Решебник Алгебра Алимов Ш.А. 11 класс гдз
Задание не найдено
Глава 1. Действительные числа
§ 1. Целые и рациональные числа
1
2
3
4
5
§ 2. Действительные числа
6
7
8
9
10
11
12
§ 3. Бесконечно убывающая геометрическая прогрессия
13
14
15
16
17
18
19
20
21
22
23
24
25
26
§ 4. Арифметический корень натуральной степени
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
§ 5. Степень с рациональным и действительным показателями
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
Упражнения к главе I
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
Глава II. Степенная функции
Степенная функции
§ 6. Степенная функция, её свойства и график
119
120
121
122
123
124
125
126
127
128
129
130
§ 7. Взаимно обратные функции
131
132
133
134
135
136
137
§ 8. Равносильные уравнения и неравенства
138
139
140
141
142
143
144
145
146
147
148
149
150
§ 9. Иррациональные уравнения
151
152
153
154
155
156
157
158
159
160
161
162
163
164
§ 10. Иррациональные неравенства
165
166
167
168
169
170
171
172
173
174
Упражнения к главе II
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
Глава III. Показательная функция
Показательная функция
§11. Показательная функция, её свойства и график
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
§ 12. Показательные уравнения
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
§ 13. Показательные неравенства
228
229
230
231
232
233
234
235
236
237
238
239
§ 14. Системы показательных уравнений и неравенств
240
241
242
243
244
245
Упражнения к главе III
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
Глава IV. Логарифмическая функция
§ 15. Логарифмы
Логарифмы
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
§ 16. Свойства логарифмов
290
291
292
293
294
295
296
297
298
299
300
§ 17. Десятичные и натуральные логарифмы
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
§ 18. Логарифмическая функция, её свойства и график
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
§ 19. Логарифмические уравнения
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
§ 20. Логарифмические неравенства
Логарифмические неравенства
354
355
356
357
358
359
360
361
362
363
364
365
366
367
Упражнения к главе IV
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
Глава V . Тригонометрические формулы
§ 21. Радианная мера угла
407
408
409
410
411
412
413
414
415
§ 22. Поворот точки вокруг начала координат
416
417
418
419
420
421
422
423
424
425
426
427
428
§ 23. Определение синуса, косинуса и тангенса угла
429
430
431
432
433
434
435
436
437
438
439
440
441
§ 24. Знаки синуса, косинуса и тангенса
Знаки синуса, косинуса и тангенса
442
443
444
445
446
447
448
449
450
451
452
453
454
455
§ 25. Зависимость между синусом, косинусом и тангенсом одного и того же угла
456
457
458
459
460
461
462
463
464
§ 26. Тригонометрические тождества
465
466
467
468
469
470
471
472
473
474
§ 27. Синус, косинус и тангенс углов α и -α
475
476
477
478
479
480
§ 28. Формулы сложения
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
§ 29. Синус, косинус и тангенс двойного угла
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
§ 30. Синус, косинус и тангенс половинного угла
Синус, косинус и тангенс половинного угла
513
514
515
516
517
518
519
520
521
522
523
§ 31. Формулы приведения
524
525
526
527
528
529
530
531
532
533
534
535
536
§ 32. Сумма и разность синусов. Сумма и разность косинусов
537
538
539
540
541
542
543
544
545
Упражнения к главе V
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
Глава VI. Тригонометрические уравнения
§ 33. Уравнение cos х = а
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
§ 34. Уравнение sin х = а
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
§ 35. Уравнение tg х = а
Уравнение tg х = а
607
608
609
610
611
612
613
614
615
616
617
618
619
§ 36. Решение тригонометрических уравнений
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
§ 37. Примеры решения простейших тригонометрических неравенств
648
649
650
651
652
653
654
Упражнения к главе VI
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
Глава VII. Тригонометрические функции
Тригонометрические функции
§ 38. Область определения и множество значений тригонометрических функций
691
692
693
694
695
696
697
698
699
§ 39. Чётность, нечётность, периодичность тригонометрических функций
700
701
702
703
704
705
706
707
§ 40. Свойства функции у = cos x и её график
708
709
710
711
712
713
714
715
716
717
718
719
§ 41. Свойства функции у = sin x и её график
720
721
722
723
724
725
726
727
728
729
730
731
732
§ 42. Свойства функции у = tg x и её график
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
§ 43. Обратные тригонометрические функции
750
751
752
753
754
755
756
757
Упражнения к главе VII
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
Тригонометрия Мордкович Тульчинская ГДЗ – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Тригонометрия Мордкович Тульчинская ГДЗ
18 Тригонометрические уравнения — Глава 3 . Тригонометрические уравнения А .Г . Мордковичи 2009 — Алгебра, 10 класс . А .Г . Мордокович, О .Л . Денищева, Т .А . Мишустина 2001-2009 Мордкович А . Г ., Денищева Л . О ., Корешкова Т . А ., Мишустина Т . Н ., Тульчинская Е . Е . .
Тригонометрические уравнения А .Г . Мордковичи 2009 — Алгебра, 10 класс . А .Г . Мордокович, О .Л . Денищева, Т .А . Мишустина 2001-2009 Мордкович А . Г ., Денищева Л . О ., Корешкова Т . А ., Мишустина Т . Н ., Тульчинская Е . Е . .
Если сомневаетесь, стоит ли школьникам пользоваться ГДЗ по алгебре 10–11 класс Мордкович , то подумайте – многим ли в жизни пригодились школьные знания по основам матанализа, комбинаторики или тригонометрии? Только тем, кто поступил в профильные ВУЗы и нашел . .
ГДЗ : готовые ответы по алгебре Учебник, Задачник за 10‐11 класс, решебник Мордкович, Базовый уровень ФГОС, часть 1, 2 онлайн решения на Данное пособие содержит шесть разделов, особое внимание в которых уделено производной и тригонометрическим функциям .
Вот, наконец, вышел совершенно новый решебник Мордковича Семенова по алгебре и начала математического анализа 10 и 11 класса . Данный сборник включает в себя очень подробный ответ на практически все задания курса учебника .
2000-2005 г Мордкович А . Г ., Тульчинская Е . Е . Мордкович А . Г ., Семенов П . В . Алгебра и начала математического анализа . 10-11 класс .
Г ., Тульчинская Е . Е . Мордкович А . Г ., Семенов П . В . Алгебра и начала математического анализа . 10-11 класс .
ГДЗ и решебник к задчнику по алгебре за 10-11 класс Мордкович , Александрова, Мишустина, Тульчинская — ответы к учебнику онлайн . Что делать если не понимаешь предмет, а двойку так не хочется получать? Просто списать решение из ГДЗ?
Тут отличные гдз по алгебре задачник для 10‐11 класса, Мордкович А .Г . от Путина . Очень удобный интерфейс с решениями . Издательство: Мнемозина . Перед вами вторая часть задачника гдз по алгебре 10-11 класс Мордковича .
«ГДЗ по алгебре 10-11 класс Мордкович » содержит готовые ответы из одноименного сборника задач с подробным пояснением хода решений . На его страницах содержатся задания шестидесяти параграфов по основным разделам и темам старшей школы
Бесплатное решение номеров из задачника по алгебре за 10 и 11 класс Мордковича ко второй части . Решебник без ошибок! §7 . Тригонометрические функции числового аргумента
Готовое Домашнее Задание (ГДЗ ) по Алгебре и началам анализа . Контрольные работы 10-11 класс А .Г . Мордкович , Е .Е . Тульчинская — Ваша домашняя работа на 5+ . А .Г . Мордкович , Е .Е . Тульчинская — Издание «Мнемозина», 2000-2005
Контрольные работы 10-11 класс А .Г . Мордкович , Е .Е . Тульчинская — Ваша домашняя работа на 5+ . А .Г . Мордкович , Е .Е . Тульчинская — Издание «Мнемозина», 2000-2005
§7 . Тригонометрические функции числового аргумента . Решебник по алгебре за 10-11 класс Мордковича включает тригонометрические, степенные и логарифмические функции, а также затрагивает интегралы, статистику, комбинаторику, с которыми невозможно разобраться без . .
Большой ужас у школьников вызывает тема «Тригонометрические уравнения» и все что с ними связано . Ведь основная навленность решебника к учебнику «Алгебра . Часть 2 . Задачник 10-11 класс» Мордкович идет на закрепление тематического материала, а не на списывание .
§22 . Преобразование сумм тригонометрических функций в произведения . Решения упражнений и примеров из учебника собраны в ГДЗ или решебнике по алгебре 11 класса Мордкович с объяснением .
Решебник (ГДЗ ) Алгебра 10, 11 класс А .Г . Мордкович , Е .Е . Тульчинская (2003 год) Контрольные работы . Авторы: А .Г . Мордкович , Е .Е . Тульчинская . Год: 2003 | .
Авторы: А .Г . Мордкович , Е .Е . Тульчинская . Год: 2003 | .
Видеоуроки, тесты и тренажёры по предмету Алгебра за 10 класс по учебнику Мордкович А .Г . ГЛАВА 3 . тригонометрические уравнения . ГЛАВА 4 . Преобразование тригонометрических выражений .
18 Тригонометрические уравнения — Глава 3 . Тригонометрические уравнения А .Г . Мордковичи 2009 — Алгебра, 10 класс . А .Г . Мордокович, О .Л . Денищева, Т .А . Мишустина 2001-2009 Мордкович А . Г ., Денищева Л . О ., Корешкова Т . А ., Мишустина Т . Н ., Тульчинская Е . Е . .
Если сомневаетесь, стоит ли школьникам пользоваться ГДЗ по алгебре 10–11 класс Мордкович , то подумайте – многим ли в жизни пригодились школьные знания по основам матанализа, комбинаторики или тригонометрии? Только тем, кто поступил в профильные ВУЗы и нашел . .
ГДЗ : готовые ответы по алгебре Учебник, Задачник за 10‐11 класс, решебник Мордкович, Базовый уровень ФГОС, часть 1, 2 онлайн решения на Данное пособие содержит шесть разделов, особое внимание в которых уделено производной и тригонометрическим функциям .
Вот, наконец, вышел совершенно новый решебник Мордковича Семенова по алгебре и начала математического анализа 10 и 11 класса . Данный сборник включает в себя очень подробный ответ на практически все задания курса учебника .
2000-2005 г Мордкович А . Г ., Тульчинская Е . Е . Мордкович А . Г ., Семенов П . В . Алгебра и начала математического анализа . 10-11 класс .
ГДЗ и решебник к задчнику по алгебре за 10-11 класс Мордкович , Александрова, Мишустина, Тульчинская — ответы к учебнику онлайн . Что делать если не понимаешь предмет, а двойку так не хочется получать? Просто списать решение из ГДЗ?
Тут отличные гдз по алгебре задачник для 10‐11 класса, Мордкович А .Г . от Путина . Очень удобный интерфейс с решениями . Издательство: Мнемозина . Перед вами вторая часть задачника гдз по алгебре 10-11 класс Мордковича .
«ГДЗ по алгебре 10-11 класс Мордкович » содержит готовые ответы из одноименного сборника задач с подробным пояснением хода решений . На его страницах содержатся задания шестидесяти параграфов по основным разделам и темам старшей школы
Бесплатное решение номеров из задачника по алгебре за 10 и 11 класс Мордковича ко второй части . Решебник без ошибок! §7 . Тригонометрические функции числового аргумента
Решебник без ошибок! §7 . Тригонометрические функции числового аргумента
Готовое Домашнее Задание (ГДЗ ) по Алгебре и началам анализа . Контрольные работы 10-11 класс А .Г . Мордкович , Е .Е . Тульчинская — Ваша домашняя работа на 5+ . А .Г . Мордкович , Е .Е . Тульчинская — Издание «Мнемозина», 2000-2005
§7 . Тригонометрические функции числового аргумента . Решебник по алгебре за 10-11 класс Мордковича включает тригонометрические, степенные и логарифмические функции, а также затрагивает интегралы, статистику, комбинаторику, с которыми невозможно разобраться без . .
Большой ужас у школьников вызывает тема «Тригонометрические уравнения» и все что с ними связано . Ведь основная навленность решебника к учебнику «Алгебра . Часть 2 . Задачник 10-11 класс» Мордкович идет на закрепление тематического материала, а не на списывание .
§22 . Преобразование сумм тригонометрических функций в произведения . Решения упражнений и примеров из учебника собраны в ГДЗ или решебнике по алгебре 11 класса Мордкович с объяснением .
Решебник (ГДЗ ) Алгебра 10, 11 класс А .Г . Мордкович , Е .Е . Тульчинская (2003 год) Контрольные работы . Авторы: А .Г . Мордкович , Е .Е . Тульчинская . Год: 2003 | .
Видеоуроки, тесты и тренажёры по предмету Алгебра за 10 класс по учебнику Мордкович А .Г . ГЛАВА 3 . тригонометрические уравнения . ГЛАВА 4 . Преобразование тригонометрических выражений .
ГДЗ 6 Класс Мерзляк Мате
ГДЗ По Английскому Языку 7 Класс Тетрадка
ГДЗ По Математике Вариант 3
Решебник Канакина 3 Класс 2
ГДЗ По Английскому Enjoy English Учебник
ГДЗ Математика Колягин Федоров 10 Класс
Решебник По Русскому 7 Класс Просвещение
ГДЗ По Алгебре Седьмого Класса Мерзляк
ГДЗ По Биологии 10 Класс Пасечник
Решебник Пасечника 5 Класс Рабочая Тетрадь
ГДЗ По Русскому 8 Класс Чешко 2009
ГДЗ По Алгебре Мордкович Звавич
ГДЗ По Русс 7 Класс Баранов
ГДЗ Англ Яз 2 Класс Рабочая Тетрадь
ГДЗ Третий Класс Математика 3 Часть
ГДЗ Алгебра Полонский 8
ГДЗ 5 Класс Учебник Гуревич
ГДЗ По Биологии 8 Класс От Путина
ГДЗ По Французскому 6 2 Часть
Фэмили Френдс 1 ГДЗ Рабочая Тетрадь
ГДЗ По Математике 3 Класс Е
ГДЗ Т А Байкова 4
ГДЗ Комарова Учебник 5
ГДЗ По Математике 4 Моро 2
ГДЗ Окружающими Тетрадь 3 Класс Плешаков
ГДЗ 2 Класс Учебник Номер 7
ГДЗ По Калининой 2
Решебник По Немецкому Языку Девятый Класс Бим
Решебник Контрольных Работ 5 Класс Никольский
Решебник По Английскому Языку Трубанева
Русский Язык Шмелева Ответы ГДЗ
ГДЗ По Математике 5 Просвещение Дорофеев
ГДЗ По Алгебре 7 Дидактические Материалы
ГДЗ По Математике Ткачева
ГДЗ По Математике 6 0
Решебник Второй Класс Канакина
ГДЗ По Литературе 4 Класс Стр 23
ГДЗ Русский Язык 3 Сильнова
ГДЗ По Математике 3 Класса Канакин
ГДЗ Английский Язык 2 Класс Минасова
ГДЗ Сборник Задач Парфентьева 10 11 Класс
Ридер 6 Класс Афанасьева Михеева ГДЗ Перевод
ГДЗ По Мат Кл
ГДЗ Русский 4 Класс Желтовская Калинина
ГДЗ Рус Яз Ладыженской
ГДЗ Гацкевич Грамматика Сборник Упражнений Книга
ГДЗ По Химии 9 Кузнецова
Решебник Мерзляк Шестой
Решебник По Математике 3 Петерсон ГДЗ
ГДЗ 5 Класс Страница 7 Упражнение 8
ГДЗ По Геометрии 8 Ершова Самостоятельные
Гдз По Окружающему Миру
ГДЗ Астрономия 11 Воронцов Вельяминов
Гдз По Русскому 9 Класс Бабайцев
ГДЗ Аргинская 2
Тригонометрия | Определение, формулы, отношения и тождества
тригонометрические функции
Просмотреть все СМИ
- Ключевые люди:
- Гиппарх Леонард Эйлер Региомонтан Абу аль-Вафах Франсуа Виет, сеньор де ла Биготьер
- Похожие темы:
- тригонометрическая таблица сферическая тригонометрия аналитическая тригонометрия сферический треугольник плоская тригонометрия
Просмотреть весь связанный контент →
тригонометрия , раздел математики, связанный с конкретными функциями углов и их применением в вычислениях.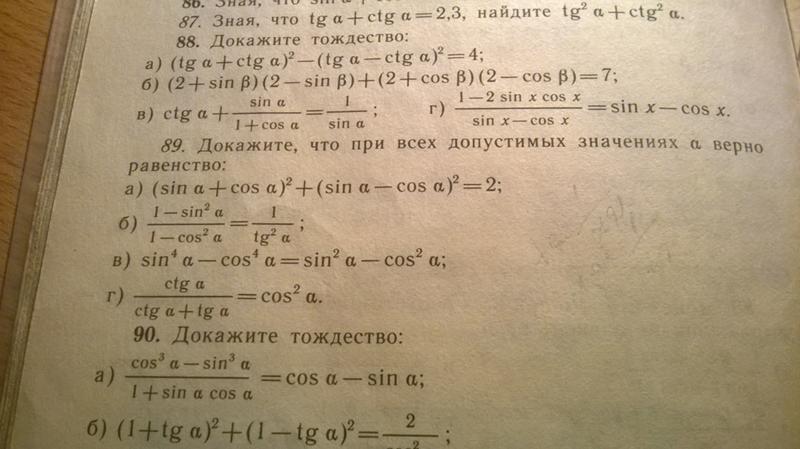 В тригонометрии обычно используются шесть функций угла. Их названия и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти шесть тригонометрических функций по отношению к прямоугольному треугольнику показаны на рисунке. Например, треугольник содержит угол
В тригонометрии обычно используются шесть функций угла. Их названия и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти шесть тригонометрических функций по отношению к прямоугольному треугольнику показаны на рисунке. Например, треугольник содержит угол
Тригонометрия возникла из-за необходимости вычислять углы и расстояния в таких областях, как астрономия, картографирование, геодезия и дальномер артиллерийских орудий. Задачи, связанные с углами и расстояниями в одной плоскости, рассматриваются в плоской тригонометрии. Приложения к подобным задачам более чем в одной плоскости трехмерного пространства рассматриваются в сферической тригонометрии.
Задачи, связанные с углами и расстояниями в одной плоскости, рассматриваются в плоской тригонометрии. Приложения к подобным задачам более чем в одной плоскости трехмерного пространства рассматриваются в сферической тригонометрии.
История тригонометрии
Классическая тригонометрия
Слово тригонометрия происходит от греческих слов тригонон («треугольник») и метрон («для измерения»). Примерно до 16 века тригонометрия в основном занималась вычислением числовых значений отсутствующих частей треугольника (или любой формы, которую можно разбить на треугольники), когда были даны значения других частей. Например, если известны длины двух сторон треугольника и величина прилежащего к нему угла, можно вычислить третью сторону и два оставшихся угла. Такие вычисления отличают тригонометрию от геометрии, которая исследует главным образом качественные отношения. Конечно, это различие не всегда абсолютно: теорема Пифагора, например, представляет собой утверждение о длинах трех сторон прямоугольного треугольника и, таким образом, носит количественный характер. Тем не менее, в своем первоначальном виде тригонометрия в целом была потомком геометрии; только в 16 веке эти две науки стали отдельными разделами математики.
Тем не менее, в своем первоначальном виде тригонометрия в целом была потомком геометрии; только в 16 веке эти две науки стали отдельными разделами математики.
Древний Египет и Средиземноморье
Несколько древних цивилизаций — в частности, египетская, вавилонская, индуистская и китайская — обладали значительными познаниями в практической геометрии, включая некоторые понятия, которые были прелюдией к тригонометрии. Папирус Райнда, египетский сборник из 84 задач по арифметике, алгебре и геометрии, датируемый примерно 1800 г. до н. э., содержит пять задач, связанных с секедом . Тщательный анализ текста и сопровождающих его рисунков показывает, что это слово означает наклон склона — важное знание для крупных строительных проектов, таких как пирамиды. Например, в задаче 56 спрашивается: «Если высота пирамиды 250 локтей, а длина стороны ее основания 360 локтей, какова ее 9 локтей?0023 секед ?» Решение дано как 51/25 ладоней на локоть, и, поскольку один локоть равен 7 ладоням, эта дробь эквивалентна чистому соотношению 18/25.
Викторина «Британника»
Числа и математика
Тригонометрия в современном понимании началась с греков. Гиппарх ( г. ок. г., 190–120 гг. до н. э.) первым составил таблицу значений тригонометрической функции. Он рассматривал каждый треугольник — плоский или сферический — как вписанный в круг, так что каждая сторона становится хордой (то есть прямой линией, соединяющей две точки на кривой или поверхности, как показано вписанным треугольником A ). B C на рисунке). Чтобы вычислить различные части треугольника, нужно найти длину каждой хорды как функцию центрального угла, который ее стягивает, или, что то же самое, длину хорды как функцию соответствующей ширины дуги.
Изучите, как Птолемей пытался использовать деференты и эпициклы для объяснения ретроградного движения
Просмотреть все видео к этой статье Щелкните здесь, чтобы просмотреть таблицу в полном размереПервой крупной древней работой по тригонометрии, дошедшей до Европы в целости и сохранности после Средневековья, был 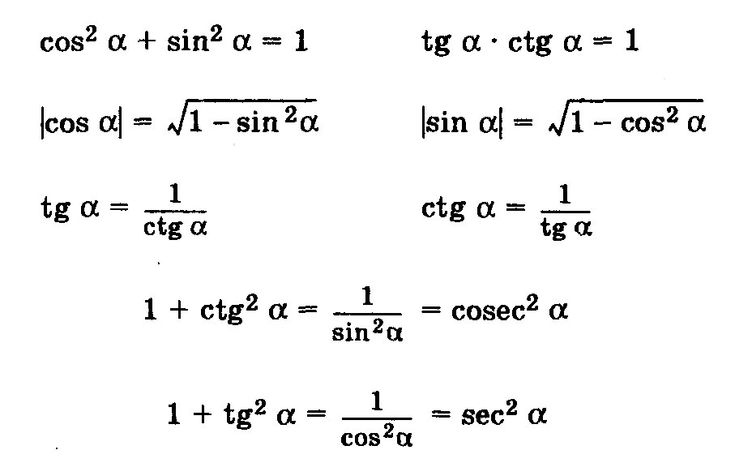 Хотя Птолемей написал работы по математике, географии и оптике, в основном он известен своими Альмагест , сборник из 13 книг по астрономии, который стал основой для картины мира человечества, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея в середине 16 века. Чтобы развить эту картину мира, сущностью которой была неподвижная Земля, вокруг которой по круговым орбитам движутся Солнце, Луна и пять известных планет, Птолемею пришлось использовать некоторую элементарную тригонометрию. Главы 10 и 11 первой книги Альмагеста касается построения таблицы хорд, в которой длина хорды в окружности дана как функция центрального угла, который ее стягивает, для углов в диапазоне от 0 ° до 180 ° с интервалами в полградуса. . По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину стягиваемой хорды c , чтобы получить c = 2 r sin A /2.
Хотя Птолемей написал работы по математике, географии и оптике, в основном он известен своими Альмагест , сборник из 13 книг по астрономии, который стал основой для картины мира человечества, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея в середине 16 века. Чтобы развить эту картину мира, сущностью которой была неподвижная Земля, вокруг которой по круговым орбитам движутся Солнце, Луна и пять известных планет, Птолемею пришлось использовать некоторую элементарную тригонометрию. Главы 10 и 11 первой книги Альмагеста касается построения таблицы хорд, в которой длина хорды в окружности дана как функция центрального угла, который ее стягивает, для углов в диапазоне от 0 ° до 180 ° с интервалами в полградуса. . По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину стягиваемой хорды c , чтобы получить c = 2 r sin A /2. Поскольку Птолемей использовал вавилонские шестидесятеричные числа и системы счисления (основание 60), он провел свои вычисления со стандартным кругом радиуса 9.0023 r = 60 единиц, так что c = 120 sin A /2. Таким образом, кроме коэффициента пропорциональности 120, это была таблица значений sin A /2 и, следовательно, (удвоением дуги) sin A . С помощью своей таблицы Птолемей усовершенствовал существующие геодезические меры мира и уточнил Гиппархову модель движения небесных тел.
Поскольку Птолемей использовал вавилонские шестидесятеричные числа и системы счисления (основание 60), он провел свои вычисления со стандартным кругом радиуса 9.0023 r = 60 единиц, так что c = 120 sin A /2. Таким образом, кроме коэффициента пропорциональности 120, это была таблица значений sin A /2 и, следовательно, (удвоением дуги) sin A . С помощью своей таблицы Птолемей усовершенствовал существующие геодезические меры мира и уточнил Гиппархову модель движения небесных тел.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подписаться
Тригонометрия | Определение, формулы, отношения и тождества
тригонометрические функции
Просмотреть все СМИ
- Ключевые люди:
- Гиппарх Леонард Эйлер Региомонтан Абу аль-Вафах Франсуа Виет, сеньор де ла Биготьер
- Похожие темы:
- тригонометрическая таблица сферическая тригонометрия аналитическая тригонометрия сферический треугольник плоская тригонометрия
Просмотреть весь связанный контент →
тригонометрия , раздел математики, связанный с конкретными функциями углов и их применением в вычислениях. В тригонометрии обычно используются шесть функций угла. Их названия и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти шесть тригонометрических функций по отношению к прямоугольному треугольнику показаны на рисунке. Например, треугольник содержит угол A , а отношение стороны, противоположной A , и стороны, противоположной прямому углу (гипотенузе), называется синусом A , или sin A ; аналогично определяются другие тригонометрические функции. Эти функции являются свойствами угла A , не зависящими от размера треугольника, и вычисленные значения были сведены в таблицы для многих углов до того, как компьютеры сделали тригонометрические таблицы устаревшими. Тригонометрические функции используются для получения неизвестных углов и расстояний от известных или измеренных углов в геометрических фигурах.
В тригонометрии обычно используются шесть функций угла. Их названия и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти шесть тригонометрических функций по отношению к прямоугольному треугольнику показаны на рисунке. Например, треугольник содержит угол A , а отношение стороны, противоположной A , и стороны, противоположной прямому углу (гипотенузе), называется синусом A , или sin A ; аналогично определяются другие тригонометрические функции. Эти функции являются свойствами угла A , не зависящими от размера треугольника, и вычисленные значения были сведены в таблицы для многих углов до того, как компьютеры сделали тригонометрические таблицы устаревшими. Тригонометрические функции используются для получения неизвестных углов и расстояний от известных или измеренных углов в геометрических фигурах.
Тригонометрия возникла из-за необходимости вычислять углы и расстояния в таких областях, как астрономия, картографирование, геодезия и дальномер артиллерийских орудий.
История тригонометрии
Классическая тригонометрия
Слово тригонометрия происходит от греческих слов тригонон («треугольник») и метрон («для измерения»). Примерно до 16 века тригонометрия в основном занималась вычислением числовых значений отсутствующих частей треугольника (или любой формы, которую можно разбить на треугольники), когда были даны значения других частей. Например, если известны длины двух сторон треугольника и величина прилежащего к нему угла, можно вычислить третью сторону и два оставшихся угла. Такие вычисления отличают тригонометрию от геометрии, которая исследует главным образом качественные отношения. Конечно, это различие не всегда абсолютно: теорема Пифагора, например, представляет собой утверждение о длинах трех сторон прямоугольного треугольника и, таким образом, носит количественный характер. Тем не менее, в своем первоначальном виде тригонометрия в целом была потомком геометрии; только в 16 веке эти две науки стали отдельными разделами математики.
Тем не менее, в своем первоначальном виде тригонометрия в целом была потомком геометрии; только в 16 веке эти две науки стали отдельными разделами математики.
Древний Египет и Средиземноморье
Несколько древних цивилизаций — в частности, египетская, вавилонская, индуистская и китайская — обладали значительными познаниями в практической геометрии, включая некоторые понятия, которые были прелюдией к тригонометрии. Папирус Райнда, египетский сборник из 84 задач по арифметике, алгебре и геометрии, датируемый примерно 1800 г. до н. э., содержит пять задач, связанных с секедом . Тщательный анализ текста и сопровождающих его рисунков показывает, что это слово означает наклон склона — важное знание для крупных строительных проектов, таких как пирамиды. Например, в задаче 56 спрашивается: «Если высота пирамиды 250 локтей, а длина стороны ее основания 360 локтей, какова ее 9 локтей?0023 секед
?» Решение дано как 51/25 ладоней на локоть, и, поскольку один локоть равен 7 ладоням, эта дробь эквивалентна чистому соотношению 18/25. На самом деле это отношение «длины к высоте» рассматриваемой пирамиды — по сути, котангенс угла между основанием и гранью. Это показывает, что египтяне хотя бы немного знали числовые отношения в треугольнике, своего рода «прототригонометрию».
На самом деле это отношение «длины к высоте» рассматриваемой пирамиды — по сути, котангенс угла между основанием и гранью. Это показывает, что египтяне хотя бы немного знали числовые отношения в треугольнике, своего рода «прототригонометрию».Викторина «Британника»
Числа и математика
Тригонометрия в современном понимании началась с греков. Гиппарх ( г. ок. г., 190–120 гг. до н. э.) первым составил таблицу значений тригонометрической функции. Он рассматривал каждый треугольник — плоский или сферический — как вписанный в круг, так что каждая сторона становится хордой (то есть прямой линией, соединяющей две точки на кривой или поверхности, как показано вписанным треугольником  Это стало главной задачей тригонометрии на следующие несколько столетий. Как астронома Гиппарха в основном интересовали сферические треугольники, такие как воображаемый треугольник, образованный тремя звездами на небесной сфере, но он также был знаком с основными формулами плоской тригонометрии. Во времена Гиппарха эти формулы выражались в чисто геометрических терминах как отношения между различными хордами и углами (или дугами), которые их стягивают; современные символы для тригонометрических функций не вводились до 17 века.
Это стало главной задачей тригонометрии на следующие несколько столетий. Как астронома Гиппарха в основном интересовали сферические треугольники, такие как воображаемый треугольник, образованный тремя звездами на небесной сфере, но он также был знаком с основными формулами плоской тригонометрии. Во времена Гиппарха эти формулы выражались в чисто геометрических терминах как отношения между различными хордами и углами (или дугами), которые их стягивают; современные символы для тригонометрических функций не вводились до 17 века.
Изучите, как Птолемей пытался использовать деференты и эпициклы для объяснения ретроградного движения
Просмотреть все видео к этой статье Щелкните здесь, чтобы просмотреть таблицу в полном размереПервой крупной древней работой по тригонометрии, дошедшей до Европы в целости и сохранности после Средневековья, был Альмагест Птолемея ( ок. 100–170 н.э.). Он жил в Александрии, интеллектуальном центре эллинистического мира, но больше о нем мало что известно. Хотя Птолемей написал работы по математике, географии и оптике, в основном он известен своими Альмагест , сборник из 13 книг по астрономии, который стал основой для картины мира человечества, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея в середине 16 века. Чтобы развить эту картину мира, сущностью которой была неподвижная Земля, вокруг которой по круговым орбитам движутся Солнце, Луна и пять известных планет, Птолемею пришлось использовать некоторую элементарную тригонометрию. Главы 10 и 11 первой книги Альмагеста касается построения таблицы хорд, в которой длина хорды в окружности дана как функция центрального угла, который ее стягивает, для углов в диапазоне от 0 ° до 180 ° с интервалами в полградуса. . По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину стягиваемой хорды c , чтобы получить c = 2 r sin A /2.
Хотя Птолемей написал работы по математике, географии и оптике, в основном он известен своими Альмагест , сборник из 13 книг по астрономии, который стал основой для картины мира человечества, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея в середине 16 века. Чтобы развить эту картину мира, сущностью которой была неподвижная Земля, вокруг которой по круговым орбитам движутся Солнце, Луна и пять известных планет, Птолемею пришлось использовать некоторую элементарную тригонометрию. Главы 10 и 11 первой книги Альмагеста касается построения таблицы хорд, в которой длина хорды в окружности дана как функция центрального угла, который ее стягивает, для углов в диапазоне от 0 ° до 180 ° с интервалами в полградуса. . По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину стягиваемой хорды c , чтобы получить c = 2 r sin A /2.
