Онлайн калькулятор дробей с запятыми: Онлайн сервис для вычислений обыкновенной и десятичной дробями, сложение, вычитание, умножение и деление десятичной и обыкновенной дробей.

alexxlab / / Разное

Содержание

Название чисел | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

В названиях арабских чисел каждая цифра принадлежит своему разряду, а каждые три цифры образуют класс. Таким образом, последняя цифра в числе обозначает количество единиц в нем и называется, соответственно, разрядом единиц. Следующая, вторая с конца, цифра обозначает десятки (разряд десятков), и третья с конца цифра указывает на количество сотен в числе – разряд сотен. Дальше разряды точно также по очереди повторяются в каждом классе, обозначая уже единицы, десятки и сотни в классах тысяч, миллионов и так далее. Если число небольшое и в нем нет цифры десятков или сотен, принято принимать их за ноль. Классы группируют цифры в числах по три, нередко в вычислительных приборах или записях между классами ставится точка или пробел, чтобы визуально разделить их. Это сделано для упрощения чтения больших чисел. Каждый класс имеет свое название: первые три цифры – это класс единиц, далее идет класс тысяч, затем миллионов, миллиардов (или биллионов) и так далее.

Поскольку мы пользуемся десятичной системой исчисления, то основная единица измерения количества – это десяток, или 101. Соответственно с увеличением количества цифр в числе, увеличивается и количество десятков 102,103,104 и т.д. Зная количество десятков можно легко определить класс и разряд числа, например, 1016 – это десятки квадриллионов, а 3×1016 – это три десятка квадриллионов. Разложение чисел на десятичные компоненты происходит следующий образом – каждая цифра выводится в отдельное слагаемое, умножаясь на требуемый коэффициент 10n, где n – положение цифры по счет слева направо.
Например: 253 981=2×106+5×105+3×104+9×103+8×102+1×101

Также степень числа 10 используется и в написании десятичных дробей: 10(-1) – это 0,1 или одна десятая. Аналогичным образом с предыдущим пунктом, можно разложить и десятичное число, n в таком случае будет обозначать положение цифры от запятой справа налево, например: 0,347629= 3×10

(-1)+4×10(-2)+7×10(-3)+6×10(-4)+2×10(-5)+9×10(-6)

Названия десятичных чисел. Десятичные числа читаются по последнему разряду цифр после запятой, например 0,325 – триста двадцать пять тысячных, где тысячные – это разряд последней цифры 5.

Таблица названий больших чисел, разрядов и классов

1-й класс единицы 1-й разряд единицы
2-й разряд десятки
3-й разряд сотни		 1 = 100
10 = 101
100 = 102
2-й класс тысячи 1-й разряд единицы тысяч
2-й разряд десятки тысяч
3-й разряд сотни тысяч		 1 000 = 103

10 000 = 104
100 000 = 105
3-й класс миллионы 1-й разряд единицы миллионов
2-й разряд десятки миллионов
3-й разряд сотни миллионов		 1 000 000 = 106
10 000 000 = 107
100 000 000 = 108
4-й класс миллиарды 1-й разряд единицы миллиардов
2-й разряд десятки миллиардов
3-й разряд сотни миллиардов		 1 000 000 000 = 109
10 000 000 000 = 1010
100 000 000 000 = 1011
5-й класс триллионы 1-й разряд единицы триллионов
2-й разряд десятки триллионов
3-й разряд сотни триллионов		 1 000 000 000 000 = 1012
10 000 000 000 000 = 1013
100 000 000 000 000 = 1014
6-й класс квадриллионы   1-й разряд единицы квадриллионов  
2-й разряд десятки  квадриллионов
3-й разряд десятки  квадриллионов		 1 000 000 000 000 000 = 1015
10 000 000 000 000 000 = 1016
100 000 000 000 000 000 = 1017
7-й класс квинтиллионы 1-й разряд единицы квинтиллионов
2-й разряд десятки квинтиллионов
3-й разряд сотни квинтиллионов		 1 000 000 000 000 000 000 = 1018
10 000 000 000 000 000 000 = 1019
100 000 000 000 000 000 000 = 1020
8-й класс секстиллионы 1-й разряд единицы секстиллионов
2-й разряд десятки секстиллионов
3-й разряд сотни секстиллионов		 1 000 000 000 000 000 000 000 = 1021
10 000 000 000 000 000 000 000 = 10
22
1 00 000 000 000 000 000 000 000 = 1023
9-й класс септиллионы 1-й разряд единицы септиллионов
2-й разряд десятки септиллионов
3-й разряд сотни септиллионов		 1 000 000 000 000 000 000 000 000 = 1024
10 000 000 000 000 000 000 000 000 = 1025
100 000 000 000 000 000 000 000 000 = 1026
10-й класс октиллион 1-й разряд единицы октиллионов
2-й разряд десятки октиллионов
3-й разряд сотни октиллионов		 1 000 000 000 000 000 000 000 000 000 = 1027
10 000 000 000 000 000 000 000 000 000 = 1028
100 000 000 000 000 000 000 000 000 000 = 1029

Таблица названий десятичных чисел

0,1 10-1 1/10 Десятые
0,01 10-2 1/100 Сотые
0,001 10-3 1/1000 Тысячные
0,0001 10-4 1/10000 Десятитысячные
0,00001 10-5 1/100000 Стотысячные
0,000001 10-6 1/1000000 Миллионные
0,0000001 10-7 1/10000000 Десятимиллионные
0,00000001   10-8   1/100000000   Стомилионные

Название чисел, классов, разрядов, перевод цифр в текст

Как из десятичного числа сделать дробь.

Как переводятся обыкновенные дроби в десятичные? Виды дробей

Материалов по дробям и изучать последовательно. Ниже для вас подробная информация с примерами и пояснениями.

1. Смешанное число в обыкновенную дробь. Запишем в общем виде число:

Запоминаем простое правило – целую часть умножаем на знаменатель и прибавляем числитель, то есть:

Примеры:


2. Наоборот, обыкновенную дробь в смешанное число. *Конечно, это возможно сделать только с неправильной дробью (когда числитель больше знаменателя).

При «небольших» числах никаких действий, в общем, и не нужно делать, результат «видно» сразу, например, дроби:

*Подробнее:

15:13 = 1 остаток 2

4:3 = 1 остаток 1

9:5 = 1 остаток 4

А вот если числа будут более, то без вычислений не обойтись. Здесь всё просто – делим уголком числитель на знаменатель до тех пор пока остаток не получится менее делителя. Схема деления:


Например:

*Числитель у нас – это делимое, знаменатель – это делитель.


Получаем целую часть (неполное частное) и остаток. Записываем – целое, затем дробь (в числителе остаток, а знаменатель оставляем тот же):

3. Десятичную переводим в обыкновенную.

Частично в первом пункте, где рассказывали про десятичные дроби мы уже коснулись этого. Как слышим так и записываем. Например — 0,3; 0,45; 0,008; 4,38; 10,00015

Первые три дроби у нас без целой части. А четвёртая и пятая её имеют, переведём их в обыкновенные, это делать уже умеем:

*Мы видим, что дроби можно ещё и сократить, например 45/100 =9/20, 38/100=19/50 и другие, но мы здесь делать этого не будем. По сокращению вас ожидает отдельный пункт ниже, где подробно всё разберём.

4. Обыкновенную переводим в десятичную.

Тут не всё так просто. По каким-то дробям сразу видно и ясно, что с ней сделать, чтобы она стала десятичной, например:

Используем наше замечательное основное свойство дроби – умножаем числитель и знаменатель соответственно на 5, 25, 2, 5, 4, 2, получим:


Если имеется целая часть, то тоже ничего сложного:

Умножаем дробную часть соответственно на 2, 25, 2 и 5, получим:

А есть такие, по которым без опыта и не определить, что их можно перевести в десятичные, например:

На какие числа умножать числитель и знаменатель?

Тут опять на помощь приходит проверенный способ – деление уголком, способ универсальный, им для перевода обыкновенной дроби в десятичную можно пользоваться всегда:


Так вы сможете всегда определить переводится ли дробь в десятичную. Дело в том, что не каждую обыкновенную дробь можно перевести в десятичную, например такие как 1/9, 3/7, 7/26 не переводятся. А что же тогда получается за дробь при делении 1 на 9, 3 на 7, 5 на 11? Отвечаю – бесконечная десятичная (говорили о них в пункте 1). Разделим:


На этом всё! Успеха вам!

С уважением, Александр Крутицких.

Зачастую дети, которые учатся в школе, интересуются, для чего в им в реальной жизни может понадобится математика, в особенности те разделы, которые уже заходят намного дальше, чем простой счет, умножение, деление, суммирование и отнимание. Многие взрослые также задаются данным вопросом, если их профессиональная деятельность очень далека от математики и разнообразных вычислений. Однако стоит понимать, что ситуации бывают всякие, и порой никак не обойтись без той самой, пресловутой школьной программы, от которой мы так пренебрежительно отказывались в детстве. К примеру, вовсе не все знают, как перевести дробь в десятичную дробь, а такие знания могут чрезвычайно пригодится, для удобства счета.

Для начала, нужно полностью убедиться, что нужная вам дробь может быть преобразована в конечную десятичную. То же самое касается и процентов, которые также можно легко перевести в десятичные дроби.

Проверка обычной дроби на возможность перевода ее в десятичную

Прежде, чем что-либо считать, необходимо убедиться, что полученная в итоге десятичная дробь будет конечной, иначе она окажется бесконечной и высчитать окончательный вариант будет попросту невозможно. Причем бесконечные дроби также могут быть периодическими и простыми, но это уже тема для отдельного раздела.

Перевести обыкновенную дробь в ее конечный, десятичный вариант можно только в том случае, если ее уникальный знаменатель способен раскладываться только на множители 5 и 2 (простые множители). Причем даже в том случае, если они повторяются произвольное количество раз.

Уточним, что оба эти числа являются простыми, так в итоге разделить без остатка их можно только на самих себя, или же, на единицу. Таблицу простых чисел можно отыскать без проблем в сети интернет, это вовсе не сложно, хотя непосредственного отношения к нашему счету она и не имеет.

Рассмотрим примеры:

Дробь 7/40 поддается преобразованию из обычной дроби в ее десятичный эквивалент, потому что ее знаменатель можно без труда разложить на множители 2 и 5.

Однако, если первый вариант даст в результате конечную десятичную дробь, то, к примеру, 7/60 уже никак не даст подобного результата, так как ее знаменатель не будет уже раскладываться на искомые нами числа, а будет иметь в числе множителей знаменателя тройку.

Перевести обычную дробь в десятичную возможно несколькими способами

После того, как стало понятно, какие дроби можно переводить из обычных в десятичные, можно приступить, собственно, к самому преобразованию. На самом деле, нет ничего сверхсложного, даже для того, у кого школьная программа окончательно «выветрилась» из памяти.

Как переводить дроби в десятичные: наиболее простой метод

Этот способ перевода обычной дроби в десятичную, действительно, является наиболее простым, однако многие люди даже не догадываются о его бренном существовании, так как в школе все эти «прописные истины» кажутся ненужными и не очень-то важными. Между тем, разобраться сможет не только взрослый, но легко воспримет подобную информацию и ребенок.

Итак, чтобы преобразовать дробь в десятичную, нужно умножить числитель, равно как и знаменатель, на одно число. Однако все не так просто, так в результате, именно в знаменателе должно получиться 10, 100, 1000, 10 000, 100 000 и так далее, до бесконечности. Не стоит забывать предварительно проверить, точно ли можно данную дробь превратить в десятичную.

Рассмотрим примеры:

Допустим, нам нужно провести преобразование дроби 6/20 в десятичную. Производим проверку:

После того, как мы убедились, что перевести дробь в десятичную дробь, да еще и конечную, все же, возможно, так как ее знаменатель легко раскладывается на двоечки и пятерки, следует приступить к самому переводу. Самым лучшим вариантом, по логике вещей, чтобы умножить знаменатель и получить результат 100, является 5, так как 20х5=100.

Можно рассмотреть дополнительный пример, для наглядности:

Второй и боле популярный способ

переводить дроби в десятичные

Второй вариант несколько сложнее, однако он пользуется большей популярностью, ввиду того, что он гораздо проще для понимания. Тут все прозрачно и ясно, потому давайте сразу же перейдем к вычислениям.

Стоит запомнить

Для того, что правильно преобразовать простую, то есть обычную дробь в ее десятичный эквивалент, нужно числитель разделить на знаменатель. По сути, дробь – это и есть деление, с этим не поспоришь.

Рассмотрим действие на примере:

Итак, первым делом, чтобы перевести дробь 78/200 в десятичную, нужно ее числитель, то есть число 78, разделить на знаменатель 200. Но первым делом, что должно войти в привычку, нужно произвести проверку, о которой уже говорилось выше.

После произведения проверки, нужно вспомнить школу и делить числитель на знаменатель «уголком» или «столбиком».

Как видите, все предельно просто, и семи пядей во лбу, чтобы легко решать подобные задачки вовсе быть не требуется. Для простоты и удобства приведем также и таблицу самых популярных дробей, которые просто запомнить, и даже не прилагать усилий, чтобы их переводить.

Как перевести проценты в десятичную дробь : нет ничего проще

Вот наконец дошел ход и до процентов, которые, оказывается, как гласит все та же, школьная программа, можно перевести в десятичную дробь. Причем тут все будет еще гораздо проще, и пугаться не стоит. Справятся с задачей даже те, кто не заканчивал университеты, а пятый класс школы вовсе прогулял и ничего не смыслит в математике.

Начать, пожалуй, нужно с определения, то есть разобраться, что такое, собственно, проценты. Процент – это одна сотая часть от какого-либо числа, то есть, абсолютно произвольно. От сотни, к примеру, это будет единица и так далее.

Таким образом, чтобы перевести проценты в десятичную дробь, нужно попросту убрать значок %, а потом разделить само число на сотню.

Рассмотрим примеры:

Причем, чтобы произвести обратную «конвертацию», нужно попросту сделать все наоборот, то есть, число нужно умножить на сотню и приписать к нему значок процента. Точно таким же образом, посредством применения полученных знаний, можно также и обычную дробь перевести в проценты. Для этого достаточно будет просто сперва преобразовать обычную дробь в десятичную, а потому уже ее перевести в проценты, а также легко можно произвести и обратное действие. Как видите, ничего сверхсложного нет, все это элементарные знания, которые просто необходимо держать в уме, в особенности, если имеете дело с цифрами.

Путь наименьшего сопротивления: удобные онлайн сервисы

Бывает и так, что считать совершенно не хочется, да и попросту нет времени. Именно для таких случаев, или же, особо ленивых пользователей, в сети интернет есть множество удобных и простых в применении сервисов, которые позволят перевести обычные дроби, а также проценты, в десятичные дроби. Это действительно дорога наименьшего сопротивления, потому пользоваться подобными ресурсами – одно удовольствие.

Полезный справочный портал «Калькулятор»

Для того, чтобы воспользоваться сервисом «Калькулятора», достаточно просто перейти по ссылке http://www.calc.ru/desyatichnyye-drobi.html , и ввести необходимые числа в нужные поля. Причем ресурс позволяет переводить в десятичные, как обычные, так и смешанные дроби.

После краткосрочного ожидания, приблизительно секунды в три, сервис выдаст конечный результат.

Точно таким же образом можно перевести в обычную дробь десятичную.

Онлайн-калькулятор на «Математическом ресурсе» Calcs.su

Еще одним, очень полезным сервисом можно назвать калькулятор дробей на «Математическом ресурсе. Тут также не придется ничего считать самостоятельно, просто выберите из предложенного списка то, что вам нужно и вперед, за орденами.

Далее, в отведенное специально для этого поле, нужно ввести искомое число процентов, которые и нужно преобразовать в обычную дробь. Причем если вам нужны десятичные дроби, то вы легко можете уже сами справиться с задачей перевода или же воспользоваться тем калькулятором, который для этого и предназначен.

В конечном итоге, стоит обязательно добавить, что сколько бы новомодных сервисов не было бы придумано, сколько ресурсов не предлагали бы вам свои услуги, но и голову тренировать периодически не помешает. Потому стоит обязательно применять полученные знания, тем более, что вы потом с гордостью сможете помогать делать уроки собственным детям, а затем и внукам.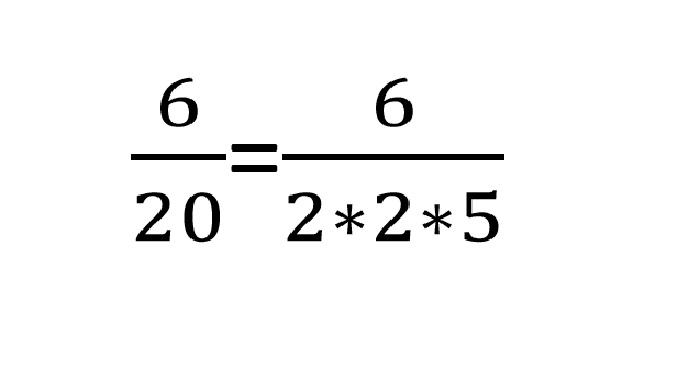 Для того же, кто страдает от вечной нехватки времени, подобные онлайн-калькуляторы на математических порталах окажутся как раз кстати и даже помогут понять, как перевести обычную дробь в десятичную.

Очень часто в школьной программе математики дети сталкиваются с проблемой, как перевести обычную дробь в десятичную. Для того чтобы перевести обычную дробь в десятичную, вспомним для начала, что такое обычная дробь и десятичная дробь. Обычная дробь – это дробь вида m/n , где m – числитель, а n – знаменатель. Пример: 8/13; 6/7 и т.д. Дроби делятся на правильные, неправильные и смешанные числа. Правильная дробь – это когда числитель меньше знаменателя: m/n, где m 3. Неправильную дробь всегда можно представить в виде смешанного числа, а именно: 4/3 = 1 и 1/3;

Перевод обычной дроби в десятичную

Теперь рассмотрим, как перевести смешанную дробь в десятичную. Любую обыкновенную дробь, будь она правильной или не правильной, можно перевести в десятичную. Для этого нужно числитель разделить на знаменатель. Пример: простая дробь (правильная) 1/2. Делим числитель 1 на знаменатель 2, получаем 0,5. Возьмем пример 45/12, сразу видно, что это дробь неправильная. Здесь знаменатель меньше числителя. Превращаем неправильную дробь в десятичную: 45: 12 = 3,75.

Перевод смешанных чисел в десятичную дробь

Пример: 25/8. Сначала мы превращаем смешанное число в неправильную дробь: 25/8 = 3х8+1/8 =3 и 1/8; затем делим числитель равный 1 на знаменатель равный 8, столбиком или на калькуляторе и получим десятичную дробь равную 0,125. В статье приведены самые легкие примеры перевода в десятичные дроби. Поняв методику перевода на простых примерах, вы легко сможете решать самые сложные из них.

То нажмите на кнопки, и задача выполнена. В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после . В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону).

Если калькулятора под рукой не , но придется . Напишите числитель дроби со знаменателем, между ними уголочек, означающий . К примеру, переведите в число дробь 10/6. Для начала 10 разделите на 6. Получится 1. Запишите результат по уголком. Перемножьте 1 на 6, получится 6. Вычтите 6 из 10. Получится остаток 4. Остаток нужно снова разделить на 6. Допишите к 4 цифру 0, и разделите 40 на 6. Получится 6. Запишите 6 в результат, после запятой. Перемножьте 6 на 6. Получится 36. Вычтите 36 из 40. Получится вновь остаток 4. Далее можно не продолжать, поскольку становится очевидным, что результатом будет число 1,66(6). Округлите данную дробь до того разряда, который вам необходим. Например, 1,67. Это и есть окончательный результат.

Связанная статья

Источники:

  • перевод дробей с целым числом

Дроби нужны для обозначения чисел, которые состоят из одной или нескольких частей единицы. Термин «дробь» произошел от латинского fractura, которое имеет значение «дробить, ломать». Различаются обыкновенные и десятичные дроби. При этом в обыкновенных дробях единицу можно разделить на любое количество частей, а в десятичной — это количество должно быть кратно 10. Любая дробь может иметь быть как обычной, так и десятичной.

Вам понадобится

  • Для подсчета результата вам понадобится калькулятор или листок и ручка.

Инструкция

Итак, для начала возьмите обыкновенную дробь и разделите ее на части. Например, 2 1\8, в которой 2 — это целая часть, а 1\8 дробь. Из нее можно увидеть, что число разделили на 8 , но взяли лишь одну. Часть, которую взяли, числитель, а количество частей, на которое делят, — знаменатель.

Обратите внимание

Зачастую встречаются дроби, которые нельзя полностью перевести в десятичные. В этом случае на помощь приходит округление. Если вы хотите округлить до тысячных, то посмотрите на четвертое число после запятой. Если оно меньше 5, то запишите в ответ, первые три цифры после запятой без изменения, в противном случае к последней цифре из трех необходимо прибавить единицу. Например, 0, 89643123 можно записать как 0,896, а вот 0, 89663123 — 0,897.

Полезный совет

Если вы подсчитываете результат вручную, то перед делением дробь лучше максимально сократить, а также выделить из нее целые части.

Источники:

  • как перевести дроби

Дробь является одним из элементов формул, для ввода которых в текстовом процессоре Word существует инструмент Microsoft Equation. С помощью него можно вводить любые сложные математические или физические формулы, уравнения и другие элементы, включающие в себя специальные символы.

Инструкция

Чтобы запустить инструмент Microsoft Equation необходимо пройти по адресу: «Вставка» -> «Объект», в открывшемся диалоговом окне, на первой вкладке из списка нужно выбрать Microsoft Equation и нажать «Ок» или два раза кликнуть на выбранном пункте. После запуска редактора , перед вами откроется панель инструментов и в отобразится поле для ввода : прямоугольник в пунктирной . Панель инструментов разделена на секции, в каждой из них находится набор знаков действий или выражений.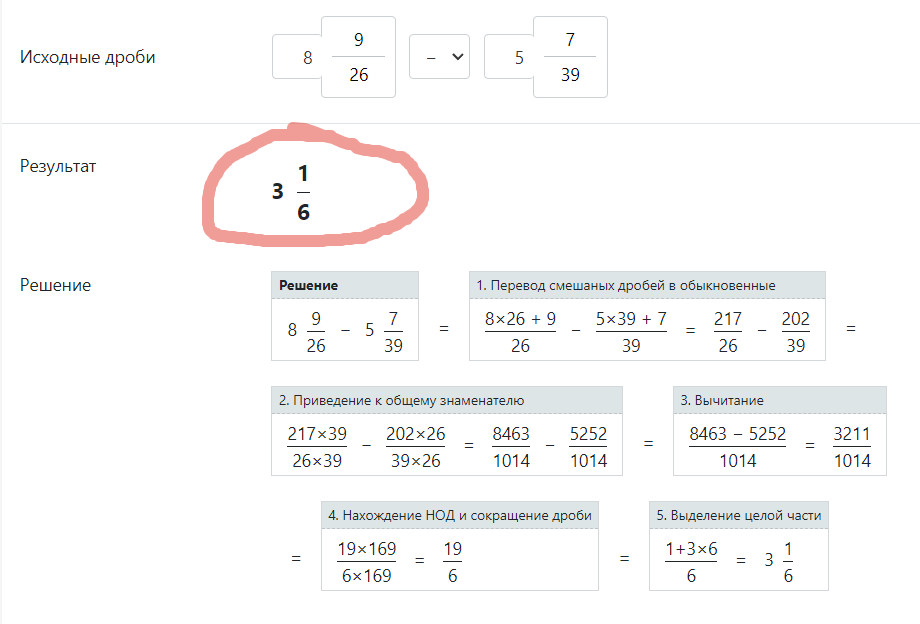 При нажатии на одну из секций, развернется список находящихся в ней инструментов. Из открывшегося списка необходимо выбрать нужный символ и кликнуть на нем. После выбора, указанный символ появится в выделенном прямоугольнике в документе.

Секция, в которой располагаются элементы для написания дробей, находится во второй строке панели инструментов. При наведении на нее курсора мыши, вы увидите подсказку «Шаблоны дробей и радикалов». Кликните секцию один раз и разверните список. В выпавшем меню есть шаблоны для дробей с горизонтальной и косой . Среди появившихся вариантов вы можете выбрать тот, который подходит для вашей задачи. Кликните на нужном варианте. После нажатия, в поле для ввода, которое открылось в документе, появится символ дроби и места для ввода числителя и знаменателя, обрамленные пунктирной линией. Курсор по умолчанию автоматически устанавливается в поле для ввода числителя. Введите числитель. Помимо цифр можно так же вводить символы, буквы или знаки действий. Их можно вводить как с клавиатуры, так и из соответствующих секций панели инструментов Microsoft Equation. После вода числителя, нажатием клавиши TAB, перейдите к знаменателю. Перейти можно и кликнув мышью в поле для ввода знаменателя. Как только написана, кликните указателем мыши в любом месте документа, панель инструментов закроется, ввод дроби будет завершен. Чтобы отредактировать , дважды нажмите на ней левой кнопкой мыши.

Если при открытии меню «Вставка» -> «Объект», в списке вы не обнаружили инструмента Microsoft Equation, его необходимо установить. Запустите установочный диск, образ диска или файл дистрибутива Word. В появившемся окне инсталлятора выберите «Добавить или удалить компоненты. Добавление или удаление отдельных компонентов» и нажмите «Далее». В следующем окне отметьте пункт «Расширенная настройка приложений». Нажмите «Далее». В следующем окне найдите пункт списка «Средства Office» и нажмите на плюсик слева. В развернувшемся списке, нас интересует пункт «Редактор формул». Кликните на значок рядом с надписью «Редактор формул» и, в открывшемся меню, нажмите «Запускать с компьютера». После этого нажмите «Обновить» и дождитесь пока пройдет установка необходимого компонента.

Десятичная дробь состоит из двух частей, которые разделены запятыми. Первая часть — это целая единица, вторая часть — это десятки (если число после запятой одно), сотни (два числа после запятой, как два нуля в ста), тысячные итд. Посмотрим на примеры десятичной дроби: 0, 2; 7, 54; 235,448; 5,1; 6,32; 0,5. Всё это — десятичные дроби. Как же перевести десятичную дробь в обыкновенную?

Пример первый

У нас есть дробь, к примеру, 0,5. Как уже выше писалось, она состоит из двух частей. Первое число 0, показывает, сколько целых единиц у дроби. В нашем случае их нет. Второе число показывает десятки. Дробь даже читается ноль целых пять десятых. Десятичное число перевести в дробь теперь не составит труда, пишем 5/10. Если видите, что у цифр есть общий делитель, можете сократить дробь. У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.

Пример второй

Возьмем более сложную дробь — 2,25. Читается она так — две целых и двадцать пять сотых. Обратите внимание — сотых, так как чисел после запятой две. Теперь можно перевести в обыкновенную дробь. Записываем — 2 25/100. Целая часть — 2, дробная 25/100. Как и в первом примере, эту часть можно сократить. Общим делителем для цифр 25 и 100 является число 25. Заметьте, что мы всегда подбираем наибольший общий делитель. Разделив обе части дроби на НОД, получили 1/4. Итак, 2, 25 это 2 1/4.

Пример третий

И для закрепления материала возьмем десятичную дробь 4,112 — четыре целых и сто двенадцать тысячных. Почему тысячных, думаю, ясно. Записываем теперь 4 112/1000. По алгоритму находим НОД чисел 112 и 1000. В нашем случае — это число 6. Получаем 4 14/125.

Вывод

  1. Разбиваем дробь на целую и дробную части.
  2. Смотрим, сколько цифр после запятой. Если одна — это десятки, две — сотни, три -тысячные итд.
  3. Записываем дробь в обыкновенном виде.
  4. Сокращаем числитель и знаменатель дроби.
  5. Записываем полученную дробь.
  6. Выполняем проверку, делим верхнюю часть дроби на нижнюю. Если есть целая часть, прибавляем к полученной десятичной дроби. Получился исходный вариант — замечательно, значит, вы все сделали правильно.

На примерах я показала, как можно перевести десятичную дробь в обыкновенную. Как видите, сделать это очень легко и просто.

Калькулятор дробей порядка

| iCalculator™

★ ★ ★ ★ ★ [ 126 голосов ]

Фракция заказа s Calculator — это бесплатный онлайн-калькулятор, который позволяет вам расположить набор дробей в порядке их размера. Калькулятор упорядочивания дробей может упорядочивать дроби от наименьшего к наибольшему количеству и от наибольшего к наименьшему количеству. Калькулятор упорядоченных дробей — отличный инструмент для расчета дробей, который помогает проверить ответы на домашние задания и/или подготовиться к экзаменам. Вы можете ввести обыкновенную дробь в Калькулятор упорядоченных дробей и десятичные дроби. Калькулятор упорядоченных дробей может вычислять простые дроби и десятичные дроби по отдельности или вместе (например, 1/2, 3/4, 0,5, 0,75).

Калькулятор порядковых дробей
Введите числа
Упорядочить от наименьшего к наибольшему Упорядочить от наибольшего к наименьшему
Порядок Fra Результаты калькулятора действий
Порядок от наименьшего к наибольшему

Как упорядочить дроби от наименьшего к наибольшему

  1. Введите дроби в калькулятор упорядочивания дробей. Дроби можно вводить, введя числитель (верхнее число дроби), затем косую черту (косая черта используется для представления винкулема) и, наконец, знаменатель (нижнее число дроби). Например, ½ равно 1/2. Кроме того, вы можете ввести десятичные числа, чтобы выразить дробь.
  2. Введите все дроби, которые вы хотите упорядочить, от наименьшего до наибольшего. Убедитесь, что вы разделяете каждую дробь запятой. Например, 3/8, 1/9, 6/7
  3. После того, как вы введете все свои дроби, нажмите «Упорядочить от наименьшего к наибольшему». чтобы упорядочить дроби от наибольшей до наименьшей
    1. Введите дроби в калькулятор упорядочивания дробей. Дроби можно вводить, введя числитель (верхнее число дроби), затем косую черту (косая черта используется для представления винкулема) и, наконец, знаменатель (нижнее число дроби). Например, 1/2 равно ½ 9.0044
    2. Введите все дроби, которые вы хотите расположить в порядке от наибольшей до наименьшей. Убедитесь, что вы разделяете каждую дробь запятой. Например, 1/2, 3/4, 6/7
    3. После того, как вы ввели все свои дроби, нажмите «Упорядочить от наибольшей к наименьшей». это дробь?

      С точки зрения математики, дробь — это числовая величина, которая не является целым числом. 1, 2, 3 и т. д. — целые числа. В математике целые числа также называют «целыми числами» и/или «натуральными числами». Обратите внимание, что это может немного сбивать с толку, поскольку целые числа являются целыми числами только в том случае, если они являются положительными целыми числами.

      Итак, дробь — это не целое число. Целое число может быть определено как:

      Целое число — это положительное число, которое НЕ является дробью, процентом и десятичным числом.

      В чем разница между целым числом и целым числом?

      Разница между целым числом и целым числом заключается в том, что целые числа могут содержать отрицательные числа

      Давайте рассмотрим пример: если мы посмотрим на таблицу ниже, мы увидим, что целые числа могут быть целыми числами, когда они являются положительными целыми числами (что то есть они больше нуля), но не все целые числа являются целыми числами (когда целое число меньше или равно нулю, оно не является целым числом).

      Целые числа V Целое число
      Отрицательное целое число Положительное целое число
      и Меньше -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 и более
      Целое число

      Итак, мы знаем, что можем определить дробь как числовое значение, которое не является целым числом, но что это означает простыми словами. Ну, проще говоря, дробь — это равная часть объекта или, в математике, часть числа. Простой способ думать об этом — торт.

      Пример дроби — разделить торт.

      Давайте представим, что у вас день рождения. Вы покупаете красивый круглый торт ко дню рождения. Это один (1) торт.

      К вам на день рождения пришли 8 друзей, поэтому вы разрезали торт на шестнадцать частей. Вы делаете это, разрезая торт посередине. Это дает вам 2 куска пирога. Затем вы разрезаете эти две части посередине. Это дает вам 4 куска пирога. Наконец, вы разрезаете 4 части посередине, чтобы получить 8 частей праздничного торта. Важное слово здесь — кусочки. У нас есть 8 кусочков торта, которые вместе образуют целый торт. Давайте посмотрим, как мы выражаем наш пример в математических терминах, это также поможет нам позже объяснить, как записываются дроби.

      90 020 2
      Понимание дробей — пример торта
      Количество штук дробь
      1 1
      ½
      4 ¼
      8 ⅛

      В приведенной выше таблице показано, как мы записываем дробь. Такой способ записи дроби называется вульгарной дробью или обыкновенной дробью.

      Что такое вульгарная дробь?

      Вульгарная дробь (или Обычная дробь) — это дробь, выраженная числителем и знаменателем (не десятичной дробью), при этом два числа разделены Винкулемом.

      Проще говоря, Обычная дробь или Обычная дробь — это одно число, написанное над другим и разделенное чертой. В математике два числа в дроби имеют специальные имена, как и линия, разделяющая верхнее и нижнее число.

      Как называется число в верхней части дроби?

      Число в верхней части дроби называется числителем

      Как называется число в нижней части дроби?

      Число в верхней части дроби называется знаменателем

      Как называется черта в дроби?

      Линия в дроби, которая разделяет верхнее число (числитель) и нижнее число (знаменатель), называется Винкулем.

      Что такое десятичная дробь?

      Десятичная дробь — это грубая дробь, знаменатель которой представляет собой степень числа 10 (10, 100, 1000, 10000, 100000 и т. д.).

      Десятичные числа могут быть выражены в виде обычной дроби или десятичного числа. Это особенно полезно при сложении, вычитании, умножении и делении дробей.

      Что такое упорядочивание дробей

      Упорядочивание дробей — это процесс упорядочивания нескольких простых дробей и/или десятичных дробей в зависимости от их относительного размера (от наименьшего к наибольшему или от наибольшего к наименьшему).

      Как рассчитать порядок смешанных дробей?

      Итак, теперь мы знаем, что существуют Обыкновенные дроби и Десятичные дроби. Мы также знаем, что с десятичными дробями довольно легко работать для сложения, вычитания, умножения и деления. Мы также можем использовать онлайн-калькулятор фракций заказа, чтобы работать с нашими фракциями и проверять наши результаты. Давайте теперь посмотрим, как мы вручную упорядочиваем дроби 9.0013

      Вульгарные дроби можно расположить по порядку:

      1. Используя общий знаменатель
      2. Используя перекрестное умножение

      Дополнительные калькуляторы дробей

      Вот некоторые из наших других калькуляторов дробей, которые вы найдете полезными. расчет обыкновенных дробей с использованием общего знаменателя и перекрестного умножения дробей.

      • Калькулятор дробей
      • Калькулятор дробей
      • Заказ калькулятора дробей
      • Калькулятор отношения к дроби
      • Повторяющийся калькулятор десятичной дроби к дроби
      • Упрощенный калькулятор сложных дробей

      Преобразователь десятичных и двоичных чисел — исследование двоичных чисел

      Преобразование десятичного числа в двоичное

      Введите десятичное число (например, 3,1415) (без запятых, пробелов, показателей степени, дробей, операторов) Преобразует в это двоичное число: Количество цифр:

      Опции:

      • Сократить бесконечные двоичные дроби до биты.

      Двоичный код в десятичный

      Введите двоичное число (например, 110.001) (без запятых, пробелов, показателей степени, дробей, операторов) Преобразует в это десятичное число: Количество цифр:

      (Хотите преобразовать в двоичное число с плавающей запятой ? Попробуйте мой конвертер с плавающей запятой. )

      (Хотите вычислить с двоичными числами? Попробуйте мой двоичный калькулятор.) Попробуйте мой преобразователь.)

      О конвертере десятичных/двоичных чисел

      Это конвертер десятичных чисел в двоичные числа и двоичных чисел в десятичные числа . Он отличается от большинства десятичных/двоичных преобразователей, таких как калькулятор Google или калькулятор Windows, потому что:

      • Он может преобразовывать как дробные, так и целые значения.
      • Может преобразовывать очень большие и очень маленькие числа — до сотен цифр.

      Десятичные числа преобразуются в «чистые» двоичные числа, а не в форматы компьютерных чисел, такие как дополнение до двух или двоичные числа с плавающей запятой IEEE.

      Преобразование реализовано с арифметикой произвольной точности, что дает преобразователю возможность преобразовывать числа больше, чем те, которые могут поместиться в стандартные компьютерные размеры слов (например, 32 или 64 бита).

      Как использовать десятичный/двоичный конвертер

      Ввод

      • Введите положительное или отрицательное число без запятых или пробелов, не выраженное в виде дроби или арифметического вычисления, а не в экспоненциальном представлении. Дробные значения обозначаются точкой счисления (‘.’, вместо ‘,’)
      • Измените количество битов, которое вы хотите отобразить в двоичном результате, если оно отличается от значения по умолчанию (применяется только при преобразовании дробного десятичного значения).
      • Нажмите «Преобразовать», чтобы преобразовать.
      • Нажмите «Очистить», чтобы сбросить форму и начать с нуля.

      Если вы хотите преобразовать другой номер, просто введите исходный номер и нажмите «Преобразовать» — нет необходимости сначала нажимать «Очистить».

      Вывод

      Кроме результата преобразования отображается количество цифр как в исходном, так и в преобразованном числах. Например, при преобразовании десятичного числа 43,125 в двоичное число 101011,001 количество цифр отображается как «от 2,3 до 6,3». Это означает, что десятичный ввод имеет 2 цифры в целой части и 3 цифры в дробной части, а двоичный вывод имеет 6 цифр в целой части и 3 цифры в дробной части.

      Дробные десятичные значения, которые являются диадическими, преобразуются в конечные дробные двоичные значения и отображаются с полной точностью. Дробные десятичные значения, не являющиеся диадическими, преобразуются в бесконечные (повторяющиеся) дробные двоичные значения, которые усекаются (а не округляются) до указанного количества битов. В этом случае к концу двоичного числа добавляется многоточие (…), а число цифр дробной части отмечается как бесконечное с помощью символа «∞».

      Изучение свойств десятичного/двоичного преобразования

      Конвертер настроен таким образом, что вы можете изучить свойства преобразования десятичных чисел в двоичные и двоичные в десятичные. Вы можете скопировать вывод десятично-двоичного преобразователя на вход двоично-десятичного преобразователя и сравнить результаты (не копируйте «…» часть числа — двоичный преобразователь пометит ее как недействительную.

      No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *