12.Матрицы, правило крамера.
Для любой квадратной матрицы может быть найдена величина, называемая определителем.
Определитель — это квадратная таблица чисел или матиматических символов (Δd).
Для матрицы второго порядка определитель вычисляется по формуле:
Разложение по строке или столбцу
Формулы разложения по строке или столбцу:
Первые n формул называются формулами разложения определителя по строке, а вторые n формул называются формулами разложения определителя по столбцу.
В этих формулах — алгебраические дополнения элементов аij матрицы А, где Mij — миноры элементов аij матрицы А.
Минором Mij элемента аij матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, получаемой из матрицы А вычеркиванием i-й строки и j-го столбца, на пересечении которых находится элемент aij/
Правило Саррюса
Дописывание
двух первых строк или столбцов.
В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33
Пример 32.2
Вычислить определитель двумя способами: с помощью разложения по первой строке и по правилу треугольника:
Решение:
Свойства определителей
Свойство (1) Определитель не изменится, если все строки заменить соответствующими столбцами и наоборот.
Свойство (2) При перестановке двух каких-либо строк или столбцов местами определитель изменяет знак.
Свойство (3) Определитель равен нулю, если он имеет две равные строки (столбца).
Свойство (4) Множитель, общий для всех элементов строки или столбца, можно выносить за знак определителя.
Свойство (5) Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, то определитель не изменится.
Следствие
из свойств 32.4 и 32.5: Если к элементам
какой-либо строки или столбца прибавить
соответствующие элементы другой строки
или столбца, умноженные на некоторое
число, то определитель не изменится.
Свойство (6) Сумма произведений элементов какой-либо строки или столбца на алгебраические дополнения соответствующих элементов другой строки или столбца равна нулю.
Пример 32.3
Вычислить определитель, используя свойства:
Решение:
1. Третью строку умножим на подходящие множители и прибавим к остальным:
получим:
ПРАВИЛО КРАМЕРА
Решение систем уравнений
Пусть имеется система уравнений:
Обозначим через Δ определитель матрицы системы и через Δj определитель, который получается из определителя Δ заметой j-го столбца столбцом правых частей системы ( j=1,2,…n).
Теорема 1
Нахождение обратной матрицы
Путь имеется матрица:
Матрица:
13. Теорема Крамера Капелли, метод гаусса
Теорема. Система
из n
уравнений с n
неизвестными
Система
из n
уравнений с n
неизвестными
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
, где = detA, а i – определитель матрицы, получаемой из матрицы системы заменой столбца iстолбцом свободных членов bi. i =
Решение систем линейных уравнений методом Крамера.
Пусть нам требуется решить систему линейных алгебраических уравнений в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, .
Пусть — определитель основной матрицы системы, а — определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:
При
таких обозначениях неизвестные переменные
вычисляются по формулам метода Крамера
как . Так находится решение системы линейных
алгебраических уравнений методом
Крамера.
Так находится решение системы линейных
алгебраических уравнений методом
Крамера.
Пример.
Решите систему линейных уравнений методом Крамера .
Решение.
Основная матрица системы имеет вид . Вычислим ее определитель (при необходимости смотрите статью определитель матрицы: определение, методы вычисления, примеры, решения):
Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.
Составим и вычислим необходимые определители (определитель получаем, заменив в матрице А первый столбец на столбец свободных членов , определитель — заменив второй столбец на столбец свободных членов, — заменив третий столбец матрицы А на столбец свободных членов):
Находим неизвестные переменные по формулам :
Ответ:
x1 =
4, x2 =
0, x3 =
-1.
Основным недостатком метода Крамера (если это можно назвать недостатком) является трудоемкость вычисления определителей, когда число уравнений системы больше трех.
МЕТОД ГАУССА
Решение систем линейных уравнений методом Гаусса.Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными определитель основной матрицы которой отличен от нуля.
Суть
метода Гаусса состоит
в последовательном исключении неизвестных
переменных: сначала исключается x1 из
всех уравнений системы, начиная со
второго, далее исключается x2из
всех уравнений, начиная с третьего, и
так далее, пока в последнем уравнении
останется только неизвестная переменная xn.
Такой процесс преобразования уравнений
системы для последовательного исключения
неизвестных переменных называется прямым
ходом метода Гаусса.
После завершения прямого хода метода
Гаусса из последнего уравнения
находитсяxn,
с помощью этого значения из предпоследнего
уравнения вычисляется xn-1,
и так далее, из первого уравнения
находится x1. Процесс вычисления неизвестных переменных
при движении от последнего уравнения
системы к первому называется
Процесс вычисления неизвестных переменных
при движении от последнего уравнения
системы к первому называется
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменнуюx1 из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на, и так далее, кn-омууравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет видгде, а.
К такому же результату мы бы пришли, если бы выразили x1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x1 исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Будем
считать, что (в
противном случае мы переставим местами
вторую строку сk-ой,
где ). Приступаем к исключению неизвестной
переменнойx2 из
всех уравнений, начиная с третьего.
Приступаем к исключению неизвестной
переменнойx2 из
всех уравнений, начиная с третьего.
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на, и так далее, кn-омууравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет видгде, а. Таким образом, переменнаяx2 исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x3, при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем

Пример.
Решите систему линейных уравнений методом Гаусса.
Решение.
Исключим неизвестную переменную x1 из второго и третьего уравнения системы. Для этого к обеим частям второго и третьего уравнений прибавим соответствующие части первого уравнения, умноженные на и насоответственно:
Теперь из третьего уравнения исключим x2, прибавив к его левой и правой частям левую и правую части второго уравнения, умноженные на :
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x3:
Из второго уравнения получаем .
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .
Ответ:
x1 = 4, x2 = 0, x3 = -1.
Алгебра и теория чисел
Алгебра и теория чисел
ОглавлениеПРЕДИСЛОВИЕГлава первая. ЭЛЕМЕНТЫ ЛОГИКИ § 1. ЛОГИКА ВЫСКАЗЫВАНИЙ Формулы логики высказываний. Законы логики. Упражнения § 2. ЛОГИЧЕСКОЕ СЛЕДСТВИЕ Схемы доказательств. § 3. ПРЕДИКАТЫ Предикаты. Операции над предикатами. Упражнения § 4. КВАНТОРЫ Запись высказываний на языке логики предикатов. Упражнения § 5. ПРЕДИКАТНЫЕ ФОРМУЛЫ.  ЗАКОНЫ ЛОГИКИ ЗАКОНЫ ЛОГИКИПредикатные формулы. Законы логики предикатов. Упражнения Глава вторая. МНОЖЕСТВА И ОТНОШЕНИЯ § 1. МНОЖЕСТВА Подмножества. Пустое множество. Операции над множествами. Основные свойства операций над множествами. Универсальное множество. Дополнение множества. Диаграммы Эйлера — Венна. Упражнения § 2. БИНАРНЫЕ ОТНОШЕНИЯ Упражнения § 3. ФУНКЦИИ Композиция функций. Инъективные функции. Обратимые функции. Ограничение функции. Упражнения § 4. ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ Отношение эквивалентности. Фактор-множество. Отношение равнообразности отображения. Упражнения § 5. ОТНОШЕНИЯ ПОРЯДКА Упорядоченное множество. Упражнения Глава третья. АЛГЕБРЫ И АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ § 1. БИНАРНЫЕ ОПЕРАЦИИ Виды бинарных операций. Нейтральные элементы. Симметричные элементы. Подмножества, замкнутые относительно операций. Аддитивная и мультипликативная формы записи.  Конгруэнция. Упражнения. § 2. АЛГЕБРЫ Гомоморфизмы алгебр. Подалгебры. Фактор-алгебра. Упражнения § 3. ГРУППЫ Примеры групп. Простейшие свойства группы. Гомоморфизмы групп. Подгруппы. Упражнения § 4. КОЛЬЦА Простейшие свойства кольца. Гомоморфизмы колец. Подкольца. Упражнения § 5. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ Изоморфизмы алгебраических систем. Подсистемы. Упражнения Глава четвертая. ОСНОВНЫЕ ЧИСЛОВЫЕ СИСТЕМЫ § 1. СИСТЕМА НАТУРАЛЬНЫХ ЧИСЕЛ Слова в однобуквенном алфавите. Система натуральных чисел. Принцип математической индукции. Упражнения § 2. СВОЙСТВА СЛОЖЕНИЯ И УМНОЖЕНИЯ НАТУРАЛЬНЫХ ЧИСЕЛ Свойства умножения. § 3. ОТНОШЕНИЕ ПОРЯДКА НА МНОЖЕСТВЕ НАТУРАЛЬНЫХ ЧИСЕЛ Полная упорядоченность множества натуральных чисел. Упражнения § 4. КОЛЬЦО ЦЕЛЫХ ЧИСЕЛ Естественное умножение в аддитивной группе целых чисел. Кольцо целых чисел. Отношение делимости в кольце целых чисел.  Упражнения § 5. ПОЛЯ. ПОЛЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ Поле рациональных чисел. Упражнения § 6. СИСТЕМА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ Система действительных чисел. Упражнения § 7. ПОЛЕ КОМПЛЕКСНЫХ ЧИСЕЛ Поле комплексных чисел. Модуль комплексного числа. Геометрическое представление комплексных чисел. Упражнения § 8. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА. ИЗВЛЕЧЕНИЕ КОРНЕЙ ИЗ КОМПЛЕКСНЫХ ЧИСЕЛ Корни n-й степени из единицы. Корни n-й степени из произвольного комплексного числа. Упражнения Глава пятая. АРИФМЕТИЧЕСКИЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ § 1. АРИФМЕТИЧЕСКИЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА Линейная зависимость и независимость системы векторов. Эквивалентные системы векторов. Базис конечной системы векторов. Ранг конечной системы векторов. Упражнения § 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Равносильные системы линейных уравнений и элементарные преобразования системы. Равенство строчечного и столбцового рангов матрицы.  Связь между решениями неоднородной линейной системы и решениями ассоциированной с ней однородной системы. Теоремы о следствиях системы линейных уравнений. Упражнения. § 3. СТУПЕНЧАТЫЕ МАТРИЦЫ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Приведенные ступенчатые матрицы. Однородные системы линейных уравнений. Фундаментальная система решений. Решение системы линейных уравнений методом последовательного исключения переменных. Упражнения Глава шестая. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ § 1. ОПЕРАЦИИ НАД МАТРИЦАМИ И ИХ СВОЙСТВА Транспонирование произведения матриц. Упражнения § 2. ОБРАТИМЫЕ МАТРИЦЫ Элементарные матрицы. Вычисление обратной матрицы. Запись и решение системы n линейных уравнений с n переменными в матричной форме. Упражнения § 3. ПОДСТАНОВКИ Четные и нечетные подстановки. Знак подстановки. Упражнения § 4. ОПРЕДЕЛИТЕЛИ Основные свойства определителей. Упражнения § 5. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ. ТЕОРЕМЫ ОБ ОПРЕДЕЛИТЕЛЯХ Разложение определителя по строке или столбцу.  Определитель произведения матриц. Необходимые и достаточные условия равенства нулю определителя. § 6. ТЕОРЕМЫ О МАТРИЦАХ. ПРАВИЛО КРАМЕРА Правило Крамера. Условия, при которых система n линейных однородных уравнений с n переменными имеет ненулевые решения. Упражнения Глава седьмая. ВЕКТОРНЫЕ ПРОСТРАНСТВА § 1. ВЕКТОРНЫЕ ПРОСТРАНСТВА Простейшие свойства векторных пространств. Линейная зависимость и независимость системы векторов. Упражнения § 2. ПОДПРОСТРАНСТВА ВЕКТОРНОГО ПРОСТРАНСТВА Линейная оболочка множества векторов. Сумма подпространств. Линейные многообразия. Упражнения § 3. БАЗИС И РАЗМЕРНОСТЬ ВЕКТОРНОГО ПРОСТРАНСТВА Дополнение независимой системы векторов до базиса. Размерность векторного пространства. Упражнения. § 4. ИЗОМОРФИЗМЫ ВЕКТОРНЫХ ПРОСТРАНСТВ Изоморфизм векторных пространств. Упражнения § 5. ВЕКТОРНЫЕ ПРОСТРАНСТВА СО СКАЛЯРНЫМ УМНОЖЕНИЕМ Ортогональная система векторов. Процесс ортогонализации. 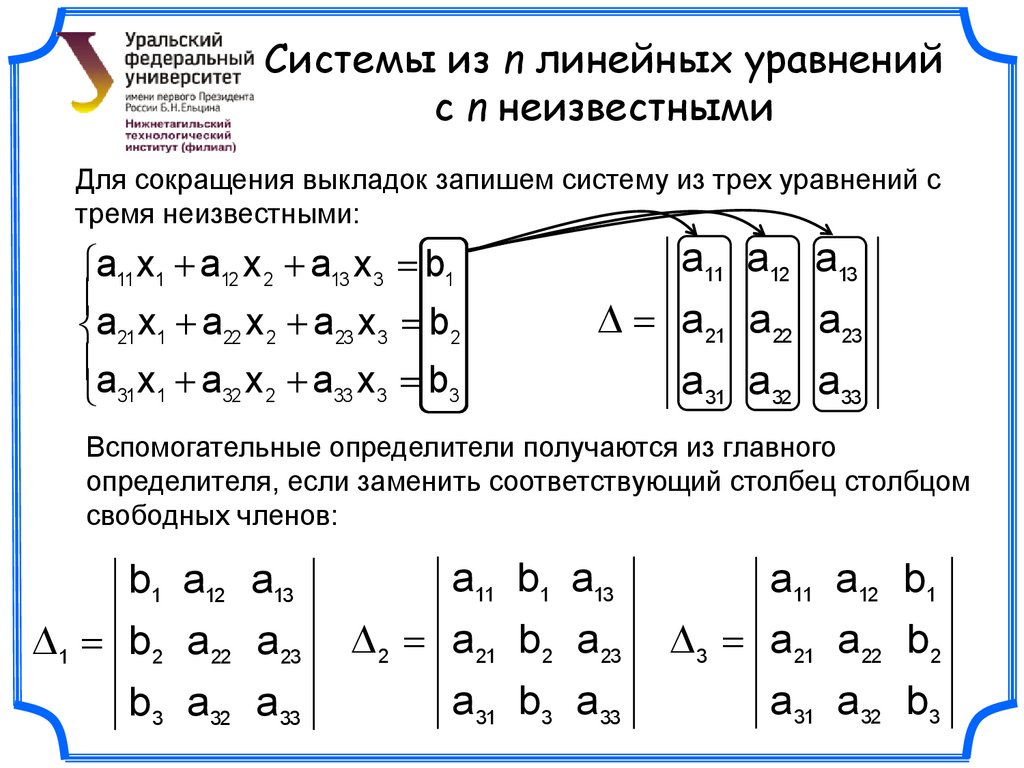 Упражнения. § 6. ЕВКЛИДОВЫ ВЕКТОРНЫЕ ПРОСТРАНСТВА Норма вектора. Ортонормированный базис евклидова пространства. Изоморфизмы евклидовых пространств. Упражнения. Глава восьмая. ЛИНЕЙНЫЕ ОПЕРАТОРЫ § 1. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ Ядро и образ линейного оператора. Операции над линейными отображениями. Упражнения § 2. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ ОПЕРАТОРОВ МАТРИЦАМИ Связь между координатными столбцами векторов х и ф(x). Ранг линейного оператора. Связь между координатными столбцами вектора относительно различных базисов. Связь между матрицами линейного оператора относительно различных базисов. Упражнения § 3. ЛИНЕЙНЫЕ АЛГЕБРЫ Алгебра линейных операторов векторного пространства Изоморфизм алгебры линейных операторов и полной матричной алгебры. Упражнения § 4. ОБРАТИМЫЕ ОПЕРАТОРЫ Полная линейная группа. Упражнения § 5. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ. ХАРАКТЕРИСТИЧЕСКИЕ УРАВНЕНИЯ Нахождение собственных векторов линейного оператора. 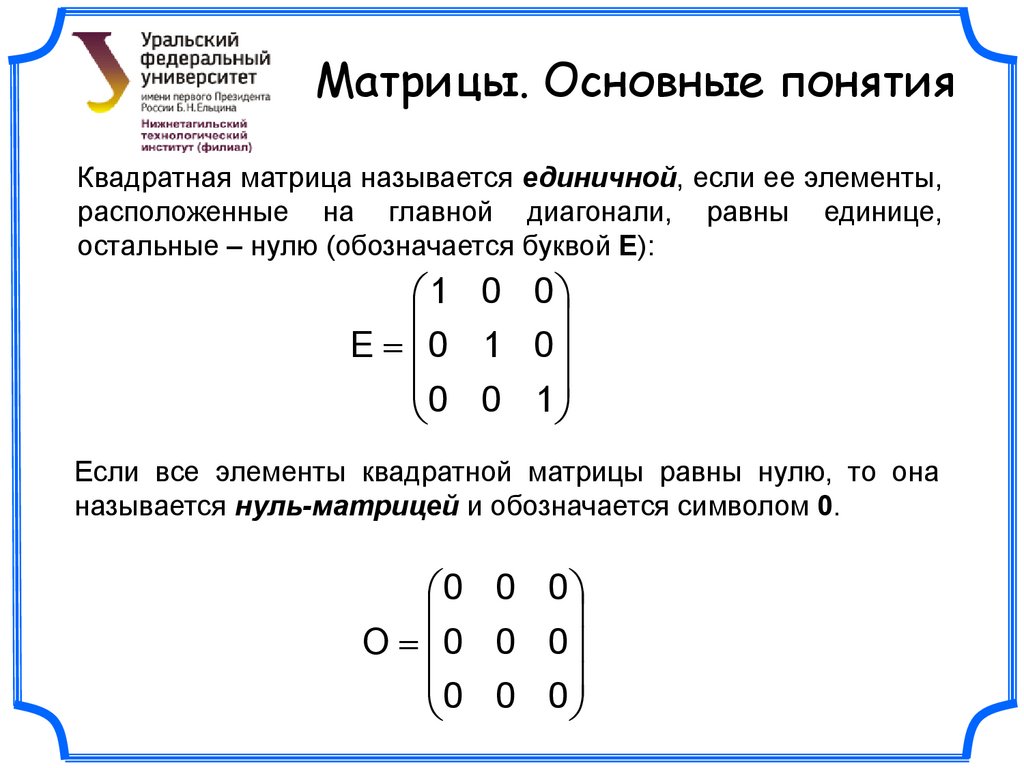 Характеристическое уравнение. Линейные операторы с простым спектром. Условия, при которых матрица подобна диагональной матрице. Упражнения Глава девятая. СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ § 1. СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ Однородные системы линейных неравенств и выпуклые конусы. Следствия однородной системы линейных неравенств. Теорема Минковского. Критерий несовместности системы линейных неравенств. Неотрицательные решения системы линейных уравнений и системы линейных неравенств. Упражнения § 2. СТАНДАРТНЫЕ И КАНОНИЧЕСКИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. ТЕОРЕМЫ ДВОЙСТВЕННОСТИ Допустимые и оптимальные векторы. Теорема двойственности для стандартных задач. Теорема двойственности для канонических задач. Теорема равновесия. Упражнения § 3. СИМПЛЕКС-МЕТОД Упражнения Глава десятая. ГРУППЫ § 1. ПОЛУГРУППЫ И МОНОИДЫ Моноиды. Обобщенный закон ассоциативности. Упражнения § 2. ПОДГРУППЫ И СМЕЖНЫЕ КЛАССЫ Смежные классы.  Теорема Лагранжа. Упражнения § 3. ЦИКЛИЧЕСКИЕ ГРУППЫ Циклические группы. Подгруппы циклической группы. Упражнения § 4. НОРМАЛЬНЫЕ ДЕЛИТЕЛИ И ФАКТОР-ГРУППЫ Фактор-группа. Ядро гомоморфизма. Упражнения Глава одиннадцатая. ТЕОРИЯ ДЕЛИМОСТИ В КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ § 1. РАЗЛОЖЕНИЕ ЦЕЛЫХ ЧИСЕЛ НА ПРОСТЫЕ МНОЖИТЕЛИ Простые числа. Разложение целых чисел на простые множители. Делители целого числа. Число и сумма натуральных делителей числа. Бесконечность множества простых чисел. Решето Эратосфена. Упражнения § 2. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ И НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Взаимно простые числа. Наименьшее общее кратное. Упражнения § 3. АЛГОРИТМ ЕВКЛИДА И КОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ Конечные цепные дроби. Подходящие дроби. Упражнения. § 4. ЦЕЛЫЕ СИСТЕМАТИЧЕСКИЕ ЧИСЛА Арифметические операции над целыми систематическими числами Перевод чисел из одной системы счисления в другую. Упражнения § 5.  РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛФункции T(х) и Л(х). Неравенства для функции Т(х). Неравенства Чебышева. Простые числа в арифметических прогрессиях. Упражнения Глава двенадцатая. ТЕОРИЯ СРАВНЕНИЙ С АРИФМЕТИЧЕСКИМИ ПРИЛОЖЕНИЯМИ § 1. СРАВНЕНИЯ И ИХ СВОЙСТВА Упражнения § 2. ПОЛНАЯ СИСТЕМА ВЫЧЕТОВ Упражнения § 3. ПРИВЕДЕННАЯ СИСТЕМА ВЫЧЕТОВ Мультипликативная группа классов вычетов, взаимно простых с модулем. Функция Эйлера. Теоремы Эйлера и Ферма. Упражнения § 4. СРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ. СРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ ПО ПРОСТОМУ МОДУЛЮ Сравнения первой степени. Сравнения высших степеней по простому модулю. Упражнения § 5. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ Первообразные корни по простому модулю. Индексы по простому модулю. Двучленные сравнения. Упражнения § 6. ОБРАЩЕНИЕ ОБЫКНОВЕННОЙ ДРОБИ В СИСТЕМАТИЧЕСКУЮ И ОПРЕДЕЛЕНИЕ ДЛИНЫ ПЕРИОДА СИСТЕМАТИЧЕСКОЙ ДРОБИ Упражнения Глава тринадцатая. КОЛЬЦА § 1.  ИДЕАЛЫ КОЛЬЦА. ФАКТОР-КОЛЬЦО ИДЕАЛЫ КОЛЬЦА. ФАКТОР-КОЛЬЦОСравнения и классы вычетов по идеалу. Фактор-кольцо. Теорема об эпиморфизмах колец. Характеристика кольца. Наименьшее подкольцо кольца. Упражнения § 2. ПОЛЕ ЧАСТНЫХ ОБЛАСТИ ЦЕЛОСТНОСТИ Изоморфизм полей частных. Упражнения § 3. КОЛЬЦА ГЛАВНЫХ ИДЕАЛОВ Простые и составные элементы области целостности. Кольца главных идеалов. Факториальность кольца главных идеалов. Евклидовы кольца. Упражнения § 4. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Наименьшее общее кратное. Упражнения Глава четырнадцатая. ПОЛИНОМЫ ОТ ОДНОЙ ПЕРЕМЕННОЙ § 1. КОЛЬЦО ПОЛИНОМОВ Теорема о существовании простого трансцендентного расширения коммутативного кольца. Степень полинома. Деление полинома на двучлен и корни полинома. Теорема о наибольшем возможном числе корней полинома в области целостности. Алгебраическое и функциональное равенства полиномов. Упражнения § 2. ПОЛИНОМЫ НАД ПОЛЕМ Алгоритм Евклида.  Неприводимые над данным полем полиномы. Разложение полинома в произведение нормированных неприводимых множителей. Упражнения § 3. ФАКТОРИАЛЬНОСТЬ КОЛЬЦА ПОЛИНОМОВ НАД ФАКТОРИАЛЬНЫМ КОЛЬЦОМ Факториальность кольца полиномов. § 4. ФОРМАЛЬНАЯ ПРОИЗВОДНАЯ ПОЛИНОМА. НЕПРИВОДИМЫЕ КРАТНЫЕ МНОЖИТЕЛИ Разложение полинома по степеням разности х – с. Неприводимые кратные множители полинома. Кратные корни полинома. Упражнения Глава пятнадцатая. ПОЛИНОМЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. КОЛЬЦО ПОЛИНОМОВ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Кольцо полиномов от нескольких переменных. Изоморфизм колец полиномов. Нормальное представление полинома и степень полинома. Факториалыюсть кольца полиномов. § 2. СИММЕТРИЧЕСКИЕ ПОЛИНОМЫ Лемма о высшем члене произведения двух полиномов. Симметрические полиномы. Леммы о симметрических полиномах. Основная теорема о симметрических полиномах. Упражнения 3. РЕЗУЛЬТАНТ ПОЛИНОМОВ И ИСКЛЮЧЕНИЕ ПЕРЕМЕННЫХ Исключение переменных.  Глава шестнадцатая. ПОЛИНОМЫ НАД ПОЛЕМ КОМПЛЕКСНЫХ ЧИСЕЛ И НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 1. АЛГЕБРАИЧЕСКАЯ ЗАМКНУТОСТЬ ПОЛЯ КОМПЛЕКСНЫХ ЧИСЕЛ Непрерывность модуля полинома. Наименьшее значение модуля полинома. Лемма Даламбера. Алгебраическая замкнутость поля комплексных чисел. Формулы Виета. Упражнения § 2. ПОЛИНОМЫ НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. УРАВНЕНИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ СТЕПЕНИ Исследование корней уравнения третьей степени с действительными коэффициентами. Уравнения четвертой степени. § 4. ОТДЕЛЕНИЕ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ ПОЛИНОМА Теорема Штурма. Глава семнадцатая. ПОЛИНОМЫ НАД ПОЛЕМ РАЦИОНАЛЬНЫХ ЧИСЕЛ И АЛГЕБРАИЧЕСКИЕ ЧИСЛА § 1. ЦЕЛЫЕ И РАЦИОНАЛЬНЫЕ КОРНИ ПОЛИНОМА. КРИТЕРИЙ НЕПРИВОДИМОСТИ § 2. ПРОСТОЕ АЛГЕБРАИЧЕСКОЕ РАСШИРЕНИЕ ПОЛЯ § 3. СОСТАВНОЕ АЛГЕБРАИЧЕСКОЕ РАСШИРЕНИЕ ПОЛЯ § 4. УСЛОВИЯ РАЗРЕШИМОСТИ УРАВНЕНИЯ ТРЕТЬЕЙ СТЕПЕНИ В КВАДРАТНЫХ РАДИКАЛАХ ЛИТЕРАТУРА |
Доказательство.

\begin{уравнение*} А \ прил А = \begin{bматрица} a_{1,1} \amp a_{1,2} \amp \cdots \amp a_{1,n} \\ a_{2,1} \amp a_{2,2} \amp \cdots \amp a_{2,n} \\ \усилитель\усилитель\вдоц\\ a_{n,1} \amp a_{n,2} \amp \cdots \amp a_{n,n} \\ \end{bmatrix} \begin{bmatrix} C_{1,1} \amp C_{2,1} \amp \cdots \amp C_{n,1} \\ C_{1,2} \amp C_{2,2} \amp \cdots \amp C_{n,2} \\ \усилитель\усилитель\вдоц\\ C_{1,n} \amp C_{2,n} \amp \cdots \amp C_{n,n} \\ \end{bmatrix} \end{уравнение*} 9n a_{i,k} C_{i,k}=\det A \end{уравнение*}
\(i\not=j\text{:}\) В этом случае мы используем новую матрицу \(B\), построенную из \(A\) путем замены \(R_j\) на \(R_i\text{, }\), то есть \(R_j\gets R_i\) (это не элементарная операция строки). Это означает \(B_{j,k}=A_{i,k}=a_{i,k}\) для \(k=1,2,\ldots n\text{.}\), поскольку \(B\ ) имеет две одинаковые строки, теорема 4.4.12 говорит нам, что \(\det B=0\text{.}\) С другой стороны, расширяя \(R_j\) строки \(B\text{,}\ ) у нас есть
\begin{уравнение*}
0
=\sum_{k=1}^n B_{j,k} C_{j,k}
=\sum_{k=1}^n a_{i,k} C_{j,k}=
(А \ прил А) _ {я, j}
\end{уравнение*} 9{-1}. \end{уравнение*}
\end{уравнение*}
Пример 4.5.4. Обратное вычисляется с использованием сопряжения \(A\).
Пусть
\begin{уравнение*} А= \begin{bmatrix} 1\усилитель 2\усилитель 1\\ 2\усилитель 3\усилитель 5 \\1\усилитель 2\усилитель 0 \end{bmatrix} \end{уравнение*}
Сначала мы вычисляем \(\det A=1\)
Далее вычисляем миноры:
\begin{уравнение*} \begin{массив}{ll} M_{1,1}= -10 \amp M_{1,2}= -5 \amp M_{1,3}= 1 \\ M_{2,1}= -2 \amp M_{2,2}= -1 \amp M_{2,3}= 0 \\ M_{3,1}= 7 \amp M_{3,2}= 3 \amp M_{3,3}= -1 \конец{массив} \end{уравнение*} 9{-1}b= \frac1{\det A} \adj Ab\text{.}\) Определяем новые матрицы \(A_1,A_2,\ldots,A_n\text{:}\) конструируем \(A_k\) путем замены \(k\)-го столбца \(A\) на \(b\text{.}\). Более конкретно, если столбцы \(A\) равны \(C_1,C_2,\ldots, C_n\text{,}\) затем
\begin{уравнение*} А_к= \begin{bmatrix} C_1 \cdots C_{k-1}\amp b\amp C_{k+1} \cdots C_n \end{bmatrix} \end{уравнение*}
Теорема 4.5.6. Правило Крамера.

Пусть
\begin{уравнение*} Ах=б \end{уравнение*} 9n b_kC_{k,i}\) — это \(i\)-е расширение столбца для оценки \(\det A_i\text{.}\) Следовательно,
\begin{уравнение*} x_i=\frac1{\det A} \det A_i=\frac{\det A_i}{\det A}. \end{уравнение*}
Пример 4.5.7. Применение правила Крамера.
Рассмотрим систему линейных уравнений
\begin{уравнение*} х_1+х_2+х_3=2\\ х_1-х_2+х_3=0\\ 2x_1-x_2+x_3=2 \end{уравнение*}
У нас есть
\begin{уравнение*} А= \begin{bmatrix} 1 \амп 1\амп 1\\ 1 \амп -1 \ампер 1\ 2 \амп -1 \ампер 1 \end{bmatrix} \qquad \дет А=2 \\ А_1= \begin{bmatrix} 2 \амп 1\амп 1\\ 0 \ампер -1 \ампер 1 \\ 2 \амп -1 \ампер 1 \end{bmatrix} \qquad \det A_1=4 \\ А_2= \begin{bmatrix} 1\амп 2\амп 1\\ 1 \ампер 0 \ампер 1 \\ 2\амп 2\амп 1 \end{bmatrix} \qquad \det A_2=2 \\ А_3= \begin{bmatrix} 1 \усилитель 1\усилитель 2\\ 1 \ампер -1 \ампер 0 \\ 2 \амп -1 \ампер 2 \end{bmatrix} \qquad \det A_3=-2 \end{уравнение*}
и так
\begin{уравнение*} x_1=\frac42=2\\ x_2=\frac22=1\\ x_3=\frac{-2}2=-1 \end{equation*}
LINALG — Правило Крамера.
 Правило Крамера, объясненное геометрически… | от Jaehoon Jang | MLearning.ai
Правило Крамера, объясненное геометрически… | от Jaehoon Jang | MLearning.aiПравило Крамера, объясненное геометрически — 3Blue1Brown
Что такое правило Крамера?
Правило Крамера — это метод, который использует определителей для анализа систем уравнений , которые имеют такое же количество уравнений, что и переменные .
Предположим, у нас есть такая система уравнений:
Мы можем представить это с помощью матриц и векторов.
Мы можем начать с определения новой матрицы Aᵢ(b), которую можно получить, заменив столбец iᵗʰ матрицы A вектором b.
Правило Крамера: когда матрица A обратима, решение x может быть представлено как xᵢ:
Например,
Итак, используя наш пример, мы сначала должны проверить, не равен ли определитель 0.
вычислив определительТеперь мы знаем, что наша матрица A обратима.
Вновь определенная матрица Aᵢ(b) будет выглядеть так:
Определитель каждой матрицы будет:
Решение будет:
Почему это правило работает именно так?
Используя определитель, мы можем лучше понять правило Крамера.
Допустим, у нас есть
, и мы хотим найти соответствующий вектор x.
Исходное состояние перед преобразованием (применением матрицы A) будет выглядеть так:
Здесь мы собираемся представить координаты x и y вектора x особым образом, используя параллелограммы.
Мы можем сказать, что координата y вектора x равна y, но эта область параллелограмма также может представлять координату y вектора x (до преобразования), потому что она умножается на единичный вектор i-шляпы (длина = 1).
<координата X>
Мы можем сказать, что координата x вектора x равна x, но эта область параллелограмма также может представлять координату x вектора x (до преобразования), потому что она умножается на единичный вектор j-шляпы (длина = 1).
Что, если мы применим здесь линейное преобразование?
<координата Y>
Определитель говорит нам о том, насколько изменилась система. Также площадь нашего параллелограмма изменится на величину определителя.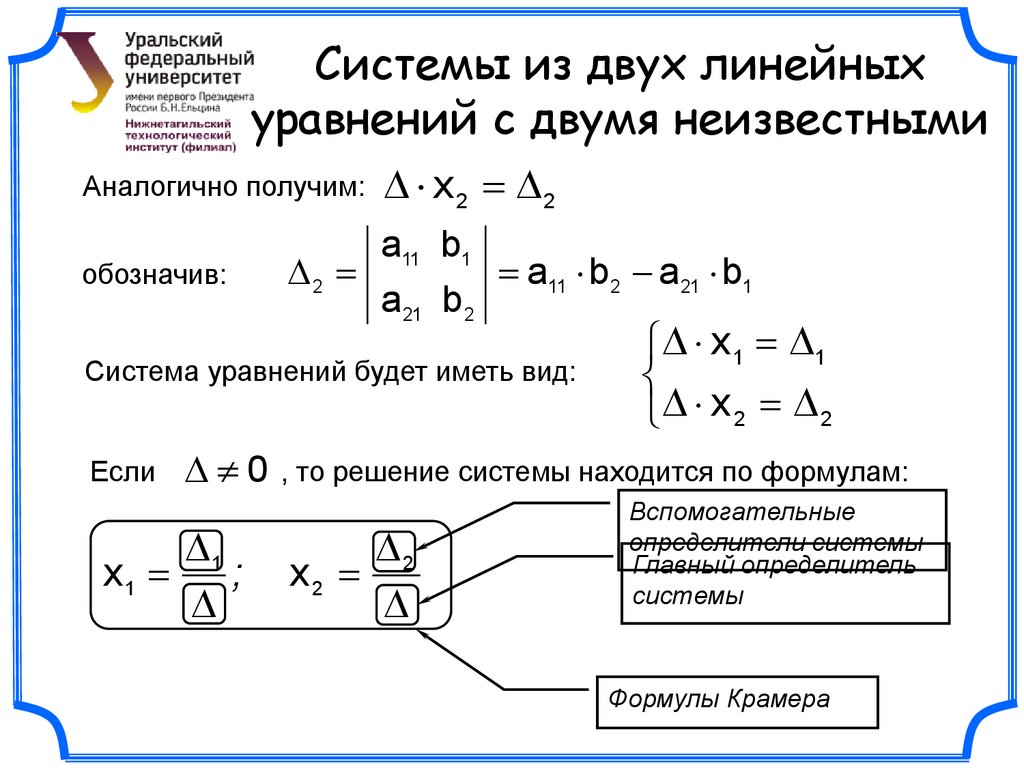

 Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтов. — М.: Высш. школа, 1979. — 559 с.
Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтов. — М.: Высш. школа, 1979. — 559 с.