Знаменатель прогрессии тогда равен:
$q = \frac{a_k}{a_{k-1}}$
Если знаменатель прогресии:
- Отрицательный, члены прогрессии будут чередоваться между позитивными и отрицатесльными.
Пример:
1, -2, 4, -8, 16, -32… — знаменатель -2 и первы член 1. - Больше, чем 1, тогда прогрессия будет иметь экспоненциальный рост до бесконечности (позитивной).
Пример:
1, 5, 25, 125, 625 … — знаменатель 5. - Меньше чем -1, тогда прогрессия будет иметь экспоненциальный рост до бесконечности (отрицательную и позитивную сторону).
Пример:
1, -5, 25, -125, 625, -3125, 15625, -78125, 390625, -1953125 … — знаменатель -5. - Между 1 и -1, тогда прогрессия будет экспоненциально приближаться к 0.
Пример:
4; 2; 1; 0,5; 0,25; 0,125; 0,0625 … — знаменатель $\frac{1}{2}$
4; -2; 1; -0,5; 0,25; -0,125; 0,0625 .
что верно только для |q| < 1
Калькулятор геометрической прогрессии
Задачи с геометрической прогрессией
Задача 1) Является ли последовательность 2, 4, 6, 8… геометрической прогрессией?
Решение: Нет. (2, 4, 8 есть геометрической прогрессией )Задача 2) Если есть геометрическая прогрессия 2, 4, 8… Чему равен ее 10-й член?
Решение: Мы можем использовать формулу an = a1 . qn-1
a10 = 2 . 210-1 = 2 . 512 = 10243) Найдите первый член и знаменатель геометрической прогресии, если
a5 — a1 = 15
a4 — a2 = 6
Решение: Здесь две геометрические прогрессии; одна из с первым членом = 1 знаменателем = 2
и вторая прогрессия с первым членом = -16 и знаменателем = 1/2 ,Геометрические прогрессии в темах нашего математического форума
Для участия в математическом форуме регистрация не требуется!
Форум о прогрессияхГеометрическая прогрессия на примерах
Геометрическая прогрессия не менее важная в математике по сравнению с арифметической.
 Геометрической прогрессией называют такую последовательность чисел b1, b2,…, b[n] каждый следующий член которой, получается умножением предыдущего на постоянное число. Это число, которое также характеризует скорость роста или убывания прогрессии называют знаменателем геометрической прогрессии и обозначают
Геометрической прогрессией называют такую последовательность чисел b1, b2,…, b[n] каждый следующий член которой, получается умножением предыдущего на постоянное число. Это число, которое также характеризует скорость роста или убывания прогрессии называют знаменателем геометрической прогрессии и обозначаютДля полного задания геометрической прогрессии кроме знаменателя необходимо знать или определить первый ее член. Для положительного значения знаменателя прогрессия является монотонной последовательностью, причем если это последовательность чисел является монотонно убывающей и при монотонно возрастающей. Случай, когда знаменатель равен единице на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса
Общий член геометрической прогрессии вычисляют по формуле
Сумма n первых членов геометрической прогрессии определяют по формуле
Рассмотрим решения классических задач на геометрическую прогрессию.
 Начнем для понимания с простейших.
Начнем для понимания с простейших.Пример 1. Первый член геометрической прогрессии равен 27, а ее знаменатель равен 1/3. Найти шесть первых членов геометрической прогрессии.
Решение: Запишем условие задачи в виде
Для вычислений используем формулу n-го члена геометрической прогрессии
На ее основе находим неизвестные члены прогрессии
Как можно убедиться, вычисления членов геометрической прогрессии несложные. Сама прогрессия будет выглядеть следующим образом
Пример 2. Даны три первых члена геометрической прогрессии : 6; -12; 24. Найти знаменатель и седьмой ее член.
Решение: Вычисляем знаменатель геомитрической прогрессии исходя из его определения
Получили знакопеременную геометрическую прогрессию знаменатель которой равен -2. Седьмой член вычисляем по формуле
На этом задача решена.
Пример 3. Геометрическая прогрессия задана двумя ее членами .
 Найти десятый член прогрессии.
Найти десятый член прогрессии.Решение:
Запишем заданные значения через формулы
По правилам нужно было бы найти знаменатель, а затем искать нужное значение, но для десятого члена имеем
Такую же формулу можно получить на основе нехитрых манипуляций с входными данными. Разделим шестой член ряда на другой, в результате получим
Если полученное значение умножить на шестой член, получим десятый
Таким образом, для подобных задач с помощью несложных преобразований в быстрый способ можно отыскать правильное решение.
Пример 4. Геометрическая прогрессия задано рекуррентными формулами
Найти знаменатель геометрической прогрессии и сумму первых шести членов.
Решение:
Запишем заданные данные в виде системы уравнений
Выразим знаменатель разделив второе уравнение на первое
Найдем первый член прогрессии из первого уравнения
Вычислим следующие пять членов для нахождения суммы геометрической прогрессии
Поскольку найти сумму в данном случае не составляет большого труда, то обходя простые выкладки сводим все слагаемые под общий знаменатель
В общем случае, при нахождении суммы знакопеременных рядов следует выделять их положительную часть и отрицательную и найти отдельно их суммы по приведенным выше формулам.
 Наконец найденные значения добавить.
Наконец найденные значения добавить.Примеры на геометрическую прогрессию не так сложны если знать несколько базовых формул. Все остальное сводится к простым математическим манипуляциям. Практикуйте с примерами самостоятельно и подобные задания будут для Вас несложными.
Похожие материалы:
- Арифметическая прогрессия. Формула суммы
- Простые примеры на прогресию
- Арифметическая и геометрическая прогрессии. Простые примеры
- Арифметическая и геометрическая прогрессии. Средний уровень сложности
- Арифметическая и геометрическая прогрессии. Сложные примеры
Геометрические ряды (последовательность), ряды и последовательности, чистая математика
Главная >> PURE MATHS, последовательности и ряды, геометрические ряды
Структура
Доказательство суммы геометрического ряда
Среднее геометрическое
Сумма до бесконечности
Геометрический ряд — структура
Геометрический ряд начинается с первого члена, обычно обозначаемого буквой « a ».

Для каждого последующего члена ряда первый член умножается на другой член.
Термин кратен букве « r », называемой «общее отношение ».
Итак, ряд имеет структуру:
, где S n — сумма слагаемых « n », буква « l » — последняя слагаемая.
Обычное отношение « r » рассчитывается путем деления любого термина на предшествующий ему термин.
n-й член (иногда называемый ‘ общий термин ‘) определяется по:
вернуться к началу
Доказательство суммы геометрического ряда
NB альтернативная формула для r > 1 , просто умножьте числитель и знаменатель на -1
Пример №1
В геометрической прогрессии сумма 3-го и 4-го членов равна 60, а сумма 4-го и 5-го членов равна 120.

Найдите 1-й член и знаменатель.
вернуться к началу
Пример №2
Какое наименьшее количество членов геометрической прогрессии:
2 + 6 + 18 + 54 + 162 …
, что даст в сумме больше 1000?
Среднее геометрическое
Это метод нахождения термина, находящегося между двумя другими терминами.
Итак, если у нас есть последовательность термов: a , b , c , где a и c известны,
отношение последовательных членов дает обыкновенное отношение .

Приравнивание этих :
Пример
Если 4-й член геометрической прогрессии равен 40, а 6-й равен 160, чему равен 5-й член?
вернуться к началу
Сумма до бесконечности
Это касается геометрических прогрессий, в которых по мере увеличения числа членов значение суммы приближается к одному определенному числу. Это число называется сумма до бесконечности .
В этом примере по мере увеличения ‘ n ‘ сумма приближается к 2 .
Значит, если член r n стремится к нулю, то с увеличением n уравнение для суммы n членов меняется:
Пример
Экспресс 0,055555.
 .. в виде дроби.
.. в виде дроби.вернуться к началу
Самый быстрый словарь в мире | Vocabulary.com
ПЕРЕЙТИ К СОДЕРЖАНИЮ
геометрическая прогрессия (математика) прогрессия, в которой каждый член умножается на константу, чтобы получить следующий член
арифметическая прогрессия (математика) прогрессия, в которой к каждому члену добавляется константа для получения следующего члена
гармоническая прогрессия (математика) последовательность членов, обратные величины которых образуют арифметическую прогрессию
8″>
геометрическая правильность свойство многоугольников: свойство иметь равные стороны и равные углы
геометрическая неправильность неправильная асимметрия формы
правонарушение нарушение закона, долга или морального принципа
геометрический ряд геометрическая прогрессия, записанная в виде суммы
геометрический шаг современная версия римского шага, который теперь принимается равным 5 футам
Future Progressive Длительное время, используемое для выражения действия, которое будет происходить в будущем
21″>возврат к прежнему состоянию
регрессневротическая депрессия термин, используемый для обозначения любого состояния депрессии, не являющегося психотическим
прогрессия действие движения вперед как к цели
-
барометрическое давление атмосферное давление по показаниям барометра
медроксипрогестерон прогестиновое соединение, используемое для лечения нарушений менструального цикла
статистическая регрессия отношение между выбранными значениями x и наблюдаемыми значениями y (на основании которых можно предсказать наиболее вероятное значение y для любого значения x)
прямолинейная регрессия отношение между переменными, когда уравнение регрессии является линейным: например, y = ax + b
незавершенная работа часть работы, которая еще не закончена


 Геометрической прогрессией называют такую последовательность чисел b1, b2,…, b[n] каждый следующий член которой, получается умножением предыдущего на постоянное число. Это число, которое также характеризует скорость роста или убывания прогрессии называют знаменателем геометрической прогрессии и обозначают
Геометрической прогрессией называют такую последовательность чисел b1, b2,…, b[n] каждый следующий член которой, получается умножением предыдущего на постоянное число. Это число, которое также характеризует скорость роста или убывания прогрессии называют знаменателем геометрической прогрессии и обозначают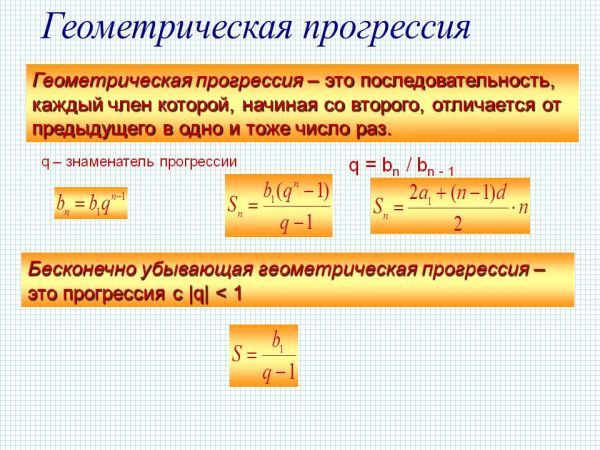 Начнем для понимания с простейших.
Начнем для понимания с простейших. Найти десятый член прогрессии.
Найти десятый член прогрессии. Наконец найденные значения добавить.
Наконец найденные значения добавить.


