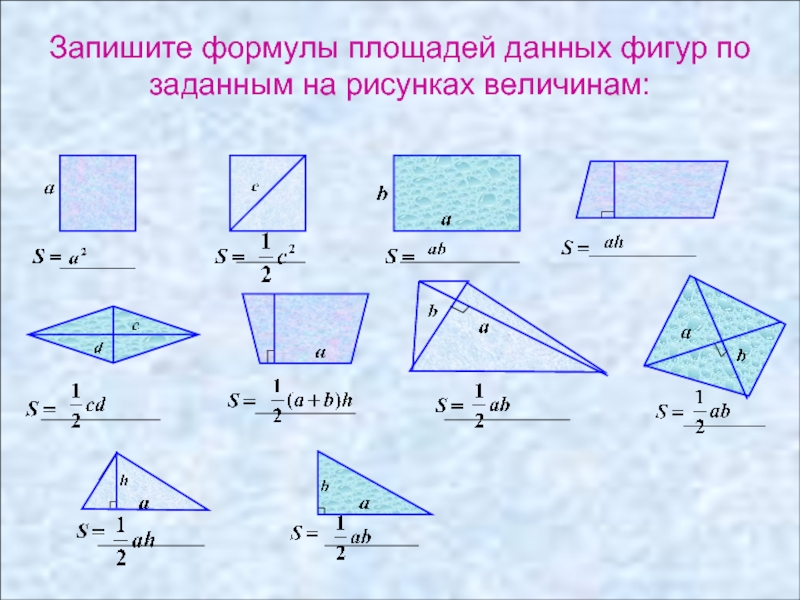
Шпаргалка: площадь многоугольников для геометрии 8 класса, формулы нахождения площади треугольника, квадрата, ромба, параллелограмма
31 августа, 2022
1 мин
Треугольник
- Площадь треугольника по основанию и высоте: S=1/2 a⋅h
- Площадь треугольника по двум сторонам и углу между ними: S=1/ a⋅b⋅sinα
- Площадь треугольника по радиусу описанной окружности и трём сторонам: S = 4R/a⋅b⋅c
- Площадь треугольника по формуле Герона: S = √p(p — a)(p — b)(p — c). Где p — полупериметр, a,b,c — стороны треугольника.
- Площадь равностороннего треугольника по стороне: S = √3/4a²
- Площадь прямоугольного треугольника по двум катетам: S= ½ a • b
- Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность: S = d • e. Где d и e — отрезки гипотенузы.
Параллелограмм
- Площадь параллелограмма по основанию и высоте: S = a • h
- Площадь параллелограмма по двум сторонам и углу между ними: S = a⋅b⋅sinα
Ромб (он же параллелограмм, у которого все стороны равны и в который можно вписать окружность)
- Площадь ромба по вписанной окружности и стороне: S = 2 • a • r
Прямоугольник и квадрат
- Площадь прямоугольника через две стороны: S = a • b
- Площадь квадрата: S = a²
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Мы обязательно поправим!
01 июля, 2022
1 мин
Лит 📚
А.Т. ТвардовскийПродолжим военную тему творчеством Твардовского. Мы разобрали для тебя его стихотворения из…
Редакция Без Сменки06 июня, 2022
1 мин
Общ 👨👩👧
Социальное обеспечениеЭто право означает обязательное участие государства в содержании тех граждан, которые из-за…
Редакция Без Сменки07 июня, 2022
1 мин
Англ 🇬🇧
Условные предложения. Третий тип
Третий тип❗️ Условные предложения третьего типа выражают НЕреальные ситуации в ПРОШЛОМ. То есть юзаешь их,…
Основные правила математики. Геометрия. Теоремы, определения. 8 класс
Основные правила математики. Геометрия. Теоремы, определения. 8 класс | Сайт учителя математики Косыхиной Н.В.-
Репетитор по математике
- /whatsapp +7(908)682-97-49
Основные правила математики. Геометрия. Теоремы, определения. 8 класс
Многоугольник
- Многоугольник — геометрическая фигура, обычно определяется как замкнутая ломаная
- Выпуклый многоугольник— многоугольник, который лежит по одну сторону от прямой, которая проходит через 2 его смежные вершины
- Диагональ многоугольника — отрезок, соединяющие 2 несоседние вершины
- Формула суммы углов -угольника
, — число вершин(сторон)
Параллелограмм
- Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны
Свойства параллелограмма
- В параллелограмме противоположные стороны равны и противоположные углы равны
- В параллелограмме противоположные стороны равны и противоположные углы равны
- Диагонали параллелограмма точкой пересечения делятся пополам
Признаки параллелограмма
- Если в четырехугольнике 2 стороны равны и параллельны, то этот четырехугольник параллелограмм
- Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник параллелограмм
- Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм
Трапеция
- Трапеция — четырехугольник, у которого две стороны параллельны, а две другие стороны — не параллельны
- Параллельные стороны трапеции называются основаниями трапеции
- Не параллельные стороны называются боковыми сторонами
- Трапеция равнобедренная, если её боковые стороны равны
- Трапеция прямоугольная, у которой одна боковая сторона, перпендикулярна основаниям
Прямоугольник
- Прямоугольник — параллелограмм, у которого все углы прямые
Свойства прямоугольника
- Диагонали прямоугольника равны
Признаки прямоугольника
- Если в параллелограмме диагонали равны, то этот параллелограмм прямоугольник
- Если в параллелограмме есть хотя бы 1 прямой угол, то этот параллелограмм прямоугольник
Ромб
- Ромб — параллелограмм у которого все стороны равны
Свойства ромба
- Диагонали ромба взаимно перпендикулярны, точкой пересечения делятся пополам, являются биссектрисами углов
Признаки ромба
- Параллелограмм, диагонали которого взаимно перпендикулярны.

- Параллелограмм, диагональ которого является биссектрисой его угла
Квадрат
- Квадрат прямоугольник, у которого все стороны равны
Свойства квадрата
- Все углы квадрата прямые
- Диагонали квадрата равны, взаимно-перпендикулярны, точкой пересечения делятся пополам, являются биссектрисами углов
Симметрия
- Две точки называются симметричными относительно прямой, если эта прямая проходит через середину отрезка и перпендикулярна к нему
- Фигура называется симметричной относительно прямой , если для каждой точки фигуры симметрична ей точка относительно прямой также принадлежит этой фигуре. Прямая называется осью симметрии фигуры
- Две точки называются симметричными относительно точки О, если О середина отрезка
- Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
 Точка О называется центром симметрии фигуры.
Точка О называется центром симметрии фигуры.
Площади
- Высота треугольника -перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону треугольника(основание)
- Высота параллелограмма -перпендикуляр, проведенный из любой точки противоположной стороны к прямой, содержащей основание
- Равные многоугольники имеют равные площади
- Высота трапеции — перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников
- Площадь квадрата равна квадрату его стороны
- Площадь прямоугольника равна произведению его смежных сторон
- Площадь треугольника равна половине произведения его основания на высоту
- Площадь прямоугольного треугольника равна половине произведения его катетов
- Если высоты двух треугольников равны, то их площади относятся как основания
- Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы
- Площадь трапеции равна произведению полусуммы ее основания на высоту
Прямоугольный треугольник
- Теорема Пифагора:в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
- Теорема, обратная теореме Пифагора: если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный
- Пифагоровы тройки: треугольники со сторонами 3,4,5; 6,8,10 и т.
 д
д - Высота прямоугольного треугольника, проведенная из вершины прямого угла есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой
- Катет прямоугольного треугольника есть среднее пропорциональное для гипотенуз и отрезка гипотенузы, заключенного между катетом и высотой проведенной из вершины прямого угла
Подобие
- Подобные треугольники -это треугольники, у которых углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
- Коэффициент подобия — это число , равное отношению сходственных сторон подобных треугольников
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия
Признаки подобия треугольников
- Первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны
- Второй признак подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы заключенные между этими сторонами равны, то такие треугольники подобны
- Третий признак подобия треугольников:если три стороны одного треугольника пропорциональным трем сторонам другого треугольника, то такие треугольники подобны
Средняя линия треугольника.

- Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
Некоторые свойства геометрических фигур
- Параллельные прямые, пересекающие стороны угла, образуют с его сторонами подобные между собой треугольники
- Теорема Фалеса Параллельные прямые, пересекающие стороны угла отсекают на них равные отрезки
- Пропорциональные отрезки Параллельные прямые, пересекающие стороны угла, отсекают от его сторон пропорциональные отрезки
Окружность
- Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
- Центральный угол — это угол, вершина которого лежит в центре окружности.
- Центральный угол равен градусной мере дуги, на которую он опирается.
- Вписанный угол — это угол, вершина которого лежит на окружности.

- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу
- Формула длины окружности
- Формула площади круга
- Описанный четырехугольник — четырехугольник, каждая сторона которого касается данной окружности. Окружность называют вписанной. Центр окружности, вписанной в четырехугольник,— точка пересечения биссектрис всех его углов.
- Свойство четырехугольника, описанного около окружности : Если четырехугольник описан около окружности, то сумма двух его противолежащих сторон равна сумме двух других его сторон.
- Признак четырехугольника, в который можно вписать окружность: Если у четырехугольника сумма двух его противолежащих сторон равна сумме двух других его сторон, то в него можно вписать окружность.
- Признак принадлежности четырех точек одной окружности: Если одна сторона выпуклого четырёхугольника видна из двух его вершин под равными углами, то около этого четырёхугольник можно описать окружность.

Окружность и треугольник
Описанный четырехугольник
2018-2023
Геометрические формулы для 8-го класса – Learn Cram
Эти формулы помогут учащимся быстро учиться и обеспечат легкий доступ к информации, когда это необходимо.
- (а + б) 2 = а 2 + 2аб + б 2
- (а – б) 2 = а 2 – 2аб + б 2
- (а + б) (a – b) = a 2 – b 2
- (x + a) (x + b) = x 2 + (a + b)x + ab
- (x + a) (x – b) = x 2 + (a – b)x – ab
- (x – a) (x + b) = x 2 + (b – a)x – ab
- (x – a) (x – b) = x 2 – (a + b)x + ab
- (a + b)3 = a 3 + b 3 + 3ab(a + b)
- (a – b)3 = a 3 – b 3 – 3ab(a – b)
Глава 10.
 Визуализация твердого тела Формы
Визуализация твердого тела Формы Объемная геометрия жизненно важна в повседневной жизни, поскольку помогает нам понять множество форм, с которыми мы сталкиваемся, и их свойства. Всестороннее понимание визуализации твердотельных объектов может помочь учащимся освоить более сложные принципы геометрии и решать реальные ситуации. В результате очень важно понимать многочисленные формулы, связанные с различными твердыми телами, которые помогут в повседневных вычислениях.
Давайте узнаем о некоторых важных понятиях и формулах, используемых в этой главе.
- Твердые тела определяются их формой и тем фактом, что они занимают место. Грани твердого тела представляют собой многоугольные сечения, из которых состоит твердое тело.
- Многогранник: Многогранник — это твердотельный объект, окаймленный многоугольниками (платоническое тело).
- Формула Эйлера: Многогранник имеет определенное количество плоских граней, ребер и вершин, удовлетворяющих формуле:
F + V – E = 2
, где F – количество граней.
Буквы V и E обозначают количество вершин и ребер соответственно.
- Призма: Призма является сплошной с параллелограммными боковыми гранями и конгруэнтными параллельными концами многоугольника (или основаниями). Две треугольные грани, три прямоугольные грани, шесть вершин и девять ребер составляют призму.
- Пирамида: Пирамида – это многогранник, основанием которого является многоугольник с любым числом сторон и дополнительными гранями, представляющими собой треугольники с одной вершиной. Одна квадратная грань, четыре треугольных грани, пять вершин и восемь ребер составляют пирамиду.
- Тетраэдр: Если основание пирамиды представляет собой треугольник, она называется треугольной пирамидой. Тетраэдр — другое название треугольной пирамиды.
- Размеры тела: Твердое тело имеет три измерения (измерения) – длину, ширину и высоту. Плоские формы имеют два измерения (измерения): длину и ширину (или глубину).
В результате они называются двумерными и трехмерными формами соответственно. Их называют двумерными и трехмерными фигурами соответственно. Треугольники, прямоугольники и круги являются двухмерными формами, тогда как кубы, цилиндры, конусы и сферы являются трехмерными фигурами. Под разными углами трехмерные объекты кажутся разными. В результате они могут быть нарисованы под разными углами, такими как вид сверху, вид спереди и вид сбоку.
- Картирование : Карта — это не то же самое, что фотография. Карта показывает, где находится одна вещь или место по отношению к другим объектам или местам. Символы используются для обозначения различных предметов и мест. На карте нет привязки или перспективы. С другой стороны, перспектива имеет решающее значение при создании изображения. Кроме того, карты имеют масштаб, который устанавливается для каждой карты.
- Грани, вершины и ребра: Грани — это многоугольные сечения, составляющие многогранник.
Ребра — это отрезки, соединяющие грани многогранника. Вершины многогранника — это точки пересечения ребер. В вершине многогранника сходятся три и более ребра.
Глава 11: Измерение
Формулы для измерения класса 8, глава 11, перечислены здесь. Здесь вы найдете ресурсы для измерения, основанные на программе CBSE (2021-2022) и самом последнем образце экзамена. Работайте с формулами и примерами, чтобы лучше понять идею измерения. Измерение — это процесс вычисления площади и периметра различных геометрических форм, таких как треугольники, трапеции, прямоугольники и т. д.
- Периметр: Длина контура любой простой замкнутой фигуры называется периметром.
- Периметр прямоугольника = 2 × (l + b) единиц.
- Периметр квадрата = 4 × сторона.
- Периметром круга называется его окружность. Следовательно, длина окружности равна 2 π r.
- Периметр параллелограмма = 2 (основание + высота)
- Периметр треугольника = a + b + c (где a, b и c — длины сторон)
- Периметр трапеции = a + b + c + d (где a, b, c, d — стороны трапеции) (где a — длина первой пары b — длина второй пары)
- Периметр ромба = 4 × сторона
- Периметр шестиугольника = 6 × сторона
- Площадь криволинейной поверхности конуса = 1/2 × l × 2πr = πrl , где «r» — радиус основания, а «l» — наклонная высота.
‘l’ = √(r 2 + H 2 )
- Объем кубоида = базовая площадь × высота = длина × ширина × высота
- Объем конуса = (1 /3) πr 2 H
- Объем счета = = (4/3) π r 3
- Объем полушария = (2/3) πr 3
Глава 12. Показатели и степени
Показатель степени представляет значение, которое относится к числу раз число умножается само на себя. Например, 5 × 5 × 5 можно записать как 5 3 . Даже очень маленькие числа могут быть выражены в виде отрицательных показателей. Вот список некоторых законов, относящихся к экспонентам:
- Закон произведения: a m × a n = a m + n
- Закон частного: a m 90 053/а n = am – n
- Закон нулевого показателя степени: a 0 = 1
- Закон отрицательного показателя степени: a -m = 1/a m
- Закон мощности степени : (а м )n = a mn
- Закон мощности произведения: (ab) n = a m b m
- Закон мощности частного: (a/b) m = a m /b m
Глава 13.
 Прямые и обратные пропорции
Прямые и обратные пропорцииЧтобы показать, как количества и количества связаны друг с другом, используется прямая и обратная пропорция. Прямо пропорциональные и обратно пропорциональные — это другие термины, используемые для их описания.
- Пропорции: Пропорциональность представлена символом ∝. Например, если мы утверждаем, что p пропорционально q, это подразумевает p ∝ q , а если мы говорим, что p обратно пропорционально q, то это подразумевает «p∝1/q». Эти отношения регулируются некоторыми правилами пропорциональности. Теперь значение «p» изменяется с точки зрения «q» в обоих случаях, или когда значение «q» изменяется, значение «p» также изменяется. Константа пропорциональности равна изменению обоих значений. По сути, пропорция указывает на то, что два отношения, такие как p/q и r/s, эквивалентны, то есть p/q = r/s.
- Прямая пропорция или вариация: Можно сказать, что любые две величины a и b находятся в прямой зависимости, если они изменяются (увеличиваются или уменьшаются) друг с другом таким образом, что отношение их соответствующих значений остается неизменным.
Отсюда следует, что если a/b = k, где k — любое положительное число, то говорят, что a и b прямо пропорциональны. например Если количество купленных вещей увеличивается, то увеличивается и общая стоимость покупки.
- Величины, которые увеличиваются или уменьшаются параллельно, не обязательно должны быть прямо пропорциональны, а обратная пропорция не всегда должна быть прямо пропорциональна.
- Обратная пропорция: Говорят, что две величины x и y находятся в обратной пропорции, если увеличение x вызывает пропорциональное уменьшение y (и наоборот ) таким образом, что произведение их соответствующих значений остается постоянный. То есть, если xy = k, то говорят, что x и y изменяются обратно пропорционально. например Если количество людей увеличивается, время, затрачиваемое на приготовление еды, уменьшается. Или если скорость увеличится, время, необходимое для преодоления заданного расстояния, уменьшится.
Глава 14: Факторизация
Факторизация — это один из наиболее распространенных способов приведения алгебраического или квадратного уравнения к его простейшей форме.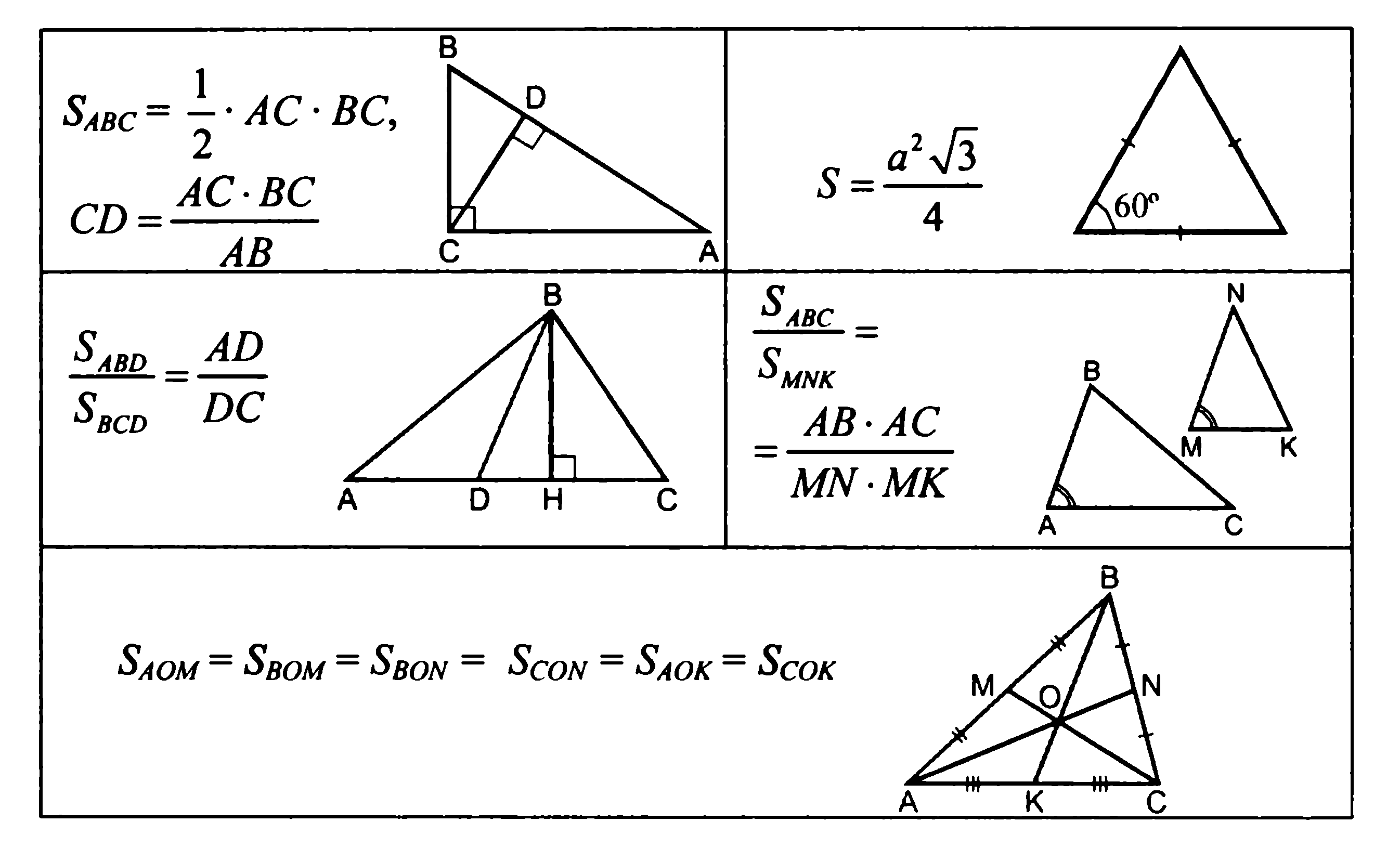 В результате нужно быть знакомым с формулами факторизации, чтобы разложить сложное уравнение. Ниже приведен список различных формул и свойств, полезных для решения задач полиномов, тригонометрии, алгебры и квадратных уравнений.
В результате нужно быть знакомым с формулами факторизации, чтобы разложить сложное уравнение. Ниже приведен список различных формул и свойств, полезных для решения задач полиномов, тригонометрии, алгебры и квадратных уравнений.
- Факторизация : Факторизация — это процесс выражения алгебраического уравнения в виде произведения его компонентов. В качестве коэффициентов можно использовать числа, переменные или алгебраические выражения.
- Несократимый множитель: Компонент, который нельзя далее сформулировать как произведение сомножителей, называется неприводимым.
- Метод факторизации: Метод общего фактора представляет собой метод методического разложения уравнения на множители. Есть три шага, чтобы решить эту проблему:
- Каждый член утверждения должен быть записан как произведение неприводимых элементов.
- Найдите и разделите похожие компоненты.
- В каждом члене соедините оставшиеся элементы в соответствии с распределительным законом.
- Все термины в данном выражении могут иногда не иметь общего множителя, но термины могут быть сгруппированы так, чтобы все термины в каждой группе имели общий делитель. Когда мы это делаем, для всех групп появляется общий множитель, что приводит к необходимой факторизации выражения. Это метод перегруппировки.
- При факторинге путем перегруппировки имейте в виду, что любая перегруппировка (т. е. перестановка) членов в предоставленном уравнении может привести или не привести к факторизации. Мы должны соблюдать язык и использовать метод проб и ошибок, чтобы прийти к желаемой перегруппировке.
- Ряд факторизуемых выражений имеет вид или может быть разложен на множители в виде: – б 2 и x 2 + (a + b)x + ab . Эти выражения можно легко разложить на множители, используя приведенные ниже тождества: – 2аб + б 2 = (a – b) 2
- a 2 – b 2 = (a + b) (a – b)
- x 2 90 053 + (а + б)х + аб = (x + a)(x + b)
Помните, что числовой член дает ab в формулировках с факторами типа (х + а) (х + б) . Его коэффициенты а и b следует выбирать так, чтобы их сумма с учетом знаков равнялась коэффициенту х.
При делении многочлена на одночлен мы можем разделить многочлен либо путем деления каждого члена на одночлен, либо с помощью метода общего множителя. Мы не можем разделить каждый член многочлена делимого на многочлен делителя при делении многочлена на другой многочлен. Вместо этого оба полинома факторизуются, а их общие делители сокращаются. У нас есть подразделения алгебраических выражений в случае подразделений алгебраических выражений, которые мы обсуждали в этой главе. Делимое = делитель × частное
или
Делимое = делитель × частное + остаток
Глава 15. Введение в графики
Использование графических инструментов для отображения данных особенно эффективно при организации и понимании информация. Ниже приведены некоторые примеры графических методов:
- При сравнении категорий гистограмма является наиболее подходящим инструментом.
- Круговые диаграммы — лучший способ сравнить части целого.
- Гистограмму можно использовать для упрощения интерпретации данных, когда они представлены с интервалами.
- Линейный график удобен в ситуации, когда данные постоянно меняются с течением времени.
- Координата x и координата y необходимы для фиксации точки на листе графика.
- График изображает отношение между зависимой переменной и независимой переменной.
Глава 16. Игра с числами
Говорят, что число имеет общую форму, если оно может быть представлено как сумма произведений его цифр и связанных с ними разрядных значений. Числа можно записывать разными способами. В результате ab = 10a +b будет выражаться двузначным числом. При решении головоломок или игре с числами полезна общая форма чисел. Когда числа изложены в общей форме, могут быть указаны причины, по которым они делятся на 10, 5, 2, 9 или 3.
Правила кратности:
- Признак делимости на 2: число делится на 2, если его единица равна 0, 2, 4, 6 или 8.



 д
д

 Буквы V и E обозначают количество вершин и ребер соответственно.
Буквы V и E обозначают количество вершин и ребер соответственно. В результате они называются двумерными и трехмерными формами соответственно. Их называют двумерными и трехмерными фигурами соответственно. Треугольники, прямоугольники и круги являются двухмерными формами, тогда как кубы, цилиндры, конусы и сферы являются трехмерными фигурами. Под разными углами трехмерные объекты кажутся разными. В результате они могут быть нарисованы под разными углами, такими как вид сверху, вид спереди и вид сбоку.
В результате они называются двумерными и трехмерными формами соответственно. Их называют двумерными и трехмерными фигурами соответственно. Треугольники, прямоугольники и круги являются двухмерными формами, тогда как кубы, цилиндры, конусы и сферы являются трехмерными фигурами. Под разными углами трехмерные объекты кажутся разными. В результате они могут быть нарисованы под разными углами, такими как вид сверху, вид спереди и вид сбоку. Ребра — это отрезки, соединяющие грани многогранника. Вершины многогранника — это точки пересечения ребер. В вершине многогранника сходятся три и более ребра.
Ребра — это отрезки, соединяющие грани многогранника. Вершины многогранника — это точки пересечения ребер. В вершине многогранника сходятся три и более ребра.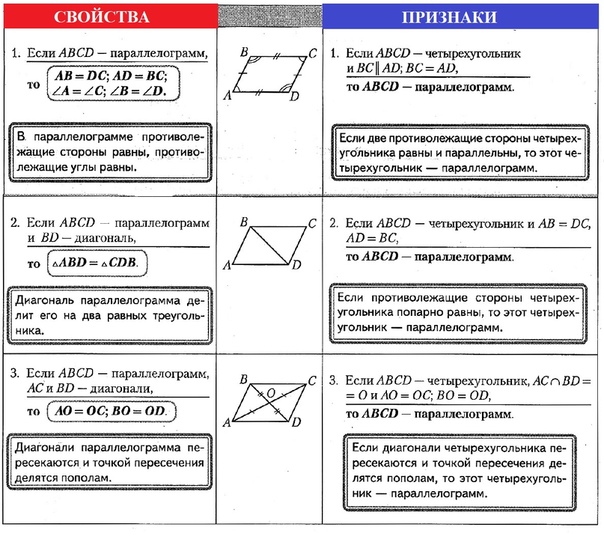 ‘l’ = √(r 2 + H 2 )
‘l’ = √(r 2 + H 2 ) Отсюда следует, что если a/b = k, где k — любое положительное число, то говорят, что a и b прямо пропорциональны. например Если количество купленных вещей увеличивается, то увеличивается и общая стоимость покупки.
Отсюда следует, что если a/b = k, где k — любое положительное число, то говорят, что a и b прямо пропорциональны. например Если количество купленных вещей увеличивается, то увеличивается и общая стоимость покупки.
 Его коэффициенты а и b следует выбирать так, чтобы их сумма с учетом знаков равнялась коэффициенту х.
Его коэффициенты а и b следует выбирать так, чтобы их сумма с учетом знаков равнялась коэффициенту х.