|
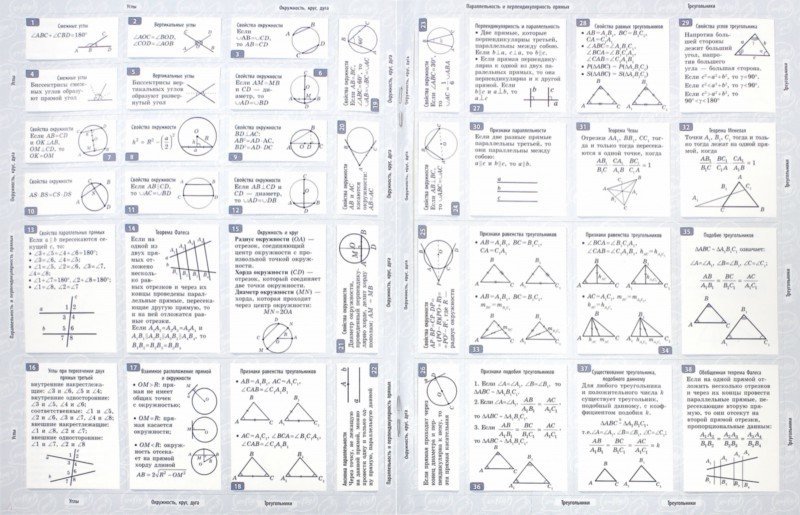
1.Признаки параллельности прямых.
|
|||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||||||
Признаки параллельности прямых |
|||||||||||||||||||||||||||
Признаки равенства треугольников |
|||||||||||||||||||||||||||
Теорема Пифагора |
|||||||||||||||||||||||||||
Рассчитать стороны прямоугольного треугольникаКатет a Катет b Гипотенуза c =
|
|||||||||||||||||||||||||||
| Гипотенуза c Катет a Катет b = | |||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
Радиус вписанной и описанной окружностей правильных многоугольников |
|||||||||||||||||||||||||||
Рассчитать радиус вписанной и описанной окружностейСторона a Число углов n Радиус R = Радиус r = |
|||||||||||||||||||||||||||
Теорема синусов |
|||||||||||||||||||||||||||
Рассчитать сторону треугольникаСторона а sin (α= °) sin (β= °) Сторона b =Рассчитать угол треугольникаСторона а sin (α= °) Сторона b Угол β = °
|
|||||||||||||||||||||||||||
Теорема косинусов |
|||||||||||||||||||||||||||
Рассчитать сторону треугольникаСторона b Сторона с cos (α= °) Сторона a =Рассчитать угол треугольникаСторона а Сторона b Сторона c Угол α = ° |
|||||||||||||||||||||||||||
Радиус вписанной и описанной окружностей |
|||||||||||||||||||||||||||
|
Рассчитать радиус описанной и вписанной окружности Сторона а Сторона b Сторона c
Площадь S = Радиус R = Радиус r = |
|||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||||||
Геометрия: уроки, тесты, задания.

- Предметы
-
-
Прямая, отрезок, точки
-
Луч, угол, обозначение угла
-
Сравнение отрезков и углов.
 Биссектриса
Биссектриса
-
Измерение отрезков и углов
-
Перпендикулярные прямые. Смежные и вертикальные углы
-
-
-
-
Медиана, биссектриса, высота треугольника
-
Второй и третий признаки равенства треугольников
-
Окружность.
 Радиус. Задачи на построение
Радиус. Задачи на построение
-
-
-
Признаки параллельности двух прямых. Свойства параллельных прямых. Аксиома параллельных прямых
-
-
-
Сумма углов треугольника. Виды треугольников
-
Теорема о соотношениях между сторонами и углами треугольника
-
Прямоугольный треугольник.
 Свойства. Признаки равенства
Свойства. Признаки равенства
-
Расстояние от точки до прямой. Построение треугольника по трём элементам
-
-
-
Ломаная. Виды ломаных. Многоугольники
-
Параллелограмм.
 Свойства параллелограмма. Трапеция
Свойства параллелограмма. Трапеция
-
Прямоугольник, квадрат. Признаки прямоугольника и квадрата. Ромб
-
-
-
Площадь многоугольника. Свойства площадей
-
Формулы площадей параллелограмма, треугольника и трапеции
-
Теорема Пифагора.
 Доказательство
Доказательство
-
-
-
Подобные треугольники. Пропорциональные отрезки
-
Признаки подобия треугольников
-
Применение подобия. Решение задач
-
Тригонометрические функции острого угла прямоугольного треугольника
-
-
-
Касательная и окружность
-
Центральные и вписанные углы.
 Свойство пересекающихся хорд окружности
Свойство пересекающихся хорд окружности
-
Замечательные точки треугольника
-
Вписанная и описанная окружности
-
-
-
Решай и получай ТОП-баллы!
-
-
-
Понятие вектора.
 Виды векторов
Виды векторов
-
Правила сложения и вычитания векторов
-
Умножение векторов на число
-
Проекция вектора на ось
-
-
-
Вектор в системе координат
-
Решение простейших задач в координатах
-
Уравнение окружности.
 Уравнение прямой
Уравнение прямой
-
-
-
Синус, косинус, тангенс угла
-
Соотношения между сторонами и углами треугольника
-
Скалярное произведение векторов. Свойства
-
-
-
Правильные многоугольники
-
Длина окружности.
 Площадь круга
Площадь круга
-
-
-
Понятие движения. Симметрия
-
Параллельный перенос и поворот
-
-
-
Многогранники. Основные формулы для расчётов
-
Цилиндр.
 Конус. Сфера
Конус. Сфера
-
-
-
Аксиомы стереометрии и их простейшие следствия
-
-
-
Определение и свойства параллельности прямых, прямой и плоскости
-
Определение и свойства скрещивающихся прямых.
 Угол между прямыми
Угол между прямыми
-
Определение, признак и свойства параллельности плоскостей
-
Элементы тетраэдра и параллелепипеда
-
-
-
Определение и свойства перпендикулярности прямой и плоскости
-
Определение перпендикуляра, наклонной.
 Теорема о трёх перпендикулярах
Теорема о трёх перпендикулярах
-
Понятие двугранного угла. Признак перпендикулярности плоскостей
-
-
-
Понятие многогранника. Призма
-
Элементы пирамиды. Виды пирамид
-
Определение и свойства правильных многогранников
-
-
-
Определение и физический смысл вектора в пространстве
-
Как складывать векторы и умножать вектор на число
-
Разложение вектора.
 Понятие компланарности
Понятие компланарности
-
-
-
Абсцисса, ордината и аппликата точки. Простейшие задачи в координатах
-
Угол между векторами. Скалярное произведение
-
Отображения пространства на себя.
 Виды движения
Виды движения
-
-
-
Элементы цилиндра. Площадь поверхности
-
Элементы конуса. Площадь поверхности
-
Элементы сферы и шара. Уравнение сферы. Сечение шара плоскостью
-
-
-
Как найти объём прямоугольного параллелепипеда
-
Как найти объём прямой призмы, цилиндра
-
Как найти объём наклонной призмы, пирамиды, конуса
-
Как найти объём шара
-
-
Коллекция интерактивных моделей
Подготовка к ЕГЭ и ОГЭ (справочник по математике для школьников — Геометрия
Подготовка к ЕГЭ и ОГЭ (справочник по математике для школьников — Геометрия — Планиметрия)Поиск по сайту:
К.
 Л. САМАРОВ, С.С.САМАРОВА
Л. САМАРОВ, С.С.САМАРОВАСправочник по математике для школьников
Тематическое содержание
Основные фигуры планиметрии | ||
| Фигуры, составляющие основу планиметрии | ||
Углы | ||
| Углы на плоскости | ||
| Теорема Фалеса | ||
| Углы, связанные с окружностью | ||
| Вписанные и центральные углы | ||
| Углы, образованные хордами, касательными и секущими | ||
| Доказательства теорем об углах, связанных с окружностью | ||
Параллельность прямых | ||
| Признаки параллельности прямых | ||
Треугольники | ||
Типы треугольников.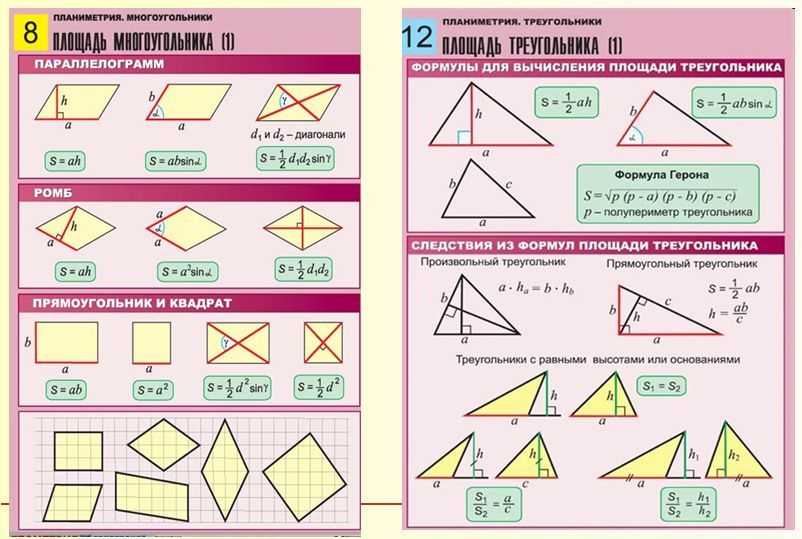 Признаки равенства треугольников Признаки равенства треугольников | ||
| Типы треугольников | ||
| Признаки равенства треугольников | ||
| Признаки равенства прямоугольных треугольников | ||
| Свойства и признаки равнобедренного треугольника | ||
| Свойства прямоугольного треугольника | ||
| Свойства сторон и углов треугольника | ||
| Подобные треугольники. Признаки подобия треугольников | ||
| Подобные треугольники | ||
| Признаки подобия треугольников | ||
| Признаки подобия прямоугольных треугольников | ||
| Теорема Пифагора. Теорема косинусов | ||
| Теорема Пифагора | ||
| Теорема косинусов | ||
Биссектриса треугольника. Свойства биссектрисы. Вычисление длины биссектрисы Свойства биссектрисы. Вычисление длины биссектрисы | ||
| Медиана треугольника. Свойства медианы. Вычисление длины медианы | ||
| Высота треугольника. Задача Фаньяно | ||
| Высота треугольника. Свойство высоты прямоугольного треугольника | ||
| Расположение высот у треугольников различных типов | ||
| Ортоцентр треугольника | ||
| Расположение ортоцентров у треугольников различных типов | ||
| Ортоцентрический треугольник | ||
| Задача Фаньяно | ||
| Средние линии треугольника | ||
| Теорема Чевы | ||
| Теорема Чевы 1 | ||
| Теорема Чевы 2 | ||
| Применения теоремы Чевы | ||
| Теорема Менелая | ||
Окружность, описанная около треугольника.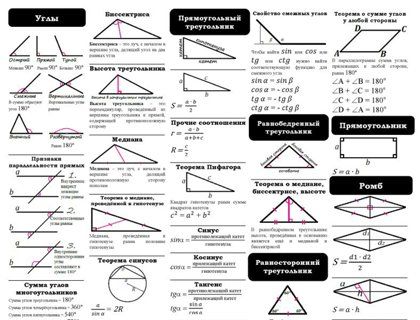 Треугольник, вписанный в окружность. Теорема синусов Треугольник, вписанный в окружность. Теорема синусов | ||
| Серединный перпендикуляр к отрезку | ||
| Окружность описанная около треугольника | ||
| Свойства описанной около треугольника окружности. Теорема синусов | ||
| Доказательства теорем о свойствах описанной около треугольника окружности | ||
| Формулы для стороны, периметра и площади правильного треугольника | ||
| Площадь треугольника | ||
| Формулы для площади треугольника | ||
| Вывод формул для площади произвольного треугольника | ||
| Вывод формул для площади равностороннего (правильного) треугольника | ||
| Вывод формул для площади прямоугольного треугольника | ||
| Вывод формулы Герона для площади треугольника | ||
Окружность, вписанная в треугольник. Основное свойство биссектрисы угла Основное свойство биссектрисы угла | ||
| Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла | ||
| Формулы для радиуса окружности, вписанной в треугольник | ||
| Вывод формул для радиуса окружности, вписанной в треугольник | ||
| Вневписанные окружности | ||
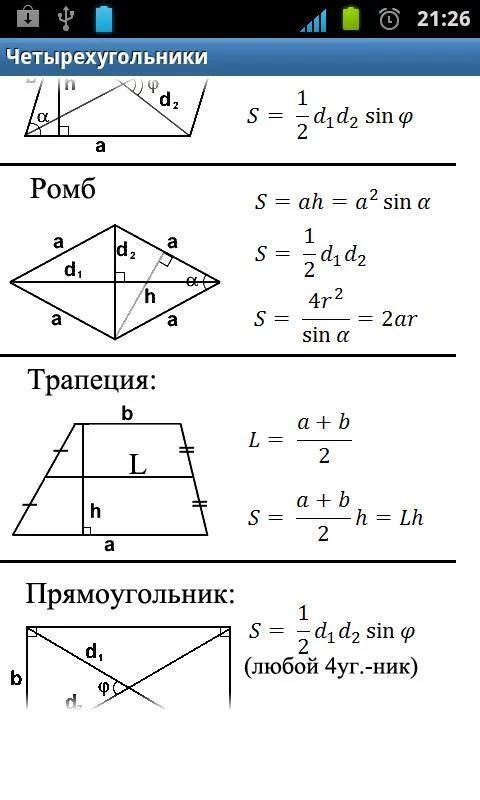
Четырехугольники | ||
| Четырехугольники | ||
| Типы четырехугольников | ||
| Типы параллелограмов | ||
| Типы трапеций | ||
| Параллелограммы | ||
| Свойства и признаки параллелограмма | ||
| Свойства и признаки прямоугольника | ||
| Свойства и признаки ромба | ||
| Свойства и признаки квадрата | ||
| Трапеции | ||
| Основные определения и свойства трапеций | ||
| Свойства и признаки равнобедренных трапеций | ||
Четырехугольники, вписанные в окружность.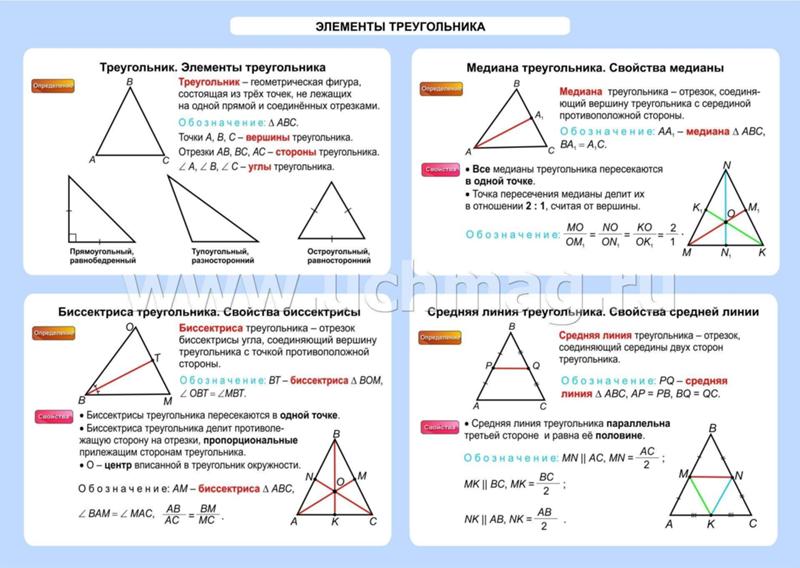 Теорема Птолемея Теорема Птолемея | ||
| Вписанные четырехугольники и их свойства | ||
| Теорема Птолемея | ||
| Описанные четырехугольники | ||
| Средние линии четырехугольников | ||
| Средняя линия трапеции | ||
| Средние линии четырехугольников. Теорема Вариньона | ||
| Формулы для стороны, периметра и площади квадрата | ||
| Площади четырехугольников | ||
| Формулы для площадей четырехугольников | ||
| Вывод формул для площадей четырехугольников | ||
| Вывод формулы Брахмагупты для площади вписанного четырехугольника | ||
Многоугольники | ||
| Многоугольники | ||
| Определение многоугольника | ||
| Диагонали n – угольника | ||
| Внешний угол многоугольника | ||
| Свойства углов треугольника | ||
| Свойства углов многоугольника | ||
| Свойства углов правильного n – угольника | ||
| Доказательства теорем о свойствах углов многоугольника | ||
| Правильные многоугольники | ||
| Формулы для стороны, периметра и площади правильного n – угольника | ||
| Формулы для стороны, периметра и площади правильного треугольника | ||
| Формулы для стороны, периметра и площади правильного шестиугольника | ||
| Формулы для стороны, периметра и площади квадрата | ||
Окружность и круг | ||
| Углы, связанные с окружностью | ||
| Вписанные и центральные углы | ||
| Углы, образованные хордами, касательными и секущими | ||
| Доказательства теорем об углах, связанных с окружностью | ||
Отрезки и прямые, связанные с окружностью. Теорема о бабочке Теорема о бабочке | ||
| Отрезки и прямые, связанные с окружностью | ||
| Свойства хорд и дуг окружности | ||
| Теоремы о длинах хорд, касательных и секущих | ||
| Доказательства теорем о длинах хорд, касательных и секущих | ||
| Теорема о бабочке | ||
| Две окружности на плоскости. Общие касательные к двум окружностям | ||
| Взаимное расположение двух окружностей | ||
| Общие касательные к двум окружностям | ||
| Формулы для длин общих касательных и общей хорды | ||
| Доказательства формул для длин общих касательных и общей хорды | ||
| Длина окружности и ее дуг. Площадь круга и его частей | ||
| Основные определения и свойства. Число π | ||
| Формулы для площади круга | ||
| Формулы для длины окружности и ее дуг | ||
| Площадь круга | ||
| Длина окружности | ||
| Длина дуги | ||
| Площадь сектора | ||
| Площадь сегмента | ||
Окружность, описанная около треугольника.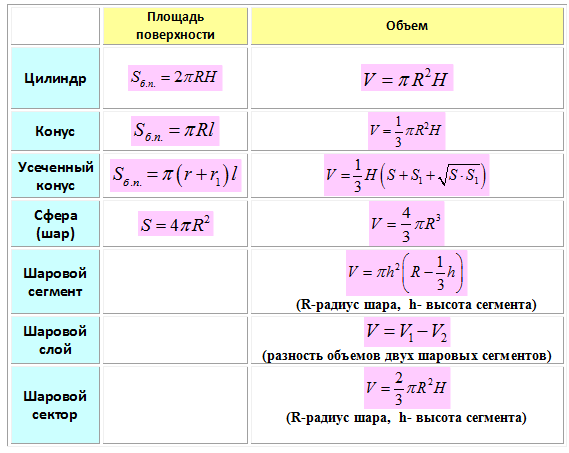 Треугольник, вписанный в окружность. Теорема синусов Треугольник, вписанный в окружность. Теорема синусов | ||
| Серединный перпендикуляр к отрезку | ||
| Окружность описанная около треугольника | ||
| Свойства описанной около треугольника окружности. Теорема синусов | ||
| Доказательства теорем о свойствах описанной около треугольника окружности | ||
| Окружность, вписанная в треугольник. Основное свойство биссектрисы угла | ||
| Существование окружности, вписанной в треугольник | ||
| Формулы для радиуса окружности, вписанной в треугольник | ||
| Вывод формул для радиуса окружности, вписанной в треугольник | ||
| Вневписанные окружности | ||
| Четырехугольники, вписанные в окружность. Теорема Птолемея | ||
| Вписанные четырехугольники и их свойства | ||
| Теорема Птолемея | ||
| Вывод формулы Брахмагупты для площади вписанного четырехугольника | ||
| Описанные четырехугольники | ||
Площади | ||
| Площади четырехугольников | ||
| Формулы для площадей четырехугольников | ||
| Вывод формул для площадей четырехугольников | ||
| Площадь треугольника | ||
| Формулы для площади треугольника | ||
| Вывод формул для площади произвольного треугольника | ||
| Вывод формул для площади равностороннего (правильного) треугольника | ||
| Вывод формул для площади прямоугольного треугольника | ||
| Вывод формул Герона и Брахмагупты | ||
| Вывод формулы Герона для площади треугольника | ||
| Вывод формулы Брахмагупты для площади вписанного четырехугольника | ||
Средние линии | ||
| Средние линии | ||
| Средние линии треугольника | ||
| Средняя линия трапеции | ||
Средние линии четырехугольников. Теорема Вариньона Теорема Вариньона | ||
| Средние линии тетраэдра | ||
Геометрические места точек на плоскости | ||
| Геометрические места точек на плоскости | ||
Преобразования плоскости | ||
| Движения плоскости. Теорема Шаля. Афинные преобразования плоскости | ||
| Преобразования плоскости | ||
| Движения плоскости | ||
| Теорема Шаля | ||
| Афинные преобразования плоскости | ||
| Классификация афинных преобразований плоскости | ||
С демонстрационными вариантами ЕГЭ и ОГЭ, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Классическая дифференциальная геометрия | Открытые видеолекции учебных курсов МГУ
Курс «Классическая дифференциальная геометрия» читается студентам механико-математического факультета МГУ имени М. В. Ломоносова на втором курсе в 4 семестре.
В рамках курса рассмотрены кривые в евклидовом пространстве, а также поверхности — их первая и вторая фундаментальные формы. Даны элементы дифференциального исчисления на поверхности, геодезические на поверхностях и криволинейные координаты в области и на поверхности. Освещены риманова и псевдориманова метрики, геометрия Лобачевского, топологические пространства, многообразия.
Освещены риманова и псевдориманова метрики, геометрия Лобачевского, топологические пространства, многообразия.
Изложены касательное пространство к многообразию, дифференциал, вложения многообразий в евклидово пространство, дополнительные структуры (риманова метрика, ориентируемость), а также классификация связных компактных двумерных многообразий.
Список всех тем лекций
Лекция 1. Введение в дифференциальную геометрию.
Что такое дифференциальная геометрия и чем она занимается
Определения кривых с точки зрения разных разделов математики
Регулярные кривые: формальные определения
Утверждение об эквивалентности различных параметризаций кривой и его применение
Краткий обзор курса
Рекомендованный список литературы, отступление про применение дифференциальной геометрии в физике
Выбор координаты кривой как регулярного параметра
Способы задания кривой в действительном векторном пространстве в дифференциальной геометрии и значение понятия регулярности
Теорема о локальной эквивалентности определений регулярной элементарной кривой
Примеры, иллюстрирующие значение регулярности в условии теоремы
Лекция 2. Основные понятия, связанные с кривыми в дифференциальной геометрии.
Основные понятия, связанные с кривыми в дифференциальной геометрии.
Регулярные, k-гладкие и k-дифференцируемые отображения (напоминание)
Теорема о локальной эквивалентности определений регулярной кривой (напоминание) и примеры к ней
Следствие теоремы о локальной эквивалентности
Касательная прямая к регулярной кривой
Утверждение (о том, что расстояние от точек кривой до касательной имеет второй порядок малости)
Натуральная параметризация кривой
Утверждение о параметризации с постоянным вектором скорости
Кривизна кривой в действительном векторном пространстве
Соприкосновение кривых в действительном векторном пространстве
Утверждение об участке кривой, кривизна которого равна нулю
Бирегулярная кривая
Его ортогональность вектору скорости
Соприкасающаяся плоскость к кривой в действительном векторном пространстве
Построение соприкасающейся окружности
Лекция 3. Плоские кривые.
Плоские кривые.
Напоминание определений с предыдущей лекции, используемых в теореме о соприкасающейся окружности
Теорема о соприкасающейся окружности: доказательство, комментарии
Два смысла понятия кривизны кривой: кривизна соприкасающейся окружности и длина вектора ускорения
Формула кривизны кривой в действительном векторном пространстве для произвольной параметризации
Плоские кривые: кривизна со знаком, коориентация
Уравнения Френе и репер Френе для плоских кривых
Ортонормированный базис на кривой в действительном векторном пространстве
Теорема о восстановлении кривой по ее кривизне: значение и формулировка
Доказательство единственности (плоские кривые с одинаковой кривизной совмещаются движением плоскости)
Доказательство существования (существует кривая с данной кривизной)
Натуральное уравнение кривой (явная формула восстановления плоской кривой по ее кривизне)
Лекция 4. Эволюта, эвольвента; пространственные кривые.
Эволюта, эвольвента; пространственные кривые.
Напоминание определений и формулы натурального уравнения кривой с прошлой лекции
Глобальный смысл кривизны кривой: связь кривизны плоской замкнутой кривой и ее коэффициента вращения
Эволюта: определение
Теорема об эволюте: формулировка и доказательство
Эвольвента: определение
Утверждение об эвольвенте: формулировка и доказательство
Анонс тем, которые будут рассматриваться на второй половине лекции; дополнительные комментарии
Кривые в трехмерном пространстве: бинормаль, репер Френе, уравнения Френе, кручение пространственных кривых
Утверждение о кручении плоской кривой в пространстве
Геометрический смысл кручения
Вектор Дарбу
Локальные проекции кривой на плоскости трехгранника Френе
Анонс тем, которые будут рассмотрены на следующей лекции
Лекция 5. Кривые в пространстве произвольной размерности.
Кривые в пространстве произвольной размерности.
Вычислительные формулы для кручения
Теорема о восстановлении пространственной кривой по ее кривизне и кручению: формулировка
Доказательство теоремы: вспомогательные наблюдения, единственность
Доказательство теоремы: существование
Теорема (критерий сохранения ортогональности матрицы, гладко зависящей от параметра)
Покомпонентная (матричная) запись уравнений Френе
Базис Френе и уравнения Френе для кривой в действительном векторном пространстве
Теорема о восстановлении кривой в действительном векторном пространстве по ее кривизне и кручению: формулировка
Теорема о восстановлении кривой в действительном векторном пространстве по ее кривизне и кручению: идеи доказательства
Лекция 6. Криволинейные системы координат.
Криволинейные системы координат.
Теорема Гаусса (формулировка)
Криволинейные системы координат в действительном векторном пространстве: введение, примеры
Регулярная система координат (определение)
Локальная система координат (определение)
Применение определений к полярным, сферическим, цилиндрическим, евклидовым координатам
Координатные поверхности
Замена координат
Матрица Грама как частный случай задания римановой метрики
Отличие от римановой метрики и примеры
Деривационные уравнения для криволинейной системы координат
Символы Кристоффеля
О классе римановых метрик, которые задают криволинейные системы координат
Лекция 7.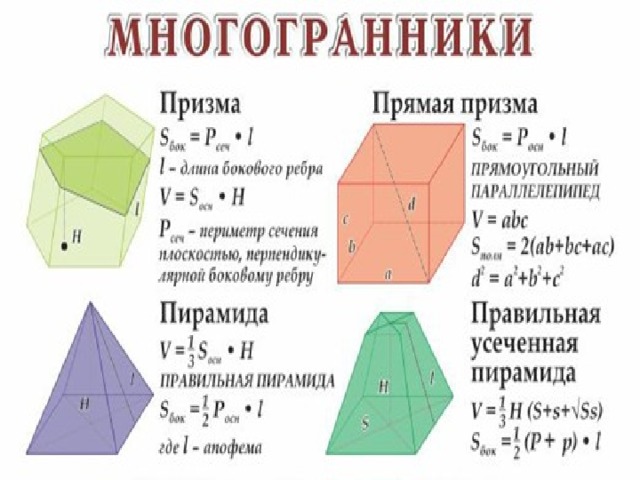 Криволинейные системы координат (продолжение).
Криволинейные системы координат (продолжение).
Криволинейные системы координат, уравнения перехода, римановы метрики (напоминание)
Теорема Дарбу о совместных системах (формулировка)
Применение теоремы к вопросу о римановых метриках, задающих криволинейные системы координат
Условие существование криволинейной системы координат для заданной римановой метрики
Утверждение о сохранении регулярности кривой при регулярной замене системы координат
Определение
Координатные линии на k-мерной поверхности
Теорема о связи с векторами скоростей кривых на поверхности
Первая квадратичная форма поверхности
Различные способы задания k-мерной поверхности
Теорема об эквивалентности этих способов
Лекция 8.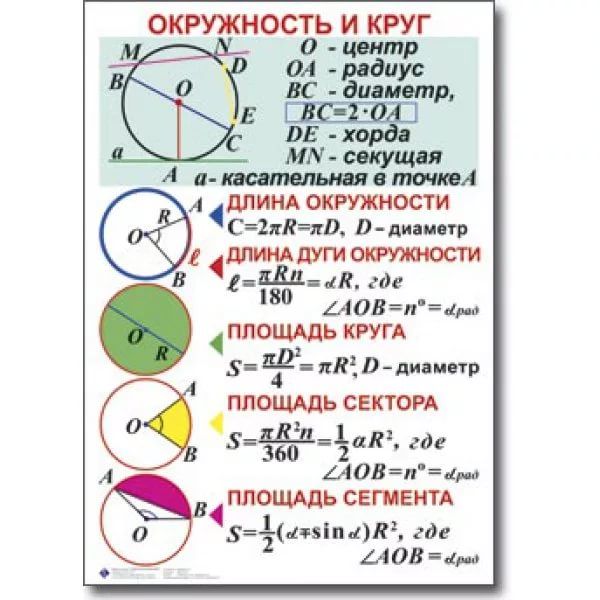 n в прямую сумму нормального и касательного пространств
Элемент объема на подмногообразии
Разложения Гаусса и Вейнгартена
Вторая квадратичная форма поверхности
Фундаментальные характеристики подмногообразия (краткая сводка)
Связь коэффициентов деривационных уравнений и фундаментальных характеристик
Фундаментальные уравнения теории подмногообразий: уравнения Гаусса
Фундаментальные уравнения теории подмногообразий: уравнения Кодацци
n в прямую сумму нормального и касательного пространств
Элемент объема на подмногообразии
Разложения Гаусса и Вейнгартена
Вторая квадратичная форма поверхности
Фундаментальные характеристики подмногообразия (краткая сводка)
Связь коэффициентов деривационных уравнений и фундаментальных характеристик
Фундаментальные уравнения теории подмногообразий: уравнения Гаусса
Фундаментальные уравнения теории подмногообразий: уравнения Кодацци
Лекция 9. Двумерные поверхности в трехмерном пространстве.
Двумерные поверхности в трехмерном пространстве: матрицы первой и второй квадратичных форм
Разложения Гаусса и Вейнгартена; уравнения Гаусса-Кодацци для двумерных поверхностей в трехмерном пространстве
Теорема Дарбу о совместных системах: общая формулировка
Следствиe: лемма Пуанкаре
Следствие: применение к вопросу о векторных полях на многообразии
Теорема Дарбу для двумерного пространства: формулировка, комментарии
Теорема Дарбу для двумерного пространства: доказательство
Теорема Бонне для двумерных поверхностей в трехмерном пространстве: формулировка, комментарии
Теорема Бонне для двумерных поверхностей в трехмерном пространстве: доказательство единственности
Теорема Бонне для двумерных поверхностей в трехмерном пространстве: доказательство существования
Лекция 10. Двумерные поверхности в трехмерном пространстве (продолжение).
Двумерные поверхности в трехмерном пространстве (продолжение).
Теорема Бонне — повторение основных моментов с предыдущей лекции и окончание доказательства
Уравнения нулевой кривизны
Кривые на поверхностях в трехмерном пространстве: формулы для длин кривых
Условие того, что две поверхности пересекаются по регулярной кривой
Формулы для кривизны нормального сечения
Лекция 11. Кривизны поверхностей.
Определения, которые были введены на прошлой лекции и понадобятся в дальнейшем (напоминания)
(определения)
Комментарии, примеры
Теорема Менье: формулировка, комментарии
Примеры к теореме Менье
Теорема Эйлера
Омбилические точки
Гауссова кривизна и средняя кривизна — определения
Линии кривизны
Формулы для вычисления гауссовой кривизны
Лекция 12.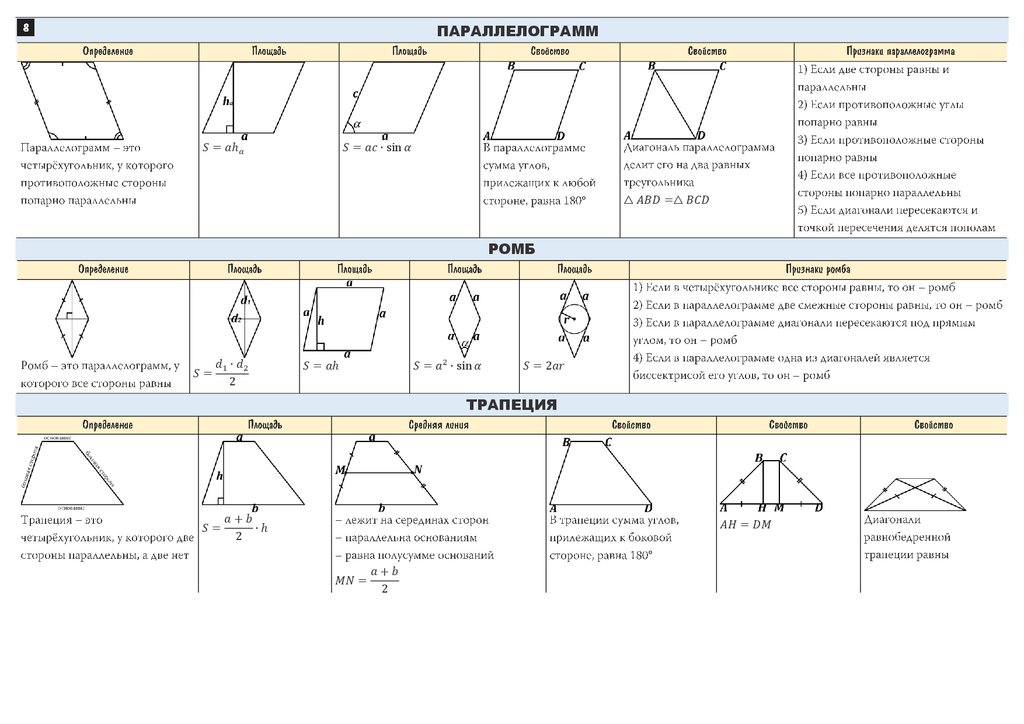 Сопряженные направления и геодезические на поверхностях.
Сопряженные направления и геодезические на поверхностях.
Оператор Вайнгартена
Формулы Родрига
Сопряженные направления в касательном пространстве
Сопряженная система координат
Линии кривизны на поверхности
Сферическое отображение (отображение Гаусса)
Соприкасающийся параболоид
Индикатриса Дюпена
Геодезические на поверхности
Лекция 13. Геодезические и их роль в дифференциальной геометрии.
Геодезические и геодезическая кривизна на регулярных поверхностях в трехмерном пространстве
Критерий того, что кривая является геодезической
Уравнения Френе (напоминание), их связь с уравнением геодезической
Примеры
Теорема Клеро
Анализ поведения геодезических на примере конуса
Уравнение геодезической
Теорема о единственности геодезической, касающейся данного направления
Уравнения Эйлера-Лагранжа
Лекция 14. Полугеодезические координаты.
Полугеодезические координаты.
Напоминание определений и фактов с предыдущей лекции
Свойство геодезической быть локально кратчайшей — комментарии на примере
Определение и свойства
Вывод теоремы о полугеодезической системе координат
Существование полугеодезической системы координат в каждой точке
Теорема о свойстве геодезической быть локально кратчайшей
Изометрии (и изгибания)
Задача о существовании диффеоморфизма поверхностей
Дифференциальные параметры Бельтрами; инварианты локальной изометрии
Изгибания
Теорема об изометрии поверхностей с постоянной гауссовой кривизной
Лекция 15. Поверхности постоянной кривизны. Теорема Гаусса-Бонне.
Теорема Гаусса-Бонне.
Теорема о классификации поверхностей постоянной гауссовой кривизны с точностью до изометрии
Формула Бибербаха
Доказательство теоремы
Общий вид метрик поверхностей различной постоянной кривизны и вывод
Реализация плоскости Лобачевского
Неизгибаемость выпуклой замкнутой поверхности — формулировка результата и комментарии
Ковариантная производная векторного поля вдоль кривой
Свойства ковариантной производной
Ковариантно постоянное (параллельное) поле вдоль кривой
Естественные векторные поля вдоль кривой
ОДУ параллельного переноса
Формулы, выражающие ковариантную производную для некоторых частных случаев
Геодезическое кручение для кривых на поверхностях
Теорема Гаусса-Бонне — формулировки и простые следствия
Теорема Гаусса-Бонне — схема доказательства
это просто.
 Понятия и формулы
Понятия и формулыОзнакомившись с материалом, читатель поймет, что планиметрия — это вовсе не сложно. В статье приведена самая важная теоретическая информация и необходимые для решения конкретных задач формулы. По полочкам разложены важные утверждения и свойства фигур.
Определение и важные факты
Планиметрия — это раздел геометрии, рассматривающий объекты на плоской двумерной поверхности. Можно выделить некоторые подходящие примеры: квадрат, круг, ромб.
Среди всего прочего стоит выделить точку и прямую. Они являются двумя основными понятиями планиметрии.
Уже на них строятся все остальное, например:
- Отрезок — часть прямой линии, ограниченная двумя точками.
- Луч — объект, аналогичный отрезку, однако, имеющий границу лишь с одной стороны.
- Угол, который состоит из двух лучей, выходящих из одной точки.
Аксиомы и теоремы
Подробнее разберемся с аксиомами. В планиметрии это наиважнейшие правила, по которым работает вся наука. Да и не только в ней. По определению, речь идет об утверждениях, не требующих доказательств.
Да и не только в ней. По определению, речь идет об утверждениях, не требующих доказательств.
Аксиомы, которые буду рассмотрены ниже, входят в так называемую Евклидовую геометрию.
- Есть две точки. Через них всегда можно провести единственную прямую.
- Если существует прямая, то есть точки, которые на ней лежат, и точки, не лежащие на ней.
Это 2 утверждения принято называть аксиомами принадлежности, а следующие – порядка:
- Если на прямой расположены три точки, то одна из них обязательно находится между двумя другими.
- Плоскость делится любой прямой на две части. Когда концы отрезка лежат на одной половине, то значит и весь объект принадлежит ей. В ином случае исходная прямая и отрезок имеют точку пересечения.
Аксиомы мер:
- Каждый отрезок имеет длину, отличную от нуля. Если точка разбивает его на несколько частей, то их сумма будет равна полной длине объекта.
- У каждого угла есть определенная градусная мера, которая не равна нулю.
 Если разбить его лучом, то исходный угол будет равен сумме образованных.
Если разбить его лучом, то исходный угол будет равен сумме образованных.
Параллельность:
- На плоскости расположена прямая. Через любую точку, не принадлежащую ей, можно провести лишь одну прямую, параллельную данной.
Теоремы в планиметрии — это уже не совсем фундаментальные утверждения. Обычно их принимают как факт, но каждая из них имеет доказательство, построенное на основных понятиях, упомянутых выше. Кроме того, их очень много. Разобрать все будет довольно трудно, но в представленном материале будут присутствовать некоторые из них.
Со следующими двумя стоит ознакомиться пораньше:
- Сумма смежных углов равна 180 градусам.
- Вертикальные углы имеют одинаковую величину.
Эти две теоремы могут пригодиться в решении геометрических задач, связанных с n-угольниками. Они довольно просты и интуитивно понятны. Стоит их запомнить.
Треугольники
Треугольник — это геометрическая фигура, состоящая из трех последовательно соединенных отрезков. Классифицируют их по нескольким признакам.
Классифицируют их по нескольким признакам.
По сторонам (соотношения выплывают из названий):
- Равносторонний.
- Равнобедренный — две стороны и противоположные им углы соответственно равны.
- Разносторонний.
По углам:
- остроугольный;
- прямоугольный;
- тупоугольный.
Два угла независимо от ситуации всегда будут острыми, а третий определяется первой частью слова. То есть у прямоугольного треугольника один из углов равен 90 градусам.
Свойства:
- Чем больше угол, тем больше противоположная ему сторона.
- Сумма всех углов — 180 градусов.
- Площадь можно вычислить по формуле: S = ½ ⋅ h ⋅ a, где a — сторона, h — проведенная к ней высота.
- Всегда можно вписать окружность в треугольник или же описать ее вокруг него.
Об одной из основных формул планиметрии говорит теорема Пифагора. Работает она исключительно для прямоугольного треугольника и звучит так: квадрат гипотенузы равен сумме квадратов катетов: AB2 = AC2 + BC2.
Под гипотенузой подразумевают сторону, противоположную углу 90°, а под катетами — прилежащие.
Четырехугольники
Информации на эту тему чрезвычайно много. Ниже приведена лишь самая важная.
Некоторые разновидности:
- Параллелограмм — противоположные стороны равны и попарно параллельны.
- Ромб — параллелограмм, чьи стороны имеют одинаковую длину.
- Прямоугольник — параллелограмм с четырьмя прямыми углами
- Квадрат — одновременно ромб и прямоугольник.
- Трапеция — лишь две противоположные стороны параллельны.
Свойства:
- Сума внутренних углов равна 360 градусам.
- Площадь всегда можно вычислить по формуле: S=√(p-a)(p-b)(p-c)(p-d), где p — половина периметра, a, b, c, d — стороны фигуры.
- Если вокруг четырехугольник можно описать окружность, тогда его называю выпуклым, если нет — невыпуклым.
Термины, определения и формулы по геометрии за 7 класс — Справочник
Все формулы по геометрии за 7 класс
Геометрия
Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).
В Планиметрии изучаются свойства фигур на плоскости. В Стереометрии изучаются свойства фигур в пространстве.
Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Лучи называются сторонами угла, а Точка — вершиной угла.
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности.
Радиус Окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.
Отрезок, соединяющий две точки окружности, называется ее Хордой.
Хорда, проходящая через центр окружности, называется диаметром.
Круг — это часть плоскости, ограниченная окружностью.
Угол называется Развёрнутым, если обе его стороны лежат на одной прямой. ( Развёрнутый угол равен 180°).
Две геометрические фигуры называются Равными, если их можно совместить наложением.
Середина отрезка — это точка отрезка, делящая его пополам, т. е. на два равных отрезка.
Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
Угол называется Прямым, если он равен 90°.
Угол называется Острым, если он меньше 90° (т. е. меньше прямого угла).
Угол называется Тупым, если он больше 90°, но меньше 180°. (т. е. больше прямого, но меньше развёрнутого).
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются Смежными. Сумма смежных углов равна 180°.
Два угла называются Вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
Вертикальные углы равны.
Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.
Перпендикулярные прямые — прямые, которые при пересечении образуют прямой угол.
Параллельные прямые — прямые, лежащие в одной плоскости и не имеющие общих точек.
Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами треугольника.
Сумма углов треугольника равна 180°.
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Если все три угла треугольника острые, то треугольник называется Остроугольным.
Если один из углов треугольника тупой, то треугольник называется Тупоугольным.
Если один из углов треугольника прямой, то треугольник называется Прямоугольным.
Сторона прямоугольного треугольника, лежащая против прямого угла, называется Гипотенузой, а две стороны, образующие прямой угол — Катетами.
(Т. о соотношениях между сторонами и углами треугольника) В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
В прямоугольном треугольнике гипотенуза Больше катета.
(Признак равнобедр. треугольника) Если два угла треугольника равны, то треугольник Равнобедренный.
(Т. Неравенство треугольника) Каждая сторона треугольника Меньше суммы двух других сторон.
Если два треугольника Равны, то элементы (т. е. стороны и углы) одного треугольника соответственно Равны элементам другого треугольника.
Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.
Сами рассуждения называются доказательством теоремы.
Первый признак равенства треугольников
«Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.»
Сокращенно его называют равенство «по двум сторонам и углу между ними».
На рисунке 1 представлен треугольник ABС. Который имеет три вершины (А, В и С). И стороны – АВ, АС и ВС.
Треугольники считаются равными, когда все их стороны и углы соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны, треугольники называются подобными). Таким образом очевидно, что равные треугольники можно наложить друг на друга – и они полностью совпадут.
Доказательство первого признака равенства треугольников
Два треугольника: ABC и DEF (рисунок 2).
По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т. е. ∠АСВ = ∠EFD).
е. ∠АСВ = ∠EFD).
Доказать, что треугольник ABC равен треугольнику DEF.
Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
При этом отрезки СА и СВ наложатся на отрезки FE и FD.
А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
Это в свою очередь даст совмещение вершин А и D, В и Е.
Следовательно, треугольники полностью совместятся, а значит, они равны.
Теорема доказана.
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Как и в доказательстве первого признака, нужно убедиться, достаточно ли этого для равенства треугольников, можно ли их полностью совместить?
1. Так как MN=PR, то эти отрезки совмещаются, если совместить их конечные точки.
2. Так как∡N=∡R и∡M=∡P, то лучи MK и NK наложатся соответственно на лучи PT и RT.
3. Если совпадают лучи, то совпадают точки их пересечения K и T.
4. Совмещены все вершины треугольников, то есть ΔMNK и ΔPRT полностью совместятся, значит они равны.
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Опять попробуем совместить треугольникиΔMNK и ΔPRT наложением и убедится, что соответственно равные стороны гарантирует и равенство соответственных углов этих треугольников и они полностью совпадут.
Совместим, например, одинаковые отрезки MK иPT. Допустим, что точки N и R при этом не совмещаются.
Пусть O — середина отрезка NR. Соответственно данной информацииMN=PR, KN=TR. Треугольники MNR и KNR равнобедренные с общим основанием NR.
Поэтому их медианы MO и KO являются высотами, значит перпендикулярны NR. Прямые MO и KO не совпадают, так как точки M, K, O не лежат на одной прямой. Но через точку O прямой NR можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.
Прямые MO и KO не совпадают, так как точки M, K, O не лежат на одной прямой. Но через точку O прямой NR можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.
Доказано, что должны совместиться и вершины N и R.
Третий признак позволяет назвать треугольник очень сильной, устойчивой фигурой, иногда говорят, что треугольник — жёсткая фигура. Если длины сторон не меняются, то углы тоже не меняются. Например, у четырёхугольника такого свойства нет. Поэтому разные поддержки и укрепления делают треугольными.
Перпендикуляр к прямой
Из точки не лежащей на прямой можно провести перпендикуляр к этой прямой и притом только один
Медианы, биссектриссы и высоты треугольника
В любом треугольнике медианы пересекаются в одной точке. Биссектрисы пересекаются в одной точке. Высоты или их продолжения также пересекаются в одной точке
Свойства равнобедренного треугольника
В равнобедренном треугольнике углы при основании равны.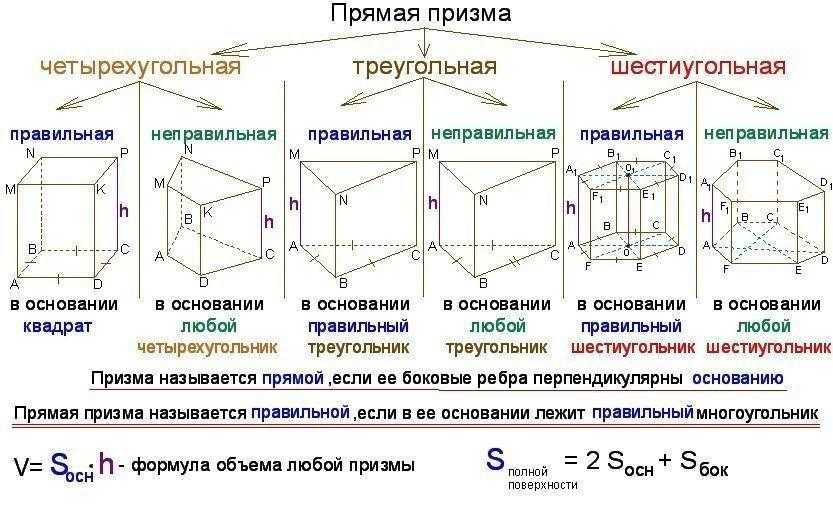 В рабнобедренном треугольнике бисссектриса проведенная к основанию является медианой и высотой. Высота равнобедренного треугольника проведенная к основанию является медианой и биссектрисой. Медиана равнобедренного треугольника проведенная к основанию является высотой и биссекрисой.
В рабнобедренном треугольнике бисссектриса проведенная к основанию является медианой и высотой. Высота равнобедренного треугольника проведенная к основанию является медианой и биссектрисой. Медиана равнобедренного треугольника проведенная к основанию является высотой и биссекрисой.
Признаки параллельности двух прямых. Теорема 1
Если при пересечении двух прямых секущей накрест лежащие углы равны то прямые параллельны.
Признаки параллельности прямых. Теорема 2
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Признаки параллельности прямых. Теорема 3.
Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰ то прямые параллельны.
Теорема об углах образованных двумя параллельными прямыми и секущей.
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Аксиома параллельных прямых.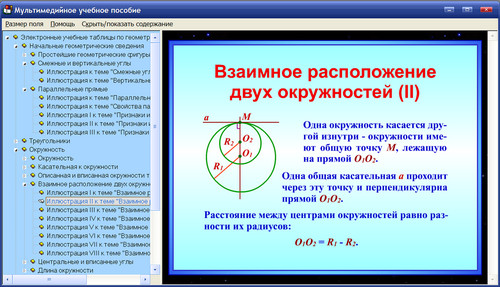
В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.
Теоремы об углах, образованных двумя параллельными прямыми и секущей
Если две параллельные прямые пересечены секущей, накрест лежащие углы равны. Если две параллельные прямые пересечены секущей, то соответственные углы равны. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°. Если при пересечении двух прямых секущей накрест лежащие углы равны, топрямые параллельны.
Теорема Сумма углов треугольника равна 180°.
Рассмотрим произвольный треугольник KLM и докажем, что ∡K+∡L+∡M=180°.
Проведём через вершину L прямую a, параллельную стороне KM.
Углы, обозначенные 1, являются накрест лежащими углами при пересечении параллельных прямых a и KMсекущей KL, а углы, обозначенные 2 — накрест лежащими углами при пересечении тех же параллельных прямых секущей ML.
Очевидно, сумма углов 1, 2 и 3 равна развёрнутому углу с вершиной L, т. е.
∡1+∡2+∡3= 180°или ∡K+∡L+∡M=180°.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
Следствие 3. В равностороннем треугольнике каждый угол равен 60°.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Из равенств ∡KML+∡BML= 180° и ∡K+∡L+∡KML=180° получаем, что ∡BML=∡K+∡L.
Четырёхугольники
Многоугольник — фигура, состоящая из нескольких точек плоскости, поочередно соединённых между собой непересекающимися отрезками.
Диагональ — это отрезок, соединяющий две несоседних вершины многоугольника.
Выпуклый многоугольник — это многоугольник, который весь лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Теорема:Сумма внутренних углов выпуклого n-угольника равна (n-2)*1800.
Параллелограмм- это четырёхугольник, у которого противоположные стороны попарно параллельны.
Свойство:в параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство:диагонали параллелограмма точкой пересечения делятся пополам.
Теорема(признакпараллелограмма): Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма): Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма): Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.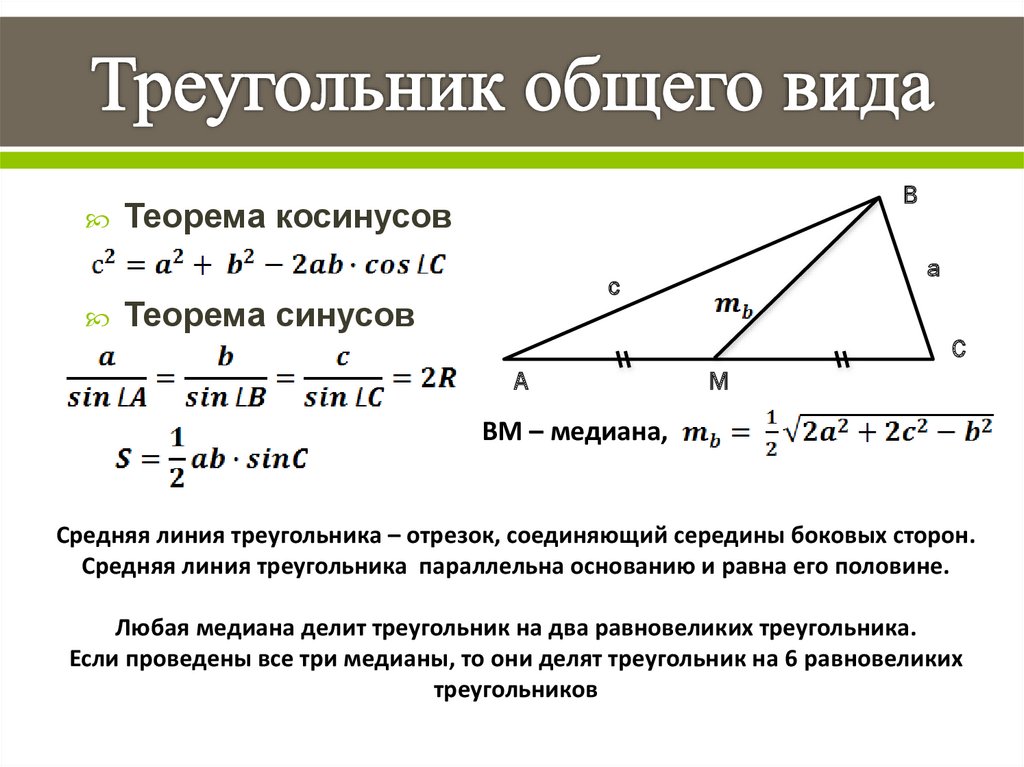
Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны. Параллельные стороны-основания, непараллельные стороны-боковые.
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Прямоугольная трапеция — это трапеция, у которой один из углов прямой.
Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пресекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Прямоугольник — это параллелограмм, у которого все углы прямые.
Свойство: диагонали прямоугольника равны.
Теорема(признакпрямоугольника): если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Ромб — это параллелограмм, у которого все стороны равны.
Свойство: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат — это прямоугольник, у которого все стороны равны.
Площадь
Площадь плоской фигуры-это количество единичных квадратов, вмещающихся в данную фигуру.
Единицы измерения площади: мм2,см2, дм2, м2, ар=100м2, км2 , га=100км2.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его смежных сторон.
Площадь параллелограмма равна произведению его основания на высоту.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна произведению его катетов.
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции равна полусумме её оснований на высоту.
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема(обр.): если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.
Подобные треугольники
Отрезки m и n пропорциональны отрезкам m1и n1,если отношения их длин равны m:m1= n: n1.
Подобные треугольники — это треугольники, у которых соответственные углы равны, а сходственные стороны пропорциональны.
Коэффициент подобия — это число, равное отношению сходственных сторон подобных треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Свойство биссектрисы тр-ка: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Теорема(первый признак подобия треугольников): если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Теорема(второй признак подобия треугольников): если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Теорема(первый признак подобия треугольников): если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Среднее пропорциональное(среднее геометрическое)двух величин – это квадратный корень из произведения этих величин.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
С. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключённым между катетом и высотой, проведённой из вершины прямого угла.
Синус острого угла прямоугольного треугольника — это отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника — это отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника — это отношение противолежащего катета к прилежащему.
Котангенс острого угла прямоугольного треугольника — это отношение прилежащего катета к противолежащему.
Окружность
Касательная к окружности – это прямая, имеющая с окружностью только одну общую точку.
Т. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Т.(обр.) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Центральный угол – это угол с вершиной в центре окружности.
Дуга окружности измеряется центральным углом, который на неё опирается.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Т.Вписанный угол равен половине дуги, на которую он опирается.
С. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
С. Вписанный угол, опирающийся на полуокружность, — прямой.
Т. Если две хорды окружности пересекаются, произведение отрезков одной хорды равно произведению отрезков другой хорды.
Геометрия
Круг это часть плоскости, ограниченная окружностью.
Na5.club
31.10.2019 15:14:32
2019-10-31 15:14:32
Источники:
Https://na5.club/geometriya/terminy-7-klass. html
Формулы геометрии. Площади фигур — материалы для подготовки к ЕГЭ и ОГЭ по Математике » /> » /> .keyword { color: red; }
Все формулы по геометрии за 7 класс
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным. Высоты этих треугольников равны и. Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга. Найдите площадь сектора круга радиуса, длина дуги которого равна.
На этом рисунке мы видим часть круга. Площадь всего круга равна, так как. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна, следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.
Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.
Найдите площадь сектора круга радиуса, длина дуги которого равна.
Ege-study. ru
15.01.2020 2:34:58
2020-01-15 02:34:58
Источники:
Https://ege-study. ru/ru/ege/materialy/matematika/formuly-geometrii/
Формулы по геометрии, скачать основные геометрические формулы для студентов и школьников » /> » /> .keyword { color: red; }
Все формулы по геометрии за 7 класс
В данном разделе собраны Основные формулы по геометрии, которые необходимы школьникам и студентам для подготовки к занятиям, решения задач и выполнения контрольных работ по геометрии./918870b1bc4a305.s.siteapi.org/img/da030ac2a7fb5c233f7bae5e5994c9ac4d7727d0.jpg) Геометрические формулы — это краткий теоретический материал, выучив которые вы легко сможет выполнить задания по геометрии.
Геометрические формулы — это краткий теоретический материал, выучив которые вы легко сможет выполнить задания по геометрии.
Все геометрические формулы и таблицы составлены нашими специалистами и снабжены дополнительными комментариями, это идеальный материал для школьников 7, 8 и 9 классов!
Если после изучения данного теоретического материала у Вас возникнут проблемы в решении задач или появятся вопросы образовательного характера, то вы всегда можете задать их на нашем форуме.
Формулы по геометрии.
Www. webmath. ru
04.07.2017 12:06:25
2017-07-04 12:06:25
Источники:
Https://www. webmath. ru/poleznoe/formules_main2.php
Геометрические формулы и понятия GMAT о треугольниках (часть 1)
Чувствуете ли вы себя подавленным, изучая множество геометрических формул GMAT[1] и понятий? Считаете ли вы, что геометрия — ваша слабая тема? Ты не одинок. Многие тестируемые избегают решать вопросы GMAT по геометрии, так как большинству из них не нравится эта тема.
В этой статье вы прочтете-
- Почему GMAT Geometry – ваше слабое место?
- Как мы поможем вам улучшить геометрию?
- Основные свойства треугольников для GMAT Geometry
- Наглядные примеры использования геометрических формул GMAT
- Вынос
- Есть слишком много формул GMAT по геометрии, чтобы запомнить . Несмотря на то, что GMAT тестирует нас по очень ограниченному количеству свойств, но поскольку эти ограниченные свойства не собраны в одном месте, тестируемому трудно с уверенностью сказать, что он знает все концепции.
- И скажем, даже если кому-то удастся найти и выучить все понятия , большинство из них не уверены, как применить эти понятия к вывести информацию из заданного вопроса и цифру в вопросах, проверенных на GMAT.
ПРИМЕЧАНИЕ: Это вторая статья из серии «Подводные камни GMAT по геометрии».
Прочитайте первую статью, нажмите на ссылку ниже.
Наиболее распространенные ошибки в вопросах GMAT по геометрии
Следующие 2 статьи из этой серии:
- Практические вопросы GMAT по геометрии – свойства треугольников (часть 2)
- Практические задачи по геометрии и специальные свойства треугольников (часть 3)
Как мы можем помочь вам с подготовкой к GMAT по геометрии?
В этой статье мы рассмотрим оба вышеупомянутых вопроса:
- Объединение НАИБОЛЕЕ важных понятий геометрии GMAT, необходимых в треугольниках .
- Сосредоточение внимания на некоторых вопросах, подобных GMAT, и официальных вопросах и иллюстрация применения вышеуказанных понятий в этих вопросах.
Основные свойства треугольников
В этом разделе рассматриваются следующие аспекты:
- Определение того, может ли набор заданных чисел быть длинами треугольника или нет
- Диапазон значений, которые может принимать сторона треугольника при заданных значениях двух других сторон, и
- Свойства углы треугольника
Концепция 1: Формулы GMAT по геометрии
Геометрия GMAT Концепция 1. Сумма длин любых двух сторон треугольника > Длина третьей стороны
Сумма длин любых двух сторон треугольника > Длина третьей стороны Предположим, вам даны три длины a, b и c, и вас спросили чтобы узнать, можем ли мы построить треугольник, используя эти три длины.
Как вы собираетесь решать эту проблему?
Теория:
Чтобы определить, образуют ли три длины треугольник или нет, нам нужно знать основное свойство треугольника:
Сумма длин любых двух сторон треугольника > Длина третьей стороны
Это означает, что:
- a + b > c
- б + в > а
- с + а > b
Обратите внимание, что все три неравенства должны удовлетворять , чтобы треугольник существовал.
Давайте поймем это с помощью очень простого вопроса типа GMAT:
Иллюстративный пример 1
Q. Три длины 5, 3 и x используются для формирования треугольника. Что из следующего может быть значением x?
Что из следующего может быть значением x?
- 6
- 9
- 10
- 12
- 14
Поскольку 5, 3 и x образуют треугольник, они должны удовлетворять свойству –
Сумма длин любых двух сторон треугольника > длины третьей стороны
Следовательно, мы можем написать –
I , 5 + 3 > x II. 3 + x > 5 III. 5 + х > 3
=> x < 8 => x > 2 => x > -2
мы можем заключить, что из диапазона x есть: попадает в этот диапазон, равно 6. Следовательно, вариант А является нашим ответом.
Итак, теперь мы знаем:
- Как определить, образуют ли данных длин треугольник или нет
- Как использовать вышеуказанное свойство до найти диапазон значений неизвестной стороны треугольника
Концепция 2: Геометрические формулы GMAT
Предположим, после того, как вы узнали, что данные длины образуют треугольник, вы хотите узнать, как длины сторон могут помочь в нахождении соотношения между углами треугольника.
Чтобы понять это, нам нужно знать еще два важных свойства:
GMAT Geometry Concept 2 – Сумма внутренних углов треугольника постоянна и равна 180°Обратите внимание, что вышеуказанное свойство верно для всех треугольников, независимо от их размера и формы.
(Обратите внимание, что я использую заглавные A, B и C для обозначения углов треугольника
, а a, b и c — для длин сторон 9026 треугольника)
Свойство 3 – В любом треугольнике наибольшая сторона всегда лежит против наибольшего угла, а наименьшая сторона всегда против наименьшего угла
Позвольте мне объяснить это немного подробнее:
Если ABC — треугольник, в котором мы знаем, что длины AB, BC и CA подчиняются соотношению AB>BC>AC, то мы можем заключить, что, поскольку АВ — наибольшая сторона противолежащего ей угла , т. е.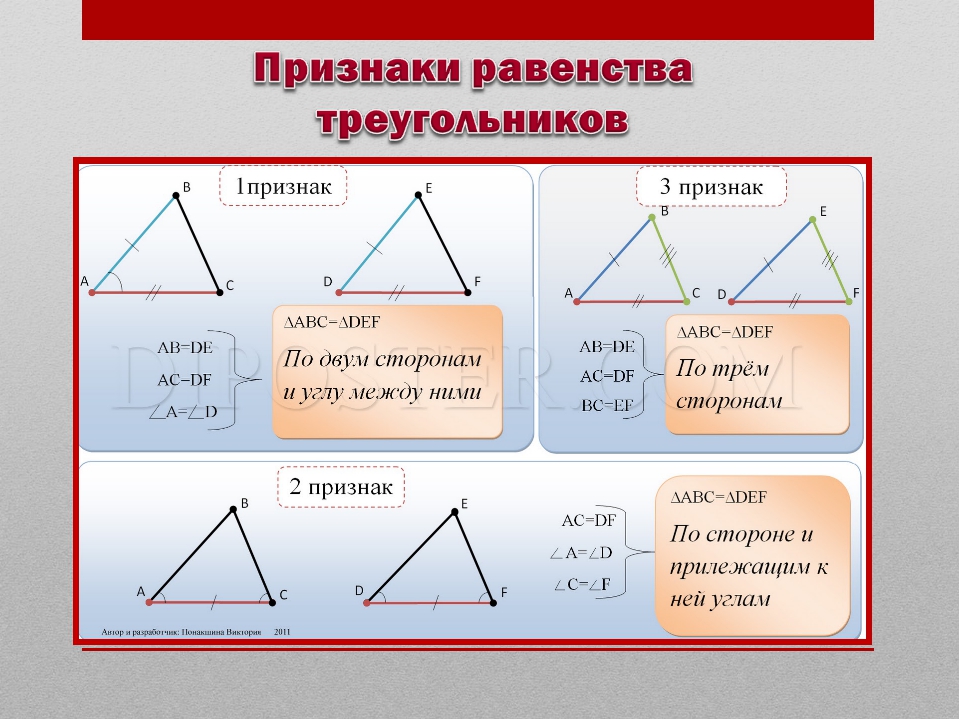 угол АСВ — наибольший угол .
угол АСВ — наибольший угол .
А так как BC > AC, то и противоположные им углы находятся в таком же соотношении, то есть угол BAC > угла ABC
Отсюда можно заключить, что: ∠ ACB > ∠ BAC > ∠ ABC
Имейте в виду, что обратное также верное , т. е. если отношение между углами задано, мы можем использовать это, чтобы найти отношение между сторонами.
Давайте разберем применение этого свойства на примере:
Иллюстративный пример 2
В приведенном ниже треугольнике все обозначенные точки не перекрываются, а углы A, B и C различны. АВ > АС > ВС?
- ∠ у 1 = ∠ с 1
- ∠ BAC < ∠ ABC и ни один из углов не является наибольшим в треугольнике ABC
Решение:
Подход
Нам нужно выяснить, верно ли утверждение AB > AC > BC. Для этого достаточно получить соотношение между углами A, B и C, так как стороны треугольника подчиняются тому же соотношению, что и противоположные им углы.
Анализ Заявление 1
T y 1 = ♂ C 1 9003
, поэтому C 1 9003
, с C 1 9003
C 1 9003
C 1 C 1
AB > BC
Однако мы не можем сделать вывод о какой-либо связи между BC и AC (или AB и AC) на основании предоставленной информации
Анализ заявления 20042 ∠ BAC < ∠ ABC, и ни один из углов не является наибольшим.
Также в постановке вопроса упоминается, что углы BAC, ABC и ACB различны, поэтому ∠ACB должен быть наибольшим углом.
Следовательно, мы можем заключить, что ∠ BAC < ∠ ABC < ∠ ACB
Таким образом, мы можем заключить, что длины BC < AC < AB
уникальный ответ.
Правильный ответ: B
Выводы – Статья 1 – Концепции треугольника геометрии GMAT
На этом мы подошли к концу первой статьи этой серии. Надеюсь, вы найдете его полезным и информативным. Прочитав это, вы сможете легко:
- Применить GMAT Geometry Concept 1 , чтобы определить, можно ли составить треугольник из заданных трех длин
- Применение концепции геометрии GMAT 1 , чтобы также найти диапазон неизвестной стороны, если известны две другие длины треугольника
- Применять GMAT Geometry Concept 2 в вопросах, где для решения задачи требуется соотношение углов и сторон
Помня об этих выводах, можете ли вы решить 2 вопроса?
- Усвоение важных понятий, проверенных GMAT в треугольниках — вопрос упражнения № 1
- Усвоение важных понятий, проверенных GMAT в треугольниках — вопрос упражнения № 2
В следующих статьях о треугольниках читайте оНачните подготовку к GMAT, подписавшись на бесплатную пробную версию и получив доступ к 10+ часам видеоуроков и более 400 вопросам.

1. Табличное представление: Различные типы треугольников с их НАИБОЛЕЕ важными свойствами.
2. Особые свойства: Несколько особых свойств, которые можно проверить с помощью GMAT.
[1] Формулы является формой множественного числа формулы , альтернативное множественное число формулы есть формулы.
Определение, типы и формулы для 2D и 3D объектов
Геометрия — это раздел математики, в котором мы изучаем различные виды фигур (безразмерные, одномерные, двухмерные и трехмерные) и их свойства. Вопросы, связанные с геометрией, оценивают зрительные способности наряду с аналитическими способностями кандидата. Различные типы фигур в геометрии позволяют нам понимать различные фигуры в математике, а также объекты нашей повседневной жизни. Также с помощью разных геометрических терминов можно найти площадь, периметр, угол, стороны, объем и другие параметры заданной фигуры. Эти темы часто задают на таких экзаменах, как SSC JE и SSC CGL, за которыми следуют банковские экзамены, такие как SBI PO, SBI Clerk, IBPS PO, IBPS Clerk и т. д.
Эти темы часто задают на таких экзаменах, как SSC JE и SSC CGL, за которыми следуют банковские экзамены, такие как SBI PO, SBI Clerk, IBPS PO, IBPS Clerk и т. д.
В этой статье вы узнаете о ключевых понятиях геометрии, за которыми следуют такие фигуры, как треугольники, четырехугольники, многоугольники, круги и их типы с изображениями. Тема также охватывает основные формулы геометрии, за которыми следуют расширенные. Внимательно прочитайте статью, чтобы развеять все сомнения относительно того же самого.
Разделы геометрииДавайте начнем обсуждение с различных разделов геометрии и узнаем о каждом из них.
Евклидова геометрия: Геометрия Евклида или евклидова геометрия занимается изучением геометрических форм, как двумерных, так и трехмерных, а также отношений между этими фигурами с точки зрения линий и углов, точек конгруэнтности и поверхностей. Книга Евклида об элементах дала введение в аксиомы и различные постулаты для твердых и плоских фигур, которые помогли в описании геометрических фигур.
Неевклидова геометрия: Как следует из названия, это раздел геометрии, включающий все, что не подпадает под евклидову геометрию. Она также известна как сферическая геометрия и гиперболическая геометрия.
Алгебраическая геометрия: Это раздел геометрии, который имеет дело с кривыми или поверхностями и включает линейные и полиномиальные алгебраические уравнения, которые используются для решения множеств нулей.
Проективная геометрия: Проективная геометрия — это раздел геометрии, изучающий связи между геометрическими фигурами, возникающие в результате проецирования объекта на другую поверхность.
Дискретная геометрия или комбинаторная геометрия: Это то, что относится к изучению геометрических объектов, дискретных по своей природе, таких как линии, треугольники, точки, окружности и т. д.
Дифференциальная геометрия: Он связан с общей теорией относительности в физике и использует методы алгебры и исчисления для решения задач.
Топология: Он имеет дело со свойствами пространства при непрерывном отображении. Он имеет приложения в различных областях, таких как метрические пространства, начальная и конечная структура, непрерывность, проксимальная непрерывность, проксимальные пространства и т. д.
Также читайте о гиперболе здесь.
Геометрические размерыВ предыдущем заголовке мы видели ветки основ геометрии, давайте теперь разберемся в различных измерениях геометрии в математике. В математике объекты можно разделить на объекты без измерений, одномерные, двухмерные и трехмерные объекты.
Безразмерная геометрияТочка может быть визуализирована как отдельная точка или место на плоскости. Обычно это определяется точкой, которая не имеет реального размера или формы. Следовательно, точечная геометрия не имеет размерности, или можно сказать, что она имеет единственное положение.
Одномерная геометрия Прямая линия и кратчайшее расстояние между двумя точками. То есть мы можем сказать, что количество точек при соединении составляет линейную геометрию. Поскольку линии обладают только длиной и не имеют ширины, поэтому они учитываются в одномерных формах/объектах. Различные типы и термины, относящиеся к линиям, следующие:
То есть мы можем сказать, что количество точек при соединении составляет линейную геометрию. Поскольку линии обладают только длиной и не имеют ширины, поэтому они учитываются в одномерных формах/объектах. Различные типы и термины, относящиеся к линиям, следующие:
| Типы | Определение | Представление |
| Прямая линия | Фигура, образованная соединением двух или более коллинеарных точек, называется прямой линией. Длина прямой линии не конечна. | |
| Отрезок | Когда мы соединяем две фиксированные точки прямой линией, то фигура, образованная таким образом, называется отрезком. Длина отрезка конечна, то есть его можно измерить. | |
| Луч | Прямая, выходящая из одной точки, называется лучом. | |
| Пересекающиеся линии | Когда две или более прямых пересекаются в одной точке, эти линии называются пересекающимися. | |
| Поперечные прямые | Прямая называется поперечной, если она пересекает две или более прямых. | |
| Параллельные прямые | Две или более прямых называются параллельными прямыми, если они не пересекаются друг с другом. | |
| Перпендикулярные прямые | Две прямые называются перпендикулярными, если угол между ними равен 90°. | |
| Параллельные прямые | Две или более прямых называются параллельными, если все они проходят через фиксированную точку. |
Когда два луча исходят из фиксированной точки, то угол поворота от одного луча к другому называется углом между лучами или углом между линиями. . Лучи называются плечами угла. Углы обычно измеряются в градусах или радианах. Различные типы углов геометрии с их определением и представлением следующие:
| Типы | Определение | Представление |
Острый ул.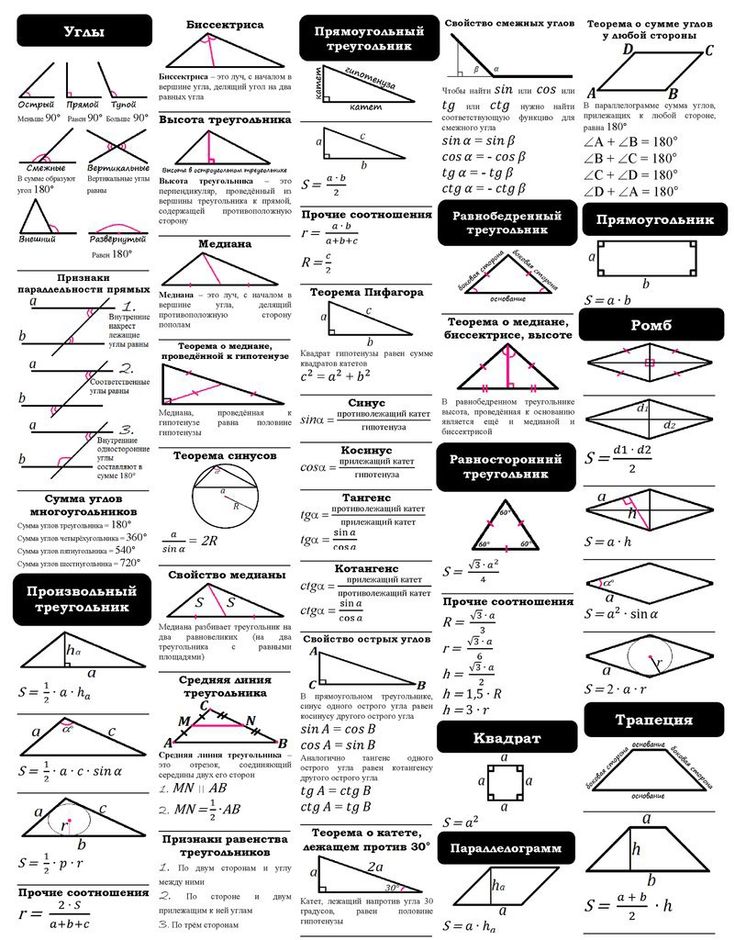 Здесь 0° <∠AOB< 90° | ||
| Прямой угол | Угол, величина которого равна 90°, называется прямым углом. Здесь ∠AOB = 90° | |
| Тупой угол | Угол, величина которого находится в пределах от 90° до 180°, называется тупым углом. Здесь 90° <∠AOB< 180° | |
| Прямой угол | Прямоугольным называется угол, величина которого равна 180°. | |
| Угол рефлекса | Угол, величина которого находится в пределах от 180° до 360°, называется углом рефлекса.
| |
| Полный угол | Угол, величина которого равна 360°, называется полным углом. |
Плоская геометрия или двумерная геометрия включает плоские фигуры, такие как круги, прямоугольники, треугольники и другие многоугольники. Двумерные объекты можно рисовать на бумаге, и они имеют длину и ширину. Различные двумерные объекты с определениями и изображениями следующие:
Различные двумерные объекты с определениями и изображениями следующие:
Многоугольник в математике называется двумерной формой. Есть разные названия по сторонам:
Треугольник: многоугольник, образованный тремя отрезками.
Четырехугольник: многоугольник, образованный четырьмя отрезками.
Точно так же существуют и другие типы многоугольников. Обратитесь к изображению ниже для того же.
Узнайте больше об измерении в 2D.
ТреугольникТреугольник — это многоугольник с 3 вершинами, скажем, P, Q и R, который представляется как △PQR. Различные типы треугольников перечислены в таблице ниже.
Типы треугольников в зависимости от сторон
Треугольники можно разделить на следующие группы в зависимости от стороны треугольника.
| Type | Definition | Representation |
| Scalene Triangle | A triangle whose all sides are different in length is called a scalene triangle. | |
| Равнобедренный треугольник | Треугольник, у которого две стороны равны, называется равнобедренным. | |
| Равносторонний треугольник | Треугольник, у которого все стороны равны, называется равносторонним треугольником. |
Также читайте о площади треугольника здесь.
Типы треугольников на основе углов
Треугольники в геометрии также можно разделить на следующие группы на основе измерения угла треугольника.
| Тип | Определение | Репрезентация |
| ОТКРЫТАЯ АНГЛИНА. | ||
| Прямоугольный треугольник | Прямоугольным треугольником называется треугольник, один из углов которого равен 90°. | |
| Тупоугольный треугольник | Треугольник, один из углов которого больше 90° называется тупоугольным треугольником.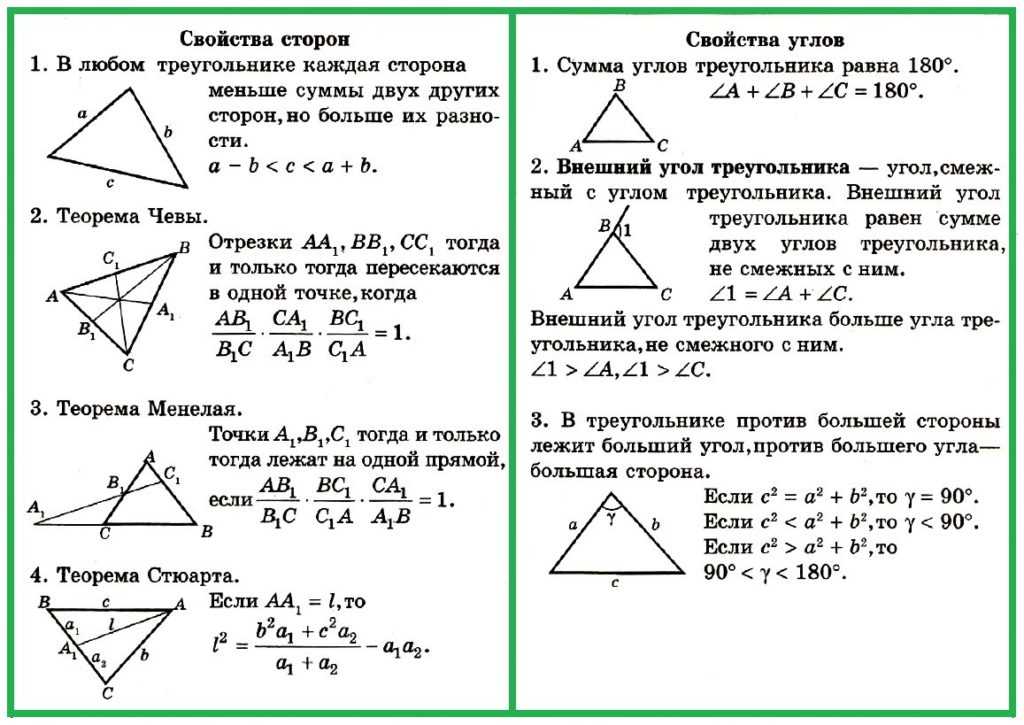 |
Прочтите эту статью о свойствах треугольников.
ЧетырехугольникиФигура, образованная отрезком из четырех прямых, называется четырехугольником. Сумма углов любого четырехугольника равна 360°. То есть, если четыре угла четырехугольника равны ∠A, ∠B, ∠C, ∠D. Тогда ∠A + ∠B + ∠C + ∠D = 360°.
Различные типы четырехугольников перечислены в таблице ниже.
| Тип | Определение | Представление |
| Параллелограмм | . | |
| Прямоугольник | Параллелограмм называется прямоугольником, если каждый угол равен 90°. | |
| Квадрат
| Параллелограмм называется квадратом, если все его стороны равны и каждый угол равен 90°. | |
| Ромб
| Параллелограмм называется ромбом, если все его стороны равны, а угол между диагоналями равен 90°.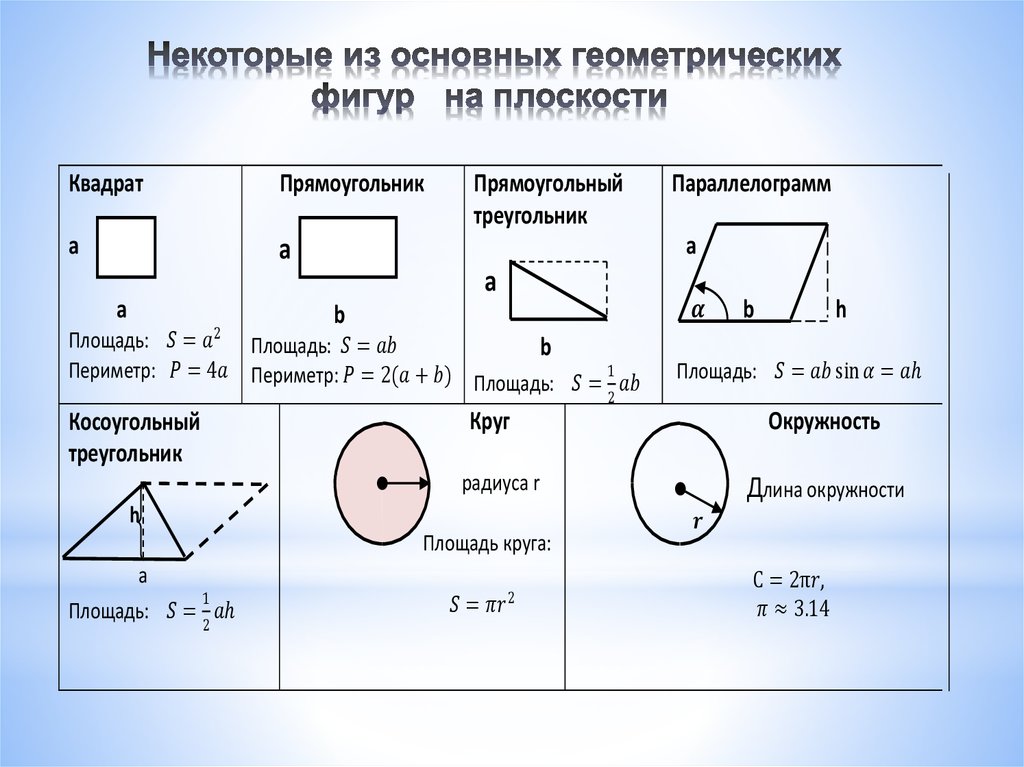 | |
| Трапеция | Четырехугольник называется трапецией, если одна пара противоположных сторон параллельна друг другу. |
Другие типы полигонов:
| Тип | Определение | Представление |
| Пятиугольник | Пятиугольник | |
| Шестиугольник | Многоугольник, образованный шестью отрезками. | |
| Семиугольник | Многоугольник, образованный семью отрезками. | |
| Восьмиугольник | Многоугольник, образованный восемью отрезками. | |
| Нонагон | Многоугольник, образованный девятью отрезками. | |
| Десятиугольник | Многоугольник, образованный десятью отрезками. |
Также узнайте о Параболе здесь.
Это геометрическое место всех точек, лежащих на плоскости так, что их расстояния от фиксированной точки всегда постоянны. Неподвижная точка называется центром окружности. Окружность с центром O и радиусом r показана ниже.
Различные части круга перечислены ниже:
| Части Circle | Определение | Radired | Radius | Радис | 2 29 29 любая точка, присутствующая на окружности круга, называется радиусом круга. Обычно радиус окружности обозначается буквой r или R. | |
| Хорда окружности
| Отрезок, образованный соединением любых двух точек на окружности окружности, в геометрии окружности называется хордой. | |||||
| Диаметр окружности
| Самая длинная хорда окружности называется диаметром окружности.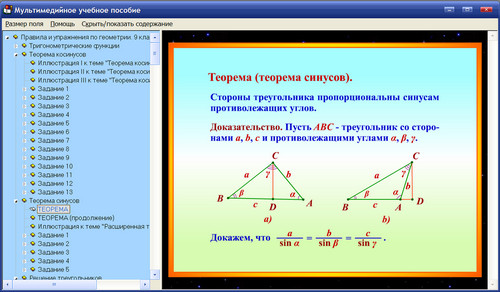 ИЛИ Хорда, проходящая через центр окружности, называется диаметром окружности. | |||||
| Секущая окружности | Прямая, пересекающая окружность в двух различных точках, называется секущей окружности. | |||||
| Тангенс окружности
| Линия, касающаяся окружности только в одной точке, называется касательной к окружности. | |||||
| Сектор окружности | Область окружности, ограниченная двумя радиусами и дугой, называется сектором окружности. |
Также узнайте о площади круга.
Трехмерная геометрия Объемная геометрия или трехмерная геометрия включает такие объекты, как кубы, прямоугольные параллелепипеды, призмы, цилиндры, конусы и сферы. Все эти объекты содержат длину, ширину и высоту. Важными характеристиками твердотельной геометрии являются ребра, грани и вершины. Давайте разберемся в каждом из них подробно.
Ребра
Ребра в 3D-форме соединяют одну угловую точку с другой угловой точкой. То есть это отрезок на границе, соединяющий одну вершину с другой. Они служат стыком двух граней.
Грани
Гранью трехмерных объектов называется плоская или изогнутая поверхность объекта. Для 3D-объекта лицо находится в 2D-формате. Конкретная форма может иметь несколько граней.
Вершины
Точка в трехмерных объектах, где пересекаются две или более линий, называется вершиной. Или можно понимать вершины как точки пересечения ребер.
Прочтите эту статью о Mensuration 3D.
Измерение в геометрии До сих пор мы читали об определении геометрии, различных ответвлениях, размерах и связанных формах с их изображениями. Давайте теперь разберемся с формулами геометрии под заголовком измерения в геометрии. Это включало формулы для расчета длины, площади, периметра и объема различных объектов.
Площадь и периметр определяются с помощью длины и ширины различных геометрических объектов. Некоторые важные формулы символов геометрии, относящиеся к 2D, перечислены ниже. 92\)
Здесь r — радиус данной окружности.
Площадь = lw
Здесь l — длина, а w — ширина данного прямоугольника.
Площадь, A = bh
Здесь a и b — смежные стороны параллелограмма, а h — высота.
Аналитическая геометрия в двух измерениях имеет дело с формулой сечения, формулой расстояния, центром тяжести треугольника, формулой середины и так далее. Все это определяется с использованием знаний о понятиях координатной геометрии.
Подобие и конгруэнтность в геометрии Когда две фигуры имеют одинаковую форму или одинаковый угол, но не имеют одинакового размера, говорят, что они подобны. Если две фигуры имеют одинаковую форму и размер, то говорят, что они равны. 93\)
Если две фигуры имеют одинаковую форму и размер, то говорят, что они равны. 93\)
Узнайте больше о Family of Lines здесь.
Некоторые другие связанные концепции твердотельной геометрии перечислены ниже.
Направляющие косинусы прямойЕсли направленная прямая, скажем, ‘R’, проходящая через начало координат, образует углы α, β и γ с осями x, y и z соответственно, то косинус этих углов, т. е. cos α, cos β и cos γ называются направляющими косинусами данной направленной линии ‘R’. Направляющие косинусы линии, соединяющей две точки: \(P(x_1,y_1,z_1)\text{ и }Q(x_2,y_2,z_2)\) определяются по формуле: 92}}\)
Уравнение прямой в трехмерной геометрииЕсли l, m, n — направляющие косинусы прямой, проходящей через точку \(\left(x_1,y_1,z_1\right)\ ), то уравнение прямой будет следующим:
\(\left(\frac{\left(x-x_1\right)}{l},\ \frac{\left(y-y_1\right)} {m},\ \frac{\left(z-z_1\right)}{n}\right)\)
Уравнение прямой, проходящей через две точки, скажем; \(\слева(x_1,y_1,z_1\справа)\) и \(\слева(x_2,y_2,z_2\справа)\) . Тогда уравнение прямой задается формулой: 92}}\right|\)
Тогда уравнение прямой задается формулой: 92}}\right|\)
Мы надеемся, что вы нашли эту статью о геометрии информативной и полезной, и, пожалуйста, не стесняйтесь обращаться к нам с любыми сомнениями или вопросами по этому поводу. Вы также можете скачать абсолютно бесплатное приложение Testbook и начать подготовку к любому государственному конкурсному экзамену, пройдя пробные тесты перед экзаменом, чтобы улучшить свою подготовку.
Часто задаваемые вопросы о геометрииВ.1 Что такое геометрия?
Ans.1 Геометрия – раздел математики, в котором изучаются различные виды фигур (безразмерные, одномерные, двухмерные и трехмерные) и их свойства.
Q.2 Кто является отцом геометрии?
Ответ 2 Отец геометрии — греческий математик; Евклид.
Q.3 Какие бывают типы линий в геометрии?
Ответ 3 Различные типы линий: прямые линии, пересекающиеся линии, поперечные линии, параллельные линии, перпендикулярные линии, параллельные линии и т. д.
д.
Q.4 Какое использование геометрии?
Ответ 4 Геометрия помимо математики и физики используется в различных инженерных областях, включая архитектуру, робототехнику, машины, астрономию, космос, автомобили и т. д.
Q.5 Какие бывают типы углов в геометрии?
Ans.5 Различные типы углов в геометрии: острый угол, прямой угол, тупой угол, прямой угол, угол отражения, полный угол и так далее.
Q.6 Какие существуют типы геометрии?
Ответ 6 Различные области геометрии включают в себя; евклидова, неевклидова, алгебраическая, проективная, дискретная и дифференциальная геометрия.
Q.7 Что такое формула координатно-геометрического расстояния?
Ответ 7 Формула расстояния между двумя точками \(A(x_1,\ y_1,\ z_1)\) и \(B(x_{2\ },y_2,\ z_2)\) в 3D самолет.
\(d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\)
Геометрия
Геометрия — это все о формах и их свойствах.
Если вы любите играть с предметами или рисовать, то геометрия для вас!
Геометрию можно разделить на:
Плоская геометрия касается плоских фигур, таких как линии, круги и треугольники… формы, которые можно нарисовать на листе бумаги
Solid Geometry — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.
| Подсказка: попробуйте нарисовать некоторые формы и углы, когда будете учиться… это поможет. |
Точка, линия, плоскость и тело
Точка не имеет размеров, только положение
Линия одномерная
Плоскость двухмерная (2D)
Твердое тело трехмерное (3D)
Почему?
Почему мы занимаемся геометрией? Чтобы открывать закономерности, находить площади, объемы, длины и углы и лучше понимать окружающий мир.
Плоская геометрия
Плоская геометрия — это формы на плоской поверхности (как на бесконечном листе бумаги).
- 2D-фигуры
- Упражнение: Сортировка фигур
- Треугольники
- Прямоугольные треугольники
- Интерактивные треугольники
- Четырехугольники (ромб, параллелограмм, и т.д.)
- Прямоугольник, ромб, квадрат, параллелограмм, трапеция и воздушный змей
- Интерактивные четырехугольники
- Параллелограмм в любом четырехугольнике
- Размеры бумаги
- Свободная игра фигур
- Периметр
- Зона
- Площадь плоских форм
- Инструмент расчета площади
- Площадь многоугольника по чертежу
- Деятельность: Сад
- Общий инструмент для рисования
- Калькулятор площади и калькулятор прямоугольника
Полигоны
Многоугольник — это двухмерная фигура, состоящая из прямых линий. Треугольники и прямоугольники являются многоугольниками.
Треугольники и прямоугольники являются многоугольниками.
Вот еще:
| Пентагон |
| Пентаграмма |
| Шестигранник |
- Свойства правильных многоугольников
- Диагонали многоугольников
- Интерактивные полигоны
Круг
- Круг
- Пи
- Площадь круга по линиям
- Круговой сектор и сегмент
- Площадь круга по секторам
- Упражнение: Бросание монеты на сетку
- Арка
- Кольцо
Теоремы о кругах (дополнительная тема)
Символы
В геометрии используется много специальных символов. Вот краткая справка для вас:
Вот краткая справка для вас:
Геометрические символы
Конгруэнтные и аналогичные
- Конгруэнтные фигуры
- Похожие формы
Углы
Типы уголков
| Острые углы | Прямые углы | Тупые углы | Прямоугольный | Рефлекторные углы | Полный оборот |
|
|
Использование чертежных инструментов
- Геометрические конструкции
- Использование транспортира
- Использование чертежного треугольника и линейки
- Использование линейки и компаса
Преобразования и симметрия
Преобразования:
- Вращение
- Отражение
- Перевод
- Изменение размера
Симметрия:
- Симметрия отражения
- Вращательная симметрия
- Точечная симметрия
- Линии симметрии плоских фигур
- Художник по симметрии
- Упражнение: Симметрия фигур
- Упражнение: Создание мандалы
- Упражнение: Раскрашивание (Четыре цвета Теорема)
- Мозаика
- Мастер тесселяции
Координаты
- Декартовы координаты
- Интерактивные декартовы координаты
- Игра «Найди координаты»
Более сложные темы плоской геометрии
Пифагор
- Теорема Пифагора
- Пифагорейские тройки
Конические секции
- Набор всех точек
- Конические секции
- Эксцентриситет
- Эллипс
- Анимация параболы и снаряда
- Гипербола
Теоремы круга
- Теоремы о кругах
- Касательные и секущие линии
- Теорема о пересекающихся секущих
- Теорема о пересекающихся хордах
- Угол пересекающихся секущих Теорема
Треугольные центры
Тригонометрия
Тригонометрия — отдельная тема, поэтому вы можете посетить:
- Введение в тригонометрию
- Индекс тригонометрии
Твердотельная геометрия
Solid Geometry — это геометрия трехмерного пространства, в котором мы живем…
. .. начнем с самых простых фигур:
.. начнем с самых простых фигур:
Общие 3D-фигуры
Многогранники и не-многогранники
Существует два основных типа твердых тел: «многогранники» и «не-многогранники»:
Многогранники (они должны иметь плоские грани) :
| куба и кубоидов (объем кубоида ) | |
| Платоновые тела | |
| Призмы | |
| Пирамиды |
Не многогранники (когда любая поверхность не плоский) :
| Сфера | Тор | |||
| Цилиндр | Конус |
- Модели многогранников
- Калькулятор объема и площади сферы
- Сфероид
- Поперечные сечения
- Вершины, грани и ребра
- Конус против сферы против цилиндра
- Пирамида против Конуса
- Призма против цилиндра
- Пирамида против Куба
- Объем горизонтального цилиндра
- Теорема Эйлера
- Пифагор в 3D
- Гиперкубы
- Математика строителя
- Моменты площади
28 важнейших математических формул SAT, которые вы ДОЛЖНЫ знать
Математический тест SAT не похож ни на один математический тест, который вы проходили раньше. Он разработан, чтобы взять концепции, к которым вы привыкли, и заставить вас применять их новыми (и часто странными) способами. Это сложно, но при внимательном отношении к деталям и знании основных формул и понятий, охватываемых тестом, вы можете улучшить свой результат.
Он разработан, чтобы взять концепции, к которым вы привыкли, и заставить вас применять их новыми (и часто странными) способами. Это сложно, но при внимательном отношении к деталям и знании основных формул и понятий, охватываемых тестом, вы можете улучшить свой результат.
Итак, какие формулы вам нужно выучить для математической секции SAT до дня экзамена? В этом полном руководстве я расскажу о каждой важной формуле, которую вы ДОЛЖНЫ знать, прежде чем сесть за тест. Я также объясню их на случай, если вам понадобится освежить память о том, как работает формула. Если вы поймете каждую формулу в этом списке, вы сэкономите драгоценное время на тесте и, возможно, ответите правильно на несколько дополнительных вопросов.
Формулы, представленные на SAT, объяснение
Это именно то, что вы увидите в начале обоих математических разделов (с калькулятором и без калькулятора). Может быть легко пройти мимо него, поэтому ознакомьтесь с формулами сейчас, чтобы не тратить время в день теста.
Вам дается 12 формул на самом тесте и три закона геометрии. Запоминание приведенных формул может быть полезным и сэкономить ваше время и усилия, но в этом, в конечном счете, нет необходимости, , поскольку они даются в каждом математическом разделе SAT.
Вам выдаются только формулы по геометрии, поэтому прежде всего запомните формулы по алгебре и тригонометрии до экзамена (мы рассмотрим их в следующем разделе). В любом случае вам следует сосредоточить большую часть своих учебных усилий на алгебре, потому что в новом SAT геометрия была уменьшена и теперь составляет всего 10% (или меньше) вопросов в каждом тесте. 92$$
- π — константа, которую для целей SAT можно записать как 3,14 (или 3,14159)
- r радиус окружности (любая линия, проведенная от центральной точки прямо к краю окружности)
Длина окружности
$C=2πr$ (или $C=πd$)
- d — диаметр окружности.
 Это линия, которая делит круг пополам через середину и касается двух концов круга на противоположных сторонах. Это в два раза больше радиуса.
Это линия, которая делит круг пополам через середину и касается двух концов круга на противоположных сторонах. Это в два раза больше радиуса.
Площадь прямоугольника
$$A = 1/2bh$$ Площадь треугольника
- В прямоугольном треугольнике две меньшие стороны ( a и b ) возведены в квадрат. Их сумма равна квадрату гипотенузы (с, самой длинной стороны треугольника).
Свойства особого прямоугольного треугольника: равнобедренный треугольник
- Равнобедренный треугольник имеет две равные по длине стороны и два равных угла, противоположных этим сторонам.
- В равнобедренном прямоугольном треугольнике всегда есть угол 90 градусов и два угла по 45 градусов.

- Длины сторон определяются по формуле: $x$, $x$, $x√2$, где гипотенуза (сторона, противоположная 90 градусам) имеет длину одной из меньших сторон *$√2$.
- Например, равнобедренный прямоугольный треугольник может иметь длины сторон $12$, $12$ и $12√2$.
Свойства особого прямоугольного треугольника: Треугольник с углами 30, 60, 90 градусов
- Треугольник со сторонами 30, 60, 90 описывает градусные меры трех углов треугольника.
- Длины сторон определяются по формуле: $x$, $x√3$ и $2x$
- Сторона, противоположная 30 градусам, является наименьшей, ее размер равен $x$.
- Сторона, противоположная 60 градусам, является средней длиной и имеет размер $x√3$.
- Сторона, противоположная 90 градусам, является гипотенузой (самая длинная сторона) и имеет длину $2x$.
- Например, треугольник 30-60-90 может иметь длины сторон $5$, $5√3$ и $10$.
92h$$
- $r$ — радиус круглой стороны конуса.

- $h$ — высота заостренной части конуса (измеряется от центра круглой части конуса).
Объем пирамиды.
Закон: количество градусов в окружности равно 360
Закон: количество радиан в окружности равно $2π$
Закон: количество градусов в треугольнике равно 1423 9000 90 Напрягите свой мозг, потому что вот формулы, которые вам нужно запомнить. Для большинства формул из этого списка вам просто нужно пристегнуться и запомнить их (извините). Некоторые из них, однако, полезно знать, но в конечном счете их не нужно запоминать, так как их результаты можно рассчитать другими способами. (Однако знать их все же полезно, так что относитесь к ним серьезно). Мы разделили список на «Необходимо знать», и «Полезно знать», в зависимости от того, являетесь ли вы тестируемым, любящим формулу, или любителем тестов меньше формул, тем лучше. $$({(x_1 + x_2)}/2, {(y_1 + y_2)}/2)$$ 2 2 2 Формулы, не указанные в тесте

Наклоны и графики
Необходимо знать

Полезно знать
Вам не нужна эта формула , так как вы можете просто изобразить свои точки, а затем создать из них прямоугольный треугольник. Расстоянием будет гипотенуза, которую можно найти по теореме Пифагора.
Круги
Полезно знать
- Длина дуги
- Зная радиус и градусную меру дуги из центра, найдите длину дуги
- Используйте формулу для длины окружности, умноженной на угол дуги, деленной на общий угол окружности (360)
- $$L_{\дуга} = (2πr)({\градус\мера\центр\из\дуги}/360)$$
- Например, дуга в 60 градусов составляет $1/6$ от общей длины окружности, потому что $60/360 = 1/6$
- Площадь сектора дуги
- Зная радиус и градусную меру дуги от центра, найдите площадь сектора дуги
- Используйте формулу для площади, умноженной на угол дуги, деленной на общий угловой размер окружности 92) ({\ степень \ мера \ центр \ из \ дуги} / 360) $ $
- Зная радиус и градусную меру дуги от центра, найдите площадь сектора дуги
- Альтернативой запоминанию «формулы» является просто остановиться и логически подумать об окружностях дуги и площади дуги.

- Вы знаете формулы площади и длины окружности (поскольку они находятся в заданном вами поле уравнения на тесте).
- Вы знаете, сколько градусов в окружности (потому что это указано в поле уравнения в тексте).
- Теперь сложите их вместе:
- Если дуга охватывает 90 градусов окружности, она должна составлять $1/4$ общей площади/длины окружности, потому что $360/90 = 4$. Если дуга находится под углом 45 градусов, то это $1/8$ окружности, потому что $360/45 = 8$.
- Концепция точно такая же, как и формула, но она может помочь вам думать о ней именно так, а не как о «формуле» для запоминания.
Алгебра
Необходимо знать 92-4ac}}/{2a}$.
Примечание: Если вы знаете, как составить квадрат, то вам не нужно запоминать квадратное уравнение. Однако, если вам не совсем удобно заполнять квадрат, то относительно легко запомнить квадратную формулу и иметь ее наготове. Я рекомендую выучить его под мелодию «Pop Goes the Weasel» или «Row, Row, Row Your Boat».
Я рекомендую выучить его под мелодию «Pop Goes the Weasel» или «Row, Row, Row Your Boat».
Средние значения
Необходимо знать
- Среднее — это то же самое, что и среднее .
- Найти среднее/среднее значение набора чисел/терминов
$$\Mean = {\sum\of\the\terms}/{\число\различных\terms}$$
- Найти среднюю скорость
$$\Speed = {\total \distance}/{\total \time}$$
Вероятности
Необходимо знать
- Вероятность — это представление вероятности того, что что-то произойдет.
$$\text»Вероятность исхода» = {\text»количество желаемых исходов»}/{\text»общее количество возможных исходов»}$$
Полезно знать
- Вероятность 1 гарантированно произойдет. Вероятность 0 никогда не произойдет.
Проценты
Необходимо знать
- Найдите x процентов от заданного числа n.

$$n(x/100)$$
- Узнать, сколько процентов составляет число n от другого числа m.
$$(n100)/m$$
- Выясните, от какого числа n составляет x процентов.
$$(n100)/x$$
Тригонометрия
Тригонометрия — это новое дополнение к новому математическому разделу SAT 2016 года. Хотя это составляет менее 5% вопросов по математике, вы не сможете ответить на вопросы по тригонометрии, не зная следующих формул.
Необходимо знать
- Найдите синус угла, зная размеры сторон треугольника.
$sin(x)$= Мера стороны, противоположной углу / Мера гипотенузы
На приведенном выше рисунке синус отмеченного угла равен $a/h$.
- Найдите косинус угла, зная длины сторон треугольника.
$cos(x)$= Мера стороны, примыкающей к углу / Мера гипотенузы
На рисунке выше косинус отмеченного угла равен $b/h$.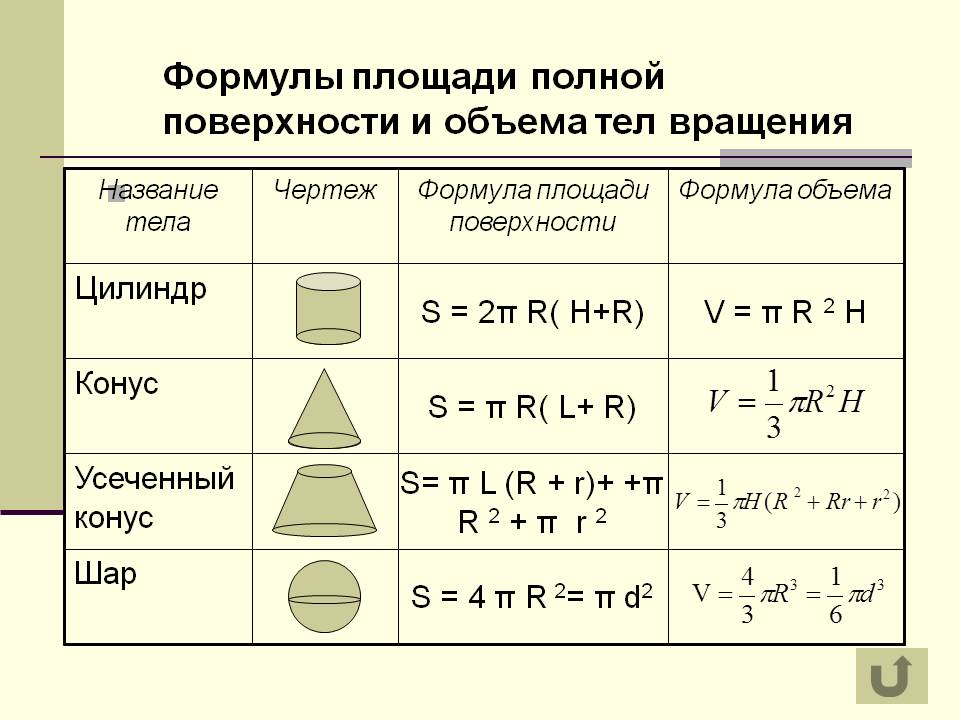
- Найдите тангенс угла, зная длины сторон треугольника.
$tan(x)$= Мера стороны, противоположной углу / Мера стороны, примыкающей к углу
На рисунке выше тангенс помеченного угла равен $a/b$.
- Полезным трюком с памятью является аббревиатура: SOHCAHTOA.
S INE равняется O PPOSITE Более H Ypotenuse
C osine Equals A DJacent более H Ypotenus
SAT Математика: за пределами формул
Хотя это все формул , которые вам понадобятся (те, что вам дали, а также те, которые вам нужно запомнить), этот список не охватывает все аспекты SAT Math. Вам также нужно будет понять, как факторизовать уравнения, как манипулировать абсолютными значениями и решать их, как манипулировать и использовать показатели степени и многое другое. Все эти темы раскрыты здесь.
Еще одна важная вещь, о которой следует помнить, это то, что запоминание формул из этой статьи, которые не были даны вам на тесте, важно, знание этого списка формул не означает, что вы готовы к SAT Math. Вам также необходимо попрактиковаться в применении этих формул для ответов на вопросы, чтобы вы знали, когда имеет смысл их использовать.
Вам также необходимо попрактиковаться в применении этих формул для ответов на вопросы, чтобы вы знали, когда имеет смысл их использовать.
Например, если вас попросили рассчитать вероятность того, что из банки, содержащей три белых и четыре черных шарика, будет вынут белый шарик, достаточно легко понять, что вам нужно воспользоваться следующей формулой вероятности:
$$\text»Вероятность исхода» = {\text»количество желаемых исходов»}/{\text»общее количество возможных исходов»}$$
и используйте его, чтобы найти ответ:
$\text»Вероятность белого шарика» = {\text»количество белых шариков»}/{\text»общее количество шариков»}$
$\text «Вероятность белого шарика» = 3/7$
Однако на математическом разделе SAT вы также столкнетесь с более сложными вероятностными вопросами, такими как этот:
Нет
от 1 до 4
5 или более
Всего
Группа Х
15
28
57
100
Группа Y
21
11
68
100
Всего
36
39
125
200
Данные в приведенной выше таблице были получены исследователем сна, изучающим количество снов, которые люди вспоминают, когда их просят записывать свои сны в течение одной недели. Группа X состояла из 100 человек, которые ложились спать раньше, а группа Y состояла из 100 человек, которые ложились спать позже. Если случайным образом выбрать человека из тех, кто вспомнил хотя бы 1 сон, какова вероятность того, что этот человек принадлежал к группе Y?
Группа X состояла из 100 человек, которые ложились спать раньше, а группа Y состояла из 100 человек, которые ложились спать позже. Если случайным образом выбрать человека из тех, кто вспомнил хотя бы 1 сон, какова вероятность того, что этот человек принадлежал к группе Y?
A) 68/100$
B) 79/100$
C) 79/164$
D) 164/200$
В этом вопросе нужно синтезировать много информации: таблица данных, длинное объяснение таблицы в два предложения, а затем, наконец, что вам нужно решить.
Если вы не решали такого рода задачи, вы не обязательно поймете, что вам понадобится заученная вами формула вероятности, и вам может потребоваться несколько минут, чтобы порыться в таблице и поломать голову, чтобы понять как получить ответ — минут, которые вы теперь не можете использовать для решения других задач в разделе или для проверки своей работы.
Если вы практиковали такие вопросы, вы сможете быстро и эффективно применить эту заученную формулу вероятности и решить задачу:
Это вопрос вероятности, поэтому я, вероятно, (ха) необходимо использовать эту формулу:
$$\text»Вероятность исхода» = {\text»количество желаемых исходов»}/{\text»общее количество возможных исходов»}$$
Итак, количество желаемых результатов — это любой из группы Y, кто помнит хотя бы один сон. Вот эти выделенные жирным шрифтом ячейки:
Вот эти выделенные жирным шрифтом ячейки:
| Нет | от 1 до 4 | 5 или более | Всего |
Группа Х | 15 | 28 | 57 | 100 |
Группа Y | 21 | 11 | 68 | 100 |
Всего | 36 | 39 | 125 | 200 |
И тогда общее количество возможных исходов равно всем людям, которые вспомнили хотя бы один сон. Чтобы получить это, я должен вычесть количество людей, которые не вспомнили хотя бы один сон (36), из общего числа людей (200). Теперь я подключу все обратно к уравнению:
$\text»Вероятность исхода» = {11+68}/{200-36}$
$\text»Вероятность исхода» = {79}/{164}$
Верно ответ: C) $79/164$
Вывод из этого примера: как только вы запомните эти математические формулы SAT, вам нужно научиться, когда и как их использовать, тренируясь на практических вопросах.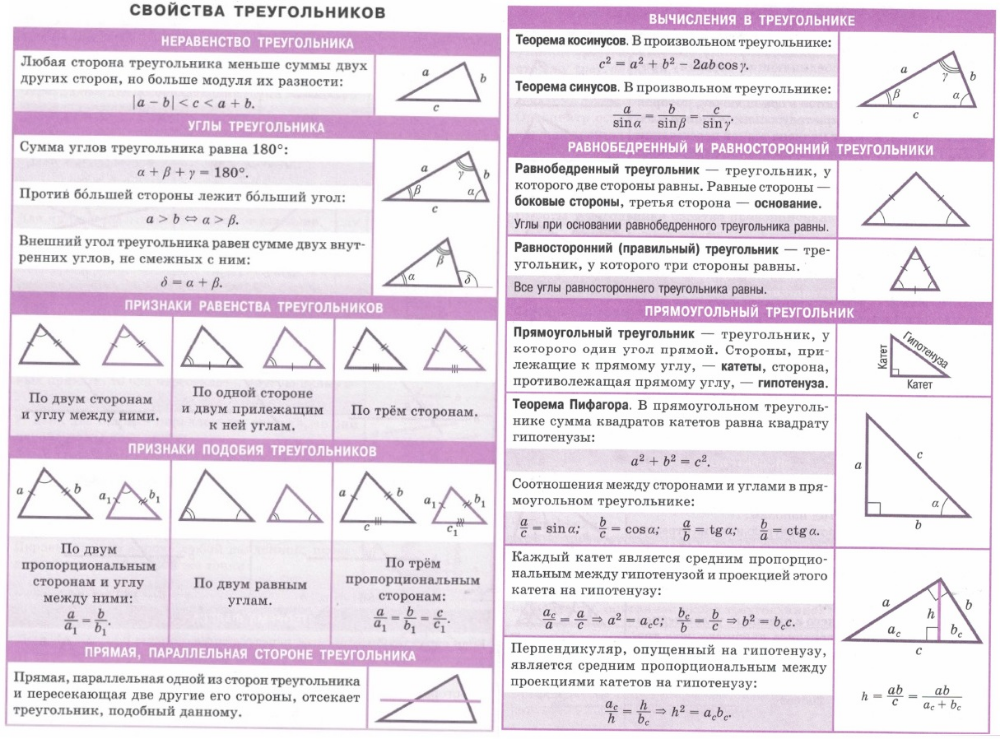
Что дальше?
Теперь, когда вы знаете основные формулы SAT, возможно, пришло время ознакомиться с полным списком математических знаний и ноу-хау SAT, которые вам понадобятся перед днем экзамена. А для тех из вас, у кого особенно высокие цели, ознакомьтесь с нашей статьей о том, как получить 800 баллов по математике SAT идеальным бомбардиром SAT.
В настоящее время средний балл по математике? Читайте нашу статью о том, как улучшить свой результат, если ваш текущий результат ниже диапазона 600.
Хотите улучшить свой результат SAT на 160 баллов?
Посетите наши лучшие в своем классе онлайн-курсы по подготовке к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой результат SAT на 160 или более баллов.
Наши занятия полностью онлайн, и их проводят эксперты SAT. Если вам понравилась эта статья, вам понравятся наши занятия. Наряду с занятиями под руководством экспертов вы получите индивидуальное домашнее задание с тысячами практических задач, организованных по индивидуальным навыкам, чтобы вы могли учиться наиболее эффективно.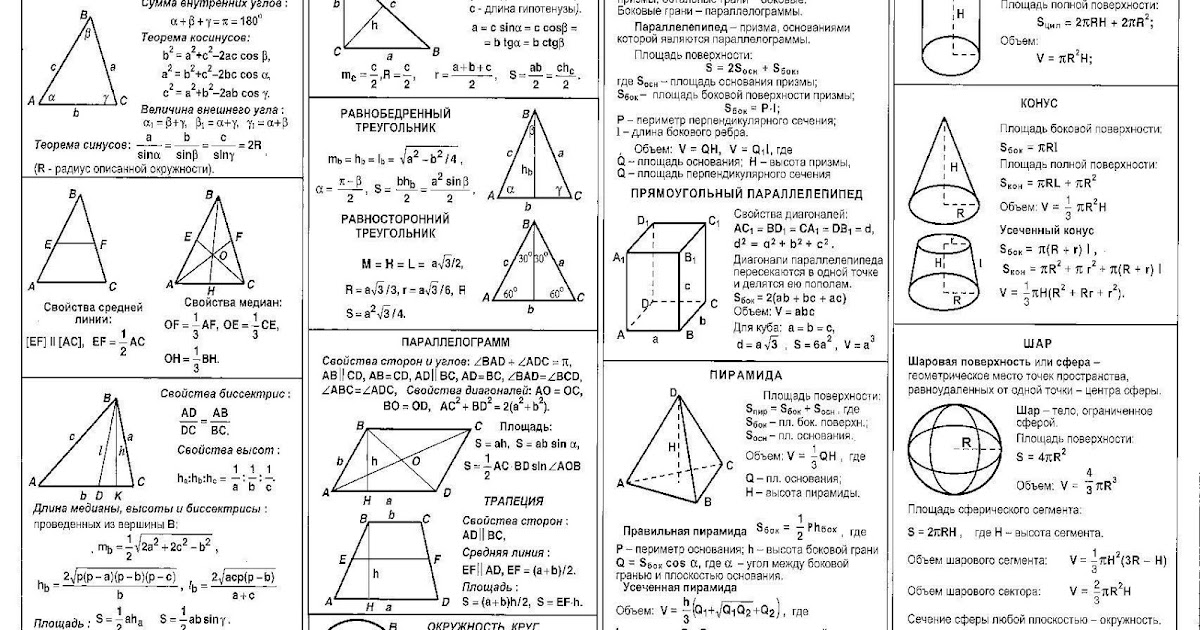 Мы также предоставим вам пошаговую индивидуальную программу, чтобы вы никогда не запутались в том, что изучать дальше.
Мы также предоставим вам пошаговую индивидуальную программу, чтобы вы никогда не запутались в том, что изучать дальше.
Попробуйте без риска сегодня:
Есть друзья, которым также нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Кортни Монтгомери
Об авторе
Кортни набрала 99-й процентиль по SAT в старшей школе и окончила Стэнфордский университет со степенью в области культурной и социальной антропологии. Она увлечена тем, чтобы предоставить образование и инструменты для достижения успеха учащимся из всех слоев общества и слоев общества, поскольку она считает, что открытое образование является одним из величайших социальных уравнителей. Имеет многолетний опыт репетиторства, в свободное время пишет творческие работы.
Карманный справочник GRE по геометрии: концепции и формулы
Геометрия в GRE Quant очень важна, когда время всегда в кризисе. Каждый студент, изучающий математику, знает, что геометрия — это глава, в которой оценивается оценка. Небольшое внимание к этой главе повысит ваш счет в геометрической прогрессии.
Каждый студент, изучающий математику, знает, что геометрия — это глава, в которой оценивается оценка. Небольшое внимание к этой главе повысит ваш счет в геометрической прогрессии.
Начнем с обзора GRE quant. Математика в GRE состоит из 2 разделов, каждый из которых содержит 20 вопросов, а общее время составляет всего 35 минут.
Как правило, в GRE quant появляются 2 типа вопросов.
- Количественный сравнение
- Проблема решение
В дополнение к этому тест имеет числовой ввод задачи, в которых студент должен ввести свои собственные ответы.
Дело в том, что все знают, что количественные рассуждения GRE учебный план до 10 -го класса. Но представление о проблема в тесте другая. Вот как GRE измеряет рассуждения способностей испытуемых.
Квант GRE включает в себя как арифметику, так и геометрию. Сегодня мы рады представить вам краткое «полное руководство по геометрии в GRE Quant».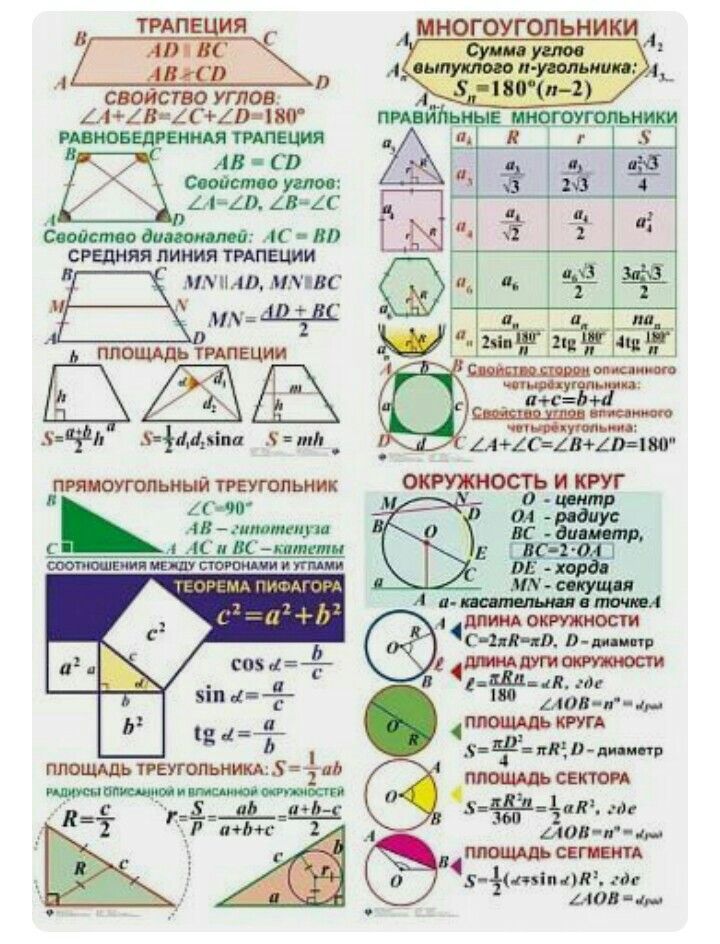 Это карманные заметки для справки с первого взгляда.
Это карманные заметки для справки с первого взгляда.
ГЕОМЕТРИЯ , as we все знают, легко понять, но кризис обычно возникает, когда вы решаете проблема. Потому что у большинства студентов неправильное представление о том, что квантовая геометрия GRE можно решить только на глазок. Но это неправда.
Чтобы преуспеть в геометрии, у нас есть набор стратегии. Теперь давайте обсудим один за другим.
Каким бы ни был расчет, если это геометрия, то Есть 3 правила вашего успеха.
- Определения
- Свойства
- Применение ( это касается практики) и теперь вы готовы к геометрии.
Как сказано; сначала определения.
Геометрия GRE: Линии- Прямая линия с конечными точками называется
линия.

- Луч исходит из точки и продолжается в только одно направление.
- Линия – сегмент является частью линии. В основном линия отрезки используются в геометрических построениях (в том числе и на схемах).
- Есть 3 основные пары линий; Пересекающиеся линии, перпендикулярные линии и параллельные линии.
- Две линии, пересекающиеся в одной точке, образуют УГОЛ с одной стороны, и эта точка называется ВЕРШИНА . Поскольку у линии нет концов, две пересекающиеся прямые образуют в общей сложности 4 угла.
- Пределы острого угла от 0 до 90 градусов.
- Прямой угол равен 90 градусов.
- Тупой угол ограничивается от 90 до 180 градусов.
- Прямой угол 180 градусов.
- Угол от 180 до 360 называется рефлекторным углом.
- Когда две прямые пересекаются в одной точке, пары противоположных углов равны.

- Два угла являются дополнительными, если их сумма углов составляет 180 градусов.
X +y =180 => x = 180 – y => y = 180 – x
- Два угла являются дополнительными, если их сумма углов составляет 90 градусов.
X +y =90 => x = 90 – y => y = 90 – x
- Перпендикулярные прямые пересекаются под прямым углом.
- Две параллельные линии имеют одинаковый наклон.
- Кратчайшее расстояние от точки до прямой равно всегда перпендикуляр.
- Когда параллельные прямые пересекаются поперечные, есть три основных соотношения углов;
Поперечная теория:
- Альтернативные внутренние углы равны
- Соответствующие углы равны
- Внутренние углы на одной стороне поперечные являются дополнительными.
«Треугольники» — действительно обширная тема для изучения.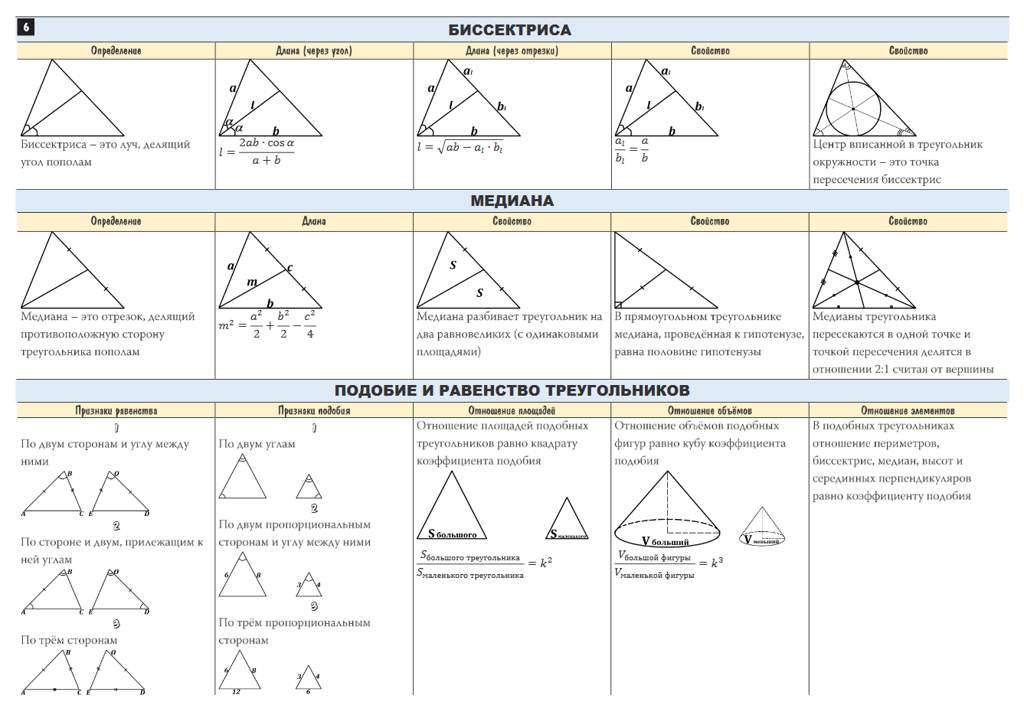 Как только вы
достичь уровня теоремы Пифагора, это скачок в другую тему.
Начнем с определений.
Как только вы
достичь уровня теоремы Пифагора, это скачок в другую тему.
Начнем с определений.
Любая замкнутая двумерная фигура с тремя сторонами называется Треугольником. У него 3 стороны и 3 угла. Есть 3 основные классификации, основанные на сторонах.
- Если все стороны треугольника равны, то это равносторонний треугольник. Следовательно, все углы равны и равны 60 градусам.
- Если 2 стороны треугольника равны, то это равнобедренный треугольник. Следовательно, 2 угла, опирающиеся на равные стороны при основании, равны
- Если все три стороны различны, то это разносторонний треугольник. Он имеет три разных угла.
Если треугольник имеет один прямой угол, то говорят, что он равен Прямоугольный треугольник . Один из углы = 90 градусов, а самая длинная сторона называется «гипотенуза» , противоположная прямому углу.
Сумма всех трех углов треугольника => A + B + C = 180
Высота треугольника – это линия, соединяющая основание
перпендикулярно от противоположного угла.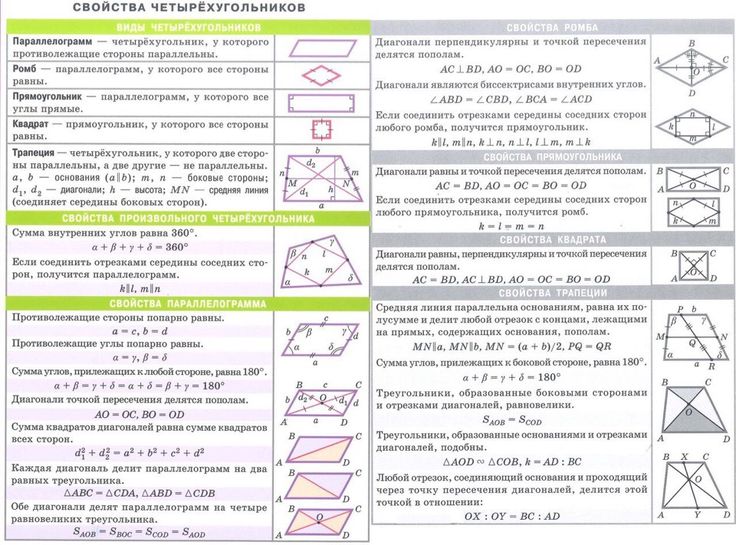
Высота равностороннего и равнобедренного треугольника треугольник делит пополам угол и основание тоже.
Для прямоугольного треугольника с прямым углом на любой стороне основание, высота измеряется как длина перпендикуляра.
В некоторых случаях, например, в случае тупоугольного треугольников, основание должно быть расширено, чтобы нарисовать высоту.
Высота также называется высотой треугольника.
Площадь треугольника ½ бх. [b — основание, h — высота треугольника]
В каждом треугольнике длинная сторона лежит против большего угла и меньшая сторона, противоположная меньшему углу.
Теорема Пифагора:Эта теорема подразумевает прямоугольные треугольники. Ее еще называют «Теорема о правой гипотенузе». Там указано, что сумма отдельных квадратов основания и высоты равна квадрату гипотенузы прямоугольного треугольника.
Пифагорейские тройки — это числа, которые чаще всего представляют стороны прямоугольного треугольника.
Пример: 3,4,5 и 5,12,13. Наибольшее число в каждом наборе представляет собой гипотенузу прямоугольного треугольника.
Конгруэнтный треугольник:Конгруэнтность треугольника обычно основана на пропорции и соответствии размеров. Конгруэнтные треугольники также называют подобными или тождественными треугольниками.
[ Также читайте: GRE Math Tips and Tricks ]
Треугольники разного размера, но с одинаковыми размерами конгруэнтны. У нас есть четыре свойства конгруэнтности треугольников. Когда у тебя есть два треугольника для сравнения конгруэнтности;
- Свойство стороны угла стороны (SAS) , в котором совпадают 2 стороны и 1 угол.
- Свойство угла стороны угла (ASA) , в котором совпадают 2 угла и 1 сторона.
- Боковая сторона боковая собственность (SSS) , в котором совпадают все 3 стороны.

- Угол Свойство угла (AAA) , в котором совпадают все 3 угла.
- Правая сторона гипотенузы (RHS), в которой любая сторона и гипотенуза прямоугольного треугольника совпадают.
Четырехугольник — замкнутая фигура с 4 прямыми линиями. Сумма всех внутренних углов четырехугольника составляет 360 градусов.
Каждая двумерная замкнутая фигура с четырьмя стороны — четырехугольник. Поэтому квадрат, прямоугольник, параллелограмм, ромб, трапеции — четырехугольники. Перейдем к их основным свойствам. площадь поверхности четырехугольника есть произведение длины и ширины. периметр это сумма всех сторон.
Четырехугольники делятся на 5 различных типов в зависимости от их свойств.
Квадрат:Все стороны равны. Каждый угол равняется 90 градусам. Диагонали пересекают друг друга под прямым углом.
Площадь = сторона * сторона
Периметр = 4 * сторона
Прямоугольник: Противоположные стороны равны. Каждый
угол равен 90 градусов. Диагонали делят друг друга пополам, но не справа
углы.
Каждый
угол равен 90 градусов. Диагонали делят друг друга пополам, но не справа
углы.
Площадь = длина * ширина
Периметр = 2* (l + b)
Параллелограмм:4 Противоположные стороны равны. Противоположный углы равны. Диагонали делят друг друга пополам, но не под прямым углом.
Площадь = длина * ширина
Периметр = 2* (l + b)
Ромб: Все стороны равны по длине. Противоположные стороны параллельны друг другу. Диагонали делятся пополам перпендикулярно.Смежные углы дополнительные (угол 1 + угол 2 = 180).
Углы при вершине ромба не равны равен 90 градусам.
Предположим, что «а» и «б» являются длины диагоналей, тогда
Площадь ромба = (a * b)/2
Периметр = 4 * длина стороны.
[ Также читайте: Как подготовиться к GRE по математике ]
Трапеция: Только основание и его противоположность
стороны параллельны друг другу.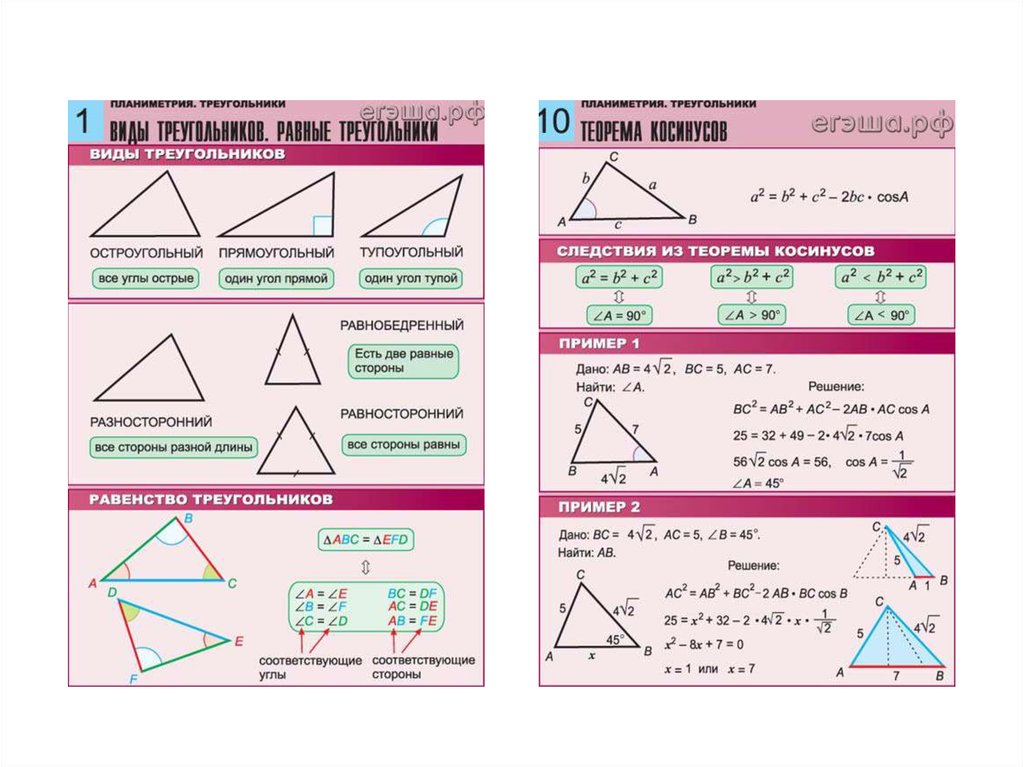 Стороны, углы или диагонали не равны.
Стороны, углы или диагонали не равны.
Площадь трапеции: ½ * высота трапеция * (длина основания + длина стороны, противоположной основанию)
Это среднее двух оснований, умноженных на высоту.
A = 1/2 [L + L2] * h
Периметр = сумма длин всех сторон = L + L1 + L2 +L3
7 GRECLES Геометрия3Окружность определяется как набор точки, равноудаленные от центра на плоской поверхности. Периметр круга называется « окружность круга ».
Теперь поговорим о кругах терминология
Радиус: Радиус окружности отрезка, соединяющего центр в любую точку окружности.
Аккорд: Аккорд — это линия отрезок, соединяющий любые две точки окружности.
Диаметр: Диаметром окружности называется отрезок, соединяющий любой две точки окружности, проходящие через центр.
Диаметр также обозначается как 2 * радиус. Это самый длинный аккорд
круг.
Это самый длинный аккорд
круг.
Диаметр = 2 * радиус => радиус = диаметр / 2
Дуга: Часть окружности – это дуга окружности.
Сектор: Площадь, ограниченная окружностью (дугой) под углом центр (как вершина) называется сектором.
СЕКАНТ — линия, проходящая через окружность пересекающиеся в 2 точках.
ТАНГЕНТ — прямая, проходящая через окружность пересекающиеся только в 1 точке.
Окружность окружности является измерением края границы круга.
C = 2 π r = π d where π = 222/7 or 3.14 approximately
Area of the circle
A = π r 2 where π = 222/7 или 3.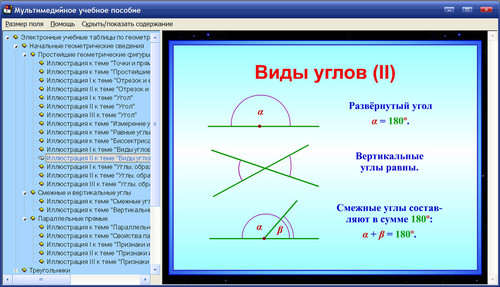 14 примерно
14 примерно
«r» можно заменить на «d/2»
SO A = πd 2 /4
ГРЕ Геометрия Формулы: ARC и Sector Formulas Если ‘ 99 2 Если‘ 999 ’ Если‘ 999 ’ Если‘ 999 ’ Если‘ 99 ’ .
угол, образуемый дугой или сектором, тогда Длина дуги = ( θ /360) * длина окружности = ( θ /360) * 2 r Площадь сектора = ( θ /360) * Площадь = ( θ /360) * π R 2 3D Геометрия. Цилиндр, конус и полусфера.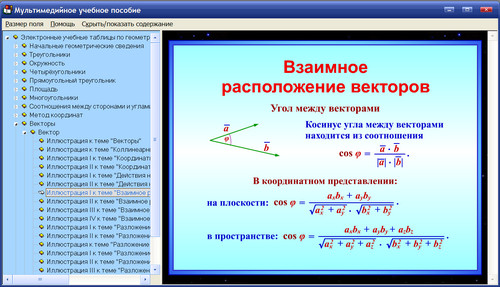
Существует два основных расчета 3D фигуры и они общей поверхности область и том . Площадь боковой поверхности представляет собой сумму всех поверхности, кроме верхней и нижней.
Прямоугольник:Прямоугольник – это объем, покрытый 6 прямоугольники, где все прямоугольники называются гранями прямоугольного параллелепипеда.
Вершины являются точками пересечение 3 ребер. Есть 8 вершин.
Краем прямоугольного параллелепипеда является линия отрезок, соединяющий соседние вершины. Всего 12 ребер.
Все углы при вершинах равны 90 градусов.
Диагонали делят друг друга пополам.
Если «l» — длина, «w» — ширина, а «h» — высота; затем
GRE Geometry Formulas: Cuboid FormulasTotal surface area = 2(lw + wh + hl)
Lateral surface area = 2h (l+w)
Volume of кубоид’ = l * w * h
Длина наибольшей диагонали = √ (l² + w² + h²)
Куб: измерения всех граней являются квадратами. У него 6 граней, 8 вершин и 12
края. Все углы при вершинах равны 90. Длина, ширина и
высота куба одинакова.
У него 6 граней, 8 вершин и 12
края. Все углы при вершинах равны 90. Длина, ширина и
высота куба одинакова.
Если «l» — длина, «b» — ширина, а «h» — высота куба. But for a cube l = b = h = x
GRE Geometry Formulas: Cube FormulaVolume = x³
Total surface area = 6x 2
Площадь боковой поверхности = 4x 2
Длина диагонали куба = √3x
CYLINDE твердое тело с двумя круглыми и параллельными гранями, соединенными криволинейной поверхностью. Главные размеры цилиндра – радиус основания и высота.«Высота» цилиндра расстояние между двумя круглыми гранями.
Обычно «h» — это высота цилиндра, а «r» — его радиус.
Volume of a cylinder = π r 2 h
Lateral surface area = 2 π rh
Цилиндр и призма подобны потому что они имеют одинаковое сечение везде.
Конус:Конус представляет собой трехмерную форму. обычно с круглым основанием, а форма постепенно сужается до одной точки. А конус очень похож на пирамиду, но пирамида имеет треугольное основание. конус не имеет граней, кроме одного кругового основания. У него нет ребер и есть только 1 вершина. Это называется вершина.
Расстояние между центром основание и вершину (вершину) называют высотой конуса(не в случае косого конуса).
Конус имеет 3 важных показания (замеры). Они есть;
- Высота (перпендикулярное расстояние от вершина)
- Радиус (радиус круглого основания) и
- Наклонная высота (расстояние между вершиной
и любую точку на окружности круглого основания).

Эти 3 измерения составляют прямоугольный треугольник. Следовательно, можно применить теорему Пифагора.
GRE Geometry Formulas: Cone FormulaThe slant height l = √(r 2 +h 2 )
Volume of a cone = ⅓ πr 2 H
Общая площадь поверхности = .
+ πr 2 => πr being a common factor, TSA of a cone = πr( l + r) A sphere is a уникальная трехмерная фигура без вершин и без ребер. Том сферы = (4/3) * π * R 3 2 . 4 * π * R 2 A Hemis. У него есть один
круговой край. У него только одна грань и нет вершины. Основным измерением является «радиус» или «r». Площадь искривленной поверхности
полусфера: 2 * π * R 2  У него нет ни граней, ни он плоский. Сфера имеет только 1 заметное измерение. Это его радиус «r».
У него нет ни граней, ни он плоский. Сфера имеет только 1 заметное измерение. Это его радиус «r».
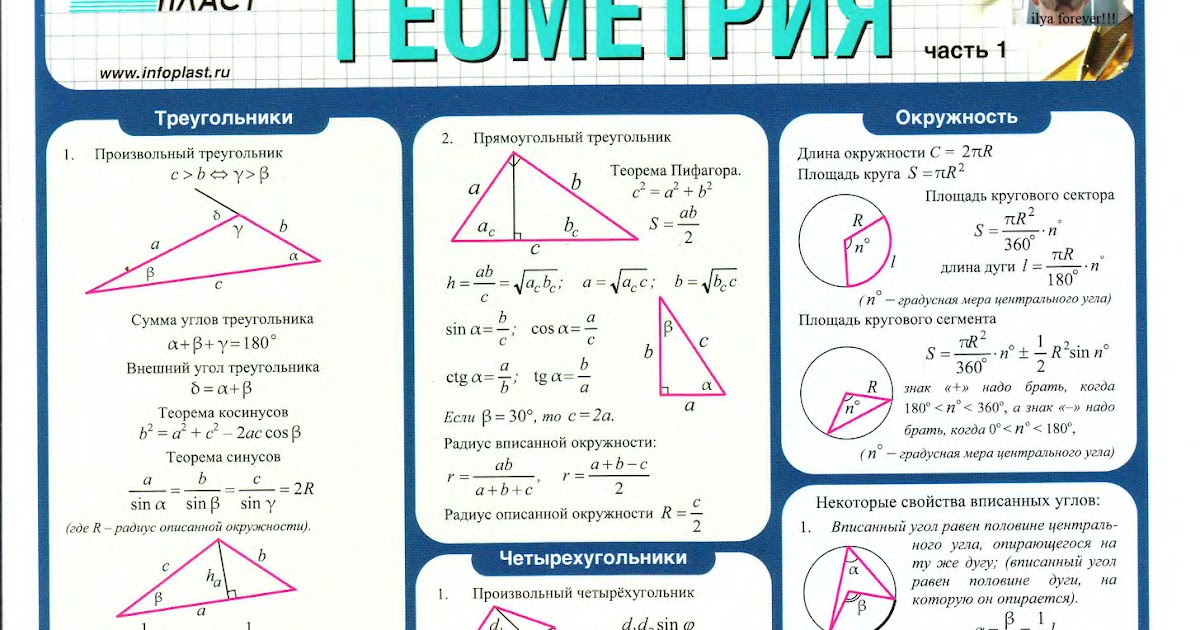 полусфера: площадь изогнутой поверхности + площадь основания круга =
полусфера: площадь изогнутой поверхности + площадь основания круга = = 2 * № * р 2 + π * r 2 = 3 * π * r 2
Volume of a hemisphere: (2/3) * π * р 3
Площадь полого полушария: Область внешней полусферы – Область внутренней полусферы
GRE Geometry Concept: Координатная геометрия Координатная плоскость: Расчеты в координатной геометрии выполняются по координатам
– ось ординат.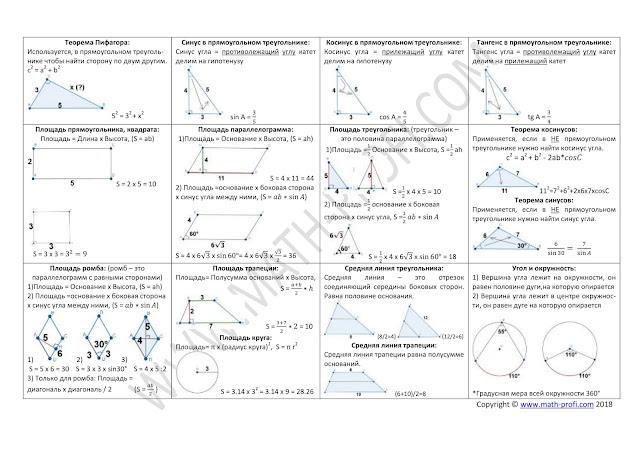 Ключевым элементом оси координат является числовая линия.
Ключевым элементом оси координат является числовая линия.
Номера расположены в порядке возрастания слева направо где числа справа от нуля положительны, а числа слева отрицательны.
Теперь нарисуйте линию, перпендикулярную числовой прямой. пересекающиеся в точке «0». Числа выше «0» положительные, а числа ниже отрицательные.
Говорят, что горизонтальная линия является осью X, а вертикальная линия – ось Y. Следовательно, это оси координат. Их точка пересечения называется началом координат (0, 0).
Теперь подумайте об оси координат, а не о числовой прямой;
По оси X числа справа от начала и положительны и увеличиваются дальше вправо, а числа слева от начала отрицательны и убавляем дальше влево
По оси Y числа выше нуля положительные и увеличиваются выше, а числа ниже отрицательные и уменьшаются дальше.
Точка на координатной плоскости: Точка на координатной плоскости представлена
упорядоченная пара (x, y), где «x» — абсцисса, а «y» — ордината. Они есть
координирует коллективно. Координаты представляют собой показания на оси
соответственно.
Они есть
координирует коллективно. Координаты представляют собой показания на оси
соответственно.
Квадрант: Оси «X» и «Y» делят координатную плоскость на 4 квадранта, считая против часовой стрелки, начиная с 1 st квадрант
Примечание : Если x ≠ y, то (x, y) и (y, x) представляют разные точки на плоскости.
Геометрические формулы GRE: Координатная геометрическая формулаФормула расстояния: Формула расстояния по координате плоскость извлечена из теоремы Пифагора. Если (x, y) и (a, b) 2 точки на плоскости то по пифагорейцу Теорема , тогда
Расстояние D 2 = (x — a) 2 + (Y — B) 2
9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 9003 ) 2 + (y − b) 2
) 2 + (y − b) 2 Формула средней точки: Предположим, что (x, y) и (a, b) равны 2 точки на плоскости;
Средняя точка между двумя точками определяется как M = (x + а/2, у + б/2)
Это среднее значение соответствующих координат 2 балла.
Формула наклона: Наклон линии измеряется по формуле уклона. Вертикальное изменение наклона называется подъемом, а горизонтальное изменение называется Run. Наклон – это отношение вертикального изменения к изменение по горизонтали.
Пусть (x, y) и (a, b) — две точки на плоскости, тогда уклон – это подъем над прогоном и определяется по формуле;
м = у – б/х – а
Примечание. Уравнение прямой на координатной плоскости можно задается формой пересечения наклона как
Y = mx + b [где ‘m’ наклон, а ‘b’ – точка пересечения y]
Форма наклона точки = (y – y1) = m(x – x1)
Площади и периметры на координатной плоскости: Здесь следует помнить самое важное:
координатная плоскость с 2 осями является двумерной плоскостью.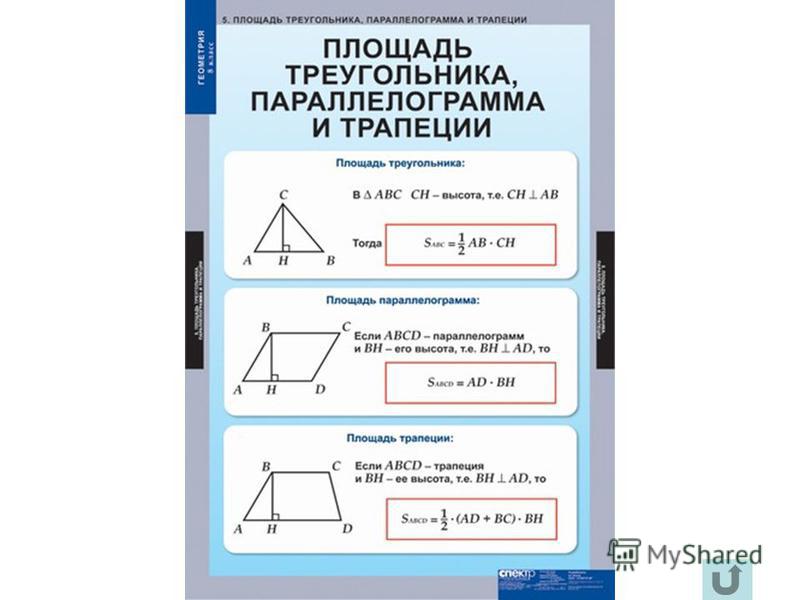
Если вас попросят найти площадь или периметр на со- плоскость ординат, то вы должны разделить фигуру на прямоугольники и треугольники и использовать свойства, чтобы понять их. Позднее применение надлежащего формулы 2D геометрии, вы сможете решить задачу без особых усилий.
Итак, это карманные заметки со всеми основными постулатами квантовой математической части GRE. Мы желаем тебе всего наилучшего!!!
Нажмите, чтобы повысить свой балл GRE
Основы геометрии | Концепция геометрии
Треугольники
Плоская фигура, ограниченная объединением трех прямых, соединяющих три не лежащие на одной прямой точки, называется треугольником.
Существует несколько специальных типов треугольников с важными свойствами. Но одно свойство, общее для всех треугольников, заключается в том, что сумма длин любых двух сторон больше длины третьей стороны или разность длин любых двух сторон меньше длины третьей стороны. как показано ниже.
Треугольники подобны, если они имеют одинаковую форму, они могут быть разных размеров. Следовательно, треугольник, полученный вращением треугольника, подобен исходному треугольнику. Точно так же зеркальное или водное изображение определенного треугольника похоже на исходный треугольник.
Треугольник определяется, в частности, шестью мерами (тремя углами и тремя сторонами). Но нам не нужно знать все это, чтобы показать, что два треугольника подобны друг другу.
Рекомендуемое действие
БЕСПЛАТНЫЕ живые мастер-классы от нашего звездного факультета с более чем 20-летним опытом. Зарегистрируйтесь сейчас
Треугольники подобны, если:
- AAA (угол угол угол): Два треугольника называются подобными, если две пары соответствующих углов равны. Это также означает, что оставшаяся пара углов также будет конгруэнтной.
- SSS (сторона сторона сторона): Два треугольника также называются подобными, если все три пары соответствующих сторон находятся в одинаковой пропорции друг к другу.

- SAS (боковой угол сторона): Два треугольника называются подобными, если две пары сторон находятся в одинаковой пропорции, а углы между ними равны.
Когда два треугольника подобны, всегда выполняются следующие свойства:
- Соответствующие углы равны друг другу (одна мера)
- Соответствующие стороны находятся в одинаковой пропорции друг к другу.
Теорема Пифагора:
Теорема Пифагора утверждает, что «квадрат гипотенузы (стороны, противоположной прямому углу) равен сумме квадратов двух других сторон». Теорему также можно записать в виде уравнения, связывающего длины сторон x, y и z, которое часто называют «уравнением Пифагора». Хотя теорема Пифагора применима только в случае прямоугольного треугольника, тем не менее она имеет много прямые и косвенные приложения. Основная формула для вычисления гипотенузы: x2 + y2 = z2, где z представляет длину гипотенузы, а x и y длины двух других сторон треугольника.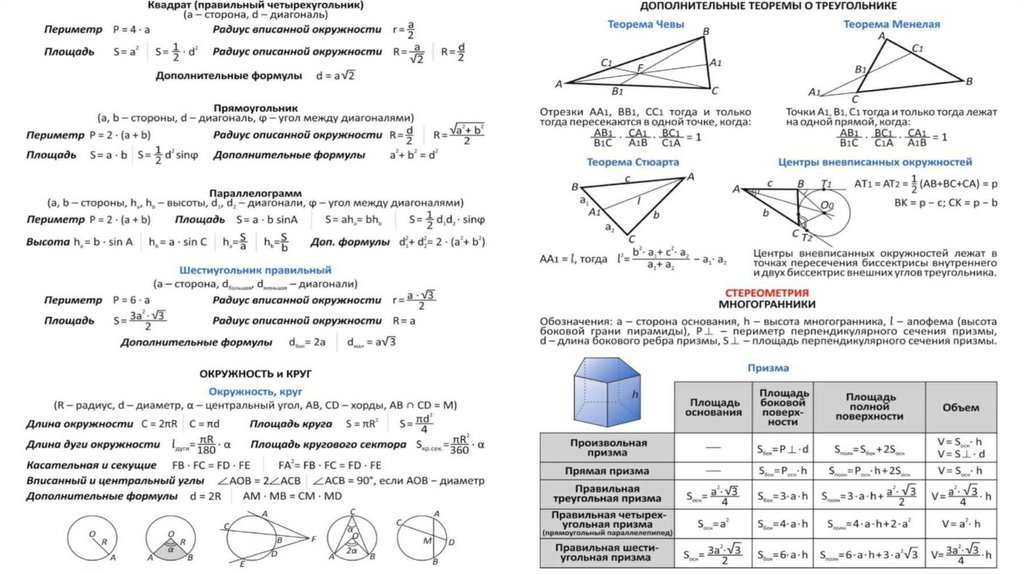
Классификация треугольников по теореме Пифагора:
- Если x 2 + y 2 < z 2 , то треугольник будет тупоугольным.
- Если x 2 + y 2 > z 2 , то треугольник будет остроугольным.
Окружности :
Окружность — это набор точек на плоскости, расположенных на одинаковом расстоянии от фиксированной точки (центра окружности).
Хорда окружности — это отрезок, концы которого лежат на окружности. Хорда, проходящая через центр окружности, является диаметром окружности. Радиус окружности – это отрезок от центра окружности до точки на окружности. Слова «диаметр» и «радиус» также используются для обозначения длин этих сегментов.
Многоугольники :
Многоугольник — это замкнутая фигура, образованная тремя или более отрезками прямых. Эти отрезки называются сторонами многоугольника. Каждая сторона многоугольника пересекает ровно две другие стороны в соответствующих конечных точках.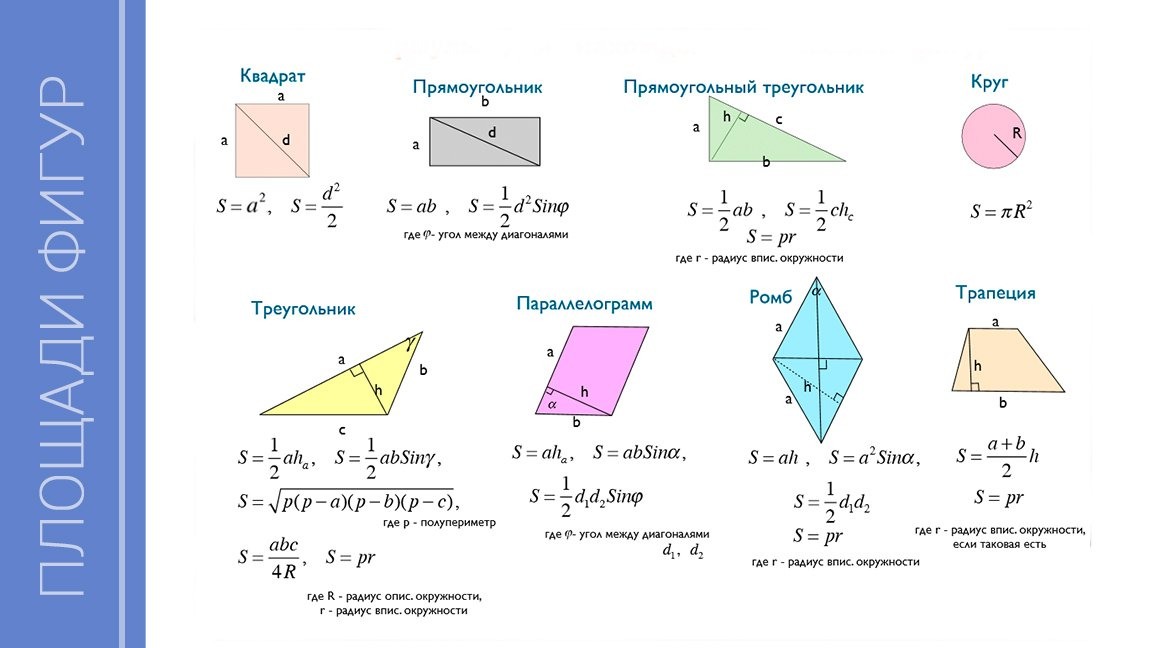 Точки пересечения сторон многоугольника называются вершинами многоугольника. Термин «многоугольник» используется для обозначения выпуклого многоугольника, то есть многоугольника, в котором каждый внутренний угол имеет меру меньше 180°.0003
Точки пересечения сторон многоугольника называются вершинами многоугольника. Термин «многоугольник» используется для обозначения выпуклого многоугольника, то есть многоугольника, в котором каждый внутренний угол имеет меру меньше 180°.0003
Выпуклый многоугольник: Тип многоугольника, в котором ни один из внутренних углов не превышает 180, называется выпуклым многоугольником.
Вогнутый многоугольник: Тип многоугольника, в котором хотя бы один из внутренних углов многоугольника больше 180, называется вогнутым многоугольником.
Правильный многоугольник: Тип многоугольника, у которого все углы и стороны равны, называется правильным многоугольником.
Многоугольник с тремя сторонами называется треугольником; с четырьмя сторонами, называется четырехугольником; с пятью сторонами называется пятиугольником; и с шестью сторонами называется шестиугольником.
Сумма всех внутренних углов треугольника всегда равна 180.


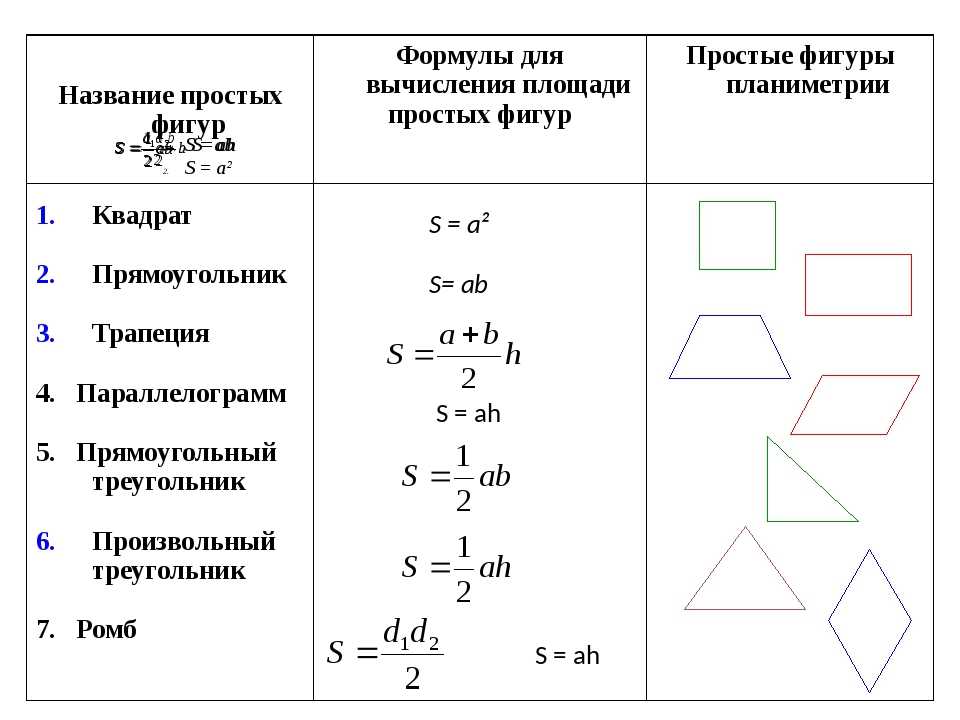 Биссектриса
Биссектриса
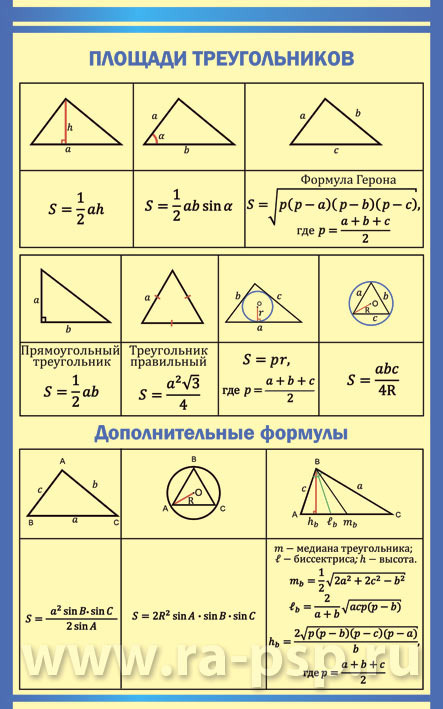 Радиус. Задачи на построение
Радиус. Задачи на построение
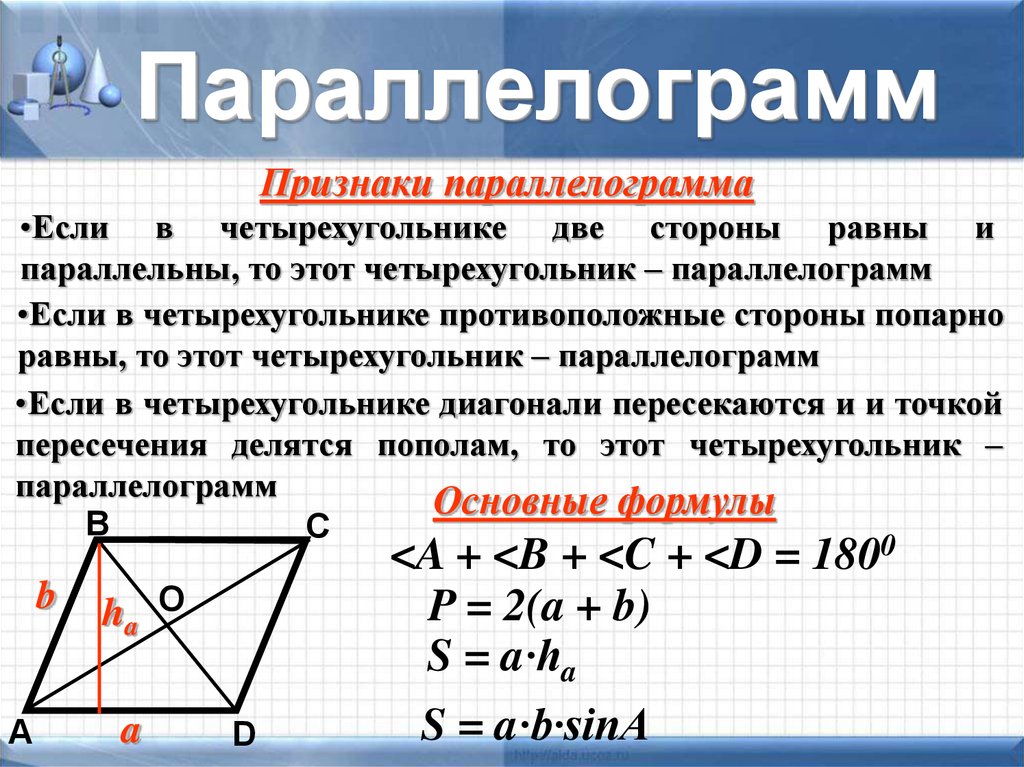 Свойства. Признаки равенства
Свойства. Признаки равенства
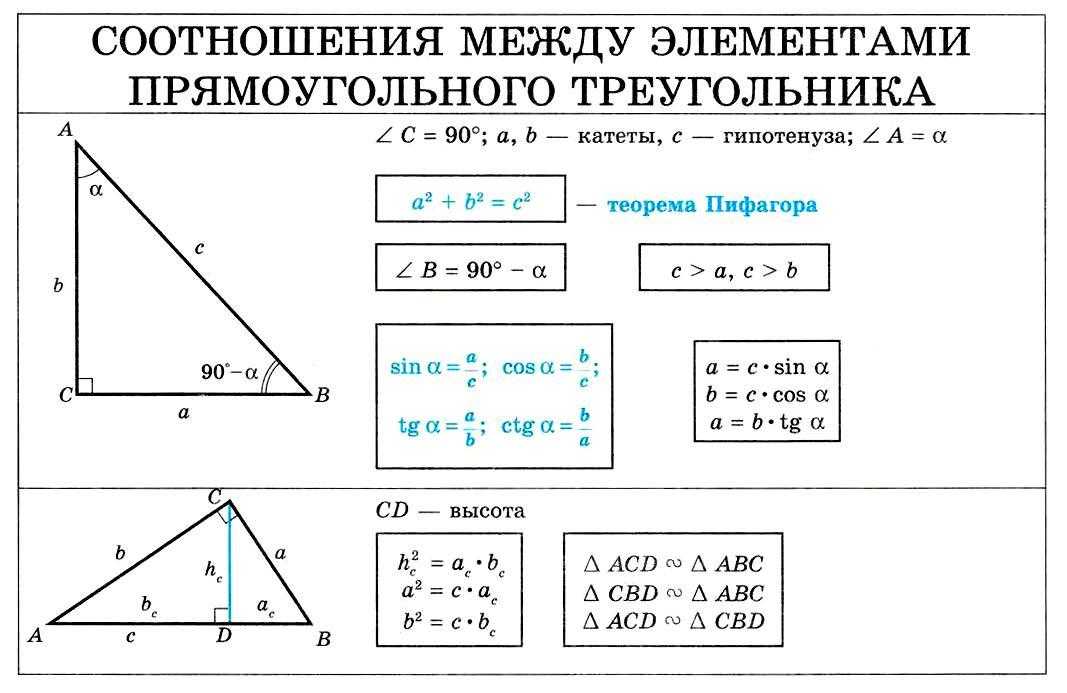 Свойства параллелограмма. Трапеция
Свойства параллелограмма. Трапеция
 Доказательство
Доказательство
 Свойство пересекающихся хорд окружности
Свойство пересекающихся хорд окружности
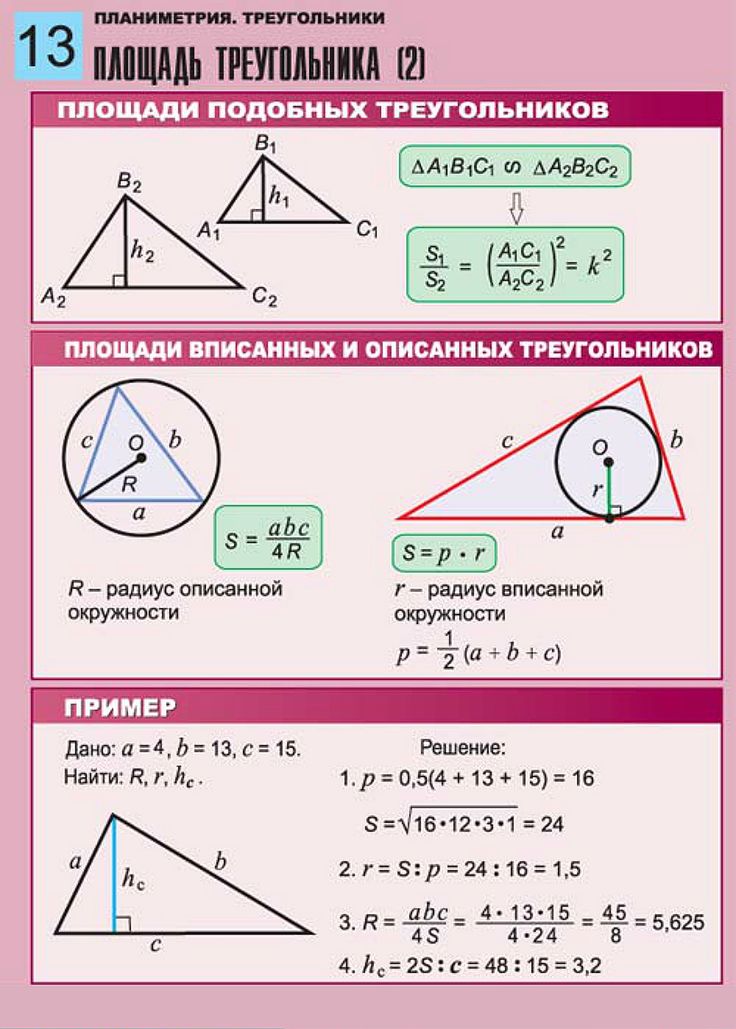 Виды векторов
Виды векторов
 Уравнение прямой
Уравнение прямой
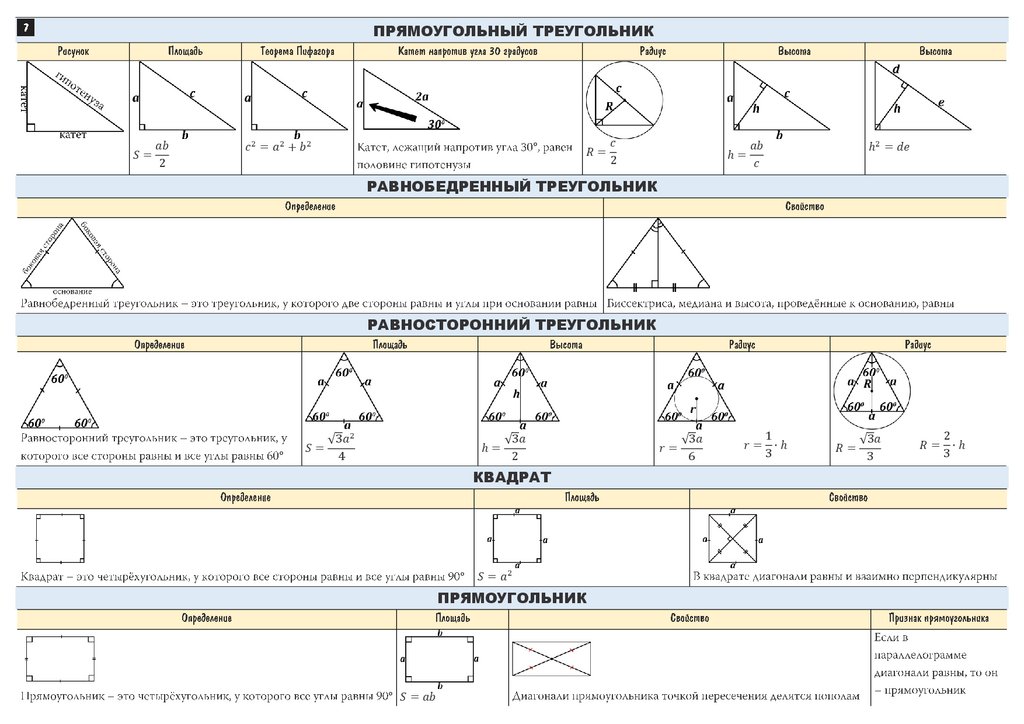 Площадь круга
Площадь круга
 Конус. Сфера
Конус. Сфера
 Угол между прямыми
Угол между прямыми
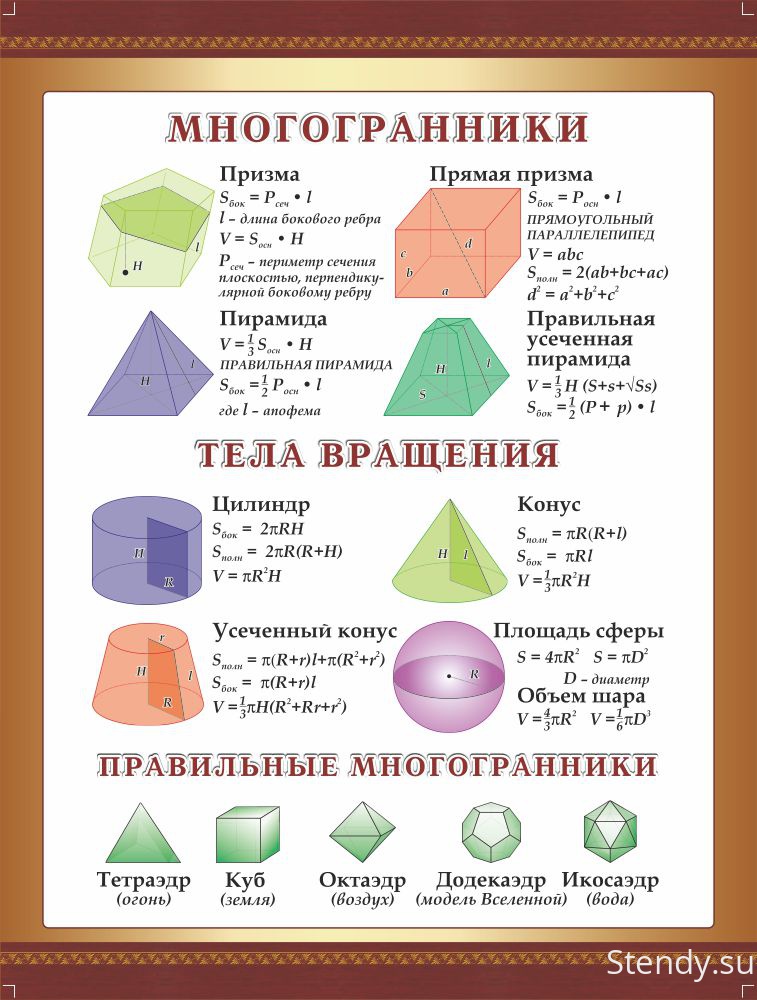 Теорема о трёх перпендикулярах
Теорема о трёх перпендикулярах
 Понятие компланарности
Понятие компланарности
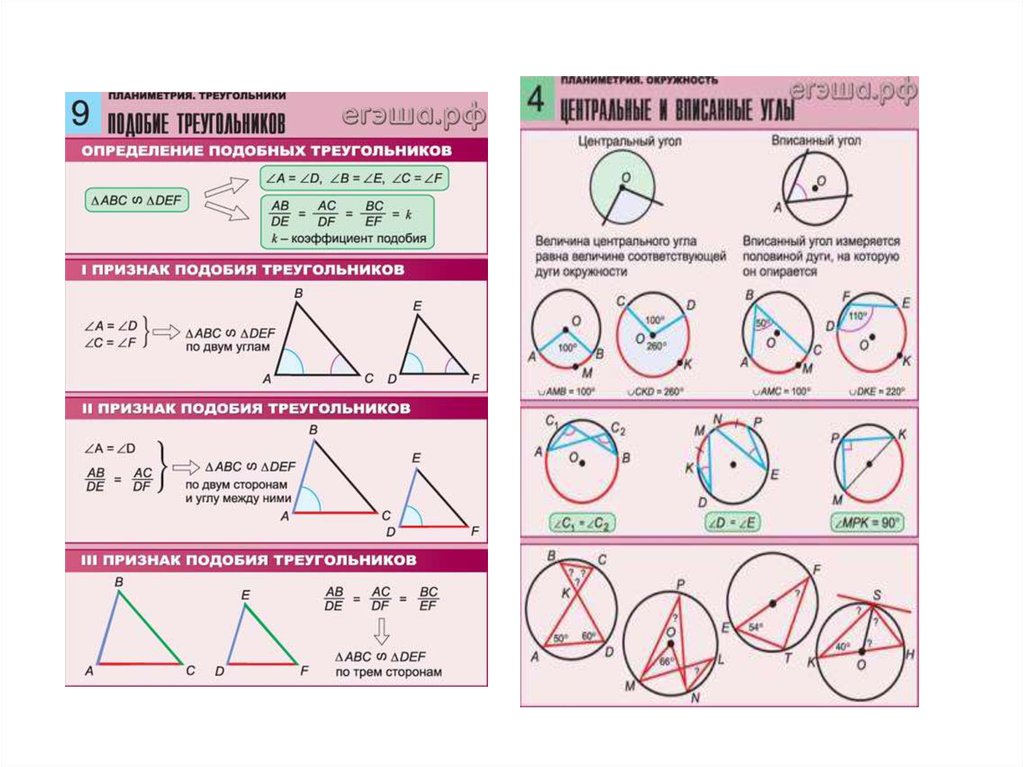 Виды движения
Виды движения
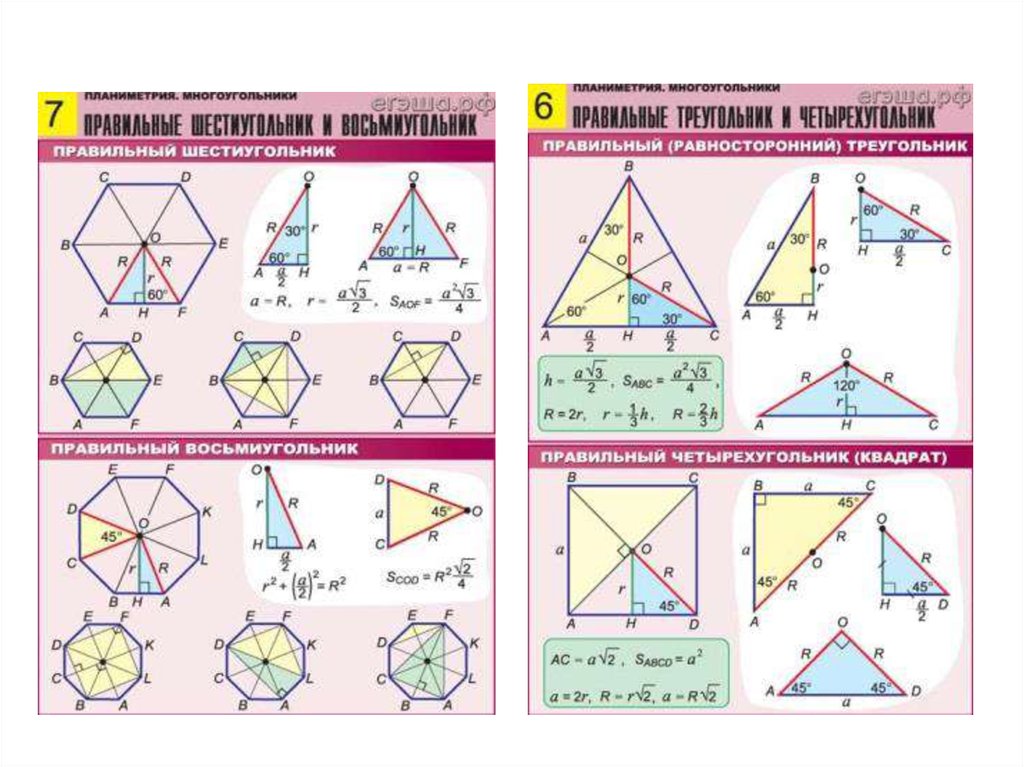 Если разбить его лучом, то исходный угол будет равен сумме образованных.
Если разбить его лучом, то исходный угол будет равен сумме образованных. Прочитайте первую статью, нажмите на ссылку ниже.
Прочитайте первую статью, нажмите на ссылку ниже.
 Это линия, которая делит круг пополам через середину и касается двух концов круга на противоположных сторонах. Это в два раза больше радиуса.
Это линия, которая делит круг пополам через середину и касается двух концов круга на противоположных сторонах. Это в два раза больше радиуса.