Производная и интеграл — проще некуда / Хабр
19 декабря 2020 г. на Хабре вышла статья «Интуитивное объяснение интеграла».
В комментариях к ней некоторые пользователи указали, что объяснение получилось не очень интуитивным, например:
“Тема сама по себе интересная, недавно снова повторял курс, но должен сказать, что на мой взгляд, в материале нет изюминки. Автор прав, что в современных изданиях часто даются темы без описания их прикладного применения, из-за чего непонятен смысл их изучения.
Но конкретно интегралы это такая тема, которую надо описать или короче, чем у вас, или намного дольше.
Иначе и школьник не поймет, и те, кто знает, ничего нового не откроют.»
Я попробую изложить материал максимально коротко и просто. Так, чтобы школьники, наконец, поняли, пусть и с помощью родителей. Итак:
Я живу на плоскости, и мой мир выглядит так:
Все мои перемещения ограничиваются прямой линией, которую я называю «ось абсцисс» и обозначаю ее латинской буквой х. Таким образом, я могу гулять от точки, обозначенной цифрой ноль (там находится мой дом), вправо до бесконечности и назад, до нуля. Цифры на оси абсцисс позволяют мне понять, как далеко я от дома. Сейчас я нахожусь в 10 делениях от него.
Таким образом, я могу гулять от точки, обозначенной цифрой ноль (там находится мой дом), вправо до бесконечности и назад, до нуля. Цифры на оси абсцисс позволяют мне понять, как далеко я от дома. Сейчас я нахожусь в 10 делениях от него.
Да, я слышал, что есть миры, в которых можно перемещаться и влево от нуля, и там расстояния обозначаются отрицательными числами: -1, -2 и т. д., до бесконечности. Кроме того, в тех мирах можно опуститься ниже оси абсцисс, но мой мир максимально прост.
Как-то раз, летящие птицы навели меня на мысль, что по нашему миру можно перемещаться не только влево или вправо, но и «вверх». Потом я узнал, что есть некие люди, умеющие строить дороги, ведущие в наши плоские небеса. Было бы неплохо бы с ними переговорить. И вот я общаюсь со специалистом (С), по строительству таких дорог:
Я: Здравствуйте, вы занимаетесь строительством дорог в небо?
С: Добрый день, да.
Я: А какие дороги вы умеете строить?
С: Самые простые варианты — прямые дороги различной крутизны.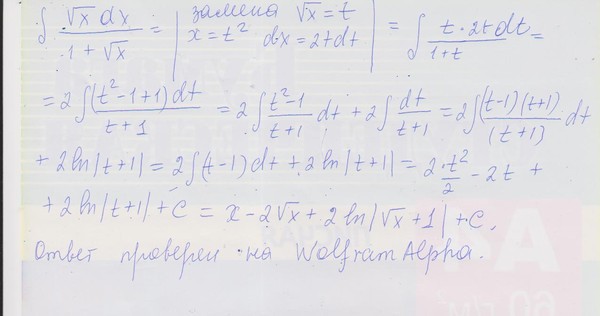
Я: А что такое «крутизна»? Я всегда жил на горизонтальной прямой, и понятия не имею, что это слово может значить.
С: «Крутизна» показывает то, насколько трудно будет вам подниматься (или опускаться) по данной дороге. Чем круче дорога, тем тяжелее подъем или спуск. Давайте нарисуем на нашей плоскости еще одну ось — вертикальную. Мы назовем ее осью ординат, и обозначим латинской буквой у. На этой оси есть цифры, обозначающие «высоту» — расстояние до оси х.
Чтобы нам было проще ориентироваться в нашем двухмерном мире, нанесем на его плоскость линии, идущие от цифр, расположенных на осях х и у:
Теперь любое место (точку) на плоскости мы можем обозначить двумя цифрами. Первая цифра будет обозначать расстояние от нуля до проекции этой точки на ось х…
Я: Простите, а что такое «проекция»?
С: Видите внизу, на оси абсцисс, тень от летящей птицы? Она находится в точке, обозначенной цифрой 6 на оси х. Эта тень и есть проекция тела птицы на ось х. А если бы Солнце находилось справа от птицы, мы бы увидели ее тень на оси у, в районе цифры 8. Это есть проекция тела птицы на ось ординат. Она показывает, на какой высоте летит птица. То есть, расстояние от «земли» (от оси х) до нее.
Эта тень и есть проекция тела птицы на ось х. А если бы Солнце находилось справа от птицы, мы бы увидели ее тень на оси у, в районе цифры 8. Это есть проекция тела птицы на ось ординат. Она показывает, на какой высоте летит птица. То есть, расстояние от «земли» (от оси х) до нее.
Мы можем обозначить положение птицы двумя цифрами (6, 8). Первая цифра — проекция на ось х, вторая — проекция на ось у. Эти две цифры мы называем координатами птицы.
Вместо запятой между целой и дробной частями чисел, я буду ставить точку (т.е., не 13,5 а 13.5) для того, чтобы не путать с запятыми между соседними числами.
Я: Отлично, что дальше?
С: Дальше мы отгоним птицу и нарисуем дорогу:
Вы можете заметить, что эта дорога поднимается на одну клеточку вверх, при перемещении проекции на ось х на одну клеточку вправо.
Когда человек перемещается из точки с координатами (4, 4) в точку с координатами (10, 10), его проекция на ось х меняется на 6 цифр.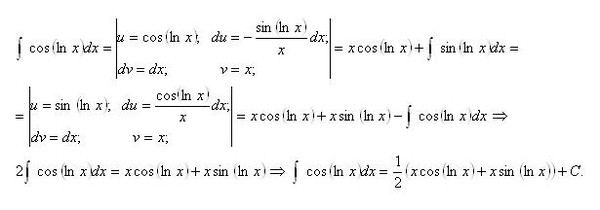 То есть, его тень перемещается вправо на 6 единиц (клеточек). Такое же изменение проекции происходит по оси у. То есть, он одновременно поднимается вверх также на 6 единиц.
То есть, его тень перемещается вправо на 6 единиц (клеточек). Такое же изменение проекции происходит по оси у. То есть, он одновременно поднимается вверх также на 6 единиц.
Изменение какого-либо параметра (например, проекции на ось х или у), мы обозначаем буквой d (дельта). Изменение высоты мы запишем как dy, а изменение проекции на ось х — как dx. То есть, в данном случае, dу = 6, и dx также = 6.
Разделив изменение высоты на изменение положение тени человека при его перемещении (dy/dx), мы узнаём крутизну данного участка дороги: 6 / 6 = 1.
В нашей проектной документации мы используем очень краткое описание маршрута прокладываемой дороги. В данном случае оно будет выглядеть как математическая формула у = 1*х.
Это значит, что у всегда равен х, и это справедливо для любой точки дороги. Если человек будет находиться, например, в точке, тень от которой падает на ось х в точке 15, он будет находиться на высоте 15. Два параметра — положение тени человека на оси абсцисс и высота, на которой он находится, жестко связаны между собой вышеуказанной формулой.
Если человек будет находиться, например, в точке, тень от которой падает на ось х в точке 15, он будет находиться на высоте 15. Два параметра — положение тени человека на оси абсцисс и высота, на которой он находится, жестко связаны между собой вышеуказанной формулой.
Разумеется, можно было просто указать крутизну дороги одно цифрой, в данном случае, единицей, но проблема в том, что во-первых, дороги не всегда начинаются у вашего дома — в точке с координатами (0, 0). Во-вторых, существуют дороги, крутизна которых не постоянна. Но о них позже. А пока давайте нарисуем еще пару прямых дорог:
Мы видим, что верхняя дорога поднимается круче, чем та, которую мы рассмотрели ранее. А нижняя дорога — наоборот, более пологая. Высота (проекция на ось у), на которой находится человек, идущий по верхней дороге, равна 10. То есть, перемещаясь от начала координат до точки, в которой он находится сейчас, он изменил свою проекцию на ось у на 10 единиц. В то же самое время, его тень (проекция на ось х) переместилась вправо всего на 5 единиц. Разделив 10 на 5, мы получаем цифру 2. Эта цифра — соотношение высоты и удаленности от нуля по оси х — есть показатель крутизны дороги. Понятно?
В то же самое время, его тень (проекция на ось х) переместилась вправо всего на 5 единиц. Разделив 10 на 5, мы получаем цифру 2. Эта цифра — соотношение высоты и удаленности от нуля по оси х — есть показатель крутизны дороги. Понятно?
Я: Да, я понял это еще на первом примере. А если мы разделим проекцию перемещения человека, идущего по нижней дороге на ось у, на перемещение его тени по оси х, (5/10), мы получим цифру 0.5, или 1/2. Это и есть показатель крутизны нижней дороги?
С: Совершенно верно! Между каждой из дорог и осью х (горизонталью) есть некоторый угол. Чем больше этот угол, тем круче поднимается дорога. Соотношение координаты любой точки дороги (если дорога прямая) по оси у и координаты этой же точки по оси х, называют тангенсом этого угла. Для каждого угла — свой тангенс. Тангенс угла верхней дороги равен 2, тангенс угла нижней, более пологой дороги, равен 0. 5. Соответственно, формулы, которыми мы опишем две последние дороги будут выглядеть как у = 2х и у = 0.5х.
5. Соответственно, формулы, которыми мы опишем две последние дороги будут выглядеть как у = 2х и у = 0.5х.
Эти формулы мы называем функциями. Мы говорим, что у — функция от х, где х независимая переменная (мы ее задаём), а у — зависимая переменная, так как мы ее вычисляем, исходя из заданного значения х. И она жестко зависит от значения х. Например, задав х = 12 для дороги, описываемой формулой у = 0.5х, мы, подставляя цифру 12 вместо х, узнаём, что у в этой точке равен 6.
В математике функции обозначают, например, так: f(x) = x. Эта функция справедлива для дороги, рассмотренной нами в самом первом примере. Для второй и третьей дорог, функции будут выглядеть соответственно, как f(x) = 2x и f(x) = 0. 5x. Не очень сложно, да?
5x. Не очень сложно, да?
Я: Не очень. Что еще мне нужно знать о дорогах?
С: Мы делаем не только прямые дороги. Например, мы можем построить дорогу, которая описывается формулой (функцией) у = x2, или f(x) = x2. Крутизна этой дороги будет увеличиваться, по мере ее удаления от оси у.
Чтобы построить рисунок этой дороги, мы найдем (вычислим) координаты нескольких ее точек. Для этого мы подставим в формулу у = x2 вместо х сначала 1, потом 2, затем 3 и т.д. И рассчитаем значение у для всех этих точек. Сначала подставим 1:
y = х2 = 12 = 1.
Это значит, что для точки, с координатой по х равной 1, ее координата по у также равна 1. Нанесем эту точку на график:
Теперь рассчитаем координату по у для точки, с координатой по х равной 2:
y = x2 = 22 = 4.
Таким образом, наша вторая точка будет иметь координаты (2, 4). Рассчитав у для точек с координатами по х 3 и 4, получим их полные координаты (3, 9) и (4, 16) соответственно. Нанесем эти точки на график:
Теперь соединим все точки линией, обозначающей дорогу:
Для любой точки этой дороги справедлива формула y = x2. Например, для точки, с координатой по х = 1,5, мы получим ее координату по у, возведя 1,5 в квадрат. То есть, ее координаты (1.5, 2.25). Таким образом, мы можем узнать высоту любой точки дороги, задавая ее абсциссу (положение ее тени на оси х).
Но возникает проблема: мы не можем посчитать крутизну какой-либо точки дороги, так как она меняется постоянно. Не получится просто взять две точки дороги сверху и снизу от исследуемой и посмотреть, насколько изменится высота при прохождении пути между ними, разделив перемещение проекции на ось у на перемещение тени по оси х.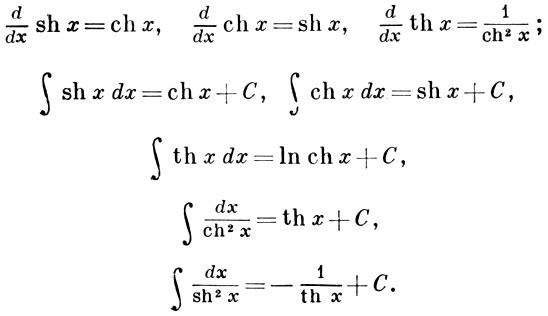 Точнее, мы можем это сделать, но полученная цифра не будет соответствовать крутизне в средней точке между ними. Смотрите:
Точнее, мы можем это сделать, но полученная цифра не будет соответствовать крутизне в средней точке между ними. Смотрите:
Допустим, мы хотим узнать крутизну нашей кривой дороги на участке от начала координат (точки с координатами (0, 0)), до точки с координатами (3, 9). На этом участке дорога поднимается на 9 единиц, в то время, как удаление от начала координат по х составляет 3 единицы. Считаем крутизну так же, как мы считали ее для прямой дороги: 9 / 3 = 3. То есть, крутизна на этому участке, вроде бы, равна 3. Но если мы проведем прямую с крутизной, равной 3, то увидим, что на самом деле дорога в самом низу идет гораздо более полого, чем прямая, а в точке пересечения прямой и дороги, крутизна дороги уже больше крутизны прямой! Крутизна кривой в центре между этими точками также не совпадает с крутизной прямой. Засада. Что же делать? Как нам узнать крутизну каждой точки в ситуации, когда первая постоянно меняется, и нет ни единого прямого участка? Вот для таких случаев господин Ньютон и придумал дифференцирование.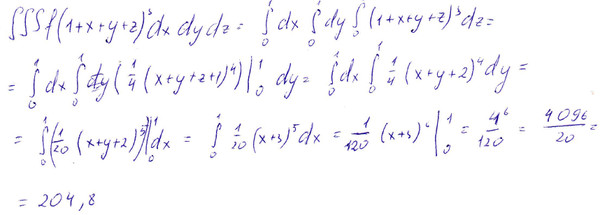
Дифференцирование преобразует нашу функцию в другую функцию, которая как раз-таки позволяет точно вычислить крутизну дороги в данной точке. Мы не будем вдаваться в то, как он пришел к своему решению, а просто воспользуемся результатом его работы — таблицей дифференциалов. Я не буду ее приводить, в Сети такого добра навалом. Можно просто ввести в строку поиска формулу, которую нужно дифференцировать.
Для нашей функции f(x) = x2 дифференцирование будет выглядеть таким образом: нам нужно перенести двойку из показателя степени влево, перед х, и уменьшить степень х на единицу. То есть, в данном случае степень х станет равна 1: f ‘(x) = 2x.
Обратите внимание на штрих после буквы f: f ‘(x) — так обозначается функция, которая произошла от нашей оригинальной функции. Поэтому ее называют производной функцией.
Но что нам теперь делать с этой производной? Как с ее помощью найти крутизну какой-либо точки оригинальной функции f(x) = x2? Очень просто. Мы подставляем в производную значение проекции на ось х, точки дороги, крутизна которой нас интересует. Допустим, мы хотим узнать, насколько круто поднимается дорога в точке, находящейся над цифрой 1 по оси х. Мы подставляем эту единицу в производную, и вычисляем значение:
Мы подставляем в производную значение проекции на ось х, точки дороги, крутизна которой нас интересует. Допустим, мы хотим узнать, насколько круто поднимается дорога в точке, находящейся над цифрой 1 по оси х. Мы подставляем эту единицу в производную, и вычисляем значение:
f ‘(x) = 2x = 2*1 = 2.
Эта двойка и показывает нам крутизну дороги над точкой 1 по оси х.
А какова крутизна дороги в точке с абсциссой 4 (проекцией на ось х = 4)? Подставляем эту четверку в производную функцию f ‘(x) = 2x = 2*4 и получаем цифру 8.
Эта восьмерка означает, что крутизна дороги в точке с абсциссой 4 равна 8. То есть, в этой точке дорога поднимается так же круто, как верхняя прямая на правом графике. Вот и весь смысл дифференцирования (нахождения производной).
Слева — график самой дороги, а справа — прямые, крутизна которых соответствует крутизне дороги в указанных точках. То есть, в указанных точках дороги подниматься так же тяжело, как по соответствующим этим точкам прямым. «Здесь так же круто, как там».
То есть, в указанных точках дороги подниматься так же тяжело, как по соответствующим этим точкам прямым. «Здесь так же круто, как там».
Давайте найдем производную нашей самой первой функции f (x) = x.
Мы проделаем такой же трюк: перенесем степень переменной вперед, перед х (это ничего не изменит, так как степень х была равна 1). Кроме того, мы уменьшим степень х на единицу. При этом степень станет равна нулю, и х превратится в единицу (потому, что любое число (кроме нуля) в нулевой степени равно 1).
Мы получили производную функции f(x) = x. Она выглядит так: f ‘(x) = 1. Что это значит? Это значит, что крутизна данной дороги на любом ее участке равна 1. То есть, при изменении абсциссы на dx, dy изменится ровно на такую же величину. В принципе, мы это знали и раньше, но теперь мы вычислили крутизну дороги через производную.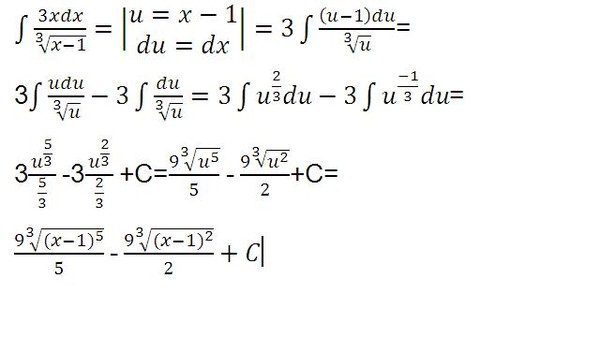
В учебниках пишут, что производная постоянной (некоторого числа) равна нулю. Почему это так?
Давайте построим дорогу, которая описывается функцией f(x) = 5. Это означает, что высота (проекция на ось у) любой точки данной дороги всегда равна 5, следовательно, dy (изменение высоты) равно нулю.
Поэтому эта дорога идет параллельно оси абсцисс, то есть, никакого изменения высоты не будет, на сколько бы мы не перемещались вправо. А раз крутизна дороги равна нулю, то и производная данной функции равна нулю (dy/dx = 0/dx = 0).
Повторим: производная отображает крутизну функции (графика, дороги), а в данном случае никакой крутизны нет. Что и имеется ввиду, когда говорят, что производная постоянной равна нулю.
Я: Хорошо, я все понял: по оригинальной функции я могу вычислить высоту дороги в любой ее точке, а по производной — крутизну в любой ее точке. Но дорога не может висеть в воздухе, она же должна опираться на ось х?
Но дорога не может висеть в воздухе, она же должна опираться на ось х?
С: Совершенно правильный вопрос. Под дорогой нам придется сделать насыпь. И чем больше материала (клеточек) мы потратим на данный участок дороги, тем больше вам придется заплатить.
Я: А как вы посчитаете, сколько клеточек вам понадобится? Для участка прямой дороги, параллельной оси абсцисс f(x) = 5, все просто:
У нас получается прямоугольник, высота которого равна постоянной 5, а длину мы можем посчитать, вычитая координату по х левой стороны прямоугольника из координаты его правой стороны: 10 — 3 = 7. То есть, ширина прямоугольника равна 7, соответственно, его площадь равна 5 * 7 = 35 клеточек. Я буду вам должен за 35 клеточек.
Нет проблем и с дорогой, которая поднимается (или опускается) по прямой.
Как и в предыдущем случае, ширину основания мы узнаём, вычитая координаты границ по оси х друг из друга: 9 — 3 = 6.
Высоту найти немного сложнее: нам придется вычислить ее среднее значение. Для этого мы берем высоту (проекцию на ось у) левой верхней точки закрашенной фигуры, прибавляем к ней высоту правой верхней точки и делим пополам:
(1.5 + 4.5) : 2 = 3. Эта тройка — средняя высота фигуры. Мы умножаем ее на ширину фигуры и получаем цифру 18. То есть, на данный участок дороги потрачено 18 клеток, верно? Но как узнать, сколько клеток потребует участок дороги типа y = x2?
С протяженностью участка дороги слева направо разобраться легко, она равна 4 — 1 = 3 клетки, но как быть с высотой? Ведь мы не можем в данном случае сложить 1 и 16, затем разделить пополам и получить среднюю высоту фигуры? Как нам посчитать площадь этой насыпи?
С: Господин Ньютон предусмотрел и это. Метод подсчета площади криволинейных фигур называется «интегрирование». Нам придется вспомнить то, как мы находили производную функции f (x) = x2Она выглядит так: f ‘(x) = 2x.
Эту, как и многие другие математические операции, можно производить и в обратную сторону. Если нам известна производная функции, мы можем восстановить эту изначальную функцию, называемую первообразной. То есть, имея функцию, показывающую изменение крутизны дороги, мы можем восстановить функцию, показывающую саму дорогу — высоту любой ее точки.
Если для нахождения производной мы переносили вперед показатель степени переменной (двойку), и уменьшали степень переменной х на единицу
f(x) = x2=> f ‘(x) = 2x,
то теперь нам следует поступить ровно наоборот: двойку, стоящую перед х следует перенести наверх, в степень: f ‘(x) = 2x => f(x) = x2.Так мы получаем первообразную функцию. То есть, ту функцию, от которой производная произошла.
Но не все так просто, давайте рассмотрим дорогу, описываемую функцией
f (x) = x2+ 4:
Она выглядит точно так же, как дорога f (x) = x2, но располагается выше. Если мы найдем производную этой функции, то обнаружим, что она выглядит точно так же, как производная от функции f (x) = x2! То есть, как f ‘(x) = 2x. Ибо при нахождении производной четверка (постоянная) будет отброшена.
Если мы найдем производную этой функции, то обнаружим, что она выглядит точно так же, как производная от функции f (x) = x2! То есть, как f ‘(x) = 2x. Ибо при нахождении производной четверка (постоянная) будет отброшена.
Я: Почему?
С: Потому, что она не влияет на крутизну графика. Вы же помните, что производная описывает крутизну оригинального (первообразного) графика на каждом его участке? А теперь посмотрите на точки обоих графиков, расположенные, к примеру над цифрой 3 на оси х. Крутизна верхнего и нижнего графиков в этих точках одинакова! То же самое касается любых двух точек этих графиков, расположенных друг под другом. Эти две дороги идут параллельно друг другу, поэтому, их крутизна везде совпадает. Отличается только высота.
Но производная — это не про высоту, а про крутизну дороги. Потому и получается, что обе функции f (x) = x2и f (x) = x2+ 4 приводят к одной и той же производной f ‘(x) = 2x.
Я: Погодите, но тогда получается, что функции, к примеру, f (x) = x2 + 5 или f (x) = x2 + 1.3 и даже f (x) = x2— 2 также приводят к одной и той же производной? Ведь они все параллельны друг другу, и их крутизна в точках, расположенных друг под другом, совпадает?
С: Да, наша производная имеет бесконечный набор первообразных. Поэтому первообразную функции f (x) = 2x записывают как F (x) = x2 + C, где буква С может быть любым числом. От этого числа зависит только высота, на которой проходит дорога. Точнее, разница высот между данной дорогой, и дорогой, у которой С = 0. Если Вы снова посмотрите на графики выше, то увидите, что любая точка верхнего графика ровно на 4 клетки выше аналогичной точки нижнего графика.
Обратите внимание также на то, что буква F в первообразной — заглавная (большая), Первообразная является «матерью» производной, поэтому мы относимся к ней с уважением, и пишем ее имя заглавной буквой.
Все множество функций, описываемых формулой F (x) = x2 + C, называется неопределенным интегралом. Самая распространенная формула для нахождения неопределенного интеграла выглядит так:
По этой формуле мы можем найти неопределенный интеграл нашей функции f (x) = x2. Для этого мы увеличиваем степень переменной на единицу, а в знаменатель просто ставим получившуюся степень переменной. Степень нашей переменной была 2, увеличив ее на единицу, получаем x3. Эту же тройку мы ставим в знаменатель (под дробную черту). Получается выражение F (x) = x3/3 + С.
Теперь вернемся к нашей криволинейной фигуре.
Чтобы узнать ее площадь, в полученный нами неопределенный интеграл нужно подставить абсциссу ее правой границы — цифру 4 (при этом постоянная С отбрасывается):
F (x) = x3/3 = 43/3 = 21 1/3 (двадцать одна целая и одна треть)
То же самое проделаем с левой границей фигуры:
F (x) = x3/3 = 13/3 = 1/3 (одна треть)
Теперь нам остается вычесть из первого числа второе: 21 1/3 — 1/3 = 21
Искомая площадь равна 21 клетке. Для проверки вы можете примерно посчитать закрашенные клетки на картинке.
Для проверки вы можете примерно посчитать закрашенные клетки на картинке.
Давайте подытожим все вышесказанное. Итак, у нас есть некоторая формула (функция) f(x), описывающая некую линию на графике.
Чтобы найти крутизну этой линии (функции) в какой-либо ее точке, мы находим производную данной функции f ‘(x), затем подставляем в полученную производную проекцию на ось х интересующей нас точки оригинальной функции, и вычисляем искомый параметр. Полученная цифра будет показывать тангенс угла наклона прямой, которая поднимается (или опускается) так же круто, как исходный график в исследуемой точке.
А чтобы найти площадь под участком графика исходной функции, следует найти ее первообразную F, затем, в эту первообразную по очереди подставить координаты по х правой и левой границы фигуры, площадь которой мы хотим найти, а затем вычесть два полученных числа друг из друга.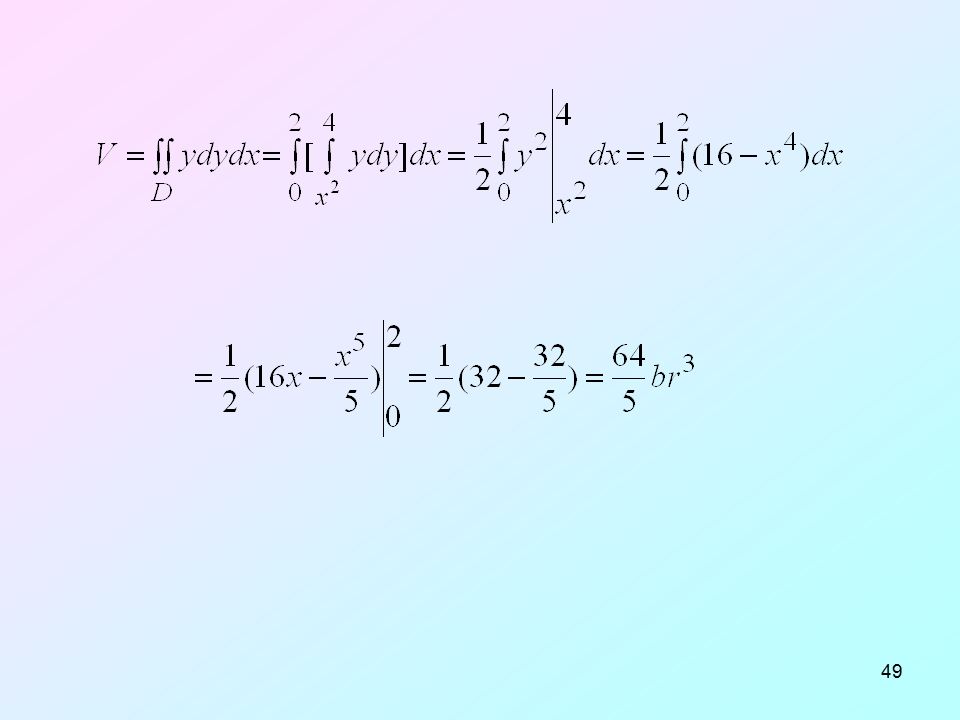 Результат вычитания и есть искомая площадь.
Результат вычитания и есть искомая площадь.
Я: А почему вы отбросили постоянную С? Разве это не приведет к тому, что площадь под участками кривых f (x) = x2и f (x) = x2+ 4, находящимися друг под другом, будут одинаковыми?
С: Не беспокойтесь, при нахождении интеграла второй функции, постоянная 4 в ее первообразной превратится в 4х, поэтому, к площади под ней добавится прямоугольник высотой 4 клеточки и ошибки не будет. Ну так что, какую дорогу Вы выбираете?
Метод интегрирования по частям.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Если $u(x)$ и $v(x) -$ дифференцируемые функции, то справедлива следующая формула интегрирования по частям: $$\int u(x)v'(x)’,dx=u(x)v(x)-\int v(x)u'(x)dx,$$
Или в краткой записи $$\int u\,dv=uv-\int v\,du.$$
Эта формула используется в тех случаях, когда подынтегральное выражение $f(x)dx$ можно так представить в виде $u\,dv$ чтобы можно было найти $v=\int\,dv$ и полученный в правой части интеграл $\int v\,du$ был проще исходного $\int u\,dv.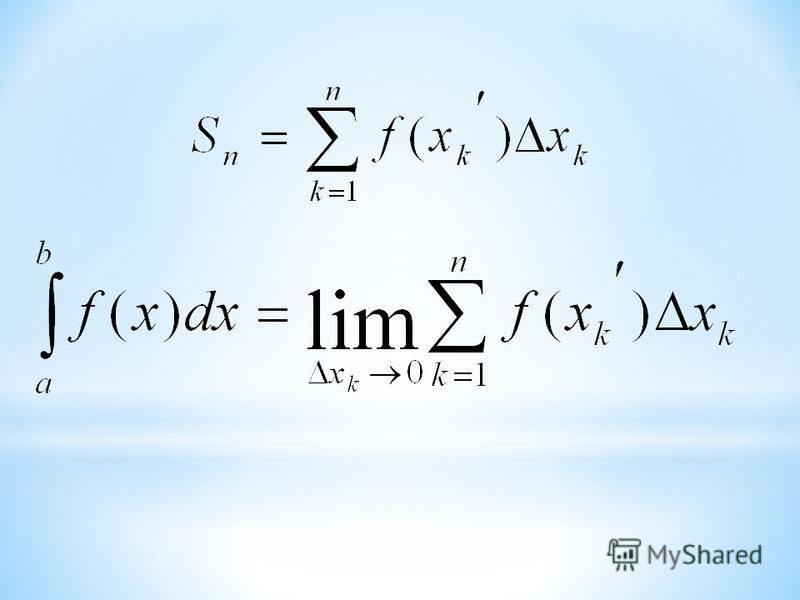 2}+C.$
2}+C.$
6.143.$\int\cos(\ln x)\,dx.$
Решение.
$$\int \cos(\ln x)\, dx=\left[\begin{array}{lcl}u=\cos(\ln x) \Rightarrow du=-\frac{1}{x}\sin(\ln x)\, dx\\dv=dx\Rightarrow v=x\end{array}\right]=$$ $$=\cos(\ln x)x-\int x\cdot\left(-\frac{1}{x}\sin(\ln x)\right)\,dx=x\cos(\ln x)+\int\sin(\ln x)\,dx.$$
$$\int \sin(\ln x)\, dx=\left[\begin{array}{lcl}u=\sin(\ln x) \Rightarrow du=\frac{1}{x}\cos(\ln x)\, dx\\dv=dx\Rightarrow v=x\end{array}\right]=$$ $$=\sin(\ln x)x-\int x\cdot\left(\frac{1}{x}\cos(\ln x)\right)\,dx=x\sin(\ln x)-\int\cos(\ln x)\,dx.$$
Таким образом, $$\int\cos(\ln x)\,dx=x\cos(\ln x)+x\sin(\ln x)-\int\cos(\ln x)\, dx.$$
Пусть $\int\cos(\ln x)\, dx=I.$ Тогда запишем и решим уравнение
$$I=x\cos(\ln x)+x\sin(\ln x)-I\Rightarrow$$ $$\Rightarrow 2I=x\cos(\ln x)+x\sin(\ln x)\Rightarrow$$ $$\Rightarrow I=\frac{1}{2}(x\cos(\ln x)+x\sin(\ln x).$$
Ответ: $\frac{1}{2}(x\cos(\ln x)+x\sin(\ln x))+C.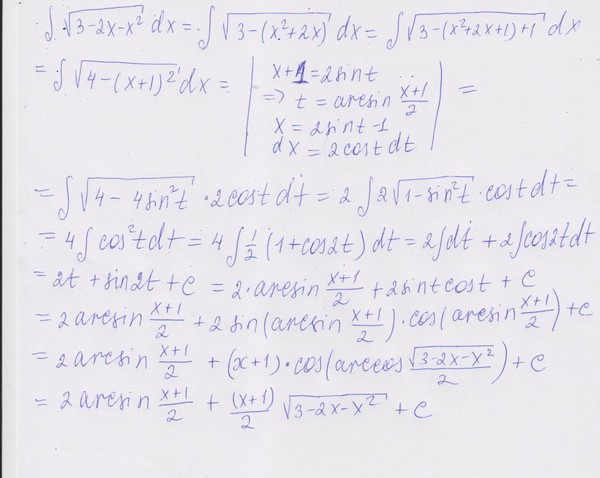 2-2x+3)\cos x\, dx.$
2-2x+3)\cos x\, dx.$
Интегрирование тригонометрических и иррациональных функций 2
Примеры решения задач по теме «Неопределенный интеграл»
Свойства неопределенного интеграла
1.f x dx f x .
2.d f x dx f x dx.
3.dF x F x c.
4.af x dx d f x dx, a — постоянная.
5.f1 x f2 x dx f1 x dx f2 x dx.
Таблица неопределенных интегралов
0dx c
xndx | xn 1 | n 1 | ||||||||||
|
|
|
|
|
| c | ||||||
|
|
|
|
|
| |||||||
| 1 |
|
| n 1 |
| |||||||
| dx ln |
| x |
| c |
| ||||||
|
|
| ||||||||||
|
| |||||||||||
| x |
| ax |
| ||||||||
|
| x |
|
| ||||||||
a |
|
| dx |
|
|
|
|
| c |
| ||
|
|
|
|
|
|
|
| |||||
|
|
|
|
| lna |
| ||||||
exdx ex c
sinxdx cosx c
cosx dx sinx c
| 1 |
| dx tgx c |
|
|
|
| |||
cos2 x |
|
|
|
| ||||||
|
|
|
|
|
|
|
| |||
| 1 |
| dx ctgx c |
|
|
|
| |||
sin2 x | x |
|
| |||||||
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| ||
| 1 |
|
|
| arcsin |
|
| c | ||
|
|
|
| a | ||||||
|
|
|
|
|
|
| ||||
|
|
|
|
|
| dx |
|
| x | |
|
|
|
|
|
|
| ||||
| a2 x2 |
|
| |||||||
|
|
|
|
|
| |||||
|
|
|
|
|
| arccos |
| c | ||
|
|
|
|
|
|
|
|
| a | |
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| dx ln | x |
| x2 a2 | |||||||||||||||
|
|
|
|
|
| |||||||||||||||||||
|
|
| ||||||||||||||||||||||
|
|
|
| x2 a2 | 1 |
|
|
|
|
| x |
|
|
|
|
| ||||||||
|
|
|
|
| arctg |
| c | |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
| dx | a |
|
|
|
|
| a |
|
|
|
|
| |||||||
| x | 2 a2 | 1 |
|
|
| x | |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| arctg |
|
|
| c | |||||||
|
|
|
|
|
|
|
|
|
|
| a |
|
|
| a | |||||||||
|
| 1 |
|
| 1 |
| x a |
|
| |||||||||||||||
|
|
| dx | ln |
| c | ||||||||||||||||||
x | 2 a2 |
|
| x a | ||||||||||||||||||||
|
|
|
|
|
|
|
| 2a |
|
|
|
|
| |||||||||||
shdx chx c
chxdx shx c
1
ch3x dx thx c
1
sh3xdx cthx c
Методы интегрирования
1. Непосредственное интегрирование. Основано на преобразовании подынтегрального выражения с помощью арифметических операций к одному из табличных интегралов либо к сумме интегралов имеющихся в таблице.
Непосредственное интегрирование. Основано на преобразовании подынтегрального выражения с помощью арифметических операций к одному из табличных интегралов либо к сумме интегралов имеющихся в таблице.
Пример 1. Найти интеграл | 1 |
|
|
| 3 |
| |
| x | dx. | |||||
|
|
|
|
| |||
x | |||||||
|
|
| |||||
Решение. Возведем числитель подынтегральной дроби в куб и полученный многочлен разделим почленно на знаменатель
| 1 |
|
|
| 3 | dx | 1 3 |
|
| 3x x |
|
| dx | ||||||||
| x | x | x | ||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
x | x | ||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
| 3 3 x x | dx | ||||||||||
|
|
|
|
|
|
|
|
| |||||||||||||
|
|
|
|
|
|
| x | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
x 12dx 3 dx 3 x12dx xdx
2x 3x 2xx x2 c.
|
|
|
|
|
| 3 |
| 2 |
|
|
|
|
| |
| 1 |
|
|
|
|
|
|
|
|
| x | 2 |
| |
|
| x |
|
|
| |||||||||
|
|
|
|
|
|
| ||||||||
Ответ: |
|
|
|
|
|
| dx 2 | x 3x 2x | x |
|
| c. | ||
|
|
|
|
|
|
| ||||||||
|
| x |
|
|
|
|
|
|
| 2 |
| |||
|
|
|
|
|
|
|
|
|
| |||||
2. Метод замены переменной (подстановки)
Пусть функция x t определена и дифференцируема на множестве t , и пусть x множество значений этой функции.
Пусть для функции f x существует на множестве x
первообразная F x , тогда на множестве t для функции f t t
существует первообразная F t .
Этот результат обычно записывают в виде
f x dx f t t dt.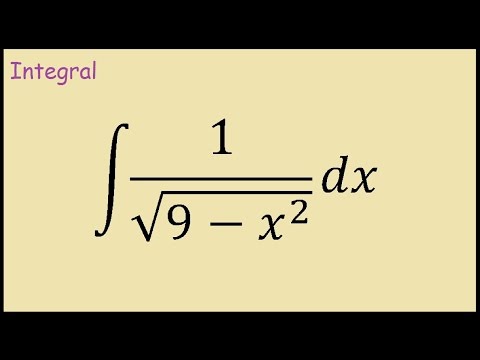
После взятия интеграла справа делают обратный переход к переменной x.
Замена переменной делается для того, чтобы свести интеграл к табличному или к интегралу, для которого известны способы интегрирования. Выбор правильной подстановки в значительной степени определяется умением анализировать подынтегральную функцию.
Пример 2. Найти интеграл | sinx coscdx . |
|
| |||||||||||||||||
Решение. | Положим u sinx, |
|
| тогда | du cosxdx и, | |||||||||||||||
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
| u sin x |
|
|
|
| 1 |
| 2 |
| 3 |
| |||||
|
|
|
|
|
|
|
|
| ||||||||||||
sin x cosxdx |
| u2du | u2 c | |||||||||||||||||
|
|
|
|
|
| |||||||||||||||
du cosxdx | 3 | |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
| 2 | sin x |
|
| c. |
|
|
|
|
|
|
| ||||
|
|
| 2 |
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
| 3 |
| 2 | 3 |
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
Ответ: | sin x cosxdx | sin x |
| c. |
|
|
|
| ||||||||||||
2 |
|
|
|
| ||||||||||||||||
|
|
|
|
| ||||||||||||||||
|
|
| 3 |
|
|
|
|
|
|
|
|
|
| |||||||
Метод замены переменной является основным методом интегрирования в неопределенном интеграле, который используется как промежуточный элемент интегрирования в сочетании с другими методами.
u x,du dx
3. Метод интегрирования по частям
Основан на использовании формулы
u x dv x u x v x v x du x ,
если u x и v x — дифференцируемые функции.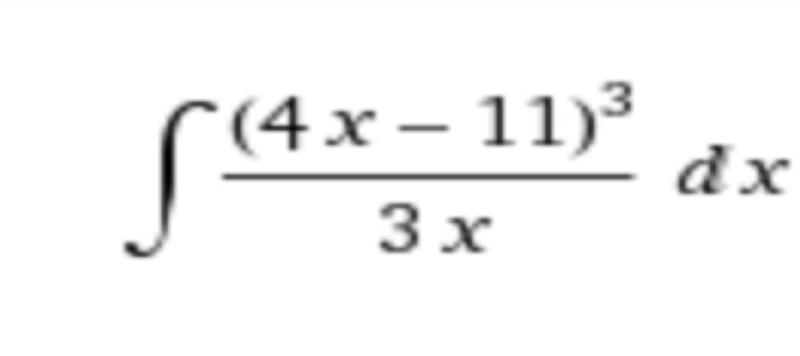 Важным условием удачного использования исходной формулы интегрирования по частям является правильный выбор функции u и выражения dv, в связи с этим можно пользоваться приведенным ниже перечнем интегралов, берущихся по частям, сгруппированных по типам (условно).
Важным условием удачного использования исходной формулы интегрирования по частям является правильный выбор функции u и выражения dv, в связи с этим можно пользоваться приведенным ниже перечнем интегралов, берущихся по частям, сгруппированных по типам (условно).
Первый тип интегралов, берущихся по частям:
p x eaxdx , p x sinaxdx, p x cosaxdx,
где p x — многочлен произвольной целой неотрицательной степени относительно x, a — постоянная.
В интегралах этого типа за u принимают многочлен p x , т.е. u p x , все остальное принимают за dv, т.е.
ax |
|
e |
|
| |
dv sinax | dx . |
|
|
cosax |
|
Пример 3. Вычислить интеграл xexdx .
Решение. Положим u x , dv exdx v ex , c 0 .
Процесс интегрирования будем записывать следующим образом:
xexdx dv exdx, v ex x ex exdx xex ex c.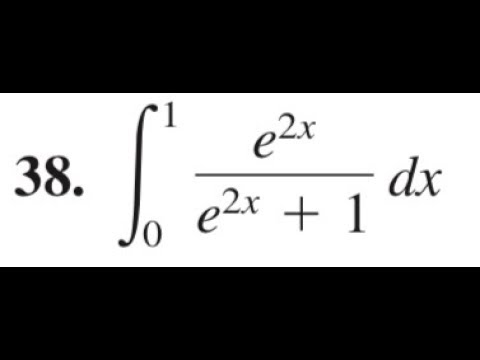
Ответ: xexdx x 1 ex c.
При нахождении функции v по известному выражению dv в
качестве произвольной постоянной удобно использовать | c 0, | так | |
как | значение c в промежуточном вычислении не | влияет | на |
выражение окончательного решения. |
|
| |
| Второй тип интегралов, берущихся по частям: |
|
|
sin x
cosx
p x lnxdx, p x arc dx, p x — многочлен.
tgx
|
|
|
| ctgx | |
В интегралах этого типа за | u | принимают либо логарифм, либо |
обратную функцию, т. |
|
|
lnx |
| |
|
|
|
| sin x | |
|
|
|
u | cosx , | |
arc |
| |
| tgx |
|
| ctgx | |
|
|
|
все остальное есть dv, т.е. dv p x dx.
Далее процесс интегрирования ведется аналогично предыдущему случаю.
| Пример 4. Вычислить интеграл xarctgxdx . |
|
| 1 |
| ||||||||||||||||
| Решение. |
| u arctgx, | dv xdx, | du | dx , | |||||||||||||||
|
| ||||||||||||||||||||
| x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 x2 |
| |||
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
| , запишем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
2 |
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
| u arctgx, | du |
| dx |
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
| xarctgxdx |
|
|
|
|
| 1 x2 |
|
|
| |||||||||
|
|
|
|
|
|
| x2 |
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
| dv xdx, | v |
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| ||
|
|
|
|
|
|
| x2 |
|
|
| x2 |
|
|
|
| ||||||
|
|
|
|
|
|
|
|
| arctgx | 21 x2 | dx ; |
|
|
|
| ||||||
|
|
|
|
|
| 2 |
|
|
|
| |||||||||||
вычислим | x2 |
|
| отдельно: |
|
|
|
|
|
|
|
|
|
|
| ||||||
21 x2 |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
| x2 |
| x2 1 1 | 1 |
| 1 |
| dx |
| |
| 21 x2 | dx | 21 x2 | dx |
| dx |
|
|
|
|
2 | 2 | 1 x2 | ||||||||
1 x 1arctgx c.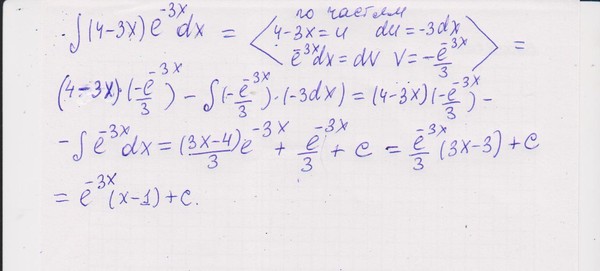
2 2
Ответ: xarctgxdx | x2 | arctgx | 1 | arctgx | 1 | x c. |
| 2 | 2 | ||||
2 |
|
|
| |||
Третий тип интегралов, берущихся по частям:
eax cosbxdx , | eax sinbxdx . |
Интегралы этого типа находятся двукратным интегрированием по частям. За u можно принимать любую из функций.
Пример 5. Найти интеграл e2x cos3xdx .
u e2x , du 2e2xdx
Решение: e2x cos3xdx dv cos3xdx, v 1sin 3x 3
1e2x sin3x 2e2x sin3xdx . 3 3
Вычислим полученный интеграл в правой части равенства еще раз по частям
ue2x, du 2e2xdx
e2x sin3xdx dv sin3xdx, v 1cos3x
3
| 1 |
|
|
| 2 | e2x cos3xdx, | ||||
3 |
|
|
| 3 | ||||||
|
|
|
|
|
| |||||
e2x cos3xdx | 1 | e2x sin3x | 2 | e2x cos3x | 4 | e2x cos3xdx . | ||||
| 9 |
| ||||||||
3 |
|
|
|
| 9 |
| ||||
В правой части равенства в результате второго интегрирования по частям получен исходный интеграл с коэффициентом. Перенесем этот интеграл в левую часть и, объединив с исходным интегралом, получим
| 13 | e2x cos3xdx | 1 | e2x sin3x | 2 | e2x cos3x , | ||||||||||||
9 |
|
|
| |||||||||||||||
|
|
| 3 |
|
|
|
| 3 |
| |||||||||
откуда e2x cos3xdx | 3 | e2x sin3x |
| 2 | e2x cos3x c. | |||||||||||||
|
| |||||||||||||||||
13 |
|
|
|
|
|
| 13 |
|
|
|
|
| ||||||
Ответ: e2x cos3xdx |
| 3 | e2x sin3x |
| 2 | e2x cos3x c. | ||||||||||||
13 | 13 | |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
Интегрирование рациональных дробей
Определение 1. | Pn x |
| называется рациональной, если ее | |
Qm x | ||||
|
| |||
числитель и знаменатель – многочлены степеней n и m n,m N с действительными коэффициентами.
Определение 2. Если n m, дробь | Pn | x |
| называется | |
Qm x | |||||
|
| ||||
неправильной. Если n m — дробь правильная.
Теорема 1. Всякая неправильная рациональная дробь может быть представлена в виде суммы многочлена и правильной дроби, а именно
P x n m | x | R x | , где R x — многочлен степени, | ||||
n |
| Wn m |
|
| |||
Qm x | Qm x | ||||||
|
|
| |||||
меньшей, чем m.
Теорема 2. Всякий многочлен степени m может быть представлен в виде произведения по корням действительным или комплексным в том числе и кратным.
Другими словами, если многочлен степени m Qm x имеет
действительные корни x1,x2,… и комплексные корни, то
Qm x
a0 x x1 x x2 … x2 p1x q1 … x2 p2x q2 ,
где a0 — действительное число, коэффициент при xm ,
x1,x2 — действительные корни, а квадратичные множители действительных корней не имеют и выполняется условие
… 2 … 2 m .
Определение 3. Правильные рациональные дроби вида:
1)A ,
xa
A
2) x a k (k — целое положительное число 2),
3) |
| Ax B |
| (корни знаменателя комплексные), |
| |||||||||||||
x2 px q |
| |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
4) |
|
| Ax B |
|
| , k 2, k N , | (корни знаменателя комплексные) | |||||||||||
| x2 | px q k | ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
| называются простейшими дробями. |
|
|
|
| |||||||||||
|
|
| Интегралы от простейших дробей, а именно, |
| ||||||||||||||
|
|
| A | dx , |
| A |
| dx, |
| Ax B |
|
| , |
| Ax B | dx . | ||
|
|
|
|
|
|
|
|
| ||||||||||
x a | x a k | x2 px qdx | x2 px q k | |||||||||||||||
|
|
|
|
| ||||||||||||||
Теорема 3. Всякая правильная рациональная дробь может быть разложена на сумму простейших дробей: если корень знаменателя действительный, то в числителе простейшей дроби пишем постоянную; если же корни комплексные, то в числителе пишем многочлен первой степени.
Всякая правильная рациональная дробь может быть разложена на сумму простейших дробей: если корень знаменателя действительный, то в числителе простейшей дроби пишем постоянную; если же корни комплексные, то в числителе пишем многочлен первой степени.
Пример разложения правильной дроби на простейшие:
|
|
|
|
|
|
|
|
| 3×2 x 1 |
|
|
|
|
|
|
| ||||||
|
|
| x 1 3 x 2 2 x2 x 4 2 x2 2x 8 3 |
| ||||||||||||||||||
|
| A1 |
| A2 |
|
| A3 |
|
| B1 |
| B2 |
| C1x D1 |
|
| ||||||
|
| x 1 2 | x 1 3 |
|
| x 2 2 |
|
| ||||||||||||||
|
| x 1 |
|
|
| x 2 |
|
| x2 x 4 |
| ||||||||||||
| C2x D2 | M1x N1 |
|
|
| M2x N2 |
|
| M3x N3 |
| ||||||||||||
|
|
|
|
|
|
|
|
| ; | |||||||||||||
x2 x 4 2 | x2 2x 8 | x2 2x 8 2 | x2 2x 8 3 | |||||||||||||||||||
коэффициенты A1, A2 , A3 , B1, B2, C1, C2, D1, D2 , M1, M2 , M3 , N1,N2,N3 называют неопределенными коэффициентами,
которые находят после приведения правой части равенства к общему
знаменателю, из условия равенства многочленов числителей справа и слева от знака равенства.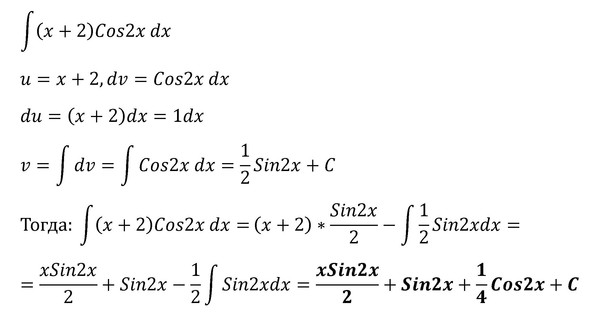
Интегрирование рациональных дробей, связанное с разложением подынтегральной дроби на простейшие с последующим нахождением неопределенных коэффициентов, называют методом неопределенных коэффициентов.
x3 x 2
Пример 6. Найти интеграл: x 3 x 4 dx .
x3 x 2
Решение. Подынтегральная дробь x 3 x 4 — неправильная,
следовательно, преобразуем ее к правильной дроби и целой части, разделив числитель на знаменатель
|
|
|
|
| _ x3 x 2 | x2 7x 12 | ||||||||||||
|
|
|
|
|
| x3 7×2 |
| 12x |
| x 7 | ||||||||
|
|
|
|
|
|
| _7x2 11x 2 |
|
|
| ||||||||
|
|
|
|
|
|
| 7×2 49x 84. | |||||||||||
|
|
|
|
|
|
|
|
|
|
| 38x 82 |
|
|
| ||||
Имеем |
| x3 x 2 |
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
| x 7 |
|
|
| 38x 82 | |||||||||
|
|
|
|
|
|
|
|
|
| . | ||||||||
Тогда |
| x 3 x 4 | x 3 x 4 | |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
| x3 x 2 |
|
|
|
|
|
|
|
|
| 38x 82 |
| ||||||
|
| dx x 7 |
|
|
|
|
|
|
|
| dx | |||||||
|
|
|
|
|
|
|
|
| ||||||||||
| x 3 x 4 |
|
|
|
| x 3 x 4 |
| |||||||||||
|
|
|
|
|
| |||||||||||||
|
|
|
| x2 |
|
|
| 38x 82 |
|
|
| |||||||
|
|
|
|
|
| 7x |
| dx. | ||||||||||
|
|
|
| 2 | x 3 x 4 | |||||||||||||
Для нахождения полученного интеграла разложим подынтегральную дробь на простейшие
38x 82 |
| A |
| B |
| A x 4 B x 3 | . | |
x 3 x 4 |
| x 3 | x 4 | x 3 x 4 | ||||
О понятии нечеткого интеграла | Статья в журнале «Молодой ученый»
Библиографическое описание: Макеева, А. В. О понятии нечеткого интеграла / А. В. Макеева. — Текст : непосредственный // Молодой ученый. — 2010. — № 5 (16). — Т. 1. — С. 34-37. — URL: https://moluch.ru/archive/16/1617/ (дата обращения: 03. 10.2022).
10.2022).
Введение понятия нечеткого интеграла связано со стремлением к разработке в нечеткой математике аналогов, используемых в статистике и теории вероятностей понятий среднего и математического ожидания. Поскольку указанные понятия базируются на свойстве аддитивности вероятностной меры, а нечеткие меры более широкий класс мер, разработка указанных аналогов привела к построению принципиально новой математической конструкции [2].
Нечеткий интеграл от функции h : X → [0, 1] на множестве AX по нечеткой мере g определяется как
h(x)g = (αg ( A ∩ Hα)), (1)
где Hα={x | h(x)≥α}.
Нечеткий интеграл принято также называть нечетким ожиданием или FEV (fuzzy expected value).
Нечеткий интеграл от функции h : X → [0,1] на нечетком множестве A={x, μA(x)} по нечеткой мере g определяется как [3]
h(x)g =(μ A (x) h( x))g (2)
Отметим основные свойства нечетких интегралов.
Пусть a[0,1], (E, FX ) и h: X → [0,1].
1. .
2. .
3. .
4. .
5. .
6. .
Можно показать, что понятие нечеткого интеграла сходно с понятием интеграла Лебега. Для этого рассмотрим разбиение множества X на непересекающиеся подмножества (рис.1):, , i ≠ j, i=1,2,…,n.
Рис. 1. Построение ступенчатой функции
Пусть — ступенчатая возрастающая функция (h:X → [0,1]), где
αi [0,1], Ei X , fEi — характеристическая функция обычного множества Ei, т. е. fEi (x) = 1, если xEi, fEi (x) = 0, x ∉ Ei. Пусть l есть мера Лебега. Интеграл Лебега от функции h по множеству A определяется как
, (3)
где i = {1, 2, 3 …. n}; α1 ≤ α2 ≤ α3 ≤ … αn.
Введем множества Fi = , i=1,2,…, n.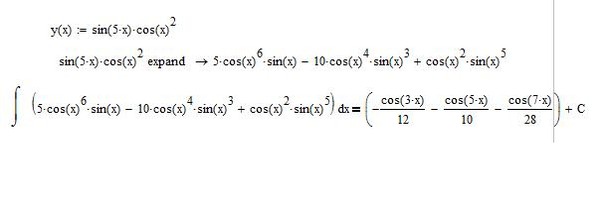 Тогда h(x) может быть представлена в виде . В этом случае нечеткий интеграл по аналогии с интегралом Лебега может быть определен в виде:
Тогда h(x) может быть представлена в виде . В этом случае нечеткий интеграл по аналогии с интегралом Лебега может быть определен в виде:
. (4)
Сопоставляя (3) и (4), можно обнаружить сходство между данными интегралами: операции сложения и умножения для интеграла (3) заменены операциями max и min соответственно для (4) [1].
Оба интеграла – лебегов и нечеткий – можно сравнить, используя вероятностную меру. Если (X, B, Р) – вероятностное пространство, а h: X → [0,1] есть B-измеримая функция, то имеем, что
. (5)
Сравнительно легко осуществлять расчет нечеткого интеграла в случае конечного множества X и соответственно конечного числа α, для которых требуется определить g(Hα). Для этого необходимо воспользоваться следующим утверждением.
Если функция h(x) принимает n+1 значение αi, то соответственно множество значений g(Hαi), отличных от 0 и 1, состоит из n элементов. В последовательности из 2n+1 элементов, составленной из элементов {αi} и {g(Hαi)}, расположенных в порядке возрастания, значение срединного n+1 элемента равно значению FEV(h).
В последовательности из 2n+1 элементов, составленной из элементов {αi} и {g(Hαi)}, расположенных в порядке возрастания, значение срединного n+1 элемента равно значению FEV(h).
На рис. 2 приведен пример графической интерпретации нахождения значения нечеткого интеграла для X = R [2]:
FEV(h)=, где Hα={x | h(x)≥α}.
Рис. 2. Графическая интерпретация нечеткого интеграла
Для описания различных видов неопределенности в теории нечетких мер используется общее понятие «степень нечеткости». В общем случае оно включает в себя «степень важности», «степень уверенности» и как отдельный случай — «степень принадлежности» в теории нечетких множеств. Нечеткая мера, таким образом, может интерпретироваться различными способами в зависимости от конкретного применения.
Определение нечеткого множества, фиксирующего степень принадлежности элемента хХ подмножеству АF(X), где F(Х) — множество всех нечетких подмножеств Х, может быть представлено с использованием нечеткого интеграла следующим образом [3].
Пусть необходимо оценить степень принадлежности некоторого элемента множеству . Очевидно, что для пустого множества эта степень принадлежности равна 0, а для равна 1, т.е. степень принадлежности для будет больше, чем для , если . Если степень принадлежности равна g(x0,E), а вместе E задано нечеткое подмножество , то .
Это говорит о том, что степень нечеткости суждения “” равна степени принадлежности нечеткому подмножеству . Таким образом, понятие степени нечеткости в теории нечетких мер включает в себя понятие степени принадлежности теории нечетких множеств.
Для непрерывного пространства X=R вычисление нечеткого интеграла может быть упрощено и сведено к нахождению значения на монограмме (или таблице).
Пусть выполняется условие:
{x|h(x)≥αi}=Fαi.
В этом случае справедливо следующее. Если f(x) – плотность нечеткой меры, значение нечеткого интеграла от h(x) по нечеткой мере равно значению , для которого справедливо:
, , (6)
где
.
Правая часть (6) зависит только от значений α и λ и может быть получена заранее в числовом виде в форме таблицы или графика. Левая часть (6) представляет собой отношение области, определяемой уровневым множеством Hα, ко всей области определения функции плотности нечеткой меры f(x).
Использование (6), таким образом, может облегчить организацию вычисления нечеткого интеграла [1].
В качестве примеров рассмотрим вычисления нечеткого интеграла для конечных множеств в случаях gλ— и gv-мep.
Пусть задано пятиэлементное множество X={хi}, i{1, 2, 3, 4, 5}. Каждому элементу хiX соответствуют значения нечетких плотностей gi из табл.1.
Таблица 1
|
i |
1 |
2 |
3 |
4 |
5 |
|
gi |
0,170 |
0,257 |
0,216 |
0,212 |
0,061 |
|
h(хi) |
0,5 |
0,7 |
0,1 |
0,2 |
0,3 |
Согласно условию нормировки для gi-меры получаем λ=0,25.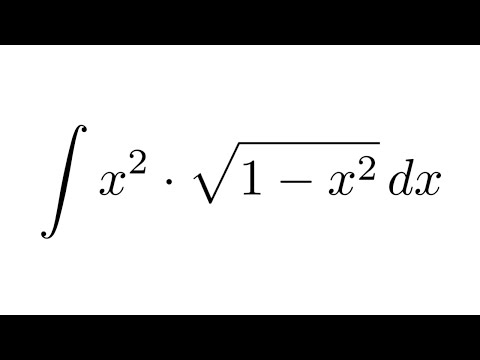 Значение нечеткого интеграла , где , Θα={i|h(xi)≥α},, принимает значение S=0,4379.
Значение нечеткого интеграла , где , Θα={i|h(xi)≥α},, принимает значение S=0,4379.
Для gv-мepы из условия нормировки можно получить
При этом значение нечеткого интеграла для gv -меры S = 0,448 [2].
Литература
Бочарников В.П. Fuzzy-технология: Математические основы. Практика моделирования в экономике. Санкт-Петер6ург: «Наука» РАН, 2001.- 328 с.
Павлов А.Н., Соколов Б.В. Принятие решений в условиях нечеткой информации. ГУАП- СПб., 2006 — 72 с.
Яхъяева Г.Э. Нечеткие множества и нейронные сети.– М.: Бином. Лаборатория знаний, 2008.- 320 с.
Основные термины (генерируются автоматически): нечеткий интеграл, FEV, нечеткая мера, множество, вероятностная мера, интеграл, мера, нечеткое множество, нечеткое подмножество, условие нормировки.
x — Формула, Доказательство, Проверка Прежде чем найти интеграл от e x , вспомним, что такое e x . Это экспоненциальная функция, поскольку она имеет переменную (x) в своем показателе и константу (e) в своем основании. Здесь «е» называется числом Эйлера, и его приблизительное значение равно 2,718. Интеграл от e x равен самому себе. Конечно, мы всегда добавляем постоянную интегрирования к значению каждого неопределенного интеграла.
Это экспоненциальная функция, поскольку она имеет переменную (x) в своем показателе и константу (e) в своем основании. Здесь «е» называется числом Эйлера, и его приблизительное значение равно 2,718. Интеграл от e x равен самому себе. Конечно, мы всегда добавляем постоянную интегрирования к значению каждого неопределенного интеграла.
Найдем интеграл от e x вместе с его проверкой дифференцированием и несколькими решенными примерами. 9Икс?
Интеграл от e x равен самому e x . Но мы знаем, что мы добавляем постоянную интегрирования после значения каждого неопределенного интеграла, и, следовательно, интеграл e x равен e x + C. Математически мы записываем это как ∫ e x dx = e x + С . Здесь
- ∫ — символ интегрирования.
- e x (за которым следует dx) является подынтегральной функцией 9x Доказательство дифференцированием
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 10743
- ОпенСтакс
- ОпенСтакс
- Подсказка
Используйте процесс из примера \(\PageIndex{8}\) для решения проблемы.
- Ответить
Есть \(116\) мух.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- расчет: да
- Интегралы экспоненциальных функций
- Формулы интегрирования с использованием логарифмических функций
е е б = e a + b
e a / e b = е ( а — б )
e 2 x
хe х
Мы используем цепное правило с
и = е u , u = 2 x
Что даету ‘ = е у , и ‘ = 2
Так что( е 2 х )’ = ( e u )(2) = 2 e 2 x
Мы используем правило произведения:
( xe x )’ = ( x )’ ( e x ) + x ( e x )’
= x
ln( e х )
e x / x 2
Начиная с
e x = ( e x )’
Мы можем объединить обе стороны, чтобы получитье х d x = e x + C
Для этого интеграла мы можем использовать замену u на
и = e x , d u = e x г х
Интегралов становится= e u + С
- Использование интегрирования по частям.
- Использование стандартной замены Исчисления I.
Мы осознаем, что интеграция и дифференциация — процессы, противоположные друг другу.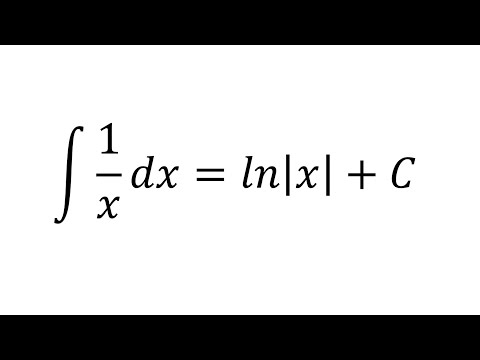 Таким образом, чтобы найти интеграл e x , мы должны увидеть, дифференцируя, какая функция даст e x . Если мы посмотрим на формулы дифференцирования, то найдем, что
Таким образом, чтобы найти интеграл e x , мы должны увидеть, дифференцируя, какая функция даст e x . Если мы посмотрим на формулы дифференцирования, то найдем, что
d/dx (e x ) = e x
Таким образом, мы можем прямо сказать, что интеграл от e x равен e x само (или) мы можем доказать это с помощью основной теоремы исчисления.
Умножение обеих частей на dx,
d/dx (e x ) dx = e x dx
Взяв интеграл от обеих частей приведенного выше уравнения,
∫ 4 x
(e 9000 ) dx = ∫ e
x dxПо основной теореме исчисления, «d/dx» и символ «∫ dx» сокращаются друг с другом, и мы получаем,
e x = ∫ e x dx
Так как мы должны добавлять постоянную интегрирования C для каждого неопределенного интеграла, 9x Использование расширения серии
Все стандартные функции имеют серийное расширение. Расширение серии e x : e x = 1 + x + x 2 /2! + х 3 /3! + . x
x
Мы знаем, что значение любого неопределенного интеграла можно проверить, используя процесс дифференцирования. Чтобы доказать, что интеграл от e x равен e x + C, нам просто нужно доказать, что производная от e x + C равна e x . Теперь найдем производную.
d/dx (e x + C) = d/dx (e x ) + d/dx (C)
= e x + 0
= e x
4 90,000 мы проверили формулу интеграла от e 9x от 0 до ∞ расходится.Интеграл показательной функции
Мы уже доказали, что интеграл экспоненциальной функции e x равен самой себе. Но вообще интеграл любой экспоненциальной функции x НЕ является самим собой. Тогда что такое ∫ a x dx? Покажи нам. Мы знаем, что производная от x есть x ln a. т. е.
d/dx (a x ) = a x ln a
Разделив обе стороны на ln a,
d/dx [ a x /ln a] = a x
говорят, что интеграл от х равен х /ln a.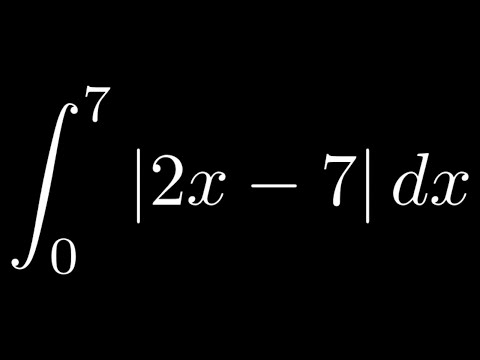 т. е.
т. е.
∫ a x dx = a x / ln a + C
Здесь C — постоянная интегрирования.
Таким образом, интеграл экспоненциальной функции a x равен x 9Икс? Чтобы найти ∫ x e x dx, предположим, что u = x и dv = e x dx. Тогда du = dx и v = e x . Затем интегрированием по частям ∫ u dv = uv — ∫ v du = x e x — ∫ e x dx = xe x — e x + C. Чтобы найти ∫ e x cos x dx, предположим, что u = cos x и dv = e x dx. Тогда du = -sin x dx и v = e x . Используя формулу интегрирования по частям, ∫ u dv = uv — ∫ v du. Отсюда ∫ e x cos x dx = (cos x) (e x ) — ∫ e x (- sin x) dx = cos x e x + ∫ e x sin x dx. Снова применяем интегрирование по частям (на этот раз с u = sin x и dv = e x dx). Мы можем записать ∫ 1/e x dx как ∫ e -x dx. Теперь предположим, что -x = u. Тогда -dx = du (или) dx = -du. Тогда приведенный выше интеграл принимает вид ∫ e u (-du) = — e u + C = -e -x + C. Экспоненциальные и логарифмические функции используются для моделирования роста населения, роста клеток и финансового роста, а также износа, радиоактивного распада и потребления ресурсов, и это лишь некоторые из приложений. В этом разделе мы исследуем интегрирование с использованием экспоненциальных и логарифмических функций. Показательная функция, пожалуй, самая эффективная функция с точки зрения операций исчисления. Распространенной ошибкой при работе с экспоненциальными выражениями является обращение с показателем степени на \(e\) так же, как мы обращаемся с показателями степени в полиномиальных выражениях. Мы не можем использовать правило степени для экспоненты на \(e\). Это может быть особенно запутанным, когда у нас есть и экспоненты, и полиномы в одном и том же выражении, как в предыдущей контрольной точке. В этих случаях мы всегда должны перепроверять, чтобы убедиться, что мы используем правильные правила для интегрируемых функций. 94}+С\) Как упоминалось в начале этого раздела, экспоненциальные функции используются во многих реальных приложениях. Число \(e\) часто ассоциируется с составным или ускоряющимся ростом, как мы видели в предыдущих разделах о производной. Хотя производная представляет собой скорость изменения или скорость роста, интеграл представляет собой общее изменение или общий рост. Функция «цена-спрос» сообщает нам о соотношении между объемом спроса на продукт и ценой продукта. Как правило, цена снижается по мере увеличения объема спроса. Функция предельной цены-спроса является производной от функции цены-спроса и говорит нам, как быстро меняется цена при данном уровне производства. Эти функции используются в бизнесе для определения ценовой эластичности спроса и помогают компаниям определить, будет ли прибыльным изменение уровня производства. 9{0,01t},\), а начальная популяция мух — \(100\) мух. Сколько мух будет в популяции через \(15\) дней? Пример \(\PageIndex{9}\): вычисление определенного интеграла с помощью подстановки Вычисление определенного интеграла с помощью подстановки: \[∫^2_1\dfrac{e^{1/x}}{x^2}\ ,дх. Правило: Основной интеграл, приводящий к натуральной логарифмической функции Следующая формула может использоваться для вычисления интегралов, в которых степень равна \(-1\), а правило степени не работает. \[ ∫\frac{1}{x}\,dx =\ln |x|+C\] Фактически, мы можем обобщить эту формулу для работы со многими рациональными подынтегральными выражениями, в которых производная знаменателя ( или его переменная часть) присутствует в числителе. Помните, что когда мы используем цепное правило для вычисления производной \(y = \ln[u(x)]\), мы получаем: \[\frac{d}{dx}\left( \ln[u(x)] \right) = \frac{1}{u(x)}\cdot u'(x) = \frac{u ‘(x)}{u(x)}\] Правило: общие интегралы, приводящие к натуральной логарифмической функции Это дает нам более общую формулу интегрирования, \[ ∫\frac{u'(x)} {u(x)}\,dx =\ln |u(x)|+C\] Пример \(\PageIndex{10}\): поиск первообразной, включающей \(\ln x\) первообразная функции \[\dfrac{3}{x−10}. Решение Первый фактор \(3\) вне интегрального символа. Затем используйте правило \(u’/u\). Таким образом, \[∫\dfrac{3}{x−10}\,dx=3∫\dfrac{1}{x−10}\,dx=3∫\dfrac{du}{u}=3\ ln |u|+C=3\ln |x−10|+C,\quad x≠10. \nonumber\] См. рисунок \(\PageIndex{3}\). Рисунок \(\PageIndex{3}\): Область определения этой функции: \(x \neq 10.\) Упражнение \(\PageIndex{8}\) Найдите первообразная от \[\dfrac{1}{x+2}.\] \[ ∫\frac{u'(x)}{u(x)}\,dx =\ln |u(x) |+C \номер\] Производная и интеграл экспоненты
Функция Определения и свойства показательной функции Экспоненциальная функция, y = e x ln x ln( e x ) = x e ln x = х Напомним, что Доказательство 2. ln[ e a / е б ]
= ln[ e a ]
— ln[ e b ] = a — b =
лн[ е а — б ] поскольку
ln( x ) равно 1-1, свойство доказано. Производная экспоненты 1 Пусть f ( x ) =
ln( x ) ф ‘( х ) =
1/ x ф ‘( г ( х ))
= 1/ e x г ‘( х )
= е x Теорема Если Примеры: Найдите производную числа Как решить интеграл от e
х потому что х? Тогда мы получаем ∫ e x cos x dx = (cos x) (e x ) + [(sin x) (e x ) — ∫ e x (cos x) dx] = e x cos x + e x sin x — ∫ e x cos x dx. Отсюда 2∫ e x cos x dx = e x 9х дх?
Тогда мы получаем ∫ e x cos x dx = (cos x) (e x ) + [(sin x) (e x ) — ∫ e x (cos x) dx] = e x cos x + e x sin x — ∫ e x cos x dx. Отсюда 2∫ e x cos x dx = e x 9х дх? Mathway | Популярные проблемы
1 Найти производную — d/dx натуральное бревно х 2 92) 21 Оценить интеграл интеграл от 0 до 1 кубического корня из 1+7x относительно x 22 Найти производную — d/dx грех(2x) 23 Найти производную — d/dx 9(3x) по отношению к x 41 Оценить интеграл интеграл от cos(2x) по x 42 Найти производную — d/dx 1/(корень квадратный из х) 43 Оцените интеграл 9бесконечность 45 Найти производную — d/dx х/2 46 Найти производную — d/dx -cos(x) 47 Найти производную — d/dx грех(3x) 92+1 68 Оценить интеграл интеграл от sin(x) по x 69 Найти производную — d/dx угловой синус(х) 70 Оценить предел ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х 85 Найти производную — d/dx лог х 86 Найти производную — d/dx арктан(х) 87 Найти производную — d/dx бревно натуральное 5х92 5.
 6: Интегралы с экспоненциальными и логарифмическими функциями
6: Интегралы с экспоненциальными и логарифмическими функциями Интегралы экспоненциальных функций
 x\) является собственной производной и собственным интегралом. 93}+С\)
x\) является собственной производной и собственным интегралом. 93}+С\)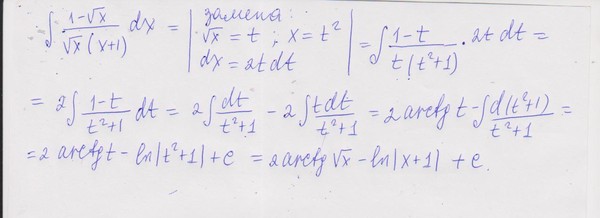 Давайте рассмотрим пример, в котором интеграция экспоненциальной функции решает обычное бизнес-приложение.
Давайте рассмотрим пример, в котором интеграция экспоненциальной функции решает обычное бизнес-приложение.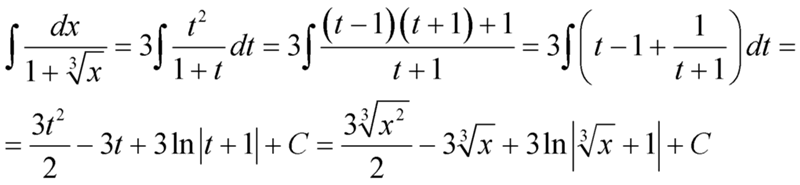 \номер\] 9{−1}\) приводят к абсолютному значению натуральной логарифмической функции, как показано в следующем правиле.
\номер\] 9{−1}\) приводят к абсолютному значению натуральной логарифмической функции, как показано в следующем правиле. \]
\]{−1}\,dx=\ln |x|+C \nonumber\]
Авторы
Производная и интеграл показательной функции
определяется как инверсия
из
Следовательно
и 
Мы будем использовать производную обратной теоремы, чтобы найти производную
экспоненциальной. Производная обратной теоремы говорит, что если f а также г обратные,
тогда
г ‘( x ) =
f ‘( г ( x ))
тогда
чтобы
Следовательно
ф ( х ) = e х
тогда
ф ‘( x ) = f ( x ) = e x
Раствор
e е x
Упражнения:
Найдите производные от
Примеры
А.
Б.
Решение
Упражнения
Интеграция:
Вернуться к Домашняя страница Math 105
Вернуться на математический факультет Дом
электронная почта Вопросы и Предложения
Исчисление II — Интегрирование по частям
Онлайн-заметки Пола
Главная
/
Исчисление II
/
Методы интеграции
/ Интеграция по частям
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-1: Интеграция по частям 92}}} + с\]
Опять же, достаточно просто сделать, если вы помните, как делать замены. Кстати, убедитесь, что вы можете делать такие замены быстро и легко. С этого момента мы будем делать такие замены в нашей голове. Если вам придется останавливаться и записывать их для каждой задачи, вы обнаружите, что вам потребуется значительно больше времени для решения этих задач.
Теперь давайте посмотрим на интеграл, который мы действительно хотим сделать. 9\prime}\,dx}} = \int{{f’\,g + f\,g’\,dx}}\]
Левую часть достаточно легко проинтегрировать (мы знаем, что интегрирование производной просто «отменяет» производную), и мы разделим правую часть интеграла.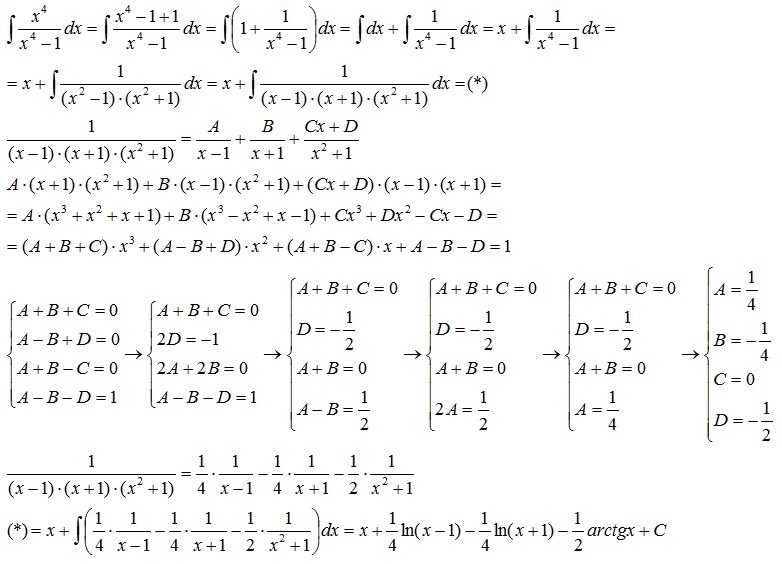
\[fg = \int{{f’\,g\,dx}} + \int{{f\,g’\,dx}}\]
Обратите внимание, что технически у нас должна была появиться константа интегрирования с левой стороны после выполнения интегрирования. Мы можем отбросить его на этом этапе, так как другие константы интеграции появятся в будущем, и они просто в конечном итоге поглотят эту.
Наконец, перепишем формулу следующим образом, и мы придем к формуле интегрирования по частям.
\[\int{{f\,g’\,dx}} = fg — \int{{f’\,g\,dx}}\]
Однако это не самая простая формула. Итак, делаем пару замен.
\[\begin{align*}u = f\left( x \right)\hspace{0.5in}v = g\left( x \right)\\ & du = f’\left( x \right)\, dx\hspace{0.5in}dv = g’\left( x \right)\,dx\end{align*}\]
Обе эти замены являются стандартными заменами Исчисления I, к которым, надеюсь, вы уже привыкли. Пусть вас не волнует тот факт, что здесь мы используем две замены. Они будут работать так же.
Они будут работать так же.
Использование этих подстановок дает нам формулу, которую большинство людей считают формулой интегрирования по частям.
Интеграция по частям
\[\int{{u\,dv}} = uv — \int{{v\,du}}\]
Чтобы использовать эту формулу, нам нужно определить \(u\) и \(dv\), вычислить \(du\) и \(v\), а затем использовать формулу. Заметьте также, что вычисление \(v\) очень просто. Все, что нам нужно сделать, это интегрировать \(dv\).
\[v = \int{{dv}}\]
Одна из самых сложных вещей при использовании этой формулы заключается в том, что вы должны уметь правильно идентифицировать как \(u\), так и \(dv\). Не всегда будет ясно, какой выбор правильный, и иногда мы делаем неправильный выбор. Это не то, о чем стоит беспокоиться. Если мы делаем неправильный выбор, мы всегда можем вернуться и попробовать другой набор вариантов.
Это приводит к очевидному вопросу: как узнать, правильный ли выбор мы сделали для \(u\) и \(dv\)? Ответ на самом деле довольно прост. Мы сделали правильный выбор для \(u\) и \(dv\), если после использования формулы интегрирования по частям новый интеграл (тот, что справа от формулы) действительно можно проинтегрировать. 9{6x}}\,dx}}\]
Мы сделали правильный выбор для \(u\) и \(dv\), если после использования формулы интегрирования по частям новый интеграл (тот, что справа от формулы) действительно можно проинтегрировать. 9{6x}}\,dx}}\]
Показать решение
Итак, на каком-то уровне проблема заключается в том, что \(x\) стоит перед экспонентой. Если бы этого не было, мы могли бы сделать интеграл. Заметьте также, что при интегрировании по частям все, что мы выбираем для \(u\), будет дифференцированным. Итак, кажется, что выбор \(u = x\) будет хорошим выбором, так как при дифференцировании \(x\) выпадет.
Теперь, когда мы выбрали \(u\), мы знаем, что \(dv\) будет всем остальным, что осталось. Итак, вот варианты для \(u\) и \(dv\), а также \(du\) и \(v\). 9{6x}} + c\end{выравнивание*}\]
После того, как мы сделали последний интеграл в задаче, мы добавим константу интегрирования, чтобы получить окончательный ответ.
Заметим также, что, как отмечено выше, мы знаем, что сделали правильный выбор для \(u\) и \(dv\), когда мы получили новый интеграл, который мы фактически вычисляем после применения формулы интегрирования по частям.
Далее рассмотрим интегрирование по частям для определенных интегралов. Формула интегрирования по частям для определенных интегралов: 9b\) в первом члене — это просто стандартная запись вычисления интеграла, с которой вы должны быть знакомы на данном этапе. Все, что мы делаем, это вычисляем термин, uv в данном случае, в точке \(b\), затем вычитаем оценку термина в точке \(a\).
На каком-то уровне нам действительно не нужна формула, потому что мы знаем, что при вычислении определенных интегралов все, что нам нужно сделать, это вычислить неопределенный интеграл, а затем выполнить вычисление. На самом деле, это, вероятно, будет немного проще, поскольку нам не нужно отслеживать оценку каждого термина таким образом. 9{- 6}}\end{выравнивание*}\]
Любой метод вычисления определенных интегралов с интегрированием по частям довольно прост, поэтому какой из них вы выберете, зависит от вас.
Поскольку нам нужно уметь вычислять неопределенный интеграл, чтобы вычислить определенный интеграл, а выполнение определенного интеграла сводится к вычислению неопределенного интеграла в нескольких точках, мы сосредоточимся на вычислении неопределенного интеграла в остальных точках. эта секция. Фактически, на протяжении большей части этой главы так и будет. Мы будем делать гораздо больше неопределенных интегралов, чем определенных интегралов.
эта секция. Фактически, на протяжении большей части этой главы так и будет. Мы будем делать гораздо больше неопределенных интегралов, чем определенных интегралов.
Давайте рассмотрим еще несколько примеров.
Пример 3. Вычислите следующий интеграл. \[\int{{\left({3t + 5} \right)\cos \left({\frac{t}{4}} \right)\,dt}}\]
Показать решение
Этот пример можно продолжить двумя способами. Для многих первое, что они пробуют, это умножить косинус через круглые скобки, разделить интеграл, а затем выполнить интегрирование по частям в первом интеграле.
Хотя это вполне приемлемый способ решения проблемы, это больше работы, чем нам действительно нужно. Вместо того, чтобы разбивать интеграл, давайте вместо этого используем следующие варианты для \(u\) и \(dv\).
\[\begin{align*}u & = 3t + 5& \hspace{0. 5in}dv & = \cos\left({\frac{t}{4}} \right)\,dt\\ du & = 3 \, dt & \ hspace {0,5 дюйма} v & = 4 \ sin \ left ( {\ frac {t} {4}} \ right) \ end {align *} \]
5in}dv & = \cos\left({\frac{t}{4}} \right)\,dt\\ du & = 3 \, dt & \ hspace {0,5 дюйма} v & = 4 \ sin \ left ( {\ frac {t} {4}} \ right) \ end {align *} \]
Тогда интеграл равен
\[\ begin{align*}\int{{\left({3t + 5} \right)\cos \left({\frac{t}{4}} \right)\,dt}} & = 4\ влево ({3t + 5} \right)\sin \left({\frac{t}}{4}} \right) — 12\int{{\sin \left({\frac{t}{4}} \ справа) \, dt}} \\ & = 4 \ влево ( {3t + 5} \ вправо) \ грех \ влево ( {\ гидроразрыва {t} {4}} \ вправо) + 48 \ соз \ влево ( {\ frac{t}{4}} \right) + c\end{align*}\]
Обратите внимание, что мы убрали все константы из интеграла, когда использовали формулу интегрирования по частям. Обычно мы будем делать это, чтобы немного упростить интеграл. 92}}}{{10}}\cos \left( {10w} \right) + \frac{1}{5}\int{{w\cos \left( {10w} \right)\,dw}} \]
В этом примере, в отличие от предыдущих примеров, новый интеграл также потребует интегрирования по частям. Для этого второго интеграла мы будем использовать следующие варианты.
Для этого второго интеграла мы будем использовать следующие варианты.
\[\begin{align*}u & = w & \hspace{0.5in}dv & = \cos \left( {10w} \right)\,dw\\ du & = \,dw & \hspace{0.5in }v & = \frac{1}{{10}}\sin \left( {10w} \right)\end{align*}\] 92}}}{{10}}\cos \left( {10w} \right) + \frac{w}{{50}}\sin \left( {10w} \right) + \frac{1}{{ 500}}\cos\left( {10w} \right) + c\end{align*}\]
Будьте осторожны с коэффициентом при интеграле для второго применения интегрирования по частям. Поскольку интеграл умножается на \(\frac{1}{5}\), нам нужно убедиться, что результаты фактического выполнения интеграла также умножаются на \(\frac{1}{5}\). Забыть сделать это — одна из самых распространенных ошибок при интегрировании по частям.
Как показал последний пример, иногда нам потребуется более одного применения интегрирования по частям, чтобы полностью вычислить интеграл. Это то, что произойдет, так что не волнуйтесь об этом, когда это произойдет.
В следующем примере мы должны отметить важный момент, касающийся методов интеграции. Некоторые интегралы можно вычислить, используя несколько различных методов. Так обстоит дело с интегралом в следующем примере.
Пример 5. Вычислите следующий интеграл \[\int{{x\sqrt {x + 1} \,dx}}\]
Показать все решения Скрыть все решения
a Использование интегрирования по частям. Показать решение
Прежде всего обратите внимание, что в этом интеграле нет триггерных функций или экспонент. В то время как многие интегрирования по частям будут включать тригонометрические функции и/или экспоненты, не все из них будут, поэтому не слишком зацикливайтесь на идее ожидания их появления. 9{\ гидроразрыва {5} {2}}} + с \ конец {выравнивание *} \]
9{\ гидроразрыва {5} {2}}} + с \ конец {выравнивание *} \]
b Используя стандартную замену Calculus I. Показать решение
Теперь сделаем интеграл с подстановкой. Мы можем использовать следующую замену.
\[u = x + 1\hspace{0,5 дюйма}x = u — 1\hspace{0,5in}du = dx\]
Обратите внимание, что на самом деле мы будем использовать замену дважды, один раз для количества под квадратным корнем и один раз для \(x\) перед квадратным корнем. Тогда интеграл равен 9{\ гидроразрыва {3} {2}}} + с \ конец {выравнивание *} \]
Итак, в этом примере мы использовали два разных метода интеграции и получили два разных ответа. Очевидный вопрос тогда должен быть: Мы сделали что-то не так?
На самом деле, мы не сделали ничего плохого. Нам нужно помнить следующий факт из исчисления I.
\[{\rm{If}}\,\,f’\left(x\right) = g’\left(x\right)\,\,\,{\rm{then}}\,\,\ ,f\влево(x\вправо) = g\влево(x\вправо) + c\]
Другими словами, если две функции имеют одинаковую производную, то они будут отличаться не более чем на константу. Итак, как это относится к вышеупомянутой проблеме? Сначала определите следующее,
Итак, как это относится к вышеупомянутой проблеме? Сначала определите следующее,
\[f’\влево( x \вправо) = g’\влево( x \вправо) = x\sqrt {x + 1} \]
Затем мы можем вычислить \(f\left( x \right)\) и \(g\left( x \right)\), интегрируя следующим образом:
\[f\left( x \right) = \int{{f’\left( x \right)\,dx}}\hspace{0.5in}g\left( x \right) = \int{{g’ \влево( х \вправо)\,dx}}\]
Мы будем использовать интегрирование по частям для первого интеграла и замену для второго интеграла. Тогда по тому, что \(f\left( x \right)\) и \(g\left( x \right)\) должны отличаться не более чем на константу. Давайте проверим это и посмотрим, так ли это. Мы можем убедиться, что они различаются не более чем на константу, если посмотрим на разницу между ними и проделаем небольшую алгебраическую манипуляцию и упрощение.
\[\ begin{array}{l}\left( {\frac{2}{3}x{{\left({x + 1} \right)}^{\frac{3}{2}}} — \frac{4}{{15}}{{\left({x + 1} \right)}^{\frac{5}{2}}}} \right) — \left({\frac{2} {5}{{\left( {x + 1} \right)}^{\frac{5}{2}}} — \frac{2}{3}{{\left( {x + 1} \right )} ^ {\ frac {3} {2}}}} \ right) \\ \ hspace {2,0 дюйма} = {\ left ( {x + 1} \ right) ^ {\ frac {3} {2}} }\left( {\frac{2}{3}x — \frac{4}{{15}}\left({x + 1} \right) — \frac{2}{5}\left({x + 1} \right) + \frac{2}{3}} \right)\\ \hspace{2. {\frac{3}{2} }}\left( 0 \right)\\ \hspace{2.0in} = 0\end{массив}\]
{\frac{3}{2} }}\left( 0 \right)\\ \hspace{2.0in} = 0\end{массив}\]
Итак, в данном случае получается, что две функции — это одна и та же функция, поскольку разница равна нулю. Обратите внимание, что это происходит не всегда. Иногда разница будет давать ненулевую константу. В качестве примера см. раздел «Константа интегрирования» в заметках «Исчисление I».
Итак, что мы узнали? Во-первых, иногда будет более одного метода вычисления интеграла. Во-вторых, мы видели, что разные методы часто приводят к разным ответам. Наконец, даже если ответы разные, можно показать, иногда с большим трудом, что они отличаются не более чем на константу.
Когда мы сталкиваемся с интегралом, первое, что нам нужно решить, это то, есть ли более одного способа вычислить интеграл. Если существует более одного способа, нам нужно определить, какой метод мы должны использовать. Общее эмпирическое правило, которое я использую на своих занятиях, состоит в том, что вы должны использовать тот метод, который вам кажется самым легким.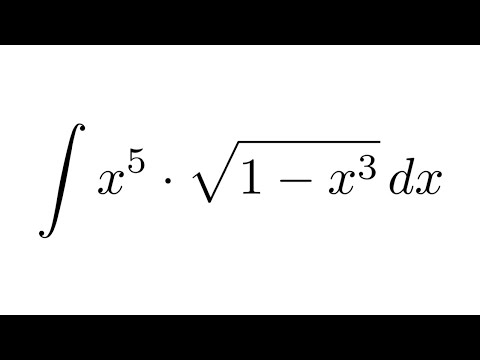 Возможно, это не тот метод, который другим кажется самым простым, но это не делает его неправильным.
Возможно, это не тот метод, который другим кажется самым простым, но это не делает его неправильным.
Одна из наиболее распространенных ошибок при интеграции по частям заключается в том, что люди слишком зацикливаются на воспринимаемых шаблонах. Например, во всех предыдущих примерах использовался базовый шаблон, когда \(u\) был полиномом, стоящим перед другой функцией, а затем пусть \(dv\) был другой функцией. Это происходит не всегда, поэтому нам нужно быть осторожными и не зацикливаться на каких-либо шаблонах, которые, как нам кажется, мы видим.
Давайте посмотрим на некоторые интегралы, которые не вписываются в приведенную выше схему.
Пример 6. Вычислите следующий интеграл. \[\int{{\ln x\,dx}}\]
Показать решение
Итак, в отличие от любого другого интеграла, который мы сделали до этого момента, в интеграле есть только одна функция и нет многочлена, стоящего перед логарифмом.
Первое, что многие здесь делают, это попытаться вписать это в шаблон, описанный выше, и сделать следующие варианты для \(u\) и \(dv\).
\[u = 1\hspace{0.5in}dv = \ln x\,dx\]
Однако это приводит к реальной проблеме, поскольку это означает, что \(v\) должно быть,
\[v = \int{{\ln x\,dx}}\]
Другими словами, нам нужно знать ответ заранее, чтобы решить задачу. Таким образом, этот выбор просто не будет работать.
Следовательно, если логарифм не принадлежит \(dv\), он должен принадлежать \(u\). Итак, давайте использовать следующие варианты вместо
\[\begin{align*}u & = \ln x & \hspace{0,5in} dv & = \,dx\\ du & = \frac{1}{x}dx & \hspace{0,5in}v & = х\конец{выравнивание*}\]
Тогда интеграл равен
\[\begin{align*}\int{{\ln x\,dx}} & = x\ln x — \int{{\frac{1}{x}\,x\,dx}}\\ & = x\ln x — \int{{dx}}\\ & = x\ln x — x + c\end{align*}\]
Пример 7. \theta}\cos \theta \,d\theta}}\]
\theta}\cos \theta \,d\theta}}\]
Показать решение
Хорошо, до сих пор мы всегда выбирали \(u\) таким образом, чтобы при дифференцировании эта часть исчезала или, по крайней мере, представляла интеграл в форме, которая облегчала бы работу с. В этом случае какую бы часть мы ни составили \(u\), она никогда не исчезнет в процессе дифференцирования.
Не так уж важно, что мы выберем в качестве \(u\), поэтому мы выберем следующим образом. Обратите внимание, однако, что мы могли бы выбрать и другой путь, и в конце концов мы получим тот же результат. 9\theta }\sin \theta } \right) + c\]
Обратите внимание, что после деления на два мы добавляем константу интегрирования в этой точке.
Эту идею интегрирования до тех пор, пока вы не получите один и тот же интеграл по обе стороны от знака равенства, а затем просто находите интеграл, неплохо запомнить. Он появляется не так уж часто, но когда появляется, это может быть единственным способом вычислить интеграл.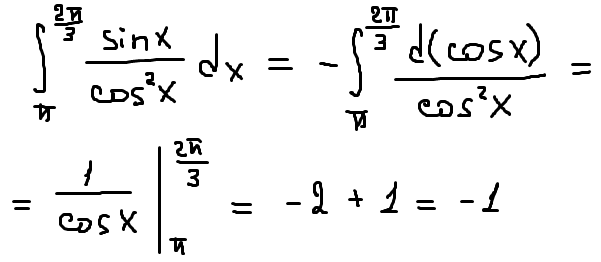
Обратите также внимание, что на самом деле это просто алгебра, правда, сделанная так, что вы, возможно, не привыкли ее видеть, но на самом деле это просто алгебра.
На этом этапе вашей математической карьеры каждый может решить,
\[x = 3 — x\hspace{0,5 дюйма} \to \hspace{0,5 дюйма} x = \frac{3}{2}\]
Мы все еще решаем «уравнение». Единственная разница в том, что вместо нахождения \(x\) в мы находим интеграл, а вместо хорошей константы «3» в приведенной выше задаче по алгебре у нас есть «более беспорядочная» функция.
У нас есть еще один пример. Как мы увидим, некоторые проблемы могут потребовать многократного интегрирования по частям, и существует короткий метод, который позволит нам быстро и легко выполнять несколько приложений интегрирования по частям. 9{\ гидроразрыва {х} {2}}} \, дх}} \]
Показать решение
Мы начинаем с выбора \(u\) и \(dv\), как обычно.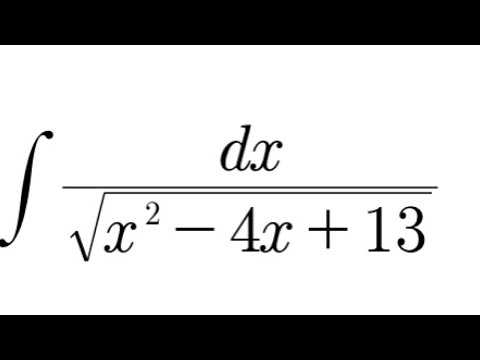 Однако вместо вычисления \(du\) и \(v\) мы помещаем их в следующую таблицу. Затем мы дифференцируем столбец, соответствующий \(u\), пока не достигнем нуля. В столбце, соответствующем \(dv\), мы интегрируем один раз для каждой записи в первом столбце. Существует также третий столбец, который мы немного объясним, и он всегда начинается с «+», а затем чередуются знаки, как показано. 9{\ гидроразрыва {х} {2}}} + с \ конец {выравнивание *} \]
Однако вместо вычисления \(du\) и \(v\) мы помещаем их в следующую таблицу. Затем мы дифференцируем столбец, соответствующий \(u\), пока не достигнем нуля. В столбце, соответствующем \(dv\), мы интегрируем один раз для каждой записи в первом столбце. Существует также третий столбец, который мы немного объясним, и он всегда начинается с «+», а затем чередуются знаки, как показано. 9{\ гидроразрыва {х} {2}}} + с \ конец {выравнивание *} \]
У нас есть интеграл. Это намного проще, чем записывать все различные \(u\) и \(dv\), которые нам пришлось бы делать в противном случае.
Итак, в этом разделе мы увидели, как выполнять интегрирование по частям. На более поздних занятиях по математике это, вероятно, будет одним из наиболее частых методов интеграции, с которыми вы столкнетесь.
Важно не слишком зацикливаться на шаблонах, которые, как вам может показаться, вы уже видели. В большинстве случаев любой шаблон, который, как вам кажется, вы видели, может (и будет) нарушен в какой-то момент времени.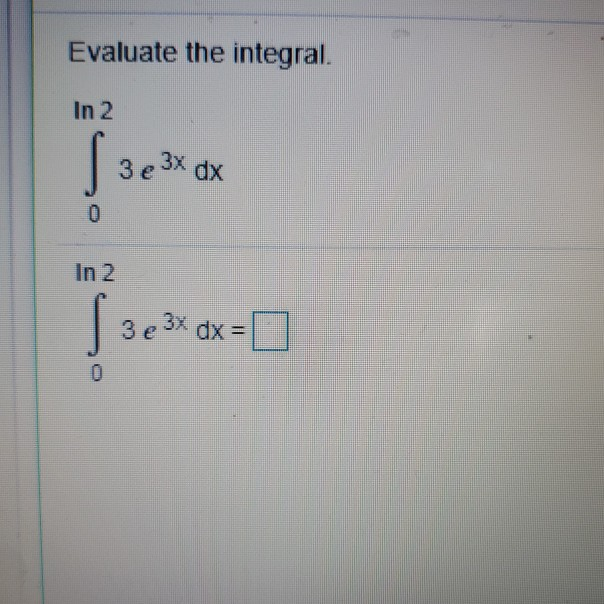 {b} f\,dx\)
{b} f\,dx\)
Примеры
SymPy может интегрировать широкий спектр функций. Он может интегрировать полиномиальные функции:
>>> из импорта sympy *
>>> init_printing(use_unicode=False, wrap_line=False)
>>> х = Символ('х')
>>> интегрировать(х**2 + х + 1, х)
3 2
х х
-- + -- + х
3 2
Рациональные функции:
>>> интегрировать(х/(х**2+2*х+1), х)
1
журнал (х + 1) + -----
х + 1
Экспоненциально-полиномиальные функции. Эти мультипликативные комбинации полиномов и функций exp , cos и sin можно интегрировать вручную, используя многократное интегрирование по частям, что является чрезвычайно утомительным процессом. К счастью, SymPy справится с этими интегралами.
>>> интегрировать(x**2 * exp(x) * cos(x), x)
2 х 2 х х х
x *e *sin(x) x *e *cos(x) x e *sin(x) e *cos(x)
------------ + ------------ - x*e *sin(x) + --------- - ----- ----
2 2 2 2
можно вычислить даже несколько неэлементарных интегралов (в частности, некоторые интегралы, включающие функцию ошибок):
>>> интегрировать(exp(-x**2)*erf(x),x)
____ 2
\/ пи *erf (x)
--------------
4
Интегральные преобразования
SymPy имеет специальную поддержку определенных интегралов и интегральных преобразований.
- sympy.integrals.transforms.mellin_transform( f , x 9{s-1} f(x) \mathrm{d}x.\]
- Для всех «разумных» функций абсолютно сходится в полосе
\(a < \operatorname{Re}(s) < b\).
Пояснение
Преобразование Меллина связано заменой переменных с преобразованием Фурье преобразования, а также к (двустороннему) преобразованию Лапласа.
Эта функция возвращает
(F, (a, b), условие)гдеF— преобразование Меллинаf,(a, b)— основная полоса (как указано выше), аcond— вспомогательные условия сходимости.Если интеграл нельзя вычислить в закрытой форме, эта функция возвращает неоцененный объект
MellinTransform.Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.doit(). Еслиnoconds=False, то будет возвращено только \(F\) (т. е. не
е. не конд, а так же не полоска(а, б)).Примеры
>>> из sympy import mellin_transform, exp >>> из sympy.abc импортировать x, s >>> mellin_transform(exp(-x),x,s) (гамма(ы), (0, оо), Истина)
См. также
inverse_mellin_transform,laplace_transform,Fourier_transform,hankel_transform,inverse_hankel_transform
- класс sympy.integrals.transforms.MellinTransform ( *args ) [источник]
Класс, представляющий невычисленные преобразования Меллина.
Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять преобразования Меллина, см.
mellin_transform()строка документации.
- sympy.integrals.transforms.inverse_mellin_transform( 9{-s} F(s) \mathrm{d}s,\]
для любого \(c\) в основной полосе.
 При определенной закономерности
условия на \(F\) и/или \(f\),
это восстанавливает \(f\) из его преобразования Меллина \(F\)
(и наоборот), для положительных действительных \(х\).
При определенной закономерности
условия на \(F\) и/или \(f\),
это восстанавливает \(f\) из его преобразования Меллина \(F\)
(и наоборот), для положительных действительных \(х\).Один из \(a\) или \(b\) может быть передан как
None; подходящим \(c\) будет предполагаемый.Если интеграл нельзя вычислить в закрытой форме, эта функция возвращает неоцененный
InverseMellinTransformобъект.Обратите внимание, что эта функция будет считать x положительным и действительным, независимо от предположений SymPy!
Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.doit().Примеры
>>> from sympy import inverse_mellin_transform, оо, гамма >>> из sympy.abc импортировать x, s >>> inverse_mellin_transform(gamma(s), s, x, (0, оо)) ехр(-х)
Основная полоса имеет значение:
>>> f = 1/(s**2 - 1) >>> inverse_mellin_transform(f,s,x,(-oo,-1)) х*(1 - 1/х**2)*Хевисайд(х - 1)/2 >>> inverse_mellin_transform(f, s, x, (-1, 1)) -x*Хевисайд(1 - х)/2 - Хевисайд(х - 1)/(2*х) >>> inverse_mellin_transform(f, s, x, (1, оо)) (1/2 - x**2/2)*Хевисайд(1 - x)/x
См.
 также
такжеmellin_transform,hankel_transform,inverse_hankel_transform
- класс sympy.integrals.transforms.InverseMellinTransform( *args )[источник]
Класс, представляющий невычисленные обратные преобразования Меллина.
Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять обратные преобразования Меллина, см.
inverse_mellin_transform()строка документации. 9{-st} f(t) \mathrm{d}t.\]Пояснение
Для всех разумных функций это сходится абсолютно в полусамолет
\[a <\operatorname{Re}(s)\]
Эта функция возвращает
(F, a, cond), гдеF— это число Лапласа. преобразованиеf, \(a\) является полуплоскостью сходимости, а \(cond\) являются вспомогательные условия сходимости.Реализация основана на правилах, и если вас интересует, какие применяются правила, и если попытка интеграции, вы можете переключить отладочная информация по настройке 9{-st} f(t) \mathrm{d}t\]
, применяя правила.

Если интеграл нельзя полностью вычислить в закрытой форме, эта функция возвращает неоцененный объект
LaplaceTransform.Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.doit(). Еслиnoconds=True, будет возвращено только \(F\) (т.е. неcond, а также не плоскостьa).Устарело, начиная с версии 1.9: устаревшее поведение для матриц, где
laplace_transformсnoconds=False(по умолчанию) возвращает матрицу, элементы которой кортежи. Поведениеlaplace_transformдля матриц изменится в будущем выпуске SymPy, чтобы вернуть кортеж преобразованного Матрица и условия сходимости матрицы в целом. Использоватьlegacy_matrix=False, чтобы включить новое поведение.Примеры
>>> из sympy import DiracDelta, exp, laplace_transform >>> из sympy.abc импортировать t, s, a >>> laplace_transform(t**4, t, s) (24/с**5, 0, правда) >>> laplace_transform(t**a, t, s) (гамма (а + 1)/(s*s**a), 0, re(a) > -1) >>> laplace_transform(DiracDelta(t)-a*exp(-a*t),t,s) (с/(а + с), Макс(0, -а), Истина)
См.
 также
такжеinverse_laplace_transform,mellin_transform,фурье_преобразование,hankel_transform,inverse_hankel_transform
- класс sympy.integrals.transforms.LaplaceTransform ( *args ) [источник]
Класс, представляющий невычисленные преобразования Лапласа.
Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять преобразования Лапласа, см. 9{st} F(s) \mathrm{d}s,\]
для \(c\) настолько больших, что \(F(s)\) не имеет сингулярностей в полуплоскость \(\operatorname{Re}(s) > c-\epsilon\).
Пояснение
Плоскость может быть указана аргумент
plane, но будет выведен, если передан как None.При определенных условиях регулярности это восстанавливает \(f(t)\) из его Преобразование Лапласа \(F(s)\), для неотрицательных \(t\) и наоборот наоборот
Если интеграл нельзя вычислить в закрытой форме, эта функция возвращает неоцененный
InverseLaplaceTransformобъект.
Обратите внимание, что эта функция всегда предполагает, что \(t\) действительно, независимо от предположения SymPy о \(t\).
Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.doit().Примеры
>>> из sympy import inverse_laplace_transform, exp, Symbol >>> из sympy.abc импортировать s, t >>> a = Symbol('a', положительный=Истина) >>> inverse_laplace_transform(exp(-a*s)/s, s, t) Хевисайд (-a + t)См. также
laplace_transform,_fast_inverse_laplace,hankel_transform,inverse_hankel_transform
- класс sympy.integrals.transforms.InverseLaplaceTransform ( *args ) [источник]
Класс, представляющий невычисленные обратные преобразования Лапласа.
Информацию об использовании этого класса см. в строке документации
IntegralTransform.
О том, как вычислять обратные преобразования Лапласа, см.
inverse_laplace_transform()строка документации.
- sympy.integrals.transforms._fast_inverse_laplace( e , s , t )[источник]
Быстрое обратное преобразование Лапласа рациональной функции, включая RootSum
- sympy.integrals.transforms.fourier_transform( f , x , 9{-2\pi x k} \mathrm{d} x.\]
Пояснение
Если преобразование не может быть вычислено в закрытой форме, это Функция возвращает неоцененный объект
FourierTransform.Другие правила преобразования Фурье см. в функции
sympy.integrals.transforms._fourier_transform().Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.doit(). Обратите внимание, что для этого преобразования по умолчаниюnoconds=True.
Примеры
>>> из sympy импорта fourier_transform, exp >>> из sympy.abc импортировать x, k >>> преобразование_фурье(exp(-x**2),x,k) sqrt(pi)*exp(-pi**2*k**2) >>> Fourier_transform(exp(-x**2), x, k, noconds=False) (sqrt(pi)*exp(-pi**2*k**2), True)
См. также
inverse_fourier_transform,sine_transform,inverse_sine_transform,cosine_transform,inverse_cosine_transform,hankel_transform,inverse_hankel_transform,mellin_transform,laplace_transform
- sympy.integrals.transforms._fourier_transform( f , x , k , a , b , имя , упростить = True 9{bixk} f(x)\, dx.\]
При подходящем выборе a и b это сводится к стандартному Фурье и обратное преобразование Фурье.
- класс sympy.
 integrals.transforms.FourierTransform( *args )[источник]
integrals.transforms.FourierTransform( *args )[источник] Класс, представляющий невычисленные преобразования Фурье.
Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять преобразования Фурье, см. 9{2\pi x k} \mathrm{d} k.\]
Пояснение
Если преобразование не может быть вычислено в закрытой форме, это Функция возвращает неоцененный объект
InverseFourierTransform.Другие правила преобразования Фурье см. в функции
sympy.integrals.transforms._fourier_transform().Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.doit(). Обратите внимание, что для этого преобразования по умолчаниюnoconds=True.Примеры
>>> из sympy import inverse_fourier_transform, exp, sqrt, pi >>> из sympy.abc импортировать x, k >>> inverse_fourier_transform(sqrt(pi)*exp(-(pi*k)**2), k, x) ехр(-х**2) >>> inverse_fourier_transform(sqrt(pi)*exp(-(pi*k)**2), k, x, noconds=False) (exp(-x**2), Истина)
См.
 также
такжеfourier_transform,sine_transform,inverse_sine_transform,cosine_transform,inverse_cosine_transform,hankel_transform,inverse_hankel_transform,mellin_transform,laplace_transform
- класс sympy.integrals.transforms.InverseFourierTransform( *args )[источник]
Класс, представляющий необработанные обратные преобразования Фурье.
Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять обратное преобразование Фурье, см.
inverse_fourier_transform()строка документации.
- sympy.integrals.transforms.sine_transform( f , x , k , **подсказки )[источник]
Вычислить унитарное синусоидальное преобразование \(f\) с обычной частотой, определенное как 9\infty f(x) \sin(2\pi x k) \mathrm{d} x.
 \]
\]Пояснение
Если преобразование не может быть вычислено в закрытой форме, это Функция возвращает неоцененный объект
SineTransform.Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.doit(). Обратите внимание, что для этого преобразования по умолчаниюnoconds=True.Примеры
>>> из sympy импортировать sine_transform, exp >>> из sympy.abc импортировать x, k, a >>> sine_transform(x*exp(-a*x**2), x, k) sqrt(2)*k*exp(-k**2/(4*a))/(4*a**(3/2)) >>> sine_transform(x**(-a), x, k) 2**(1/2 - а)*k**(а - 1)*гамма(1 - а/2)/гамма(а/2 + 1/2)
See also
fourier_transform,inverse_fourier_transform,inverse_sine_transform,cosine_transform,inverse_cosine_transform,hankel_transform,inverse_hankel_transform,mellin_transform,laplace_transform
- класс sympy.
 integrals.transforms.SineTransform ( *args ) [источник]
integrals.transforms.SineTransform ( *args ) [источник] Класс, представляющий невычисленные синусоидальные преобразования.
Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять синусоидальные преобразования, см.
sine_transform()строка документации.
- sympy.integrals.transforms.inverse_sine_transform( F , k , x , **подсказки )[источник]
Вычисление унитарного обратного синусоидального преобразования с обычной частотой \(F\), определяется как 9\infty F(k) \sin(2\pi x k) \mathrm{d} k.\]
Пояснение
Если преобразование не может быть вычислено в закрытой форме, это Функция возвращает неоцененный объект
InverseSineTransform.Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.. Обратите внимание, что для этого преобразования по умолчанию doit()
doit() noconds=True.Примеры
>>> из sympy import inverse_sine_transform, exp, sqrt, gamma >>> из sympy.abc импортировать x, k, a >>> inverse_sine_transform(2**((1-2*a)/2)*k**(a - 1)* ... гамма(-а/2 + 1)/гамма((а+1)/2), к, х) х**(-а) >>> inverse_sine_transform(sqrt(2)*k*exp(-k**2/(4*a))/(4*sqrt(a)**3), k, x) х*ехр(-а*х**2)
See also
fourier_transform,inverse_fourier_transform,sine_transform,cosine_transform,inverse_cosine_transform,hankel_transform,inverse_hankel_transform,mellin_transform,laplace_transform
- класс sympy.integrals.transforms.InverseSineTransform ( *args ) [источник]
Класс, представляющий необработанные обратные синусоидальные преобразования.

Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять обратное синусоидальное преобразование, см.
inverse_sine_transform()строка документации.
- sympy.integrals.transforms.cosine_transform( f , x , k , **подсказки )[источник]
Вычислить унитарное косинусное преобразование \(f\) с обычной частотой, определенное как 9\infty f(x) \cos(2\pi x k) \mathrm{d} x.\]
Пояснение
Если преобразование не может быть вычислено в закрытой форме, это Функция возвращает неоцененный объект
CosineTransform.Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.doit(). Обратите внимание, что для этого преобразования по умолчаниюnoconds=True.Примеры
>>> из sympy import cosine_transform, exp, sqrt, cos >>> из sympy.
 abc импортировать x, k, a
>>> cosine_transform(exp(-a*x),x,k)
sqrt(2)*a/(sqrt(pi)*(a**2 + k**2))
>>> cosine_transform(exp(-a*sqrt(x))*cos(a*sqrt(x)), x, k)
а*ехр(-а**2/(2*к))/(2*к**(3/2))
abc импортировать x, k, a
>>> cosine_transform(exp(-a*x),x,k)
sqrt(2)*a/(sqrt(pi)*(a**2 + k**2))
>>> cosine_transform(exp(-a*sqrt(x))*cos(a*sqrt(x)), x, k)
а*ехр(-а**2/(2*к))/(2*к**(3/2))
See also
fourier_transform,inverse_fourier_transform,sine_transform,inverse_sine_transform,inverse_cosine_transform,hankel_transform,inverse_hankel_transform,mellin_transform,laplace_transform
- класс sympy.integrals.transforms.CosineTransform ( *args ) [источник]
Класс, представляющий невычисленные косинусные преобразования.
Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять косинусные преобразования, см.
cosine_transform()строка документации.
- sympy.integrals.transforms.inverse_cosine_transform( F , k , x , **подсказки )[источник]
Вычислить унитарное обратное косинусное преобразование \(F\) с обычной частотой, определяется как 9\infty F(k) \cos(2\pi x k) \mathrm{d} k.\]
Пояснение
Если преобразование не может быть вычислено в закрытой форме, это Функция возвращает неоцененный объект
InverseCosineTransform.Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.doit(). Обратите внимание, что для этого преобразования по умолчаниюnoconds=True.Примеры
>>> из sympy import inverse_cosine_transform, sqrt, pi >>> из sympy.abc импортировать x, k, a >>> inverse_cosine_transform(sqrt(2)*a/(sqrt(pi)*(a**2 + k**2)), k, x) ехр(-а*х) >>> inverse_cosine_transform(1/sqrt(k), k, x) 1/кв.(х)
См.
 также
такжепреобразование фурье,преобразование_фурье_обратное,преобразование_синуса,преобразование_обратного_синуса,преобразование_косинуса,hankel_transform,inverse_hankel_transform,mellin_transform,laplace_transform
- класс sympy.integrals.transforms.InverseCosineTransform ( *args ) [источник]
Класс, представляющий невычисленные арккосинусные преобразования.
Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять арккосинусные преобразования, см. 9\infty f(r) J_\nu(k r) r \mathrm{d} r.\]
Пояснение
Если преобразование не может быть вычислено в закрытой форме, это Функция возвращает неоцененный объект
HankelTransform.Описание возможных подсказок см.
 в строке документации
в строке документации sympy.integrals.transforms.IntegralTransform.doit(). Обратите внимание, что для этого преобразования по умолчаниюnoconds=True.Примеры
>>> из sympy import hankel_transform, inverse_hankel_transform >>> из sympy import exp >>> из sympy.abc импортировать r, k, m, nu, a
>>> ht = hankel_transform(1/r**m, r, k, nu) >>> чт 2*k**(m - 2)*gamma(-m/2 + nu/2 + 1)/(2**m*gamma(m/2 + nu/2))
>>> inverse_hankel_transform(ht,k,r,nu) г**(-м)
>>> ht = hankel_transform(exp(-a*r), r, k, 0) >>> чт а/(к**3*(а**2/к**2 + 1)**(3/2))
>>> inverse_hankel_transform (ht, k, r, 0) exp(-a*r)
См. также
fourier_transform,inverse_fourier_transform,sine_transform,inverse_sine_transform,cosine_transform,inverse_cosine_transform,inverse_hankel_transform,mellin_transform,laplace_transform
- класс sympy.
 integrals.transforms.HankelTransform ( *args ) [источник]
integrals.transforms.HankelTransform ( *args ) [источник] Класс, представляющий невычисленные преобразования Ганкеля.
Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять преобразования Ганкеля, см.
hankel_transform()строка документации.
- sympy.integrals.transforms.inverse_hankel_transform ( F , k , r , nu , ** подсказки ) [источник]
Вычисление обратного преобразования Ганкеля \(F\), определенного как
9\infty F_\nu(k) J_\nu(k r) k \mathrm{d} k.\]Пояснение
Если преобразование не может быть вычислено в закрытой форме, это Функция возвращает неоцененный объект
InverseHankelTransform.Описание возможных подсказок см. в строке документации
sympy.integrals.transforms.IntegralTransform.doit(). Обратите внимание, что для этого преобразования по умолчаниюnoconds=True.
Примеры
>>> из sympy import hankel_transform, inverse_hankel_transform >>> из sympy import exp >>> из sympy.abc импортировать r, k, m, nu, a
>>> ht = hankel_transform(1/r**m, r, k, nu) >>> чт 2*k**(m - 2)*gamma(-m/2 + nu/2 + 1)/(2**m*gamma(m/2 + nu/2))
>>> inverse_hankel_transform(ht,k,r,nu) г**(-м)
>>> ht = hankel_transform(exp(-a*r), r, k, 0) >>> чт а/(к**3*(а**2/к**2 + 1)**(3/2))
>>> inverse_hankel_transform (ht, k, r, 0) exp(-a*r)
See also
fourier_transform,inverse_fourier_transform,sine_transform,inverse_sine_transform,cosine_transform,inverse_cosine_transform,hankel_transform,mellin_transform,laplace_transform
- класс sympy.integrals.transforms.InverseHankelTransform( *args )[источник]
Класс, представляющий невычисленные обратные преобразования Ханкеля.

Информацию об использовании этого класса см. в строке документации
IntegralTransform.О том, как вычислять обратные преобразования Ганкеля, см.
inverse_hankel_transform()строка документации.
- класс sympy.integrals.transforms.IntegralTransform( *args )[источник]
Базовый класс для интегральных преобразований.
Пояснение
Этот класс представляет невычисленные преобразования.
Чтобы реализовать конкретное преобразование, сделайте производным от этого класса и реализуйте
_compute_transform(f, x, s, **подсказки)и_as_integral(f, x, s)функции. Если преобразование не может быть вычислено, поднимитеIntegralTransformError.Также установлено
cls._name. Например,>>> из sympy import LaplaceTransform >>> Трансформация Лапласа._имя 'Лаплас'
Реализуйте
self., если ваша функция возвращает больше, чем просто число и, возможно, условие сходимости. _collapse_extra
_collapse_extra - doit( **подсказка )[источник]
Попробуйте оценить трансформацию в закрытом виде.
Пояснение
Эта общая функция обрабатывает линейность, но кроме этого оставляет практически все для _compute_transform.
Стандартные подсказки следующие:
упростить: упрощать или нет результатnoconds: если True, не возвращать условия сходимости-
needeval: если True, поднять IntegralTransformError вместо возврат объектов IntegralTransform
-
Значения этих подсказок по умолчанию зависят от конкретного преобразования, обычно по умолчанию
(упрощение, несоответствие, потребность) = (Истина, Ложь, Ложь).
- свойство функция
Преобразуемая функция.

- свойство function_variable
Зависимая переменная преобразуемой функции.
- свойство transform_variable
Независимая переменная преобразования.
- исключение sympy.integrals.transforms.IntegralTransformError ( преобразование , функция , сообщение ) [источник]
Исключение, связанное с проблемами вычисления преобразований.
Пояснение
Этот класс в основном используется внутри; если интегралы не могут быть вычислены обычно возвращаются объекты, представляющие невычисленные преобразования.
Подсказка
needeval=Trueможет использоваться для отключения возвращаемого преобразования объектов и вместо этого вызвать это исключение, если интеграл не может быть вычислено.
Внутренние элементы
SymPy использует ряд алгоритмов для вычисления интегралов. Алгоритмы опробованы
по порядку, пока не будет получен ответ. Большинство из этих алгоритмов могут быть включены
или отключается вручную с помощью различных флагов до
Алгоритмы опробованы
по порядку, пока не будет получен ответ. Большинство из этих алгоритмов могут быть включены
или отключается вручную с помощью различных флагов до интегрировать() или сделать() .
SymPy сначала применяет несколько эвристических алгоритмов, так как они самые быстрые:
Если функция является рациональной функцией, существует полный алгоритм для интегрируя рациональные функции, называемые Lazard-Rioboo-Trager и Алгоритмы Горовица-Остроградского. Они реализованы в
ratint().- sympy.integrals.rationaltools.ratint( f , x , **флаги )[источник]
Выполняет бесконечную интеграцию рациональных функций.
Пояснение
Для данного поля \(K\) и рациональной функции \(f = p/q\), где \(p\) и \(q\) — многочлены от \(K[x]\), возвращает функцию \(g\), такую что \(f = g’\).
Примеры
>>> из sympy.integrals.
 rationaltools импортировать ratint
>>> из sympy.abc импортировать x
rationaltools импортировать ratint
>>> из sympy.abc импортировать x
>>> ratint(36/(x**5 - 2*x**4 - 2*x**3 + 4*x**2 + x - 2), x) (12*x + 6)/(x**2 - 1) + 4*log(x - 2) - 4*log(x + 1)
См. также
sympy.integrals.integrals.Integral.doit,sympy.integrals.rationaltools.ratint_logpart,sympy.integrals.rationaltools.ratint_ratpartСсылки
[Р525]
М. Бронштейн, Символическая интеграция I: Трансцендентальное Функции, второе издание, Springer-Verlag, 2005, стр. 35-70
- sympy.integrals.rationaltools.ratint_ratpart( f , g , x )[источник]
Алгоритм Горовица-Остроградского.
Пояснение
Для данного поля K и полиномов f и g в K[x], таких что f и g взаимно просты и deg(f) < deg(g), возвращает дроби A и B в K(x), такое, что f/g = A’ + B и B имеет бесквадратный знаменатель.

Примеры
>>> из sympy.integrals.rationaltools импортировать ratint_ratpart >>> из sympy.abc импортировать x, y >>> из импорта sympy Poly >>> ratint_ratpart(Poly(1, x, домен='ZZ'), ... Poly(x + 1, x, domain='ZZ'), x) (0, 1/(х + 1)) >>> ratint_ratpart(Poly(1, x, домен='EX'), ... Poly(x**2 + y**2, x, домен='EX'), x) (0, 1/(х**2 + у**2)) >>> ratint_ratpart(Poly(36, x, домен='ZZ'), ... Poly(x**5 - 2*x**4 - 2*x**3 + 4*x**2 + x - 2, x, domain='ZZ'), x) ((12*x + 6)/(x**2 - 1), 12/(x**2 - x - 2))
См. также
ratint,ratint_logpart
- sympy.integrals.rationaltools.ratint_logpart( f , g , x , t=None )[источник]
Алгоритм Лазара-Риобу-Трагера.
Пояснение
Для данного поля K и полиномов f и g в K[x], таких что f и g взаимно просты, deg(f) < deg(g) и g не содержит квадратов, возвращает список наборов (s_i, q_i) многочленов, для i = 1.
 .n, таких, что s_i
в K[t, x] и q_i в K[t], и:
.n, таких, что s_i
в K[t, x] и q_i в K[t], и:___ ___ д ж д \ ` \ ` -- - = -- )) a log(s_i(a, x)) дх г дх /__, /__, i=1..n а | q_i (а) = 0Примеры
>>> из sympy.integrals.rationaltools импортировать ratint_logpart >>> из sympy.abc импортировать x >>> из импорта sympy Poly >>> ratint_logpart(Poly(1, x, домен='ZZ'), ... Poly(x**2 + x + 1, x, domain='ZZ'), x) [(Poly(x + 3*_t/2 + 1/2, x, домен = 'QQ[_t]'), ...Poly(3*_t**2 + 1, _t, домен='ZZ'))] >>> ratint_logpart(Poly(12, x, домен='ZZ'), ... Poly(x**2 - x - 2, x, домен='ZZ'), x) [(Poly(x - 3*_t/8 - 1/2, x, домен='QQ[_t]'), ...Poly(-_t**2 + 16, _t, домен='ZZ'))]
См. также
ratint,ratint_ratpart
trigintegrate()решает интегралы тригонометрических функций, используя сопоставление с образцом- sympy.integrals.trigonometry.trigintegrate( f , x , conds=’кусочно’ )[источник]
Проинтегрировать f = Mul(trig) по x.

Примеры
>>> из sympy import sin, cos, tan, sec >>> из sympy.integrals.trigonometry импортировать trigintegrate >>> из sympy.abc импортировать x
>>> Trigintegrate(sin(x)*cos(x), x) грех(х)**2/2
>>> Trigintegrate(sin(x)**2, x) х/2 - грех(х)*cos(х)/2
>>> Trigintegrate(tan(x)*sec(x), x) 1 / cos (х)
>>> Trigintegrate(sin(x)*tan(x), x) -log(sin(x) - 1)/2 + log(sin(x) + 1)/2 - sin(x)
См. также
sympy.integrals.integrals.Integral.doit,sympy.integrals.integrals.IntegralСсылки
[Р526]
http://en.wikibooks.org/wiki/Calculus/Integration_techniques
deltaintegrate()решает интегралы собъектами DiracDelta.- sympy.integrals.deltafunctions.deltaintegrate( f , x )[источник]
Пояснение
Идея интеграции следующая:
Если мы имеем дело с выражением DiracDelta, то есть DiracDelta(g(x)), мы пытаемся упростить его.

Если бы можно было упростить, то интегрируем полученное выражение. Мы уже знаем, что можем интегрировать упрощенное выражение, потому что только используются простые выражения DiracDelta.
Если бы мы не могли упростить это, есть два случая:
Выражение представляет собой простое выражение: мы возвращаем интеграл, заботясь о том, имеем ли мы дело с производным или с надлежащим ДиракДельта.
Выражение не простое (т.е. DiracDelta(cos(x))): мы можем сделать вообще ничего.
Если узел является узлом умножения, имеющим термин DiracDelta:
Сначала мы расширяем его.
Если расширение сработало, то пытаемся интегрировать расширение.
Если нет, мы пытаемся извлечь простой термин DiracDelta, тогда у нас есть два корпусов:
У нас есть простой член DiracDelta, поэтому мы возвращаем интеграл.
У нас не было простого терма, но у нас есть выражение с упрощенные термины DiracDelta, поэтому мы интегрируем это выражение.

Примеры
>>> из sympy.abc импортировать x, y, z >>> из sympy.integrals.deltafunctions импортировать deltaintegrate >>> из sympy импортировать sin, cos, DiracDelta >>> deltaintegrate(x*sin(x)*cos(x)*DiracDelta(x - 1), x) грех(1)*cos(1)*Хевисайд(х - 1) >>> deltaintegrate(y**2*DiracDelta(x - z)*DiracDelta(y - z), y) z**2*Дельта Дирака(x - z)*Хевисайда(y - z)
См. также
sympy.functions.special.delta_functions.DiracDelta,sympy.integrals.integrals.Integral
singleityintegrate()применяется, если функция содержитSingularityFunction- sympy.integrals.singularityfunctions.singularityintegrate( f , x )[источник]
Эта функция обрабатывает неограниченные интеграции функций Singularity.
интегрироватьфункция вызывает эту функцию внутри всякий раз, когда экземпляр SingularityFunction передается в качестве аргумента.
Пояснение
Идея интеграции следующая:
Если мы имеем дело с выражением SingularityFunction, то есть
SingularityFunction(x, a, n), мы просто возвращаемсяSingularityFunction(x, a, n + 1)/(n + 1), еслиn >= 0иSingularityFunction(x, a, n + 1), еслиn < 0.Если узел является узлом умножения или мощности, имеющим SingularityFunction мы перепишем все выражение в терминах Heaviside и DiracDelta, а затем интегрировать выходные данные. Наконец, мы перепишите результат интегрирования обратно в терминах SingularityFunction.
Если ни один из вышеперечисленных случаев не возникает, мы возвращаем None.
Примеры
>>> from sympy.integrals.singularityfunctions import singleityintegrate >>> from sympy import SingularityFunction, символы, функция >>> x, a, n, y = символы ('x a n y') >>> f = Функция ('f') >>> сингулярностьинтегрировать(Функция сингулярности(х, а, 3), х) Функция сингулярности (x, a, 4)/4 >>> сингулярностьинтегрировать(5*Функция сингулярности(х, 5, -2), х) 5*Функция сингулярности(x, 5, -1) >>> сингулярностьинтегрировать(6*сингулярностьфункция(х, 5, -1), х) 6*Функция сингулярности(x, 5, 0) >>> сингулярностьинтегрировать(х*сингулярностьфункция(х, 0, -1), х) 0 >>> сингулярностьинтегрировать(Функция сингулярности(x, 1, -1) * f(x), x) f(1)*SingularityFunction(x, 1, 0)
Если эвристические алгоритмы не могут быть применены, используется
risch_integrate(). попробовал дальше. Алгоритм Риша представляет собой общий метод вычисления
первообразные элементарных функций. Алгоритм Риша – это решение
процедура, которая может определить, существует ли элементарное решение, и в
в этом случае вычислить его. Его можно расширить для обработки многих неэлементарных
функции в дополнение к элементарным. Однако версия, реализованная
в SymPy поддерживает только небольшое подмножество полного алгоритма, в частности, на
часть трансцендентного алгоритма для экспонент и логарифмов
реализовано. Преимущество
попробовал дальше. Алгоритм Риша представляет собой общий метод вычисления
первообразные элементарных функций. Алгоритм Риша – это решение
процедура, которая может определить, существует ли элементарное решение, и в
в этом случае вычислить его. Его можно расширить для обработки многих неэлементарных
функции в дополнение к элементарным. Однако версия, реализованная
в SymPy поддерживает только небольшое подмножество полного алгоритма, в частности, на
часть трансцендентного алгоритма для экспонент и логарифмов
реализовано. Преимущество risch_integrate()по сравнению с другими методами что если он возвращает экземплярNonElementaryIntegral, алгоритмом доказано, что интеграл неэлементарен, т.е. интеграл не может быть представлен с помощью комбинации экспонент, логарифмов, триггеров функции, степени, рациональные функции, алгебраические функции и функция сочинение.- sympy.integrals.risch.risch_integrate( f , x , extension=None , handle_first='log' , single_integral=False , rewrite_complex=None , conds='piecely' )[источник]
Алгоритм интеграции Риша.

Пояснение
Поддерживаются только трансцендентные функции. Сейчас только экспоненты и логарифмы поддерживаются, но поддержка тригонометрических функций отсутствует. предстоящий.
Если эта функция возвращает невычисленный интеграл в результате, это означает что он доказал, что интеграл неэлементарен. Любые ошибки будут привести к возникновению NotImplementedError. Невычисленный интеграл будет экземпляр NonElementaryIntegral, подкласса Integral.
handle_first может быть либо «exp», либо «log». Это меняет порядок в которого построено расширение, и может привести к другому (но эквивалентное) решение (пример этого см. в выпуске 5109). Это также возможно, что интеграл может быть вычислен с одним, но не с другим, потому что еще не все кейсы реализованы. По умолчанию это «журнал», поэтому что внешнее расширение является экспоненциальным, когда это возможно, потому что больше реализован экспоненциальный случай.
Если
, отдельный_интегралравенTrue, результат возвращается в виде кортежа (ans, i), где интеграл есть ans + i, ans элементарный, i либо a NonElementaryIntegral или 0. Это полезно, если вы хотите попробовать дальше
интегрирование части NonElementaryIntegral с использованием других алгоритмов для
возможно получить решение с точки зрения специальных функций. Это неверно
дефолт.
Это полезно, если вы хотите попробовать дальше
интегрирование части NonElementaryIntegral с использованием других алгоритмов для
возможно получить решение с точки зрения специальных функций. Это неверно
дефолт.Примеры
>>> из sympy.integrals.risch импортировать risch_integrate >>> из sympy импортировать exp, log, pprint >>> из sympy.abc импортировать x
Сначала мы пытаемся интегрировать exp(-x**2). За исключением постоянного коэффициента 2/sqrt(pi) — это знаменитая функция ошибок.
>>> pprint(risch_integrate(exp(-x**2),x)) / | | 2 | -Икс | е дх | /
Невычисленный интеграл в результате означает, что risch_integrate() имеет доказано, что exp(-x**2) не имеет элементарной антипроизводной.
Во многих случаях risch_integrate() может разделить элементарный антипроизводная часть от неэлементарной антипроизводной части. Например,
>>> pprint(risch_integrate((2*log(x)**2 - log(x) - x**2)/(log(x)**3 - .
 .. х**2*лог(х)), х))
/
|
журнал (-х + журнал (х)) журнал (х + журнал (х)) | 1
- ---------------- + --------------- + | ------ дх
2 2 | журнал (х)
|
/
.. х**2*лог(х)), х))
/
|
журнал (-х + журнал (х)) журнал (х + журнал (х)) | 1
- ---------------- + --------------- + | ------ дх
2 2 | журнал (х)
|
/
Это означает, что доказано, что интеграл от 1/log(x) равен неэлементарная. Эта функция также известна как логарифмический интеграл, и часто обозначается как Li(x).
risch_integrate() в настоящее время принимает только чисто трансцендентные функции с экспонентами и логарифмами, хотя обратите внимание, что это может включать вложенные экспоненты и логарифмы, а также экспоненты с основанием кроме E.
>>> pprint (risch_integrate (exp (x) * exp (exp (x)), x)) / Икс\ \ е / е >>> pprint(risch_integrate(exp(exp(x)), x)) / | | / Икс\ | \ е / | е дх | /
>>> pprint(risch_integrate(x*x**x*log(x) + x**x + x*x**x, x)) Икс х*х >>> pprint(risch_integrate(x**x, x)) / | | Икс | х дх | /
>>> pprint(risch_integrate(-1/(x*log(x)*log(log(x))**2), x)) 1 ----------- журнал (журнал (х))
- класс sympy.
 integrals.risch.NonElementaryIntegral( функция , * символы , **допущения )[источник]
integrals.risch.NonElementaryIntegral( функция , * символы , **допущения )[источник] Представляет неэлементарный интеграл.
Пояснение
Если результатом интегрировать() является экземпляр этого класса, он гарантированно неэлементарна. Обратите внимание, что по умолчанию интегрировать() попытается найти любое решение в замкнутой форме, даже в терминах специальных функций, которые сами по себе не могут быть элементарными. Чтобы интегрировать () только дайте элементарные решения, или, в случаях, когда он может доказать интеграл от быть неэлементарными, экземпляры этого класса, используйте интеграцию (risch=True). В этом случае интегрировать () может вызвать NotImplementedError, если он не может сделать такая решимость.
интегрировать() использует детерминированный алгоритм Риша для интегрирования элементарных функций или доказать, что они не имеют элементарного интеграла. В некоторых случаях, этот алгоритм может разбить интеграл на элементарный и неэлементарный часть, так что результатом интегрирования будет сумма элементарной выражение и NonElementaryIntegral.

Примеры
>>> из импорта sympy интегрировать, опыт, журнал, интеграл >>> из sympy.abc импортировать x
>>> a = интегрировать (exp (-x ** 2), x, risch = True) >>> напечатать(а) Интеграл(ехр(-х**2), х) >>> тип(а) <класс 'sympy.integrals.risch.NonElementaryIntegral'>
>>> выражение = (2*log(x)**2 - log(x) - x**2)/(log(x)**3 - x**2*log(x)) >>> b = интегрировать(expr, x, risch=True) >>> печатать(б) -log(-x + log(x))/2 + log(x + log(x))/2 + Integral(1/log(x), x) >>> type(b.atoms(Integral).pop()) <класс 'sympy.integrals.risch.NonElementaryIntegral'>
Для неэлементарных определенных интегралов SymPy использует так называемые G-функции Мейера. Подробности описаны в разделе «Вычисление интегралов с использованием G-функций Мейера».
Все алгоритмы, упомянутые до сих пор, либо основаны на сопоставлении с образцом, эвристика, или решать интегралы с использованием алгоритмов, которые сильно отличаются от так, как большинство людей учат на курсах математического анализа.
 SymPy также
реализует метод, который может решать интегралы почти так же, как в
исчисление. Преимущество этого метода в том, что можно извлечь
шагов интегрирования, чтобы можно было увидеть, как вычислить интеграл «по
рука". Это используется SymPy Gamma. Это
реализовано в
SymPy также
реализует метод, который может решать интегралы почти так же, как в
исчисление. Преимущество этого метода в том, что можно извлечь
шагов интегрирования, чтобы можно было увидеть, как вычислить интеграл «по
рука". Это используется SymPy Gamma. Это
реализовано в функция manualintegrate(). Шаги для интеграла можно увидеть с помощью функцииintegral_steps().- sympy.integrals.manualintegrate.manualintegrate( f , var )[источник]
Пояснение
Вычислить неопределенный интеграл от одной переменной, используя алгоритм, который напоминает то, что ученик сделал бы руками.
В отличие от
интегрировать(), var может быть только одним символом.Примеры
>>> из sympy импортировать sin, cos, tan, exp, log,интегрировать >>> из sympy.integrals.manualintegrate импортировать manualintegrate >>> из sympy.abc импортировать x >>> интегрирование вручную (1 / x, x) журнал (х) >>> интегрировать(1/х) журнал (х) >>> интегрировать вручную (журнал (x), x) х * журнал (х) - х >>> интегрировать (журнал (х)) х * журнал (х) - х >>> интегрирование вручную (exp(x) / (1 + exp(2 * x)), x) атан (ехр (х)) >>> интегрировать (exp(x) / (1 + exp(2 * x))) RootSum(4*_z**2 + 1, Lambda(_i, _i*log(2*_i + exp(x)))) >>> интегрирование вручную (cos(x)**4 * sin(x), x) -cos(x)**5/5 >>> интегрировать (cos(x)**4 * sin(x), x) -cos(x)**5/5 >>> интегрирование вручную (cos(x)**4 * sin(x)**3, x) соз(х)**7/7 - соз(х)**5/5 >>> интегрировать(cos(x)**4 * sin(x)**3, x) соз(х)**7/7 - соз(х)**5/5 >>> интегрировать вручную (tan(x), x) -лог (потому что (х)) >>> интегрировать (загар (х), х) -лог (потому что (х))
См.
 также
такжеsympy.integrals.integrals.integrate,sympy.integrals.integrals.Integral.doit,sympy.integrals.integrals.Integral
- sympy.integrals.manualintegrate.integral_steps( подынтегральная функция , символ , **опции )[источник]
Возвращает шаги, необходимые для вычисления интеграла.
- Возвраты:
правило : именованный кортеж
Первый шаг; большинство правил имеют подшаги, которые также должны быть считается. Эти подэтапы можно оценить с помощью
manualintegrateдля получения результата.
Пояснение
Эта функция пытается отразить то, что учащийся сделал бы вручную, как как можно ближе.
SymPy Gamma использует это для предоставления пошагового объяснения интеграл. Код, который он использует для форматирования результатов этой функции, может быть найдено в https://github.
 com/sympy/sympy_gamma/blob/master/app/logic/intsteps.py.
com/sympy/sympy_gamma/blob/master/app/logic/intsteps.py.Примеры
>>> из sympy import exp, sin >>> из sympy.integrals.manualintegrate импортировать integer_steps >>> из sympy.abc импортировать x >>> print(repr(integral_steps(exp(x) / (1 + exp(2 * x)), x))) URule(u_var=_u, u_func=exp(x), константа=1, substep=ArctanRule(a=1, b=1, c=1, context=1/(_u**2 + 1), symbol=_u), контекст=exp(x)/(exp(2*x) + 1), символ=x) >>> print(repr(integral_steps(sin(x), x))) TrigRule(func='sin', arg=x, context=sin(x), symbol=x) >>> print(repr(integral_steps((x**2 + 3)**2, x))) RewriteRule (переписано = x ** 4 + 6 * x ** 2 + 9, substep=AddRule(substeps=[PowerRule(base=x, exp=4, context=x**4, symbol=x), ConstantTimesRule (константа = 6, другое = x ** 2, substep=PowerRule(база=x, выражение=2, контекст=x**2, символ=x), контекст=6*x**2, символ=x), ConstantRule(константа=9, контекст=9, символ=x)], контекст=x**4 + 6*x**2 + 9, символ=x), контекст=(x**2 + 3)**2, символ=x)
Наконец, если все вышеперечисленное терпит неудачу, SymPy также использует упрощенную версию Алгоритм Риша, называемый Алгоритм Риша-Нормана .
 Этот алгоритм опробован
последний, потому что он часто самый медленный для вычислений. Это реализовано в
Этот алгоритм опробован
последний, потому что он часто самый медленный для вычислений. Это реализовано в Heurisch():- sympy.integrals.heurisch.heurisch( f , x , rewrite=False , hints=None , mappings=None , retries=3 , degree_offset=0 , unnecessary_permutations=None , _try_heurisch=Нет )[источник]
Вычисление неопределенного интеграла с использованием эвристического алгоритма Риша.
Пояснение
Это эвристический подход к бесконечному интегрированию в конечных терминов с помощью расширенного эвристического (параллельного) алгоритма Риша, основанного на по роману Мануэля Бронштейна «Интегратор для бедняков».
Алгоритм поддерживает различные классы функций, включая трансцендентные элементарные или специальные функции, такие как Эйри, Бессель, Уиттакер и Ламберт.
Обратите внимание, что этот алгоритм не является процедурой принятия решения.
 Если это не так
в состоянии вычислить первообразную для данной функции, то это
не доказательство того, что такой функции не существует. Следует использовать
рекурсивный алгоритм Риша в таком случае. Это открытый вопрос, если
этот алгоритм можно сделать полной процедурой принятия решений.
Если это не так
в состоянии вычислить первообразную для данной функции, то это
не доказательство того, что такой функции не существует. Следует использовать
рекурсивный алгоритм Риша в таком случае. Это открытый вопрос, если
этот алгоритм можно сделать полной процедурой принятия решений.Это внутренняя процедура интегратора. Вы должны использовать верхний уровень «интегрировать» функцию в большинстве случаев, так как эта процедура требует некоторого этапы предварительной обработки и в противном случае может произойти сбой.
Спецификация
heurisch(f, x, переписать=ложь, подсказки=нет)
- где
f : выражение х : символ
переписать -> принудительно перезаписать «f» с точки зрения «tan» и «tanh» подсказки -> список функций, которые могут появиться в антидеривате
подсказки = нет -> вообще нет предложений
подсказки = [ ] -> попытаться вычислить
подсказки = [f1, …, fn] -> мы лучше знаем
Примеры
>>> от sympy import tan >>> из sympy.
 integrals.heurisch импортировать heurisch
>>> из sympy.abc импортировать x, y
integrals.heurisch импортировать heurisch
>>> из sympy.abc импортировать x, y
>>> Heurisch(y*tan(x), x) у*лог(загар(х)**2 + 1)/2
См. «Интегратор для бедняков» Мануэля Бронштейна:
См. также
sympy.integrals.integrals.Integral.doit,sympy.integrals.integrals.Integral,sympy.integrals.heurisch.componentsСсылки
[Р527]
http://www-sop.inria.fr/cafe/Manuel.Bronstein/pmint/index.html
Для получения дополнительной информации о реализованном алгоритме см.:
[Р528]
К. Геддес, Л. Стефанус, Об интеграции Риша-Нормана Метод и его реализация в Maple, Труды ИССАК’89, ACM Press, 212-217.
[Р529]
Дж. Х. Давенпорт, О параллельном алгоритме Риша (I), Материалы EUROCAM’82, LNCS 144, Springer, 144–157.
[Р530]
Дж.
 Х. Давенпорт, О параллельном алгоритме Риша (III):
Использование касательных, Бюллетень SIGSAM 16 (1982), 3-6.
Х. Давенпорт, О параллельном алгоритме Риша (III):
Использование касательных, Бюллетень SIGSAM 16 (1982), 3-6.[Р531]
Дж. Х. Давенпорт, Б. М. Трагер, На параллельном берегу Алгоритм (II), транзакции ACM на математических Программное обеспечение 11 (1985), 356-362.
- sympy.integrals.heurisch.components( f , x )[источник]
Возвращает набор всех функциональных компонентов данного выражения который включает в себя символы, функциональные приложения и композиции и нецелые степени. Дробные полномочия собираются с минимальные, положительные показатели.
Примеры
>>> from sympy import cos, sin >>> из sympy.abc импортировать x >>> из компонентов импорта sympy.integrals.heurisch
>>> компоненты (sin(x)*cos(x)**2, x) {х, грех(х), соз(х)}См. также
Heurisch
Ссылка API
- sympy.
 integrals.integrals.integrate( f , var , ... )[источник]
integrals.integrals.integrate( f , var , ... )[источник] Устарело, начиная с версии 1.6: использование
интегрировать()сPolyустарело. ИспользоватьPoly.integrate() 9вместо 2999. См. Использование интеграции с Poly.Пояснение
Вычисление определенного или неопределенного интеграла от одной или нескольких переменных с использованием алгоритма Риша-Нормана и поиска в таблице. Эта процедура способен обрабатывать элементарные алгебраические и трансцендентные функции а также огромный класс специальных функций, включая Airy, Бессель, Уиттакер и Ламберт.
переменная может быть:
a символ – неограниченная интеграция
- кортеж (символ, а) – бесконечное интегрирование с результатом
дается с
символ
кортеж (символ, а, б) – определенное интегрирование
Можно указать несколько переменных, в этом случае результат множественная интеграция.
 (Если var опущен, а подынтегральная функция
одномерный, будет выполнен неопределенный интеграл по этой переменной.)
(Если var опущен, а подынтегральная функция
одномерный, будет выполнен неопределенный интеграл по этой переменной.)Неопределенные интегралы возвращаются без членов, которые являются независимыми переменных интегрирования. (см. примеры)
Определенные несобственные интегралы часто влекут за собой тонкую сходимость условия. Передайте conds=’piecewise’, ‘separate’ или ‘none’, чтобы иметь они возвращаются, соответственно, как кусочная функция, как отдельная результат (т.е. результат будет кортежем) или вообще не будет (по умолчанию «кусочно»).
Стратегия
SymPy использует различные подходы к определенной интеграции. Один из методов заключается в найти первообразную для подынтегральной функции, а затем использовать фундаментальную теорема исчисления. Различные функции реализованы для интеграции полиномиальные, рациональные и тригонометрические функции и подынтегральные выражения содержащие термины DiracDelta.
SymPy также реализует часть алгоритма Риша, которая является решением процедура интегрирования элементарных функций, т.
 е. алгоритм может
либо найти элементарную первообразную, либо доказать, что она не
существует. Существует также (весьма удачный, хотя и несколько медлительный) общий
реализация эвристического алгоритма Риша. Этот алгоритм будет
в конечном итоге будет прекращено, поскольку все больше полного алгоритма Риша
реализовано. Подробнее см. строку документации Integral._eval_integral().
подробности о вычислении первообразной алгебраическими методами.
е. алгоритм может
либо найти элементарную первообразную, либо доказать, что она не
существует. Существует также (весьма удачный, хотя и несколько медлительный) общий
реализация эвристического алгоритма Риша. Этот алгоритм будет
в конечном итоге будет прекращено, поскольку все больше полного алгоритма Риша
реализовано. Подробнее см. строку документации Integral._eval_integral().
подробности о вычислении первообразной алгебраическими методами.Параметр risch=True может использоваться для использования только (полного) алгоритма Риша. Это полезно, если вы хотите узнать, имеет ли элементарная функция элементарная первообразная. Если неопределенный интеграл, возвращенный этим функция является экземпляром NonElementaryIntegral, это означает, что Алгоритм Риша доказал, что интеграл неэлементарен. Обратите внимание, что по умолчанию дополнительные методы (например, описанный метод Meijer G ниже) проверяются на этих интегралах, поскольку они могут быть выражены в терминах специальных функций, поэтому, если вас интересуют только элементарные ответы, используйте риш = Верно.
 Также обратите внимание, что невычисленный интеграл, возвращенный этим
функция не обязательно является NonElementaryIntegral, даже если risch=True,
поскольку это может быть просто указанием на то, что конкретная часть Риша
алгоритм, необходимый для интеграции этой функции, еще не реализован.
Также обратите внимание, что невычисленный интеграл, возвращенный этим
функция не обязательно является NonElementaryIntegral, даже если risch=True,
поскольку это может быть просто указанием на то, что конкретная часть Риша
алгоритм, необходимый для интеграции этой функции, еще не реализован.Другое семейство стратегий происходит от перезаписи подынтегральной функции в в терминах так называемых G-функций Мейера. Неопределенные интегралы единственную G-функцию всегда можно вычислить, а определенный интеграл произведения двух G-функций можно вычислить от нуля до бесконечность. Различные стратегии реализованы для перезаписи подынтегральных выражений как G-функции и использовать эту информацию для вычисления интегралов (см. модуль
meijerint).Опция manual=True может использоваться только для алгоритма, который пытается для имитации интеграции вручную. Этот алгоритм не обрабатывает столько подынтегральные выражения, как и другие реализованные алгоритмы, но могут возвращать результаты в более привычная форма.

manualintegrate Модульимеет функции, которые вернуть использованные шаги (дополнительную информацию см. в строке документации модуля).В целом алгебраические методы лучше всего подходят для вычисления первообразные (возможно, сложные) комбинаций элементарных функции. Методы G-функций лучше всего подходят для вычисления определенных интегралы от нуля до бесконечности умеренно сложных комбинации специальных функций или неопределенные интегралы очень простые комбинации специальных функций.
Код интеграции использует следующую стратегию:
Если при вычислении определенного интеграла оба предела действительны, и по крайней мере один предел +- оо, попробуйте метод G-функции сначала определенная интеграция.
Попробуйте найти первообразную, используя все доступные методы, заказанные по производительности (то есть сначала попробуйте самый быстрый метод, а затем самый медленный; в сначала пробуется конкретное полиномиальное интегрирование, Мейер G-функции предпоследние и эвристические Риша последними).

Если все еще не удается, попробуйте G-функции независимо от пределы.
Параметр meijerg=True, False, None можно использовать соответственно для: всегда используйте методы G-функции и никакие другие, никогда не используйте G-функцию методы, либо использовать все доступные методы (в порядке, описанном выше). По умолчанию установлено значение «Нет».
Примеры
>>> из импорта sympy интегрировать, журнал, опыт, оо >>> из sympy.abc импортировать a, x, y
>>> интегрировать(х*у, х) х**2*у/2
>>> интегрировать (лог(х), х) х * журнал (х) - х
>>> интегрировать (журнал (х), (х, 1, а)) а*лог(а) - а + 1
>>> интегрировать(х) х**2/2
Термины, не зависящие от x, отбрасываются при интегрировании на неопределенный срок:
>>> из sympy import sqrt >>> интегрировать (sqrt (1 + x), (x, 0, x)) 2*(х + 1)**(3/2)/3 - 2/3 >>> интегрировать(sqrt(1 + x), x) 2*(х + 1)**(3/2)/3
>>> интегрировать(х*у) Traceback (последний последний вызов): .
 ..
ValueError: укажите переменные интеграции для интеграции x*y
..
ValueError: укажите переменные интеграции для интеграции x*y
Обратите внимание, что синтаксис
интегрировать(х)предназначен только для удобства. в интерактивных сеансах, и его следует избегать в библиотечном коде.>>> интегрировать(x**a*exp(-x), (x, 0, oo)) # то же, что и conds='кусочно' Кусочная ((гамма (а + 1), re (а) > -1), (Интеграл(x**a*exp(-x), (x, 0, оо)), True))>>> интегрировать (x**a*exp(-x), (x, 0, oo), conds='none') гамма (а + 1)
>>> интегрировать(x**a*exp(-x), (x, 0, oo), conds='separate') (гамма (а + 1), ре (а) > -1)
См. также
Интеграл,Интеграл.doit
- sympy.integrals.integrals.line_integrate ( поле , кривая , переменные ) [источник]
Вычислите линейный интеграл.
Примеры
>>> из sympy import Curve, line_integrate, E, ln >>> из sympy.abc импортировать x, y, t >>> C = Curve([E**t + 1, E**t - 1], (t, 0, ln(2))) >>> line_integrate(x + y, C, [x, y]) 3*кв(2)
См.
 также
такжеsympy.integrals.integrals.integrate,Интеграл
Класс Интеграл представляет невычисленный интеграл и имеет несколько методов, помогающих интегрировать выражение.
- класс sympy.integrals.integrals.Integral ( функция , * символы , ** предположения ) [источник]
Представляет невычисленный интеграл.
- is_commutative
Возвращает значение, указывающее, являются ли все свободные символы в интеграле коммутативными.
- as_sum( n=Нет , method='midpoint' , Assessment=True )[источник]
Приближает определенный интеграл суммой.
- Параметры:
номер :
Количество используемых подынтервалов, необязательно.
метод :
Один из: «левый», «правый», «средняя точка», «трапеция».

оценка : логическое значение
Если False, возвращает невычисленное выражение Sum. По умолчанию Верно, оцените сумму.
Примечания
Эти методы приближенного интегрирования описаны в [1].
Примеры
>>> из импорта sympy Integral, sin, sqrt >>> из sympy.abc импортировать x, n >>> e = Интеграл(sin(x), (x, 3, 7)) >>> е Интеграл (грех (х), (х, 3, 7))
В демонстрационных целях этот интервал будет разделен только на 2 области, ограниченные [3, 5] и [5, 7].
Правило левой руки использует оценку функции слева от каждой интервал:
>>> e.as_sum(2, 'левый') 2*грех(5) + 2*греш(3)
Правило средней точки использует оценки в центре каждого интервала:
>>> e.as_sum(2, 'средняя точка') 2*грех(4) + 2*греш(6)
Правило правой руки использует оценку функции справа от каждой интервал:
>>> e.
 as_sum(2, 'правильно')
2*грех(5) + 2*греш(7)
as_sum(2, 'правильно')
2*грех(5) + 2*греш(7)
Правило трапеций использует вычисления функций с обеих сторон интервалы. Это эквивалентно взятию среднего левого и результаты правила правой руки:
>>> e.as_sum(2, 'трапеция') 2*грех(5) + грех(3) + грех(7) >>> (e.as_sum(2, 'левый') + e.as_sum(2, 'правый'))/2 == _ Истинный
Здесь разрыва в точке x = 0 можно избежать, используя метод средней точки или метод правой руки:
>>> e = Интеграл (1/sqrt(x), (x, 0, 1)) >>> e.as_sum(5).n(4) 1.730 >>> e.as_sum(10).n(4) 1.809 >>> e.doit().n(4) # фактическое значение равно 2 2.000
Метод левой или трапециевидной формы столкнется с разрывом и вернуть бесконечность:
>>> e.as_sum(5, 'левый') зоопарк
Количество интервалов может быть символическим. Если опущено, фиктивный символ будет использоваться для этого.
>>> e = Интеграл (x**2, (x, 0, 2)) >>> e.as_sum(n, 'право').expand() 8/3 + 4/н + 4/(3*н**2)
Это показывает, что правило средней точки является более точным, так как его ошибка член распадается как квадрат n:
>>> e.
 as_sum(method='midpoint').expand()
8/3 - 2/(3*_n**2)
as_sum(method='midpoint').expand()
8/3 - 2/(3*_n**2)
Возвращается символическая сумма с оценкой = False:
>>> e.as_sum(n, 'средняя точка', оценка=ложь) 2*Сумма((2*_k/n - 1/n)**2, (_k, 1, n))/n
См. также
-
Integral.doit Выполнить интегрирование по любым подсказкам
Ссылки
[Р532]
https://en.wikipedia.org/wiki/Riemann_sum#Методы
- doit( **подсказка )[источник]
Выполните интеграцию, используя любые подсказки.
Примеры
>>> из импорта sympy Покусочно, S >>> из sympy.abc импортировать x, t >>> p = x**2 + Piecewise((0, x/t < 0), (1, True)) >>> p.integrate((t, S(4)/5, 1), (x, -1, 1)) 1/3
See also
sympy.integrals.trigonometry.trigintegrate,sympy.integrals.heurisch.heurisch,sympy.integrals. rationaltools.ratint
rationaltools.ratint -
as_sum Approximate the integral using a sum
-
- свойство free_symbols
Этот метод возвращает символы, которые будут существовать, когда оценивается интеграл. Это полезно, если кто-то пытается определить, зависит ли интеграл от некоторого символ или нет.
Примеры
>>> от Симпи импорт Интеграл >>> из sympy.abc импортировать x, y >>> Интеграл(х, (х, у, 1)).free_symbols {г}См. также
sympy.concrete.expr_with_limits.ExprWithLimits.function,sympy.concrete.expr_with_limits.ExprWithLimits.limits
- главное_значение( **kwargs )[источник]
Вычисление главного значения Коши определенного интеграла действительной функции в заданном интервале на реальной оси.
Пояснение
В математике основное значение Коши — это метод присвоения значений некоторым неправильным интегралы, которые в противном случае были бы неопределенными.

Примеры
>>> from sympy import Интеграл, оо >>> из sympy.abc импортировать x >>> Интеграл(x+1, (x, -oo, oo)).principal_value() оо >>> f = 1 / (x**3) >>> Интеграл(f, (x, -oo, oo)).principal_value() 0 >>> Интеграл(f, (x, -10, 10)).principal_value() 0 >>> Интеграл(f, (x, -10, оо)).главное_значение() + Интеграл(f, (х, -оо, 10)).главное_значение(). 0
Ссылки
[Р533]
https://en.wikipedia.org/wiki/Cauchy_principal_value
[Р534]
http://mathworld.wolfram.com/CauchyPrincipalValue.html
- преобразование ( x , и ) [источник]
Выполняет замену переменных с \(x\) на \(u\), используя отношение задается \(x\) и \(u\), которые будут определять преобразования \(f\) и \(F\) (которые являются обратными друг другу) следующим образом:
Если \(x\) является символом (который является переменной интегрирования), то \(u\) будет интерпретироваться как некоторая функция f(u) с обратной F(u).
 Фактически это просто замена x на f(x).
Фактически это просто замена x на f(x).Если \(u\) является символом, то \(x\) будет интерпретироваться как некоторая функция, F(x) с обратным f(u). Это обычно называют у-замещение.
После определения f и F преобразование выполняется следующим образом: следует: 9{F(b)} f(x) \ гидроразрыва {\ mathrm {d}} {\ mathrm {d} x} \]
, где \(F(x)\) является инверсией \(f(x)\), а пределы и подынтегральная функция имеют были скорректированы, чтобы сохранить то же значение после интегрирования.
Примечания
Отображения F(x) или f(u) должны приводить к единственному интегралу. Линейный или рациональное линейное выражение,
2*x,1/xиsqrt(x), будет всегда работать; допустимы квадратичные выражения, такие какx**2 - 1если полученное подынтегральное выражение не зависит от знака решения (см. примеры).Интеграл будет возвращен без изменений, если
xне является переменной интеграция.
xдолжен быть (или содержать) только одну из переменных интегрирования. Еслиuимеет более одного свободного символа, тогда он должен быть отправлен в виде кортежа (u,uvar) гдеuvarопределяет, какая переменная заменяет переменная интегрирования. XXX может ли он содержать другую переменную интегрирования?Примеры
>>> из sympy.abc импортировать a, x, u >>> из sympy import Integral, cos, sqrt
>>> i = Интеграл (x*cos(x**2 - 1), (x, 0, 1))
Преобразованиеможет изменить переменную интеграции
>>> i.transform(x, u) Интеграл(u*cos(u**2 - 1), (u, 0, 1))
Преобразованиеможет выполнять u-подстановку до тех пор, пока уникальный получается подынтегральная функция:
>>> i.transform(x**2 - 1, u) Интеграл (cos (и)/2, (и, -1, 0))
Эта попытка не удалась, так как x = +/-sqrt(u + 1) и знак не отменяется вне подынтегральной функции:
>>> Интеграл(cos(x**2 - 1), (x, 0, 1)).
Преобразование transform(x**2 - 1, u)
Traceback (последний последний вызов):
...
ЗначениеОшибка:
Отображение между F (x) и f (u) не дало единственного подынтегрального выражения.
transform(x**2 - 1, u)
Traceback (последний последний вызов):
...
ЗначениеОшибка:
Отображение между F (x) и f (u) не дало единственного подынтегрального выражения.
может выполнять замену. Здесь, предыдущий результат преобразуется обратно в исходное выражение с использованием «u-замены»:
>>> пользовательский интерфейс = _ >>> _.transform(sqrt(u + 1), x) == i Истинный
То же самое можно сделать обычной заменой:
>>> ui.transform(u, x**2 - 1) == я Истинный
Если \(x\) не содержит знака интегрирования, то интеграл вернется без изменений. Интеграл \(i\) делает не имеет переменной интегрирования \(a\), поэтому никаких изменений не производится:
>>> i.transform(a, x) == i Истинный
Когда \(u\) имеет более одного свободного символа, символ, замена \(x\) должна быть идентифицирована передачей \(u\) как кортежа:
>>> Интеграл(х, (х, 0, 1)).преобразование(х, (и + а, и)) Интеграл (а + и, (и, -а, 1 - а)) >>> Интеграл(x, (x, 0, 1)).
 transform(x, (u + a, a))
Интеграл (а + и, (а, -и, 1 - и))
transform(x, (u + a, a))
Интеграл (а + и, (а, -и, 1 - и))
См. также
-
sympy.concrete.expr_with_limits.ExprWithLimits.variables Перечисляет переменные интегрирования
-
as_dummy Заменить интеграционные переменные фиктивными
Integral подклассов от ExprWithLimits , который является
общий суперкласс Integral и Sum .
- класс sympy.concrete.expr_with_limits.ExprWithLimits (функция , * символы , ** предположения ) [источник]
- свойство bound_symbols
Возвращает только фиктивные переменные.
Примеры
>>> от Симпи импорт Интеграл >>> из sympy.abc импортировать x, i, j, k >>> Интеграл(x**i, (i, 1, 3), (j, 2), k).bound_symbols [я, дж]
См. также
Функция,лимиты,free_symbols-
as_dummy Переименовать фиктивные переменные
-
sympy. integrals.integrals.Integral.transform
integrals.integrals.Integral.transform Выполнить отображение фиктивной переменной
-
- свойство free_symbols
Этот метод возвращает символы в объекте, за исключением тех, которые принимают определенное значение (т. е. фиктивные символы).
Примеры
>>> из суммы импорта sympy >>> из sympy.abc импортировать x, y >>> Сумма(х, (х, у, 1)).free_symbols {г}
- свойство функция
Возвращает функцию, применяемую вне пределов.
Примеры
>>> от Симпи импорт Интеграл >>> из sympy.abc импортировать x >>> Интеграл(x**2, (x,)).функция х**2
См. также
лимиты,переменные,free_symbols
- свойство has_finite_limits
Возвращает True, если известно, что пределы конечны либо по явные границы, предположения об этих границах или предположения о переменные.
 False, если известно, что он бесконечен, исходя из границ.
Нет, если недостаточно информации для определения.
False, если известно, что он бесконечен, исходя из границ.
Нет, если недостаточно информации для определения.Примеры
>>> из sympy import Сумма, Интеграл, Продукт, оо, Символ >>> х = Символ('х') >>> Сумма(x, (x, 1, 8)).has_finite_limits Истинный>>> Интеграл(x, (x, 1, оо)).has_finite_limits ЛОЖЬ
>>> М = Символ('М') >>> Сумма(x, (x, 1, M)).has_finite_limits>>> N = Символ ("N", целое число = Истина) >>> Произведение(x, (x, 1, N)).has_finite_limits ИстинныйСм. также
has_reversed_limits
- свойство has_reversed_limits
Возвращает True, если известно, что пределы находятся в обратном порядке, либо явными границами, предположениями об оценках или предположениями о переменные. False, если известно, что он находится в нормальном порядке на основе границ. Нет, если недостаточно информации для определения.
Примеры
>>> из sympy import Сумма, Интеграл, Продукт, оо, Символ >>> х = Символ('х') >>> Сумма(x, (x, 8, 1)). has_reversed_limits
Истинный
has_reversed_limits
Истинный
>>> Сумма(х, (х, 1, оо)).has_reversed_limits ЛОЖЬ
>>> М = Символ('М') >>> Интеграл(x, (x, 1, M)).has_reversed_limits>>> N = Символ('N', целое=Истина, положительное=Истина) >>> Сумма(x, (x, 1, N)).has_reversed_limits ЛОЖЬ>>> Продукт(х, (х, 2, N)).has_reversed_limits
>>> Product(x, (x, 2, N)).subs(N, N + 2).has_reversed_limits ЛОЖЬ
См. также
sympy.concrete.expr_with_intlimits.ExprWithIntLimits.has_empty_sequence
- свойство is_number
Возвращает True, если в Sum нет свободных символов, иначе False.
- свойство ограничения
Вернуть пределы выражения.
Примеры
>>> от Симпи импорт Интеграл >>> из sympy.abc импортировать x, i >>> Интеграл(x**i, (i, 1, 3)).пределы ((я, 1, 3),)
См. также
функция,переменные,free_symbols
- свойство переменные
Возвращает список предельных переменных.

>>> из суммы импорта sympy >>> из sympy.abc импортировать x, i >>> Сумма(x**i, (i, 1, 3)).переменные [я]
См. также
функция,пределы,free_symbols-
as_dummy Переименовать 009 переменные
-
sympy.integrals.integrals.Integral.transform Выполнение отображения фиктивной переменной
-
TODO и ошибки
Есть еще много функций, которые SymPy не умеет интегрировать. Об ошибках, связанных с этим модулем, см. https://github.com/sympy/sympy/issues?q=is%3Aissue+is%3Aopen+label%3Aintegrals
.Числовые интегралы
SymPy имеет функции для вычисления точек и весов для гауссовой квадратуры любой порядок и любая точность:
- sympy.integrals.quadrature.gauss_legendre ( n , n_digits ) [источник]
Вычисляет точки и веса в квадратуре Гаусса-Лежандра [R535].

- Параметры:
номер :
Порядок квадратур.
n_цифр :
Количество значащих цифр точек и весов для возврата. 92}\]
Примеры
>>> из sympy.integrals.quadrature import gauss_legendre >>> x, w = gauss_legendre(3, 5) >>> х [-0,7746, 0, 0,7746] >>> ш [0,55556, 0,88889, 0,55556] >>> x, w = gauss_legendre(4, 5) >>> х [-0,86114, -0,33998, 0,33998, 0,86114] >>> ш [0,34785, 0,65215, 0,65215, 0,34785]
См. также
gauss_laguerre,GAUSS_GEN_LAGUERRE,GAUSS_HERMITE,GAUSS_CHEBYSHEV_T,GAUSS_CHEBYSHEV_U,GAUSS_JACOBI 9299,,GAUSS_JACOBI 9299,,,GAUSS_JACOBI 9299,,GAUSS_JACOBI,.Ссылки
[Р535] (1,2)
https://en.
 wikipedia.org/wiki/Gaussian_quadrature
wikipedia.org/wiki/Gaussian_quadrature[Р536]
http://people.sc.fsu.edu/~jburkardt/cpp_src/legendre_rule/legendre_rule.html
- sympy.integrals.quadrature.gauss_laguerre( n , n_digits )[источник]
Вычисляет точки и веса в квадратуре Гаусса-Лагерра [R537].
- Параметры:
номер :
Порядок квадратур.
n_цифр :
Количество значащих цифр точек и весов для возврата.
- Возвратов:
92}\]
Примеры
>>> из sympy.integrals.quadrature import gauss_laguerre >>> х, ш = гаусс_лагерр (3, 5) >>> х [0,41577, 2,2943, 6,2899] >>> ш [0,71109, 0,27852, 0,010389] >>> x, w = gauss_laguere(6, 5) >>> х [0,22285, 1,1889, 2,9927, 5,7751, 9,8375, 15,983] >>> ш [0,45896, 0,417, 0,11337, 0,010399, 0,00026102, 8,9855e-7]
См.
 также
такжеgauss_legendre,gauss_gen_laguerre,gauss_hermite,gauss_chebyshev_t,gauss_chebyshev_u,gauss_jacobi,gauss_lobattoСсылки
[Р537] (1,2)
https://en.wikipedia.org/wiki/Gauss%E2%80%93Laguerre_quadrature
[Р538]
http://people.sc.fsu.edu/~jburkardt/cpp_src/laguerre_rule/laguerre_rule.html
- sympy.integrals.quadrature.gauss_hermite ( n , n_digits ) [источник]
Вычисляет точки и веса в квадратуре Гаусса-Эрмита [R539].
- Параметры:
номер :
Порядок квадратур.
n_цифр :
Количество значащих цифр точек и весов для возврата. 92}\]
Примеры
>>> из sympy.
 integrals.quadrature импортировать gauss_hermite
>>> х, ш = gauss_hermite(3, 5)
>>> х
[-1,2247, 0, 1,2247]
>>> ш
[0,29541, 1,1816, 0,29541]
integrals.quadrature импортировать gauss_hermite
>>> х, ш = gauss_hermite(3, 5)
>>> х
[-1,2247, 0, 1,2247]
>>> ш
[0,29541, 1,1816, 0,29541]
>>> х, ш = gauss_hermite(6, 5) >>> х [-2,3506, -1,3358, -0,43608, 0,43608, 1,3358, 2,3506] >>> ш [0,00453, 0,15707, 0,72463, 0,72463, 0,15707, 0,00453]
See also
gauss_legendre,gauss_laguerre,gauss_gen_laguerre,gauss_chebyshev_t,gauss_chebyshev_u,gauss_jacobi,gauss_lobattoСсылки
[Р539] (1,2)
https://en.wikipedia.org/wiki/Gauss-Hermite_Quadrature
[Р540]
http://people.sc.fsu.edu/~jburkardt/cpp_src/hermite_rule/hermite_rule.html
[Р541]
http://people.sc.fsu.edu/~jburkardt/cpp_src/gen_hermite_rule/gen_hermite_rule.
 html
html
- sympy.integrals.quadrature.gauss_gen_laguerre( n , альфа , n_digits ) [источник]
Вычисляет точки и веса в обобщенной квадратуре Гаусса-Лагерра [R542].
- Параметры:
номер :
Порядок квадратур.
альфа :
Показатель сингулярности, \(\alpha > -1\).
n_цифр :
Количество значащих цифр точек и весов для возврата.
- Возвратов:
(x, w) :
9{\альфа+1}_{n-1}(x_i)}\]xиw— это списки точек и весов в виде чисел с плавающей запятой.Примеры
>>> из импорта sympy S >>> из sympy.integrals.quadrature импортировать gauss_gen_laguerre >>> x, w = gauss_gen_laguerre(3, -S.Half, 5) >>> х [0,19016, 1,7845, 5,5253] >>> ш [1,4493, 0,31413, 0,00906]
>>> x, w = gauss_gen_laguerre(4, 3*S.
 Half, 5)
>>> х
[0,97851, 2,9904, 6,3193, 11,712]
>>> ш
[0,53087, 0,67721, 0,11895, 0,0023152]
Half, 5)
>>> х
[0,97851, 2,9904, 6,3193, 11,712]
>>> ш
[0,53087, 0,67721, 0,11895, 0,0023152]
See also
gauss_legendre,gauss_laguerre,gauss_hermite,gauss_chebyshev_t,gauss_chebyshev_u,gauss_jacobi,gauss_lobattoСсылки
[Р542] (1,2)
https://en.wikipedia.org/wiki/Gauss%E2%80%93Laguerre_quadrature
[Р543]
http://people.sc.fsu.edu/~jburkardt/cpp_src/gen_laguerre_rule/gen_laguerre_rule.html
- sympy.integrals.quadrature.gauss_chebyshev_t( n , n_digits )[источник]
Вычисляет квадратурные точки Гаусса-Чебышёва [R544] и веса первый вид.
- Параметры:
номер :
Порядок квадратур.
n_цифр :
Количество значащих цифр точек и весов для возврата.
 9n w_i f(x_i)\]
9n w_i f(x_i)\]Узлы \(x_i\) порядка \(n\) квадратурного правила являются корнями \(T_n\) а веса \(w_i\) задаются как:
\[w_i = \frac{\pi}{n}\]
Примеры
>>> из sympy.integrals.quadrature import gauss_chebyshev_t >>> x, w = gauss_chebyshev_t(3, 5) >>> х [0,86602, 0, -0,86602] >>> ш [1,0472, 1,0472, 1,0472]
>>> x, w = gauss_chebyshev_t(6, 5) >>> х [0,96593, 0,70711, 0,25882, -0,25882, -0,70711, -0,96593] >>> ш [0,5236, 0,5236, 0,5236, 0,5236, 0,5236, 0,5236]
See also
gauss_legendre,gauss_laguerre,gauss_hermite,gauss_gen_laguerre,gauss_chebyshev_u,gauss_jacobi,gauss_lobattoСсылки
[Р544] (1,2)
https://en.wikipedia.org/wiki/Чебышев%E2%80%93Гаусс_квадратура
[Р545]
http://people.
 sc.fsu.edu/~jburkardt/cpp_src/chebyshev1_rule/chebyshev1_rule.html
sc.fsu.edu/~jburkardt/cpp_src/chebyshev1_rule/chebyshev1_rule.html
- sympy.integrals.quadrature.gauss_chebyshev_u( n , n_digits )[источник]
Вычисляет квадратурные точки Гаусса-Чебышёва [R546] и веса второй вид.
- Параметры:
n : порядок квадратуры
n_digits : количество значащих цифр точек и весов для возврата
- Возвратов:
(x, w) :
xиw— это списки точек и весов в виде чисел с плавающей запятой.Точки \(x_i\) и веса \(w_i\) возвращаются как
(x, w)кортеж списков.
Пояснение
Квадратура Гаусса-Чебышёва второго рода аппроксимирует интеграл: 92 \влево(\frac{i}{n+1}\pi\вправо)\]
Примеры
>>> из sympy.integrals.quadrature import gauss_chebyshev_u >>> x, w = gauss_chebyshev_u(3, 5) >>> х [0,70711, 0, -0,70711] >>> ш [0,3927, 0,7854, 0,3927]
>>> x, w = gauss_chebyshev_u(6, 5) >>> х [0,, 0,62349, 0,22252, -0,22252, -0,62349, -0,] >>> ш [0,084489, 0,27433, 0,42658, 0,42658, 0,27433, 0,084489]
See also
gauss_legendre,gauss_laguerre,gauss_hermite,gauss_gen_laguerre,gauss_chebyshev_t,gauss_jacobi,gauss_lobattoСсылки
[Р546] (1,2)
https://en.
 wikipedia.org/wiki/Chebyshev%E2%80%93Gauss_quadrature
wikipedia.org/wiki/Chebyshev%E2%80%93Gauss_quadrature[Р547]
http://people.sc.fsu.edu/~jburkardt/cpp_src/chebyshev2_rule/chebyshev2_rule.html
- sympy.integrals.quadrature.gauss_jacobi( n , альфа , бета , n_digits ) [источник]
Вычисляет квадратурные точки и веса Гаусса-Якоби [R548].
- Параметры:
n : порядок квадратуры
альфа : первый параметр многочлена Якоби, \(\alpha > -1\)
бета : второй параметр полинома Якоби, \(\бета > -1\)
n_digits : количество значащих цифр точек и весов для возврата
- Возвратов:
(x, w) :
xиw— это списки точек и весов в виде чисел с плавающей запятой.
9{(\альфа,\бета)}_{n+1}(x_i)}\]Точки \(x_i\) и веса \(w_i\) возвращаются как
(x, w)кортеж списков.
Примеры
>>> из импорта sympy S >>> из sympy.integrals.quadrature импортировать gauss_jacobi >>> x, w = gauss_jacobi(3, S.Half, -S.Half, 5) >>> х [-0,, -0,22252, 0,62349] >>> ш [1,7063, 1,0973, 0,33795]
>>> x, w = gauss_jacobi(6, 1, 1, 5) >>> х [-0,87174, -0,5917, -0,2093, 0,2093, 0,5917, 0,87174] >>> ш [0,050584, 0,22169, 0,39439, 0,39439, 0,22169, 0,050584]
See also
gauss_legendre,gauss_laguerre,gauss_hermite,gauss_gen_laguerre,gauss_chebyshev_t,gauss_chebyshev_u,gauss_lobattoСсылки
[Р548] (1,2)
https://en.wikipedia.org/wiki/Gauss%E2%80%93Jacobi_quadrature
[Р549]
http://people.sc.fsu.edu/~jburkardt/cpp_src/jacobi_rule/jacobi_rule.
 html
html[Р550]
http://people.sc.fsu.edu/~jburkardt/cpp_src/gegenbauer_rule/gegenbauer_rule.html
- sympy.integrals.quadrature.gauss_lobatto( n , n_digits )[источник]
Вычисляет точки и веса в квадратуре Гаусса-Лобатто [R551].
- Параметры:
n : порядок квадратуры
n_digits : количество значащих цифр точек и весов для возврата 92},\quad x\neq\pm 1\\ &w_i = \frac{2}{n(n-1)},\quad x=\pm 1\end{split}\]
Примеры
>>> из sympy.integrals.quadrature import gauss_lobatto >>> x, w = gauss_lobatto(3, 5) >>> х [-1, 0, 1] >>> ш [0,33333, 1,3333, 0,33333] >>> x, w = gauss_lobatto(4, 5) >>> х [-1, -0,44721, 0,44721, 1] >>> ш [0,16667, 0,83333, 0,83333, 0,16667]
См. Также
GAUSS_LEGENDRE,GAUSS_LAGUERRE,GAUSS_GEN_LAGUERRE,GAUSS_HERMITE,GAUSSSH_CHEVISHEV_T999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999. 9999.
9999.Ссылки
[Р551] (1,2)
https://en.wikipedia.org/wiki/Gaussian_quadrature#Gauss.E2.80.93Lobatto_rules
[Р552]
http://people.math.sfu.ca/~cbm/aands/page_888.htm
Интеграция по многогранникам
Модуль
intpolyв SymPy реализует методы для вычисления интеграла полинома по 2/3-многогранникам. Использует методы оценки, описанные в Chin et al. (2015) [1].Входные данные для 2-Polytope или Polygon используют уже существующую структуру данных
Polygonв SymPy. Видетьsympy.geometry.polygonдля того, как создать многоугольник.Для трехмерного многогранника или многогранника наиболее экономичное представление заключается в том, чтобы указать список вершин, а затем предоставить каждую составляющую грань (полигон) в виде списка индексов вершин.
Например, рассмотрим единичный куб.
 Вот как это будет представлено.
Вот как это будет представлено.-
unit_cube = [[(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)], [3, 7, 6, 2], [1, 5, 7, 3], [5, 4, 6, 7], [0, 4, 5, 1], [2, 0, 1, 3], [2, 6, 4, 0]]
Здесь первый подсписок — это список вершин. Другие меньшие списки, такие как
[3, 7, 6, 2], представляют двумерное лицо. многогранников с вершинами, имеющими индекс3, 7, 6 и 2в первом подсписке (именно в таком порядке).Основным методом в этом модуле является
polytope_integrate()polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), x)возвращает интеграл от \(x\) по треугольнику с вершинами (0, 0), (0, 1) и (1, 0)polytope_integrate(unit_cube, x + y + z)возвращает интеграл от \(x + y + z\) по единичному кубу.
Каталожные номера
[1]: Чин, Эрик Б.
 , Жан Б. Лассер и Н. Сукумар. «Численное интегрирование однородных функций на выпуклых и невыпуклых многоугольниках и многогранниках». Вычислительная механика 56.6 (2015): 967-981
, Жан Б. Лассер и Н. Сукумар. «Численное интегрирование однородных функций на выпуклых и невыпуклых многоугольниках и многогранниках». Вычислительная механика 56.6 (2015): 967-981Ссылка в формате PDF: http://dilbert.engr.ucdavis.edu/~suku/quadrature/cls-integration.pdf
Примеры
Для 2D полигонов
Один полином:
>>> из импорта sympy.integrals.intpoly * >>> init_printing(use_unicode=False, wrap_line=False) >>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), x) 1/6 >>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), x + x*y + y**2) 7/24
Список заданных полиномов:
>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), [3, x*y + y**2, x**4], max_степень=4) 4 2 {3: 3/2, х: 1/30, х*у + у: 1/8} >>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), [1.125, x, x**2, 6.89*x**3, x*y + y** 2, х**4], max_степень=4) 2 3 689 4 2 {1,125: 9/16, х: 1/6, х: 1/12, 6,89*х: ----, х: 1/30, х*у + у: 1/8} 2000 г.
Вычисление всех мономов до максимальной степени:
>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)),max_степень=3) 2 3 2 3 2 2 {0: 0, 1: 1/2, х: 1/6, х: 1/12, х: 1/20, у: 1/6, у: 1/12, у: 1/20, х*у : 1/24, х*у : 1/60, х*у: 1/60}Для 3-многогранников/многогранников
Один полином:
>>> из импорта sympy.integrals.intpoly * >>> куб = [[(0, 0, 0), (0, 0, 5), (0, 5, 0), (0, 5, 5), (5, 0, 0), (5, 0, 5), (5, 5, 0), (5, 5, 5)], [2, 6, 7, 3], [3, 7, 5, 1], [7, 6, 4, 5 ], [1, 5, 4, 0], [3, 1, 0, 2], [0, 4, 6, 2]] >>> polytope_integrate(cube, x**2 + y**2 + z**2 + x*y + y*z + x*z) -21875/4 >>> октаэдр = [[(S(-1) / sqrt(2), 0, 0), (0, S(1) / sqrt(2), 0), (0, 0, S(-1) / sqrt(2)), (0, 0, S(1) / sqrt(2)), (0, S(-1) / sqrt(2), 0), (S(1) / sqrt(2) , 0, 0)], [3, 4, 5], [3, 5, 1], [3, 1, 0], [3, 0, 4], [4, 0, 2], [4, 2, 5], [2, 0, 1], [5, 2, 1]] >>> polytope_integrate(октаэдр, x**2 + y**2 + z**2 + x*y + y*z + x*z) ___ \/ 2 ----- 20
Список заданных полиномов:
>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), [3, x*y + y**2, x**4], max_степень=4) 4 2 {3: 3/2, х: 1/30, х*у + у: 1/8} >>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)), [1. 125, x, x**2, 6.89*x**3, x*y + y** 2, х**4], max_степень=4)
2 3 689 4 2
{1,125: 9/16, х: 1/6, х: 1/12, 6,89*х: ----, х: 1/30, х*у + у: 1/8}
2000 г.
125, x, x**2, 6.89*x**3, x*y + y** 2, х**4], max_степень=4)
2 3 689 4 2
{1,125: 9/16, х: 1/6, х: 1/12, 6,89*х: ----, х: 1/30, х*у + у: 1/8}
2000 г.
Вычисление всех мономов до максимальной степени:
>>> polytope_integrate(Polygon((0, 0), (0, 1), (1, 0)),max_степень=3) 2 3 2 3 2 2 {0: 0, 1: 1/2, х: 1/6, х: 1/12, х: 1/20, у: 1/6, у: 1/12, у: 1/20, х*у : 1/24, х*у : 1/60, х*у: 1/60}Ссылка API
- sympy.integrals.intpoly.polytope_integrate( поли , expr=Нет , * , по часовой стрелке=Ложь , max_степень=Нет )[источник]
Интегрирует многочлены по 2/3-многогранникам.
- Параметры:
poly : Входной полигон.
expr : Входной полином.
по часовой стрелке : Двоичное значение для сортировки входных точек 2-многогранника по часовой стрелке.


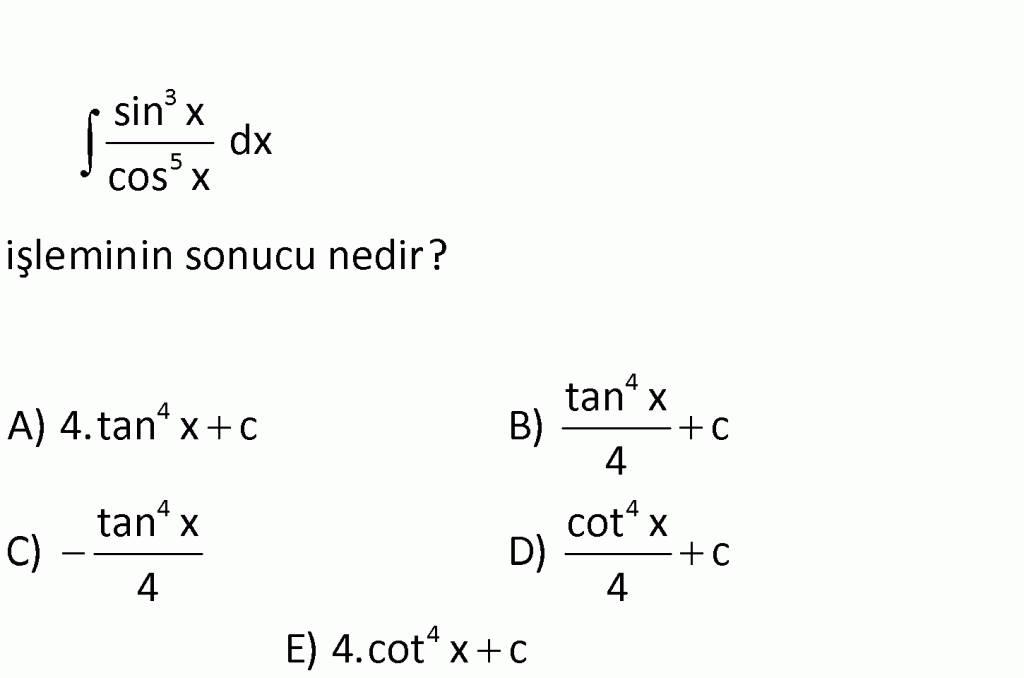


 е.
е.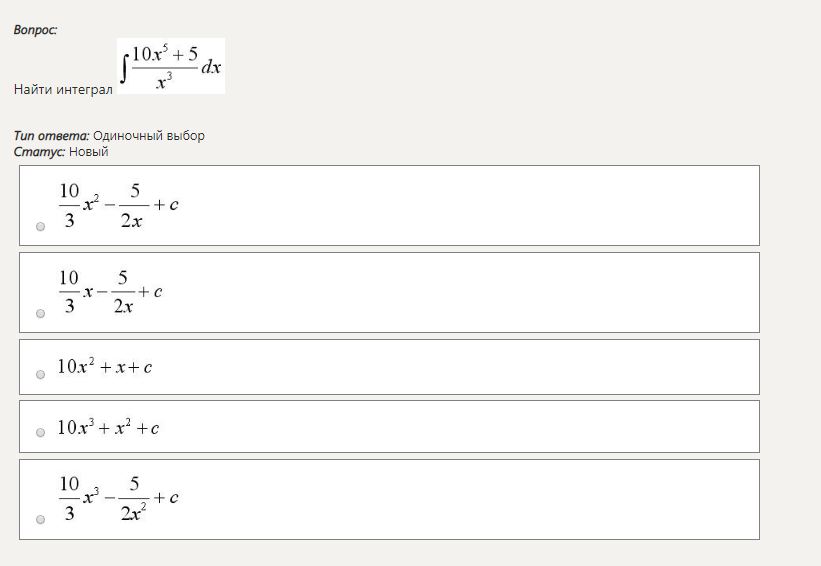 Положим
Положим

 Дробь
Дробь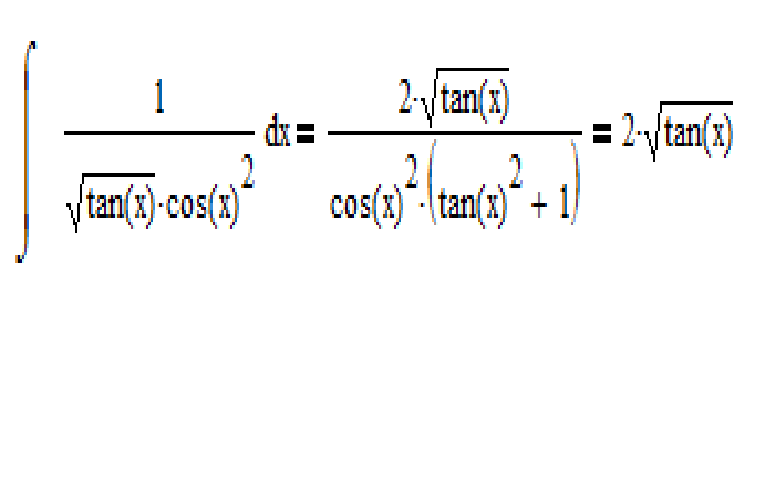
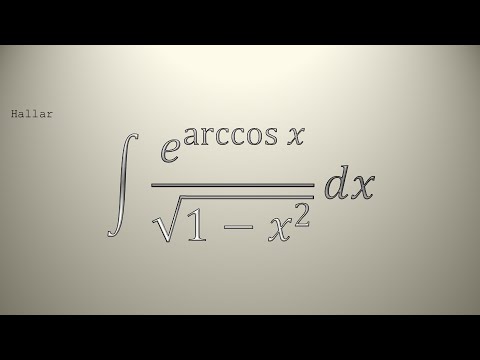


 е. не
е. не 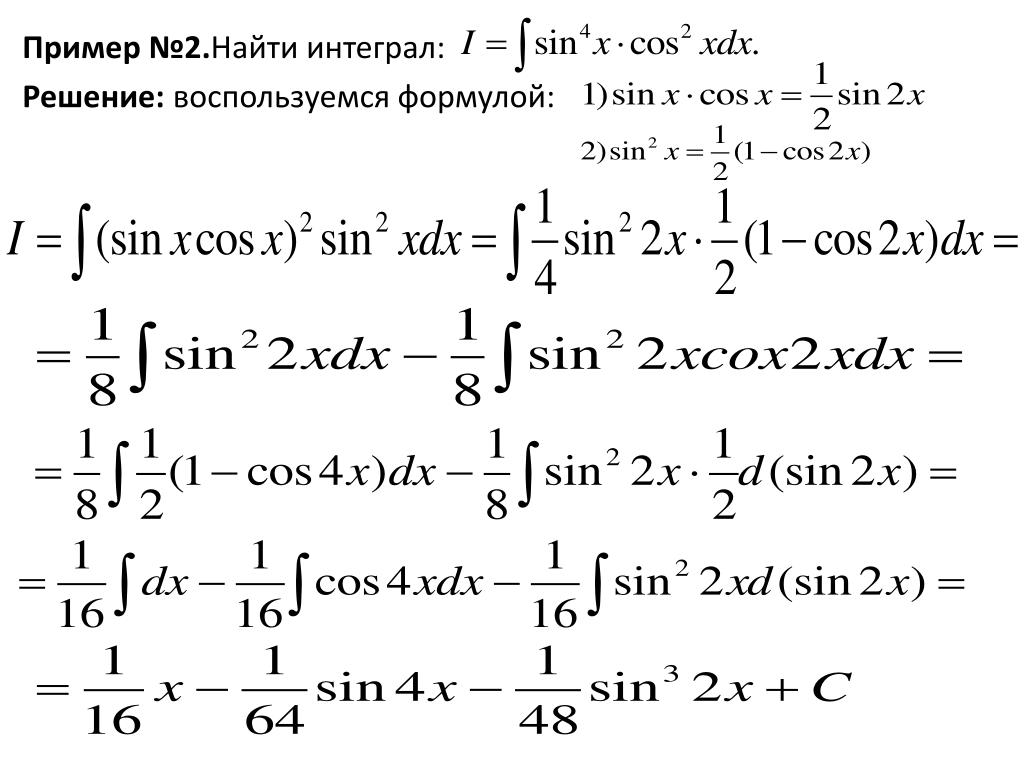 При определенной закономерности
условия на \(F\) и/или \(f\),
это восстанавливает \(f\) из его преобразования Меллина \(F\)
(и наоборот), для положительных действительных \(х\).
При определенной закономерности
условия на \(F\) и/или \(f\),
это восстанавливает \(f\) из его преобразования Меллина \(F\)
(и наоборот), для положительных действительных \(х\).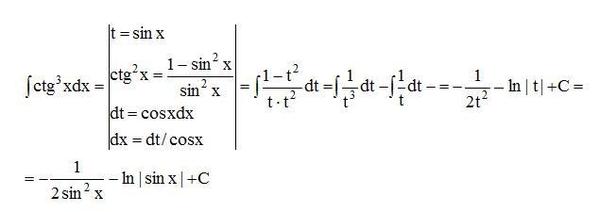 также
также
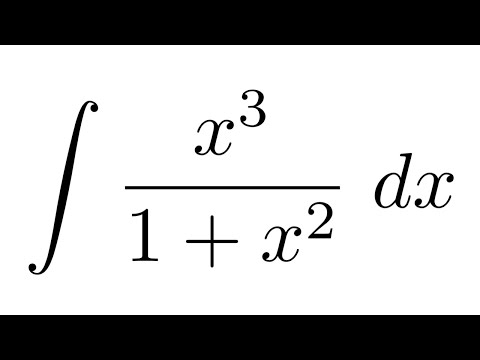 также
также


 integrals.transforms.FourierTransform( *args )[источник]
integrals.transforms.FourierTransform( *args )[источник]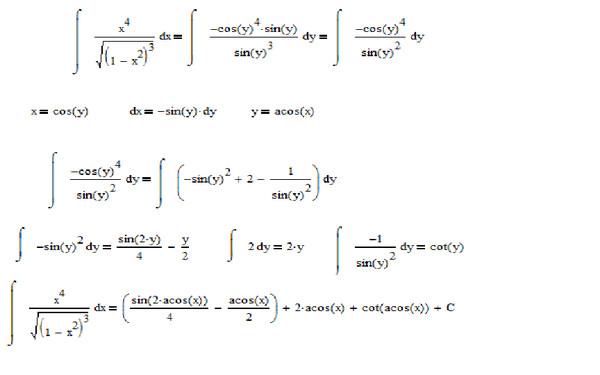 также
также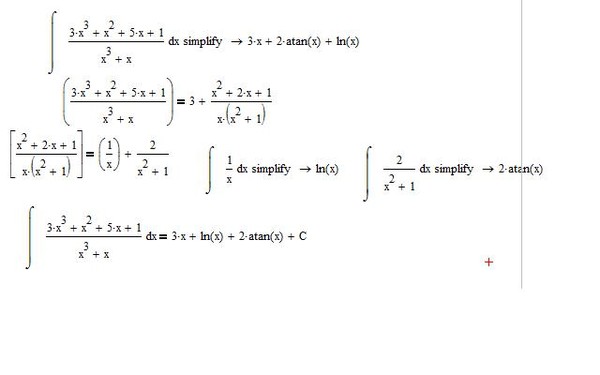 \]
\] integrals.transforms.SineTransform ( *args ) [источник]
integrals.transforms.SineTransform ( *args ) [источник]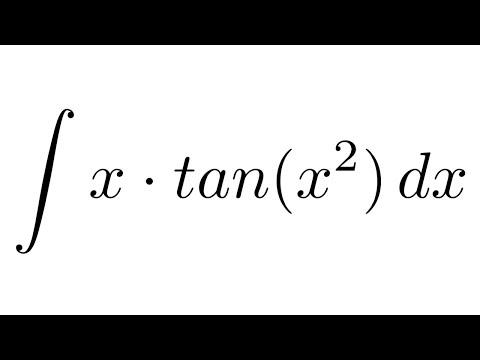 doit()
doit() 
 abc импортировать x, k, a
>>> cosine_transform(exp(-a*x),x,k)
sqrt(2)*a/(sqrt(pi)*(a**2 + k**2))
>>> cosine_transform(exp(-a*sqrt(x))*cos(a*sqrt(x)), x, k)
а*ехр(-а**2/(2*к))/(2*к**(3/2))
abc импортировать x, k, a
>>> cosine_transform(exp(-a*x),x,k)
sqrt(2)*a/(sqrt(pi)*(a**2 + k**2))
>>> cosine_transform(exp(-a*sqrt(x))*cos(a*sqrt(x)), x, k)
а*ехр(-а**2/(2*к))/(2*к**(3/2))
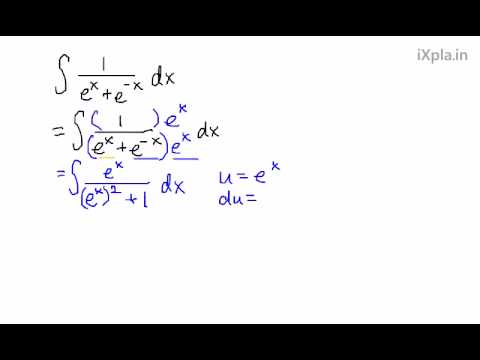
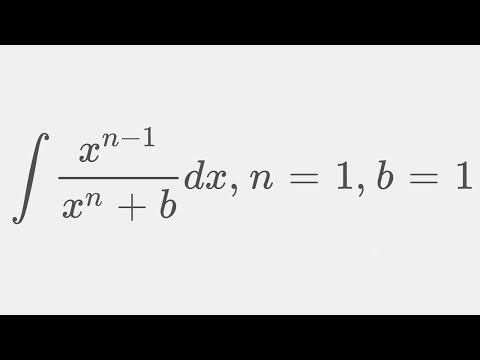 также
также в строке документации
в строке документации 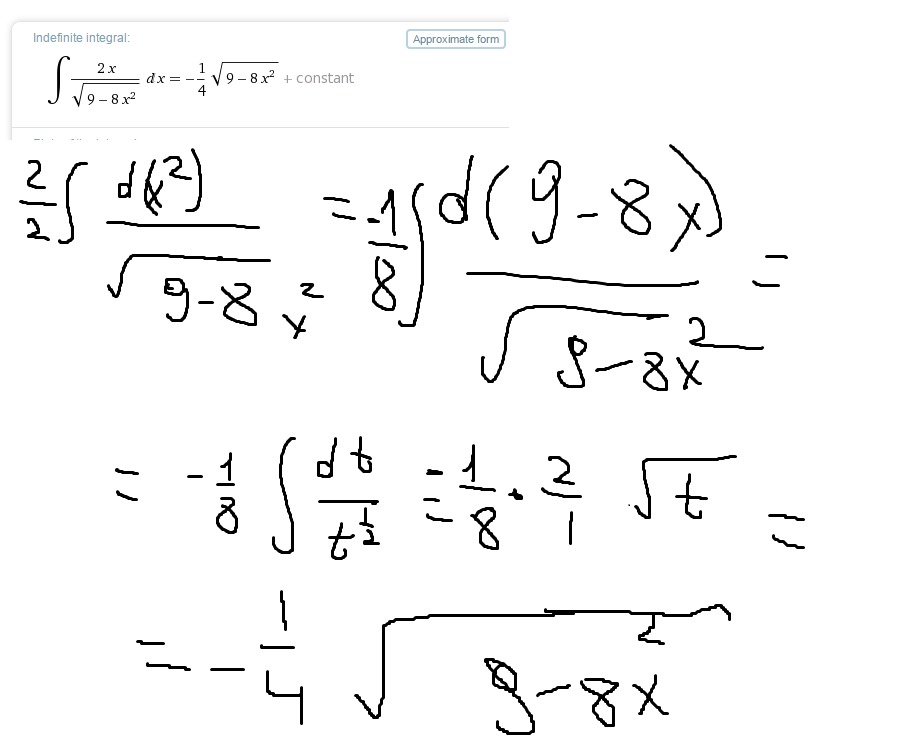 integrals.transforms.HankelTransform ( *args ) [источник]
integrals.transforms.HankelTransform ( *args ) [источник]
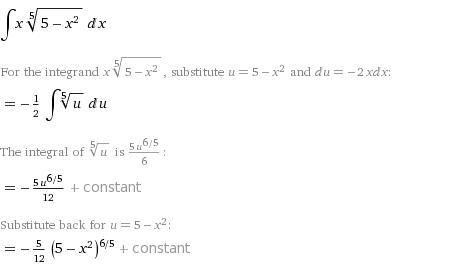
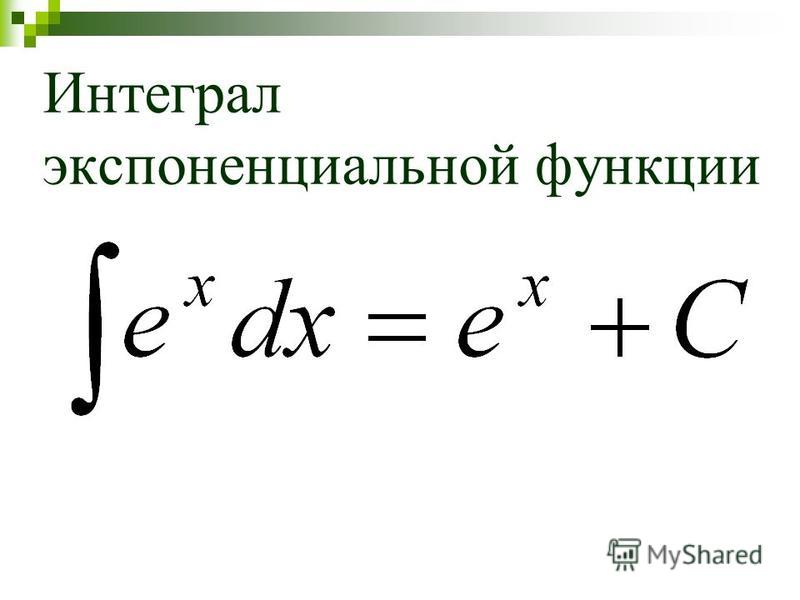 _collapse_extra
_collapse_extra 
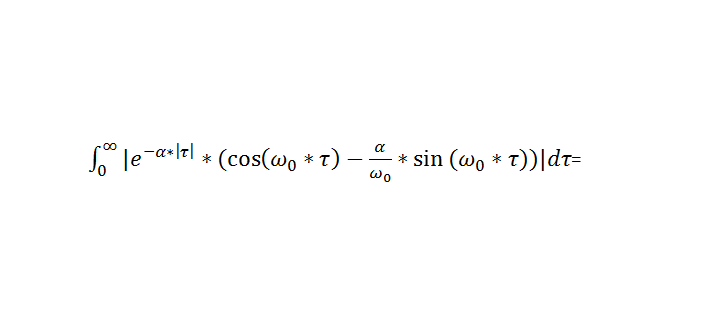 rationaltools импортировать ratint
>>> из sympy.abc импортировать x
rationaltools импортировать ratint
>>> из sympy.abc импортировать x
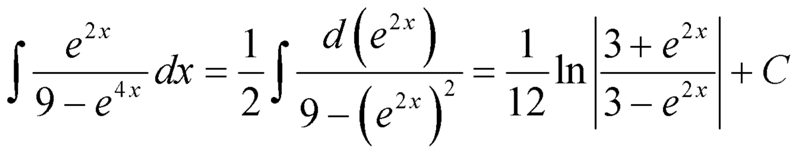
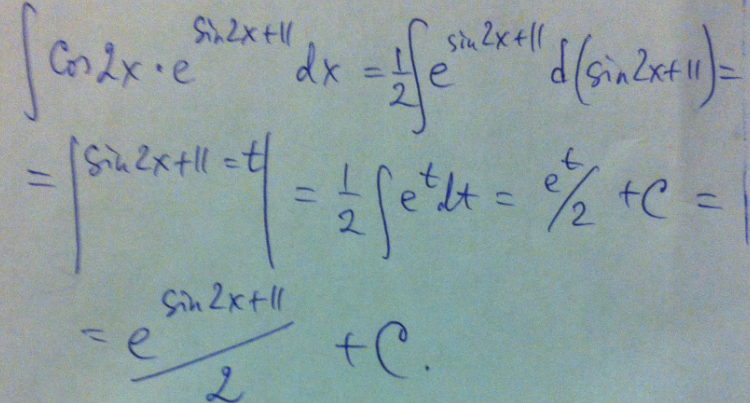 .n, таких, что s_i
в K[t, x] и q_i в K[t], и:
.n, таких, что s_i
в K[t, x] и q_i в K[t], и: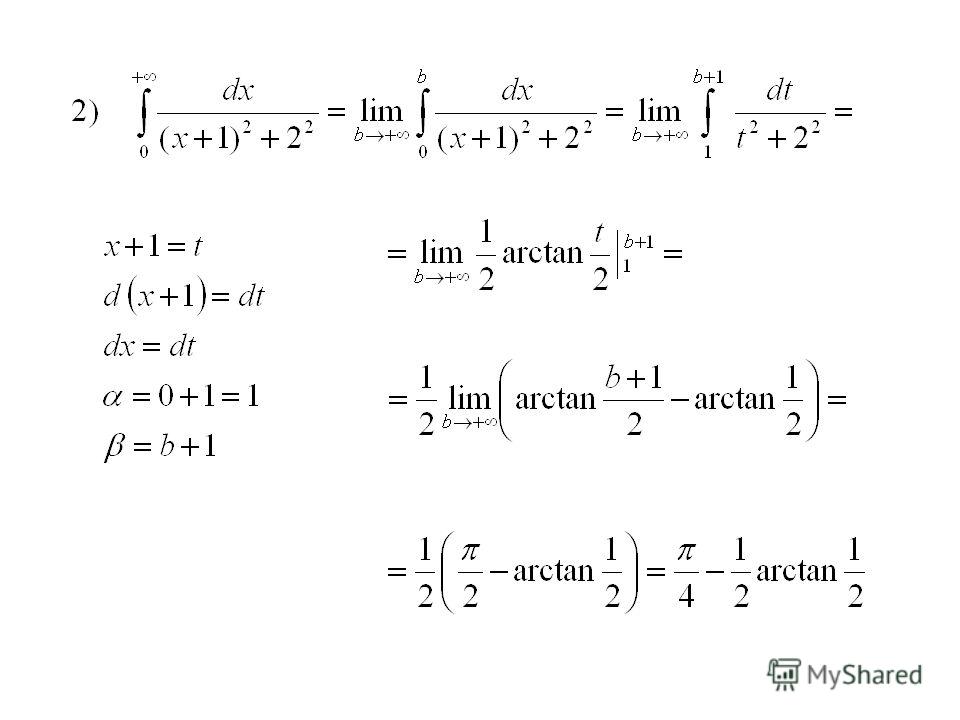

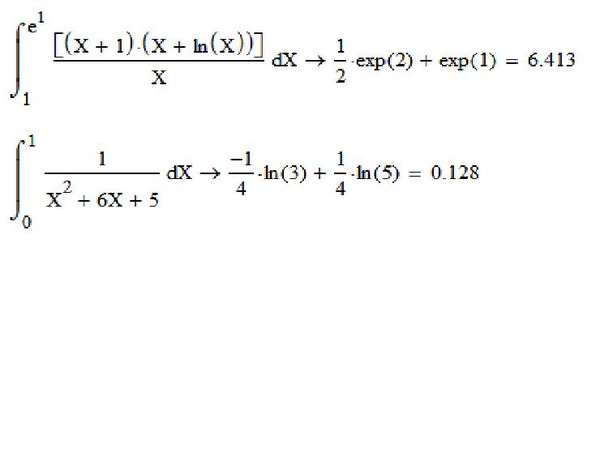

 попробовал дальше. Алгоритм Риша представляет собой общий метод вычисления
первообразные элементарных функций. Алгоритм Риша – это решение
процедура, которая может определить, существует ли элементарное решение, и в
в этом случае вычислить его. Его можно расширить для обработки многих неэлементарных
функции в дополнение к элементарным. Однако версия, реализованная
в SymPy поддерживает только небольшое подмножество полного алгоритма, в частности, на
часть трансцендентного алгоритма для экспонент и логарифмов
реализовано. Преимущество
попробовал дальше. Алгоритм Риша представляет собой общий метод вычисления
первообразные элементарных функций. Алгоритм Риша – это решение
процедура, которая может определить, существует ли элементарное решение, и в
в этом случае вычислить его. Его можно расширить для обработки многих неэлементарных
функции в дополнение к элементарным. Однако версия, реализованная
в SymPy поддерживает только небольшое подмножество полного алгоритма, в частности, на
часть трансцендентного алгоритма для экспонент и логарифмов
реализовано. Преимущество 
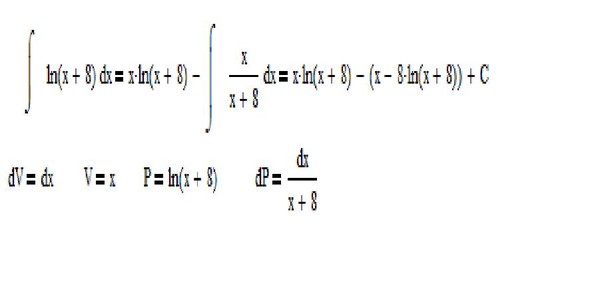 Это полезно, если вы хотите попробовать дальше
интегрирование части NonElementaryIntegral с использованием других алгоритмов для
возможно получить решение с точки зрения специальных функций. Это неверно
дефолт.
Это полезно, если вы хотите попробовать дальше
интегрирование части NonElementaryIntegral с использованием других алгоритмов для
возможно получить решение с точки зрения специальных функций. Это неверно
дефолт.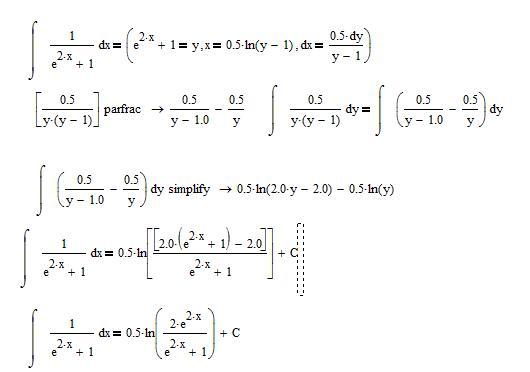 .. х**2*лог(х)), х))
/
|
журнал (-х + журнал (х)) журнал (х + журнал (х)) | 1
- ---------------- + --------------- + | ------ дх
2 2 | журнал (х)
|
/
.. х**2*лог(х)), х))
/
|
журнал (-х + журнал (х)) журнал (х + журнал (х)) | 1
- ---------------- + --------------- + | ------ дх
2 2 | журнал (х)
|
/
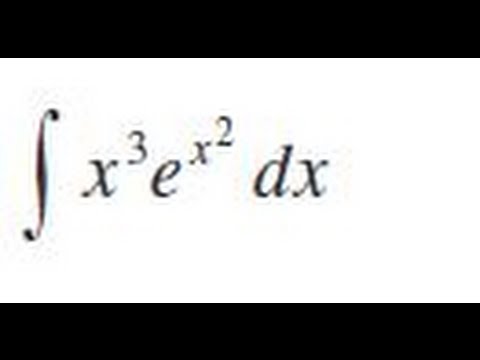 integrals.risch.NonElementaryIntegral( функция , * символы , **допущения )[источник]
integrals.risch.NonElementaryIntegral( функция , * символы , **допущения )[источник]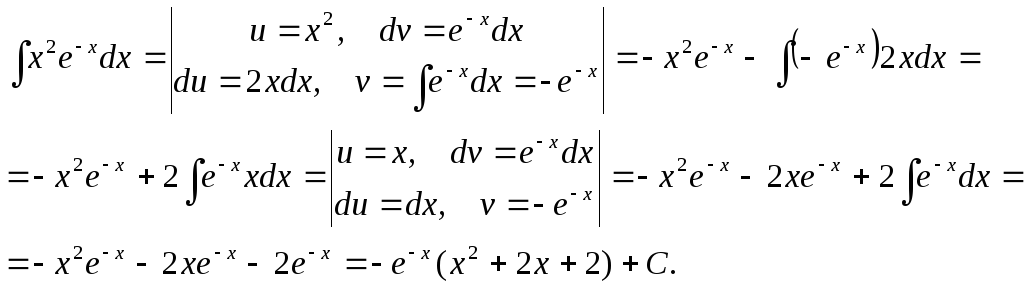
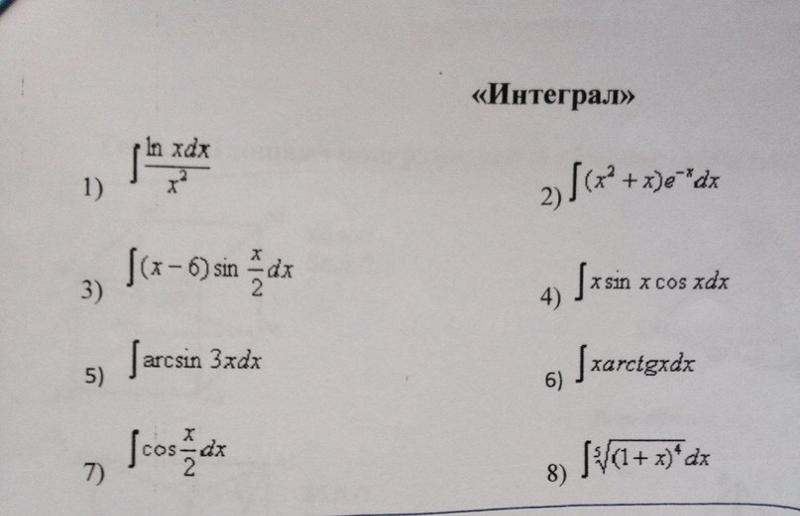 SymPy также
реализует метод, который может решать интегралы почти так же, как в
исчисление. Преимущество этого метода в том, что можно извлечь
шагов интегрирования, чтобы можно было увидеть, как вычислить интеграл «по
рука". Это используется SymPy Gamma. Это
реализовано в
SymPy также
реализует метод, который может решать интегралы почти так же, как в
исчисление. Преимущество этого метода в том, что можно извлечь
шагов интегрирования, чтобы можно было увидеть, как вычислить интеграл «по
рука". Это используется SymPy Gamma. Это
реализовано в  также
также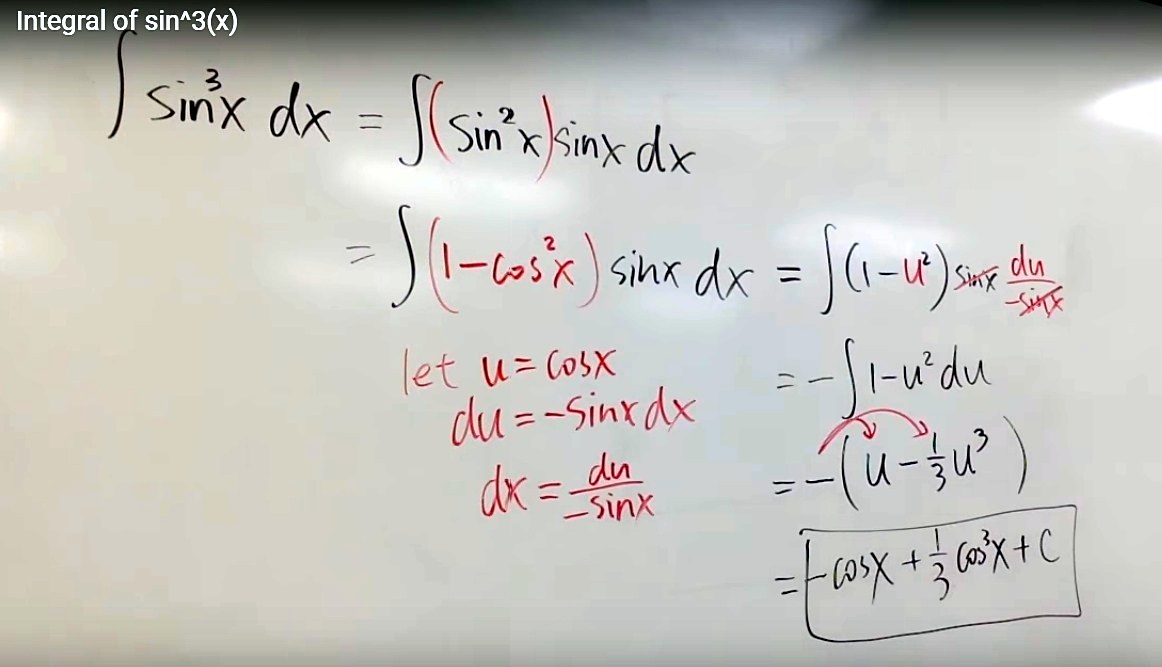 com/sympy/sympy_gamma/blob/master/app/logic/intsteps.py.
com/sympy/sympy_gamma/blob/master/app/logic/intsteps.py. Этот алгоритм опробован
последний, потому что он часто самый медленный для вычислений. Это реализовано в
Этот алгоритм опробован
последний, потому что он часто самый медленный для вычислений. Это реализовано в  Если это не так
в состоянии вычислить первообразную для данной функции, то это
не доказательство того, что такой функции не существует. Следует использовать
рекурсивный алгоритм Риша в таком случае. Это открытый вопрос, если
этот алгоритм можно сделать полной процедурой принятия решений.
Если это не так
в состоянии вычислить первообразную для данной функции, то это
не доказательство того, что такой функции не существует. Следует использовать
рекурсивный алгоритм Риша в таком случае. Это открытый вопрос, если
этот алгоритм можно сделать полной процедурой принятия решений.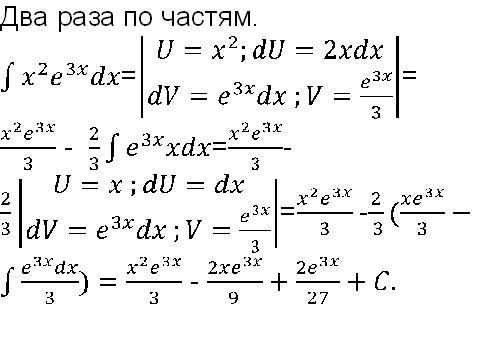 integrals.heurisch импортировать heurisch
>>> из sympy.abc импортировать x, y
integrals.heurisch импортировать heurisch
>>> из sympy.abc импортировать x, y
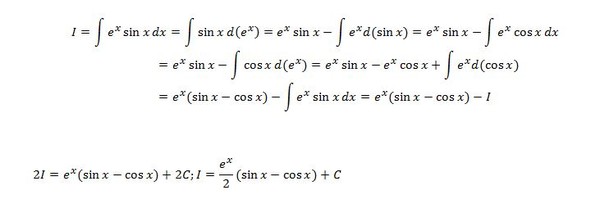 Х. Давенпорт, О параллельном алгоритме Риша (III):
Использование касательных, Бюллетень SIGSAM 16 (1982), 3-6.
Х. Давенпорт, О параллельном алгоритме Риша (III):
Использование касательных, Бюллетень SIGSAM 16 (1982), 3-6.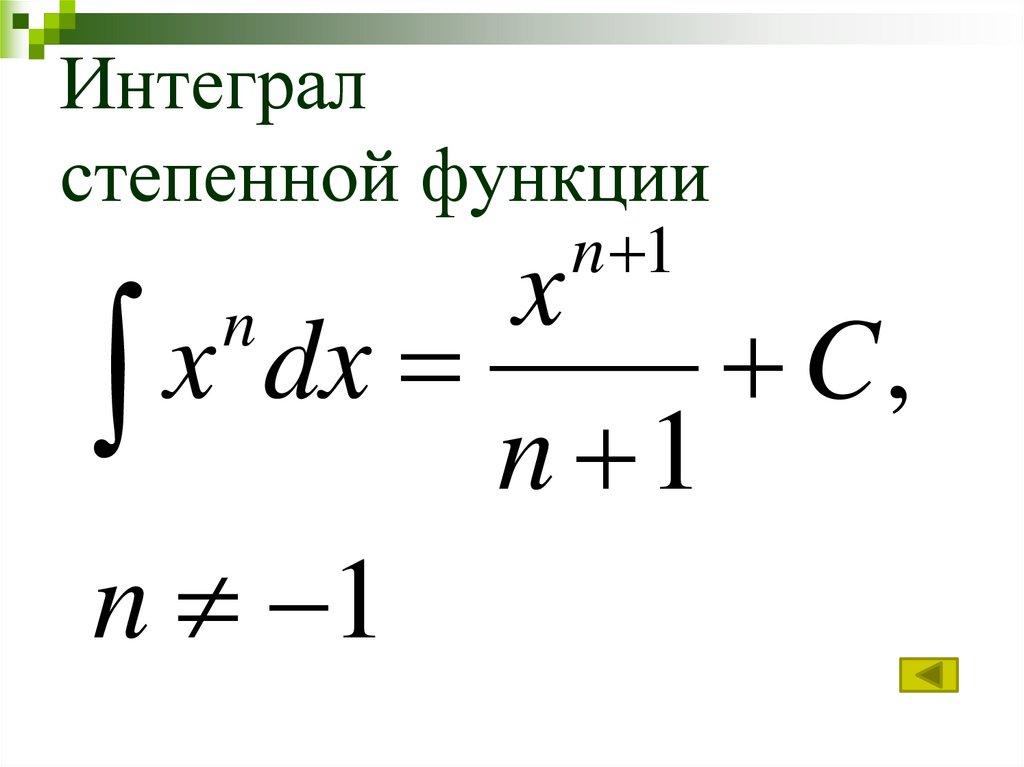 integrals.integrals.integrate( f , var , ... )[источник]
integrals.integrals.integrate( f , var , ... )[источник] (Если var опущен, а подынтегральная функция
одномерный, будет выполнен неопределенный интеграл по этой переменной.)
(Если var опущен, а подынтегральная функция
одномерный, будет выполнен неопределенный интеграл по этой переменной.) е. алгоритм может
либо найти элементарную первообразную, либо доказать, что она не
существует. Существует также (весьма удачный, хотя и несколько медлительный) общий
реализация эвристического алгоритма Риша. Этот алгоритм будет
в конечном итоге будет прекращено, поскольку все больше полного алгоритма Риша
реализовано. Подробнее см. строку документации Integral._eval_integral().
подробности о вычислении первообразной алгебраическими методами.
е. алгоритм может
либо найти элементарную первообразную, либо доказать, что она не
существует. Существует также (весьма удачный, хотя и несколько медлительный) общий
реализация эвристического алгоритма Риша. Этот алгоритм будет
в конечном итоге будет прекращено, поскольку все больше полного алгоритма Риша
реализовано. Подробнее см. строку документации Integral._eval_integral().
подробности о вычислении первообразной алгебраическими методами. Также обратите внимание, что невычисленный интеграл, возвращенный этим
функция не обязательно является NonElementaryIntegral, даже если risch=True,
поскольку это может быть просто указанием на то, что конкретная часть Риша
алгоритм, необходимый для интеграции этой функции, еще не реализован.
Также обратите внимание, что невычисленный интеграл, возвращенный этим
функция не обязательно является NonElementaryIntegral, даже если risch=True,
поскольку это может быть просто указанием на то, что конкретная часть Риша
алгоритм, необходимый для интеграции этой функции, еще не реализован.

 ..
ValueError: укажите переменные интеграции для интеграции x*y
..
ValueError: укажите переменные интеграции для интеграции x*y
 также
также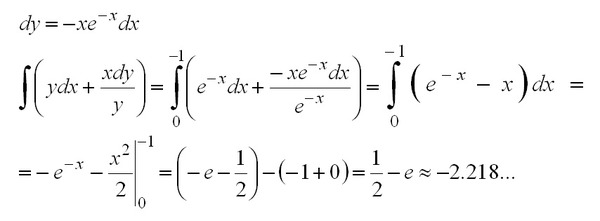
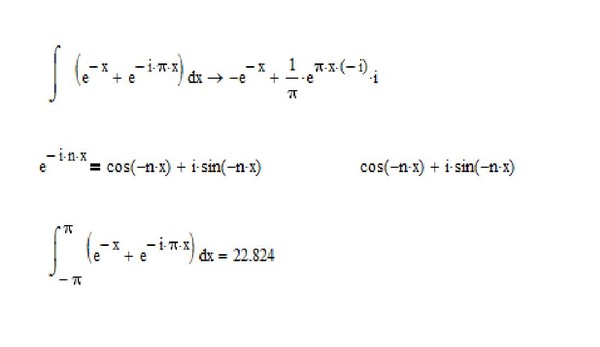 as_sum(2, 'правильно')
2*грех(5) + 2*греш(7)
as_sum(2, 'правильно')
2*грех(5) + 2*греш(7)
 as_sum(method='midpoint').expand()
8/3 - 2/(3*_n**2)
as_sum(method='midpoint').expand()
8/3 - 2/(3*_n**2)
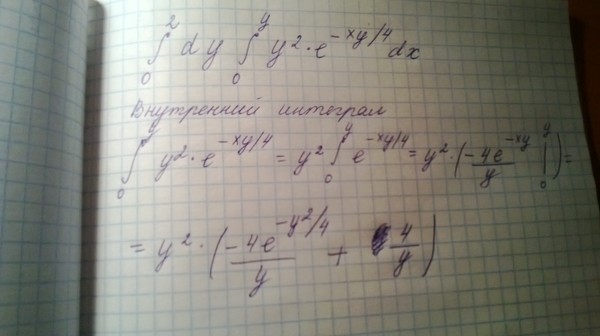 rationaltools.ratint
rationaltools.ratint 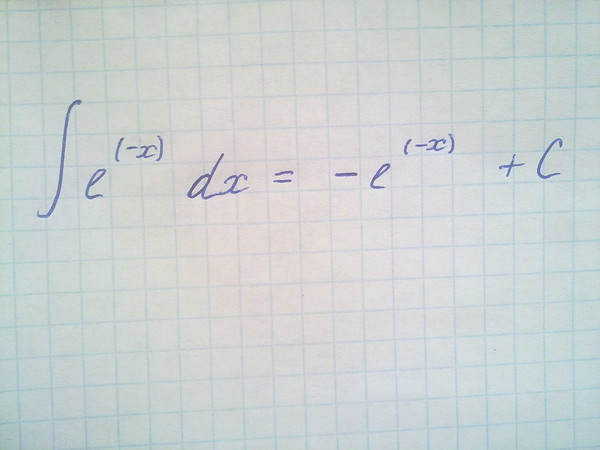
 Фактически это просто замена x на f(x).
Фактически это просто замена x на f(x).
 transform(x**2 - 1, u)
Traceback (последний последний вызов):
...
ЗначениеОшибка:
Отображение между F (x) и f (u) не дало единственного подынтегрального выражения.
transform(x**2 - 1, u)
Traceback (последний последний вызов):
...
ЗначениеОшибка:
Отображение между F (x) и f (u) не дало единственного подынтегрального выражения.
 transform(x, (u + a, a))
Интеграл (а + и, (а, -и, 1 - и))
transform(x, (u + a, a))
Интеграл (а + и, (а, -и, 1 - и))
 integrals.integrals.Integral.transform
integrals.integrals.Integral.transform  False, если известно, что он бесконечен, исходя из границ.
Нет, если недостаточно информации для определения.
False, если известно, что он бесконечен, исходя из границ.
Нет, если недостаточно информации для определения.