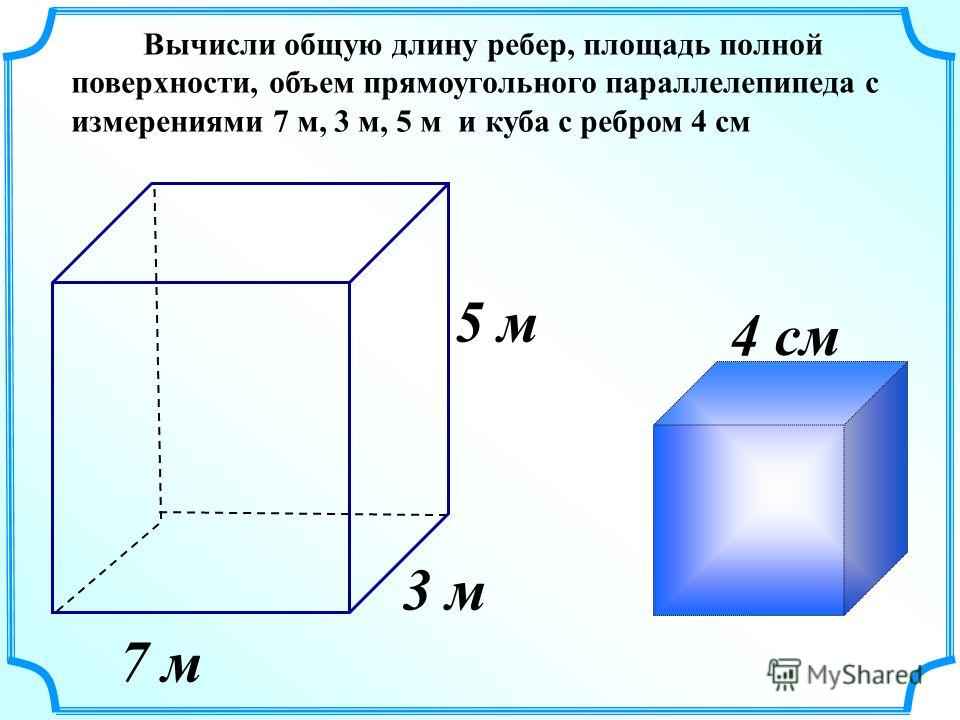
Вычислите объем прямоугольного параллелепипеда площадь. Параллелепипед формула площади и объема.
- Альфашкола
- Статьи
- Объем и площадь параллелепипеда
Прямоугольный параллелепипед
У этой геометрической фигуры \(6\) граней, которые являются прямоугольниками.
Третье ребро прямоугольного параллелепипеда \(c \) является высотой параллелепипеда .
Формула объема параллелепипеда:
\(V=a⋅b⋅c\)
Сторона прямоугольного параллелепипеда a:
Сторона прямоугольного параллелепипеда b:
Высота прямоугольного параллелепипеда h:
Формула площади параллелепипеда:
\(S= 2(a⋅b+a⋅c+b⋅c)\)
V=a⋅b⋅c
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Елена Александровна Гинько
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный педагогический университет имени Максима Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-7 классов.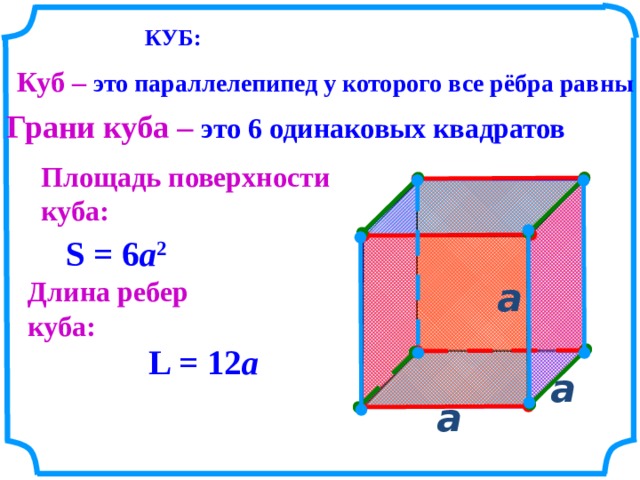 У меня высшее педагогическое образование и работаю я по методике преподавания математики. Любовь к предмету мне привила мой школьный учитель. Мне стало интересным решать разного рода задачи и примеры. И я добилась много в жизни благодаря математике. На уроках и занятиях я располагаю к себе учеников и стараюсь преподносить материал интересным способом. С уверенностью могу сказать, что мои ученики в школе полюбили математику и прилагали все усилия, чтобы совершенствоваться. И на мой взгляд, математику может понять и полюбить каждый, потому что всё зависит от самого человека и того, кто про нее рассказывает.
У меня высшее педагогическое образование и работаю я по методике преподавания математики. Любовь к предмету мне привила мой школьный учитель. Мне стало интересным решать разного рода задачи и примеры. И я добилась много в жизни благодаря математике. На уроках и занятиях я располагаю к себе учеников и стараюсь преподносить материал интересным способом. С уверенностью могу сказать, что мои ученики в школе полюбили математику и прилагали все усилия, чтобы совершенствоваться. И на мой взгляд, математику может понять и полюбить каждый, потому что всё зависит от самого человека и того, кто про нее рассказывает.
Валерия Сергеевна Хусаинова
Репетитор по математике
Стаж (лет)
Образование:
МГУ им. Ломоносова
Ломоносова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Помогу качественно подготовиться к ОГЭ и ЕГЭ ученикам 9, 10 и 11 классов. Вспомним весь школьный курс биологии с самого начала, разберем все типы заданий на реальных вариантах прошлого года, расскажу все об актуальных изменениях этого года и дам много классных готовых конспектов в виде схем и таблиц. Мои ученики хорошо сдают и успешно поступают!
Юлия Геннадьевна Ючко
Репетитор по математике
Стаж (лет)
Образование:
Минский государственный лингвистический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-9 классов. Я фанат английского языка. Хочу, чтобы и мои ученики выучили английский язык даже так же как и я и даже лучше! Коммуникативная методика, преподавание с креативом и энергией, индивидуальный подход к каждому ученику.
Я фанат английского языка. Хочу, чтобы и мои ученики выучили английский язык даже так же как и я и даже лучше! Коммуникативная методика, преподавание с креативом и энергией, индивидуальный подход к каждому ученику.
Похожие статьи
- Что такое дробные числа?
- Простые и составные числа
- Биотехнологический факультет МГУ: приёмная комиссия, проходной балл, отзывы
- ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 3)
- ЕГЭ по математике, базовый уровень. Задачи на совместную работу (вариант 4)
- Как выбрать велосипед для школьника
- Что делать, если школьник придумывает истории и жалуется родителям на преподавателя?
- Подборка логических задач для школьников 3-4 класса
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Площадь поверхности и объем параллелепипеда
Примечание. Это часть урока с задачами по геометрии (раздел теорема стереометрия — параллелепипед). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√»Задача
Основание прямоугольного параллелепипеда — ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений равны P и Q
Это часть урока с задачами по геометрии (раздел теорема стереометрия — параллелепипед). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√»Задача
Основание прямоугольного параллелепипеда — ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений равны P и QРешение.
Площадь первого сечения выразим как
P = hd1 , где
h — высота параллелепипеда
d1 — длина диагонали
Площадь второго сечения выразим как
Q= hd2 , где
h — высота параллелепипеда
d2 — длина диагонали
Соответственно,
d1 = P / h
d2 = Q / h
Площадь боковой поверхности равна
S = 4ah, где
a — длина стороны ромба
По теореме Пифагора
a = sqrt( ( d1 / 2 )2 + ( d2 / 2 )2 )
a = sqrt( d12 / 4 + d22 / 4 )
a = sqrt( d12 + d22 ) / 2
Тогда
S = 4ah
S = 4h sqrt( d12 + d22 ) / 2
S = 2h sqrt( d12 + d22 )
поскольку
d1 = P / h
d2 = Q / h
то
S = 2h √( ( P / h )2 + ( Q / h )2 )
S = 2h √( P 2 + Q2 ) / h
S = 2 √( P 2 + Q2 )
Ответ: S = 2 √( P 2 + Q2 )
Задача
|
Вычислить объем прямоугольного параллелепипеда, диагональ которого а образует с плоскостью основания угол а, а с боковой гранью – угол β. |
Обчислити об’єм прямокутного паралелепіпеда, діагональ якого а утворює з площиною основи кут а, а з бічною гранню кут β. |
Решение. Рiшення.
|
По условию AC’ = a ∠C’AC = α ∠AC’B = β Тогда V = AB х BC х CC´; AB = a sin β; AC = a cos α; CC´ = a sin α; BC2 = AC2 — AB2 a2cos2α — a2sin2β = a2( cos2α — sin2β ) (cos2α — sin2β > 0 т. к. АС – гипотенуза, а АВ – катет). к. АС – гипотенуза, а АВ – катет).
|
За умовою AC’ = a ∠C’AC = α ∠AC’B = β ТодіV = AB х BC х CC´; AB = a sin β; AC = a cos α; CC´ = a sin α; BC2 = AC2 — AB2 a2cos2α — a2sin2β = a2( cos2α — sin2β ) (cos2α — sin2β > 0 т.к. АС – гіпотенуза, а АВ – катет).
|
Задача
|
В параллелепипеде длины трех ребер, выходящих из одной вершины, равны а, b, с. Ребра а и b взаимно перпендикулярны, а ребро с образует с каждым из них угол α. Найти объем параллелепипеда. |
У паралелепіпеді довжини трьох ребер, що виходять з однієї вершини, дорівнюють а, b, с. Ребра а і b взаємно перпендикулярні, а ребро с утворює з кожним з них кут α. Знайти об’єм паралелепіпеда. |
Решение. Рiшення.
|
Так как углы, образуемые ребром с с ребрами а и b, равны, то треугольник АОВ равнобедренный и прямоугольный, катеты которого АВ=ОВ=с*cosα, а гипотенуза ОА= *c*cosα |
Так як кути, утворені ребром с з ребрами а і b рівні, то трикутник АОВ і прямокутний рівнобедрений, катети якого АВ=ОВ=с*cosα, а гіпотенуза ОА= *c*cosα |
0
Параллепипед | Описание курса | Призма с треугольником в основании
Объем параллелепипеда: формула, примеры решения задач
Содержание
- 1 Формулы нахождения объема параллелепипеда
- 2 Параллелепипед: определение, виды и свойства
- 3 Формула объема прямоугольного параллелепипеда
- 4 Формула для нахождения объема наклонного параллелепипеда
- 5 Примеры решения задач
Формулы нахождения объема параллелепипеда
Любое геометрическое тело можно охарактеризовать площадью (S) поверхности и объемом (V). Площадь и объем совсем не одно и то же. Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Площадь и объем совсем не одно и то же. Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Параллелепипед: определение, виды и свойства
Параллелепипед – это четырехугольная призма, в основании которой находится параллелограмм. Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.
У фигуры 6 граней – параллелограммов и 12 ребер, две произвольно выбранные грани называют основаниями. Параллелепипед может быть нескольких видов. Различия обусловлены углами между смежными ребрами. Формулы для нахождения V-ов различных многоугольников немного отличаются.
Если 6 граней геометрической фигуры представляют собой прямоугольники, то ее тоже называют прямоугольной. Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Для решения задач понадобятся знания не только готовых формул, но свойств фигуры. Перечень основных свойств прямоугольной призмы невелик и очень прост для понимания:
- Противолежащие грани фигуры равны и параллельны. Это значит, что ребра расположенные напротив одинаковы по длине и углу наклона.
- Все боковые грани прямого параллелепипеда – прямоугольники.
- Четыре главные диагонали геометрической фигуры пересекаются в одной точкой, и делятся ею пополам.
- Квадрат диагонали параллелепипеда равен суме квадратов измерений фигуры (следует из теоремы Пифагора).
Теорема Пифагора гласит, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.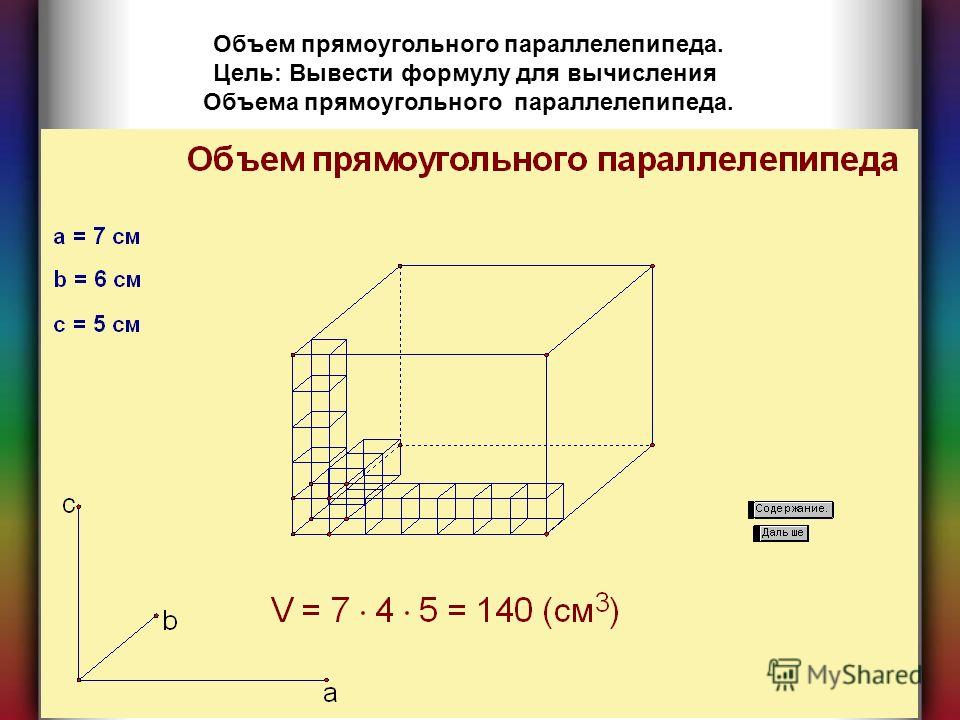
Доказательство последнего свойства можно разобрать на изображении представленном ниже. Ход решения поставленной задачи прост и не требует подробных объяснений.
Формула объема прямоугольного параллелепипеда
Формула нахождения для всех видов геометрической фигуры одна: V=S*h, где V- искомый объем, S – площадь основания параллелепипеда, h – высота, опущенная из противоположной вершины и перпендикулярная основанию. В прямоугольнике h совпадает с одной из сторон фигуры, поэтому чтобы найти объем прямоугольной призмы необходимо перемножить три измерения.
Объем принято выражать в см3. Зная все три значения a, b и c найти объем фигуры совсем не сложно. Наиболее часто встречающийся тип задач в ЕГЭ – это поиск объема или диагонали параллелепипеда. Решить многие типовые задания ЕГЭ без формулы объема прямоугольника – невозможно. Пример задания и оформления его решения приведен на рисунке ниже.
Примечание 1. Площадь поверхности прямоугольной призмы можно найти, если умножить на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ac).
Примечание 2. Площадь поверхности боковых граней легко узнать умножив периметр основания на высоту параллелепипеда.
Исходя из первого свойства параллелепипедов AB = A1B1, а грань B1D1 = BD. Согласно следствиям из теоремы Пифагора сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла в 30°, равен гипотенузы. Применив данные знания для треугольника, легко находим длину сторон AB и AD. Затем перемножаем полученные значения и вычисляем объем параллелепипеда.
Формула для нахождения объема наклонного параллелепипеда
Чтобы найти объем наклонного параллелепипеда необходимо площадь основания фигуры умножить на высоту, опущенную на данное основание из противоположного угла.
Таким образом, искомый V можно представить в виде h — количества листов с площадью S основания, так объем колоды складывается из V-ов всех карт.
Примеры решения задач
Задания единого экзамена должны быть выполнены за определенное время. Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Как видно из примера на изображении выше, ничего сложного в решении подобных задач нет. Задания из более сложных разделов предполагают знания теоремы Пифагора и ее следствий, а так же формулу длины диагонали фигуры. Для успешного решения заданий тестов достаточно заранее ознакомится с образцами типовых задач.
Поделиться с друзьями:
Формулы для нахождения объема параллелепипеда. Объем параллелепипеда Примеры решения задач
Любое геометрическое тело можно охарактеризовать площадью (S) поверхности и объемом (V). Площадь и объем совсем не одно и то же. Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Параллелепипед: определение, виды и свойства
Параллелепипед – это четырехугольная призма, в основании которой находится параллелограмм. Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.
У фигуры 6 граней – параллелограммов и 12 ребер, две произвольно выбранные грани называют основаниями. Параллелепипед может быть нескольких видов. Различия обусловлены углами между смежными ребрами. Формулы для нахождения V-ов различных многоугольников немного отличаются.
Если 6 граней геометрической фигуры представляют собой прямоугольники, то ее тоже называют прямоугольной. Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Для решения задач понадобятся знания не только готовых формул, но свойств фигуры. Перечень основных свойств прямоугольной призмы невелик и очень прост для понимания:
- Противолежащие грани фигуры равны и параллельны. Это значит, что ребра расположенные напротив одинаковы по длине и углу наклона.
- Все боковые грани прямого параллелепипеда – прямоугольники.
- Четыре главные диагонали геометрической фигуры пересекаются в одной точкой, и делятся ею пополам.
- Квадрат диагонали параллелепипеда равен суме квадратов измерений фигуры (следует из теоремы Пифагора).
Теорема Пифагора гласит, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.
Доказательство последнего свойства можно разобрать на изображении представленном ниже. Ход решения поставленной задачи прост и не требует подробных объяснений.
Формула объема прямоугольного параллелепипеда
Формула нахождения для всех видов геометрической фигуры одна: V=S*h, где V- искомый объем, S – площадь основания параллелепипеда, h – высота, опущенная из противоположной вершины и перпендикулярная основанию. В прямоугольнике h совпадает с одной из сторон фигуры, поэтому чтобы найти объем прямоугольной призмы необходимо перемножить три измерения.
Объем принято выражать в см3. Зная все три значения a, b и c найти объем фигуры совсем не сложно. Наиболее часто встречающийся тип задач в ЕГЭ – это поиск объема или диагонали параллелепипеда. Решить многие типовые задания ЕГЭ без формулы объема прямоугольника – невозможно. Пример задания и оформления его решения приведен на рисунке ниже.
Примечание 1 . Площадь поверхности прямоугольной призмы можно найти, если умножить на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ac).
Примечание 2 . Площадь поверхности боковых граней легко узнать умножив периметр основания на высоту параллелепипеда.
Исходя из первого свойства параллелепипедов AB = A1B1, а грань B1D1 = BD. Согласно следствиям из теоремы Пифагора сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла в 30°, равен гипотенузы. Применив данные знания для треугольника, легко находим длину сторон AB и AD. Затем перемножаем полученные значения и вычисляем объем параллелепипеда.
Формула для нахождения объема наклонного параллелепипеда
Чтобы найти объем наклонного параллелепипеда необходимо площадь основания фигуры умножить на высоту, опущенную на данное основание из противоположного угла.
Таким образом, искомый V можно представить в виде h — количества листов с площадью S основания, так объем колоды складывается из V-ов всех карт.
Примеры решения задач
Задания единого экзамена должны быть выполнены за определенное время. Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Как видно из примера на изображении выше, ничего сложного в решении подобных задач нет. Задания из более сложных разделов предполагают знания теоремы Пифагора и ее следствий, а так же формулу длины диагонали фигуры. Для успешного решения заданий тестов достаточно заранее ознакомится с образцами типовых задач.
Если говорить просто, то это овощи, приготовленные в воде по специальному рецепту. Я буду рассматривать два исходных компонента (овощной салат и воду) и готовый результат — борщ. Геометрически это можно представить как прямоугольник, в котором одна сторона обозначает салат, вторая сторона обозначает воду. Сумма этих двух сторон будет обозначать борщ. Диагональ и площадь такого «борщевого» прямоугольника являются чисто математическими понятиями и никогда не используются в рецептах приготовления борща.
Как салат и вода превращаются в борщ с точки зрения математики? Как сумма двух отрезков может превратиться в тригонометрию? Чтобы понять это, нам понадобятся линейные угловые функции.
В учебниках математики вы ничего не найдете о линейных угловых функциях. А ведь без них не может быть математики. Законы математики, как и законы природы, работают независимо от того, знаем мы о их существовании или нет.
Линейные угловые функции — это законы сложения. Посмотрите, как алгебра превращается в геометрию, а геометрия превращается в тригонометрию.
Можно ли обойтись без линейных угловых функций? Можно, ведь математики до сих пор без них обходятся. Хитрость математиков заключается в том, что они всегда рассказывают нам только о тех задачах, которые они сами умеют решать, и никогда не рассказывают о тех задачах, которые они решать не умеют. Смотрите. Если нам известен результат сложения и одно слагаемое, для поиска другого слагаемого мы используем вычитание. Всё. Других задач мы не знаем и решать не умеем. Что делать в том случае, если нам известен только результат сложения и не известны оба слагаемые? В этом случае результат сложения нужно разложить на два слагаемых при помощи линейных угловых функций. Дальше мы уже сами выбираем, каким может быть одно слагаемое, а линейные угловые функции показывают, каким должно быть второе слагаемое, чтобы результат сложения был именно таким, какой нам нужен. Таких пар слагаемых может быть бесконечное множество. В повседневной жизни мы прекрасно обходимся без разложения суммы, нам достаточно вычитания. А вот при научных исследованиях законов природы разложение суммы на слагаемые очень может пригодиться.
Дальше мы уже сами выбираем, каким может быть одно слагаемое, а линейные угловые функции показывают, каким должно быть второе слагаемое, чтобы результат сложения был именно таким, какой нам нужен. Таких пар слагаемых может быть бесконечное множество. В повседневной жизни мы прекрасно обходимся без разложения суммы, нам достаточно вычитания. А вот при научных исследованиях законов природы разложение суммы на слагаемые очень может пригодиться.
Ещё один закон сложения, о котором математики не любят говорить (ещё одна их хитрость), требует, чтобы слагаемые имели одинаковые единицы измерения. Для салата, воды и борща это могут быть единицы измерения веса, объема, стоимости или единицы измерения.
На рисунке показаны два уровня различий для математических . Первый уровень — это различия в области чисел, которые обозначены a , b , c . Это то, чем занимаются математики. Второй уровень — это различия в области единиц измерения, которые показаны в квадратных скобках и обозначены буквой U . Этим занимаются физики. Мы же можем понимать третий уровень — различия в области описываемых объектов. Разные объекты могут иметь одинаковое количество одинаковых единиц измерения. Насколько это важно, мы можем увидеть на примере тригонометрии борща. Если мы добавим нижние индексы к одинаковому обозначению единиц измерения разных объектов, мы сможем точно говорить, какая математическая величина описывает конкретный объект и как она изменяется с течением времени или в связи с нашими действиями. Буквой W я обозначу воду, буквой S обозначу салат и буквой B — борщ. Вот как будут выглядеть линейные угловые функции для борща.
Этим занимаются физики. Мы же можем понимать третий уровень — различия в области описываемых объектов. Разные объекты могут иметь одинаковое количество одинаковых единиц измерения. Насколько это важно, мы можем увидеть на примере тригонометрии борща. Если мы добавим нижние индексы к одинаковому обозначению единиц измерения разных объектов, мы сможем точно говорить, какая математическая величина описывает конкретный объект и как она изменяется с течением времени или в связи с нашими действиями. Буквой W я обозначу воду, буквой S обозначу салат и буквой B — борщ. Вот как будут выглядеть линейные угловые функции для борща.
Если мы возьмем какую-то часть воды и какую-то часть салата, вместе они превратятся в одну порцию борща. Здесь я предлагаю вам немного отвлечься от борща и вспомнить далекое детство. Помните, как нас учили складывать вместе зайчиков и уточек? Нужно было найти, сколько всего зверушек получится. Что же нас тогда учили делать? Нас учили отрывать единицы измерения от чисел и складывать числа. Да, одно любое число можно сложить с другим любым числом. Это прямой путь к аутизму современной математики — мы делаем непонятно что, непонятно зачем и очень плохо понимаем, как это относится к реальности, ведь из трех уровней различия математики оперируют только одним. Более правильно будет научиться переходить от одних единиц измерения к другим.
Да, одно любое число можно сложить с другим любым числом. Это прямой путь к аутизму современной математики — мы делаем непонятно что, непонятно зачем и очень плохо понимаем, как это относится к реальности, ведь из трех уровней различия математики оперируют только одним. Более правильно будет научиться переходить от одних единиц измерения к другим.
И зайчиков, и уточек, и зверушек можно посчитать в штуках. Одна общая единица измерения для разных объектов позволяет нам сложить их вместе. Это детский вариант задачи. Давайте посмотрим на похожую задачу для взрослых. Что получится, если сложить зайчиков и деньги? Здесь можно предложить два варианта решения.
Первый вариант . Определяем рыночную стоимость зайчиков и складываем её с имеющейся денежной суммой. Мы получили общую стоимость нашего богатства в денежном эквиваленте.
Второй вариант . Можно количество зайчиков сложить с количеством имеющихся у нас денежных купюр. Мы получим количество движимого имущества в штуках.
Как видите, один и тот же закон сложения позволяет получить разные результаты. Всё зависит от того, что именно мы хотим знать.
Но вернемся к нашему борщу. Теперь мы можем посмотреть, что будет происходить при разных значениях угла линейных угловых функций.
Угол равен нулю. У нас есть салат, но нет воды. Мы не можем приготовить борщ. Количество борща также равно нулю. Это совсем не значит, что ноль борща равен нулю воды. Ноль борща может быть и при нуле салата (прямой угол).
Лично для меня, это основное математическое доказательство того факта, что . Ноль не изменяет число при сложении. Это происходит потому, что само сложение невозможно, если есть только одно слагаемое и отсутствует второе слагаемое. Вы к этому можете относиться как угодно, но помните — все математические операции с нулем придумали сами математики, поэтому отбрасывайте свою логику и тупо зубрите определения, придуманные математиками: «деление на ноль невозможно», «любое число, умноженное на ноль, равняется нулю», «за выколом точки ноль» и прочий бред. Достаточно один раз запомнить, что ноль не является числом, и у вас уже никогда не возникнет вопрос, является ноль натуральным числом или нет, потому что такой вопрос вообще лишается всякого смысла: как можно считать числом то, что числом не является. Это всё равно, что спрашивать, к какому цвету отнести невидимый цвет. Прибавлять ноль к числу — это то же самое, что красить краской, которой нет. Сухой кисточкой помахали и говорим всем, что » мы покрасили». Но я немного отвлекся.
Достаточно один раз запомнить, что ноль не является числом, и у вас уже никогда не возникнет вопрос, является ноль натуральным числом или нет, потому что такой вопрос вообще лишается всякого смысла: как можно считать числом то, что числом не является. Это всё равно, что спрашивать, к какому цвету отнести невидимый цвет. Прибавлять ноль к числу — это то же самое, что красить краской, которой нет. Сухой кисточкой помахали и говорим всем, что » мы покрасили». Но я немного отвлекся.
Угол больше нуля, но меньше сорока пяти градусов. У нас много салата, но мало воды. В результате мы получим густой борщ.
Угол равен сорок пять градусов. Мы имеем в равных количествах воду и салат. Это идеальный борщ (да простят меня повара, это просто математика).
Угол больше сорока пяти градусов, но меньше девяноста градусов. У нас много воды и мало салата. Получится жидкий борщ.
Прямой угол. У нас есть вода. От салата остались только воспоминания, поскольку угол мы продолжаем измерять от линии, которая когда-то обозначала салат.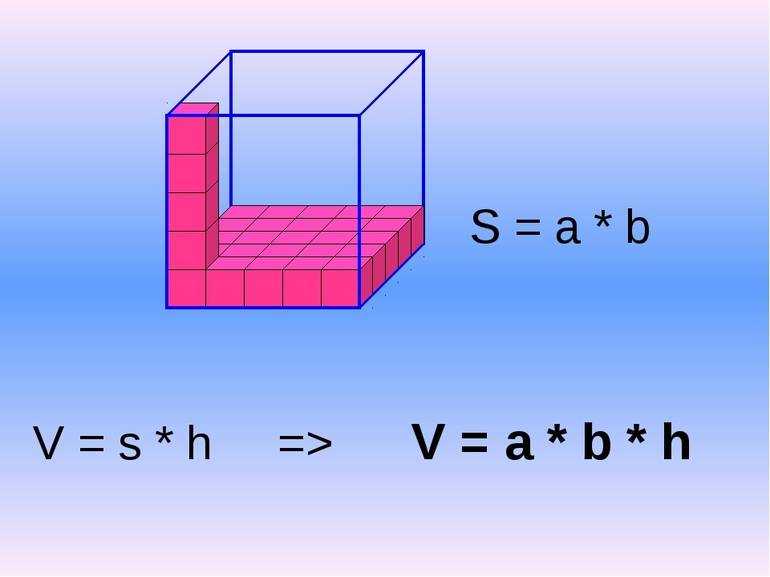 Мы не можем приготовить борщ. Количество борща равно нулю. В таком случае, держитесь и пейте воду, пока она есть)))
Мы не можем приготовить борщ. Количество борща равно нулю. В таком случае, держитесь и пейте воду, пока она есть)))
Вот. Как-то так. Я могу здесь рассказать и другие истории, которые будут здесь более чем уместны.
Два друга имели свои доли в общем бизнесе. После убийства одного из них, всё досталось другому.
Появление математики на нашей планете.
Все эти истории на языке математики рассказаны при помощи линейных угловых функций. Как-нибудь в другой раз я покажу вам реальное место этих функций в структуре математики. А пока, вернемся к тригонометрии борща и рассмотрим проекции.
суббота, 26 октября 2019 г.
Просмотрел интересное видио про ряд Гранди Один минус один плюс один минус один — Numberphile . Математики врут. Они не выполнили проверку равенства в ходе своих рассуждений.
Это перекликается с моими рассуждениями о .
Давайте более детально рассмотрим признаки обмана нас математиками. В самом начале рассуждений, математики говорят, что сумма последовательности ЗАВИСИТ от того, четное количество элементов в ней или нет. Это ОБЪЕКТИВНО УСТАНОВЛЕННЫЙ ФАКТ. Что происходит дальше?
Это ОБЪЕКТИВНО УСТАНОВЛЕННЫЙ ФАКТ. Что происходит дальше?
Дальше математики из единицы вычитают последовательность. К чему это приводит? Это приводит к изменению количества элементов последовательности — четное количество изменяется на нечетное, нечетное изменяется на четное. Ведь мы добавили к последовательности один элемент, равный единице. Несмотря на всю внешнюю схожесть, последовательность до преобразования не равна последовательности после преобразования. Даже если мы рассуждаем о бесконечной последовательности, необходимо помнить, что бесконечная последовательность с нечетным количеством элементов не равна бесконечной последовательности с четным количеством элементов.
Ставя знак равенства между двумя разными по количеству элементов последовательностями, математики утверждают, что сумма последовательности НЕ ЗАВИСИТ от количества элементов в последовательности, что противоречит ОБЪЕКТИВНО УСТАНОВЛЕННОМУ ФАКТУ. Дальнейшие рассуждения о сумме бесконечной последовательности являются ложными, поскольку основаны на ложном равенстве.
Если вы видите, что математики в ходе доказательств расставляют скобки, переставляют местами элементы математического выражения, что-нибудь добавляют или убирают, будьте очень внимательны, скорее всего вас пытаются обмануть. Как карточные фокусники, математики различными манипуляциями с выражением отвлекают ваше внимание, чтобы в итоге подсунуть вам ложный результат. Если карточный фокус вы не можете повторить, не зная секрета обмана, то в математике всё гораздо проще: вы даже ничего не подозреваете об обмане, но повторение всех манипуляций с математическим выражением позволяет вам убедить других в правильности полученного результата, точно так же, как когда-то убедили вас.
Вопрос из зала: А бесконечность (как количество элементов в последовательности S), она четная или нечётная? Как можно поменять четность у того, что четности не имеет?
Бесконечность для математиков, как Царство Небесное для попов — никто никогда там не был, но все точно знают, как там всё устроено))) Согласен, после смерти вам будет абсолютно безразлично, четное или нечетное количество дней вы прожили, но.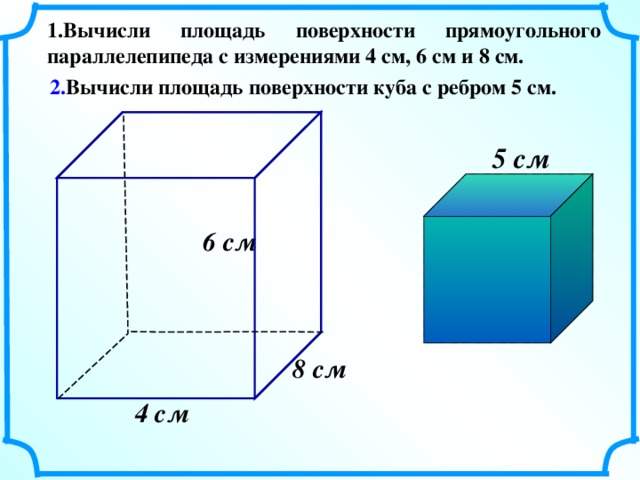 .. Добавив всего один день в начало вашей жизни, мы получим совсем другого человека: фамилия, имя и отчество у него точно такие же, только дата рождения совсем другая — он родился за один день до вас.
.. Добавив всего один день в начало вашей жизни, мы получим совсем другого человека: фамилия, имя и отчество у него точно такие же, только дата рождения совсем другая — он родился за один день до вас.
А теперь по существу))) Допустим, конечная последовательность, имеющая четность, теряет эту четность при переходе к бесконечности. Тогда и любой конечный отрезок бесконечной последовательности должен потерять четность. Мы этого не наблюдаем. То, что мы не можем точно сказать, четное или нечетное количество элементов у бесконечной последовательности, совсем не означает, что четность исчезла. Не может четность, если она есть, бесследно исчезнуть в бесконечности, как в рукаве шулера. Для этого случая есть очень хорошая аналогия.
Вы никогда не спрашивали у кукушки, сидящей в часах, в каком направлении вращается стрелка часов? Для неё стрелка вращается в обратном направлении тому, которое мы называем «по часовой стрелке». Как это не парадоксально звучит, но направление вращения зависит исключительно от того, с какой стороны мы вращение наблюдаем. И так, у нас есть одно колесо, которое вращается. Мы не можем сказать, в каком направлении происходит вращение, поскольку мы его можем наблюдать как с одной стороны плоскости вращения, так и с другой. Мы можем только засвидетельствовать факт, что вращение есть. Полная аналогия с четностью бесконечной последовательности S .
И так, у нас есть одно колесо, которое вращается. Мы не можем сказать, в каком направлении происходит вращение, поскольку мы его можем наблюдать как с одной стороны плоскости вращения, так и с другой. Мы можем только засвидетельствовать факт, что вращение есть. Полная аналогия с четностью бесконечной последовательности S .
Теперь добавим второе вращающееся колесо, плоскость вращения которого параллельна плоскости вращения первого вращающегося колеса. Мы по прежнему не можем точно сказать, в каком направлении вращаются эти колеса, но мы абсолютно точно можем сказать, вращаются оба колеса в одну сторону или в противоположные. Сравнивая две бесконечные последовательности S и 1-S , я при помощи математики показал, что у этих последовательностей разная четность и ставить знак равенства между ними — это ошибка. Лично я верю математике, я не доверяю математикам))) Кстати, для полного понимания геометрии преобразований бесконечных последовательностей, необходимо вводить понятие «одновременность» . Это нужно будет нарисовать.
Это нужно будет нарисовать.
среда, 7 августа 2019 г.
Завершая разговор о , нужно рассмотреть бесконечное множество. Дало в том, что понятие «бесконечность» действует на математиков, как удав на кролика. Трепетный ужас перед бесконечностью лишает математиков здравого смысла. Вот пример:
Первоисточник находится . Альфа обозначает действительное число. Знак равенства в приведенных выражениях свидетельствует о том, что если к бесконечности прибавить число или бесконечность, ничего не изменится, в результате получится такая же бесконечность. Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:
Для наглядного доказательства своей правоты математики придумали много разных методов . Лично я смотрю на все эти методы, как на пляски шаманов с бубнами. По существу, все они сводятся к тому, что либо часть номеров не занята и в них заселяются новые гости, либо к тому, что часть посетителей вышвыривают в коридор, чтобы освободить место для гостей (очень даже по-человечески).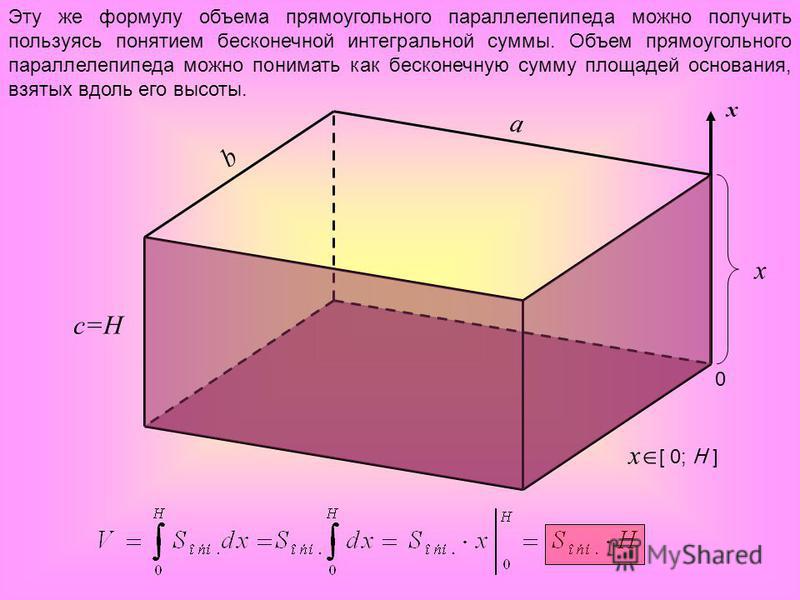 Свой взгляд на подобные решения я изложил в форме фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Переселение бесконечного количества посетителей требует бесконечно много времени. После того, как мы освободили первую комнату для гостя, один из посетителей всегда будет идти по коридору из своего номера в соседний до скончания века. Конечно, фактор времени можно тупо игнорировать, но это уже будет из разряда «дуракам закон не писан». Всё зависит от того, чем мы занимаемся: подгоняем реальность под математические теории или наоборот.
Свой взгляд на подобные решения я изложил в форме фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Переселение бесконечного количества посетителей требует бесконечно много времени. После того, как мы освободили первую комнату для гостя, один из посетителей всегда будет идти по коридору из своего номера в соседний до скончания века. Конечно, фактор времени можно тупо игнорировать, но это уже будет из разряда «дуракам закон не писан». Всё зависит от того, чем мы занимаемся: подгоняем реальность под математические теории или наоборот.
Что же такое «бесконечная гостиница»? Бесконечная гостиница — это гостиница, в которой всегда есть любое количество свободных мест, независимо от того, сколько номеров занято. Если все номера в бесконечном коридоре «для посетителей» заняты, есть другой бесконечный коридор с номерами «для гостей». Таких коридоров будет бесконечное множество. При этом у «бесконечной гостиницы» бесконечное количество этажей в бесконечном количестве корпусов на бесконечном количестве планет в бесконечном количестве вселенных, созданных бесконечным количеством Богов. Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».
Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».
Логику своих рассуждений я вам продемонстрирую на примере бесконечного множества натуральных чисел. Для начала нужно ответить на очень простой вопрос: сколько множеств натуральных чисел существует — одно или много? Правильного ответа на это вопрос не существует, поскольку числа придумали мы сами, в Природе чисел не существует. Да, Природа отлично умеет считать, но для этого она использует другие математические инструменты, не привычные для нас. Как Природа считает, я вам расскажу в другой раз. Поскольку числа придумали мы, то мы сами будем решать, сколько множеств натуральных чисел существует. Рассмотрим оба варианта, как и подобает настоящим ученым.
Вариант первый. «Пусть нам дано» одно-единственное множество натуральных чисел, которое безмятежно лежит на полочке. Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:
Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:
Я записал действия в алгебраической системе обозначений и в системе обозначений, принятой в теории множеств, с детальным перечислением элементов множества. Нижний индекс указывает на то, что множество натуральных чисел у нас одно и единственное. Получается, что множество натуральных чисел останется неизменным только в том случае, если из него вычесть единицу и прибавить эту же единицу.
Вариант второй. У нас на полочке лежит много разных бесконечных множеств натуральных чисел. Подчеркиваю — РАЗНЫХ, не смотря на то, что они практически не отличимы.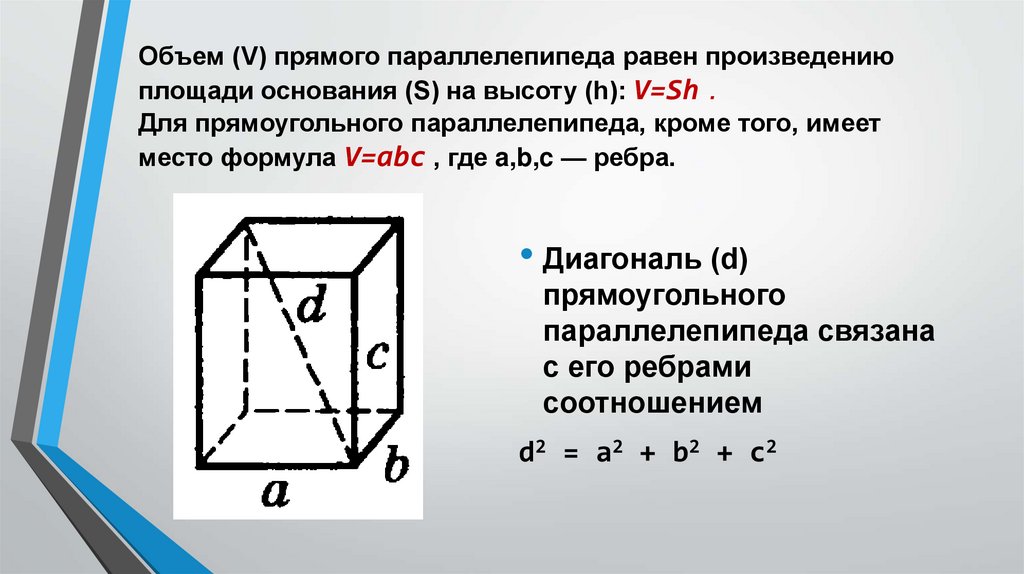 Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:
Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:
Нижние индексы «один» и «два» указывают на то, что эти элементы принадлежали разным множествам. Да, если к бесконечному множеству прибавить единицу, в результате получится тоже бесконечное множество, но оно не будет таким же, как первоначальное множество. Если к одному бесконечному множеству прибавить другое бесконечное множество, в результате получится новое бесконечное множество, состоящее из элементов первых двух множеств.
Множество натуральных чисел используется для счета так же, как линейка для измерений. Теперь представьте, что к линейке вы добавили один сантиметр. Это уже будет другая линейка, не равная первоначальной.
Вы можете принимать или не принимать мои рассуждения — это ваше личное дело. Но если когда-то вы столкнетесь с математическими проблемами, задумайтесь, не идете ли вы по тропе ложных рассуждений, протоптанной поколениями математиков. Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).
Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).
pozg.ru
воскресенье, 4 августа 2019 г.
Дописывал постскриптум к статье о и увидел в Википедии этот замечательный текст:
Читаем: «… богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приемов, лишенных общей системы и доказательной базы.»
Вау! Какие мы умные и как хорошо можем видеть недостатки других. А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:
Богатая теоретическая основа современной математики не имеет целостного характера и сводится к набору разрозненных разделов, лишенных общей системы и доказательной базы.
За подтверждением своих слов я далеко ходить не буду — имеет язык и условные обозначения, отличные от языка и условных обозначений многих других разделов математики.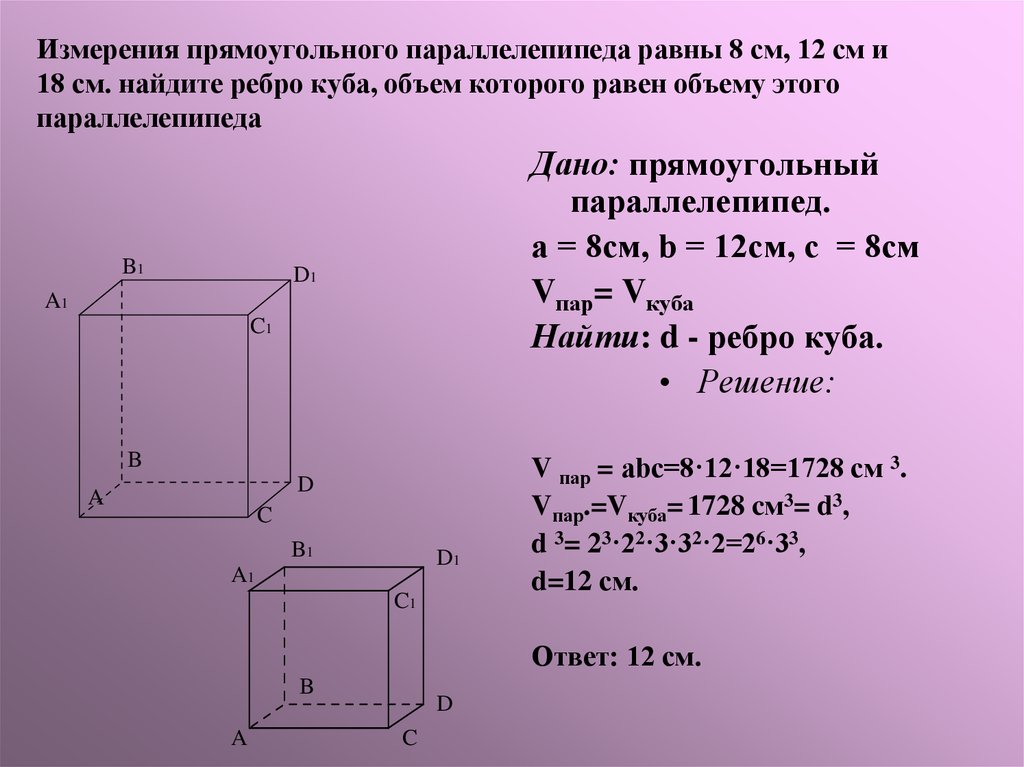 Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.
Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.
суббота, 3 августа 2019 г.
Как разделить множество на подмножества? Для этого необходимо ввести новую единицу измерения, присутствующую у части элементов выбранного множества. Рассмотрим пример.
Пусть у нас есть множество А , состоящее из четырех человек. Сформировано это множество по признаку «люди» Обозначим элементы этого множества через букву а , нижний индекс с цифрой будет указывать на порядковый номер каждого человека в этом множестве. Введем новую единицу измерения «половой признак» и обозначим её буквой b . Поскольку половые признаки присущи всем людям, умножаем каждый элемент множества А на половой признак b . Обратите внимание, что теперь наше множество «люди» превратилось в множество «люди с половыми признаками». После этого мы можем разделить половые признаки на мужские bm и женские bw половые признаки.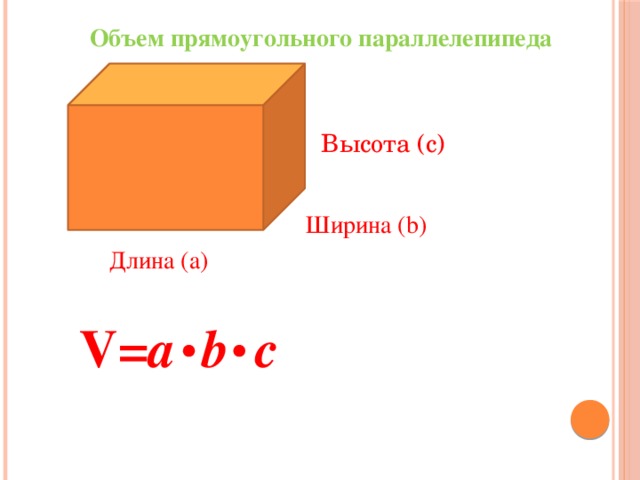 Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
После умножения, сокращений и перегруппировок, мы получили два подмножества: подмножество мужчин Bm и подмножество женщин Bw . Приблизительно так же рассуждают математики, когда применяют теорию множеств на практике. Но в детали они нас не посвящают, а выдают готовый результат — «множество людей состоит из подмножества мужчин и подмножества женщин». Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в изложенных выше преобразованиях? Смею вас заверить, по сути преобразований сделано всё правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики. Что это такое? Как-нибудь в другой раз я вам об этом расскажу.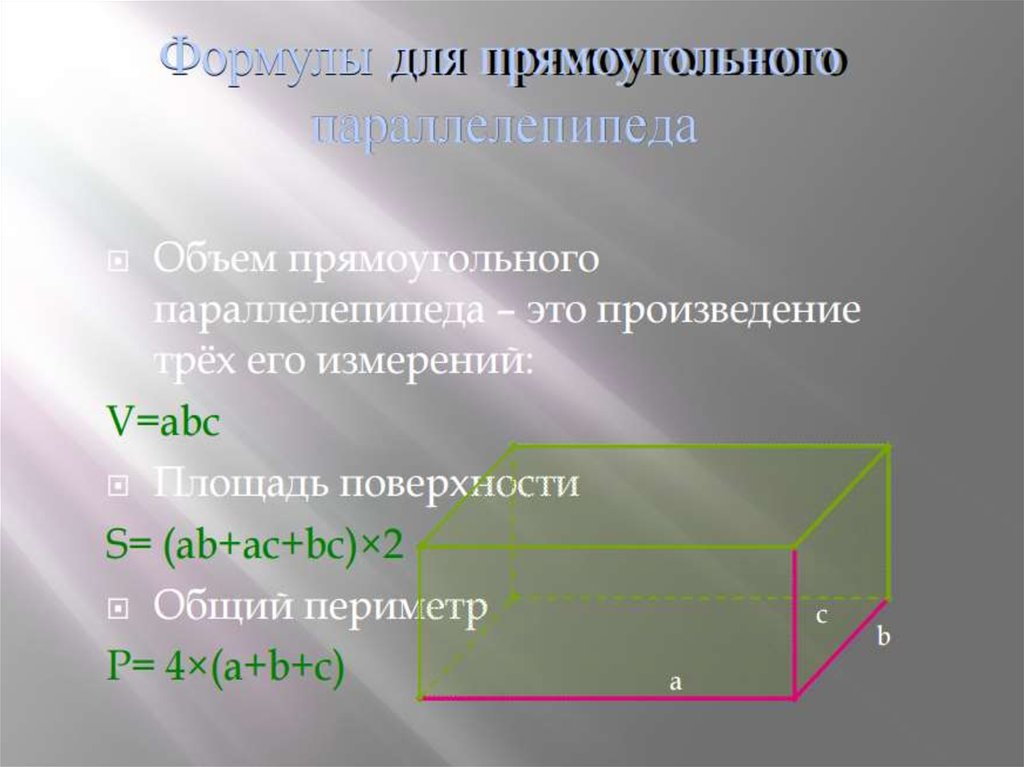
Что касается надмножеств, то объединить два множества в одно надмножество можно, подобрав единицу измерения, присутствующую у элементов этих двух множеств.
Как видите, единицы измерения и обычная математика превращают теорию множеств в пережиток прошлого. Признаком того, что с теорией множеств не всё в порядке, является то, что для теории множеств математики придумали собственный язык и собственные обозначения. Математики поступили так, как когда-то поступали шаманы. Только шаманы знают, как «правильно» применять их «знания». Этим «знаниям» они обучают нас.
В заключение, я хочу показать вам, как математики манипулируют с
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Покажу процесс на примере. Отбираем «красное твердое в пупырышку» — это наше «целое». При этом мы видим, что эти штучки есть с бантиком, а есть без бантика. После этого мы отбираем часть «целого» и формируем множество «с бантиком». Вот так шаманы добывают себе корм, привязывая свою теорию множеств к реальности.
А теперь сделаем маленькую пакость. Возьмем «твердое в пупырышку с бантиком» и объединим эти «целые» по цветовому признаку, отобрав красные элементы. Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.
Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.
Этот простой пример показывает, что теория множеств совершенно бесполезна, когда речь заходит о реальности. В чем секрет? Мы сформировали множество «красное твердое в пупырышку с бантиком». Формирование происходило по четырем разным единицам измерения: цвет (красное), прочность (твердое), шероховатость (в пупырышку), украшения (с бантиком). Только совокупность единиц измерения позволяет адекватно описывать реальные объекты на языке математики . Вот как это выглядит.
Буква «а» с разными индексами обозначает разные единицы измерения. В скобках выделены единицы измерения, по которым выделяется «целое» на предварительном этапе. За скобки вынесена единица измерения, по которой формируется множество. Последняя строчка показывает окончательный результат — элемент множества.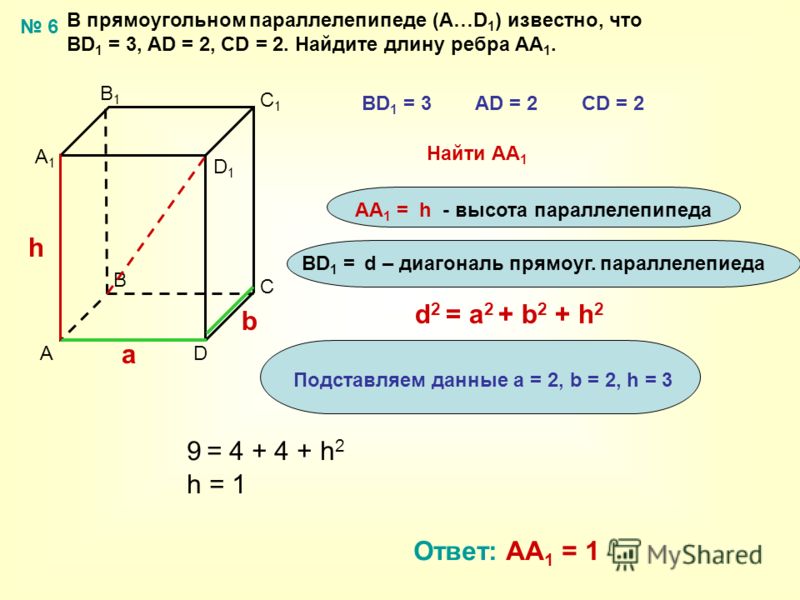 Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
При помощи единиц измерения очень легко разбить одно или объединить несколько множеств в одно надмножество. Давайте более внимательно рассмотрим алгебру этого процесса.
Лемма 1. Объемы прямоугольных параллелепипедов, имеющих равные основания, относятся, как их высоты.
Если прямоугольные параллелепипеды имеют равные основания, то их можно вложить один в другой.
Пусть AG и AP (рис.) два таких параллелепипеда. Рассмотрим два случая.
1. Высоты BF и BN соизмеримы.
Пусть общая мера высот содержится m раз в BF и n раз в BN.
Проведем через точки деления ряд плоскостей, параллельных основанию.
Тогда параллелепипед AG разделится на m, а параллелепипед AP на n равных частей.
Таким образом мы получим:
\(\frac{BF}{BN}=\frac{m}{n}\) и \(\frac{Объем AG}{Объем AP}=\frac{m}{n} \)
Следовательно:
\(\frac{Объем AG}{Объем AP}=\frac{BF}{BN} \)
2. Высоты BF и BN несоизмеримы.
Разделим BN на n равных частей и одну часть отложим на BF столько раз, сколько можно.
Пусть 1/n доля BN содержится в BF более m раз, но менее m+1 раз.
Тогда, проведя попрежнему ряд плоскостей, параллельных основанию, мы разделим пар-д AP на n таких равных частей, каких в пар-де AG содержится более m, но менее m+1.
Следовательно:
прибл.отн. \(\frac{BF}{BN}=\frac{m}{n}\) и прибл.отн. \(\frac{Объем AG}{Объем AP}=\frac{m}{n}\)
Таким образом, приближенные отношения, вычисленные с произвольной, но одинаковой точностью, равны. А в этом и состоит равенство несоизмеримых отношений.
Лемма 2. Объемы прямоугольных параллелепипедов, имеющих равные высоты, относятся как площади их оснований.
Пусть (рис.) P и P 1 два прямоугольных параллелепипеда. Обозначим неравные основания одного из них через a и b, а другого через a 1 и b 1 .
Возьмем вспомогательный прямоугольный параллелепипед Q, у которого высота такая же, как у данных тел, а основанием служит прямоугольник со сторонами a и b 1 .
У параллелепипедов P и Q передние грани равны. Если примем эти грани за основания, то высоты будут b и b 1 , и следовательно:
Объем P/Объем Q = b/b1
У параллелепипедов Q и P 1 боковые грани равны. Если примем эти грани за основания, то высоты будут a и a 1 , и следовательно:
Объем Q/Объем P 1 = a/a1
Перемножив равенства и , найдем:
Объем P/Объем P 1 = ab/a 1 b 1
Так как ab выражает площадь основания пар-да P, а a 1 b 1 — площадь основания пар-да P 1 , то лемма доказана.
Теорема. Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
Пусть (рис.) P есть прямоугольный параллелепипед, а P 1 какая-нибудь кубическая единица.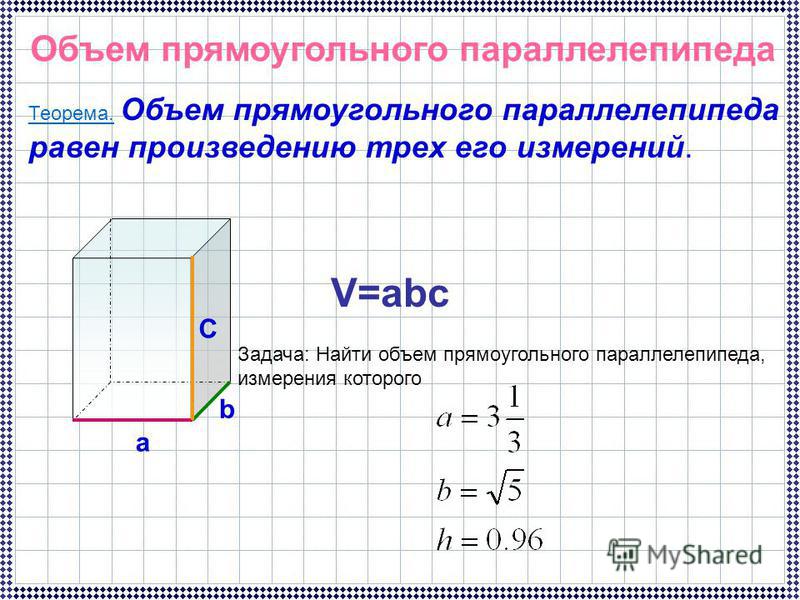
Обозначим площадь основания и высоту первого через B и H, а второго через B 1 и H 1 .
Возьмем вспомогательный прямоугольный параллелепипед Q, у которого площадь основания B 1 , а высота H.
Сравнивая P с Q, а затем Q с P 1 , находим:
Об. P/Об. Q = B/B1 и об. Q/об. P1 = H/h2
Перемножив эти равенства, получим:
Об. P/Об. P1 = B/B1 * H/h2
Отношения, входящие в это равенство есть числа, выражающие объем, площадь основания и высоту данного параллелепипеда в соответствующих кубических, квадратных и линейных единицах. Поэтому последнее равенство можно выразить так:
Число, выражающее объем прямоугольного параллелепипеда, равно произведению чисел, выражающих площадь основания и высоту в соответствующих единицах.
Это выражают сокращенно так: объем прямоугольного параллелепипеда равен произведению площади основания на высоту, т.е.
где под V, B и H разумеются числа, выражающие в соответствующих единицах объем, площадь основания и высоту прямоугольного параллелепипеда.
Обозначая буквами a, b и с три измерения прямоугольного пар-да (выраженные в числах), можем написать:
потому что площадь основания выражается произведением двух из этих измерений, а высота равна третьему измерению.
Следствия:
- Объем куба равен третьей степени его ребра.
- Отношение двух кубических единиц равно третьей степени отношения соответствующих линейных единиц. Так, отношение м3 к дм3 равно 10 3 , т.е. 1000.
Объем любого параллелепипеда
Лемма. Наклонная призма равновелика такой прямой призме, у которой основание равно перпендикулярному сечению наклонной призмы, а высота — ее боковому ребру.
Через какую-нибудь точку a (рис.) одного из боковых ребер наклонной призмы A 1 d проведем перпендикулярное сечение abcde. Затем продолжим все боковые грани вниз, отложим aa 1 =AA 1 и через точку a 1 проведем перпендикулярное сечение a 1 b 1 с 1 d 1 e 1 .
Так как плоскости двух сечений параллельны, то части боковых ребер, заключенные между ними, равны, т. е.
е.
bb 1 = сс 1 = dd 1 = ee 1 = aa 1 = AA 1 .
Вследствие этого многогранник a 1 d есть прямая призма, у которой основанием служит перпендикулярное сечение, а высота (или, что то же самое, боковое ребро) равна боковому ребру наклонной призмы.
Докажем, что наклонная призма равновелика прямой призме.
Для этого предварительно убедимся, что многогранники aD и a 1 D 1 равны.
Основания их abcde и a 1 b 1 с 1 d 1 e 1 равны, как основания призмы a 1 d.
С другой стороны, отняв от обеих частей равенства A 1 A = a 1 a по одной и той же прямой A 1 a , получим aA = a 1 A 1 .
Подобно этому: bB = b 1 B 1 , сС = с 1 С 1 и т.д.
Вообразим теперь, что многогранник aD вложен в a 1 D 1 так, чтобы основания их совпали. Тогда боковые ребра, будучи перпендикулярны к основаниям и соответственно равны, также совпадут.
Поэтому многогранник aD совместится с a 1 D 1 . Значит, эти тела равны.
Теперь заметим, что если от целого многогранника a 1 D , отнимем часть aD , то получим прямую призму.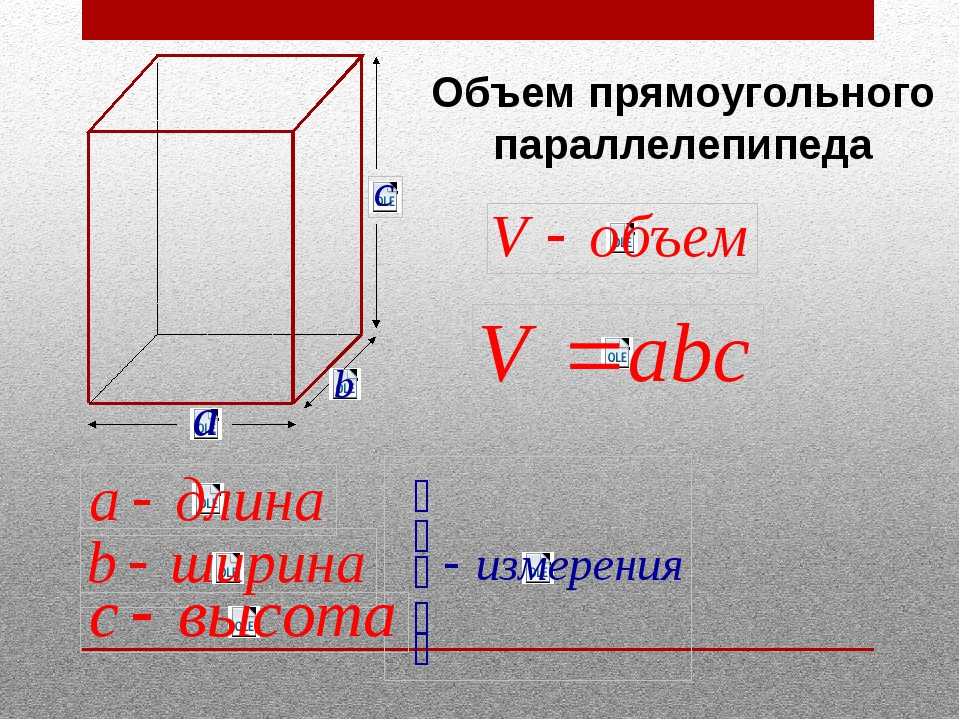 А если от того же многогранника отнимем часть a 1 D 1 , то получим наклонную призму.
А если от того же многогранника отнимем часть a 1 D 1 , то получим наклонную призму.
Из этого следует, что эти две призмы равновелики, так как объемы их представляют собой разности объемов равных тел.
Теорема. Объем параллелепипеда равен произведению площади основания на высоту.
Ранее мы доказали эту теорему для параллелепипеда прямоугольного, теперь докажем ее для параллелепипеда прямого, а потом наклонного.
1. Пусть (рис.) AC 1 прямой пар-д, т.е. такой, у которого основание ABCD какой-нибудь параллелограмм, а все боковые грани — прямоугольники.
Возьмем в нем за основание грань AA 1 B 1 B. Тогда параллелепипед будет наклонный.
Рассматривая его, как частный случай наклонной призмы, мы, на основании леммы предыдущего параграфа, можем утверждать, что этот пар-д равновелик такому прямому, у которого основание есть перпендикулярное сечение MNPQ, а высота BC.
Четырехугольник MNPQ есть прямоугольник, потому что его углы служат линейными углами прямых двугранных углов. Поэтому прямой параллелепипед, имеющий это основание должен быть прямоугольным, и, следовательно, его объем равен произведению площади основания MNPQ на высоту BC.
Поэтому прямой параллелепипед, имеющий это основание должен быть прямоугольным, и, следовательно, его объем равен произведению площади основания MNPQ на высоту BC.
Но площадь MNPQ равна MN * MQ. Значит:
Объем AC1 = MN * MQ * BC
Произведение MQ * BC выражает площадь параллелограмма ABCD. Поэтому:
Объем AC 1 = (площ.ABCD) * MN
2. Пусть (рис.) AC 1 есть пар-д наклонный. Он равновелик такому прямому, у которого основанием служит перпендикулярное сечение MNPQ, а высотой ребро BC.
Но, по доказанному, объем прямого параллелепипеда равен произведению площади основания на высоту. Значит:
Объем AC 1 = (площ.MNPQ) * BC
Если RS есть высота сечения MNPQ, то площадь MNPQ = MQ * RS. Поэтому:
Объем AC1 = MQ * RS * BC
Произведение BC * MQ выражает площадь параллелограмма ABCD. Следовательно:
Объем AC 1 = (площ.ABCD) * RS
Т.е. объем всякого параллелепипеда равен произведению площади основания на высоту .
Следствие. Если V, B и H — числа, выражающие в соответствующих единицах объем, площадь основания и высоту какого — нибудь паралллелепипеда, то можем написать:
Если V, B и H — числа, выражающие в соответствующих единицах объем, площадь основания и высоту какого — нибудь паралллелепипеда, то можем написать:
Задача. Основанием прямого параллелепипеда является ромб, площадь которого равна S. Площади диагональных сечений равны S 1 и S 2 . Найти объем параллелепипеда.
Для нахождения объема параллелепипеда нужно найти его высоту Н (рис. 242).
Обозначим длины диагоналей основания через d 1 и d 2 . Тогда
d 1 H = S 1 , d 2 H = S 2 , d 1 d 2 = 2S.
Из этих уравнений находим
$$ \frac{S_1}{H}\cdot \frac{S_2}{H} = 2S, \;\; H=\sqrt{\frac{S_1 S_2}{2S}} $$
Следовательно,
$$ V=S\cdot H = S\sqrt{\frac{S_1 S_2}{2S}}=\sqrt{\frac{S\cdot S_1\cdot S_2}{2}} $$
Призма называется параллелепипедом , если её основания — параллелограммы. См.Рис.1 .
Свойства параллелепипеда:
Противоположные грани параллелепипеда параллельны (т. е. лежат в параллельных плоскостях) и равны.
е. лежат в параллельных плоскостях) и равны.
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Смежные грани параллелепипеда – две грани, имеющие общее ребро.
Противоположные грани параллелепипеда – грани, не имеющих общих рёбер.
Противоположные вершины параллелепипеда – две вершины, не принадлежащие одной грани.
Диагональ параллелепипеда – отрезок, который соединяет противоположные вершины.
Если боковые ребра перпендикулярны плоскостям оснований, то параллелепипед называется прямым .
Прямой параллелепипед, основания которого – прямоугольники, называется прямоугольным . Призма, все грани которой — квадраты, называется кубом .
Параллелепипед – призма, у которой основаниями служат параллелограммы.
Прямой параллелепипед – параллелепипед, у которого боковые ребра перпендикулярны плоскости основания.
Прямоугольный параллелепипед – это прямой параллелепипед, основаниями которого являются прямоугольники.
Куб – прямоугольный параллелепипед с равными ребрами.
Параллелепипедом называется призма, основание которой – параллелограмм; таким образом, параллелепипед имеет шесть граней и все они — параллелограммы.
Противоположные грани попарно равны и параллельны. Параллелепипед имеет четыре диагонали; все они пересекаются в одной точке и делятся в ней пополам. За основание может быть принята любая грань; объем равен произведению площади основания на высоту: V = Sh.
Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым.
Прямой параллелепипед, у которого все шесть граней — прямоугольники, называется прямоугольным. См.Рис.2 .
Объем (V) прямого параллелепипеда равен произведению площади основания (S) на высоту (h): V = Sh .
Для прямоугольного параллелепипеда, кроме того, имеет место формула V=abc , где a,b,c — ребра.
Диагональ (d) прямоугольного параллелепипеда связана с его ребрами соотношением d 2 = а 2 + b 2 + c 2 .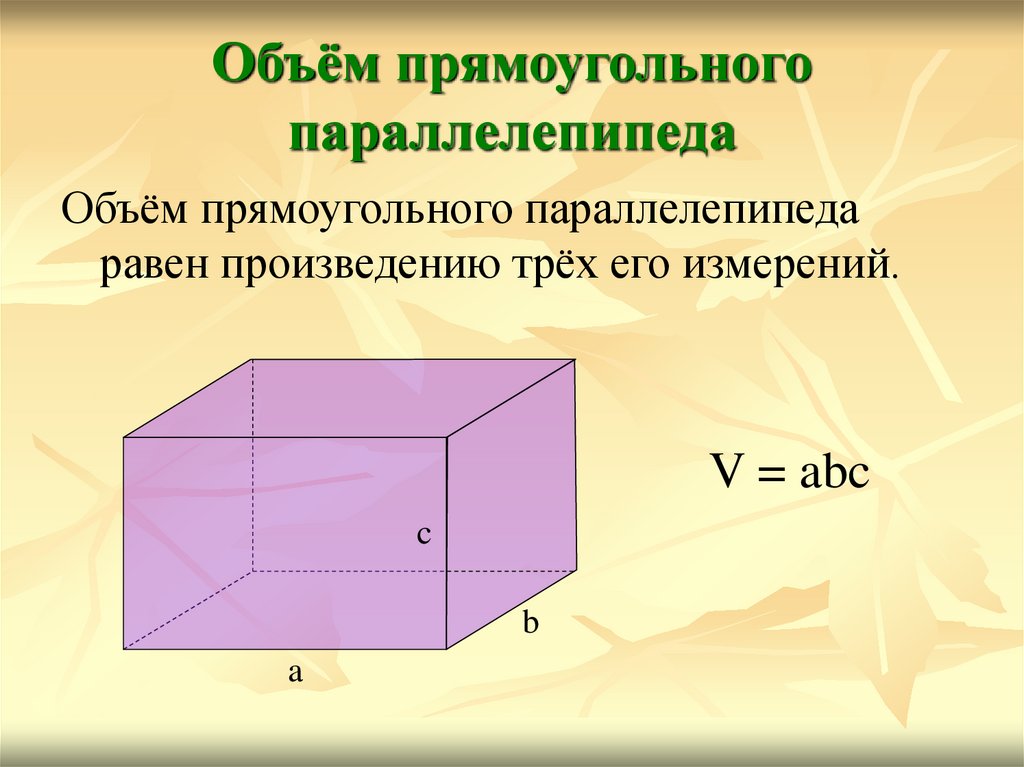
Прямоугольный параллелепипед – параллелепипед, у которого боковые рёбра перпендикулярны основаниям, а основания прямоугольниками.
Свойства прямоугольного параллелепипеда:
В прямоугольном параллелепипеде все шесть граней – прямоугольники.
Все двугранные углы прямоугольного параллелепипеда прямые.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений (длин трёх рёбер, имеющих общую вершину).
Диагонали прямоугольного параллелепипеда равны.
Прямоугольный параллелепипед, все грани которого — квадраты, называется кубом. Все ребра куба равны; объем (V) куба выражается формулой V=a 3 , где a — ребро куба.
В данном уроке мы поговорим о прямоугольном параллелепипеде. Вспомним
некоторые из его свойств. А затем подробно выведем формулы для вычисления
объема прямоугольного параллелепипеда.
Конспект урока «Объем прямоугольного параллелепипеда»
На этом уроке мы поговорим о прямоугольном параллелепипеде. Вспомним
некоторые из его свойств. А затем подробно выведем формулы для вычисления
объёма прямоугольного параллелепипеда.
Ранее мы с вами уже познакомились с прямоугольным параллелепипедом.
Напомним, что параллелепипед называетсяпрямоугольным, если все его шесть
граней прямоугольники.
Представление о форме прямоугольного параллелепипеда дают спичечный
коробок, коробка, холодильник и др.
Давайте представим себе, комнату, которая имеет форму прямоугольного
параллелепипеда. Если говорить о её размерах, то обычно употребляют слова «длина», «ширина» и
«высота», имея в виду длины трех рёбер с общей вершиной. В геометрии эти три
величины объединяются общим названием: измерения прямоугольного
параллелепипеда.
На экране изображён прямоугольный параллелепипед
качестве его измерений можно взять,например, длины рёбер
эти рёбра имеют общую вершину
параллелепипеда,
– ширина и
Прямоугольный параллелепипед обладает следующими свойствами:
1) квадрат диагонали прямоугольного параллелепипеда равен сумме
квадратов трёх его измерений.
Вспомним
некоторые из его свойств. А затем подробно выведем формулы для вычисления
объёма прямоугольного параллелепипеда.
Ранее мы с вами уже познакомились с прямоугольным параллелепипедом.
Напомним, что параллелепипед называетсяпрямоугольным, если все его шесть
граней прямоугольники.
Представление о форме прямоугольного параллелепипеда дают спичечный
коробок, коробка, холодильник и др.
Давайте представим себе, комнату, которая имеет форму прямоугольного
параллелепипеда. Если говорить о её размерах, то обычно употребляют слова «длина», «ширина» и
«высота», имея в виду длины трех рёбер с общей вершиной. В геометрии эти три
величины объединяются общим названием: измерения прямоугольного
параллелепипеда.
На экране изображён прямоугольный параллелепипед
качестве его измерений можно взять,например, длины рёбер
эти рёбра имеют общую вершину
параллелепипеда,
– ширина и
Прямоугольный параллелепипед обладает следующими свойствами:
1) квадрат диагонали прямоугольного параллелепипеда равен сумме
квадратов трёх его измерений. – это есть длина данного. Тогда ребро
– его высота.
. В
и, все 2) объём прямоугольного параллелепипеда равен произведению трёх его
измерений.
Итак, справедлива следующая теорема: объём прямоугольного параллелепипеда
равен произведению трёх его измерений.
Докажем эту теорему. Пусть дан прямоугольный параллелепипед
его измерения буквами
Докажем, что объём прямоугольного параллелепипеда равен, а его объём буквой. Обозначим
и.
,
.
Возможны два случая:
Рассмотрим первый случай. Измерения
десятичные дроби, у которых число знаков после запятой не превосходит
представляют собой конечные
и
(,).
В этом случае числа,
и
являются целыми.
Разделим каждое ребро параллелепипеда на равные части длины. Затем
через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Тогда наш параллелепипед
разобьётся на равные кубы с длиной каждого
ребра. Общее же количество таких кубов будет равно.
Так как объём каждого такого куба равен, то объём всего
параллелепипеда
будет равен.
Этим мы доказали, что объём прямоугольного параллелепипеда равен
произведению трёх его измерений.
– это есть длина данного. Тогда ребро
– его высота.
. В
и, все 2) объём прямоугольного параллелепипеда равен произведению трёх его
измерений.
Итак, справедлива следующая теорема: объём прямоугольного параллелепипеда
равен произведению трёх его измерений.
Докажем эту теорему. Пусть дан прямоугольный параллелепипед
его измерения буквами
Докажем, что объём прямоугольного параллелепипеда равен, а его объём буквой. Обозначим
и.
,
.
Возможны два случая:
Рассмотрим первый случай. Измерения
десятичные дроби, у которых число знаков после запятой не превосходит
представляют собой конечные
и
(,).
В этом случае числа,
и
являются целыми.
Разделим каждое ребро параллелепипеда на равные части длины. Затем
через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Тогда наш параллелепипед
разобьётся на равные кубы с длиной каждого
ребра. Общее же количество таких кубов будет равно.
Так как объём каждого такого куба равен, то объём всего
параллелепипеда
будет равен.
Этим мы доказали, что объём прямоугольного параллелепипеда равен
произведению трёх его измерений.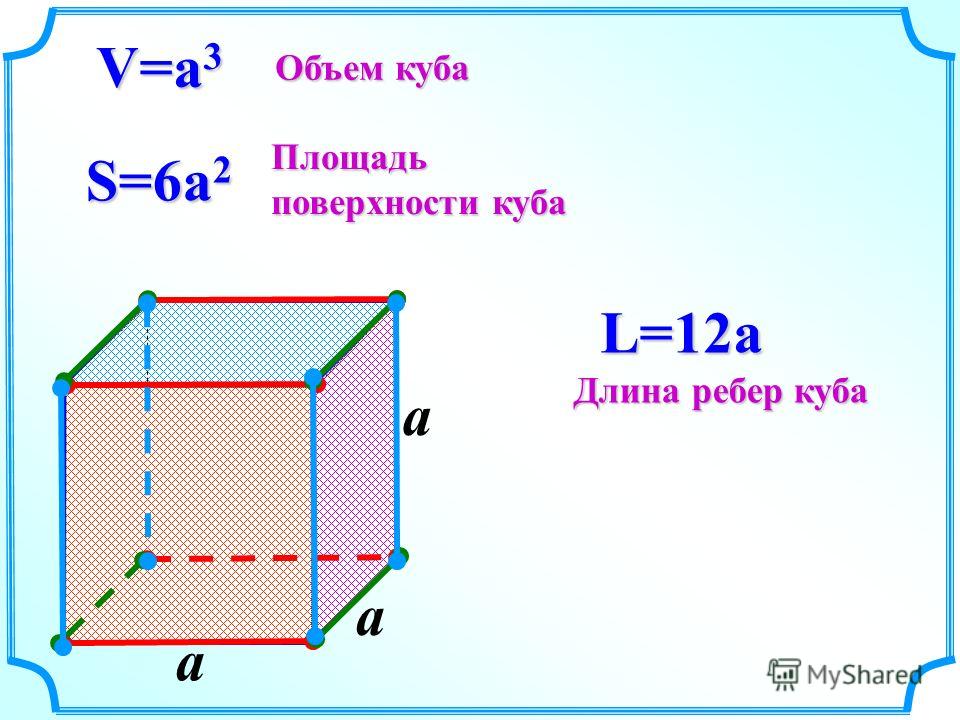 Что и требовалось доказать.
Перейдём ко второму случаю. Хотя бы одно из измерений
собой бесконечную десятичную дробь.
,
и
представляет
Рассмотрим конечные десятичные дроби
чисел
с,
-ой.
, которые получаются из, если отбросить в каждом из них все цифры после запятой, начиная
Заметим, что тогда справедливо неравенство
Аналогичные неравенства будут выполняться и для чисел, где
и:
.
, где,
.
Перемножим эти неравенства. Тогда видим, что. Из неравенства понятно, что параллелепипед
параллелепипед, а сам содержится в параллелепипеде
содержит в себе.
А это говорит о том, что.
Теперь давайте будем неограниченно увеличивать
становиться сколь угодно малым, и поэтому число
мало отличаться от числа.
. Тогда число
будет
будет сколь угодно
В итоге, они станут равны. Т.е.
. Что и требовалось доказать.
Из этой теоремы справедливы следующие следствия.
Первое следствие. Объём прямоугольного параллелепипеда равен
произведению площади основания на высоту.
Доказательство. Пусть грань с рёбрами
прямоугольного параллелепипеда.
Что и требовалось доказать.
Перейдём ко второму случаю. Хотя бы одно из измерений
собой бесконечную десятичную дробь.
,
и
представляет
Рассмотрим конечные десятичные дроби
чисел
с,
-ой.
, которые получаются из, если отбросить в каждом из них все цифры после запятой, начиная
Заметим, что тогда справедливо неравенство
Аналогичные неравенства будут выполняться и для чисел, где
и:
.
, где,
.
Перемножим эти неравенства. Тогда видим, что. Из неравенства понятно, что параллелепипед
параллелепипед, а сам содержится в параллелепипеде
содержит в себе.
А это говорит о том, что.
Теперь давайте будем неограниченно увеличивать
становиться сколь угодно малым, и поэтому число
мало отличаться от числа.
. Тогда число
будет
будет сколь угодно
В итоге, они станут равны. Т.е.
. Что и требовалось доказать.
Из этой теоремы справедливы следующие следствия.
Первое следствие. Объём прямоугольного параллелепипеда равен
произведению площади основания на высоту.
Доказательство. Пусть грань с рёбрами
прямоугольного параллелепипеда. Тогда площадь основания
высота параллелепипеда
и.
является основанием, а Тогда можно заметить, что формулу для вычисления объёма прямоугольного
параллелепипеда
–
площадь основания,
– высота прямоугольного параллелепипеда.
можно записать в виде, где
Таким образом, мы доказали, что объём прямоугольного параллелепипеда
равен. Что и требовалось доказать.
Второе следствие. Объём прямой призмы, основанием которой является
прямоугольный треугольник, равен произведению площади основания на высоту.
Доказательство. Для доказательства этого утверждения достроим прямую
треугольную призму с основанием
параллелепипеда так, как показано на экране.
Учитывая первое следствие, объём этого параллелепипеда равен
где
– площадь основания) до прямоугольного
(,
– высота призмы.
,
разбивает параллелепипед на две равные прямые призмы, одна
Плоскость
из которых – данная. Эти призмы равны, так как имеют равные основания и
равные высоты.
Следовательно, объём
данной призмы равен, т.е.
равен
доказать.
Замечание.
Тогда площадь основания
высота параллелепипеда
и.
является основанием, а Тогда можно заметить, что формулу для вычисления объёма прямоугольного
параллелепипеда
–
площадь основания,
– высота прямоугольного параллелепипеда.
можно записать в виде, где
Таким образом, мы доказали, что объём прямоугольного параллелепипеда
равен. Что и требовалось доказать.
Второе следствие. Объём прямой призмы, основанием которой является
прямоугольный треугольник, равен произведению площади основания на высоту.
Доказательство. Для доказательства этого утверждения достроим прямую
треугольную призму с основанием
параллелепипеда так, как показано на экране.
Учитывая первое следствие, объём этого параллелепипеда равен
где
– площадь основания) до прямоугольного
(,
– высота призмы.
,
разбивает параллелепипед на две равные прямые призмы, одна
Плоскость
из которых – данная. Эти призмы равны, так как имеют равные основания и
равные высоты.
Следовательно, объём
данной призмы равен, т.е.
равен
доказать.
Замечание.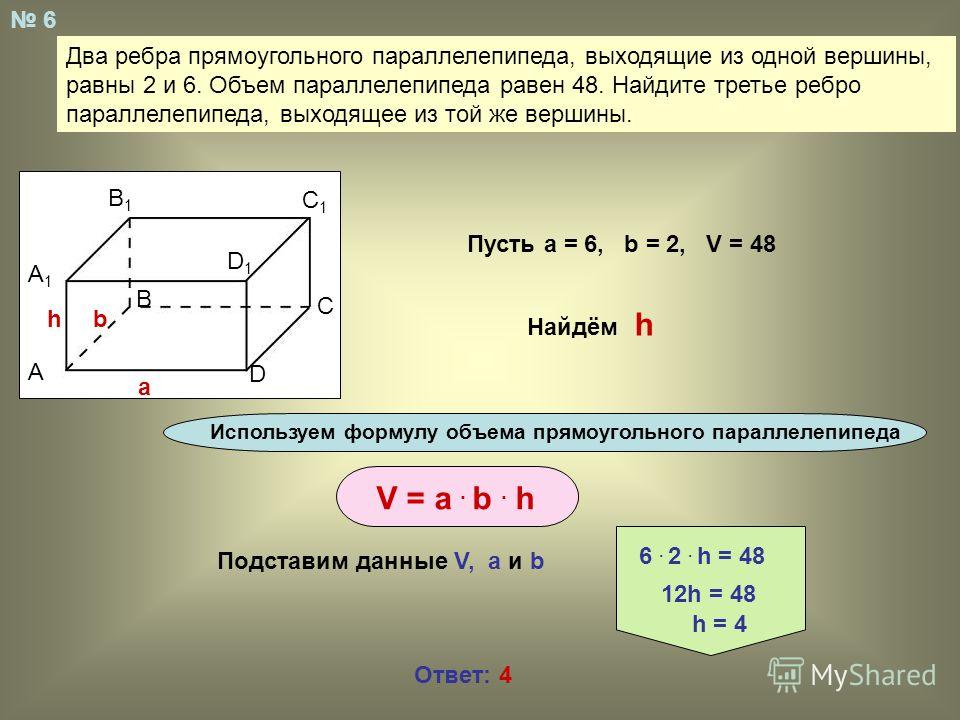 Рассмотрим квадрат со стороной а.
. Что и требовалось Исходя из теоремы Пифагора его диагональ равна. Поэтому площадь
построенного на ней квадрата вдвое больше площади данного квадрата. Таким
образом, не составляет труда построить сторону квадрата, площадь которого
вдвое больше площади данного квадрата.
Рассмотрим теперь куб со стороной а.
Возникает вопрос: можно ли с помощью циркуля и линейки построить сторону
куба, объём которого вдвое больше объёма данного куба, т.е. построить отрезок,
равный?
Эта задача была сформулирована ещё в глубокой древности. Она получила
название «задача об удвоении куба». Лишь в 1837 году французский математик
Пьер Лоран Ванцель доказал, что такое построение невозможно. Одновременно
им была доказана неразрешимость ещё одной задачи на построение – задачи о
трисекции угла (произвольный данный угол разделить на три равных угла).
Напомним, что к числу классических неразрешимых задач на построение
относится также задача о квадратуре круга (построить квадрат, площадь
которого равна площади данного круга).
Рассмотрим квадрат со стороной а.
. Что и требовалось Исходя из теоремы Пифагора его диагональ равна. Поэтому площадь
построенного на ней квадрата вдвое больше площади данного квадрата. Таким
образом, не составляет труда построить сторону квадрата, площадь которого
вдвое больше площади данного квадрата.
Рассмотрим теперь куб со стороной а.
Возникает вопрос: можно ли с помощью циркуля и линейки построить сторону
куба, объём которого вдвое больше объёма данного куба, т.е. построить отрезок,
равный?
Эта задача была сформулирована ещё в глубокой древности. Она получила
название «задача об удвоении куба». Лишь в 1837 году французский математик
Пьер Лоран Ванцель доказал, что такое построение невозможно. Одновременно
им была доказана неразрешимость ещё одной задачи на построение – задачи о
трисекции угла (произвольный данный угол разделить на три равных угла).
Напомним, что к числу классических неразрешимых задач на построение
относится также задача о квадратуре круга (построить квадрат, площадь
которого равна площади данного круга).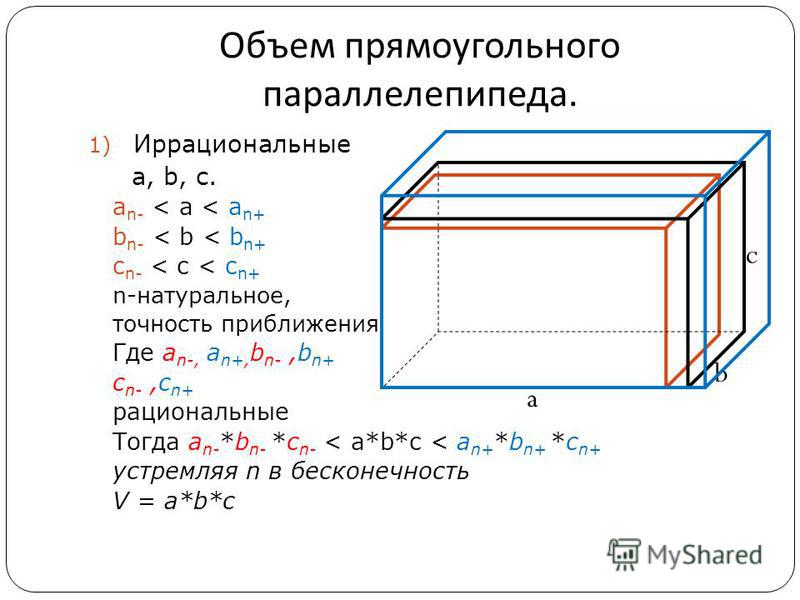 Невозможность такого построения была
доказана в 1882 году немецким математиком Карлом Луизом Фердинандом
Линдеманом. Задача: найдите объём прямоугольного параллелепипеда с диагональю
сторонами основания
Решение: запишем формулу для вычисления объёма прямоугольного
параллелепипеда через его измерения.
см и
см.
см и
Из условия задачи нам известны длина, ширина и диагональ прямоугольного
параллелепипеда, но неизвестна его высота. Напомним, что.
Выразим из этой формулы высоту
что высота равна
(см).
прямоугольного параллелепипеда. Получим,
и равна
Подставим измерения нашего прямоугольного параллелепипеда в формулу
объёма. Посчитаем. Получим, что объем параллелепипеда
равен
Не забудем записать ответ.
(см3).
Задача:
квадрат. Объем прямоугольного параллелепипеда равен
высоту прямоугольного параллелепипеда, если
прямоугольный параллелепипед, основание
–
см3. Определите
см. Решение: на этом уроке мы доказали, что объём прямоугольного
параллелепипеда равен. Выразим из формулы высоту. Отсюда,
высота равна.
Невозможность такого построения была
доказана в 1882 году немецким математиком Карлом Луизом Фердинандом
Линдеманом. Задача: найдите объём прямоугольного параллелепипеда с диагональю
сторонами основания
Решение: запишем формулу для вычисления объёма прямоугольного
параллелепипеда через его измерения.
см и
см.
см и
Из условия задачи нам известны длина, ширина и диагональ прямоугольного
параллелепипеда, но неизвестна его высота. Напомним, что.
Выразим из этой формулы высоту
что высота равна
(см).
прямоугольного параллелепипеда. Получим,
и равна
Подставим измерения нашего прямоугольного параллелепипеда в формулу
объёма. Посчитаем. Получим, что объем параллелепипеда
равен
Не забудем записать ответ.
(см3).
Задача:
квадрат. Объем прямоугольного параллелепипеда равен
высоту прямоугольного параллелепипеда, если
прямоугольный параллелепипед, основание
–
см3. Определите
см. Решение: на этом уроке мы доказали, что объём прямоугольного
параллелепипеда равен. Выразим из формулы высоту. Отсюда,
высота равна.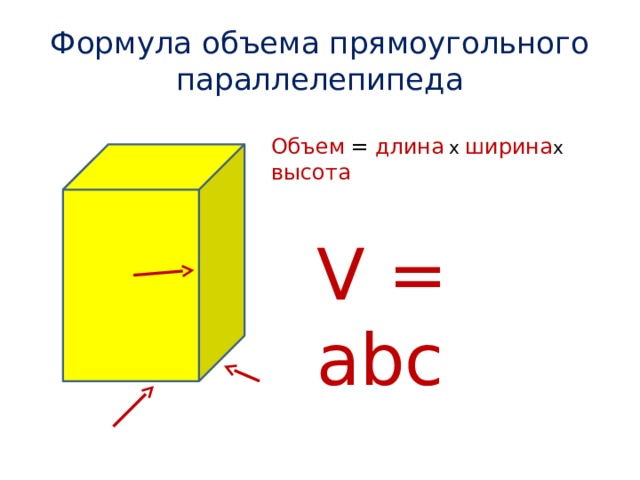 Так как в основании нашего прямоугольного
параллелепипеда лежит квадрат по условию, то площадь основания
равна
объём прямоугольного параллелепипеда равен
(см2). По условию задачи, также известно, что. Отсюда, высота
(см). Запишем ответ.
равна
Итоги:
На этом уроке мы вспомнили понятие прямоугольного параллелепипеда.
Доказали, что объём прямоугольного параллелепипеда равен произведению трёх
его измерений. Доказали, что объём прямоугольного параллелепипеда можно
вычислить как произведение площади основания на высоту. А также доказали,
что объём прямой призмы, основанием которой является прямоугольный
треугольник, равен произведению площади основания на высоту.
Так как в основании нашего прямоугольного
параллелепипеда лежит квадрат по условию, то площадь основания
равна
объём прямоугольного параллелепипеда равен
(см2). По условию задачи, также известно, что. Отсюда, высота
(см). Запишем ответ.
равна
Итоги:
На этом уроке мы вспомнили понятие прямоугольного параллелепипеда.
Доказали, что объём прямоугольного параллелепипеда равен произведению трёх
его измерений. Доказали, что объём прямоугольного параллелепипеда можно
вычислить как произведение площади основания на высоту. А также доказали,
что объём прямой призмы, основанием которой является прямоугольный
треугольник, равен произведению площади основания на высоту.
| Прямой параллелепипед – это параллелепипед с ребром, перпендикулярным плоскости основания. | ||
| Геометрические фигуры. Прямой параллелепипед. | ||
| Призма — многогранник, 2 грани это конгруэнтные (равные) многоугольники, которые лежат в параллельных плоскостях, а оставшиеся грани — параллелограммы, имеющие общие стороны с этими многоугольниками. | ||
| Геометрические фигуры. Призма. Объем призмы. | ||
| V = | 1 | So · h |
| 3 |
где V – объем пирамиды,
So – площадь основания пирамиды,
h – длина высоты пирамиды.
Онлайн калькулятор для расчета объема пирамиды
Формулы площади геометрических фигур для определения площади основания пирамиды
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.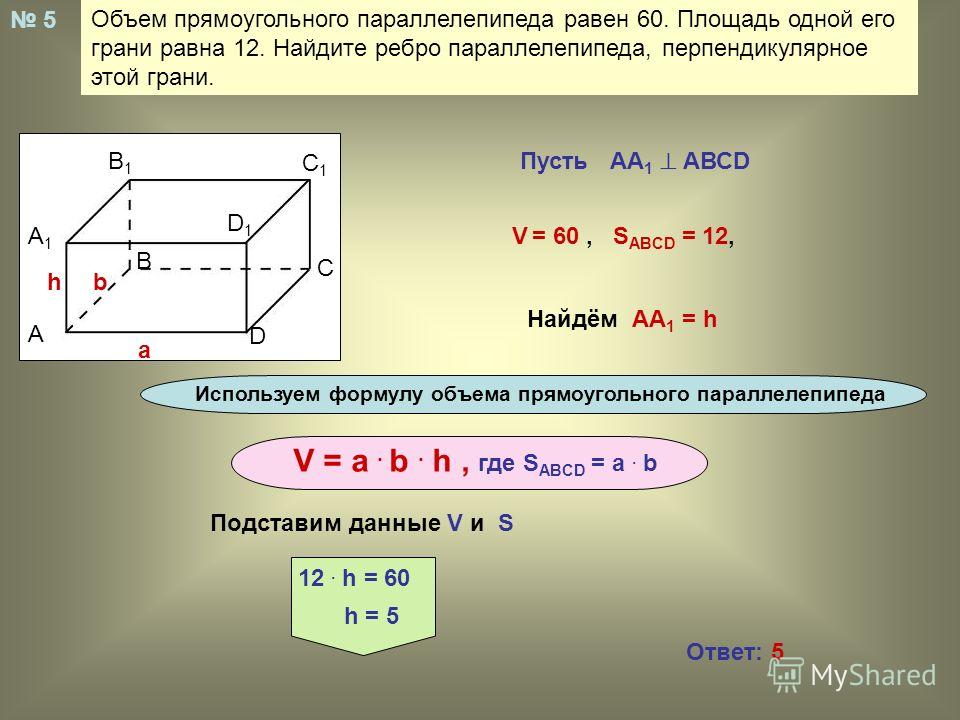
Формула объема призмы:
V = So h
где V – объем призмы,
So – площадь основания призмы,
h – высота призмы.
Онлайн калькулятор для расчета объема призмы
Формулы площади геометрических фигур для определения площади основания призмы
Сложности запоминания
Бывают случаи, когда слово параллелепипед путают со словом параллелограмм.
И, действительно, эти слова созвучны.
В чем же отличие параллелепипеда от параллелограмма?
Параллелогра́мм — это четырехугольник, у которого противоположные стороны параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб
Параллелограмм – плоская фигура.
Параллелепипед – объёмное тело, все грани которого – параллелограммы.
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Шутка:
“Иногда, нерадивые ученики пытаются посчитать сколько грамм в параллелограмме и сколько параллельных пипедов в параллелепипеде!”
Свойства параллелепипеда.
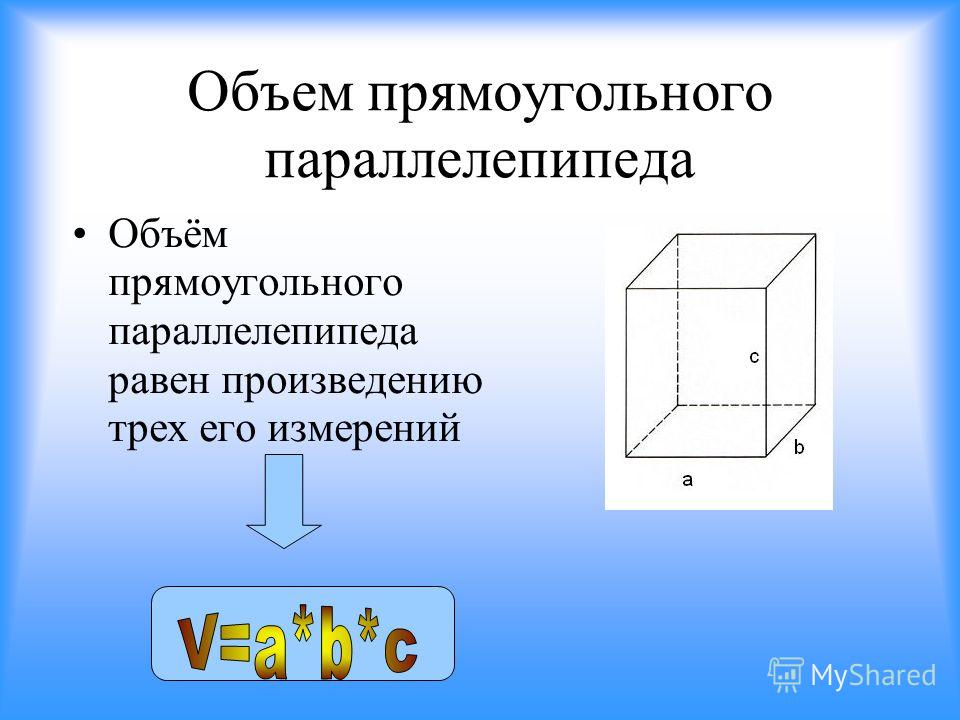
- Параллелепипед симметричен относительно середины его диагонали.
- Всякий отрезок с концами, которые принадлежат поверхности параллелепипеда и который проходит через середину его диагонали, делится ею на две равные части. Все диагонали параллелепипеда пересекаются в 1-ой точке и делятся ею на две равные части.
- Противоположные грани параллелепипеда параллельны и имеют равные размеры.
- Квадрат длины диагонали прямоугольного параллелепипеда равняется сумме квадратов 3-х его измерений.
В параллелепипед вписывают тетраэдр. Объем этого тетраэдра будет равняться третьей части объема параллелепипеда.
Геометрические фигуры. Наклонный параллелепипед. Объем наклонного параллелепипеда.

Источники
- https://elhow.ru/ucheba/geometrija/stereometrija/kak-najti-vysotu-parallelepipeda
- https://www.calc.ru/Geometricheskiye-Figury-Parallelepiped.html
- https://www.calc.ru/Geometricheskiye-Figury-Pryamougolniy-Parallelepiped.html
- https://ru.onlinemschool.com/math/formula/volume/
- https://mnogogranniki.ru/parallelepiped.html
- https://mnogoformul.ru/obem-parallelepipeda
- https://karate-ege.ru/matematika/obem-parallelepipeda.html
- https://planetcalc.ru/131/
- https://obrazovaka.ru/matematika/obem-pryamougolnika-formula.html
Объем параллелепипеда
Объем прямоугольного параллелепипеда
Лемма 1. Объемы прямоугольных параллелепипедов, имеющих равные основания, относятся, как их высоты.
Если прямоугольные параллелепипеды имеют равные основания, то их можно вложить один в другой.
Пусть AG и AP (рис. ) два таких параллелепипеда. Рассмотрим два случая.
) два таких параллелепипеда. Рассмотрим два случая.
1. Высоты BF и BN соизмеримы.
Пусть общая мера высот содержится m раз в BF и n раз в BN.
Проведем через точки деления ряд плоскостей, параллельных основанию.
Тогда параллелепипед AG разделится на m, а параллелепипед AP на n равных частей.
Таким образом мы получим:
\(\frac{BF}{BN}=\frac{m}{n}\) и \( \frac{Объем AG}{Объем AP}=\frac{m}{n} \)
Следовательно:
\( \frac{Объем AG}{Объем AP}=\frac{BF}{BN} \)
2. Высоты BF и BN несоизмеримы.
Разделим BN на n равных частей и одну часть отложим на BF столько раз, сколько можно.
Пусть 1/n доля BN содержится в BF более m раз, но менее m+1 раз.
Тогда, проведя попрежнему ряд плоскостей, параллельных основанию, мы разделим пар-д AP на n таких равных частей, каких в пар-де AG содержится более m, но менее m+1.
Следовательно:
прибл.отн. \(\frac{BF}{BN}=\frac{m}{n}\) и прибл.отн. \(\frac{Объем AG}{Объем AP}=\frac{m}{n}\)
Таким образом, приближенные отношения, вычисленные с произвольной, но одинаковой точностью, равны. А в этом и состоит равенство несоизмеримых отношений.
А в этом и состоит равенство несоизмеримых отношений.
Лемма 2. Объемы прямоугольных параллелепипедов, имеющих равные высоты, относятся как площади их оснований.
Пусть (рис.) P и P1 два прямоугольных параллелепипеда. Обозначим неравные основания одного из них через a и b, а другого через a1 и b1.
Возьмем вспомогательный прямоугольный параллелепипед Q, у которого высота такая же, как у данных тел, а основанием служит прямоугольник со сторонами a и b1.
У параллелепипедов P и Q передние грани равны. Если примем эти грани за основания, то высоты будут b и b1, и следовательно:
Объем P/Объем Q = b/b1 [1]
У параллелепипедов Q и P1 боковые грани равны. Если примем эти грани за основания, то высоты будут a и a1, и следовательно:
Объем Q/Объем P1 = a/a1 [2]
Перемножив равенства [1] и [2], найдем:
Объем P/Объем P1 = ab/a1b1
Так как ab выражает площадь основания пар-да P, а a1b1 — площадь основания пар-да P1, то лемма доказана.
Теорема. Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
Пусть (рис.) P есть прямоугольный параллелепипед, а P1 какая-нибудь кубическая единица.
Обозначим площадь основания и высоту первого через B и H, а второго через B1 и H1.
Возьмем вспомогательный прямоугольный параллелепипед Q, у которого площадь основания B1, а высота H.
Сравнивая P с Q, а затем Q с P1, находим:
Об. P/Об. Q = B/B1 и об. Q/об. P1 = H/h2
Перемножив эти равенства, получим:
Об. P/Об. P1 = B/B1 * H/h2
Отношения, входящие в это равенство есть числа, выражающие объем, площадь основания и высоту данного параллелепипеда в соответствующих кубических, квадратных и линейных единицах. Поэтому последнее равенство можно выразить так:
Число, выражающее объем прямоугольного параллелепипеда, равно произведению чисел, выражающих площадь основания и высоту в соответствующих единицах.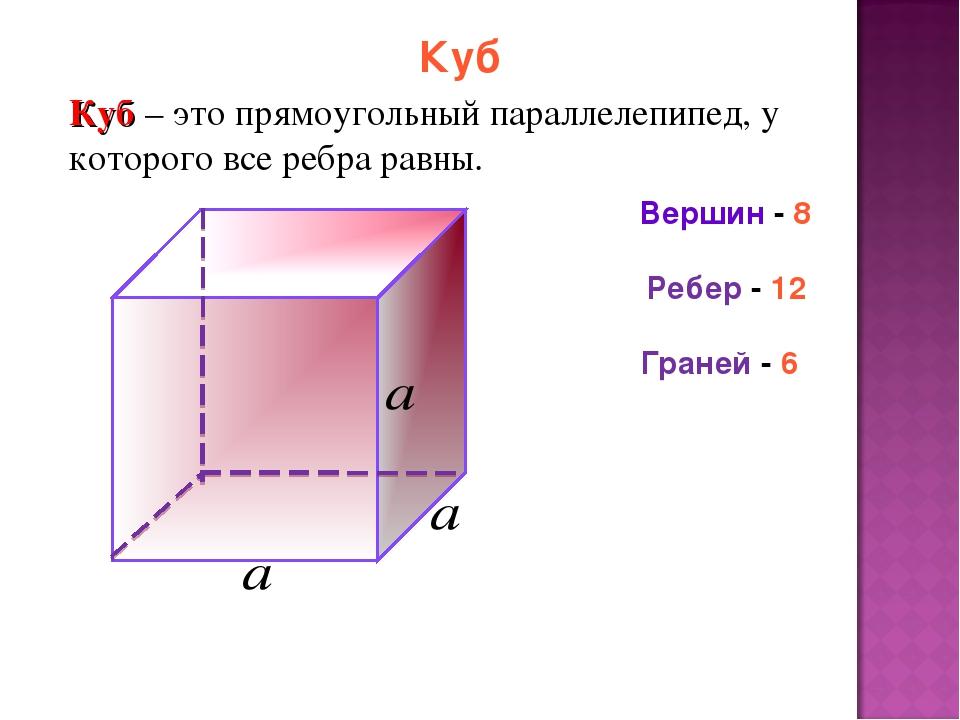
Это выражают сокращенно так: объем прямоугольного параллелепипеда равен произведению площади основания на высоту, т.е.
V = BH,
где под V, B и H разумеются числа, выражающие в соответствующих единицах объем, площадь основания и высоту прямоугольного параллелепипеда.
Обозначая буквами a, b и с три измерения прямоугольного пар-да (выраженные в числах), можем написать:
V = abс
потому что площадь основания выражается произведением двух из этих измерений, а высота равна третьему измерению.
Следствия:
- Объем куба равен третьей степени его ребра.
- Отношение двух кубических единиц равно третьей степени отношения соответствующих линейных единиц. Так, отношение м3 к дм3 равно 103, т.е. 1000.
Объем любого параллелепипеда
Лемма. Наклонная призма равновелика такой прямой призме, у которой основание равно перпендикулярному сечению наклонной призмы, а высота — ее боковому ребру.
Через какую-нибудь точку a (рис.) одного из боковых ребер наклонной призмы A1d проведем перпендикулярное сечение abcde. Затем продолжим все боковые грани вниз, отложим aa1=AA1 и через точку a1 проведем перпендикулярное сечение a1b1с1d1e1.
Так как плоскости двух сечений параллельны, то части боковых ребер, заключенные между ними, равны, т.е.
bb1 = сс1 = dd1 = ee1 = aa1 = AA1.
Вследствие этого многогранник a1d есть прямая призма, у которой основанием служит перпендикулярное сечение, а высота (или, что то же самое, боковое ребро) равна боковому ребру наклонной призмы.
Докажем, что наклонная призма равновелика прямой призме.
Для этого предварительно убедимся, что многогранники aD и a1D1 равны.
Основания их abcde и a1b1с1d1e1 равны, как основания призмы a1d.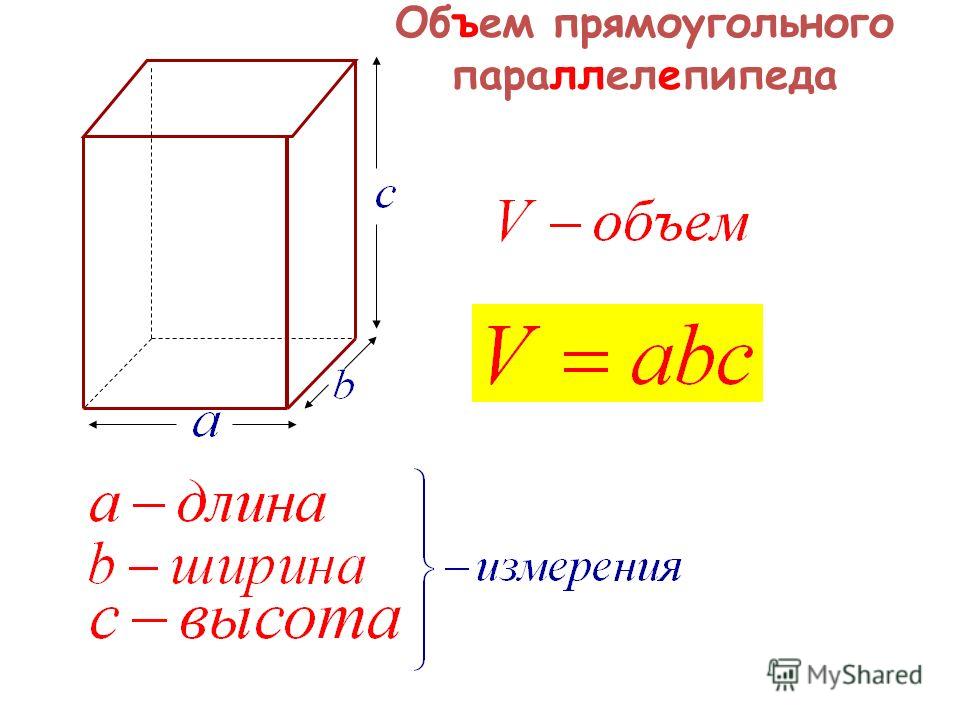
С другой стороны, отняв от обеих частей равенства A1A = a1a по одной и той же прямой A1a , получим aA = a1A1.
Подобно этому: bB = b1B1, сС = с1С1 и т.д.
Вообразим теперь, что многогранник aD вложен в a1D1 так, чтобы основания их совпали. Тогда боковые ребра, будучи перпендикулярны к основаниям и соответственно равны, также совпадут.
Поэтому многогранник aD совместится с a1D1. Значит, эти тела равны.
Теперь заметим, что если от целого многогранника a1D , отнимем часть aD , то получим прямую призму. А если от того же многогранника отнимем часть a1D1, то получим наклонную призму.
Из этого следует, что эти две призмы равновелики, так как объемы их представляют собой разности объемов равных тел.
Теорема. Объем параллелепипеда равен произведению площади основания на высоту.
Ранее мы доказали эту теорему для параллелепипеда прямоугольного, теперь докажем ее для параллелепипеда прямого, а потом наклонного.
1. Пусть (рис.) AC1 прямой пар-д, т.е. такой, у которого основание ABCD какой-нибудь параллелограмм, а все боковые грани — прямоугольники.
Возьмем в нем за основание грань AA1B1B. Тогда параллелепипед будет наклонный.
Рассматривая его, как частный случай наклонной призмы, мы, на основании леммы предыдущего параграфа, можем утверждать, что этот пар-д равновелик такому прямому, у которого основание есть перпендикулярное сечение MNPQ, а высота BC.
Четырехугольник MNPQ есть прямоугольник, потому что его углы служат линейными углами прямых двугранных углов. Поэтому прямой параллелепипед, имеющий это основание должен быть прямоугольным, и, следовательно, его объем равен произведению площади основания MNPQ на высоту BC.
Но площадь MNPQ равна MN * MQ. Значит:
Объем AC1 = MN * MQ * BC
Произведение MQ * BC выражает площадь параллелограмма ABCD.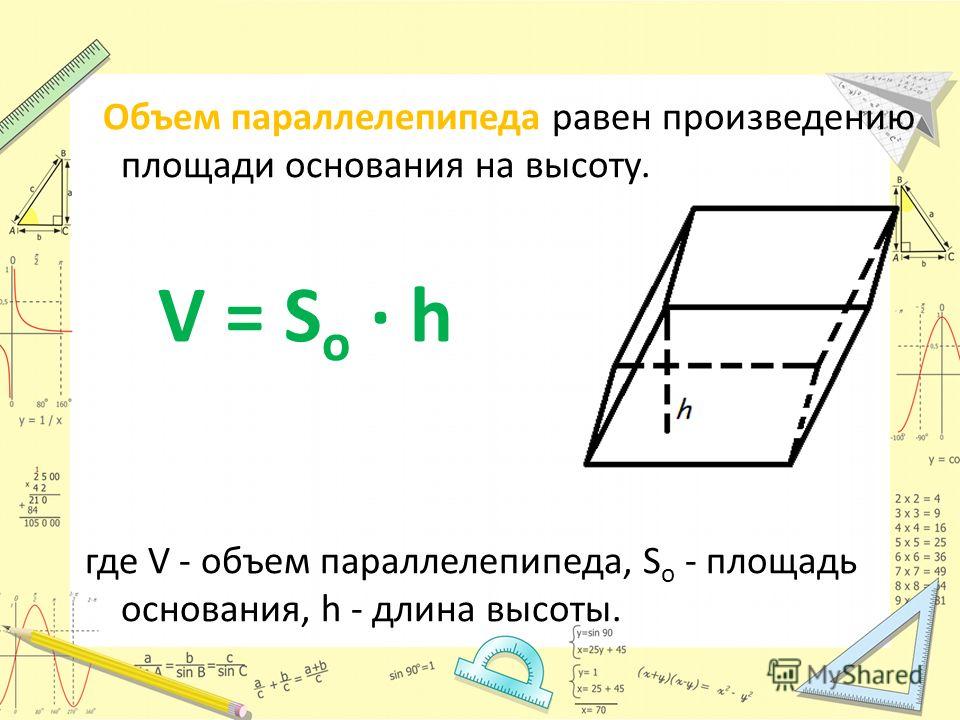 Поэтому:
Поэтому:
Объем AC1 = (площ.ABCD ) * MN
2. Пусть (рис.) AC1 есть пар-д наклонный. Он равновелик такому прямому, у которого основанием служит перпендикулярное сечение MNPQ, а высотой ребро BC.
Но, по доказанному, объем прямого параллелепипеда равен произведению площади основания на высоту. Значит:
Объем AC1 = (площ.MNPQ ) * BC
Если RS есть высота сечения MNPQ, то площадь MNPQ = MQ * RS. Поэтому:
Объем AC1 = MQ * RS * BC
Произведение BC * MQ выражает площадь параллелограмма ABCD. Следовательно:
Объем AC1 = (площ.ABCD ) * RS
Т.е. объем всякого параллелепипеда равен произведению площади основания на высоту.
Следствие. Если V, B и H — числа, выражающие в соответствующих единицах объем, площадь основания и высоту какого — нибудь паралллелепипеда, то можем написать:
V = BH
Задача. Основанием прямого параллелепипеда является ромб, площадь которого равна S.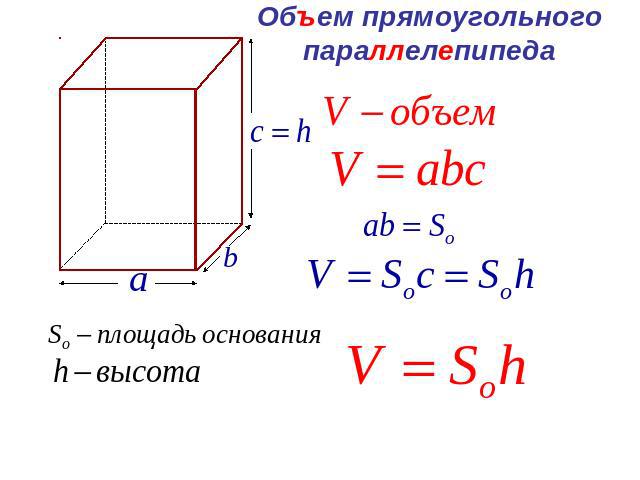 Площади диагональных сечений равны S1 и S2. Найти объем параллелепипеда.
Площади диагональных сечений равны S1 и S2. Найти объем параллелепипеда.
Для нахождения объема параллелепипеда нужно найти его высоту Н (рис. 242).
Обозначим длины диагоналей основания через d1 и d2. Тогда
d1•H = S1, d2•H = S2, d1• d2 = 2S.
Из этих уравнений находим
$$ \frac{S_1}{H}\cdot \frac{S_2}{H} = 2S, \;\; H=\sqrt{\frac{S_1 S_2}{2S}} $$
Следовательно,
$$ V=S\cdot H = S\sqrt{\frac{S_1 S_2}{2S}}=\sqrt{\frac{S\cdot S_1\cdot S_2}{2}} $$
Параллелепипед
Свойства параллелепипеда
1) Параллелепипед — это трехмерная фигура.
2) Имеет 6 граней.
3) Имеет 12 ребер и 8 вершин.
4) Грани параллелепипеда — параллелограмм.
5) Это призма с параллелограммом в основании.
6) Каждое лицо кажется зеркальным отражением противоположного лица.
7) Диагональ каждой грани называется диагональю грани.
8) Диагональ трехмерного тела параллелепипеда называется диагональю тела.
объем параллелепипленных
для данного параллелепипмента, пусть «A» — это область нижней поверхности, а «H» — высота, тогда формула объема дается:
× h
Поскольку нижняя грань является параллелограммом, ее площадь «A» можно рассчитать по формуле:
A = площадь параллелограмма = основание × высота.
В векторной форме:
Объем параллелепиппа, охватываемый A, B и C, дается:
Объем = площадь основания × высота
= | а × б | |с| cos ø
= | (а × б). с |
с |
Площадь поверхности параллелепипеда
1) Площадь боковой поверхности (L.S.A.)
Это произведение периметра основания и высоты параллелепипеда.
L.S.A. = Периметр основания × высота
2) Общая площадь поверхности (TSA)
Это сумма LSA и площади двух оснований.
T.S.A. = L.S.A. + 2(базовая площадь)
Существует два основных типа параллелепипедов:
1. Куб
2. Прямоугольник
Куб
Куб представляет собой параллелепипед, все шесть граней которого имеют квадратную форму.
Пример: игральные кости, кубик льда, кубик Рубика и т. д.
Пусть каждая сторона куба равна a единиц. Затем,
1. Объем кубоида = площадь нижней поверхности (квадратная) × высота
= (a × a) × (a)
= A3 единицы
2.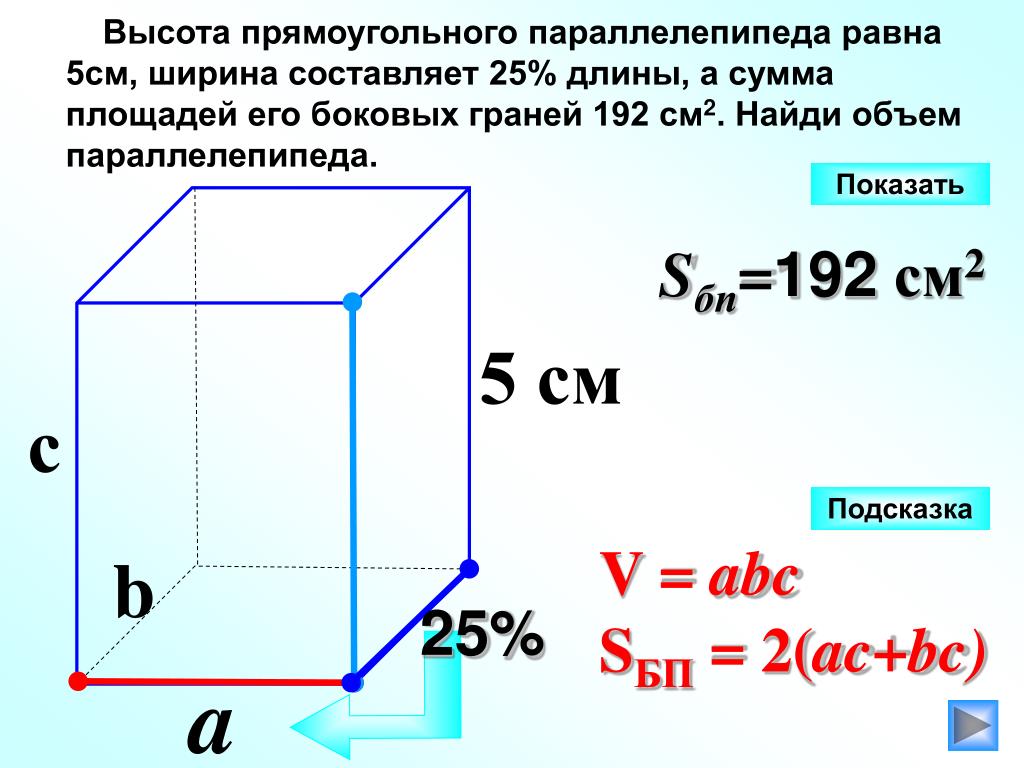 L.S.A. = периметр основания (квадрат) × высота
L.S.A. = периметр основания (квадрат) × высота
= (4a) × (a)
= 4a2 единицы
3. T.S.A. = L.S.A. + 2(базовая площадь)
= (4a2)+ 2(a2) 92}} = \sqrt 3 \times \left( a \right)\] единиц
Кубоид
Кубоид — это параллелепипед, все шесть граней которого имеют прямоугольную форму.
Это трехмерная структура в форме коробки.
Пример: коробка для спичек, тряпка, кирпичи, коробка для инструментов и т. д.
Обозначим длину, ширину и высоту прямоугольного параллелепипеда l, b и h соответственно. Тогда
1) Объем прямоугольного параллелепипеда = площадь нижней грани (прямоугольной) × высота
= (l × b) × (h)
= l × b × h
2) L. S.A. = периметр основания (прямоугольник) × высота
S.A. = периметр основания (прямоугольник) × высота
= 2(l + b) × (h)
= 2(l + b) h
L.S.A. кубоида также можно принять как площадь четырех стен прямоугольного помещения.
3) Т.С.А. = L.S.A. + 2(площадь основания)
= 2(l + b) h + 2(lb)
= 2(lb + bh + lh) 92}}\]
Решено Примеры:
Q.1. Найдите сторону куба, площадь поверхности которого равна 600 см2.
Ответ. Площадь поверхности куба = 6 (сторона) 2
Данная, площадь поверхности куба = 600 см2
⇒ 6 (сторона) 2 = 600 см2
⇒ (сторона) 2 = 100 см2
⇒ Сторона = = 10 см.
Q.2. Найдите объем, L.S.A., T.S.A. Диагональ тела прямоугольного параллелепипеда, длина которого 3 см, ширина 4 см, высота 5 см.
Ответ. а.) Объем кубоида = L × B × H
= 3 см × 4 см × 5 см
= 60 см3
B.) L.S.A. = 2(l + b) h
= 2 × (3 см + 4 см) × 5 см
= 70 см2
А. = 2(lb + bh + hl)
= 2 × {(3 см × 4 см) + (4 см × 5 см) + (5 см × 3 см)}
92}}\]= \[\sqrt{9 + 16 + 25}\] см
= \[\sqrt{50}\] см
= 5\[\sqrt{2}\] см
Q.3. Внутренние размеры прямоугольной комнаты составляют 12 м × 8 м × 4 м. Найдите общую стоимость побелки всех четырех стен комнаты, если стоимость побелки составляет 500 руб. 5 за кв. метр.
Ответ. Пусть длина комнаты = l = 12 м
ширина комнаты = b = 8 м
высота комнаты = h = 4 м
Площадь четырех стен комнаты = L. S.A. кубической комнаты = 2(l + b) × h
S.A. кубической комнаты = 2(l + b) × h
= 2 (12+8) × 4
= 2 × 20 × 4
= 160 м2
, стоимость белого промывки на м2 = рупий. 5
Отсюда общая стоимость побелки четырех стен комнаты = Rs.(160 × 5) = Rs. 800.
Том
ТомЧасть 4: Объем параллелепипеда
Если u , v и w имеют общую начальную точку, то множество конечных точек векторов s u + t v + r w для 0 r , s , t 1 называется параллелепипедом , натянутым на u , v , и w :
Maple/javaview изображение
Чтобы найти объем параллелепипеда, сначала заметим, что параллелепипед может быть «нарезан» на части, которые могут быть переставлены, чтобы сформировать новый параллелепипед, натянутый на u , v и proj u × v ( w ). Щелкните стрелки слайд-шоу
ниже изображения, чтобы увидеть нарезку и перестановку в действии.
Щелкните стрелки слайд-шоу
ниже изображения, чтобы увидеть нарезку и перестановку в действии.
| ||||||||||||||
| ||||||||||||||||||||
ПРИМЕР 7 Найдите объем параллелепипеда, натянутого на u = б 2,0,0 с, v = á1,3,0 ñ, и w = а 1,0,3 с .рисунок ниже нарисован так, как будто все векторы имеют свои начальные точки в источник.
Maple/javaview изображение
Решение: Перекрестное произведение на и на равноСкалярное произведение с на дает объем:
.
u × v =
, ,
знак равно 0,0,6 –
Объем = | ( u × v ) · w | = | а 1,0,3 с · 0,0,6 с | = 18
Площадь и объем параллелограммов и параллелепипедов
Площадь и объем параллелограммов и параллелепипедов1 Площадь параллелограмма
Предположим, мы хотим нарисовать параллелограмм.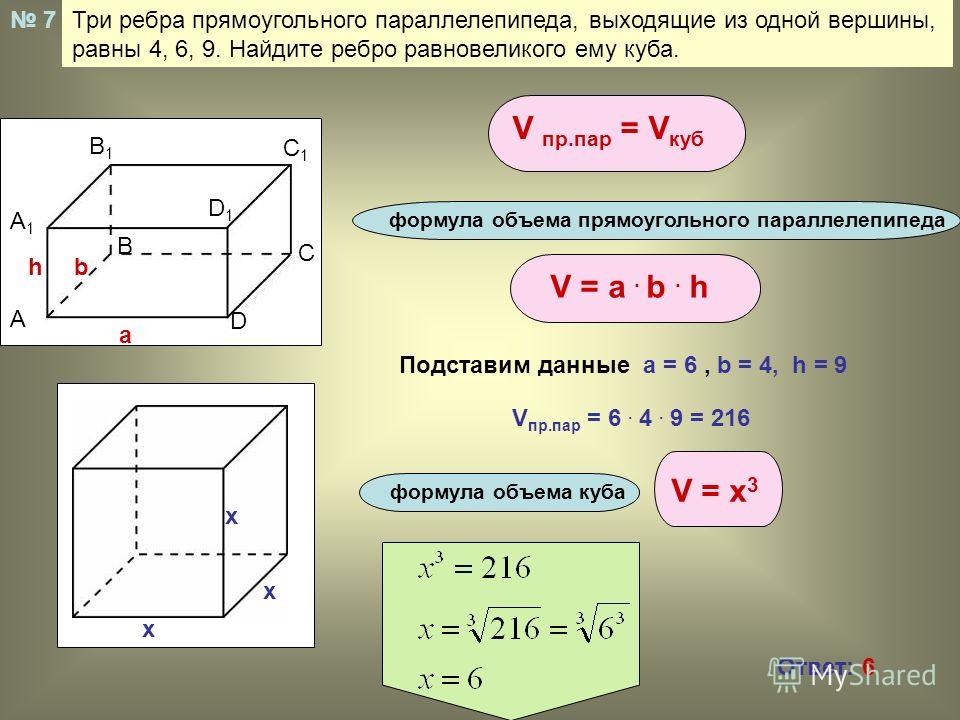 Сколько краски нам нужно?
Давайте посмотрим, как выразить ответ в терминах алгебры Клиффорда (она же
геометрическая алгебра).
Сколько краски нам нужно?
Давайте посмотрим, как выразить ответ в терминах алгебры Клиффорда (она же
геометрическая алгебра).
Этот документ также доступен в PDF формат. Вы можете найти это выгодным, если ваш браузер не может отображать стандартные математические символы HTML.
Для введения в алгебру Клиффорда и ее применение по геометрии и физике см. ссылку 1, ссылку 2, ссылка 3 и ссылка 4.
Ребрами параллелограмма являются векторы A и B. Мы почти уверены
- количество краски является скаляром,
- это симметричная функция A и B, и
- положительно.
В геометрической алгебре нам говорят, что произведение клина A∧B представляет площадь. Но это не прямой ответ к проблеме с краской. В частности
- A∧B не скаляр; это какое-то высшее измерение геометрическая абстракция.
- антисимметрично: A∧B = − B∧A
- мы даже не можем определить оператор «>» для бивекторов, поэтому
мы, конечно, не можем сказать, что A ∧ B будет «>» нулем.

Ответ заключается в том, что мы должны спрашивать о норме A∧B, пишется ||A∧B||.
Покажем, что
| площадь = ||A∧B|| = ||А|| ||Б|| |греш(θ)| (1) |
где θ — угол между векторами. Это правильный ответ на задачу с краской. Посмотрим, где это результат исходит из.
Для любого мультивектора M квадрат нормы определяется выражением
| ||М|| 2 := M M∼ (2) |
где M∼ — обращение M, образованное записью векторов которые составляют М в обратном порядке. Особенно
| (А∧В)∼ = (В∧А) (3) |
И для простого (оценка = 1) вектора
| (4) |
Предполагая, что мы имеем дело с пространственноподобными векторами, мы можем написать
| А = ||А|| а’ (5) |
, где a′ — единичный вектор в направлении A.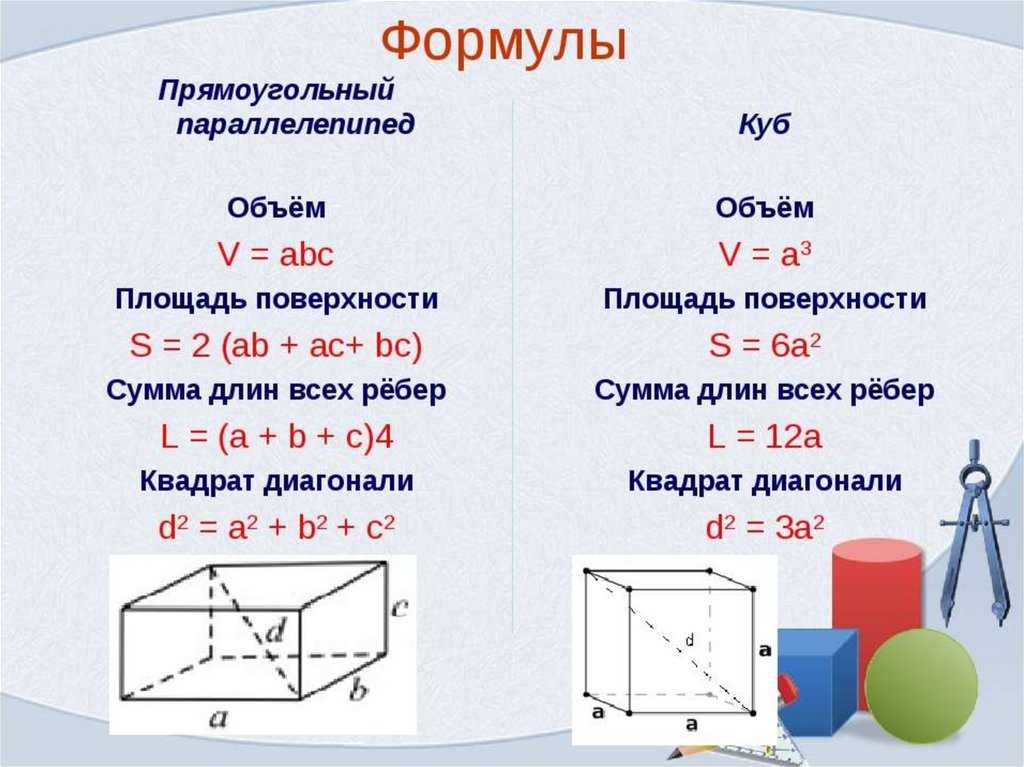
Другой вектор B можно записать как
| Б = ||Б|| (a′ cos(θ) + a» sin(θ)) (6) |
, где а» — некоторый единичный вектор, перпендикулярный А. Тогда просто возьмите эти выражения для A и B, подключите их в определение ||A∧B|| и поверните рукоятка. Мы нашли
| (7) |
где члены косинуса исчезли, потому что a′∧a′ = 0.
Затем мы используем тот факт, что произведение клина (a′∧a») равно
к геометрическому произведению (a′a»), поскольку два множителя равны
ортогональный; см. уравнение 17. Это полезно, потому что
геометрическое произведение геометрических произведений проще, чем геометрическое
продукт клиновых изделий. В этом случае (a′∧a»)(a»∧a′) =
a′a»a»a′ = 1, и сразу следует результат:
В этом случае (a′∧a»)(a»∧a′) =
a′a»a»a′ = 1, и сразу следует результат:
| площадь = ||A∧B|| = ||А|| ||Б|| |греш(θ)| (8) |
Более общий способ получения геометрического произведения двух клиньев продуктов заключается в расширении обоих клиновых продуктов с точки зрения геометрического произведения в соответствии с уравнением 16, а затем умножив все по срокам. В данном случае речь идет о том же, потому что
| (9) |
, где мы использовали уравнение антикоммутационного отношения 14.
(Рано или поздно нам придется использовать тот факт, что а’ и а»
перпендикулярно. )
)
Это хорошее домашнее задание для укрепления уверенности в себе в формализме.
2 Объем параллелепипеда
Перейдем к еще более интересной задаче.
Предположим, у нас есть параллелепипед с ребрами A, B и C, и мы хотим рассчитать объем.
Старомодным способом сделать это было бы использование «тройное скалярное произведение» A·B×C. Но крест продукты — плохие новости, и нам было бы намного лучше используя формулировку геометрической алгебры. Желаемый выражение
| объем = ||A∧B∧C|| (10) |
Обратите внимание, что, несмотря на то, что мы использовали клиновидное изделие
чтобы избавиться от перекрестных произведений, это не один к одному
замена. Вы не можете вслепую заменить A·B×C
через A·B∧C. Тройное скалярное произведение правильно
написано ||A∧B∧C|| с двумя клиновидными изделиями и без точки
товары. У этого есть хорошая геометрическая интерпретация: A∧B
визуализируется как подметание A в направлении B, используя
это как кисть, чтобы вымести область A∧B. Сходным образом
A ∧ B ∧ C визуализируется как подметание области A ∧ B в
направление C, используя его, чтобы выметать объем
А∧В∧С.
Сходным образом
A ∧ B ∧ C визуализируется как подметание области A ∧ B в
направление C, используя его, чтобы выметать объем
А∧В∧С.
Мы можем убедиться, что величина громкости ведет себя как рекламируется, используя ту же процедуру, что и раньше:
| (11) |
где ab′ — любой единичный вектор в плоскости AB, а ab» — единица вектор, перпендикулярный плоскости АВ. Результат:
| ||А∧В∧С|| = ||А|| ||Б|| ||С|| |греш(θ)| |греш(ф)| (12) |
что имеет смысл.
3 Примечания
Мы получили эти результаты без установления каких-либо базисных векторов
и без расширения A, B и C с точки зрения компонентов. (Это признак того, что мы все делаем правильно.) Все, что вам нужно, это
основные аксиоматические свойства
(Это признак того, что мы все делаем правильно.) Все, что вам нужно, это
основные аксиоматические свойства
| A B = B A если A и B коллинеарны (13) |
| A B = − B A если A и B перпендикулярны (14) |
| А· В = (А В + В А)/2 (15) |
| A∧B = (A B − B A)/2 (16) |
| А В = А·В + А∧В (17) |
везде, предполагая, что A и B являются простыми старыми векторами класса = 1.
Кстати, даже слегка произвольное разложение по синусам и можно обойтись без косинуса, если у нас есть аксиоматическое определение что означает «ротация», но это более сложная тема. Видеть номер 5.
4 Номера по каталогу
1.
Стивен Галл, Энтони Ласенби и Крис Доран, «Геометрическая алгебра Пространство-время» http://www.mrao.cam. ac.uk/~clifford/introduction/intro/intro.html
ac.uk/~clifford/introduction/intro/intro.html2.
Ричард Э. Харк, «Введение в математику Алгебра пространства-времени» http://www.harke.org/ps/intro.ps.gz3.
Дэвид Хестенес, «Лекция, посвященная медали Эрстеда, 2002 г.: Реформирование Математический язык физики»
Аннотация: http://geocalc.clas.asu.edu/html/Overview.html Полная статья: http://geocalc.clas.asu.edu/pdf/OerstedMedalLecture.pdf4.
Джон Денкер, «Введение в алгебру Клиффорда» www.av8n.com/physics/clifford-intro.htm5.
Джон Денкер, «Многомерные вращения, включая ускорение» www.av8n.com/physics/rotations.htm
и в частности раздел «расчеты».
Mathwords: прямоугольный параллелепипед
Mathwords: прямоугольный параллелепипед
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Обзор, вопросы, простые приемы, правила, подготовка
Содержание
- Что такое параллелепипед?
- Вес параллелепипеда
- Наглядный пример на параллелепипеде
- Часто задаваемые вопросы о параллелепипеде
Что такое параллелепипед?
Любая трехмерная фигура, все шесть граней которой являются параллелограммами, называется параллелепипедом. Их также называют призмами с тремя парами параллельных граней. Три случая параллелепипеда:
Кубовидный:- Призма с основанием в виде параллелограмма
Ромбовидный:- Шестигранник с тремя наборами параллельных граней
Куб:- Многогранник с шестью гранями в виде параллелограмма.
Характеристики параллелепипеда
Вот некоторые из основных характеристик параллелепипеда:
a. В данный момент можно увидеть любые три лица.
б. Это объемная трехмерная фигура.
в. Он имеет три пары по 4 параллельных ребра.
д. Все ребра равны по длине.
д. Каждой грани параллелепипеда соответствует диагональ.
Объем параллелепипеда
Рассмотрим параллелепипед, площадь основания которого равна B, а высота H. Объем параллелепипеда определяется по формуле:
V = B x H.
В векторной форме объем параллелепипеда равен рассчитывается с учетом трех различных измерений a, b и c. Формула:
V = I (a x b).c I
Площадь поверхности параллелепипеда
Общая площадь поверхности параллелепипеда определяется из площади боковой поверхности параллелепипеда. Площадь боковой поверхности параллелепипеда равна произведению высоты граней параллелепипеда на периметр основания. Таким образом, формула для расчета площади боковой поверхности (LSA) параллелепипеда:
LSA = высота x периметр основания.
Таким образом, общая площадь поверхности (TSA) есть не что иное, как арифметическая сумма площади боковой поверхности и верхнего и нижнего оснований параллелепипеда. Следовательно, формула для расчета TSA:
TSA = площадь боковой поверхности + 2 x площадь основания.
Вес параллелепипеда
Тема параллелепипеда взята из главы «Векторная алгебра». В главе представлены другие важные понятия скалярных скалярных произведений и перекрестных произведений, сложения и умножения векторов и скалярных тройных произведений векторов. Эта глава дает ценные 14 баллов на выпускных экзаменах в 12 классе. Кроме того, эта тема имеет важное значение на вступительных экзаменах национального уровня.
Наглядный пример на параллелепипеде
1. Даны ребра параллелепипеда as = и . Найдите объем параллелепипеда.
Раствор.
Объем параллелепипеда = 2[(2 х 2) — (-1 х -1)] — (-3)[(1 х 2) — (2 х -1)] + 4[(1 х -1) ) — (2 x 2)]
= 2[4 -1] + 3(2+2) + 4[-1-4]
= 2(3) + 3(4) + 4(-5)
= 6 + 12 — 20
= -2
Следовательно, объем параллелепипеда равен 2 кубическим единицам.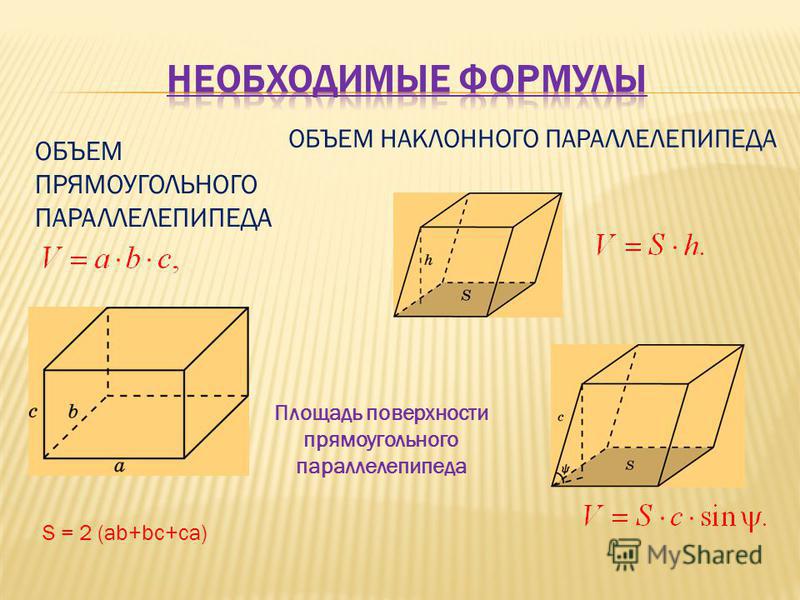
2. Параллелепипед длиной 5 дюймов имеет вершину и основание размером 10 дюймов и 15 дюймов соответственно. Если стоимость покраски коробки составляет 2 индийских рупии за кв. дюйм, найдите общую стоимость покраски?
Раствор.
Полную стоимость покраски можно вычислить только с учетом площади боковой поверхности.
Следовательно, LSA = высота x периметр основания
LSA = 2 (10 + 15) x 5
LSA = 250 кв. дюймов
Таким образом, общая стоимость покраски коробки = 250 x 2 = рупий. 500/-
3. Объем 40 куб. футов. Сколько тонн должен иметь угольный ковш, чтобы иметь высоту 18 футов, ширину 7 футов и глубину 10 футов при максимальном уровне?
Раствор.
Теперь,
Объем угольного ковша можно рассчитать как:
V = 18x7x10
V = 1260 фут3
Необходимое количество тонн:
W = 1 тонна/40 фут3 (1260 фут3)
W = 31,5 тонны
Часто задаваемые вопросы о параллелепипеде
В: Какова двумерная форма объемной фигуры в виде параллелепипеда?
A: Двумерная форма объемной фигуры в виде параллелепипеда известна как параллелограмм.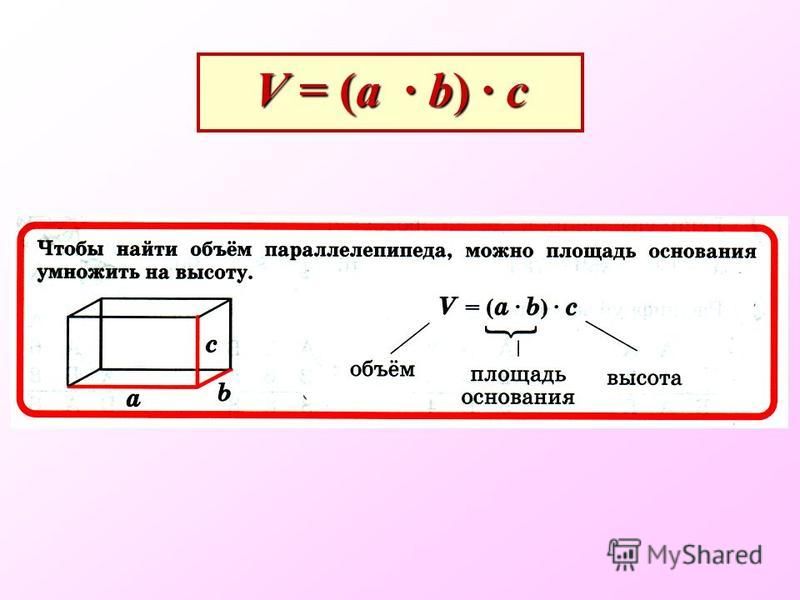
В: Как называется трехмерный ромб?
A: Трехмерный ромб называется ромбоэдр.
В: На какую двумерную форму похожа форма параллелепипеда?
A: Форма параллелепипеда напоминает параллелограмм.
В: Когда параллелепипед называют прямоугольным параллелепипедом?
A: Параллелепипед называется прямоугольным параллелепипедом, если все шесть его граней напоминают прямоугольник.
В: Какова формула диагонали грани и тела параллелепипеда?
A: Формула диагонали грани параллелепипеда и диагонали тела:
Прямоугольник или параллелепипед
Параллелепипед и пирамида вместе
Куб и параллелепипед вместе
Параллелепипед и сфера вместе
Параллелепипед и призма вместе
Параллелепипед и конус вместе
Параллелепипед и цилиндр вместе
Они дают дорожки, некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.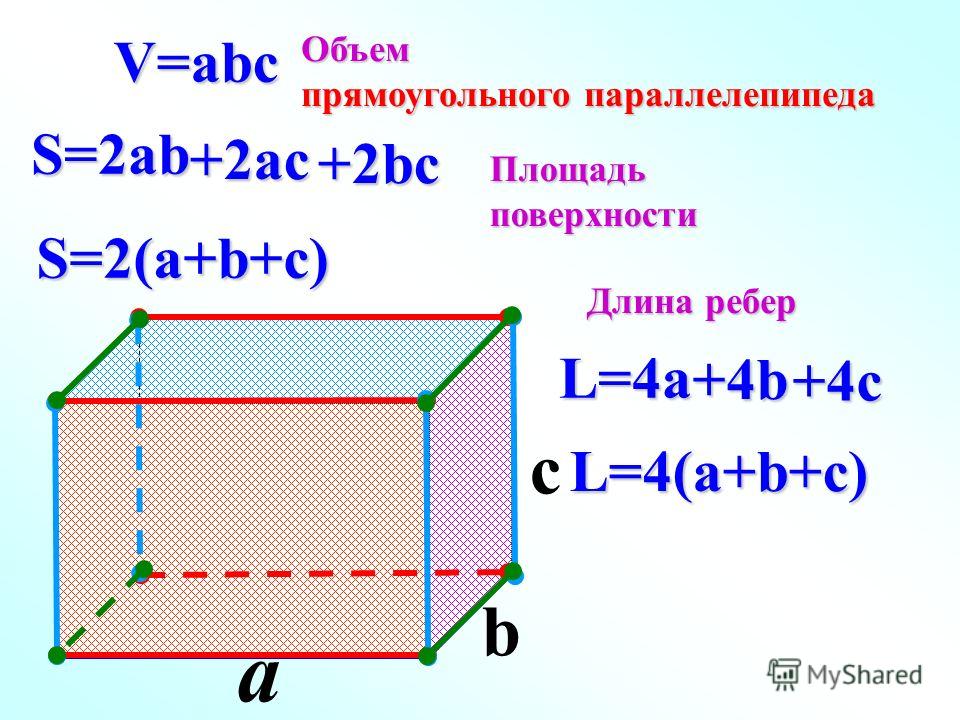
Дорожка 1
Прямоугольный параллелепипед имеет прямоугольное основание с размерами 30 см и 50 см, высота 100 см. Вычислите объем твердого тела и боковой поверхности.
Направляющая 2
Сколько уходит на бетонную стену длиной 500 см, высотой 300 см и шириной 20 см?
Трек 3
Контейнер имеет внутреннюю площадь 14200 см, площадь внутреннего основания 1500 см, размер 3/5 от другого. Рассчитывает высоту сосуда и его вместимость, зная, что имеет форму прямоугольного параллелепипеда.
Дорожка 4
Размеры основания прямоугольного параллелепипеда составляют 3/4 размера другого, а диагональ основания длиной 30 см равна высоте параллелепипеда. Вычислите площадь всей площади коробки.
Дорожка 5
Рассчитайте общую площадь поверхности прямоугольного параллелепипеда, зная, что сумма мер трех его измерений равна 17 см, а два из них составляют соответственно 1/2 и 1/5 высоты .
Направляющая 6
В прямоугольном параллелепипеде сумма мер трех измерений равна 60 см; зная, что размеры основания составляют 3/4 другого, а высота составляет 5/3 меньшего размера, вычисляет площадь всей площади и объем твердого тела.
Дорожка 7
Ребро куба совпадает с диагональю прямоугольного параллелепипеда с размерами 24 см, 32 см и 30 см. Вычислите площадь полной площади куба.
Дорожка 8
Ребро куба имеет длину 30 см. Определяет размер основания прямоугольника параллелепипеда высотой 30 см, зная, что размер основания в два раза больше другого и что боковая поверхность параллелепипеда эквивалентна боковой поверхности куба.
Дорожка 9
Прямоугольный параллелепипед имеет размеры соответственно 10 см, 20 см, 30 см. Вычислите боковую площадь, общую площадь и объем.
Путь 10
Длина и ширина прямоугольного параллелепипеда равны 20 м и 30 м. Зная, что общая площадь равна 6200 м, вычисляем высоту ящика и измеряем объем.
Зная, что общая площадь равна 6200 м, вычисляем высоту ящика и измеряем объем.
Дорожка 11
Вычислите объем и диагональ прямоугольного параллелепипеда с размерами 14 см, 48 см и 120 см.
Дорожка 12
На одном листе вырезал ящик длиной 20 см, шириной 25 см и высотой 30 см. Если бы бумага имела площадь 1 м, сколько квадратных метров бумаги было свободно?
Дорожка 13
Параллелепипед состоит из трех конгруэнтных кубов, сложенных друг на друга. Зная, что ребро каждого куба размером 10 см, вычисляют площадь всей поверхности и объем твердого тела.
Дорожка 14
Площадь полной поверхности куба равна площади боковой поверхности прямоугольного параллелепипеда с размерами основания соответственно 30 см и 10 см. Вычислите объем куба, зная, что периметр основания коробки равен 8/3 высоты.
Дорожка 15
Площадь полной поверхности куба равна одной стороне прямоугольного параллелепипеда высотой 30 см. Вычислите объем куба, зная, что размеры одного параллелепипеда втрое меньше другого и их сумма равна 40 см.
Вычислите объем куба, зная, что размеры одного параллелепипеда втрое меньше другого и их сумма равна 40 см.
Путь 16
Высота прямоугольного параллелепипеда 100 см, а объем 150000 см . Вычислите боковую площадь и общую площадь, зная, что размеры основания составляют 3/5 других.
Путь 17
Площадь боковой поверхности прямоугольного параллелепипеда 160 дм ; Зная, что размер основания и высота твердого тела составляют соответственно 5 дм и 10 дм, вычислить вес параллелепипеда. ( Ps = 8 кг/дм )
След 18
Площадь боковой поверхности прямоугольного параллелепипеда 11200 см , размер основания 50 см , высота равна 7/5. Определяет площадь полной поверхности и объем параллелепипеда.
Дорожка 19
Площадь полной поверхности параллелепипеда 14200 см, а площадь основания 1500 см. В прямоугольнике основания одна сторона составляет 3/5 другой.


 Призма. Объем призмы.
Призма. Объем призмы.
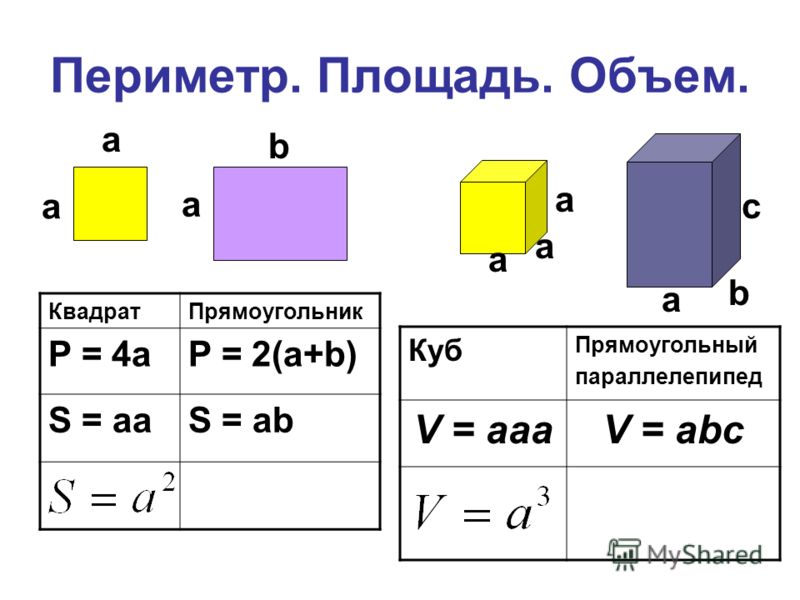 Соотношение между длинами сторон параллелепипеда и углами между ними показывает утверждение, что определитель Грама данных 3-х векторов равняется квадрату их смешанного произведения.
Соотношение между длинами сторон параллелепипеда и углами между ними показывает утверждение, что определитель Грама данных 3-х векторов равняется квадрату их смешанного произведения.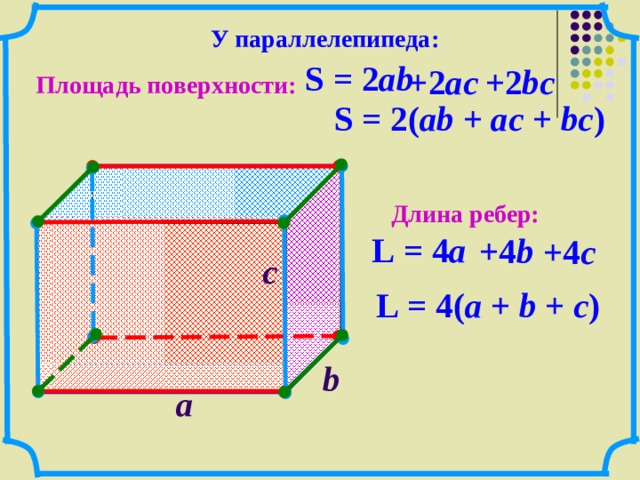

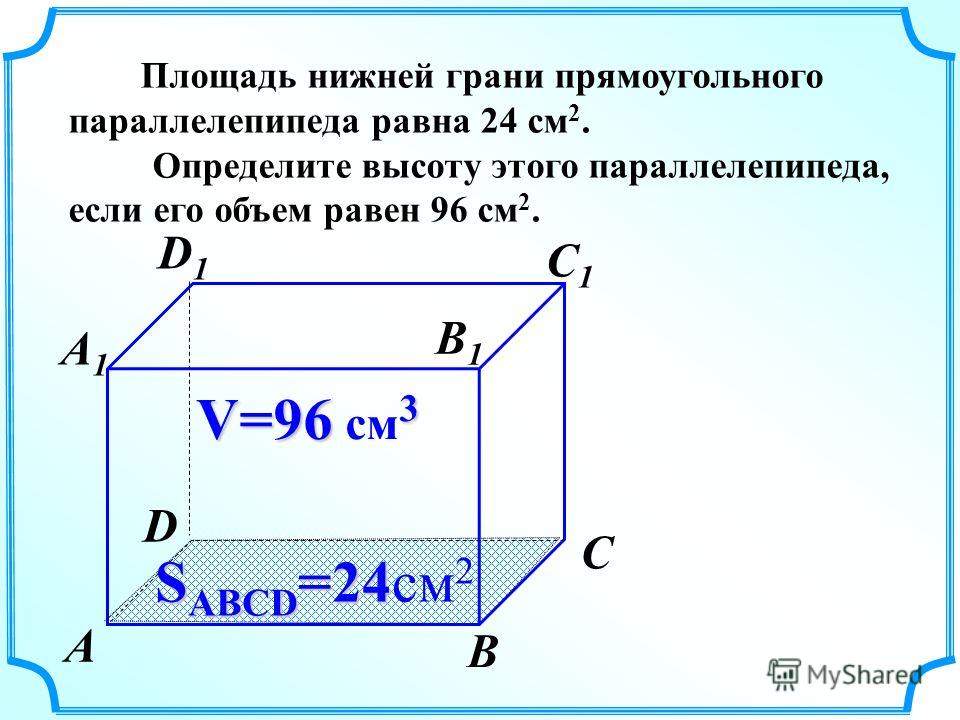
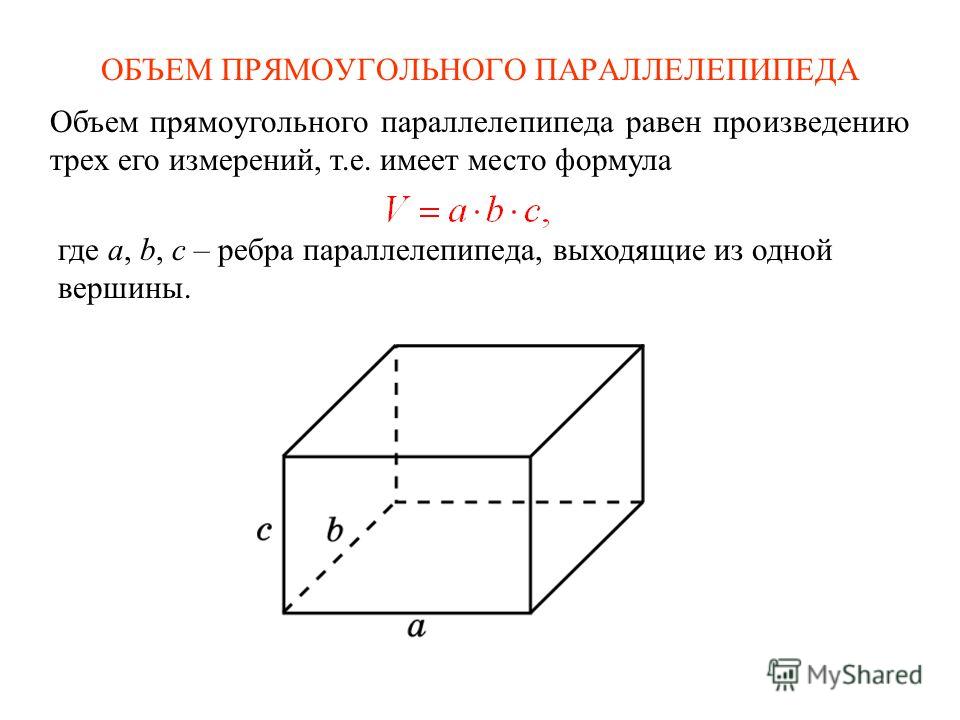 В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.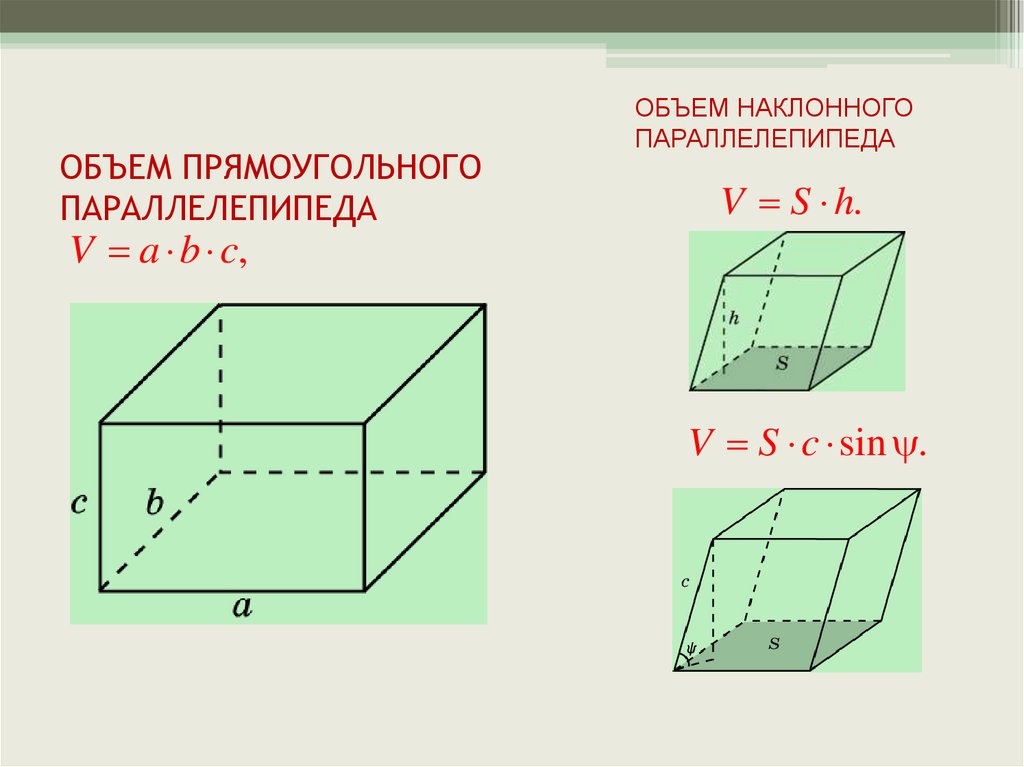 Ход решения поставленной задачи прост и не требует подробных объяснений.
Ход решения поставленной задачи прост и не требует подробных объяснений.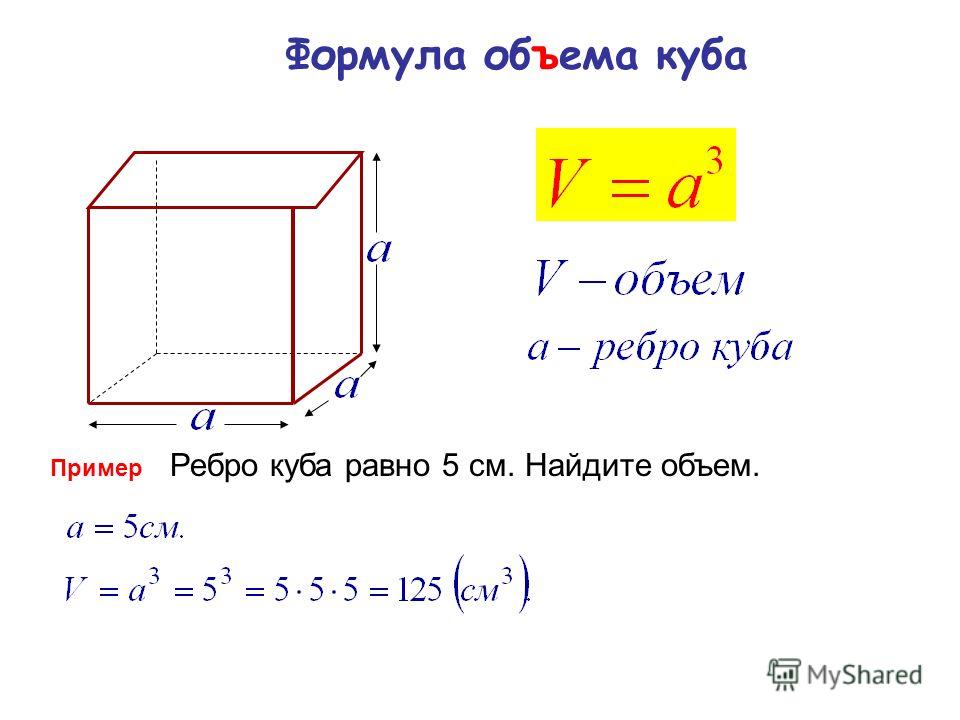
 Точное определение объема было дано лишь в 19 веке учеными Пеано и Жорданом.
Точное определение объема было дано лишь в 19 веке учеными Пеано и Жорданом.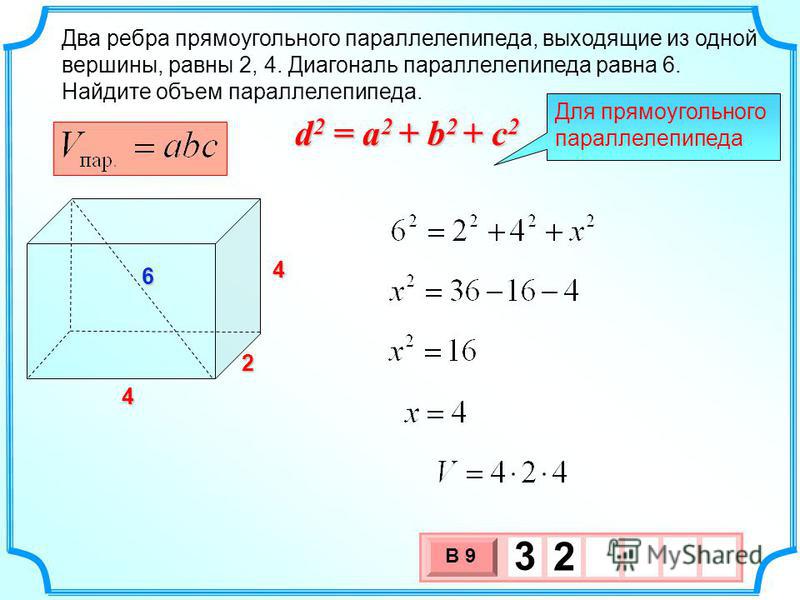
 рисунок ниже нарисован так, как будто все векторы имеют свои начальные точки в
источник.
рисунок ниже нарисован так, как будто все векторы имеют свои начальные точки в
источник.
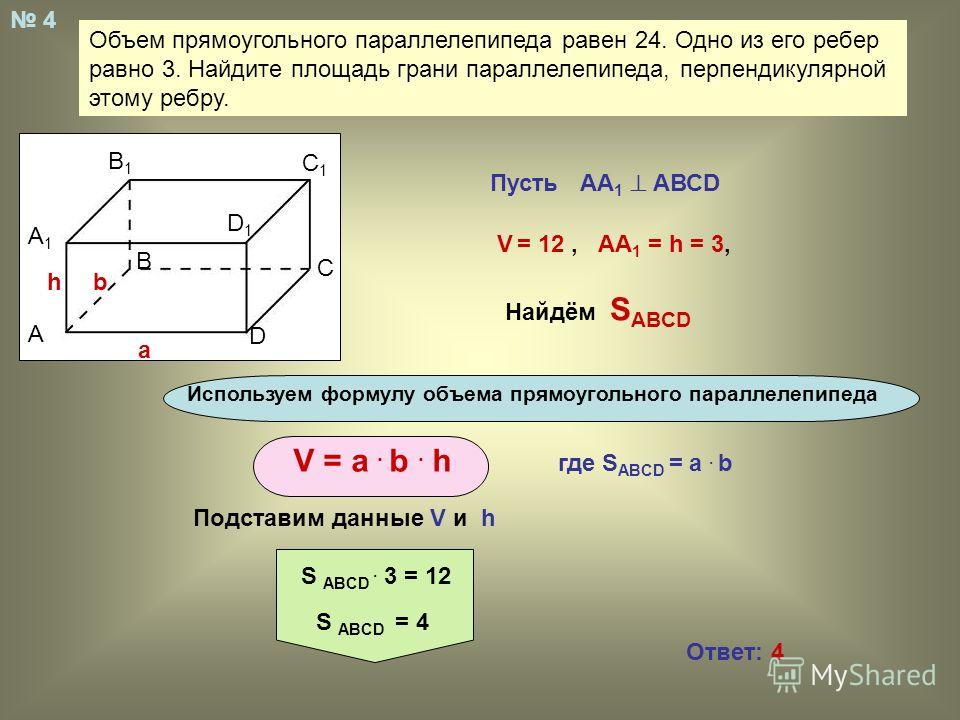 ac.uk/~clifford/introduction/intro/intro.html
ac.uk/~clifford/introduction/intro/intro.html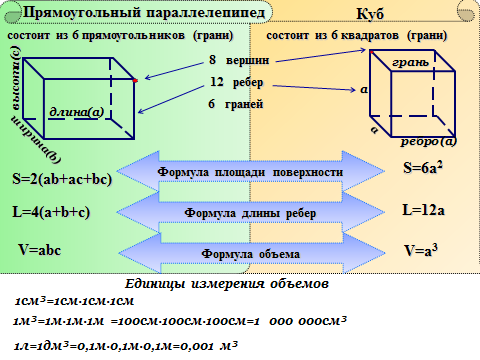 Формально многогранник, у которого все грани
прямоугольники.
Формально многогранник, у которого все грани
прямоугольники.