Таблица значений функции Лапласа
Примеры решенийКоэффициент СпирменаКоэффициент Фехнера Множественная регрессияНелинейная регрессия Уравнение регрессии Автокорреляция Расчет параметров трендаОшибка аппроксимации
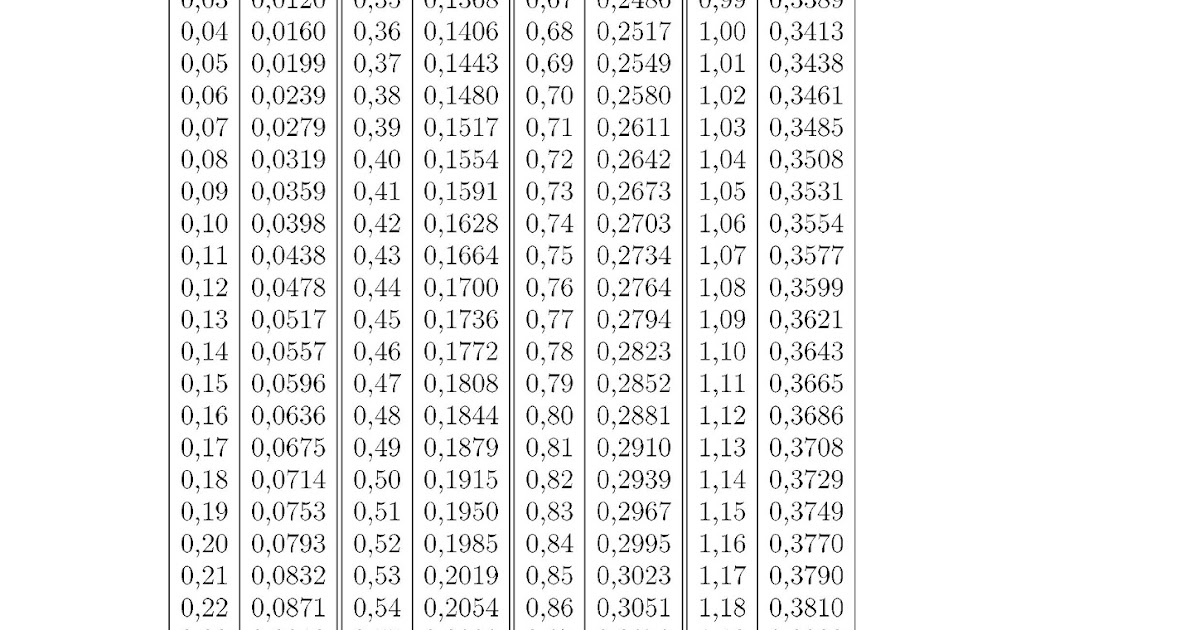
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0.00 | 0.0000 | 0.32 | 0.1255 | 0.64 | 0.2389 | 0.96 | 0.3315 |
| 0.01 | 0.0040 | 0.33 | 0.1293 | 0.65 | 0.2422 | 0. | 0.3340 |
| 0.02 | 0.0080 | 0.34 | 0.1331 | 0.66 | 0.2454 | 0.98 | 0.3365 |
| 0.03 | 0.0120 | 0.35 | 0.1368 | 0.67 | 0.2486 | 0.99 | 0.3389 |
| 0.04 | 0.0160 | 0.36 | 0.1406 | 0.68 | 0.2517 | 1.00 | 0.3413 |
| 0.05 | 0.0199 | 0.37 | 0.1443 | 0.69 | 0.2549 | 1.01 | 0.3438 |
| 0.06 | 0.0239 | 0.38 | 0.1480 | 0. 70 70
| 0.2580 | 1.02 | 0.3461 |
| 0.07 | 0.0279 | 0.39 | 0.1517 | 0.71 | 0.2611 | 1.03 | 0.3485 |
| 0.08 | 0.0319 | 0.40 | 0.1554 | 0.72 | 0.2642 | 1.04 | 0.3508 |
| 0.09 | 0.0359 | 0.41 | 0.1591 | 0.73 | 0.2673 | 1.05 | 0.3531 |
| 0.10 | 0.0398 | 0.42 | 0.1628 | 0.74 | 0.2703 | 1.06 | 0.3554 |
| 0.11 | 0.0438 | 0. 43 43
| 0.1664 | 0.75 | 0.2734 | 1.07 | 0.3577 |
| 0.12 | 0.0478 | 0.44 | 0.1700 | 0.76 | 0.2764 | 1.08 | 0.3599 |
| 0.13 | 0.0517 | 0.45 | 0.1736 | 0.77 | 0.2794 | 1.09 | 0.3621 |
| 0.14 | 0.0557 | 0.46 | 0.1772 | 0.78 | 0.2823 | 1.10 | 0.3643 |
| 0.15 | 0.0596 | 0.47 | 0.1808 | 0.79 | 0.2852 | 1.11 | 0.3665 |
0. 16 16
| 0.0636 | 0.48 | 0.1844 | 0.80 | 0.2881 | 1.12 | 0.3686 |
| 0.17 | 0.0675 | 0.49 | 0.1879 | 0.81 | 0.2910 | 1.13 | 0.3708. |
| 0.18 | 0.0714 | 0.50 | 0.1915 | 0.82 | 0.2939 | 1.14 | 0.3729 |
| 0.19 | 0.0753 | 0.51 | 0.1950 | 0.83 | 0.2967 | 1.15 | 0.3749 |
| 0.20 | 0.0793 | 0.52 | 0.1985 | 0.84 | 0.2995 | 1. 16 16
| 0.3770 |
| 0.21 | 0.0832 | 0.53 | 0.2019 | 0.85 | 0.3023 | 1.17 | 0.3790 |
| 0.22 | 0.0871 | 0.54 | 0.2054 | 0.86 | 0.3051 | 1.18 | 0.3810 |
| 0.23 | 0.0910 | 0.55 | 0.2088 | 0.87 | 0.3078 | 1.19 | 0.3830 |
| 0.24 | 0.0948 | 0.56 | 0.2123 | 0.88 | 0.3106 | 1.20 | 0.3849 |
| 0.25 | 0.0987 | 0.57 | 0.2157 | 0. 89 89
| 0.3133 | 1.21 | 0.3869 |
| 0.26 | 0.1026 | 0.58 | 0.2190 | 0.90 | 0.3159 | 1.22 | 0/3883 |
| 0.27 | 0.1064 | 0.59 | 0.2224 | 0.91 | 0.3186 | 1.23 | 0.3907 |
| 0.28 | 0.1103 | 0.60 | 0.2257 | 0.92 | 0.3212 | 1.24 | 0.3925 |
| 0.29 | 0.1141 | 0.61 | 0.2291 | 0.93 | 0.3238 | 1.25 | 0.3944 |
| 0.30 | 0.1179 | 0. 62 62
| 0.2324 | 0.94 | 0.3264 | ||
| 0.31 | 0.1217 | 0.63 | 0.2357 | 0.95 | 0.3289 |
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 1.26 | 0.3962 | 1.59 | 0.4441 | 1.92 | 0.4726 | 2.50 | 0.4938 |
| 1.27 | 0.3980 | 1.60 | 0.4452 | 1.93 | 0.4732 | 2.52 | 0.4941 |
| 1.28 | 0.3997 | 1.61 | 0. 4463 4463
| 1.94 | 0.4738 | 2.54 | 0.4945 |
| 0.4015 | 1.62 | 0.4474 | 1.95 | 0.4744 | 2.56 | 0.4948 | |
| 1.30 | 0.4032 | 1.63 | 0.4484 | 1.96 | 0.4750 | 2.58 | 0.4951 |
| 1.31 | 0.4049 | 1.64 | 0.4495 | 1.97 | 0.4756 | 2.60 | 0.4953 |
| 1.32 | 0.4066 | 1.65 | 0.4505 | 1.98 | 0.4761 | 2.62 | 0.4956 |
1. 33 33
| 0.4082 | 1.66 | 0.4515 | 1.99 | 0.4767 | 2.64 | 0.4959 |
| 1.34 | 0.4099 | 1.67 | 0.4525 | 2.00 | 0.4772 | 2.66 | 0.4961 |
| 1.35 | 0.4115 | 1.68 | 0.4535 | 2.02 | 0.4783 | 2.68 | 0.4963 |
| 1.36 | 0.4131 | 1.69 | 0.4545 | 2.04 | 0.4793 | 2.70 | 0.4965 |
| 1.37 | 0.4147 | 1.70 | 0.4554 | 2.06 | 0.4803 | 2. 72 72
| 0.4967 |
| 1.38 | 0.4162 | 1.71 | 0.4564 | 2.08 | 0.4812 | -2.74 | 0.4969 |
| 1.39 | 0.4177 | 1.72 | 0.4573 | 2.10 | 0.4821 | 2.76 | 0.4971 |
| 1.40 | 0.4192 | 1.73 | 0.4582 | 2.12 | 0.4830 | 2.78 | 0.4973 |
| 1.41 | 0.4207 | 1.74 | 0.4591 | 2.14 | 0.4838 | 2.80 | 0.4974 |
| 1.42 | 0.4222 | 1.75 | 0. 4599 4599
| 2.16 | 0.4846 | 2.82 | 0.4976 |
| 1.43 | 0.4236 | 1.76 | 0.4608 | 2.18 | 0.4854 | 2.84 | 0.4977 |
| 1.44 | 0.4251 | 1.77 | 0.4616 | 2.20 | 0.4861 | 2.86 | 0.4979 |
| 1.45 | 0.4265 | 1.78 | 0.4625 | 2.22 | 0.4868 | 2.88 | 0.4980 |
| 1.46 | 0.4279 | 1.79 | 0.4633 | 2.24 | 0.4875 | 2.90 | 0.4981 |
1. 47 47
| 0.4292 | 1.80 | 0.4641 | 2.26 | 0.4881 | 2.92 | 0.4982 |
| 1.48 | 0.4306 | 1.81 | 0.4649 | 2.28 | 0.4887 | 2.94 | 0.4984 |
| 1.49 | 0.4319 | 1.82 | 0.4656 | 2.30 | 0.4893 | 2.96 | 0.4985 |
| 1.50 | 0.4332 | 1.83 | 0.4664 | 2.32 | 0.4898 | 2.98 | 0.4986 |
| 1.51 | 0.4345 | 1.84 | 0.4671 | 2.34 | 0.4904 | 3.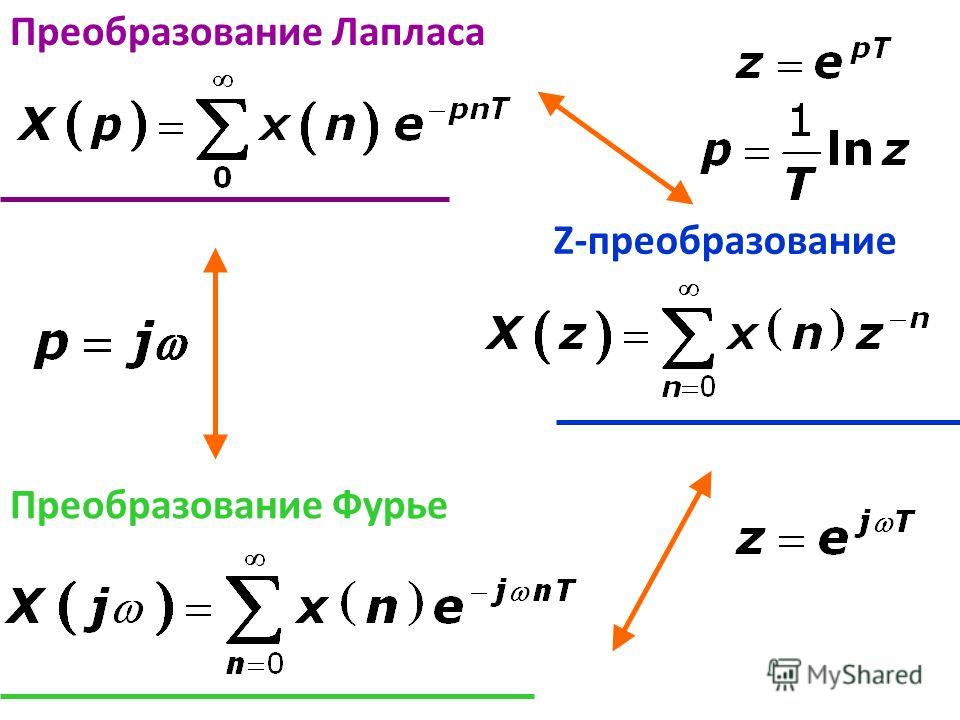 00 00
| 0.49865 |
| 1.52 | 0.4357 | 1.85 | 0.4678 | 2.36 | 0.4909 | 3.20 | 0.49931 |
| 1.53 | 0.4370 | 1.86 | 0.4686 | 2.38 | 0.4913 | 3.40 | 0.49966 |
| 1.54 | 0.4382 | 1.87 | 0.4693 | 2.40 | 0.4918 | 3.60 | 0.49984 |
| 1.55 | 0.4394 | 1.88 | 0.4699 | 2.42 | 0.4922 | 3.80 | 0.49992 |
| 1.56 | 0.4406 | 1.89 | 0. 4706 4706
| 2.44 | 0.4927 | 4.00 | 0.49996 |
| 1.57 | 0.4418 | 1.90 | 0.4713 | 2.46 | 0.4931 | 4.50 | 0.49999 |
| 1.58 | 0.4429 | 1 1.91 | 0.4719 | 2.48 | 0.4934 | > 5.00 | 0.49999 |
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Функция Лапласа. Полная таблица значений интегральной функции Лапласа онлайн. Теория вероятностей и математическая статистика
В таблице даны значения функции
для положительных значений
и для
;
для
пользуются той же таблицей, так как функция
нечетна, то есть
. В таблице приведены значения интеграла лишь до
,
так как для
можно принять
.
Эту функцию называют функцией Лапласа.
В таблице приведены значения интеграла лишь до
,
так как для
можно принять
.
Эту функцию называют функцией Лапласа.
Таблица значений функции Лапласа в теории вероятностей и математической статистике используется довольно часто. На сайте можно посмотреть примеры ее использования в следующих задачах:
- Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
- Интегральная теорема Муавра – Лапласа
- Доверительные интервалы для среднего и дисперсии
- Проверка гипотезы о равенстве средних
Цветом в таблице подсвечены аргументы функции Лапласа, рядом, в соседнем столбце — значения функции Лапласа.
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 | 0,0000 | 0,32 | 0,1255 | 0,64 | 0,2389 | 0,96 | 0,3315 |
| 0,01 | 0,0040 | 0,33 | 0,1293 | 0,65 | 0,2422 | 0,97 | 0,3340 |
| 0,02 | 0,0080 | 0,34 | 0,1331 | 0,66 | 0,2454 | 0,98 | 0,3365 |
| 0,03 | 0,0120 | 0,35 | 0,1368 | 0,67 | 0,2486 | 0,99 | 0,3389 |
| 0,04 | 0,0160 | 0,36 | 0,1406 | 0,68 | 0,2517 | 1,00 | 0,3413 |
| 0,05 | 0,0199 | 0,37 | 0,1443 | 0,69 | 0,2549 | 1,01 | 0,3438 |
| 0,06 | 0,0239 | 0,38 | 0,1480 | 0,70 | 0,2580 | 1,02 | 0,3461 |
| 0,07 | 0,0279 | 0,39 | 0,1517 | 0,71 | 0,2611 | 1,03 | 0,3485 |
| 0,08 | 0,0319 | 0,40 | 0,1554 | 0,72 | 0,2642 | 1,04 | 0,3508 |
| 0,09 | 0,0359 | 0,41 | 0,1591 | 0,73 | 0,2673 | 1,05 | 0,3531 |
| 0,10 | 0,0398 | 0,42 | 0,1628 | 0,74 | 0,2703 | 1,06 | 0,3554 |
| 0,11 | 0,0438 | 0,43 | 0,1664 | 0,75 | 0,2734 | 1,07 | 0,3577 |
| 0,12 | 0,0478 | 0,44 | 0,1700 | 0,76 | 0,2764 | 1,08 | 0,3599 |
| 0,13 | 0,0517 | 0,45 | 0,1736 | 0,77 | 0,2794 | 1,09 | 0,3621 |
| 0,14 | 0,0557 | 0,46 | 0,1772 | 0,78 | 0,2823 | 1,10 | 0,3643 |
| 0,15 | 0,0596 | 0,47 | 0,1808 | 0,79 | 0,2852 | 1,11 | 0,3665 |
| 0,16 | 0,0636 | 0,48 | 0,1844 | 0,80 | 0,2881 | 1,12 | 0,3686 |
| 0,17 | 0,0675 | 0,49 | 0,1879 | 0,81 | 0,2910 | 1,13 | 0,3708 |
| 0,18 | 0,0714 | 0,50 | 0,1915 | 0,82 | 0,2939 | 1,14 | 0,3729 |
| 0,19 | 0,0753 | 0,51 | 0,1950 | 0,83 | 0,2967 | 1,15 | 0,3749 |
| 0,20 | 0,0793 | 0,52 | 0,1985 | 0,84 | 0,2995 | 1,16 | 0,3770 |
| 0,21 | 0,0832 | 0,53 | 0,2019 | 0,85 | 0,3023 | 1,17 | 0,3790 |
| 0,22 | 0,0871 | 0,54 | 0,2054 | 0,86 | 0,3051 | 1,18 | 0,3810 |
| 0,23 | 0,0910 | 0,55 | 0,2088 | 0,87 | 0,3078 | 1,19 | 0,3830 |
| 0,24 | 0,0948 | 0,56 | 0,2123 | 0,88 | 0,3106 | 1,20 | 0,3849 |
| 0,25 | 0,0987 | 0,57 | 0,2157 | 0,89 | 0,3133 | 1,21 | 0,3869 |
| 0,26 | 0,1026 | 0,58 | 0,2190 | 0,90 | 0,3159 | 1,22 | 0,3883 |
| 0,27 | 0,1064 | 0,59 | 0,2224 | 0,91 | 0,3186 | 1,23 | 0,3907 |
| 0,28 | 0,1103 | 0,60 | 0,2257 | 0,92 | 0,3212 | 1,24 | 0,3925 |
| 0,29 | 0,1141 | 0,61 | 0,2291 | 0,93 | 0,3238 | 1,25 | 0,3944 |
| 0,30 | 0,1179 | 0,62 | 0,2324 | 0,94 | 0,3264 | ||
| 0,31 | 0,1217 | 0,63 | 0,2357 | 0,95 | 0,3289 |
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Продолжение таблицы
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 1,26 | 0,3962 | 1,59 | 0,4441 | 1,92 | 0,4726 | 2,50 | 0,4938 |
| 1,27 | 0,3980 | 1,60 | 0,4452 | 1,93 | 0,4732 | 2,52 | 0,4941 |
| 1,28 | 0,3997 | 1,61 | 0,4463 | 1,94 | 0,4738 | 2,54 | 0,4945 |
| 1,29 | 0,4015 | 1,62 | 0,4474 | 1,95 | 0,4744 | 2,56 | 0,4948 |
| 1,30 | 0,4032 | 1,63 | 0,4484 | 1,96 | 0,4750 | 2,58 | 0,4951 |
| 1,31 | 0,4049 | 1,64 | 0,4495 | 1,97 | 0,4756 | 2,60 | 0,4953 |
| 1,32 | 0,4066 | 1,65 | 0,4505 | 1,98 | 0,4761 | 2,62 | 0,4956 |
| 1,33 | 0,4082 | 1,66 | 0,4515 | 1,99 | 0,4767 | 2,64 | 0,4959 |
| 1,34 | 0,4099 | 1,67 | 0,4525 | 2,00 | 0,4772 | 2,66 | 0,4961 |
| 1,35 | 0,4115 | 1,68 | 0,4535 | 2,02 | 0,4783 | 2,68 | 0,4963 |
| 1,36 | 0,4131 | 1,69 | 0,4545 | 2,04 | 0,4793 | 2,70 | 0,4965 |
| 1,37 | 0,4147 | 1,70 | 0,4554 | 2,06 | 0,4803 | 2,72 | 0,4967 |
| 1,38 | 0,4162 | 1,71 | 0,4564 | 2,08 | 0,4812 | -2,74 | 0,4969 |
| 1,39 | 0,4177 | 1,72 | 0,4573 | 2,10 | 0,4821 | 2,76 | 0,4971 |
| 1,40 | 0,4192 | 1,73 | 0,4582 | 2,12 | 0,4830 | 2,78 | 0,4973 |
| 1,41 | 0,4207 | 1,74 | 0,4591 | 2,14 | 0,4838 | 2,80 | 0,4974 |
| 1,42 | 0,4222 | 1,75 | 0,4599 | 2,16 | 0,4846 | 2,82 | 0,4976 |
| 1,43 | 0,4236 | 1,76 | 0,4608 | 2,18 | 0,4854 | 2,84 | 0,4977 |
| 1,44 | 0,4251 | 1,77 | 0,4616 | 2,20 | 0,4861 | 2,86 | 0,4979 |
| 1,45 | 0,4265 | 1,78 | 0,4625 | 2,22 | 0,4868 | 2,88 | 0,4980 |
| 1,46 | 0,4279 | 1,79 | 0,4633 | 2,24 | 0,4875 | 2,90 | 0,4981 |
| 1,47 | 0,4292 | 1,80 | 0,4641 | 2,26 | 0,4881 | 2,92 | 0,4982 |
| 1,48 | 0,4306 | 1,81 | 0,4649 | 2,28 | 0,4887 | 2,94 | 0,4984 |
| 1,49 | 0,4319 | 1,82 | 0,4656 | 2,30 | 0,4893 | 2,96 | 0,4985 |
| 1,50 | 0,4332 | 1,83 | 0,4664 | 2,32 | 0,4898 | 2,98 | 0,4986 |
| 1,51 | 0,4345 | 1,84 | 0,4671 | 2,34 | 0,4904 | 3,00 | 0,49865 |
| 1,52 | 0,4357 | 1,85 | 0,4678 | 2,36 | 0,4909 | 3,20 | 0,49931 |
| 1,53 | 0,4370 | 1,86 | 0,4686 | 2,38 | 0,4913 | 3,40 | 0,49966 |
| 1,54 | 0,4382 | 1,87 | 0,4693 | 2,40 | 0,4918 | 3,60 | 0,499841 |
| 1,55 | 0,4394 | 1,88 | 0,4699 | 2,42 | 0,4922 | 3,80 | 0,499928 |
| 1,56 | 0,4406 | 1,89 | 0,4706 | 2,44 | 0,4927 | 4,00 | 0,499968 |
| 1,57 | 0,4418 | 1,90 | 0,4713 | 2,46 | 0,4931 | 4,50 | 0,499997 |
| 1,58 | 0,4429 | 1,91 | 0,4719 | 2,48 | 0,4934 | 5,00 | 0,499997 |
Таблица лапласа, полная таблица значений функции Лапласа на сайте webmath.
 ru
ruСодержание:
- Объяснение
- Таблица значений функции Лапласа
Таблица значений функции Лапласа — это вероятность того, что случайная величина примет значение, принадлежащее заданному интервалу. При решении задач по теории вероятности, как правило, требуется найти значение функции Лапласа по известному значению аргумента или, наоборот, по известному значению функции Лапласа требуется найти значение аргумента. Для этого пользуются таблицей значений функции Лапласа. Таблица значений функции Лапласа незаменима при изучении теории вероятности, так как решать интеграл (функцию Лапласа) сложно, а запомнить таблицу значений функции Лапласа просто невозможно.
Функцию Лапласа и данную таблицу чаще всего изучают на втором курсе университета, при изучении
математики и теории вероятности, если Вам в данной теме,
что-то не понятно, то Вы всегда можете задать вопрос на нашем
форуме, мы будем рады вам помочь. {2}}{2}} d t$$
{2}}{2}} d t$$
При разных значениях t; F(–t) = –F(t) (функция нормального распределения).
|
|
|
|
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
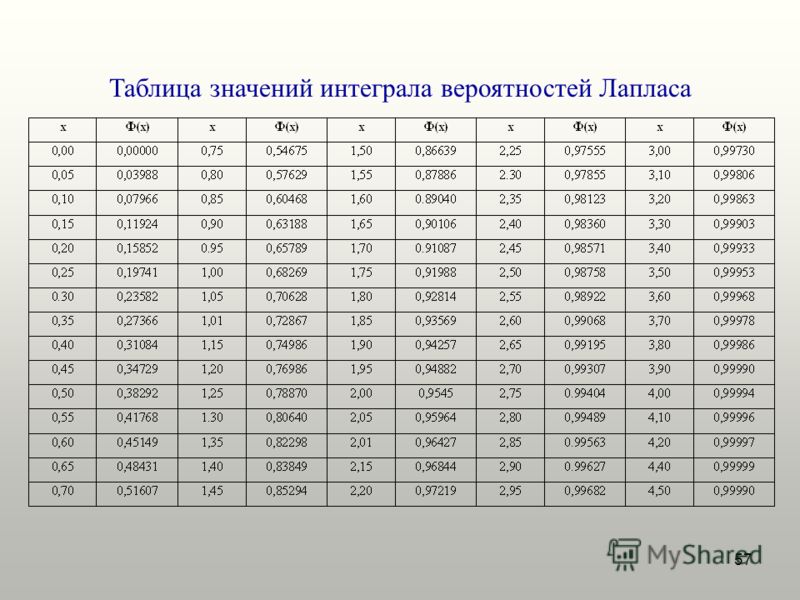
Таблица значений функции Лапласа | matematicus.ru
Artman Таблицы
Таблица значений функции Муавра Лапласа
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 | 0,00000 | 0,50 | 0,19146 | 1,00 | 0,34134 | 1,50 | 0,43319 | 2,00 | 0,47725 | 3,00 | 0,49865 |
| 0,01 | 0,00399 | 0,51 | 0,19497 | 1,01 | 0,34375 | 1,51 | 0,43448 | 2,02 | 0,47831 | 3,05 | 0,49886 |
| 0,02 | 0,00798 | 0,52 | 0,19847 | 1,02 | 0,34614 | 1,52 | 0,43574 | 2,04 | 0,47932 | 3,10 | 0,49903 |
| 0,03 | 0,01197 | 0,53 | 0,20194 | 1,03 | 0,34849 | 1,53 | 0,43699 | 2,06 | 0,48030 | 3,15 | 0,49918 |
| 0,04 | 0,01595 | 0,54 | 0,20540 | 1,04 | 0,35083 | 1,54 | 0,43822 | 2,08 | 0,48124 | 3,20 | 0,49931 |
| 0,05 | 0,01994 | 0,55 | 0,20884 | 1,05 | 0,35314 | 1,55 | 0,43943 | 2,10 | 0,48214 | 3,25 | 0,49942 |
| 0,06 | 0,02392 | 0,56 | 0,21226 | 1,06 | 0,35543 | 1,56 | 0,44062 | 2,12 | 0,48300 | 3,30 | 0,49952 |
| 0,07 | 0,02790 | 0,57 | 0,21566 | 1,07 | 0,35769 | 1,57 | 0,44179 | 2,14 | 0,48382 | 3,35 | 0,49960 |
| 0,08 | 0,03188 | 0,58 | 0,21904 | 1,08 | 0,35993 | 1,58 | 0,44295 | 2,16 | 0,48461 | 3,40 | 0,49966 |
| 0,09 | 0,03586 | 0,59 | 0,22240 | 1,09 | 0,36214 | 1,59 | 0,44408 | 2,18 | 0,48537 | 3,45 | 0,49972 |
| 0,10 | 0,03983 | 0,60 | 0,22575 | 1,10 | 0,36433 | 1,60 | 0,44520 | 2,20 | 0,48610 | 3,50 | 0,49977 |
| 0,11 | 0,04380 | 0,61 | 0,22907 | 1,11 | 0,36650 | 1,61 | 0,44630 | 2,22 | 0,48679 | 3,55 | 0,49981 |
| 0,12 | 0,04776 | 0,62 | 0,23237 | 1,12 | 0,36864 | 1,62 | 0,44738 | 2,24 | 0,48745 | 3,60 | 0,49984 |
| 0,13 | 0,05172 | 0,63 | 0,23565 | 1,13 | 0,37076 | 1,63 | 0,44845 | 2,26 | 0,48809 | 3,65 | 0,49987 |
| 0,14 | 0,05567 | 0,64 | 0,23891 | 1,14 | 0,37286 | 1,64 | 0,44950 | 2,28 | 0,48870 | 3,70 | 0,49989 |
| 0,15 | 0,05962 | 0,65 | 0,24215 | 1,15 | 0,37493 | 1,65 | 0,45053 | 2,30 | 0,48928 | 3,75 | 0,49991 |
| 0,16 | 0,06356 | 0,66 | 0,24537 | 1,16 | 0,37698 | 1,66 | 0,45154 | 2,32 | 0,48983 | 3,80 | 0,49993 |
| 0,17 | 0,06749 | 0,67 | 0,24857 | 1,17 | 0,37900 | 1,67 | 0,45254 | 2,34 | 0,49036 | 3,85 | 0,49994 |
| 0,18 | 0,07142 | 0,68 | 0,25175 | 1,18 | 0,38100 | 1,68 | 0,45352 | 2,36 | 0,49086 | 3,90 | 0,49995 |
| 0,19 | 0,07535 | 0,69 | 0,25490 | 1,19 | 0,38298 | 1,69 | 0,45449 | 2,38 | 0,49134 | 3,95 | 0,49996 |
| 0,20 | 0,07926 | 0,70 | 0,25804 | 1,20 | 0,38493 | 1,70 | 0,45543 | 2,40 | 0,49180 | 4,00 | 0,49997 |
| 0,21 | 0,08317 | 0,71 | 0,26115 | 1,21 | 0,38686 | 1,71 | 0,45637 | 2,42 | 0,49224 | 4,05 | 0,49997 |
| 0,22 | 0,08706 | 0,72 | 0,26424 | 1,22 | 0,38877 | 1,72 | 0,45728 | 2,44 | 0,49266 | 4,10 | 0,49998 |
| 0,23 | 0,09095 | 0,73 | 0,26730 | 1,23 | 0,39065 | 1,73 | 0,45818 | 2,46 | 0,49305 | 4,15 | 0,49998 |
| 0,24 | 0,09483 | 0,74 | 0,27035 | 1,24 | 0,39251 | 1,74 | 0,45907 | 2,48 | 0,49343 | 4,20 | 0,49999 |
| 0,25 | 0,09871 | 0,75 | 0,27337 | 1,25 | 0,39435 | 1,75 | 0,45994 | 2,50 | 0,49379 | 4,25 | 0,49999 |
| 0,26 | 0,10257 | 0,76 | 0,27637 | 1,26 | 0,39617 | 1,76 | 0,46080 | 2,52 | 0,49413 | 4,30 | 0,49999 |
| 0,27 | 0,10642 | 0,77 | 0,27935 | 1,27 | 0,39796 | 1,77 | 0,46164 | 2,54 | 0,49446 | 4,35 | 0,49999 |
| 0,28 | 0,11026 | 0,78 | 0,28230 | 1,28 | 0,39973 | 1,78 | 0,46246 | 2,56 | 0,49477 | 4,40 | 0,49999 |
| 0,29 | 0,11409 | 0,79 | 0,28524 | 1,29 | 0,40147 | 1,79 | 0,46327 | 2,58 | 0,49506 | 4,45 | 0,50000 |
| 0,30 | 0,11791 | 0,80 | 0,28814 | 1,30 | 0,40320 | 1,80 | 0,46407 | 2,60 | 0,49534 | 4,50 | 0,50000 |
| 0,31 | 0,12172 | 0,81 | 0,29103 | 1,31 | 0,40490 | 1,81 | 0,46485 | 2,62 | 0,49560 | 4,55 | 0,50000 |
| 0,32 | 0,12552 | 0,82 | 0,29389 | 1,32 | 0,40658 | 1,82 | 0,46562 | 2,64 | 0,49585 | 4,60 | 0,50000 |
| 0,33 | 0,12930 | 0,83 | 0,29673 | 1,33 | 0,40824 | 1,83 | 0,46638 | 2,66 | 0,49609 | 4,65 | 0,50000 |
| 0,34 | 0,13307 | 0,84 | 0,29955 | 1,34 | 0,40988 | 1,84 | 0,46712 | 2,68 | 0,49632 | 4,70 | 0,50000 |
| 0,35 | 0,13683 | 0,85 | 0,30234 | 1,35 | 0,41149 | 1,85 | 0,46784 | 2,70 | 0,49653 | 4,75 | 0,50000 |
| 0,36 | 0,14058 | 0,86 | 0,30511 | 1,36 | 0,41309 | 1,86 | 0,46856 | 2,72 | 0,49674 | 4,80 | 0,50000 |
| 0,37 | 0,14431 | 0,87 | 0,30785 | 1,37 | 0,41466 | 1,87 | 0,46926 | 2,74 | 0,49693 | 4,85 | 0,50000 |
| 0,38 | 0,14803 | 0,88 | 0,31057 | 1,38 | 0,41621 | 1,88 | 0,46995 | 2,76 | 0,49711 | 4,90 | 0,50000 |
| 0,39 | 0,15173 | 0,89 | 0,31327 | 1,39 | 0,41774 | 1,89 | 0,47062 | 2,78 | 0,49728 | 4,95 | 0,50000 |
| 0,40 | 0,15542 | 0,90 | 0,31594 | 1,40 | 0,41924 | 1,90 | 0,47128 | 2,80 | 0,49744 | 5,00 | 0,50000 |
| 0,41 | 0,15910 | 0,91 | 0,31859 | 1,41 | 0,42073 | 1,91 | 0,47193 | 2,82 | 0,49760 | ||
| 0,42 | 0,16276 | 0,92 | 0,32121 | 1,42 | 0,42220 | 1,92 | 0,47257 | 2,84 | 0,49774 | ||
| 0,43 | 0,16640 | 0,93 | 0,32381 | 1,43 | 0,42364 | 1,93 | 0,47320 | 2,86 | 0,49788 | ||
| 0,44 | 0,17003 | 0,94 | 0,32639 | 1,44 | 0,42507 | 1,94 | 0,47381 | 2,88 | 0,49801 | ||
| 0,45 | 0,17364 | 0,95 | 0,32894 | 1,45 | 0,42647 | 1,95 | 0,47441 | 2,90 | 0,49813 | ||
| 0,46 | 0,17724 | 0,96 | 0,33147 | 1,46 | 0,42785 | 1,96 | 0,47500 | 2,92 | 0,49825 | ||
| 0,47 | 0,18082 | 0,97 | 0,33398 | 1,47 | 0,42922 | 1,97 | 0,47558 | 2,94 | 0,49836 | ||
| 0,48 | 0,18439 | 0,98 | 0,33646 | 1,48 | 0,43056 | 1,98 | 0,47615 | 2,96 | 0,49846 | ||
| 0,49 | 0,18793 | 0,99 | 0,33891 | 1,49 | 0,43189 | 1,99 | 0,47670 | 2,98 | 0,49856 |
21846
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Все разделы / Таблицы функций Лапласа
Таблица значений локальной функции Лапласа Как пользоваться таблицей Скачать таблицу (8Kb) Локальная теорема Лапласа Свойства функции Лапласа Задачи на применение локальной функции Лапласа
Таблица значений интегральной функции Лапласа Как пользоваться таблицей Скачать таблицу (9Kb) Интегральная теорема Лапласа Свойства функции Лапласа Задачи на применение локальной функции Лапласа
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Смотри также
Формула Бернулли Биография Бернулли Якова I
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva. Поделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица преобразования Лапласа ( F(s) = L{ f(t) } )
- Преобразование Лапласа функция
- Таблица преобразования Лапласа
- Свойства преобразования Лапласа
- Преобразование Лапласа примеры
Преобразование Лапласа преобразует функцию временной области в функцию s-области путем интегрирования от нуля до бесконечности
функции временной области, умноженной на e -st .
Преобразование Лапласа используется для быстрого нахождения решений дифференциальных уравнений и интегралов.
Вывод во временной области преобразуется в умножение на s в s-области.
Интегрирование во временной области преобразуется в деление на s в s-области.
Функция преобразования Лапласа
Преобразование Лапласа определяется оператором L {}:
Обратное преобразование Лапласа
Обратное преобразование Лапласа можно вычислить напрямую.
Обычно обратное преобразование дается из таблицы преобразований.
Таблица преобразования Лапласа
| Имя функции | Функция временной области | преобразование Лапласа |
|---|---|---|
ф ( т ) | F ( s ) = L { f ( t )} | |
| Константа | 1 | |
| Линейный | т | |
| Сила | т н | |
| Мощность | т а | Γ( a +1) ⋅ с -( a +1) |
| Экспонента | и по | |
| Синус | грех на | |
| Косинус | соз на | |
| Гиперболический синус | с по | |
| Гиперболический косинус | кош по | |
| Растущий синус | т син ат | |
| Растущий косинус | т соз в | |
| Затухающий синус | е -ат sin ωt | |
| Затухающий косинус | е -ат cos ωt | |
| Дельта-функция | δ( т ) | 1 |
| Дельта с задержкой | δ( т-а ) | е -как |
Свойства преобразования Лапласа
| Имя свойства | Функция временной области | преобразование Лапласа | Комментарий |
|---|---|---|---|
ф ( т ) | Ф ( с ) | ||
| Линейность | а ф ( т )+ бг ( т ) | аФ ( с ) + бГ ( с ) | а , б а константа |
| Смена шкалы | ф ( по ) | а >0 | |
| Смена | е -ат ф ( т ) | Ф ( с + а ) | |
| Задержка | ф ( т-а ) | e — как F ( с ) | |
| Производная | сф ( с ) — ф (0) | ||
| N-ая производная | с н ф ( с ) — s n -1 f (0) — s n -2 f ‘(0)-. ..- ф ( н -1) (0) ..- ф ( н -1) (0) | ||
| Мощность | т н ф ( т ) | ||
| Интеграция | |||
| Обратный | |||
| Свертка | ф ( т ) * г ( т ) | Ф ( с ) ⋅ Г ( с ) | * это свертка оператор |
| Периодическая функция | ф ( т ) = ф ( т + т ) |
Laplace transform examples
Example #1
Find the transform of f(t):
f ( t ) = 3 t + 2 t 2
Solution:
ℒ{ t } = 1/ s 2
ℒ{ t 2 } = 2/ s 3
F ( s ) = ℒ{ f ( t )} = ℒ{3 t + 2 t 2 } = 3ℒ { T } + 2ℒ { T 2 } = 3/ S 2 + 4/ S 3
57574747474747474747474747474747474747474747474747474747474747474747474 474747474747474747474747. F(s):
F(s):F ( с ) = 3 / ( с 2 + s — 6)
Решение:
Чтобы найти обратное преобразование, нам нужно изменить s доменной функции к более простой форме:
F ( с ) = 3 / ( с 2 + s — 6) = 3 / [( s -2)( s +3)] = a / ( s -2) + б / ( с +3)
[ а ( с +3) + б ( с -2)] / [( с -2)] / [( с — +3)] = 3 / [( с -2)( с +3)]
a ( с +3) + b ( с -2) = 3
Чтобы найти a и b, получаем 2 уравнения — одно из s коэффициентов и второе из остальных:
a + B = 0, 3 A -2 B = 3
A = 3/5, B = -3/5
40018 ( S = -3/5
( S = -3/5
( S = -3/5
. ) = 3 / 5( с -2) — 3 / 5( с +3)
Теперь F(s) можно легко преобразовать с помощью таблицы преобразований для экспоненциальной функции:
f ( t ) = (3/5) e 2 t — (3/5) e -3 t
See also
- Производная
- Символы исчисления
6.
 {-st}g(t)=0\) когда \(s>c\). Затем 9{-st}g(t)dt=-g(0)+s \mathcal{L}\{g(t)\}. \nonumber \]
{-st}g(t)=0\) когда \(s>c\). Затем 9{-st}g(t)dt=-g(0)+s \mathcal{L}\{g(t)\}. \nonumber \]Повторим эту процедуру для высших производных. Результаты перечислены в таблице \(\PageIndex{1}\). Процедура также работает для кусочно-гладких функций, то есть функций, кусочно-непрерывных с кусочно-непрерывной производной. Тот факт, что функция имеет экспоненциальный порядок, используется, чтобы показать, что указанные выше пределы существуют. Мы не будем сильно беспокоиться об этом факте.
Решение ОДУ с помощью преобразования Лапласа
Обратите внимание, что преобразование Лапласа превращает дифференцирование в умножение на \(s\). Посмотрим, как применить этот факт к дифференциальным уравнениям.
Пример \(\PageIndex{1}\)
Возьмем уравнение
\[ x»(t) + x(t) = \cos (2t),~~~~~~~ x(0) =0, ~~~~~~~ х'(0)=1. 2X(s) — sx(0) — x'(0)\) и так далее. Решим уравнение для \(X(s)\). Затем, выполняя обратное преобразование, если возможно, находим \(x(t)\).
2X(s) — sx(0) — x'(0)\) и так далее. Решим уравнение для \(X(s)\). Затем, выполняя обратное преобразование, если возможно, находим \(x(t)\).
Следует отметить, что поскольку не каждая функция имеет преобразование Лапласа, не каждое уравнение можно решить таким образом. Также, если уравнение не является линейным постоянным коэффициентом ОДУ, то, применяя преобразование Лапласа, мы можем не получить алгебраическое уравнение.
Использование функции Хевисайда
Прежде чем мы перейдем к более общим уравнениям, чем те, которые мы могли решить раньше, мы хотим рассмотреть функцию Хевисайда. График см. на рисунке \(\PageIndex{1}\).
\[u(t)=\left\{ \begin{array}{cc} 0 & {\rm{if~}}t<0, \\ 1 & {\rm{if~}}t \geq 0 .\end{массив} \right. \nonumber \]
Рисунок \(\PageIndex{1}\): График функции Хевисайда (единичный шаг) \(u(t)\). Эта функция полезна для объединения функций или отключения функций. Чаще всего он используется как \(u(t-a)\) для некоторой константы \(a\). \[f(t)=\left\{ \begin{array}{cc} 0 & {\rm{if~}}t< \pi , \\ \sin t & {\rm{if~}} т \geq \pi . \end{массив} \right. \nonumber \] Используя функцию Хевисайда, \(f(t)\) можно записать как \[ f(t) = u(t- \pi) \sin t \nonumber \] Аналогично ступенчатая функция, равная \(1\) на интервале \([1,2)\) и равная нулю в остальных местах, может быть записана как \[ u(t-1) — u(t-2). \nonumber \] Функция Хевисайда полезна для определения функций, определенных кусочно. Если вы хотите определить \(f(t)\) таким образом, что \(f(t)=t\), когда \(t\) находится в \([0,1]\), \(f(t) = -t +2\), когда \(t\) находится в \([1,2)\) и \(f(t)=0\) в противном случае, вы можете использовать выражение 9{-as} \mathcal{L} \{ f(t) \}. Предположим, что вынуждающая функция не является периодической. Например, предположим, что у нас есть система масса-пружина \[ x»(t) + x(t) = f(t), ~~~~~~ x(0) = 0,~~~~ ~~ x'(0) = 0, \nonumber \] , где \(f(t)=1\), если \(1 \le t < 5\), и ноль в противном случае. Мы могли бы представить систему масса-пружина, в которой ракета запускается в течение 4 секунд, начиная с \(t=1\). Или, возможно, схема RLC, в которой напряжение повышается с постоянной скоростью в течение 4 секунд, начиная с \(t=1\), а затем снова удерживается на одном уровне, начиная с \(t=5\). 9{-5s}\mathcal{L}\{1-\cos t \} \}=(1-\cos(t-5))u(t-5). \nonumber \] Следовательно, решение \[ x(t) = \left( 1 — \cos (t-1) \right) u(t-1) — \left(1-\cos ( t-5) \right) u(t-5). \nonumber \] График этого решения показан на рисунке \(\PageIndex{2}\). Преобразование Лапласа приводит к следующей полезной концепции для изучения стационарного поведения линейной системы. \[ Lx = f(t), \nonnumber \] где \(L\) — линейный дифференциальный оператор с постоянными коэффициентами. Тогда \(f(t)\) обычно считается входом системы, а \(x(t)\) — выходом системы. Например, для системы масса-пружина входом является функция силы, а выходом — поведение массы. Нам хотелось бы иметь удобный способ изучения поведения системы при различных входных данных. Предположим, что все начальные условия равны нулю, и преобразуя уравнение по Лапласу, мы получаем уравнение \[ A(s)X(s) = F(s). \nonumber \] Находя отношение \(\frac{X(s)}{F(s)}\), мы получаем так называемую передаточную функцию \(H(s)=\frac{1} {В качестве)}\). \[ H(s) = \dfrac{X(s)}{F(s)} \nonumber \] Другими словами, \(X(s) = H(s)F(s)\) . Получаем алгебраическую зависимость выхода системы от входа. Теперь мы можем легко изучить стационарное поведение системы при различных входных данных, просто умножив на передаточную функцию. Эта страница под названием 6.2: Преобразования производных и ОДУ распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Йиржи Леблом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу. Частный вид интегрального преобразования известен как преобразование Лапласа , обозначаемое L . Определение этого оператора Результат, называемый преобразованием Лапласа из f — будет функцией p , так что в общем Пример 1 : Найдите преобразование Лапласа функции f ( x ) = x . По определению, Интегрирование по частям дает Следовательно, функция F ( p ) = 1/ p 2 является преобразованием Лапласа функции f ( х ) = х . [Техническое примечание: сходимость несобственного интеграла здесь зависит от положительности p , поскольку только тогда ( x/p ) e − px и e − В общем случае можно показать, что для любого неотрицательного целого числа н , Подобно операторам D и I — впрочем, как и всем операторам — оператор преобразования Лапласа L воздействует на функцию, производя другую функцию. Кроме того, с и оператор преобразования Лапласа L также является линейным. [Техническое примечание: точно так же, как не все функции имеют производные или интегралы, не все функции имеют преобразования Лапласа. Для функции f для преобразования Лапласа достаточно, чтобы f ( x ) было непрерывным (или хотя бы кусочно-непрерывным) для x ≥ 0 и имело экспоненциального порядка (что означает, что для некоторых констант c и λ неравенство выполняется для всех x ). Пример 2 : Найдите преобразование Лапласа функции Отзыв с образованием первого утверждения следующего примера 1 о том, что преобразование Лапласа F ( x ) = x N IS F ( P ) = N N ( P ) = n N ( P ). Пример 3 : Определить преобразование Лапласа f ( x ) = e kx . Применить определение и выполнить интеграцию: Чтобы этот несобственный интеграл сходился, коэффициент ( p – k ) в экспоненте должен быть положительным (вспомним техническое примечание к Примеру 1). Таким образом, для р > k , вычисление дает Пример 4 : Найдите преобразование Лапласа f ( x ) = sin kx . По определению, Этот интеграл вычисляется путем двойного интегрирования по частям следующим образом: значит Следовательно, для p > 0. Аналогичным вычислением можно показать, что Пример 5 : Определение преобразования Лапласа функции изображен на рис. Рисунок 1 Это пример ступенчатой функции . Он не непрерывен, но кусочно непрерывен, а так как он ограничен, то, конечно, имеет экспоненциальный порядок. Следовательно, оно имеет преобразование Лапласа. В таблице 1 собраны преобразования Лапласа нескольких наиболее часто встречающихся функций, а также некоторые важные свойства оператора преобразования Лапласа л . Пример 6 : Используйте Таблицу 1 , чтобы найти преобразование Лапласа f ( x ) = sin 2 x . Вызов тригонометрического тождества линейность L подразумевает Пример 7 : Используйте таблицу 1, чтобы найти преобразование Лапласа для g ( x ) x 3 e 5x . Наличие множителя e 5x предполагает использование формулы сдвига с k = 5 . Переключающая формула говорит, что преобразование Лапласа F ( x ) E 5x = x 3 E 5x E 5 5 E 5 5 E 5 5 . 5). Другими словами, преобразование Лапласа x 3 e 5x равно преобразованию Лапласа x 3 с аргументом p , сдвинутым на p 0 – 1:0 Пример 8 : Используйте таблицу 1, чтобы найти преобразование Лапласа f ( x ) = e −2x sin x – 3, Во-первых, поскольку L [sin x ] = 1/( p 2 + 1), формула сдвига (с к = -2) говорит Теперь, поскольку L [3] = 3 · L [1] = 3/ p , линейность подразумевает Пример 9 : Используйте Таблицу 1 , чтобы найти непрерывную функцию , преобразование Лапласа которой равно F ( p ) = 12 / p 5 . В этом примере представлена идея оператора обратного преобразования Лапласа, , L −1 . Оператор L −1 «отменит» действие L . Символически, Если вы думаете об операторе L как о замене f ( x ) на F ( p ), то оператор L −1 просто меняет P обратно в f ( x ). Как и L , обратный оператор L −1 является линейным. Более формально результат применения L −1 функция F ( p ) предназначена для восстановления непрерывной функции f ( x ), преобразование Лапласа которой является заданным F ( p ). [Эта ситуация должна напомнить вам об операторах D и I (которые, по сути, являются обратными друг другу). Каждый отменит действие другого в том смысле, что если, скажем, I изменит f ( x ) на F ( x ), то D изменит F ( x ) обратно на f ( x ). Используя Таблицу 1 (читая ее слева направо), Пример 10 : Найдите непрерывную функцию, преобразование Лапласа которой равно F ( p ) = 1/( стр 2 – 1). Разложением на неполные дроби, Следовательно, по линейности L −1 , Пример 11 : Определить Во-первых, обратите внимание, что p было сдвинуто на p + 2 = p – (-2). Следовательно, с формула сдвига (с k = −2) подразумевает Пример 12 : Оценить Хотя p 2 – 6 p + 25 нельзя разложить на множители целых чисел, его можно выразить в виде суммы двух квадратов: Следовательно, Использование преобразования Лапласа для решения исходной
Проблемы со стоимостью Теперь, когда мы знаем, как найти преобразование Лапласа, пришло время использовать его для
решать дифференциальные уравнения. Теорема. Преобразование Лапласа
Производной Пусть f(t)
быть непрерывным с f ‘(t)
кусочно-непрерывный. Также предположим, что f(t) < Ke при для некоторого положительного K
и постоянная а.
Затем L{f ‘(t)} = sL(f(t)} — f(0) Доказательство Чтобы доказать эту теорему, мы просто воспользуемся определением преобразования Лапласа и
интегрирование по частям. Мы докажем теорему для случая, когда f’ равно
непрерывный. Если он кусочно непрерывен, мы можем просто разбить интеграл
на части и доказательство аналогично. Для функций f таких, что f,
f’ и f» удовлетворяют
условия теоремы имеем Л{ф
»(t)} = -f ‘(0) + sL{f ‘(t)} = -f ‘(0) + s[-f(0) + sL{f(t)}] Мы будем часто использовать это. Перепишем результат как Этот процесс будет работать и для производных более высокого порядка. С быстрым
по индукции можно показать, что Это говорит нам о том, что если у нас есть дифференциальное уравнение, то
Преобразование Лапласа превратит его в алгебраическое уравнение. Пример Решить у» + у’ —
2y = 4 y(0) =
2 y'(0) = 1 Раствор Мы могли бы решить эту проблему, используя метод
неопределенных коэффициентов, однако это потребует нахождения y h ,
у р , а
две константы. Начнем с применения преобразования Лапласа к обеим сторонам. По линейности
преобразования Лапласа имеем Л{у»}
+ L{y’} — 2L{y} = L{4} Здесь пригодится таблица преобразований Лапласа. Есть в
учебник или вы можете найти его в Интернете здесь.
Получаем (s 2 L{y}
— 2s — 1) + (sL{y} — 2) — 2L{y} = 4/s Затем объедините одинаковые термины, чтобы получить (с 2 + s — 2)L{y} = 4/s + 2s + 3 Обратите внимание, что коэффициент перед L{y} равен
характеристическое уравнение дифференциального уравнения. Это не
стечение обстоятельств. Подведя под общий знаменатель, разделив и разложив мы
получить 2 с 2 + 3 с + 4 Чтобы найти y, нам нужно выполнить обратное преобразование Лапласа правой руки
сторона. 2 с 2 + 3 с +
4
А
B C что дает A(s — 1)(s +
2) + Bs(s + 2) + Cs(s — 1) = 2s 2 + 3s + 4 Пусть s =
0 дает
-2A = 4 A = -2 Пусть s = 1 дает
3B = 9 B = 3 Пусть s =
-2 дает
6C = 6 C = 1 Теперь решим -2 3
1 или -2
3
1 Теперь мы можем использовать таблицу, чтобы получить г
= -2 + 3e t + e -2t Назад
на домашнюю страницу методов степенных рядов и преобразований Лапласа Назад
на домашнюю страницу дифференциальных уравнений Назад к математике
Домашняя страница отдела электронная почта Вопросы и предложения \(\)Приблизительно в 1785 году Пьер-Симон, маркиз де Лаплас, французский математик и физик, первым изобрел метод решения дифференциальных уравнений с использованием интегрального преобразования. В разделах ниже представлены часто используемые свойства, общие функции ввода и начальные/конечные значения.
теоремы ценности, упомянутые в моих различных статьях по электронике. Многие основаны на
отличные заметки группы линейной физики в Swarthmore College, и
воспроизведены здесь в основном для моего собственного понимания и ссылки. Доказательство каждого из этих преобразований можно найти ниже. Из чего следует $$
\def\lfz#1{\overset{\Large#1}{\,\circ\kern-6mu-\kern-7mu-\kern-7mu-\kern-6mu\bullet\,}}
\ деф \ Лаплас {\ lfz {\ mathscr {L}}}
\затененный{
а\cdotf(t)+b\cdotg(t)
\лаплас
a\cdot F(s) + b\cdot G(s)
}
\label{экв:линейность}
$$ Первая производная по времени используется для получения преобразования Лапласа для импеданса конденсатора и катушки индуктивности. Введем \(g(t)=\frac{\mathrm{d}}{\mathrm{d}t}f(t)\) $$
\оставил\{
\начать{выравнивать}
u (t) & = \ frac {\ mathrm {d}} {\ mathrm {d} t} g (t) \ nonumber \\
g (t) & = \ frac {\ mathrm {d}} {\ mathrm {d} t} f (t) \ nonumber
\end{выравнивание}
\Правильно.
$$ Из преобразования первой производной \(\eqref{eq:derivative}\) мы находим преобразования Лапласа \(\frac{\mathrm{d}}{\mathrm{d}t}g(t)\) и \ (\ frac {\ mathrm {d}} {\ mathrm {d} t} f (t) \)
9-} f(\тау)\матрм{д}\тау}
\Правильно)
+
\frac{1}{s}F(s)
\end{выравнивание}
$$ Первый член стремится к нулю, потому что \(f(\infty)\) конечно, что является условием существования преобразования. Во втором члене экспонента равняется единице, а интеграл равен \(0\), поскольку пределы равны. Дает нам перенос Лапласа для свойства свертки $$
\def\lfz#1{\overset{\Large#1}{\,\circ\kern-6mu-\kern-7mu-\kern-7mu-\kern-6mu\bullet\,}}
\ деф \ Лаплас {\ lfz {\ mathscr {L}}}
\затененный{
f(t)\ast g(t)
\лаплас
F(s)\,G(s)
}
\label{eq:свертка}
$$ Импульсная функция \(\delta(t)\) часто используется в качестве теоретического входного сигнала для изучения поведения системы. Определение $$
и (т) = \ дельта (т) =
\begin{случаи}
\mathrm{undefined}, & t=0 \\
0 и \neq 0
\end{случаи}
\label{eq:impuls_def1}
$$
9{\infty}\delta(t)=1\) из \(\eqref{eq:impuls_def2}\) дает нам преобразование Лапласа импульсной функции $$
\def\lfz#1{\overset{\Large#1}{\,\circ\kern-6mu-\kern-7mu-\kern-7mu-\kern-6mu\bullet\,}}
\ деф \ Лаплас {\ lfz {\ mathscr {L}}}
\затененный{
\дельта(т)
\лаплас
1
}
\label{экв:импульс}
$$ Единица или ступенчатая функция Хевисайда, обозначаемая \(\gamma(t)\), определяется как функция \(\gamma(t)\). $$
и(т) = \гамма(т) =
\begin{случаи}
0 & t<0 \\
1 & т\geq 0 \\
\end{случаи}
\label{eq:unitstep_def_a}
$$ Функция единичного шага связана с функцией импульса как
9{-s0}\справа)
= -\frac{1}{s}\left(0-1\right)
\end{выравнивание}
$$ Дает нам перенос Лапласа единичной ступенчатой функции $$
\def\lfz#1{\overset{\Large#1}{\,\circ\kern-6mu-\kern-7mu-\kern-7mu-\kern-6mu\bullet\,}}
\ деф \ Лаплас {\ lfz {\ mathscr {L}}}
\затененный{
\ гамма (т)
\лаплас
\фракция{1}{с}
}
\label{eq:unitstep}
$$ Единица или ступенчатая функция Хевисайда, обозначаемая \(\gamma(t)\), определяется, как показано ниже [smathmore]. Замените \(\eqref{eq:sin3}\) $$
\начать{выравнивать}
Ф (с)
&= \frac{1}{2j}\left( \frac{1}{s-j\omega} \right)
– \frac{1}{2j}\left( \frac{1}{s+j\omega} \right) \nonumber \\
&= \frac{1}{2j}\left( \frac{1}{s-j\omega} – \frac{1}{s+j\omega} \right)
\end{выравнивание}
$$
92}
}\
метка {экв: синус}
$$ Еще одним популярным входным сигналом является косинусоидальная волна, начинающаяся с \(t=0\) $$
u(t) = f(t) = \cos(\omega t)\,\gamma(t)
\label{eq:cos_def}
$$ Преобразование Лапласа косинуса аналогично преобразованию функции синуса, за исключением того, что оно использует тождество Эйлера для косинуса. Мы распознаем экспоненциальные функции и применяем их преобразования Лапласа \(\eqref{eq:exponential}\) $$
\начать{выравнивать}
Ф (с)
&= \frac{1}{2j}\left(
\frac{1}{s-(j\omega-\alpha)}-
\frac{1}{s+(j\omega+\alpha)}
\справа)\номер\\
&= \frac{1}{2j}\left(
\frac{1}{s+\alpha-j\omega}-
\frac{1}{s+\alpha+j\omega}
\Правильно)
\end{выравнивание}
$$ Подведите к общему знаменателю $$
\начать{выравнивать}
Ф (с)
&= \frac{1}{2j}\left(
\frac{1}{s+\alpha-j\omega}-
\frac{1}{s+\alpha+j\omega}
\справа) \номер\\
&= \frac{1}{2j}\left(
\frac{1}{(s+\alpha-j\omega)}\frac{(s+\alpha+j\omega)}{(s+\alpha+j\omega)} —
\frac{1}{(s+\alpha+j\omega)}\frac{(s+\alpha-j\omega)}{(s+\alpha-j\omega)}
\справа) \номер\\
&= \frac{1}{2j}\left(
\frac{(s+\alpha+j\omega) -(s+\alpha-j\omega)}{(s+\alpha)^2-(j\omega)^2}
\Правильно)
=\frac{1}{2j}\left(
\frac{\cancel{s}\cancel{+\alpha}+j\omega\cancel{-s}\cancel{-\alpha}+j\omega}{(s+\alpha)^2+\omega^2 }
\справа) \номер\\
&= \frac{1}{\cancel{2j}}\left(
\frac{\cancel{2j}\omega}{(s+\alpha)^2+\omega^2}
\Правильно)
\end{выравнивание}
$$
9{-\alpha t}\cos(\omega t)\,\gamma(t)
\label{eq:decayingcosine_def}
$$ Преобразование Лапласа затухающего косинуса похоже на преобразование затухающей синусоидальной функции, за исключением того, что оно использует тождество Эйлера для косинуса. Задержка во временной области, начиная с \(t-a=0\) $$
u(t) = f(t-a)\cdot \gamma(t-a)
$$ Функция задержанного шага \(\gamma(t)\) $$
\ гамма (т-а) =
\begin{случаи}
0 & т&а \\
1&t\geq a\\
\end{случаи}
$$
9{-su}\mathrm{d}u}_{F(s)}
\end{выравнивание}
$$ Последний интеграл — это просто определение преобразования Лапласа. Вместе это дает нам преобразование Лапласа функции с задержкой по времени. $$
\def\lfz#1{\overset{\Large#1}{\,\circ\kern-6mu-\kern-7mu-\kern-7mu-\kern-6mu\bullet\,}}
\ деф \ Лаплас {\ lfz {\ mathscr {L}}}
\затененный{
f(t-a)\,\gamma(t-a)
\лаплас
е ^ {-су} F (ы)
}
\label{eq:timedelay}
$$
9+)
знак равно
\lim_{s\to\infty}\left(s\,F(s)\right)
}
\label{eq:начальное значение}
$$ Окончательное значение функции \(f(\infty)\) следует из ее преобразования Лапласа производной \(\eqref{eq:derivative}\). Теорема об окончательном значении выглядит следующим образом: $$
\затененный{
f(\infty) = \lim_{s\to0}\left( s\,F(s) \right)
}
\label{eq:finalvalue}
$$ Предлагаемая следующая литература — Передаточные функции. Математика 340 Дом,
Содержание учебника,
Домашнее задание онлайн Дом Предупреждение: MathJax
требует JavaScript для обработки математики на этой странице. Следующая тема, которую мы рассмотрим в этом семестре, — преобразования Лапласа. Обратите внимание, что преобразование Лапласа переводит функцию одной переменной $t$ в другую
функция переменной $s$. (Именно это и имеется в виду под термином
трансформировать). Также обратите внимание, что преобразование Лапласа функции только
зависит от значений функции при $0\le t$, а не от
значения функции для $t
Есть два способа вычислить преобразование Лапласа. Это долгий путь. Другой способ — искать
ответ в
Таблица преобразований Лапласа, которую я составил
предоставил вам. Это
короткий путь. Конечно, поиск вещей страдает от
недостатком является то, что таблица не может перечислить все функции, но перечисляет достаточно
для наших целей в этом классе. Использование таблицы преобразования Лапласа аналогично
пользоваться таблицей интегралов; вы несете ответственность за манипулирование
выражения, чтобы они соответствовали формам в таблице. Чтобы манипулировать выражениями так
они соответствуют формам в таблице, полезно отметить, что Лапласов
преобразование является линейным оператором. Теорема Пусть $f(t)$ — функция, а $c$ — константа. затем
$$\begin{выравнивание}
{\ mathcal L} \ {f (t) + g (t) \} & = {\ mathcal L} \ {f (t) \} + {\ mathcal L} \ {g (t) \}
\\
{\ mathcal L} \ {cf (t) \} & = c {\ mathcal L} \ {f (t) \}
\end{выравнивание} $$
Это важно
потому что это позволяет нам уменьшить проблему нахождения преобразования Лапласа
сложной функции в набор более простых задач, переписывая
сложная функция как сумма более простых частей.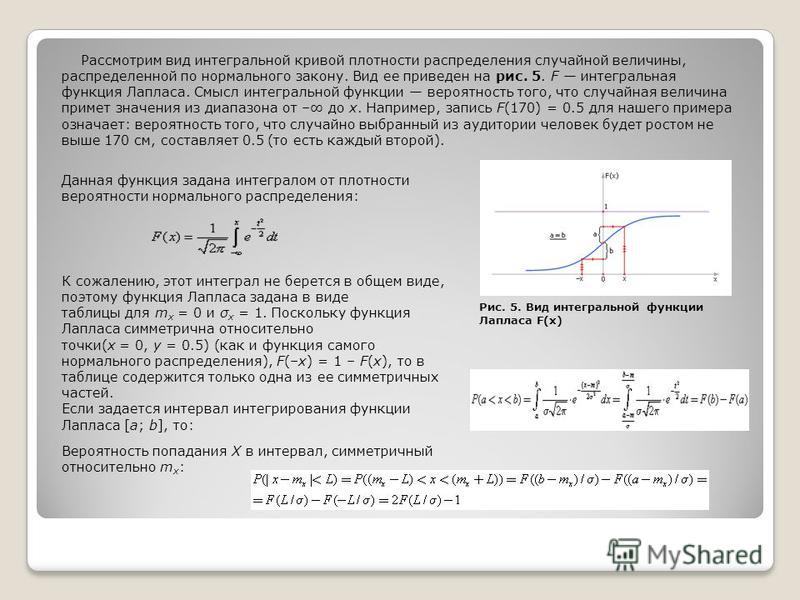 Это просто сдвигает график вправо на \(a\). То есть это функция, которая равна 0, когда \(
Это просто сдвигает график вправо на \(a\). То есть это функция, которая равна 0, когда \( \]
\] Пример \(\PageIndex{2}\)
Передаточные функции
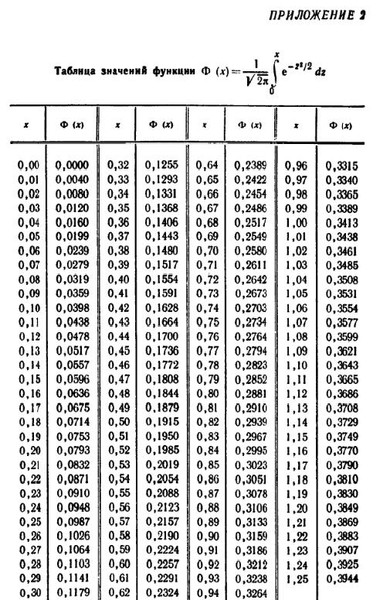 Предположим, у нас есть уравнение вида
Предположим, у нас есть уравнение вида 9{-т}т. \номер\]
9{-т}т. \номер\] jirka.org/diffyqs
jirka.org/diffyqs Оператор преобразования Лапласа
4 px приближаются к конечный предел (а именно 0) как x → ∞.  Следовательно, преобразование Лапласа f ( x ) = x определено только для p > 0.]
Следовательно, преобразование Лапласа f ( x ) = x определено только для p > 0.] Любая ограниченная функция (то есть любая функция f , которая всегда удовлетворяет условию | f ( x )| ≤ M для некоторого M ≥ 0) автоматически имеет экспоненциальный порядок (просто возьмите c = M и λ = 0 в определяющем неравенстве). Следовательно, sin kx и cos kx имеют преобразование Лапласа, поскольку они являются непрерывными и ограниченными функциями. Кроме того, любая функция вида e kx , как и любой многочлен, непрерывна и, хотя и неограничена, имеет экспоненциальный порядок и, следовательно, имеет преобразование Лапласа. Короче говоря, большинство функций, с которыми вы, вероятно, столкнетесь на практике, будут иметь преобразования Лапласа.]
Любая ограниченная функция (то есть любая функция f , которая всегда удовлетворяет условию | f ( x )| ≤ M для некоторого M ≥ 0) автоматически имеет экспоненциальный порядок (просто возьмите c = M и λ = 0 в определяющем неравенстве). Следовательно, sin kx и cos kx имеют преобразование Лапласа, поскольку они являются непрерывными и ограниченными функциями. Кроме того, любая функция вида e kx , как и любой многочлен, непрерывна и, хотя и неограничена, имеет экспоненциальный порядок и, следовательно, имеет преобразование Лапласа. Короче говоря, большинство функций, с которыми вы, вероятно, столкнетесь на практике, будут иметь преобразования Лапласа.]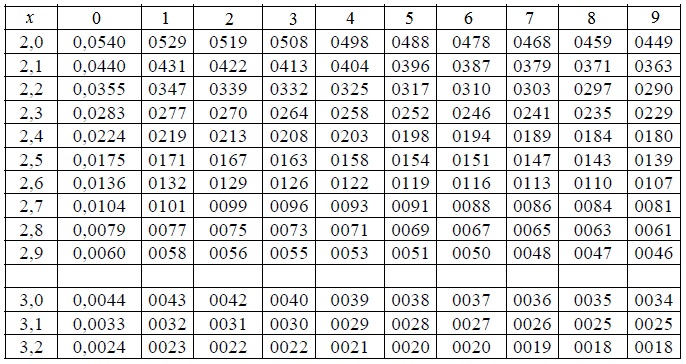 n + 1 . Следовательно, поскольку оператор преобразования Лапласа L линейный,
n + 1 . Следовательно, поскольку оператор преобразования Лапласа L линейный,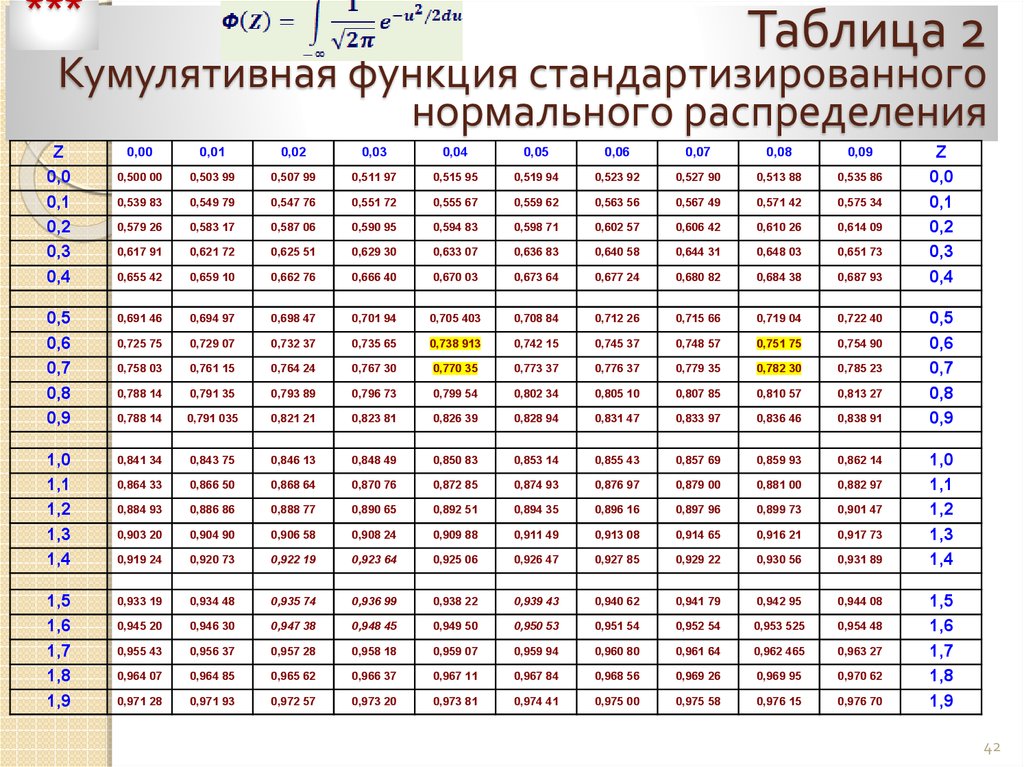 1:
1: С
С
 Другими словами, D = I −1 , поэтому, если вы примените I , а затем D , вы вернетесь к тому, с чего начали.]
Другими словами, D = I −1 , поэтому, если вы примените I , а затем D , вы вернетесь к тому, с чего начали.] Использование преобразования Лапласа для решения задач с начальными значениями
 Ключевая особенность преобразования Лапласа
что делает его инструментом для решения дифференциальных уравнений, является то, что Лаплас
преобразование производной функции является алгебраическим выражением, а не
дифференциальное выражение. У нас есть
Ключевая особенность преобразования Лапласа
что делает его инструментом для решения дифференциальных уравнений, является то, что Лаплас
преобразование производной функции является алгебраическим выражением, а не
дифференциальное выражение. У нас есть У нас есть
У нас есть L{f »(t)} = s 2 L{f(t)} — sf(0) — f
‘(0) Л{ф (n) (t)} = s n L{f(t)} — s n-1 f
(0) — … — сф (н-2) (0) — ф (н-1) (0)  Вместо этого мы увидим, что метод преобразований Лапласа
решает всю проблему одним махом.
Вместо этого мы увидим, что метод преобразований Лапласа
решает всю проблему одним махом.
L{y} =
с(с — 1)(с + 2)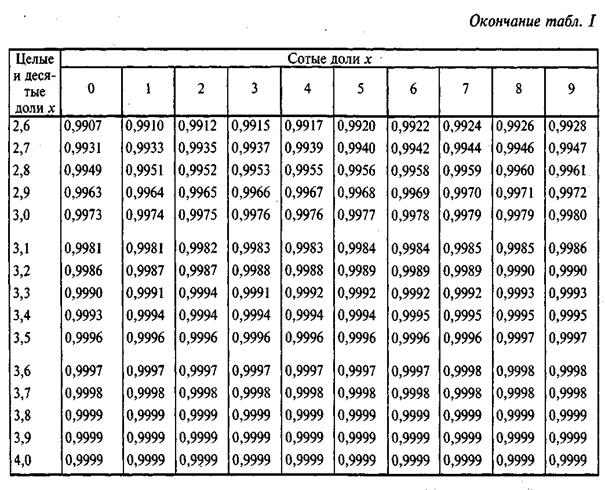 К сожалению, найти функцию y, правая часть которой равна
преобразование Лапласа y — непростая задача. Техника, которая просто
о всегда работает частично
дроби. Мы пишем
К сожалению, найти функцию y, правая часть которой равна
преобразование Лапласа y — непростая задача. Техника, которая просто
о всегда работает частично
дроби. Мы пишем
знак равно
+
+
с(с — 1)(с +
2)
SS —
1 с + 2
Л{у}
знак равно
+
+
SS —
1 с + 2
у
= L -1 + Л -1 + L -1
SS
— 1 с + 2 Преобразование Лапласа, доказательство свойств и функций
 Это преобразование Лапласа превращает дифференциальные уравнения во времени в алгебраические уравнения в области Лапласа, что упрощает их решение.
9-\) подчеркивает, что значение в \(t=0\) полностью захвачено преобразованием.
Это преобразование Лапласа превращает дифференциальные уравнения во времени в алгебраические уравнения в области Лапласа, что упрощает их решение.
9-\) подчеркивает, что значение в \(t=0\) полностью захвачено преобразованием. Обзор
Характеристики
Временная область Домен Лапласа Линейность $$a\cdot f(t)+b\cdot g(t)\nonumber$$ $$a\cdot F(s) + b\cdot G(s)\nonumber$$ доказательство 9t f(\tau)\mathrm{\tau}\nonumber$$ $$\frac{1}{s}F(s)\nonumber$$ доказательство Свертка $$f(t)\ast g(t)\nonumber$$ $$F(s)\,G(s)\номер$$ доказательство Функции
г. 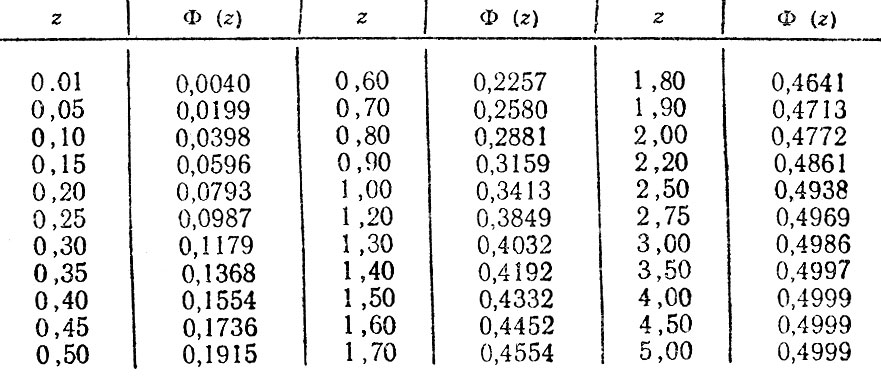
Временная область Домен Лапласа Импульс $$\дельта(т)\номер$$ $$1\номер$$ доказательство Шаг блока $$\gamma(t)\номер$$ $$\frac{1}{s}\nonumber$$ 9+)\номер$$ $$\номер$$ доказательство Окончательное значение $$f(\infty)\nonumber$$ $$\номер$$ доказательство Доказательства собственности
Свойство линейности
9{-st}\mathrm{d}t}_{G(s)}
\end{выравнивание}
$$
Первое производное свойство
 -)
}
\label{экв: производная}
$$
92}f(t)
$$
-)
}
\label{экв: производная}
$$
92}f(t)
$$ т f (\ тау) \ mathrm {\ тау}
\лаплас
\frac{1}{s}F(s)
}
\label{eq:интеграция}
$$
9{-su}\mathrm{d}u}_{G(s)} &\mathrm{это\ являются\ преобразованиями Лапласа}
\end{выравнивание}
$$
т f (\ тау) \ mathrm {\ тау}
\лаплас
\frac{1}{s}F(s)
}
\label{eq:интеграция}
$$
9{-su}\mathrm{d}u}_{G(s)} &\mathrm{это\ являются\ преобразованиями Лапласа}
\end{выравнивание}
$$ Функциональные доказательства
Импульсная функция
Функция единичного шага
Функция рампы
 {-st}\sin(\omega t)
\,\mathrm{d}t
\end{align}\label{eq:sinlaplace}
$$
9{-(s+a) t}\,\mathrm{d}t = \frac{1}{s+a} ,\ a
\label{eq:sin3}
$$
{-st}\sin(\omega t)
\,\mathrm{d}t
\end{align}\label{eq:sinlaplace}
$$
9{-(s+a) t}\,\mathrm{d}t = \frac{1}{s+a} ,\ a
\label{eq:sin3}
$$ Функция косинуса
 9{-(j\omega+\alpha) t}\right)\gamma(t)
\end{выравнивание}
$$
9{-(j\omega+\alpha) t}\right)\gamma(t)
\end{выравнивание}
$$ 2}
\конец{выравнивание*}
}
\label{eq:распадающийсякосинус}
$$
2}
\конец{выравнивание*}
}
\label{eq:распадающийсякосинус}
$$ Функция задержки времени
Теорема конечного значения
 -)
\end{выравнивание}
$$
9-)}
\end{выравнивание}
$$
-)
\end{выравнивание}
$$
9-)}
\end{выравнивание}
$$ Элементарные дифференциальные уравнения
Если ваш браузер поддерживает JavaScript, убедитесь, что он включен. Преобразования Лапласа
Обсуждение
 Это
метод решения дифференциальных уравнений, который сильно отличается от любого из
методы, которые мы использовали ранее, но имеет очень много важных
Приложения. Это также самый простой из целого семейства методов.
называются методами преобразования. Преобразование Лапласа — единственное, что мы будем
использовать в этом классе.
Пусть $f(t)$ — функция. 9{-ст}\,дт$$
Нам следует побеспокоиться о сходимости несобственного интеграла, но мы не будем
в этом курсе, пока вы обещаете мне помнить, что конвергенция
возможная проблема, которую следует рассмотреть на более поздних курсах, где у вас есть
больше времени на эту тему. Если вы хотите обсудить конвергенцию сейчас,
Вы можете зайти в мой офис.
Это
метод решения дифференциальных уравнений, который сильно отличается от любого из
методы, которые мы использовали ранее, но имеет очень много важных
Приложения. Это также самый простой из целого семейства методов.
называются методами преобразования. Преобразование Лапласа — единственное, что мы будем
использовать в этом классе.
Пусть $f(t)$ — функция. 9{-ст}\,дт$$
Нам следует побеспокоиться о сходимости несобственного интеграла, но мы не будем
в этом курсе, пока вы обещаете мне помнить, что конвергенция
возможная проблема, которую следует рассмотреть на более поздних курсах, где у вас есть
больше времени на эту тему. Если вы хотите обсудить конвергенцию сейчас,
Вы можете зайти в мой офис. Один из способов — вычислить
неправильный интеграл.
9{\ бесконечность} \\
&=\frac{1}{s-r}
\end{выравнивание} $$
при $s>r$ (иначе интеграл расходится и преобразование Лапласа
неопределенный).
Один из способов — вычислить
неправильный интеграл.
9{\ бесконечность} \\
&=\frac{1}{s-r}
\end{выравнивание} $$
при $s>r$ (иначе интеграл расходится и преобразование Лапласа
неопределенный).

 05
05 10348
10348 22
22 23582
23582 39
39 36164
36164 56
56 47783
47783 73
73 58206
58206 90
90 67291
67291 05
05 74152
74152 22
22 80640
80640 39
39 85844
85844 56
56 89899
89899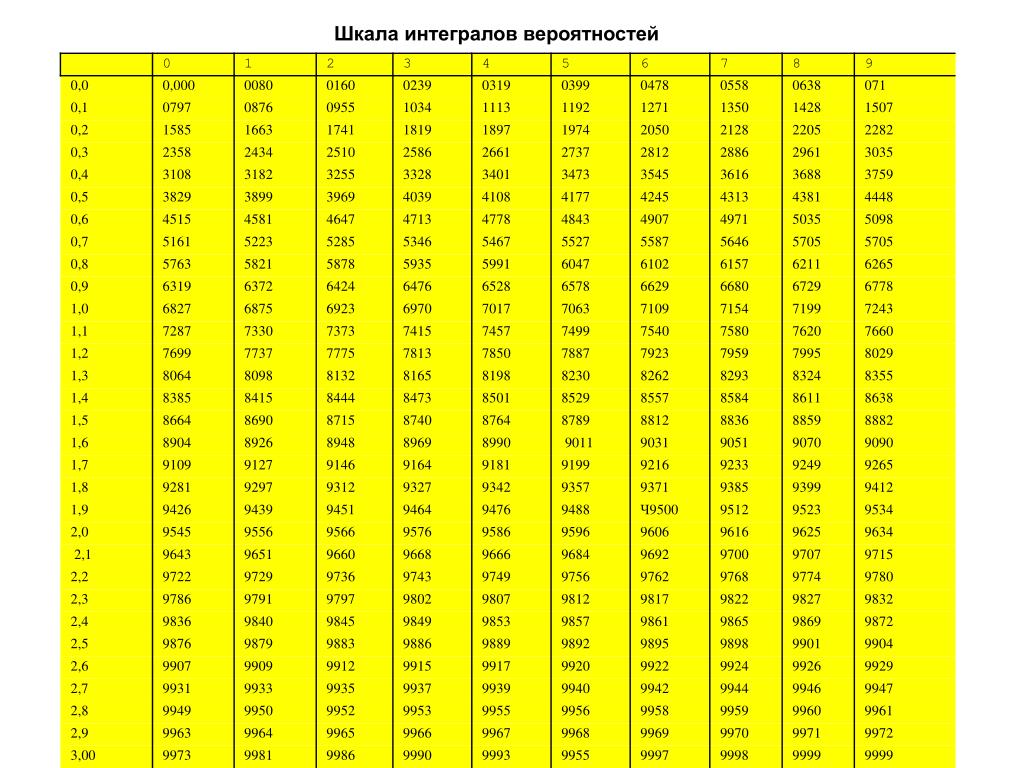 73
73 92970
92970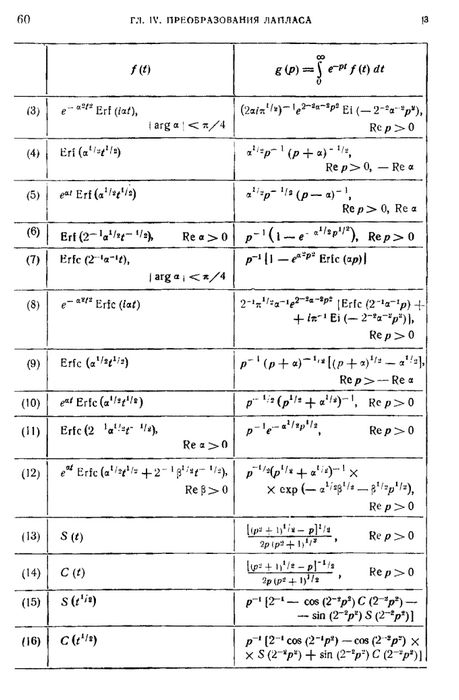 90
90 95230
95230 05
05 96683
96683 22
22 97855
97855 39
39 98649
98649 56
56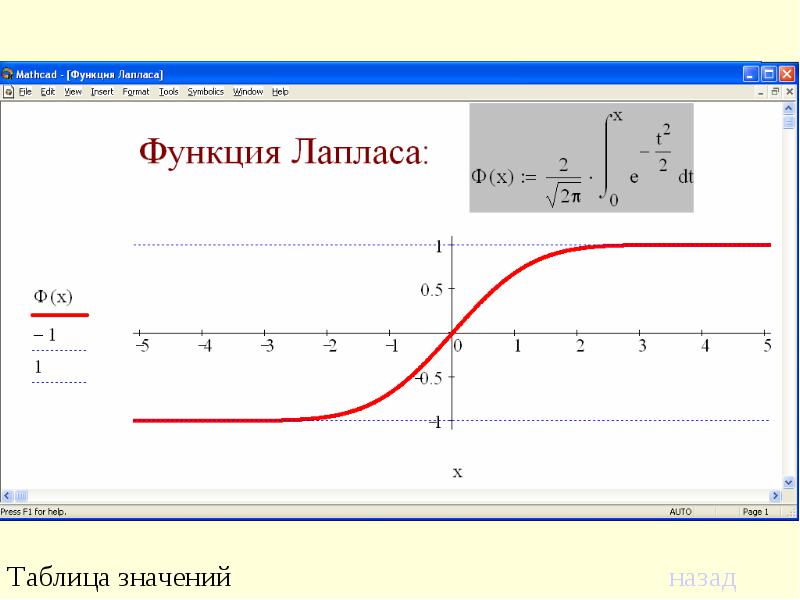 99171
99171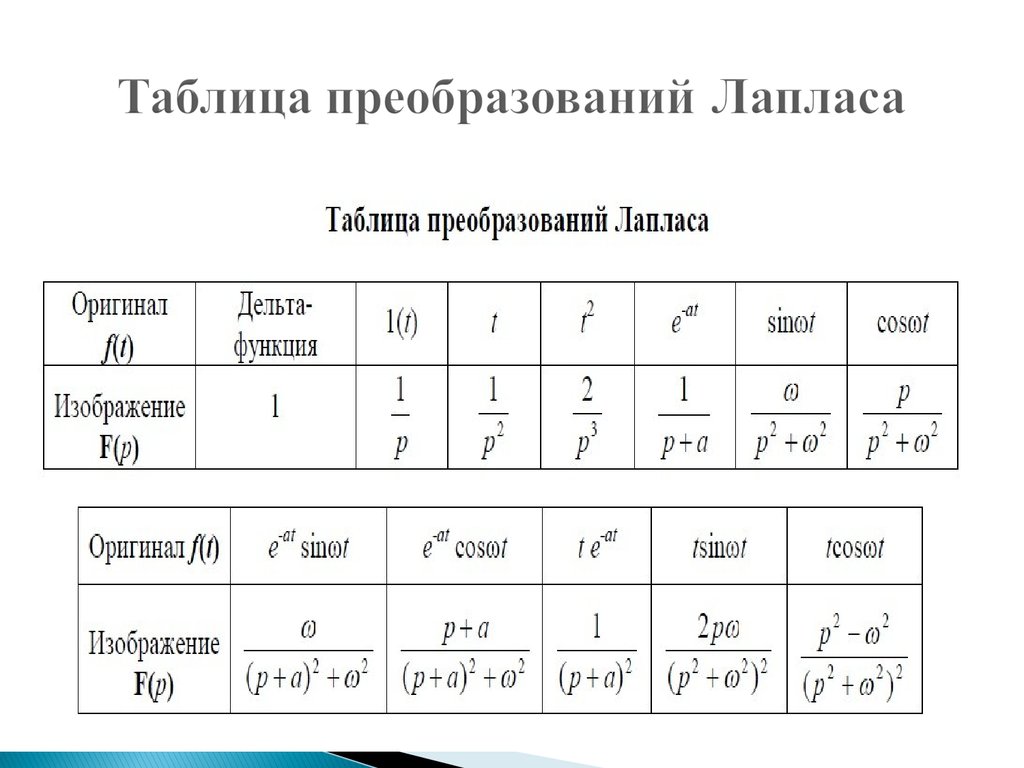 73
73 99505
99505 90
90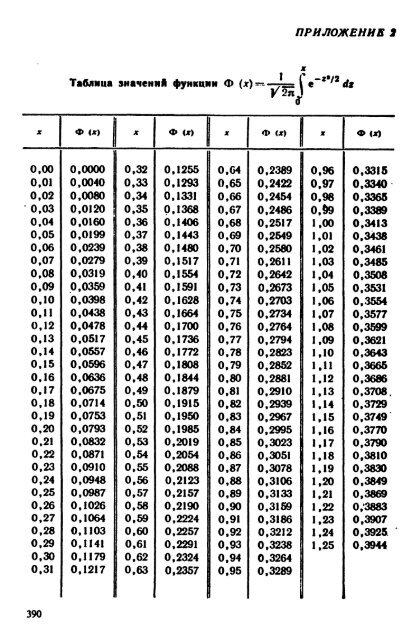 99712
99712 05
05 99825
99825 22
22 99903
99903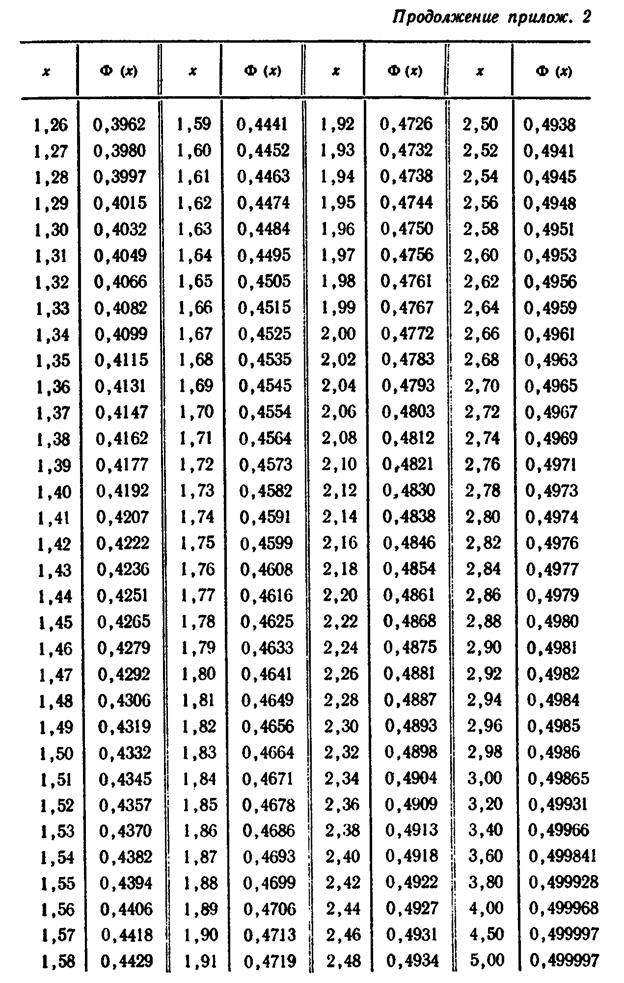 39
39 99948
99948 56
56 99973
99973 73
73 99986
99986 90
90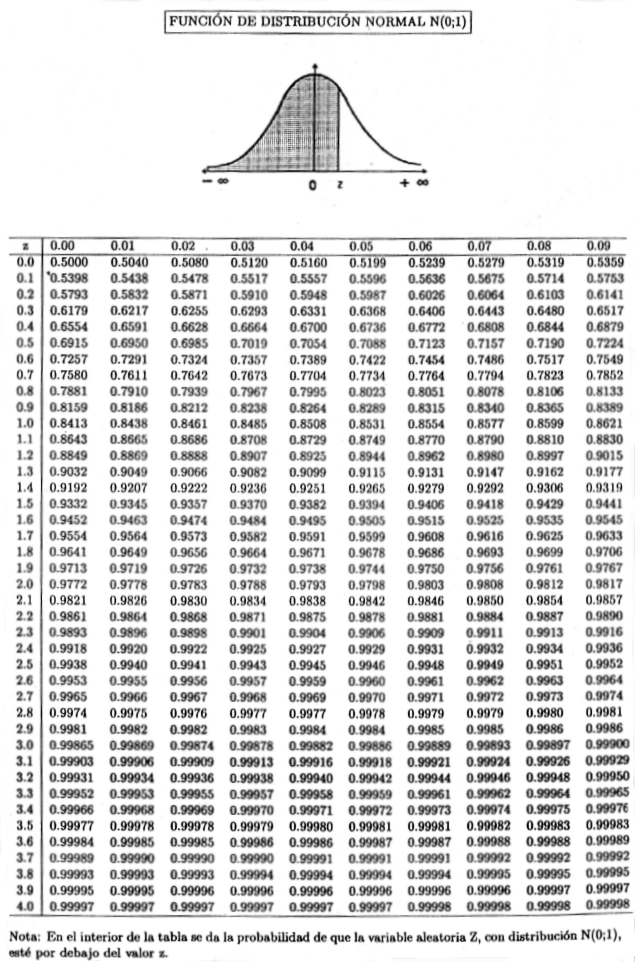 99993
99993 ru
решение математики и теории вероятностей на заказ
ru
решение математики и теории вероятностей на заказ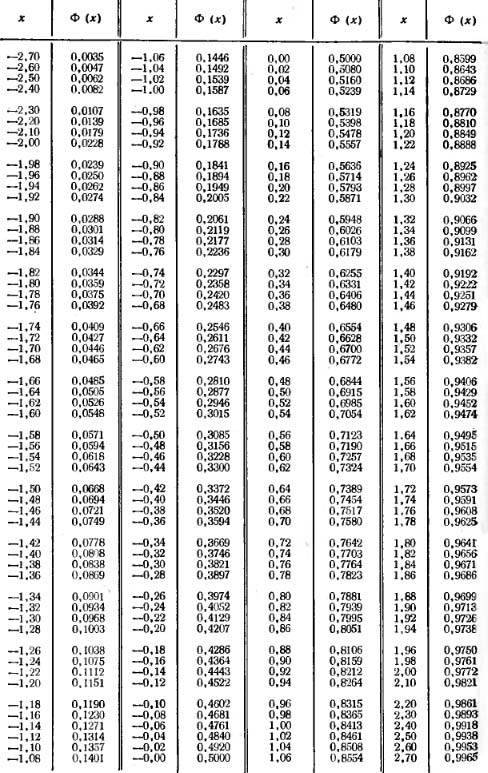 ru
— решение математики и теории вероятностей на заказ
ru
— решение математики и теории вероятностей на заказ ru: главная страница / / Техническая информация/ / Математический справочник / / Теория вероятностей. Математическая статистика. Комбинаторика. / / Таблица. Нормированный интеграл вероятностей (нормированная функция Лапласа). Таблица значений нормированной функции Лапласа. Она же нормированная функция ошибок.
ru: главная страница / / Техническая информация/ / Математический справочник / / Теория вероятностей. Математическая статистика. Комбинаторика. / / Таблица. Нормированный интеграл вероятностей (нормированная функция Лапласа). Таблица значений нормированной функции Лапласа. Она же нормированная функция ошибок.