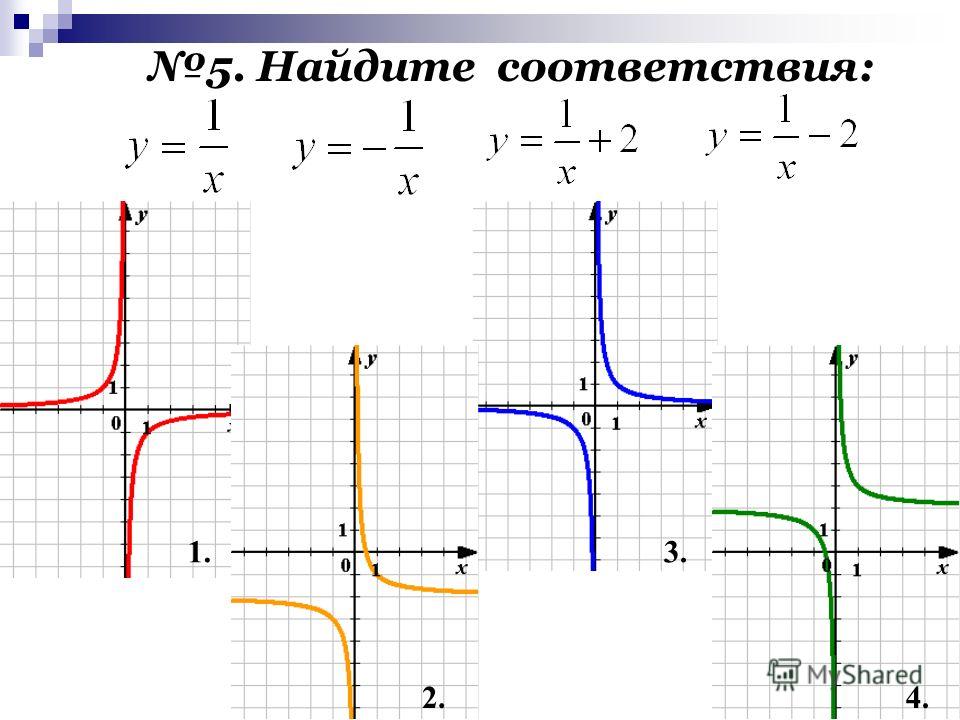
Гипербола x y 1 x: Гипербола в Математике. Формула, примеры, уравнение.

2

Гипербола

К содержанию

Гипербола — это плоская кривая второго порядка, которая состоит из двух отдельных кривых, которые не пересекаются.
Формула гиперболы y = k/x, при условии, что k не равно 0. То есть вершины гиперболы стремятся к нолю, но никогда не пересекаются с ним.

Гипербола — это множество точек плоскости, модуль разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.

Основные понятия

1. Гипербола состоит из двух отдельных кривых, которые называют ветвями.
2. Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
3. Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
4. Середина большой оси называется центром гиперболы.
5. Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы. Обычно обозначается a.
6. Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием. Обычно обозначается c.
7. Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.
8. Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой или сопряженной осью гиперболы.
9. Отрезок между фокусом гиперболы и гиперболой, перпендикулярный к её действительной оси, называется фокальным параметром.
10. Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром. Обычно обозначается b.

• Каноническое уравнение гиперболы в декартовых координатах:

x² / a² — y² / b² = 1

• Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:

x_ox / a² — y_oy / b² = 1

или

y = y_o + (b²x_o)(x — x_o) / (a²y_o)

• Уравнение нормали к гиперболе имеет вид:

y = y_o — (a²y_o)(x — x_o) / (b²x_o)

Некоторые типы гипербол

Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением:

xy = a² / 2,

при этом фокусы гиперболы располагаются в точках (a, a)

и (−a,−a).

Гиперболы, связанные с треугольником:

1. гипербола Енжабека — кривая, изогонально сопряженная прямой Эйлера.
2. гипербола Киперта — кривая, изогонально сопряженная прямой проходящей через точку Лемуана и центр описанной окружности данного треугольника.

Свойства гиперболы

1. Оптическое свойство: свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
   Иначе говоря, если F1 и F2 фокусы гиперболы, то касательная в любой точки X гиперболы является биссектрисой угла ∠F1XF2.
2. Для любой точки, лежащей на гиперболе, отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
3. Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей
   , а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
4. Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними.

---

Другие заметки по алгебре и геометрии

Полезная информация?

есть ли связь между графиком y=1/x и гиперболой? если да то объясните как?

Гипербола

Каснов В.

спросил 29.09.13

есть ли график с таким же описанием?

 

Подписаться І 2

Подробнее

Отчет

1 ответ эксперта

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Роберт Дж. ответил 29.09.13

Репетитор

4.6 (13)

Сертифицированный учитель исчисления и физики средней школы AP

См. таких репетиторов

Смотрите таких репетиторов

На этот вопрос Дюк ответил пять лет назад. Вот копия его ответа: 92/2 = 1. Эта гипербола имеет центр в начале координат, а фокусы находятся на оси x. Он симметричен относительно оси x (поэтому «открывается» влево и вправо).
Если вы возьмете эту гиперболу и повернете ее на 45 градусов против часовой стрелки, вы можете показать, что уравнение принимает вид
xy = 1. Что можно записать как y = 1/x. («Перекрестный термин» xy указывает на то, что он был повернут).

Гипербола принадлежит к тому же классу, что и окружность, эллипс и парабола. Они известны как «конические сечения» (поскольку их можно получить путем пересечения конуса и плоскости), и все они имеют уравнения второй степени.

Наиболее общее уравнение этого класса: 9Икс.
Если f(x) = 1/x, то обратной функцией f является сама функция ! А именно
г(х) = 1/х. Вы видите, например, что f(2)=1/2, а затем g(1/2) = 2. В общем, g(f(x)) будет = g(1/x) = 1/(1/ х) = х.

Функции обычно не называют «обратными». Взаимное обычно означает просто 1 больше количества. Таким образом, с алгебраической точки зрения, если y = 1/x, то x и y обратны, но это не имеет ничего общего с классификацией этой функции».

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.

Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

конических сечений — Как уравнение гиперболы может быть $xy=1$?

спросил 6 лет, 1 месяц назад

Изменено 6 лет, 1 месяц назад 92+Dx+Ey=F$. Тогда это уравнение можно записать в виде $$q(x,y)=\begin{pmatrix}x&y\end{pmatrix}\begin{pmatrix}A&B\\B&C\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}+\ begin{pmatrix}D&E\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}=F$$ Найдите собственные значения и собственные векторы $\begin{pmatrix}A&B\\B&C\end{pmatrix}$, а именно $v_1,\lambda_1,v_2,\lambda_2$ . Тогда матрица вращения $R$ может быть определена как $$R=\begin{pmatrix}\frac{v_1}{|v_1|}&\frac{v_2}{|v_2|}\end{pmatrix}\text{ if }\det\begin{pmatrix}\frac{ v_1}{|v_1|}&\frac{v_2}{|v_2|}\end{pmatrix}=1$$ $$R=\begin{pmatrix}\frac{v_1}{|v_1|}&-\frac{v_2}{|v_2|}\end{pmatrix}\text{ if }\det\begin{pmatrix}\frac {v_1}{|v_1|}&\frac{v_2}{|v_2|}\end{pmatrix}=-1$$ Таким образом, $\begin{pmatrix}x\\y\end{pmatrix}=R\begin{pmatrix}u\\v\end{pmatrix}$.