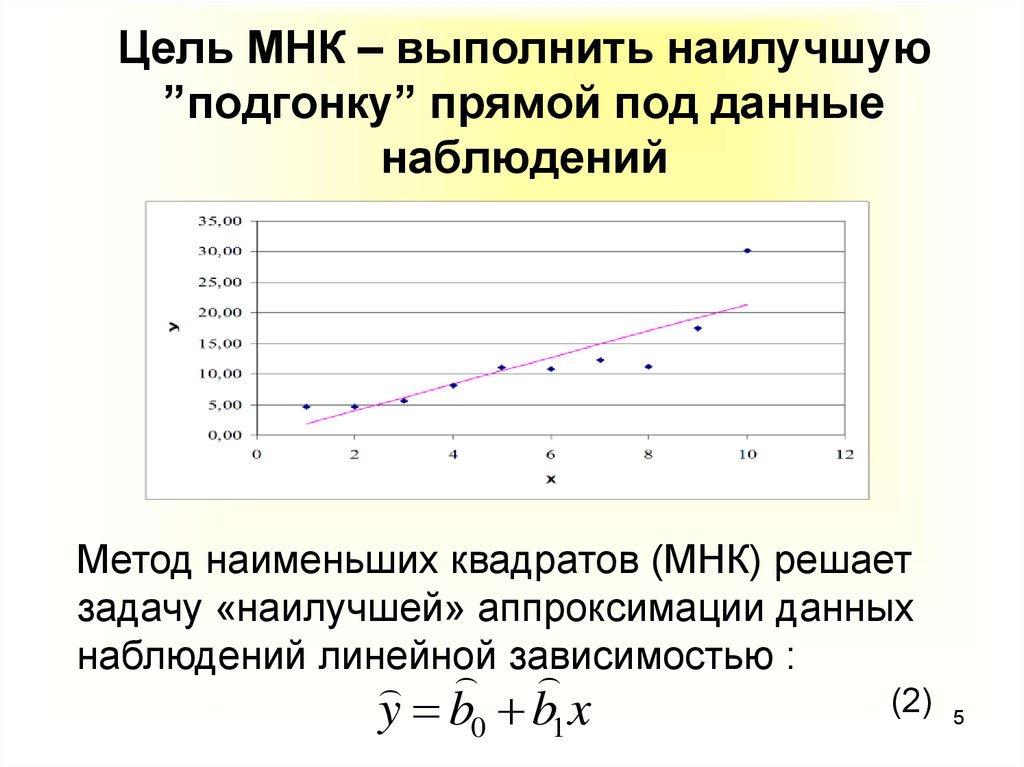
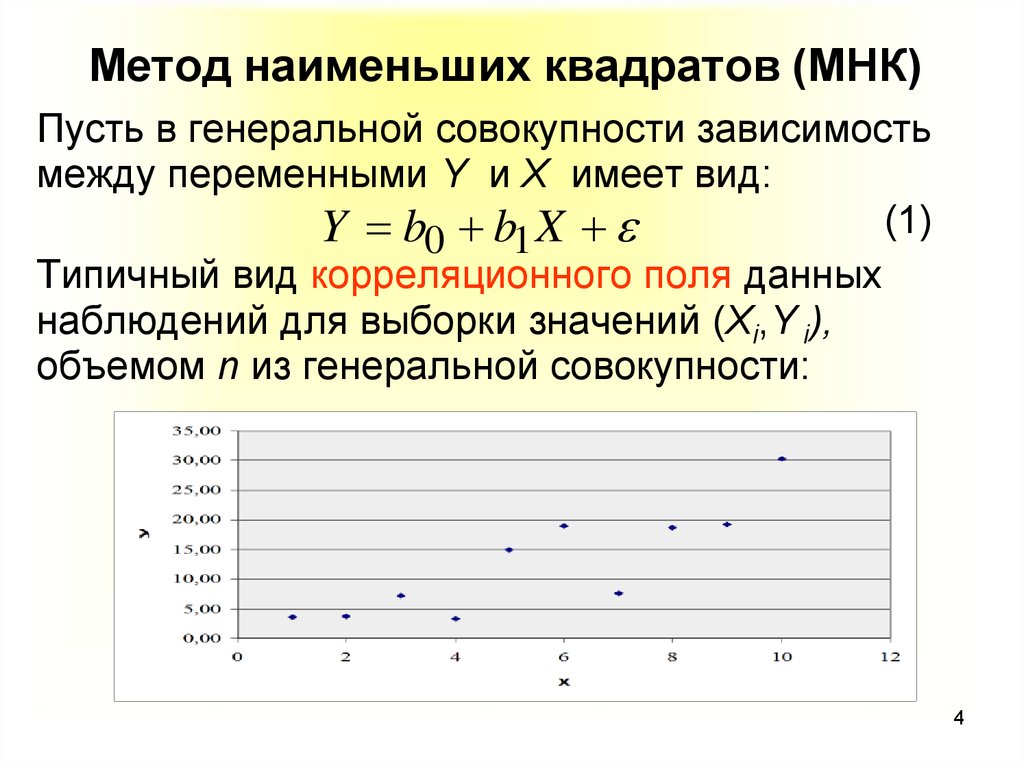
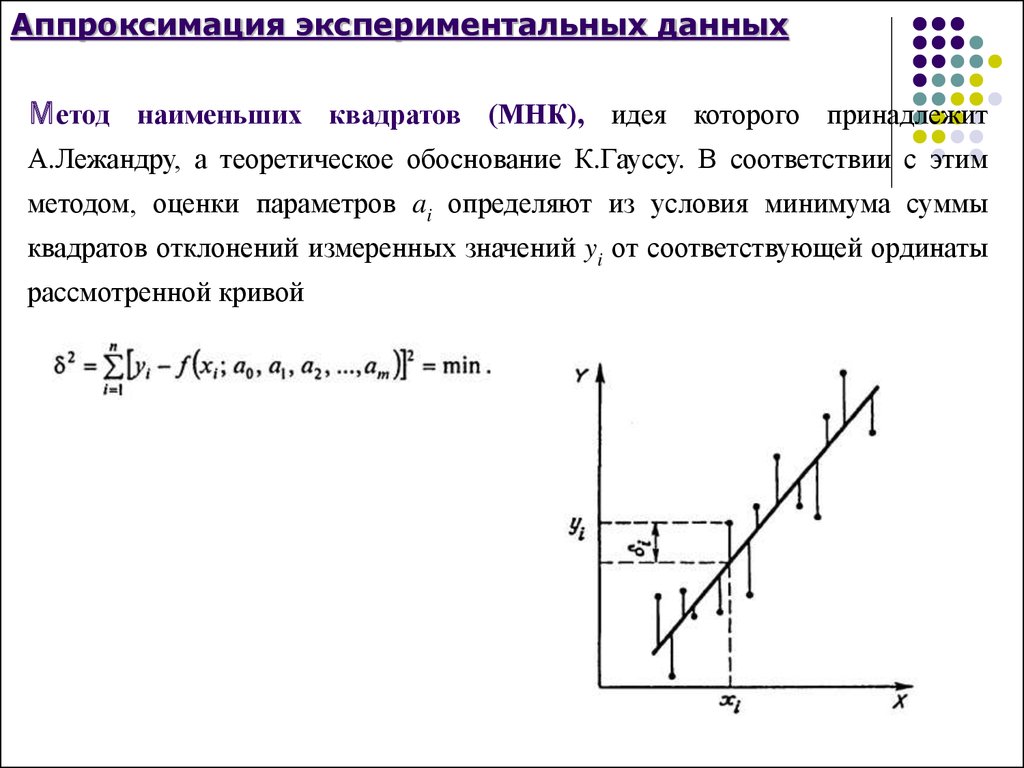
6.6. Линейная аппроксимация по мнк
Пусть зависимоcть y от x задана в дискретной форме: {x1, y1; x2,y2; … xn,yn}. По этим данным можно построить такую аппроксимирующую функцию, график которой будет располагаться между узлами интерполяции близко к ним, но не обязательно точно проходить через все узлы. Такая зависимость носит сглаживающий характер и строится, например, для того, чтобы описать экспериментальные данные с помощью функции заданного вида. Необходимо определить лишь параметры этой функции. Для решения такой задачи используется метод наименьших квадратов — МНК. Его суть заключается в минимизации полной квадратичной невязки между построенной функцией и значениями yi в узловых точках:
где F(x) – искомая аппроксимирующая функция.
Часто в качестве приближения, строящегося по МНК, берутся полиномы степени l, , гдеl<n-1. В простейшем случае строится полином первой степени, т.е. линейная функция: F(x) =ax+b. Коэффициенты a и b находятся с помощью метода наименьших квадратов по следующим формулам:
, .
Для нахождения коэффициентов, можно использовать стандартные функции системы MathCAD и Excel.
В MathCAD имеется функция line(vx, vy), которая возвращает линейные коэффициенты по значениям векторных аргументов vx и vy.
В Excel
имеется функция ЛИНЕЙН, у которой также
имеются два аргумента, состоящих из
диапазонов ячеек. На первом месте
диапазон ячеек соответствующий ординате.
После ввода этой функции (например,
«=ЛИНЕЙН(F10:F12;E1:E3)» ) выводится только
один линейный коэффициент.
Лабораторная работа №8
Используя исходные данные из предыдущей работы, построить линейную функцию по методу наименьших квадратов. Вычислить полную квадратичную невязку полученной функции. Вычислить значение функции при заданном значении аргумента.
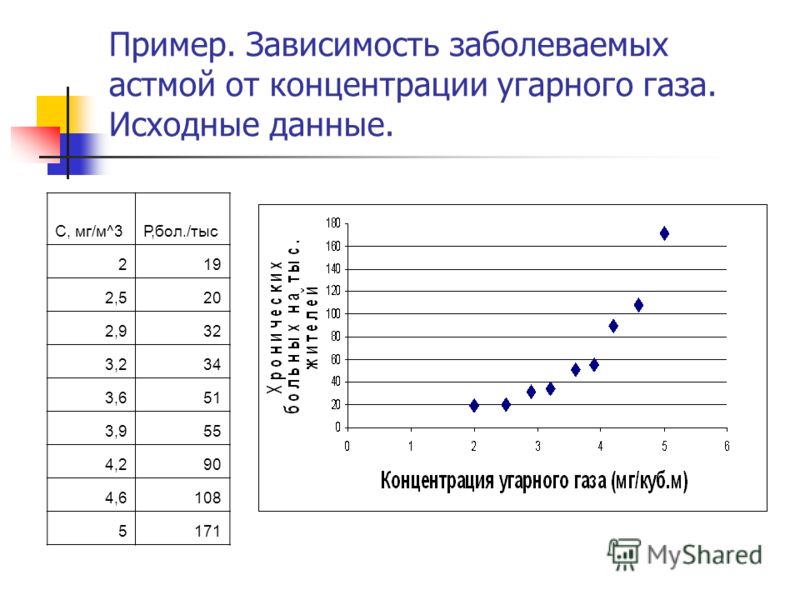
Физическая задача №3
Полагаем, что измерение интенсивности радиоактивного распада было выполнено для (К+1) моментов времени с заданным интервалом времени . Эти измерения дали таблицу, состоящую из К+1 (К=3-5) значений количества распадовдля моментов времени.
Используя метод наименьших квадратов, определить константу распада, период полураспада и значение суммы квадратов невязок.
Знание закона радиоактивного распада
(1)
подсказывает
вычислить значения
и использовать метод наименьших
квадратов для величин,
отыскивая параметры линейной зависимости. Тангенс угла наклона линейной зависимости
определяет константу радиоактивного
распада.
Тангенс угла наклона линейной зависимости
определяет константу радиоактивного
распада.
В отчете должен быть представлен график прямой вместе с экспериментальными точками. Заметим, что закон радиоактивного распада является вероятностным и выполняется сравнительно точно для больших значений. Периоды полураспада радиоактивных изотопов изменяются в очень широких пределах. Например, период полураспада изотопа азота равен 10 минутам, а период полураспада изотопа хлора 300 000 лет [1]. В заданиях период полураспада равен часам (и ответ следует выдавать в часах).
Из определения периода полураспада следует его связь с постоянной распада:
. (2)
Параметры задачи преподаватель выдает студенту по аналитическим формулам
, .
В этих формулах
— номер студента в группе, а-
номер измерения (,
время в этой формуле измеряется в часах. Между номером студента и периодом
полураспада имеется линейная зависимость.
Между номером студента и периодом
полураспада имеется линейная зависимость.
В отчете показать вывод уравнений, позволяющих решить задачу, график с прямой в логарифмическом масштабе для и экспериментальными точками, выписать значения постоянной распада и времени полураспада в часах.
275
провести прямую через набор точек
Дмитрий Хизбуллин
ведущий инженер в исследовательском центре Huawei
Будучи энтузиастом в области беспилотных автомобилей, я проходил собеседования в ряд компаний на позицию разработчика программного обеспечения. Чаще всего компании, занимающиеся беспилотными автомобилями, разрабатывают машину, которая может проехать по местности и хорошо ориентируется в 3D окружении. Следовательно, фирмы беспокоятся о том, насколько хорош кандидат в вычислительной геометрии, и в частности, как легко и быстро он/она может закодить решение. Один из вопросов на собеседовании меня особенно заинтересовал. Задача формулируется следующим образом:
Представьте, что ваш автономный автомобиль едет по дороге прямо, и его 2D позиции определяются при помощи ГНСС (Глобальной Навигационной Спутниковой Системы, например GPS) не очень точно, а с определенной погрешностью.
Требуется найти наиболее вероятные положения автомобиля такие, что они лежат на одной прямой.
Эту задачу, как и практически любую другую, можно решать несколькими способами. В этой статье мы рассмотрим 3 решения на языке Python и сравним их: посмотрим на достоинства и недостатки. С математической точки зрения задание формулируется как задача линейной регрессии: найти аппроксимацию набора точек при помощи прямой. С программисткой стороны нам понадобится подходящая библиотека по манипулированию векторами и матрицами. Мы будем использовать NumPy для этой цели.
Подход 1: Метод наименьших квадратов
На первый взгляд, нам подойдет стандартное решение линейной регрессии: метод наименьших квадратов.
Нам дан массив 2D координат, представляющих собой пары точек (x, y). Мы можем считать x за аргумент, а y — за значение функции. Тогда, проконсультировавшись с Википедией, мы можем рассчитать коэффициенты прямой при помощи следующей формулы.
Это хорошее решение в том плане, что оно прямолинейное (непреднамеренный каламбур), то есть нам нужно взять и рассчитать все по формуле и получить ответ. Недолго думая, закодим решение. Далее я предлагаю читателю следовать за комментариями в коде.
def least_squares(points: np.ndarray, axis: Optional[Any] = None) \
-> np.ndarray:
"""
Функция для аппроксимации массива точек прямой, основанная на
методе наименьших квадратов.
:param points: Входной массив точек формы [N, 2]
:return: Numpy массив формы [N, 2] точек на прямой
"""
x = points[:, 0]
y = points[:, 1]
# Для метода наименьших квадратов нам нужно, чтобы X был матрицей,
# в которой первый столбец - единицы, а второй - x координаты точек
X = np.vstack((np.ones(x.shape[0]), x)).T
normal_matrix = np.dot(X.T, X)
moment_matrix = np.dot(X.T, y)
# beta_hat это вектор [перехват, наклон], рассчитываем его в
# в соответствии с формулой. beta_hat = np.dot(np.linalg.inv(normal_matrix), moment_matrix)
intercept = beta_hat[0]
slope = beta_hat[1]
# Теперь, когда мы знаем параметры прямой, мы можем
# легко вычислить y координаты точек на прямой.
y_hat = intercept + slope * x
# Соберем x и y в единую матрицу, которую мы собираемся вернуть
# в качестве результата.
points_hat = np.vstack((x, y_hat)).T
return points_hat
beta_hat = np.dot(np.linalg.inv(normal_matrix), moment_matrix)
intercept = beta_hat[0]
slope = beta_hat[1]
# Теперь, когда мы знаем параметры прямой, мы можем
# легко вычислить y координаты точек на прямой.
y_hat = intercept + slope * x
# Соберем x и y в единую матрицу, которую мы собираемся вернуть
# в качестве результата.
points_hat = np.vstack((x, y_hat)).T
return points_hat
Посмотрим, что мы получили на выходе.
Выглядит в точности так, как мы и хотели, — линия прямая и максимально подогнана под набор точек. Однако у метода наименьших квадратов есть один существенный недостаток — он не работает в случае, если траектория вертикальная. В таком случае наклон прямой обращается в бесконечность, и программа или упадет, или выдаст NaN — «не число». Таким образом, данный подход не может претендовать на продуктовый уровень.
Подход 2: RANSAC
RANSAC — метод достижения консенсуса на основе случайных выборок, предложенный в 1981 году.
В нашем двумерном случае мы будем случайно выбирать две точки (суппорт) из входного массива и проверять, насколько хорошо все входные точки вписывается в полосу ближайшей окрестности прямой, задаваемой суппортом. Конечно же не каждая попытка даст удачно угаданную прямую, поэтому алгоритм RANSAC — итерационный. Для RANSAC есть формула, позволяющая по ожидаемому проценту выбросов и желаемой вероятности успешного решения вычислить необходимое количество итераций алгоритма.
где p
— вероятность успеха, ω — доля выбросов, n — размер суппорта. В нашем случае размер суппорта равен двум точкам для прямой в двумерном пространстве. Для прямой в трехмерном пространстве n было бы тоже равно двум, а для трехмерной плоскости в 3D — уже трем точкам. В примере кода количество итераций получилось 16, что является вполне небольшим значением. Я предлагаю читателю далее следовать за комментариями в коде.def ransac(points: np.ndarray,
min_inliers: int = 4,
max_distance: float = 0. 15,
outliers_fraction: float = 0.5,
probability_of_success: float = 0.99) -> Optional[np.ndarray]:
"""
RANdom SAmple Consensus метод нахождения наилучшей
аппроксимирующей прямой.
:param points: Входной массив точек формы [N, 2]
:param min_inliers: Минимальное количество не-выбросов
:param max_distance: максимальное расстояние до поддерживающей прямой,
чтобы точка считалась не-выбросом
:param outliers_fraction: Ожидаемая доля выбросов
:param probability_of_success: желаемая вероятность, что поддерживающая
прямая не основана на точке-выбросе
:param axis: Набор осей, на которых рисовать график
:return: Numpy массив формы [N, 2] точек на прямой,
None, если ответ не найден.
"""
# Давайте вычислим необходимое количество итераций
num_trials = int(math.log(1 - probability_of_success) /
math.
15,
outliers_fraction: float = 0.5,
probability_of_success: float = 0.99) -> Optional[np.ndarray]:
"""
RANdom SAmple Consensus метод нахождения наилучшей
аппроксимирующей прямой.
:param points: Входной массив точек формы [N, 2]
:param min_inliers: Минимальное количество не-выбросов
:param max_distance: максимальное расстояние до поддерживающей прямой,
чтобы точка считалась не-выбросом
:param outliers_fraction: Ожидаемая доля выбросов
:param probability_of_success: желаемая вероятность, что поддерживающая
прямая не основана на точке-выбросе
:param axis: Набор осей, на которых рисовать график
:return: Numpy массив формы [N, 2] точек на прямой,
None, если ответ не найден.
"""
# Давайте вычислим необходимое количество итераций
num_trials = int(math.log(1 - probability_of_success) /
math.
log(1 - outliers_fraction**2))
best_num_inliers = 0
best_support = None
for _ in range(num_trials):
# В каждой итерации случайным образом выбираем две точки
# из входного массива и называем их "суппорт"
random_indices = np.random.choice(
np.arange(0, len(points)), size=(2,), replace=False)
assert random_indices[0] != random_indices[1]
support = np.take(points, random_indices, axis=0)
# Здесь мы считаем расстояния от всех точек до прямой
# заданной суппортом. Для расчета расстояний от точки до
# прямой подходит функция векторного произведения.
# Особенность np.cross в том, что функция возвращает только
# z координату векторного произведения, а она-то нам и нужна.
cross_prod = np.cross(support[1, :] - support[0, :],
support[1, :] - points)
support_length = np.linalg. norm(support[1, :] - support[0, :])
# cross_prod содержит знаковое расстояние, поэтому нам нужно
# взять модуль значений.
distances = np.abs(cross_prod) / support_length
# Не-выбросы - это все точки, которые ближе, чем max_distance
# к нашей прямой-кандидату.
num_inliers = np.sum(distances < max_distance)
# Здесь мы обновляем лучший найденный суппорт
if num_inliers >= min_inliers and num_inliers > best_num_inliers:
best_num_inliers = num_inliers
best_support = support
# Если мы успешно нашли хотя бы один суппорт,
# удовлетворяющий всем требованиям
if best_support is not None:
# Спроецируем точки из входного массива на найденную прямую
support_start = best_support[0]
support_vec = best_support[1] - best_support[0]
# Для расчета проекций отлично подходит функция
# скалярного произведения.
norm(support[1, :] - support[0, :])
# cross_prod содержит знаковое расстояние, поэтому нам нужно
# взять модуль значений.
distances = np.abs(cross_prod) / support_length
# Не-выбросы - это все точки, которые ближе, чем max_distance
# к нашей прямой-кандидату.
num_inliers = np.sum(distances < max_distance)
# Здесь мы обновляем лучший найденный суппорт
if num_inliers >= min_inliers and num_inliers > best_num_inliers:
best_num_inliers = num_inliers
best_support = support
# Если мы успешно нашли хотя бы один суппорт,
# удовлетворяющий всем требованиям
if best_support is not None:
# Спроецируем точки из входного массива на найденную прямую
support_start = best_support[0]
support_vec = best_support[1] - best_support[0]
# Для расчета проекций отлично подходит функция
# скалярного произведения. offsets = np.dot(support_vec, (points - support_start).T)
proj_vectors = np.outer(support_vec, offsets).T
support_sq_len = np.inner(support_vec, support_vec)
projected_vectors = proj_vectors / support_sq_len
projected_points = support_start + projected_vectors
return projected_points
offsets = np.dot(support_vec, (points - support_start).T)
proj_vectors = np.outer(support_vec, offsets).T
support_sq_len = np.inner(support_vec, support_vec)
projected_vectors = proj_vectors / support_sq_len
projected_points = support_start + projected_vectors
return projected_points
Что мы получим, запустив код?
Полученная прямая хорошо аппроксимирует набор точек. Черными квадратами отмечены точки, которые были выбраны в качестве суппорта.
В чем недостатки метода RANSAC? В том, что он не гарантирует успешного результата. Вероятность того, что генератор случайных чисел будет выбирать исключительно выбросы или просто неудачные точки, например очень близкие друг к другу, достаточно мала. Тем не менее, в применениях, требующий высокой надежности, например, в беспилотных автомобилях, RANSAC может не подойти. Также RANSAC не подойдет там, где доступ к генератору случайных или псевдослучайных чисел затруднен. Помимо того у RANSAC есть много параметров, которые надо подбирать под задачу. В частности,
Помимо того у RANSAC есть много параметров, которые надо подбирать под задачу. В частности, max_distance довольно сложно оценить, не потратив длительное время на изучение интенсивности шума.
Подход 3: PCA
Метод главных компонент (Principal Component Analysis, PCA) часто используется для уменьшения размерности данных, когда нужно аффинно преобразовать облако точек таким образом, чтобы по большинству размерностей дисперсия была малой (или хотя бы меньшей, чем по важным размерностям). В таком случае можно отбросить эти размерности, как не несущие информации. Очень похоже на нашу ситуацию, когда нам нужно отбросить шум в направлении, перпендикулярном общему направлению разброса точек, и таким образом спроецировать точки на соответствующую прямую.
В результате вычисления собственных чисел и собственных векторов мы получим пары (собственное число, собственный вектор). Чем больше собственное число, тем выше разброс точек в направлении соответствующего собственного вектора. Применительно к нашему случаю нам как раз нужно найти собственный вектор с наибольшим собственным значением. Он и задаст прямую, на которую мы будем проецировать точки. Код с комментариями:
Применительно к нашему случаю нам как раз нужно найти собственный вектор с наибольшим собственным значением. Он и задаст прямую, на которую мы будем проецировать точки. Код с комментариями:
def pca(points: np.ndarray, axis: Optional[Any] = None) -> np.ndarray: """ Метод главных компонент (PCA) оценки направления максимальной дисперсии облака точек. :param points: Входной массив точек формы [N, 2] :param axis: Набор осей, на которых рисовать график :return: Numpy массив формы [N, 2] точек на прямой """ # Найдем главные компоненты. # В первую очередь нужно центрировать облако точек, вычтя среднее mean = np.mean(points, axis=0) centered = points - mean # Функция вычисления собственных значений и векторов np.linalg.eig # требует ковариационную матрицу в качестве аргумента. cov = np.cov(centered.T) # Теперь мы можем посчитать главные компоненты, заданные # собственными значениями и собственными векторами.eigenval, eigenvec = np.linalg.eig(cov) # Мы хотим параметризовать целевую прямую в координатной системе, # заданной собственным вектором, собственное значение которого # наиболее велико (направление наибольшей вариативности). argmax_eigen = np.argmax(eigenval) # Нам понадобятся проекции входных точек на наибольший собственный # вектор. loc_pca = np.dot(centered, eigenvec) loc_maxeigen = loc_pca[:, argmax_eigen] max_eigenval = eigenval[argmax_eigen] max_eigenvec = eigenvec[:, argmax_eigen] # Ре-параметризуем прямую, взяв за начало отрезка проекции # первой и последней точки на прямую. loc_start = mean + max_eigenvec * loc_maxeigen[0] loc_final = mean + max_eigenvec * loc_maxeigen[-1] linspace = np.linspace(0, 1, num=len(points)) # Получаем позиции точек, которые идут с одинаковым интервалом, # таким образом удаляя шум измерений и вдоль траектории движения.
positions = loc_start + np.outer(linspace, loc_final - loc_start) return positions
Запустив код, получаем следующий график.
PCA также справился с задачей! При этом этот метод лишен недостатка метода наименьших квадратов: PCA отлично аппроксимирует вертикальные линии. Также PCA всегда даст результат в отличие от вероятностного RANSAC. Однако, в отличие от RANSAC метод PCA чувствителен к сильным выбросам в локациях точек.
Заключение
Данная задача понравилась мне тем, что у нее есть несколько существенно разных решений со своими присущими достоинствами и недостатками. Также задача позволяет разобраться с матричными операциями в NumPy на простом примере. Посмотрим на все три решения на одном изображении.
Из трех решений мой личный фаворит — метод главных компонент PCA.
Дорогой читатель, надеюсь статья тебе понравилась и ты приобрел навыки превращения задач аналитической геометрии в код. Полный код доступен на GitHub.
Спасибо за внимание и удачи на собеседованиях!
Методнаименьших квадратов | Определение и объяснение
метод наименьших квадратов
Просмотреть все СМИ
- Ключевые люди:
- Карл Фридрих Гаусс Адриан-Мари Лежандр
- Похожие темы:
- корреляционная диаграмма приближение регрессионный анализ
Просмотреть весь связанный контент →
метод наименьших квадратов , также называемый приближением методом наименьших квадратов , в статистике метод оценки истинного значения некоторой величины, основанный на учете ошибок в наблюдениях или измерениях. In particular, the line (the function y i = a + b x i , where x i are the values at which y i измеряется и i обозначает отдельное наблюдение), которое минимизирует сумму квадратов расстояний (отклонений) от линии до каждого наблюдения, используется для аппроксимации зависимости, которая считается линейной. То есть сумма по всем I из ( Y I — A — B x I ) 2 минимализированные настройки. в отношении а и b равно 0. Метод также можно обобщить для использования с нелинейными отношениями.
То есть сумма по всем I из ( Y I — A — B x I ) 2 минимализированные настройки. в отношении а и b равно 0. Метод также можно обобщить для использования с нелинейными отношениями.
Одним из первых применений метода наименьших квадратов было разрешение спора о форме Земли. Английский математик Исаак Ньютон утверждал в Principia (1687 г.), что Земля имеет сплюснутую (грейпфрутовую) форму из-за своего вращения, в результате чего экваториальный диаметр превышает полярный диаметр примерно на 1 часть из 230. В 1718 г. директор Парижская обсерватория Жак Кассини утверждал на основании собственных измерений, что Земля имеет вытянутую (лимонную) форму.
Дополнительная информация по этой теме
Статистика: метод наименьших квадратов
Либо простая, либо модель множественной регрессии первоначально ставится в качестве гипотезы относительно взаимосвязи между зависимыми и независимыми. ..
..
Для разрешения спора в 1736 г. Французская академия наук отправила геодезические экспедиции в Эквадор и Лапландию. Однако расстояния невозможно измерить идеально, а ошибки измерения в то время были достаточно велики, чтобы создать существенную неопределенность. Было предложено несколько методов подбора линии по этим данным, т. е. получения функции (линии), которая лучше всего соответствует данным, связывающим измеренную длину дуги с широтой. По общему мнению, этот метод должен минимизировать отклонения в y -направление (длина дуги), но вариантов было много, включая минимизацию наибольшего такого отклонения и минимизацию суммы их абсолютных размеров (как показано на рисунке). Измерения, казалось, подтверждали теорию Ньютона, но относительно большие оценки ошибок измерений оставляли слишком много неопределенности для окончательного вывода, хотя это не сразу было признано. На самом деле, хотя Ньютон был в основном прав, более поздние наблюдения показали, что его предсказание избыточного экваториального диаметра было примерно на 30 процентов больше.
В 1805 году французский математик Адриан-Мари Лежандр опубликовал первую известную рекомендацию использовать линию, минимизирующую сумму квадратов этих отклонений, т. е. современный метод наименьших квадратов. Немецкий математик Карл Фридрих Гаусс, который, возможно, ранее использовал тот же метод, внес важные вычислительные и теоретические достижения. Метод наименьших квадратов в настоящее время широко используется для подгонки линий и кривых к диаграммам рассеяния (дискретным наборам данных).
Ричард Рутледж
Регрессия наименьших квадратов
Линия наилучшего соответствия
Представьте, что у вас есть несколько точек, и вы хотите получить линию , которая лучше всего подходит для них, например:
«: старайтесь располагать линию как можно ближе ко всем точкам и одинаковое количество точек выше и ниже линии.
Но для большей точности давайте посмотрим, как рассчитать линию, используя регрессию наименьших квадратов .
Линия
Наша цель состоит в том, чтобы вычислить значения m (наклон) и b (y-пересечение) в уравнении прямой:
y = mx + b
Где:
8
3 7
7 y = как далеко вверх
Шаги
Чтобы найти линию наилучшего соответствия для N точек:
Шаг 1 : Для каждой точки (x,y) вычислить x 2 и xy
Шаг 2 : Суммировать все x, y, x 2 и xy, что дает нам Σx, σy, σx 2 и σxy (σ означает «sum up»)
Шаг 3 : Рассчитайте наклон M :
M = N σ (XY) σx σx = N σ (xy) σx σy N σ (xy) σx σx 9 N σ (xy) σx N σ (xy) σx σx N σ (xy) σx σx
= N σ (xy) σx . (x 2 ) − (Σx) 2
(x 2 ) − (Σx) 2 (N — количество точек.)
Шаг 4 : Рассчитайте перехват B :
B = σy — M σx N
Шаг 5 : Соберите уравнение линии
Y = MX + B
!
Пример
Давайте посмотрим на примере, как это сделать!
Пример: Сэм нашел, сколько
часов солнечного света и сколько мороженого было продано в магазине с понедельника по пятницу:| «x» Солнечные часы | «y» Мороженое продано |
|---|---|
| 2 | 4 |
| 3 | 5 |
| 5 | 7 |
| 7 | 10 |
| 9 | 15 |
Найдем наилучшие м (наклон) и b (пересечение по оси Y), которые подходят для этих данных
y = mx + b
Шаг 1 : Для каждого (x,y) вычислить x 2 и xy:
| x | г | х 2 | ху |
|---|---|---|---|
| 2 | 4 | 4 | 8 |
| 3 | 5 | 9 | 15 |
| 5 | 7 | 25 | 35 |
| 7 | 10 | 49 | 70 |
| 9 | 15 | 81 | 135 |
Шаг 2 : Сумма x, y, x 2 и xy (дает нам Σx, Σy, Σx 2 и Σxy):
2 2 4| г | х 2 | ху | |
|---|---|---|---|
| 2 | 4 | 4 | 8 |
| 3 | 5 | 9 | 15 |
| 5 | 7 | 25 | 35 |
| 7 | 10 | 49 | 70 |
| 9 | 15 | 81 | 135 |
| Σх: 26 | Σг: 41 | Σx 2 : 168 | Σxy: 263 |
Также N (количество значений данных) = 5
Шаг 3 : Рассчитайте наклон M :
M = N σ (XY) — σy M = N σ (XY) — σy M = N σ (XY) – σy M = N σ (XY) — σy . Н Σ(х 2 ) — (Σх) 2
Н Σ(х 2 ) — (Σх) 2
= 5 х 263 — 26 х 41 5 x 168 − 26 2
= 1315 − 1066 840 − 676
= 249 164 = 1.5183…
Step 4 : Calculate Intercept b :
б = Σy − м Σx Н
= 41 − 1,5183 x 26 5
= 0,3049…
Шаг 5 : Составить уравнение прямой:
y = mx + b
y = 1,518x + 0,305
Посмотрим, что получится:
| x | г | у = 1,518х + 0,305 | ошибка |
|---|---|---|---|
| 2 | 4 | 3,34 | −0,66 |
| 3 | 5 | 4,86 | −0,14 |
| 5 | 7 | 7,89 | 0,89 |
| 7 | 10 | 10,93 | 0,93 |
| 9 | 15 | 13,97 | −1,03 |
Вот точки (x,y) и линия y = 1,518x + 0,305 на графике:
Отлично подходит!
Сэм слышит прогноз погоды, в котором говорится: «Мы ожидаем, что завтра будет 8 часов солнца», поэтому он использует приведенное выше уравнение, чтобы оценить, что он продаст 9 часов.

 beta_hat = np.dot(np.linalg.inv(normal_matrix), moment_matrix)
intercept = beta_hat[0]
slope = beta_hat[1]
# Теперь, когда мы знаем параметры прямой, мы можем
# легко вычислить y координаты точек на прямой.
y_hat = intercept + slope * x
# Соберем x и y в единую матрицу, которую мы собираемся вернуть
# в качестве результата.
points_hat = np.vstack((x, y_hat)).T
return points_hat
beta_hat = np.dot(np.linalg.inv(normal_matrix), moment_matrix)
intercept = beta_hat[0]
slope = beta_hat[1]
# Теперь, когда мы знаем параметры прямой, мы можем
# легко вычислить y координаты точек на прямой.
y_hat = intercept + slope * x
# Соберем x и y в единую матрицу, которую мы собираемся вернуть
# в качестве результата.
points_hat = np.vstack((x, y_hat)).T
return points_hat
 15,
outliers_fraction: float = 0.5,
probability_of_success: float = 0.99) -> Optional[np.ndarray]:
"""
RANdom SAmple Consensus метод нахождения наилучшей
аппроксимирующей прямой.
:param points: Входной массив точек формы [N, 2]
:param min_inliers: Минимальное количество не-выбросов
:param max_distance: максимальное расстояние до поддерживающей прямой,
чтобы точка считалась не-выбросом
:param outliers_fraction: Ожидаемая доля выбросов
:param probability_of_success: желаемая вероятность, что поддерживающая
прямая не основана на точке-выбросе
:param axis: Набор осей, на которых рисовать график
:return: Numpy массив формы [N, 2] точек на прямой,
None, если ответ не найден.
"""
# Давайте вычислим необходимое количество итераций
num_trials = int(math.log(1 - probability_of_success) /
math.
15,
outliers_fraction: float = 0.5,
probability_of_success: float = 0.99) -> Optional[np.ndarray]:
"""
RANdom SAmple Consensus метод нахождения наилучшей
аппроксимирующей прямой.
:param points: Входной массив точек формы [N, 2]
:param min_inliers: Минимальное количество не-выбросов
:param max_distance: максимальное расстояние до поддерживающей прямой,
чтобы точка считалась не-выбросом
:param outliers_fraction: Ожидаемая доля выбросов
:param probability_of_success: желаемая вероятность, что поддерживающая
прямая не основана на точке-выбросе
:param axis: Набор осей, на которых рисовать график
:return: Numpy массив формы [N, 2] точек на прямой,
None, если ответ не найден.
"""
# Давайте вычислим необходимое количество итераций
num_trials = int(math.log(1 - probability_of_success) /
math.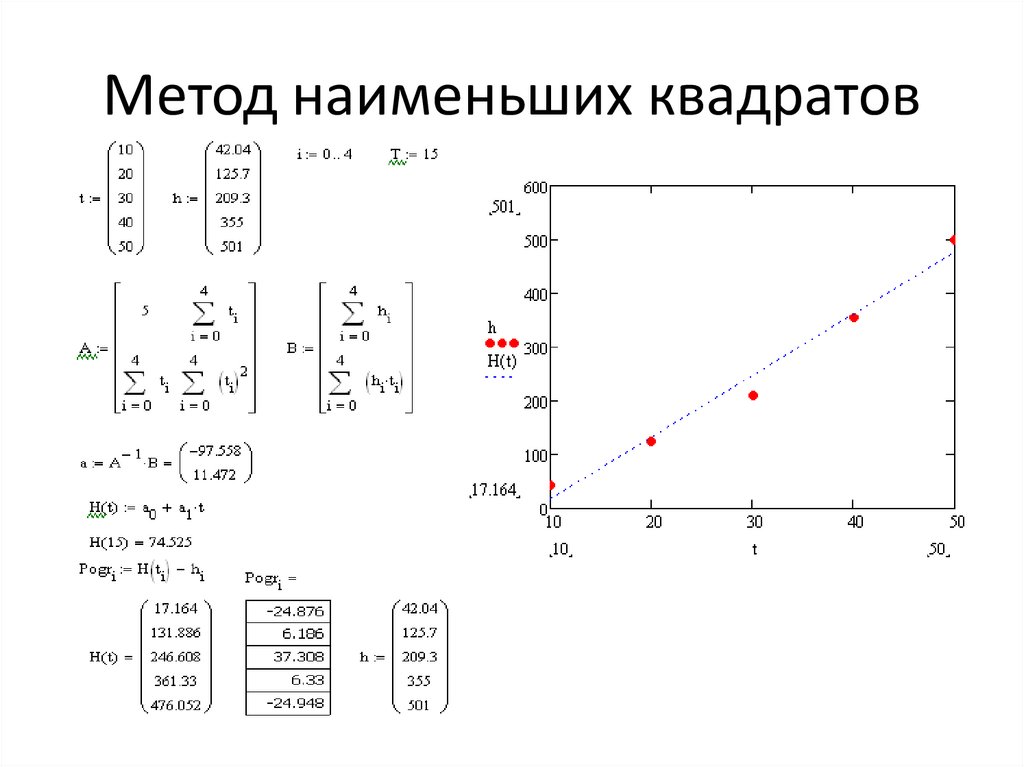
 norm(support[1, :] - support[0, :])
# cross_prod содержит знаковое расстояние, поэтому нам нужно
# взять модуль значений.
distances = np.abs(cross_prod) / support_length
# Не-выбросы - это все точки, которые ближе, чем max_distance
# к нашей прямой-кандидату.
num_inliers = np.sum(distances < max_distance)
# Здесь мы обновляем лучший найденный суппорт
if num_inliers >= min_inliers and num_inliers > best_num_inliers:
best_num_inliers = num_inliers
best_support = support
# Если мы успешно нашли хотя бы один суппорт,
# удовлетворяющий всем требованиям
if best_support is not None:
# Спроецируем точки из входного массива на найденную прямую
support_start = best_support[0]
support_vec = best_support[1] - best_support[0]
# Для расчета проекций отлично подходит функция
# скалярного произведения.
norm(support[1, :] - support[0, :])
# cross_prod содержит знаковое расстояние, поэтому нам нужно
# взять модуль значений.
distances = np.abs(cross_prod) / support_length
# Не-выбросы - это все точки, которые ближе, чем max_distance
# к нашей прямой-кандидату.
num_inliers = np.sum(distances < max_distance)
# Здесь мы обновляем лучший найденный суппорт
if num_inliers >= min_inliers and num_inliers > best_num_inliers:
best_num_inliers = num_inliers
best_support = support
# Если мы успешно нашли хотя бы один суппорт,
# удовлетворяющий всем требованиям
if best_support is not None:
# Спроецируем точки из входного массива на найденную прямую
support_start = best_support[0]
support_vec = best_support[1] - best_support[0]
# Для расчета проекций отлично подходит функция
# скалярного произведения. offsets = np.dot(support_vec, (points - support_start).T)
proj_vectors = np.outer(support_vec, offsets).T
support_sq_len = np.inner(support_vec, support_vec)
projected_vectors = proj_vectors / support_sq_len
projected_points = support_start + projected_vectors
return projected_points
offsets = np.dot(support_vec, (points - support_start).T)
proj_vectors = np.outer(support_vec, offsets).T
support_sq_len = np.inner(support_vec, support_vec)
projected_vectors = proj_vectors / support_sq_len
projected_points = support_start + projected_vectors
return projected_points
 eigenval, eigenvec = np.linalg.eig(cov)
# Мы хотим параметризовать целевую прямую в координатной системе,
# заданной собственным вектором, собственное значение которого
# наиболее велико (направление наибольшей вариативности).
argmax_eigen = np.argmax(eigenval)
# Нам понадобятся проекции входных точек на наибольший собственный
# вектор.
loc_pca = np.dot(centered, eigenvec)
loc_maxeigen = loc_pca[:, argmax_eigen]
max_eigenval = eigenval[argmax_eigen]
max_eigenvec = eigenvec[:, argmax_eigen]
# Ре-параметризуем прямую, взяв за начало отрезка проекции
# первой и последней точки на прямую.
loc_start = mean + max_eigenvec * loc_maxeigen[0]
loc_final = mean + max_eigenvec * loc_maxeigen[-1]
linspace = np.linspace(0, 1, num=len(points))
# Получаем позиции точек, которые идут с одинаковым интервалом,
# таким образом удаляя шум измерений и вдоль траектории движения.
eigenval, eigenvec = np.linalg.eig(cov)
# Мы хотим параметризовать целевую прямую в координатной системе,
# заданной собственным вектором, собственное значение которого
# наиболее велико (направление наибольшей вариативности).
argmax_eigen = np.argmax(eigenval)
# Нам понадобятся проекции входных точек на наибольший собственный
# вектор.
loc_pca = np.dot(centered, eigenvec)
loc_maxeigen = loc_pca[:, argmax_eigen]
max_eigenval = eigenval[argmax_eigen]
max_eigenvec = eigenvec[:, argmax_eigen]
# Ре-параметризуем прямую, взяв за начало отрезка проекции
# первой и последней точки на прямую.
loc_start = mean + max_eigenvec * loc_maxeigen[0]
loc_final = mean + max_eigenvec * loc_maxeigen[-1]
linspace = np.linspace(0, 1, num=len(points))
# Получаем позиции точек, которые идут с одинаковым интервалом,
# таким образом удаляя шум измерений и вдоль траектории движения.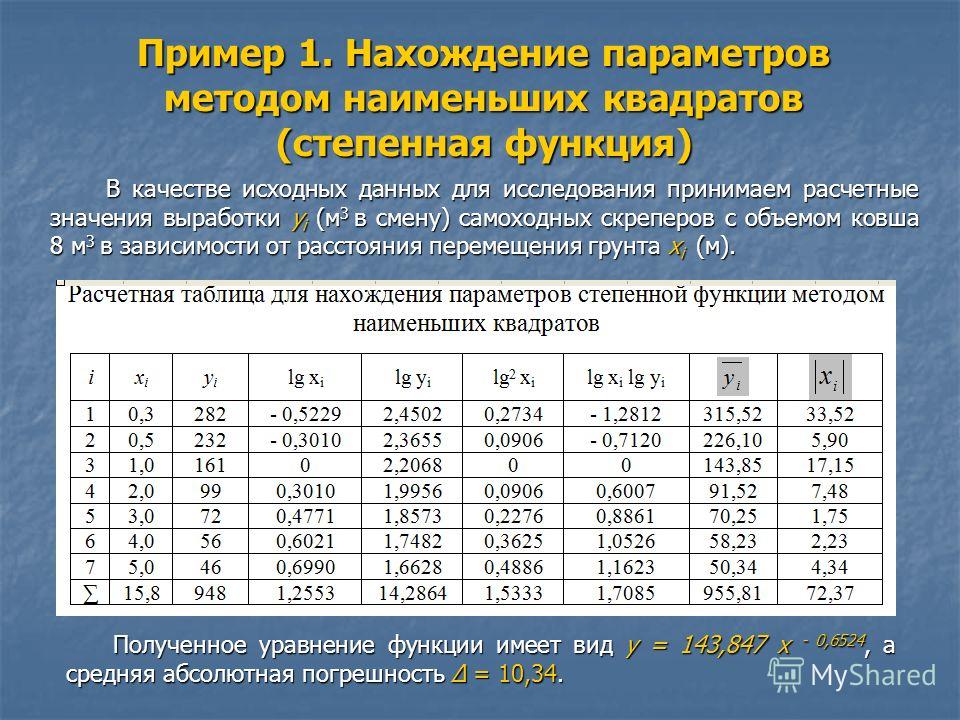 positions = loc_start + np.outer(linspace, loc_final - loc_start)
return positions
positions = loc_start + np.outer(linspace, loc_final - loc_start)
return positions