17. Гиперболические функции:
–синус гиперболический, – косинус гиперболический,– тангенс гиперболический ,– котангенс гиперболический.
, .
Гиперболические функции можно выразить через тригонометрические и наоборот.
3. Преобразование графиков
3.1. Сдвиг
График функции у=f(x–a)+b совпадает с графиком функции y=f(x), если Х=х–а, Y=у–b – новые оси координат.
3.2. Изменение масштаба
График функции y=af(x) совпадает с графиком функции y=f(x), если сделано масштабное преобразование осей координат по правилу Х=x, . В частном случаеа= –1 происходит зеркальное отражение от оси х, а в частном случае = –1 – от оси у.
Пример. y=kx
y=kx
Пример. y=cosx. Так как , то график этой функции совпадает с графиком функцииY=sinX, если Y=y, .
3.3. График функции y=|f(x)|
По определению модуля,
Таким образом, график функции y=|f(x)| совпадает с графиком функции f(x) в верхней полуплоскости и зеркально отражается от оси в нижней полуплоскости.
3.4. График функции f(|X|)
Этот
график получается зеркальным отражением
правой полуплоскости графика y=f(x)
на левую.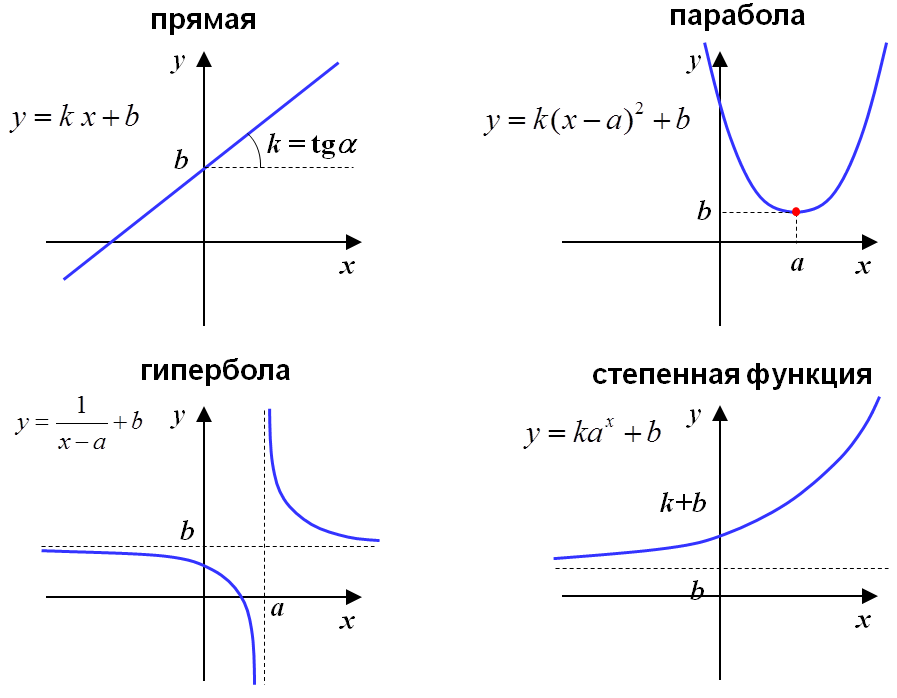
3.5. Функция типа «единица на эф»
Пусть дана функция y=f(x). Она может касаться или пересекать ось абсцисс, а может проходить выше нее. Соответственно рассмотрим обе возможности.
а) Рассмотрим только точких0 и х1 (а):
х + f(x)+
хх0 + f(x)min
хх0 – f(x)min
хх1 + f(x)max
хх1 – f(x)max
х – f(x)+
(запись ха+ читается: х стремится к а со стороны плюсов, т.е. справа, а
На основании этого исследования строим график . Рассмотрим только точких0 и х1 (б):
х + f(x) –
хх0 + f(x) 0 –
хх0 – f(x) 0 +
хх1 + f(x)max
хх1 – f(x)max
х – f(x)+
На основании этого исследования строим график.
3.6. Обратная функция.
Пусть
функция y=f(x)
задана на сегменте [a, b],
а множеством ее значений на этом сегменте
является сегмент [ , ].
Если каждому y[, ]
соответствует единственное значение x[a, b],
для которого y=f(x),
то на [, ]
можно определить функцию x=(y). Эта функция называется обратной по
отношению к функции y=f(x),
т.е. f((y))=y, f((x))=x.
Очевидно, что y=f(x)
и x=f(y)
описывают одну и ту же функцию на
плоскости XOY.
Но принято значения аргументов откладывать
по оси x,
а значения функции – по оси y,
т.е. вместе с функцией y=f(x)
рассматривать ее обратную функцию как y=(x).
Тогда очевидно, что графики прямой и
обратной функций будут симметричны
относительно биссектрисы 1-го и 3-го
координатных углов.
Эта функция называется обратной по
отношению к функции y=f(x),
т.е. f((y))=y, f((x))=x.
Очевидно, что y=f(x)
и x=f(y)
описывают одну и ту же функцию на
плоскости XOY.
Но принято значения аргументов откладывать
по оси x,
а значения функции – по оси y,
т.е. вместе с функцией y=f(x)
рассматривать ее обратную функцию как y=(x).
Тогда очевидно, что графики прямой и
обратной функций будут симметричны
относительно биссектрисы 1-го и 3-го
координатных углов.
Примеры. 1. у=5х+7.
Эта функция монотонно возрастает на
всей числовой оси, и каждому у соответствует единственное значение
,
тогда функциябудет обратной функцией по отношению
к функцииу=5х+7.
Достаточным условием существования
обратной функции (но не необходимым!)
является строгая монотонность «прямой»
функции y=f(x).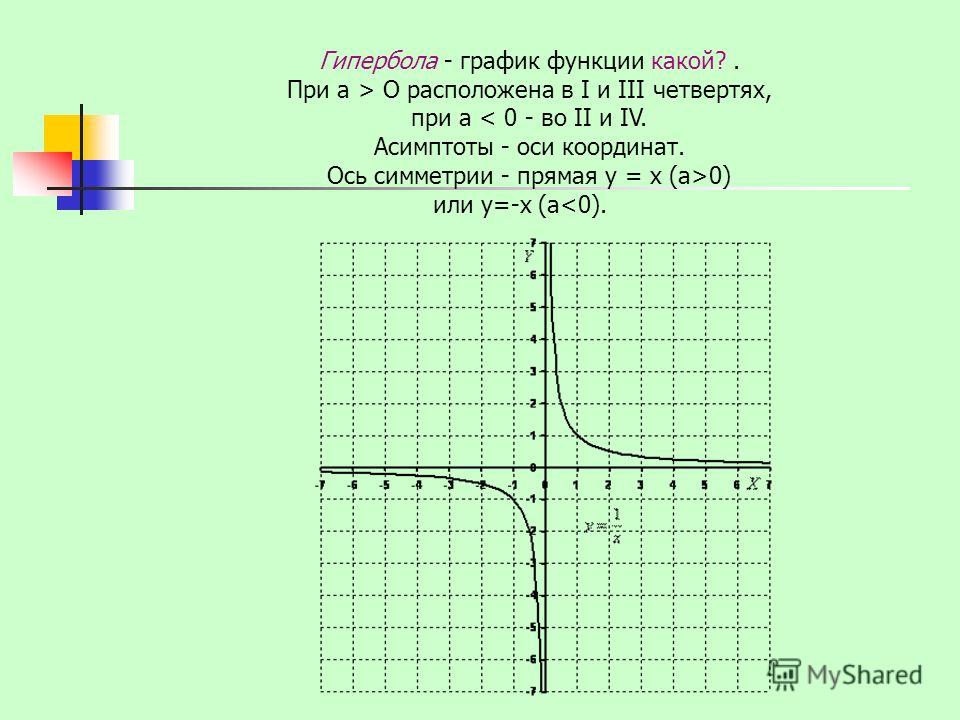 При этом, если функция y=f(x)
возрастает (убывает), то и обратная
функция возрастает (убывает). График
обратной функции совпадает с графиком
прямой, если аргументом считать теперь у,
но, как уже отмечалось, аргументом будем
считать х,
тогда график обратной функции получается
из графика прямой зеркальным отражением
от биссектрисы 1-го и 3-го координатных
углов. Обозначается обратная функция
так: y=f –1(x).
Таким образом, она может пересекаться
с прямой функцией только на прямой у=х.
При этом, если функция y=f(x)
возрастает (убывает), то и обратная
функция возрастает (убывает). График
обратной функции совпадает с графиком
прямой, если аргументом считать теперь у,
но, как уже отмечалось, аргументом будем
считать х,
тогда график обратной функции получается
из графика прямой зеркальным отражением
от биссектрисы 1-го и 3-го координатных
углов. Обозначается обратная функция
так: y=f –1(x).
Таким образом, она может пересекаться
с прямой функцией только на прямой у=х.
2. y=sinx. Очевидно,
что для этой функции не выполнено условие
существования обратной функции. Разобьем
ось х на промежутки
;
еслиk=2
(четное), то на них функция y=sinx возрастает, если k=n+1
(нечетное), то на этих промежутках y=sinx убывает. Причем на концах промежутков
|y|=1.
Таким образом, на каждом из этих
промежутков существует обратная функция,
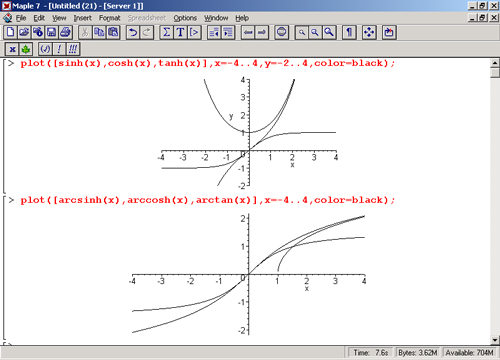
определенная на [–1; 1] и называемая y=arcsinx.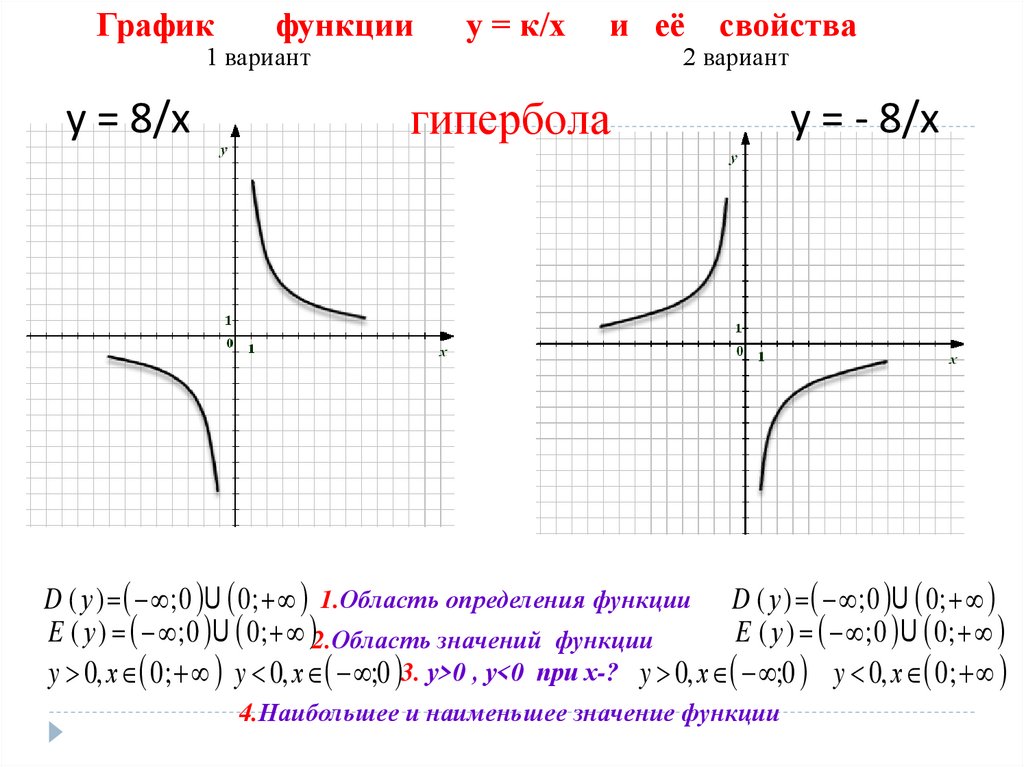 Отрезок
называется основным (k=0),
и на нем определена обратная функция y=arcsinx,
симметричная на этом промежутке
относительно биссектрис 1-го и 3-го
координатных углов функции y=sinx. Аналогично
определяются остальные обратные
тригонометрические функции. Мы их
изобразим на одном чертеже.
Отрезок
называется основным (k=0),
и на нем определена обратная функция y=arcsinx,
симметричная на этом промежутке
относительно биссектрис 1-го и 3-го
координатных углов функции y=sinx. Аналогично
определяются остальные обратные
тригонометрические функции. Мы их
изобразим на одном чертеже.
Пример. Построить обратную функцию на промежутках монотонности:
а)–f(x)=ax; б) –f(x)=х2.
Ответ:
2. Может ли немонотонная функцияy=f(x), х(–; +) иметь обратную? Рассмотрите пример:
Указание. Может, если уравнение y=f(x)
при каждом фиксированном у(–;
+)
имеет единственное решение. Обладает
ли этим свойством предложенная функция?
Обладает
ли этим свойством предложенная функция?
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать ИзбранныеТоп: Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит… Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства… Интересное: Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы. Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 2 Свойства 3. Чётность Разность квадратов Формулы суммы и разности аргументов Формулы произведений гиперболического синуса и косинуса Формулы суммы и разности гиперболических функций Формулы производных Формулы интегралов Формулы неравенства Формулы разложения в степенные ряды Появление названия «гиперболическая функция» Применение гиперболических функций.
Введение Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы. Цель данной работы – изучить гиперболические функции и их применение.
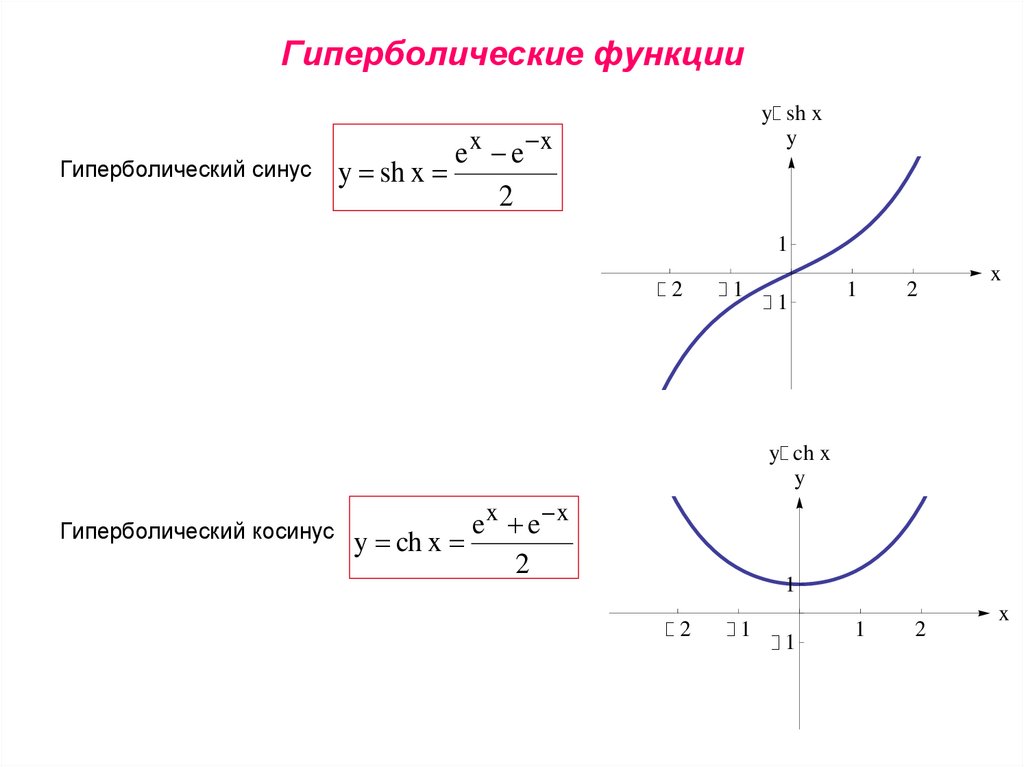
Определения гиперболических синусов, косинусов, тангенсов и котангенсов Гиперболическим синусом называется функция:
Гиперболическим тангенсом называется функция: Гиперболическим котангенсом называется функция: Гиперболическим секансом и косекансом называется функции: , .
⇐ Предыдущая12 Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… |
 Если мы введем систему координат так, чтобы нижняя точка цепи лежала вдоль оси [latex]y[/latex], мы можем описать высоту цепи в терминах гиперболической функции. Сначала определим гиперболические функции. 9{−x}}[/latex]
Если мы введем систему координат так, чтобы нижняя точка цепи лежала вдоль оси [latex]y[/latex], мы можем описать высоту цепи в терминах гиперболической функции. Сначала определим гиперболические функции. 9{−x}}[/latex]Имя cosh рифмуется со словом «черт возьми», тогда как имя sinh произносится как «cinch». Tanh , sech , csch и coth произносятся как «tanch», «seech», «coseech» и «cotanch» соответственно.
Используя определение [латекс]\cosh(x)[/латекс] и принципы физики, можно показать, что высота висящей цепи, такой как на рис. 6, может быть описана функцией [ латекс]h(x)=a \cosh(x/a)+c[/latex] для некоторых констант [latex]a[/latex] и [latex]c[/latex]. 9{−x}[/latex] в качестве направляющих мы рисуем графики [latex]\cosh x[/latex] и [latex]\sinh x[/latex]. Для построения графика [латекс]\tanh x[/латекс] мы используем тот факт, что [латекс]\танген(0)=0, \, -1<\танген(х)<1[/латекс] для всех [латекс] x, \, \tanh x \to 1[/latex] как [латекс]x \to \infty[/latex], и [латекс]\tanh x \to −1[/latex] как [латекс]x \to −\infty[/латекс]. {−x}[/latex]. 92 t[/latex], показанное на рис. 7, является одним из нескольких тождеств, включающих гиперболические функции, некоторые из которых перечислены ниже. Первые четыре свойства легко следуют из определений гиперболического синуса и гиперболического косинуса. За исключением некоторых различий в знаках, большинство этих свойств аналогичны тождествам для тригонометрических функций.
{−x}[/latex]. 92 t[/latex], показанное на рис. 7, является одним из нескольких тождеств, включающих гиперболические функции, некоторые из которых перечислены ниже. Первые четыре свойства легко следуют из определений гиперболического синуса и гиперболического косинуса. За исключением некоторых различий в знаках, большинство этих свойств аналогичны тождествам для тригонометрических функций.
Идентичности, включающие гиперболические функции
- [латекс]\cosh(−x)=\cosh x[/латекс]
- [латекс]\шп(-х)=-\шп х[/латекс] 92 х[/латекс]
- [латекс]\sin(x \pm y)=\sinx x \cosh y \pm \cosh x \sinh y[/latex]
- [латекс]\cosh (x \pm y)=\cosh x \cosh y \pm \sinx x \sinhy[/latex]
Пример: вычисление гиперболических функций
- Упростить [latex]\sinh(5 \ln x)[/latex].
- Если [latex]\sinh x=\frac{3}{4}[/latex], найдите значения оставшихся пяти гиперболических функций.
Показать раствор
Посмотрите следующее видео, чтобы увидеть работающее решение примера: Оценка гиперболических функций
Скрытые субтитры и расшифровка информации для видео
Попробуйте
Упростить [латекс]\cosh(2 \ln x)[/латекс].
Показать раствор
Обратные гиперболические функции
Из графиков гиперболических функций мы видим, что все они взаимно однозначны, кроме [латекс]\ш х[/латекс] и [латекс]\текст{sech} \, х [/латекс]. Если мы ограничим области определения этих двух функций интервалом [latex][0,\infty)[/latex], то все гиперболические функции будут взаимно однозначными, и мы сможем определить 9{-1}\left(\frac{1}{2}\right)[/latex].
Показать раствор
Графики гиперболических функций — Алгебра II
Все ресурсы по Алгебре II
10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
Алгебра II Помощь » Функции и графики » Квадратичные функции » Гиперболические функции » Графики гиперболических функций
В каком направлении открывается график приведенной выше гиперболы?
Возможные ответы:
по вертикали
по горизонтали
Правильный ответ:
по горизонтали
Объяснение:
Чтобы определить, в каком направлении открывается гипербола, сначала приведите уравнение к стандартной форме для конического сечения: член (но не оба!) отрицательный. В этой задаче коэффициент перед членом, возведенным в квадрат х, положителен, а коэффициент перед членом, возведенным в квадрат у, отрицателен. Вот правила для направлений гиперболы:
В этой задаче коэффициент перед членом, возведенным в квадрат х, положителен, а коэффициент перед членом, возведенным в квадрат у, отрицателен. Вот правила для направлений гиперболы:
- Если коэффициент при квадрате х положительный, а коэффициент при квадрате у отрицательный, то это гипербола, открывающаяся горизонтально.
- Если коэффициент при квадрате х отрицательный, а коэффициент при квадрате у положительный, то это гипербола, открывающаяся вертикально.
Итак, у нас есть график горизонтальной гиперболы.
Сообщить об ошибке
Каковы вершины этой гиперболы?
Возможные ответы:
Правильный ответ:
Пояснение:
Первое, что нам нужно найти для этой гиперболы, это центр. Это просто точка, где и оба равны , то есть . Поскольку термин положительный, гипербола открывается горизонтально, а это значит, что нам нужно посмотреть на знаменатель этого термина.
Знаменатель равен , поэтому наши вершины равны , или
и .
Сообщить об ошибке
Запишите выражение для этой гиперболы в стандартной форме:
Возможные ответы:
Правильный ответ:
1 9 Объяснение:
Стандартная форма гиперболы –
или аналогичная форма с положительным и отрицательным членами. Итак, чтобы начать приводить это уравнение в стандартную форму, мы должны заполнить квадрат квадрата в и .
коэффициент равен , таким образом, завершая квадрат, мы получаем
и аналогично с мы получаем
и поэтому наше начальное выражение можно записать как
Разделив на с обеих сторон, мы получим стандартное представление гипербола,
Сообщить об ошибке
Найдите вершины следующей гиперболической функции:
Возможные ответы:
Правильный ответ:
Объяснение:
Начнем с того, что заметим, что наша гипербола имеет следующую форму:
Чтобы определить вершины гиперболы, мы должны сначала найти ее центр.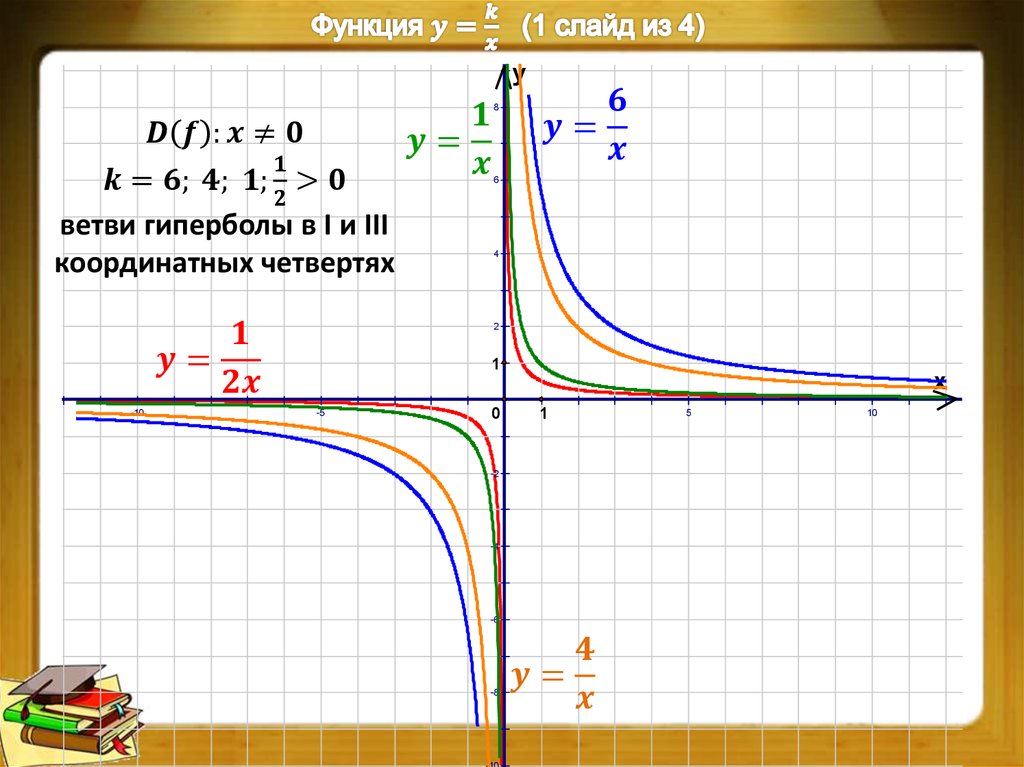

 ..
.. 1. Связь (сумма)
1. Связь (сумма) Винсент Риккати (итал. Vincenzo de Riccati; 11 января 1707, Кастель-Франко — 17 января 1775, Тревизо) — итальянский математик, иностранный почётный член Петербургской Академии Наук с 17 января 1760 года. Известен как создатель гиперболических функций. Отец Винсента Якопо Франческо Риккати (в честь которого названо уравнение Риккати) был одним из крупных итальянских математиков того времени. Винсент Риккати унаследовал интересы отца в области дифференциальных уравнений, которые естественно возникали при решении геометрических задач. Это привело его к изучению конических сечений в декартовых координатах и к заинтересованности в изучении гиперболы1.
Винсент Риккати (итал. Vincenzo de Riccati; 11 января 1707, Кастель-Франко — 17 января 1775, Тревизо) — итальянский математик, иностранный почётный член Петербургской Академии Наук с 17 января 1760 года. Известен как создатель гиперболических функций. Отец Винсента Якопо Франческо Риккати (в честь которого названо уравнение Риккати) был одним из крупных итальянских математиков того времени. Винсент Риккати унаследовал интересы отца в области дифференциальных уравнений, которые естественно возникали при решении геометрических задач. Это привело его к изучению конических сечений в декартовых координатах и к заинтересованности в изучении гиперболы1.  Риккати не только рассмотрел эти новые функции, но и на основе связанных с ними интегральных формул и с помощью геометрических методов получил интегральную формулу для тригонометрических функций. Его книга «Institutiones» признана как первый обширный трактат по интегральному исчислению. Работы Эйлера и Ламберта изданы позже. Саладини и Риккати также рассматривали другие геометрические проблемы, в том числе трактрису, строфоиду. Риккати применял для гиперболических функций обозначения и в дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой.
Риккати не только рассмотрел эти новые функции, но и на основе связанных с ними интегральных формул и с помощью геометрических методов получил интегральную формулу для тригонометрических функций. Его книга «Institutiones» признана как первый обширный трактат по интегральному исчислению. Работы Эйлера и Ламберта изданы позже. Саладини и Риккати также рассматривали другие геометрические проблемы, в том числе трактрису, строфоиду. Риккати применял для гиперболических функций обозначения и в дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой.