Умножения корень на корень – . . ? .

Как умножить корень на число

Вы решаете школьную задачу по математике. В процессе выполнения задачи появилась надобность умножить корень на число . Вы не знаете, как это сделать, корень и число кажутся вам идеально различными категориями. На самом деле корень – это такое же число . Разглядим задачу на примере простого квадратного корня.

Инструкция

1. Посмотрите на ваш корень . Если число , записанное под корнем, является полным квадратом иного числа (1, 4, 9, 16, 25, 36, 49, 64, 81, 100, … ), извлеките корень . То еесть обнаружьте такое целое число , квадратом которого является число , записанное под корнем. Умножьте его на 2-й множитель. Запишите результат.

2. Если квадратный корень

не извлекается, то традиционно результат дозволено записать, примитивно убрав знак умножения. Получается число , состоящее из целого числа и рядом стоящего корня. Это будет обозначать, что данный корень берется такое-то целое число раз. Целое число принято записывать слева от корня.

3. Если нужно всё число внести под корень , сделайте следующее. Возведите целую часть в квадрат. Домножьте на число , стоящее под корнем. Запишите полученное число под корнем. Это и будет ваш результат.

Одна из четырех простейших математических операций (умножение) породила иную, несколько больше усложненную – возведение в степень. Та, в свою очередь, добавила дополнительную трудность в обучение математике, породив обратную себе операцию – извлечение корня. К всякий из этих операций дозволено использовать все остальные математические действия, что еще больше запутывает постижение предмета. Дабы все это каким-то образом систематизировать, существуют комплекты правил, одно из которых регламентирует порядок умножения корней.

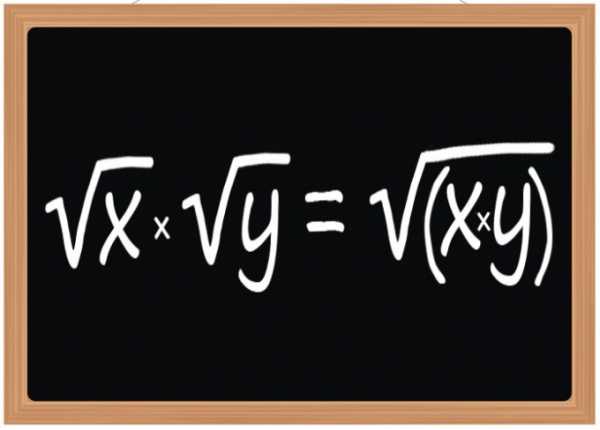
Инструкция

1. Используйте для умножения квадратных корней правило – итогом этой операции должен стать квадратный корень , подкоренным выражением которого будет произведение подкоренных выражений корней-множителей. Это правило действует при умножении 2-х, 3 и всякого иного числа квадратных корней. Однако, оно относится не только к корням квадратным, но и к кубическим либо с любым иным показателем степени, если данный показатель идентичен у всех участвующих в операции радикалов.

2. Если под знаками умножаемых корней стоят численные значения, то перемножьте их между собой и поставьте полученную величину под знак корня. Скажем, при умножении ?3,14 на ?7,62 это действие дозволено записать так: ?3,14 * ?7,62 = ?(3,14*7,62) = ?23,9268.

3. Если подкоренные выражения содержат переменные, то вначале запишите их произведение под одним знаком радикала, а после этого испробуйте упростить полученное подкоренное выражение. Скажем, если нужно умножить ?(x+7) на ?(x-14), то операцию дозволено записать так: ?(x+7) * ?(x-14) = ?((x+7) * (x-14)) = ?(x?-14*x+7*x-7*14) = ?(x?-7*x-98).

4. При необходимости перемножить огромнее 2-х квадратных корней действуйте верно так же – собирайте под одним знаком радикала подкоренные выражения всех умножаемых корней в качестве множителей одного трудного выражения, а после этого упрощайте его. Скажем, при перемножении квадратных корней из чисел 3,14, 7,62 и 5,56 операцию дозволено записать так: ?3,14 * ?7,62 * ?5,56 = ?(3,14*7,62*5,56) = ?133,033008. А умножение квадратных корней, извлекаемых из выражений с переменными x+7, x-14 и 2*x+1 – так: ?(x+7) * ?(x-14) * ?(2*x+1) = ?((x+7) * (x-14) * (2*x+1)) = ?((x?-14*x+7*x-7*14) * (2*x+1)) = ?((x?-7*x-98) * (2*x+1)) = ?(2*x*x?-2*x*7*x-2*x*98 + x?-7*x-98) = ?(2*x?-14*x?-196*x+x?-7*x-98) = ?(2*x?-13*x?-205*x-98).

Видео по теме

Возведение числа в степень – это сокращенная форма записи операции многократного умножения, в котором все множители равны начальному числу. А извлечение корня обозначает обратную операцию – определение множителя, тот, что должен быть задействован в операции многократного умножения, дабы в ее итоге получилось подкоренное число. Как показатель степени, так и показатель корня указывают на одно и то же – сколько сомножителей должно быть в такой операции умножения.

Вам понадобится

• Доступ в интернет.

Инструкция

1. Если к числу либо выражению требуется применить единовременно и операцию извлечения корня, и возведения его в степень, сведите оба действия в одно – в возведение в степень с дробным показателем. В числителе дроби должен стоять показатель степени, а в знаменателе – корня. Скажем, если необходимо построить в квадрат кубический корень , то две эти операции будут равнозначны одному возведению числа в степень ?.

2. Если в условиях требуется построить в квадрат корень с показателем степени, равным двойке, это задача не на вычисление, а на проверку ваших умений. Воспользуйтесь методом из первого шага, и вы получите дробь 2/2, т.е. 1. Это значит, что итогом возведения в квадрат квадрат ного корня из всякого числа будет само это число.

3. При необходимости построить в квадрат корень с четным показателем степени, неизменно есть вероятность упростить операцию. Потому что у двойки (числителя дробного показателя степени) и всякого четного числа (знаменателя) есть всеобщий делитель, то позже облегчения дроби в числителе останется единица, а это значит, что возводить в степень при расчетах не требуется, довольно извлечь

корень с половинным показателем степени. Скажем, возведение в квадрат корня шестой степени из восьмерки дозволено свести к извлечению из нее кубического корня, т.к. 2/6=1/3.

4. Для вычисления итога при всяких показателях степени корня воспользуйтесь, скажем, калькулятором, встроенным в поисковую систему Google. Это, вероятно, самый легкий метод расчетов при наличии выхода в интернет с вашего компьютера. Общепризнанным заменителем знака операции возведения в степень является вот такая «крышка»: ^. Используйте ее при вводе в Google поискового запроса. Скажем, если требуется построить в квадрат корень пятой степени из числа 750, сформулируйте запрос так: 750^(2/5). Позже его ввода поисковик даже без нажатия кнопки отправки на сервер покажет итог вычислений с точностью до семи знаков позже запятой: 750^(2 / 5) = 14,1261725.

Обратите внимание!
Квадратный корень – это корень степени 2. Если в задаче применяются корни других целых степеней, измените соответствующие степени в алгорифме решения.

Полезный совет
Рекомендуем вам чаще заглядывать в учебник по математике. Там вы обнаружите много пригодной и ценной информации, которая всенепременно сгодится вам в решении математических задач.

jprosto.ru

можно ли умножать корень на корень?

ЕСЛИ КОРНИ ОДИНАКОВОЙ СТЕПЕНИ, ТО ПЕРЕМНОЖАЮТСЯ ПОДКОРЕННЫЕ ВЫРАЖЕНИЯ, РЕЗУЛЬТАТ ПОД КОРНЕМ ТОЙ ЖЕ СТЕПЕНИ ЕСЛИ КОРНИ РАЗНОЙ СТЕПЕНИ, НО ОДИНАКОВЫЕ ПОДКОРЕННЫЕ ВЫРАЖЕНИЯ, ТО СКЛАДЫВАЮТСЯ СТЕПЕНИ КОРНЕЙ, А ПОДКОРЕННЫЕ ОСТАЮТСЯ ТЕ ЖЕ. ПРИ РАЗНЫХ СТЕПЕНЯХ КОРНЕЙ И ПОДКОРЕННЫХ, ТО ВЫДЕЛЯЮТСЯ, ЕСЛИ МОЖНО, ИЗ МНОЖИТЕЛЕЙ ОДИНАКОВЫЕ СТЕПЕНИ ИЛИ ПОДКОРЕННЫЕ ВЫРАЖЕНИЯ.

Да пожалуйста, умножай

можно и нужно)))

ДААААААААА ДА ДА ДА ДА

Кто мешает? Умножайте!

touch.otvet.mail.ru

Как перемножить квадратные корни Как? Так!

Содержимое:

2 метода:

Квадратные корни можно умножать так же, как целые числа. Иногда перед квадратным корнем находится множитель (целое число), но это лишь немного удлиняет процесс умножения, но не меняет его. Перед тем как перемножить квадратные корни, рекомендуется упростить их, но это довольно легко, если вы знаете, что такое полный квадрат.

Шаги

Метод 1 Перемножение квадратных корней без множителей

1. 1 Перемножьте подкоренные числа. Это числа, которые находятся под знаком корня. Перемножьте подкоренные числа как целые числа. Результат перемножения запишите под одним знаком корня.
   • Например, 15×5 2 Вынесите множитель из-под корня. Для этого выясните, можно ли разложить подкоренное число на два множителя, один из которых является полным квадратом. Если полного квадрата нет, результат упростить нельзя; в этом случае запишите его в ответе.
     • Полный квадрат – это число, которое является квадратом (произведением самого на себя) целого числа. Например, 25 – это полный квадрат, потому что 5×5=25 3 Извлеките квадратный корень из полного квадрата, а результат запишите перед знаком корня. Другой множитель оставьте под знаком корня. Так вы упростите подкоренное выражение.
       • Например, 75 4 Возведите квадратный корень в квадрат. В некоторых задачах квадратный корень умножается сам на себя. Возведение в квадрат и извлечение квадратного корня – это две противоположные операции, то есть они отменяют друг друга. Результатом возведения квадратного корня в квадрат является подкоренное число.
         • Например, 25×25=25

           Метод 2 Перемножение квадратных корней с множителями

           1. 1 Перемножьте множители. Здесь множитель – это число, которое находится перед знаком корня. На этом этапе не обращайте внимания на подкоренные числа – просто перемножьте множители. Результат запишите перед первым знаком корня.
              • При перемножении множителей не забудьте про их знаки. Помните, что при умножении отрицательного числа на положительное получится отрицательное число, а при умножении отрицательного числа на отрицательное получится положительное число.
              • Например, 32×26 2 Перемножьте подкоренные числа. Перемножьте подкоренные числа как целые числа. Результат перемножения запишите под одним знаком корня.
                • В нашем примере 62×6 3 Вынесите множитель из-под корня. Для этого выясните, можно ли разложить подкоренное число на два множителя, один из которых является полным квадратом. Если полного квадрата нет, результат упростить нельзя; в этом случае запишите его в ответе.
                  • Полный квадрат – это число, которое является квадратом (произведением самого на себя) целого числа. Например, 4 – это полный квадрат, потому что 2×2=4 4 Извлеките квадратный корень из полного квадрата, а результат умножьте на множитель, стоящий перед знаком корня. Другой множитель оставьте под знаком корня. Так вы упростите подкоренное выражение.
                    • В нашем примере 612{displaystyle 6{sqrt {12}}} подкоренное число раскладывается на два множителя: 64×3{displaystyle 6{sqrt {4 imes 3}}}. Таким образом, из числа 4 можно извлечь корень, а результат нужно умножить на 6:
                      612{displaystyle 6{sqrt {12}}}
                      = 64×3{displaystyle 6{sqrt {4 imes 3}}}
                      = 6×23{displaystyle 6 imes 2{sqrt {3}}}
                      
                      = 123{displaystyle 12{sqrt {3}}}

           Советы

           • Не забывайте про полные квадраты, которые облегчают процесс вычисления.
           • Следуйте правилам перемножения отрицательных и положительных чисел, чтобы определить знак конечного множителя. Если положительный множитель умножить на отрицательный, конечный множитель будет отрицательным. Если перемножить два положительных или два отрицательных множителя, конечный множитель будет положительным.
           • Подкоренные числа всегда положительные, поэтому при перемножении подкоренных чисел конечный результат будет всегда положительным.

           Что вам понадобится

           • Карандаш
           • Бумага
           • Калькулятор

Прислал: Cr1stal . 2017-11-06 20:02:51

kak-otvet.imysite.ru