График arccos cosx: Элементарная математика

Тригонометрическая функция и график обратной тригонометрической функции

вперед от:http://math001.com/inverse_trigonometric_functions/

вТригонометрическая функцияДобавить передarc, Означает ихОбратная функция f-1 (x). То есть текущий угол можно получить из тригонометрической функции.

 

1. Синус-функция sin x, арксинус-функция arcsin x

• y = sin x, x∈R, y∈ [–1,1], период равен 2π, изображение функции принимает x = (π / 2) + kπ в качестве оси симметрии
• y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]

1. sin x = 0    ←→     arcsin x = 0
2. sin x = 1/2     ←→     arcsin x = π/6
3. sin x = √2/2    ←→     arcsin x = π/4
4. sin x = 1    ←→     arcsin x = π/2

 

 

2. Функция косинуса cos x, функция обратного косинуса arccos x

• y = cos x, x∈R, y∈ [–1,1], период равен 2π, изображение функции принимает x = kπ в качестве оси симметрии
• y = arccos x， x∈[–1，1]， y∈[0，π]

1. cos x = 0    ←→     arccos x = π/2
2. cos x = 1/2     ←→     arccos x = π/3
3. cos x = √2/2    ←→     arccos x = π/4
4. cos x = 1    ←→     arccos x = 0 

 

 

3.

Функция обратного синуса arcsin x, функция обратного косинуса arccos x

• y = arcsin x и y = arccos x Диапазон независимой переменной x∈ [–1, 1]
• Образы y = arcsin x и y = arccos x симметричны относительно прямой y = π / 4, пересекаются с точкой (√2 / 2, π / 4)

 

 

4. Функция тангенса tan x, функция котангенса cot x

• y = tan x, x∈ ((–π / 2) + kπ, (π / 2) + kπ), y∈R, период равен π, при x → ± (π / 2) + kπ функцияпределБесконечно ∞
• y = cot x = 1 / tan x, x∈ (0, kπ), y∈R, период равен π, при x → kπ предел функции равен бесконечности ∞
• Образы y = tan x и y = cot x симметричны относительно x = (π / 4) + kπ / 2
• За один период (первый) изображение y = tan x и y = cot x пересекается с точкой (π / 4, 1). Когда x = (π / 4) + kπ / 2, значения y = tan x и y = cot x равны, что равно ± 1

 

 

5. Функция обратного тангенса arctan x, обратного котангенса arccot ​​x

• y = arctan x и y = arccot ​​x Диапазон независимой переменной x∈R
• Образы y = arctan x и y = arccot ​​x симметричны относительно прямой y = π / 4, пересекаются с точкой (1, π / 4)

1. tan x = 0    ←→     arctan x = 0
2. tan x = 1    ←→     arctan x = π/4
3. tan x = √3    ←→     arctan x = π/6

 

6.

Функция косеканса csc x

• y = csc x = 1 / sin x, x∈ (0, kπ), y∈ (–∞, –1] ∪ [1, ∞), период равен π, при x → kπ предел функции бесконечен ∞

 

 

7. Секущая функция sec x

• y = sec x = 1 / cosn x, x∈ ((–π / 2) + kπ, (π / 2) + kπ), y∈ (–∞, –1] ∪ [1, ∞), период равен π , При x → (π / 2) + kπ предел функции бесконечен ∞

---

Интеллектуальная рекомендация

FFMPEG и VS2010

Скомпилируйте ffmpeg — это болезненная вещь, которая обычно используется напрямуюZeranoe FFmpeg Builds。 Если вы используете эту версию, вам нужно обратить внимание на абзац о помощи FFMPEG: То есть фа…

Встроенная идея + Maven + Sprilboot Project Project Prience Integration MVC

Используйте идею + Maven + Springboot Создание новых проектов (1) Интегрированный MVC 1. Создайте новый файл проекта -> Новый -> Проект maven —> next 2. Заполните идентификатор организации и…

Redis Обзор и общие инструкции

Redis использует два — инструкции Окружающая среда: Redis-5.

0.3, Centos605 Обзор Redis — это высокоскоростная база данных памяти NoSQL, которая является системой хранения структуры данных в памяти, а …

Режим цепочки режима дизайна режима

основная концепция Что такое цепь Цепь представляет собой коллекцию узлов. Каждый узел цепи может быть разделен и реорганизован. Режим цепочки обязанностей Сделайте несколько объектов иметь возможност…

Проникновение в сеть/динамическое сетевые сети/видео Shangyun Gateway Easynts Network Platform Номер учетной записи и пароль нельзя войти в систему, как решить

Easynts, как Gateway Video Cloud, имеет такие функции, как сети видеопотоков, удаленная работа и техническое обслуживание. До запуска он будет протестирован отделом департамента исследований и разрабо…

Вам также может понравиться

Аплет WeChat сообщил об ошибке: не удалось прочитать свойство 0 из undefined

Сегодня я столкнулся с ошибкой: VM4735:2 Uncaught TypeError: Cannot read property ‘0’ of undefined После долгих поисков было обнаружено, что тринокулярный расчет был неправильным.

Такую низкоуровневую …

beaurifulsoup считывает данные локальной веб-страницы и сохраняет их в csv

Градуированная бедная собака использовала paperYY для проверки дубликатов. Контент проверки дубликатов отображается в формате html. Чтобы облегчить изменение повторяющихся мест в документе, содержание…

【CCF】201609-1

 …

Два элемента управления JS — список и пейджер

В последние месяцы я выполнял различные работы по техническому обслуживанию, и блог не обновляется часто. В мгновение ока наступит 2011 год, и я надеюсь, что в наступающем году я найду свою страсть. З…

Начало работы с сопоставлением точек функций python opencv + цель поиска по гомографии (39)

Контент поступает из само переведенных и организованных учебных пособий OpenCV-Python. цели: Мы объединим сопоставление характерных точек и поиск гомографии, а также будем использовать модуль calib3d …

© 2020-2022 All rights reserved by russianblogs.com

Урок 6.

обратные тригонометрические функции — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №6. Обратные тригонометрические функции.

Перечень вопросов, рассматриваемых в теме

• Рассмотреть свойства арксинуса и арккосинуса;
• Рассмотреть свойства арктангенса и арккотангенса;
• Объяснять расположение промежутков монотонности;
• Определять наибольшее и наименьшее значение функции;
• Применять знания при решении задач.

Глоссарий по теме

Арксинус ( y = arcsin x )  – это функция, обратная к синусу ( x = sin y ). Он имеет область определения  и множество значений  .

Арккосинус ( y = arccos x )  – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения   и множество значений  

Арктангенс ( y = arctg x )  – это функция, обратная к тангенсу ( x = tg y ).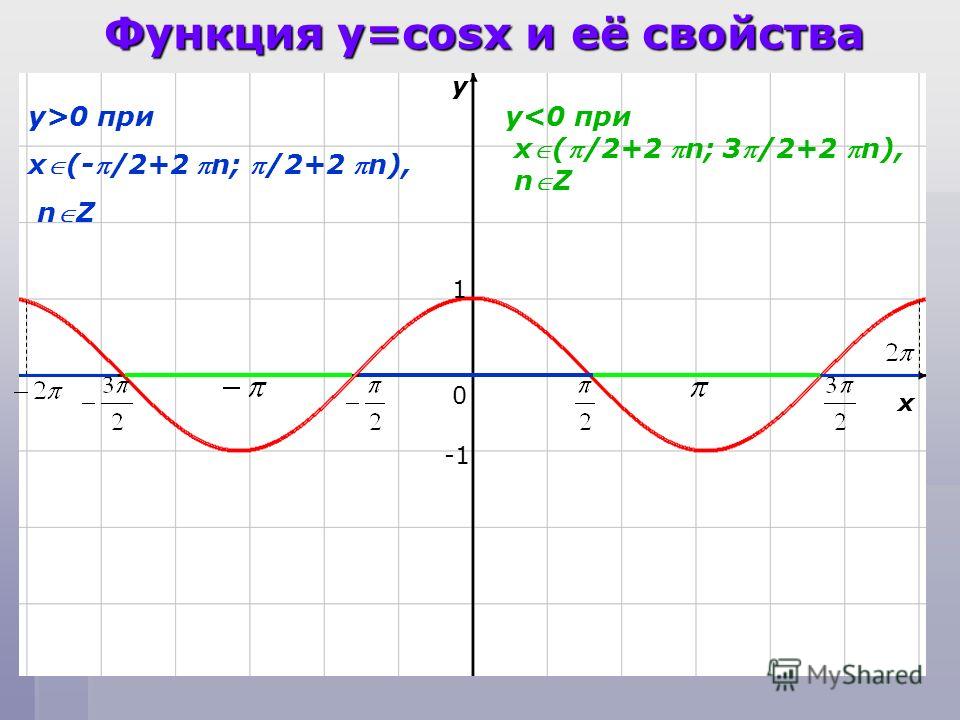 Он имеет область определения и множество значений  .

Арккотангенс ( y = arcctg x )  – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения    и множество значений

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.

Дополнительная литература:

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Актуализация знаний

Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен  ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.

Объяснение нового материала

Рассмотрим свойства функции y=arcsin x и построим ее график.

Арксинус ( y = arcsin x )  – это функция, обратная к синусу ( x = sin y ).

Свойства	Функции y=arcsin х
E(f)
D(f)
Чётность	Нечётная, т.к. arcsin(-x)= — arcsin x
Промежутки монотонности	Возрастающая

Рис. 1 График функции y=arcsin х

Рассмотрим свойства функции y=arcos x и построим ее график.

Арккосинус ( y = arccos x )  – это функция, обратная к косинусу ( x = cos y ).

Свойства	Функции y=arccos х
E(f)
D(f)
Чётность	Ни чётная, ни нечётная
Промежутки монотонности	Убывающая

Рис.2 График функции y=arccos х

Рассмотрим свойства функции y=arctgx и y=arcctgx и построим их графики.

Арктангенс ( y = arctg x )  – это функция, обратная к тангенсу ( x = tg y ).

Арккотангенс ( y = arcctg x )  – это функция, обратная к котангенсу ( x = ctg y ).

Свойства	y=arctg х	y=arcctg х
E(f)	R	R
D(f)
Чётность	Нечётная	Нечётная
Промежутки монотонности	Возрастающая	Убывающая

Рис. 3 График функции y=arctgx

Рис.4 График функции y=arcсtgx

Примеры и разборы решения заданий тренировочного модуля:

Пример 1.

Найдите значение выражения

Обозначим , по определения арктангенса получаем х=60°, т.е. нам нужно найти

Ответ:

Пример 2.

Решите неравенство

;

;

;

;

Накладываем ограничения по свойствам арксинуса:

;

Ответ:

Открытая Математика. Алгебра. Обратные тригонометрические функции

Обратные тригонометрические функции

Вернемся к определению функции, данному в § 2.2.1. Отметим, что в этом определении функция f не обязана разным элементам x1 и x2 множества X ставить в соответствие разные элементы множества Y.

Если Y – множество значений функции f (x) и для любого элемента y∈Y существует единственный элемент x∈X такой, что f (x) = y, то говорят, что функция осуществляет взаимнооднозначное соответствие между множествами X и Y.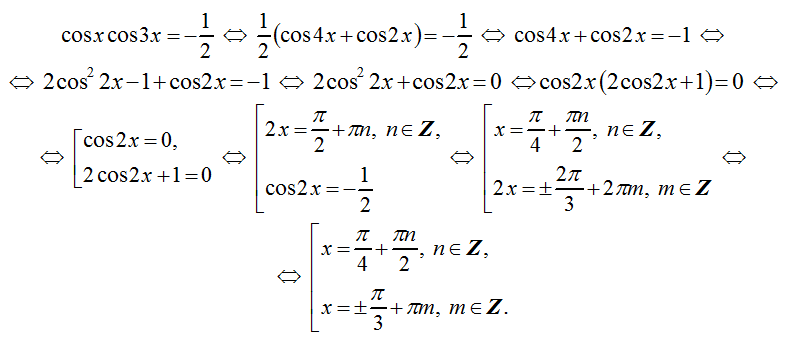 Другими словами, соответствие называется взаимнооднозначным, если каждому элементу x∈X соответствует единственный элемент y∈Y и наоборот, каждому элементу y∈Y соответствует единственный элемент x∈X. Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции

f существует обратная функция. Такая функция обозначается f-1 и каждому элементу y∈Y ставит в соответствие такой элемент x∈X, что f (x) = y; этот факт записывают так: x=f-1 (y). Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных x↔y, что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что y=f-1 (x) − обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции: D (f-1)=E (f)=Y. Область значений обратной функции совпадает с множеством определения самой функции: E (f-1)=D (f)=X.

Рассмотрим функцию f (x) = sin x для x∈[-π2; π2]. Тогда D (f)=[-π2; π2], E (f)=[-1; 1]. При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения D (f-1)=[-1;  1] и областью значений E (f-1)=[-π2; π2]. Эта обратная функция называется арксинусом. Её обозначение: y = arcsin x. График функции y = arcsin x изображён на рисунке.

Арксинус Функция y = arcsin x

Аналогично, на промежутке D (f^–1) = E (f) = [–1; 1] можно определить функцию, обратную cos x, c областью значений E (f^–1) = D (f) = [0; π] Эта обратная функция называется арккосинусом. Её обозначение: y = arccos x

. График функции y = arccos x изображён на рисунке.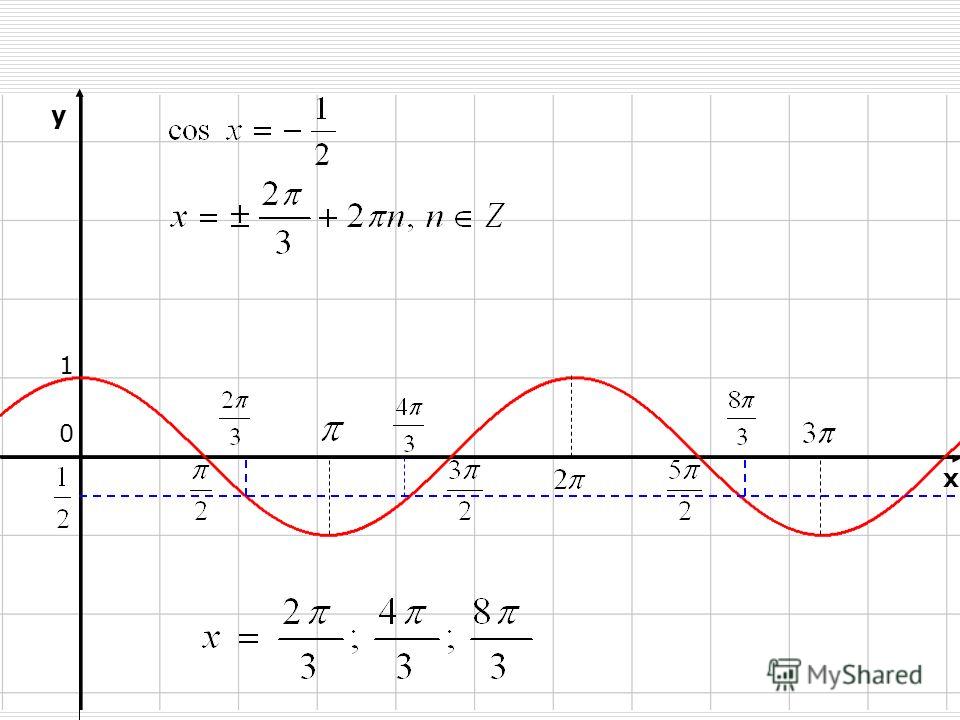

Арккосинус Функция y = arccos x

Рассмотрим функцию f (x) = tg x для x∈(-π2; π2). Тогда D (f)=(-π2; π2), E (f)=R. При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения D (f-1)=R и областью значений E (f-1)=(-π2; π2). Эта обратная функция называется арктангенсом. Её обозначение y = arctg x. График функции y = arctg x изображён на рисунке.

Арктангенс Функция y = arctg x

Для построения арккотангенса выберем промежуток x ∈ (0; π). Тогда D (f)=(0; π), E (f)=R. Построим обратную функцию с областью определения D (f-1)=E (f)=R и областью значений E (f-1)=D (f)=(0; π). Эта обратная функция называется арккотангенсом. Её обозначение

y = arcctg x. График функции y = arcctg x изображён на рисунке.

Арккотангенс Функция y = arcctg x

Итак, запись b = arcsin a обозначает, что b∈[-π2; π2] и sin b = a. Аналогичные соотношения справедливы и для остальных обратных тригонометрических функций.

Докажите тождество arcsinx+arccosx=π2.

Пусть y=arcsinx⇔{-π2≤y≤π2, sin y=x;  пусть также z=arccosx⇔{0≤z≤π, cos z=x. Следовательно, требуется доказать неравенство y+z=π2. Перенесём z в правую часть и возьмём синус от обеих частей получившегося равенства: y=π2-z⇒sin y=sin(π2-z)=cos z.

Но sin y = x и cos z = x, значит, наше равенство принимает вид

x = x. Однако для того, чтобы доказать нужное нам тождество, мы должны обосновать возможность перехода от верного равенства x = x к исходному. В самом деле, переход от равенства sin y = cos z к равенству y=π2-z, вообще говоря, не является равносильным преобразованием.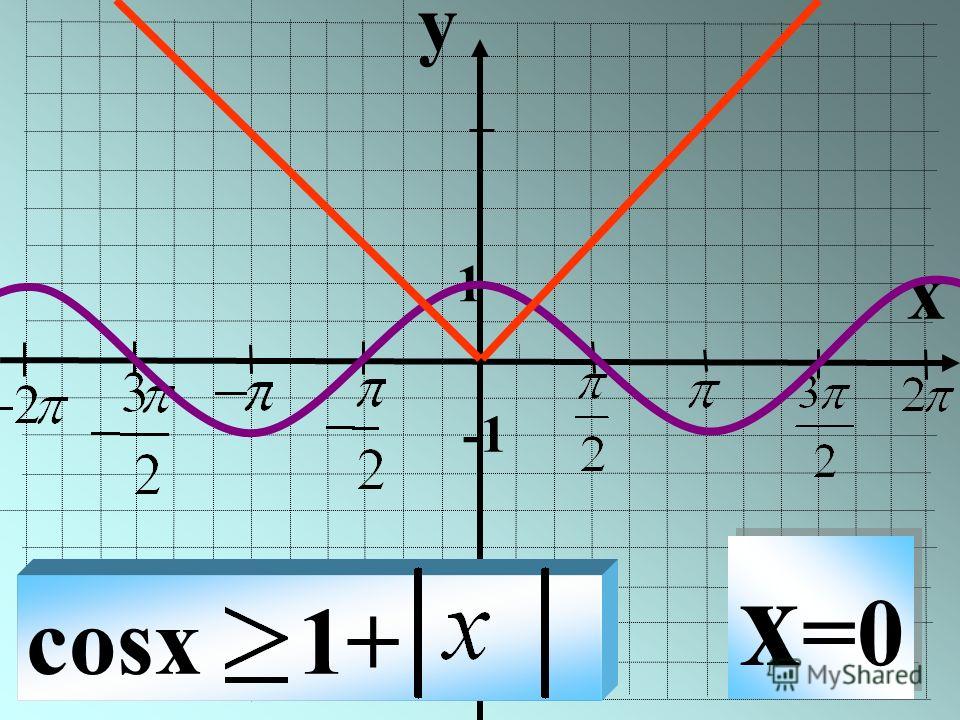 Но у нас есть ограничения на y и z в виде неравенств -π2≤y≤π2, 0≤z≤π, а для таких y и z равенство sin y = cos z возможно только при y=π2-z. Следовательно, y+z=π2 и наконец arcsinx+arccosx=π2, что и требовалось доказать.

Найти соотношение между A (x) = arcsin (cos (arcsin x)) и B (x) = arccos (sin (arccos x)).

Обозначим через y переменную, для которой выполняется равенство: y=arcsinx⇔{-π2≤y≤π2, sin y=x, тогда cos y = cos (arcsin x). Значит, cos y=+1-sin2 (arcsin x)=+1-x2. Здесь поставлен знак «+», поскольку

y − угол первой или четвёртой четверти, в которых косинус положителен. Равенство sin (arcsin x) = x справедливо по определению функции арксинус. Значит, cos(arcsinx)=1-x2.

Вычислим sin (arccos x) = sin z, где z=arccosx⇔{0≤z≤π,cos z=x. Значит, sin z=+1-cos2 (arccos x)=+1-x2. Здесь поставлен знак плюс, поскольку z − угол первой или второй четверти, в которых синус положителен.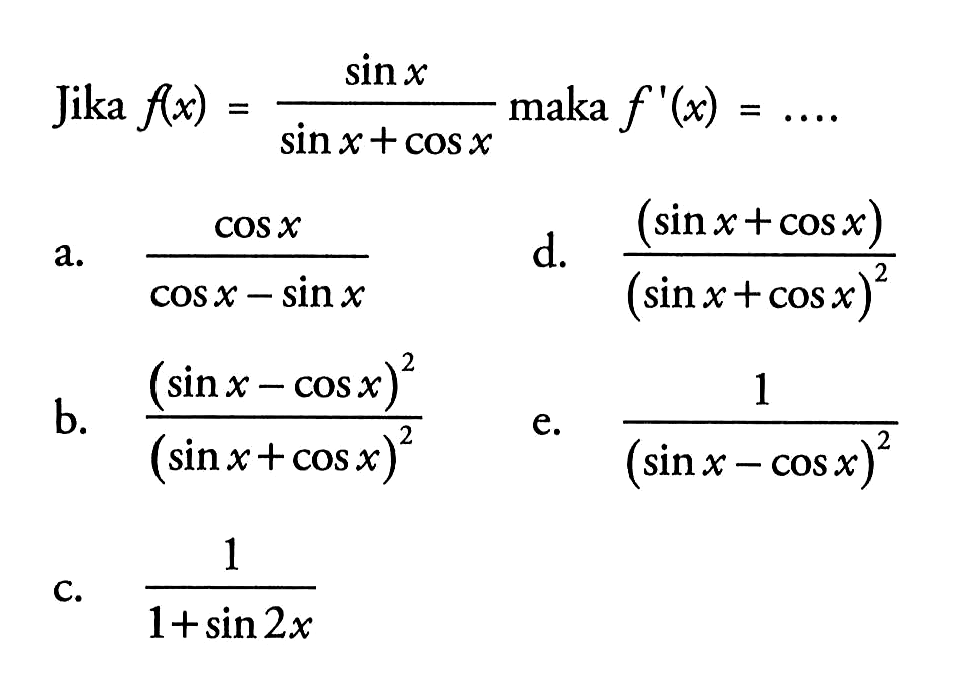 Равенство cos (arccos x) = x справедливо по определению функции арккосинус. Отсюда sin(arccosx)=1-x2.

Итак, A (x)=arcsin1-x2 и B (x)=arccos1-x2. В предыдущем примере мы установили, что сумма арксинуса и арккосинуса одного и того же аргумента равна π2. Окончательно, A (x)+B (x)=π2.

Ответ. A (x)+B (x)=π2.





 

Функция, производная которой равна y ‘ = — cos x, имеет вид …. Выбери… — Учеба и наука

Ответы

02. 03.21

Екатерина Читать ответы

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Здравствуйте! Прошу помощи! Алеша сказал: «У Змея Горыныча больше трех голов». Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея больше

Решено

В прямоугольной трапеции диагональ является биссектрисой острого угла. Найдите. площадь трапеции, если боковые стороны равны 8 см и 10 см

Решено

Начертите треугольник АВС. Постройте вектор: 1) АС+СВ 2)ВА-ВС 3)АС+АВ

Периметр правильного треугольника, вписанного в окружность, равен 6√3 дм. Найдите периметр правильного шестиугольника описанного около той же окружности.

Решено

В лесу на разных кустах висят 100 шнурков. Сова утверж-дает, что в среднем три шнурка из четырёх, которые мож-но найти в лесу, ей не подходят,

Пользуйтесь нашим приложением

Функция у=arccos x — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

y
y = cos x
2
3
2
2
1
0
-1
Функция y=cosx, взятая на
всей области определения, не
имеет обратной, т.к. одно и
тоже её значение достигается
при разных значениях
аргумента.
2
x
3
2
Кривая симметричная
косинусоиде относительно
прямой у=х не является
функцией (функциональная
зависимость предполагает
соответствие каждому
значению аргумента
единственное значение
функции).
2
y
Рассмотрим функцию
y=cosx только на отрезке
[0; ]
2
2
3
2
y = cos x
-1
1
0
1
-1
2
D
E( y) : yx 1;1
; 1
0
0;;1
2
x
3
2
Обратная
функция
y = arccos
x
D
E( у) : yх 0;
101;;;0
2
2
y = arccosx
y
D( y) : x 1;1
E( у) : y 0;
-1
0
1
x
Функция ни четная ни нечетная
Функция убывает
Функция непрерывна
Повторим
y = f(x)
y
y = f(x)
y = — f(x)
-1
x
1
y = — f(x)
y
y = — arccosx
D( y) : x 1;1
2
Найдем E(y) методом оценки
0 arccos x
(-1)
0 arccos x
arccos x 0
E( у) : y ; 0
1
-1
2
x
Повторим
y = f(x)
y = f(-x)
y
y = f(x)
y = f(-x)
-1
1
x
y
y = arccos(-x)
Найдем D(y) методом оценки
1 x 1
(-1)
2
1 x 1
1 x 1
D( y) : x 1;1
E( у) : у 0;
1
-1
2
x
y
y = 2arccos x
2
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
2
0 2 arccos x 2
0 y 2
2
E( у) : у 0; 2
-1
1
x
y
1
=
y — 2 arccos x
D( y) : х 1;1
2
Найдем E(y) методом оценки
0 arccos x
0 0,5 arccos x
2
(–0,5)
0,5 arccos x 0
E ( у ) : у ; 0
2
1
-1
2
2
x
y
y = arccos 12 x
Найдем D(y) методом оценки
1
1 x 1
2
2 x 2
2
2
D( y) : х 2; 2
E( у) : у 0;
-2
1
-1
2
2
x
y
y = arccos 2x
Найдем D(y) методом оценки
1 2x 1 : 2
1
1
x
2
2
2
1 1
D( y ) : х ;
2 2
E( у) : у 0;
-1– 1
2
1 1
2
2
x
y
y = 1,5arccosx +
2
2
3
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
* 1,5
0 1,5 arccos x 1,5 + 2
3
2
13
1,5 arccos x
3
6
2 13
E ( у ) : у
;
3
6
2
-1
1
x
Повторим
y = f(x)
y = f(x)
y
y = f(x)
1
x
y
Повторим
1
y = f(x)
y= f x
Функция четная
(график симметричен
относительно оси Оу)
x
y
y = arccosx
2
1
-1
2
График y =arccosx не изменится.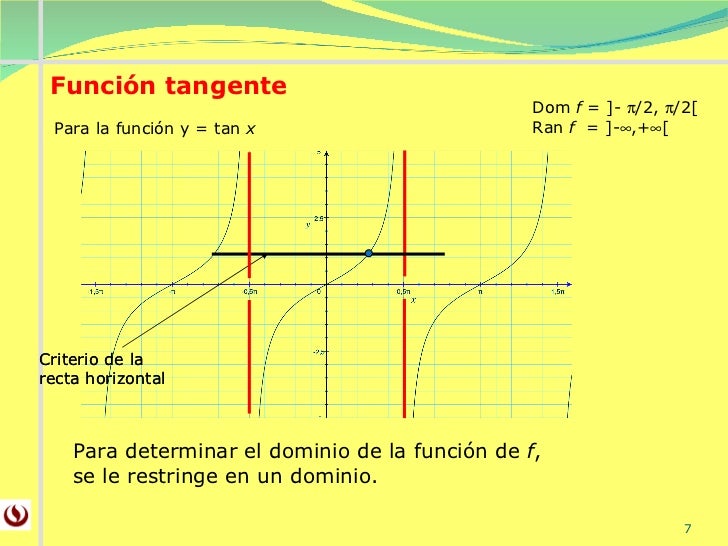
Почему?
x
y = arccos x –
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
0 arccos x
–6
2
arccos x
6 3
6
0
E ( у ) : у 0;
3
y
6
g ( x) = x
При x [ 1; 1]
x [0; 1]
-1
0
1
x
1
x
y
y( x) = arccos x
При x [0; 1]
arccos x [0;
2
]
-1
0
y = arccos x –
y
6
D( y) : х 1;1
E ( у ) : у 0;
3
Функция четная
(график симметричен
относительно оси Оу)
2
-1
1
2
x
y 3
Найдем область определения и
множество значений, затем
построим график.
2
y = -1,5arccos (x–2)
3
1 x 2 1 +2
1 x 3
D( y ) : x 1; 3
[ 1; 1]
0 arccos( x 2)
(-1,5)
1,5 2 arccos( x 2) 0
1,5 y 0
E ( y ) : y 1,5 ; 0
4
2
1
-1
3
4
3
2
3
x
3
y = arccos( x – )
4
D( y )
3
1 х 1
4
+3
4
1
3
х 1
4
4
3
х 1
4
3
3
1 х 1
4
4
3 3
D ( y ) : х 1 ;1
4 4
y( x) = arccos g ( x)
3
При g ( x) [ ; 1]
4
E ( y)
3
y = arccos( x – )
4
y
3
g ( x) = x
4
x 0
3
arccos
4
–3
4
3
3
x
4
4
3
1 х 1
4
3
3
х 1
4
4
-1– 3 0
1
x
4
3
E ( у ) : у 0; arccos
4
y
3
y = arccos( x – )
4
3 3
D ( y ) : х 1 ;1
4 4
2
3
–1
3 4
E ( у ) : у 0; arccos
4
Функция четная
(график симметричен
относительно оси Оу)
3
arccos
4
-1
1
2
1
3
4
x

English     Русский Правила

Вычисление производных сложных функций

Вычисление производных сложных функций

Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3 Архитектура Биология География Другое Иностранные языки Информатика История Культура Литература Математика Медицина Механика Образование Охрана труда Педагогика Политика Право Программирование Психология Религия Социология Спорт Строительство Физика Философия Финансы Химия Экология Экономика Электроника

Практическая работа № 14

Вычисление производных сложных функций

Цель урока. Проверить навыки и умения студентов по вычислению производных простейших функций.

Задания

2.

2.1. 2.2.

2.3. 2.4.

2.5. 2.6.

2.7. 2.8.

2.9. 2.10.

2.11. 2.12.

2.13. 2.14.

2.15. 2.16.

2.17. 2.18.

2.19. 2.20.

2.21. 2.22.

2.23. 2.24.

2.25. 2.26.

2.27. 2.28.

2.29. 2.30.

3.

3. 18. y = e^{cos x} * ctg8x³.

3.19. у = cos⁵x * arccos4x. 3.20. у = sin³7x * arcctg5x².

3.21. y = sin²3x * arcctg3x⁵. 3.22. у = cos * arctg x⁴

3.23. y = tg⁶2x * cos7x². 3.24. y = ctg³4x * arcsin .

3.25. y = ctg1/x * arccos x⁴ 3.26. у = tg * arcctg 3x⁵.

3.27. у = tg³2x * arccos2x³. 3.28. y = 2^{tg x} * arctg⁵ 3x.

3.29. y = sin⁵3x * arctg . 3.30. у = cos⁴3x * arcsin3x².

4.

4.1. y = arcctg²5x * ln(x — 4). 4.2. у = аrctg³2x * ln(x + 5).

4.3. у = arccos⁴x * ln(x² + x — 1). 4.4.

4.5. y = tg⁴3x * arctg7x². 4.6. у = 5^-x2 * arcsin3x³.

4.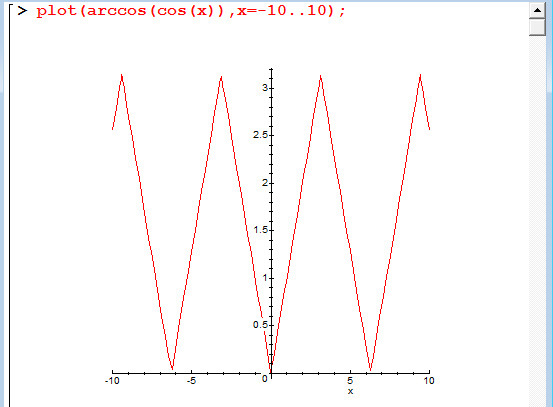 7. у = arctg⁵x * log₂(x — 3). 4.8. у = log₃(x + 5) * arccos 3x.

4.9. у = е^-x * arcsin²5x. 4.10. у = log₄(x — 1) * arcsin⁴ x.

4.11. у = (x — 4)⁵ * arcctg 3x². 4.12. y = ctg³4x * arctg 2x³.

4.13. y = e^{-cos x} * arctg7x⁵. 4.14. y = (x + l) * arccos3x⁴

4.15. у = 2 ^sinx * arcctg x⁴. 4.16. y = 3^-x3 * arctg 2x⁵.

4.17. у = 3^{cos x} * arcsin² 3x. 4.18. y = ln(x — 10) * arccos²4x.

4.19. у = lg(x — 2) * arcsin⁵ x. 4.20. у = log₃(x + 1) * arctg⁵ 7x.

4.21. y = ln(x + 9) * arcctg³2x. 4.22. у = lg(x + 2) * arcsin² 3x.

4.23. y = 4^{-sin x} * arctg 3x. 4.24. у = 2^{cos x} * arcctg³ x

4.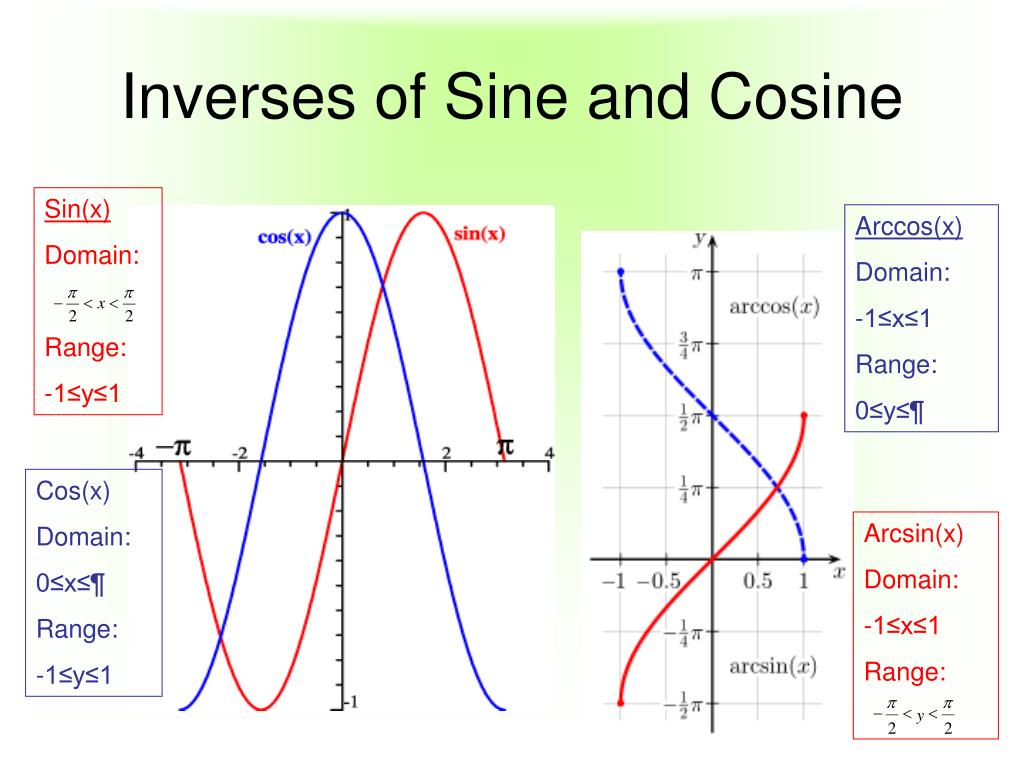 25. у = lg(x — 3) * arcsin² 5x. 4.26. y = log₂(x + 3) * arccos²x.

4.27. y = 2^-x * arctg³ 4x. 4.28. y = ln(x — 4) * arcctg⁴ 3x.

4.29. y = lg(x + 3) * arcctg² 5x. 4.30. у = log₅(x + 1) * arctg² x³.

5.

5.1. у = tg⁴3x * arcsin 2x³. 5.2. y = (x — 2)⁴ * arcsin 5x⁴.

5.3. у = 2^—x3 * arctg 7x⁴. 5.4. у = (x + 6)⁵ * arcctg 3x⁵.

5.5. у = 3^{cos x} * ln(x² — 3x + 7). 5.6. y = log₂(x -7) * arctg

5.7. y = arccos³5x * tgx⁴. 5.8. y = (x — 5)⁷ * arcctg 7x³

5.9. у = arccos x² * ctg 7x³. 5.10. у = 5^-x2 * arccos 5x⁴.

5.11. y = arctg⁴x * cos 7x⁴. 5.12. у = 4(x — 7)⁶ * arcsin 3x⁵.

5.13. у = (x + 5)² arccos³ 5x. 5.14. y = 2^{-sin x} * arcsin³2x

5.15. у = (x + 2)⁷ * arccos 5.16. у = (x — 7)⁵ * arcsin 7x⁴

5.17. y = ln(x — 3) * arccos 3x⁴ 5.18. у = log₂(x — 4) * arctg³ 4x.

5.19. y = (x — 7)⁴ * arcctg² 7x 5.20.

5.21. 5.22. y = (x – 3)⁵arccos 3x⁶

5.23. 5.24.

5.25. y = tg³ x * arcctg 3x 5.26.

5.27. 5.28. y = arcsin³ 4x * ctg 3x

5.29. y = e^{-cos x} arcsin 2x 5.30.

6.

6.1. у = (х — 3)⁴ * arccos 5x³. 6.2. у = (3х — 4)³ * arccos 3x².

6.3. у = sh³ 4x * аrссоs . 6.4. у = th² * arcctg3x².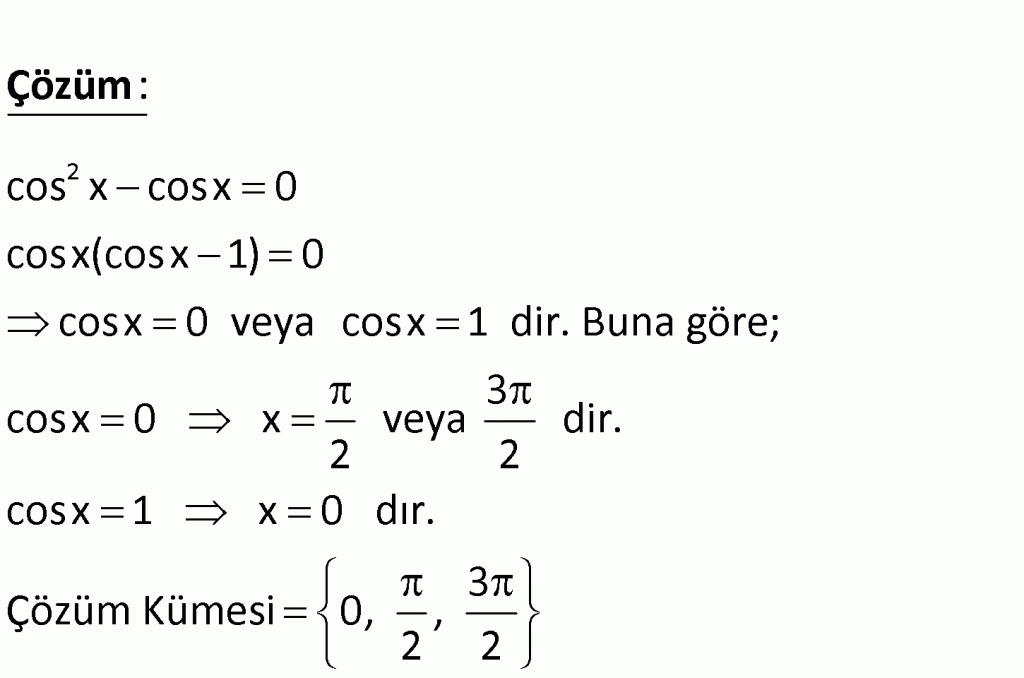

6.5. y = cth³ 5x * arcsin 3x². 6.6. y = ch2/x * arctg(7x + 2).

6.7. у = ch³ 4x * arccos 4x². 6.8. y = sh³3x * arcctg5x².

6.9. у = th⁵ Зx * arcsin . 6.10. у = сth²(x + 1) * arccos1/x.

6.11. у = sh⁴ 2x * arccos x². 6.12. y = ch³(3x + 2) * arctg3x.

6.13. у = th³4x * аrссtg3x⁴ 6.14. у = cth⁴ 7x * arcsin .

6.15. у = sh³ 2x * arcsin 7x². 6.16. у = th⁵ 4x * arccos 3x⁴.

6.17. у = ch² 5x * arctg . 6.18. y = cth⁴2x * arctg x³.

6.19. y = sh⁴ 5x * arccos 3x². 6.20. у = ch³ 9x * arctg(5x — 1).

6.21. y = th⁴x * arcctg 1/x. 6.22. у = cth³ 4x * arcsin (3x + 1).

6.23. y = ch²5x * arctgx⁴. 6.24. у = th⁴ 7x * arccos x³.

6.25. у = cth 4х⁵ * arccos 2x. 6.26. у = cth 3х * arcsin⁴ 2x.

6.27. у = th⁵ 3х * arcctg 6.28. у = sh⁴ 3х * arccos 5x⁴.

6.29. у = cth² 4x * arcsin x³. 6.30. у = th³ 5x * arcctg(2x — 5).

7.

7.1. 7.2.

7.3. 7.4.

7.5. 7.6.

7.7. 7.8.

7.9. 7.10.

7.11. 7.12.

7.13. 7.14.

7.15. 7.16.

7.17. 7.18.

7.19. 7.20.

7.21. 7.22.

7.23. 7.24.

7.25. 7.26.

7.27. 7.28.

 

7.29. 7.30.

8.

8.1. 8.2.

8.3. 8.4.

8.5. 8.6.

8.7. 8.8.

8.9. 8.10.

8.11. 8.12.

8. 13. 8.14.

8.15. 8.16.

8.17. 8.18.

8.19. 8.20.

8.21. 8.22.

8.23. 8.24.

8.25. 8.26.

8.27. 8.28.

8.29. 8.30.

9.

9.1. 9.2.

9.3. 9.4.

9.5. 9.6.

9.7. 9.8.

9.9. 9.10.

9.11. 9.12.

9.13. 9.14.

9.15. 9.16.

9.17. 9.18.

9.19. 9.20.

9.21. 9.22.

9.23. 9.24.

9.25. 9.26.

9.27. 9.28.

9.29. 9.30.

10.

10.1. 10.2.

10.3. 10.4.

10.5. 10.6.

10.7. 10.8.

10.9. 10.10.

10.11. 10.12.

10.13. 10.14.

10.15. 10.16.

10.17. 10.18.

10.19. 10.20.

10. 21. 10.22.

10.23. 10.24.

10.25. 10.26.

10.27. 10.28.

10.29. 10.30.

11.

11.1. 11.2.

11.3. 11.4.

11.5. 11.6.

11.7. 11.8.

11.9. 11.10.

11.11. 11.12.

11.13. 11.14.

11.15. 11.16.

11.17. 11.18.

11.19. 11.20.

11.21. 11.22.

11.23. 11.24.

11.25. 11.26.

11.27. 11.28.

11.29. 11.30.

12.

12.1. y = (cth 3x)^{arcsin x} 12.2. y = (cos (x+2))^{ln x}

12.3. y = (sin 3x)^{arccos x} 12.4. y = (th 5x)^{arcsin (x+1)}

12.5. y = (sh (x+2))^{arcsin 2x} 12.6.

12.7. 12.8.

12.9. y = (log₂(x+4))^ctg7x 12. 10. y = (sh 3x)^{arctg (x+2)}

12.11. y = (ch 3x)^{ctg 1/x} 12.12.

12.13. y = (arccos 5x)^{ln x} 12.14. y = (arctg 2x)^{sin x}

12.15. y = (ln (x+7))^{ctg 2x} 12.16.

12.17. 12.18. y = (cth 1/x)^{arcsin 7x}

12.19. y = (cos (x+5))^{arcsin 3x} 12.20.

12.21. y = (sin 4x)^{arctg 1/x} 12.22.

12.23. 12.24.

12.25. 12.26. y = (ctg 7x)^sh(x+3)

12.27. y = (sh 5x)^arctg(x+2) 12.28. y = (arctg x)^th(3x+1)

12.29. 12.30. y = (sh 3x)^{arcctg 2x}

 

Решние типового варианта

Продифференцировать данные функции.

 

1.

2.

3.

4.

 

5.

6.

7.

8.

 

 

9.

10.

11.

 

12.

Прологарифмируем данную функцию:

тогда

Отсюда выразим y`:

 

 

 

---

Дата добавления: 2015-08-27; просмотров: 590 | Нарушение авторских прав

---

---

	|	следующая лекция ==>
Министерство образования и науки Российской Федерации	|	Правила общения с ГАИ (Украина)

---

mybiblioteka. su — 2015-2022 год. (0.105 сек.)

Мэтуэй | Популярные задачи

92

1	Найти точное значение	грех(30)
2	Найти точное значение	грех(45)
3	Найти точное значение	грех(30 градусов)
4	Найти точное значение	грех(60 градусов)
5	Найти точное значение	загар (30 градусов)
6	Найти точное значение	угловой синус(-1)
7	Найти точное значение	грех(пи/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	грех(45 градусов)
10	Найти точное значение	грех(пи/3)
11	Найти точное значение	арктан(-1)
12	Найти точное значение	cos(45 градусов)
13	Найти точное значение	cos(30 градусов)
14	Найти точное значение	желтовато-коричневый(60)
15	Найти точное значение	csc(45 градусов)
16	Найти точное значение	загар (60 градусов)
17	Найти точное значение	сек(30 градусов)
18	Найти точное значение	cos(60 градусов)
19	Найти точное значение	cos(150)
20	Найти точное значение	грех(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	загар (45 градусов)
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 градусов)
25	Найти точное значение	сек(45 градусов)
26	Найти точное значение	csc(30 градусов)
27	Найти точное значение	грех(0)
28	Найти точное значение	грех(120)
29	Найти точное значение	соз(90)
30	Преобразовать из радианов в градусы	пи/3
31	Найти точное значение	желтовато-коричневый(30)
32
35	Преобразовать из радианов в градусы	пи/6
36	Найти точное значение	детская кроватка(30 градусов)
37	Найти точное значение	арккос(-1)
38	Найти точное значение	арктан(0)
39	Найти точное значение	детская кроватка(60 градусов)
40	Преобразование градусов в радианы	30
41	Преобразовать из радианов в градусы	(2 шт. )/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	тан(пи/2)
45	Найти точное значение	грех(300)
46	Найти точное значение	соз(30)
47	Найти точное значение	соз(60)
48	Найти точное значение	соз(0)
49	Найти точное значение	соз(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	сек(60 градусов)
53	Найти точное значение	грех(300 градусов)
54	Преобразование градусов в радианы	135
55	Преобразование градусов в радианы	150
56	Преобразовать из радианов в градусы	(5 дюймов)/6
57	Преобразовать из радианов в градусы	(5 дюймов)/3
58	Преобразование градусов в радианы	89 градусов
59	Преобразование градусов в радианы	60
60	Найти точное значение	грех(135 градусов)
61	Найти точное значение	грех(150)
62	Найти точное значение	грех(240 градусов)
63	Найти точное значение	детская кроватка(45 градусов)
64	Преобразовать из радианов в градусы	(5 дюймов)/4
65	Найти точное значение	грех(225)
66	Найти точное значение	грех(240)
67	Найти точное значение	cos(150 градусов)
68	Найти точное значение	желтовато-коричневый(45)
69	Оценить	грех(30 градусов)
70	Найти точное значение	сек(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	КСК(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	загар((5pi)/3)
75	Найти точное значение	желтовато-коричневый(0)
76	Оценить	грех(60 градусов)
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3 пи)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	угловой синус(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	КСК(45)
83	Упростить	арктан( квадратный корень из 3)
84	Найти точное значение	грех(135)
85	Найти точное значение	грех(105)
86	Найти точное значение	грех(150 градусов)
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	загар((2pi)/3)
89	Преобразовать из радианов в градусы	пи/4
90	Найти точное значение	грех(пи/2)
91	Найти точное значение	сек(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	угловой синус(0)
95	Найти точное значение	грех(120 градусов)
96	Найти точное значение	желтовато-коричневый ((7pi)/6)
97	Найти точное значение	соз(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразование градусов в радианы	88 градусов

Arccos

Арккосинус, записывается как arccos или cos-1 (не путать с ), является функцией арккосинуса. Косинус имеет обратный только в ограниченной области, 0≤x≤π. На рисунке ниже часть графика, выделенная красным цветом, показывает часть графика cos(x), которая имеет обратную.

Домен должен быть ограничен, поскольку для того, чтобы у функции была обратная функция, она должна быть взаимно однозначной, то есть никакая горизонтальная линия не может пересекать график функции более одного раза. Поскольку косинус является периодической функцией, без ограничения области определения горизонтальная линия будет периодически пересекать функцию бесконечно много раз.

Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, то точка (b, a) находится на графике обратной функции. Это фактически означает, что график обратной функции является отражением графика функции через прямую y = x.

График y = arccos(x) показан ниже.

Как видно из рисунка, y = arccos(x) является отражением cos(x) для ограниченной области 0≤x≤π через прямую y = x. Домен arccos(x), -1≤x≤1, является диапазоном cos(x), а его диапазон, 0≤x≤π, является доменом cos(x).

Калькулятор Arccos

Ниже приведен калькулятор для определения либо значения arccos числа от -1 до 1, либо значения косинуса угла.

арккос		=		деградировать

Использование специальных углов для нахождения арккосинуса

Хотя мы можем найти значение арккосинуса для любого значения x в интервале [-1, 1], существуют определенные углы, которые часто используются в тригонометрии (0°, 30°, 45°, 60°, 90° и их кратные и эквиваленты в радианах), значения косинуса и арккосинуса которых стоит запомнить. Ниже приведена таблица, показывающая эти углы (θ) в градусах и их соответствующие значения косинуса, cos(θ).

θ	0°	30°	45°	60°	90°	120°	135°	150°	180°
соз(θ)	1				0				-1

Один из методов, который может помочь в запоминании этих значений, заключается в выражении всех значений cos(θ) в виде дробей с квадратным корнем. Начиная с 0° и увеличивая до 90°, cos(0°)=1=. Последующие значения cos(30°), cos(45°), cos(60°) и cos(90°) следуют шаблону, так что используя значение cos(0°) в качестве эталона, чтобы найти значения косинуса для последующих углов, мы просто уменьшаем число под знаком радикала в числителе на 1, как показано ниже:

θ	0°	30°	45°	60°	90°
соз(θ)					0

От 90° до 180° вместо этого мы увеличиваем число под радикалом на 1, но также должны учитывать квадрант, в котором находится угол. Косинус отрицателен в квадрантах II и III, поэтому значения будут равны но отрицательный. В квадрантах I и IV значения будут положительными. Этот шаблон периодически повторяется для соответствующих угловых измерений.

После того, как мы запомнили значения или если у нас есть какая-то ссылка, становится относительно просто распознавать и определять значения косинуса или арккосинуса для специальных углов.

Пример:

Найти arccos() , arccos() и arccos(2) в радианах.

, .

, .

arccos(2) не определен, так как 2 не находится в интервале -1≤arccos(θ)≤1, домене arccos(x).

Обратные свойства

Как правило, функции и их обратные свойства демонстрируют отношение

f(f ^-1 (x)) = x   и   f ^-1 (f(x)) = x

при условии, что x находится в области определения функции. То же самое верно для cos(x) и arccos(x) в пределах их соответствующих ограниченных доменов:

cos(arccos(x)) = x для всех x в [-1, 1]

и

arccos(cos (x)) = x, для всех x в [0, π]

Эти свойства позволяют нам оценить композицию тригонометрических функций.

Композиция арккосинуса и косинуса

Если x находится в области определения, вычисление композиции арккосинуса и косинуса относительно просто.

Примеры:

1.

2.

Если x не входит в область значений, нам необходимо определить опорный угол, а также соответствующий квадрант. Учитывая arccos(cos()), мы не можем оценить это, как мы сделали выше, потому что x не находится в пределах [0, π], поэтому решение не может быть . Чтобы оценить это, нам нужно сначала определить cos() перед использованием arccos:

3.

В приведенном выше примере опорный угол равен , а cos() равен , но поскольку он лежит в квадранте III, его косинус отрицательный, и единственный угол, косинус которого равен , который лежит в области определения arccos(x), равен .

Композиция других тригонометрических функций

Мы также можем составить композиции, используя все другие тригонометрические функции: синус, тангенс, косеканс, секанс и котангенс.

Пример:

Найти sin(arccos()).

Так как не является одним из отношений для специальных углов, мы можем использовать прямоугольный треугольник, чтобы найти значение этой композиции. Учитывая arccos() = θ, мы можем найти, что cos(θ) = . Прямоугольный треугольник ниже показывает θ и отношение его смежной стороны к гипотенузе треугольника.

Чтобы найти синус, нам нужно найти противоположную сторону, так как sin(θ)=. Пусть а — длина противоположной стороны. Используя теорему Pythagorean,

A ² + 12 ² = 13 ²

A ² + 144 = 169

A ² = 25907 = 169

A ² = 25907 = 169

A ² = 94907

A ² = 94 = 169

A ² = 144 = 169

A ² = 144 = 169

A ² . (arccos()) = sin(θ) =

Тот же процесс можно использовать с переменным выражением.

Пример:

Найдите tan(arccos(4x)).

Учитывая arccos(4x) = θ, мы можем найти, что cos(θ)= и построить следующий прямоугольный треугольник:

Чтобы найти касательную, нам нужно найти противоположную сторону, так как tan(θ)=. Пусть b — длина противоположной стороны. Using the Pythagorean theorem,

(4x) ² + b ² = 1 ²

16x ² + b ² = 1

b ² = 1 — 16x ²

b =

и

tan(arccos(4x)) = tan(θ) = , где —

Использование арккосинуса для решения тригонометрических уравнений

Арккосинус также можно использовать для решения тригонометрических уравнений, включающих функцию косинуса.

Пример:

Решите следующие тригонометрические уравнения относительно x, где 0≤x<2π.

1. 2cos(x) =

2cos(x) =

cos(x) =

x = arccos()

Косинус отрицателен в квадрантах II и III, поэтому есть два решения: x= и х=. Это единственные два угла в пределах 0≤x<2π, значение косинуса которых равно .

2. 6cos ² (x) + 9cos(x) — 36 = 0

6cos ² (x) + 9sin(x) — 6 = 0

(6cos(x) — 3)(cos (x) + 2) = 0

6cos(x) — 3 = 0 или cos(x) + 2 = 0

cos(x) = или cos(x) = -2

x = arccos() или x = arccos(-2)

Решение для x = arccos(),

x = или

Мы не можем решить для x = arccos(-2), потому что оно не определено, поэтому x= или являются единственными решениями.

тригонометрия — Почему Arccos(Sin(x)) выглядит так??

спросил 6 лет, 9 месяцев назад

Изменено 6 лет, 9 месяцев назад

Просмотрено 8к раз

$\begingroup$

Я вроде как могу понять основное направление (наклон) $y$ на разных интервалах $x$, но я не могу понять, почему значения $y$ принимают форму прямых линий, а не кривых, выглядящих больше похоже на греховные, потому что. ..

РЕДАКТИРОВАТЬ : Я понимаю, что производная от Arccos(Sin(x)) дает 1 или -1 в зависимости от интервала x, но это не дает мне интуитивно понять, почему это так.

тригонометрия обратная композиция функций и отношений

$\endgroup$

3

$\begingroup$

Что ж, чтобы подумать об уравнении $$y=\arccos(\sin(x))$$, давайте сначала рассмотрим более простое уравнение, полученное путем наложения косинуса обеих сторон (отметив, что $\cos(\arccos( x))=x$ — то есть $\arccos$ является правой инверсией $\cos$): $$\cos(y)=\sin(x).$$ Если мы построим это, мы получим следующий график:

$\hskip1.5in$

который представляет собой просто набор диагональных линий, идущих в двух направлениях. Эта тайна раскрывается, когда мы переписываем $$\cos(y)=\cos\left(x+\frac{\pi}2\right)$$ и обратите внимание, что из симметрии и периодичности мы имеем, что $\cos(u)=\cos(v)$ всякий раз, когда $u=2\pi k \pm v$ для некоторого целого числа $k$. Это дает нам, что есть линия $y=x+\frac{\pi}2$, а также линия $y=x-\frac{\pi}2$ и любой их сдвиг по горизонтали (или вертикали) на $2\pi$, что приводит к решетчатому узору.

Однако определение $\arccos$, которое вы используете, кажется, требует, чтобы его выходные данные попадали в интервал $[0,\pi]$, следовательно, $y$ должен быть там. Если мы выделим подходящий диапазон $y$ серым цветом и обведем линии, которые он покрывает красным, мы восстановим наблюдаемую вами закономерность:

$\hskip1.5in$

, из чего становится ясно, что чередование является лишь небольшой частью более крупного шаблона, чем невозможно полностью представить из-за того, что диапазон $\arccos$ ограничен.

$\endgroup$

1

$\begingroup$

Инверсия косинуса определена на $[-1, 1]$ и отображается в $[0, \pi]$.
Функция синуса на $[-\pi/2, \pi/2]$ отображается в $[-1,1]$. $$ \арккос(\грех(х)) = \arccos(\cos(\pi/2 — x)) = -х + \пи/2 $$ Функция синуса на $[\pi/2, \pi/2 + \pi]$ равна $$ \sin(x) = -\sin(x-\pi) = \sin(\pi — x) $$ и отображается в $[-1,1]$. Мы получаем $$ \arccos(\sin(x)) = \arccos(\cos(\pi/2 — (\pi -x)) = x — \pi/2 $$ В обоих случаях мы можем добавить целое число, кратное $2\pi$, к аргументу функции косинуса. Это дает

$$ \арккос(\грех(х)) = \begin{случаи} -x + \pi/2 + 2\pi k & \text{for } x \in [-\pi+2\pi k, \pi/2 + 2\pi k] \\ x — \pi/2 + 2\pi k & \text{for} x \in [\pi/2+2\pi k, \pi/2 + \pi + 2\pi k] \\ \end{случаи} $$ где $k \in \mathbb{Z}$.

$\endgroup$

$\begingroup$

Обратите внимание, что $$cos(x-\pi)=sin(x)$$ $$x-\pi=arccos(sin(x))$$ $$and$$ $$cos(x)=cos( x\pm 2n\pi), n=0,1,2,3,…$$

Вы получаете решения между $\pi$ и $0$ из-за $arccos$. Это объясняет, почему ваше решение является линейным с наклоном, равным единице.

ТАКЖЕ: $$cos(x)=cos(-x)$$

Это означает, что ваше решение является положительным и отрицательным. Объединение всех этих результатов дает $$arccos(sin(x))=\pm(x-\pi\pm2n\pi)$$ $$=x\pm(2n-1)\pi,-x\pm(2n -1)\pi$$

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

9-1({\tan{x}})$ и получил это как: — из wolfram alpha

Я даже проверил это с помощью wolfram alpha и понял правильно, но проблема с $\cos$ заключается в том, что когда я пытаюсь решить его так же, как я сделал с $\tan$, и получаю интервал, в котором $n$ лежит, крайние точки интервала отличаются на $0,5$, из-за чего для некоторых значений их нижний и верхний предел совпадают, но для некоторых значений в этом интервале нет целочисленного значения, как это :- из wolfram alpha

поэтому что делать в таком случае и что означает отсутствие значения $n$, лежащего в интервале? 9{-1}$. По определению, $$\arccos(\cos y)=y\qquad(0\leq y\leq\pi)\ .$$ Для произвольного $x\in{\mathbb R}$ определим $$d(x):=\min\bigl\{|x-2k\pi|\,\bigm|\,k\in{\mathbb Z}\bigr\}$$ быть расстоянием $x$ от ближайшего целого числа, кратного $2\pi$. затем $$0\leq d(x)\leq\pi,\quad \cos x=\cos\bigl(d(x)\bigr)\qquad\forall x\in{\mathbb R}\ .$$ Это следует из того $$\arccos(\cos x)=\arccos\bigl(\cos\bigr(d(x)\bigr)\bigr)=d(x)\qquad(x\in{\mathbb R})\ ,$ $ что показывает, что $\arccos\circ\cos$ является пилообразной функцией. 9{-1}\left[\cos\left(\left(k+1\right)\pi-x\right)\right]\overset{1}{=}\left(k+1\right)\pi -Икс. \tag*{∎}$$

---

(Читатель может проверить $\overset{2}{=}$ и $\overset{3}{=}$, используя формулы вычитания для косинуса.)

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Арккосинус (Arccos) — определение, примеры, график

Арккосинус является одной из обратных тригонометрических функций и также записывается как cos ^-1 . Поскольку cos ^-1 (x) является обратной функцией cos(x), арккосинус (x) является обратной функцией cos x. У нас есть 6 обратных тригонометрических функций, таких как

• arcsin = инверсия sin = sin ^-1
• arccos = инверсия cos = cos ^-1
• arctan = инверсия tan = tan ^-1
• arccsc = инверсия csc = csc ^-1
• угловых секунд = инверсия секунды = секунда ^-1
• arccot ​​= инверсия cot = кроватка ^-1

Здесь мы подробно изучим обратную функцию косинуса (арккосинус), а также ее график, область значений, диапазон, формулы, производную и интеграл, а также несколько решенных примеров.

1.	Что такое арккосинус?
2.	Домен, диапазон и график арккосинуса
3.	Свойства арккосинуса
4.	Производная Arccos x
5.	Интеграл Arccos x
6.	Часто задаваемые вопросы по Arccosine

Что такое арккосинус?

Арккосинус  — это функция, обратная косинусу и, следовательно, одна из обратных тригонометрических функций. Арккосинус произносится как «арккосинус». Арккосинус x также может быть записан как «acosx» (или) «cos ^-1 x» или «arccos». Если f и f ^-1 являются обратными функциями друг друга, то f(x) = y ⇒ x = f ^-1 (y). Итак, y = cos x ⇒ x = cos ^-1 (y) . В этом смысл арккосинуса. Давайте рассмотрим несколько примеров, чтобы увидеть, как работает функция арккосинуса.

Примеры арккосинуса

• cos 0 = 1 ⇒ 0 = arccos (1)
• потому что π/2 = 0 ⇒ π/2 = arccos (0)
• потому что π = -1 ⇒ π = arccos (-1)

Арккосинус Определение

В прямоугольном треугольнике косинус угла (θ) представляет собой отношение прилежащего катета к гипотенузе. т. е. cos θ = (прилежащая сторона) / (гипотенуза). Тогда по определению арккосинуса θ = cos ^-1 [(прилежащая сторона)/(гипотенуза)] .

Таким образом, функция арккосинуса используется для нахождения неизвестных углов в прямоугольном треугольнике. Кроме того, его можно использовать для нахождения неизвестных углов в любом треугольнике, используя закон косинусов. Например, в треугольнике ABC, если AB = c, BC = a и CA = b, то по закону косинусов

a ² = b ² + c ² — 2bc cos A

Используя это,

cos A = (b ² + c ² — a ² ) / (2bc)

A = cos ^-1 [(b ² + c ² — a ² ) / (2bc)] ([или (2bc) арксинус)] б ² + с ² — а ² ) / (2bc)].

Точно так же мы можем найти другие углы треугольника, зная длины его сторон.

Домен, диапазон и график арккосинуса

В этом разделе мы посмотрим, как можно найти домен и диапазон функции арккосинуса. Кроме того, мы увидим, как изобразить его в его основной области.

Домен и диапазон арккосинуса

Мы знаем, что функция косинуса является функцией из R → [-1, 1]. Но функция косинуса НЕ является биекцией (поскольку она НЕ является однозначной) в области R. Следовательно, она не может иметь обратную, если ее областью определения является R. Чтобы функция косинуса была однозначной, ее область определения может быть ограничена единицей. интервалов [-π, 0], [0, π], [π, 2π] и т. д. Каждому из этих интервалов соответствует ветвь арккосинуса. Ветвь арккосинуса с диапазоном [0, π] называется главной ветвью. Таким образом, область определения косинуса обычно ограничивается значением [0, π], а его диапазон — [-1, 1].

Мы знаем, что область определения и область значений функции будут соответственно областью значений и областью значений обратной функции. Следовательно, область обратного косинуса, который является арккосинусом, равна [-1, 1], а его диапазон равен [0, π] . т. е.,

arccos x (или) cos ^-1 x : [-1, 1] → [0, π]

График арккосинуса

График функции арккосинуса с диапазоном значений главной ветви [0, π] можно нарисовать с помощью следующей таблицы. Здесь мы выбрали случайные значения для x в области арккосинуса, которая равна [-1, 1].

х	y = cos -1 x (или) arccos x
-1	потому что -1 (-1) = π — 0 = π
-0,5	потому что -1 (-0,5) = π — π/3 = 2π/3
0	потому что -1 (0) = π/2
0,5	, потому что -1 (0,5) = π/3
1	, потому что -1 (1) = 0

Нанеся эти точки на график, мы получим график arccos.

Свойства арккосинуса

Вот некоторые свойства/формулы арккосинуса. Они очень полезны при решении задач, связанных с обратными косами в тригонометрии.

• cos(cos ^-1 x) = x только тогда, когда x ∈ [-1, 1]
  ([Когда x ∉ [-1, 1], cos(cos ^-1 х) НЕ определено)
• cos ^-1 (cos x) = x, только когда x ∈ [0, π]
  (Когда x ∉ [0, π], либо найдите котерминальный угол x, либо примените тригонометрические тождества, чтобы найти эквивалентный угол x, лежащий в [0, π] )
• потому что ^-1 (-х) = π — потому что ^-1 х
• cos ^-1 (1/x) = сек ^-1 x, когда |x| ≥ 1
• sin ^-1 x + cos ^-1 x = π/2, когда x ∈ [-1, 1]

Производная Arccos x

Найдем производную от y = cos ^-1 x. По определению арккосинуса y = cos ^-1 x можно записать как cos y = x. Дифференцируя это с обеих сторон по x с использованием цепного правила,

— sin y (dy/dx) = 1

dy/dx = -1/sin y . .. (1)

Теперь у нас есть sin ² y + cos ² y = 1 ⇒ sin ² y = 1 — cos ² y ⇒ sin y = √(1 — cos²y) = √1 — x².

Подставив это в (1),

dy/dx = -1/√1 — x²

Таким образом, производная арккосинуса (или) производная от cos ^-1 x равна -1/√(1 — x² ).

Интеграл Arccos x

∫cos ^-1 x dx найдем с помощью интегрирования по частям. Для этого запишем приведенный выше интеграл в виде

∫cos ^-1 x · 1 dx

Используя LIATE, f(x) = cos ^-1 x и g(x) = 1.

Интегрируя по части,

∫f(x) . g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) ∫g(x) dx) dx + C

∫cos ^-1 x · 1 dx = cos ^{— 1} x ∫1 dx — ∫ [d/dx(cos ^-1 x) ∫x dx] + C

∫cos ^-1 x dx = cos ^-1 x (x) — ∫ [- 1/√1 — x²] x dx + C

Мы вычислим этот интеграл с помощью u-подстановки. Для этого пусть 1-х ² = u. Тогда -2x dx = du (или) x dx = -1/2 du.

∫cos ^-1 x dx = x cos ^-1 x — ∫(-1/√u) (-1/2) du + C

= x cos ^-1 x — 1/2 ∫u ^-1/2 du + C

= x cos ^-1 x — (1/2) (u ^1/2 /( 1/2)) + C

= x cos ^-1 x — √u + C

= x cos ^-1 x — √1 — x² + C

Следовательно, ∫cos ^-1 x dx = x cos ^-1 x — √(1 — x²) + C.

Важные примечания по арккосинусу:

Вот несколько важных замечаний, связанных с функцией арккосинуса.

• арккосинус можно записать как cos ^-1 (или) arccos (или) acos, и это функция с доменом [-1, 1] и диапазоном [0, π].
• арккосинус НЕ совпадает с (cos x) ^-1 как (cos x) ^-1 = 1/(cos x) = sec x.
• cos ^-1 (-x) НЕ -cos ^-1 (x), а cos ^-1 (-x) = π — cos ^-1 x.
• cos(cos ^-1 x) НЕ всегда x. cos(cos ^-1 x) = x только тогда, когда x ∈ [-1, 1].
• cos ^-1 (cos x) НЕ всегда x. потому что ^-1 (cos x) = x только тогда, когда x ∈ [0, π].

☛ Связанные темы:

Вот некоторые темы, которые могут вас заинтересовать при чтении об арккосинусе.

• грех кост тан
• Тригонометрические функции
• Закон синусов
• Тригонометрическая таблица
• Калькулятор арккосинуса

Часто задаваемые вопросы по арккосинусу

Что такое арккосинус?

Арккосинус является обратной функцией тригонометрической функции cos x и, следовательно, является обратной тригонометрической функцией. По определению обратной функции y = cos x ⇒ x = cos ^-1 (y).

Что такое формула арккосинуса?

В прямоугольном треугольнике, если θ — один из острых углов, то cos θ = (прилежащий)/(гипотенуза). Тогда θ = arccos((соседний)/(гипотенуза). Это формула арккосинуса (или arccos).

Является ли арккосинус x таким же, как cos⁻¹x?

Арккосинус является обратным cos x, поэтому да, арккосинус x равен cos⁻¹x.

Является ли арккосинус таким же, как (cos x)⁻¹?

Нет. Арккосинус является обратной функцией косинуса, т. е. arccos x = cos ^-1 x. Но оно НЕ равно (cos x) ^-1 , поскольку (cos x) ^-1 = 1/ cos x = sec x.

Что такое произношение арккосинуса?

«Арккосинус» является одной из обратных тригонометрических функций и может произноситься как «арккосинус» или «арккосинус».

Что такое домен Arccos x?

Область определения арккосинуса (или) арккосинуса x ^{равна [-1, 1], так как диапазон его обратной функции (которая является функцией косинуса) равен [-1, 1].}

Каков ассортимент Arccos x?

Диапазон значений arccos x (или) cos ^-1 x ^{равен [0, π], поскольку ограниченная область значений обратной функции (которая является функцией косинуса) равна [0, π], чтобы сделать функцию косинуса однократной. один.}

Что такое арккосинус Cos x?

Арккосинус cos x равен x (или) cos ^-1 (cos x) = x, если x ∈ [0, π]. Если x ∉ [0, π], то либо найдите котерминальный угол x, либо примените тригонометрические тождества, чтобы найти эквивалентный угол x, лежащий в [0, π], а затем примените cos ^-1 (cos x) = x .

Что такое косинус арккосинуса x?

Косинус арккосинуса числа x равен x (или) cos(cos ^-1 x) = x, если x ∈ [-1, 1]. Если x ∉ [-1, 1], то cos(cos ^-1 x) НЕ определен.

Калькулятор — arccos(cos(x)) — Solumaths

Arccos, расчет онлайн

Резюме:

Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.

arccos online

---

Описание:

Функция арккосинуса является обратной функцией функция косинуса, это вычисляет арккосинус числа онлайн .

Число, к которому вы хотите применить функцию функции арккосинуса, должно принадлежать диапазону [-1,1].

1. Расчет арккосинуса

Чтобы вычислить арккосинус числа , просто введите число и примените функция arccos . Таким образом, для , вычисляющего , арккосинус числа, следующего за 0,4, вы должны ввести arccos(`0.4`) или сразу 0.4, если кнопка arccos уже есть, результат 1.1592)`.

2. Таблица замечательных значений
arccos(sqrt`-4 2)/2`) `

arccos(`-1`)	`pi`
arccos(`-sqrt(3)/2`)	`5*pi/6`
`3*pi/4`
arccos(`-1/2`)	`2*pi/3`
arccos(`0`)		`2*pi/3` pi/2`
arccos(`1/2`)	`pi/3`
arccos(`sqrt(2)/2`)	`pi/4`
Arccos (` sqrt (3)/2`)	`pi/6`
Arccos (` 1`)	`0`

888888888894 `0`

88888888888888888888888888888 :

arccos(x), где x — число.

Иногда используются другие обозначения: acos

---

Примеры:

arccos(`1`) возвращает 0

---

Производная арккосинуса :

Чтобы дифференцировать функцию арккосинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции арккосинуса 92)`

---

Предел арккосинуса :

Калькулятор предела позволяет вычислить пределы функции арккосинуса.

предел arccos(x) is limit(`»arccos»(x)`)

---

Обратная функция арккосинуса :

обратная функция арккосинуса — это функция косинуса, отмеченная как cos.

---

---

Графический арккосинус :

Графический калькулятор может отображать функцию арккосинуса в заданном интервале.

---

Расчет онлайн с арккосинусом

См. также

Список связанных калькуляторов:

• Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
• Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
• Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
• Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
• Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
• Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
• Тригонометрическое расширение: expand_trigo.

  No related posts.