Терминология теории функций: f(x) и f(-x)
| bssgrad |
| ||
14/09/16 |
| ||
| |||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Karan |
| ||
19/10/15 | |||
| |||
| Karan |
| |||||
19/10/15 |
| |||||
| ||||||
| bssgrad |
| ||
14/09/16 |
| ||
| |||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| grizzly |
| |||
09/09/14 |
| |||
| ||||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| bssgrad |
| ||
14/09/16 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 11 ] |
Модераторы: Модераторы Математики, Супермодераторы
3-8
Примечание: Хотя ваши ответы содержат некоторые истинные аспекты, ваши рассуждения не вполне удовлетворительны.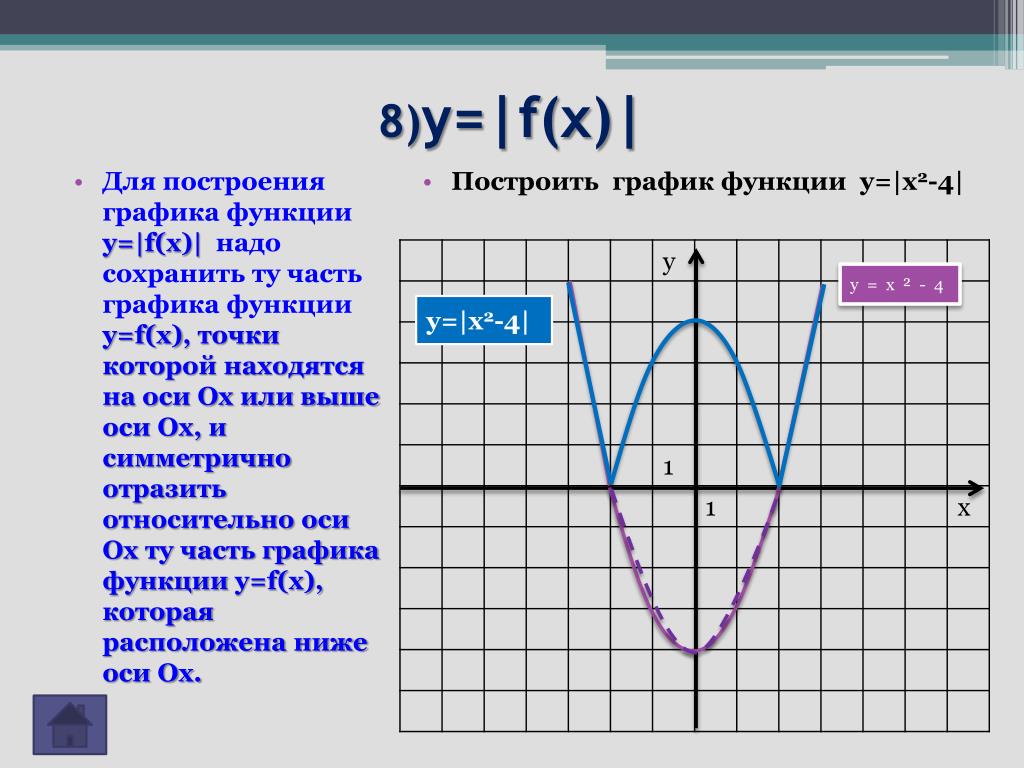 Большинство из них связано с неполным заданием функции $f$. абсолютно необходимо полностью знать домен и кодовый домен функции. В противном случае точный анализ проблемы невозможен. Вы можете проверить пример в разделе , формальное определение 9.{-\frac{1}{3}}$, и пусть $A$ обозначает площадь области, ограниченной $f(x)$ и осью $X$, когда $x$ изменяется от $-1$ до $1 $. Какое из следующих утверждений ВЕРНО?
Большинство из них связано с неполным заданием функции $f$. абсолютно необходимо полностью знать домен и кодовый домен функции. В противном случае точный анализ проблемы невозможен. Вы можете проверить пример в разделе , формальное определение 9.{-\frac{1}{3}}$, и пусть $A$ обозначает площадь области, ограниченной $f(x)$ и осью $X$, когда $x$ изменяется от $-1$ до $1 $. Какое из следующих утверждений ВЕРНО?
$f$ непрерывна в $[-1, 1]$
$f$ не ограничен в $[-1, 1]$
$A$ отличен от нуля и конечен
$$ $$
Ответ:
Утверждение 1. ЛОЖНО. Рассуждение: Чтобы быть непрерывной в $[-1,1]$, функция $f$ должна быть непрерывной в каждой точке $[-1,1]$. Поскольку $f$ равно не определено при $x=0$, оно не является ни непрерывным, ни прерывистым при $0$. Но $f$ непрерывна в $[-1,1]\setminus{\{0\}}$.
Комментарий к вашему рассуждению , поскольку левый предел не эквивалентен правому пределу :
Вы обращаетесь к точке $0$, поэтому вы должны указать ее, потому что во всех остальных точках $[-1,1]\setminus{\ {0\}}$ левый предел $f$ равен правому пределу. Термин , эквивалентный , имеет особое математическое значение, поэтому вместо него следует использовать термин 9.-}=-\infty$.
Комментарий к вашим рассуждениям , так как $f(x)$ возрастает до $infinite$ при $x=0$ :
Поскольку функция $f$ не определена при $x=0$, лучше написать поскольку $f(x)$ возрастает до $infinite$, когда $x$ стремится к нулю . Эта формулировка рассматривает только значения $x$ в пределах области определения $f$.
Утверждение 3. ЛОЖНО. Обоснование: Предполагается, что $x$ изменяется в пределах области $[-1,1]\setminus{\{0\}}$ $f$, и мы также предполагаем, что область $A$ является областью со знаком.
1 = \ гидроразрыва {3} {2} \конец{выравнивание*} которое конечно, получаем в силу симметрии $A=0$.
Комментарий к вашему рассуждению , так как мы можем вычислить его, проинтегрировав функцию .
Формулировка недостаточно точная, так как мы умеем вычислять интеграл и результатом может быть $\pm\infty$. Мы должны заявить, что мы получаем окончательное значение путем интегрирования.
Обычно при интеграции мы рассматриваем области как со знаком . Вот почему я вычислил $A=0$. Но, может быть, согласно вашим условностям в отношении таких вопросов, вам приходится рассматривать неподписанную область. В этом случае мы получаем $A=3$ и ваш ответ ИСТИННЫЙ.
[2015-09-29] Дополнение к термину разрывность
Термин непрерывная функция определяется по отношению к своей области определения. Поэтому крайне важно указать область определения функции, если мы хотим проанализировать функцию с точки зрения непрерывности. Вне области определения функции эта функция не является непрерывной, так как она даже не определена там.
Вне области определения функции эта функция не является непрерывной, так как она даже не определена там.
Обратите внимание, что когда мы говорим о разрывах функции с одной переменной, мы классифицируем их либо как съемная несплошность , скачкообразная несплошность или существенная несплошность соответственно. бесконечный разрыв . Ключевым моментом здесь является то, что каждый из этих разрывов определен относительно области $f$ . Мы заключаем, что разрывы определяются только в области определения $f$.
К сожалению, мы часто встречаем различные объяснения, говорящие о разрывах в точках, где функция не определена . Типичный пример
\начать{выравнивать*}
&f:\mathbb{R}\setminus{\{0\}}\стрелка вправо \mathbb{R}\\
&f(x)=\frac{1}{x}
\конец{выравнивание*}
$f$ не является непрерывным в точке $x=0$, поскольку она там даже не определена. Но мы не должны говорить, что $f$ равно прерывистый при $x=0$, поскольку термин прерывистый обусловлен его классификацией в различных типах , определяющих только в области $f$.


 10.2016, 12:12
10.2016, 12:12 
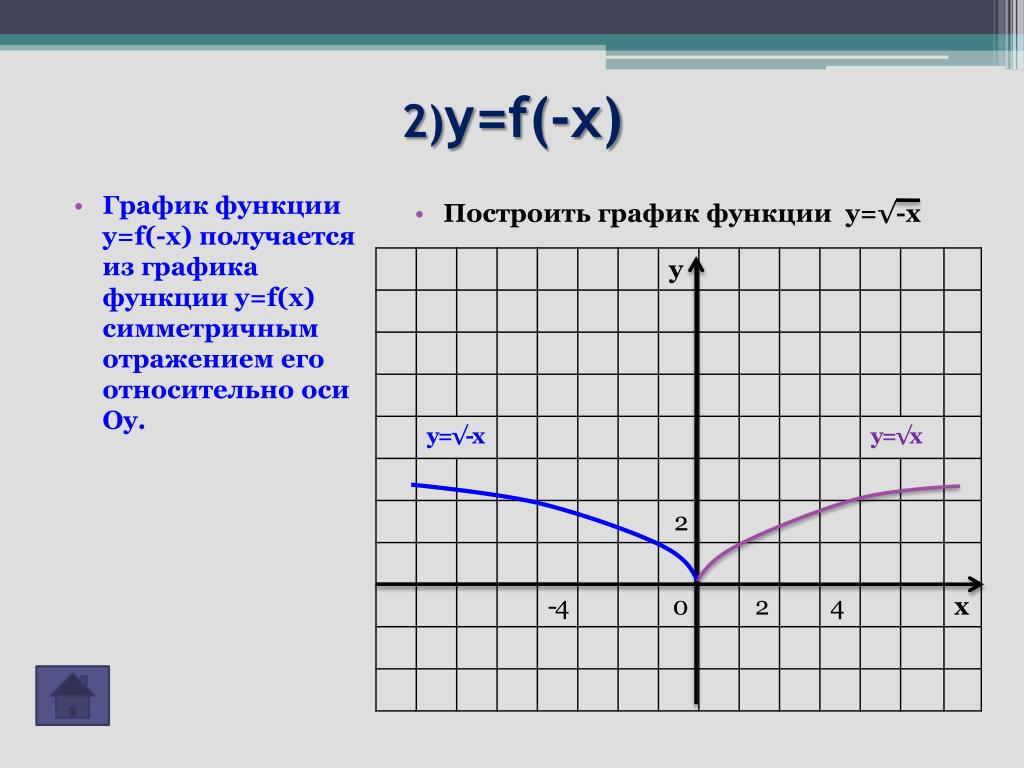 Хотя вещи связанные, и часто одинаково обозначаемые. Как правило, из контекста понятно, о чём речь. В частности, подразумевает, что переменная-аргумент имеет определённое значение, равное , где x принимает известное значение.
Хотя вещи связанные, и часто одинаково обозначаемые. Как правило, из контекста понятно, о чём речь. В частности, подразумевает, что переменная-аргумент имеет определённое значение, равное , где x принимает известное значение. 10.2016, 13:21
10.2016, 13:21 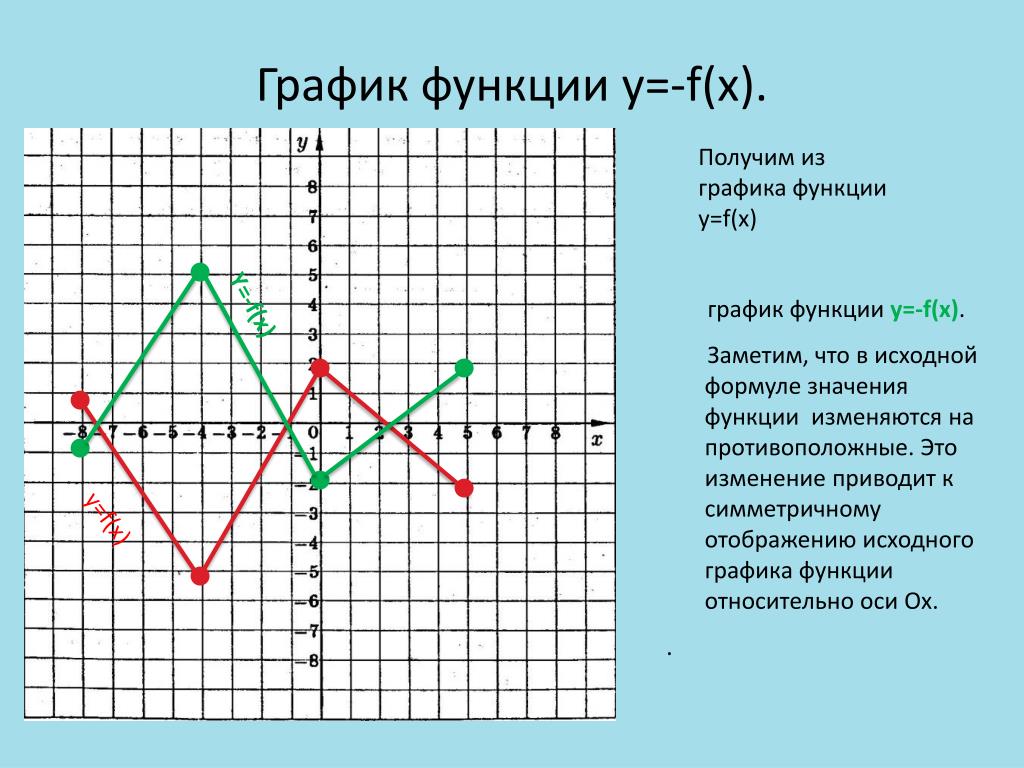 10.2016, 14:14
10.2016, 14:14 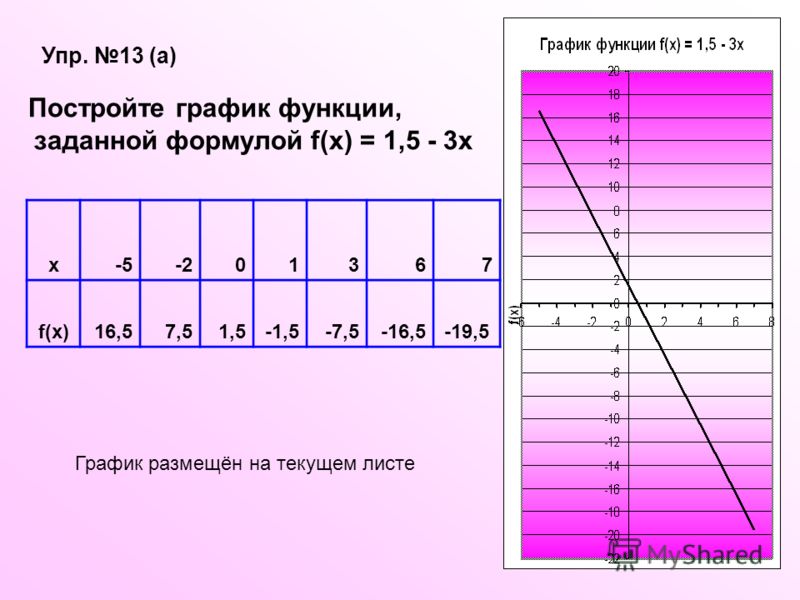 10.2016, 14:24
10.2016, 14:24 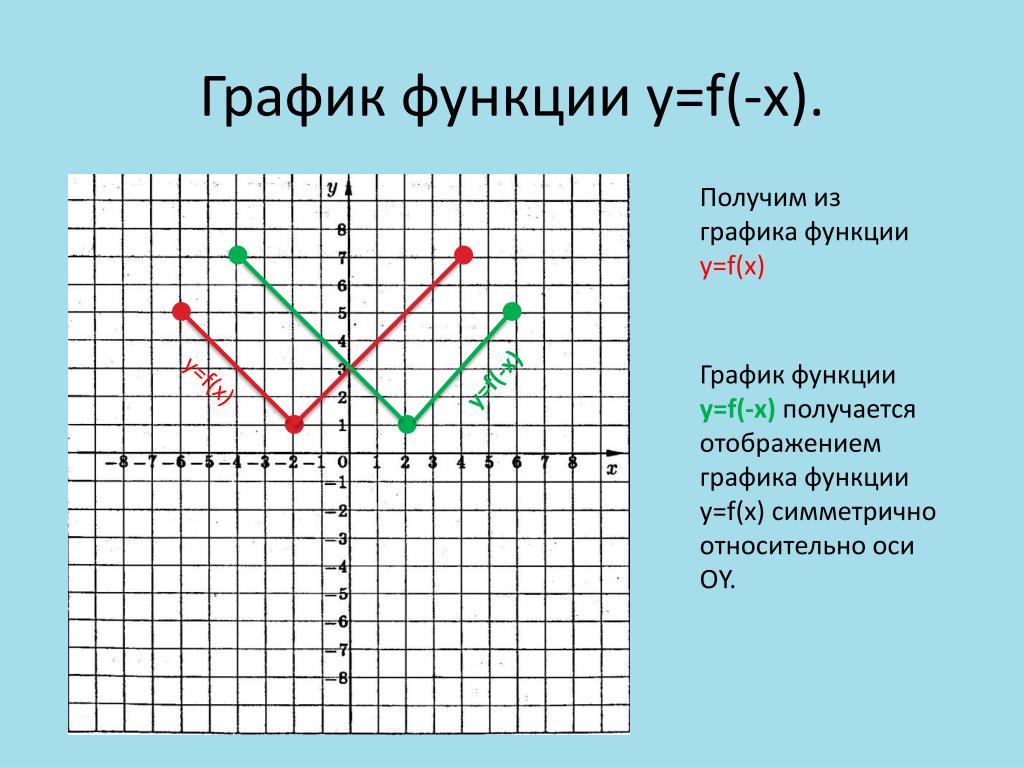
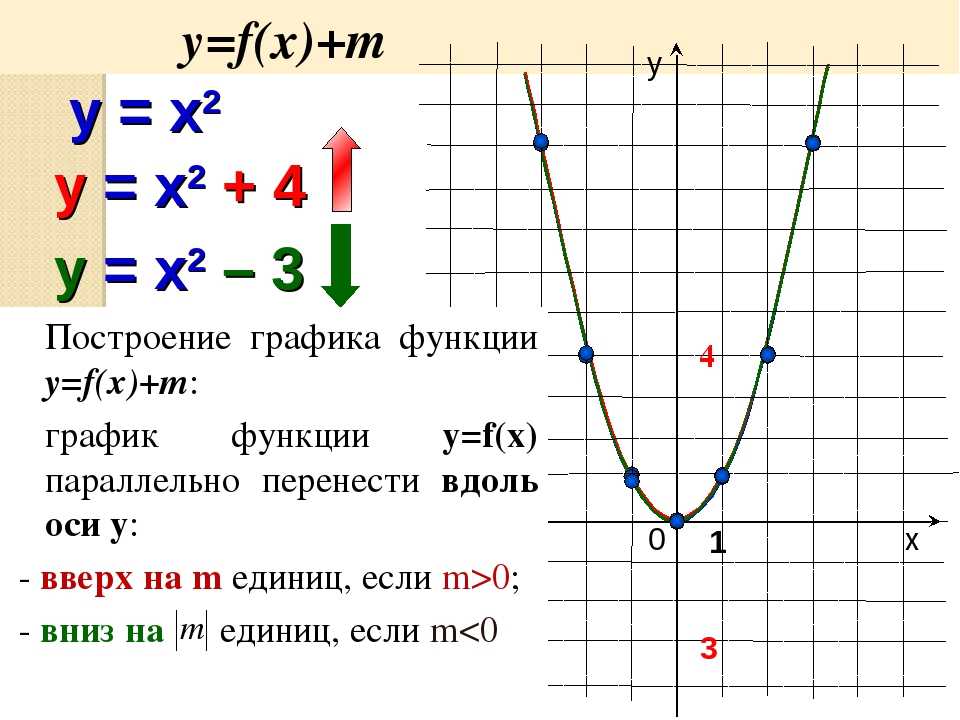 Вот у каждой точки этого графика имеются координаты: абсцисса и ордината — и , соответственно. Как раз о них и шла речь в учебнике.
Вот у каждой точки этого графика имеются координаты: абсцисса и ордината — и , соответственно. Как раз о них и шла речь в учебнике.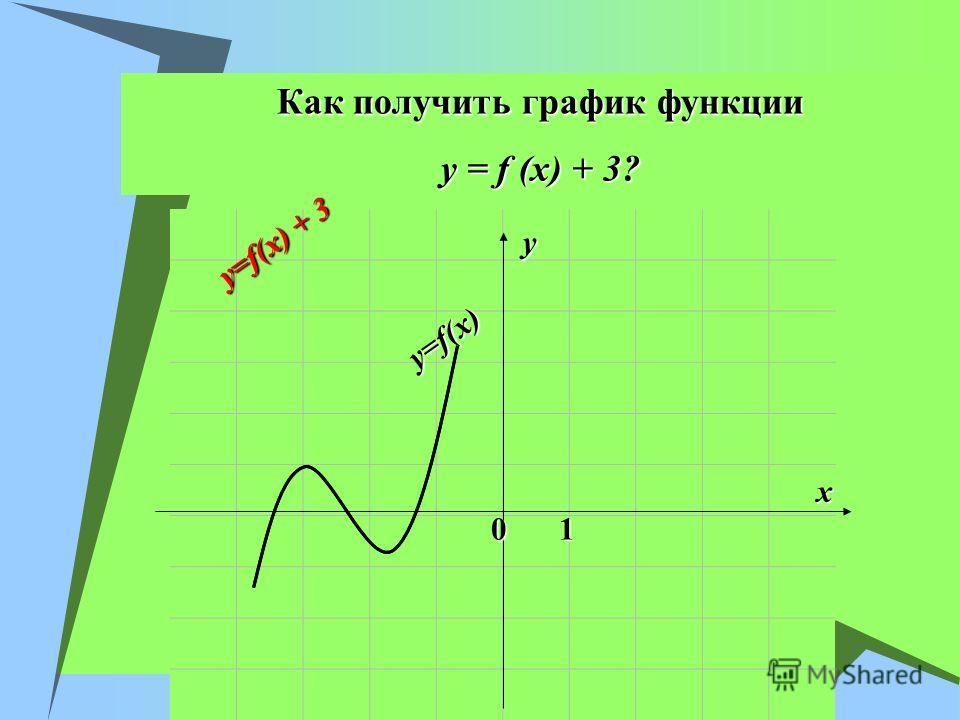
 10.2016, 21:06
10.2016, 21:06 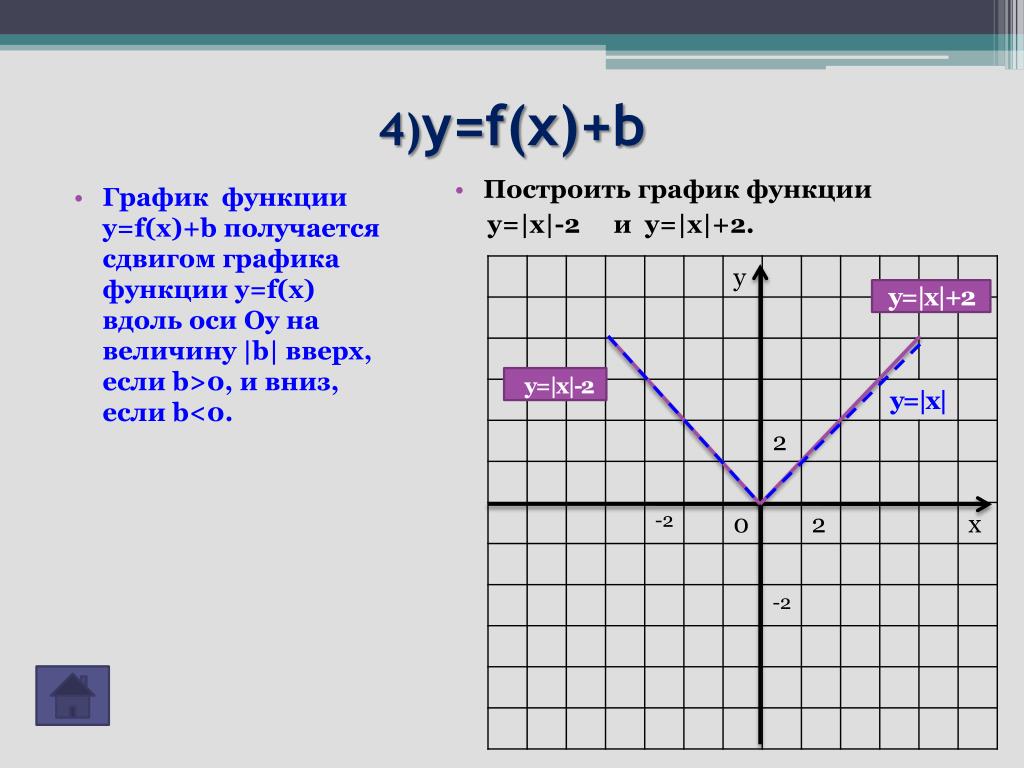 И это происходит для всех возможных вариантов выбрать из множества
И это происходит для всех возможных вариантов выбрать из множества Сверьтесь, пожалуйста, с учебником.
Сверьтесь, пожалуйста, с учебником.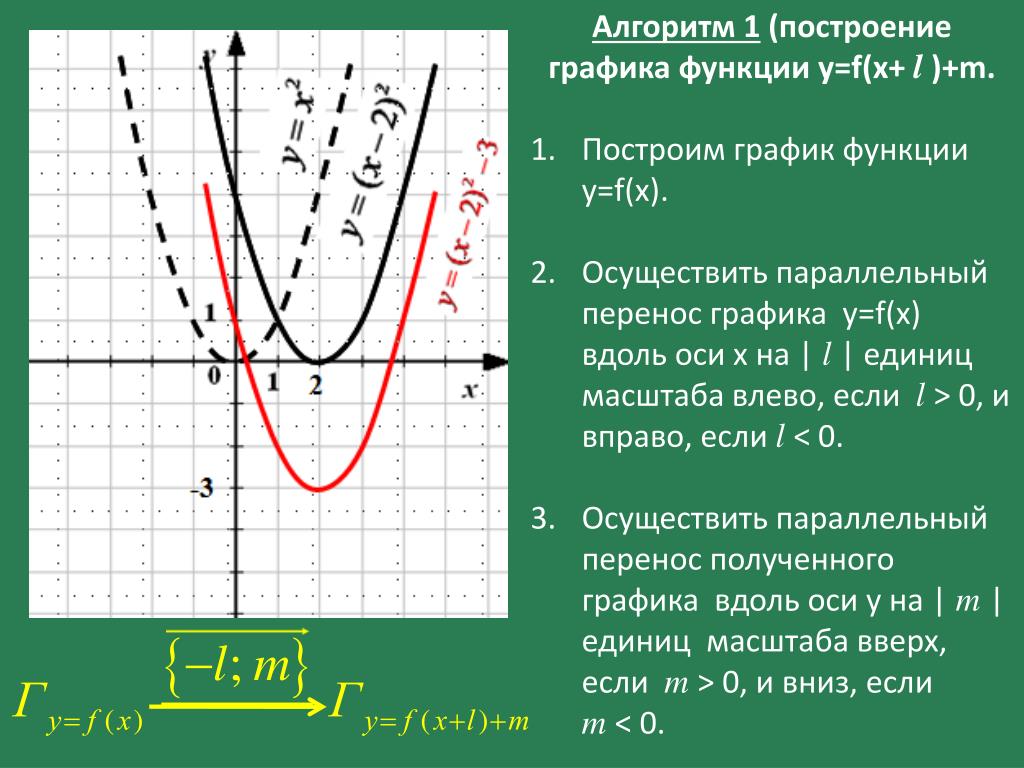
 1 = \ гидроразрыва {3} {2}
\конец{выравнивание*}
которое конечно, получаем в силу симметрии $A=0$.
1 = \ гидроразрыва {3} {2}
\конец{выравнивание*}
которое конечно, получаем в силу симметрии $A=0$.