Обобщение [ править | править код ]
- Кардиоида есть Синусоидальная спираль при n = 1 2 1>
2>>>
;История [ править | править код ]
Кардиоида впервые встречается в трудах французского учёного Луи Карре (Louis Carrè, 1705 г.). Название кривой дал в 1741 году Джованни Сальвемини ди Кастиллоне (он упоминается также как Johann Francesco Melchiore Salvemini Castillon).
«Спрямление», то есть вычисление длины кривой, выполнил Ла Ир (Philippe de La Hire), который открыл кривую независимо, в 1708 году. Также независимо описал кардиоиду голландский математик Й. Коерсма (J. Koersma, 1741 год). В дальнейшем к кривой проявляли интерес многие видные математики XVIII—XIX веков.
Один и один — получается два. Все одиноки — здесь ты, а там я.
Люди всегда одиноки вдвойне сами с собою наедине.
Если б их что-то сблизить могло, сразу б из двух получилось одно.Пусть математика сложит сердца — чтобы проделать нам путь до конца.
Уильямс Джей, «Герои Ниоткуда»
Вероятно, пост следовало назвать «Как нарисовать анимированное сердечко ко дню Святого Валентина, используя математику не по назначению». Я отверг это название в пользу более поэтичного: как-никак, надвигается замечательный романтический праздник, который мы, айтишники и прочие нёрды, должны встретить во всеоружии. Я сразу покажу вам результат, а под хабракатом будет много букв о том, как я этого результата достиг.
Дисклеймер
Я осознаю, что красивое мигающее сердечко можно сделать и без малейшего знания математики. Но разве это интересно?
Шаг 1. Параметризуем сердечко.
Для начала нам нужен математический объект, хотя бы отдалённо напоминающий сердечко. К счастью, для меня этот шаг был тривиален: ещё пару лет назад я обнаружил замечательную формулу как раз для такого случая (из эстетических соображений график на рисунке растянут по горизонтали, на самом деле он должен умещаться между -1 и 1).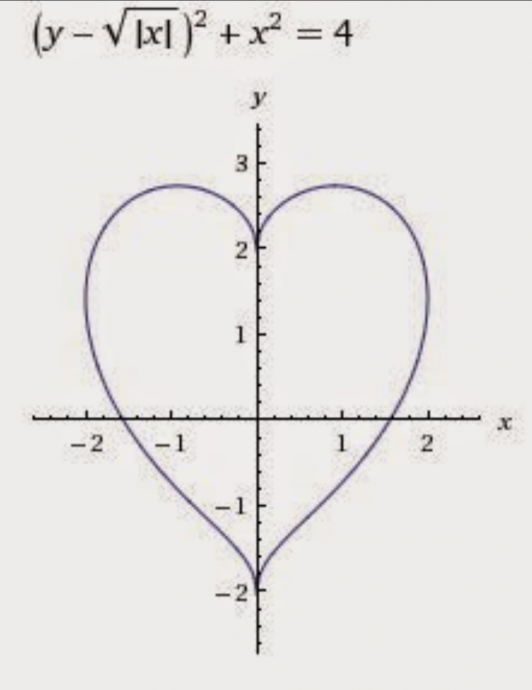
Формула была обнаружена из следующий соображений: возьмём обыкновенную окружность и представим, что она состоит из желе, будучи при этом жёстко прикреплена к оси ординат. Теперь «подуем» на неё снизу: прибавим к координате игрек некую функцию w(x) = w(x(t)), равную нулю при x=0, монотонно возрастающую при x>0 и чётную по x. После такого «дуновения» половинки окружности сместятся вверх, образуя «выпуклости» сердечка, а благодаря жёсткому креплению к оси Y образуется нижний «хвостик» и верхняя «вмятинка». В данном случае w(x(t)) = |x| 1/2 = |cos(t)| 1/2 . Можете самостоятельно попробовать другую «функцию дуновения» и посмотреть, что из этого выйдет.
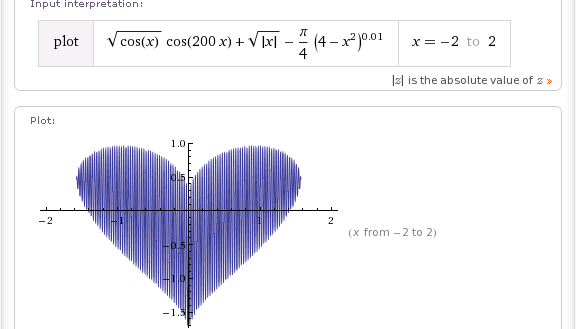
Шаг 2. От параметрического задания к неявной функции.
x = cos(t)
y = sin(t) + |cos(t)| 1/2
y — |x| 1/2 = sin(t)
(y — |x| 1/2 ) 2 + x 2 = 1
f(x,y) = (y — |x| 1/2 ) 2 + x 2 — 1 = 0
Шаг 3. От неявной функции к функции двух переменных. Функция цвета.
Имея на руках f(x,y), мы наконец можем осуществить свою мечту: нарисовать красивую цветную картинку.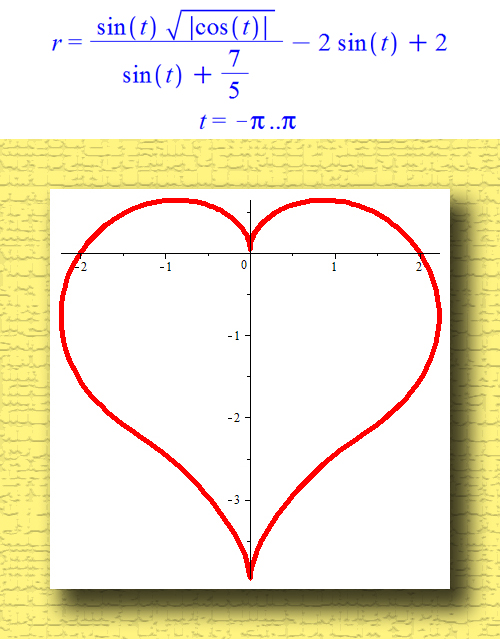
Для этого нам понадобится ещё одна функция: функция цвета. Она должна принимать вещественный аргумент r и возвращать целое значение от 0 до 255. Также желательно, чтобы она была монотонна на каждой полуоси и имела максимум в точке нуль. В качестве такой функции можно взять, например, эту:
Здесь 100 — «магическое число», позднее мы его в полном соответствии с «хорошим стилем программирования» заменим параметром.
Теперь для каждой точки (x,y) мы можем задать цвет как rgb(c(f(x,y)), 0, 0). Те точки, которые раньше принадлежали непосредственно графику «сердечка», стали ярко-красными (обратите внимание на неподвижный светлый контур на гифке). По мере удаления от графика цвет будет тускнеть, пока на некотором расстоянии от него не станет чёрным.
Шаг 4. Добавляем параметр, создаём анимацию.
Теперь заменим магическое число 100 параметром k. Новая функция цвета выглядит так:
Пусть k — это некоторая функция времени. Тогда для каждой точки изображения в каждый момент времени мы можем вычислить её цвет (что и является, по сути, математическим определением анимации).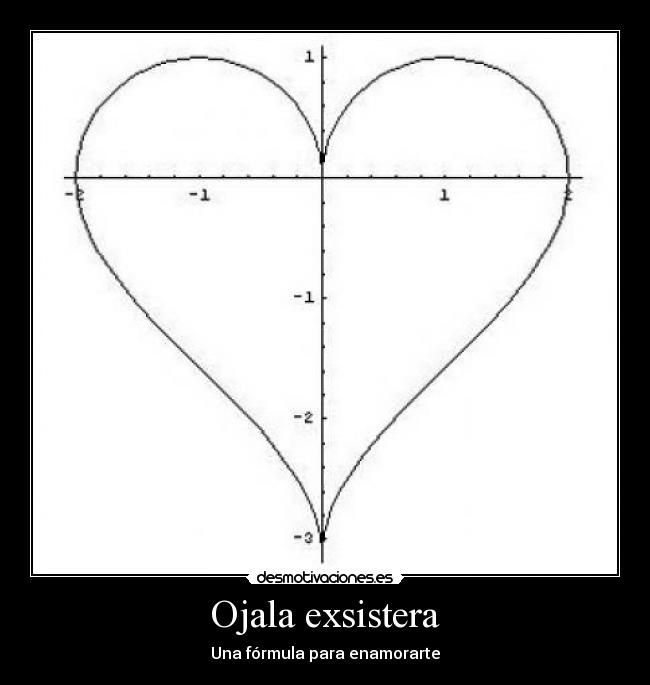
Сначала я хотел взять что-нибудь типа k(t) = 80(sin(t)+1). Потом, однако, я понял, что при большом количестве кадров гифка будет весить более 640 килобайт. С другой стороны, при малом количестве кадров нет смысла заморачиваться с аналитическим заданием k(t). В итоге, чтобы добиться пульсирования сердца, я последовательно присвоил k значения 80, 90, 100, 110, 120, 110, 100, 90, а затем изображения, сгенерированные для этих значений, объединил в циклический GIF. В общем-то, всё.
Дубликаты не найдены
С лекции по анатомии, например.
Поясняю: в норме у человека пульс меняется. Всегда. ЧСС меняется +- несколько ударов в минуту за каждые несколько секунд — поставьте себе постоянный измеритель и поймёте, о чём я. Всего 2 недели назад мерил в течение 2 суток, потому, поверьте, я знаю, о чём я говорю.
В случае инфаркта I-й водитель ритма (в терминологии могу чуть косячить, никогда с ней в ладах не был) отключается, работает II-й (вторичный), который задаёт исключительно ровный пульс, уже не зависящий от состояния организма)
Есть ещё III-й, третичный, водитель ритма (забыл, какая это система), но он не может поддерживать пульс выше 30 ударов в минуту, а потому в случае её работы человек обычно лежит без сознания.
Это если отказал II-й, более устойчивый.
III-й же почти неуязвим сам по себе.
«>2>0>
Curve Heart Alt code График функции Символ, сердце, угол, текст, треугольник png
Curve Heart Alt code График функции Символ, сердце, угол, текст, треугольник pngтеги
- угол,
- текст,
- треугольник,
- сердце,
- симметрия,
- график функции,
- объекты,
- круговая диаграмма,
- точка,
- квадрат,
- символ,
- линейная диаграмма,
- линия,
- информация,
- диаграмма,
- кривая,
- круг,
- площадь,
- alt Key,
- alt Code,
- algebraicкривая,
- png,
- прозрачный,
- бесплатная загрузка
Об этом PNG
- Размер изображения
- 1067x1024px
- Размер файла
- 59.92KB
- MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Лицензия
Некоммерческое использование, DMCA Contact Us
org/ImageGallery» align=»middle»>
org/ImageObject»> декоры розовое сердце, сердце, плавающие сердца, любовь, угол, текст png
2850x2075px
367.62KB
org/ImageObject»> Треугольная форма фона, черный и белый абстракция, текстура, компьютерная сеть, угол png
2480x3508px
524.6KB
org/ImageObject»> Декартова система координат Линейный график График функции, бумажный фейерверк, шаблон, угол, текст png
4167x4167px
90.04KB
65KB
04KB
84KB
61KB
org/ImageObject»> Синий, Синий абстрактная графика, синий фон, текстура, угол, треугольник png
3553x5075px
726.6KB
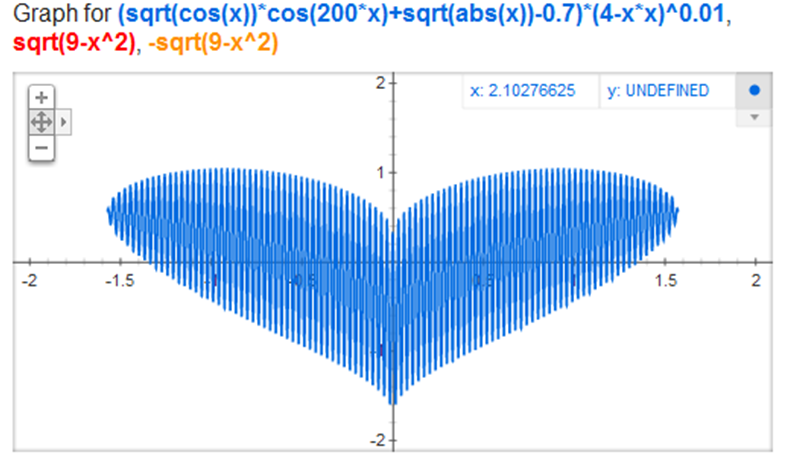2MBУравнение Сердца – Академия Онлайн
День святого Валентина – один из самых широко отмечаемых праздников в нашем календаре. Вся школа, автостоянка, окрестности (практически везде) кажутся наполненными потоками красных и розовых сердечек, конфет и херувимов.
У нас много разнообразных и популярных праздников, но, видимо, в День святого Валентина мы можем «почувствовать любовь в воздухе», и большинство людей либо ненавидят День святого Валентина, либо любят его.
Я считаю День святого Валентина особенным, но не потому, что это день любви.
На каждой открытке, на каждом украшении и на каждом признании в любви изображена одна форма: сердце. Разве День святого Валентина не похож на день любви, а не на день сердечек? Когда мы идем по улицам, кажется, что сердец больше, чем любви. Целый день, посвященный одной конкретной форме… Треугольники и круги, наверное, завидуют.
Так что неудивительно, что существует так много математических и научных аналогий любви, поскольку это прямо аллея математика или ученого. И когда мы видим формы, мы всегда думаем об уравнениях, чтобы воссоздать их. Точно так же, как есть много типов форм сердца, есть много способов построить график уравнения сердца. 92), кардиоида, как известно, является частным случаем эпициклоиды, показанной ниже, которая создается путем прокатки по окружности по окружности другой окружности.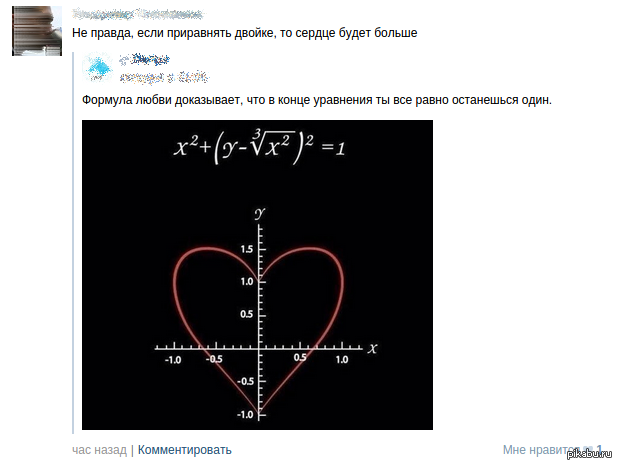
Выше показаны другие уравнения, которые можно использовать для создания формы сердца.
Если вы хотите узнать больше о других уравнениях для создания большего количества форм сердца или о том, как сердца могут быть созданы с использованием других форм, ремесел и архитектурных проектов, вы можете посетить http://www.mathematische-basteleien.de/heart.htm Узнать больше!
Автор: Саанви Гутта
Под редакцией Кирти Селвам и Трифены Пилли Математическая Бастель. http://www.mathematische-basteleien.de/heart.htm
Льюис, Х. (1 февраля 2018 г.). Математика ко Дню святого Валентина: какое уравнение для сердца? Математика Карьера. https://www.mathscareers.org.uk/valentines-day-maths-what-is-the-equation-for-a-heart/
ИСТОЧНИКИ ИЗОБРАЖЕНИЙ:
Кривая сердца [График]. Вольфрам MathWorld. https://mathworld.wolfram.com/HeartCurve.html
Эпициклоида [График]. Математика Карьера.
https://www.mathscareers.org.uk/valentines-day-maths-what-is-the-equation-for-a-heart/
Кардиоид [фотография]. Математика Карьера. https://www.mathscareers.org.uk/valentines-day-maths-what-is-the-equation-for-a-heart/
[Конфеты любви по фону сердца] [Фотография]. По дизайну. https://www.ftd.com/blog/celebrate/valentines-day-puns
Примечание. Первое сердце и кардиоида были построены (мной) с помощью Desmos, графического онлайн-калькулятора, доступ к которому можно получить через LCPS Go. .
Сердечная кривая
|
.Что такое кривая сердца?
| Кривая сердца представляет собой замкнутую кривую, имеющую вид
сердца. Сердце хорошо известно как фигура на игральных картах. кроме бубнов, крестов и пик. |
Если вы говорите о сердце, вы имеете в виду сердце фигура, чем кривая в форме сердца.
| …… | В простейшем случае сердце образуется квадратом, стоящим на острие и два полукруга сидят по бокам. Характеристики фигуры сердца, очевидно, представляют собой бороздку вверху и точку внизу. |
. ….. | Фигура сердечка складывается также, если поставить два полукруга
на треугольник. Но здесь вы получаете два неприятных угла. Очевидно, вы ожидаете, что эти стороны закруглены. |
| Если пункт ниже отсутствует, то не говорите о сердце
а скорее фигура в форме сердца. Однако эта форма более
подобно человеческому сердцу. Фигура слева образована тремя полукружиями. |
Нарисованные кривые сердца вверху
Метод 1
| 1 Нарисуйте равнобедренный треугольник. 2 Проведите перпендикуляры к ножкам. Получается второй равнобедренный треугольник. 3 Нарисуйте два полукруга на ножках (теперь желтые) треугольник.  |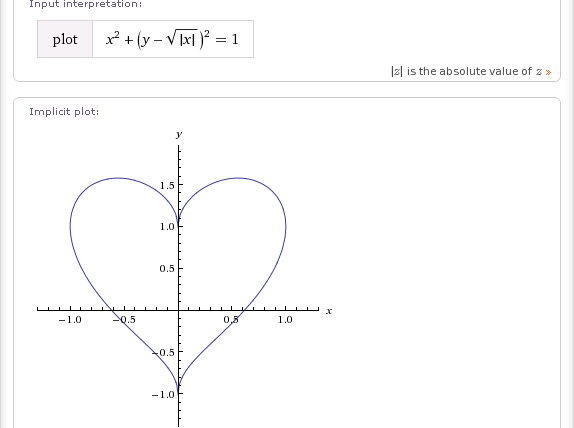
Метод 2
| 1 Нарисуйте два соприкасающихся равных круга. 2 Проведите общую касательную. 3 Проведите две дополнительные (внешние) касательные из одной точки касательная. |
Метод 3
| …… | 1 Нарисуйте квадрат. 2 Нарисуйте четыре одинаковых круга. Центры — это углы квадрата, а общий радиус равен «стороне полуквадрата». |
Метод 4
| 1 Нарисуйте эллипс. 2 Поверните примерно на 45°. 3 Отражение. 4 Сформируйте два сердца. |
Метод 5
. ….. | 1 Нарисуйте график функции f(x)=sin(x), 0 3 Сформируйте треугольник из этих двух кривых и прямой линия. 4 Установите два полукруга на треугольник. |
Метод 6
| …… | 1 Нарисуйте график функции f(x)=sin(x), -pi/2 3 Сформируйте треугольник из этих двух кривых и прямой линия. 4 Установите два полукруга на треугольник. |
Рассчитано
Изгибы сердца вверху
Сложно найти формулы
которые производят сердца.
| Метод 4 можно описать формулами. Черный эллипс имеет формулу 2x²-2xy+y²-1=0. |
домен {х| х>=0}. Тогда y=|x|+sqrt(1-x²) и y=|x|-sqrt(1-x²) описать сердечную кривую [(7)].
Формулы y=sqr(|x|)+sqrt(1-x²) /\ y=sqrt(|x|)-sqrt(1-x²) еще лучше.
Другие кривые
(Изображение 1) Книга 8, Ойген Бейтель (1901) (2) Бух 4, Ауфгабе 8.5.5., (3) MathWorld (упрощенные формулы), (4) Х.-Дж. Веб-сайт Caspar (URL-адрес ниже), (6) Jurjen N.E. Бос
Со стола Торстена Силлке
Трехмерный
Если вы выберете y=0 соответственно x=0, вы получите уравнение двухмерного сердца вверху слева.
Источник: Габриэль Таубин [например, MathWorld (URL
ниже)]
Графики сделаны бесплатная программа «winplot» (версия 23.05.2000, URL ниже).
Winword Hearts верх
А как художники оформляют сердце?
Сердце появляется как известная фигура персонажа
наборы программ под MS Windows. Там фигура играющая
карты, кроме бубнов, крестов и пик.
| Вот набор известных наборов символов. |
Наборы Normaler Text, Arial, Courier New, Estrangelo
Edessa, Lucida Console, Symbol, Times New Roman, Webdings .
Если вы увеличите количество букв с 12 до 72, вы узнаете
формы.
Первоначальный черный цвет заменен на цвет сердца красный.
Верхняя часть фигуры сердца образована кривыми
похожие на дуги.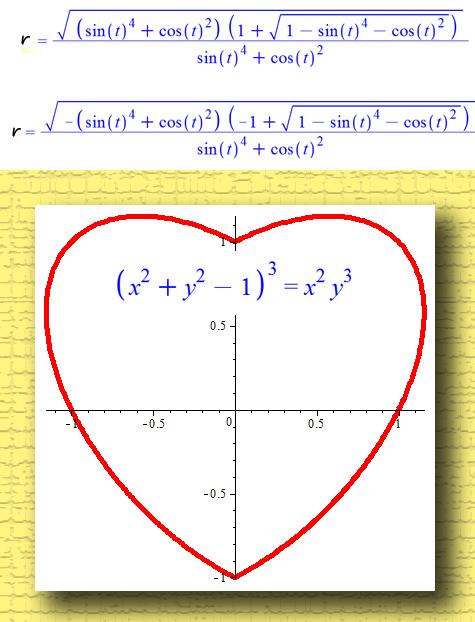
Нижние линии не приближаются линейно к
точки, но обычно сначала изогнуты внутрь, а затем наружу. Что
придает сердцу особый размах.
Найдено в стандарте Unicode, Версия 4.0
| 1 ЧЕРНЫЙ КОСТЮМ С СЕРДЦЕМ 2665 2 БЕЛЫЙ КОСТЮМ С СЕРДЦЕМ 2664 3 ТЯЖЕЛОЕ ЧЕРНОЕ СЕРДЦЕ 2764 |
Сердца учеников вверх
А как ученики рисуют сердце?
23 ученика HS Lohfeld в Бад-Зальцуфлене (Германия) были
нарисовать простое сердце.
Результаты:
Спасибо Классу 7а, Jg.2003/2004, около 12 лет
старый.
Сердечная кривая или кардиоидная
Топ
Как это сделать
| …… | Нарисуйте круг (слева, желтый) и бросьте равный
кружок на нем.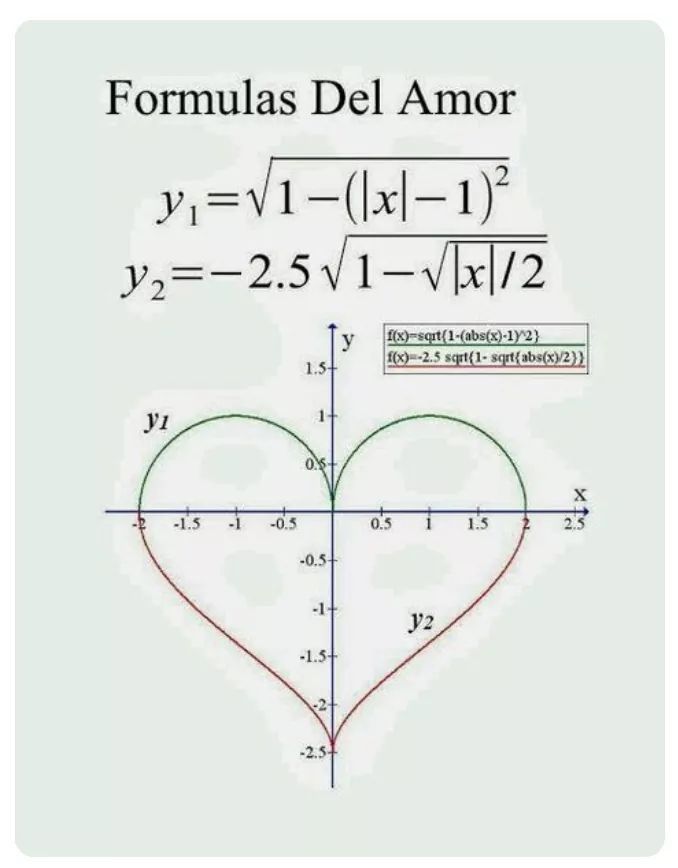 Зафиксируйте одну точку на линии движущегося круга и следуйте этому точка. Он описывает сердечную кривую или кардиоидную (справа). | …… |
Другое способ изготовления сердца
| …… | Кардиоиду также можно рассматривать как огибающую кругов. Нарисуйте круг (желтый) и фиксированную точку P на круге линия. Все окружности, проходящие через фиксированную точку P и имеющие их центры на (желтом) круге имеют кардиоиду в качестве огибающей. |
Площадь и периметр сердечной кривой
Используйте полярную форму r=2a[1+cos (t)] как самую простую уравнение для вычисления площади A и периметра U. Происхождение система координат лежит в точке кардиоиды.
Периметр — рациональное число. Площадь с.
сторона 4а имеет такой же.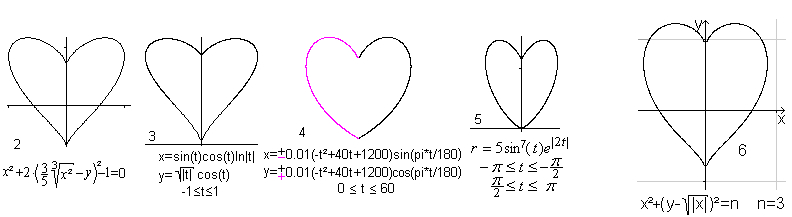
Мандельброт Набор и кардиоида
| …… | «Главная фигура» множества Мандельброта имеет вид
кардиоиды. Немецкое имя Apfelmännchen (человек-яблоко) использует это
форма. На самом деле основная фигура — это кардиоида. Точки множества Мандельброта, имеющие сходящиеся последовательности, лежат внутри кардиоиды. Источник: (5), стр. 208 и далее. Там вы найдете доказательство и многое другое использованная литература. |
Катакаустика и кардиоидный
| …… | Если свет падает на сферическое зеркало (обручальное кольцо
при солнечном свете) отражающие лучи образуют особую поверхность — катакаустику.
Это не кардиоида, а нефроид. Кардиоида развивается как огибающая,
если лучи начинаются в точке окружности и отражаются от окружности
(рисунок справа). | …… |
Характеристика Кривая микрофона
| …… | Микрофоны имеют определенную характеристику. в
плоскости это круг для «приемника звукового давления» и похож на
лежащая восьмерка для «приемника скорости звука». Специальные приемники, такие как конденсаторные микрофоны, имеют оба емкости. Их характеристическая кривая развивается путем наложения на кардиоиду. |
Разбитое сердце верх
Разбитое сердце (Das gebrochene Herz) — это танграм-игра.
| …… | Поместите внутри квадрата два круга и нарисуйте несколько линий.
Развивается сердце, которое разделено на девять частей. Веселье состоит в том, чтобы положить
сердце с кусочками или открывать новые фигуры, как те, что справа. | …… |
Плетеное сердце верх
1 Нарисуйте квадрат и два сидящих на нем полукруга.
2 Разрежьте по красной линии.
3 Скопируйте. Раскрасьте бумагу двумя разными цветами.
или начните с цветной бумаги.
4 Вставьте синюю деталь в зеленую.
5,6 Сердце нормально работает с большим количеством щелей
также.
| Если хочешь, посмотри на сердце страница корзины, сделанная Кристофером Хэмкинсом. |
Мозаика Сердца топ
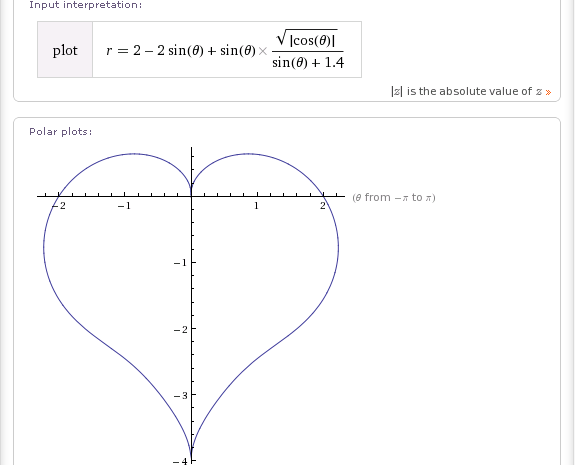. ….. | 1 Дайте спираль. 2 Отразите спираль в конечной точке. 3 Соедините обе спирали, чтобы получилась двойная спираль. 4 Отразите двойную спираль. Это образует сердце вместе с первой двойной спиралью. Много сердец приводят к тесселяции (справа). | …… |
Венеция богата сердцем грили.
Розетки Фигурки Сердца топ
четырехлистный клевер | И снова фото Венеции, подкрашенное красным. | Шесть вафель |
| Пара лебедей во время ухаживания |
Смайлики сверху
Каталожные номера сверху
(1) Питер ван Делфт, Джек Ботерманс: Denkspiele der
Welt, Мюнхен, 1998 ISBN 3-88034-87-0]
(2) Карл-Хайнц Кох: .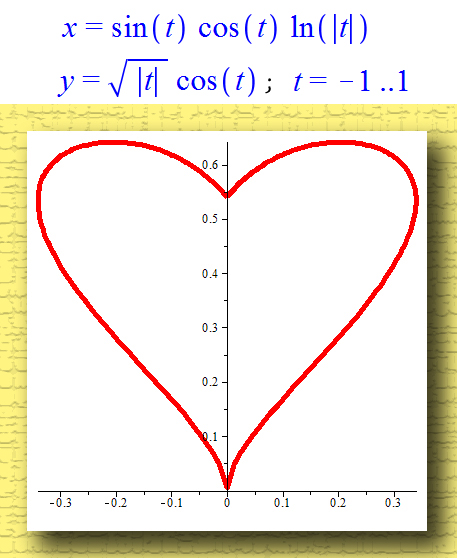
..lege Spiele, Köln 1987 (dumont
taschenbuch2480) [ISBN 3-7701-2097-3]
(3) Heinz Nickel ua: Algebra und Geometrie für Ingenieur- und Fachschulen, Франкфурт / Цюрих, 1966 г.
(4) Ханс Шупп, Хайнц Даброк: Höhere Kurven, BI Wissenschaftsverlag 19(1/2) и а=2
Кривые сердца в Интернете топ
немецкий
33. Evangelischer Kirchentag в Дрездене, 2011 г.
Гугл
фотографии
Армин Дитц
Герцсимвол
Кристиан Уке и Кристиан Энгельхардт
Каустик
в дер Каффитассе
[erschienen in: Physik in unserer Zeit, 29(1998), Сайт
120-122]
| Бенуцер:Георг-Иоганн (Википедия) Фон Пункт за пунктом | х(t)=12sin(t)-4sin(3t) y(t)=13cos(t)-5cos(2t)-2cos(3t)-cos(4t) |
Умереть Лютерроуз
| Эрнст-Мориц-Арндт-Университет Грайфсвальд Герцкартенентвурф фон Стабиус-Вернер (Математика и искусство) | Dies ist die Formel des Randes des «Герцкартенентвурф фон Стабиус-Вернер» X = t sin( 3,14 sin(т)/т) Y = — abs(t) cos( 3,14 sin(t)/t ) -пи <= т <= пи (Mitteilung von Torsten Sillke) |
Фрюлингсгефюле (Томас Т.
) Ханс-Юрген (Matroids Matheplanet)
Герцкурвен
Ханс-Юрген Каспар
Курвен
х = а (-фи² + 40 фи +1200)
грех(пи*фи/180)
92 = 0 (кардиоид)
NN (Матепланета)
Геометрия
ин-дер-Титассе
| Томас Яре (Хемницер Шульмодель) Ein Herz für die Mathematik |
Торстен Зиллке
Герцкурвен
Википедия
Кардиоиде,
Герц
(Символ), Герц
(Геральдик),
Герц
(Фарбе)
Английский
Алексей Богомольный (Разруби узел!)
Сердечный
Жевать кардиоиды
Эрик В. Вайсштейн (MathWorld)
| Кардиоидная Сердце Изгиб (x²+y²-1)³-x²y³ (Зихе Бейтель) х=sin(t)cos(t)ln|t| ; у=|т| 0,3 [cos(t)] 0,5 мит 0<=t<=1 | Бонн
Проекция Сердце Поверхность [x²+(9/4)y²+z²]³-x²z³-(8/90)y²z³=0 (2x²+2y²+z²-1)³-(1/10)x²z³-y²z³=0 |
