Лучший ответ по мнению автора
| |||||||||||||||||
Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
| Похожие вопросы |
чему равны индуктивность и энергия магнитного поля соленоида , если при силе тока, равной 4А, магнитный поток через соленоид и равен 0,4 вб
Решено
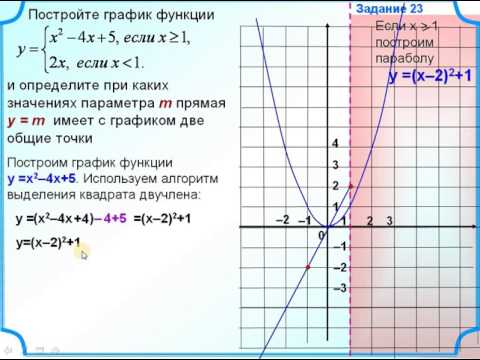
Постройте график функции у=cos (x-пи/6) б) укажите промежутки возрастания и убывания функции; в) определите нули функции.
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружность. На пишите пожалуйста решение
Из колоды в 36 карт вынимают сразу 3 карты. Найти вероятность того что эти карты будут дамой, семеркой тузом
найти массу 10%раствора азотной кислоты необходимой для получения 15г нитроэтана
Пользуйтесь нашим приложением
Графики арифметических корней n-й степени, взаимно обратные функции
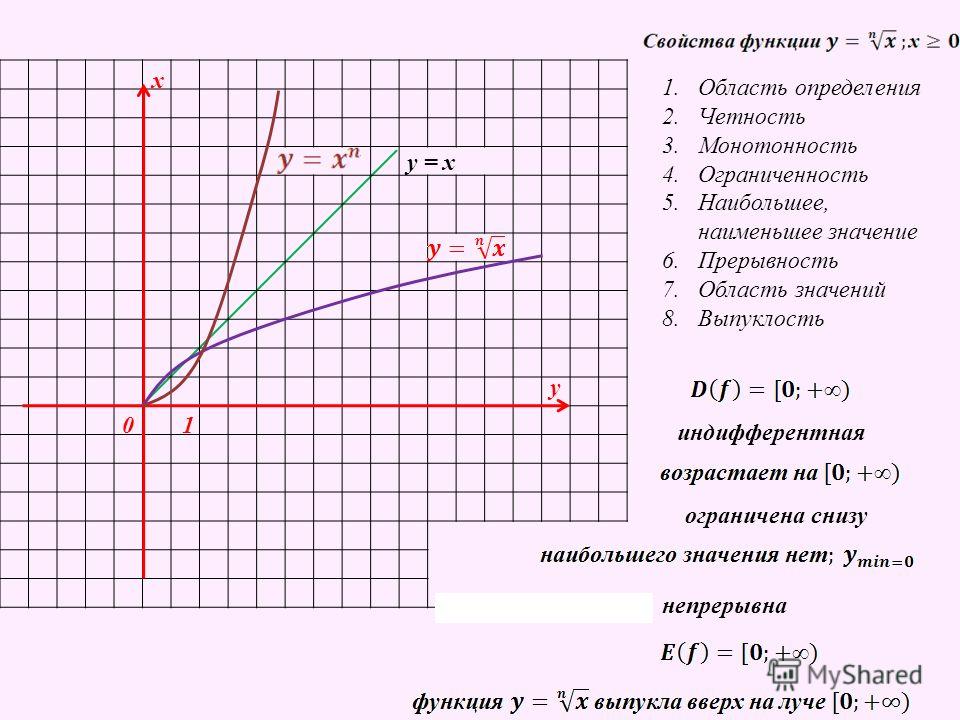
Графики функций $y = \sqrt{x}, y = \sqrt[3]{x}, y = \sqrt[4]{x}, y = \sqrt[5]{x}$
С графиком $y = \sqrt{x}$ – «половиной» параболы — мы уже встречались
(см. §22 справочника для 8 класса).
Построим по точкам графики $y = \sqrt[3]{x}, y = \sqrt[4]{x}, y = \sqrt[5]{x}$ и изобразим все графики в одной системе координат.
Заметим, что при $0 \lt x \lt 1$ выполняется неравенсто $\sqrt{x} \lt \sqrt[3]{x} \lt \sqrt[4]{x} \lt \sqrt[5]{x}$
А при $x \gt 1$ выполняется неравенство $\sqrt[5]{x} \lt \sqrt[4]{x} \lt \sqrt[3]{x} \lt \sqrt{x}$
Графики корня n-й степени $y = \sqrt[n]{x}$
Корень $y = \sqrt[n]{x}$ с натуральным чётным показателем n возрастает на всей области определения Область определения $x \ge 0,т. Область значений $y \ge 0,т.е.y \in [0;+ \infty)$ | |
Корень $y = \sqrt[n]{x}$ с натуральным нечётным показателем n возрастает на всей области определения Область определения $x \in \Bbb R, т.е. x \in (- \infty;+ \infty)$ Область значений $y \in \Bbb R, т.е. y \in (- \infty;+ \infty)$ График симметричен относительно начала координат. Функция нечётная y(-x) = -y(x) |
Т.к. функция возрастает, можно утверждать, что для неотрицательных $a \ge 0$ и $b \ge 0$ и любом натуральном $n \ge 2$:
$$ a \gt b \iff \sqrt[n]{a} \gt \sqrt[n]{b}, a = b \iff \sqrt[n]{a} = \sqrt[n]{b}, a \lt b \iff \sqrt[n]{a} \lt \sqrt[n]{b} $$
Знак сравнения между аргументами сохраняется для функции.
Если n – нечётное, знак сравнения сохраняется для любых действительных $a, b \in \Bbb R$.
Например:
Для чётной степени:
$4 \gt 3 \Rightarrow 4^2 \gt 3^2$, т.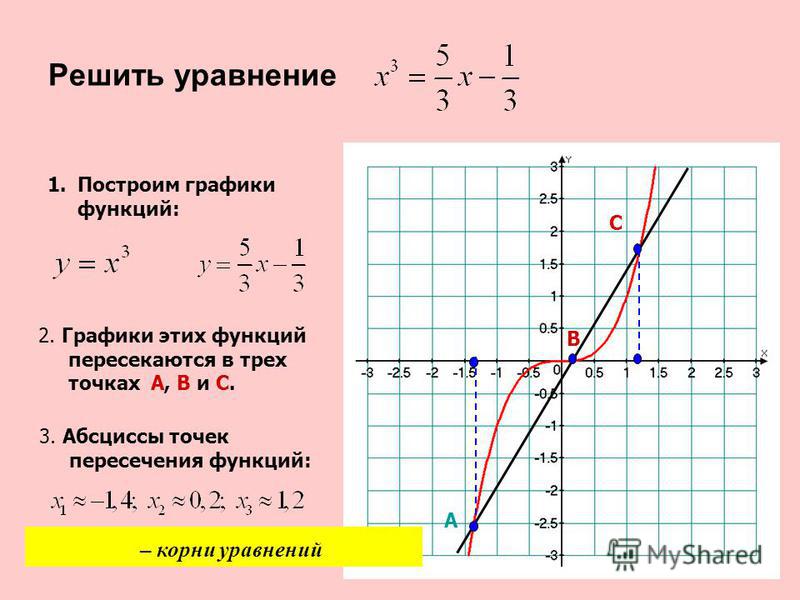 4 $
4 $
$ 12+x \gt 16 $
$ x \gt 4 $
$ x \in (4;+ \infty) $
$ г)\sqrt[4]{12+x} \gt -2 $
Корень чётной степени всегда неотрицательный. Решение сводится к поиску ОДЗ:
$ 12+x \ge 0 $
$ x \ge -12 $
$ x \in [-12;+\infty) $
Пример 3. Решите графически уравнение $\sqrt[3]{x} = 2-x$
При каких x выполняется неравенство $\sqrt[3]{x} \gt 2-x, \sqrt[3]{x} \lt 2-x$?
Корень уравнения: x = 1
$\sqrt[3]{x} \gt 2-x$ при $x \gt 1$ (кривая расположена над прямой)
$\sqrt[3]{x} \lt 2-x$ при $x \lt 1$ (кривая расположена под прямой)
Пример 4. Решите графически уравнение $\sqrt[4]{x} = x$
При каких x выполняется неравенство $\sqrt[4]{x} \gt x, \sqrt[4]{x} \lt x$?
Корни уравнения: $x_1 = 0, x_2 = 1$
$\sqrt[4]{x} \gt x$ при $0 \lt x \lt 1$ (кривая расположена над прямой)
$\sqrt[4]{x} \lt x$ при $x \gt 1$ (кривая расположена под прямой)
Пример 5*. Постройте в одной системе координат графики функций:
$$ y = \sqrt[3]{x}, y = \sqrt[6]{x^2-2x+1}, y = -|x-1|^{\frac{1}{3}} $$
Сделайте выводы. 2-2x+1}$ относительно оси абсцисс OX.
2-2x+1}$ относительно оси абсцисс OX.
Построение графиков функций по заданным параметрам»
Цели урока:
- научить строить графики элементарных математических функций с помощью табличного процессора Excel;
- показать возможности использования программы Excel для решения задач по математике;
- закрепить навыки работы с Мастером диаграмм.
Задачи урока:
- образовательная – знакомство учащихся с основными приемами построения графиков функций в программе Excel;
- развивающие – формирование у учащихся логического и алгоритмического мышления; развитие познавательного интереса к предмету; развитие умения оперировать ранее полученными знаниями; развитие умения планировать свою деятельность;
- воспитательные – воспитание умения
самостоятельно мыслить, ответственности за
выполняемую работу, аккуратности при выполнении
работы.

Тип урока:
- комбинированный
Учебники:
Информатика. Базовый курс 2-е издание/Под ред. С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.
- Проектор
Раздаточный материал:
- Карточки с индивидуальными заданиями на построение графиков функций.
План урока.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока. Домашнее задание – 7 мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный
опрос)
(фронтальный
опрос)
Вопросы для проверки
- Что представляет собой рабочая область программы Excel?
- Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она задается?
- Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как изменить ориентацию бумаги?
- Что такое функциональная зависимость у = f(х)? Какая переменная является зависимой, а какая независимой?
- Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.
При объяснении нового материала может быть использован файл Excel с шаблонами задач (Приложение 1), который выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного процессора Excel для графиков функций. На предыдущих практических вы уже строили диаграммы к различным задачам, используя Мастер диаграмм. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Excel.
Рассмотрим построение графиков функций на примере функции у = sin x.
Вид данного графика хорошо известен вам по урокам математики, попробуем построить его средствами Excel.
Программа будет строить график по точкам: точки с известными значениями будут плавно соединяться линией. Эти точки нужно указать программе, поэтому, сначала создается таблица значений функции у = f(х).
Чтобы создать таблицу, нужно определить
- отрезок оси ОХ, на котором будет строиться
график.

- шаг переменной х, т.е. через какой промежуток будут вычисляться значения функции.
Задача 1.Построить график функции у = sin x на отрезке [– 2; 2] с шагом h = 0,5.
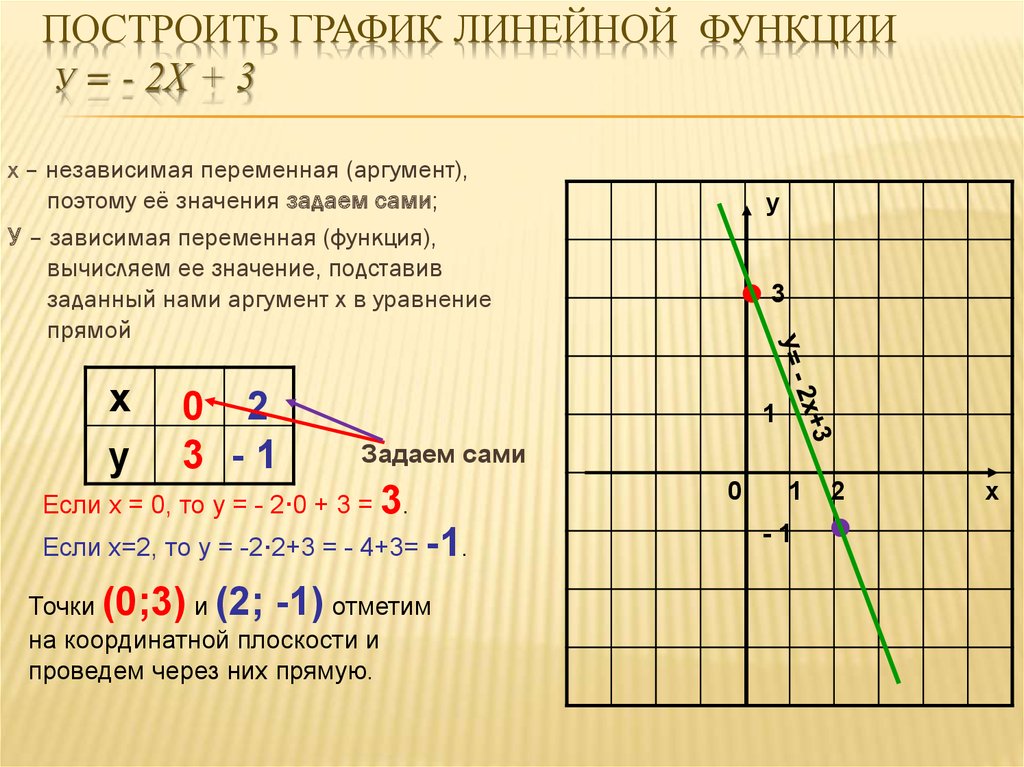
1. Заполним таблицу значений функции. В ячейку С4 введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево ячейки строки 4, до тех пор, пока получим значение другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в категории математические выберем функцию SIN, в качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов (х) и значений (у) функции у = sin x на отрезке [-2;2] с шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,6816 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 | 0,9092 |
6.
Следующий шаг. Выделим таблицу и вызовем Мастер диаграмм. На первом шаге выберем во вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
В поле Подписи оси Х нажать на кнопку. Выделить в таблице ячейки со значениями х и нажмите на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
8. На третьем шаге заполним вкладку Заголовки.
9. Пример полученного графика.
На самом деле пока это мало похоже на график функции в нашем привычном понимании.
Для форматирования графика:
- Вызовем контекстное меню оси ОУ. Затем, выберем
пункт Формат оси…. Во вкладке Шкала установим:
цена основного деления: 1.
 Во вкладке Шрифт
установим размер шрифта 8пт.
Во вкладке Шрифт
установим размер шрифта 8пт. - Вызовем контекстное меню оси ОХ. Выберем пункт Формат оси….
Во вкладке Шкала установим: пересечение с осью ОУ установите номер категории 5 (чтобы ось ОУ пересекала ось ОХ в категории с подписью 0, а это пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт. Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на построение графика функций. Эту задачу попробуйте решить самостоятельно, сверяясь с экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и сформулировать следующую задачу.
Задача 2. Построить график функции у = х3 на отрезке [– 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица значений функции у = f(х).
2.
3
6. Маркером заполнения скопировать формулу в ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица аргументов (х) и значений (у) функции у = х3 на отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7.
Выделить таблицу и вызвать мастер диаграмм. На первом шаге выбрать во второй вкладке Гладкие графики.
8. На втором шаге во вкладке Ряд выполнить:
- В поле Ряд выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
- В поле Подписи оси Х нажать на кнопку . Выделить в таблице ячейки со значениями х и нажать на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры диаграмм таким образом, что бы все поместилось на одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (Вид Колонтитулы…):
14.Верхний колонтитул слева: график функции у = x3
Сохранить документ своей папке под именем График.
Самостоятельная работа.
Работа по карточкам с индивидуальными заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде, выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с шагом h=c
2. Установить параметры страницы и размеры графика таким образом, что бы все поместилось на одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (Вид Колонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный график”
5. Вывести документ на печать.
После выполнения задания правильность каждого
варианта проверяется с помощью проектора.
Подведение итогов.
Домашнее задание.
Оценки за урок.
3 способа расчета полинома в Excel. | Тренды
Есть 3 способа расчета значений полинома в Excel:
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН();
- 3-й способ с помощью Forecast4AC PRO;
Подробнее о полиноме и способе его расчета в Excel далее в нашей статье.
Полиномиальный тренд применяется для описания значений временных рядов, попеременно возрастающих и убывающих. Полином отлично подходит для анализа большого набора данных нестабильной величины (например, продажи сезонных товаров).
Что такое полином? Полином — это степенная функция y=ax2+bx+c (полином второй степени) и y=ax3+bx2+cx+d (полином третей степени) и т.д. Степень полинома определяет количество экстремумов (пиков), т.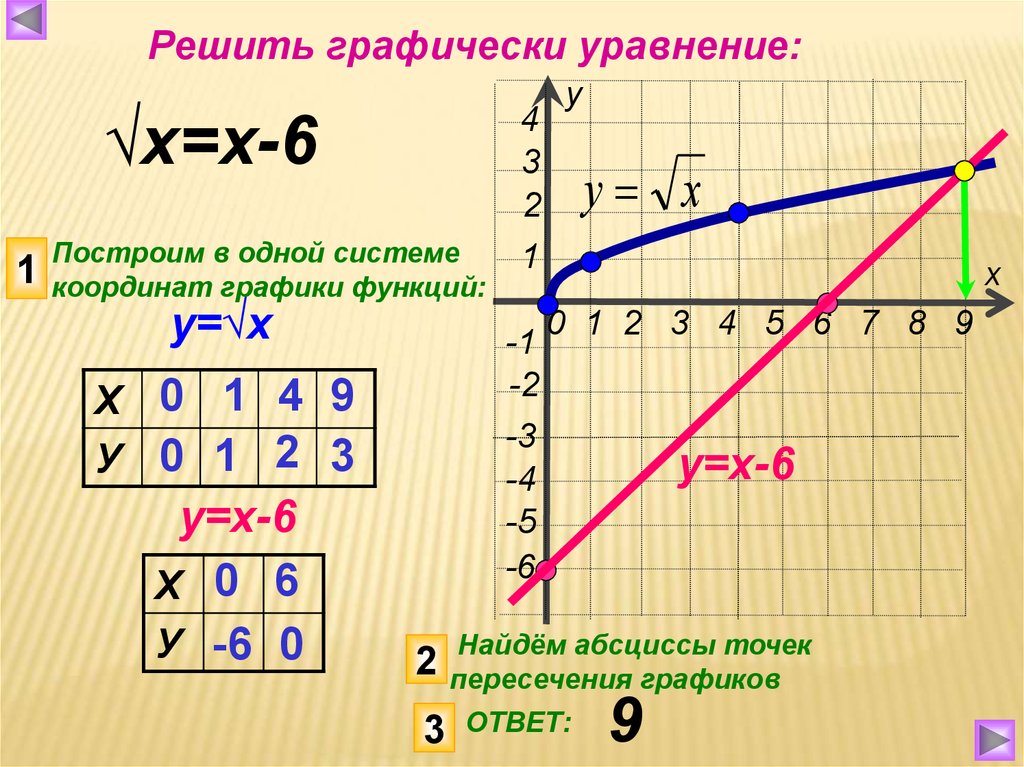 е. максимальных и минимальных значений на анализируемом промежутке времени.
е. максимальных и минимальных значений на анализируемом промежутке времени.
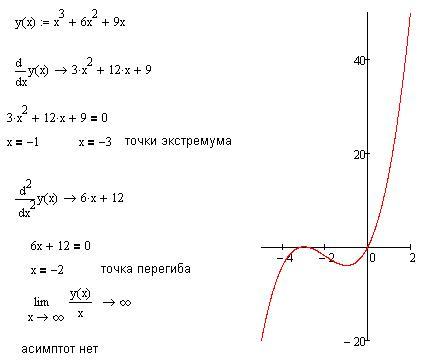
У полинома второй степени y=ax2+bx+c один экстремум (на графике ниже 1 максимум).
У Полинома третьей степени y=ax3+bx2+cx+d может быть один или два экстремума.
Один экстремум
Два экстремума
У Полинома четвертой степени не более трех экстремумов и т.д.
Есть 3 способа расчета значений полинома в Excel:
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН;
- 3-й способ с помощью Forecast4AC PRO;
1-й способ расчета полинома — с помощью графика
Выделяем ряд со значениями и строим график временного ряда.
На график добавляем полином 6-й степени.
Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»
После этого уравнение выводится на график y = 3,7066x6 — 234,94x5 + 4973,6x4 — 35930x3 — 7576,8x2 + 645515x + 5E+06.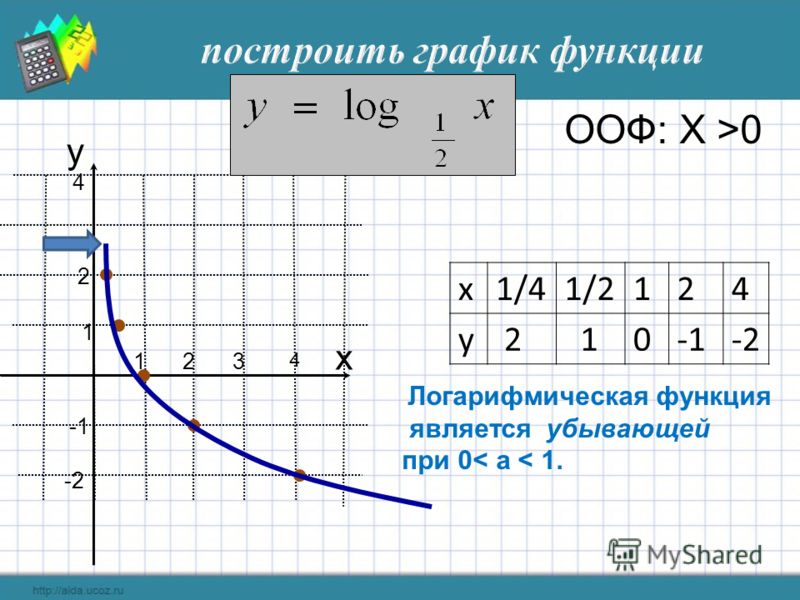 Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома
Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома
Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»
В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».
Получаем уравнение полинома в читаемом формате:
y = 3,71x6 — 234,94x5 + 4 973,59x4 — 35 929,91x3 — 7 576,79x2 + 645 514,77x + 4 693 169,35
Из этого уравнения берем коэффициенты a, b, c, d, g, m, v, и вводим в соответствующие ячейки Excel
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.
Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71x6 — 234,94x5 + 4 973,59x4 — 35 929,91x3 — 7 576,79x2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см.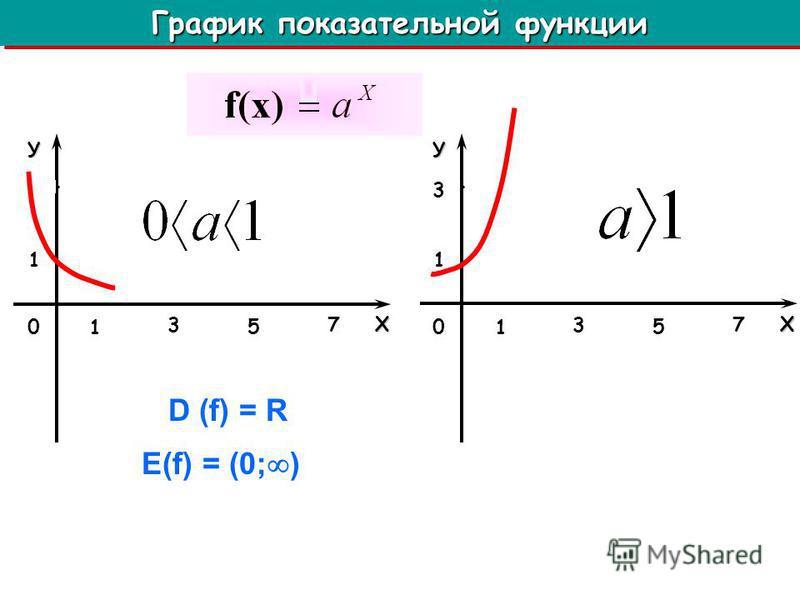 2+R7C8*RC[-3]+R8C8
2+R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
Скачать файл с примером расчета значений полинома.
2-й способ расчета полинома в Excel — функция ЛИНЕЙН()
Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()
Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:
- «известные значения y» (объёмы продаж за периоды),
- «известные значения x» (порядковый номер временного ряда),
- в константу ставим «1»,
- в статистику «0»
Получаем следующего вида формулу:
=ЛИНЕЙН(R[-4]C:R[-4]C[24];R[-5]C:R[-5]C[24];1;0),
Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать. 2+R7C8*RC[-3]+R8C8
2+R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
Скачать файл с примером расчета значений полинома.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.
3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO
Устанавливаем курсор в начало временного ряда
Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».
Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:
Копируем значения в наш лист.
Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:
Скачать файл с примером расчета значений полинома.
- Коэффициентов полиномиального тренда выведенных на график;
- Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
- и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.

Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
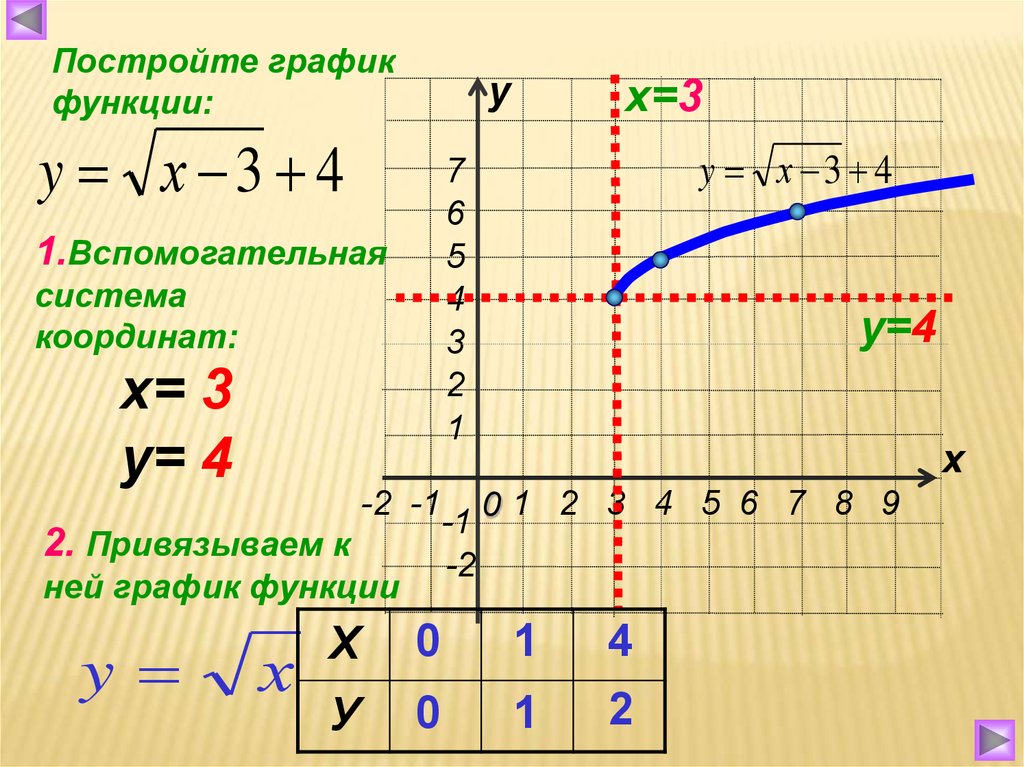
Функция корень n — степени из x, свойства и график
Урок 2. Алгебра 11 класc
На этом уроке мы рассматриваем свойства и график функции корень n – ой степени из x. Рассматриваем примеры на построение и нахождение свойств функций этого вида.
Рассматриваем примеры на построение и нахождение свойств функций этого вида.
Конспект урока «Функция корень n — степени из x, свойства и график»
Вопросы занятия:
· рассмотреть свойства функции корень n-ой степени из x;
· рассмотреть график функции корень n-ой степени из x;
· рассмотреть примеры на построение и нахождение свойств функций этого вида.
Материал урока
Прежде чем перейти к изучению нового материала, давайте повторим основные понятия, с которыми мы познакомились на предыдущих уроках.
Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.
Корнем нечётной степени n-ой из
отрицательного числа а называют такое
отрицательное число, при возведении которого в степень n получается а.
Обозначают:
Число а – это подкоренное число, число n – показатель корня.
Обобщая эти понятия, можно сказать, что из любого неотрицательного числа можно извлечь корень любой степени (второй, третьей, четвертой и так далее), а из отрицательного числа можно извлечь только корень нечётной степени.
То есть на [0; +∞) каждому числу x можно поставить в соответствие единственное число корень n-ой степени из x при любом значении n.
Другими словами, на множестве [0; +∞) можно говорить о функции:
Давайте попробуем найти свойства этой функции и построить её график.
Основные свойства:
Областью определения будет являться промежуток [0; +∞).
Поскольку
корнем n-ой степени из неотрицательного числа является неотрицательное
число, то областью значений функции будет промежуток [0; +∞).
Поскольку область определения функции не является симметричным множеством, то функция не является ни чётной, ни нечётной.
Операцию извлечения корня мы вводили как операцию обратную возведению в соответствующую степень.
Тогда можно сказать, что:
Зная это, нетрудно построить график функции.
Используя построенный график, мы можем записать оставшиеся свойства функции.
Функция возрастает на промежутке [0; +∞).
Функция не ограничена сверху, но ограничена снизу, например, прямой y = -0,5.
Наименьшим значением функции будет 0, наибольшего значения функция не имеет.
Функция непрерывна на всей области определения.
Функция выпукла вверх на всей области определения.
При изучении темы дифференцирование
функций, мы говорили, что если функция дифференцируема в каждой точке
некоторого промежутка, то она непрерывна на данном промежутке. Из курса базовой
школы мы знаем:
Из курса базовой
школы мы знаем:
Тогда:
Эта производная существует в любой точке промежутка [0; +∞) за исключением точки 0.
Таким образом, функция имеет производную в любой точке промежутка (0; +∞), то есть функция дифференцируема на промежутке (0; +∞).
Рассмотрим несколько примеров.
Пример.
Пример.
Мы с вами говорили о функции y равно корень n—ой степени из x только для неотрицательных значений аргумента.
Но если эн нечётное число, то выражение корень n—ой степени из x имеет смысл и для отрицательных x. Значит, можно говорить о функции:
Теперь давайте запишем свойства этой функции.
Областью определения будет промежуток (– ∞; + ∞).
Областью значений будет промежуток (– ∞; + ∞).
Поскольку область определения является симметричным множеством, то можно исследовать данную функцию на чётность:
Получаем, что функция при нечётном n
будет нечётной.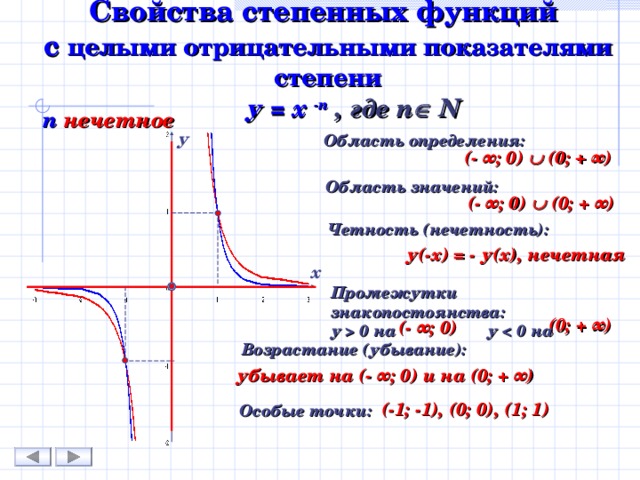
Давайте построим график функции.
Воспользуемся свойством нечётности функции и добавим к этой ветви ветвь, симметричную ей относительно начала координат.
По графику легко записать оставшиеся свойства функции.
Функция возрастает на всей области определения.
Функция не ограничена ни сверху ни снизу.
Функция не имеет ни наименьшего, ни наибольшего значений.
Функция непрерывна на всей области определения.
Функция выпукла вниз на промежутке (– ∞; 0) и выпукла вверх на промежутке (0; + ∞).
Функция дифференцируема на всей области определения за исключением точки 0.
Рассмотрим несколько примеров.
Пример.
Пример.
Пример.
Предыдущий урок 1 Понятие корня n — степени из действительного числа
Следующий урок 3 Свойства корня n — степени
Получите полный комплект видеоуроков, тестов и презентаций Алгебра 11 класc
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 93-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92Степенная функция — свойства, графики и приложения
Вы когда-нибудь работали с функцией, содержащей один термин? Скорее всего, вы работали с силовой функцией. Этот тип функции настолько разнообразен, что если вы изучаете функции, мы на 100% уверены, что вы уже встречались с типом степенной функции, не зная, что это один из них.
Этот тип функции настолько разнообразен, что если вы изучаете функции, мы на 100% уверены, что вы уже встречались с типом степенной функции, не зная, что это один из них.
Почему бы нам не начать с определения степенных функций?
Степенная функция — это одночленная функция, в основе которой лежит переменная, а показатель степени — константа.
Это означает, что существует множество родительских функций, которые также являются степенными функциями. В этой статье мы узнаем:
- Концепция силовых функций.
- Специальные свойства, которыми может обладать степенная функция.
- Примените эти свойства для построения графиков и определения степенных функций.
Убедитесь, что у вас под рукой блокнот, так как это будет подробное обсуждение функций питания. Мы даже научимся применять степенные функции в текстовых задачах.
Почему бы нам не начать с его определения и некоторых примеров степенных функций?
Что такое степенная функция? Прежде чем мы углубимся в важные свойства степенной функции, мы должны понять основное определение степенной функции.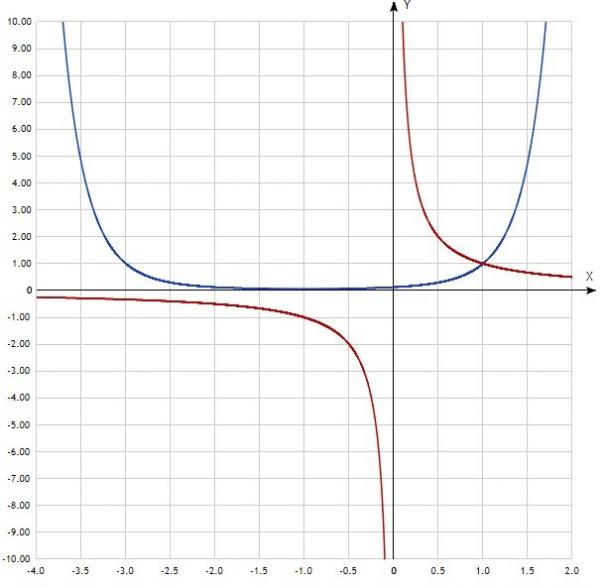 Вот общая форма степенных функций:
Вот общая форма степенных функций:
Давайте разберем эту общую форму и найдем примеры степенных функций, использующих это определение.
Обязательно ознакомьтесь с этой формой, так как мы будем неоднократно использовать ее на протяжении всей статьи.
Определение и примеры степенных функцийКак показано в предыдущем разделе, степенные функции представляют собой функции в форме f(x) = kx a 59×17 81820 или 0 a , где k — ненулевой коэффициент, а a — действительное число.
Вот несколько примеров степенных функций:
- y = -5x 2
- y = 2 √x
- f(x) = 3/x 2
- g(x) = 2x 3
Обратите внимание, что каждая функция содержит только один термин – an20 для 918 важный идентификатор силовых функций. Показатели степенных функций также должны быть действительными числами, поэтому давайте проверим каждый показатель из примеров, чтобы подтвердить это.
Показатели степенных функций также должны быть действительными числами, поэтому давайте проверим каждый показатель из примеров, чтобы подтвердить это.
- Функция y = -5x 2 и g(x) = 2x 3 являются функциями с целыми числами в качестве их показателей, поэтому они являются степенными функциями.
- Функция квадратного корня, y = 2 √x, может быть переписана как y = 2x 1/2 , поэтому ее показатель степени является действительным числом, поэтому это также степенная функция.
- Мы применяем тот же процесс с f(x) = 3/x 2 и имеем f(x) = 3x -2 , подтверждая, что это степенная функция, поскольку -2 является действительным числом.
Ниже приведены лишь некоторые родительские функции, и давайте посмотрим, почему все они также считаются степенными функциями.
| Parent Function | Function Form |
| Constant Function | y = a |
| Linear Function | y = x |
| Quadratic Function | y = x 2 |
| Кубическая функция | y = x 3 |
| Обратная функция | y = 1/ x, y = 1/ x 2 |
| Функция0004 y = √x |
Поскольку каждая из этих родительских функций содержит по одному члену и действительные числа для показателей степени, все они являются степенными функциями.
При построении графика степенных функций мы должны помнить о двух важных свойствах степенных функций: их симметрии и конечном поведении .
Вот краткое руководство о том, как мы строим графики функций мощности, чтобы показать вам, почему эти две функции могут помочь вам сэкономить время:
- Определите, является ли степенная функция четной или нечетной.
- Применяйте преобразования всякий раз, когда можете.
- Найдите несколько точек, которые помогут построить график половины степенной функции.
- Применить свойство симметрии заданной степенной функции.
- Дважды проверьте их конечное поведение.
Почему бы нам не освежить наши знания о нечетных и четных функциях и посмотреть, как они влияют на график степенной функции?
Симметрия четных степенных функций и граничное поведение Степенные функции либо четные, либо нечетные, поэтому они также симметричны относительно оси Y и начала координат . Мы также можем предсказать конечное поведение степенных функций на основе их коэффициента и мощности .
Мы также можем предсказать конечное поведение степенных функций на основе их коэффициента и мощности .
Давайте посмотрим на график этих четных степенных функций: y = 2x 2 и y = -4x 4 . Чтобы построить график каждой функции, нанесите несколько точек справа и отразите эту кривую по оси Y.
Для обоих графиков, поскольку показатели степени четны, функции также четны и, следовательно, их графики симметричны относительно оси ординат.
Начнем с четных степенных функций с положительным коэффициентом , таких как y = 2x 2 .
- Поскольку коэффициент 2 положительный, график открывается вверх .
- Мы видим, что при x < 0 функция убывает, а при x > 0 функция убывает.
- Следовательно, и левая, и правая стороны кривой будут повышаться (↑) .
Теперь посмотрим даже степенные функции, где коэффициент отрицательный , например y = -4x 4 .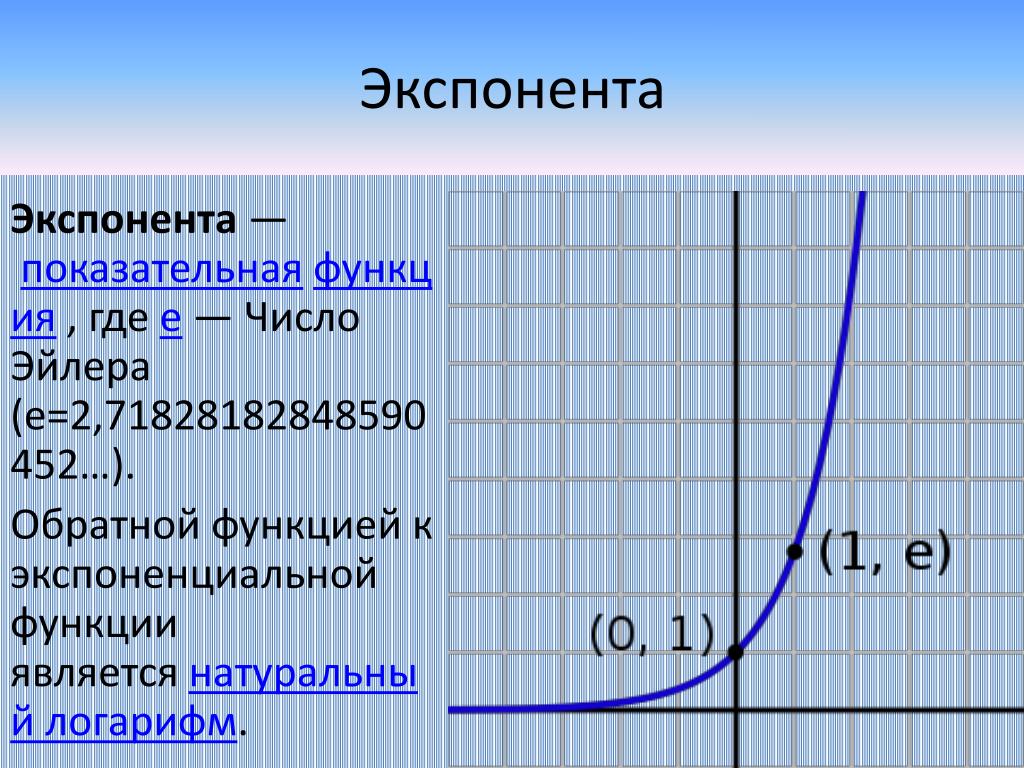
- Поскольку коэффициент -4 отрицательный, график открывается вниз .
- Здесь мы видим, что при x < 0 функция возрастает, а при x > 0 функция убывает.
- Это означает, что для с обеих сторон мы ожидаем, что кривая пойдет вниз (↓).
Как насчет функций нечетной мощности? Давайте продолжим и посмотрим на эти две функции: y = 3x 3 и y = -x 5 .
Чтобы построить график двух функций, мы можем нанести некоторые значения либо на левую, либо на правую сторону координатной плоскости. Отразите график над началом координат.
Из определения нечетных функций видно, что обе степенные функции симметричны относительно начала координат .
Вот некоторые вещи, которые мы можем наблюдать на основе графика y = 3x 3 , где коэффициент положительный :
- Мы можем видеть, что при x < 0 функция возрастает, , а при x > 0 функция возрастает .

- Следовательно, левая сторона идет вниз (↓) , а правая сторона идет вверх (↑) .
Теперь посмотрим на поведение нечетных функций при отрицательном коэффициенте .
- Мы видим, что когда x < 0 и x > 0, функция убывает
- Следовательно, левая сторона увеличивается (↑) , а правая сторона идет вниз (↓) .
Мы подробно обсудили влияние на график степенной функции на основе ее четности и значения k. Теперь давайте попробуем пронаблюдать разницу, когда а — дробь, а когда а — целое число.
Случай 1: Когда a = 0 и a = 1 , мы ожидаем, что график сведется к постоянной функции и линейной функции соответственно.
Графики y = 2 и y = 2x могут подтвердить это. То же самое относится ко всем значениям k.
Областью определения в этом случае будут все действительные числа или в интервальной записи, то есть (-∞, ∞).
Случай 2: Когда a < 0 . Рассмотрим графики y = x -1 и y = x -2 :
Когда a отрицательно, а функция мощности возвращает рациональное выражение, мы можем видеть, что графики приближаются, но никогда не равны 0 . Это означает, что доменом этих степенных функций будет любое действительное число, кроме 0, , поэтому домен равен (-∞, 0) U (0, ∞) .
Два графика также вогнуты вверх с обеих сторон .
Случай 3: Когда 1< a < 0 . Посмотрим на графики y = x 1/2 и y = x 1/3 :
Когда a является дробью, а функция степени возвращает подкоренное выражение. Мы видим, что область определения будет зависеть от того, четный или нечетный знаменатель:
- Если знаменатель четный, то только положительные значения x будут частью области определения или [0, ∞).

- Если знаменатель нечетный, все его области определения могут быть действительными числами или (-∞, ∞).
Два графика также вогнуты вниз с обеих сторон .
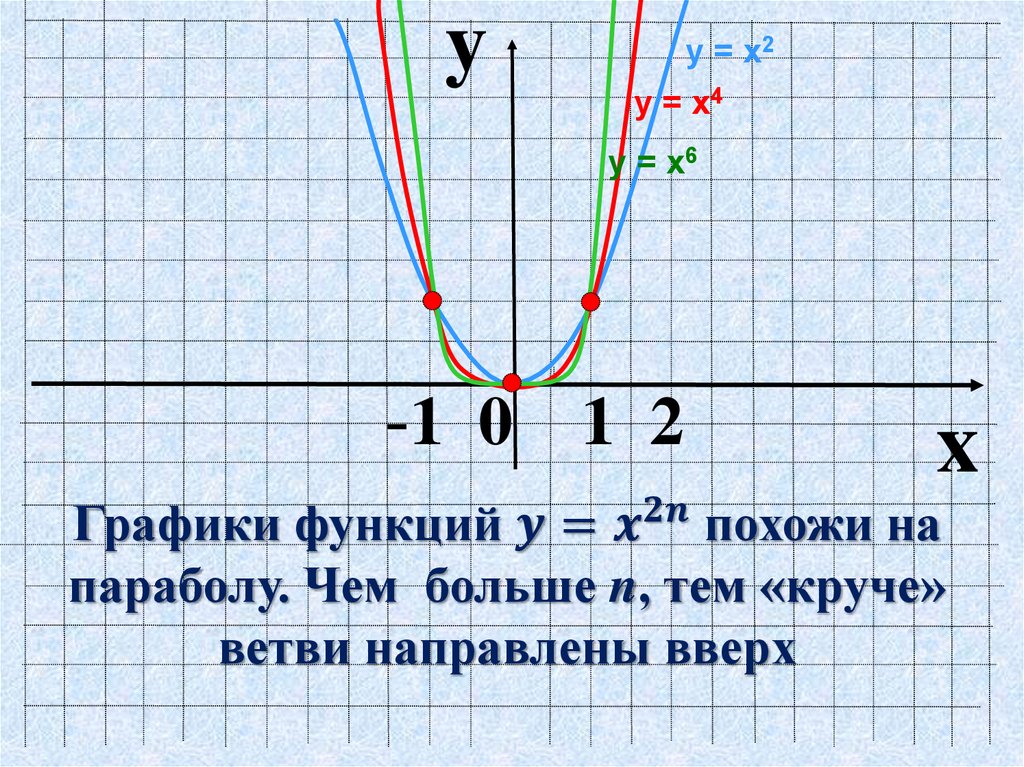
Случай 4: Когда a > 1 , давайте посмотрим на графики y = x 5 и y = x 6 .
Когда показатель степени положительный, мы ожидаем, что графики будут вогнутыми вверх . Областью определения для этого типа степенной функции будут все действительные числа или интервальных обозначений, (-∞, ∞) .
Как найти силовую функцию?
Иногда нам дают график степенной функции или несколько точек, проходящих через ее график. Мы все еще можем найти выражение, представляющее степенную функцию, используя две точки.
- Подставьте эти две точки в общий вид степенных функций: y = kx a .
- Найдите способ сохранить k или a в одном из уравнений.

- Определите значения для k и a и подставьте их обратно в общий вид степенных функций.
Допустим, мы хотим найти степенную функцию, проходящую через (2, 16) и (3, 54). Подставим эти значения в общий вид:
9000 41810 54111111119 (3, 54). ) A54 /3 A = K
| (2, 16) | 16 = K (2) A 16/2 A = K |
| (3, 54) | |
Let’s Againing оба правых побочных экспрессии и имеют:
16/2 A = 541818
16/2 A = 54 /3 918
16/2 A = 541810 16 /2 A = 541810 16 /2 A = 541810 16 /2 A = 541810 16 /2 A = 541818
. 2 a = 27 / 3 a
2 3 / 2 a = 3 3 / 3 a
2 3 – a = 3 3 – a
должно быть равно 0. Следовательно, a = 3,
Следовательно, a = 3,
. Подставим это обратно в любое из выражений k: имеем a = 3 и k = 2, теперь мы можем записать выражение степенной функции: y = 2x 3 .
Что, если мы хотим найти выражение степенной функции на основе ее графика? Просто обратите внимание на две точки, через которые проходит график функции, а затем примените тот же процесс.
Прежде чем мы попробуем ответить еще на несколько вопросов, связанных со степенными функциями, почему бы нам не обобщить все, что мы уже знаем о степенных функциях?
Краткое изложение формул степенных функций и их свойствВот несколько полезных напоминаний при работе со степенными функциями и их приложениями:
- При определении того, является ли функция степенной функцией, убедитесь, что выражение является одним термином , k является константой , а a является действительным числом .
- Графики степенных функций будут зависеть от значений k и a.

- Примените свойства нечетных и четных функций, когда это применимо.
- При нахождении выражения для степенной функции всегда используйте общую форму, y = kx а .
- Используйте приведенную ниже таблицу для прогнозирования конечного поведения силовых функций.
| Условие для K | Evel Power Functions | ODD Power Functions |
| , когда k> 0 | функция снижается. ∞, y → ∞ Функция возрастает, когда x > 0: При x → ∞, y → ∞ | Функция возрастает на всем интервале x: При x → – ∞, y → -∞ При x → ∞, y → ∞ |
| При k < 0 | Функция возрастает при x < 0: При x → – ∞, y → – ∞ Функция убывает при x > 0: При x → ∞, y → – ∞ | Функция убывает на всем интервале x: При x → – ∞, y → ∞ При x → ∞, y → – ∞ |
Убедитесь, что понимаете концепцию силовых функций и ознакомьтесь с различными вариантами конечного поведения. Когда вы будете готовы, давайте продолжим и попробуем решить несколько задач!
Когда вы будете готовы, давайте продолжим и попробуем решить несколько задач!
Пример 1
Какие из следующих функций считаются степенными?
а. f(x) = -2x 2 · 3x
б. g(x) = 2√x + 5
c. h(x) = 0,5x π
d. m(x) = -(x + 1) 2
e. п (х) = 1 / х 3
Решение
Проверьте каждую из заданных функций и по возможности упростите выражения.
а. Функцию все еще можно упростить до f(x) = -6x 3 . Мы видим, что он содержит только один член и имеет действительное число для коэффициента и показателя степени, поэтому f(x) является степенной функцией .
Следующие два пункта (b и d) содержат более одного члена и не могут быть упрощены, поэтому функции g(x) и m(x) не рассматриваются как степенные функции .
г. Мы всегда возвращаемся к фундаментальному определению степенных функций: они содержат один член, а коэффициент и показатели степени действительны.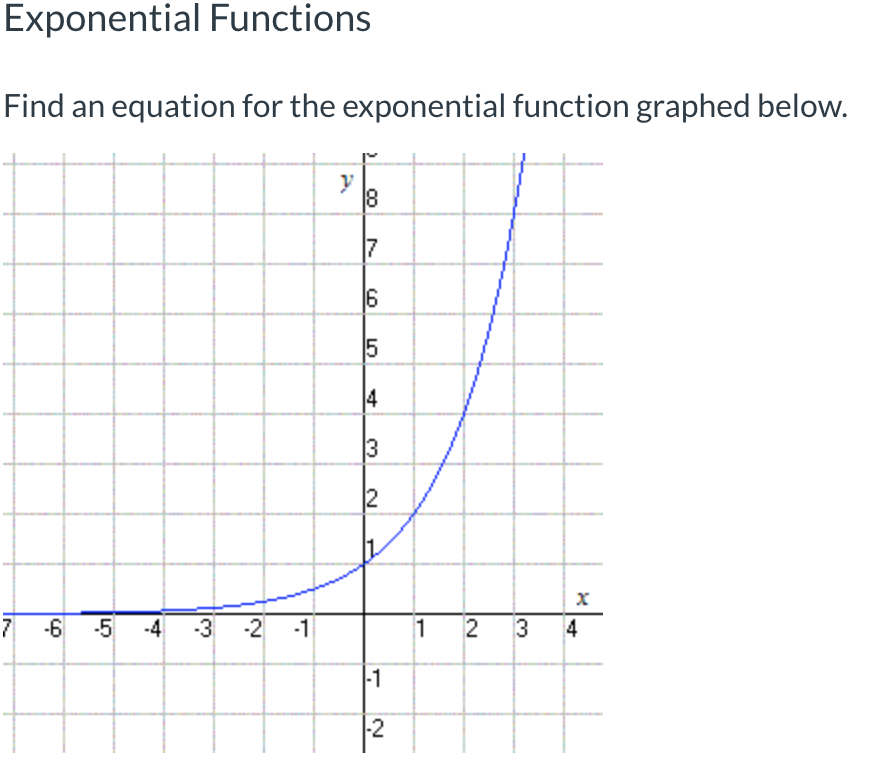 И 0,5, и π — действительные числа, поэтому h(x) также является степенной функцией .
И 0,5, и π — действительные числа, поэтому h(x) также является степенной функцией .
эл. Поскольку 1/ x 3 = 1 · x -3 , мы можем убедиться в результате проверки, что оно удовлетворяет условиям степенных функций, поэтому n(x) также является степенной функцией .
Следовательно, функции в a, c и e являются степенными функциями .
Пример 2
Заполните пропуски всегда , иногда и никогда , чтобы сделать следующие утверждения верными.
а. Кубические функции – это ______________ степенные функции.
б. Постоянные функции — это _____________ степенные функции.
с. Степенные функции будут ___________ иметь отрицательные показатели.
Решение
Давайте продолжим и проверим каждое утверждение:
а. Некоторые примеры кубических функций: 2x 3 и x 3 — x 2 + x — 1. Мы видим, что первый пример является степенной функцией, а второй — нет. Это означает, что кубические функции могут быть степенными функциями.
Мы видим, что первый пример является степенной функцией, а второй — нет. Это означает, что кубические функции могут быть степенными функциями.
б. Общая форма постоянных функций такова: y = c, где c — любая ненулевая константа. Из общей формы видно, что независимо от значения c постоянные функции всегда будут иметь один член с действительными числами для их коэффициента и показателя степени. Следовательно, постоянные функции будут всегда — степенные функции.
г. Пока функция содержит один член и показатель действительного числа, она будет считаться степенной функцией. Это означает, что в степенной функции могут быть положительные и отрицательные показатели. Таким образом, они могут иногда иметь отрицательные показатели степени.
Пример 3
Определите конечное поведение следующих степенных функций:
a. f(x) = x 3
б. г(х) = -4х 4
в. h(x) = (-3x) 3
Решение
При прогнозировании конечного поведения степенной функции проверьте знак коэффициента и значение показателя степени. Используйте предоставленную нами таблицу, чтобы спрогнозировать конечное поведение.
Используйте предоставленную нами таблицу, чтобы спрогнозировать конечное поведение.
а. Функция f(x) = x 3 имеет коэффициент 1 и положительный показатель степени 3. Поскольку степень нечетна, ожидается, что функция будет возрастать во всей области определения.
Это означает, что левая сторона его кривой идет вниз, а правая – вверх: (↓↑).
б. Для второй функции g(x) = -4x 4 имеет отрицательный коэффициент и четный положительный показатель степени. Это означает, что ожидается открытие графика вниз. Функция также будет возрастать, когда x < 0, и уменьшаться, когда x > 0.
Это означает, что и левая, и правая стороны кривой должны идти вниз: (↓↓).
г. Сначала упростим выражение для h(x): h(x) = -27x 3 . Мы видим, что h(x) имеет отрицательный коэффициент и нечетный показатель степени. Когда это происходит, функция убывает по всей области определения.
Кривая графика идет вверх с левой стороны и спускается с правой стороны: (↑↓).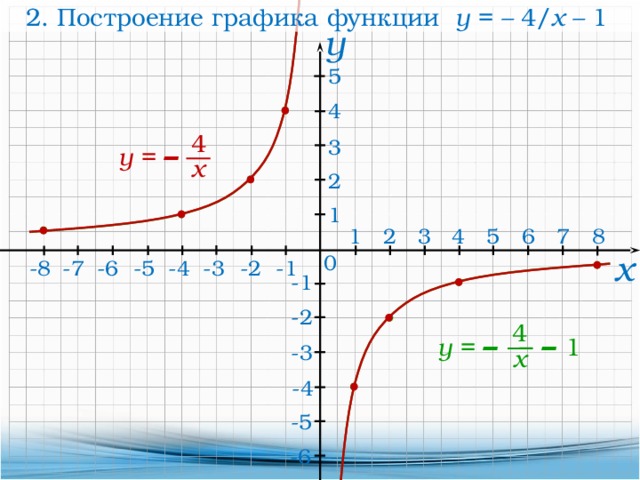
Пример 4
Покажите, что произведение двух степенных функций также всегда возвращает степенную функцию.
Решение
Пусть две степенные функции равны f(x) = mx p и g(x) = nx q , где m и n — действительные числовые коэффициенты. Показатели p и q также являются действительными числами.
Умножение двух функций даст:
f(x) · g(x) = (mx p ) · (nx q )
= mn x p + q Пусть
= mn
k и p + q = a, поэтому f(x) · g(x) = kx a .
Поскольку mn и p + q — действительные числа, k и a также будут действительными числами. Произведение по-прежнему возвращает степенную функцию, поэтому мы только что подтвердили, что произведение двух степенных функций также будет степенной функцией.
Пример 5
Постройте график степенной функции f(x) = -3x 5 и ответьте на следующие вопросы.
а. Каковы область определения и диапазон функции?
б. Если график переместить на 6 единиц вверх, будет ли результирующая функция по-прежнему степенной?
Решение
Поскольку f(x) — нечетная функция, мы ожидаем, что график будет симметричным относительно начала координат.
| х | F (x) |
| 0 | 0 |
| 1 | -3 |
| 2 | -96 |
Мы можем построить эти очки на график и размышления. над происхождением.
а. Поскольку показатель степени положителен и нечетен, область определения и диапазон f(x) будут действительными числами или (-∞, ∞) . В этом также можно убедиться, изучив график.
б. Когда мы переводим f(x) на 6 единиц, мы добавляем 6 к выражению. Следовательно, выражение новой функции теперь будет -3x 5 + 6. Это выражение будет содержать два члена, и, таким образом, новая функция больше не будет степенной функцией .
Пример 6
Используйте приведенный ниже график, чтобы найти выражение для h(x).
Решение
Поскольку график h(x) проходит через (-1, -2), (1, -2) и (1/2, -8), мы можем использовать любой из этих три точки в общем виде степенной функции: y = kx a .
: Заметили что-нибудь на графике? Кривые приближаются, но никогда не могут быть равны 0, поэтому мы ожидаем, что показатель степени будет дробным.
Сначала подставим (1, -2) в общую форму степенной функции. (Это будет лучший вариант, поскольку k1 a уменьшится до k .)
-2 = k(1) a
-2 = k
Примените тот же процесс для (1/2, -8), но на этот раз давайте также используем k = -2.
-8 = (-2)(-1/2) а
4 = (-1/2) a
(-1/2) -2 = (-1/2) a
Чтобы это было правдой, a должно быть равно — 2. Следовательно, мы имеем h(x) = -2x -2 .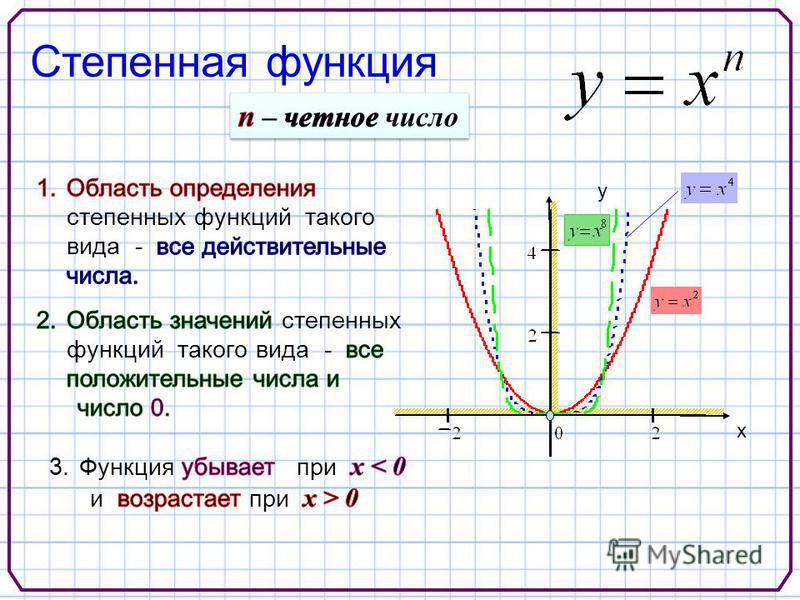
Пример 7
Степенная функция g(x) проходит через точки (4, -6) и (9, -9).
а. Какое выражение для g(x)?
б. Постройте график функции g(x).
г. Найдите его домен и диапазон, затем опишите его конечное поведение.
Решение
Подставим каждую пару значений в общий вид степенных функций: y = kx a и упростим полученное уравнение.
| (4, -6) | -6 = k(4) a -6= k4 a -6/4 a = k |
| ( 9, -9) | -9 = k(9) a -9= k9 a -9/9 a = k |
Теперь, когда у нас есть k в обеих правых частях уравнений, давайте приравняем выражения в левой части. Найдите а из полученного уравнения.
-6/4 A = -9/9 A
-2/4 A = -3/9 A
-2 1 /2
2A-2 1 /2
2A-2 1 /2
2A-2 1 /2
2A-2 1 /2
2A-2 1 /2
2A-2 1 2
. 1 / 3 2a
1 / 3 2a
-2 1 – 2a = -3 1 – 2a
Это уравнение будет верным только тогда, когда обе стороны равны 1, поэтому показатели степени должны быть равны 0
1 – 2a = 0
1 = 2a
a = ½
Подставьте значение a в одно из выражений для k.
k = -6/4 a
= -6/ 4 1/2
= -6/ 2
= -3
Подставим эти два значения обратно в общую форму степенных функций найдите выражение для g(x).
g(x) = kx a
= -3x 1/2
= -3√x
а. Следовательно, мы имеем g(x) = -3√x .
Давайте используем две заданные точки, чтобы соединить кривую. Вспомните форму родительской функции функции квадратного корня, чтобы знать, чего ожидать от графика g(x).
б.
Мы можем найти область определения и диапазон значений g(x), изучив график. Поскольку g(x) имеет рациональный показатель с четным знаменателем, мы ожидаем, что для x будут только положительные значения. График также может подтвердить это.
График также может подтвердить это.
Поскольку график g(x) никогда не поднимается выше отрицательной оси y, мы ожидаем, что его диапазон будет состоять только из отрицательных чисел.
гр. Следовательно, область функции g(x) равна [0, ∞) , а диапазон равен (-∞, 0] . График показывает, что она непрерывно уменьшается, а кривая последовательно идет вниз .
Пример 8
Площадь круга прямо пропорциональна квадрату его радиуса, г. Площадь круга с радиусом 10 единиц составляет 314 единиц 2, и круга с радиусом 20 единиц это 1256 единиц 2 .
а. Найдите степенную функцию A(r), представляющую площадь круга через r. Что представляет собой коэффициент при A(r)?
б. Независимо от ограничений на r, является ли A(r) нечетным или четным?
г. Каково конечное поведение A(r)?
д. Если мы учтем тот факт, что r представляет собой радиус окружности, изменится ли домен?
Решение
Поскольку площадь прямо пропорциональна r 2 , мы можем выразить A(r) как kr 2 , где k — ненулевая константа.
Давайте используем любую из двух заданных пар значений, чтобы найти k.
A(r) = kr 2
314 = k(10) 2
314 = 100k
k = 3,14
а. Подставим k обратно в выражение, и мы получим A(r) = 3,14r 2 . Напомним, что 3,14 — это приближенное значение π, , поэтому коэффициент A(r) представляет π .
б. Поскольку A(r) — квадратичное выражение; это даже функция .
г. Коэффициент при A(r) положительный, а его показатель четный, поэтому мы ожидаем, что график будет уменьшаться, когда x < 0, и увеличиваться, когда x > 0. Следовательно, ожидается, что оба конца кривой будут двигаться до .
д. Первоначально, поскольку A(r) представляет собой квадратное выражение, мы ожидаем, что оно будет иметь область определения (-∞, ∞). Но с учетом того факта, что измерения должны быть больше 0, область теперь становится (0, ∞).
5.2 — Справочник — Графики восьми основных типов функций
5.2 — Справочник — Графики восьми основных типов функций5.2 — Справочник — Графики восьми основных типов функций
Цель этого справочного раздела — показать вам графики различных типов функций для того, чтобы вы могли ознакомиться с типами. Вы обнаружите, что каждый тип имеет свой характерный график. Показывая несколько графиков на одном графике, вы уметь видеть их общие черты. В этой галерее показаны примеры следующих типов функций:- линейный
- квадратичный
- сила
- многочлен
- рациональное
- экспоненциальный
- логарифмический
- синусоидальный
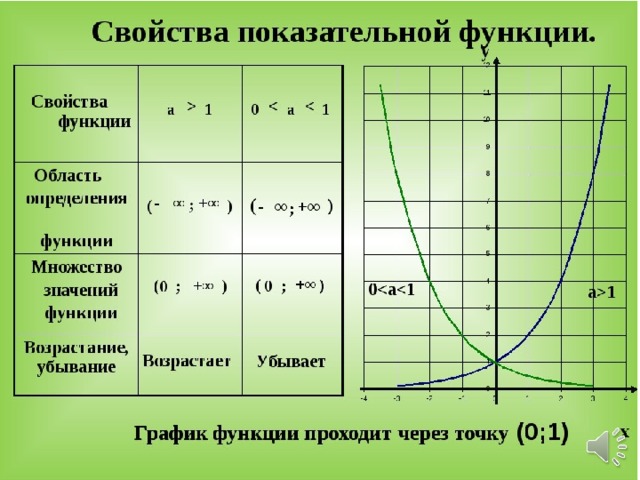
Линейные функции. Это функции вида:
y = m x + b ,где m и b — константы. Типичное использование для линейные функции преобразуют одну величину или набор единиц в другую. Графики этих функций представляют собой прямых линий . м — уклон, b — точка пересечения y . Если м положительно, то линия поднимается вправо, а если м отрицательно, тогда линия падает вправо. Линейные функции подробно описаны здесь.
Квадратичные функции. Это функции вида:
у = а х 2 + б х + с ,где a , b и c — константы. Их графики называются парабол . Это следующий простейший тип функции после линейной функции. Падающие предметы движутся по параболическим траекториям. Если a — положительное число, то парабола открывается вверх, а если a — отрицательное число, тогда парабола открывается вниз.
 Квадратичные функции подробно описаны здесь.
Квадратичные функции подробно описаны здесь.Силовые функции. Это функции вида:
y = a x b ,где a и b — константы. Они получили свое название от факта что переменная x возведена в некоторую степень. Многие физические законы (например, гравитационная сила как функция расстояния между двумя объектами или изгиб балки в зависимости от нагрузки на нее) имеют вид степенных функций. Будем считать, что a = 1 и посмотрите на несколько случаев для b :
Степень b является положительным целым числом. См. график справа. Когда x = 0, все эти функции равны нулю. Когда x большое и положительные они все большие и положительные. Когда x большое и отрицательное тогда те, у кого четные степени, большие и положительные, а числа с нечетными степенями большие и отрицательные.
Мощность b — отрицательное целое число. См. график справа.
Когда x = 0, эти функции подвергаются делению на ноль и, следовательно,
все бесконечны. Когда x большое и
положительные они маленькие и положительные. Когда x большое и отрицательное
тогда те, у которых четные степени, малы и положительны, а те, у которых
нечетные степени малы и отрицательны.
См. график справа.
Когда x = 0, эти функции подвергаются делению на ноль и, следовательно,
все бесконечны. Когда x большое и
положительные они маленькие и положительные. Когда x большое и отрицательное
тогда те, у которых четные степени, малы и положительны, а те, у которых
нечетные степени малы и отрицательны.
Степень b представляет собой дробь от 0 до 1. См. график справа. Когда x = 0, все эти функции равны нулю. Кривые вертикальны в начала координат, и по мере увеличения x они увеличиваются, но изгибаются к оси x .
Функция мощности подробно обсуждается здесь.
Полиномиальные функции. Это функции вида:
y = a n · x n + a n -1 · x n -1 + … + a 2 · x 2 + a 1 · x + a 0 ,где a n , a n −1 , … , и 2 , и 1 , a 0 — константы.
 Допускаются только целые степени x .
Наивысшая степень x , которая встречается, называется степенью многочлена.
На графике показаны примеры полиномов степени 4 и степени 5.
Градус дает максимальное количество « подъемов и спадов», которые
многочлен может иметь, а также максимальное количество пересечений x ось, которую он может иметь.
Допускаются только целые степени x .
Наивысшая степень x , которая встречается, называется степенью многочлена.
На графике показаны примеры полиномов степени 4 и степени 5.
Градус дает максимальное количество « подъемов и спадов», которые
многочлен может иметь, а также максимальное количество пересечений x ось, которую он может иметь.Полиномы полезны для создания гладких кривых в компьютерной графике. приложений и для аппроксимации других типов функций. Полиномы подробно описаны здесь.
Рациональные функции. Эти функции являются отношением двух многочленов. Одна область исследования, где они важны при анализе устойчивости механических и электрических систем. (который использует преобразования Лапласа).
Когда многочлен в
знаменатель равен нулю, тогда рациональная функция становится бесконечной, как указано
вертикальной пунктирной линией (называемой асимптотой ) на его графике. Для
пример справа
это бывает когда x = -2 и когда x = 7.
Когда x становится очень большим, кривая может выровняться. Кривая справа выходит на уровень y = 5.
На графике справа показан еще один пример рациональной функции. У этого есть деление на ноль при x = 0. Он не выравнивается, но приближается к прямой линии y = x , когда x — это большое значение, на что указывает пунктирная линия (еще одна асимптота).
Экспоненциальные функции. Это функции вида:
y = a b x ,где x в экспоненте (не в базе, как в случае с силовыми функциями) а a и b являются константами. (Обратите внимание, что только b возводится в степень x , а не a .) Если основание b больше 1, то результат экспоненциальный рост. Многие физические величины растут экспоненциально (например, популяции животных и денежные потоки). на процентном счете).

Если основание b меньше 1, то результат экспоненциальный спад. Многие величины затухают экспоненциально (например, солнечный свет, достигающий заданной глубины океана и скорость тела, замедляющегося из-за трения).
Экспоненциальные функции подробно описаны здесь.
Логарифмические функции. Существует много эквивалентных способов определения логарифмических функций. Мы будем определить их в виде:
y = a ln ( x ) + b ,где x в натуральном логарифме, а a и b константы. Они определены только для положительных x . Для маленьких x они отрицательны, а для больших x они положительны, но остаются маленькими. Логарифмические функции точно описывают реакцию человеческого уха на звуки различной громкости и реакцию человеческого глаза на свет различной яркость. Логарифмические функции подробно описаны здесь.

Синусоидальные функции. Это функции вида:
y = a sin ( b x + c ),где a , b и c — константы. Синусоидальные функции полезны для описания всего, что имеет форму волны по отношению к положение или время. Примерами являются волны на воде, высота прилива во время течения. день и переменный ток в электричестве. Параметр а (называемая амплитудой) влияет на высоту волны, b (угловая скорость) влияет на ширину волны и c (фазовый угол) сдвигает волну влево или вправо. Синусоидальные функции подробно описаны здесь.
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Графики экспоненциальных функций | Алгебра и тригонометрия
Цели обучения
- График экспоненциальных функций.
 {x},[/latex][латекс]\,b\,[/latex] равно постоянный коэффициент функции. Это означает, что при увеличении ввода на 1 выходное значение будет произведением базы и предыдущего вывода, независимо от значения [латекс]\,а.[/латекс] 9{х}[/латекс] [латекс]8[/латекс] [латекс]4[/латекс] [латекс]2[/латекс] [латекс]1[/латекс] [латекс]\фракция{1}{2}[/латекс] [латекс]\фракция{1}{4}[/латекс] [латекс]\фракция{1}{8}[/латекс]
{x},[/latex][латекс]\,b\,[/latex] равно постоянный коэффициент функции. Это означает, что при увеличении ввода на 1 выходное значение будет произведением базы и предыдущего вывода, независимо от значения [латекс]\,а.[/латекс] 9{х}[/латекс] [латекс]8[/латекс] [латекс]4[/латекс] [латекс]2[/латекс] [латекс]1[/латекс] [латекс]\фракция{1}{2}[/латекс] [латекс]\фракция{1}{4}[/латекс] [латекс]\фракция{1}{8}[/латекс]Опять же, поскольку ввод увеличивается на 1, каждое выходное значение является произведением предыдущего вывода и базы, или постоянным отношением[латекс]\,\фракция{1}{2}.[/латекс]
Обратите внимание на таблицу, что
9{x},[/latex][latex]\,b>0,[/latex][latex]\,b\ne 1,[/latex]имеет следующие характеристики:- функция «один к одному»
- горизонтальная асимптота:[латекс]\,y=0[/латекс]
- домен:[латекс]\,\левый(–\infty , \infty \правый)[/латекс]
- диапазон:[латекс]\,\влево(0,\infty\вправо)[/латекс]
- x- перехват: нет
- y- перехват:[латекс]\,\влево(0,1\вправо)\,[/латекс]
- увеличивается, если[латекс]\,b>1[/латекс]
- уменьшается, если[латекс]\,b<1[/латекс] 9{x},[/latex] нарисуйте график функции.

- Создайте таблицу точек.
- Нанесите на график хотя бы [латекс]\,3\,[/латекс]точку из таблицы, включая и -intercept[латекс]\,\влево(0,1\вправо).[/латекс]
- Нарисуйте плавную кривую через точки.
- Укажите домен,[latex]\,\left(-\infty ,\infty \right),[/latex]диапазон,[latex]\,\left(0,\infty \right),[/latex] и горизонтальная асимптота, [латекс]\,у=0.[/латекс]
Эскиз графика экспоненциальной функции формы 9{x}-3:[/латекс]
- Перехват y- сдвигает вниз [латекс]\,3\,[/латекс]единицы к [латекс]\,\влево(0,-2\вправо).[/латекс]
- Асимптота также смещается вниз [latex]\,3\,[/latex]единицы до [latex]\,y=-3.[/latex]
- Диапазон становится [латекс]\,\влево(-3,\infty \вправо).[/латекс]
График горизонтального смещения
Следующее преобразование происходит, когда мы добавляем константу[latex]\,c\,[/latex] на вход родительской функции[latex]\,f\left(x\right)= {b}^{x},[/latex] дает нам сдвиг по горизонтали[latex]\,c\,[/latex]единиц в 9{x+c}+d\,[/latex]for[latex]\,x,[/latex] используйте графический калькулятор для приближенного решения.

- Нажмите [Y=] . Введите данное показательное уравнение в строку под названием « Y 1 = ».
- Введите заданное значение для [латекс]\,f\влево(х\вправо)\,[/латекс] в строку с заголовком « Y 2 = ».
- Нажмите [ОКНО] . Отрегулируйте ось y так, чтобы она включала значение, введенное для “ Y 2 = ”.
- Нажмите [GRAPH] , чтобы просмотреть график экспоненциальной функции вместе с линией для указанного значения [latex]\,f\left(x\right).[/latex]
- Чтобы найти значение [латекс]\,х,[/латекс], мы вычисляем точку пересечения. Нажмите [2ND] , затем [CALC] . Выберите «пересечение» и нажмите [ENTER] три раза. Точка пересечения дает значение x для указанного значения функции. 9{x}[/latex]
- растягивается по вертикали с коэффициентом [latex]\,a\,[/latex]if[latex]\,|a|>1.
 ( -1), 1), домен остается (0, бесконечность), а диапазон остается (-бесконечность, бесконечность). Во втором столбце показан сдвиг уравнения g(x)=log_b(x) влево, когда b>1, и отмечены следующие изменения: отраженная функция убывает по мере того, как x движется от 0 до бесконечности, асимптота остается x=0, x-пересечение изменяется на (-1, 0), ключевая точка изменяется на (-b, 1), домен изменяется на (-бесконечность, 0), а диапазон остается (-бесконечность, бесконечность)».> 9{x},[/latex][latex]\,b>1,[/latex]это
( -1), 1), домен остается (0, бесконечность), а диапазон остается (-бесконечность, бесконечность). Во втором столбце показан сдвиг уравнения g(x)=log_b(x) влево, когда b>1, и отмечены следующие изменения: отраженная функция убывает по мере того, как x движется от 0 до бесконечности, асимптота остается x=0, x-пересечение изменяется на (-1, 0), ключевая точка изменяется на (-b, 1), домен изменяется на (-бесконечность, 0), а диапазон остается (-бесконечность, бесконечность)».> 9{x},[/latex][latex]\,b>1,[/latex]это- сдвинутых по горизонтали[latex]\,c\,[/latex]единиц влево.
- растянуто по вертикали с коэффициентом [латекс]\,|а|\,[/латекс]если[латекс]\,|а|>0.[/латекс]
- сжато по вертикали в [латекс]\,|а|\,[/латекс]если[латекс]\,0<|а|<1.[/латекс]
- смещено по вертикали[латекс]\,д\,[/латекс]единиц.
- отражается относительно оси x- , когда [латекс]\,а<0.[/латекс]
Обратите внимание, что порядок сдвигов, преобразований и отражений соответствует порядку операций.
 {x}[/latex] 9{x}\,[/latex] имеет пересечение y- в [latex]\,\left(0, 1\right),[/latex]домен[latex]\,\left(-\infty , \ infty \right),[/latex]range[latex]\,\left(0, \infty \right),[/latex] и горизонтальная асимптота[latex]\,y=0.\,[/latex]См. ( Фигура).
{x}[/latex] 9{x}\,[/latex] имеет пересечение y- в [latex]\,\left(0, 1\right),[/latex]домен[latex]\,\left(-\infty , \ infty \right),[/latex]range[latex]\,\left(0, \infty \right),[/latex] и горизонтальная асимптота[latex]\,y=0.\,[/latex]См. ( Фигура). - Если[latex]\,b>1,[/latex]функция возрастает. Левый хвост графика будет приближаться к асимптоте[латекс]\,у=0,[/латекс], а правый хвост неограниченно увеличиваться.
- Если[латекс]\,0
- (a + b) 2 = a 2 + b 2 + 2ab
- (a – b) 2 = a 2 + b 2 – 2ab
- (A + B) 2 = A 2 + B 2 = A 2 + B 2 + 2AB 6 + 2 + 2 + 2 + 2 + 2 + 2 . – б) 2 = а 2 + б 2 – 2аб
Раздел Упражнения
Вербальный
Какую роль играет горизонтальная асимптота экспоненциальной функции, говоря нам о конечном поведении графика?
Показать решение
В чем преимущество знания того, как алгебраически распознавать преобразования графика родительской функции?
Алгебраический
График [латекс]\,f\left(x\right)={3}^{x}\,[/latex]отражен относительно 9{x-20}[/latex] смещено влево[latex]\,2\,[/latex]единиц, растянуто по вертикали с коэффициентом[latex]\,4,[/latex]отражено относительно x — оси, а затем сдвинуты вниз[латекс]\,4\,[/латекс]единицы.
 Каково уравнение новой функции,[латекс]\,г\влево(х\вправо)?\,[/латекс]Укажите ее и — точку пересечения, домен и диапазон.
Каково уравнение новой функции,[латекс]\,г\влево(х\вправо)?\,[/латекс]Укажите ее и — точку пересечения, домен и диапазон.Показать решение
Графический
Для следующих упражнений начертите график функции и ее отражения относительно оси y на тех же осях и задайте 9{x}.[/latex]
Рисунок 13.
Какой график имеет наибольшее значение для [latex]\,b?[/latex]
Показать решение
Какой график имеет наименьшее значение для [latex]\,b?[/latex]
Какой график имеет наибольшее значение для [latex]\,a?[/latex]
Показать решение
Какой график имеет наименьшее значение для [латекс]\,а?[/латекс]
Для следующих упражнений нарисуйте функцию и ее отражение относительно оси x на тех же осях. 9{x}.\,[/latex]Затем напишите функцию, которая получается в результате данного преобразования.

Сдвиг [латекс]f\влево(х\вправо)[/латекс] на 4 единицы вверх
Сдвиг[латекс]\,f\влево(х\вправо)\,[/латекс]3 единицы вниз
Показать решение
Сдвиг[латекс]\,f\влево(х\вправо)\,[/латекс]2 единицы влево
Сдвиг[латекс]\,f\влево(х\вправо)\,[/латекс]5 единиц вправо
Показать решение
Reflect[латекс]\,f\left(x\right)\,[/latex]о оси x
Reflect[латекс]\,f\left(x\right)\,[/latex ] о 9{x}\,[/latex]для любого действительного числа n и действительного числа[latex]\,b>0.[/latex]
Показать решение
Докажите предположение, сделанное в предыдущем упражнении.
Найдите степенную функцию, на которую похож график f при больших значениях |x|, учитывая функцию f(x) = (x + 6)2 (x — 2)2
Математика — это не только числа, но и речь идет о различных вычислениях с использованием чисел и переменных. Это то, что в основном известно как алгебра.
 Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Цифры могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.
Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Цифры могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.Экспоненты и степени
используемые для упрощения сложных вычислений, включающих многократное самоумножение, самоумножение — это в основном числа, умноженные сами на себя. Например, 7 × 7 × 7 × 7 × 7 можно просто записать как 7 5 . Здесь 7 — базовое значение, 5 — показатель степени, а значение равно 16807. 11 × 11 × 11 можно записать как 11 3 , здесь 11 — базовое значение, а 3 — показатель степени или степень числа 11. Значение 11 3 равно 1331.
умножается на себя. Если выражение записано как cx y , где c — константа, c — коэффициент, x — основание, а y — показатель степени. Если число, например p, умножить n раз, то n будет показателем степени p.
 Это будет записано как
Это будет записано какp × p × p × p … n раз = p n
Функции
Функцию можно определить как набор правил, относящихся к данному набору входных данных, которые обеспечивают некоторые возможные выходные данные. Только те выражения обозначаются как функции, в которых есть один выход для одного входа. Могут ли быть два входа для одного и того же выхода? Да. Однако не может быть двух выходов для одного входа.
Функции могут быть представлены как f(x), g(x), h(x) и т. д. Здесь f(x) — результат для заданного входного значения полинома. Например, значение f(x) при x = -2 в функции f(x) = 2x + 20 будет равно 16. Его можно получить, подставив значение x в выражение и решив его.
Функции умножения и деления
Чтобы умножать или делить две функции, первое требование состоит в том, чтобы понять, что умножение и деление являются основными математическими операциями умножения и деления. Точно так же, как числа умножаются или делятся, точно так же умножаются и делятся многочлены.
 Их можно представить как f(x).g(x) для умножения и f(x)/g(x) для деления.
Их можно представить как f(x).g(x) для умножения и f(x)/g(x) для деления.Степенная функция
Произведение действительного числа, коэффициента и переменной, возведенное в фиксированное действительное или натуральное число, называется степенной функцией. Простыми словами, степенную функцию можно обозначить как переменную, возведенную в действительное число. Степенная функция представлена как y = x R , где R — любое действительное число. Например, y = x 2 является степенной функцией, y = 1/x также является степенной функцией и так далее.
Вопрос: Найдите степенную функцию, на которую похож график f при больших значениях |x|, учитывая функцию f(x) = (x + 6)
2 (x – 2) 2 .Решение:
Сначала разверните выражение в правой части, используя следующую формулу:
f(x) = (x 2 3x 1 x 2 0 2 + 4 — 4x)
Теперь, умножьте оба термина,
F (x) = (x 4 + 4x 2 — 4x 3 + 36x 2 + 144 –144x + 12x + 12x + 12x + 12x + 12x + 12x + 12x + 12x + 12x + 36x 2 + 144 – 144 – 144x 144x + 36x 2 .
 3 + 48x – 48x 2 )
3 + 48x – 48x 2 )f(x) = x 4 + 8x 3 – 18x 2 – 96x + 144)
0 Поскольку степень функции очевидна 0 4. Следовательно, степенная функция, на которую похож график f при больших значениях |x| х 4 .Аналогичные задачи
Вопрос 1. Дана функция f(x) = x 5 + 56x 4 – 78x + 2. Найдите степенную функцию, на которую похож график f.
Решение:
Поскольку функция, указанная в вопросе, уже расширена. Таким образом, нет необходимости в расширении функции.
f(x) = x 5 + 56x 4 – 78x + 2
Поскольку ясно, что степень функции равна 5. Следовательно, степенная функция, на которую похож график f, равна x 5 .
Вопрос 2: Дана функция f(x) = (x + 1) 2 (x – 1) 2 . Найдите степенную функцию, на которую похож график f при больших значениях |x|.

Решение:
Сначала разверните экспрессию на RH, используя следующую формулу,
f(x) = (x 2 + 1 + 2x)(x 2 + 1 – 2x)
Теперь умножьте оба члена,
f(x) = (x 4 + x 2 — 2x 3 + x 2 + 1 — 2x + 2x 3 + 2x — 4x 2 )
F (x) = x 4 — 2x 918
F (x) = x 4 — 2x
2 9181818181818181818181818 гг.Поскольку ясно, что степень функции равна 4. Следовательно, степенная функция, на которую похож график f при больших значениях |x| х 4 .
Вопрос 3: Дана функция f(x) = (x 5 ) (x + 3) 2 .


 10.17
10.17
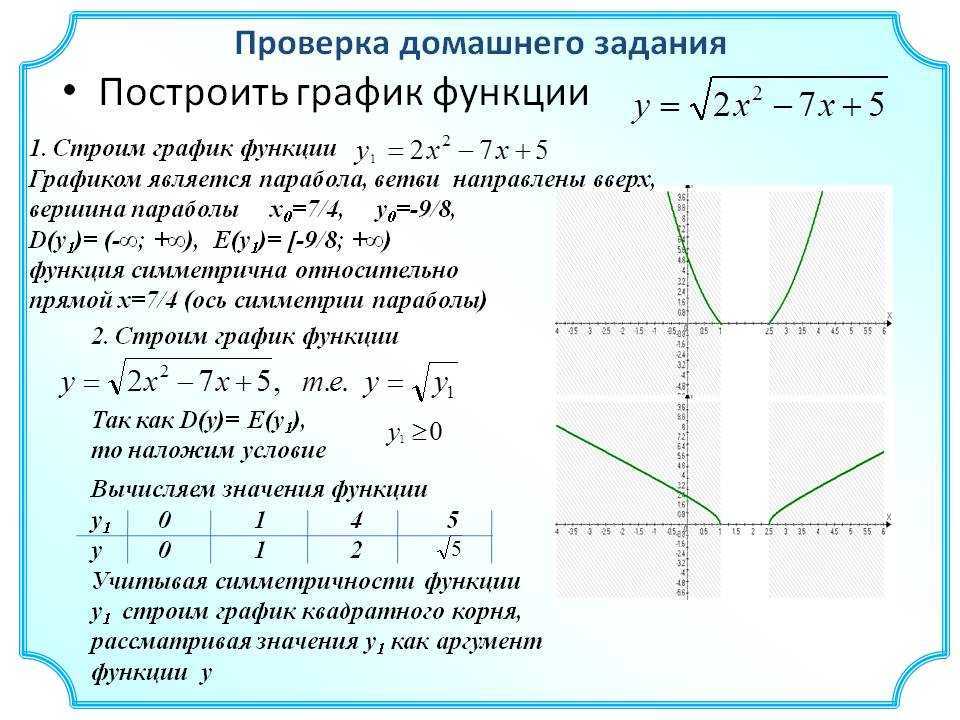 е.x \in [0;+ \infty)$
е.x \in [0;+ \infty)$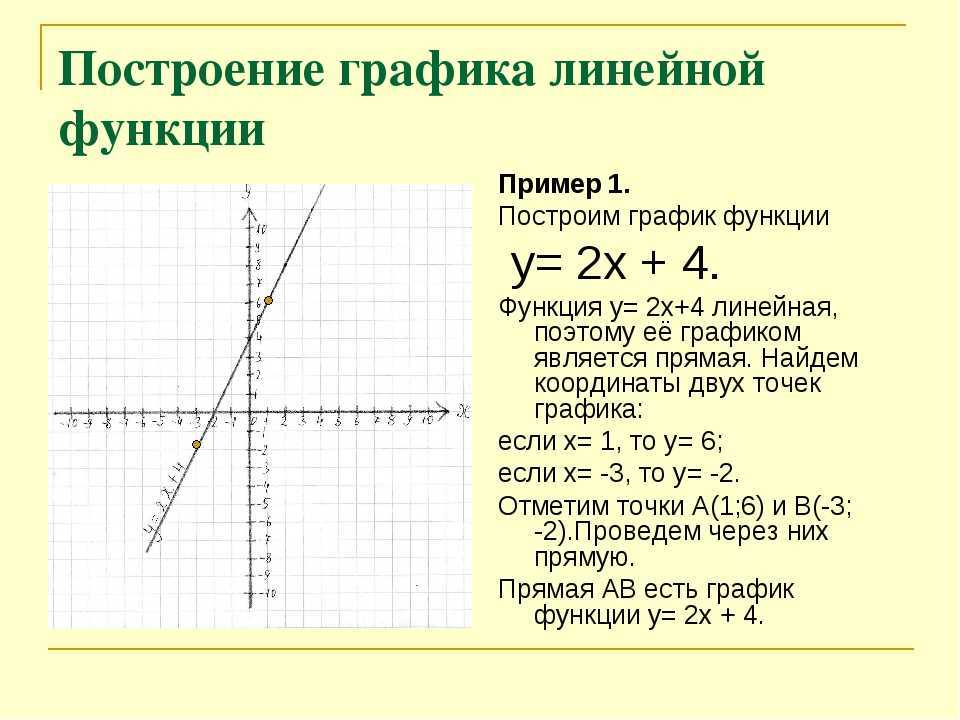
 Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики.
Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики.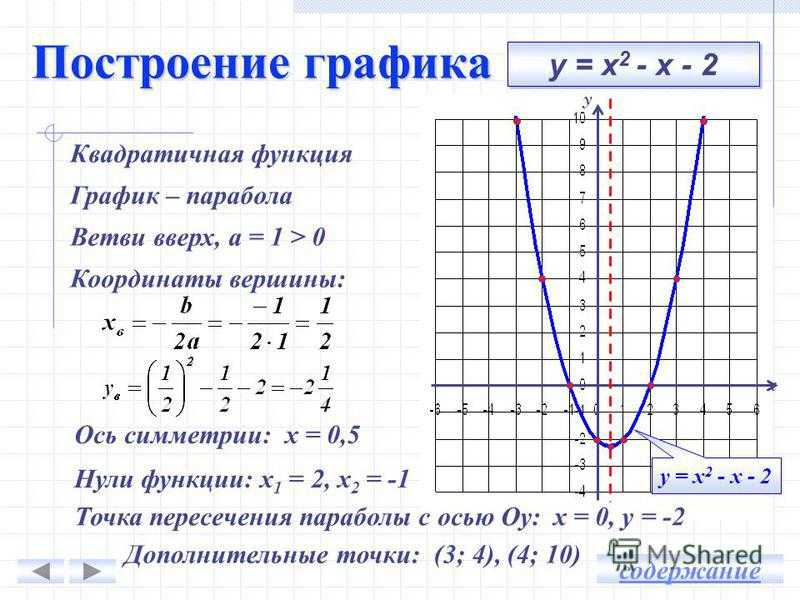 Во вкладке Шрифт
установим размер шрифта 8пт.
Во вкладке Шрифт
установим размер шрифта 8пт.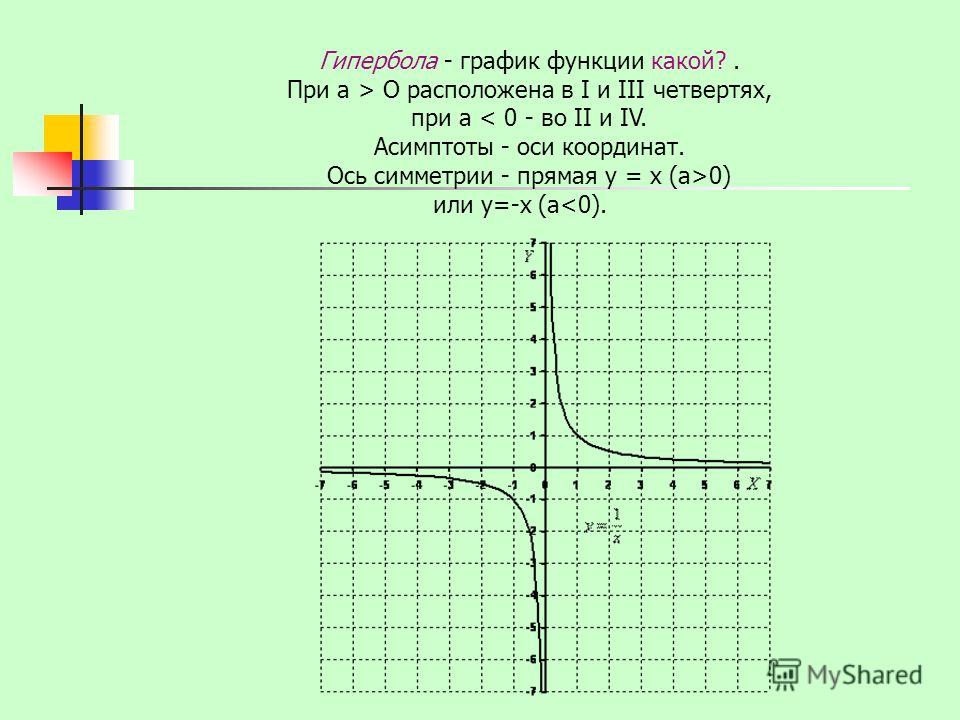 3
3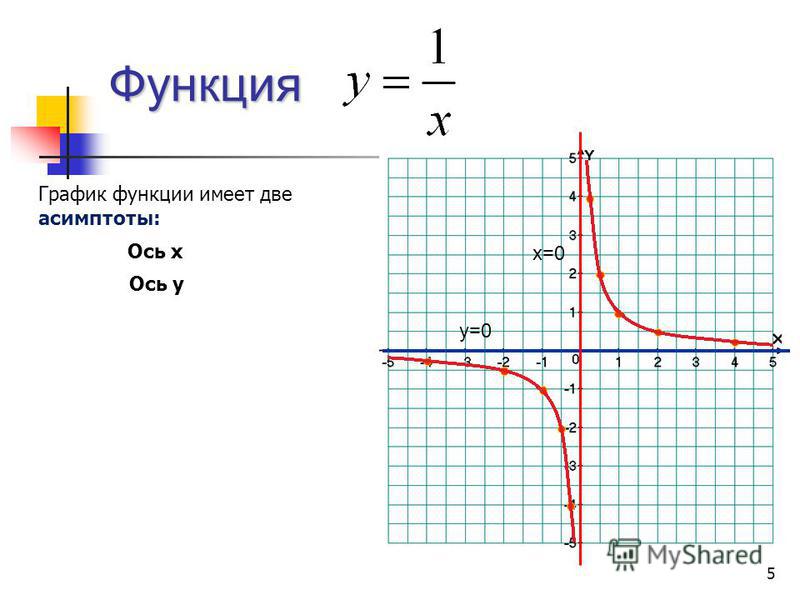 Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики.
Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики.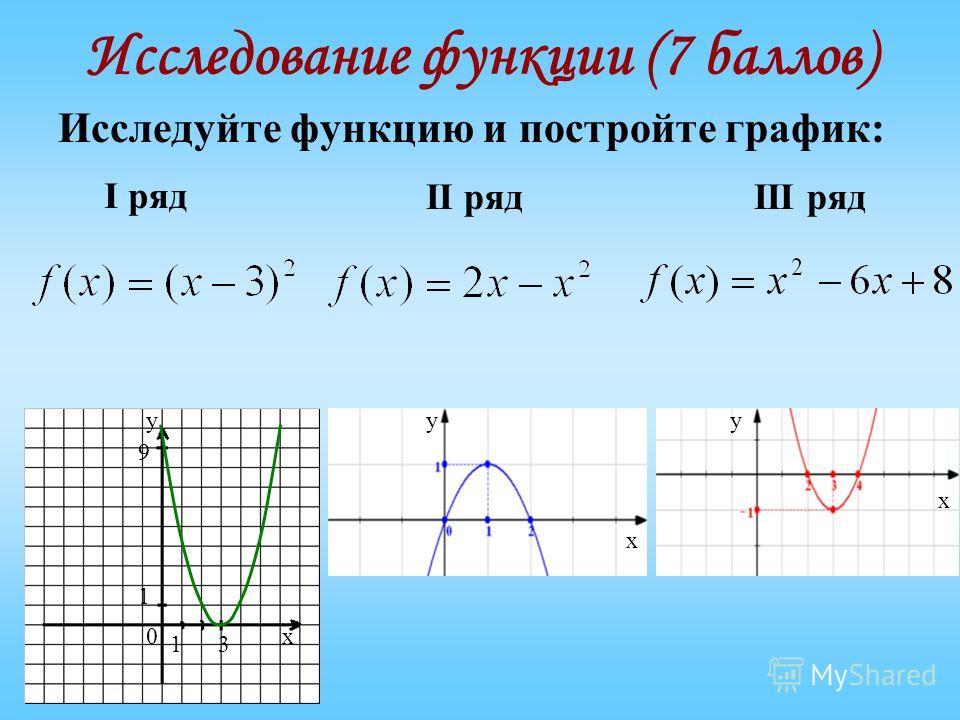 Верхний колонтитул слева: график функции у = x3
Верхний колонтитул слева: график функции у = x3
 {x},[/latex][латекс]\,b\,[/latex] равно постоянный коэффициент функции. Это означает, что при увеличении ввода на 1 выходное значение будет произведением базы и предыдущего вывода, независимо от значения [латекс]\,а.[/латекс] 9{х}[/латекс] [латекс]8[/латекс] [латекс]4[/латекс] [латекс]2[/латекс] [латекс]1[/латекс] [латекс]\фракция{1}{2}[/латекс] [латекс]\фракция{1}{4}[/латекс] [латекс]\фракция{1}{8}[/латекс]
{x},[/latex][латекс]\,b\,[/latex] равно постоянный коэффициент функции. Это означает, что при увеличении ввода на 1 выходное значение будет произведением базы и предыдущего вывода, независимо от значения [латекс]\,а.[/латекс] 9{х}[/латекс] [латекс]8[/латекс] [латекс]4[/латекс] [латекс]2[/латекс] [латекс]1[/латекс] [латекс]\фракция{1}{2}[/латекс] [латекс]\фракция{1}{4}[/латекс] [латекс]\фракция{1}{8}[/латекс]

 ( -1), 1), домен остается (0, бесконечность), а диапазон остается (-бесконечность, бесконечность). Во втором столбце показан сдвиг уравнения g(x)=log_b(x) влево, когда b>1, и отмечены следующие изменения: отраженная функция убывает по мере того, как x движется от 0 до бесконечности, асимптота остается x=0, x-пересечение изменяется на (-1, 0), ключевая точка изменяется на (-b, 1), домен изменяется на (-бесконечность, 0), а диапазон остается (-бесконечность, бесконечность)».> 9{x},[/latex][latex]\,b>1,[/latex]это
( -1), 1), домен остается (0, бесконечность), а диапазон остается (-бесконечность, бесконечность). Во втором столбце показан сдвиг уравнения g(x)=log_b(x) влево, когда b>1, и отмечены следующие изменения: отраженная функция убывает по мере того, как x движется от 0 до бесконечности, асимптота остается x=0, x-пересечение изменяется на (-1, 0), ключевая точка изменяется на (-b, 1), домен изменяется на (-бесконечность, 0), а диапазон остается (-бесконечность, бесконечность)».> 9{x},[/latex][latex]\,b>1,[/latex]это {x}[/latex] 9{x}\,[/latex] имеет пересечение y- в [latex]\,\left(0, 1\right),[/latex]домен[latex]\,\left(-\infty , \ infty \right),[/latex]range[latex]\,\left(0, \infty \right),[/latex] и горизонтальная асимптота[latex]\,y=0.\,[/latex]См. ( Фигура).
{x}[/latex] 9{x}\,[/latex] имеет пересечение y- в [latex]\,\left(0, 1\right),[/latex]домен[latex]\,\left(-\infty , \ infty \right),[/latex]range[latex]\,\left(0, \infty \right),[/latex] и горизонтальная асимптота[latex]\,y=0.\,[/latex]См. ( Фигура). Каково уравнение новой функции,[латекс]\,г\влево(х\вправо)?\,[/латекс]Укажите ее и — точку пересечения, домен и диапазон.
Каково уравнение новой функции,[латекс]\,г\влево(х\вправо)?\,[/латекс]Укажите ее и — точку пересечения, домен и диапазон.
 Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Цифры могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.
Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Цифры могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д. Это будет записано как
Это будет записано как Их можно представить как f(x).g(x) для умножения и f(x)/g(x) для деления.
Их можно представить как f(x).g(x) для умножения и f(x)/g(x) для деления. 3 + 48x – 48x 2 )
3 + 48x – 48x 2 )