Решением уравнения (7) является выражение:
\[\varphi ={\varphi }_0{\cos \left({\omega }_0t+\alpha \right)\left(8\right),\ }\]
где $\alpha $ — начальная фаза колебаний; ${\varphi }_0$ — амплитуда колебаний.
Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической или квантовой механики.
Примеры задач с математическим маятником
Пример 1
Задание. Каков период (T) колебаний математического маятника, который подвешен к потолку кабины лифта, движущегося вертикально вниз 1) равномерно; 2) с ускорением $a$? Длина нити маятника равна $l$.
Решение. Сделаем рисунок.
Период колебаний при равномерном движении математического маятника равен:
\[T=2\pi \sqrt{\frac{l}{g}}\left(1.1\right).\]
При движении с ускорением вниз период равен:
\[T=2\pi \sqrt{\frac{l}{g-a}}\left(1. 2m\ Дж$
2m\ Дж$
Читать дальше: механика.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Математический и пружинный маятники. Энергия колебаний
Физика. Уровень стандарта. 10 класс. Барьяхтар
Колебательные движения очень разнообразны. При этом существует «классика» колебательных движений — они описаны сотни лет назад, их изучением занимались Галилео Галилей (1564-1642) и Христиан Гюйгенс (1629-1695). Это колебания пружинного и математического маятников. Именно о них пойдет речь в данном параграфе.
1. Колебания пружинного маятника
Пружинный маятник — это колебательная система, представляющая собой закрепленное на пружине тело.
Рассмотрим колебания горизонтального пружинного маятника — тележки массой m, закрепленной на пружине жесткостью k.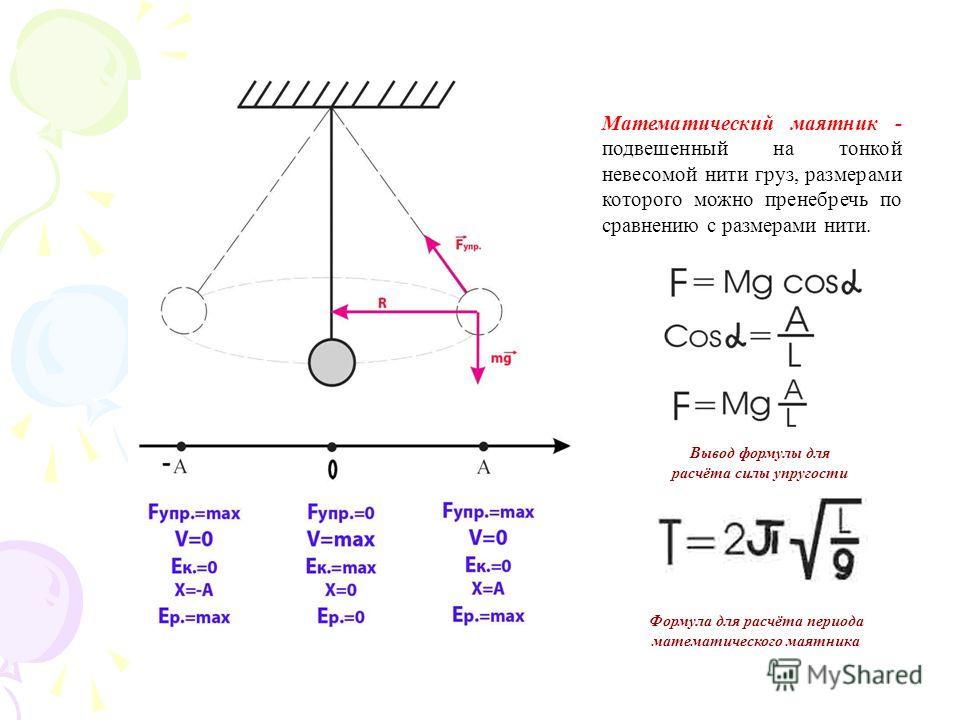
Колебания пружинного маятника
Обратите внимание! В течение всего времени колебания сила упругости направлена в сторону, противоположную смещению тележки, — сила упругости все время «толкает» тележку к положению равновесия.
Итак, причины свободных колебаний пружинного маятника:
- 1) действующая на тело сила всегда направлена к положению равновесия;
- 2) колеблющееся тело инертно, поэтому оно не останавливается в положении равновесия (когда равнодействующая сил становится равной нулю), а продолжает движение в том же направлении.
2. Как вычислить период колебаний пружинного маятника
Обратите внимание! Период колебаний пружинного маятника не зависит ни от амплитуды колебаний, ни от места расположения маятника (на поверхности Земли или Луны, в космическом корабле и т.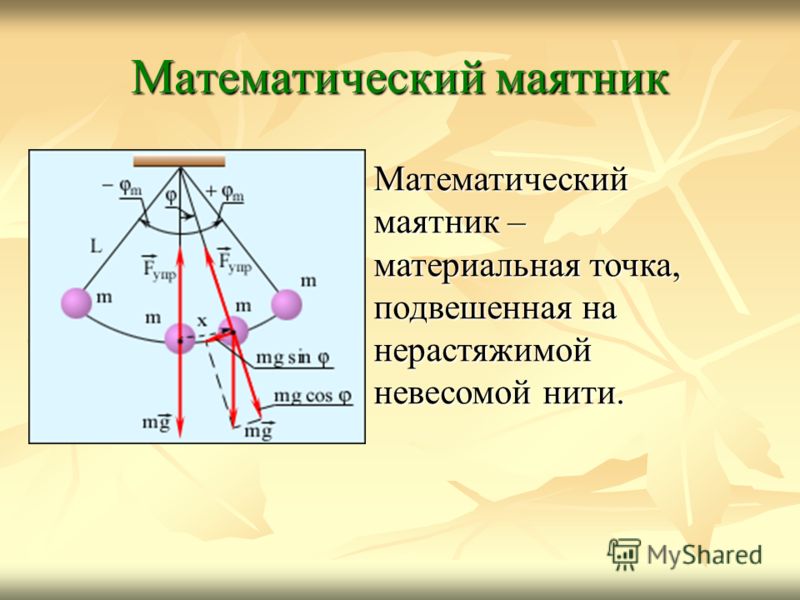 д.), — он определяется только характеристиками самой колебательной системы «тело — пружина». Если период Т колебаний тела и жесткость — пружины известны, можно найти массу m тела. Такой способ определения массы используют в состоянии невесомости, когда обычные весы не работают.
д.), — он определяется только характеристиками самой колебательной системы «тело — пружина». Если период Т колебаний тела и жесткость — пружины известны, можно найти массу m тела. Такой способ определения массы используют в состоянии невесомости, когда обычные весы не работают.
3. Что называют математическим маятником
Любое твердое тело, которое совершает или может совершать колебания относительно оси, проходящей через точку подвеса, называют физическим маятником. Примером может быть игрушка, подвешенная на нити в салоне автомобиля. Если игрушку вывести из положения равновесия, она начнет колебаться. Однако изучать такие колебания сложно: их характер определяется размерами и формой игрушки, свойствами нити и другими факторами.
Чтобы размеры тела не влияли на характер его колебаний, следует взять нить, длина которой намного больше размеров тела, а масса незначительна по сравнению с его массой. В таком случае тело можно считать материальной точкой. А чтобы во время колебаний тело все время находилось на одинаковом расстоянии от точки подвеса, нить должна быть нерастяжимой.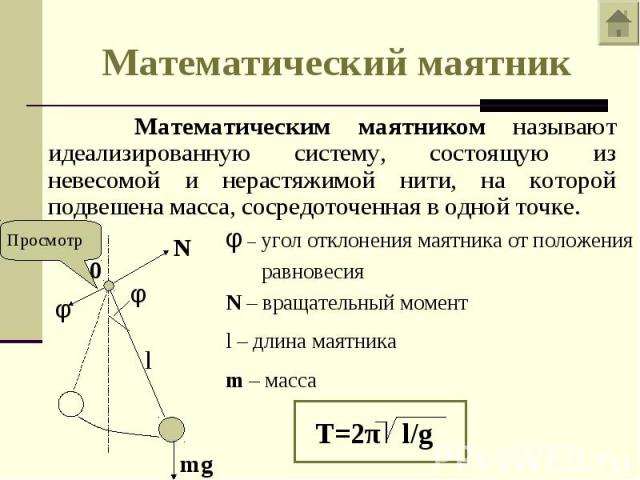 Таким образом будет получена физическая модель — математический маятник.
Таким образом будет получена физическая модель — математический маятник.
Математический маятник — это физическая модель колебательной системы, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити, и гравитационного поля.
4. Колебания математического маятника
Возьмем небольшой, но достаточно тяжелый шарик и подвесим его на длинной нерастяжимой нити — такой маятник можно считать математическим. Если отклонить шарик от положения равновесия и отпустить, то в результате действия гравитационного поля Земли (силы тяжести) и силы натяжения нити шарик начнет колебаться около положения равновесия. Поскольку сопротивление воздуха пренебрежимо мало, а силы, действующие в системе, являются консервативными, полная механическая энергия шарика будет сохраняться: потенциальная энергия шарика будет превращаться в его кинетическую энергию, и наоборот.
Рис. 20.2. Колебания математического маятника — свободные, так как происходят под действием внутренних сил системы. Причины, по которым математический маятник совершает свободные колебания, те же, что и в случае колебаний пружинного маятника: 1) равнодействующая сил, приложенных к телу, всегда направлена к положению равновесия; 2) колеблющееся тело инертно
Причины, по которым математический маятник совершает свободные колебания, те же, что и в случае колебаний пружинного маятника: 1) равнодействующая сил, приложенных к телу, всегда направлена к положению равновесия; 2) колеблющееся тело инертно
• Рассмотрите колебательное движение шарика (рис. 20.2). Объясните причины его движения. Какие происходят превращения энергии?
5. Как вычислить период колебаний математического маятника
Математический маятник, отклоненный от положения равновесия на небольшой угол (3-5°), будет совершать гармонические колебания, то есть ускорение его движения все время будет прямо пропорционально смещению и направлено в сторону, противоположную смещению: ax = -ω2x.
где l — длина маятника; g — ускорение свободного падения.
Данную формулу впервые получил в XVII в. голландский ученый Христиан Гюйгенс, поэтому ее называют формулой Гюйгенса.
Период колебаний математического маятника не зависит от массы маятника, а определяется только длиной нити и ускорением свободного падения в том месте, где расположен маятник.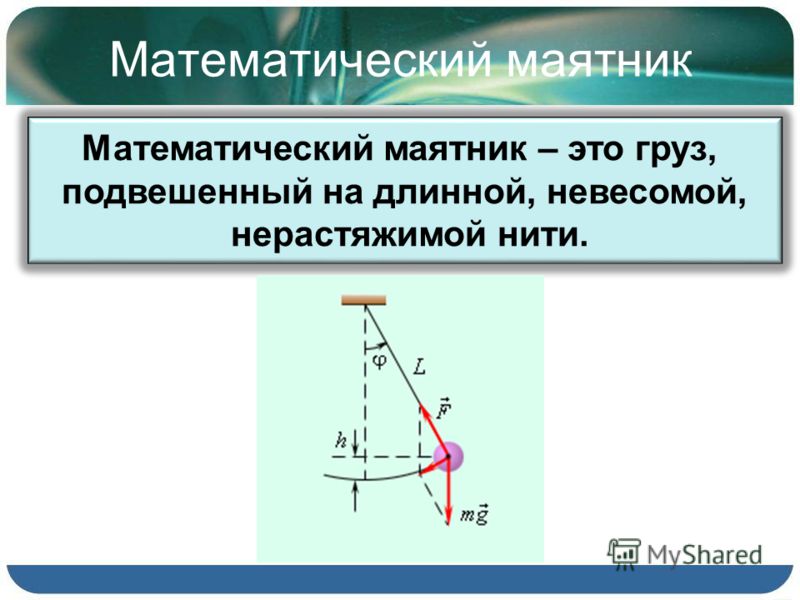
6. Учимся решать задачи
Подводим итоги
• Во время свободных колебаний маятника его потенциальная и кинетическая энергии непрерывно изменяются: потенциальная энергия максимальна в точках поворота и равна нулю в момент прохождения маятником положения равновесия; кинетическая энергия в точках поворота равна нулю и достигает максимального значения в момент прохождения маятником положения равновесия.
Контрольные вопросы
1. Опишите колебания пружинного маятника. Почему тело не останавливается, когда проходит положение равновесия? 2. По какой формуле определяют период колебаний пружинного маятника? 3. Дайте определение математического маятника. 4. Опишите колебания математического маятника. По какой формуле находят период его колебаний? 5. Какие преобразования энергии происходят во время колебаний пружинного маятника? математического маятника? 6.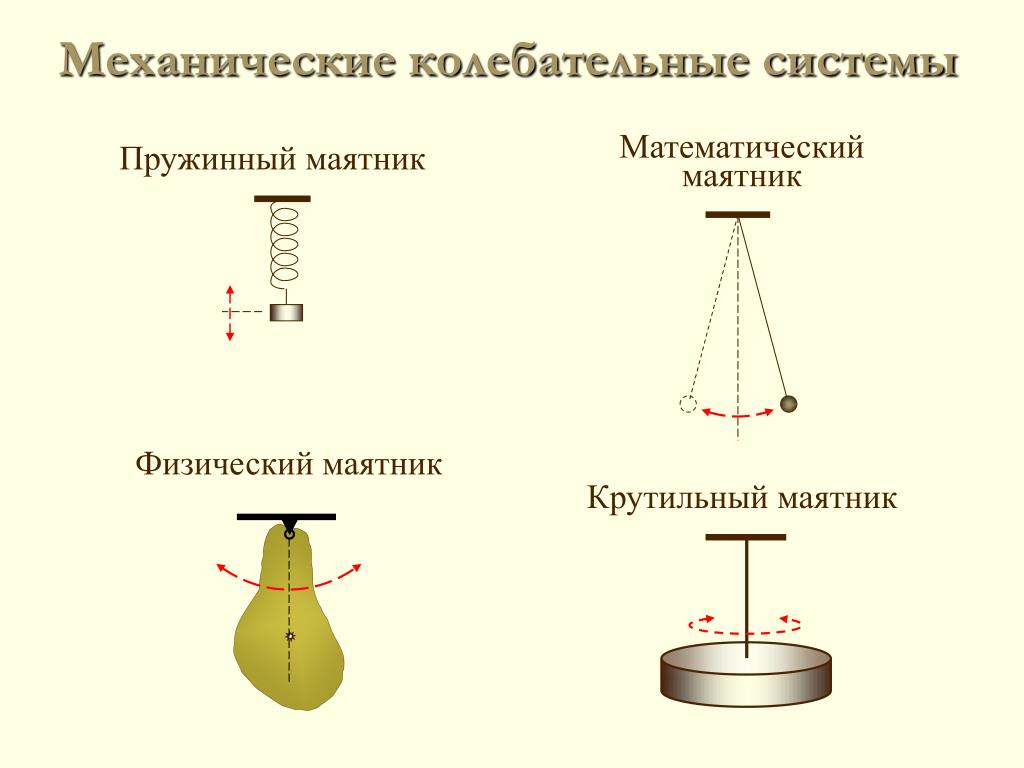
Упражнение № 20
1. В системе «тележка — пружина» происходят свободные колебания. Как изменится период этих колебаний, если: 1) увеличить амплитуду колебаний? 2) уменьшить массу тележки? 3) увеличить жесткость пружины?
2. Будет ли колебаться математический маятник в невесомости?
3. Как изменится ход маятниковых часов, если их из теплой комнаты вынести в холодную кладовую? поднять с первого этажа небоскреба на крышу?
4. Какова масса тела, подвешенного на пружине жесткостью 40 Н/м, если после отклонения тела от положения равновесия оно совершает 8 колебаний за 12 с?
5. На какую максимальную высоту отклоняется математический маятник, если в момент прохождения положения равновесия он движется со скоростью 0,2 м/с? Какова длина маятника, если период его колебаний 2 с?
6. Уравнение колебаний пружинного маятника массой 5 кг имеет вид: x = 0,2cos10пt. Определите: 1) циклическую частоту и период колебаний; 2) жесткость пружины; 3) полную механическую энергию колебаний; 4) смещение, кинетическую и потенциальную энергии маятника при t = 0,025 с.
Определите: 1) циклическую частоту и период колебаний; 2) жесткость пружины; 3) полную механическую энергию колебаний; 4) смещение, кинетическую и потенциальную энергии маятника при t = 0,025 с.
7. Наблюдая за колебаниями большой люстры в Пизанском кафедральном соборе, раскачивающейся из-за сквозняка, Г. Галилей измерил период ее колебаний и установил… Выясните, что установил Г. Галилей и как он измерял период колебаний без часов. Вычислите период колебаний большой люстры в соборе (найдите информацию о длине ее подвеса).
Экспериментальное задание
Изготовьте маятник, закрепив на длинной нити достаточно тяжелое тело, и измерьте ускорение свободного падения в вашем доме. Убедитесь, что оно действительно примерно равно 9,8 м/с2.
Попередня
СторінкаНаступна
СторінкаЗміст
Цей контент створено завдяки Міністерству освіти і науки України
№5 Математический маятник
ЛАБОРАТОРНАЯ РАБОТА № 5
Тема: «Изучение зависимости периода колебаний нитяного маятника от длины нити»
Цель: установить математическую
зависимость периода нитяного маятника
от длины нити маятника.
Оборудование: штатив с держателем, шарик на нити, измерительная лента или линейка, секундомер.
Теоретическая часть
Математическим маятником называется материальная точка, подвешенная на невесомой и нерастяжимой нити. Моделью может служить тяжёлый шарик, размеры которого весьма малы по сравнению с длинной нити, на которой он подвешен (не сравнимы с расстоянием от центра тяжести до точки подвеса).
Учёные Галилей, Ньютон, Бессель и др. установили следующие законы колебания математического маятника:
1.Период колебания математического маятника не зависит от массы маятника и от амплитуды, если угол размаха не превышает 10.
2.Период колебания математического
маятника прямо пропорционален квадратному
корню из длины маятника и обратно пропорционален квадратному
корню из ускорения свободного падения
.
На основании этих законов можно написать
формулу для периода колебаний
математического маятника: .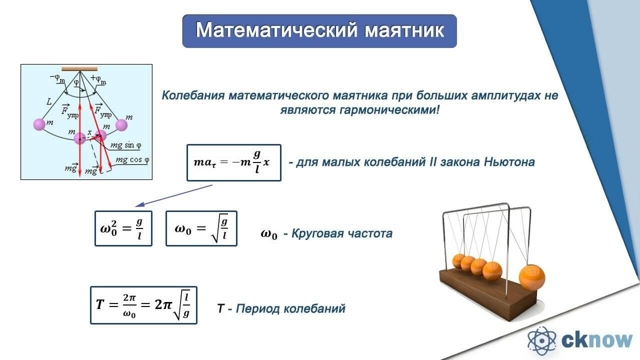
Используя модель и законы колебаний математического маятника, можно пронаблюдать свободные колебания, а так же с их помощью определить ускорение свободного падения для своей местности и сравнить со справочным значением g .
Порядок выполнения работы:
Укрепить нить маятника в держателе штатива.
Измерить длину маятника (длина маятника считается от точки подвеса до центра тяжести шарика).
Отклонить шарик на угол не более 10° и отпустить.
Определить время, за которое маятник совершил 20 колебаний.
Вычислить период колебания маятника, используя формулу Т= t/N.
Повторить опыт еще три раза, уменьшая (или увеличивая) длину нити маятника.
Данные всех опытов и результаты расчетов внести в таблицу.

№ опыта | Длина нити маятника l, м | Число полных колебаний N | Время колебаний t, с | Период колебаний T, с |
1 | 20 | |||
2 | 20 | |||
3 | 20 | |||
4 | 20 |
Проанализировать результаты опытов и сделать вывод о зависимости периода нитяного маятника от длины его нити.

ОТЧЕТ ПО РАБОТЕ
ВЫВОД: |
Контрольные вопросы:
Изобразите математический маятник в крайней правой точке и покажите на чертеже силы, действующие на шарик в данной точке траектории.
 Нарисуйте равнодействующую
сил. Как меняется величина и направление
равнодействующей сил в течение периода?
Нарисуйте равнодействующую
сил. Как меняется величина и направление
равнодействующей сил в течение периода?Каким будет характер движения маятника А) при его перемещении от положения равновесия до амплитудного значения координаты? Б) при его перемещении от амплитудного значения к положению равновесия?
Как будет меняться период колебаний ведерка с водой, подвешенного на очень длинном шнуре: А) если из отверстия в его дне постепенно будет вытекать вода?; Б) если увеличить длину шнура? Какой математический закон или формулу вы использовали при ответе на данные вопросы?
ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. | |
2.Каким будет характер движения маятника А) при его перемещении от положения равновесия до амплитудного значения координаты? Б) при его перемещении от амплитудного значения к положению равновесия? | |
3. | |
Урок-презентация «Колебательные движения» | План-конспект урока по физике (9 класс) по теме:
Механические колебания.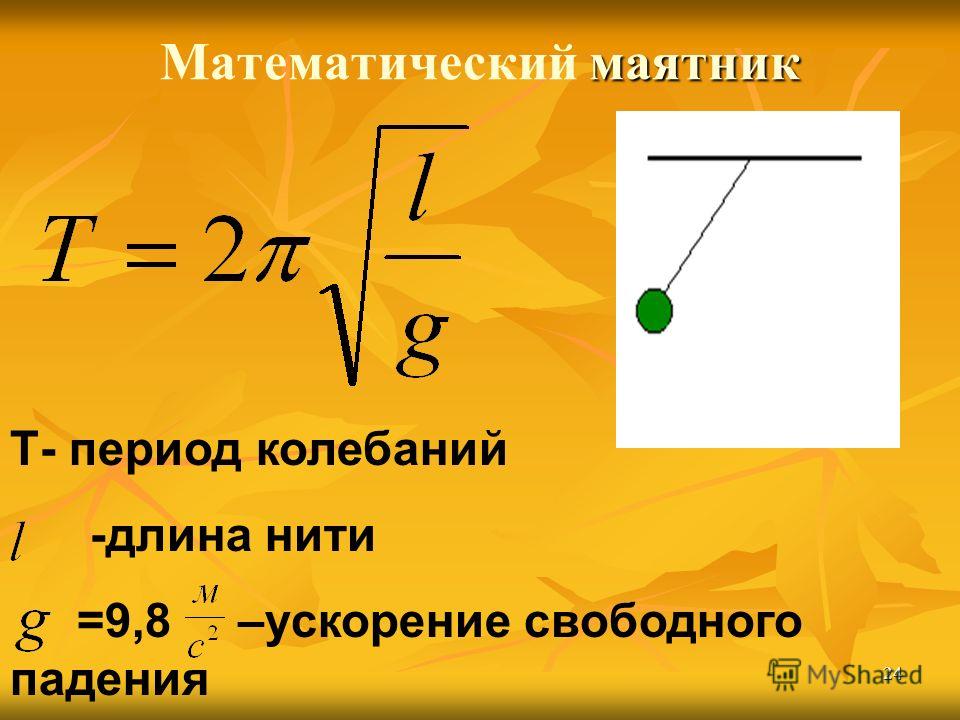
Урок в 9 классе.
(слайд 1) Цель урока:
Образовательная: ознакомить учащихся с новыми понятиями; механические колебания, положения устойчивого равновесия, колебательная система, свободные колебания, выявить основные свойства колебаний и существенные признаки колебательной системы.
Развивающая: развивать умения учащихся анализировать, сопоставлять, проводить сравнения и аналогии, проводить классификацию, обобщение, познавательной, информационно-коммуникативной и рефлексивной деятельности.
Воспитательная: формировать увлеченность, активность смелости, воспитание культуры речи, познавательного интереса к учебному предмету и окружающему миру.
Задачи:
Вспомнить виды колебательных движений; понятие «свободные колебания», выяснить общие свойства колебательных систем.
Оборудование: плакаты; нитяной, пружинный маятники, весы, метроном; презентация.
Основное содержание. Опираясь на демонстрационный эксперимент ввести понятие механического колебания; обсудить свойства, которыми обладают колебательные системы. Продемонстрировать колебания нитяного и пружинного маятников.
Продемонстрировать колебания нитяного и пружинного маятников.
План-конспект
Урок сопровождается показом компьютерной презентации.
I. Организационный момент
Тема урока, цель урока, готовность к уроку.
- Мотивация (2 мин)
- Изучение нового материала – лекция (30 мин)
- Упражнения и вопросы для закрепления (10 мин)
- Итог урока, домашнее задание (3 мин)
II. Мотивация
В начале урока обучающимся выдаются бланки, в которых нужно дописать определения по ходу объяснения нового материала.
- Колебательным движением называется …
- Колебания бывают …
- Периодом колебаний называют …
- Амплитудой называют …
- Свободными колебаниями называют …
- Виды колебательных систем …
- Общее у всех колебательных систем …
III. Изучение нового материала
(слайд 2) Колебания — один из самых распространенных процессов в природе и технике.
Приведите примеры колебаний.
Колеблются высотные здания и высоковольтные провода под действием ветра, маятник заведенных часов и автомобиль на рессорах во время движения, уровень реки в течение года и температура человеческого тела при болезни.
Звук — это колебания плотности и давления воздуха, радиоволны — периодические изменения напряженностей электрического и магнитного полей, видимый свет — тоже электромагнитные колебания, только с несколько иными длиной волны и частотой. Землетрясения — колебания почвы, приливы и отливы — изменение уровня морей и океанов, вызываемое притяжением Луны и достигающее в некоторых местностях 18 метров, биение пульса — периодические сокращения сердечной мышцы человека и т.д.
Смена бодрствования и сна, труда и отдыха, зимы и лета…
Даже наше каждодневное хождение на работу и возвращение домой попадает под определение колебаний, которые трактуются как процессы, точно или приближенно повторяющиеся через равные промежутки времени (повторяющееся движение по одной и той же траектории).
Колебания играют огромную роль в жизни человека. Без знания законов колебаний нельзя было создать радио, телевидение, многие современные устройства и машины. Колебания многогранны. Иногда они выступают как друг и помощник, а иногда как коварный враг.
IV.Историческая справка (слайд 3)
Специальный раздел физики – теория колебаний – занимается изучением закономерностей этих явлений. Знать их необходимо судо- и самолетостроителям, специалистам промышленности и транспорта, создателям радиотехнической и акустической аппаратуры.
Первыми учеными, изучавшими колебания, были Галилео Галилей (1564-1642) и Христиан Гюйгенс (1629-1692). Полагают, что соотношение между длиной маятника и временем каждого качания открыл Галилей. Однажды в церкви он наблюдал, как качалась огромная люстра, и засекал время по своему пульсу. Позже он открыл, что время, за которое происходит один взмах, зависит от длины маятника. Время наполовину уменьшается, если укоротить маятник на три четверти.
Гюйгенс изобрел первые часы с маятником (1657) и во втором издании своей монографии «Маятниковые часы» (1673) исследовал ряд проблем, связанных с движением маятника, в частности нашел центр качания физического маятника.
Большой вклад в изучение колебаний внесли многие ученые: английские – У. Томсон (лорд Кельвин) и Дж. Рэлей, русские – А.С. Попов и П.Н. Лебедев, советские – А.Н. Крылов, Л.И. Мандельштам, Н.Д. Папалекси, Н.Н. Боголюбов, А.А. Андронов и другие.
Томсон (лорд Кельвин) и Дж. Рэлей, русские – А.С. Попов и П.Н. Лебедев, советские – А.Н. Крылов, Л.И. Мандельштам, Н.Д. Папалекси, Н.Н. Боголюбов, А.А. Андронов и другие.
(слайд 4) Колебания бывают механические, электромагнитные, химические, термодинамические и различные другие. Несмотря на такое разнообразие, все они имеют между собой много общего.
(слайд 5) На рисунке изображены тела, которые могут совершать колебательные движения, если вывести их из положения равновесия (т.е. отклонить или сместить от линии ОО/). В движении этих тел можно найти много различий. Например, шарик на нити (рис. а) движется криволинейно, а цилиндр на резиновом шнуре (рис. б) – прямолинейно; верхний конец линейки (рис. в) колеблется с большим размахом, чем средняя точка струны (рис. г).
(слайд 6) За одно и то же время одни тела могут совершать большее количество колебаний, чем другие. Но при всем разнообразии этих движений у них есть важная общая черта: через определенный промежуток времени движение любого тела повторяется.
Минимальный промежуток времени, через который движение повторяется, называют периодом колебаний. Поэтому говорят, что колебательное движение периодично.
Если тело, подвешенное на нити, отведем влево на некоторое расстояние и отпустим, тело будет двигаться с ускорением вправо – вниз, пройдет положение равновесие и вследствие инерции отклонится вправо – вверх и т.д.
Отклонение тела от положения равновесия называют смещением.
Наибольшее (по модулю) отклонение тела от положения равновесия называют амплитудой.
Как и другие движения, колебательное движение характеризуется скоростью и ускорением. При колебательном движении обе эти величины изменяются от точки к точке, от одного момента времени к другому. В точках максимального отклонения от положения равновесия скорость равна нулю. В точке равновесия скорость максимальна. Ускорение – наоборот.
(слайд 7) Группу тел, движение которых мы изучаем, называют системой тел.
Силы, действующие между телами системы, называют внутренними.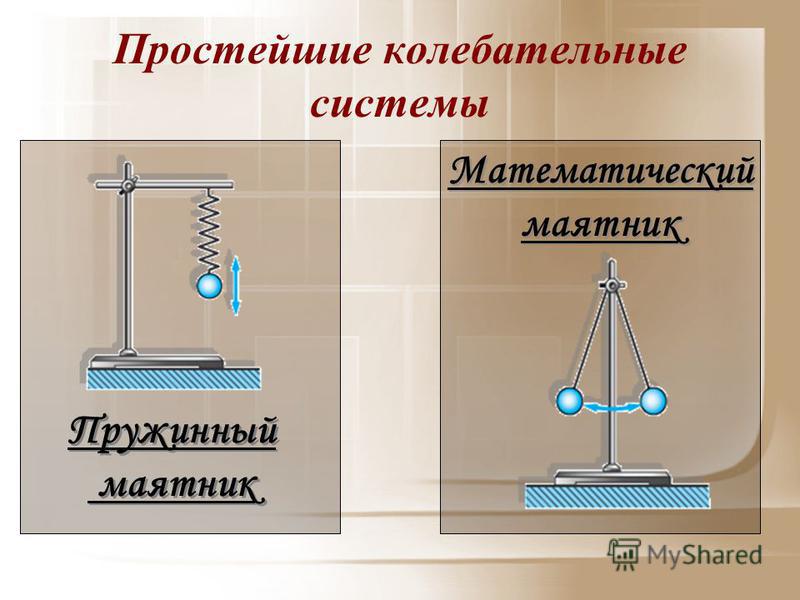
Силы, действующие на тела системы со стороны тел, не входящих в нее, называют внешними .
Самым простым видом колебаний являются свободные колебания.
(слайд 8) Свободными колебаниями называются колебания, происходящие благодаря начальному запасу энергии, приданному колеблющемуся телу.
Чтобы тело совершало свободные колебания, необходимо вывести его из состояния равновесия.
Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел, которая получила название колебательной системы.
(слайд 9) Т.е. системы тел, которые способны совершать свободные колебания, называются колебательными системами.
(слайд 10) Рассмотрим колебательную систему, которую называют маятником. Существует несколько типов маятников: нитяные и пружинные.
— Земля, штатив, пружина и груз образуют вертикальный пружинный маятник (Земля на рис. не показана).
— Земля, подставка и подвешенный на легкой и прочной нити к подставке шарик, причем размеры груза много меньше длины нити, а его масса много больше массы нити, образуют колебательную систему, называемую математическим маятником или, просто маятником.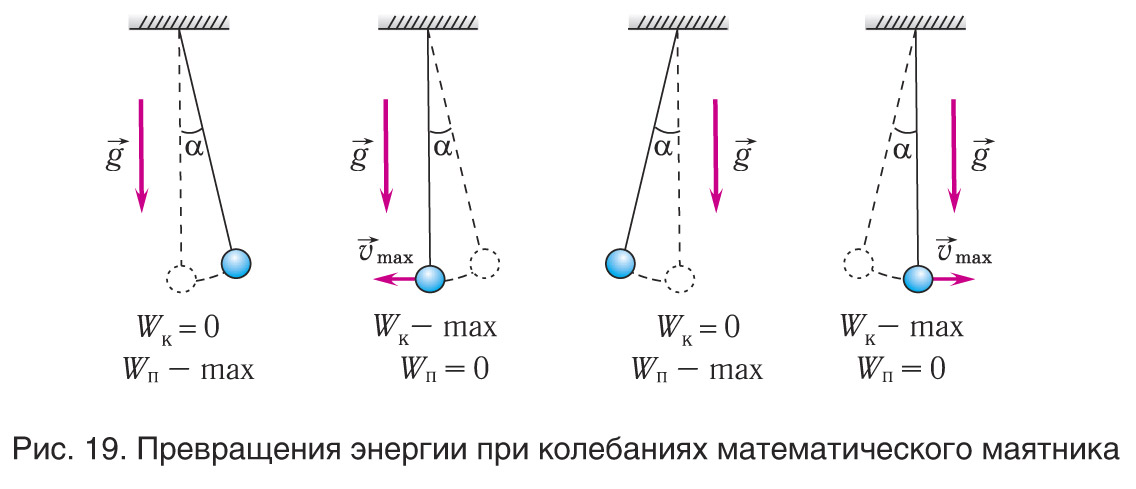
— Два штатива, две пружины и тело массой m образуют колебательную систему, которую называют горизонтальным пружинным маятником.
(слайд 11) Всем колебательным системам присущ ряд общих свойств:
- Наличие положения устойчивого равновесия, при котором равнодействующая сила равна нулю.
- Хотя бы одна сила должна зависеть от координаты.
- Наличие в колеблющемся теле избыточной энергии.
- Если вывести тело из положения равновесия, то равнодействующая уже не будет равна нулю.
Силы трения в системе достаточно малы.
- Упражнения и вопросы для закрепления, работа с бланками:
(слайд 12)
— Какое движение называют колебательным?
— Что называют колебанием тела?
-Что называют амплитудой колебания? Периодом? Смещением?
-Что такое маятник? Какой маятник называют математическим?
— Какой маятник называют пружинным?
— Какие из перечисленных ниже движений являются механическими колебаниями:
а) движение качелей;
б) движение мяча, падающего на землю;
в) движение звучащей струны гитары?
— Приведите другие примеры механических колебаний.
Домашнее задание: (слайд 13)
п.24-26 (Физика-9, А.В.Перышкин,Е.М.Гутник)
Прочитать, выучить определения и формулы
Выполнить практическую работу (по выбору)
(слайд 14)
Изготовьте математический маятник из подручных средств. Приведите его в движение, подсчитайте частоту колебаний. Измерьте длину маятника, так чтобы частота увеличилась вдвое. Проверьте правильность своего расчета на опыте. Сделайте вывод о том, как меняется частота математического маятника в зависимости от его длины.
Литература
1. Мякишев Г.Я. Физика. Колебания и волны : учеб. пособие / Г.Я. Мякишев, А.З. Синяков. — М.: Дрофа, 2001. – 288 с.
2. Боброва А.И. Колебания и маятники : учеб. пособие / А.И. Боброва, А.Н. Херувимов.- М.: Наука, 1981.- 177 с.
3. Шишкин Н.Н. Клуб юных физиков: Кн. для учителя: Из опыта работы. – М.: Просвещение, 1991. – 144.
4. Яндекс. Мультимедиа по физике. Демонстрационный эксперимент по физике. Платонова Т.И. Применение электронной презентации на школьном уроке // www.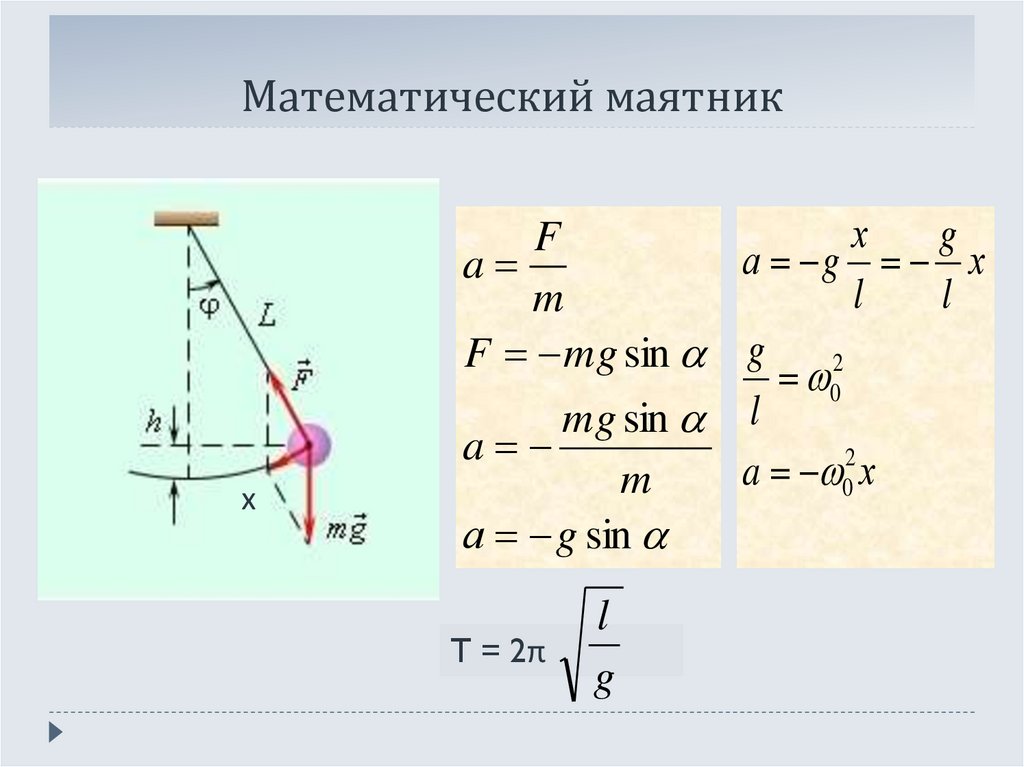 Mendeleev.upeg.net
Mendeleev.upeg.net
- Интернет-ресурсы:
Анимации по физике:
http://somit.ru
- http://physics.nad.ru
- http://anna.vega-int.ru
| Главная Контакты Случайная статья
|
gif» bgcolor=»#FDFCF7″/> | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Лабораторная работа 1 «Изучение колебаний груза на нити» Цель: изучение зависимости характеристик математического маятника от амплитуды колебаний, массы груза, длины нити. Оборудование: два математических маятника с подвесами (шариками различной массы), штатив с зажимом, линейка, секундомер, весы, разновес. Ход работы 1. Найдите массу шарика первого маятника путем взвешивания: m1=200г =0.2 кг. 2. Измерьте длину маятника (от точки подвеса до центра шарика). Длина должна быть не менее 1м. l1= 40 см = 0.4м. 3. Изучите зависимость периода колебаний маятника от амплитуды его колебаний
Таблица 1.
4. По результатам измерений и вычислений сделайте вывод, зависит ли период малых колебаний маятника от амплитуды его колебаний.
5. Найдите массу шарика второго маятника путем взвешивания: m2= 100 г = 0.1 кг. Таблица 2.
6. Сравните полученное значение периода колебаний с полученным в таблице 1. По результатам измерений и вычислений сделайте вывод, зависит ли период малых колебаний маятника от массы шарика.
Исходя из формулы периода малых колебаний мятника не зависит от массы шарика
7. Измените длину маятника: сначала l2=75см и затем l3=50см. Повторите измерение периода колебаний, оставив неизменными массу m2 шарика и амплитуду его колебаний. Таблица 3.
8. По результатам измерений и вычислений сделайте вывод, зависит ли период колебаний маятника от его длины.
Период колеб. маятника зависит от 2 его длины
Контрольные вопросы: 1) Какую длину имеет математический маятник, период колебаний которого π секунд? T=2π√(L/g) L=gT²/4π²
2)Как изменится период колебаний маятника, если массу шарика уменьшить в 3 раза, а длину нити маятника увеличить в 3 раза? Масса не влияет ,а при увеличении длины в 3 раза ,период увеличивается в 3 раза Выводы: Мы научились: изучение зависимости характеристик математического маятника от амплитуды колебаний, массы груза, длины нити Суперзадание. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
См. также « Программа заочной нелинейной школы« 1. Оценки в физикеОдна из задач физики — определение численных значений физических величин. В жизни мы непрерывно сталкиваемся с оценками, которые делаем интуитивно. Например,
вы оцениваете, сколько времени уйдет на выполнение домашнего задания. Стоя в очереди,
нетрудно оценить, сколько времени уйдет на покупку товара. Для этого нужно «прикинуть»,
сколько человек стоит в очереди, и сколько времени уходит на отпуск товара одному
покупателю. Теперь понятно, почему в физике столь полезна запись в виде числа порядка единицы, умноженного на 10 в соответствующей степени. Ведь эта степень сразу дает порядок самого числа. Итак, для физика очень ценно представлять примерный порядок величины. Это дает
важную информацию о том, что учитывать, а что не учитывать в теории. Например,
нужно ли учитывать электромагнитные поля звезд при описании образования галактик?
С помощью метода оценок можно быстро получать ответы на совершенно неожиданные
вопросы. Давайте решим две задачи на определение порядка величин. Сначала оценим период колебаний математического маятника (рис.). Пусть в начальный
момент времени маятник находится в точке А, которой на рисунке соответствует
максимальное удаление маятника от точки В — положения равновесия. Тогда
период колебаний есть учетверенный промежуток времени, за который маятник
пройдет дугу АВ. Для оценки заменим его истинное движение по дуге окружности
движением по хорде. Тогда движение маятника — это просто скольжение по наклонной
плоскости, угол которой с горизонтом составляет .
Значит, ускорение будет равно .
Длина наклонной плоскости ,
где l — длина нити. Сравним наш результат с тем, что на самом деле известно о движении маятника.
Период малых колебаний строго вычисляется и дается формулой
.
Итак, с помощью нашей оценки мы обнаружили, что период малых колебаний не зависит
от их амплитуды, а это правильный результат. Далее, мы правильно определили зависимость
периода от длины нити l и ускорения свободного паденияg.
Наконец, мы получили оценку численного коэффициента в формуле для периода 8, которая
отличается от точного значения
на 27%. Однако, для оценки порядка величины это не плохой результат. А в чем мы
ошиблись? Как мы уже сказали — в величине точного численного коэффициента. Кроме
того, из нашего рассуждения следует, что период колебаний вообще не зависит от
начального отклонения маятника (т.е. от его амплитуды), что на самом деле не так. Вы решили задачу и продолжаете читать дальше, но вас раздражает писк влетевшего
в комнату комара. Оценим частоту звука, генерируемого летящим комаром. Предположим,
что звук возникает от периодического взмахивания крылышек комара. Конечно, на
самом деле физика полета комара сложнее. Но мы воспользуемся грубой моделью. Пусть
сила тяжести, действующая на комара, компенсируется изменением импульса воздуха
в единицу времени, которое создается взмахами крылышек, т.е.
,
— изменение импульса воздуха,
— время движения крылышек, т — масса комара, g — ускорение
свободного падения. Масса воздуха с плотностью ,
отбрасываемая вниз за время
движения крылышек площадью S со скоростью v, может быть
выражена формулой: .
При этом массе сообщается импульс ,
что создает силу ,
действующую на крылышко вверх. В качестве характерного размера комара введем его
длину l (1-4 мм) и будем считать, что размах его крыльев порядка длины. , . А поскольку, F~mg, то получаем . Если подставит сюда численные значения всех величин, то найдем f~400 Гц. Получился вполне разумный порядок величины частоты. Из нашей формулы следует,
что частота обратно пропорциональна корню квадартному из размера насекомого l.
Это значит, что чем крупнее насекомое, тем ниже издаваемый им звук. Действительно,
вас раздражает тонкий звенящий звук (писк) комара, но вы уважительно прислуживаетесь
к жужжанию пчелы или гудению шмеля. Большим мастером оценок физических величин был выдающийся физик Энрико Ферми. На своих лекциях он проводил за считанные минуты оценку числа настройщиков роялей в Чикаго. (Как это сделать?) Давайте сделаем еще несколько занимательных оценок. Оценим число домашних кошек в Саратове. В Саратове порядка 106 человек. В каждой семье около 3-5 человек. Значит, в Саратове порядка 2·105семей. Зная сколько человек сидит в классе, можно быстро подсчитать долю семей, в которых есть кошки. Это число колеблется от 1/4 до 1/2. Таким образом, в Саратове около 5·104 -105 домашних кошек. Точно также можно оценить число домашних собак, телефонов и т.д. Оценки можно делать из разных соображений, здесь важен не столько путь решения,
сколько результат. Например, число домашних телефонов можно оценить так. Практически
каждый видел телефонные справочники, это две книги по 300-400 страниц. В физике оценки позволяют очень быстро получать важные результаты. Например, во время испытания первой атомной бомбы Энрико Ферми почти мгновенно оценил мощность ядерного взрыва, измерив вызванное ударной волной смещение клочков бумаги, которые он сыпал на землю. Итак, нужно уметь оценивать физические величины. Это умение должно стать очень
естественным для вас, настолько, чтобы вы могли в своей работе следовать правилу
физика, специалиста по теории атомного ядра и гравитации Уилера, учителя другого
выдающегося физика Ричарда Фейнмана: «Никогда не начинай вычислений, пока
не знаешь ответа. Каждому вычислению предпосылай оценочный расчет: привлеки простые
физические соображения (симметрию! инвариантность!) до того, как начинать подробный
вывод; продумай возможные ответы на каждую загадку. Задачи
2. Размерности физических величинКроме численных значений, физические величины характеризуются своей размерностью.
С понятием размерности мы знакомимся еще до того, как начинаем изучать физику.
Например, мы хорошо знаем, что длина измеряется в метрах, масса в граммах и т. Давайте поговорим о размерности подробнее. Не указав размерности, нельзя сопоставить физической величине какое-либо число. Например, бессмысленно сказать, что длина предмета равна 10. Надо обязательно уточнить, чего 10? Метров, сантиметров, а может быть парсек? Вот эта дополняющая число информация и называется размерностью. Таким образом, размерность физической величины устанавливает, с каким эталоном надо соотнести число. Если длина стены равна 10 метров, это означает, что вдоль стены можно уложить 10 раз линейку метровой длины. Существуют основные размерности. Они соответствуют физическим величинам, которые
людям проще измерять. В физических соотношениях размерности правой и левой части всегда должны быть равны. Невозможна запись 3 бегемота — 2 бегемота = 1 крокодилу. Также не верна запись 100 бегемотов = 100 килобегемотов, хотя, казалось бы, цифры одинаковы. Это правило позволяет быстро находить ошибку, когда вы проводите большое количество промежуточных расчетов. Но простая проверка преобразований — это далеко не все выгоды размерности. [V] = м3, [R] = м. Единственный способ, с помощью которого из размерности «м» можно получить «м3«, состоит в том, чтобы возвести радиус в куб. Поэтому искомая формула имеет вид: V=CR3. В полученное соотношение вошел некоторый неизвестный нам численный коэффициент,
который мы обозначили через C. Это число нельзя определить с помощью метода
размерностей. Решим с помощью метода размерностей еще одну, более сложную задачу. Чему равно
время, за которое маятник совершает одно полное колебание? Строгое математическое
решение этой задачи приводит к дифференциальному уравнению. Не будем, однако,
пытаться написать уравнение движения, а попробуем ответить на вопрос: от каких
физических величин зависит период колебаний T? Мы знаем, что период малых
колебаний не зависит от начального угла отклонения маятника. Нить, на которой
подвешен маятник, очень легкая, поэтому период колебаний не может зависеть от
ее массы. Грузик имеет очень маленький размер, так что этот размер тоже не может
быть существенным. Если пренебречь сопротивлением воздуха, то останутся всего
три величины: длина нити l, ускорение свободного падения g, масса
маятника m. Итак, ответ к нашей задаче должен выглядеть в виде формулы, в левой части которой должен стоять период колебаний T, а в правой — неизвестная нам пока комбинация из длины нити l, ускорения свободного падения g, массы маятника m. Выпишем размерности величин, входящих в искомую формулу: [T] = c; [l] = м, [g] = м/с2, [m] = кг. Размерности левой и правой части любого равенства должны быть равны. Как «приготовить» из м, м/с2, кг секунды? Способ один: . Следовательно, ответ к задаче имеет следующий вид: . Здесь C — какое-то неизвестное нам безразмерное число. Определим константу
C экспериментально. Изготовим маятник длиной 1 м, и измерим период колебаний.
Он окажется около 2 с. Мы получили, что период колебаний зависит от длины маятника как . Поэтому, если увеличить длину маятника в 2 раза, то период колебаний возрастет в раз. Кроме того, мы установили, что период колебаний маятника не зависит от массы грузика. Это существенные результаты, которые могут быть проверены экспериментально. Давайте еще немного поразмышляем над задачей о маятнике. Что будет, если маятник совершает колебания с большим размахом? Тогда период колебаний должен зависеть от начального угла отклонения j. Это величина безразмерная. Но ведь размерности левой и правой частей уравнений все равно должны быть одинаковы. Это с неизбежностью приводит нас к выводу о том, что формула для периода колебаний выглядит так: В этом соотношении
— некоторая функция, которую установить из соображений размерности невозможно.
Можно проделать несколько серий измерений зависимости периода колебаний от начального
угла отклонения
при разных значениях длины нити l. Построим эти зависимости, отложив по
вертикальной оси величину . Тогда все они должны представлять собой одну и ту же кривую! Ведь фактически,
мы каждый раз строим график функция ,
а она одинакова во всех случаях. Когда возникает такая ситуация, у физиков принято
рисовать одну серию результатов точечками, другую — крестиками, третью — квадратиками
и т. Задачи
На уроках в школе Вы постоянно получаете новые знания. Практически так же
протекают занятия и во всех высших учебных заведениях. Но совсем другая ситуация
возникнет, если Вы станете заниматься наукой. Ведь в этом случае Вам необходимо
самими получить новые знания, которые до Вашей работы были неизвестны. Это совсем
другая ситуация, чем та, к которой приучает школа. Поясним эту мысль на простом
примере. В школе знания даются поэтапно, в соответствии с учебной программой.
При этом нельзя, например, пользоваться теми теоремами, которые еще «не прошли»
на уроках. Особенность предложенных задач в том, что они не имеют строго определенных
решений — каждая из них допускает множество подходов и дальнейшее развитие. «Арсенал»
Вашего исследования не фиксирован. Используйте теоретические соображения, эксперименты,
компьютерное моделирование, по своим наклонностям и возможностям — в тексте даются
лишь отдельные советы. Обсуждайте Вашу задачу с другими учениками. Ознакомитесь с теоретическим материалом по колебаниям, помещенным на странице Открытого колледжа МФТИ по адресу http://www.college.ru/physics/Theory/op25part1/content/content.html Задачи
Ознакомитесь с теоретическим материалом по волнам, помещенным на странице Открытого колледжа МФТИ по адресу http://www.college.ru/physics/Theory/op25part1/content/content.html Задачи
Саратовская группа теоретической нелинейной динамики |
маятник | Определение, формула и типы
маятник
Смотреть все СМИ
- Ключевые люди:
- Галилео Христиан Гюйгенс Марин Мерсенн
- Похожие темы:
- баллистический маятник боб физический маятник сферический маятник составной маятник
Просмотреть весь связанный контент →
Популярные вопросы
Что такое маятник?
Маятник представляет собой тело, подвешенное к фиксированной точке, так что оно может раскачиваться вперед и назад под действием силы тяжести. Интервал времени полного возвратно-поступательного движения маятника постоянен.
Интервал времени полного возвратно-поступательного движения маятника постоянен.
Для чего используются маятники?
Различные типы маятников имеют различное применение. Примеры простых маятников можно найти в часах, качелях и даже в естественной механике раскачивания ног. Tetherballs являются примерами сферических маятников. Маятники Шулера используются в некоторых инерциальных системах наведения, а некоторые составные маятники применяются для измерения ускорения свободного падения.
Как питаются маятниковые часы?
Маятниковые часы приводятся в действие механизмами, которые заставляют маятник качаться с постоянным периодом. Традиционно для этой цели используются весовые или пружинные механизмы, но в некоторых часах для питания маятника используется электричество. Маятниковые часы с приводом от веса требуют перемотки, когда их вес полностью опущен, в то время как часы с пружинным приводом должны быть свернуты, как только пружины вытянутся.
Когда были изобретены маятниковые часы?
Одни авторы приписывают изобретение маятниковых часов Галилею, другие – Христиану Гюйгенсу. Это разногласие возникает из-за того, что Галилей впервые отметил относительное постоянство периода маятника около 1583 г., а Гюйгенс в 1656 г. создал часы, основанные на движении маятника с действительно постоянной скоростью.
Раскройте силы потенциальной энергии, кинетической энергии и силы трения маятника напольных часов
Посмотреть все видео к этой статьемаятник , тело, подвешенное к фиксированной точке так, что оно может раскачиваться вперед и назад под действием силы тяжести. Маятники используются для регулирования движения часов, потому что интервал времени для каждого полного колебания, называемый периодом, является постоянным. Формула для периода T маятника: T = 2π Квадратный корень из √ L / g , где L — длина маятника, а 9051 g
2 — ускорение свободного падения.
Итальянский ученый Галилей впервые отметил (ок. 1583 г.) постоянство периода маятника, сравнив движение качающейся лампы в пизанском соборе с частотой его пульса. Голландский математик и ученый Христиан Гюйгенс изобрел часы, управляемые движением маятника, в 1656 г. Приоритет изобретения маятниковых часов был приписан одними авторитетами Галилею, а другими — Гюйгенсу, но Гюйгенс решил основную проблему создания часов. период маятника действительно постоянный, изобретая стержень, который заставлял подвешенное тело, или груз, качаться по дуге циклоиды, а не по дуге окружности.
Подробнее по этой теме
механика: Движение маятника
Согласно легенде, Галилей открыл принцип действия маятника во время службы в Дуомо (соборе), расположенном…
Простой маятник состоит из шарика, подвешенного на конце нити, настолько легкой, что ее можно считать невесомой. Срок действия такого устройства можно увеличить, увеличив его длину, измеряемую от точки подвеса до середины боба. Однако изменение массы боба не влияет на период, если при этом не изменяется длина. С другой стороны, на период влияет положение маятника по отношению к Земле. Поскольку сила гравитационного поля Земли не везде одинакова, данный маятник качается быстрее и, следовательно, имеет более короткий период на малых высотах и на полюсах Земли, чем на больших высотах и на экваторе.
Однако изменение массы боба не влияет на период, если при этом не изменяется длина. С другой стороны, на период влияет положение маятника по отношению к Земле. Поскольку сила гравитационного поля Земли не везде одинакова, данный маятник качается быстрее и, следовательно, имеет более короткий период на малых высотах и на полюсах Земли, чем на больших высотах и на экваторе.
Существуют и другие виды маятников. Составной маятник имеет вытянутую массу, как качающийся стержень, и может свободно колебаться вокруг горизонтальной оси. Специальный обратимый составной маятник, называемый маятником Катера, предназначен для измерения величины г , ускорения свободного падения.
Другой тип — маятник Шулера. Когда маятник Шулера подвешен вертикально, он остается выровненным с местной вертикалью, даже если точка, из которой он подвешен, ускоряется параллельно поверхности Земли. Этот принцип маятника Шулера применяется в некоторых инерциальных системах наведения для поддержания правильной внутренней вертикальной привязки даже при быстром ускорении.
Сферический маятник подвешен к шарнирному креплению, что позволяет ему качаться в любой из бесконечного числа вертикальных плоскостей через точку подвеса. Фактически плоскость колебаний маятника свободно вращается. Простая версия сферического маятника, маятник Фуко, используется, чтобы показать, что Земля вращается вокруг своей оси. См. также баллистический маятник .
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Редакция Британской энциклопедии Эта статья была недавно отредактирована и дополнена Эриком Грегерсеном.
Колебание во времени — Действие
(2 оценки)Нажмите здесь, чтобы оценить
Quick Look
Уровень: 8 (7-9)
Необходимое время: 45 минут
Расходные материалы Стоимость/группа: 1,00 долл. США
Размер группы: 3
Зависимость от действий: Нет
Предметные области: Алгебра, физика, физика
Поделиться:
TE Информационный бюллетень
youtube.com/embed/3FsQ5y7ZuYA?modestbranding=1&wmode=transparent&rel=0″ frameborder=»0″ webkitallowfullscreen=»» mozallowfullscreen=»» allowfullscreen=»» title=»Youtube embedded video»>Резюме
Учащиеся изучают движение маятников и приходят к выводу, что чем длиннее нить маятника, тем меньше число колебаний за заданный интервал времени. Группы учащихся проводят эксперимент, собирая и отображая данные на рабочем листе. Они видят, что изменение веса маятника не влияет на период.Эта учебная программа по инженерному делу соответствует научным стандартам следующего поколения (NGSS).
Инженерное подключение
Инженеры используют концепции движения, извлеченные из маятников, во многих приложениях, включая хронометраж, обнаружение землетрясений, спутниковые орбиты и рассеяние энергии. Инженеры по управлению включают маятники в системы виброизоляции для производственного и промышленного оборудования, а также управляют шагающими роботами и ракетными двигателями. Системы перевернутого маятника контролируют характеристики плотины и поведение конструкции, обнаруживая угловое движение. Программное обеспечение для защиты от раскачивания основано на концепции маятника, чтобы обеспечить более безопасную и эффективную работу строительных кранов, кранов на верфи, кранов с телескопической стрелой и судовых кранов.
Системы перевернутого маятника контролируют характеристики плотины и поведение конструкции, обнаруживая угловое движение. Программное обеспечение для защиты от раскачивания основано на концепции маятника, чтобы обеспечить более безопасную и эффективную работу строительных кранов, кранов на верфи, кранов с телескопической стрелой и судовых кранов.
Цели обучения
После этого задания учащиеся должны уметь:
- Описать движение маятников.
- Собирайте данные, экспериментируя с маятниками, и используйте эти данные для прогнозирования будущего поведения.
- Используйте собранные данные, чтобы объяснить взаимосвязь между длиной маятника и его частотой.
- Приведите примеры ситуаций, в которых инженеры используют маятники.
- (расширение деятельности) Используйте знания, полученные в результате анализа данных, для создания маятника, который решает задачу проектирования.
Образовательные стандарты
Каждый урок или занятие TeachEngineering связано с одной или несколькими науками K-12,
технологические, инженерные или математические (STEM) образовательные стандарты.
Все более 100 000 стандартов K-12 STEM, включенных в TeachEngineering , собираются, поддерживаются и упаковываются Сеть стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты структурированы иерархически: сначала по источнику; напр. , по штатам; внутри источника по типу; напр. , естественные науки или математика; внутри типа по подтипу, затем по классам, и т.д. .
NGSS: Научные стандарты следующего поколения — Наука
Общие базовые государственные стандарты — математика
- Свободно складывать, вычитать, умножать и делить многозначные десятичные числа, используя стандартный алгоритм для каждой операции.
(Оценка
6) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- Представляйте данные с помощью графиков на линии действительных чисел (точечные графики, гистограммы и диаграммы).
 (Оценки
9 —
12) Подробнее
(Оценки
9 —
12) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии – Технология
ГОСТ
Предложите выравнивание, не указанное вышеКакое альтернативное выравнивание вы предлагаете для этого контента?
Подписывайся
Подпишитесь на нашу рассылку новостей, чтобы получать внутреннюю информацию обо всем, что связано с TeachEngineering, например, о новых функциях сайта, обновлениях учебных программ, выпусках видео и многом другом!
PS: Мы никому не передаем личную информацию и электронные письма.
Список материалов
Каждой группе нужно:
- 110 см веревки
- рыболовные грузила (1 унция и 2 унции)
- лента
- метрическая линейка или рулетка
- цветные маркеры
- транспортир
- секундомер
Рабочие листы и вложения
Рабочий лист «Колебание во времени» (pdf)
Посетите [www.teachengineering.org/activities/view/cub_mechanics_lesson09_activity1], чтобы распечатать или загрузить.Больше учебных программ, подобных этому
Урок средней школы
Качание на веревке
Студенты изучают, как работают маятники и почему они полезны в повседневных приложениях. В практической деятельности они экспериментируют с длиной струны, весом маятника и углом выпуска.
Качание на струне
Начальный урок
Наука свинга
Студенты узнают, что такое маятник и как он работает в контексте аттракционов в парке развлечений. Изучая физику маятников, они также знакомятся с первым законом движения Ньютона — о непрерывном движении и инерции.
Наука свинга
Нижняя элементарная деятельность
Качание со стилем
Учащиеся на собственном опыте узнают о характеристиках простого физического явления — маятника — катаясь на качелях на игровой площадке. Они используют условия маятника и таймер, чтобы экспериментировать с переменными колебаниями. Они расширяют свои знания, следуя этапам процесса инженерного проектирования, чтобы проектировать …
Они расширяют свои знания, следуя этапам процесса инженерного проектирования, чтобы проектировать …
Свинг со стилем
Урок средней школы
В вихре вещей
После просмотра видеоклипа 1940 года об обрушении моста «Скачущая Герти» и демонстрации учителя с простым маятником группы студентов обсуждают, а затем исследуют идею повторяющегося движения, в частности концепции периодического и гармонического движения. Они изучают основные свойства этого типа…
В качели вещей
Предварительные знания
Базовое понимание сил, таких как подъемная сила, вес, тяга и сопротивление, а также вращательное движение и угловой момент.
Введение/Мотивация
Волны в воде поднимаются и опускаются, автомобили подпрыгивают, когда наезжают на кочки, а люди качаются взад и вперед, когда играют на качелях. Можете ли вы придумать другие вещи, которые имеют регулярное движение вперед и назад? Элементы, которые перемещаются вперед и назад, регулярно перемещаются аналогичным образом. Если ученые и инженеры смогут понять один вид возвратно-поступательного движения, например качание, то они смогут применить это понимание к другим объектам, которые совершают возвратно-поступательное движение.
Можете ли вы придумать другие вещи, которые имеют регулярное движение вперед и назад? Элементы, которые перемещаются вперед и назад, регулярно перемещаются аналогичным образом. Если ученые и инженеры смогут понять один вид возвратно-поступательного движения, например качание, то они смогут применить это понимание к другим объектам, которые совершают возвратно-поступательное движение.
В этом упражнении вы изучите движение маятника. Если вы когда-либо играли на качелях, вы уже знакомы с некоторыми способами движения маятника. В этой лабораторной работе вы изучите конкретные факторы, которые могут повлиять на колебания маятника. Вы замерите колебания маятника взад-вперед и увидите, какие факторы заставляют его ускоряться, а какие — замедлять.
Движение маятника было впервые математически описано человеком по имени Галилео Галилей в конце 1500-х годов. Галилей также исследовал падение предметов, движение планет и многие другие научные явления. Многие из его открытий выросли из его наблюдений за тем, как качаются маятники. Только подумайте — может быть, вы сможете понять, как что-то работает, разобравшись с маятниками!
Только подумайте — может быть, вы сможете понять, как что-то работает, разобравшись с маятниками!
использовались не только в 1500-х годах. Сегодня инженеры используют движение маятников. На самом деле, некоторые из самых передовых строительных конструкций включают в себя большие маятники для рассеивания энергии, если здание сотрясается от землетрясения. Инженеры используют маятники в роботах и часах. Можете ли вы придумать полезные способы использования маятника?
Процедура
Перед занятием
- Отрезать отрезки ниток длиной 110 см.
- Прикрепите либо 1 унцию. или 2 унции. вес всем маятникам.
- Этикетка рыболовных грузиков 1 унция. и 2 унции.
- Сделайте копии рабочего листа Swing in Time, по одной на каждого учащегося.
Со студентами
- Введите задание: Спросите учащихся, знают ли они, что такое маятник.
 Спросите их, знают ли они, как используются маятники. Скажите им, что они узнают больше о маятниках и их движениях в этом упражнении. Дополнительные сведения и мотивацию см. в соответствующем уроке.
Спросите их, знают ли они, как используются маятники. Скажите им, что они узнают больше о маятниках и их движениях в этом упражнении. Дополнительные сведения и мотивацию см. в соответствующем уроке. - Раздайте рабочие листы. Предложите учащимся использовать рабочие листы для выполнения задания.
- Работая в группах по три человека, попросите учащихся измерить и отметить свою веревку с интервалом в 10 см, начиная измерение с середины груза и отмечая до 100 см.
- Попросите учащихся прикрепить маятник к своим партам на отметке 10 см.
- Потяните вес назад под углом 45 градусов для равномерности замаха.
- Предскажите и проверьте: сначала попросите учащихся предсказать, сколько раз маятник вернётся в исходную точку (качание или колебание) в течение 30 секунд для проверяемых длины и веса маятника, и запишите это в таблицу. рабочий лист таблицы. Затем попросите одного учащегося замерить замах в течение 30 секунд, а два других ученика подсчитают количество полных замахов (колебаний) и запишут это в таблицу рабочего листа.

- Повторите процесс «прогнозируйте и проверьте», наклеивая ленту на следующие 10 см (20 см). Повторите еще раз до длины 50 см.
- Предложите учащимся построить гистограммы с числом колебаний (колебаний) по вертикальной оси и длиной маятника по горизонтальной оси. Ожидайте, что учащиеся наблюдают закономерность.
- Повторите процедуру со вторым грузом. Попросите учащихся отметить любые различия между двумя весами (разницы быть не должно).
- Ожидайте, что их гистограммы будут похожи на приведенный ниже пример. (Примечание: вес оказывает незначительное влияние на количество махов, но из-за экспериментальной ошибки может быть небольшое расхождение.)
- Следуя шаблону, учащиеся должны уметь прогнозировать результаты на отрезках от 60 до 100 смn.
- Пусть учащиеся продолжат записывать свои прогнозы, тестировать и записывать результаты в рабочий лист.
- Завершите обсуждение в классе, чтобы просмотреть и поделиться результатами, ответами и выводами из рабочих листов.

Словарь/Определения
боб: качающийся груз на конце маятника.
гравитация: сила, притягивающая тела к центру Земли.
колебание: колебательное движение маятника вперед и назад. Одно колебание завершается, когда груз возвращается в исходное положение.
маятник: Нить с грузом на одном конце, подвешенная к неподвижной опоре, так что она свободно качается взад и вперед под действием силы тяжести.
период: количество времени, которое требуется грузу маятника, чтобы вернуться в исходное положение.
Оценка
Предварительная оценка
Вопрос для обсуждения: Запрашивайте, объединяйте и обобщайте ответы учащихся. Спросите учащихся: Что такое маятник? Затем придумайте примеры маятников. (Возможные ответы: детские качели, качели из веревок или шин, свисающие с деревьев, напольные часы, цирковые качели-трапеции и веревки, балансировочные механизмы для некоторых роботов и т. д.)
д.)
Встроенная оценка деятельности
Рабочий лист: Предложите учащимся следить за выполнением задания с помощью рабочего листа Swing in Time и использовать его для записи своих лабораторных наблюдений и измерений. Просмотрите их данные, ответы и графики, чтобы оценить их глубину вовлеченности и понимания.
Проверка в парах: После того, как группы учащихся закончат работу с рабочими листами, попросите их сравнить ответы с ответами другой заполненной группы, дав всем учащимся время закончить рабочий лист.
Оценка после активности
Обсуждение рабочего листа: Просмотрите и обсудите ответы на рабочем листе со всем классом. Ответы учащихся свидетельствуют об их владении предметом.
Вопросы безопасности
Небольшие веса могут быть причиной удушья.
Советы по устранению неполадок
Может быть полезно смоделировать это задание для учащихся.
Убедитесь, что учащиеся ведут точный подсчет колебаний маятника. Пусть два ученика посчитают и договорятся о количестве взмахов.
Расширения деятельности
Песчаный маятник: Сделайте конусообразную чашу и наполните ее песком или солью. Раскачивайте конус как маятник, позволяя песку высыпаться из отверстия на дне конуса. Наблюдайте за узором, который он делает.
Эксперимент с двумя или более маятниками одновременно: качайте маятники в одном направлении, в противоположных направлениях, два в одну сторону и один в другую, крест-накрест и т. д.
Предскажите, сколько времени потребуется маятнику, чтобы полностью остановиться.
Попросите учащихся найти длину нити, при которой маятник качается ровно 60 раз в минуту. Чем это может быть полезно? (Ответ: маятник можно было бы использовать как часы, если бы каждое колебание занимало одну секунду.)
Задача на проектирование: Предложите учащимся сконструировать маятник, который качается взад-вперед 10 раз за 1 минуту. Поощряйте учащихся «быстро ошибаться», чтобы они могли протестировать множество различных проектов за отведенное время. Также предложите учащимся использовать то, что они узнали о маятниках из этого упражнения , чтобы внести необходимые коррективы в свои конструкции.
Поощряйте учащихся «быстро ошибаться», чтобы они могли протестировать множество различных проектов за отведенное время. Также предложите учащимся использовать то, что они узнали о маятниках из этого упражнения , чтобы внести необходимые коррективы в свои конструкции.
Масштабирование активности
- Для младших школьников попросите их нарисовать что-нибудь, что качается, например, качели из шины или маятник в часах. После того, как они закончат рисовать, попросите их показать классу, что они нарисовали. Спросите учащихся, что, по их мнению, влияет на скорость качания маятника — масса или длина маятника?
- Предложите учащимся старшего возраста построить линейные графики, а не гистограммы.
Авторские права
© 2004 Регенты Университета КолорадоАвторы
Сэйбер Дюрен; Бен Хивнер; Малинда Шефер Зарске; Дениз В. Карлсон
КарлсонПрограмма поддержки
Комплексная программа преподавания и обучения, Инженерный колледж Колорадского университета в БоулдереБлагодарности
Содержание этой учебной программы цифровой библиотеки было разработано в рамках грантов Фонда улучшения высшего образования (FIPSE), Министерства образования США и Национального научного фонда (грант GK-12 № 0338326). Однако это содержание не обязательно отражает политику Министерства образования или Национального научного фонда, и вы не должны исходить из того, что оно одобрено федеральным правительством.
Последнее изменение: 19 июля 2021 г.
Маятники – Гиперучебник по физике
[закрыть]
простой маятник
Маятник представляет собой массу, подвешенную к точке вращения , которая может свободно раскачиваться вперед и назад. Поскольку движение колебательное (причудливый способ сказать туда-сюда) и периодическое (повторяющееся с характерным временем), маятники использовались в часах с 17 века. Сырые маятники дешевы и просты в изготовлении — все, что вам нужно, это небольшой груз, кусок веревки и что-то, на чем его можно повесить — и сделать подходящие практические устройства для вводных курсов физики. Руки и ноги идущего человека также являются маятниками, поэтому типичный серийный человек поставляется с маятниками.
Поскольку движение колебательное (причудливый способ сказать туда-сюда) и периодическое (повторяющееся с характерным временем), маятники использовались в часах с 17 века. Сырые маятники дешевы и просты в изготовлении — все, что вам нужно, это небольшой груз, кусок веревки и что-то, на чем его можно повесить — и сделать подходящие практические устройства для вводных курсов физики. Руки и ноги идущего человека также являются маятниками, поэтому типичный серийный человек поставляется с маятниками.
Простой маятник представляет собой математическую идеализацию, используемую для аппроксимации поведения реальных маятников. Простых маятников не существует, но с их помощью реализуется настоящая физика. Начните с простого и доведите до реального. Вся масса простого маятника сосредоточена в одной точке (называемой грузом ) на конце нерастяжимого, несжимаемого, невесомого стержня, соединенного с неподвижным шарниром без трения. Груз простого маятника движется вперед и назад по дуге окружности с центром в центре. Неподвижный маятник любого типа будет покоиться на положение равновесия с центром масс ниже оси вращения.
Груз простого маятника движется вперед и назад по дуге окружности с центром в центре. Неподвижный маятник любого типа будет покоиться на положение равновесия с центром масс ниже оси вращения.
Две силы действуют на простой маятник независимо от того, движется он или нет, — вес (сила тяжести) и напряжение. (Сопротивление воздуха игнорируется, как это часто бывает. Плохое сопротивление воздуха. Всегда игнорируется.) В положении равновесия, когда маятник покоится, две силы равны и противоположны. Не очень интересно.
Поскольку весь маятник зафиксирован в точке поворота (существительное), любая попытка двигать маятник из стороны в сторону заставляет его вращаться (глагол) с угловым смещением θ. Теперь все становится интереснее.
Это проблема, когда радиально-тангенциальная система координат работает лучше, чем типичная вертикально-горизонтальная. Натяжение указывает радиально внутрь к оси и считается «хорошим» вектором. Вес — это «плохой» вектор, и его необходимо разбить на составляющие — одну радиальную ( мг sin θ) и одну тангенциальную ( мг cos θ).
Радиальная составляющая и натяжение вносят вклад в центростремительную силу. Напряжение является положительным, поскольку оно направлено к центру. Радиус ( r ) в уравнении центростремительного ускорения можно заменить длиной маятника (ℓ), поскольку это одно и то же. Тангенциальную скорость ( v ) также можно записать в виде производной для тех, кто любит исчисление. Нет никакой реальной причины делать это сейчас, кроме как потому, что это выглядит круто. На самом деле нет никакой причины писать об этом сейчас, кроме как для ощущения завершенности.
| ∑ F r = | мА с | ||||||||
| T − мг cos θ = |
| ||||||||
| T − мг cos θ = |
| ||||||||
Более интересна тангенциальная составляющая. Она описана как возвращающая сила , потому что она увеличивается с увеличением смещения и толкает груз обратно к его положению равновесия. По этой причине он получает отрицательный знак. Когда смещение положительное, оно указывает в отрицательном направлении. Когда смещение отрицательное, оно указывает в положительном направлении. В неформальном языке все наоборот. Теперь тангенциальное ускорение действительно должно быть записано в причудливых математических обозначениях. Так полезнее. Также компенсируется масса, что интересно.
Она описана как возвращающая сила , потому что она увеличивается с увеличением смещения и толкает груз обратно к его положению равновесия. По этой причине он получает отрицательный знак. Когда смещение положительное, оно указывает в отрицательном направлении. Когда смещение отрицательное, оно указывает в положительном направлении. В неформальном языке все наоборот. Теперь тангенциальное ускорение действительно должно быть записано в причудливых математических обозначениях. Так полезнее. Также компенсируется масса, что интересно.
| ∑ F т = | ма т | ||||
| − мг sin θ = |
| ||||
| − г sin θ = |
| ||||
Это дифференциальное уравнение второго порядка, которое чрезвычайно сложно решить. Я никогда не делал этого сам. Вы можете подумать, что это конец этого обсуждения, но вы забыли одну вещь. Это простой маятник . В ней уже полно предположений, которые не соответствуют действительности (точечные массы, нерастяжимые струны и т. д.). Еще одно упрощение не помешает.
Я никогда не делал этого сам. Вы можете подумать, что это конец этого обсуждения, но вы забыли одну вещь. Это простой маятник . В ней уже полно предположений, которые не соответствуют действительности (точечные массы, нерастяжимые струны и т. д.). Еще одно упрощение не помешает.
аппроксимация малого угла
Вернемся к определению синуса как отношения стороны, противоположной ( x ) углу (θ) к гипотенузе ( r ). Вот (возможно, новый) факт для вас, известный как аппроксимация малого угла : длина противоположной стороны ( x ) приближается к длине дуги ( s ), когда угол (θ) приближается к нулю (0).
| θ→ 0 | ⇒ | x → с |
Это означает, что…
| sin θ = | х |
| р |
можно заменить на…
| sin θ ≈ | с |
| ℓ |
…для простого маятника, когда угол мал. Это дает нам дифференциальное уравнение, которое гораздо легче решить.
Это дает нам дифференциальное уравнение, которое гораздо легче решить.
| − г sin θ = |
| |||||||
|
| |||||||
|
|
Нам нужна функция, вторая производная которой равна самой себе со знаком минус. У нас есть два варианта: синус и косинус. Любой из них в порядке, поскольку они в основном идентичны по функциям с 9фазовый сдвиг 0° между ними. Без ограничения общности я выберу синус с произвольным фазовым углом (φ), который может быть равен 90°, если мы позволим. Или он равен 0° или какому-то другому углу. Другими параметрами общей синусоидальной функции являются амплитуда смещения ( с 0 ) и угловая частота (ω).
У нас есть два варианта: синус и косинус. Любой из них в порядке, поскольку они в основном идентичны по функциям с 9фазовый сдвиг 0° между ними. Без ограничения общности я выберу синус с произвольным фазовым углом (φ), который может быть равен 90°, если мы позволим. Или он равен 0° или какому-то другому углу. Другими параметрами общей синусоидальной функции являются амплитуда смещения ( с 0 ) и угловая частота (ω).
Основной метод, который я начал, называется « угадать и проверить «. Моя догадка состоит в том, что функция выглядит как обычная синусоидальная функция…
с = с 0 sin(ω t + φ)
и проверка состоит в том, чтобы снова включить его в дифференциальное уравнение и посмотреть, что произойдет.
| г 2 | с 0 sin(ω t + φ) | = − | г | с 0 sin(ω t + φ) |
| дт 2 | ℓ | |||
| − ω 2 s 0 sin(ω t + φ) | = − | г | с 0 sin(ω t + φ) | |
| ℓ | ||||
| ω 2 | = | г | ||
| ℓ | ||||
Отменяется в принципе все, кроме одного из трех моих параметров — угловой частоты.
| ω = √ | г |
| ℓ |
Я не думаю об угловых частотах. Они слишком абстрактны. Я хочу частоту — частоту без прилагательного впереди. Что-то, что использует герц [Гц] в качестве единицы измерения.
| f = | ω | = | 1 | √ | г |
| 2π | 2π | ℓ |
На самом деле, я даже этого не хочу. Маятники, как правило, медлительны. Я бы предпочел обратную частоту — период. Период простого маятника с малыми угловыми амплитудами определяется следующим уравнением…
| Т = 2π√ | ℓ |
| г |
Где…
| Т = | период [с], время совершения одного цикла движения |
| π = | математическая константа [безразмерная] |
| ℓ = | длина [м], измеренная от точки подвеса до массы |
| г = | гравитация [м/с 2 ], напряженность гравитационного поля в том месте, где работает маятник |
Что это говорит о простых маятниках…
- Период простого маятника от него не зависит масса .
 Легкий боб, тяжелый боб, без разницы. Это должно иметь смысл, поскольку ускорение свободно падающего тела не зависит от его массы. Однако по практическим причинам, возможно, стоит учитывать массу, когда добавляется сопротивление воздуха. Тяжелые массы менее подвержены аэродинамическому сопротивлению, чем более легкие, поскольку ускорение обратно пропорционально массе. Вы хотите, чтобы ваш маятник продолжал бороздить воздух? Тогда сделайте его массовым.
Легкий боб, тяжелый боб, без разницы. Это должно иметь смысл, поскольку ускорение свободно падающего тела не зависит от его массы. Однако по практическим причинам, возможно, стоит учитывать массу, когда добавляется сопротивление воздуха. Тяжелые массы менее подвержены аэродинамическому сопротивлению, чем более легкие, поскольку ускорение обратно пропорционально массе. Вы хотите, чтобы ваш маятник продолжал бороздить воздух? Тогда сделайте его массовым. - Период простого маятника пропорционален квадратному корню из его длина ( T ∝ √ℓ). Более длинным маятникам требуется больше времени, чтобы один раз качнуться вперед и назад, чем коротким. Удвоение периода простого маятника требует четырехкратного увеличения его длины. Это должно иметь интуитивно понятный смысл на каком-то уровне. Длинным ногам требуется больше времени, чтобы раскачиваться вперед и назад, чем коротким. Слон делает меньше шагов, чем мышь с той же скоростью.
- Период простого маятника обратно пропорционален квадратному корню из местной напряженности гравитационного поля ( T ∝ 1/√ г ).
 Не очень хорошо скатывается с языка, не так ли? Увеличение гравитации в четыре раза уменьшило бы вдвое период простого маятника. Не совсем та ситуация, с которой я мог столкнуться. Местная гравитация не сильно различается по поверхности Земли — по крайней мере, с точки зрения непосредственного человеческого восприятия — но она имеет значение, когда маятники — это то, как вы точно отслеживаете время.
Не очень хорошо скатывается с языка, не так ли? Увеличение гравитации в четыре раза уменьшило бы вдвое период простого маятника. Не совсем та ситуация, с которой я мог столкнуться. Местная гравитация не сильно различается по поверхности Земли — по крайней мере, с точки зрения непосредственного человеческого восприятия — но она имеет значение, когда маятники — это то, как вы точно отслеживаете время.
Чего только не скажешь о простых маятниках…
- Период простого маятника увеличивается с увеличением амплитуда таким образом, который трудно описать, трудно объяснить и часто не имеет значения.
коррекция большого угла
Уравнение для периода простого маятника, учитывающее большие углы, представляет собой приближение малых углов…
| Т = 2π√ | ℓ |
| г |
умножить на бесконечную сумму все меньших поправок. Первые 5 терминов показаны ниже. Я не буду пытаться вывести это уравнение.
Первые 5 терминов показаны ниже. Я не буду пытаться вывести это уравнение.
| T = 2π√ | ℓ | ⎡ ⎢ ⎣ | 1 + | ⎛ ⎜ ⎝ | 1 | ⎞ 2 ⎟ ⎠ | грех 2 | ⎛ ⎜ ⎝ | θ | ⎞ ⎟ ⎠ |
| г | 2 | 2 |
| + | ⎛ ⎜ ⎝ | 1 · 3 | ⎞ 2 ⎟ ⎠ | грех 4 | ⎛ ⎜ ⎝ | θ | ⎞ ⎟ ⎠ |
| 2 · 4 | 2 |
| + | ⎛ ⎜ ⎝ | 1 · 3 · 5 | ⎞ 2 ⎟ ⎠ | грех 6 | ⎛ ⎜ ⎝ | θ | ⎞ ⎟ ⎠ |
| 2 · 4 · 6 | 2 |
| + | ⎛ ⎜ ⎝ | 1 · 3 · 5 · 7 | ⎞ 2 ⎟ ⎠ | грех 8 | ⎛ ⎜ ⎝ | θ | ⎞ ⎟ ⎠ | + … | ⎤ ⎥ ⎦ |
| 2 · 4 · 6 · 8 | 2 |
Поскольку каждое слагаемое в этом бесконечном звере положительно, истинный период простого маятника всегда будет больше периода, рассчитанного с использованием приближения малых углов. Поправка добавляет <0,1% до 7°, <1% до 22°, <10% до 69°.° и около 18% при 90°.
Поправка добавляет <0,1% до 7°, <1% до 22°, <10% до 69°.° и около 18% при 90°.
Если допускаются еще большие углы, то поправка на большой угол достигает максимума +116% для маятников с углом отклонения 180°.
Другой вариант бесконечной суммы поправок показан ниже. Этот начинается с уравнения, полученного выше, и заменяет все синусоидальные функции их разложениями Тейлора (каждая из которых представляет собой бесконечную сумму сама по себе). Соберите одинаковые термины, удалите общие множители, и вот что вы получите…
| T = 2π√ | ℓ | ⎡ ⎢ ⎣ | 1 + | 1 | θ 2 |
| г | 16 |
| + | 11 | θ 4 |
| 3 072 |
| + | 173 | θ 6 |
| 737 280 |
| + | 22 931 | θ 8 | + … | ⎤ ⎥ ⎦ |
| 1 321 205 760 |
Определение маятника и уравнение | Что такое маятник в физике? — Видео и стенограмма урока
Научные курсы / AP Physics 1: подготовка к экзамену Курс / AP Physics 1: Колебания Глава
Кэтрин Кайлегян-Старки, Дэвид Вуд, Аманда Робб- Автор Кэтрин Кейлегиан-Старки
Кэтрин имеет степень бакалавра в области физики, и она стремится получить степень магистра в области прикладной физики.
Посмотреть биографию В настоящее время она преподает учащимся, испытывающим затруднения в области STEM, в муниципальном колледже Лейн.
В настоящее время она преподает учащимся, испытывающим затруднения в области STEM, в муниципальном колледже Лейн. - Инструктор Дэвид Вуд
Дэвид преподавал физику с отличием, физику AP, физику IB и курсы общих наук. Имеет степень магистра педагогики и степень бакалавра физики.
Посмотреть биографию - Экспертный участник Аманда Робб
Аманда преподает науку в средней школе более 10 лет. Она имеет степень магистра клеточной и молекулярной физиологии Медицинской школы Тафтса и степень магистра преподавания Колледжа Симмонса. Она также имеет сертификаты по среднему специальному образованию, биологии и физике в Массачусетсе.
Посмотреть биографию
Понять определение маятника в физике. Узнайте, как ньютоновская механика описывает движение маятников, их период и частоту с помощью уравнений. Обновлено: 17.10.2021
Содержание
- Определение маятника в физике
- Уравнение маятника
- Пример вычислений маятника
- Краткое содержание урока
Определение маятника в физике
Маятник определяется как свободно качающаяся масса, прикрепленная к фиксированной точке. В физике при изучении маятников принято моделировать движение с помощью простого маятника . Простой маятник — это упрощенная модель, в которой предполагается, что трос не имеет массы, а масса представляет собой сферическую и однородную точечную массу. Помимо физического строения маятника есть еще две определяющие характеристики: простое гармоническое движение и зависимость от гравитации. Простое гармоническое движение, или ГГМ, представляет собой колебательное движение , создаваемое восстанавливающей силой вокруг точки равновесия , а движение маятника является лишь одной из форм ГГМ. Гравитация также является определяющей характеристикой маятника, потому что, хотя некоторые маятники имеют внешнюю движущую силу, именно гравитация пытается вернуть массу обратно в равновесие, что создает характерное колебательное движение маятника.
В физике при изучении маятников принято моделировать движение с помощью простого маятника . Простой маятник — это упрощенная модель, в которой предполагается, что трос не имеет массы, а масса представляет собой сферическую и однородную точечную массу. Помимо физического строения маятника есть еще две определяющие характеристики: простое гармоническое движение и зависимость от гравитации. Простое гармоническое движение, или ГГМ, представляет собой колебательное движение , создаваемое восстанавливающей силой вокруг точки равновесия , а движение маятника является лишь одной из форм ГГМ. Гравитация также является определяющей характеристикой маятника, потому что, хотя некоторые маятники имеют внешнюю движущую силу, именно гравитация пытается вернуть массу обратно в равновесие, что создает характерное колебательное движение маятника.
Простое гармоническое движение в физике маятников
Понятия «колебательное движение» и «точка равновесия» имеют решающее значение для понимания маятников.
Колебательное движение : Движение, которое предсказуемо повторяется. Его часто математически моделируют синусоидальными волнами.
Точка равновесия : Место в системе, где система сбалансирована. Некоторые точки равновесия устойчивы, и системе трудно выйти из этой точки. Другие точки равновесия неустойчивы, и система легко меняется.
Когда маятник качается, его масса описывает дугу. Ближайшая к земле точка обычно является центром дуги и является точкой равновесия маятника. Однако он нестабилен, поэтому при раскачивании маятник легко выходит из равновесия. Гравитация притягивает массу, и она снова несется по дуге, пытаясь остаться как можно ближе к земле. Вот почему зависимость от гравитации является определяющей характеристикой маятника. При каждом последующем переходе к равновесию кинетическая энергия маятника превращается в потенциальную энергию, и колебания становятся все ниже и ниже.0101 амплитуды . Амплитуда волны определяется тем, насколько далеко она простирается выше 0. Если маятник приводится в движение, то каждый последующий взмах будет иметь ту же кинетическую энергию, что и раньше, поэтому амплитуда дуги останется постоянной. Именно это повторяющееся движение через равновесие делает маятниковое движение простым гармоническим движением.
Если маятник приводится в движение, то каждый последующий взмах будет иметь ту же кинетическую энергию, что и раньше, поэтому амплитуда дуги останется постоянной. Именно это повторяющееся движение через равновесие делает маятниковое движение простым гармоническим движением.
Что такое маятник?
Маятник представляет собой груз, подвешенный к неподвижной точке таким образом, что он может свободно качаться вперед и назад. Простой маятник — это маятник, в котором груз маятника рассматривается как точечная масса, а нить, на которой он висит, имеет незначительную массу. Простые маятники интересны с точки зрения физики, потому что они являются примером простого гармонического движения, очень похожего на пружины или резиновые ленты.
Простое гармоническое движение — это любое периодическое движение, в котором применяется восстанавливающая сила, пропорциональная смещению и направленная в направлении, противоположном этому смещению. Или, другими словами, чем больше вы тянете его в одну сторону, тем больше он хочет вернуться в середину. Это легко представить с помощью пружины, потому что вы чувствуете возрастающее усилие по мере того, как растягиваете ее все больше и больше.
Это легко представить с помощью пружины, потому что вы чувствуете возрастающее усилие по мере того, как растягиваете ее все больше и больше.
А маятник? Что ж, когда вы поднимаете маятник в одну сторону, сила тяжести хочет тянуть его обратно вниз, а натяжение нити хочет тянуть его влево (или вправо). Эти объединенные силы работают вместе, чтобы вернуть его к середине (положение равновесия). В конечном итоге, достигнув середины, скорость маятника увеличилась, поэтому он продолжает движение за пределы положения равновесия и уходит в другую сторону. Затем эта схема продолжается.
При маятнике (или любом простом гармоническом движении) скорость наибольшая в середине, но возвращающая сила (и, следовательно, ускорение) наибольшая на внешних краях.
Произошла ошибка при загрузке этого видео.
Попробуйте обновить страницу или обратитесь в службу поддержки.
Вы должны создать учетную запись, чтобы продолжить просмотр
Зарегистрируйтесь, чтобы просмотреть этот урок
Вы студент или преподаватель?
Создайте учетную запись, чтобы продолжить просмотр
В качестве члена вы также получите неограниченный доступ к более чем 84 000
уроки математики, английского языка, науки, истории и многое другое. Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспеть.
Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспеть.
Получите неограниченный доступ к более чем 84 000 уроков.
Попробуй это сейчас
Настройка занимает всего несколько минут, и вы можете отменить ее в любое время.
Уже зарегистрированы? Войдите здесь для доступ
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. 900:50 Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Назад
Далее: Различия между поступательным и вращательным движением
пройти викторину Смотреть Следующий урок
Повторить
Просто отмечаюсь.
 Вы все еще смотрите? Да! Продолжай играть.
Вы все еще смотрите? Да! Продолжай играть.Ваш следующий урок будет играть в 10 секунд
- 0:01 Что такое маятник?
- 1:30 Уравнения
- 2:55 Пример задачи
- 4:26 Итоги урока
Сохранить Сохранить Сохранить
Хронология
Автовоспроизведение
Автовоспроизведение
Скорость
Скорость
Уравнение маятника
СГМ маятника можно описать с помощью Ньютоновская механика . Ньютоновская механика связывает силу с массой и ускорением уравнением F = ma. Для простого маятника единственной силой, действующей на него, является сила тяжести, поэтому a = -g, если предположить, что +y находится вверху в системе координат. Поскольку движение маятника образует дугу, гравитация не может быть просто g. Масса будет по-разному ощущать гравитацию в зависимости от своего положения вдоль дуги, и уравнение силы должно представлять это. Эта последняя часть включена, рассматривая всю систему как треугольник и используя {eq}sin (\theta) {/eq}, так что {eq}F = -mgsin( \theta) {/eq}.
На практике найти {eq}\theta {/eq} часто невозможно, но угол, под которым проходит масса, совпадает с его угловой частотой, умноженной на времени, {eq}\omega t {/eq}. Частота — это количество колебаний, происходящих за заданное время, а угловая частота соотносит это время со временем, которое потребуется массе, чтобы пройти полный круг. Угловая частота равна {eq}\omega = \sqrt(g/L) {/eq}, а частота равна {eq}(1/2\pi) \sqrt(g/L) {/eq}, где L – расстояние масса от точки вращения.
Частота — это количество колебаний, происходящих за заданное время, а угловая частота соотносит это время со временем, которое потребуется массе, чтобы пройти полный круг. Угловая частота равна {eq}\omega = \sqrt(g/L) {/eq}, а частота равна {eq}(1/2\pi) \sqrt(g/L) {/eq}, где L – расстояние масса от точки вращения.
Что означает период маятника?
Почти невозможно говорить о частоте, не говоря о периоде. Период маятника — это время, которое требуется маятнику, чтобы пройти через точку равновесия и снова вернуться. Математически это величина, обратная частоте, {eq}T = 2\pi \sqrt(L/g) {/eq}. T — это обычный способ представления периода, а L, как и в предыдущих уравнениях, — это расстояние, на котором находится масса от точки вращения. Коэффициент {eq}2\pi {/eq} появляется потому, что типичное синусоидальное колебание имеет период {eq}2\pi {/eq}, а все колебания представляют собой преобразование основной синусоиды. 9{-2} {/eq}
L = {eq}2m {/eq}
Частота = {eq}1/2 \pi \sqrt(9,81/2) {/eq}
{eq}= 3,4788 {/eq}
2) Чтобы найти угловую частоту, просто удалите {eq}1/2 \pi {/eq} из приведенного выше вычисления, чтобы получить {eq}\sqrt(9,81/2) = 2,214 {/eq}
Пример 2. {\circ} {/eq} с осью Y. 9{\circ} {/eq} маятник испытывает силу 480 Н в направлении -x. N означает ньютоны и является мерой силы. Этот расчет можно было бы так же легко сделать для силы, которую маятник испытывает в направлении y, используя вместо этого {eq}cos(\theta) {/eq}.
{\circ} {/eq} с осью Y. 9{\circ} {/eq} маятник испытывает силу 480 Н в направлении -x. N означает ньютоны и является мерой силы. Этот расчет можно было бы так же легко сделать для силы, которую маятник испытывает в направлении y, используя вместо этого {eq}cos(\theta) {/eq}.
Краткий обзор урока
Маятник представляет собой свободно качающуюся массу, закрепленную на одном конце и подверженную простому гармоническому движению (SHM). Простое гармоническое движение — это колебательное движение , потому что он движется предсказуемым образом вокруг точки равновесия , положения, в котором система уравновешена. Если равновесие устойчиво, система будет стремиться остаться в равновесии, но маятник имеет неустойчивое равновесие, и именно эта неустойчивость приводит к его СГМ. Графически простое гармоническое движение является синусоидальным, и ведомый маятник будет иметь постоянную амплитуду или расстояние от оси x, в то время как невключенный маятник будет иметь амплитуду, уменьшающуюся до нуля.
Любое движение можно описать с помощью механики, и самый простой способ изучить маятник — это Ньютоновская механика , которая связывает силу, которую испытывает объект, с его массой и ускорением. Силы являются векторами , что означает, что они имеют величину и направление, поэтому важно обращать внимание на ориентацию оси при расчете ньютоновских сил. В уравнении силы для маятника {eq}-mgsin(\theta) {/eq}, {eq}\theta {/eq} можно заменить на {eq}\omega {/eq}, что представляет угловая частота . Будь то тангенциальная или угловая частота, частота подразумевает, как часто синусоидальный цикл повторяется за заданный промежуток времени. Обратная частота равна периоду , а период — это измерение того, сколько времени требуется системе, чтобы совершить один оборот.
Уравнения
Существует множество уравнений для описания маятника. Одно уравнение говорит нам, что период времени маятника, T , равен 2π, умноженным на квадратный корень из 9. 0453 L над g , где L — длина струны, а g — ускорение свободного падения (которое на Земле равно 9,8).
0453 L над g , где L — длина струны, а g — ускорение свободного падения (которое на Земле равно 9,8).
Но поскольку все простые гармонические движения синусоидальны, мы также имеем синусоидальное уравнение:
Здесь говорится, что смещение в направлении x равно амплитуде вариации, A (иначе максимальное водоизмещение), умноженное на синус омега- t , где омега — угловая частота вариации, а t — время. В этом уравнении вы запускаете свой математический секундомер посередине — время, t = 0, находится прямо посередине, когда оно проходит мимо.
Наконец, вам может быть интересно: что такое угловая частота? Ну, угловая частота — это количество радиан, которое проходит каждую секунду. Полные 360 градусов составляют 2 пи радиана, и это представляет собой одно полное колебание: от середины к одной стороне, обратно к середине к другой стороне, а затем снова к середине. Вы можете преобразовать эту угловую частоту в обычную частоту, разделив угловую частоту на 2pi. Обычная частота просто говорит вам о количестве полных циклов в секунду и измеряется в герцах.
Вы можете преобразовать эту угловую частоту в обычную частоту, разделив угловую частоту на 2pi. Обычная частота просто говорит вам о количестве полных циклов в секунду и измеряется в герцах.
Пример проблемы
Хорошо, давайте рассмотрим пример. Маятник длиной 4 м совершает полный оборот 0,25 раза в секунду. Максимальное смещение маятника достигает 0,1 метра от центра. Каков период колебаний? А какое водоизмещение через 0,6 секунды?
Прежде всего, мы должны записать то, что мы знаем. L , длина маятника равна 4 метрам. Частота маятника f 0,25, амплитуда (или максимальное смещение) A равно 0,1, а время t равно 0,6. Также г , как всегда, 9,8. Мы пытаемся найти T , а также x .
Прежде всего, чтобы найти T , мы просто подставляем числа в это уравнение и решаем. 2pi умножить на квадратный корень из 4, деленный на 9,8. Получается 4,01 секунды.
Далее, чтобы найти x , нам сначала нужно вычислить угловую частоту. Обычная частота составляет 0,25 Гц, поэтому просто умножьте ее на 2pi, и мы получим омегу. Получается угловая частота 1,57 радиана в секунду. Теперь подставьте числа в уравнение смещения, и, убедившись, что ваш калькулятор находится в режиме радианов, мы получим смещение 0,08 метра.
Обычная частота составляет 0,25 Гц, поэтому просто умножьте ее на 2pi, и мы получим омегу. Получается угловая частота 1,57 радиана в секунду. Теперь подставьте числа в уравнение смещения, и, убедившись, что ваш калькулятор находится в режиме радианов, мы получим смещение 0,08 метра.
Вот и все; у нас есть ответ.
Краткий обзор урока
Маятник представляет собой груз, подвешенный к неподвижной точке таким образом, что он может свободно качаться вперед и назад. Простой маятник — это маятник, в котором груз маятника рассматривается как точечная масса, а нить, на которой он висит, имеет незначительную массу.
Простой маятник совершает простое гармоническое движение. Простое гармоническое движение — это любое движение, при котором применяется восстанавливающая сила, пропорциональная смещению и направленная в направлении, противоположном этому смещению. При маятнике (или любом простом гармоническом движении, если на то пошло) скорость наибольшая в середине, но восстанавливающая сила (и, следовательно, ускорение) наибольшая на внешних краях.
Эти уравнения можно использовать для решения задач с маятниками:
Здесь х — смещение маятника, А — амплитуда, омега — угловая частота, t — время, g — ускорение свободного падения (которое всегда равно 9,8). на Земле), T — период времени маятника, L — длина струны, f — регулярная (неугловая) частота.
Результаты обучения
После завершения этого урока вы сможете:
- Дать определение маятнику
- Объясните простое гармоническое движение маятника
- Определите уравнения, используемые для решения задач маятника
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свой аккаунт
Что такое маятник?
Маятник представляет собой груз, подвешенный к неподвижной точке таким образом, что он может свободно качаться вперед и назад. Простой маятник — это маятник, в котором груз маятника рассматривается как точечная масса, а нить, на которой он висит, имеет незначительную массу. Простые маятники интересны с точки зрения физики, потому что они являются примером простого гармонического движения, очень похожего на пружины или резиновые ленты.
Простой маятник — это маятник, в котором груз маятника рассматривается как точечная масса, а нить, на которой он висит, имеет незначительную массу. Простые маятники интересны с точки зрения физики, потому что они являются примером простого гармонического движения, очень похожего на пружины или резиновые ленты.
Простое гармоническое движение — это любое периодическое движение, в котором применяется восстанавливающая сила, пропорциональная смещению и направленная в направлении, противоположном этому смещению. Или, другими словами, чем больше вы тянете его в одну сторону, тем больше он хочет вернуться в середину. Это легко представить с помощью пружины, потому что вы чувствуете возрастающее усилие по мере того, как растягиваете ее все больше и больше.
А маятник? Что ж, когда вы поднимаете маятник в одну сторону, сила тяжести хочет тянуть его обратно вниз, а натяжение нити хочет тянуть его влево (или вправо). Эти объединенные силы работают вместе, чтобы вернуть его к середине (положение равновесия). В конечном итоге, достигнув середины, скорость маятника увеличилась, поэтому он продолжает движение за пределы положения равновесия и уходит в другую сторону. Затем эта схема продолжается.
В конечном итоге, достигнув середины, скорость маятника увеличилась, поэтому он продолжает движение за пределы положения равновесия и уходит в другую сторону. Затем эта схема продолжается.
При маятнике (или любом простом гармоническом движении) скорость наибольшая в середине, но возвращающая сила (и, следовательно, ускорение) наибольшая на внешних краях.
Уравнения
Существует множество уравнений для описания маятника. Одно уравнение говорит нам, что период времени маятника, T , равен 2π, умноженным на квадратный корень из L из g , где L — длина струны, а g — это ускорение свободного падения (которое составляет 90,8 на Земле).
Но поскольку все простые гармонические движения синусоидальны, мы также имеем синусоидальное уравнение:
Здесь говорится, что смещение в направлении x равно амплитуде вариации, A (также известной как максимальное смещение), умноженной на синусоиду омега- t , где омега равна угловая частота вариации, т это время. В этом уравнении вы запускаете свой математический секундомер посередине — время, t = 0, находится прямо посередине, когда оно проходит мимо.
В этом уравнении вы запускаете свой математический секундомер посередине — время, t = 0, находится прямо посередине, когда оно проходит мимо.
Наконец, вам может быть интересно: что такое угловая частота? Ну, угловая частота — это количество радиан, которое проходит каждую секунду. Полные 360 градусов составляют 2 пи радиана, и это представляет собой одно полное колебание: от середины к одной стороне, обратно к середине к другой стороне, а затем снова к середине. Вы можете преобразовать эту угловую частоту в обычную частоту, разделив угловую частоту на 2pi. Обычная частота просто говорит вам о количестве полных циклов в секунду и измеряется в герцах.
Пример проблемы
Хорошо, давайте рассмотрим пример. Маятник длиной 4 м совершает полный оборот 0,25 раза в секунду. Максимальное смещение маятника достигает 0,1 метра от центра. Каков период колебаний? А какое водоизмещение через 0,6 секунды?
Прежде всего, мы должны записать то, что мы знаем. L , длина маятника равна 4 метрам. Частота маятника f 0,25, амплитуда (или максимальное смещение) A равно 0,1, а время t равно 0,6. Также г , как всегда, 9,8. Мы пытаемся найти T , а также x .
Частота маятника f 0,25, амплитуда (или максимальное смещение) A равно 0,1, а время t равно 0,6. Также г , как всегда, 9,8. Мы пытаемся найти T , а также x .
Прежде всего, чтобы найти T , мы просто подставляем числа в это уравнение и решаем. 2pi умножить на квадратный корень из 4, деленный на 9,8. Получается 4,01 секунды.
Далее, чтобы найти x , нам сначала нужно вычислить угловую частоту. Обычная частота составляет 0,25 Гц, поэтому просто умножьте ее на 2pi, и мы получим омегу. Получается угловая частота 1,57 радиана в секунду. Теперь подставьте числа в уравнение смещения, и, убедившись, что ваш калькулятор находится в режиме радианов, мы получим смещение 0,08 метра.
Вот и все; у нас есть ответ.
Краткий обзор урока
Маятник представляет собой груз, подвешенный к неподвижной точке таким образом, что он может свободно качаться вперед и назад. Простой маятник — это маятник, в котором груз маятника рассматривается как точечная масса, а нить, на которой он висит, имеет незначительную массу.
Простой маятник совершает простое гармоническое движение. Простое гармоническое движение — это любое движение, при котором применяется восстанавливающая сила, пропорциональная смещению и направленная в направлении, противоположном этому смещению. При маятнике (или любом простом гармоническом движении, если на то пошло) скорость наибольшая в середине, но восстанавливающая сила (и, следовательно, ускорение) наибольшая на внешних краях.
Эти уравнения можно использовать для решения задач с маятниками:
Здесь х — смещение маятника, А — амплитуда, омега — угловая частота, t — время, g — ускорение свободного падения (которое всегда равно 9,8). на Земле), T — период времени маятника, L — длина струны, f — регулярная (неугловая) частота.
Результаты обучения
После завершения этого урока вы сможете:
- Дать определение маятнику
- Объясните простое гармоническое движение маятника
- Определите уравнения, используемые для решения задач маятника
Чтобы разблокировать этот урок, вы должны быть участником Study. com.
com.
Создайте свой аккаунт
Соберите свой собственный маятник
В этом упражнении учащиеся должны построить свой собственный маятник и вычислить период, используя уравнение урока, и сравнить его с фактическим измерением, полученным при наблюдении за маятником. Для выполнения этого упражнения вам понадобится подставка для колец, С-образный зажим, веревка длиной около 20 см и шайба.
Инструкции для учащихся
Теперь, когда вы знакомы с маятником и некоторыми уравнениями, пришло время составить свой собственный маятник. Следуйте инструкциям ниже, чтобы построить маятник, затем мы рассчитаем и , наблюдая за периодом и сравнивая наши результаты.
- Прикрепите С-образный зажим к кольцевой стойке так, чтобы он был перпендикулярен стойке.
- Отрежьте веревку длиной 0,2 м или достаточной длины, чтобы между землей и веревкой, когда она будет привязана, оставался дюйм. Привяжите веревку к С-образному зажиму.
- Затем привяжите шайбу к нижней части веревки.

- Измерьте расстояние между верхней частью струны и нижней частью шайбы. Это длина ( L ) маятника.
- Используйте уравнение урока для расчета периода. Запишите свою работу и свой окончательный ответ.
- Затем поднимите маятник и отпустите его. Запишите, сколько времени требуется маятнику, чтобы совершить одно движение вперед и назад в секундах. Это наблюдаемый период.
- Далее, повторите это испытание четыре раза и возьмите средний наблюдаемый период.
Вопросы
- Как расчетный период сравнивается с наблюдаемым периодом? Если была разница, объясните, почему вы думаете, что это могло произойти.
- Чем средний период наблюдения отличался от единичного наблюдения? Почему мы берем среднее значение в науке?
- Объясните, как этот эксперимент продемонстрировал простое гармоническое движение.
- Какие есть приложения для изучения периода маятника?
Ожидаемые результаты
Учащиеся должны увидеть небольшое расхождение между фактическим периодом и наблюдаемым. Наблюдаемый период может быть больше из-за взаимодействия с сопротивлением воздуха и трением. Точность измерений студентов также может вызвать расхождение между расчетными и наблюдаемыми результатами. Маятник показывает простое гармоническое движение, потому что, когда маятник тянут в одну сторону, движение при отпускании равно, но противоположно. Со временем маятник замедляется из-за сопротивления воздуха.
Наблюдаемый период может быть больше из-за взаимодействия с сопротивлением воздуха и трением. Точность измерений студентов также может вызвать расхождение между расчетными и наблюдаемыми результатами. Маятник показывает простое гармоническое движение, потому что, когда маятник тянут в одну сторону, движение при отпускании равно, но противоположно. Со временем маятник замедляется из-за сопротивления воздуха.
Зарегистрируйтесь для просмотра этого урока
Вы студент или преподаватель?
Разблокируйте свое образование
Убедитесь сами, почему 30 миллионов человек используют Study.com
Станьте участником Study.com и начните учиться прямо сейчас.
Стать участником
Уже являетесь участником? Войти
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков
и учебные ресурсы‐все
в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Спинка
myPhysicsLab Simple Pendulum
myPhysicsLab Simple Pendulumпоказать сима Терминал
команда >
Физическое моделирование простого маятника.
Измените гравитацию, массу или трение (демпфирование). Перетащите маятник, чтобы изменить начальную должность. Или нажмите ниже, чтобы установить начальные условия:
Математика моделирования показана ниже. Также доступны: открытый исходный код, документация и просто-скомпилированная версия который более настраиваемый.
Для небольших колебаний простой маятник имеет линейное поведение, что означает, что его уравнение движения можно охарактеризовать линейным уравнением (без квадратов членов или синус или косинус), но для больших колебаний он становится очень нелинейным с синусоидальный член в уравнении движения.
Пазлы
Попробуйте использовать график и изменить параметры, такие как масса, длина, гравитация, чтобы ответить эти вопросы (для простоты оставьте демпфирование равным нулю):
- Какая связь между угловым ускорением и углом?
- Как масса, длина или гравитация влияют на взаимосвязь между угловыми ускорение и угол?
- Как для малых колебаний длина или сила тяжести влияют на период или частота колебаний?
Ниже вы найдете ответы.
Физика — метод вращения
маятниковые переменные
Маятник моделируется как точечная масса на конце безмассового стержня. Мы определяем следующие переменные:
- θ = угол маятника ( 0= вертикально)
- Р = длина стержня
- Т = натяжение в тяге
- м = масса маятника
- г = гравитационная постоянная
Выведем уравнение движения маятника, используя вращательный аналог Второй закон Ньютона для движения вокруг неподвижной оси, который τ = I α где
- т = чистый крутящий момент
- я = инерция вращения
- α = θ» = угловое ускорение
Вращательная инерция вокруг оси составляет I = м R 2 . Крутящий момент может быть
рассчитывается как векторное векторное произведение вектора положения и силы. величина крутящего момента из-за силы тяжести получается равной т = — R м г sin θ . Итак, у нас есть
величина крутящего момента из-за силы тяжести получается равной т = — R м г sin θ . Итак, у нас есть
− R м г sin θ = м R 2 α
, что упрощается до
| θ» = − г ⁄ R sin θ | (1) |
Это уравнение движения маятника.
Физика — Прямой метод
Большинство людей менее знакомы с вращательной инерцией и крутящим моментом, чем с простая масса и ускорение, найденные во втором законе Ньютона, F = м а . Чтобы показать, что во вращательной версии второго закона Ньютона нет ничего нового, мы вывести здесь уравнение движения без вращательной динамики. Как вы увидите, этот метод включает в себя больше алгебры.
силы маятника
Нам понадобятся стандартные единичные векторы,
я, дж
. Мы используем жирный шрифт и зачеркивание, чтобы
указать вектор.
- я = единичный вектор в горизонтальном направлении
- Дж = единичный вектор в вертикальном направлении
Кинематика маятника следующая
позиция = R sin θ i − R cos θ j
скорость = R θ’ cos θ i + R θ’ sin θ j
ускорение = R ( θ» cos θ я — θ’ 2 sin θ i + θ» sin θ j + θ’ 2 cos θ j)
Положение определяется довольно простым применением тригонометрии. скорость и ускорение являются тогда первой и второй производными положения.
Далее рисуем диаграмму свободного тела маятника. Силы на маятник равны напряжение в стержне Т и гравитация. Таким образом, мы можем записать чистую силу как:
F = T cos θ Дж − T sin θ i − м г Дж
Используя закон Ньютона F = м а и ускорение маятника, которое мы нашли ранее у нас было
T cos θ j − T sin θ i − m g j = м R ( θ» cos θ i − θ’ 2 sin θ i + θ» sin θ j + θ’ 2 cos θ j)
Запишите векторные компоненты приведенного выше уравнения в виде отдельных уравнений. Это дает
два одновременных уравнения: первое для
я
компонента, а второй для
в
Дж
составная часть.
Это дает
два одновременных уравнения: первое для
я
компонента, а второй для
в
Дж
составная часть.
− T sin θ = м R ( θ» cos θ − θ’ 2 sin 90 5 sin 90 5
Т COS θ — M g = M R ( θ ‘ SIN θ + θ 595559555955595545595545595549554954549545454545454549545495549545495454545454545454545454974454545454545454545454549н
Теперь выполните некоторые алгебраические операции, чтобы исключить неизвестное. Т . Умножить первое уравнение cos θ а второй по грех θ .
− T sin θ cos θ = м R ( θ» cos 2 θ − θ’ 2 sin θ cos θ )
T cos θ sin θ − м г sin θ = м R ( θ» sin 2 θ + θ’ 2 sin θ cos θ )
Используйте первое уравнение для замены T cos θ sin θ во-вторых уравнение и проделайте еще немного алгебры, чтобы получить:
— θ » COS 2 θ + θ ‘ 2 SIN θ COS θ = θ’ SIN 2 29458 29458 2 2 29458 29458 2 29458 2 9058 2 9058 29458 2 9058 2 9058 2 9058 2 9058 2 9058 2 9058 2 9058 2 9058 2 9058. θ’ 2 sin θ cos θ + г ⁄ R sin θ
θ’ 2 sin θ cos θ + г ⁄ R sin θ
С идентификатором триггера cos 2 θ + sin 2 θ = 1 это упрощает уравнение (1)
θ» = − г ⁄ R sin θ
Физика — энергетический метод
Есть еще третий способ вывести уравнения движения маятника. Это использовать «косвенный» энергетический метод, связанный с терминами «лагранжиан», «Уравнения Эйлера-Лагранжа», «Гамильтониан» и другие. Пока этот метод не показан здесь вы можете увидеть пример этого на Страница моделирования Pendulum+Cart.
Численное решение
Чтобы решить уравнения движения численно, чтобы мы могли управлять симуляцией,
мы используем метод Рунге Кутта
для решения систем обыкновенных дифференциальных уравнений. Сначала мы определяем переменную для
угловая скорость ω = θ’ . Тогда мы можем записать уравнение второго порядка (1) в виде двух
уравнения первого порядка.
Тогда мы можем записать уравнение второго порядка (1) в виде двух
уравнения первого порядка.
θ’ = ω
ω ‘ = — г ⁄ R sin θ
Это бланк, необходимый для использования метода Рунге-Кутта.
Ответы на головоломки
Вопрос: Какова связь между угловым ускорением и углом?
Ответ: Это синусоидальное соотношение, заданное уравнением (1):
θ» = − г ⁄ R sin θ
Вопрос: Как масса, длина или сила тяжести влияют на соотношение между угловым ускорением и углом?
Ответ: Из уравнения (1) мы видим, что:
- Масса вообще не влияет на движение.
- Амплитуда синусоидального соотношения пропорциональна силе тяжести.
- Амплитуда синусоидального соотношения обратно пропорциональна длине
маятника.

Вопрос: Как для малых колебаний длина или сила тяжести влияют на период или частота колебаний?
Ответ: Для малых колебаний мы можем использовать приближение, что грех θ = θ . Тогда уравнение движения принимает вид
θ» = − г ⁄ R θ
Это линейная зависимость. Вы можете видим, что график зависимости ускорения от угла представляет собой прямую линию для малых колебания. Это та же форма уравнения, что и для имитация одной пружины. Аналитическое решение:
$$\theta(t) = \theta_0 \cos(\sqrt{g/R} \; t)$$
, где θ 0 — начальный угол и т время. Период это время, необходимое для θ ( т )
$$period = \frac{2 \pi}{\sqrt{g/R}}$$
Частота колебаний обратно пропорциональна периоду:
$$frequency = \frac{ 1}{2 \pi} \sqrt{g/R}$$
Итак, мы предсказываем, что
- увеличение длины в 4 раза удваивает период и вдвое уменьшает частоту;
- увеличение силы тяжести в 4 раза сокращает вдвое период и удваивает частоту;
Эта веб-страница была впервые опубликована в апреле 2001 года.
Маятниковая змея: физико-математическая деятельность
Десять маятников качаются взад-вперед с немного разной скоростью, определяемой длиной струн. Начавшись синхронно, модель со временем меняется, пока, наконец, маятники не перестраиваются.
Предмет:
Математика
Физика
Механика
Ключевые слова:
маятник
период
frequency
exhibit-based
NGSS and EP&Cs:
PS
PS2
CCCs
Patterns
Cause and Effect
Structure and Function
Stability and Change
Tools and Materials
- Труба из ПВХ, сортамент 40, внутренний диаметр 1/2 дюйма (1,25 см), длина 10 футов (3 м)
Примечание. Это стандартная длина, которую вы найдете в магазинах товаров для дома. Для удобства транспортировки вы можете разрезать его на две 1,5-метровые части. - Резак для ПВХ
- Измерительная лента или измерительная линейка с английскими и метрическими единицами измерения.

- Линейка длиной не менее 2 футов (60 см)
- Карандаш
- Сверлильный станок или направляющая сверла
- Сверлильный шаблон (или деревянные блоки, горячий клей и зажимы для его изготовления) или другой метод крепления ПВХ во время сверления.
- Электрическая дрель и сверло 1/8 дюйма (3 мм)
- Двадцать винтов с плоской головкой Phillips для листового металла, № 6 x 1/2 дюйма (13 мм)
- Крестообразная отвертка
- 30-футовая (9-метровая) веревка (плетеная веревка, такая как бечевка каменщика или меловая бечевка, подойдет лучше всего, так как она не расплетается)
- Ножницы
- Десять шестигранных гаек 3/4 дюйма (2 см)
- Гобеленовая игла № 16, прямая (не изогнутая), продается в магазинах для рукоделия (если нет, можно заменить скрепкой; инструкции приведены ниже).
- Два 1/2-дюймовых (1 см) колена из ПВХ под углом 90 градусов
- Два 1/2-дюймовых (1 см) Т-образных соединения из ПВХ
- Четыре 1/2-дюймовых (1 см) муфты или колпачка из ПВХ.

- 21-дюймовая (50-сантиметровая) деревянная доска 1 x 4 или эквивалент
Примечание. «1 x 4» — это стандартное обозначение для пиломатериалов толщиной 3/4 дюйма (2 см) и шириной 3 1/2 дюйма (9 см).
Сборка
Обратите внимание, что эта закуска состоит из четырех частей. В части I вы разрежете ПВХ и отметите расположение отверстий, из которых будут висеть маятники. В Части II вы просверлите отверстия в трубе. В части III вы добавите маятники. В Части IV вы завершите сборку и запустите маятниковую змею.
Часть I. Разрежьте ПВХ и отметьте расположение отверстий
- Используя ножницы для ПВХ и измерительную ленту с метрическими единицами измерения, отрежьте следующие семь отрезков трубы из ПВХ:
- Один кусок 58 см
- Два куска по 45 см.
- Четыре куска по 25 см.
Отложите все, кроме самой длинной трубы. Другие части будут использованы для создания каркаса в Части IV.

- С помощью карандаша и линейки начертите три прямые линии по длине трубы длиной 58 см. Линии должны быть параллельны друг другу и примерно в 1 см друг от друга.
- Работая только по центральной линии, установите трубу горизонтально и начните делать следующие отметки:
- Первую отметку сделайте в 5 см от конца трубы
- Сделайте вторую отметку на 3 см дальше.
- Сделайте третью отметку в 2 см от второй отметки.
- Сделайте четвертую отметку на 3 см дальше.
- Сделайте пятую отметку в 2 см от этой отметки.
- Карандашом пронумеруйте сделанные вами точки от 1 до 20.
- Перейдите к верхней строке и поставьте точку прямо над каждым нечетным числом, отмеченным на центральной линии (то есть над 1, 3, 5 и т.
 д.). Затем перейдите к нижней строке и поставьте точку непосредственно под каждым четным числом, отмеченным на центральной линии (то есть под 2, 4, 6 и т. д.). Когда вы закончите, у вас должно быть 10 меток в верхней строке, 20 (пронумерованных) меток в центральной линии и 10 меток в нижней строке (щелкните, чтобы увеличить диаграмму ниже).
д.). Затем перейдите к нижней строке и поставьте точку непосредственно под каждым четным числом, отмеченным на центральной линии (то есть под 2, 4, 6 и т. д.). Когда вы закончите, у вас должно быть 10 меток в верхней строке, 20 (пронумерованных) меток в центральной линии и 10 меток в нижней строке (щелкните, чтобы увеличить диаграмму ниже).
Часть II: Просверлите отверстия
- Найдите способ прочно удерживать размеченную ПВХ-трубу на месте, чтобы вы могли просверлить ее. Расположите трубу так, чтобы центральная линия с нарисованными карандашом цифрами проходила вдоль верхней части трубы.
Примечание. Сверлильный кондуктор будет надежно удерживать трубу, предотвращая ее скатывание во время работы и защищая поверхность под ней. Если у вас нет приспособления для сверления, вы можете сделать его, приклеив деревянные обрезки к основанию, а затем прикрепив приспособление к столу или сверлильному станку (см. фото ниже).
- Как только труба закреплена, пора начинать бурение.
 Первые отверстия будут сделаны на пронумерованных метках центральной линии. Однако вам нужно будет сделать отверстия, которые проходят как через верхнюю стенку трубы, так и через нижнюю стенку, прямо под ними.
Первые отверстия будут сделаны на пронумерованных метках центральной линии. Однако вам нужно будет сделать отверстия, которые проходят как через верхнюю стенку трубы, так и через нижнюю стенку, прямо под ними.Вы можете либо просверлить оба набора отверстий одновременно (см. Вариант А ниже), либо просверлить одну сторону, повернуть трубу и просверлить другую (см. Вариант Б ниже). Используйте вариант А, если у вас есть доступ к сверлильному станку и вы знакомы с его использованием, или если вы уверены в своей способности сверлить почти идеально вертикально ручной дрелью. (Может помочь недорогой направитель для сверла.) В противном случае используйте вариант Б.
- Вариант А:
В каждой отметке на средней линии просверлите отверстия диаметром 1/8 дюйма (3 мм) в верхней стенке трубы и продолжайте сверлить в нижней стенке.
- Вариант Б:
В каждой отметке на средней линии просверлите отверстия диаметром 1/8 дюйма (3 мм) в верхней стенке трубы.
 Когда вы закончите, поверните трубу так, чтобы линия просверленных отверстий оказалась на дне трубы. Затем в верхней части трубы (непосредственно над набором отверстий, которые вы только что просверлили) нарисуйте прямую линию по длине трубы и отметьте ее точно так же, как вы делали это в шаге 3 выше. Когда вы закончите, просверлите отверстия диаметром 1/8 дюйма (3 мм) в этих местах, как вы делали это на противоположной стороне трубы.
Когда вы закончите, поверните трубу так, чтобы линия просверленных отверстий оказалась на дне трубы. Затем в верхней части трубы (непосредственно над набором отверстий, которые вы только что просверлили) нарисуйте прямую линию по длине трубы и отметьте ее точно так же, как вы делали это в шаге 3 выше. Когда вы закончите, просверлите отверстия диаметром 1/8 дюйма (3 мм) в этих местах, как вы делали это на противоположной стороне трубы.
- Вариант А:
- Когда центральные отверстия просверлены, переориентируйте трубу так, чтобы одна из двух «боковых линий» теперь находилась в верхней части трубы. В каждой отметке на линии просверлите отверстие диаметром 1/8 дюйма (3 мм) в первой стенке трубы. (Не сверлите противоположную стену насквозь!) Когда вы закончите, у вас должно получиться 10 отверстий.
- Снова поверните трубу и повторите для второй боковой линии. Когда все отверстия просверлены, можно приступать к установке маятников.
- Вверните шуруп для листового металла на несколько витков (не до конца) в каждое отверстие, которое вы просверлили на двух боковых линиях.
 Всего должно быть 20 винтов, по 10 на каждой боковой линии (нажмите, чтобы увеличить фото ниже).
Всего должно быть 20 винтов, по 10 на каждой боковой линии (нажмите, чтобы увеличить фото ниже).
Часть III: добавление маятников
- Ножницами отрежьте 10 отрезков плетеной нити следующим образом:
- Два куска по 100 см.
- Две части по 90 см.
- Два куска по 80 см.
- Четыре куска по 70 см.
- Наденьте на гобеленовую иглу отрезок нити длиной 100 см. Проденьте иглу вниз через первый набор отверстий (сверху вниз) на центральной линии. Наденьте шестигранную гайку на струну, а затем снова проденьте струну через следующий набор отверстий (снизу вверх) на центральной линии (см. фото ниже).
Примечание. Если у вас нет гобеленовой иглы, выпрямите скрепку и используйте небольшой кусочек малярного скотча, чтобы скрепить проволоку и нить.
- Снимите гобеленовую иглу и оберните каждый конец нити вокруг ближайшего к нему винта на боковой линии. Затем затяните винты настолько, чтобы удерживать струну на месте (см.
 фото ниже).
фото ниже). - Повторите шаги 2 и 3 для второго отрезка веревки длиной 100 см, используя третий и четвертый наборы отверстий. (Не забудьте добавить шестигранную гайку!) Затем используйте тот же процесс, чтобы добавить остальные маятники, как показано ниже:
- Повторите для двух отрезков веревки длиной 90 см, используя 5-й и 6-й наборы отверстий, а также 7-й и 8-й наборы отверстий.
- Повторите то же самое для двух отрезков веревки длиной 80 см, используя 9-й и 10-й наборы отверстий, а также 11-й и 12-й наборы отверстий.
- Повторите то же самое для четырех отрезков веревки длиной 70 см, используя четыре оставшиеся пары наборов отверстий (13 и 14; 15 и 16; 17 и 18; 19 и 20).
- Теперь у вас должно быть 10 петель с шестигранными гайками: каждая представляет собой отдельный маятник.
Часть IV. Соберите раму и приведите маятниковую змею в движение
- Используйте оставшиеся куски ПВХ, чтобы собрать раму, как показано на фото ниже (нажмите, чтобы увеличить).
 Когда сборка завершена, пришло время отрегулировать длину маятников.
Когда сборка завершена, пришло время отрегулировать длину маятников. - Начиная с первого маятника, в который вы продели нити (первые 100 см длины нити), тщательно отрегулируйте каждый из них до следующих длин: 38,8 см, 35,8 см, 33,1 см, 30,7 см, 28,5 см, 26,6 см, 24,8 см, 23,3 см, 21,8 см, 20,5 см
Для этого измерьте расстояние от нижней части трубы из ПВХ, посередине между двумя подвесными нитями, до центра отверстия в шестигранной гайке (центр масс шестигранной гайки). Когда маятник станет нужной длины, плотно затяните винты, оставив лишние струны на месте.
- Используя тот же метод, отрегулируйте все струны, пока не будет достигнута желаемая длина и все винты не будут затянуты.
- Наконец, дважды проверьте длину каждого маятника. Затем используйте ножницы, чтобы обрезать лишнюю нить, которая может мешать ее движению. (Однако обязательно оставьте немного веревки на случай, если вам понадобится внести изменения позже.) Установите рядом 21-дюймовую (50-сантиметровую) доску, чтобы заставить маятниковую змейку двигаться, и вы готовы к работе ( смотрите фото ниже).

Действия и уведомления
Встаньте лицом к ряду маятников и используйте деревянную доску, чтобы потянуть их все к себе одновременно (см. фото ниже). Переверните доску, чтобы быстро убрать ее с дороги, а затем откиньтесь на спинку кресла и смотрите шоу!
Сначала все маятники двигаются вместе. Затем появляется змеевидный узор (см. левое фото ниже), растворяющийся в беспорядочной мешанине. Далее маятники чередуются и движутся в идеальном противоборстве (см. правое фото ниже). Снова появляется случайный беспорядок, за которым в конце концов следует возврат к исходному идеальному выравниванию. Затем весь цикл повторяется.
Если вы не видите этих закономерностей, попробуйте «настроить» маятники, слегка изменив их длину. Если конкретный маятник приходит слишком рано в тот момент, когда все должно быть синхронизировано, то немного удлините его; если он прибывает поздно, то укоротите его немного. Отрегулируйте длину струны, ослабив любой винт, сдвинув струну и снова затянув винт.
Что происходит?
Каждый маятник качается вперед и назад с разной скоростью, определяемой длиной поддерживающей его нити. Это приводит к тому, что они падают в ногу друг с другом, когда они качаются.
Однако через определенные промежутки времени шарики складываются в узнаваемые узоры. Например, через 15 секунд соседние маятники находятся на расстоянии одного полуколебания друг от друга, заставляя их качаться в идеальном противодействии. Через 30 секунд шары снова выстраиваются в линию, и цикл рисунков повторяется (см. таблицу ниже).
Дальше
Люди часто удивляются, когда узнают, что время, необходимое маятнику для раскачивания вперед и назад, называемое периодом маятника, не зависит от массы качающегося маятника или от того, насколько далеко качается маятник.
Вы можете доказать это себе, покачивая бутылку с водой на веревочке: сначала попробуйте с полной бутылкой, а затем вылейте половину воды. Затем попробуйте маленькие махи и большие, широкие махи. Изменяется ли период маятника?
Затем попробуйте маленькие махи и большие, широкие махи. Изменяется ли период маятника?
Математический корень
Уравнение для периода (T) простого маятника:
где T — период в секундах на один взмах, L — длина (в метрах) и г — ускорение свободного падения (9,8 м/с 2 ).
Частота F маятника — это количество раскачиваний маятника вперед и назад за одну секунду (выраженное в колебаниях в секунду). Частота обратно пропорциональна периоду, или 1/ T . Таким образом, уравнение для расчета частоты маятника является обратным приведенной выше формуле, или
Сравнивая обе стороны,
Решение для L,
Вы можете использовать это уравнение для расчета длины маятника для заданной частоты. Например, самый длинный маятник вашего Pendulum Snake качается вперед и назад 24 раза за 30 секунд. Частота выражается в колебаниях в секунду, поэтому 24 колебания/30 секунд = 0,8 колебания в секунду.



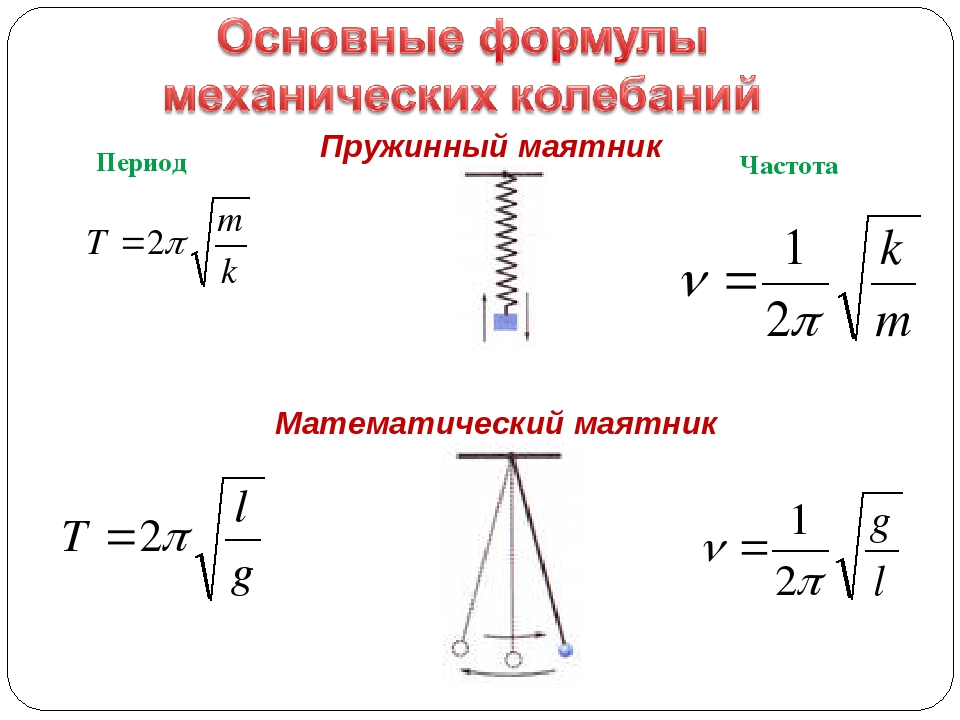 Нарисуйте равнодействующую
сил. Как меняется величина и направление
равнодействующей сил в течение периода?
Нарисуйте равнодействующую
сил. Как меняется величина и направление
равнодействующей сил в течение периода? Изобразите
математический маятник в крайней
правой точке и покажите на чертеже силы, действующие
на шарик в данной точке траектории.
Нарисуйте равнодействующую сил. Как
меняется величина и направление
равнодействующей сил в течение
периода?
Изобразите
математический маятник в крайней
правой точке и покажите на чертеже силы, действующие
на шарик в данной точке траектории.
Нарисуйте равнодействующую сил. Как
меняется величина и направление
равнодействующей сил в течение
периода?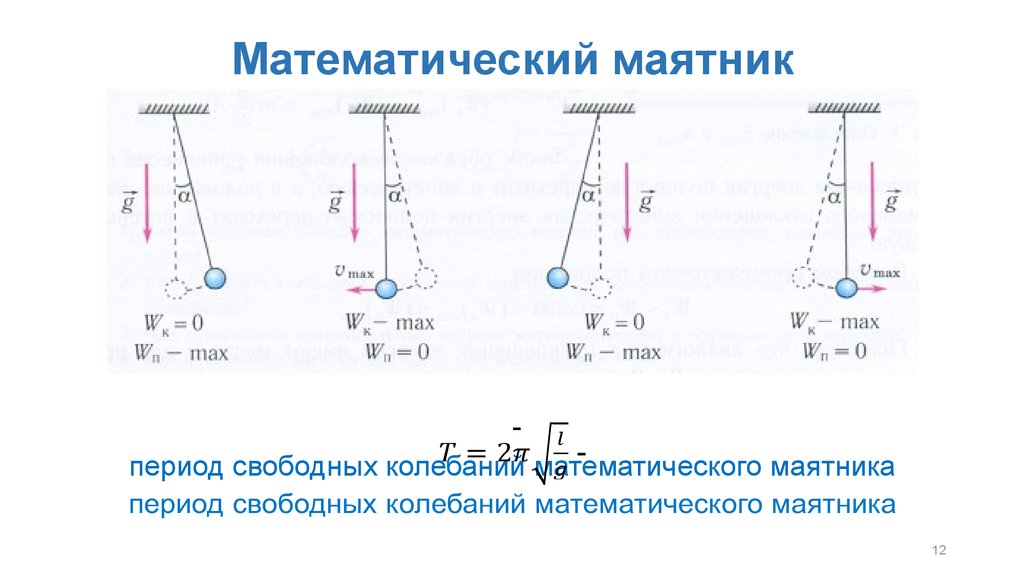 Как
будет меняться период колебаний
ведерка с водой, подвешенного на очень
длинном шнуре: А) если из отверстия в
его дне постепенно будет вытекать
вода?
Б) если увеличить длину шнура?
Какой
математический закон или формулу вы
использовали при ответе на данные
вопросы?
Как
будет меняться период колебаний
ведерка с водой, подвешенного на очень
длинном шнуре: А) если из отверстия в
его дне постепенно будет вытекать
вода?
Б) если увеличить длину шнура?
Какой
математический закон или формулу вы
использовали при ответе на данные
вопросы?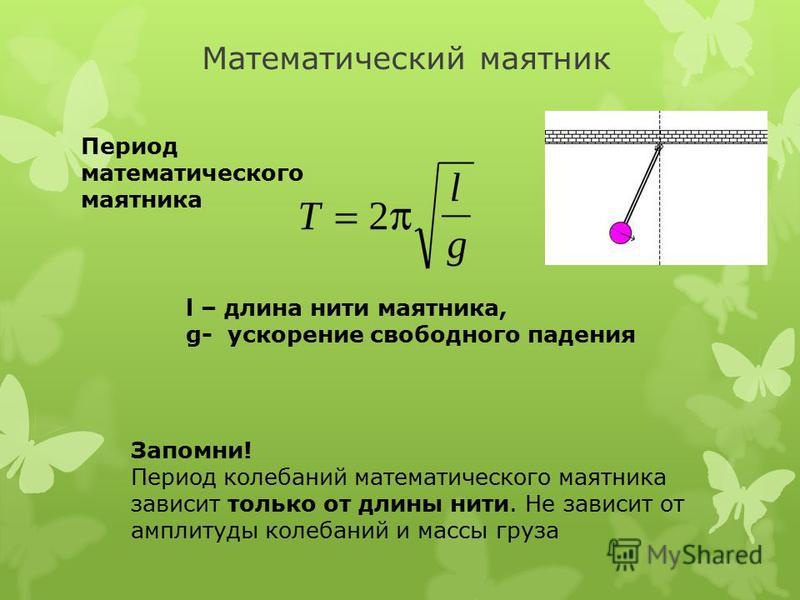 4
4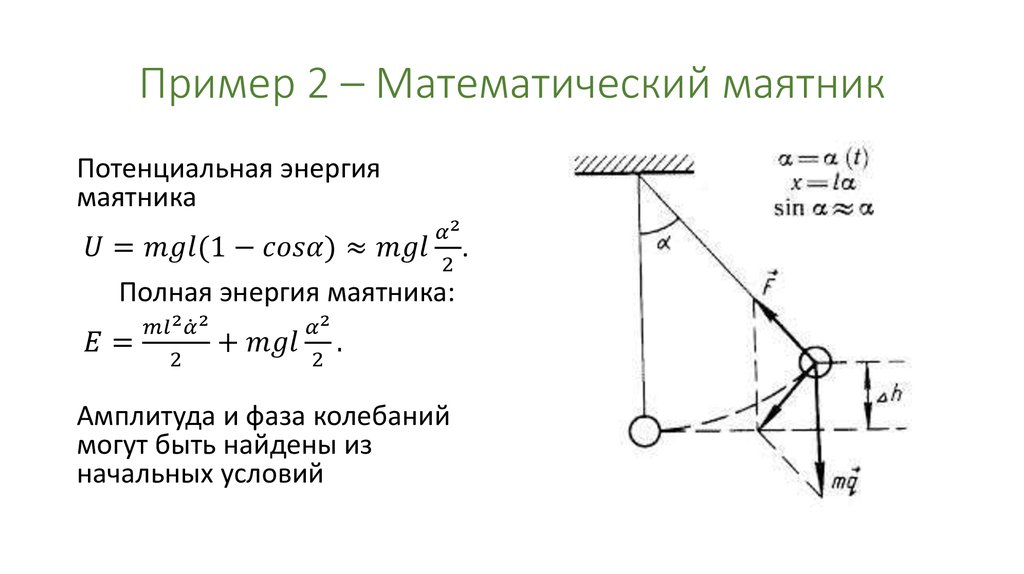 Исходя из формулы период малых колебаний маятника не зависит от амплитуды его колебаний ( Ответ на 4)
Исходя из формулы период малых колебаний маятника не зависит от амплитуды его колебаний ( Ответ на 4)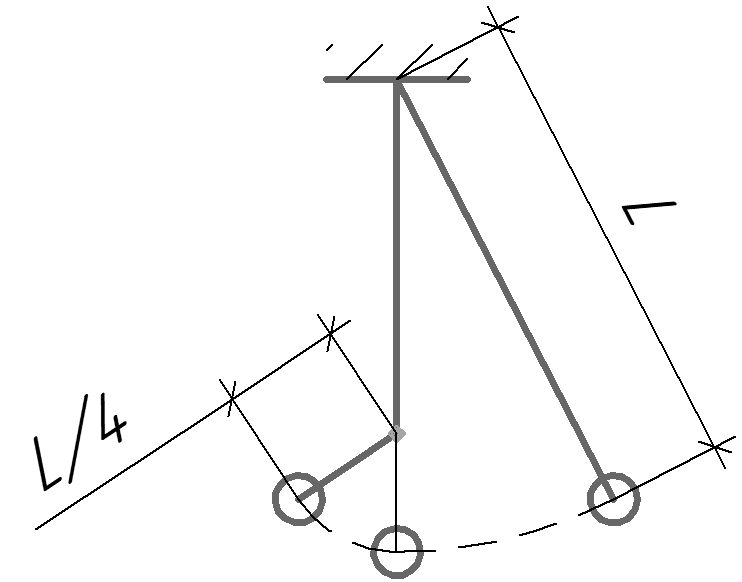 268
268
 736
736
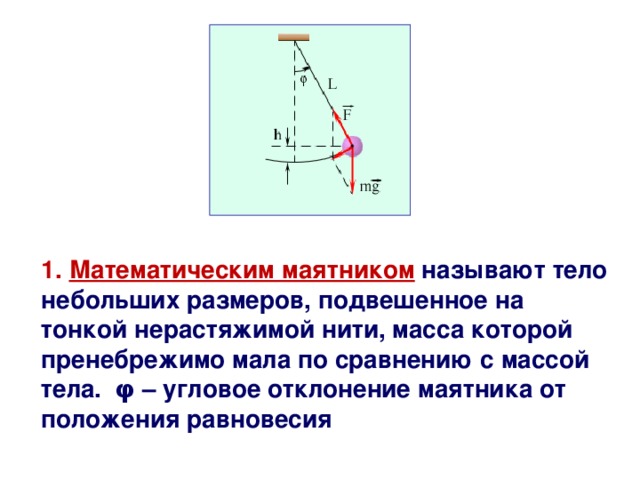 Изготовьте математический маятник длиной 1 м. Экспериментально определите период его колебаний. Результат проанализируйте и сделайте вывод.
Изготовьте математический маятник длиной 1 м. Экспериментально определите период его колебаний. Результат проанализируйте и сделайте вывод. Однако,
для этого иногда нужно построить слишком сложную теорию или выполнить громоздкие
расчеты. Поэтому бывает очень полезно определить приближенное, примерное значение
физической величины. Как говорят физики, нужно оценить физическую величину. Один
из известных наших физиков академик А.Б. Мигдал писал: “Решение большинства задач
теоретической физики начинается с применения качественных методов, которые составляют
наиболее привлекательную и красивую особенность этой науки. Под качественными
методами мы понимаем размерные оценки и оценки с помощью простых моделей”
Однако,
для этого иногда нужно построить слишком сложную теорию или выполнить громоздкие
расчеты. Поэтому бывает очень полезно определить приближенное, примерное значение
физической величины. Как говорят физики, нужно оценить физическую величину. Один
из известных наших физиков академик А.Б. Мигдал писал: “Решение большинства задач
теоретической физики начинается с применения качественных методов, которые составляют
наиболее привлекательную и красивую особенность этой науки. Под качественными
методами мы понимаем размерные оценки и оценки с помощью простых моделей” Поскольку вы делаете оценку, а не хотите знать результат точно, то
ответы 1 час 15 минут и 1 час 33 минуты будут одинаково правильными. Действительно,
ситуация, когда вам надо ждать 1 час с минутами совершенно иная, чем та, когда
надо ждать 2-3 минуты. Таким образом, числа, которые отличаются в 2 — 3 раза -
это числа одного порядка. Если же числа отличаются в 10 раз, говорят, что они
отличаются на один порядок, если в 100 — на два порядка и т.д.
Поскольку вы делаете оценку, а не хотите знать результат точно, то
ответы 1 час 15 минут и 1 час 33 минуты будут одинаково правильными. Действительно,
ситуация, когда вам надо ждать 1 час с минутами совершенно иная, чем та, когда
надо ждать 2-3 минуты. Таким образом, числа, которые отличаются в 2 — 3 раза -
это числа одного порядка. Если же числа отличаются в 10 раз, говорят, что они
отличаются на один порядок, если в 100 — на два порядка и т.д. Например, каково давление в центре Земли? С какой высоты можно прыгать
в воду, чтобы не разбиться? Какова толщина льда, при которой машина не провалится?
(Такую оценку делали физики в Ленинграде во время войны.)
Например, каково давление в центре Земли? С какой высоты можно прыгать
в воду, чтобы не разбиться? Какова толщина льда, при которой машина не провалится?
(Такую оценку делали физики в Ленинграде во время войны.) Теперь с помощью известного соотношения кинематики
находим
время движения по хорде , а значит период колебаний
.
Теперь с помощью известного соотношения кинематики
находим
время движения по хорде , а значит период колебаний
. Говорят, что большие колебания маятника неизохронны.
Говорят, что большие колебания маятника неизохронны. Тогда площадь пары крыльев S~l2. Так
как поперечные размеры комара без крылышек существенно меньше его длины, оценим
его объем как 1/10l3. Плотность голодного комара примем
равной плотности воды r. Если частота взмаха крылышек f,
то скорость крыла v~lf. Из условия равновесия комара
F~mg, используя полученные оценочные соотношения,
находим:
Тогда площадь пары крыльев S~l2. Так
как поперечные размеры комара без крылышек существенно меньше его длины, оценим
его объем как 1/10l3. Плотность голодного комара примем
равной плотности воды r. Если частота взмаха крылышек f,
то скорость крыла v~lf. Из условия равновесия комара
F~mg, используя полученные оценочные соотношения,
находим:
 На каждой
странице около сотни телефонов. Значит, число домашних телефонов, зарегистрированных
на момент создания справочника, порядка 80 тысяч.
На каждой
странице около сотни телефонов. Значит, число домашних телефонов, зарегистрированных
на момент создания справочника, порядка 80 тысяч.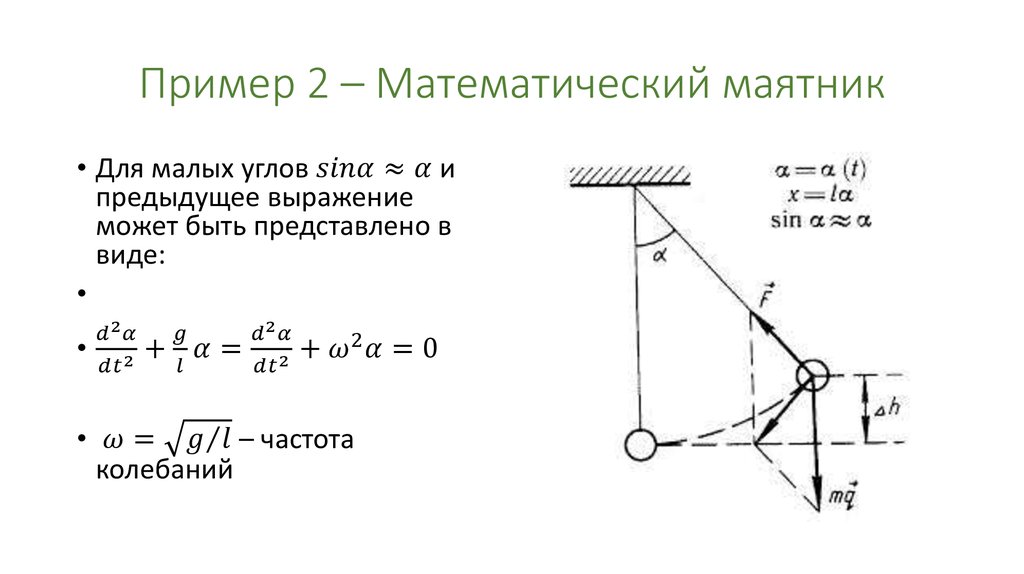 Будь смелее: ведь никому нет
дела до того, что именно ты предположил. Поэтому делай предположения быстро, интуитивно.
Удачные предположения укрепляют эту интуицию. Ошибочные предположения дают полезную
встряску». Если вернуться к началу нашего задания, то нетрудно увидеть, что
мы все время пользовались правилом Уилера, которое хорошо коррелирует с высказываниями
А.Б.Мигдала.
Будь смелее: ведь никому нет
дела до того, что именно ты предположил. Поэтому делай предположения быстро, интуитивно.
Удачные предположения укрепляют эту интуицию. Ошибочные предположения дают полезную
встряску». Если вернуться к началу нашего задания, то нетрудно увидеть, что
мы все время пользовались правилом Уилера, которое хорошо коррелирует с высказываниями
А.Б.Мигдала. Как соотносится ваш
результат с данными наблюдений с автоматических космических станций?
Как соотносится ваш
результат с данными наблюдений с автоматических космических станций? д.
На первый взгляд кажется, что размерность играет вспомогательную роль. На самом
деле это не так. Размерность — хороший помощник физика. Умение обращаться с размерностью
помогает избежать ошибок в преобразованиях, а иногда дает возможность получить
ответ к задаче, когда другие способы решения найти не удается.
д.
На первый взгляд кажется, что размерность играет вспомогательную роль. На самом
деле это не так. Размерность — хороший помощник физика. Умение обращаться с размерностью
помогает избежать ошибок в преобразованиях, а иногда дает возможность получить
ответ к задаче, когда другие способы решения найти не удается.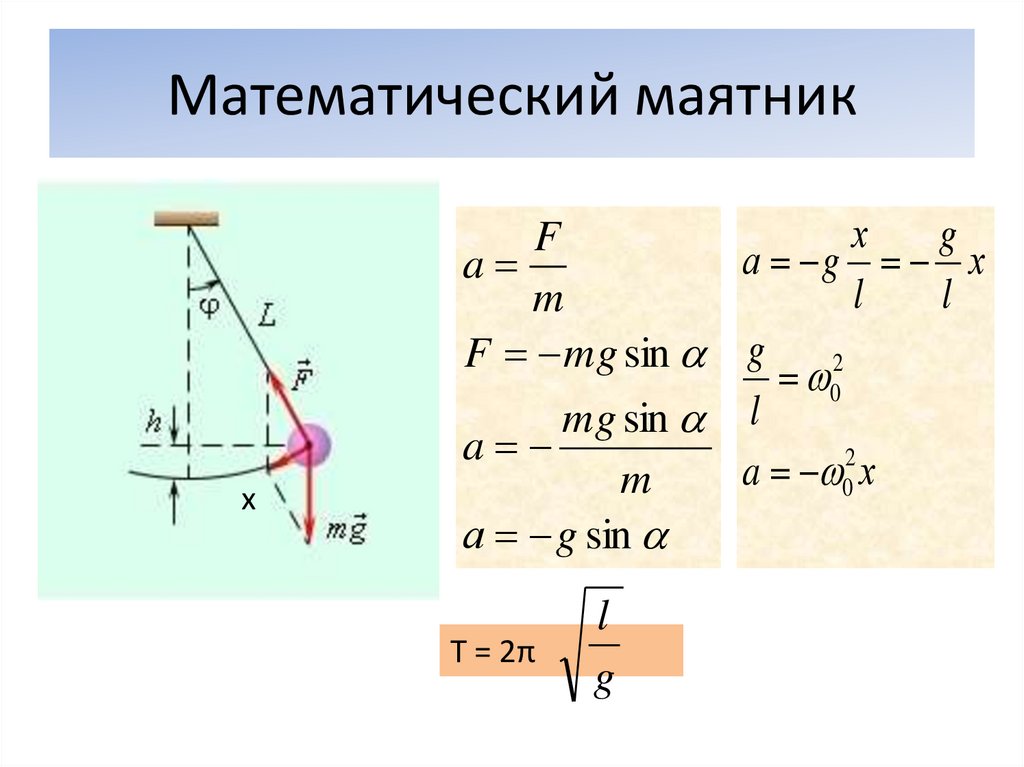 Обычно это длина, масса, время. Им соответствуют размерности
«метр», «килограмм», «секунда» или сокращенно «м»,
«кг», «с». Остальные физические величины имеют производную
размерность, например, размерность скорости — «м/с», ускорения — «м/с2«
и т.д. Вообще-то, можно придумать единицу скорости, и считать ее основной. Тогда
производной станет единица длины. Принципиальных возражений против этого нет,
но это очень неудобно.
Обычно это длина, масса, время. Им соответствуют размерности
«метр», «килограмм», «секунда» или сокращенно «м»,
«кг», «с». Остальные физические величины имеют производную
размерность, например, размерность скорости — «м/с», ускорения — «м/с2«
и т.д. Вообще-то, можно придумать единицу скорости, и считать ее основной. Тогда
производной станет единица длины. Принципиальных возражений против этого нет,
но это очень неудобно. Оказывается, анализ размерности физических величин позволяет получать новые формулы.
Соответствующий прием называют методом размерностей. Давайте научимся пользоваться
этим методом. Отыщем формулу для объема шара. Первый этап решения задачи с помощью
метода размерности состоит в том, что определяются все величины, которые могут
войти в искомую формулу. Ясно, что объем шара может зависеть только от его радиуса
R. Выпишем размерности всех интересующих нас величин:
Оказывается, анализ размерности физических величин позволяет получать новые формулы.
Соответствующий прием называют методом размерностей. Давайте научимся пользоваться
этим методом. Отыщем формулу для объема шара. Первый этап решения задачи с помощью
метода размерности состоит в том, что определяются все величины, которые могут
войти в искомую формулу. Ясно, что объем шара может зависеть только от его радиуса
R. Выпишем размерности всех интересующих нас величин: Константу C можно отыскать экспериментально, с помощью компьютерного
моделирования или строго решив задачу.
Константу C можно отыскать экспериментально, с помощью компьютерного
моделирования или строго решив задачу.
 Значит число приближенно равно 6,3. (Точное значение .)
Значит число приближенно равно 6,3. (Точное значение .)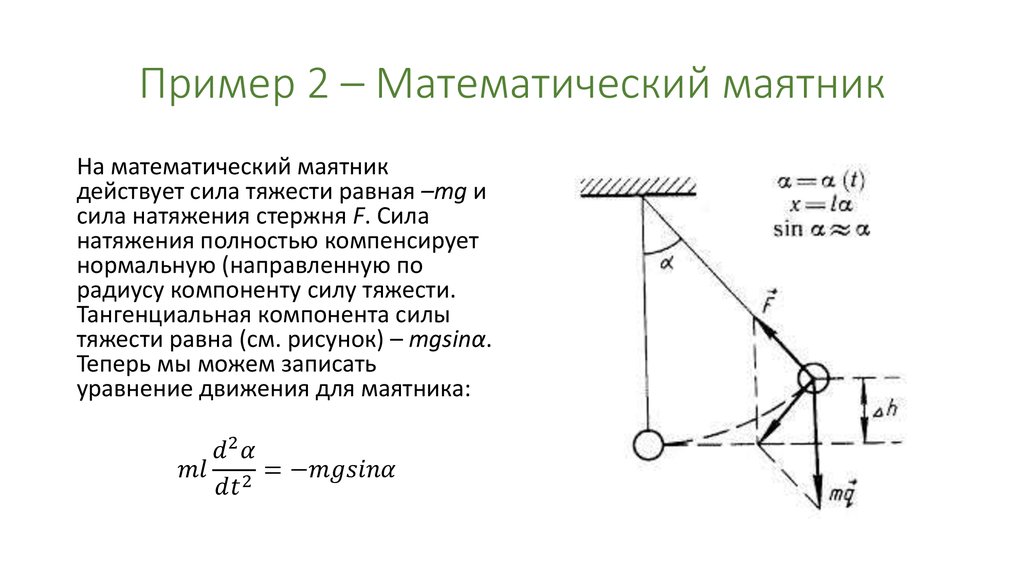 Однако ее график можно построить экспериментально. Для этого надо установить зависимость
для какой-то одной фиксированной длины l. Если затем построить график измеренной
зависимости, отложив по горизонтальной оси угол ,
а по вертикальной — комбинацию , то это и будет график функции .
Кстати, у нас обязательно при этом получится
(почему?). Кроме того, при малых значениях
функция будет почти не зависеть от
(почему?).
Однако ее график можно построить экспериментально. Для этого надо установить зависимость
для какой-то одной фиксированной длины l. Если затем построить график измеренной
зависимости, отложив по горизонтальной оси угол ,
а по вертикальной — комбинацию , то это и будет график функции .
Кстати, у нас обязательно при этом получится
(почему?). Кроме того, при малых значениях
функция будет почти не зависеть от
(почему?).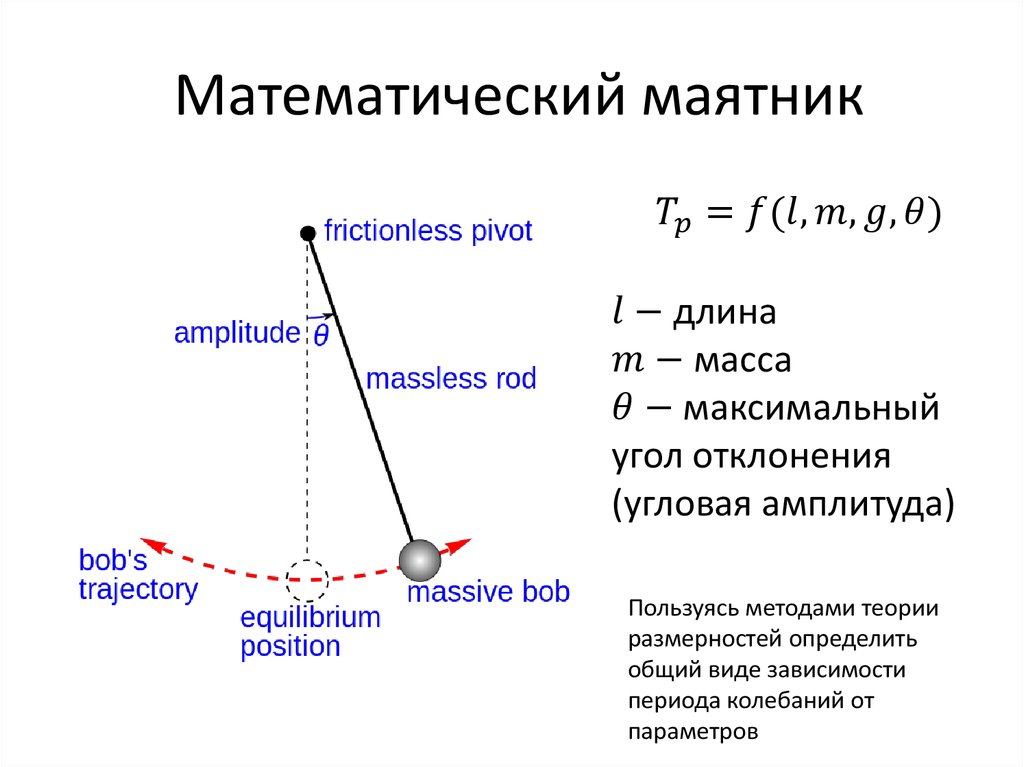 д. Тогда результаты, относящиеся к разным значениям длины, оказываются выделенными.
Получается следующая картинка. Взглянув на такой график, можно сразу сказать,
хорошо ли работает наша формула. Критерием этого является, ложатся или нет точки,
крестики, квадратики на одну кривую. Если да, то в этом случае говорят, что получилась
универсальная функция. Она является универсальной в том смысле, что она пригодна
одновременно для всех маятников, какова бы ни была длина их подвеса.
д. Тогда результаты, относящиеся к разным значениям длины, оказываются выделенными.
Получается следующая картинка. Взглянув на такой график, можно сразу сказать,
хорошо ли работает наша формула. Критерием этого является, ложатся или нет точки,
крестики, квадратики на одну кривую. Если да, то в этом случае говорят, что получилась
универсальная функция. Она является универсальной в том смысле, что она пригодна
одновременно для всех маятников, какова бы ни была длина их подвеса.
 За какое время змея, лежащая на гладкой горизонтальной поверхности вдоль прямой
линии, может свернуться, образовав кольцо? Масса змеи M, ее длина l.
За какое время змея, лежащая на гладкой горизонтальной поверхности вдоль прямой
линии, может свернуться, образовав кольцо? Масса змеи M, ее длина l.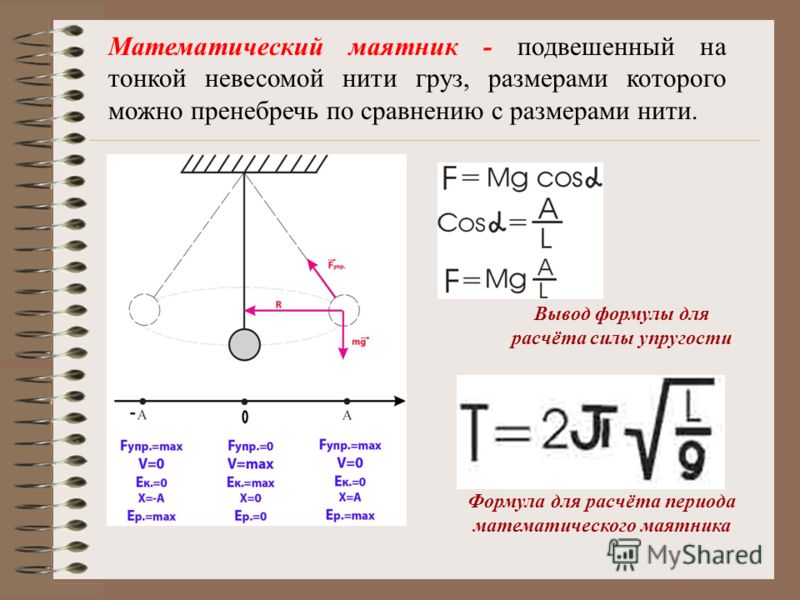 Из соображений размерности получите формулу для площади
прямоугольного треугольника. Постройте качественно универсальную функцию, характеризующую
зависимость площади прямоугольного треугольника от угла .
Из соображений размерности получите формулу для площади
прямоугольного треугольника. Постройте качественно универсальную функцию, характеризующую
зависимость площади прямоугольного треугольника от угла . Или, например, комплексными числами, которые тоже пока не изучили.
В науке же ситуация совершенно другая — можно (и нужно!) пользоваться любыми известными
знаниями. Для этого можно обращаться к справочникам, литературе, консультациями
других исследователей. На традиционных же уроках это все не разрешается. Второе,
очень существенное отличие от школьного способа обучения состоит в том, что одна
задача решается долго (неделю, месяц, год). Задачи же, которые Вы решаете в школе
и на олимпиадах совершенно другие. Урок и олимпиада скоротечны, и на каждую задачу
Вы тратите не так много времени — ведь необходимо решать их довольно большое число.
В третьих, школьная задача, как правило, имеет единственное четкое решение, именно
то, которое предполагал в учебных целях ее автор. Те же задачи, которые решает
ученый-исследователь не обладают такой степенью определенности. Можно, однако,
сформулировать задачи, содержащие традиционные для учебного курса физики ситуации,
но требующие не «ученического», а научного подхода к их решению.
Или, например, комплексными числами, которые тоже пока не изучили.
В науке же ситуация совершенно другая — можно (и нужно!) пользоваться любыми известными
знаниями. Для этого можно обращаться к справочникам, литературе, консультациями
других исследователей. На традиционных же уроках это все не разрешается. Второе,
очень существенное отличие от школьного способа обучения состоит в том, что одна
задача решается долго (неделю, месяц, год). Задачи же, которые Вы решаете в школе
и на олимпиадах совершенно другие. Урок и олимпиада скоротечны, и на каждую задачу
Вы тратите не так много времени — ведь необходимо решать их довольно большое число.
В третьих, школьная задача, как правило, имеет единственное четкое решение, именно
то, которое предполагал в учебных целях ее автор. Те же задачи, которые решает
ученый-исследователь не обладают такой степенью определенности. Можно, однако,
сформулировать задачи, содержащие традиционные для учебного курса физики ситуации,
но требующие не «ученического», а научного подхода к их решению. Наиболее
известна подборка таких задач, придуманных выдающимся ученым П.Л.Капицей для студентов
и молодых людей, поступающих в аспирантуру. Мы хотим предложить несколько задач
исследовательского характера, которые близки к научному исследованию. Из приведенных
ниже задач лучше выбрать всего одну — ту, которая Вам понравится. Значение имеет
не число решенных задач, а глубина проработки решения. Такие задачи,
можно надеяться, помогут Вам лучше понять науку, как профессию, состоящую в получении
новых результатов «своими руками».
Наиболее
известна подборка таких задач, придуманных выдающимся ученым П.Л.Капицей для студентов
и молодых людей, поступающих в аспирантуру. Мы хотим предложить несколько задач
исследовательского характера, которые близки к научному исследованию. Из приведенных
ниже задач лучше выбрать всего одну — ту, которая Вам понравится. Значение имеет
не число решенных задач, а глубина проработки решения. Такие задачи,
можно надеяться, помогут Вам лучше понять науку, как профессию, состоящую в получении
новых результатов «своими руками». Используйте
литературу — для решения некоторых задач это полезно, а решение некоторых из них
без этого и невозможно.
Используйте
литературу — для решения некоторых задач это полезно, а решение некоторых из них
без этого и невозможно.
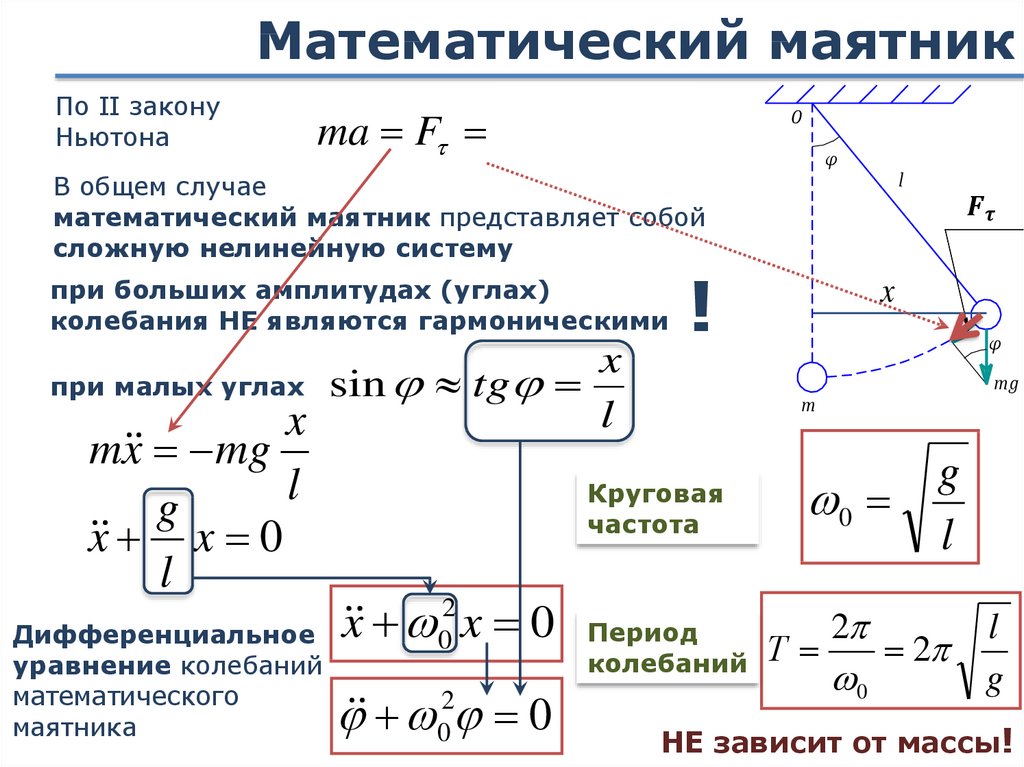
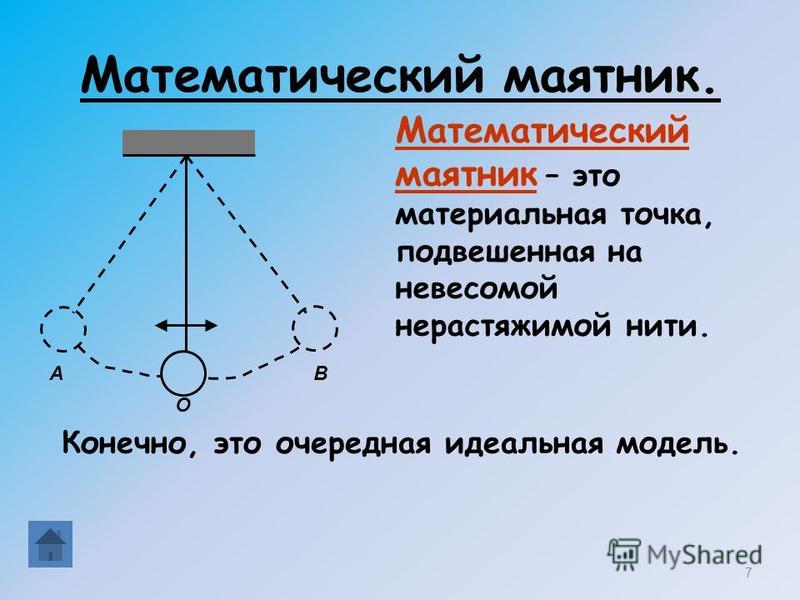
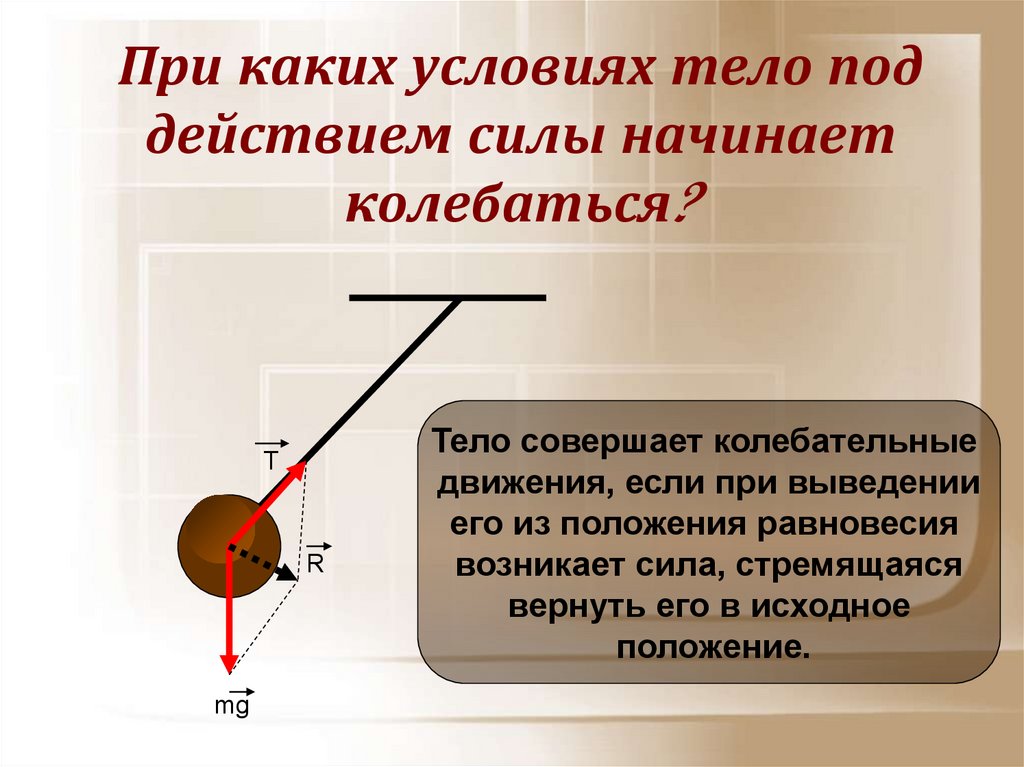 Покажите, что при небольших деформациях
время соударения не зависит от начальной скорости мяча. Оцените это время. Массу
мяча примите ,
радиус ,
избыточное давление внутри него равно одной атмосфере, т.е. 105 Па.
Оцените скорость мяча, при которой деформация мяча не будет малой.
Покажите, что при небольших деформациях
время соударения не зависит от начальной скорости мяча. Оцените это время. Массу
мяча примите ,
радиус ,
избыточное давление внутри него равно одной атмосфере, т.е. 105 Па.
Оцените скорость мяча, при которой деформация мяча не будет малой.