Функция y = ctg x, её свойства и график катангенса с примерами
- Развертка котангенса движения точки по числовой окружности в функцию от угла
- Свойства функции y=ctgx
- Примеры
п.1. Развертка котангенса движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности на горизонтальной касательной, проведенной через точку (0;1), отображаются значения котангенсов соответствующих углов (см. §3 данного справочника).
Рассмотрим, как изменяется котангенс, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=ctgx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривые продолжатся влево.
В результате получаем график y=ctgx для для всех x из области допустимых значений.
График котангенса называют «тагненцоидой», термин «котангенцоида» не используют.
Часть графика c \(0\lt x\lt\pi\) называют главной ветвью графика котангенса.
п.2. Свойства функции
y=ctgx1. Область определения \(x\ne\pi k\) — множество действительных чисел, кроме точек, в которых \(sinx=0\).
2. Функция не ограничена сверху и снизу. Область значений \(y\in\mathbb{R}\)
3. Функция нечётная $$ ctg(-x)=-ctgx $$
4. Функция периодическая с периодом π $$ ctg(x+\pi k)=ctgx $$
5. Функция стремится к \(-\infty\) при приближении слева к точкам \(x=\pi k\).
Приближение к точке a слева записывается как \(x\rightarrow a-0\) $$ \lim_{x\rightarrow \pi k-0} ctgx=-\infty $$ Функция стремится к \(+\infty\) при приближении справа к точкам \(x=\pi k\).
Приближение к точке a справа записывается как \(x\rightarrow a+0\) $$ \lim_{x\rightarrow \pi k+0} ctgx=+\infty $$ Нули функции \(y_{0}=0\) достигаются в точках \(x_0=\frac\pi2+\pi k\)
6. Функция убывает на всей области определения.
Функция убывает на всей области определения.
7. Функция имеет разрывы в точках \(x=\pi k\), через эти точки проходят вертикальные асимптоты. На интервалах между асимптотами \((\pi k;\ \pi+\pi k)\) функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=ctgx на заданном промежутке:
a) \(\left[\frac{2\pi}{3}; \pi\right)\) $$ y_{min}=\lim_{x\rightarrow\pi-0}ctgx=-\infty,\ \ y_{max}=ctg\left(\frac{2\pi}{3}\right)=-\frac{1}{\sqrt{3}} $$ б) \(\left(0; \frac{\pi}{4}\right]\) $$ y_{min}=ctg\left(\frac{\pi}{4}\right)=1,\ \ y_{max}=\lim_{x\rightarrow +0}ctgx=+\infty $$ в) \(\left[\frac{7\pi}{6}; \frac{7\pi}{4}\right]\) $$ y_{min}=ctg\left(\frac{7\pi}{4}\right)=-1,\ \ y_{max}=ctg\left(\frac{7\pi}{6}\right)=\sqrt{3} $$
Пример 2. Решите уравнение:
a) \(ctgx=-\sqrt{3}\)
Бесконечное множество решений: \(x=\frac{5\pi}{6}+\pi k,\ k\in\mathbb{Z}\)
б) \(ctg\left(x+\frac\pi2\right)=0\)
\(x+\frac\pi2=\frac\pi2+\pi k\)
Бесконечное множество решений: \(x=\pi k,\ k\in\mathbb{Z}\)
в) \(ctg(2x)=1\)
\(2x=\frac\pi4+\pi k\)
Бесконечное множество решений: \(x=\frac{\pi}{8}+\frac{\pi k}{2},\ k\in\mathbb{Z}\)
г) \(ctg\left(\frac{x}{3}-1\right)=-1\)
\(\frac{x}{3}-1=-\frac{\pi}{4}+\pi k\)
\(\frac{x}{3}=1-\frac{\pi}{4}+\pi k\)
Бесконечное множество решений: \(x=3-\frac{3\pi}{4}+3\pi k,\ k\in\mathbb{Z}\)
Пример 3.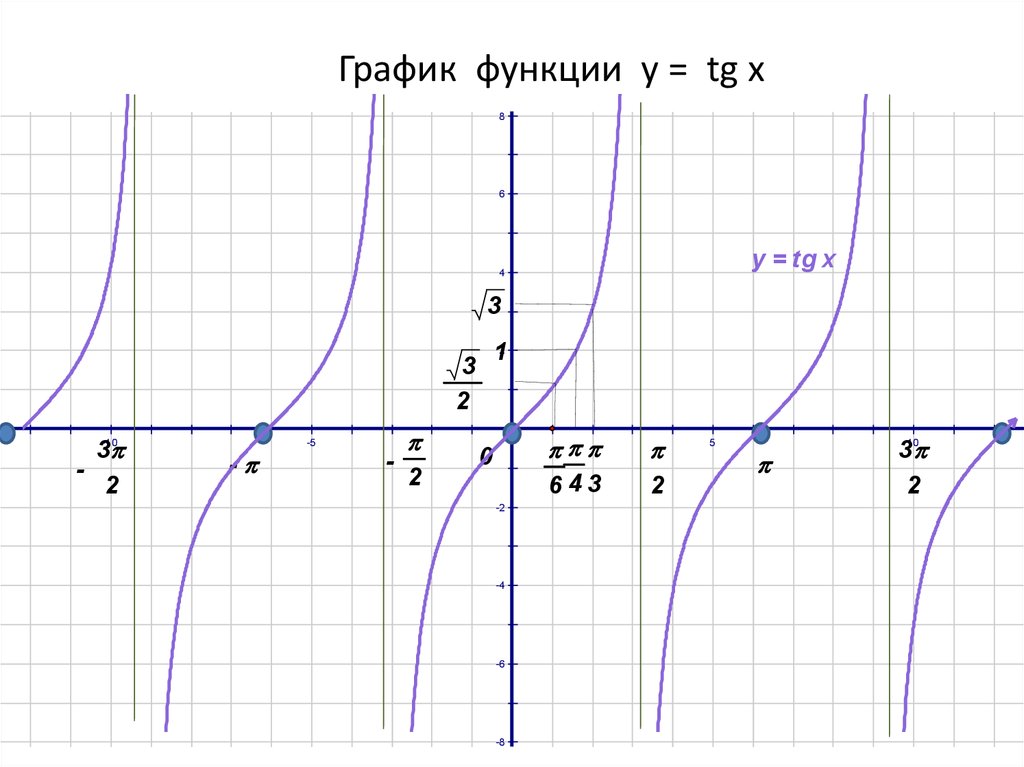 2(tgx)=1\). При этом ограничивается область определения функции \(y(x)\), т.к. \(tgx\) имеeт разрывы.
2(tgx)=1\). При этом ограничивается область определения функции \(y(x)\), т.к. \(tgx\) имеeт разрывы.
Точки разрыва отмечены на числовой окружности: \(x\ne\frac{\pi}{2}+\pi k\).
Получаем: $$ \begin{cases} 1-x\\ x\ne\frac{\pi}{2}+\pi k,\ \ k\in\mathbb{Z} \end{cases} $$ Строим график прямой и выкалываем точки, не входящие в ОДЗ.
Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3. ВЫЧИТАНИЕ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11.  ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ§ 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11.  ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯКонтрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2.  СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ§ 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2.  § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6.  ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА§ 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. 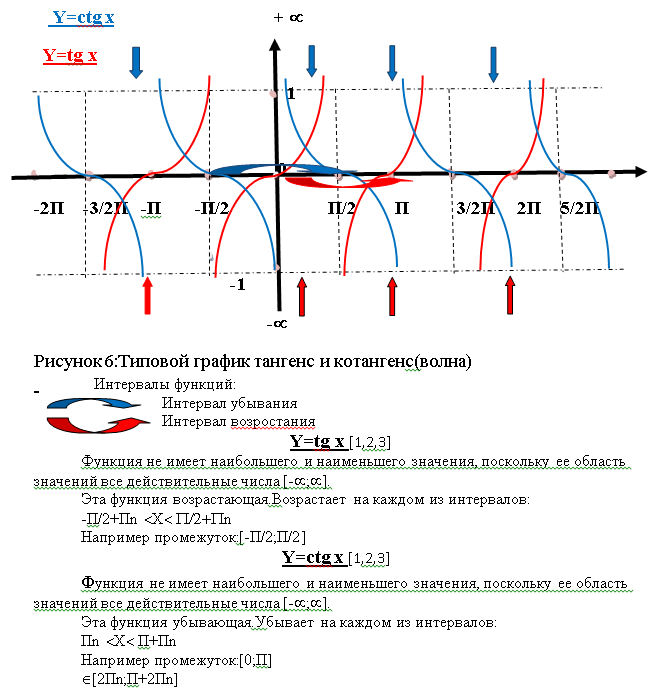 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. ПРЕДЕЛ ФУНКЦИИ § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4.  ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙКонтрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3.  СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ§ 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Графики тангенса и котангенса — тригонометрия
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
Помощь по тригонометрии » Тригонометрические функции и графики » Тригонометрические графики » График тангенса и котангенса
Что из следующего лучше всего описывает расположение асимптот на графике тангенса?
Возможные ответы:
Меры угла, где косинус равен 0, например
Меры угла, где синус и косинус равны, например .
Меры угла, где синус равен 0, например .
Угловые меры, для которых нельзя вычислить тангенс.
Правильный ответ:
Угловые меры, где косинус равен 0, например
Пояснение:
В тригонометрии
.
Его также можно рассматривать как .
Это потому, что
и
.
Это означает, что всякий раз, когда косинус равен 0, тангенс не определен, потому что он будет вычисляться путем деления на 0.
Сообщить об ошибке
Какое из следующих утверждений не является решением следующего уравнения?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы можем разложить исходное выражение следующим образом:
Таким образом, из этого уравнения мы делаем вывод, что: решение исходного уравнения.
Единственный такой выбор , то есть ; n не является целым числом, поэтому это не решение.
Сообщить об ошибке
Ниже приведен график какой функции?
Возможные ответы:
Правильный ответ:
Объяснение:
График имеет бесконечный диапазон, но несколько вертикальных асимптот. Это означает, что мы можем ограничить наш выбор касательными и котангенсными графами.
Кроме того, мы видим, что график начинается снизу и увеличивается слева направо, что согласуется с касательными графиками. Поэтому мы сужаем наше внимание до выбора, касающегося касательных.
Чтобы выбрать между оставшимися двумя графиками, обратите внимание, что точка пересечения по оси y (где x=0) нашего графика равна (0,1).
Теперь оценивается как , а это значит, что нам нужен сдвиг по вертикали на единицу.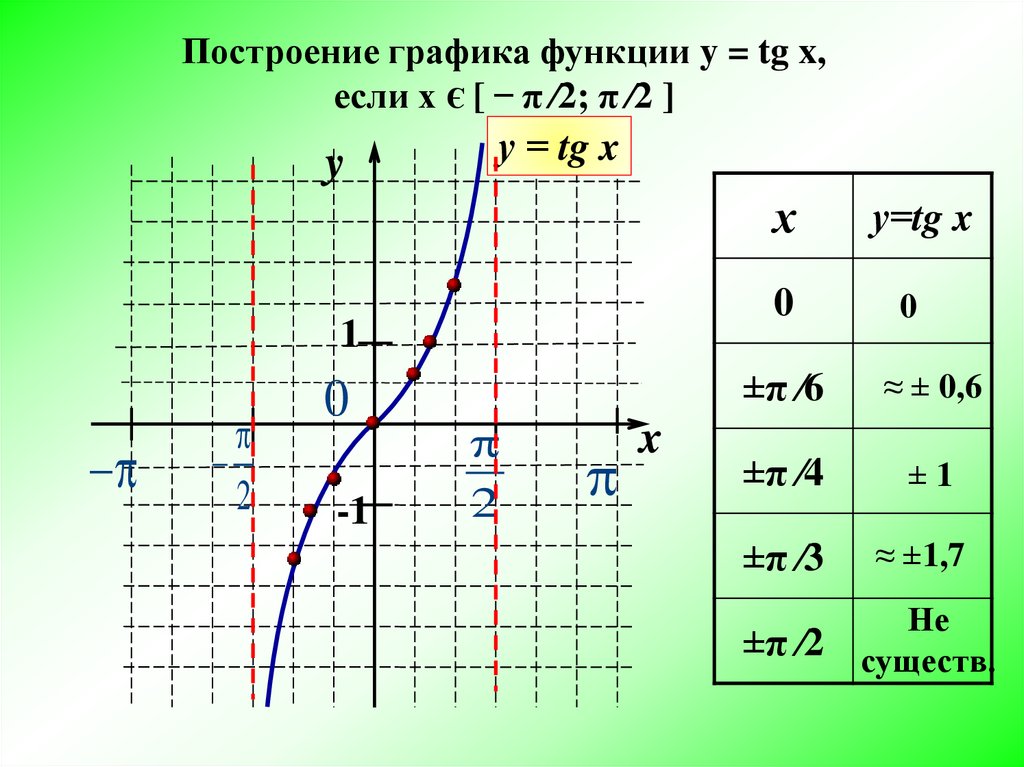
Следовательно, лучший выбор:
Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы вывести график , вспомните, что . График – это
, а график –
. Это связано с тем, что знаменатель функции тангенса будет равен нулю всякий раз, когда функция косинуса равна нулю, и тогда вся функция будет неопределенной в этих точках. Везде, где косинус пересекает ось x, возникает вертикальная асимптота. Если мы наложим графики синуса и косинуса, мы увидим следующее:
Таким образом, наш график касательной будет иметь ту же форму, что и графики синуса и косинуса, когда они возрастают, но будет иметь вертикальные асимптоты везде, где косинус пересекает ось x.
И у нас остался наш график
Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы начнем с рассмотрения общего графика и последовательно применим преобразования, чтобы построить график . График это
Общее равенство уравнения касательного преобразования . A — амплитуда графика касательной. Здесь, поэтому нам не нужно применять здесь преобразование. Далее рассмотрим период. Период касательной функции равен . Таким образом, период нашего графика будет
Период =
Период =
Таким образом, период сокращается с до .
Теперь рассмотрим . фазовый сдвиг нашего графика.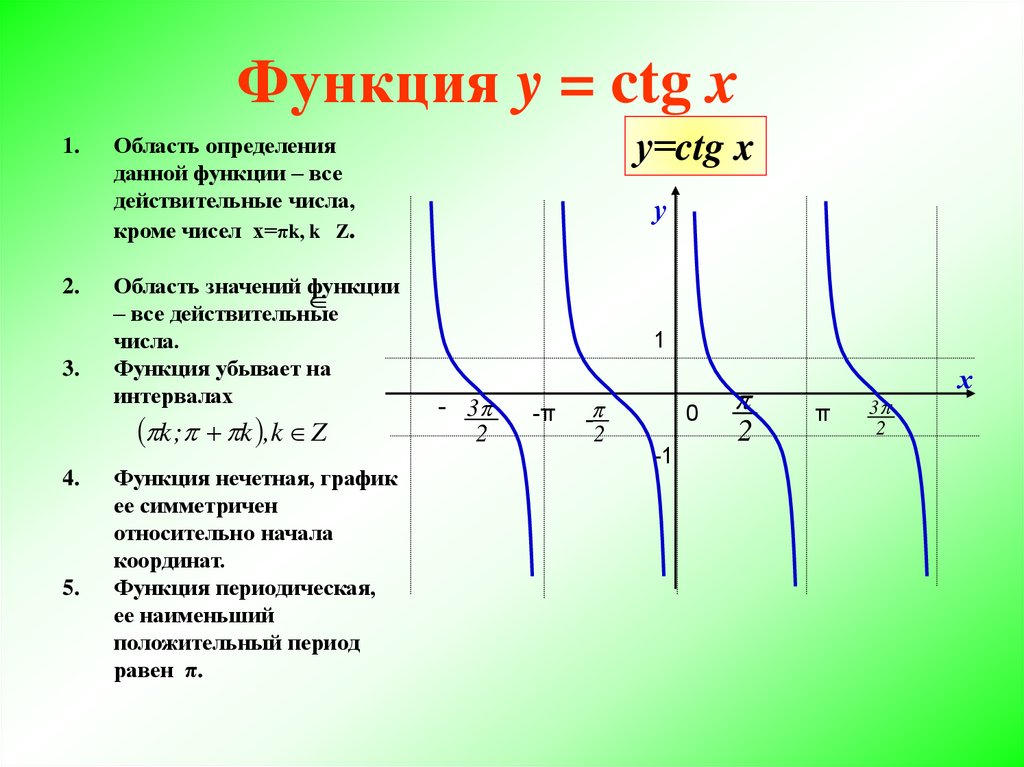 Поэтому мы сдвинем наши единицы графика влево. Это не меняет наш график визуально из-за того, что сейчас период равен . Наконец, мы рассмотрим. является вертикальным сдвигом нашего графика, поэтому мы должны сдвинуть наш график на 1 единицу вверх.
Поэтому мы сдвинем наши единицы графика влево. Это не меняет наш график визуально из-за того, что сейчас период равен . Наконец, мы рассмотрим. является вертикальным сдвигом нашего графика, поэтому мы должны сдвинуть наш график на 1 единицу вверх.
И у нас остался график .
Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы построить график вспоминания, вспомните, что . Таким образом, графики тангенса и котангенса обратны друг другу. Мы рассмотрим касательный граф, так как он нам больше знаком:
Теперь мы просто инвертируем касательный граф, чтобы получить котангенс-график
И у нас остался наш котангенс-график
Сообщить об ошибке
Что из следующего является графиком .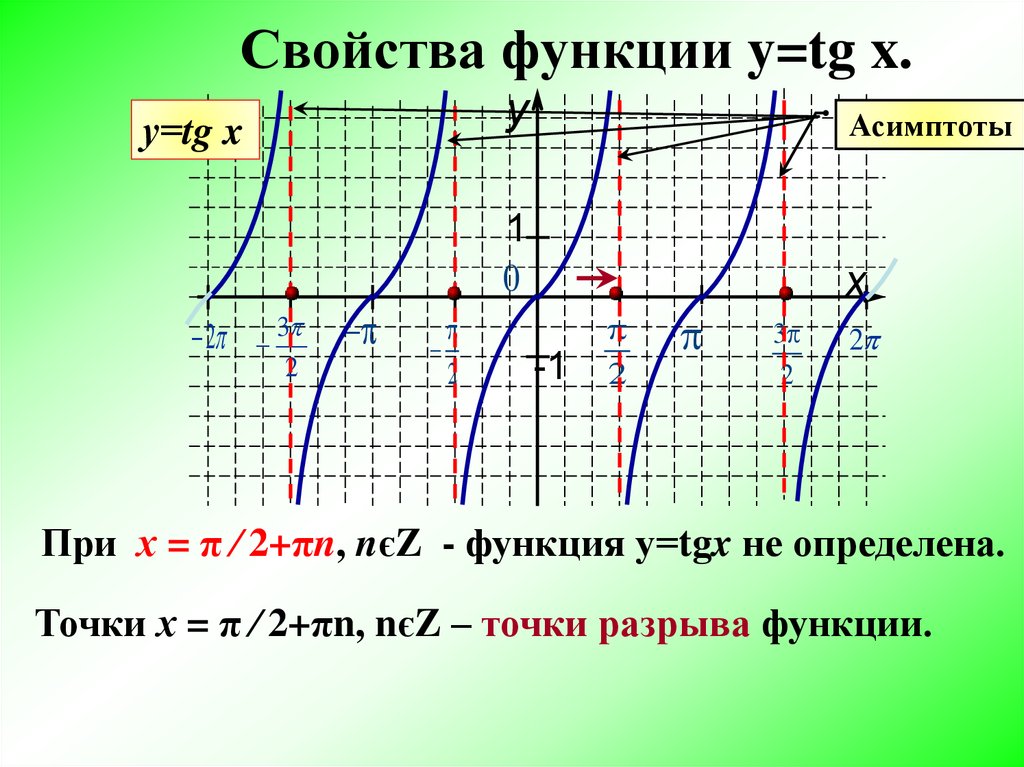
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала мы рассмотрим график и пошагово применим преобразования. График это
Общая форма функции преобразования котангенса . Для нашей функции и поэтому нам нужно увеличить амплитуду на 4 единицы.
здесь, поэтому нам не нужно вносить какие-либо изменения в период этого графика. , что дает нам отрицательный фазовый сдвиг единиц.
Остается наш график .
Сообщить об ошибке
Верно или неверно: период функции тангенса и котангенса .
Возможные ответы:
Верно
Неверно
Правильный ответ:
Верно
Объяснение:
Это связано с тем, что и вызывает неопределенность функции касательной в этих точках и формирует вертикальную асимптоту.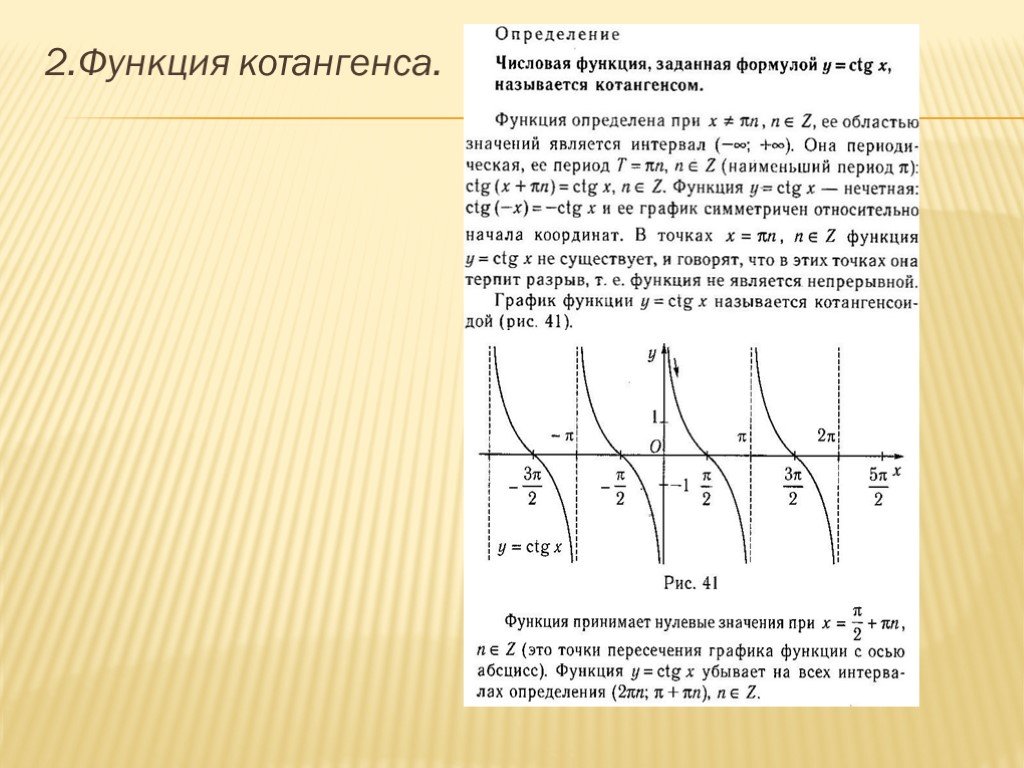

 Она может быть использована при подготовке к экзаменам в высшие учебные заведения.
Она может быть использована при подготовке к экзаменам в высшие учебные заведения.