Онлайн-олимпиады и тесты по алгебре
- Главная /
- Олимпиады /
- По предметам и областям знаний /
- Математика /
7 класс
- Арифметические операции над многочленами
- Арифметические операции над одночленами
- Базовые свойства степеней с натуральным показателем
- Взаимное расположение графиков линейных функций
- Деление многочлена на одночлен
- Деление одночленов
- Запись функции в виде y = f(x)
- Итоговый тест по математике (7 класс)
- Квадратичная функция y = x²
- Квадратичная функция и её график
- Координатная плоскость • Координаты точки
- Координатная прямая и числовые промежутки
- Линейная функция
- Линейная функция y = kx
- Линейная функция y = kx + m и её график
- Линейное уравнение с двумя переменными и его график
- Математические модели
- Математические модели реальных ситуаций
- Математический язык
- Основные понятия многочлена: теория и практика
- Понятие одночлена и его стандартный вид
- Понятие системы линейных уравнений с двумя переменными
- Понятие степени с натуральным показателем
- Понятие степени с нулевым показателем
- Произведение одночленов и возведение одночлена в степень
- Решение систем линейных уравнений методом подстановки
- Решение систем линейных уравнений методом сложения
- Решение уравнений графическим методом
- Свойства степеней с натуральным показателем
- Системы линейных уравнений как математические модели реальных ситуаций
- Системы линейных уравнений с двумя переменными
- Сложение и вычитание многочленов
- Сложение и вычитание одночленов
- Таблица основных степеней (часто используемые степени)
- Умножение и деление степеней с одинаковыми натуральными показателями
- Умножение многочлена на многочлен
- Умножение многочлена на одночлен
- Формулы сокращённого умножения многочленов
- Числовые и алгебраические выражения
8 класс
- Базовые свойства квадратных корней
- Виды квадратных уравнений
- Действительные числа
- Иррациональные числа
- Итоговый тест по математике (8 класс)
- Квадратные уравнения
- Методы решения квадратных неравенств
- Множество рациональных чисел
- Модуль действительного числа и его геометрический смысл
- Монотонность функций
- Неравенства
- Понятие квадратного корня
- Преобразование иррациональных выражений
- Решение линейных неравенств
- Свойства числовых неравенств
- Способы решения квадратных уравнений
- Стандартный вид положительного числа
- Теорема Виета
- Функция y = |x| и функция квадратного корня y = √x
- Функция квадратного корня y = √x, её свойства и график
- Числовые промежутки
9 класс
- Арифметическая прогрессия
- Геометрическая прогрессия
- Итоговый тест по математике (9 класс)
- Комбинаторика • Статистика • Теория вероятностей
- Комбинаторные задачи
- Методы обработки информации (статистика)
- Методы решения систем рациональных уравнений
- Множества и подмножества • Объединение и пересечение множеств
- Неравенства и системы неравенств
- Определение числовой функции и способы её задания
- Простейшие вероятностные задачи
- Решение рациональных неравенств методом интервалов
- Свойства основных функций
- Системы рациональных неравенств
- Системы уравнений
- Системы уравнений как математические модели реальных ситуаций
- Способы решения линейных и квадратных неравенств
- Степенная функция с натуральным показателем
- Степенная функция с отрицательным целым показателем
- Функция кубического корня
- Чётные и нечётные функции • Определение чётности и нечётности
- Числовая последовательность
- Числовые последовательности и прогрессии
- Числовые функции и их свойства
- Экспериментальные данные и вероятности событий
10 класс
- Арккосинус и решение уравнения cos x = a
- Арксинус и решение уравнения sin x = a
- Арктангенс и арккотангенс • Решение уравнений tg x = a, ctg x = a
- Итоговый тест по математике (10 класс)
- Методы, используемые для решения тригонометрических уравнений
- Нахождение значений синуса и косинуса, тангенса и котангенса
- Обратимая и обратная функции
- Периодические функции
- Предел числовой последовательности
- Применение свойств функций к решению иррациональных уравнений
- Производная • Применение производной для исследования функций
- Тригонометрические уравнения
- Тригонометрические функции
- Тригонометрические функции углового аргумента
- Тригонометрические функции числового аргумента
- Числовые функции
11 класс
- Базовые свойства логарифмов
- Бином Ньютона и треугольник Паскаля
- Вероятность события
- Итоговый тест по математике (11 класс)
- Комбинаторика
- Комбинации событий
- Логарифмы • Показательная и логарифмическая функции
- Независимые события
- Определение логарифма, основное логарифмическое тождество
- Перестановки (комбинаторика)
- Правило произведения (комбинаторика)
- Правило суммы (комбинаторика)
- Размещения (комбинаторика)
- Сложение вероятностей
- Случайные события
- Сочетания и их свойства (комбинаторика)
- Статистическая вероятность
- Теория вероятностей
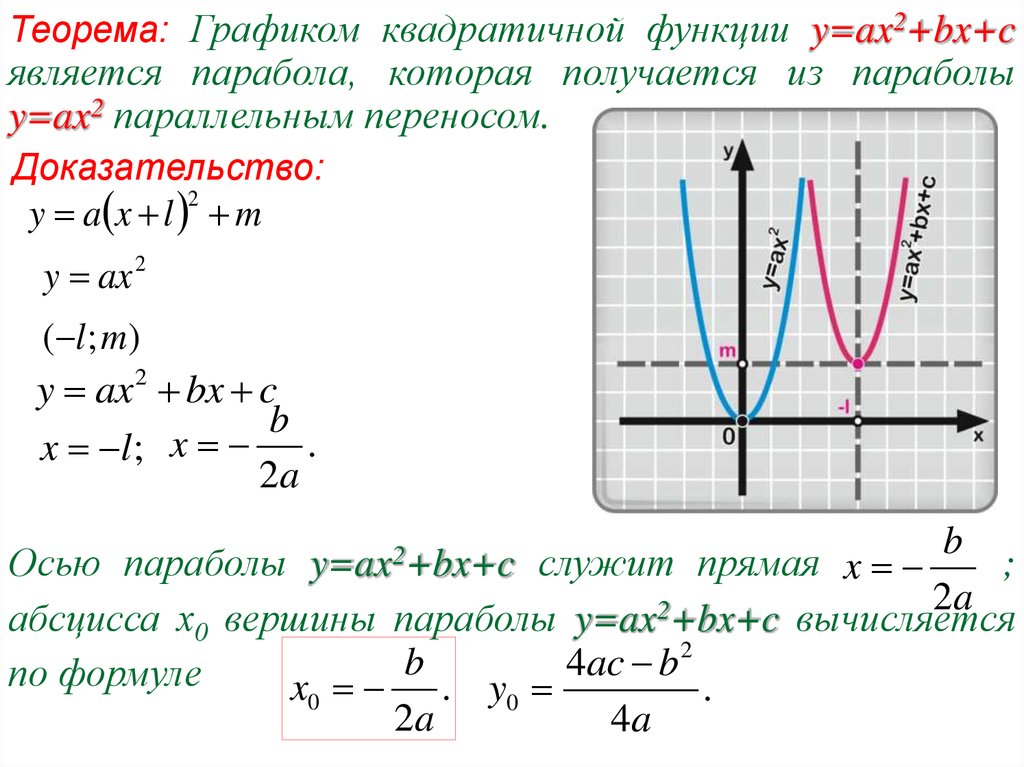
Построение графика квадратичной функции — презентация онлайн
Похожие презентации:
График квадратичной функции.
Построение графика квадратичной функци
Построение графика квадратичной функции
Построение графика квадратичной функции
Функция у = а (х -x0) +y0
Построение графика квадратичной функции
Квадратичная функция, ее график и свойства
Построение графиков квадратичной функции
Еще один способ построения графика квадратичной функции
Построение графика квадратичной функции выделением полного квадрата
Построение графиков квадратичной функции
1. Функция у = а (х -x0) +y0
Функция2
у = а (х -x ) +y
0
0
2. Указать координаты вершины параболы
21)у=-2(х-7) +3
(7;3)
2)у=3(х-8)
2
2
(8;0)
3)у=-(х+2) -6
(-2;-6)
2
4)у=4х -1
(0;-1)
y x
2
y x 3
2
y x 3
2
y x
2
y x 2
2
y x 2
2
y 2x
2
y 2 x 1
2
y 2 x 1 3
2
2
у=(х+2)
2
у=(х+2)
2
2)у = (х-3)
2
4)у = — х +1
2
6)y= (х+2) + 1
2
3) y = х — 2
2
5)y= — (х — 1) — 3
2
2
уУ=
= |х
х — -22|
2
у=│Х — 2│
2
у=│1-х │
2
У=│1 – Х │
у=1-х
2
Построить график функции
2
у=││-х +4│- 5│
2y=│-x 2+4│
y=││-x +4│-5│
2
y=│-x +4│-5
2
y=-x +4
16.
Решите графически уравнение (х-2) = -x +10Решите графически уравнение2
2
(х-2) = -x +10
y = (x-2)
2
2
y = (x-2)
2
y=-x +10
-1
2
y=-x +10
3
Ответ:х=-1;х=3
17. Преобразование графика функции y= f(x)
y=f(x-m)y=f(x+m)
вправо на m
влево на m
y=f(x)-n
y=f(x)+n
вниз на n
на n
вверх
y=f(x-m)+n
вправо на m вверх на n
у=│f(x)│
m>0
n>0
№1 Найдите пары: «Квадратичная функция-график этой
функции» и отметьте знаком «+»
у=-(х-1) 2-2
2
у=(х-2) +1
2
у=-(х+1) +2
2
у=(х+2) +1
у=х 2-2х+3
№2 Даны пары: «Квадратичная функция- координаты вершины
параболы».Укажите верные и неверные соответствия
№
Квадратичная функция
2
1
у=(х+4) — 5
2
у=(х+12) — 4
3
у=-(х- 5) +3
4
у=-(х+8) — 9
5
у=(х+12) +20
2
2
2
2
Координаты вершины параболы
(- 4;- 5)
(12;- 4)
(- 5;- 3)
(- 8;- 9)
(-12;20)
19.
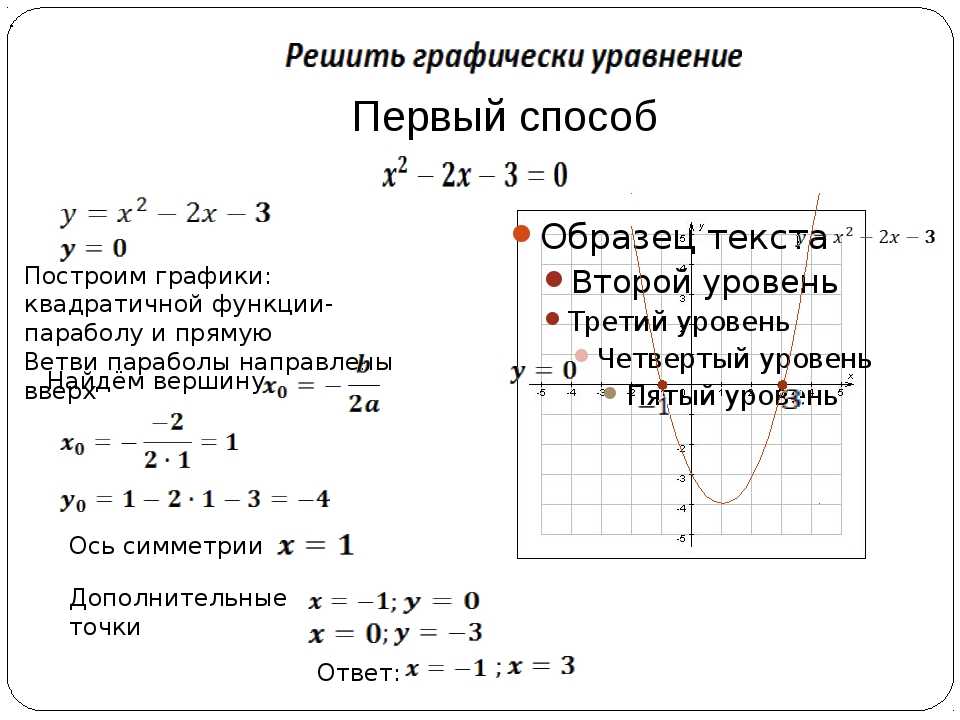Домашнее заданиеРешить графически уравнения:2
2
1)х +2= — (х+2)
2
2
2)х +2= 5(х-3)
20. Частное суммы смежных углов и наибольшего числа корней квадратного уравнения
21. К сумме углов треугольника прибавить произведение корней квадратного трехчлена х-3х-10
К сумме углов треугольникаприбавить произведение
корней квадратного
2
трехчлена х-3х-10
22. Спасибо за урок !
23. Библиография:
1)Беляцкая Н.А. «Квадратичная функция и ее график»English Русский Правила
Квадратичный график — MathCracker.com
Инструкции: Используйте этот калькулятор Quadratic Graph, чтобы построить график любой предоставленной вами квадратичной функции, показывающий все шаги.
Пожалуйста, введите квадратичную функцию, которую вы хотите изобразить в форме ниже.
92 — 1/5, при условии, что это правильный квадратичный
функция.
После того, как вы введете действительное квадратное выражение, вы можете нажать кнопку «Рассчитать», и будет построен график функции, показывающий вам шаги вычисления вершины параболы и также ось симметрии.
Квадратичные функции играют преобладающую роль в основах алгебры, так как они часто используются в контексте решения квадратные уравнения и прикладные задачи. По сути, это базовые полиномы, в которых есть много интересного. характеристики.
Как построить график квадратичных уравнений?
Сделать квадратичный график просто, в том смысле, что вы знаете, что ВСЕ квадратичные функции будут иметь форму параболы. Но все же есть
бесконечные параболы. Нам нужно знать немного больше, чтобы определить точную параболу, которая представляет данную квадратичную функцию.
Шаги по нахождению графика квадратичной функции
- Шаг 1: Четко определите заданную квадратичную функцию и при необходимости упростите
- Шаг 2: После упрощения определите функцию в виде f(x) = ax² + bx + c. Обратите внимание, что a не может быть нулевым
- Шаг 3: Если a > 0, вы знаете, что график будет представлять собой параболу, направленную вверх, тогда как если a
- Шаг 4: Ось симметрии находится в точке x* = -b/(2a), что говорит вам о «центре» параболы
- Шаг 5: обратите внимание, что x* = -b/(2a) является координатой x вершины параболы, а y* = f(x*) = a(x*)² + b(x*) + c координата y вершины
Этого должно быть достаточно, чтобы иметь четкое представление о соответствующем квадратичном графе. Следующим шагом было бы нанести несколько точек на график,
выбор различных точек на оси x и нахождение их соответствующего изображения с помощью функции, чтобы помочь процессу нахождения
график функции.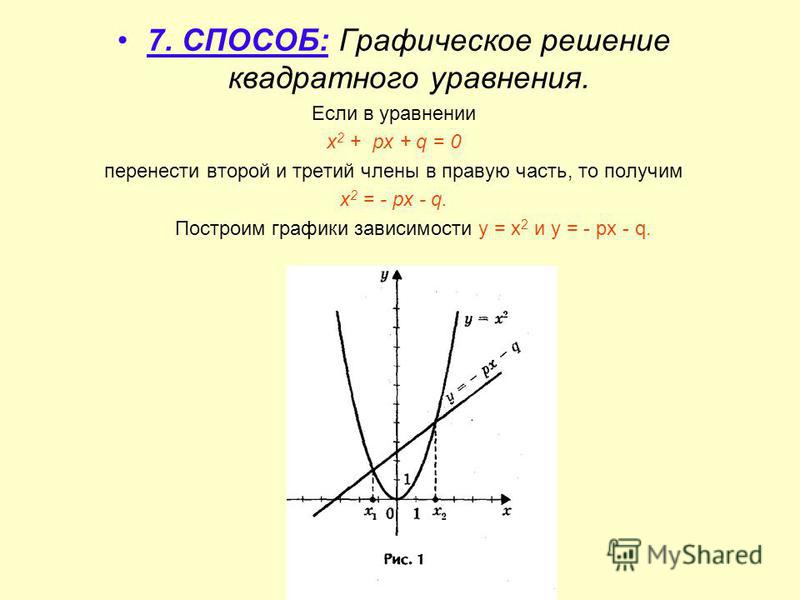
Квадратичная формула
Связана ли квадратичная формула с графиком квадратичной функции? Вы держите пари! Геометрически говоря, при решении квадратное уравнение 92 + Ьх + с = 0 \]
вы получаете корни квадратного уравнения, и когда корни действительны, они представляют собой точки, в которых парабола пересекает ось x.
Особый случай возникает, когда корни комплексные, и в этом случае парабола не пересекает ось x.
Типы квадратичных графиков
Как мы упоминали ранее, ВСЕ одномерные квадратичные функции будут представлены параболами, но в зависимости от того, a > 0 или a
92+2x-3\), из чего следует, что соответствующие коэффициенты равны:\[а = \фракция{1}{3}\] \[б = 2\] \[с = -3\]
Подставив известные значения \(a\) и \(b\) в формулу координаты x вершины, получим:
\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{2}{2 \cdot \frac{1}{3}} = -3\]
Теперь нам нужно подставить значение \(x_V = \displaystyle -3\) в квадратичную функцию, так что мы получим: 92+3x-2\), из чего следует, что соответствующие коэффициенты равны:
\[а = \фракция{4}{3}\] \[б = 3\] \[с = -2\]
Подставив известные значения \(a\) и \(b\) в формулу координаты x вершины, получим:
\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot \frac{4}{3}} = -\frac{9}{8}\]
Теперь нам нужно подставить значение \(x_V = \displaystyle -\frac{9}{8}\) в квадратичную функцию, так что мы получим: 92+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\ frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}\]
Следовательно, координата x вершины равна \(x_V = \displaystyle -\frac{9}{8}\), а координата y вершины равна \(y_V = \displaystyle -\frac{59 {16}\).
Это указывает на то, что точкой, представляющей вершину, является \( \displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)\).
Графически получается следующее:
Другие квадратичные калькуляторы
Большинство приложений базовой алгебры основаны на решении какого-либо квадратного уравнения, поэтому оно имеет сильный педагогический эффект. Цель узнать об этом.
Квадратичная формула — один из самых печально известных обучаемых объектов в математике. Дело не в том, что уравнений кубической или четвертой степени не существует, дело в том, что квадратные уравнения — это те, которые мы можем легко объяснить.
Калькулятор квадратных уравнений с делением
Калькулятор квадратных уравнений с делением
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
12.2004 
Каждый вопрос ставит новую задачу, которая кажется сложнее, чем восхождение на Эверест! Мне нужна помощь как можно скорее. Кто-нибудь, пожалуйста, направьте меня.
Что ж, я читал ваш пост и поверьте мне: я знаю, каково это. Некоторое время назад я столкнулся с той же проблемой, но прежде чем вы найдёте учителя, я хотел бы порекомендовать вам одну действительно полезную программу: Алгебратор. Я действительно пробовал много других способов, но этот определенно лучший! Удачи в этом! Дайте мне знать, что вы думаете!.
Я определенно думаю, что вам стоит попробовать.
06.2004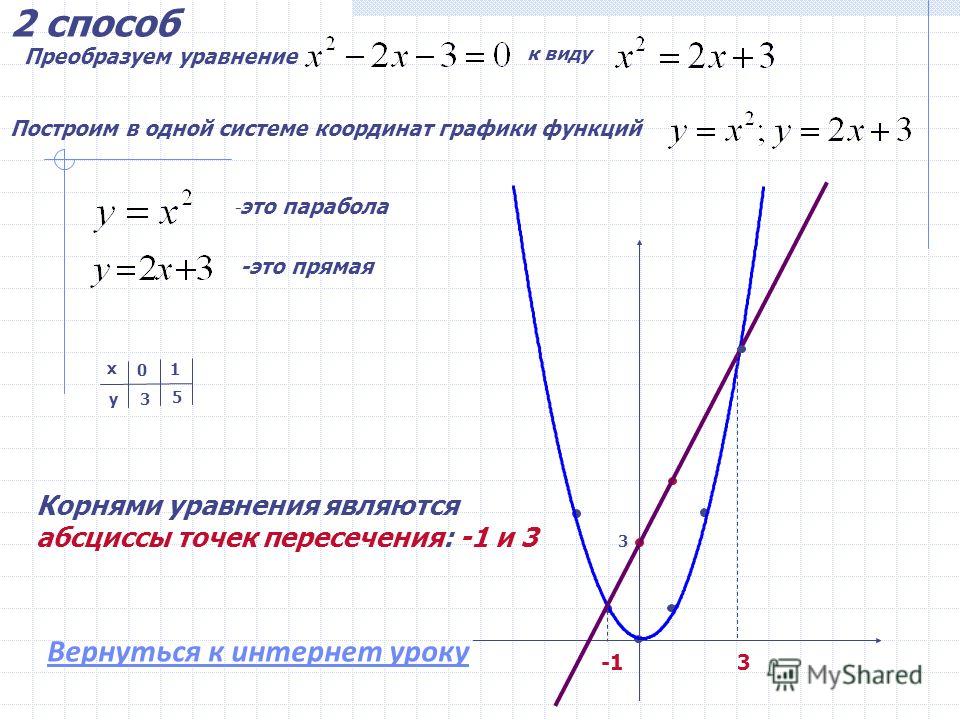 
Даже несмотря на то, что я предполагаю, что вам это понравится, мне очень интересно услышать от вас, есть ли функция, при которой программное обеспечение не работает. Я не хочу защищать Algebrator за то, что он не может сделать. Но следующая проблема, о которой сообщают, вероятно, будет первой!