Графики функций и их производных.
ИССЛЕДОВАНИЕ ФУНКЦИИ ПРИ ПОМОЩИ ПРОИЗВОДНОЙ
возрастание
убывание
функции.
Алгоритм нахождения промежутков возрастания (убывания) функции
1. Находим область определения функции
2.Находим производную функции
3.Находим точки, в которых f’(x) =0
или f’(x) не существует
4.Отмечаем эти точки на числовой прямой
и определяем знаки производной
на полученных промежутках
5.Делаем выводы о промежутках
возрастания и убывания
Исследование
по формуле
по графику
Признаки:
Если f / (x) 0,
значит, функция возрастает.
Если f / (x)
значит, функция убывает.
По формуле функции
Практикум:
Найдите промежутки возрастания
(убывания) функции.
Задания:
1 вариант
D(f)
2 вариант
f ‘ (x)
f ‘ (x) = 0
(не существует)
Знаки
Промежутки возрастания
производной
Промежутки убывания
1 вариант
D(f)
2 вариант
f ‘ (x)
R
f ‘ (x) = 0
R
(не существует)
Знаки
-1; 1
1
Промежутки возрастания
производной
-1; 1
Промежутки убывания
—
—
—
-1
+
+
+
-1
1
Графики.
Графики
функций
Графики
производных
График
функции
Если функция возрастает ,
то производная
положительна
y
4
2
1
-1
0
x
Если функция убывает ,
то производная
отрицательна
В7(ЕГЭ) На рисунке изображен график функции у = f(x) и касательная к этому графику.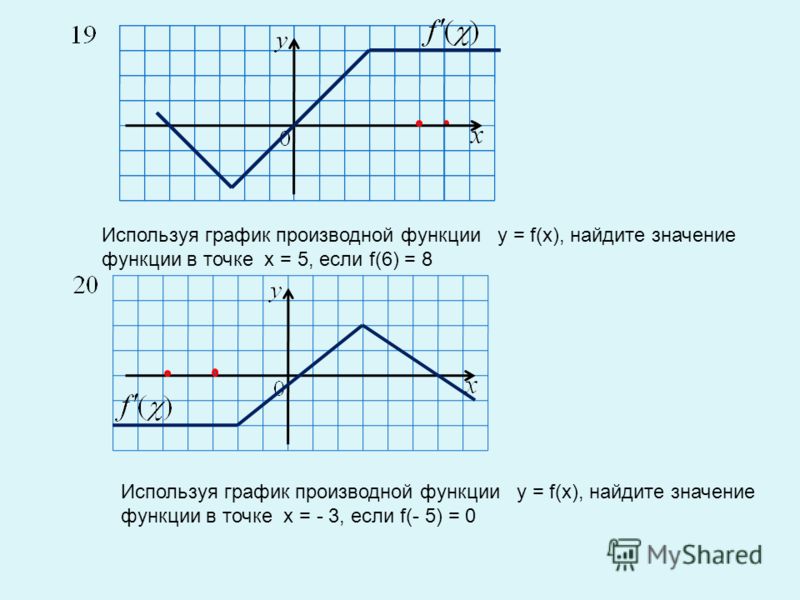 Определите знак производной в точке касания.
Определите знак производной в точке касания.
В7 (ЕГЭ) На рисунке изображен график функции у = f(x) и касательная к этому графику. Определите знак производной в точке касания.
В7 .егэ .
В7 (егэ). На рисунке изображен график функции , определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна .
- В7(егэ). На рисунке изображен график функции , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции отрицательна.
Задание 7 № 6871.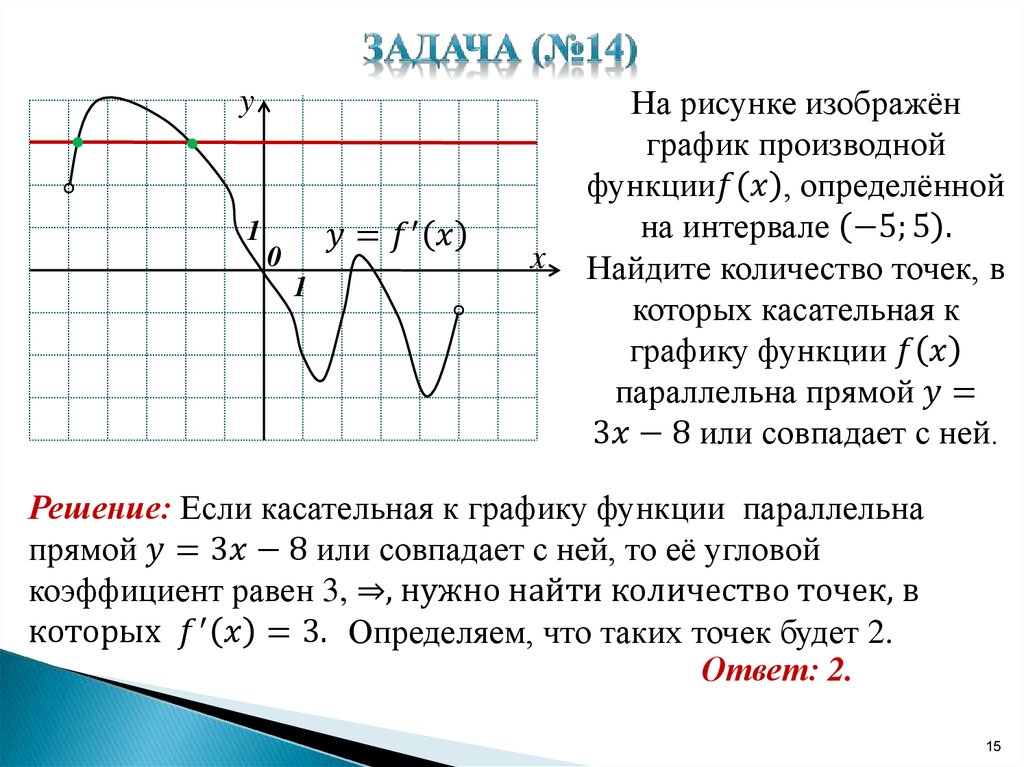 На рисунке изображен график функции , определенной на интервале (-1;12) .Определите количество целых точек, в которых производная функции отрицательна.
На рисунке изображен график функции , определенной на интервале (-1;12) .Определите количество целых точек, в которых производная функции отрицательна.
Графики производных
Задания В7 (ЕГЭ)
Если f / (x) 0,
значит, функция возрастает.
Признаки:
Если f / (x)
значит, функция убывает.
Если f / (x) 0,
значит, функция возрастает.
На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-6;8) .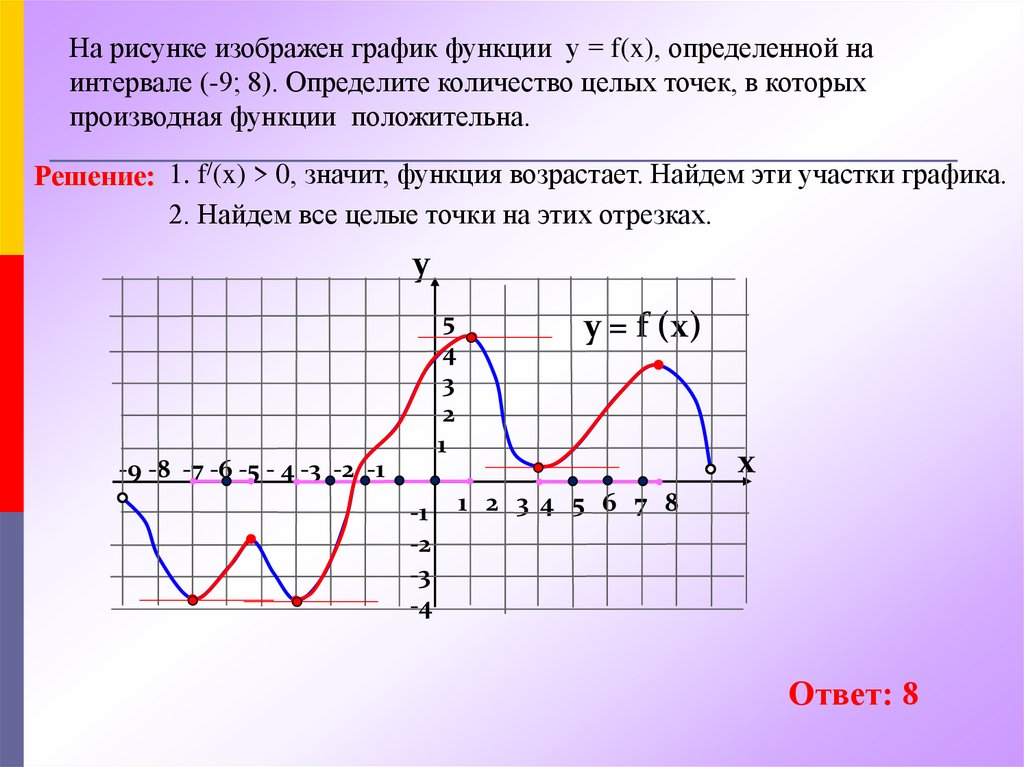
График производной
Функция задана на отрезке. На рисунке изображен график ее производной.
- Укажите количество
промежутков
возрастания функции.
у
y=f ‘(x)
1
0
b
1
х
а
На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-8;6) . Найдите количество промежутков убывания функции f(x).
Если f / (x)
значит, функция убывает.
Функция задана на отрезке. На рисунке изображен график ее производной.
у
- Укажите количество
промежутков
убывания функции
y=f ‘(x)
1
0
b
1
х
а
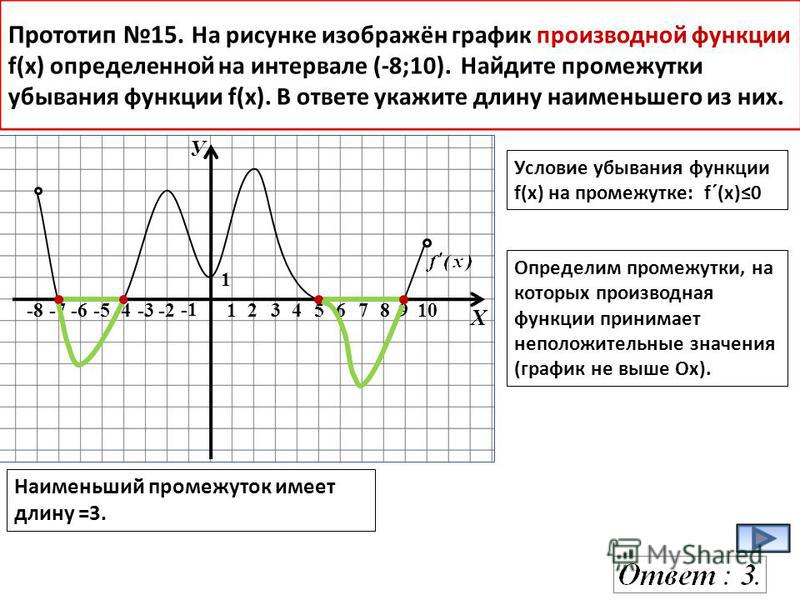
На рисунке изображен график производной функции f(x),
определенной на интервале (a;b).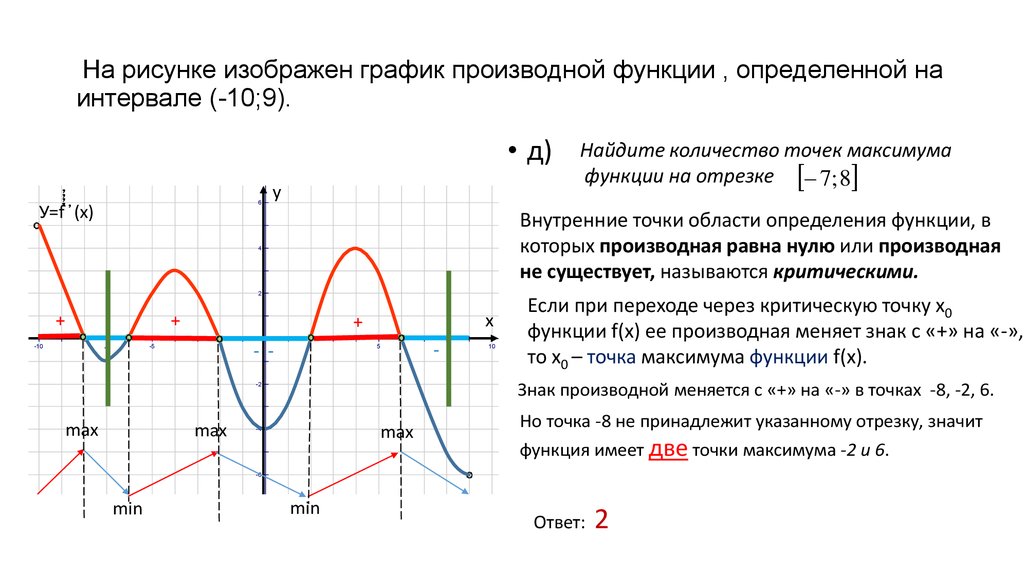 Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
у
y=f ‘(x)
1
b
0
а
1
х
(1)
На рисунке изображен график производной функции f(x),
определенной на интервале (a;b). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
у
y=f ‘(x)
1
b
0
а
1
х
(2)
Задание 7 .На рисунке изображен график производной функции , определенной на интервале (-6;6) . В какой точке отрезка[-5;-1] функция принимает наибольшее значение.
Задание 7 .На рисунке изображен график производной функции , определенной на интервале (-6;6) .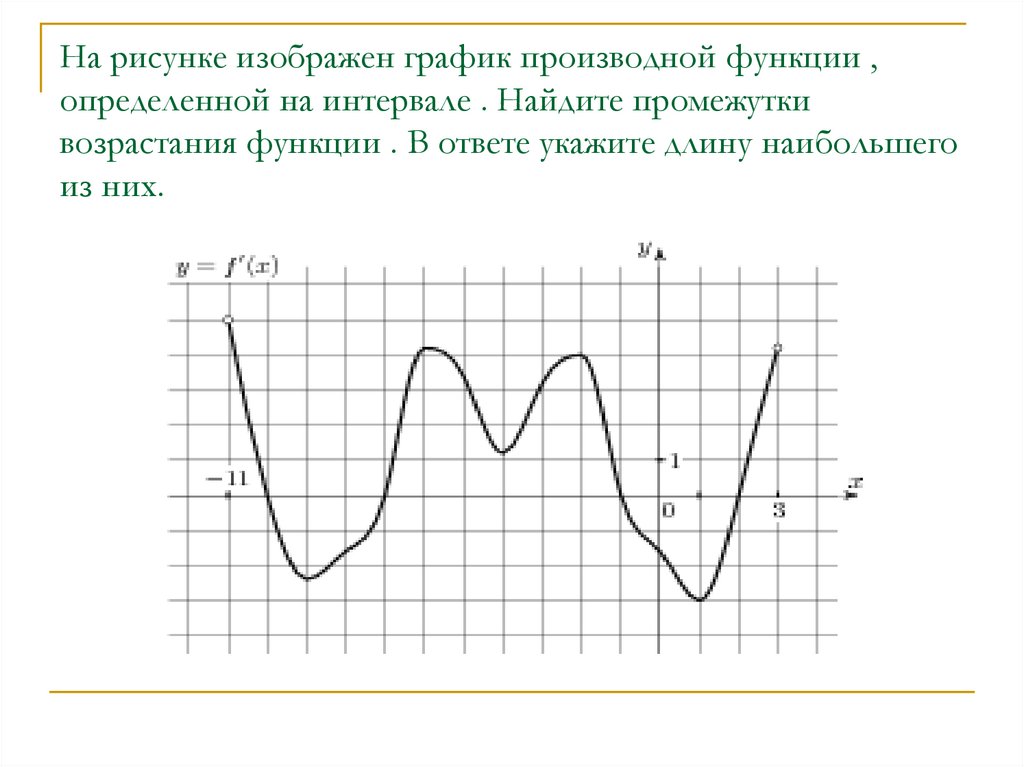 Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.
Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.
Задание 7.На рисунке изображен график производной функции, определенной на интервале (-9;2). Найдите промежутки убывания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.
На рисунке изображен график производной функции , определенной на интервале .Найдите промежутки возрастания функции . В ответе укажите длину наибольшего из них.
Домашнее задание:
Составить подборку однотипных заданий В7 из сборника егэ, прорешать.
Спасибо
за урок!
23
10. Производная функции, ее геометрический. И физический смысл
Введение бесконечно малых и больших величин связано с процессом их изменения. Изменения, как правило, характеризуют разностью между конечным (или соседним) и начальным значением. В математике, как и в физике, такую разность называют приращением. Приращение может быть положительным, когда соседнее (последующее) значение больше начального, и отрицательным. Мы постоянно встречаемся с характеристиками функции в точке: предел, непрерывность, значение самой функции. Определим понятие производной (от) функции в точке.
Изменения, как правило, характеризуют разностью между конечным (или соседним) и начальным значением. В математике, как и в физике, такую разность называют приращением. Приращение может быть положительным, когда соседнее (последующее) значение больше начального, и отрицательным. Мы постоянно встречаемся с характеристиками функции в точке: предел, непрерывность, значение самой функции. Определим понятие производной (от) функции в точке.
На рис.6 приведен график некоторой непрерывной функции .
Рисунок 6 – Касательная прямая в М0 к графику функции есть предельное положение секущей М0 М1 При
Геометрический смысл производной: .
Точке М0 отвечает пара чисел , где . Изменим значение Х0, т. е. дадим ему приращение DХ и, таким образом, от точки Х0 на оси абсцисс перейдем в точку Х0 + DХ. Вследствие этого точка М0 на графике передвинется в точку М1. Изменение функции в результате этого перехода обозначим . Отношение показывает, как быстро изменяется функция с изменением Х. Предел этого отношения при называется производной функции в точке Х0.
Отношение показывает, как быстро изменяется функция с изменением Х. Предел этого отношения при называется производной функции в точке Х0.
Def: Производной функции У по аргументу Х называется предел отношения приращения функции D У к приращению аргумента DХ, вычисленный в процессе, когда приращение аргумента стремится к нулю.
На рис.6 прямая линия, соединяющая две соседние точки М0 и М1, будет секущей для графика. Она наклонена к оси ОХ под углом j, и .
Если DХ устремим к нулю, то точка М1 начнет передвигаться по графику к точке М0, а секущая М0М1 поворачиваться относительно точки М0.
В пределе, при слиянии движущейся точки М1 с неподвижной М0 секущая займет положение касательной. Угол наклона касательной к оси ОХ равен . Таким образом,
Отсюда следует геометрический смысл производной:
Производная функции в точке равна тангенсу угла наклона касательной к графику функции в этой точке: .
В начальной школе мы проходили уравнение прямой с угловым коэффициентом: . В старших классах мы обнаружили, что угловой коэффициент равняется тангенсу угла наклона прямой к оси
Кроме касательной в каждой точке графика часто рассматривают еще одну прямую, называемую нормалью.
Def: Прямая, проходящая через точку М0 перпендикулярно к касательной, называется нормалью к кривой в точке М0.
Уравнение нормали:
Для потребностей техники приходится рассматривать пространственные кривые, извивающиеся и закручивающиеся. Каждую точку такой кривой «сопровождает» совокупность трех единичных векторов, направленных один по касательной, второй по нормали, а третий вектор перпендикулярен к каждому из двух названных. Положение этих векторов определяют через производную от функции (или функций), описывающих кривую. И этот приём применения производных оказался исключительно эффективным при решении многих задач. Соответствующий раздел математики получил название дифференциальной геометрии.
И этот приём применения производных оказался исключительно эффективным при решении многих задач. Соответствующий раздел математики получил название дифференциальной геометрии.
Мы уже рассматривали функции, имеющие точки разрыва. В этих точках функция не имеет предела. Естественно ожидать, что предел отношения двух приращений и тоже не везде существует, т. е. не везде существует производная.
Def: Функция называется дифференцируемой в точке, если она имеет производную в этой точке. Функция называется дифференцируемой на интервале, если она имеет производную в каждой точке этого интервала.
Конечно, в точках разрыва, функция не может быть дифференцируема. А вот обратное утверждение неверно.
На рис.7 представлен график функции, непрерывной во всех точках, но не имеющей производных в точках М1, М2, М3.
В точке М1 функция не дифференцируема. К этой точке непрерывности примыкают два разных участка с разными касательными. В точке М2 также примыкают две разные ветви, но они имеют общую касательную, перпендикулярную оси ОХ. Следовательно, тоже не существует. Точка М3 разделяет вогнутый (слева) участок графика от выпуклого. В этой точке касательная тоже перпендикулярна к оси абсцисс: .
В точке М2 также примыкают две разные ветви, но они имеют общую касательную, перпендикулярную оси ОХ. Следовательно, тоже не существует. Точка М3 разделяет вогнутый (слева) участок графика от выпуклого. В этой точке касательная тоже перпендикулярна к оси абсцисс: .
Рисунок 7 – График непрерывной во всех точках функции.
В точках X1, X2, X3 функция не дифференцируема. В точке X1 примыкают две ветви графика с разными касательными; в точках X2 и X3 касательная к графику наклонена к оси ОХ
Под углом 90° (tg 90° – не существует)
Рассмотрим классический пример применения производной. Он связан с прямолинейным движением. Измерим время DT движения от одного дорожного столба до соседнего. Зная, с каким шагом DS устанавливаются столбы, находим среднюю скорость движения на этом конкретном участке . Переходя к пределу (уменьшая DT)Находим мгновенную скорость.
| < Предыдущая | Следующая > |
|---|
Как построить график функции по ее производной (4 ключевых шага) – JDM Educational
Производные. Одно из основных понятий в исчислении. Большая часть исчисления зависит от производных и скорости изменения.
Одно из основных понятий в исчислении. Большая часть исчисления зависит от производных и скорости изменения.
Обычно производные вводятся в начале курса исчисления и используются на протяжении всего курса.
Предположим, нам дан график функции, и мы хотим найти график исходной функции. Как мы это сделаем? Мы рассмотрим 4 ключевых шага.
Начнем.
Напомним: когда мы впервые узнали о производных, мы узнали, что графически производную функции можно интерпретировать как формулу наклона касательной.
Прежде чем мы посмотрим на график производной функции, давайте посмотрим на несколько изображений касательных линий к различным кривым. На каждом из приведенных ниже графиков касательная проведена к кривой.
Касательная к функции будет горизонтальной на относительном минимуме или максимуме (центральный график). Обратите внимание, что на второй диаграмме касательная — это горизонтальная линия, касательная к графику в относительном минимуме.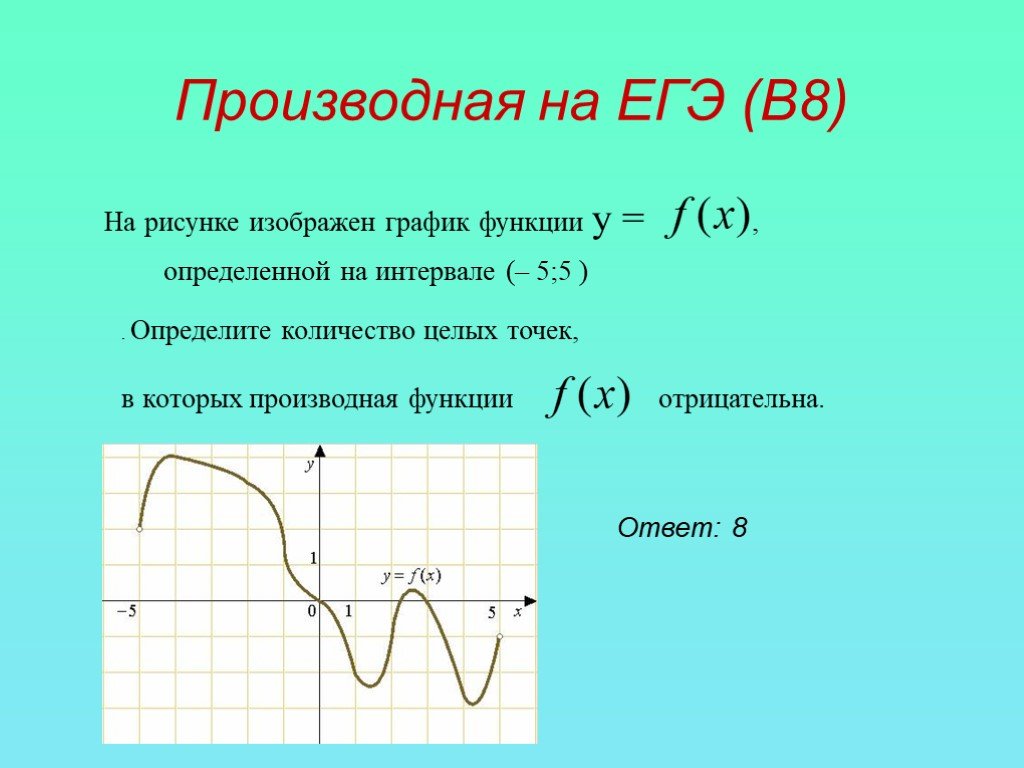 Мы будем использовать эту идею при работе с проблемами.
Мы будем использовать эту идею при работе с проблемами.
Обычная задача, возникающая на занятиях по математическому анализу, представляет собой следующий вопрос: по заданному графику производной найти возможный график исходной функции.
Что график производной говорит вам об исходной функции?
Пример 1
Начнем с простого:
Здесь у нас есть график производной f'(x) = x.Это график функции y = x . Помните, что этот график представляет производную функции. Наша задача — найти возможный график функции.
Во-первых, обратите внимание, что производная равна 0, когда x = 0. Из исчисления мы знаем, что если производная равна 0 в точке, то это критическое значение исходной функции.
Мы можем использовать критические значения, чтобы найти возможные максимумы и минимумы. Также на интервале (- ∞, 0) f ‘( x ) < 0, что означает, что исходная функция f ( x ) убывает.
На интервале (0, ∞) f ’( x ) > 0, что означает, что исходная функция f ( x ) является возрастающей.
Поскольку знак f ‘( x ) меняется с убывающего на возрастающий, мы имеем минимум при x = 0. Подведем итоги в таблице:
Таблица анализа знаков
| Interval/ Critical Value | (- ∞, 0) | (- ∞, 0) | (0, ∞) |
|---|---|---|---|
| f ‘( x ) | Отрицательный | F ‘ ( x ) = 0 | Положительный |
| F 9004 | |||
| F | |||
| F 9004 | |||
| F 9004 | |||
| F 9004 | |||
. 0097 относительное 0097 относительное минимум при x = 0 | увеличение |
Отлично! Теперь у нас есть некоторая информация об исходной функции.
Мы можем начать с построения относительного минимума в точке (0, f ( x )). Для простоты сделаем минимум в (0, 0). Мы поговорим об этом чуть позже.
Так как наша производная является линейной функцией, то исходная функция должна быть квадратичной. Это означает, что минимум (0, 0) является вершиной параболы.
Но как построить график остальной функции? Насколько узкой или широкой мы должны сделать параболу?
Мы можем использовать наклоны касательных линий, чтобы выяснить это. Помните: y — значения f ‘( x ) сообщат нам наклон касательных исходной функции .
Давайте посмотрим на значение f ‘( x ) на различных входных данных (значения x) в таблице, чтобы получить представление о том, что здесь происходит:
| x | f ‘( x ) = x |
| -4 | -4 |
| -2 | -2 |
| 0 | 0 |
| 2 | 2 |
| 4 | 4 |
Это было довольно легко определить с тех пор, как мы дали идентификационную функцию.
На интервале (- ∞, 0) наклоны начинаются очень круто и становятся менее крутыми по мере приближения к 0.
В точке (0, 0) касательная горизонтальна, затем от (0, ∞ ), склоны начинаются небольшими, а затем становятся все круче и круче.
Мы можем получить представление о том, как выглядит исходная функция, вставив несколько таких наклонов. Это называется полем наклона .
Здесь мы видим поле наклона для функции.Наклоны служат направляющими для нашей первоначальной функции. Вот график возможной функции:
Эта кривая совпала бы с показанным выше полем наклона, если бы мы наложили их на один и тот же график.Конечно, мы можем быть уверены, что наш график верен, потому что наш пример дал нам уравнение линейной функции, и мы можем легко интегрировать его, чтобы найти исходную функцию.
Если f ‘( x ) = x , то f ( x ) = ½ x 2 (возможно, с добавлением на наш график константы )0029 f ( x ), функция убывает на (-∞, 0) и возрастает на (0, ∞).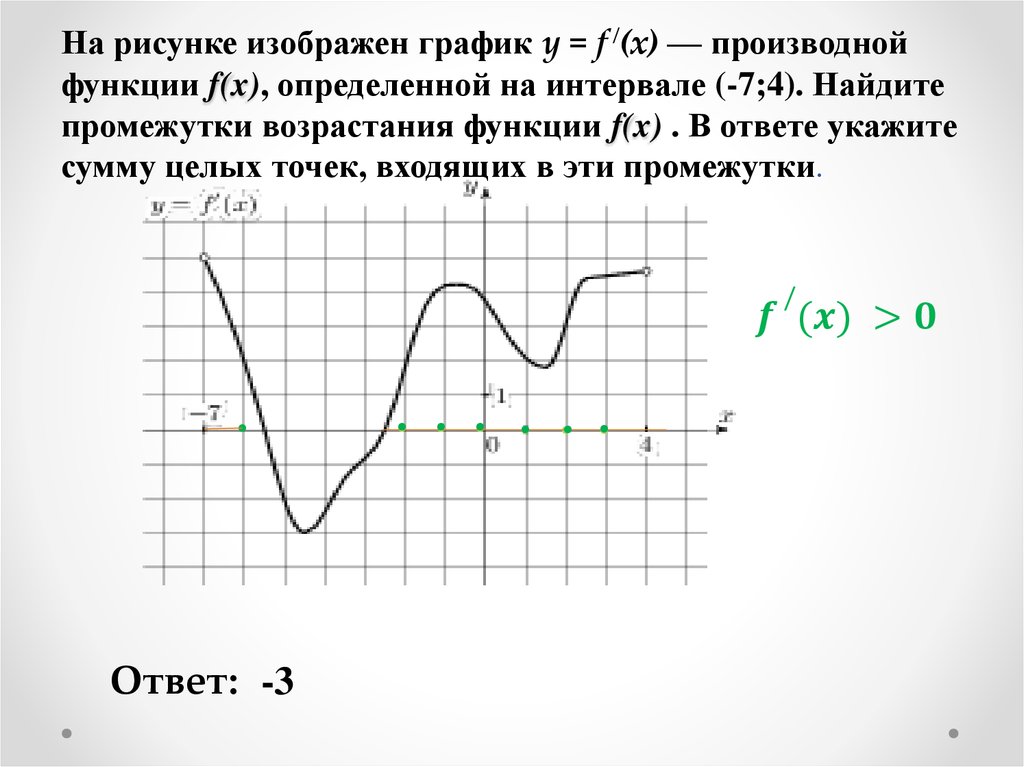
Это единственный график функции, производная которой равна f ‘( x ) = x ? № Из исчисления мы знаем, что существует бесконечное число функций, производная которых равна x .
Эти функции отличаются константой. Графически семейство функций, производная которых равна х , сдвинуты по вертикали вверх или вниз.
На диаграмме ниже все показанные параболы имеют производную f ‘( x ) = x .
Все приведенные выше параболы имеют производную от f'(x) = x.Прежде чем мы перейдем к другой задаче, давайте ответим на вопрос:
Что график производной говорит вам об исходной функции?
Используя наш первый пример, мы обнаружили следующую информацию.
- x — пересечения f ’( x ) — возможные максимумы или минимумы функции.
- Если f ’ ( x ) выше оси x , то f ( x ) увеличивается.
 Если f ’ ( x ) ниже оси x , то f ( x ) уменьшается.
Если f ’ ( x ) ниже оси x , то f ( x ) уменьшается. - Значения y f ’ ( x ) дают нам наклоны касательных f ( x ).
Наш первый пример был относительно простым. График производной был линейным, а исходный график был квадратичным.
Не все проблемы будут такими простыми. В нашем следующем примере мы рассмотрим график производной степени 2, чтобы увидеть, что мы можем узнать об исходной функции. Давайте сначала ответим на этот вопрос:
Что вторая производная говорит вам о графике?Вторая производная говорит нам о вогнутости исходной функции.
Давайте поговорим о второй производной. Напомним, что вторая производная говорит нам о вогнутости исходной функции.
Если f ‘’( x ) > 0 на интервале, то исходная функция f ( x ) равна вогнутой вверх на этом интервале.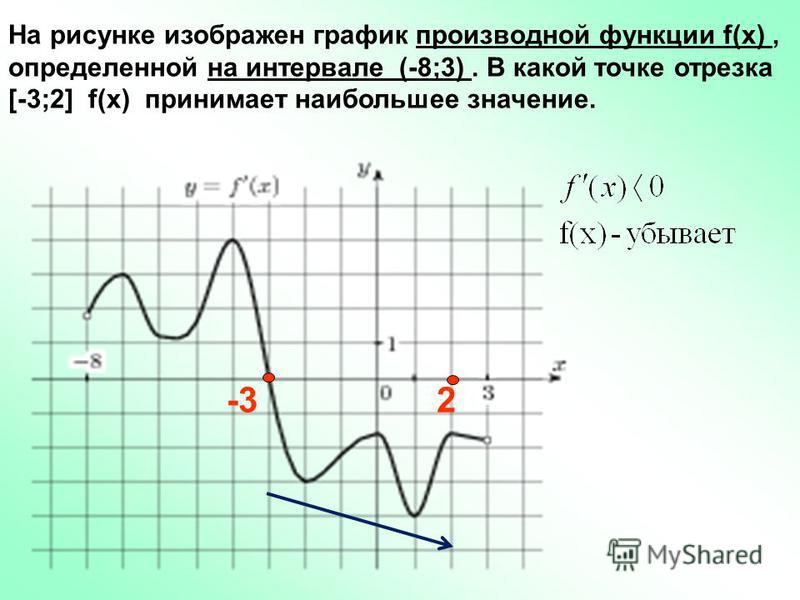 Если f ‘’( x ) < 0 на интервале, то исходная функция f ( x ) равна вогнутой вниз на этом интервале.
Если f ‘’( x ) < 0 на интервале, то исходная функция f ( x ) равна вогнутой вниз на этом интервале.
В нашем следующем примере мы также будем использовать вторую производную, чтобы узнать больше информации об исходной функции.
Пример 2
Нарисуйте возможный график функции f ( x ) график ее производной.
Этот график производной функции f'(x) представляет собой параболу, предполагающую кубическую форму исходной функции f(x).Ключевые шаги
- Найдите возможные максимумы и минимумы, идентифицируя точки пересечения x f ’. Из графика мы видим, что наши x -перехваты равны 1 и 5. Это означает, что у нас есть возможные максимумы или минимумы в этих точках.

- Определите интервалы, в которых f ’ находится выше оси x и ниже оси x . Это скажет нам, где f увеличивается или уменьшается. Мы можем создать таблицу для анализа знаков.
Sign Analysis Table
| Interval/ Critical Value | (- ∞, 1) | x = 1 | (1, 5) | x = 5 | (5, ∞) |
|---|---|---|---|---|---|
f ‘( x )| отрицательный | 0097 f ‘( x ) = 0 | positive | f ‘( x ) = 0 | negative | |
| f ( x ) | decreasing | Относительно мин | Увеличение | Относительно MAX | Уменьшение |
также, F ‘( x ) ниже — — ‘ ( x ) ниже — — — x — x — x — x — x — x — x .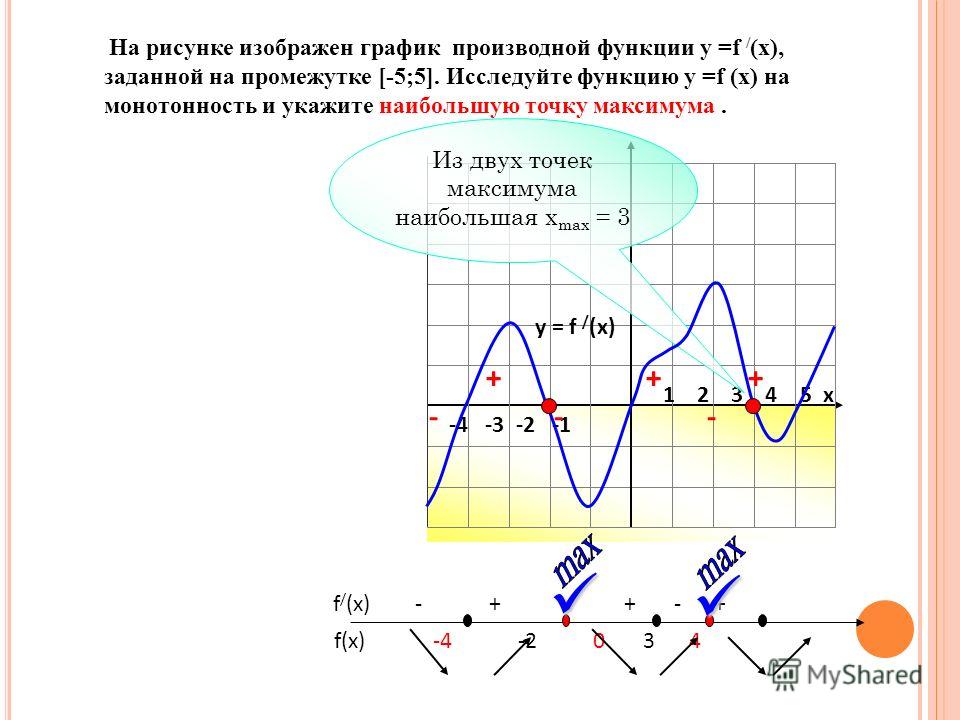 ) и (5, ∞), что означает f ( x ) равно уменьшению на этих интервалах.
) и (5, ∞), что означает f ( x ) равно уменьшению на этих интервалах.
Поскольку f ‘( x ) выше оси x на интервалах из (1, 5), это означает, что f ( x ) равно , увеличивая на этом интервале.
Поскольку функция переходит от убывания к возрастанию при x = 1, функция имеет относительного минимума .
Аналогично, поскольку функция переходит от возрастания к убыванию в точке x = 5 , имеется относительный максимум при x = 5.
Из таблицы видно, что мы имеем относительный минимум при (1, f (1)) и относительный максимум при (5, f (5). Предположим, что мы не знаем уравнения для производной функции.
Это означает, что мы не можем интегрировать его, чтобы найти возможную функцию. Итак, мы можем просто оценить эти точки.
- Найдите наклоны некоторых касательных f с помощью y значения производной.
 В этом случае нам не дано масштабирование значений по оси y , поэтому будет сложно использовать наклоны в качестве ориентиров для нашего графика. Мы пропустим этот шаг, так как здесь он не особенно полезен.
В этом случае нам не дано масштабирование значений по оси y , поэтому будет сложно использовать наклоны в качестве ориентиров для нашего графика. Мы пропустим этот шаг, так как здесь он не особенно полезен.
- Используйте вторую производную f ‘’(x), чтобы узнать о вогнутости исходной функции f(x) и найти возможные точки перегиба. Возможные точки перегиба возникают на относительных максимумах или минимумах ф ’ ( х ). На нашем графике производной ниже мы видим, что в максимуме (3, f (3)) наклоны касательных линий по обе стороны от точки имеют разные знаки. Помните, что наклоны тангенса f’(x) на самом деле являются секундной производной f’’(x). С левой стороны от точки (3, f ’(3)) мы видим, что наклоны касательных (зеленым цветом) положительны; с правой стороны наклоны касательных (выделены розовым цветом) отрицательны.

Что это значит? Если вторая производная f »(x) меняет знак, когда x = 3, имеется точки перегиба в точке (3, f(3)). Мы можем провести анализ знаков, как мы это делали с первой производной, чтобы убедиться, что у нас есть точка перегиба: Возможный
POI
(точка перегиба
)
up
inflection
down
Действительно, поскольку знак меняется, у нас есть точка перегиба на (3, f (3)) .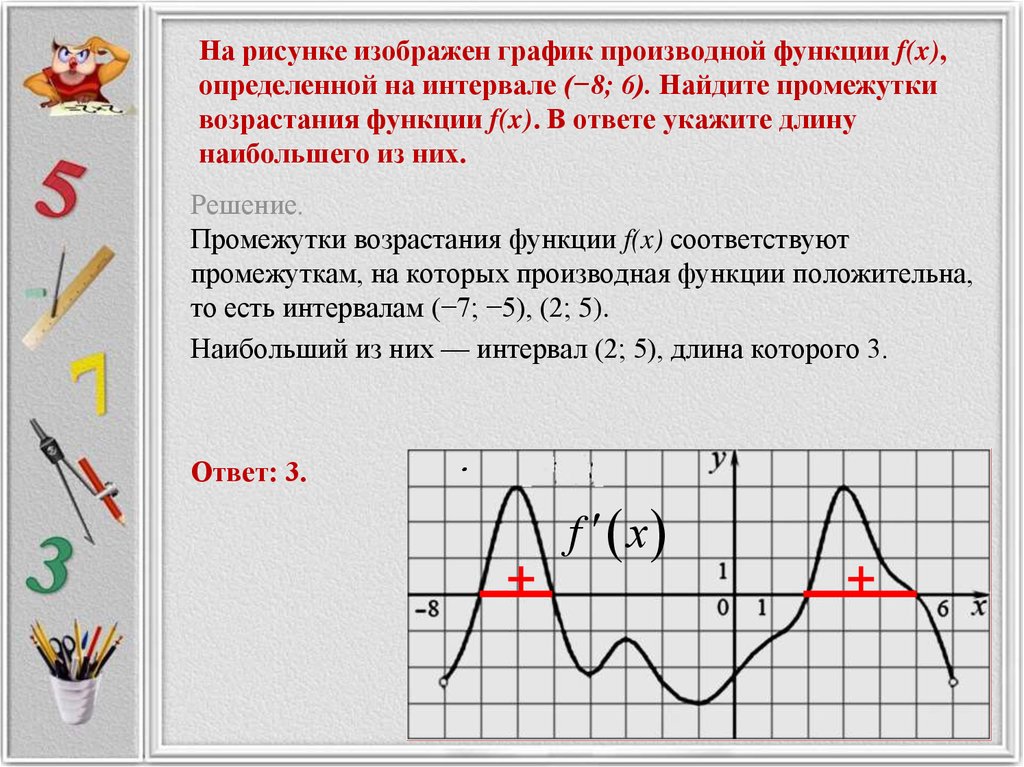 Это означает, что в этой точке вогнутость меняется с вогнутой вверх на вогнутую вниз.
Это означает, что в этой точке вогнутость меняется с вогнутой вверх на вогнутую вниз.
Соединяя все эти части вместе, мы получаем следующий эскиз. Имейте в виду, мы могли сдвинуть график по вертикали вверх или вниз, чтобы получить другую возможную функцию, производной которой был данный график.
Это возможная функция f(x), которая совпадает с производной f'(x).Обратите внимание, если мы наложим производную (выделенную зеленым цветом) на возможный график исходной функции, мы сможем довольно легко увидеть взаимосвязь между производной и исходной функцией.
Мы можем увидеть, как f(x) и f'(x) совпадают, если нанести их на один и тот же график.Давайте рассмотрим другую задачу. Как и прежде, мы пройдем через наши 4 ключевых шага.
Пример 3
Учитывая график производной и точку на исходной функции (0, 5), нарисуйте график исходной функции f ( x ).
Вот график производной функции f'(x), который предполагает квартику исходной функции f(x).
Ключевые этапы
- Найдите возможные максимумы и минимумы, идентифицируя x пересечений f ’. x — пересечения f ‘( x ) равны -2 и 4. -ось. В этом случае f ’ находится ниже оси x от (- ∞, -2) и (-2, 4) и выше x — ось из (4, ∞). Давайте используем нашу информацию из этих первых двух шагов, чтобы определить максимумы и минимумы функции.
- Найдите склоны из некоторых линейков F 9 9003 9003 9003 .
 Поскольку мы не знаем масштабирования по оси y , мы можем пропустить этот шаг.
Поскольку мы не знаем масштабирования по оси y , мы можем пропустить этот шаг. - Используйте вторую производную f ‘’(x), чтобы узнать о вогнутости исходной функции f ( x ) и найти возможные точки перегиба. Помните, что возможные точки перегиба находятся на максимумах и минимумах f ’ ( x ). Глядя на наш график, мы видим, что у нас есть максимум, когда х = -2 и минимум, когда x = 2. Когда x < -2, наклоны касательных положительны. На интервале (-2, 2) касательные отрицательны; на интервале (2, ∞) касательные снова положительны. Давайте суммируем эти выводы в таблице:
- График y = x 3 2 x 2 5 x + 6 в окне [-5, 5] x [-10, 10]
- Отобразите меню Math, нажав
- Выделите 6: Производные с помощью клавиш перемещения курсора
- Откройте подменю Производные, нажав
- Выберите dy/dx , нажав
- Введите -2 в качестве координаты x , нажав
- Установите значение координаты x , нажав
- Откройте меню Math и выберите A:Tangent.
- Введите -2. Затем нажмите
- Перерисуйте график и очистите касательную, нажав
- Установите y2 = d (y1 (x), x)
- Отобразите график функции и ее производной, нажав
- Выберите функцию Zero в меню F5:Math.
- Выберите график производной, нажав
В правом верхнем углу должна появиться маленькая цифра 2, указывающая на то, что выбран граф, определенный в y2. - Установите нижнюю границу, переместив курсор влево от нужного нуля и нажав
- Установите верхнюю границу, переместив курсор вправо от нужного нуля и нажав
| Interval/ Critical Value | (- ∞, -2) | x = -2 | (-2, 4) | x = 4 | (4, ∞) |
|---|---|---|---|---|---|
| f ‘( x ) | отрицательный | f ‘( x ) = 0 | negative | f ‘( x ) = 0 | positive |
| f ( x ) | Уменьшение | NO Заключение | Уменьшение | Относительное мин | Увеличение |
Анализ знаков F » ( x )
| Интервал/ POI 08080 ( 08080 08080 | (- ∞, -2) | x = -2 | (-2, 2) | x = 2 | (2, ∞) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
F 40095| F4 9003 » ‘ | 9 4 | 9003 | positive | f »( x ) = 0 | negative | f »( x ) = 0 | positive | f ( x ) | вогнутый вверх | точка перегиба | вогнутая вниз | точка перегиба | вогнутая вверх | |
Итак, мы имеем точки перегиба при (-2, f 2 (2)). Теперь у нас есть хорошее представление о том, как выглядит график f(x)! Используя всю приведенную выше информацию, вот возможный эскиз:
Теперь у нас есть хорошее представление о том, как выглядит график f(x)! Используя всю приведенную выше информацию, вот возможный эскиз:
Вы можете найти ключевые точки приведенного выше графика f ( x ), чтобы сопоставить его с тем, что мы нашли из производной. Идите вперед и убедитесь, что все имеет смысл!
С практикой вы очень привыкнете к интерпретации графика производной для определения графика исходной функции!
Здесь вы можете найти ответы на распространенные вопросы о функциях.
Здесь вы можете узнать, как использовать производные и графики для нахождения максимумов функций.
Надеюсь, эта статья была вам полезна. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на наш канал YouTube и получать обновления о новых математических видео!
Подпишитесь на наш канал на YouTube!
Об авторе:
Жан-Мари Гард — независимый учитель математики и репетитор из Массачусетса. Вы можете связаться с Жан-Мари по адресу https://testpreptoday.com/.
Вы можете связаться с Жан-Мари по адресу https://testpreptoday.com/.
Модуль 9. Связь между функцией и ее первой и второй производной
В Модуле 8 мы видели, что значение производной f при x определяется наклоном линии, касательной к графику f при x . В этом уроке вы узнаете, что говорит первая производная о графике исходной функции, используя функции калькулятора «Производная» и «Касательная».
Если f является функцией, то ее первая производная обозначается как f ‘, что читается как « f простое число», а значение первой производной при x = a равно f ‘. ( а ). Калькулятор обозначает первую производную от f как , что является альтернативной записью. Если y = f ( x ), другие обозначения включают и dy/dx.
Использование функции производной на экране графика
Следуйте приведенной ниже процедуре, чтобы построить график функции, и используйте функцию «Производная» в меню «Математика» экрана «График» для вычисления ее производной.
Найдите значение производной при x = -2 с помощью функции «Производная» в меню F5:Математика.
Вы должны увидеть график и подсказку для координаты x , в которой должна быть оценена производная.
Значение производной f ( x ) = x 3 2 x 2 5 x + 6 = x -90.
Использование касательной функции
Вы можете использовать функцию Tangent в меню Graph Math, чтобы увидеть график касательной линии в определенной точке вместе с уравнением для этой касательной линии.
После того, как вы сделаете выбор, вы должны увидеть график функции и подсказку для x — координаты точки касания.
TI-89 отображает график касательной, а ее уравнение отображается в нижней части экрана. Уравнение касательной в приведенном выше примере: y = 15 x + 30.
9.1.1 Как уравнение касательной отображает значение производной на х = -2? Щелкните здесь, чтобы получить ответ.
9.1.2 В таблице ниже приведены точки на графике функции f ( x ) = x 3 2 x 2 5 x + 6. найдите производную в каждой показанной точке и запишите значения.
| х | 2 | 1 | 0 | 1 | 2 | 3 |
| ф ( х ) | 0 | 8 | 6 | 0 | 4 | 0 |
| f ‘ ( x ) |
Щелкните здесь, чтобы получить ответ.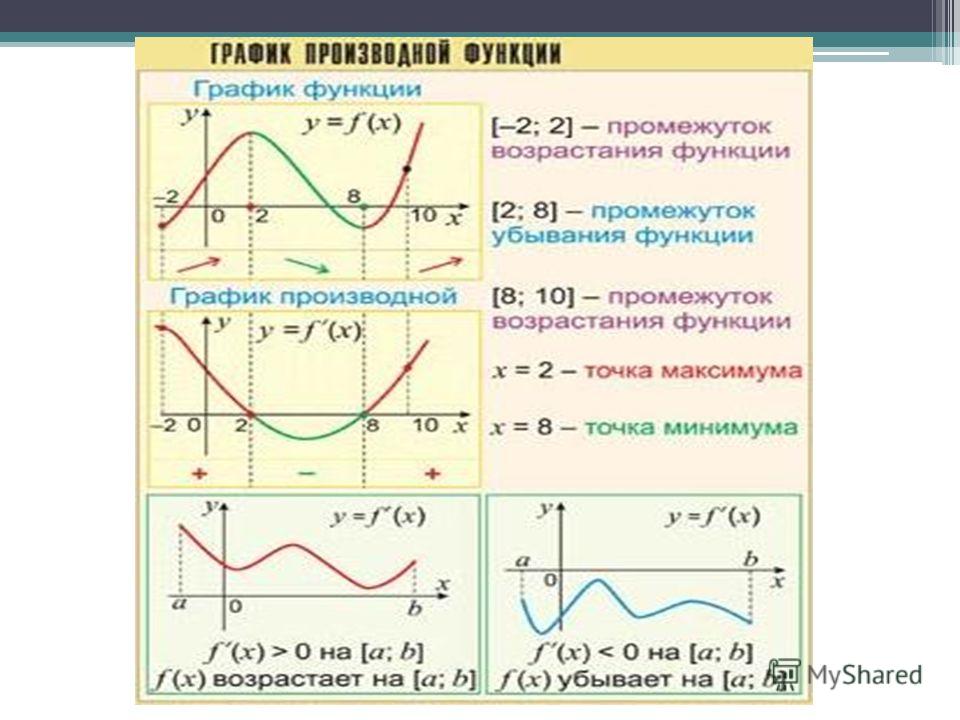
9.1.3 Что вы заметили в значениях функции на интервалах, где производная положительна, по сравнению со значениями функции на интервалах, где производная отрицательна?
Щелкните здесь для ответа.
| |||
Нахождение точек поворота в производной
Каждый
| ti.com/images/online_courses/t3/calculus/images/pd/GlossaryBackground.gif»> | |||
| Точка поворота графика функции – это точка, в которой функция меняется с возрастающей на убывающую или с убывающей на возрастающую. |
Функция возрастает ровно там, где производная положительна, и убывает там, где производная отрицательна. На графике производной найдите x-значение нуля слева от начала координат.
Один из нулей производной приблизительно равен х = -0,7863.
9.1.4 Используйте функцию Zero в меню F5:Math, чтобы найти другой нуль производной. Щелкните здесь, чтобы получить ответ.
Подводя итог взаимосвязи между f и f ‘
Следующие характеристики функции f ( х ) = х 3 2 х 2 5 х + 6 можно определить из графика его первой производной.
Производная равна нулю при x = -0,7863 и при x = 2,11963, которые являются значениями x поворотных точек.

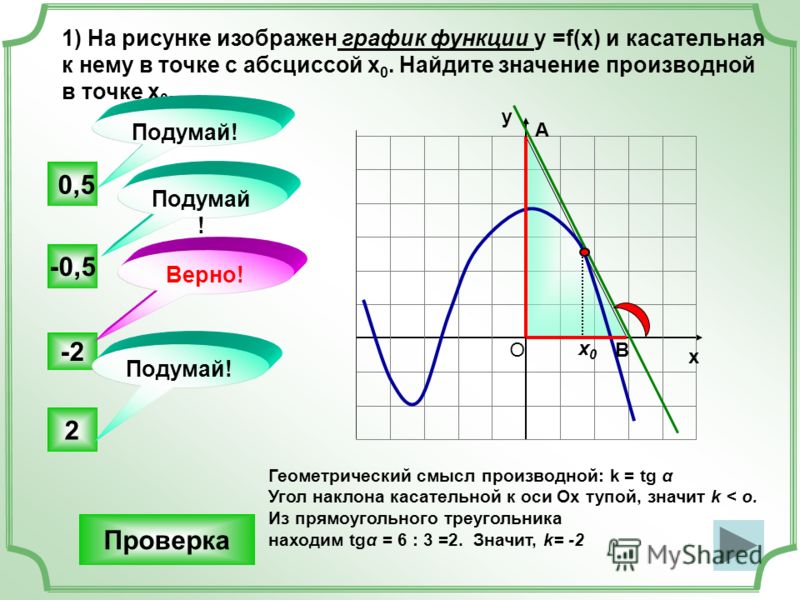 Если f ’ ( x ) ниже оси x , то f ( x ) уменьшается.
Если f ’ ( x ) ниже оси x , то f ( x ) уменьшается.
 В этом случае нам не дано масштабирование значений по оси y , поэтому будет сложно использовать наклоны в качестве ориентиров для нашего графика. Мы пропустим этот шаг, так как здесь он не особенно полезен.
В этом случае нам не дано масштабирование значений по оси y , поэтому будет сложно использовать наклоны в качестве ориентиров для нашего графика. Мы пропустим этот шаг, так как здесь он не особенно полезен. Поскольку мы не знаем масштабирования по оси y , мы можем пропустить этот шаг.
Поскольку мы не знаем масштабирования по оси y , мы можем пропустить этот шаг. 08080
08080