График суммы функций: — — — DirectEducation.ru

Элементарная математика

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) Оглавление ВВЕДЕНИЕ Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 33. Элементарное исследование поведения функции. 34. Сложная функция. 35. Обратная функция. 36. n. 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 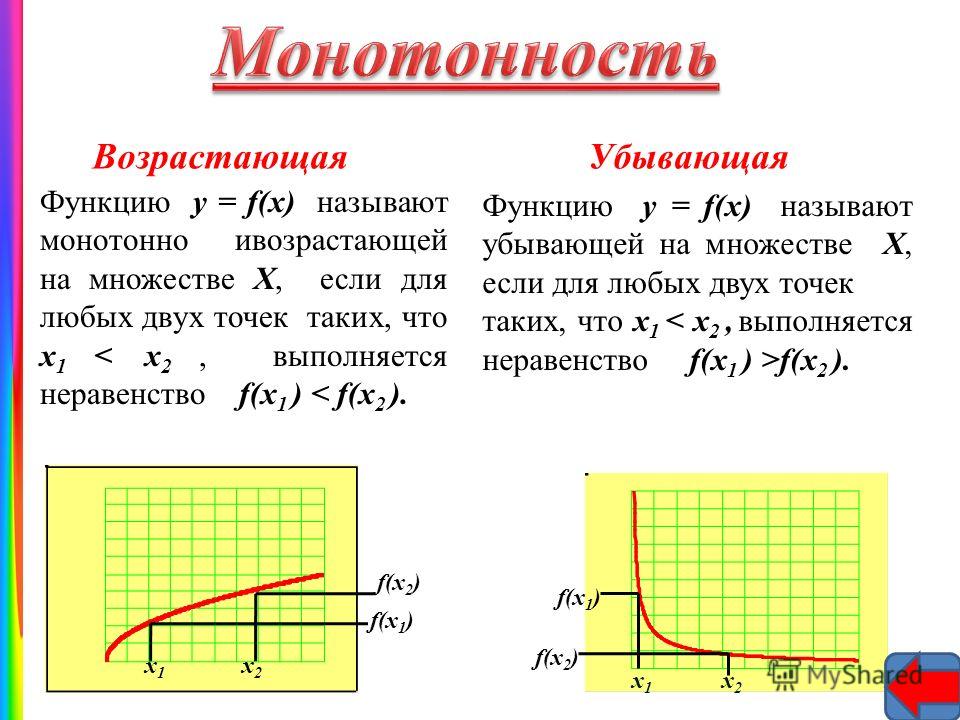60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства. Равносильные неравенства. 77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 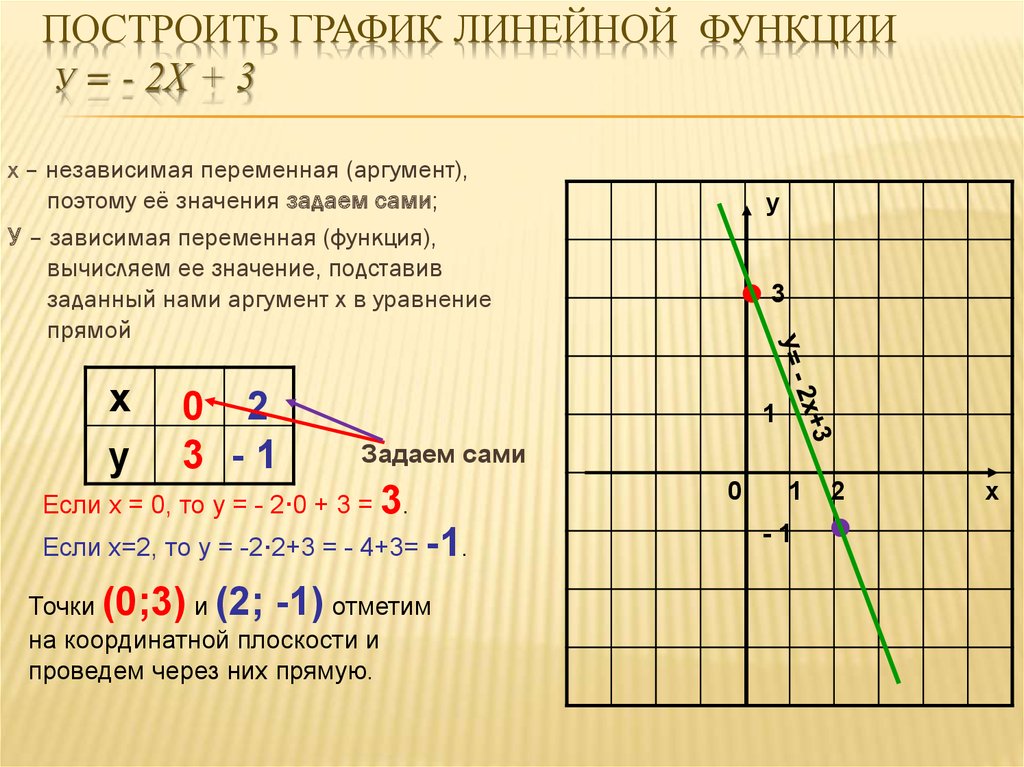94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. Тригонометрические функции числового аргумента 108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. Функция у = arcsin (sin x). 138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора. 218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 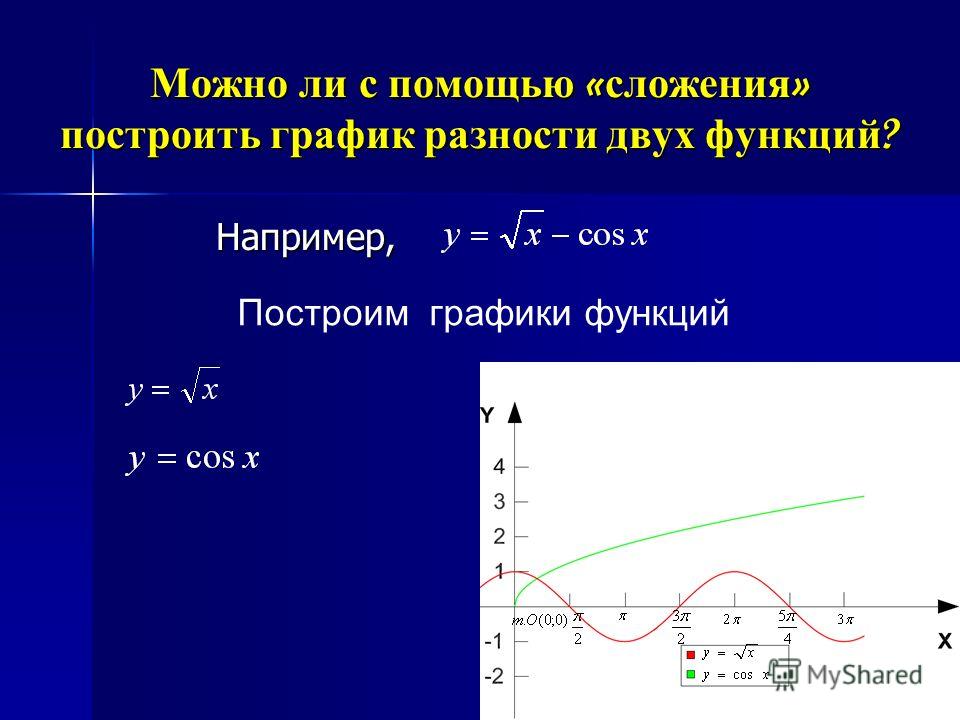232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения

1.Графики и свойства основных элементарных функций

• 1.Четность и нечетность. Функция у = f(х) называется четной, если для любых значений х из области определения f(—х)= f(х) и нечетной, если f(—х) = — f(х). В противном случае функция у = f(х) называется функцией общего вида.

• Например, функция у = х, является нечетной, так как f(—х) = — х = —f(х).

• График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

• 2.Монотонность. Функция у = f(х) называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

• Функции возрастающие и убывающие называются строго монотонными функциями.

• Например, функция у = х, является возрастающей для всех хÎR.

• 3.Ограниченность. Функция у = f(х) называется ограниченной на промежутке Х, если существует такое положительное число М, что | f(х)| £ М для любого хÎ Х.

• Например, функция у = sin х ограниченна на всей числовой оси, т.к. | sin х | £ 1 для любого хÎR.

• 4.Периодичность. Функция у = f(х) называется периодической с периодом Т ¹ 0, если для любых х из области определения функции f(х+Т) = f(х).

• Например, функция у = sin х имеет наименьший положительный период Т = 2p, так как для любых х sin (х+2p) = sin х.

• Основными элементарными функциями называются следующие функции:

• степенная у = хⁿ, где nÎN;

• показательная у = а^х, где а > 0, а ¹ 1;

• логарифмическая у = log_ax ,где а > 0, а ¹ 1;

• тригонометрические: у = sin x, y = cos x, y = tg x, y = ctg x.

Четность четная при нечетная при четная нечетная 5. Корни при x = 0 x = 0 6. Монотон-ность при a < 0 убывает при a > 0 возрастает при a = 0 постоянная убывает на возрастает на Возрастает 7. Экстремумы –– min при x = 0 –– Функция   1. D(x) 2. E(y) 3. Период ––– ––– 4. Четность нечетная ––– 5. Корни нет x = 0 6. Монотонность убывает на каждом из интервалов и возрастает 7. Экстремумы ––– min при x = 0 

Графики элементарных функций

2.Предел функции

Преде́л фу́нкции (предельное значение функции) — одно из основных понятий математического анализа, значение, к которому функция в определённом смысле приближается при приближении аргумента к определённой точке. Функция имеет предел в точке , если для всех значений , достаточно близких к , значение близко к .

3.Основные теоремы о пределах.Асимптоды графика функций

Теорема 1. Функция не может иметь более одного предела

Теорема 2. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.

Теорема 3. Предел произведения конечного числа функций равен произведению пределов этих функций, т.е.

Следствие.1. Постоянный множитель можно выносить за знак предела, т.е.

Следствие 2. Предел степени равен степени предела, т.е

Теорема 4. Предел частного двух функций равен частному пределов этих функций, при условии, что предел делителя не равен нулю, т.е.

Асимптоты графика функции

Определение 11 (вертикальная асимптота). Прямая x = a называется вертикальной асимптотой графика функции y = f(x), если хотя бы один из пределов

lim_{x a+0}f(x) или lim_{x a-0}f(x)

равен + или -.

Определение 12 (наклонная асимптота). Говорят, что прямая y = kx+b является наклонной асимптотой графика функции y = f(x) при x, если f(x) имеет вид

f(x) = kx+b+ (x),

где lim_{x} (x) = 0.

Справедлива

Теорема 13 (существование асимптот). Для того чтобы график функции y = f(x) имел при x асимптоту y = kx+b, необходимо и достаточно, чтобы существовали два предела

lim_{x}f(x)/x = k, lim_{x}(f(x)-kx) = b.

Доказательство.

1. Необходимость. Пусть график функции y = f(x) имеет при x асимптоту y = kx+b, то есть для f(x) имеет вид

f(x) = kx+b+(x),

тогда

lim_{x}f(x)/x = (kx+b+(x))/x = k,

lim_{x}(f(x)-kx) = lim_{x}(b+(x)) = b.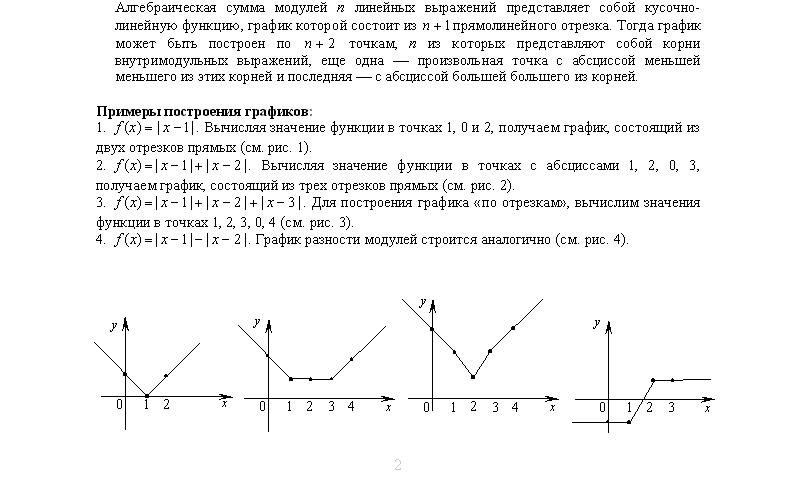

2. Достаточность. Пусть существуют пределы, фигурирующие в условии теоремы. Тогда величина f(x)-kx-b является бесконечно малой при x. Обозначив f(x)-kx-b = (x) получим, что f(x) имеет асимптоту согласно определению наклонной асимптоты.

Замечание. Аналогично определяется наклонная асимптота и доказывается теорема 13 при x.

Замечание. Если k=0 в определении наклонной асимптоты, то наклонная асимптота является горизонтальной.

• Асимптотой графика функции у =¦( х) называется прямая, обладающая следующим свойством, что расстояние от переменной точки на графике до этой прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.

• Теорема 1. Пусть функция у = ¦( х) определена в некоторой окрестности точки х₀ (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при х® х₀ – 0 (слева) или при х® х₀ + 0 (справа) – равен бесконечности, тогда прямая при х = х₀ является вертикальной асимптотой графика функции у = ¦( х).

• Замечание. Вертикальные асимптоты следует искать в точках разрыва функции у = ¦( х) или на концах ее области определения (а, b) если а и b — конечные числа.

• Теорема 2. Пусть функция у = ¦(х) определена при достаточно больших х и существует конечный предел функции при х ® ¥ и он равен числу b. Тогда прямая у = b есть горизонтальная асимптота графика функции у = ¦( х).

Замечание. Если конечен лишь один из пределов слева или справа, то функция имеет лишь левостороннюю или правосторонюю асимптоту.

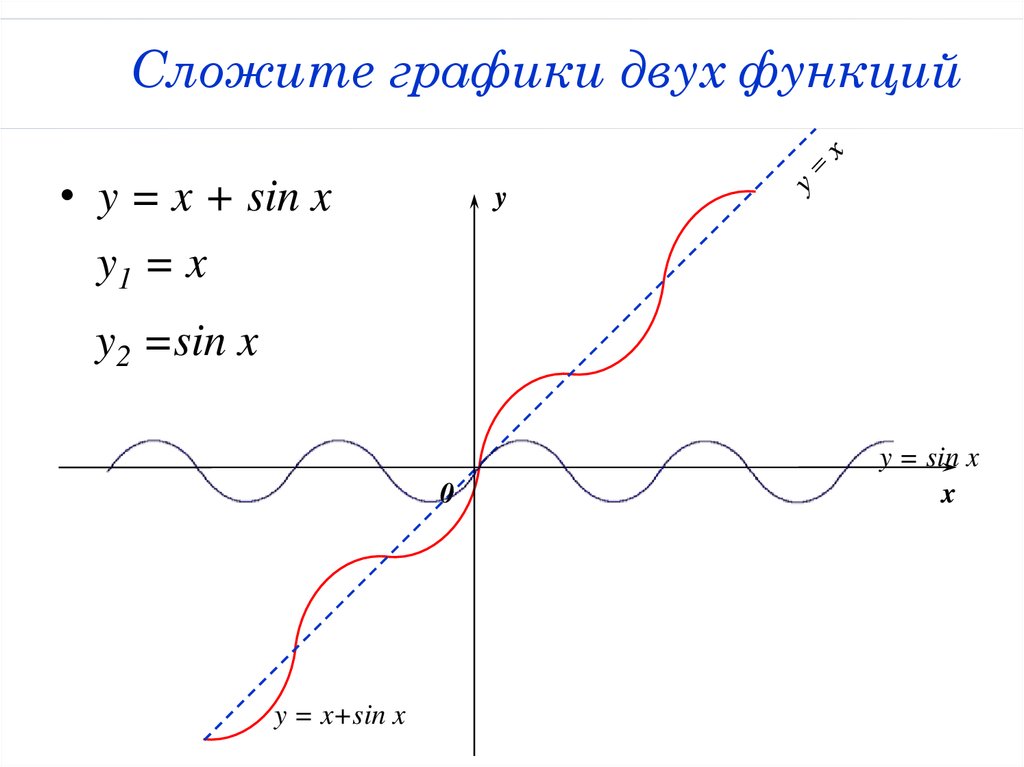
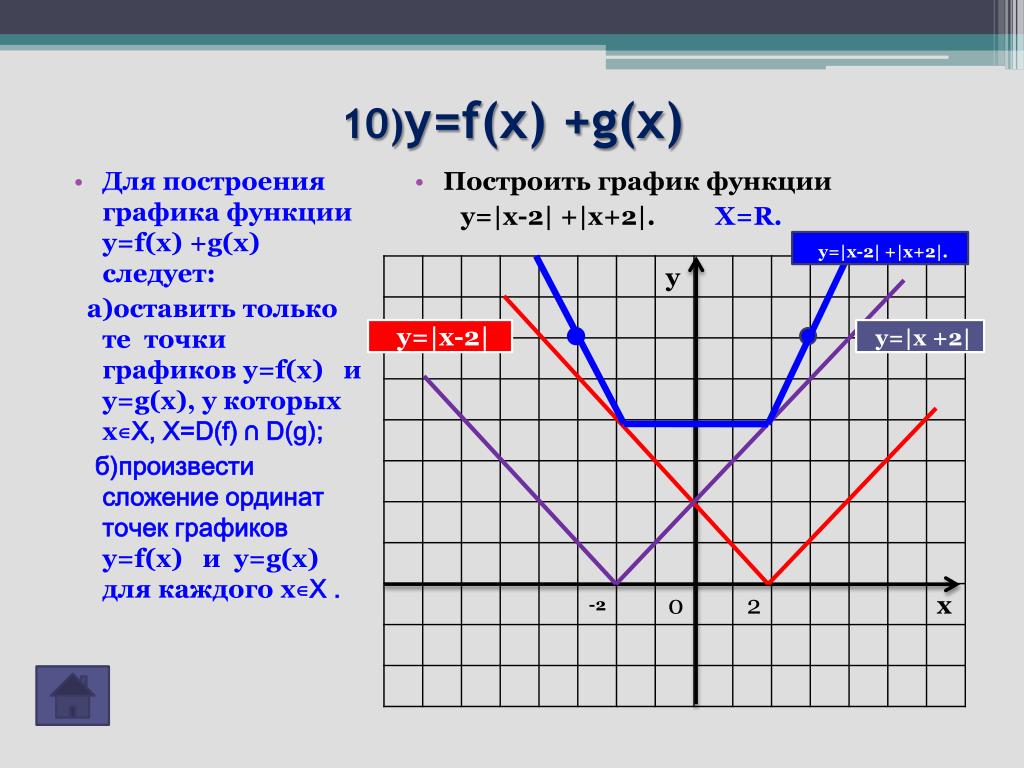
Как найти график суммы двух функций

спросил 7 лет, 6 месяцев назад

Изменено 4 года, 1 месяц назад

Просмотрено 20 тысяч раз

$\begingroup$

Предположим, мне известны графики двух функций $f(x)$ и $g(x)$.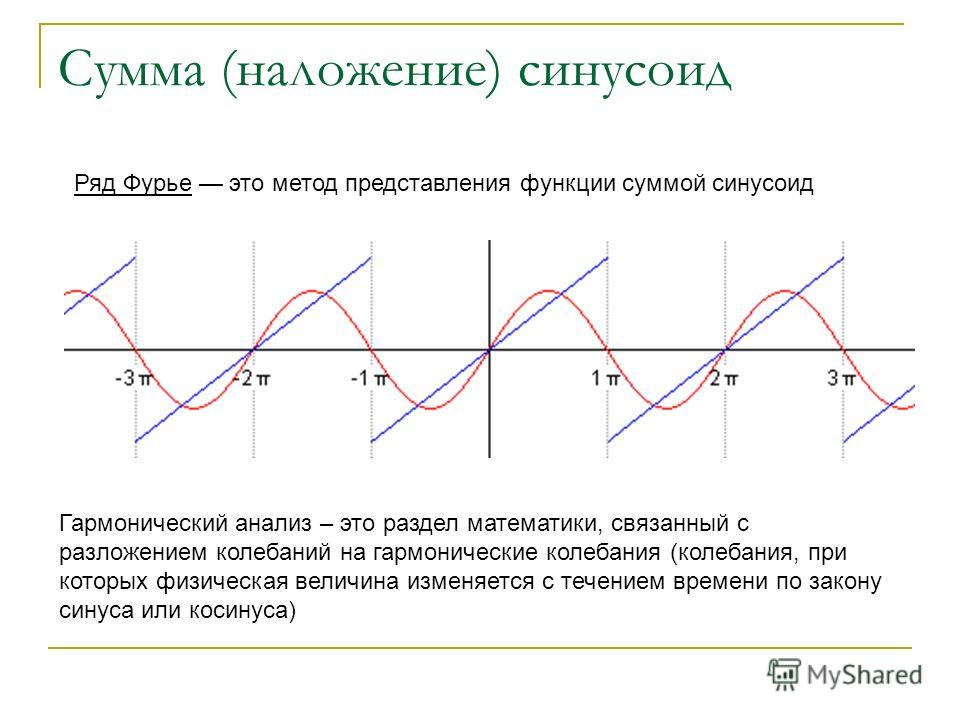 Как мне найти график $h(x)=f(x)+g(x)$? Какие правила следует соблюдать?

P.S. Если мой вопрос покажется глупым, по крайней мере дайте мне ссылку или что-то еще, чтобы я мог учиться!

• функции
• графические функции

$\endgroup$

3

$\begingroup$

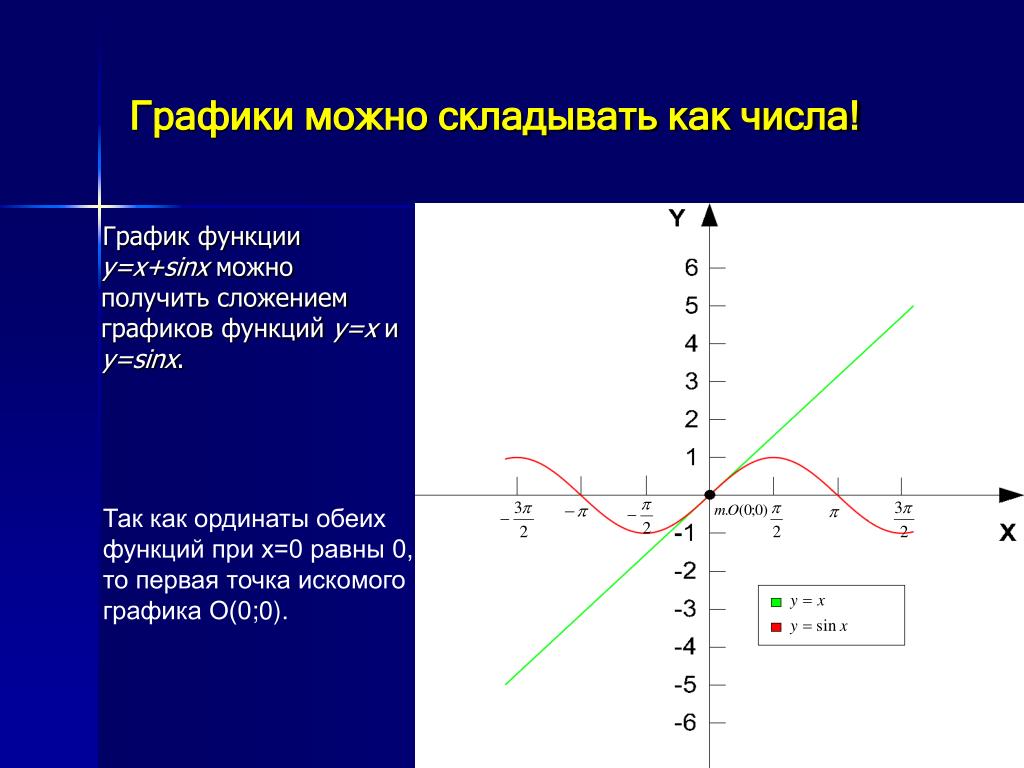
Так как $h(x)=(f+g)(x):=f(x)+g(x)$ для каждого $x$ в области, график получается суммированием двух функций точечный.

То есть при $x=x_0$ будет соответствовать точка $h(x_0)=f(x_0)+g(x_0)$.

Отредактировано после просмотра комментария о разрывах : если одна из функций $f$ и $g$ имеет разрыв, помните, что областью определения $f+g$ является $\mathcal {D}_{f+g }=\mathcal{D}_f \cap \mathcal{D}_g$. Вы можете суммировать две функции только там, где они обе существуют, и в этих точках применяется одна и та же логика.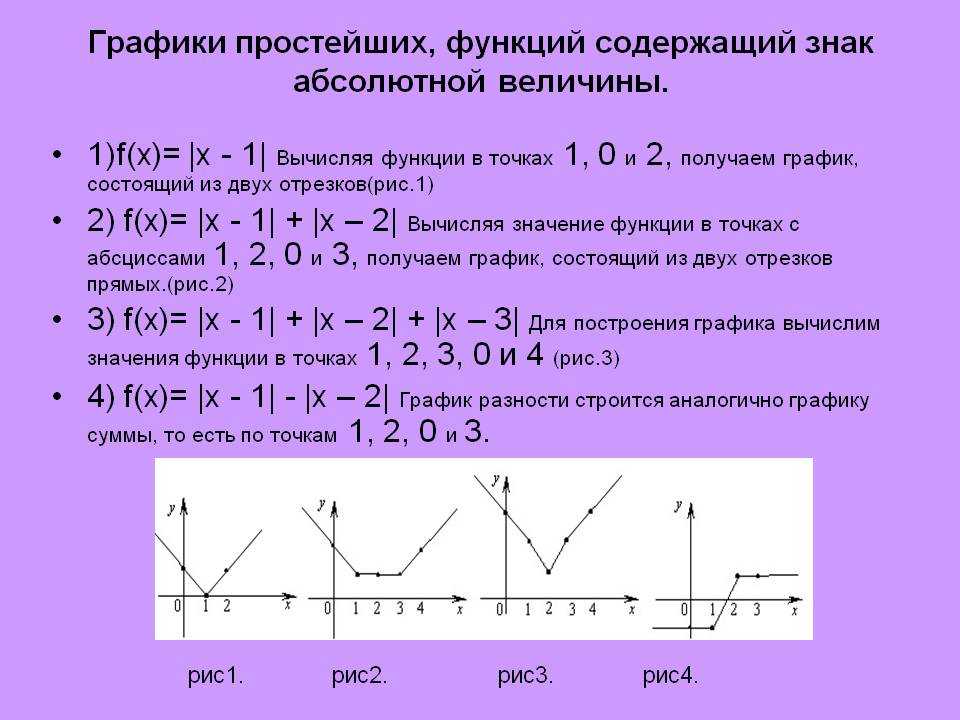

$\endgroup$

1

$\begingroup$

Вам нужно провести анализ. Я рекомендую взять следующие пункты.

Из базовой функции f и g:

1. Посмотреть, когда f и g равны нулю

2. Найдите максимальное и минимальное значения f и g (пример: для sin(x) +1 и -1)

3. Нарисуйте огибающие фигуры в увеличенном размере, чтобы получить представление о графике.

   ИЛИ

4. Вычислите корни функции (суммы), если это возможно.

5. Проанализируйте значение в корне.

6. Найти дифференциал и проанализировать дифференцируемость

7. Найдите локальные максимумы и минимумы и на основе дифференцируемости постройте кривую.

8. Вы можете проанализировать вогнутость и выпуклость. Для этого найдите двойной дифференциал.

Вы можете посмотреть это видео. Эскиз кривой

$\endgroup$

$\begingroup$

Можно представить график $h(x)$ поточечно, добавив высоты двух графиков $f(x)$ и $g(x)$ в каждой точке $x$. Например, если $f(1) = 2$ и $g(1) = 3$. $$h(1) = f(1) + g(1) = 2 + 3 = 5$$

Теперь все хорошо.

$\endgroup$

Графические линейные функции Суммирование Алгебра деятельности 1 | Цифровой

» График Линейных функций Суммируйте Упражнение — Алгебра 1 — Цифровой — Дистанционное обучение »

ЦИФРОВОЙ И ПЕЧАТНЫЙ: Семь станций включают в себя практику или просмотр графических линейных уравнений в стандартной форме, форме пересечения наклона и форме точка-наклон . Упражнение включает в себя определение точки пересечения по оси x, точки по оси y, наклона или значения x при заданном значении y.

Учащиеся работают в группах по три человека, называя себя «Ученик А», «Ученик Б» и «Ученик С». Каждый учащийся решает свою задачу на рабочем месте в своей тетради или на бланке для ответов. Затем учащиеся складывают свои три ответа вместе, чтобы получить «Сумму». Они проверяют обратную сторону станции/страницы, чтобы убедиться, что «Сумма» их ответов верна, прежде чем перейти к следующей станции. Студенты могут перемещаться по станциям в любом порядке.

***ЦИФРОВАЯ СОВМЕСТИМОСТЬ: Через Easel Activity этот продукт содержит ИНТЕРАКТИВНЫЙ PDF-файл. Текстовые поля и инструкции для использования в Интернете уже включены. Вы сможете дополнительно аннотировать и настраивать его для своих потребностей в цифровом обучении. Основной контент не редактируется. Ваши ученики заполнят цифровой PDF-файл и отправят его вам на проверку через Google Classroom или другую LMS.

CCSS: определение, оценка и сравнение функций.

8.F.A.1 Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции представляет собой набор упорядоченных пар, состоящих из входа и соответствующего выхода.

CCSS: Интерпретировать функции, возникающие в приложениях, с точки зрения контекста.

HSF.IF.B4 Для функции, которая моделирует взаимосвязь между двумя величинами, интерпретируйте ключевые характеристики графиков и таблиц с точки зрения величин и набросайте графики, показывающие ключевые характеристики с учетом словесного описания взаимосвязи.

CCSS: Анализ функций с использованием различных представлений.

HSF.IF.C.7 Графические функции, выраженные символически и отображающие ключевые особенности графа, вручную в простых случаях и с использованием технологий в более сложных случаях.

HSF.IF.C.7a Графики линейных и квадратичных функций и отображение точек пересечения, максимумов и минимумов.

TEKS: Линейные функции, уравнения и неравенства

A1.3.A Линейные функции, уравнения и неравенства. Учащийся применяет стандарты математического процесса при использовании графиков линейных функций, ключевых функций и связанных преобразований для представления различными способами и решения уравнений, неравенств и систем уравнений с использованием технологий и без них. Ожидается, что учащийся: определит наклон линии по таблице значений, графику, двум точкам на линии и уравнению, записанному в различных формах, включая y = mx + b , Ax + By = C и y — y1 = m ( x — x1).

A1.3.C Линейные функции, уравнения и неравенства. Учащийся применяет стандарты математического процесса при использовании графиков линейных функций, ключевых функций и связанных преобразований для представления различными способами и решения уравнений, неравенств и систем уравнений с использованием технологий и без них. Ожидается, что учащийся: начертит линейные функции на координатной плоскости и определит ключевые функции, в том числе  x — точка пересечения, y — точка пересечения, нули и наклон в математических и реальных задачах.

VA SOL: Уравнения и неравенства

EI.A.6.a Учащийся определит наклон прямой, если ему дано уравнение прямой, график прямой или две точки на прямой.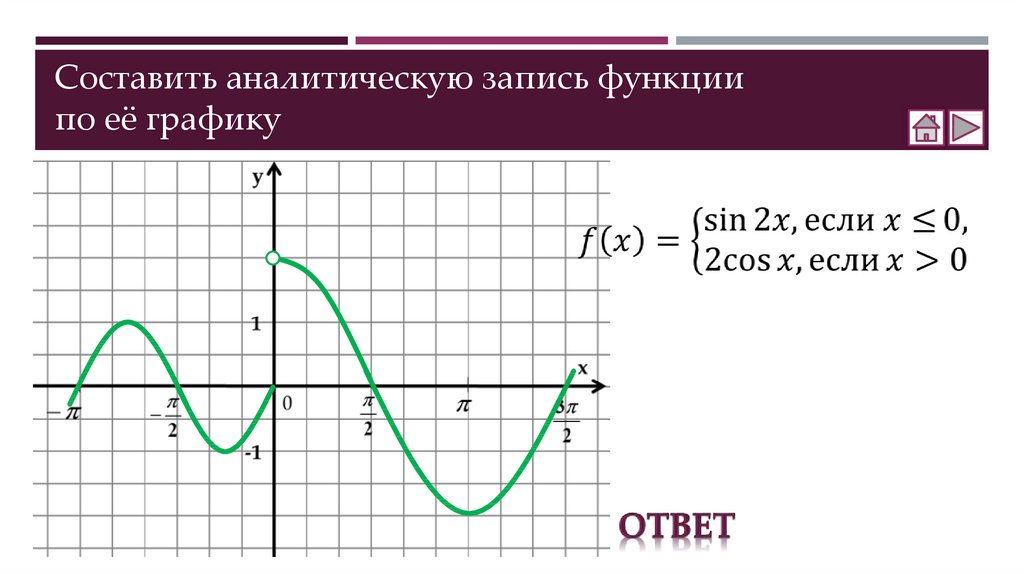

EI.A.6.c Учащийся начертит линейные уравнения с двумя переменными.

VA SOL: Функции

F.A.7.e Студент будет исследовать и анализировать семейства линейных и квадратичных функций и их характеристики как алгебраически, так и графически, включая значения функции для элементов в ее области определения.

Настройка учителя:

Распечатайте каждую страницу на картоне или бумаге. На обратной стороне соответствующей страницы напишите только цифру «Сумма» трех ответов, чтобы учащиеся могли ее проверить. Прикрепите страницы к стенам вокруг комнаты, чтобы ученики могли их посещать.

Входит в комплект:

• Семь страниц/станций «Суммируйте», каждая с тремя задачами, для размещения на стенах в классе

• Ответы «Суммируйте» для написания на обратной стороне каждой страницы/ станция для студентов

• Подробный ключ для ответов для учителя

• Чистый лист для ответов для учащихся (по желанию)

Это упражнение хорошо подходит для выполнения в середине урока или в качестве повторения.

Инструкции четко обозначены на странице учащихся, и к ним прилагается ключ для ответа.

Вам также может понравиться:

• Линейные графики Scavenger Hunt (6 станций)

• График линейных уравнений Смешанный обзор Задание по прохождению задачи (12 раундов)

• График линейных функций с использованием таблицы значений Релейное задание (6 раундов)

• График линейных функций в форме «точка-наклон» (6 раундов)

• График линейных функций в форме «наклон-пересечение» (6 раундов)

• График линейных функций в стандартной форме (6 раундов)

• Графики линейных функций Смешанный обзор Эстафетное задание (6 раундов)

• Графические линейные уравнения в форме наклона-пересечения Упражнение на выполнение задач (12 раундов)

• Графические линейные уравнения в стандартной форме Упражнение на выполнение задач (12 раундов)

• Графики линейных уравнений в форме «точка-наклон». Упражнение «Прохождение задачи» (12 раундов)

Эта покупка предназначена только для одного учителя.