Матрица умноженная на обратную матрицу равна: Действия с матрицами

Строительная механика

Строительная механика

Дарков А. В., Шапошников Н. Н. Строительная механика: Учеб. для строит. спец. вузов. —8-е изд., перераб. и доп. — М.: Высш. шк., 1986. — 607 с. В учебнике отражены вопросы курса строительной механики (статика и динамика сооружений). Изложение материала иллюстрируется конкретными примерами. В отличие от предыдущего издания (7-е— 1976 г.) рассматриваются методы расчета с использованием ЭВМ, указываются особенности этих методов. В учебнике отражено современное состояние строительной механики. Предназначается для студентов строительных специальностей вузов. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ Глава 1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ СООРУЖЕНИЙ § 1. 2. УСЛОВИЯ ГЕОМЕТРИЧЕСКОЙ НЕИЗМЕНЯЕМОСТИ СТЕРЖНЕВЫХ СИСТЕМ § 1.3. УСЛОВИЯ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ГЕОМЕТРИЧЕСКИ НЕИЗМЕНЯЕМЫХ СТЕРЖНЕВЫХ СИСТЕМ Глава 2. БАЛКИ § 2.2. ЛИНИИ ВЛИЯНИЯ ОПОРНЫХ РЕАКЦИЙ ДЛЯ ОДНОПРОЛЕТНЫХ И КОНСОЛЬНЫХ БАЛОК § 2.3. ЛИНИИ ВЛИЯНИЯ ИЗГИБАЮЩИХ МОМЕНТОВ И ПОПЕРЕЧНЫХ СИЛ ДЛЯ ОДНОПРОЛЕТНЫХ И КОНСОЛЬНЫХ БАЛОК § 2.4. ЛИНИИ ВЛИЯНИЯ ПРИ УЗЛОВОЙ ПЕРЕДАЧЕ НАГРУЗКИ § 2.5. ОПРЕДЕЛЕНИЕ УСИЛИЙ С ПОМОЩЬЮ ЛИНИЙ ВЛИЯНИЯ § 2.6. ОПРЕДЕЛЕНИЕ НЕВЫГОДНЕЙШЕГО ПОЛОЖЕНИЯ НАГРУЗКИ НА СООРУЖЕНИИ. ЭКВИВАЛЕНТНАЯ НАГРУЗКА § 2.7. МНОГОПРОЛЕТНЫЕ СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ БАЛКИ § 2.8. ОПРЕДЕЛЕНИЕ УСИЛИЙ В МНОГОПРОЛЕТНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ ОТ НЕПОДВИЖНОЙ НАГРУЗКИ § 2.9. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ ДЛЯ МНОГОПРОЛЕТНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК § 2.10. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ С ЛОМАНЫМИ ОСЯМИ ОТ НЕПОДВИЖНОЙ НАГРУЗКИ § 2.11. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ В БАЛКАХ КИНЕМАТИЧЕСКИМ МЕТОДОМ Глава 3. ТРЕХШАРНИРНЫЕ АРКИ И РАМЫ § 3. 1. ПОНЯТИЕ ОБ АРКЕ И СРАВНЕНИЕ ЕЕ С БАЛКОЙ § 3.2. АНАЛИТИЧЕСКИЙ РАСЧЕТ ТРЕХШАРНИРНОЙ АРКИ § 3.3. ГРАФИЧЕСКИЙ РАСЧЕТ ТРЕХШАРНИРНОЙ АРКИ. МНОГОУГОЛЬНИК ДАВЛЕНИЯ § 3.4. УРАВНЕНИЕ РАЦИОНАЛЬНОЙ ОСИ ТРЕХШАРНИРНОЙ АРКИ § 3.5. РАСЧЕТ ТРЕХШАРНИРНЫХ АРОК НА ПОДВИЖНУЮ НАГРУЗКУ § 3.6. ЯДРОВЫЕ МОМЕНТЫ И НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ Глава 4. ПЛОСКИЕ ФЕРМЫ § 4.1. ПОНЯТИЕ О ФЕРМЕ. КЛАССИФИКАЦИЯ ФЕРМ § 4.2. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ПРОСТЕЙШИХ ФЕРМ § 4.3. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ СЛОЖНЫХ ФЕРМ § 4.4. РАСПРЕДЕЛЕНИЕ УСИЛИЙ В ЭЛЕМЕНТАХ ФЕРМ РАЗЛИЧНОГО ОЧЕРТАНИЯ § 4.5. ИССЛЕДОВАНИЕ НЕИЗМЕНЯЕМОСТИ ФЕРМ § 4.6. ЛИНИИ ВЛИЯНИЯ УСИЛИИ В СТЕРЖНЯХ ПРОСТЕЙШИХ ФЕРМ § 4.7. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ В СТЕРЖНЯХ СЛОЖНЫХ ФЕРМ § 4.8. ШПРЕНГЕЛЬНЫЕ СИСТЕМЫ § 4,9. ТРЕХШАРНИРНЫЕ АРОЧНЫЕ ФЕРМЫ И КОМБИНИРОВАННЫЕ СИСТЕМЫ Глава 5. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В УПРУГИХ СИСТЕМАХ § 5.2. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ § 5.3. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЙ § 5.4. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ. ИНТЕГРАЛ МОРА § 5.5. ПРАВИЛО ВЕРЕЩАГИНА § 5.6. ПРИМЕРЫ РАСЧЕТА § 5.7. ТЕМПЕРАТУРНЫЕ ПЕРЕМЕЩЕНИЯ § 5.8. ЭНЕРГЕТИЧЕСКИЙ ПРИЕМ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ § 5.9. ПЕРЕМЕЩЕНИЯ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ, ВЫЗЫВАЕМЫЕ ПЕРЕМЕЩЕНИЯМИ ОПОР Глава 6. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ СИЛ § 6.2. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 6.3. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ НА ДЕЙСТВИЕ ЗАДАННОЙ НАГРУЗКИ § 6.4. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ § 6.5. СОСТАВЛЕНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ПРИ РАСЧЕТЕ СИСТЕМ НА ПЕРЕМЕЩЕНИЯ ОПОР § 6.6. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМАХ § 6.7. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ. ПРОВЕРКА ЭПЮР § 6.8. СПОСОБ УПРУГОГО ЦЕНТРА § 6.9. ЛИНИИ ВЛИЯНИЯ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 6.10. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 6.11. ГРУППИРОВКА НЕИЗВЕСТНЫХ § 6.12. СИММЕТРИЧНЫЕ И ОБРАТНОСИММЕТРИЧНЫЕ НАГРУЗКИ § 6.13. СПОСОБ ПРЕОБРАЗОВАНИЯ НАГРУЗКИ § 6. 14. ПРОВЕРКА КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ § 6.15. ПРИМЕРЫ РАСЧЕТА РАМ § 6.16. «МОДЕЛИ» ЛИНИЙ ВЛИЯНИЯ УСИЛИИ ДЛЯ НЕРАЗРЕЗНЫХ БАЛОК Глава 7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДАМИ ПЕРЕМЕЩЕНИЙ И СМЕШАННЫМ § 7.2. ОПРЕДЕЛЕНИЕ ЧИСЛА НЕИЗВЕСТНЫХ § 7.3. ОСНОВНАЯ СИСТЕМА § 7.4. КАНОНИЧЕСКИЕ УРАВНЕНИЯ § 7.5. СТАТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ § 7.6. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ ПЕРЕМНОЖЕНИЕМ ЭПЮР § 7.7. ПРОВЕРКА КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ МЕТОДА ПЕРЕМЕЩЕНИЙ § 7.8. ПОСТРОЕНИЕ ЭПЮР M, Q И N В ЗАДАННОЙ СИСТЕМЕ § 7.9. РАСЧЕТ МЕТОДОМ ПЕРЕМЕЩЕНИЙ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ § 7.10. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ ПРИ РАСЧЕТЕ РАМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ § 7.11. ПРИМЕР РАСЧЕТА РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ § 7.12. СМЕШАННЫЙ МЕТОД РАСЧЕТА § 7.13. КОМБИНИРОВАННОЕ РЕШЕНИЕ ЗАДАЧ МЕТОДАМИ СИЛ И ПЕРЕМЕЩЕНИЙ § 7. 14. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ МЕТОДОМ ПЕРЕМЕЩЕНИЙ Глава 8. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ СТЕРЖНЕВЫХ СИСТЕМ И МЕТОДЫ ЕЕ РЕШЕНИЯ § 8.2. СОСТАВЛЕНИЕ УРАВНЕНИЙ РАВНОВЕСИЯ, СТАТИЧЕСКИЕ УРАВНЕНИЯ. ИССЛЕДОВАНИЕ ОБРАЗОВАНИЯ СИСТЕМ § 8.3. СОСТАВЛЕНИЕ УРАВНЕНИЙ СОВМЕСТНОСТИ, ГЕОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. ПРИНЦИП ДВОЙСТВЕННОСТИ § 8.4. ЗАКОН ГУКА. ФИЗИЧЕСКИЕ УРАВНЕНИЯ § 8.5. СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ. СМЕШАННЫЙ МЕТОД § 8.6. МЕТОД ПЕРЕМЕЩЕНИЙ § 8.7. МЕТОД СИЛ § 8.8. УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ И ИХ СВЯЗЬ С УРАВНЕНИЯМИ СТРОИТЕЛЬНОЙ МЕХАНИКИ Глава 9. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ЭВМ § 9.2. ПОЛУАВТОМАТИЗИРОВАННЫЙ РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ КАЛЬКУЛЯТОРОВ § 9.3. АВТОМАТИЗАЦИЯ РАСЧЕТА СТЕРЖНЕВЫХ СИСТЕМ. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ ДЛЯ СТЕРЖНЯ § 9.4. МАТРИЦЫ РЕАКЦИЙ (ЖЕСТКОСТИ) ДЛЯ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ СТЕРЖНЕЙ И ИХ ИСПОЛЬЗОВАНИЕ § 9.5. ОПИСАНИЕ УЧЕБНОГО КОМПЛЕКСА ПО РАСЧЕТУ СТЕРЖНЕВЫХ СИСТЕМ. ВНУТРЕННЕЕ И ВНЕШНЕЕ ПРЕДСТАВЛЕНИЕ ИСХОДНЫХ ДАННЫХ. БЛОК-СХЕМА КОМПЛЕКСА ПО РАСЧЕТУ СТЕРЖНЕВЫХ СИСТЕМ Глава 10. УЧЕТ ГЕОМЕТРИЧЕСКОЙ И ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ ПРИ РАСЧЕТЕ СТЕРЖНЕВЫХ СИСТЕМ § 10.2. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С УЧЕТОМ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ § 10.3. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ § 10.4. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С УЧЕТОМ ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ Глава 11. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ (МКЭ) § 11.2. СВЯЗЬ МКЭ С УРАВНЕНИЯМИ СТРОИТЕЛЬНОЙ МЕХАНИКИ § 11.3. ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ РЕШЕНИЯ ПЛОСКОЙ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ § 11.4. ПРЕДЕЛЬНЫЙ ПЕРЕХОД ДЛЯ ПЛОСКОЙ ЗАДАЧИ § 11.5. ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ РЕШЕНИЯ ОБЪЕМНОЙ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ § 11.6. СЛОЖНЫЕ ЭЛЕМЕНТЫ, ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ ЭЛЕМЕНТОВ С ИСКРИВЛЕННОЙ ГРАНИЦЕЙ § 11.7. ПОСТРОЕНИЕ МАТРИЦ РЕАКЦИЙ ДЛЯ РАСЧЕТА ПЛАСТИНОК И ОБОЛОЧЕК § 11.8. ОСОБЕННОСТИ КОМПЛЕКСОВ ДЛЯ РАСЧЕТА КОНСТРУКЦИЙ ПО МКЭ. СУПЕРЭЛЕМЕНТНЫЙ ПОДХОД Глава 12. ОСНОВЫ ДИНАМИКИ СООРУЖЕНИЙ § 12. 2. СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 12.3. РАСЧЕТ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ ДЕЙСТВИИ ПЕРИОДИЧЕСКОЙ НАГРУЗКИ § 12.4. РАСЧЕТ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ ДЕЙСТВИИ ПРОИЗВОЛЬНОЙ НАГРУЗКИ. ИНТЕГРАЛ ДЮАМЕЛЯ § 12.5. ДВИЖЕНИЕ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ. ПРИВЕДЕНИЕ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ К ДВУМ СИСТЕМАМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 12.6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ. УРАВНЕНИЕ ЛАГРАНЖА § 12.7. ПРИВЕДЕНИЕ КИНЕМАТИЧЕСКОГО ВОЗДЕЙСТВИЯ К СИЛОВОМУ § 12.8. СВЕДЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДИНАМИКИ К РАЗДЕЛЯЮЩИМСЯ УРАВНЕНИЯМ С ПОМОЩЬЮ РЕШЕНИЯ ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ § 12.9. МЕТОД ПОСТОЯННОГО УСКОРЕНИЯ И ЕГО ИСПОЛЬЗОВАНИЕ ДЛЯ РЕШЕНИЯ ДИНАМИЧЕСКИХ ЗАДАЧ Глава 13. СВЕДЕНИЯ ИЗ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ, ИСПОЛЬЗУЕМЫЕ В СТРОИТЕЛЬНОЙ МЕХАНИКЕ § 13.2. МАТРИЦЫ, ИХ ВИДЫ, ПРОСТЕЙШИЕ ОПЕРАЦИИ НАД МАТРИЦАМИ § 13.3. ПЕРЕМНОЖЕНИЕ МАТРИЦ. ОБРАТНАЯ МАТРИЦА § 13.4. МЕТОД ГАУССА ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ. РАЗЛОЖЕНИЕ МАТРИЦЫ В ПРОИЗВЕДЕНИЕ ТРЕХ МАТРИЦ § 13.5. ИССЛЕДОВАНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. ОДНОРОДНЫЕ УРАВНЕНИЯ. РЕШЕНИЕ n УРАВНЕНИЙ С m НЕИЗВЕСТНЫМИ С ИСПОЛЬЗОВАНИЕМ МЕТОДА ГАУССА § 13.6. КВАДРАТИЧНАЯ ФОРМА. МАТРИЦА КВАДРАТИЧНОЙ ФОРМЫ. ПРОИЗВОДНАЯ ОТ КВАДРАТИЧНОЙ ФОРМЫ § 13.7. СОБСТВЕННЫЕ ЧИСЛА И СОБСТВЕННЫЕ ВЕКТОРЫ ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННОЙ МАТРИЦЫ § 13.8. ОДНОРОДНЫЕ КООРДИНАТЫ И ИНТЕГРИРОВАНИЕ ПО ТРЕУГОЛЬНОЙ ОБЛАСТИ § 13.9. СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ, ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ И ЭКСПОНЕНЦИАЛЬНОЙ ФУНКЦИЕЙ ЗАКЛЮЧЕНИЕ ЛИТЕРАТУРА

07. Обратная матрица и её свойства

Матрицу называют обратной к , если Удовлетворяет условиям

.

Справедлива следующая теорема.

Теорема (о существовании и единственности обратной матрицы).

Любая квадратная матрица имеет единственную обратную матрицу, вычисляемую по формуле , тогда и только тогда, когда исходная матрица невырожденная.

МатрицаНазывается присоединенной по отношению к матрице , и ее столбцы состоят из алгебраических дополнений к элементам, расположенным в соответствующих строках исходной матрицы .

Доказательство.

Докажем, что условие , является достаточным условием для существования обратной матрицы. На главной диагонали произведения матрицы на обратную матрицу стоят суммы произведений элементов строк матрицы на соответствующие этим элементам строк алгебраические дополнения. Эти суммы дают значения определителя, который по условию теоремы не равен нулю. Любые элементы произведения матриц , не лежащие на главной диагонали, равны нулю, так как там стоят суммы произведений элементов строк матрицы на алгебраические дополнения к элементам других строк.

Таким образом: .

Аналогично доказывается, что произведение , что означает существование обратной матрицы в виде, указанном в формулировке теоремы.

Покажем, что эта матрица единственная. Предположим, что имеется хотя бы одна матрица , также удовлетворяющая условиям . Умножая равенство слева на матрицу , получим цепочку следований:

,

Что доказывает единственность обратной матрицы.

Докажем, что условие является необходимым, то есть из существования обратной матрицы должна следовать невырожденность исходной матрицы . Действительно, из теоремы об определителе произведения матриц и определения обратной матрицы следует, что . Отсюда можно сделать вывод, что и, так как иначе их произведение не могло бы равняться отличному от нуля числу 1. Теорема полностью доказана.

Отметим, что в процессе доказательства теоремы было показано, что определитель обратной матрицы равен обратной величине определителя исходной матрицы, то есть вычисляется по формуле .

Квадратная матрица , обладающая свойством , называется ортогональной. Следующие основные свойства обратных матриц:

1) , 2) , 3)

Доказываются обычно по методу представления в общем виде элементов матриц, стоящих слева и справа от знаков равенств.

Рассмотрим пример вычисления обратной матрицы методом присоединенной матрицы, то есть путем составления алгебраических дополнений, для следующей матрицы третьего порядка . Ее определитель вычислим методом разложения по первой строке . Так как определитель матрицы не равен нулю, то матрица неособенная, и поэтому можно составлять обратную матрицу . Вычислим алгебраические дополнения элементов матрицы :

, , ,

, ,,

, , .

Обратной матрицей для матрицы является следующая матрица:

.

Для того чтобы проверить правильность составления обратной матрицы, следует исходную матрицу умножить на обратную ей матрицу. В результате должна получиться единичная матрица соответствующего размера.

С помощью обратной матрицы, найденной вышеуказанным способом, удобно решать невырожденные квадратные системы с небольшим числом неизвестных. При этом решение системы находится за конечное число шагов и явно выражается через коэффициенты системы и свободные члены. Правило решения такой системы формулируется в следующей теореме.

< Предыдущая		Следующая >

{-1}[A]=[I][A][A]−1=[A]−1[A]=[I]

.

Цели обучения

Потренируйтесь находить обратную матрицу и опишите ее свойства

Ключевые выводы

Ключевые моменты

• Определение обратной матрицы требует коммутативности — умножение должно работать одинаково в любом порядке.
• Чтобы матрица была обратимой, она должна быть квадратной, потому что единичная матрица тоже должна быть квадратной.
• Для определения обратной матрицы

  (3456)\begin{pmatrix} 3 и 4 \\ 5 и 6 \end{pmatrix}(35​46​)

  , установите

  (3456)(abcd)=(1001)\begin{pmatrix} 3 и 4 \\ 5 & 6 \end{pmatrix} \begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}(35​ 46​)(ac​bd​)=(10​01​)

  . Затем найдите

  aaa

  ,

  bbb

  ,

  ccc

  и

  ddd

  .

Ключевые термины

• сингулярная матрица : Матрица, не имеющая обратной.
• матрица : прямоугольное расположение чисел или терминов, имеющее различное применение, такое как преобразование координат в геометрии, решение систем линейных уравнений в линейной алгебре и представление графов в теории графов.
• обратная матрица : Квадратная матрица

  [A][A][A]

  со связанной матрицей

  [B][B][B]

  , так что

  [A][A][A]

  умножается на

  [B][B][B]

  и

  [B][B][B]

  умножить на

  [A][A][A]

  оба равны единичной матрице.
• Единичная матрица : Диагональная матрица, все диагональные элементы которой равны

  111

  , а остальные равны

  000

  .

Видя, что число

111

играет особую роль в умножении,

1x=x1x=x1x=x

, обратное число определяется как число, которое умножается на это число, чтобы получить

111

. Матрица 9{-1}[A]=[I][A][A]−1=[A]−1[A]=[I]

Где

[I][I][I]

 – единичная матрица.

Обратите внимание, что, как и в определении единичной матрицы, это определение требует коммутативности — умножение должно работать одинаково в любом порядке.

Обратите внимание, что только квадратные матрицы могут иметь обратную. Определение обратной матрицы основано на единичной матрице

[I][I][I]

, и уже было установлено, что только квадратные матрицы имеют ассоциированную единичную матрицу.

Метод нахождения обратной матрицы исходит непосредственно из определения вместе с небольшим количеством алгебры. Нахождение обратной матрицы Во-первых, пусть верно следующее:

(3456)(abcd)=(1001)\displaystyle \begin{pmatrix} 3 и 4 \\ 5 и 6 \end{pmatrix} \begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}(35​46​)(ac​bd​)=(10​01​)

Это ключевой шаг. Он устанавливает

(abcd)\begin{pmatrix} a & b \\ c & d \end{pmatrix}(ac​bd​)

как искомое обратное, утверждая, что оно заполняет определение обратная матрица. При умножении этой загадочной матрицы на исходную матрицу получается

[I][I][I]

. При решении для четырех переменных

aaa

,

bbb

,

ccc

и

ddd

, то будет найдена обратная матрица.

Далее выполните умножение:

(3a+4c3b+4d5a+6c5b+6d)=(1001)\displaystyle \begin{pmatrix} 3a+4c & 3b+4d \\ 5a+6c & 5b+6d \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}(3a+4c5a+ 6c​3b+4d5b+6d​)=(10​01​)

Чтобы две матрицы были равны, каждый элемент слева должен быть равен соответствующему элементу справа. Итак, чтобы эти две матрицы были равны друг другу:

3a+4c=1\displaystyle 3a+4c=13a+4c=1

3b+4d=0\displaystyle 3b+4d=03b+4d=0

5a+6c=0\displaystyle 5a+6c=05a+6c=0

5b+6d=1\displaystyle 5b+6d = 15b+6d = 1

Решение первых двух уравнений для

AAA

и

CCC

и вторые два уравнения для

BBB

и

DDD

с помощью любого из Elmine или

DDD

. замена.

Результаты:

a=−3\displaystyle а=-3а=-3

b=2\displaystyle b=2b=2

c=212\displaystyle c=2 \frac12c=221​

d=−112\displaystyle d= -1 \frac 12d=−121​

После решения для четырех переменных результат будет обратным

(−32212−112)\begin{pmatrix} -3 & 2 \\ 2 \frac 12 & — 1 \frac 12 \end{pmatrix}(−3221​​2−121​​)

.

Если обратная матрица была найдена, то быстрой проверкой ее правильности является умножение ее на исходную матрицу и проверка результатов идентификации матрицы:

(−32212−112)(3456)\displaystyle \begin{pmatrix} -3 & 2 \\ 2 \frac 12 & -1 \frac 12 \end{pmatrix} \begin{pmatrix} 3 & 4 \\ 5 & 6 \end{pmatrix} (−3221​​2 −121​)(35​46​)

После умножения получается:

((−3)(3)+(2)(5)(−3)(4)+(2)(6 )(212)(3)+(−112)(5)(212)(4)+(−112)(6))\displaystyle \begin{pmatrix} (-3)(3)+(2)(5) & (-3)(4)+(2)(6) \\ (2 \frac 12)(3)_+(-1 \frac 12)(5) & (2 \frac 12)(4)+(-1 \frac 12)(6) \end{pmatrix} ((−3)(3)+(2)(5)(221 ​)(3)+​(-121​)(5)​(-3)(4)+(2)(6)(221​)(4)+(-121​)(6)​)

Упрощение задачи дает:

(−9+10−12+12712−71210−9)=(1001)\displaystyle \begin{pmatrix} -9+10 & -12+12 \\ 7 \frac 12 -7 \frac 12 & 10-9 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end {pmatrix}(−9+10721−721−12+1210−9​)=(10​01​)

Следовательно, работает обратное. Но ждать!

Обратите внимание, что для полной проверки нужно попробовать умножение в обоих порядках, потому что, как правило, изменение порядка умножения матриц меняет ответ. Определение обратной матрицы указывает, что она должна работать в обоих направлениях.

(3456)(−32212−112)\displaystyle \begin{pmatrix} 3 и 4 \\ 5 и 6 \end{pmatrix} \begin{pmatrix} -3 & 2 \\ 2 \frac 12 & -1 \frac 12 \end{pmatrix} (35​46​)(−3221​​2−121​​)

После умножения получается :

((3)(−3)+(4)(212)(3)(2)+(4)(−112)(5)(−3)+(6)(212)(5)( 2)+(6)(−112))\displaystyle \begin{pmatrix} (3)(-3)+(4)(2\frac 12) & (3)(2)+(4)(-1 \frac 12) \\ (5)(-3)_ +(6)(2\frac 12) & (5)(2)+(6)(-1\frac 12) \end{pmatrix}((3)(-3)+(4)(221​)( 5)(−3)+​(6)(221​)​(3)(2)+(4)(−121​)(5)(2)+(6)(–121​)​)

Упрощение задачи дает:

(−9+106−6−15+1510−9)=(1001)\displaystyle \begin{pmatrix} -9+10 & 6-6 \\ -15+15 & 10-9 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}(-9 +10−15+15​6−610−9​)=(10​01​)

Таким образом, обратная матрица работает в обе стороны.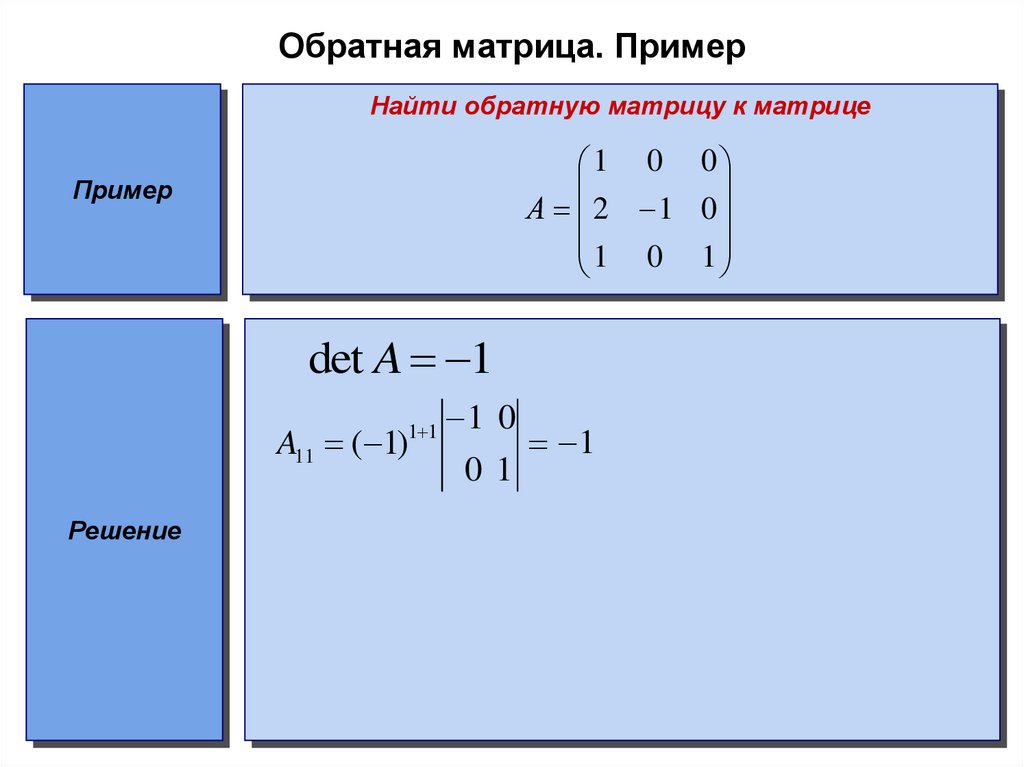

В некоторых случаях обратной квадратной матрицы не существует. Это называется сингулярной матрицей.

Решение систем уравнений с использованием обратной матрицы

Систему уравнений можно легко решить, используя концепцию обратной матрицы и умножения матриц.

Цели обучения

Попрактикуйтесь в использовании обратных матриц для решения системы линейных уравнений

Ключевые выводы

Ключевые моменты

• Использование матриц для решения систем уравнений может значительно снизить вашу рабочую нагрузку. Например, рассмотрим следующие три уравнения:

  x+2y-z=11x+2y-z=11x+2y-z=11

  ,

  2x-y+3z=72x-y+3z=72x-y+3z= 7

   и

  7x−3y−2z=27x-3y-2z = 27x−3y−2z=2

  .
• Чтобы решить эти уравнения с помощью матриц, мы сначала определим

  3×33 \times 33×3

  матрица

  [A][A][A]

  , которые являются коэффициентами всех переменных слева от знаков равенства:

  [A]=[12−12− 137−3−2][A] = \begin{bmatrix} 1&2&-1\\2&-1&3\\7&-3&-2 \end{bmatrix}[A]=⎣

  ⎡​127​2−1− 3​−13−2​⎦

  ⎤​

   Затем определите

  3×13 \times 13×1

  матрицу

  [B][B][B]

  , которые являются числами в правой части равенства знаки: 

  [B]=[1172]. [B] = \begin{bmatrix} 11\\7\\2 \end{bmatrix}.[B]=⎣

  ⎡​1172​⎦

  ⎤​.

• Чтобы определить значения переменных, мы просто умножаем обратное число

  [A][A][A]

  на

  [B][B][B]

  . Проще всего это сделать с помощью калькулятора. Калькулятор отвечает матрицей

  3×13 х 13×1

  , которая включает в себя решение системы как:

  x=3x=3x=3

  ,

  y=5y=5y=5

  и

  z= 2z=2z=2

  .

Ключевые термины

• обратная матрица : Для матрицы

  [A][A][A]

  , если существует матрица

  [B][B][B]

  такая, что

  [A][A][A]

  умножить на

  [B ][B][B]

  и

  [B][B][B]

  умноженные на

  [A][A][A]

  оба равны единичной матрице, тогда

  [B][B][B]

  является инверсией

  [A][A][A]

  .
• линейное уравнение : полиномиальное уравнение первой степени (например,

  x=2y−7x=2y-7x=2y−7

  ).

Систему уравнений можно легко решить, используя понятия обратной матрицы и матричного умножения. В главе об одновременных уравнениях мы видели, как решать два уравнения с двумя неизвестными. Но предположим, что у нас есть три уравнения с тремя неизвестными? Или четыре, или пять? Такие ситуации более распространены, чем вы можете себе представить в реальном мире. И даже если вам разрешено пользоваться калькулятором, совсем не очевидно, как решить такую ​​задачу за разумное время.

Пример 1. Решите следующую систему линейных уравнений:

x+2y−z=112x−y+3z=77x−3y−2z=2\displaystyle х+2у-г = 11 \\ 2x-y+3z = 7\\ 7x-3y-2z = 2x+2y-z=112x-y+3z=77x-3y-2z=2

Шаг 1. Создайте матрицу

AAA

, которая состоит из коэффициентов всех переменных из каждого уравнения слева от знака равенства:

[A]=[12−12−137−3−2]\displaystyle [A] = \begin{bmatrix} 1&2&-1\\2&-1&3\\7&-3&-2 \end{bmatrix}[A]=⎣

⎡​127​2−1−3​−13−2​⎦

⎤​

Шаг 2: Увеличить матрицу

BBB

, которая состоит из констант в правой части равенства знак:

[B]=[1172]\displaystyle [B] = \begin{bmatrix} 11\\7\\2 \end{bmatrix}[B]=⎣

⎡​1172​⎦

⎤​

Теперь, чтобы определить значения

xxx

,

yyy

и

zzz

, мы просто умножаем обратное число 9{-1}][B][A−1][B]

, то есть обратная матрица

[A][A][A]

, умноженная на матрицу

[B][B ][B]

.

Калькулятор отвечает

3×13 \times 13×1

матрицей, которая включает решение системы в виде: 5

и

z=2z=2z=2

. Решение линейных уравнений таким способом быстро и легко.

Лицензии и атрибуты

Контент под лицензией CC, опубликованный ранее

• Курирование и доработка. Автор: : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права

Лицензионный контент CC, конкретное указание авторства

• Обратная матрица. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Кенни Фелдер, Advanced Algebra II: Conceptual Explanations. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]:af2ce775-9674-4820-9e3c-bc43e5f89065. Лицензия : CC BY: Attribution
• матрица. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
• идентификационная матрица. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
• обратная матрица. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
• Кенни Фелдер, Advanced Algebra II: Conceptual Explanations. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]:bdbb2879-7959-4b36-a75c-5294298a3134. Лицензия : CC BY: Attribution
• линейное уравнение. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
• обратная матрица. Предоставлено : Викисловарь. License : CC BY-SA: Attribution-ShareAlike

Видео урока: Свойства обратных матриц

Стенограмма видео

В этом уроке мы узнаем, как использовать некоторые свойства обратной матрицы. В этот момент вы должны быть знакомый с нахождением определителя и обратным к два на два и матрицы три на три. Во-первых, прежде чем мы начнем, вспомните единичную матрицу, матрицу, элементы которой вдоль главной диагонали, то есть диагональ от верхнего левого угла к нижнему правому равна единице, а остальные нуль. Итак, тождественная матрица два на два это единица, ноль, ноль, единица. И личность три на три матрица один, ноль, ноль, ноль, один, ноль, ноль, ноль, один.

Напомним, что квадратная матрица 𝐴 есть называется обратимым, если существует обратный 𝐴 такой, что 𝐴, умноженное на обратный 𝐴, равно то же самое, что и обратное 𝐴, умноженное на 𝐴, что дает нам единичную матрицу. Итак, что мы можем сказать из этого определение состоит в том, что если 𝐵 является обратным 𝐴, то произведение 𝐴𝐵 и произведение 𝐵𝐴 дает нам единичную матрицу. И мы можем использовать это, чтобы проверить являются ли две матрицы 𝐴 и 𝐵 обратными друг другу.

Итак, давайте теперь посмотрим на свойства обратная матрица. Из определения матрицы инверсия, мы имеем, что инверсия инверсии 𝐴 — это просто 𝐴. Во-вторых, мы имеем обратное произведения 𝐴𝐵 является обратным 𝐵, умноженным на обратный 𝐴. Мы должны быть очень осторожны с это, потому что может быть легко подумать, что это обратное произведение 𝐴 обратным 𝐵. Но мы знаем эту матрицу умножение не коммутативно.

Мы можем сделать быстрое доказательство, чтобы показать, как это работает. Помните, мы говорили, что если мы умножив матрицу на обратную, получим единичную матрицу. Итак, если мы возьмем матрицу 𝐴𝐵 и умножьте его на обратное, то есть 𝐵 обратное, умноженное на 𝐴 обратное, мы должны получить единичную матрицу. Итак, давайте перепроверим это. Благодаря ассоциативному свойству матричного умножения, это то же самое, что 𝐴, умноженное на 𝐵, умноженное на 𝐵 инверсия, умноженная на инверсию 𝐴. И мы знаем, что 𝐵, умноженное на 𝐵 обратная должна дать нам единичную матрицу, потому что это просто из определения обратимой матрицы. Итак, у нас есть 𝐴, умноженное на единичная матрица, умноженная на обратную 𝐴. Но умножая любую матрицу на единичная матрица просто дает нам ту же матрицу. Так что это просто 𝐴, умноженное на 𝐴. обратный. И снова из определения обратимая матрица, мы знаем, что 𝐴, умноженное на обратную 𝐴, дает нам единичная матрица.

Итак, когда мы умножаем 𝐴𝐵 на его инверсия, которая представляет собой инверсию 𝐵, умноженную на инверсию 𝐴, и мы получаем тождество матрицы, мы показали, что 𝐵 обратная, умноженная на 𝐴 обратная, определенно является инверсия 𝐴𝐵. И для окончательного доказательства мы тем же методом можно показать, что 𝐵 обратное, умноженное на 𝐴 обратное, умноженное на 𝐴𝐵 также дает нам единичную матрицу.

Идем дальше и смотрим на третью свойство обратной матрицы. 𝐴 транспонированная обратная равна 𝐴 обратное транспонирование. Помните, что это обозначение 𝑇 означает транспонировать матрицу. И мы транспонируем матрицу поменять местами строки со столбцами. Например, если у нас есть матрица 𝐴 один, четыре, шесть, два, то транспонированная матрица 𝐴 равна единице, шести, четыре, два. Опять же, мы можем проверить этот результат потому что мы знаем, что мы можем взять матрицу и умножить ее на обратную, чтобы получить единичная матрица. Итак, если мы возьмем матрицу 𝐴 транспонированный и умножить его на обратный, который является обратным транспонированным 𝐴, мы должны получить единичную матрицу.

Чтобы продолжить отсюда, мы вспоминаем свойство матрицы транспонировать. Транспонирование 𝐴𝐵 равно 𝐵 транспонировать, умноженное на 𝐴 транспонировать. Это означает, что это равно 𝐴 обратное, умноженное на транспонированное 𝐴. Но из определения обратная матрица, мы знаем, что 𝐴 обратная, умноженная на 𝐴, дает нам тождество матрица. Таким образом, мы получаем единичную матрицу транспонировать. Но если мы транспонируем тождество матрица, мы просто получаем единичную матрицу. Итак, мы показали, что умножение 𝐴 транспонировать на 𝐴 обратное транспонирование дает нам единичную матрицу, которая подтверждает это свойство. И для окончательного доказательства аналогичным методом, мы можем показать, что 𝐴 обратное транспонирование умножается на 𝐴 транспонирование также дает нам единичную матрицу.

И, наконец, у нас есть 𝐴 к 𝑛-я степень, обратная, равна 𝐴, обратному 𝑛-й степени. Опять же, мы можем показать это, доказав что 𝐴 в 𝑛-й степени, умноженное на 𝐴, обратное 𝑛-й степени, будет дайте нам единичную матрицу. Мы видим, что мы собираемся быть в состоянии соединить 𝐴 с обратным 𝐴. И каждый раз, когда мы это делаем, мы получаем тождественная матрица. Мы знаем, что у нас есть то же самое количество 𝐴 как обратное 𝐴. Таким образом, соединив их и умножая их вместе, мы знаем, что в итоге получим тождество матрица. И аналогичным методом мы можем покажите, что произведение, обратное 𝐴 в 𝑛-й степени, на 𝐴 в 𝑛-й степени также дает нам единичную матрицу. Итак, давайте теперь посмотрим, как мы можем использовать эти свойства, чтобы ответить на некоторые вопросы.

Если 𝐴 — матрица, какая из следующее равно обратному квадрату 𝐴? 𝐴 в половину мощности, 𝐴 в квадрате, 𝐴, обратное половинной степени, или 𝐴, обратное в квадрате.

Мы можем ответить на этот вопрос, вспоминая свойство обратных матриц. То есть 𝐴 в 𝑛-й степени inverse равно 𝐴, обратному 𝑛-й степени, поскольку 𝑛 — целое положительное число. Итак, имея это в виду, мы можем сказать что обратный квадрат 𝐴 равен обратному квадрату 𝐴. Но давайте перепроверим это отношение просто для уверенности. Мы обнаружили, что инверсия 𝐴 квадрат равен 𝐴 обратному квадрату. И мы знаем, если мы возьмем матрицу и умножьте его на обратное, мы должны получить единичную матрицу. Итак, давайте проверим это.

Если мы возьмем матрицу 𝐴 в квадрате и умножить его на обратный 𝐴 обратный квадрат, мы должны получить тождество матрица. Мы можем просто написать это как 𝐴 умножить на 𝐴 умножить на 𝐴 обратное умножить на 𝐴 обратное. А из-за ассоциативности свойство матричного умножения, мы можем записать его таким образом. Мы знаем, что 𝐴 умножить на 𝐴 обратное дает нам единичную матрицу. И мы знаем умножение любой матрицы по единичной матрице просто дает нам ту же матрицу. Так что это просто 𝐴, умноженное на 𝐴. обратная, что дает нам единичную матрицу.

Если 𝐴 — матрица, какая из следующее равно 𝐴 обратному транспонированию?

Напомним, что это обозначение означает транспонировать матрицу. Это просто означает, что мы меняем строки с колоннами. Например, если у нас есть матрица 𝑋 равно двум, одному, шести, семи, 𝑋 транспонировать равно двум, шести, одному, семи. Чтобы ответить на этот вопрос, вспомним свойство обратной матрицы. То есть транспонированная инверсия 𝐴 есть равно 𝐴 обратно транспонированному. И это дает нам, что наш ответ это первый вариант. 𝐴 обратно транспонированное равно 𝐴 транспонированный инверсный. Итак, мы говорим, что если мы возьмем матрицу 𝐴, найдем ее обратную, а затем транспонируем ее, это как раз и есть тот же результат мы получили бы, взяв матрицу 𝐴, транспонировав ее, а затем найдя обратный.

Считаем, что матрица 𝐴 равна минус три, один, минус два, пять. Найдите 𝐴 обратное обратное.

Напомним определение обратная 𝐴 матрица такая, что 𝐴, умноженное на обратную 𝐴, равно единичная матрица. У нас есть способ найти обратная матрица два на два. То есть, если матрица 𝑋 равна 𝑎, 𝑏, 𝑐, 𝑑, 𝑋 обратное равно единице на 𝑎𝑑 минус 𝑏𝑐, умноженной на матрица 𝑑, отрицательная 𝑏, отрицательная 𝑐, 𝑎. Таким образом, чтобы найти обратную инверсию 𝐴, мы могли бы использовать этот метод, чтобы найти инверсию 𝐴, а затем повторить метод, чтобы найти обратное этому.

Однако у нас есть одно свойство обратная матрица, которая может помочь нам сделать это немного быстрее. То есть обратное обратному 𝐴 просто равно 𝐴. Итак, если мы возьмем матрицу и найдем ее инвертировать, а затем инвертировать эту матрицу, мы получаем исходную матрицу. Так что на самом деле обратная сторона обратная нашей матрицы 𝐴 — это просто матрица 𝐴 минус три, один, минус два, пять.

Даны матрицы 𝐴 и 𝐵, где 𝐴 равно единице, минус два, три, ноль, минус единица, четыре, ноль, ноль, единица и 𝐵 равно единице, минус два, пять, ноль, минус единица, четыре, ноль, ноль, единица, найти 𝐴𝐵. И вторая часть вопроса говорит: «Не выполняя никаких дальнейших вычислений, найдите 𝐴 обратное».

Итак, первое, что мы собираемся сделать здесь найти продукт 𝐴𝐵. Используя обычный метод для умножая вместе матрицы три на три, мы находим, что 𝐴𝐵 равно единице, нулю, нулю, ноль, один, ноль, ноль, ноль, один. И мы замечаем, что это на самом деле единичная матрица три на три. Так что же это значит для нашего матрицы 𝐴 и 𝐵?

Ну и определение обратное состоит в том, что это обратная 𝐴 такая, что 𝐴, умноженное на обратную 𝐴, равно единичная матрица. Итак, тот факт, что мы нашли произведение 𝐴𝐵, чтобы быть единичной матрицей, означает, что матрица 𝐵 должна быть обратной матрицы 𝐴.

Вторая часть вопроса говорит: «Не выполняя никаких дальнейших вычислений, найдите 𝐴 обратное». Ну, потому что, когда мы находим произведения 𝐴𝐵 получаем единичную матрицу, это означает, что матрица 𝐵 является инверсия 𝐴. Следовательно, обратной 𝐴 является матрица 𝐵, то есть один, минус два, пять, ноль, минус один, четыре, ноль, ноль, один.

Учитывая, что 𝐴𝐵 обратный равен одна шестая умножается на пять, минус три, минус 33, 21 и 𝐴 равно минус два, минус один, минус три, минус два, определить 𝐵 обратное.

Начнем с быстрого напоминания что такое обратная матрица. Обратная квадратная матрица 𝐴, 𝐴 обратная матрица такая, что 𝐴, умноженное на 𝐴 обратную, дает нам единичная матрица. И одно свойство матрицы обратное, которое нам здесь пригодится: 𝐴𝐵 обратное равно 𝐵 инверсия, умноженная на инверсию 𝐴. Итак, поскольку нам сказали обратное произведения 𝐴𝐵 составляет одну шестую, умноженную на матрицу пять, минус три, отрицательное 33, 21, то из этого свойства обратной матрицы можно сказать, что это это то же самое, что 𝐵 обратное, умноженное на 𝐴 обратное. Но чем это нам поможет найти 𝐵 обратный?

Ну, есть немного трюк, который мы можем применить здесь. И все, что для этого требуется, это помнить определение обратной матрицы. Мы можем найти обратную матрицу 𝐵, 𝐴 наоборот, 𝐴 путем умножения 𝐵 обратного, 𝐴 обратного на 𝐴 справа. Итак, давайте теперь умножим эти два матрицы вместе, чтобы увидеть, что мы получаем. Делаем это обычным способом умножение двух матриц два на два вместе. И тогда мы можем упростить каждый вход. И мы получаем одну шестую умножить на матрицу минус один, один, три, минус девять. Затем мы вспоминаем, когда у нас есть скаляр, умноженный на матрицу, мы можем просто умножить каждую запись на этот скаляр. И это дает нам матрицу минус один больше шести, один больше шести, один больше двух, минус три больше двух. Но как это на самом деле помогло нам найти обратную матрицу 𝐵?

Итак, мы нашли матрицу 𝐵 обратное, умноженное на 𝐴 обратное, умноженное на 𝐴. И из определения обратная матрица, 𝐴 обратная, умноженная на 𝐴, дает нам единичную матрицу. Итак, что мы на самом деле нашли, так это обратная матрица 𝐵, умноженная на единичную матрицу. Но умножая любую матрицу на единичная матрица просто дает нам эту матрицу. Итак, мы нашли матрицу 𝐵 инверсия. Таким образом, используя определение обратной матрицы и одно из свойств обратной матрицы, мы смогли найти неизвестное с использованием обратной матрицы.

Давайте теперь суммируем ключевые моменты с этого урока. Для квадратных матриц 𝐴 и 𝐵 мы есть, что инверсия инверсии 𝐴 просто равна 𝐴. Обратное произведение 𝐴𝐵 равно равно обратному 𝐵, умноженному на обратное 𝐴. 𝐴 обратное транспонирование равно 𝐴 обратное транспонирование. Итак, транспонируем ли мы матрицу а затем инвертировать его или инвертировать матрицу и затем транспонировать ее, мы получаем то же самое результат. И, наконец, поднятие матрицы 𝐴 в 𝑛-й степени, а затем инвертирование дает нам тот же результат, что и инвертирование матрицу 𝐴 и возведение ее в 𝑛-ю степень.