Примеры решение матриц: основные определения, обозначение, формулы и элементы матрицы

Примеры решения задач

1. Найти линейную комбинацию матриц , где,.

Решение:

.

2. Пусть – матрица размерности 2x 3, – матрица размерности 3 х 3. Найти произведенияи(если это возможно).

Решение: Используем формулу (2.1):

Произведение не существует, так как число столбцов матрицыB не совпадает с числом строк матрицы A: .

3. Найти, если.

Решение: .

.

4. Найти значение матричного многочлена , если , .

Решение: .

.

5. Транспонировать матрицу .

Решение: Так как у матрицы A две строки и три столбца, то у матрицы будет три строки и два столбца:.

6.

Дана матрица . Найти обратную матрицу.

Решение: Воспользуемся первым способом нахождения обратной матрицы, т.е. формулой (2.2). Вычисляем определитель матрицы A:

.

Так как , то матрицасуществует. Найдем алгебраические дополнения ко всем элементам матрицыA:

; ;

; ;

; ;

;

;

.

Составим присоединенную матрицу: . Находим обратную матрицу, поделив каждый элемент присоединенной матрицы на определитель матрицы A. Получаем ответ:

.

7. Решить матричное уравнение: .

Решение: Запишем данное матричное уравнение в виде . Его решением является матрица (если существует матрица). Найдем определитель матрицыA: . Значит, обратная матрица существует, и исходное уравнение имеет (единственное) решение.

Найдем обратную матрицу: , ; , . Найдем решение матричного уравнения:

.

8. Найти обратную к матрице , используя метод элементарных преобразований.

Решение: Припишем справа единичную матрицу

.

Разделив первую строку на три и обнулив элемент в первом столбце ниже тройки, получим

.

Умножив вторую строку на три и обнулив элемент во втором столбце выше , получим

.

Таким образом, .

Задачи для самостоятельного решения

1. Найти линейную комбинацию матриц , где

.

2. Найти произведения матриц и (если они существуют), где

.

3. Проверить коммутируют ли матрицы

и .

4. Найти значение матричного многочлена , еслии.

5. Вычислить произведение при заданной матрице .

6. Привести к ступенчатому виду матрицу .

7. Найти произведения матриц и, где

.

8. Найти обратную матрицу к матрице .

Решить матричные уравнения:

9. ;

10. .

11. Найти линейную комбинацию матриц , где

.

12. Найти произведения матриц и (если они существуют), где

.

13. Проверить, коммутируют ли матрицы и .

14. Найти значение матричного многочлена , если .

15. Вычислить произведение при заданной матрице.

16. Привести к ступенчатому виду матрицу .

17. Найти произведения матриц и, если

.

18. Найти обратную матрицу к матрице .

Решить матричные уравнения:

19. ;

20. .

Ответы:

1) ; 2) ;3) Да; 4) ;5) ; 6) ;7) ;8) ;9) ;10) ;11) ; 12) ;13) Нет; 14) ;15) ; 16) ;17) ;18) ;19) ;20) .

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3

Решение систем линейных уравнений методом Крамера и Гаусса

1. Метод Крамера.

Система уравнений вида

(3.1)

называется системой m линейных уравнений с n неизвестными.

Коэффициенты этих уравнений записываются в виде матрицы А, называемой матрицей системы, а числа, стоящие в правой части системы, образуют столбец В, называемый столбцом свободных членов. Неизвестные системы так же записываются в столбец, называемый столбец неизвестных:

, ,

Используя произведение матриц, можно записать данную систему в матричном виде: .

Совокупность чисел называетсярешением системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел вместо неизвестных.

Системы, не имеющие решения, называются несовместными.

Системы, имеющие решения, называются

совместными. Заметим, что система может иметь единственное решение, а может иметь бесконечно много решений.

Для нахождения единственного решения систем с одинаковым количеством уравнений и неизвестных есть метод, называемый метод Крамера.

Система n уравнений с n неизвестными

имеет единственное решение, если определитель матрицы системы отличен от нуля. Это решение находится по формулам Крамера:

, (3.2)

где  – определитель матрицы системы, а _k – определитель матрицы, полученной из матрицы системы заменой k-го столбца столбцом свободных членов.

лекции_1_курс_1_поток_осень_2020 | Кафедра высшей алгебры

Лекции по алгебре, 1 курс, 1 поток

Лектор: Д.А.Тимашёв

Лекции читаются

дистанционно в Zoom на 1-й паре (9:00-10:35) по вторникам на каждой чётной неделе и по пятницам на каждой неделе.

Доступны рабочие видеозаписи лекций (см. ниже).

Литература

1. А.И.Кострикин. Введение в алгебру. Часть I. Основы алгебры.

2. Э.Б.Винберг. Курс алгебры.

---

4 сентября 2020

Лекция 1

Системы линейных уравнений (СЛУ) и их решения. Совместные и несовместные, определённые и неопределённые СЛУ. n, пространство функций на множестве), простейшие следствия аксиом (единственность нулевого и противоположного векторов, умножение вектора на 0 и -1, умножение нулевого вектора на число).

Линейные комбинации векторов, их значения, тривиальная комбинация. Линейная зависимость, примеры (случай одного и двух векторов). Свойства линейной зависимости: сохранение линейной зависимости/независимости при увеличении/уменьшении системы векторов, эквивалентное определение (один из векторов системы линейно выражается через остальные), однозначное выражение вектора, добавление которого делает систему линейно зависимой. Основная лемма о линейной зависимости. Обобщение на бесконечные системы векторов.

Видеозапись лекции

---

11 сентября 2020

Лекция 3

Эквивалентность условий максимальности линейно независимой подсистемы в системе векторов и выражаемости остальных векторов системы через эту подсистему. Базис системы векторов: определение, примеры — базисы в пространствах геометрических векторов, стандартный базис в R^n. n), её геометрический смысл.

Видеозапись лекции

---

24 сентября 2020

Лекция 5

Линейные отображения векторных пространств: определение, геометрические примеры (поворот плоскости, проекция пространства на плоскость). Линейные отображения арифметических векторных пространств и их матрицы. Интерпретация СЛУ на языке линейных отображений.

Алгебраические операции над линейными отображениями и матрицами (сложение и умножение, умножение на числа). Матричная запись линейных отображений и СЛУ. Свойства матричных операций: коммутативность и ассоциативность сложения, ассоциативность и дистрибутивность умножения матриц на числа и между собой, некоммутативность умножения матриц, нулевая и противоположная матрицы, умножение на 0 и на 1. Векторное пространство матриц размера m×n.

Видеозапись лекции

---

25 сентября 2020

Лекция 6

Матричные операции и транспонирование.

Ранг произведения матриц.

Тождественное отображение и единичная матрица. Символы Кронекера. Обратная матрица: определение, единственность, связь с обратным линейным отображением. Произведение обратимых матриц обратимо. Невырожденные квадратные матрицы. Матрица обратима тогда и только тогда, когда она невырождена. Алгоритм нахождения обратной матрицы (с примером).

Элементарные матрицы, их основное свойство.

Видеозапись лекции

---

25 сентября 2020

Лекция 7

Обратимость элементарных матриц. Разложение произвольной невырожденной матрицы в произведение элементарных матриц.

Перестановки, их количество. Подстановки степени n, их двухрядная запись. Взаимно однозначное соответствие между перестановками и подстановками, количество подстановок степени n равно n!.

Умножение подстановок, его ассоциативность. Тождественная подстановка и подстановка, обратная к данной. Некоммутативность умножения подстановок.

Циклические подстановки (циклы), их орбиты, однорядная запись цикла. Независимость циклов, разложение произвольной подстановки в произведение независимых циклов, его единственность (с точностью до порядка сомножителей).

Видеозапись лекции

---

8 октября 2020

Лекция 8

Транспозиции, разложение произвольной подстановки в произведение транспозиций.

Инверсии в перестановке, чётность и знак перестановки и подстановки. Изменение чётности перестановки при транспозиции двух её элементов. Количество чётных и нечётных перестановок n элементов (или подстановок степени n) одинаково и равно n!/2. Определение знака подстановки по числу сомножителей в её разложении на транспозиции. Знак произведения подстановок. Знак обратной подстановки.

Определители квадратных матриц: определение по развёрнутой формуле. Свойства определителя как функции от набора строк матрицы: полилинейность, кососимметричность, определитель матрицы с нулевой строкой, с одинаковыми и с пропорциональными строками, неизменность при элементарных преобразованиях 1-го типа.

Определитель транспонированной матрицы, свойства определителя как функции от набора столбцов.

Определитель треугольной матрицы. Метод вычисления определителя приведением матрицы к треугольному виду.

Видеозапись лекции

---

9 октября 2020

Лекция 9

Определитель матрицы — единственная, с точностью до пропорциональности, полилинейная кососимметрическая функция от её строк.

Квадратная матрица невырождена тогда и только тогда, когда её определитель не равен 0.

Определитель матрицы с углом нулей. Определитель Вандермонда, его основное свойство. Определитель произведения матриц.

Миноры прямоугольной матрицы. Дополнительный минор и алгебраическое дополнение к элементу квадратной матрицы. Разложение определителя по строке и по столбцу. Лемма о фальшивом разложении определителя.

Видеозапись лекции

---

16 октября 2020

Лекция 10

Присоединённая матрица, её основное свойство. Формула для обратной матрицы.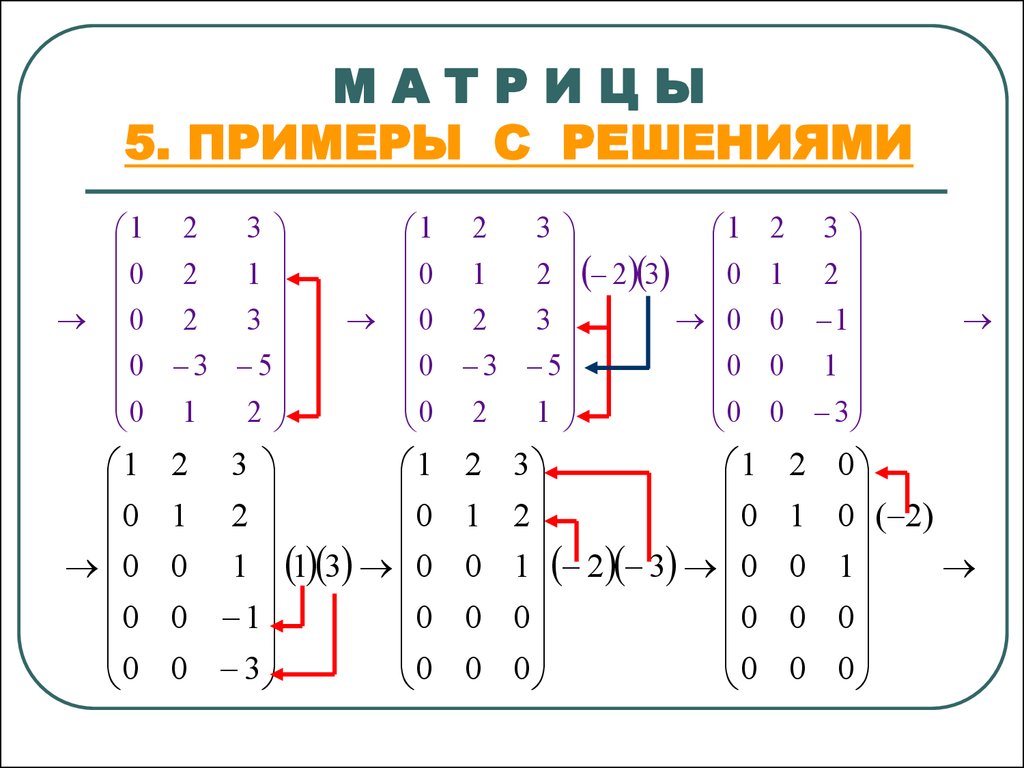 Пример: формула для обратной к матрице размера 2×2.

Правило Крамера для решения квадратных СЛУ.

Теорема о ранге матрицы (его совпадение с наибольшим порядком ненулевого минора), метод окаймляющих миноров для вычисления ранга матрицы.

Видеозапись лекции

---

20 октября 2020

Лекция 11

Группы: определение, единственность нейтрального и обратного элемента.

Примеры групп (в т.ч. симметрическая группа S_n). Абелевы группы. Сравнение мультипликативной и аддитивной терминологий в теории групп. Подгруппы: определение и примеры (в т.ч. знакопеременная группа A_n).

Кольца: определение, аддитивная группа кольца. Классы колец: ассоциативные, коммутативные, кольца с единицей. Примеры колец (кольцо целых чисел Z, кольцо квадратных матриц Mat_n, кольцо геометрических векторов в пространстве с векторным умножением). Простейшие следствия аксиом кольца (единственность 0, 1 и противоположного элемента, умножение на 0 и на -1).

Обратимые элементы в ассоциативных кольцах с единицей, примеры: 1 обратима, 0 не обратим в кольцах с числом элементов >1. Мультипликативная группа кольца, примеры (в т.ч. полная матричная группа GL_n).

Делители нуля, их необратимость. Возможность сокращения на множитель, не являющийся делителем нуля.

Поля: определение и примеры. Подкольца и подполя: определение и примеры (Z⊂Q⊂R). Перенос теории линейных уравнений, векторов, матриц и определителей с поля R на произвольное поле.

Видеозапись лекции: 1-я часть; 2-я часть (смотреть до 43-й минуты).

---

23 октября 2020

Лекция 12

Сравнимость целых чисел по модулю m, классы вычетов. Операции над вычетами, корректность их определения. Кольцо вычетов Z_m.

Делители нуля и обратимые элементы в кольцах вычетов. Z_m — поле тогда и только тогда, когда m — простое число.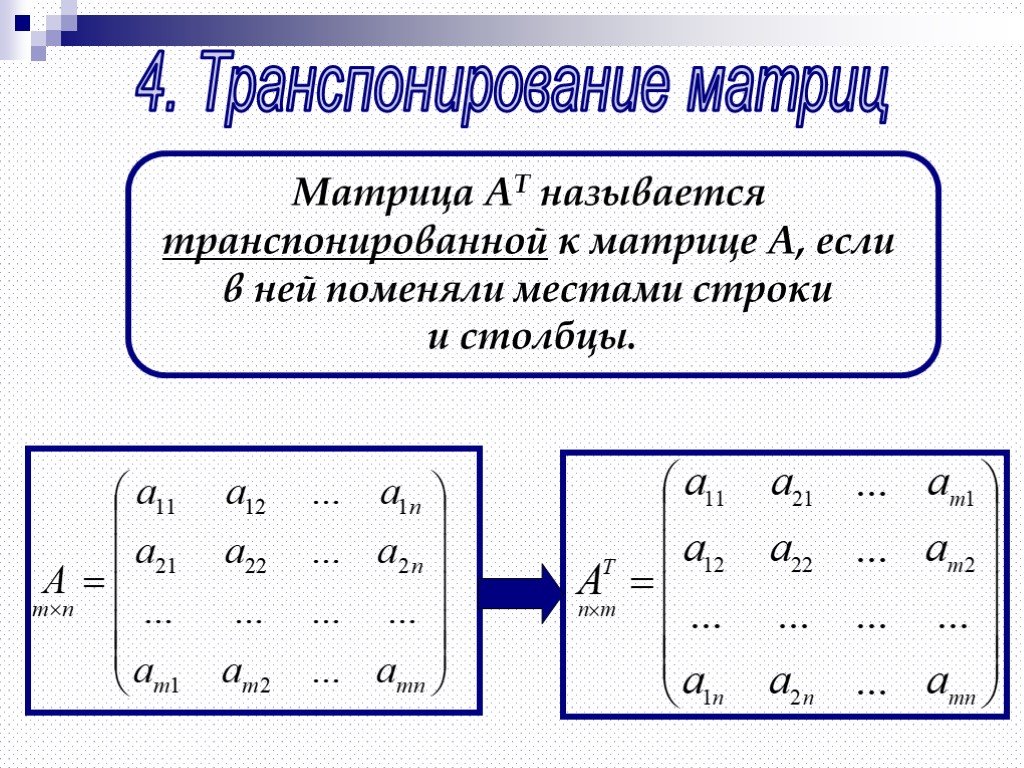 2.

Геометрическая интерпретация комплексных чисел как точек или векторов на координатной плоскости. Геометрический смысл операций сложения и вычитания комплексных чисел. Модуль комплексного числа и сопряжённое число, их геометрический смысл, свойства операции сопряжения. Деление комплексных чисел в алгебраической форме.

Видеозапись лекции

---

3 ноября 2020

Лекция 14

Аргумент комплексного числа, его главная ветвь. Тригонометрическая форма записи комплексных чисел, её экспоненциальная версия. Свойства модуля и аргумента комплексного числа, умножение и деление комплексных чисел в тригонометрической форме, геометрический смысл этих операций, формула Муавра.

Извлечение корней из комплексных чисел. Корни из единицы, первообразные корни.

Многочлены: неформальное определение, функциональная точка зрения на многочлены, её недостаток на примере поля вычетов Z_p (разные многочлены x и x^p задают одинаковые функции). ∞ финитных последовательностей элементов кольца K.

Целостные кольца (области целостности). Кольцо многочленов над областью целостности целостно. Аддитивность степени многочлена. Обратимые элементы в кольце многочленов над областью целостности.

Многочлены над полем и полиномиальные функции. Задача о (полиномиальной) интерполяции. Теорема об интерполяции, интерполяционная формула Лагранжа.

Видеозапись лекции

---

13 ноября 2020

Лекция 16

Эквивалентность формального и функционального равенства многочленов над бесконечным полем.

Деление с остатком в кольце многочленов. Теорема Безу. Корни многочленов, кратность корня, простые и кратные корни. Число корней многочлена, с учётом их кратностей, не превосходит его степени.

Производная многочлена, её свойства. Высшие производные. Связь кратности корня со значениями производных.

Разложение многочлена по степеням линейного двучлена. Формула Тейлора.

Видеозапись лекции

---

17 ноября 2020

Лекция 17

Делимость в целостных кольцах. Ассоциированные элементы. Наибольший общий делитель (НОД) двух элементов целостного кольца, его единственность с точностью до ассоциированности. Евклидовы кольца, примеры. Существование НОД в евклидовом кольце, алгоритм Евклида для его нахождения. Линейное выражение НОД через исходные элементы.

Простые элементы целостного кольца, примеры: простые числа и неприводимые многочлены. Разложение элемента евклидова кольца на простые множители, его единственность с точностью до перестановки множителей и ассоциированности. Факториальные кольца, факториальность евклидовых колец. Выяснение делимости элементов факториального кольца друг на друга, нахождение их НОД и НОК в терминах разложения на простые множители.

Видеозапись лекции

---

20 ноября 2020

Лекция 18

Пример нефакториального целостного кольца.

Неприводимость многочлена зависит от поля коэффициентов. Многочлены 1-й степени неприводимы над любым полем. Неприводимые многочлены степени >1 не имеют корней (над данным полем).

Основная теорема алгебры комплексных чисел (ОТА): любой многочлен положительной степени над полем C имеет комплексный корень. Её следствия: неприводимые многочлены над полем C — это многочлены 1-й степени, разложение многочлена над полем C на линейные множители, число комплексных корней многочлена, с учётом кратностей, равно степени многочлена. Алгебраически замкнутые поля.

Основные понятия и факты математического анализа над полем C: ε-окрестности, пределы последовательностей и функций, непрерывность, существование минимума R-значной непрерывной функции на компакте. Лемма о неограниченном возрастании модуля многочлена. Лемма Д’Алабмера. Доказательство ОТА.

Комплексные корни многочлена с действительными коэффициентами, их разбиение на пары сопряжённых друг другу корней одинаковой кратности. Разложение многочлена над неприводимые множители (линейные и квадратичные с отрицательным дискриминантом) над полем R.

Видеозапись лекции

---

27 ноября 2020

Лекция 19

Проблема приближённого вычисления действительных (комплексных) корней многочлена сводится к нахождению количества корней в заданном интервале (заданной области). Теорема Декарта (правило знаков), оценка числа действительных корней (с учётом кратности) по одну сторону от заданной границы. Избавление от кратных корней (над полем характеристики 0).

Дроби над целостным кольцом как классы эквивалентности пар элементов кольца, определение алгебраических операций над дробями.

Видеозапись лекции

---

1 декабря 2020

Лекция 20

Свойства алгебраических операций над дробями, поле дробей целостного кольца.

Поле рациональных дробей K(x). Интерпретация рациональных дробей как функций.

Несократимые дроби. Представление элемента поля K(x) несократимой дробью, его единственность.

Правильные дроби. Представление рациональной дроби в виде суммы многочлена и правильной дроби, его единственность.

Простейшие дроби, их описание над полями C и R. Разложение правильной дроби в сумму простейших дробей.

Кольцо K[x_1,…,x_n] многочленов от нескольких переменных над ассоциативным коммутативным кольцом K с единицей: аксиоматическое определение, существование и единственность с точностью до изоморфизма (без доказательства).

Видеозапись лекции

---

4 декабря 2020

Лекция 21

Доказательство существования кольца многочленов от нескольких переменных (путём индуктивного построения) и его единственности (с точностью до изоморфизма).

Полиномиальные функции от нескольких переменных. Эквивалентность формального и функционального равенства многочленов от нескольких переменных над бесконечным полем.

Степень одночлена и многочлена (полная и по отдельным переменным), однородные многочлены, разложение многочлена в сумму однородных компонент.

Лексикографический порядок на одночленах, его свойства. Старший член ненулевого многочлена. Старший член произведения многочленов над целостным кольцом K, целостность кольца K[x_1,…,x_n].

Многочлены от одной переменной над факториальным кольцом A, примитивные многочлены, лемма Гаусса. Факториальность кольца многочленов A[x], факториальность колец Z[x] и K[x_1,…,x_n], где K — поле.

Видеозапись лекции

---

11 декабря 2020

Лекция 22

Симметрические многочлены: определение и примеры. Степенные суммы и элементарные симметрические многочлены.

Теорема Виета: выражение значений элементарных симметрических многочленов на корнях многочлена от одной переменной через его коэффициенты.

Основная теорема о симметрических многочленах: существование и единственность выражения произвольного симметрического многочлена через элементарные симметрические многочлены.

Выражение значения симметрического многочлена на корнях многочлена от одной переменной через его коэффициенты.

Дискриминант многочлена от одной переменной, его основное свойство: дискриминант равен 0 тогда и только тогда, когда многочлен имеет кратные корни. Вычисление дискриминанта через определитель из степенных сумм корней многочлена.

Видеозапись лекции

---

15 декабря 2020

Лекция 23

Инвариантность дискриминанта относительно сдвига переменной на константу, сведение к дискриминанту неполного многочлена. Дискриминант неполного кубического трёхчлена, его связь с количеством вещественных корней.

Результант двух многочленов от одной переменной, его свойства, вычисление результанта через определитель из коэффициентов многочленов. Связь дискриминанта многочлена c результантом многочлена и его производной.

Видеозапись лекции

---

18 декабря 2020

Лекция 24

Возведение элемента группы в целую степень, свойства степени.

Порядок элемента группы, его свойства. Пример: порядок подстановки.

Циклическая подгруппа, порождённая элементом группы, циклические группы, примеры: аддитивные группы колец Z и Z_m. n=e в группе порядка n. Теорема Эйлера о вычетах.

Видеозапись лекции

Система линейных уравнений в матрицах

В математике система линейной системы представляет собой набор из двух или более линейных уравнений с одним и тем же набором переменных. Например: 2x – y = 1, 3x + 2y = 12. Это система двух уравнений с двумя переменными, то есть x и y, которая называется двумя линейными уравнениями с двумя неизвестными x и y, а решение линейного уравнения представляет собой значение переменных, такое, что все уравнения выполняются.

В матрице каждое уравнение в системе становится строкой, а каждая переменная в системе становится столбцом, переменные удаляются, а коэффициенты помещаются в матрицу.

Система двух линейных уравнений с двумя неизвестными x и y выглядит следующим образом: 

Пусть  ,  , .

Тогда система уравнений может быть записана в матричной форме как: 

=  т.е. AX = B и  X = .

Если правая сторона, а именно B, равна 0, то система является гомогенной, в противном случае — негомогенной.

— однородная система двух уравнений с двумя неизвестными x и y.

— неоднородная система уравнений.

Система из трех линейных уравнений с тремя неизвестными x, y, z:  

.

Пусть , , .

Тогда система уравнений может быть записана в матричной форме как:

= , то есть AX = B и X = .

Алгоритм решения линейного уравнения с помощью матрицы

1. Запишите данную систему в виде матричного уравнения в виде AX = B.
2. Найдите определитель матрицы. Если определитель |A| = 0, то не существует, значит, решения не существует. Напишите «Система несовместима».
3. Если определитель существует, то найти обратную матрицу, т.е.
4. Найдите обратную матрицу.
5. Решите уравнение матричным методом линейного уравнения по формуле и найдите значения x,y,z.

Пример 1:  Решите уравнение: 4x+7y-9 = 0 , 5x-8y+15 = 0

Решение:  Данное уравнение можно записать в матричной форме: ,  , записывается как: AX = B, где .

Найдем определитель : |A| = 4*(-8) – 5*7 = -32-35 = -67 Итак, решение существует.

Минор и Кофактор матрицы A:  = -8  = -8,  = 5 = -5,  = 7 = -7,  = 4 = 4.

Матрица кофакторов =   и Adj A = 

  .

=  =  = 

x =  и y = 

Пример 2:  Решите уравнение: 2x+y+3z = 1, x+z = 2, 2x+y+z = 3

Решение:  Данное уравнение можно записать в матричной форме как : , , .

Данную систему можно записать в виде: AX = B, где .

Найдем определитель : |A| = 2(0-1) – 1(1-2) + 3(1-0) = -2+1+3 = 2. Итак, решение существует.

Минор и сомножитель матрицы A:  = -1  = -1,  = -1 = 1, = 1 = 1, = -2 = 2,  = -4 = -4, = 0 = 0 = 1 = -1 ,  = -1 = -1, = -1 = 1.

и 

  .

=  =  =  = .

х = 3, у = -2, г = -1.

Упражнение

Решите следующие уравнения:

1. 2x+3y=9, -x+y=-2.
2. х+3у=-2, 3х+5у=4.
3. x+y=1, 3y+3z=5, 3z+3x=4.
4. x+y+z=1, 2x+y+2z=3, 3x+3y+4z=4.
5. x+y+z=6, 3x-y+3z=10, 5x+5y-4z=3.

Примеры линейной алгебры

Теперь мы готовы увидеть, как матричная алгебра может быть полезна при анализе данных. Мы начнем с нескольких простых примеров и, в конце концов, придем к основному: как писать линейные модели с обозначениями матричной алгебры и решать задачу наименьших квадратов.

Среднее

Чтобы вычислить выборочное среднее и дисперсию наших данных, мы используем эти формулы и . Мы можем представить их с помощью матричного умножения. Во-первых, определите эту матрицу, состоящую только из единиц:

Отсюда следует, что:

Обратите внимание, что мы умножаем на скаляр . В R мы умножаем матрицу, используя библиотеку %*% :

 (используя R)
у <- отец.сын$рост
печать (среднее (y))
 

 ## [1] 68.68407
 

 N <- длина(y)
Y<-матрица(y,N,1)
A <- матрица (1, N, 1)
барY=t(A)%*%Y / N
печать (барY)
 

 ## [1]
## [1,] 68.68407
 

Дисперсия

Как мы увидим позже, умножение транспонирования одной матрицы на другую очень распространено в статистике. На самом деле это настолько распространено, что в R есть функция:

 барY=перекрестный(A,Y)/N
печать (барY)
 

 ## [1]
## [1,] 68.68407
 

Для дисперсии отметим, что если:

В R, если вы отправляете только одну матрицу в crossprod , она вычисляет: поэтому мы можем просто ввести:

 r <- y - barY
перекрестный продукт (r) / N
 

 ## [1]
## [1,] 7.915196
 

Что почти эквивалентно:

 библиотека (rafalib)
попвар(у)
 

 ## [1] 7.915196
 

Линейные модели

Теперь мы готовы использовать все это. Начнем с примера Гальтона. Если мы определим эти матрицы:

, то мы можем записать модель:

как:

или просто:

, что намного проще.

Уравнение наименьших квадратов также становится проще, поскольку оно представляет собой следующее векторное произведение:

Итак, теперь мы готовы определить, какие значения минимизируют вышеуказанное, что мы можем сделать, используя вычисления, чтобы найти минимум.

Дополнительно: нахождение минимума с помощью исчисления

Существует ряд правил, которые позволяют нам вычислять уравнения в частных производных в матричной записи. Приравняв производную к 0 и найдя , мы получим наше решение. Единственное, что нам нужно здесь, говорит нам, что производная приведенного выше уравнения:

, и у нас есть наше решение. Обычно мы надеваем шляпу на то, что решает эту проблему, так как это оценка «реального», сгенерированного данными.

Помните, что наименьшие квадраты подобны квадрату (умножить что-то само на себя) и что эта формула похожа на производную от бытия.

Поиск LSE в R

Давайте посмотрим, как это работает в R:

 библиотека (используя R)
х=отец.сын$fвысота
у=отец.сын$рост
X <- cbind(1,x)
betahat <- решить( t(X) %*% X ) %*% t(X) %*% y
###или
betahat <- решить( crossprod(X)) %*% crossprod( X, y )
 

Теперь мы можем увидеть результаты этого, вычислив оценку для любого значения:

 newx <- seq(min(x),max(x),len=100)
X <- cbind(1,newx)
установлено <- X%*%betahat
plot(x,y,xlab="рост отца",ylab="рост сына")
линии (новые, подогнанные, столбец = 2)
 92)
установлено <- X%*%betahat
график (tt, y, xlab = "время", ylab = "высота")
линии (ньют, подгонка, столбец = 2)
 

И получаемые оценки такие, какие мы ожидаем:

 betahat
 

 ## [1]
## 56. 5317368
## тт 0,5013565
## -5.0386455
 

Высота Пизанской башни около 56 метров. Поскольку мы просто сбрасываем объект, начальной скорости нет, а половина гравитационной постоянной равна 9,8/2=4,9 метра в секунду в квадрате.

лм Функция 92) подходит = lm (y ~ X) резюме (подходит)

 ##
## Вызов:
## lm(формула = y ~ X)
##
## Остатки:
## Мин. 1 кв. Медиана 3 кв. Макс.
## -2,5295 -0,4882 0,2537 0,6560 1,5455
##
## Коэффициенты:
## Оценить стандарт. Значение ошибки t Pr(>|t|)
## (Перехват) 56,5317 0,5451 103,701 <2e-16 ***
## Xtt 0,5014 0,7426 0,675 0,507
## X -5,0386 0,2110 -23,884 <2e-16 ***
## ---
## Значение. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1
##
## Остаточная стандартная ошибка: 0,9822 по 22 степеням свободы
## Множественный R-квадрат: 0,9973, скорректированный R-квадрат: 0,997
## F-статистика: 4025 на 2 и 22 DF, p-значение: < 2.2e-16
 

Обратите внимание, что мы получаем те же значения, что и выше.

Резюме

Мы показали, как писать линейные модели с помощью линейной алгебры.