Графики и функций y=m sinx+n и y=m cosx+n
Невозможно отобразить презентацию
Похожие презентации:
Тригонометрические функции y = sin x и y = cos x . Их свойства и графики
Графики тригонометрических функций
Тригонометрия. Учебное пособие для техникума
Свойства и графики тригонометрических функций
Понятие обратной функции. Определение обратных тригонометрических функций
Обратные функции. Свойства взаимно обратных функций
Производная сложной функции
Построение графиков функции y = sinx и y = cosx
Область определения и множество значений тригонометрических функций
Розв’язування найпростіших тригонометричних рівнянь
Графики и функций y=m sinx+n и y=m cosx+n.
Выполнил: Кадет52 учебнойгруппы2 учебнойгруппы .
ЛёвинАлексей .
ЛёвинАлексей 900igr.net Содержание:1.
Функция1.
Функция y=sin x, еёсвойстваиразновидности, еёсвойстваиразновидности;2.
Функция2.
Функция y=cos x, еёсвойстваиразновидности, еёсвойстваиразновидности;
3.
.
Примерызадач 3.
.
Примерызадач 4.
.
Закончитьпросмотр 4.
.
Закончитьпросмотр Функцияy=sinx и её свойства.1.
D(f)=(-,+) ∞∞ D(f)=(-,+) ∞∞.2.
.
Функциянечётна .
Функциянечётна3.
Возрастаетнаотрезке3.
Возрастаетнаотрезке[ 0,/2∏ 0,/2∏] убываетнаотрезке[∏[∏/2,]∏,]∏.4.
.
Ограниченасверхуиснизу .
Ограниченасверхуиснизу5.y.
наим.
наим =-1;
y.
наиб.
наиб=1.
6.
.
Функциянепрерывна 6.
.
Функциянепрерывна7.
E(f)= [-1;1].
Смещения графикаy=sinx по вертикали.
Данафункцияy=sin x+1.
, Длятогочтобы , Длятогочтобы построитьеё, графикнужно, графикнужно построитьграфик функцииy=sinxи 1 сместитьегона 1 сместитьегона.
вверх.
вверх Смещение графикаy=sinx по горизонтали.
Данафункция y=sinx+∏ y=sinx+∏/2.
Чтобыпостроитьеё, график, график нужнографикфункции y=sin x сместить Влевона∏/2.
Растяжение графика y=sinx по осиy Данафункция y=3sinx.
, Чтобыпостроитьеёграфикнужно , Чтобыпостроитьеёграфикнужно Растянутьграфик y=sinx, такчтобы, такчтобы E(y): (-3;
3).
График функции y=m*sin x , Длятогочтобы , Длятогочтобы вернуться содержаниюнажмите.
сюда.
сюда Чтобыпродолжить .
нажмитенал .
нажмитенал .
Кнопкумыши .
Кнопкумыши КСОДЕРЖАНИЮ Функцияy=cosx и её свойства.1.
D(f)=(-;+) ∞∞ D(f)=(-;+) ∞∞.
2.
.
Чётнаяфункция 2.
.
Чётнаяфункция3.
Убываетнаотрезке3.
Убываетнаотрезке [0,]∏ [0,]∏, возрастаетнаотрезке [,2].
∏∏ [,2].
∏∏4.
Функцияограниченасверхуи4.
Функцияограниченасверхуи.
снизу.
снизу5.y наим =-1;
y наиб=1.
6.
.
Функциянепрерывна 6.
.
Функциянепрерывна7.
E(f)=[-1;1].
Смещения графикаy=cosx по вертикали.
Данафункцияy=cos x+1.
, Длятогочтобы , Длятогочтобы построитьеё, графикнужно, графикнужно построитьграфик функцииy=cosxи 1 сместитьегона 1 сместитьегона.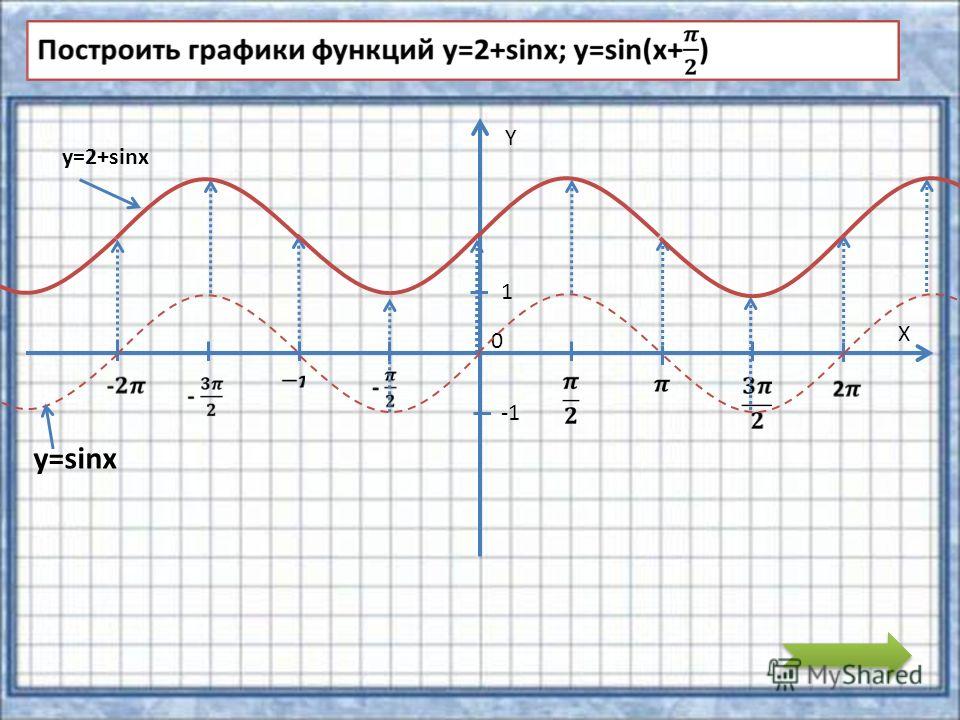
вверх.
вверх Смещение графикаy=cosx по горизонтали.
Данафункция y=cosx+∏ y=cosx+∏/2.
, Чтобыпостроитьеёграфик , Чтобыпостроитьеёграфик нужнографикфункции y=cos x сместить Влевона∏/2.
Растяжение графика y=cosx по осиy Данафункция y=3cosx.
Чтобыпостроитьеё, графикнужно, графикнужно Растянутьграфик y=cosx, такчтобы, такчтобы E(y): (-3;
3).
График функции y= m*cos x Чтобывернуться Ксодержанию .
нажмитесюда .
нажмитесюда Чтобыперейтик примерамзадач .
щёлкнител .
кнопкоймышки .
кнопкоймышки КСОДЕРЖАНИЮ Самостоятельная работа.
: Данафункция : Данафункция y=sin (x+/2)∏ y=sin (x+/2)∏.
.
Постройтеграфикфункции .
Постройтеграфикфункции.
Ответ.
Ответ Чтобывернутьсяк .
содержаниюнажмитесюда .
содержаниюнажмитесюда КСОДЕРЖАНИЮ Lelik productions .
2006 год.! Ответ! Ответ Чтобывернуться .
English Русский Правила
2. Введение в анализ
72.
Построить
график функции
преобразованием графика функцииy=sinx.
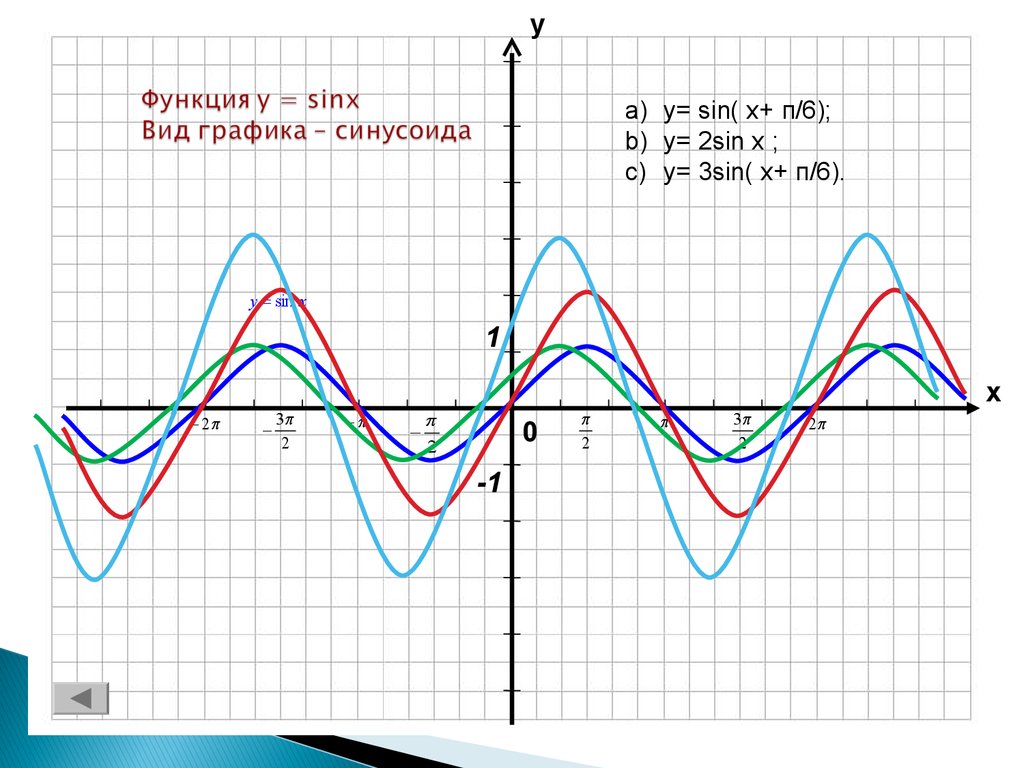
Записав данную функцию в виде замечаем, что у неё А=-3,.
1. Строим одну волну синусоиды и отмечаем на ней несколько точек.
2. Увеличивая в три раза ординаты выбранных точек графика функции и оставляя неизменными абсциссы, затем, отображая полученную линию зеркально относительно оси ОХ, графика y=sinx, строим график функции y=-3sinx.
3. Увеличивая в 2 раза абсциссы точек графика функции y=-3sinx и сохраняя неизменными ординаты, строим график функции .
4. Перенося точки графика функции в направлении оси абсцисс на 3/2 единицы масштаба этой оси влево, строим искомый график функции .
y=sinx
y=-3sinx
82. Линия задана
уравнением
в
полярной системе координат. Требуется:
1) построить линию по точкам начиная от
φ=0 до φ=2π и придавая φ значения через
промежуток π/8; 2) найти уравнение данной
линии в декартовой прямоугольной системе
координат, у которой начало совпадает
с плюсом, а положительная полуось абсцисс
– с полярной осью и по уравнению в
декартовой прямоугольной системе
координат определить, какая это линия.
φ | r |
0 | 1,2 |
π/8 | 1,237685273 |
π/4 | 1,359245518 |
3π/8 | 1,593470229 |
π/2 | 2 |
5π/8 | 2,685004489 |
3π/4 | 3,783611625 |
7π/8 | 5,207244265 |
π | 6 |
9π/8 | 5,207244265 |
5π/4 | 3,783611625 |
11π/8 | 2,685004489 |
3π/2 | 2 |
13π/8 | 1,593470229 |
7π/4 | 1,359245518 |
| 15π/8 | 1,237685273 |
2π | 1,2 |
2) Найдем уравнение данной линии в декартовой прямоугольной системе координат
Подставим это значение в уравнение линии:
Это уравнение
данной линии в декартовой системе
координат.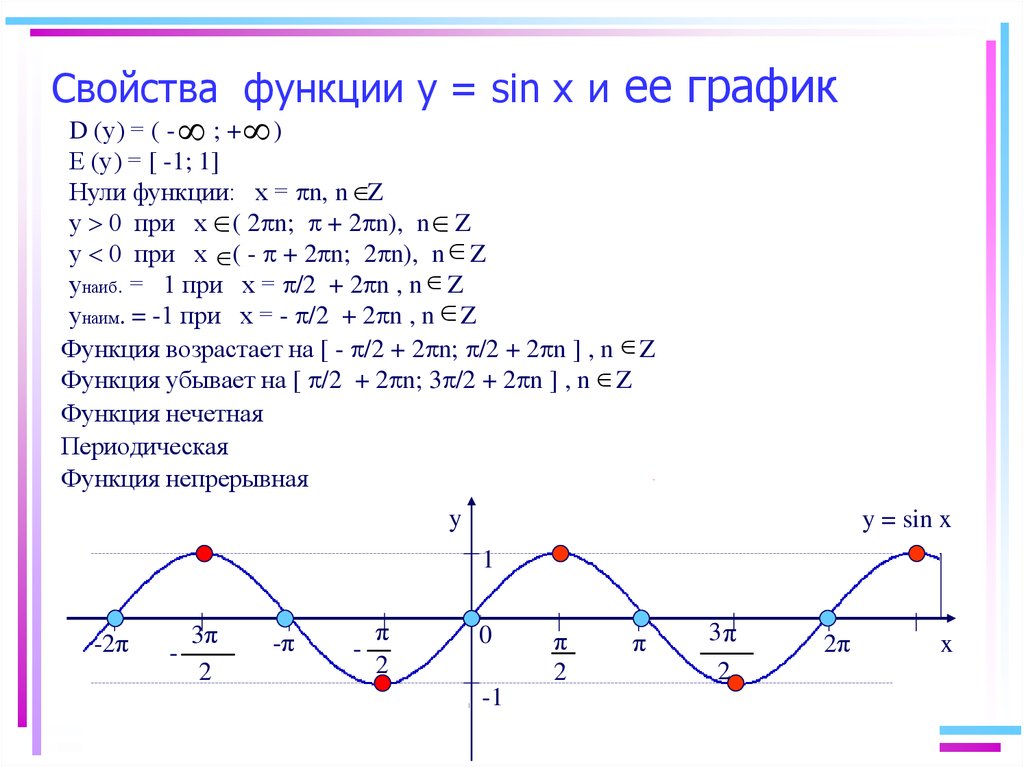
Эта линия является эллипсом, с центром в точке (,0).
а)
б)
в)
г)
102. Дана функция и два значения аргумента х1=2, х2=4. Требуется: установить, является ли данная функция непрерывной или разрывной для каждого из данных значений х; 2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа; 3) сделать схематический чертеж..
Данная функция определена и непрерывна на интервалах (-∞;4),(4;+∞).
Исследуем поведение функции в точках х1=2, х2=4. Найдём односторонние пределы.
При х=2 функция имеет одинаковые односторонние пределы, значит, в этой точке функция непрерывна. При х=4 функция имеет бесконечные пределы, значит, в этих точках функция разрывна.
112. Задана функция y=f(x)
различными аналитическими выражениями
для различных областей изменения
независимой переменной.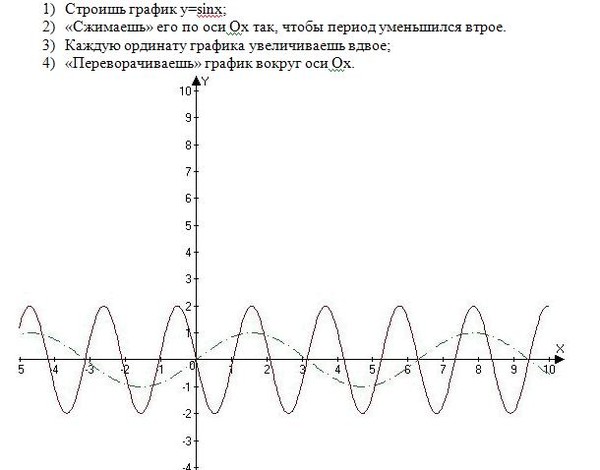
Найти точки
разрыва функции, если они существуют.
Сделать чертеж.
При х=4 функция имеет одинаковые односторонние пределы, значит, в этой точке функция непрерывна. Т.к. односторонние пределы при х=0 различны, то функция терпит в точке разрыв. А т.к. односторонние пределы конечны, то х=0 – точка разрыва первого рода. Функция имеет скачок в этой точке равный 1+3=4.
График этой функции:
Соответствующие граф-граф и уравнение-Ключ-Google Suce
AllebilderVideosshoppingMapsNewsbücher
Sucoptionen
Bilder
Alleighen
Allegeigen
winwoodmaths.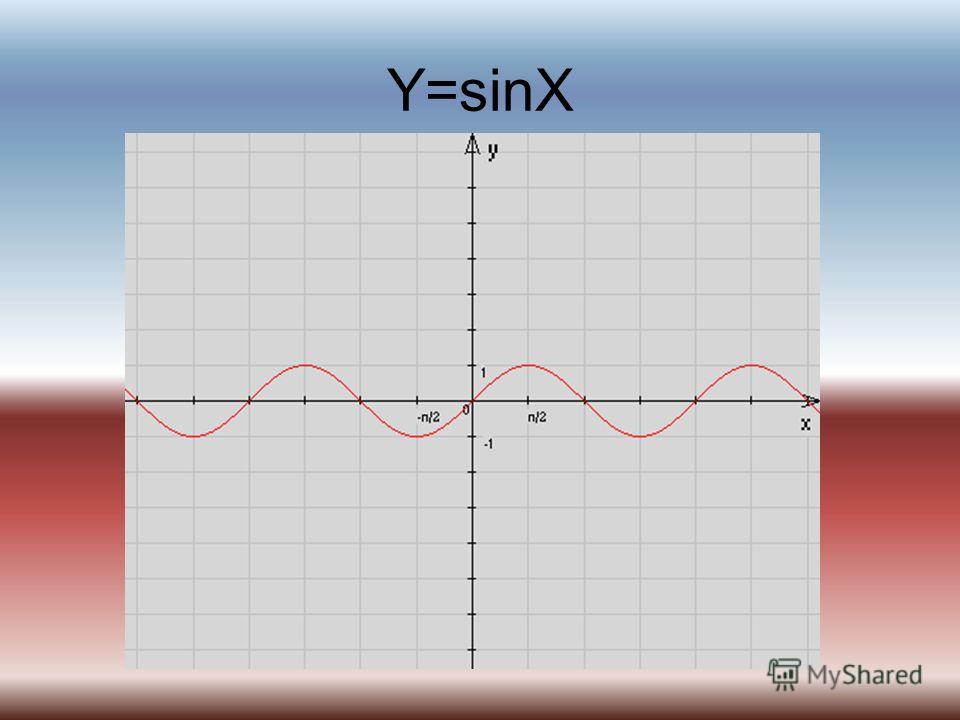
online › wp-content › uploads › 2020/05 › Graph-Ma…
Graph Matching 1 – Ответы. Сопоставьте одну группу с другой. Будет «запасной» — нарисуйте график на пустых осях внизу. Уравнение.
[PDF] Упражнение на сопоставление: уравнения, графики и таблицы
mrsrauvola.weebly.com › linearequationtableandgraphmatchingactivity
Как использовать это упражнение. • Материалы – ножницы, рабочие листы (клей и плотная бумага по желанию). • Объедините учащихся в пары и раздайте им только графики …
Сопоставление графиков и линейных уравнений | KS3-4 математика — Teachit
www.teachit.co.uk › ресурсы › графики сопоставления-а…
10.08.2021 · Сопоставление графиков и уравнений … Использование градиентов и точек пересечения прямых графиков дается для сопоставления каждой строки с ее уравнением. Два …
Результаты сопоставления уравнений и графиков — TPT
www.teacherspayteachers.com › Обзор › Search:m.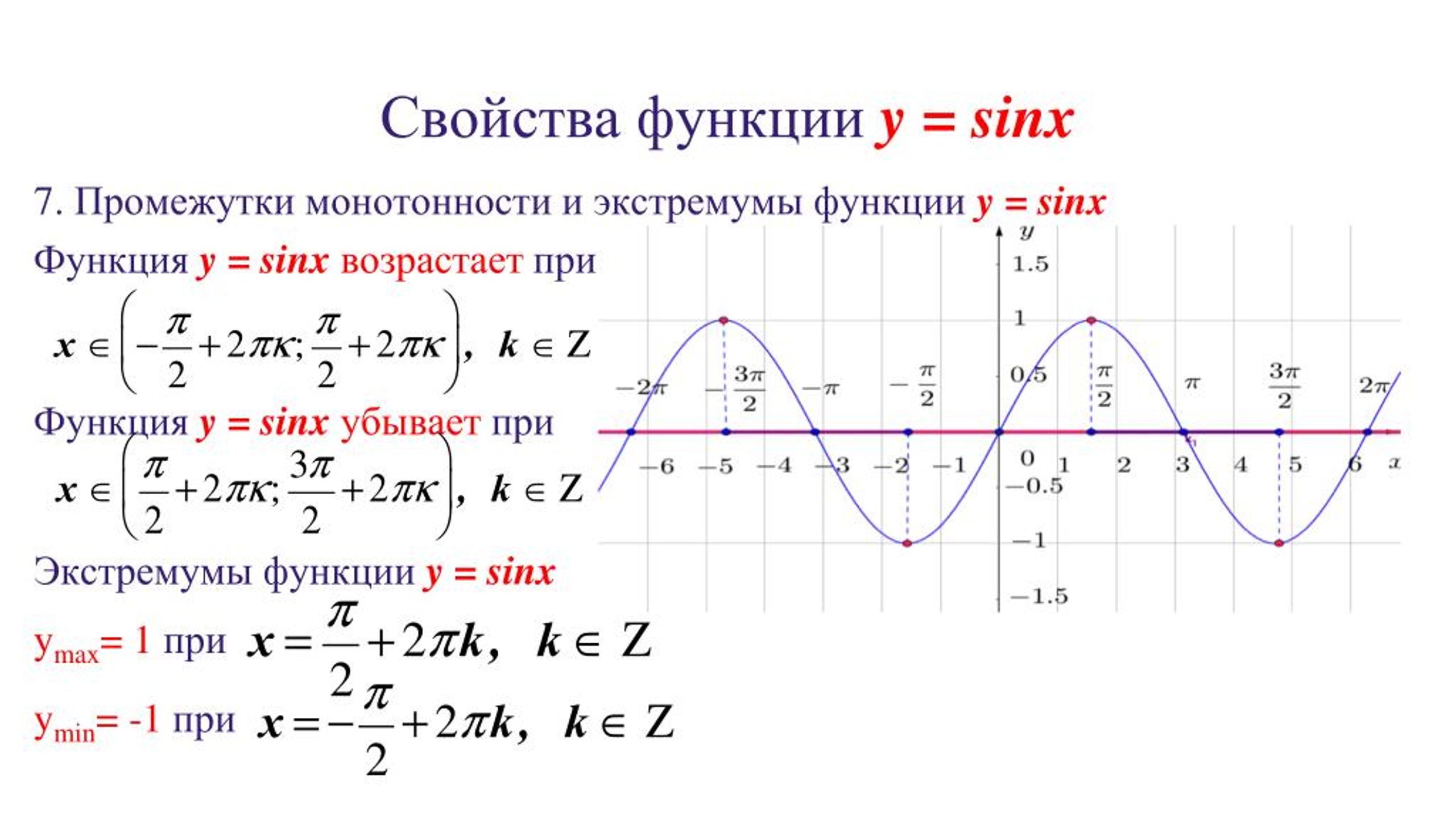
..
Результаты 1–24 из 3200+ · Если вы работаете с линейными уравнениями и их графиками, это деятельность является забавным способом обзора. Намного веселее, чем скучный рабочий лист …
Сопоставление графиков с уравнениями Учебные ресурсы — TPT
www.teacherspayteachers.com › Обзор › Search:m…
Результаты 1–24 из 5100+ · Используйте это практическое задание по сопоставлению карт, чтобы помочь учащимся попрактиковаться в сопоставлении графиков с соответствующими линейными уравнениями! Шесть …
Сопоставление графиков | Учебные ресурсы — Tes
www.tes.com › graphs-matching-11671572
Bewertung 4,9
(9) · Kostenlos
учитель об уравнениях графиков/функций и …
Таблица сопоставления графика с уравнением — Liveworksheets.com
www.liveworksheets.com › …
Онлайн-таблица с графиками и уравнениями для 9.