Способы решения квадратных уравнений | Творческие проекты и работы учащихся
Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения (Приложение 1).
Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно остановимся на каждом из них.
1 способ: разложение левой части уравнения на множители.
Решим уравнение
х2 + 10х — 24 = 0
Разложим левую часть на множители:
х2 + 10х — 24 = х2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х — 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х2 + 10х — 24 = 0.
2 способ: метод выделения полного квадрата.
Решим уравнение х2 + 6х — 7 = 0.
Выделим в левой части полный квадрат.
Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2• х • 3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как х2 + 2• х • 3 + 32 = (х + 3)2.
Преобразуем теперь левую часть уравнения
х2 + 6х — 7 = 0,
прибавляя к ней и вычитая 32. Имеем:
х2 + 6х — 7 = х2 + 2• х • 3 + 32 — 32 — 7 = (х + 3)2 — 9 — 7 = (х + 3)2 — 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 — 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 — 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
3 способ: решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах2 + bх + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) — b2 + 4ac = 0,
(2ax + b)2 = b2 — 4ac,
2ax + b = ± √ b2 — 4ac,
2ax = — b ± √ b2 — 4ac,
Примеры. Сколько корней имеет уравнение?
а) 4х2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b2 — 4ac = 72 — 4 • 4 • 3 = 49 — 48 = 1,
D > 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т. е. при
е. при
b2 — 4ac >0 , уравнение ах2 + bх + с = 0 имеет два различных корня.
б) 4х2 — 4х + 1 = 0,
а = 4, b = — 4, с = 1, D = b2 — 4ac = (-4)2 — 4 • 4 • 1= 16 — 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 — 4ac = 0, то уравнение
ах2 + bх + с = 0 имеет единственный корень,
в) 2х2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b2 — 4ac = 32 — 4 • 2 • 4 = 9 — 32 = — 13 , D < 0.
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b2 — 4ac < 0,
уравнение ах2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4 способ: решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
x1 + x2 = — p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р > 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Если р > 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Например, x2 – 3x + 2 = 0;
x1 = 2 иx2 = 1, так какq = 2 > 0 иp = — 3 < 0;x2 + 8x + 7 = 0; x1 = — 7 иx2 = — 1, так какq = 7 > 0 иp= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .
Пример: x2 + 4x – 5 = 0; x1 = — 5 иx2 = 1, так какq= — 5 < 0 иp = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 иx2 = — 1, так какq = — 9 < 0 иp = — 8 < 0.
5 способ: решение уравнений способом «переброски»( Приложение 2).
Рассмотрим квадратное уравнение
Умножая обе его части на а, получаем уравнение
а2х2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у2 + by + ас = 0, равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = у1/а и х1 = у2/а.
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример. Решим уравнение 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2 – 11у + 30 = 0.
Согласно теореме Виета
у1 = 5 х1 = 5/2 x1 = 2,5
у2 = 6 x2 = 6/2 x2 = 3.
Ответ: 2,5; 3.
6 способ: свойства коэффициентов квадратного уравнения (Приложение 2)
А.Пусть дано квадратное уравнение
ах2 + bх + с = 0, где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1
х2 = с/а.
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x2 + b/a • x + c/a = 0.
Согласно теореме Виета
x1 + x2 = — b/a,
x1x2 = 1• c/a.
По условию а – b + с = 0, откуда b = а + с. Таким образом,
x1 + x2 = — а
x1x2 = — 1• ( — c/a),
т.е. х1 = -1 и х2 = c/a, что м требовалось доказать.
Примеры.
1) Решим уравнение 345х2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
х1 = 1, х2 = c/a = -208/345.
Ответ: 1; -208/345.
2)Решим уравнение 132х2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
х1 = 1, х2 = c/a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2k – четное число, то формулу корней.
Пример.
Решим уравнение 3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16,
k = — 7;D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D > 0, два различных корня;
Ответ: 2; 8/3
В. Приведенное уравнение х2 + рх + q= 0 совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней принимает вид:
Поэтому для приведенного квадратного уравнения формула корней принимает вид:
Формулу (3) особенно удобно использовать, когда р — четное число.
Пример. Решим уравнение х2 – 14х – 15 = 0.
Решение. Имеем: х1,2 =7± 8,
Ответ: х1 = 15; х2 = -1.
7 способ: Графическое решение квадратного уравнения.
Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = — px —
Построим графики зависимости у = х2 и у = — px — q.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости — прямая (рис.1). Все данные вводим в программу«Advanced Grapher» и получаем ответы [13].
Искомая окружность пересекает ось абсцисс в точках B (х1 ;0) и D (х2 ;0), где х1 и х2 – корни уравнения ах2 + bх + с=0, и проходит через точки А (0;1) и С (0; ) на оси ординат. [5, c.34]
[5, c.34]
Возможны следующие случаи:
- прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
- прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
- прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Примеры.
1) Решим графически уравнение х2 — 3х — 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13). Прямая и парабола пересекаются в двух точках А и В с абсциссами х1 = — 1 и х2 = 4.
Ответ: х1 = — 1; х2 = 4.
2) Решим графически уравнение (рис. 3) х2 — 2х + 1 = 0.
Решение. Запишем уравнение в виде х2 = 2х — 1.
Запишем уравнение в виде х2 = 2х — 1.
Построим параболу у = х2 и прямую у = 2х — 1.
Прямую у = 2х — 1 построим по двум точкам М (0; — 1)
и N(1/2; 0). Прямая и парабола пересекаются в точке А с
абсциссой х = 1. Ответ: х = 1.
3) Решим графически уравнение х2 — 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х2 = 5х — 5. Построим параболу у = х2 и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х2 — 2х + 5 = 0 корней не имеет.
8 способ:: решение квадратных уравнений с помощью циркуля и линейки.
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика. Найти корни квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 5). [5, c.34]
Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика. Найти корни квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 5). [5, c.34]
Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 — корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD.
Итак: 1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах2 + bх + с = 0.
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
Пример. Решим уравнение х2 — 2х — 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1).
Ответ: х1 = — 1; х2 = 3.
9 способ: решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990) [ 3, c.83] .
Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение
z2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
Примеры.
1) Для уравнения z2 — 9z + 8 = 0 номограмма дает корниz1 = 8,0 и z2 = 1,0 (рис.12).
(рис.12)
2) Решим с помощью номограммы уравнение
2z2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z2 — 4,5z + 1 = 0.
Номограмма дает корни z1 = 4 иz2 = 0,5.
3) Для уравнения
z2 — 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение t2 — 5t + 2,64 = 0, которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откудаz1 = 5t1 = 3,0 иz2 = 5t2 = 22,0.
10 способ: геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
Примеры.
1) Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х2 + 10х + 25. Заменяя
х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т. е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
А вот, например, как древние греки решали уравнение у2 + 6у — 16 = 0.
Решение представлено на рис. 16, где у2 + 6у = 16,
или у2 + 6у + 9 = 16 + 9.
Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = — 8 (рис.16).
3) Решить геометрически уравнение у2 — 6у — 16 = 0.
Преобразуя уравнение, получаему2 — 6у = 16.
На рис. 17 находим «изображения» выражения у2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у2 — 6у равным ему числом 16,
Заменяя выражение у2 — 6у равным ему числом 16,
получаем: (у — 3)2 = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у1 = 8 и у2 = — 2.
Заключение
Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.
Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней. Здесь мы остановилась на вопросе решения квадратных уравнений, а что, если существуют и другие способы их решения?! Опять находить красивые закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое.
Но это вопросы уже следующих работ. В результате изучения новых способов решения квадратных уравнений мы получили возможность решать уравнения не только по формуле, но и более интересными способами. Решили множество уравнений, изучили программу «Advanced Grapher». Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи.
Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт. Данная исследовательская работа может быть использована учителями математики на уроках и элективных курсах по математике при изучении темы «Квадратные уравнения» (Приложения 1-3), учениками для расширения и углубления знаний по решению квадратных уравнений. Любой учащийся, используя эту исследовательскую работу, может самостоятельно изучить данную тему (Приложения 1-2).
Литература
- Алимов, Ш.А., Ильин В.А.
 и др. Алгебра, 6-8. / Пробный учебник для 6-8 классов средней школы. — М., Просвещение, 1981.
и др. Алгебра, 6-8. / Пробный учебник для 6-8 классов средней школы. — М., Просвещение, 1981. - Арутюнян, Е.Б.Занимательная математика/ Е.Б. Арутюнян Москва «Аст – пресс» 1999.
- Брадис, В.М. Четырехзначные математические таблицы для средней школы. Изд. 57-е. — М., Просвещение, 1990. С. 83.
- Глейзер, Г.И. История математики в школе. 7-8 классы. – М., Просвещение, 1982.
- Окунев , А.К. Квадратичные функции, уравнения и неравенства. / Пособие для учителя. — М., Просвещение, 1972.
- Пресман, А.А. Решение квадратного уравнения с помощью циркуля и линейки. — М., Квант, № 4/72. С. 34.
- Соломник , В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. — 4-е, дополн. — М., Высшая школа, 1973.
- Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. — М., Просвещение,
- Пичурин, Л.Ф. За страницами учебника алгебры/ Л.Ф. Пичурин. Москва «Просвещение» 1990г.
- Энциклопедический словарь юного математика.
 – 2-е издание, испр. и доп. – М.:Педагогика, 1989.
– 2-е издание, испр. и доп. – М.:Педагогика, 1989. - Энциклопедия для детей. Т.11. Математика.- М.: Аванта+, 1999.
- Ресурсы сети Интернет.
- Программы «Advanced Grapher» и «Открытая математика».
Перейти к разделу: 3. Что необходимо знать для решения квадратных уравнений?
10 способов решения квадратных уравнений (стр. 2 из 4)
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала каждый из них.
1. СПОСОБ: Разложение левой части уравнения на множители.
Решим уравнение
х2 + 10х — 24 = 0.
Разложим левую часть на множители:
х2 + 10х — 24 = х2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х — 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х2 + 10х — 24 = 0.
2. СПОСОБ: Метод выделения полного квадрата.
Решим уравнение х2 + 6х — 7 = 0.
Выделим в левой части полный квадрат.
Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2• х • 3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как
х2 + 2• х • 3 + 32 = (х + 3)2.
Преобразуем теперь левую часть уравнения
х2 + 6х — 7 = 0,
прибавляя к ней и вычитая 32. Имеем:
Имеем:
х2 + 6х — 7 = х2 + 2• х • 3 + 32 — 32 — 7 = (х + 3)2 — 9 — 7 = (х + 3)2 — 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 — 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 — 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
3. СПОСОБ: Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах2 + bх + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) — b2 + 4ac = 0,
(2ax + b)2 = b2 — 4ac,
2ax + b = ± √ b2 — 4ac,
2ax = — b ± √ b2 — 4ac,
Примеры.
а) Решим уравнение: 4х2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b2 — 4ac = 72 — 4 • 4 • 3 = 49 — 48 = 1,
D > 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b2 — 4ac >0 , уравнение ах2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х2 — 4х + 1 = 0,
а = 4, b = — 4, с = 1, D = b2 — 4ac = (-4)2 — 4 • 4 • 1= 16 — 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 — 4ac = 0, то уравнение
ах2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b2 — 4ac = 32 — 4 • 2 • 4 = 9 — 32 = — 13 , D < 0.
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b2 — 4ac < 0,
уравнение ах2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х2 + px + c = 0. (1)
(1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
x1 +x2 = — p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Например,
x2 – 3x + 2 = 0; x1 = 2 иx2 = 1, так какq = 2 > 0 иp = — 3 < 0;
x2 + 8x + 7 = 0; x1 = — 7 иx2 = — 1, так какq = 7 > 0 иp= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .
Например,
x2 + 4x – 5 = 0; x1 = — 5 иx2 = 1, так какq= — 5 < 0 иp = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 иx2 = — 1, так какq = — 9 < 0 иp = — 8 < 0.
5. СПОСОБ: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах2 + bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2х2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у2 + by + ас = 0,
равносильно данному. Его корни у1и у2 найдем с помощью теоремы Виета.
Окончательно получаем
х1 = у1/а и х1 = у2/а.
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример.
Решим уравнение 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2 – 11у + 30 = 0.
Согласно теореме Виета
у1 = 5 х1 = 5/2 x1 = 2,5
у2 = 6 x2 = 6/2 x2 = 3.
Ответ: 2,5; 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение
ах2 + bх + с = 0, где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,
х2 = с/а.
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x2 + b/a• x + c/a = 0.
Согласно теореме Виета
x1 + x2 = — b/a,
x1x2 = 1• c/a.
По условию а – b + с = 0, откуда b = а + с. Таким образом,
x1 + x2 = — а + b/a= -1 – c/a,
x1x2 = — 1• ( — c/a),
т. е. х1 = -1 и х2 = c/a, что м требовалось доказать.
е. х1 = -1 и х2 = c/a, что м требовалось доказать.
Примеры.
1) Решим уравнение 345х2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
х1 = 1, х2 = c/a = -208/345.
Ответ: 1; -208/345.
2)Решим уравнение 132х2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
х1 = 1, х2 = c/a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2k– четное число, то формулу корней
Пример.
Решим уравнение 3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;
D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D > 0, два различных корня;
Ответ: 2; 8/3
В. Приведенное уравнение
Приведенное уравнение
х2 + рх + q= 0
совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней
Основные способы решения полных квадратных уравнений
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Казачкова Р.Г. 1
1Рассветский филиал МКОУ «СОШ г.Нариманов»
Криволапова Е.В. 1
1Рассветский филиал МКОУ «СОШ г.Нариманов»
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Актуальность выбранной темы продиктована желанием показать разнообразие способов решения квадратных уравнений. Необходимость решать уравнения первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площади земельного участка и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Необходимость решать уравнения первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площади земельного участка и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Начиная с 8 класса, умение решать квадратные уравнения является основополагающим, так как они находят широкое применение в решении тригонометрических, логарифмических, иррациональных, показательных и других видов уравнений. Квадратное уравнение широко распространено: во многих строительных и архитектурных расчётах, сооружениях, спорте, описании траектории движения планет. Поэтому исследование способов решения полных квадратных уравнений считаю актуальным.
Проблема: какие существуют способы решения полных квадратных уравнений?
Цель работы: изучить и систематизировать способы решения полных квадратных уравнений.
Задачи:
Изучить литературу по теме исследования.
Выбрать и изучить способы решения полных квадратных уравнений.
Сделать выводы.
Объект исследования: полные квадратные уравнения.
Методы исследования: теоретический (изучение литературы), математический (построение графиков, вычисления).
Рассмотрим основные способы решения таких уравнений в нашей работе.
2.1 Квадратное уравнение: определение, виды, способы решения
Квадратным уравнением называется уравнение вида ax² + bx + c =0, где х-переменная, a,b и c – некоторые числа, причём а¹0. Коэффициенты имеют свои названия: а – первый или старший коэффициент, в – второй коэффициент, с – свободный член. Если а=1, то уравнение называется приведённым. Если в=0 или с=0, то квадратное уравнение называют неполным (рис.1).
Рис.1 Виды квадратных уравнений
Примеры полных квадратных уравнений: 3x2-5x+2=0, x2-16x+24=0;
неполные: x2 + 3x=0, 2x2 — 128=0, 62x2 = 0.
Корнями квадратного уравнения называются значения переменной, при которых уравнение обращается в верное равенство. Квадратное уравнение может иметь два, один или ни одного корня. [1]
В школьном курсе математики изучается несколько способов решения полных квадратных уравнений. Однако имеются и другие способы, которые позволяют очень быстро и рационально решать многие уравнения, всего насчитывается более десятка способов. Рассмотрим основные: решение квадратных уравнений по формуле, решение уравнения выделением полного квадрата, решение уравнения путём разложения левой части на множители, решение с помощью теоремы Виета и графический способ. Но сначала обратимся к историческим сведениям: как давно возникли квадратные уравнения и как их решали раньше?
2.2 Из истории квадратных уравнений
Квадратные уравнения в Индии.
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499г. индийским математиком и астрономом Ариабахаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
индийским математиком и астрономом Ариабахаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ах2 + bх = с, а > 0
В уравнении все коэффициенты, кроме а, могут быть отрицательными. Правило Брахмагупта (приложение 1) по существу совпадает с ныне существующими.
Квадратные уравнения в Древнем Вавилоне
Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне. Если применить современную алгебраическую запись, то в их клинописных текстах можно встретить неполные и полные квадратные уравнения, например:
х2 + х = , х2 – х = 14
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. [5]
Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. [5]
Квадратные уравнения в Европе XIII—XVII вв.
Формулы решения квадратных уравнений по образцу аль-Хорезми (приложение 1) в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардо Фибоначчи. Этот объемный труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошёл к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники XVI-XVII вв. и частично XVIII век.
и частично XVIII век.
Общее правило решения квадратных уравнений, приведённых к единому каноническому виду
х2 + bх = с,
при всевозможных комбинациях знаков коэффициентов b и с было сформулировано в Европе лишь в 1544г. М.Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, кроме положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других учёных способ решения квадратных уравнений принимает современный вид. [3]
2.3 Решение квадратных уравнений по формуле
Решение квадратных уравнений сводится к нахождению дискриминанта, чтобы определить количество корней: D=b2 — 4aс.
Если D>0, то уравнение имеет два корня и находим эти корни по формуле:
Если D=0, то уравнение имеет один корень
Если D<0, то уравнение не имеет вещественных корней. [1]
Рассмотрим пример 1: нужно найти корни уравнения 3x2 — 2x — 16=0.
Записываем сначала, чему равны числовые коэффициенты a, b и c:
a=3,b= -2,c= -16. Находим дискриминант: D=b2-4ac = (-2)2-4∙2∙(-16)=4+192=196
Дискриминант больше нуля, следовательно, у нас два корня, найдем их:
Х1= (2 – 14) /6 = -2 Х2 = (2 + 14) /6 = 8/3
Ответ: x1= -2; x2= 8/3.
Рассмотрим пример 2: найти корни уравнения x2 — 6x + 11=0.
a=1,b= -6,c= 11. Находим дискриминант: D=b2-4ac = (-6)2-4∙1∙11= 36 — 44= — 8
Дискриминант меньше нуля, следовательно, корней нет.
Ответ: корней нет.
Рассмотрим пример 3: найти корни уравнения 4x2 — 12x + 9=0.
a=4,b= -12,c= 9. Находим дискриминант: D=b2-4ac = (-12)2-4∙4∙9= 144 -144= 0
Дискриминант равен нулю, следовательно, у нас один корень:
Х = 12/8=1,5
Ответ: х=1,5.
2.4 Решение квадратных уравнений методом выделения полного квадрата
Поясним этот метод на примере 4: решим уравнение х2 + 6х – 7 = 0.
Выделим в левой части полный квадрат. Для этого запишем выражение
х2 + 6х в виде: х2 + 6х = х2 + 2· х ·3.
В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3, поэтому, чтобы получить полный квадрат, нужно прибавить 32 , так как х2 + 2· х ·3 + 32 = (х + 3)2 .
Преобразуем теперь левую часть уравнения х2 + 6х – 7 = 0, прибавляя к ней и вычитая 32. Имеем:
х2 + 6х – 7 = х2 + 2· х ·3 + 32 – 32 – 7 = (х + 3)2 – 9 – 7 = (х + 3)2 – 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 –16 = 0, т.е. (х + 3)2 = 16.
Следовательно, х + 3 = 4, х1 = 1, или х + 3 = — 4 , х2 = – 7.
Ответ: x1= 1; x2= — 7.
2.5 Разложение левой части квадратного уравнения на множители
Рассмотрим пример 5: решим уравнение х2 + 10х – 24 = 0.
Разложим левую часть уравнения на множители:
х2 + 10х – 24 = х2 + 12х – 2х – 24 = х(х + 12) – 2(х +12) = (х + 12)(х – 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х – 2) = 0.
Так как произведение равно нулю, то, по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = — 12. Это означает, что числа 2 и – 12 являются корнями уравнения х2 + 10х – 24 = 0.
Ответ: x1= 2; x2= — 12.
2.6 Графический способ решения
Если в уравнении x2 + bx + c = 0
перенести второй и третий члены в правую часть, то получим x2 = – bx – c .
Построим графики зависимостей у = х2 и у = – bx – c .
График первой зависимости – парабола, проходящая через начало координат.
График второй зависимости – прямая. Возможны следующие случаи:
прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
прямая и парабола могут касаться (только одна общая точка), т. е. уравнение имеет одно решение;
е. уравнение имеет одно решение;
прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней. [2]
Пример 6: решим графически уравнение х2 –3х – 4 = 0.
Запишем уравнение в виде х2 = 3х + 4. Построим параболу у = х2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М(0;4) и N (3;13).
Прямая и парабола пересекаются в двух точках А и B с абсциссами х1 = – 1 и х2 = 4. (Рис.2)
Ответ: х1 = – 1; х2 = 4.
2.7 Решение квадратных уравнений с помощью теоремы Виета
1. Приведенное квадратное уравнение имеет вид х2 + px + q = 0.
Его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид
Отсюда можно сделать следующие выводы (по коэффициентам p и qможно предсказать знаки корней).
Если свободный член qприведенного уравнения положителен (q >0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p.
Если p>0, то оба корня отрицательные, если p<0, то оба корня положительны.
Например,
х2 – 3х + 2 = 0; х1 = 2 и х2 = 1, так как q = 2 > 0 и p = – 3 <0;
х2 +8х + 7 = 0; х1 = – 7 и х2 = – 1, так как q = 7 > 0 и p = 8 >0.
Если свободный член qприведенного уравнения отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p<0, или отрицателен, если p>0.
Например,
х2 + 4х – 5 = 0; х1 = – 5 и х2 = 1, так как q = – 5<0 и p = 4 > 0;
х2 – 8х – 9 = 0; х1 = 9 и х2 = – 1, так как q = – 9<0 и p = – 8 >0.
2. Теорема Виета для квадратного уравнения ах2 +bх +с = 0 имеет вид
Справедлива теорема, обратная теореме Виета:
Если числа х1 и х2 таковы, что х1+х2 = -b, х1х2 = c, то х1 и х2 – корни квадратного уравнения х2 +bх + c = 0.
Эта теорема позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней. [4]
Пример 7: решим уравнение х2 – 9х + 14 =0.
Найдём два числа х1 и х2 , такие, что
х1 +х2 = 9
х1х2 = 14
Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.
Ответ: х1 = 2; х2 = 7.
Заключение
При решении квадратного уравнения не надо ограничиваться одним
способом решения уравнения, который изучается в школьном курсе математики, а для каждой ситуации можно использовать свой способ решения.
Особенно популярным способом является решение квадратного уравнения по формуле и теорема Виета. Изучив материалы для подготовки к ГИА, я пришла к выводу: материалы содержат много квадратных уравнений, при решении которых можно использовать различные способы.
Интересным для меня оказался графический способ решения квадратного уравнения. Но недостаток этого способа – не всегда значения абсцисс точек пересечения графиков будут являться целыми и точными значениями.
Более подробно изучив тему «Решение полных квадратных уравнений», я углубила знания в истории развития математики и открыла много полезного и нового для себя. Кроме вышеперечисленных мною основных способов решения квадратных уравнений в разных источниках выделяют ещё: решение уравнений способом «переброски», решение с помощью циркуля и линейки, решение с помощью номограммы, геометрический способ и использование свойств коэффициентов квадратного уравнения.
Такая широкая тема позволяет всем желающим находить в книгах, научных журналах, сайтах всё новые пути решения уравнений, создавать основу для дальнейших исследований в мире математики, получать необходимые интересующие сведения, применение которых на практике способствует развитию мышления и повышению уровня знаний. Каждый из способов удобен по-своему, интересен и значим в общей копилке умений каждого.
Каждый из способов удобен по-своему, интересен и значим в общей копилке умений каждого.
Список использованных источников и литературы
Мерзляк А.Г. Алгебра: 8 класс: учебник для общеобразовательных организаций/А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М.:Вентана – Граф, 2017.
Окунев А.К. Квадратичные функции, уравнения и неравенства / Пособие для учителя. — М.: Просвещение, 2016.
Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. — 4-е, дополн. — М.: Высшая школа, 2017.
Якушева Г.Н. Математика. Справочник школьника. — М., Просвещение, 2015.
История возникновения квадратных уравнений: [Электронный ресурс]. URL: https://ru.wikipedia.org/wiki/Квадратное_уравнение (Дата обращения 26.03.2019).
Приложение 1
Индийский математик Брахмагупта и среднеазиатский учёный, математик, астроном Абу́ Абдулла́х Муха́ммад ибн Муса́ аль-Хорезми́
Просмотров работы: 1009
Как быстро найти корни квадратного уравнения без дискриминанта
Способы решения квадратных уравнений
Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала каждый из них.
1. СПОСОБ: Разложение левой части уравнения на множители.
х 2 + 10х — 24 = 0.
Разложим левую часть на множители:
х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х — 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х 2 + 10х — 24 = 0.
Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х 2 + 10х — 24 = 0.
2. СПОСОБ: Метод выделения полного квадрата.
Решим уравнение х 2 + 6х — 7 = 0.
Выделим в левой части полный квадрат.
Для этого запишем выражение х 2 + 6х в следующем виде:
х 2 + 6х = х 2 + 2* х * 3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 3 2 , так как
х 2 + 2* х * 3 + 3 2 = (х + 3) 2 .
Преобразуем теперь левую часть уравнения
х 2 + 6х — 7 = 0,
прибавляя к ней и вычитая 3 2 . Имеем:
х 2 + 6х — 7 = х 2 + 2* х * 3 + 3 2 — 3 2 — 7 = (х + 3) 2 — 9 — 7 = (х + 3) 2 — 16.
Таким образом, данное уравнение можно записать так:
(х + 3) 2 — 16 =0, (х + 3) 2 = 16.
Следовательно, х + 3 — 4 = 0, х1= 1, или х + 3 = -4, х2 = -7.
3. СПОСОБ: Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах 2 + bх + с = 0, а ? 0
на 4а и последовательно имеем:
4а 2 х 2 + 4аbх + 4ас = 0,
((2ах) 2 + 2ах * b + b 2 ) — b 2 + 4ac = 0,
(2ax + b) 2 = b 2 — 4ac,
2ax + b = ± v b 2 — 4ac,
2ax = — b ± v b 2 — 4ac,
Примеры.
а) Решим уравнение: 4х 2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b 2 — 4ac = 7 2 — 4 * 4 * 3 = 49 — 48 = 1,
D > 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т. е. при
е. при
b 2 — 4ac >0 , уравнение ах 2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х 2 — 4х + 1 = 0,
а = 4, b = — 4, с = 1, D = b 2 — 4ac = (-4) 2 — 4 * 4 * 1= 16 — 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 — 4ac = 0, то уравнение
ах 2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х 2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b 2 — 4ac = 3 2 — 4 * 2 * 4 = 9 — 32 = — 13 , D < 0.
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b 2 — 4ac < 0,
уравнение ах 2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах 2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х 2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2= q,
x1 + x2= — p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
x 2 — 3x + 2 = 0; x1= 2 и x2= 1, так как q = 2 > 0 и p = — 3 < 0;
x 2 + 8x + 7 = 0; x1 = — 7 и x2= — 1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .
x 2 + 4x — 5 = 0; x1= — 5 и x2= 1, так как q= — 5 < 0 и p = 4 > 0;
x 2 — 8x — 9 = 0; x1 = 9 и x2= — 1, так как q = — 9 < 0 и p = — 8 < 0.
5. СПОСОБ: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах 2 + bх + с = 0, где а ? 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у 2 + by + ас = 0,
равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета.
х1= у1/а и х1= у2/а.
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.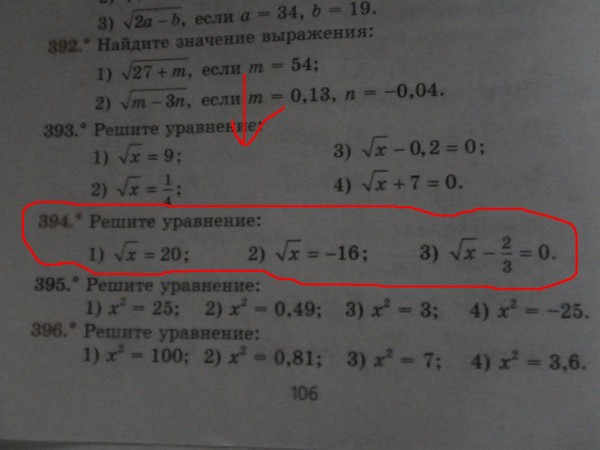
Решим уравнение 2х 2 — 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у 2 — 11у + 30 = 0.
Согласно теореме Виета
у1 = 5 х1= 5/2 x1= 2,5
у2= 6 x2= 6/2 x2= 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение
ах 2 + bх + с = 0, где а ? 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,
Доказательство. Разделим обе части уравнения на а ? 0, получим приведенное квадратное уравнение
x 2 + b/a * x + c/a = 0.
Согласно теореме Виета
x1+ x2= — b/a,
x1x2= 1* c/a.
По условию а — b + с = 0, откуда b = а + с. Таким образом,
x1+ x2= — а + b/a= -1 — c/a,
x1x2= — 1* ( — c/a),
т.е. х1= -1 и х2= c/a, что м требовалось доказать.
1) Решим уравнение 345х 2 — 137х — 208 = 0.
Решение. Так как а + b + с = 0 (345 — 137 — 208 = 0), то
х1= 1, х2= c/a = -208/345.
Ответ: 1; -208/345.
2)Решим уравнение 132х 2 — 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 — 247 + 115 = 0), то
х1= 1, х2= c/a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2k — четное число, то формулу корней
Пример.
Решим уравнение 3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;
D = k 2 — ac = (- 7) 2 — 3 * 16 = 49 — 48 = 1, D > 0, два различных корня;
В. Приведенное уравнение
х 2 + рх + q= 0
совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней
Формулу (3) особенно удобно использовать, когда р — четное число.
Пример. Решим уравнение х 2 — 14х — 15 = 0.
Решение. Имеем: х1,2=7±
Ответ: х1= 15; х2= -1.
7. СПОСОБ: Графическое решение квадратного уравнения.
Если в уравнении
х 2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
х 2 = — px — q.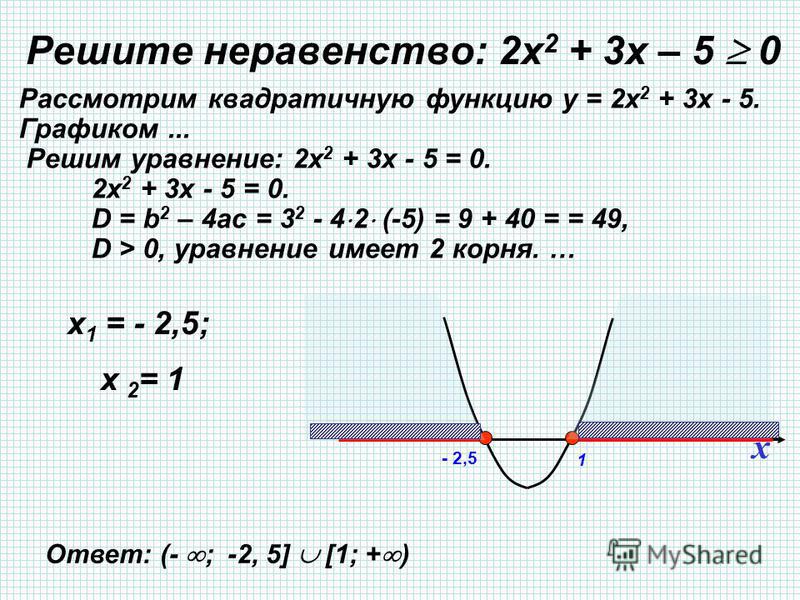
Построим графики зависимости у = х 2 и у = — px — q.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости —
прямая (рис.1). Возможны следующие случаи:
— прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квад- ратного уравнения;
— прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
1) Решим графически уравнение х 2 — 3х — 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х 2 = 3х + 4.
Построим параболу у = х 2 и прямую у = 3х + 4. Прямую
у = 3х + 4 можно построить по двум точкам М (0; 4) и
N (3; 13). Прямая и парабола пересекаются в двух точках
А и В с абсциссами х1= — 1 и х2 = 4. Ответ: х1= — 1;
Ответ: х1= — 1;
2) Решим графически уравнение (рис. 3) х 2 — 2х + 1 = 0.
Решение. Запишем уравнение в виде х 2 = 2х — 1.
Построим параболу у = х 2 и прямую у = 2х — 1.
Прямую у = 2х — 1 построим по двум точкам М (0; — 1)
и N(1/2; 0). Прямая и парабола пересекаются в точке А с
абсциссой х = 1. Ответ: х = 1.
3) Решим графически уравнение х 2 — 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х 2 = 5х — 5. Построим параболу у = х 2 и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х 2 — 2х + 5 = 0 корней не имеет.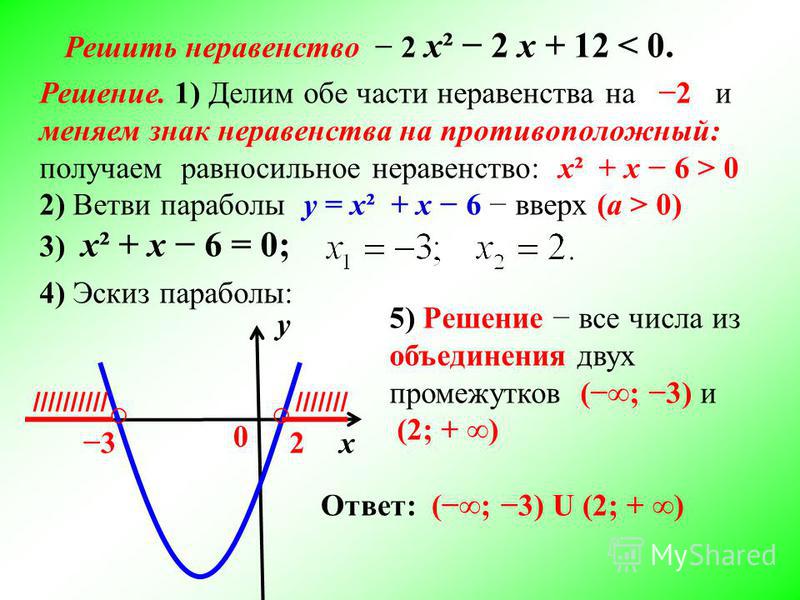
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки.
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + bх + с = 0 с помощью циркуля и линейки (рис. 5).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 — корни уравнения ах 2 + bх + с = 0, и проходит через точки
А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB * OD = OA * OC, откуда OC = OB * OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах 2 + bх + с = 0.
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
Решим уравнение х 2 — 2х — 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1).
Ответ: х1= — 1; х2= 3.
9. СПОСОБ: Решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен там определить корни уравнения.
Криволинейная шкала номограммы построена по формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение
z 2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни
z1= 8,0 и z2= 1,0 (рис. 12).
12).
2) Решим с помощью номограммы уравнение
2z 2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z 2 — 4,5z + 1 = 0.
Номограмма дает корни z1= 4 и z2= 0,5.
3) Для уравнения
z 2 — 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение
t 2 — 5t + 2,64 = 0,
которое решаем посредством номограммы и получим t1= 0,6 и t2= 4,4, откуда z1= 5t1= 3,0 и z2= 5t2= 22,0.
10. СПОСОБ: Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
1) Решим уравнение х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4* 2,5х = 10х ) и четырех пристроенных квадратов (6,25* 4 = 25), т.е. S = х 2 + 10х + 25. Заменяя
х 2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т. е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
2) А вот, например, как древние греки решали уравнение у 2 + 6у — 16 = 0.
Решение представлено на рис. 16, где
у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9.
Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у 2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1= 2, у2= — 8 (рис.16).
3) Решить геометрически уравнение у 2 — 6у — 16 = 0.
Преобразуя уравнение, получаем
у 2 — 6у = 16.
На рис. 17 находим «изображения» выражения у 2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у 2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у 2 — 6у равным ему числом 16,
Значит, если к выражению у 2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у 2 — 6у равным ему числом 16,
получаем: (у — 3) 2 = 16 + 9, т.е. у — 3 = ± v25, или у — 3 = ± 5, где у1= 8 и у2= — 2.
Квадратное уравнение
Квадратное уравнение — важное уравнение не только в школьном курсе алгебры. Квадратное уравнение часто используется в геометрии при расчете. Поэтому знать формулы корней квадратного уравнения, чтобы решать его быстрее, нужно всем.
Определение квадратного уравнения
Квадратное уравнение — это уравнение вида , где — переменная, , , — некоторые числа, причем . В квадратном уравнении коэффициент называют первым коэффициентом, — вторым коэффициентом, — свободным членом.
Формула корней
Формула корней квадратного уравнения имеет вид:
Выражение называется дискриминантом квадратного уравнения и обозначается буквой .
Влияние дискриминанта на корни квадратного уравнения
Максимальное количество корней квадратного уравнения равно степени уравнения. Квадратное уравнение имеет вторую степень переменной, поэтому и должно иметь два корня. Однако возможны случаи совпадения корней, тогда формально говорят, что «уравнение имеет один корень», хотя правильнее говорить — «уравнение имеет одно значение переменной», или «корни уравнения совпадают и равны…» Есть еще вариант, что уравнение не имеет действительных корней или не имеет действительных решений. Узнать о том — решается квадратное уравнение и сколько имеет корней можно вычислив дискриминант.
- Если , то существует только одно значение переменной, удовлетворяющее уравнению . Однако условились говорить, что в этом случае квадратное уравнение имеет два равных действительных корня, а само число называют корнем кратности два.
- Если , то квадратное уравнение не имеет действительных корней.
- Если , то квадратное уравнение имеет два различных действительных корня.

Приведенное квадратное уравнение
Пусть дано квадратное уравнение . Так как , то, разделив обе части уравнения на , получим уравнение . Считая, что и , получим уравнение , в котором первый коэффициент равен 1. Это уравнение называется приведенным.
Формула корней приведенного квадратного уравнения имеет вид:
Неполные квадратные уравнения
Уравнения вида , и называются квадратными уравнениями.
Биквадратное уравнение
Уравнение вида называется биквадратным уравнением. Оно решается с помощью замены переменной по формуле и приводится к квадратному уравнению .
Примеры решения квадратного уравнения
Уравнение 1
Решите уравнение
Решение:Найдем дискриминант , .
Найдем корни уравнения по формуле корней квадратного уравнения: .
, .
Ответ: , .
Уравнение 2
Решите уравнение .
Решение: находим дискриминант , . Применим формулу корней квадратного уравнения: . Тогда
Тогда
, .
Ответ: , .
Уравнение 3
Решите уравнение .
Решение: найдем дискриминант , . Так как дискриминант отрицателен, то уравнение не имеет корней.
Ответ: нет корней.
Уравнение 4
Решите уравнение
Решение: находим дискриминант , . Применим формулу корней квадратного уравнения
.
,
Таким образом, уравнение имеет единственный корень .
Ответ:
Уравнение 5
Решите квадратное уравнение
Решение: Применим формулу корней для приведенного квадратного уравнения: . Отсюда , .
Ответ: , .
Квадратные уравнениягде a, b и c – произвольные вещественные числа, отличные от нуля.
Неполными квадратными уравнениями называют квадратные уравнения следующих типов:
Решение неполных квадратных уравнений
Покажем, как решаются неполные квадратные уравнения на примерах.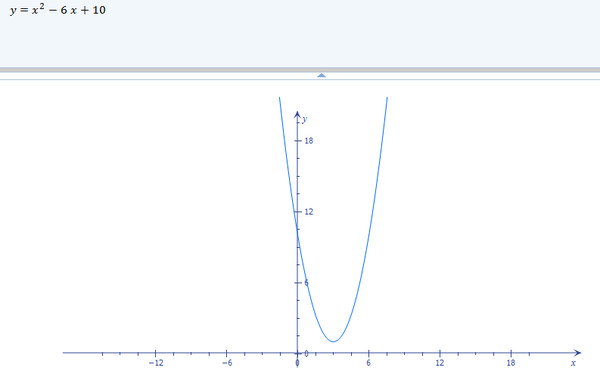
Пример 1 . Решить уравнение
Пример 2 . Решить уравнение
| 2x 2 + 3x= 0 . | (3) |
Решение . Вынося в левой части уравнения (3) переменную x за скобки, перепишем уравнение в виде
| x (2x+ 3) = 0 . | (4) |
Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:
Пример 3 . Решить уравнение
Пример 4 . Решить уравнение
| 3x 2 + 11 = 0 . | (5) |
Решение . Поскольку левая часть уравнения (5) положительна при всех значениях переменной x , а правая часть равна 0, то уравнение решений не имеет.
Выделение полного квадрата
Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:
Для того, чтобы получить формулу (6), совершим следующие преобразования:
Формула (6) получена.
Дискриминант
Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой D и вычисляется по формуле:
| D = b 2 – 4ac. | (7) |
Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.
Используя дискриминант, формулу (6) можно переписать в виде
Разложение квадратного трёхчлена на множители
Утверждение . В случае, когда , квадратный трёхчлен (1) разлагается на линейные множители. В случае, когда D < 0 , квадратный трехчлен нельзя разложить на линейные множители.
Доказательство . В случае, когда D = 0 , формула (8) и является разложением квадратного трехчлена на линейные множители:
В случае, когда D > 0 , выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:
Таким образом, в случае, когда D > 0 , разложение квадратного трехчлена (1) на линейные множители имеет вид
В случае, когда D < 0 , выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.
Замечание . В случае, когда D < 0 , квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.
Формула для корней квадратного уравнения
Из формул (9) и (10) вытекает формула для корней квадратного уравнения .
Действительно, в случае, когда D = 0 , из формулы (9) получаем:
Следовательно, в случае, когда D = 0 , уравнение (1) обладает единственным корнем, который вычисляется по формуле
В случае, когда D > 0 , из формулы (10) получаем:
Таким образом, в случае, когда D > 0 , уравнение (1) имеет два различных корня , которые вычисляются по формулам
| (12) |
| (13) |
Замечание 1 . Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
Замечание 2 . В случае, когда D = 0 , обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0 , квадратное уравнение (1) имеет два совпавших корня , вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
Поэтому часто говорят, что в случае, когда D = 0 , квадратное уравнение (1) имеет два совпавших корня , вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
Замечание 3 . В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.
В случае, когда D = 0 , разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):
| ax 2 + bx + c = = a (x – x1) 2 . | (16) |
В случае, когда D > 0 , разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:
| ax 2 + bx + c = = a (x – x1) (x – x2) . | (17) |
Замечание 4 .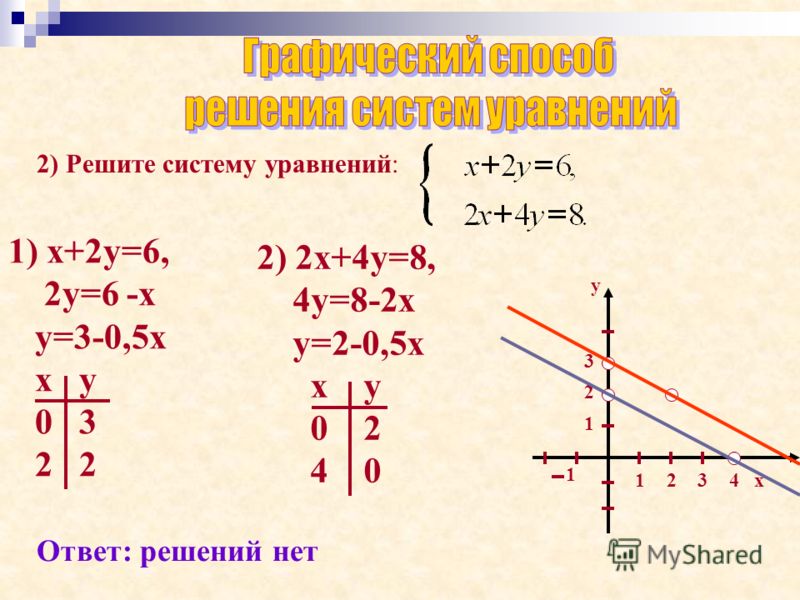 В случае, когда D = 0 , корни x1 и x2 совпадают, и формула (17) принимает вид (16).
В случае, когда D = 0 , корни x1 и x2 совпадают, и формула (17) принимает вид (16).
Прямая и обратная теоремы Виета
Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство
Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена
равны соответствующим коэффициентам многочлена
Таким образом, справедливы равенства
следствием которых являются формулы
Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета) .
Словами прямая теорема Виета формулируется так: — «Если числа x1 и x2 являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».
Обратная теорема Виета формулируется так: — «Если числа x1 и x2 являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».
Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».
Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.
Способы решения квадратных уравнений доклад, проект
Способы решения квадратных уравнений.
Определение квадратного уравнения, его виды
Квадратным уравнением называется уравнение вида
a + bx + c = 0,
где х- переменная, а,b и с-некоторые числа, причем, а ≠ 0.
Из истории квадратных уравнений
Квадратные уравнения в Древнем Вавилоне
Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта(VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ах2+вх=с, а0.
В этом уравнении коэффициенты, кроме а,могут быть и отрицатель-ными. Правило Брахмагупты по существу совпадает с нашим.
Квадратные уравнения в Европе XIII-XVII вв.
Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Книга способствовала распространению алгебраических знаний в Италии, в Германии, Франции и др. странах Европы.
Книга способствовала распространению алгебраических знаний в Италии, в Германии, Франции и др. странах Европы.
Квадратные уравнения в Европе XIII-XVII вв.
В глубокой древности была найдена формула для решения квадратного уравнения с помощью радикалов (корней). Вывод формулы имеется у Виета,но он признавал только положительные корни. Итальянские математики Тарталья, Кордано, Бомбелли в XVI в.учитывают и отрицательные корни. В XVII в. благодаря трудам Жирара, Декарта, Ньютона способ решения квадратных уравнений принимает современный вид.
Различные способы решения квадратных уравнений
1. Разложение левой части уравнения на множители
Решим уравнение х2 + 10х – 24 = 0.
Разложим левую часть уравнения на множители:
х2 + 10х – 24 = х2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х – 2) = 0.
Разложение левой части уравнения на множители
Так как произведение равно нулю, то по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = — 12. это означает, что числа 2 и – 12 являются корнями уравнения х2 + 10х – 24 = 0.
Метод выделения полного квадрата
Решим уравнение х + 6х – 7 = 0
Выделим в левой части полный квадрат.
Решение квадратных уравнений по формуле
Х1,2 =
4х + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b – 4ас = 72 – 4· 4 ·3 = 49 – 48 = 1
Х=
Х=
, х2 = –1
х1 =
4х – 4х + 1 = 0,
а =4, b = — 4, с = 1.
D = b – 4ас= 16 – 4∙4∙1 = 0,
D = 0, один корень;
Х=
2х +3х + 4 = 0
а =2, b= 3, с = 4
D = b – 4ас=9 – 4∙2∙4 =9 – 32 =
— 13
D
Решение уравнений с использованием теоремы Виета
(прямой и обратной)
Как известно, приведенное квадратное уравнение имеет вид
+ px + q = 0.
Его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
Теорема Виета для квадратного уравнения Aх +вх +с = 0
имеет вид
Примеры
Решить уравнение х – 9х + 14 =0
Попробуем найти два числа х и х ,
такие, что х +х = 9 ,х х = 14
Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.
По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.
Примеры
Решим уравнение 2х – 11х + 15 = 0.
«Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение у – 11y +30 = 0.
Согласно теореме Виета
Свойства коэффициентов квадратного уравнения.
Если а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю),
то х1 = 1, х2 = .
Если а — b + с = 0, или b = а + с, то
х1 = – 1, х2 = –
Решим уравнение 345х – 137х – 208 = 0.
Так как а + b + с = 0 (345 – 137 – 208 = 0)
, то х1 = 1, х2 = .
Решим уравнение
132х + 247х + 115 = 0
Т. к. а-b+с = 0 (132 – 247 +115=0), то
х1= — 1, х2= —
Если второй коэффициент b = 2k – четное число, то формулу корней можно записать в виде
Х =
Графическое решение квадратного уравнения
Решим графически уравнение
х – 3х – 4 = 0.
Решение. Запишем уравнение в виде
х = 3х + 4 . Построим параболу у = х и прямую у = 3х + 4.
Прямую у = 3х + 4 можно построить по двум точкам М (0;4) и N (3;13).
Прямая и парабола пересекаются в двух точках А и B с абсциссами х1 = – 1 и
х2 = 4.
квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни.
Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников.
3-8

Шаг за шагом Решение:
Шаг 1:
Пытаясь фактор равен 1.
Средний член равен -10x, его коэффициент равен -10.
Последний член, «константа», равен -24
Шаг 1: Умножьте коэффициент первого члена на константу 1 • -24 = -24
Шаг 2. Найдите два множителя -24 , сумма которых равна коэффициенту среднего члена, который равен -10 .
| -24 | + | 1 | = | -23 | ||
| -12 | + | 2 | = | -10 | That’s it |
Шаг 3. Перепишите полином, разделяющий средний член, используя два множителя, найденные на шаге 2 выше, -12 и 2.1813
Шаг 4 : Сложите первые 2 слагаемых, выделив одинаковые множители :
x • (x-12)
Сложите последние 2 слагаемых, выделив общие множители :
5 : Сложите четыре условия шага 4 :
(x+2) • (x-12)
Какая нужна факторизация
Уравнение в конце шага 1 :
x(x +) 12) = 0Шаг 2 :
Теория — корни произведения:
2.
1 Произведение нескольких слагаемых равно нулю.
Если произведение двух или более слагаемых равно нулю, то хотя бы одно из слагаемых должно быть равно нулю.
Теперь мы будем решать каждый термин = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов в произведении
Любое решение термина = 0 также решает произведение = 0.
Решение уравнения с одной переменной :
2.2 Решение : x+2 = 0
Вычитание 2 с обеих сторон уравнения:
x = -2Решение единого переменного уравнения:
2,3 Решай: X -12 = 0
Добавить 12 к обеим сторонам уравнения:
x = 12
12.Дополнение: прямое решение квадратного уравнения
прямое решение x 2 -10x-24 = 0Ранее мы разложили этот многочлен на множители, разделив средний член. давайте теперь решим уравнение, заполнив квадрат и используя квадратную формулу
Парабола, нахождение вершины :
3.
1 Найдите вершину y = x 2 -10x-24
Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили "у", потому что коэффициент первого члена, 1 , положителен (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Ax 2 +Bx+C, x-координата вершины определяется как -B/(2A) . В нашем случае координата x равна 5,0000
Подключение к формуле параболы 5.0000 Для x Мы можем рассчитать y -координату:
y = 1,0 * 5,00 * 5,00 -10,0 * 5,00 -24,0
или y = -49,000Parabola, график вершины и X -Intercess:
11111820, график вершины и X -Intercess:Корневой график для: y = x 2 -10x-24
Ось симметрии (штриховая) {x}={ 5,00}
Вершина в {x,y} = { 5,00,-49,00}
x -Перехваты (корни ) :
Корень 1 в точке {x, y} = {-2,00, 0,00}
Корень 2 в точке {x, y} = {12,00, 0,00}Решить квадратное уравнение, заполнив квадрат
3.2 Решение x 2 -10x-24 = 0, заполнив квадрат .
Прибавьте 24 к обеим частям уравнения:
x 2 -10x = 24Теперь немного хитрости: возьмем коэффициент при x, равный 10, разделим на два, получим 5, и, наконец, возведем его в квадрат, получим 25
Добавьте 25 к обеим частям уравнения:
В правой части у нас есть :
24 + 25 или, (24/1)+(25/1)
Общий знаменатель двух дробей равен 1 Сложение (24/1)+(25/1) дает 49/1
Таким образом, складывая обе части, мы окончательно получаем:
x 2 -10x+25 = 49Складывая 25 дополнил левую часть до полного квадрата:
x 2 -10x+25 =
(x-5) • (x-5) =
(x-5) 2
Вещи, равные одно и то же равно друг другу.Поскольку
x 2 -10x+25 = 49 и
x 2 -10x+25 = (x-5) 2
тогда, согласно закону транзитивности,
(x-5) 2 = 49#3.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x-5) 2 равен
(x-5) 2/2 =
(x-5) 1 =
Принцип квадратного корня в уравнении #3.2.1 получаем:
x-5 = √ 49Добавьте 5 к обеим частям, чтобы получить:
x = 5 + √ 49Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 - 10x - 24 = 0
имеет два раствора:
x = 5 + √ 49
или
x = 5 -√ 49Решение квадратичного уравнения с использованием квадратичной формулы
3.3 Решение x 2 -10x -24 = 0 по квадратичной формале.
Согласно квадратичной формуле, x , решение для Ax 2 +bx +c = 0, где A, B и C цифры, часто называемые коэффициентами, определяются как:
-B ± √ B 2 -4AC
x = ————————————————————————————————————————— ——
2AВ нашем случае A = 1
B = -10
C = -24Соответственно, B 2 -4AC =
100-(-96) =
196Применяя формулу квадрата:
10 ± √ 196
x = —————
2Можно упростить?
Да! Разложение числа 196 на простые множители равно
2•2•7•7
Чтобы иметь возможность удалить что-то из-под корня, должно быть 2 этих экземпляра (потому что мы берем квадрат, т.е. второй корень). 14
2/х-5)+(10х/х-5)-24=0
Автор: Цзышан Хан 3 года, 2 месяца назад
CBSE > Класс 10 > Математика
- 1 ответ
Найдите площадь четырехугольника ABCD с вершинами A(1,1), B(7,-3), C(12,2) и D(7,21).
Автор: Рима Гупта 2 дня, 12 часов назад
CBSE > Класс 10 > Математика
- 2 ответа
Если A.P. Sn =2n²+3n, найти A. 2-5+11=0 равен
2-5+11=0 равен
Автор: Образование Шри Мати 4 дня, 10 часов назад
CBSE > Класс 10 > Математика
- 2 ответа
грех желтовато-коричневый
Автор: Сия Шарма 2 дня, 15 часов назад
CBSE > Класс 10 > Математика
- 0 ответов
какова вероятность p(E)
Автор: Мокш Шах 3 дня, 11 часов назад
CBSE > Класс 10 > Математика
- 2 ответа
Желто-коричневый 7° tan23° tan60° tan67° tan83°= √3
Автор: Сакшам Сингх 3 дня, 12 часов назад
CBSE > Класс 10 > Математика
- 2 ответа
2 tan30° __________ 1-tan2 30°
Автор: Анант Дакка 21 час назад
CBSE > Класс 10 > Математика
- 0 ответов
Докажите, что касательная, проведенная из середины дуги окружности, параллельна хорде, соединяющей концы дуги.
Автор: Киртимаан Кумар 2 дня, 13 часов назад
CBSE > Класс 10 > Математика
- 0 ответов
myCBSEguide
Доверяют 1 крор+ студентов
Установить сейчас
- Создавайте документы за считанные минуты
- Печать с вашим именем и логотипом
- Скачать в формате PDF
- 5 лакхов+ Вопросы
- Включенные решения
- На основе учебного плана CBSE
- Подходит для школ и репетиторов
Создание документов
Тестовый генератор
Создание статей по цене 10 ₹/- за бумагу
Try Now
Ecuaciones de Segundo Grado: Ejercicios Resueltos
Repaso sobre la formula general
Para resolver ejercicios propuestos, se utilizara la formula general para ecuaciones de segundo grado :
La cual se utiliza para resolver toda ecuación de segundo grado del tipo
donde
Utilizar este método es muy sencillo, dado que solo debemos igualar las ecuaciones a cero y sustituir los valores de a,b,c и формула родов l.
Аль-резольвер una ecuación de segundo grado, pueden ocurrir 3 cosas:
- Existen 2 valores для переменной x que satisfacen la ecuación.
- Существует одно решение .
- La solucion no pertenece al conjunto de los números Reales .
Ejercicios de ecuaciones cuadraticas
1
1 Identificamos los valores de a, b y c
2 Sustituimos en la fórmula general y resolvemos
3 La ecuación tiene dos soluciones reales distintas
2
1 Identificamos los valores de a, y c
2 Sustituimos en la формула общая и разрешающая
3 La ecuación tiene dos soluciones reales distintas
3
1 Identificamos los valores de a, y c
2 Sustituimos en la формула общая и разрешающая
3 La ecuación tiene dos soluciones reales distintas
4
1 Identificamos los valores de a, y c
2 Sustituimos en la формула генеральная и разрешающая
3 La ecuación tiene solamente una solución real
5
1 Identificamos los valores de a, y c
2 Sustituimos en la формула общая и разрешающая
3 LaCuaci no Ecuaci no.
6
1 Identificamos los valores de a, b y c
2 Sustituimos en la fórmula general y resolvemos
3
7
1 Pasamos todos los términos a un sólo miembro de la ecuación para tenerla de la forma
2 Identificamos los valores de a , б у с
3 Sustituimos en la fórmula general y resolvemos
3 La ecuación tiene solamente una solución real.
8
11813
2 Pasamos todos los términos de un sólo lado y los agrupamos para escribir la ecuación en la forma
3 Identificamos los valores de a, b y c
4 Sustituimos en la формула General y Resolutionos
1812
5 La ecuación tiene dos soluciones reales.
9
1 En este caso, podemos dividir ambos miembros de la ecuación por 7 para simplificarla
2 Identificamos los valores de a, b y c
3 Sustituimos en la формула General y Resolutionos
.
10
1 Multiplicamos los dos miembros por −1 para obtener una ecuación equivalente con a > 0
2 La ecuación no tiene soluciones reales
11
1 Utilizamos la propiedad distributiva para operar el paréntesis y obtenemos:
2 Operamos y pasamos todo al primer miembro
3 Identificamos los valores de a, y c
4 Sustituimos en la fórmula general y resolvemos
5 La ecuación tiene dos soluciones reales.
12
1 Identificamos Los Valores de A -C y C.
1 IdentificAmos Los Valores de A -C
1 IdentificAmos Los Valores de, By C
1 Los Valores de, by y c c c c
1 Identificamos de, by y c c c y c c c c
1 идентификация.1812
2 Sustituimos en la fórmula general y resolvemos
3 La ecuación tiene dos soluciones reales distintas
13
1 Resolvemos el binomio al cuadrado
2 Pasamos todos los términos de un sólo lado y los agrupamos para escribir la ecuación en la forma
3 Dividimos ambos miembros de la ecuación por 2 para simplificarla
4 Identificamos los valores de a, y c
51812
6 La ecuación tiene dos soluciones reales.
14
1 Identificamos los valores de a, b y c
2 Sustituimos en la fórmula general y resolvemos
3 La ecuación tiene dos soluciones reales distintas
15
1 Identificamos los valores de a, y c
2 Sustituimos en la формула генеральная и разрешающая
3 La ecuación tiene dos soluciones reales distintas
16
1 Multiplicamos el primer miembro de la ecuación por 6, y el el ultimo por 2 para eliminar el denominador (6), y así obtenemos:
2 Identificamos los valores de a, b y c
3 Sustituimos en la fórmula general y resolvemos
4 La ecuación tiene dos soluciones reales.
Recuerda que, en Superprof, también te podemos ayudar encontrar clases de matematicas con un profesor que se pueda adapter atus necesidades.
Окситоциновая и орексиновая системы двунаправленно регулируют способность опиоидных сигналов сказываться на стремлении к вознаграждению
Abstract
Поскольку количество смертельных случаев, связанных с опиоидами, продолжает расти, потребность в новых методах лечения расстройств, связанных с употреблением опиоидов (OUD), не может быть более актуальной. Две отдельные гипоталамические нейропептидные системы продемонстрировали многообещающие результаты в доклинических моделях OUD. Система окситоцина, образующаяся в паравентрикулярном ядре (PVN), может защищать от тяжести OUD. Напротив, орексиновая система, возникающая в латеральном гипоталамусе (ЛГ), может усугублять тяжесть OUD. Таким образом, активация системы окситоцина или ингибирование системы орексина являются потенциальными терапевтическими стратегиями. Однако конкретная роль этих систем в отношении конкретных результатов OUD до конца не изучена. Здесь мы исследовали терапевтическую эффективность фармакологических вмешательств, нацеленных на систему орексина или окситоцина, по двум различным показателям тяжести OUD у крыс — выбор героина (по сравнению с выбором естественного вознаграждения, то есть еды) и поиск вознаграждения по сигналу. Используя доклиническую модель, которая дает примерно равный выбор между героином и пищевым вознаграждением, мы исследовали влияние экзогенно вводимого окситоцина, антагониста рецептора окситоцина (L-368,89).9) и двойной антагонист орексиновых рецепторов (DORA-12) при выборе опиоидов. В то время как эти агенты не влияли на выбор героина, когда были доступны вознаграждения (героин и еда), окситоцин и DORA-12 значительно снижали стремление к героину при наличии конкурирующих сигналов вознаграждения, когда вознаграждения не было. Кроме того, количество орексиновых нейронов ЛГ и окситоциновых нейронов PVN коррелировало с конкретными поведенческими экономическими переменными, свидетельствующими о мотивации употребления героина по сравнению с пищевой.
Однако конкретная роль этих систем в отношении конкретных результатов OUD до конца не изучена. Здесь мы исследовали терапевтическую эффективность фармакологических вмешательств, нацеленных на систему орексина или окситоцина, по двум различным показателям тяжести OUD у крыс — выбор героина (по сравнению с выбором естественного вознаграждения, то есть еды) и поиск вознаграждения по сигналу. Используя доклиническую модель, которая дает примерно равный выбор между героином и пищевым вознаграждением, мы исследовали влияние экзогенно вводимого окситоцина, антагониста рецептора окситоцина (L-368,89).9) и двойной антагонист орексиновых рецепторов (DORA-12) при выборе опиоидов. В то время как эти агенты не влияли на выбор героина, когда были доступны вознаграждения (героин и еда), окситоцин и DORA-12 значительно снижали стремление к героину при наличии конкурирующих сигналов вознаграждения, когда вознаграждения не было. Кроме того, количество орексиновых нейронов ЛГ и окситоциновых нейронов PVN коррелировало с конкретными поведенческими экономическими переменными, свидетельствующими о мотивации употребления героина по сравнению с пищевой. Эти данные указывают на новую двунаправленную роль систем окситоцина и орексина в способности сигналов, связанных с опиоидами, влиять на поиск вознаграждения.
Эти данные указывают на новую двунаправленную роль систем окситоцина и орексина в способности сигналов, связанных с опиоидами, влиять на поиск вознаграждения.
Введение
Выбор наркотика и способность сигналов к употреблению наркотиков мотивировать поиск наркотиков являются концептуально несовместимыми процессами, которые способствуют распространенному употреблению и поиску опиоидов, которые характеризуют расстройство, связанное с употреблением опиоидов (OUD). За последние несколько десятилетий доклинические модели рецидива были в центре внимания усилий по совершенствованию методов лечения OUD. Напротив, доклинические модели выбора опиоидов только недавно стали привлекать значительное внимание. Подавляющее большинство этих доклинических моделей выбора выявило, что грызуны в первую очередь будут выбирать естественное вознаграждение (например, пищу, социальное вознаграждение) вместо лекарственного вознаграждения в условиях взаимоисключающего выбора, эквивалентной цены (например, требования «нажать рычаг» для вознаграждения) и равных условий. задержка [1]. Таким образом, некоторые предполагают, что эти модели охватывают компоненты ситуационной терапии, поскольку они обычно приводят к добровольному воздержанию и снижению частоты рецидивов для опиоидов [2,3,4]. К сожалению, ситуационное управление имеет относительно низкий уровень успеха для долгосрочного лечения OUD, и не все люди с OUD реагируют на него [5]. Таким образом, модели, которые идентифицируют субпопуляции людей, выбирающих опиоиды, жизненно важны для скрининга новых потенциальных фармакотерапевтических средств для OUD. Недавно мы разработали доклиническую модель выбора, которая идентифицирует субпопуляцию крыс, которые предпочитают героин еде, и приводит к увеличению поиска вознаграждения за героиновые сигналы, а не за пищевые сигналы [6]. Таким образом, мы располагаем уникальными возможностями для проверки новых потенциальных методов лечения OUD, которые нацелены на поведение выбора, чтобы уменьшить потребление и поиск опиоидов.
задержка [1]. Таким образом, некоторые предполагают, что эти модели охватывают компоненты ситуационной терапии, поскольку они обычно приводят к добровольному воздержанию и снижению частоты рецидивов для опиоидов [2,3,4]. К сожалению, ситуационное управление имеет относительно низкий уровень успеха для долгосрочного лечения OUD, и не все люди с OUD реагируют на него [5]. Таким образом, модели, которые идентифицируют субпопуляции людей, выбирающих опиоиды, жизненно важны для скрининга новых потенциальных фармакотерапевтических средств для OUD. Недавно мы разработали доклиническую модель выбора, которая идентифицирует субпопуляцию крыс, которые предпочитают героин еде, и приводит к увеличению поиска вознаграждения за героиновые сигналы, а не за пищевые сигналы [6]. Таким образом, мы располагаем уникальными возможностями для проверки новых потенциальных методов лечения OUD, которые нацелены на поведение выбора, чтобы уменьшить потребление и поиск опиоидов.
Окситоцин представляет собой нейропептид, продуцируемый подмножеством нейронов, расположенных в паравентрикулярном ядре гипоталамуса (ПВЯ). Помимо своей известной роли в родах и материнском поведении [7], окситоцин играет важную роль в процессах социального вознаграждения [8,9,10], тревоге [11, 12], а также в реакции на стресс [13, 14]. Более того, появляется все больше данных, указывающих на то, что окситоцин обладает антиаддиктивными свойствами, что указывает на то, что этот нейропептид может использоваться для лечения многих злоупотребляемых веществ [15, 16]. У крыс системное введение окситоцина снижает мотивацию к самостоятельному приему метамфетамина [17], кокаина [18] и алкоголя [19]., 20], а окситоцин снижает индуцированный сигналом поиск метамфетамина [17, 21] и кокаина [18], а также индуцированный стрессом поиск алкоголя [22, 23]. У людей интраназальное лечение окситоцином уменьшает симптомы отмены алкоголя [24], тягу [25] и метаболическую активность мозга, вызванную сигналами, связанными с алкоголем [26], а также снижает баллы тяги у пациентов с героином [27] и кокаином [28]. использовать расстройства. В совокупности эти данные подчеркивают потенциальную эффективность терапии на основе окситоцина для снижения рецидивов злоупотребления наркотиками [29].
Помимо своей известной роли в родах и материнском поведении [7], окситоцин играет важную роль в процессах социального вознаграждения [8,9,10], тревоге [11, 12], а также в реакции на стресс [13, 14]. Более того, появляется все больше данных, указывающих на то, что окситоцин обладает антиаддиктивными свойствами, что указывает на то, что этот нейропептид может использоваться для лечения многих злоупотребляемых веществ [15, 16]. У крыс системное введение окситоцина снижает мотивацию к самостоятельному приему метамфетамина [17], кокаина [18] и алкоголя [19]., 20], а окситоцин снижает индуцированный сигналом поиск метамфетамина [17, 21] и кокаина [18], а также индуцированный стрессом поиск алкоголя [22, 23]. У людей интраназальное лечение окситоцином уменьшает симптомы отмены алкоголя [24], тягу [25] и метаболическую активность мозга, вызванную сигналами, связанными с алкоголем [26], а также снижает баллы тяги у пациентов с героином [27] и кокаином [28]. использовать расстройства. В совокупности эти данные подчеркивают потенциальную эффективность терапии на основе окситоцина для снижения рецидивов злоупотребления наркотиками [29]. ].
].
Орексины А и В представляют собой нейропептиды, вырабатываемые в латеральном гипоталамусе (ЛГ), которые регулируют мотивированный поиск наркотиков. Нейроны, экспрессирующие орексин, активируются стимулами, связанными с морфином, кокаином и алкоголем [30, 31, 32, 33, 34, 35], и величина их активности напрямую связана с поведением, связанным с поиском наркотиков [36, 37]. Подавляющее большинство исследований было сосредоточено на рецепторе орексина 1 (Ox1R) как на основном месте передачи сигналов орексина при воздействии наркотиков [38]. Например, системное лечение антагонистом рецептора Ox1R SB-334867 снижает мотивированную реакцию и поиск вознаграждения, вызванного сигналом, для всех протестированных наркотиков, вызывающих зависимость, включая опиоиды оксикодон, героин, фентанил и ремифентанил [30, 39].,40,41]. Хотя роль передачи сигналов орексинового рецептора 2 (Ox2R) в вознаграждении за наркотики изучена менее широко, системное или центральное введение антагонистов Ox2R снижает самостоятельный прием героина и алкоголя в дозах, которые не влияют на самостоятельный прием пищи [42, 43]. Эти данные повышают вероятность того, что соединения, которые блокируют передачу сигналов как в Ox1R, так и в Ox2R (двойные антагонисты рецепторов орексина; DORA), могут иметь более выраженные терапевтические свойства по сравнению с антагонистами одиночных рецепторов орексина [44,45,46]. Действительно, первоначальные доклинические исследования показывают, что DORA снижают потребление и поиск наркотиков среди нескольких классов наркотиков, вызывающих зависимость [47,48,49]., 50], а предварительное клиническое исследование показало, что суворексант DORA (продаваемый Merck как Belsomra TM ) снижает несколько индексов тяги, связанных с рецидивом и самооценкой, у пациентов с расстройством, связанным с употреблением кокаина или опиоидов [51, 52]. Основываясь на успехе этих исследований, Национальный институт по борьбе со злоупотреблением наркотиками (NIDA) объявил орексиновую систему первоочередной целью разработки новых лекарств для борьбы с опиоидной эпидемией [53], хотя необходимы дополнительные исследования для изучения эффективности DORA.
Эти данные повышают вероятность того, что соединения, которые блокируют передачу сигналов как в Ox1R, так и в Ox2R (двойные антагонисты рецепторов орексина; DORA), могут иметь более выраженные терапевтические свойства по сравнению с антагонистами одиночных рецепторов орексина [44,45,46]. Действительно, первоначальные доклинические исследования показывают, что DORA снижают потребление и поиск наркотиков среди нескольких классов наркотиков, вызывающих зависимость [47,48,49]., 50], а предварительное клиническое исследование показало, что суворексант DORA (продаваемый Merck как Belsomra TM ) снижает несколько индексов тяги, связанных с рецидивом и самооценкой, у пациентов с расстройством, связанным с употреблением кокаина или опиоидов [51, 52]. Основываясь на успехе этих исследований, Национальный институт по борьбе со злоупотреблением наркотиками (NIDA) объявил орексиновую систему первоочередной целью разработки новых лекарств для борьбы с опиоидной эпидемией [53], хотя необходимы дополнительные исследования для изучения эффективности DORA. в доклинических моделях OUD.
в доклинических моделях OUD.
Несмотря на растущую популярность моделей выбора в доклинических исследованиях зависимостей, до настоящего времени ни одно исследование не исследовало вклад гипоталамических нейропептидных систем в условиях выбора. Чтобы заполнить этот пробел в знаниях, мы проверили, может ли фармакологическое лечение окситоцином или DORA изменить поведение выбора в условиях, когда вознаграждение доступно или недоступно (т. Е. Когда поиск управляется сигналами, связанными с вознаграждением). Мы также применили принципы из области поведенческой экономики [54], чтобы исследовать мотивацию употребления героина по сравнению с естественным вознаграждением (еда) и оценить взаимосвязь между переменными поведенческой экономики и количеством гипоталамических окситоциновых и орексиновых нейронов. Мы обнаружили, что фармакологическая модуляция систем орексина и окситоцина не влияла на выбор героина, когда было доступно вознаграждение, но что манипуляции с этими системами специфически снижали потребность в героине в условиях, когда присутствовали и героиновые, и пищевые сигналы, но не вознаграждение. Более того, количество нейронов, экспрессирующих окситоцин и орексин, коррелировало с конкретными переменными экономического спроса на каждое вознаграждение. Эти данные подтверждают центральную роль гипоталамической системы в специфических показателях результатов, связанных с OUD, и дополняют растущий объем литературы, предполагающей, что терапевтические стратегии, модулирующие передачу сигналов окситоцина и/или орексина, являются многообещающими путями для снижения рецидивов опиоидов.
Более того, количество нейронов, экспрессирующих окситоцин и орексин, коррелировало с конкретными переменными экономического спроса на каждое вознаграждение. Эти данные подтверждают центральную роль гипоталамической системы в специфических показателях результатов, связанных с OUD, и дополняют растущий объем литературы, предполагающей, что терапевтические стратегии, модулирующие передачу сигналов окситоцина и/или орексина, являются многообещающими путями для снижения рецидивов опиоидов.
Материалы и методы
Животные
Все процедуры с животными проводились в соответствии с рекомендациями, утвержденными Комитетом по уходу и использованию животных Медицинского кампуса Университета Колорадо Anschutz. Субъектами были соответствующие по возрасту (P55–60) самцы ( n = 32) и самки ( n = 32) крыс Wistar (Charles River, Raleigh, NC). Животных содержали по отдельности в помещении с контролируемой температурой и влажностью (свет с 8:00 до 20:00) со свободным доступом к стандартному лабораторному корму (Envigo 2020X) и воде. Процедуры соответствовали рекомендациям, изложенным в Руководстве по уходу и использованию лабораторных животных [55].
Процедуры соответствовали рекомендациям, изложенным в Руководстве по уходу и использованию лабораторных животных [55].
Экспериментальные агенты
Синтетический человеческий окситоцин (Cell Sciences, CRO300GB) растворяли в стерильной воде и вводили в дозах 1 или 3 мг/кг (1 мл/кг, внутрибрюшинно) за 30 мин до тестирования. Этот интервал перед лечением и диапазон доз были основаны на предыдущей литературе, показывающей эффективное снижение поиска наркотиков с минимальными побочными эффектами [17, 56, 57]. Антагонист рецептора окситоцина L-368,899 гидрохлорид (Tocris, 2641) растворяли в стерильной воде и вводили в дозе 5 мг/кг (1 мл/кг, внутрибрюшинно) за 30 мин до тестирования, что, как было показано, эффективно блокирует эффекты окситоцина у крыс [58]. Двойной антагонист орексиновых рецепторов DORA-12 (Merck) растворяли в 5% ДМСО + 40% каптизола в стерильной воде и вводили в дозах 10 мг/кг (1 мл/кг, внутрибрюшинно) или 30 мг/кг (3 мл/сут). кг, внутрибрюшинно) на основе эффективных доз других DORA, описанных в литературе [47,48,49,50]. Героин (диаморфина гидрохлорид) растворяли в 0,9% физиологическом растворе (вливание 0,04 мг/50 мкл на награду). Беспыльные пищевые гранулы на зерновой основе (45 мг каждая, Bio-Serv, F0165) поставлялись по 3 гранулы на награду.
Героин (диаморфина гидрохлорид) растворяли в 0,9% физиологическом растворе (вливание 0,04 мг/50 мкл на награду). Беспыльные пищевые гранулы на зерновой основе (45 мг каждая, Bio-Serv, F0165) поставлялись по 3 гранулы на награду.
Самостоятельный прием пищи и героина
Крысам хирургическим путем имплантировали внутривенный яремный катетер, как описано ранее [6]. После выздоровления крыс обучали самостоятельному приему пищи и героина в тандеме в течение ежедневных (в будние дни) сеансов в стандартных крысиных оперативных камерах (Med Associates, St. Albans, VT, USA). В течение первых 30 минут каждого сеанса были доступны рычаг для еды (правый) и сигнал (тон 3,5 кГц, 5 с), после чего следовал 10-минутный тайм-аут с убранными рычагами. После этого рычаг героина (левый) и сигнал (свет над рычагом, 5 секунд) были доступны в течение 2 часов. Обучение началось по графику подкрепления с фиксированным соотношением 1 (FR1). Сигналы для каждой награды были инициированы одновременно с началом доставки вознаграждения, и рычаги убирались во время представления сигнала. После 8 занятий тренировка прошла через 8 дополнительных шагов FR (FR3, FR8, FR20, FR50, FR125, FR313, FR783, FR19).58) не менее чем по 1 дню на каждом ФР. Для предотвращения инфекции и окклюзии катетера, соответственно, цефазолин и раствор тауролидина цитрата (TCS) вводили после каждого сеанса самостоятельного введения. Проходимость катетера периодически проверяли с помощью метогекситала натрия (1 мг/0,1 мл, внутривенно). Пять крыс были исключены из окончательного набора данных из-за дефектных катетеров.
После 8 занятий тренировка прошла через 8 дополнительных шагов FR (FR3, FR8, FR20, FR50, FR125, FR313, FR783, FR19).58) не менее чем по 1 дню на каждом ФР. Для предотвращения инфекции и окклюзии катетера, соответственно, цефазолин и раствор тауролидина цитрата (TCS) вводили после каждого сеанса самостоятельного введения. Проходимость катетера периодически проверяли с помощью метогекситала натрия (1 мг/0,1 мл, внутривенно). Пять крыс были исключены из окончательного набора данных из-за дефектных катетеров.
Поведенческая экономика и кривые спроса
Мы использовали парадигму поведенческой экономики между сессиями, в которой цена (т.]. Кривые спроса на корм и героин были построены для каждого животного с использованием реагирующих на каждую точку цен FR по формуле [54]:
$$\ln Q = {{{\mathrm{ln}}}}Q_0 + k (e - \propto Q_0C - 1)$$
, где C указывает потребление (т. е. количество наград в виде еды или героина, заработанных на каждом шаге FR), а константа k (установленная на 8,85) указывает диапазон значений потребления [60 ]. Эластичная кривая спроса, при которой потребление быстро падает с ростом цены, предполагает, что животное считает вознаграждение «предметом роскоши». В то время как кривая неэластичного спроса, при которой повышение цены хорошо переносится для защиты желаемого потребления, предполагает, что животное считает вознаграждение «предметом первой необходимости». На рис. 1а показан пример кривой эластичного и неэластичного спроса, иллюстрирующий эти концепции. Из полученных кривых спроса мы извлекли следующие переменные: 9{ - 1}$$
Эластичная кривая спроса, при которой потребление быстро падает с ростом цены, предполагает, что животное считает вознаграждение «предметом роскоши». В то время как кривая неэластичного спроса, при которой повышение цены хорошо переносится для защиты желаемого потребления, предполагает, что животное считает вознаграждение «предметом первой необходимости». На рис. 1а показан пример кривой эластичного и неэластичного спроса, иллюстрирующий эти концепции. Из полученных кривых спроса мы извлекли следующие переменные: 9{ - 1}$$
a Пример «эластичных» и «неэластичных» кривых спроса и определение поведенческих экономических параметров, проанализированных в настоящем исследовании (серая рамка). b Хронология экспериментов по самостоятельному приему героина и продуктов питания, поведенческой экономике, тестированию выбора и сигнализированному рецидиву. Животных обучали самостоятельно принимать пищу (30 минут) и героин (2 часа) в тандеме в течение 8 сеансов (FR1), после чего следовали 8 дополнительных шагов с фиксированным соотношением, используемых для извлечения переменных поведенческой экономики.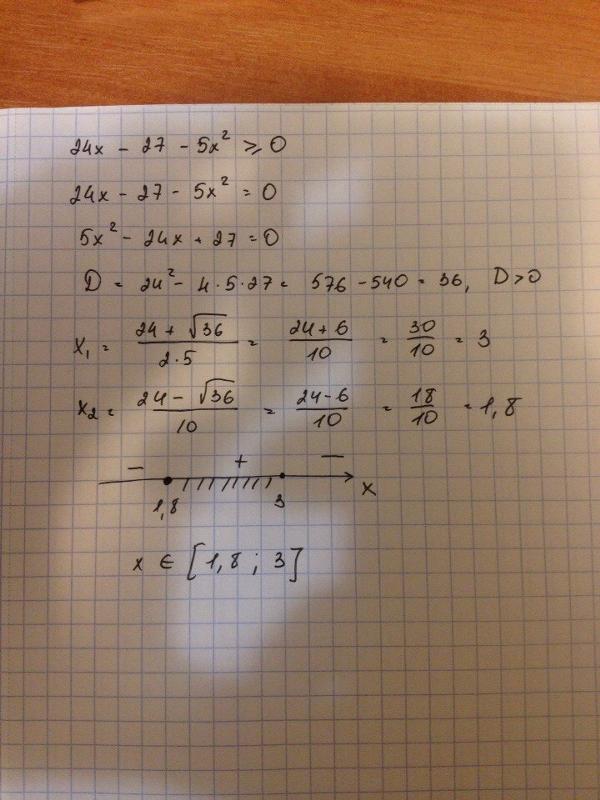 Через 3 дня самостоятельного введения по схеме FR3 животные были разделены на две разные группы лечения (DORA-12 и окситоцин) и вступили в фазу выбора. В конце тестирования выбора животные получали пищу и героин самостоятельно в течение 3 дней в соответствии с графиком FR3, прежде чем их тестировали в тесте поиска вознаграждения.
Через 3 дня самостоятельного введения по схеме FR3 животные были разделены на две разные группы лечения (DORA-12 и окситоцин) и вступили в фазу выбора. В конце тестирования выбора животные получали пищу и героин самостоятельно в течение 3 дней в соответствии с графиком FR3, прежде чем их тестировали в тесте поиска вознаграждения.
Изображение в полный размер
Поскольку EV не зависит от величины подкрепления, его полезно использовать для непосредственного сравнения различных подкреплений [59, 62]. Поэтому мы сообщаем здесь как α, так и EV, так как мы хотим напрямую сравнить вознаграждение за героин и еду. Рисунок 1а определяет каждый из этих показателей мотивационного состояния поведенческой экономики и иллюстрирует их связь с кривой спроса.
Выбор между едой и героином
Процедуры выбора были реализованы после обучения самостоятельному приему. Во время сеансов выбора крысам давали 14 попыток выбрать пищу или героин (FR3). Как только требование FR на одном рычаге было достигнуто, соответствующее вознаграждение и сигнал были доставлены, затем рычаги убирались на 10-минутный перерыв между испытаниями. Первые две сессии выбора начинались с двух попыток принудительного выбора для каждого подкрепления (всего 4 попытки, выполненных всеми крысами), во время которых в чередующемся порядке продлевались только рычаг еды или героина, за которыми следовали 10 попыток свободного выбора с обоими вариантами рычага. . После этого испытания с принудительным выбором были исключены и проводились только сеансы со свободным выбором (оба варианта рычага для всех 14 испытаний). После не менее 6 стабильных сеансов выбора (≤20% вариабельности общего выбора за последние 2 сеанса) крысы начали повторное тестирование выбора, при этом каждый тест был разделен двумя сеансами выбора. Выбор героина был выражен как процент выбора героина по сравнению с общим количеством испытаний выбора. Важно отметить, что не было упущений; все крысы завершили все 14 испытаний в каждом тесте. Сеансы выбора (включая тесты на выбор) были единственными поведенческими сеансами, в которых одновременно были доступны и еда, и героин, а рычаги как еды, так и героина расширялись одновременно.
Первые две сессии выбора начинались с двух попыток принудительного выбора для каждого подкрепления (всего 4 попытки, выполненных всеми крысами), во время которых в чередующемся порядке продлевались только рычаг еды или героина, за которыми следовали 10 попыток свободного выбора с обоими вариантами рычага. . После этого испытания с принудительным выбором были исключены и проводились только сеансы со свободным выбором (оба варианта рычага для всех 14 испытаний). После не менее 6 стабильных сеансов выбора (≤20% вариабельности общего выбора за последние 2 сеанса) крысы начали повторное тестирование выбора, при этом каждый тест был разделен двумя сеансами выбора. Выбор героина был выражен как процент выбора героина по сравнению с общим количеством испытаний выбора. Важно отметить, что не было упущений; все крысы завершили все 14 испытаний в каждом тесте. Сеансы выбора (включая тесты на выбор) были единственными поведенческими сеансами, в которых одновременно были доступны и еда, и героин, а рычаги как еды, так и героина расширялись одновременно. Крыс распределяли для исследования окситоцина или орексина сбалансированным образом в зависимости от процента выбора героина и пола. На рисунке 1b показана экспериментальная временная шкала и разделение групп лечения. Препараты окситоцина и орексина вводили за 30 мин до помещения в поведенческую камеру для тестирования. Окситоциновые крысы получали носитель (воду) или окситоцин (1 или 3 мг/кг, внутрибрюшинно). Поскольку влияния окситоцина на выбор опиоидов не наблюдалось (см. Результаты), крыс дополнительно тестировали с носителем (водой) или антагонистом окситоцина L-368,899 (5 мг/кг, внутрибрюшинно), чтобы оценить участие эндогенной системы окситоцина в выборе героина. Таким образом, препараты вводили в следующем порядке: 1 мг/кг окситоцина, носитель, 3 мг/кг окситоцина, носитель, 5 мг/кг L-368,899. Орексиновые крысы получали носитель или DORA-12 (10 или 30 мг/кг, внутрибрюшинно). Были проведены два теста с носителем для учета различных объемов, необходимых для доставки низкой (1 мл/кг) дозы соединения DORA по сравнению с высокой (3 мл/кг) из-за пределов растворимости.
Крыс распределяли для исследования окситоцина или орексина сбалансированным образом в зависимости от процента выбора героина и пола. На рисунке 1b показана экспериментальная временная шкала и разделение групп лечения. Препараты окситоцина и орексина вводили за 30 мин до помещения в поведенческую камеру для тестирования. Окситоциновые крысы получали носитель (воду) или окситоцин (1 или 3 мг/кг, внутрибрюшинно). Поскольку влияния окситоцина на выбор опиоидов не наблюдалось (см. Результаты), крыс дополнительно тестировали с носителем (водой) или антагонистом окситоцина L-368,899 (5 мг/кг, внутрибрюшинно), чтобы оценить участие эндогенной системы окситоцина в выборе героина. Таким образом, препараты вводили в следующем порядке: 1 мг/кг окситоцина, носитель, 3 мг/кг окситоцина, носитель, 5 мг/кг L-368,899. Орексиновые крысы получали носитель или DORA-12 (10 или 30 мг/кг, внутрибрюшинно). Были проведены два теста с носителем для учета различных объемов, необходимых для доставки низкой (1 мл/кг) дозы соединения DORA по сравнению с высокой (3 мл/кг) из-за пределов растворимости. Лекарства вводили в следующем порядке: 1 мл/кг носителя или 10 мг/кг DORA, затем 3 мл/кг носителя или 30 мг/кг DORA. Поскольку статистических различий между испытаниями транспортных средств с малым и большим объемом не наблюдалось, данные испытаний транспортных средств были усреднены перед статистическим анализом.
Лекарства вводили в следующем порядке: 1 мл/кг носителя или 10 мг/кг DORA, затем 3 мл/кг носителя или 30 мг/кг DORA. Поскольку статистических различий между испытаниями транспортных средств с малым и большим объемом не наблюдалось, данные испытаний транспортных средств были усреднены перед статистическим анализом.
Тест поиска вознаграждения по сигналу
После завершения тестирования выбора крыс возвращали к процедурам самостоятельного введения FR3, идентичным тем, которые применялись во время обучения. В течение первых 30 минут каждого сеанса рычаг для еды был доступен, затем рычаги были убраны в течение 10 минут, а затем рычаг для героина был доступен в течение 2 часов. По крайней мере, после трех сеансов повторного приобретения крысы прошли тест на поиск вознаграждения с одним сигналом. Во время теста и пища, и героин были одновременно доступны в течение 1 часа. Нажатие на каждый рычаг приводило к подаче сигнала (пища или героин) по графику FR3 (с отведением рычага во время доставки сигнала, как и во время предыдущих сеансов самостоятельного введения), но без вознаграждения. Обратите внимание, что повторное тестирование в этих условиях невозможно, так как реакция быстро исчезает; следовательно, для тестирования была выбрана разовая доза каждого агента. Каждая крыса получала либо носитель (вода, либо 5% ДМСО+40% каптизола в воде), 1 мг/кг окситоцина или 30 мг/кг DORA-12 за 30 мин до теста с сигналом. В других исследованиях доза окситоцина 1 мг/кг обычно использовалась для уменьшения стремления к вознаграждению [17, 18]. Доза 30 мг/кг DORA-12 была выбрана потому, что в литературе нет прецедентов эффективности этого соединения при поиске наркотиков, но исследования с использованием других антагонистов рецепторов орексина со структурным сходством с DORA-12 (например, суворексант) показывают что доза 30 мг/кг может быть более эффективной, чем 10 мг/кг, для снижения потребности в наркотиках [48, 63].
Обратите внимание, что повторное тестирование в этих условиях невозможно, так как реакция быстро исчезает; следовательно, для тестирования была выбрана разовая доза каждого агента. Каждая крыса получала либо носитель (вода, либо 5% ДМСО+40% каптизола в воде), 1 мг/кг окситоцина или 30 мг/кг DORA-12 за 30 мин до теста с сигналом. В других исследованиях доза окситоцина 1 мг/кг обычно использовалась для уменьшения стремления к вознаграждению [17, 18]. Доза 30 мг/кг DORA-12 была выбрана потому, что в литературе нет прецедентов эффективности этого соединения при поиске наркотиков, но исследования с использованием других антагонистов рецепторов орексина со структурным сходством с DORA-12 (например, суворексант) показывают что доза 30 мг/кг может быть более эффективной, чем 10 мг/кг, для снижения потребности в наркотиках [48, 63].
Иммуногистохимия и подсчет клеток
Количество орексиновых нейронов и окситоциновых нейронов подсчитывали в мозгу самцов крыс из нашего предыдущего исследования [6], которые подвергались аналогичным поведенческим процедурам, но никогда не подвергались воздействию фармакологических агентов, нацеленных на орексин или окситоцин. системы. Этим крысам транскардиально перфузировали фосфатно-солевым буфером (PBS), а затем формалином. Мозг постфиксировали в течение 1 часа и перед разрезанием подвергали криозащите в 30% сахарозе. Срезы головного мозга (40 мкм) инкубировали в блокирующем буфере, состоящем из PBS-Triton X-100 (0,3%; PBS-T) с 2% нормальной ослиной сывороткой, в течение 2 ч при комнатной температуре и инкубировали при 4°C в течение ночи с мышиными антигенами. -окситоцин (1:1000, Millipore Cat# MAB5296, RRID:AB_2157626) или мышиный антиорексин A (1:500, Santa Cruz Biotechnology Cat# sc-80263, RRID:AB_1126868). После 3 промывок в PBS срезы инкубировали в течение 2 ч со вторичным антителом ослиного антимышиного Alexafluor ® 594 (1:500; Jackson ImmunoResearch Labs, кат. № 715-585-151, RRID: AB_2340855). Срезы монтировали на предметные стекла и покрывали покровным стеклом с помощью монтажной среды ProLong Diamond Antifade с DAPI (Invitrogen, кат. № P36971). Изображения были получены с помощью сканирующего микроскопа для слайдов (Olympus VS120; 10-кратный воздушный объектив) и импортированы в программное обеспечение Imaris (Imaris, RRID: SCR_007370).
системы. Этим крысам транскардиально перфузировали фосфатно-солевым буфером (PBS), а затем формалином. Мозг постфиксировали в течение 1 часа и перед разрезанием подвергали криозащите в 30% сахарозе. Срезы головного мозга (40 мкм) инкубировали в блокирующем буфере, состоящем из PBS-Triton X-100 (0,3%; PBS-T) с 2% нормальной ослиной сывороткой, в течение 2 ч при комнатной температуре и инкубировали при 4°C в течение ночи с мышиными антигенами. -окситоцин (1:1000, Millipore Cat# MAB5296, RRID:AB_2157626) или мышиный антиорексин A (1:500, Santa Cruz Biotechnology Cat# sc-80263, RRID:AB_1126868). После 3 промывок в PBS срезы инкубировали в течение 2 ч со вторичным антителом ослиного антимышиного Alexafluor ® 594 (1:500; Jackson ImmunoResearch Labs, кат. № 715-585-151, RRID: AB_2340855). Срезы монтировали на предметные стекла и покрывали покровным стеклом с помощью монтажной среды ProLong Diamond Antifade с DAPI (Invitrogen, кат. № P36971). Изображения были получены с помощью сканирующего микроскопа для слайдов (Olympus VS120; 10-кратный воздушный объектив) и импортированы в программное обеспечение Imaris (Imaris, RRID: SCR_007370). Окситоциновые нейроны подсчитывали полуавтоматически с использованием функции обнаружения пятна Imaris. Количество окситоциновых клеток в PVN подсчитывали в обоих полушариях и усредняли по двум срезам на животное. Для подсчета орексина изображения получали с использованием микроскопа Zeiss Axio Zoom V16. Мозаичные фотографии были скомпилированы с 20-кратным увеличением с использованием программного обеспечения для обработки изображений Zen 2 (Carl Zeiss Microscopy). Как и в наших предыдущих исследованиях [60, 64], количество орексиновых клеток подсчитывали отдельно в ЛГ по сравнению с орексиновыми клеточными полями дорсомедиального гипоталамуса (DMH) и перифорникальной области (PF) в обоих полушариях с использованием функции ручного количественного определения программного обеспечения Zen 2. и в среднем по трем секциям на животное. Подполя орексина очерчивали, как описано ранее [60, 64], проводя линию на 100 микрон латеральнее свода, причем поле медиальнее этой линии представляло PF/DMH, а латеральнее этой линии представляло поле орексина LH.
Окситоциновые нейроны подсчитывали полуавтоматически с использованием функции обнаружения пятна Imaris. Количество окситоциновых клеток в PVN подсчитывали в обоих полушариях и усредняли по двум срезам на животное. Для подсчета орексина изображения получали с использованием микроскопа Zeiss Axio Zoom V16. Мозаичные фотографии были скомпилированы с 20-кратным увеличением с использованием программного обеспечения для обработки изображений Zen 2 (Carl Zeiss Microscopy). Как и в наших предыдущих исследованиях [60, 64], количество орексиновых клеток подсчитывали отдельно в ЛГ по сравнению с орексиновыми клеточными полями дорсомедиального гипоталамуса (DMH) и перифорникальной области (PF) в обоих полушариях с использованием функции ручного количественного определения программного обеспечения Zen 2. и в среднем по трем секциям на животное. Подполя орексина очерчивали, как описано ранее [60, 64], проводя линию на 100 микрон латеральнее свода, причем поле медиальнее этой линии представляло PF/DMH, а латеральнее этой линии представляло поле орексина LH. Подсчет окситоциновых и орексиновых клеток проводился отдельными исследователями, не осведомленными об экспериментальном состоянии животных.
Подсчет окситоциновых и орексиновых клеток проводился отдельными исследователями, не осведомленными об экспериментальном состоянии животных.
Статистические анализы
Все статистические анализы проводились в Prism (GraphPad Prism, RRID:SCR_002798; V9.1). Различия в переменных поведенческой экономики оценивались с использованием двухфакторного дисперсионного анализа с повторными измерениями (RM) (ANOVA) с вознаграждением (еда и героин) в качестве внутрисубъектного фактора и полом в качестве межсубъектного фактора. Данные о выборе и нажатии на рычаг для еды или героина во время тестирования выбора были проанализированы с использованием однофакторного RM-ANOVA с обработкой как внутрисубъектного фактора или двустороннего парного анализа.3238 t испытание, если необходимо. Данные теста поиска вознаграждения с сигналом были проанализированы с использованием двухстороннего RM-ANOVA с рычагом (героин или еда) в качестве внутрисубъектного фактора и лечением в качестве межсубъектного фактора с последующими апостериорными тестами Сидака. Линейные отношения между переменными анализировали с использованием коэффициента корреляции Пирсона.
Линейные отношения между переменными анализировали с использованием коэффициента корреляции Пирсона.
Результаты
Мотивация к употреблению героина превышает мотивацию к еде
Репрезентативные кривые спроса на продовольствие и самостоятельный прием героина при повышении цен на одно животное показаны на рис. 2a, b. Ответы на этапе самоуправления и поведенческой экономики показаны на дополнительных рисунках 1a, b. В соответствии с нашей предыдущей работой [6], крысы были более мотивированы на героин, чем на еду, по нескольким показателям поведенческих экономических переменных. EV (рис. 2c; двухсторонний RM-ANOVA: основной эффект вознаграждения, F (1,24) = 15,39, p = 0,0006; paired t test: t (25) = 3.826, p = 0.0008) and P max (Fig. 2d; 2-way RM-ANOVA: main effect of reward, F (1,24) = 20,77, р = 0,0001; Парные T Тест: T (25) = 4,582, P = 0,0001) были значительно более высокими, чем для еда, и Heroin α α α α α α, и Heroin α α α, а Heroin α α и Heroin α и Heroin α и Heroin. ниже, чем у пищи α (рис. 2e; двухсторонний RM-ANOVA: основной эффект вознаграждения, F (1,24) = 12,30, p = 0,0018; парные t тест: t (25) = 3,14, p = 0,0043). Эти результаты показывают, что кривая спроса на героин у крыс была более неэластичной, предполагая, что в этих экспериментальных условиях крысы относятся к героину как к необходимости, а к еде как к роскоши (см. рис. 1a, b для объяснения концепций и переменных). Еда Q 0 была выше, чем героин Q 0 (рис. 2f; 2-сторонний RM-ANOVA: основной эффект вознаграждения, F (1,24) = 22,63, p < 0,0001; парный тест t : t (25) = 4,8436, p < 0,0001), что указывает на то, что крысы значительно больше реагируют на пищу, чем на героин, в условиях «свободного» доступа, что согласуется с нашей предыдущей работой [6] .
ниже, чем у пищи α (рис. 2e; двухсторонний RM-ANOVA: основной эффект вознаграждения, F (1,24) = 12,30, p = 0,0018; парные t тест: t (25) = 3,14, p = 0,0043). Эти результаты показывают, что кривая спроса на героин у крыс была более неэластичной, предполагая, что в этих экспериментальных условиях крысы относятся к героину как к необходимости, а к еде как к роскоши (см. рис. 1a, b для объяснения концепций и переменных). Еда Q 0 была выше, чем героин Q 0 (рис. 2f; 2-сторонний RM-ANOVA: основной эффект вознаграждения, F (1,24) = 22,63, p < 0,0001; парный тест t : t (25) = 4,8436, p < 0,0001), что указывает на то, что крысы значительно больше реагируют на пищу, чем на героин, в условиях «свободного» доступа, что согласуется с нашей предыдущей работой [6] .
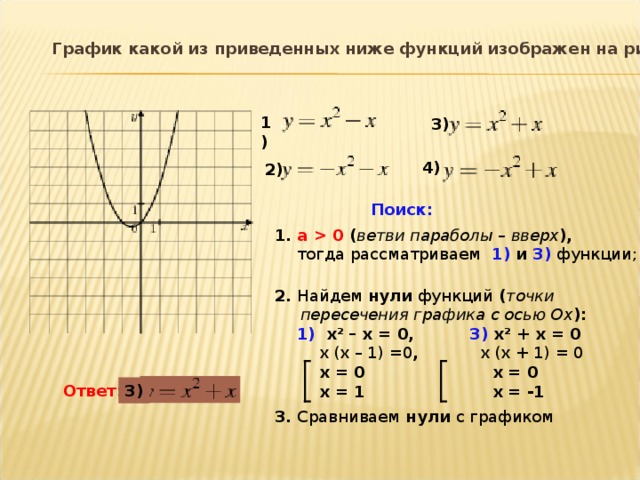
Репрезентативные кривые спроса на продукты питания ( a ) и героин ( b ) демонстрируют более неэластичный спрос на героин по сравнению с едой у крыс. c Эссенциальная ценность (EV) и d максимальная цена, которую крысы были готовы заплатить, чтобы защитить желаемое потребление ( P max ), были выше для героина, чем для еды. e Эластичность спроса ( α ) и f потребление по нулевой стоимости ( Q 0 ) были выше для продуктов питания, чем для героина. ** р < 0,01, *** р < 0,001 при сравнении еды и героина (двусторонний парный тест t ). Данные представлены как среднее ± SEM ( c – f ).
Изображение в полный размер
Как и ожидалось, исходя из нашей предыдущей работы, некоторые переменные поведенческой экономики коррелировали с другими для данного подкрепления (героин против еды; дополнительная рис. 2). Кроме того, наблюдались некоторые корреляции в переменных поведенческой экономики между подкреплениями; однако никакие переменные поведенческой экономики не коррелировали с выбором (дополнительная рис. 2). Последнее согласуется с нашим предыдущим выводом о том, что выбор является отдельной мерой аддиктивного поведения, возможно, отражающей более когнитивные, а не мотивационные аспекты аддиктивного поведения [6]. Дальнейший анализ показал, что спрос на героин был менее эластичен, чем спрос на пищу у самок крыс (дополнительный рис. 3c; двухфакторный RM-ANOVA: вознаграждение × сексуальное взаимодействие, F (1,24) = 7,18, p = 0,0131; α еда против α героин: p = 0,0004). Однако существенных различий между полами не наблюдалось ни по каким переменным поведенческой экономики (дополнительная рис. 3).
2). Последнее согласуется с нашим предыдущим выводом о том, что выбор является отдельной мерой аддиктивного поведения, возможно, отражающей более когнитивные, а не мотивационные аспекты аддиктивного поведения [6]. Дальнейший анализ показал, что спрос на героин был менее эластичен, чем спрос на пищу у самок крыс (дополнительный рис. 3c; двухфакторный RM-ANOVA: вознаграждение × сексуальное взаимодействие, F (1,24) = 7,18, p = 0,0131; α еда против α героин: p = 0,0004). Однако существенных различий между полами не наблюдалось ни по каким переменным поведенческой экономики (дополнительная рис. 3).
Крысы, предпочитающие героин, были определены как те, у которых >65% выбора героина, а крысы, предпочитающие пищу, были определены как <35% выбора героина, оставляя тех, кто выбирает 35–65%, как равных предпочитающих. Семь из десяти крыс, предпочитающих героин в этом исследовании, были самками; равные предпочитающие крысы были примерно одинакового пола (5 самок, 4 самца), тогда как крысы, предпочитающие гранулы, были преимущественно самцами (всего 6 из 7). Таким образом, в этом исследовании ~ 38% населения предпочитали героин, ~ 35% одинаково предпочитали и ~ 27% предпочитали гранулы, что дает в среднем 56 ± 6 % выбора героина (дополнительный рисунок 1c). Кроме того, у женщин исходный уровень выбора героина был значительно выше, чем у мужчин, до начала тестирования выбора (дополнительная рис. 3e; непарные t тест: t (24) = 2,21, p = 0,0366).
Таким образом, в этом исследовании ~ 38% населения предпочитали героин, ~ 35% одинаково предпочитали и ~ 27% предпочитали гранулы, что дает в среднем 56 ± 6 % выбора героина (дополнительный рисунок 1c). Кроме того, у женщин исходный уровень выбора героина был значительно выше, чем у мужчин, до начала тестирования выбора (дополнительная рис. 3e; непарные t тест: t (24) = 2,21, p = 0,0366).
Ни окситоцин, ни орексин не опосредуют выбор опиоида
После стабилизации поведения выбора и определения фенотипов предпочтений для отдельных крыс началось тестирование выбора. Различные фармакологические агенты использовались для оценки участия гипоталамической нейропептидной системы, окситоцина и орексина, в выборе опиоидов. Окситоцин (1 или 3 мг/кг, внутрибрюшинно) или носитель вводили за 30 минут до сеанса теста выбора крысам, назначенным для исследования окситоцина. Использовался внутрисубъектный дизайн, по крайней мере, с двумя сеансами выбора без наркотиков между тестами. Никакого лечебного эффекта окситоцина не наблюдалось при выборе опиоидов (рис. 3а, слева), жиме героином (рис. 3а, в центре) или жиме рычагом пищи (рис. 3а, справа) в этих условиях. Затем эти же крысы подверглись дополнительному тесту с антагонистом окситоцина L-368,89.9 (5 мг/кг, внутрибрюшинно) или носитель, и не было никакого влияния на выбор опиоидов (рис. 3b, слева), нажатие рычага героина (рис. 3b, в центре) или нажатие рычага еды (рис. 3b, справа).
Никакого лечебного эффекта окситоцина не наблюдалось при выборе опиоидов (рис. 3а, слева), жиме героином (рис. 3а, в центре) или жиме рычагом пищи (рис. 3а, справа) в этих условиях. Затем эти же крысы подверглись дополнительному тесту с антагонистом окситоцина L-368,89.9 (5 мг/кг, внутрибрюшинно) или носитель, и не было никакого влияния на выбор опиоидов (рис. 3b, слева), нажатие рычага героина (рис. 3b, в центре) или нажатие рычага еды (рис. 3b, справа).
Ни низкая доза (1 мг/кг), ни высокая доза (3 мг/кг) окситоцина не повлияли на выбор героина ( a , слева), ни рычажные нажатия на героин ( a , посередине) или еду ( и , справа). Антагонист окситоцина, L-368,899 (5 мг/кг), не повлиял на выбор (9).3276 b , слева), рычажные прессы для героина ( b , посередине) или еды ( b , справа). Двойной антагонист орексиновых рецепторов DORA-12 не влиял на выбор героина ( c , слева), нажатие рычага для героина ( c , в центре) или пищи ( c , справа) ни при низких дозах (10 мг/ кг) или высокой дозой (30 мг/кг). Данные показаны как среднее значение ± SEM.
Данные показаны как среднее значение ± SEM.
Изображение в полный размер
Крысам, включенным в исследование орексина, двойной антагонист рецептора орексина DORA-12 (10 или 30 мг/кг, внутрибрюшинно) или носитель вводили за 30 мин до сеанса теста выбора, опять же с использованием внутрибрюшинного введения. - дизайн предметов, с сессиями выбора без наркотиков, отделяющими каждый тест. В этих условиях DORA-12 не влиял на выбор опиоидов (рис. 3с, слева), героиновые рычажные жимы (рис. 3с, в центре) или пищевые рычажные жимы (рис. 3с, справа).
Системы окситоцина и орексина двунаправленно регулируют поиск опиоидов в присутствии конкурирующих сигналов
После завершения тестирования выбора всех крыс возвращали к самостоятельному приему пищи и героина (на FR3) в течение как минимум 3 сеансов перед тестом поиска вознаграждения. . Во время этого последнего теста крысы могли реагировать как на героин, так и на пищу, которые давали сигналы, связанные с героином или едой (на FR3), но не давали вознаграждения. Таким образом, это был тест на угасание сигнала, аналогичный другим формам восстановления сигнала [6, 65], проводимый во время острой (~ 24 часов) отмены опиоидов в условиях конкурирующих сигналов, связанных с вознаграждением. Окситоцин (1 мг/кг), антагонист орексина DORA-12 (30 мг/кг) или носитель вводили за 30 мин до теста. На рис. 4а показано среднее число активных нажатий рычага в течение последних 3 дней самоуправления, предшествующих тесту поиска вознаграждения. Нажатие рычага для еды было выше, чем для героина (2-факторный дисперсионный анализ; рычаг: F (1,21) = 49,93, p < 0,0001), но априорных различий между группами лечения не было.
Таким образом, это был тест на угасание сигнала, аналогичный другим формам восстановления сигнала [6, 65], проводимый во время острой (~ 24 часов) отмены опиоидов в условиях конкурирующих сигналов, связанных с вознаграждением. Окситоцин (1 мг/кг), антагонист орексина DORA-12 (30 мг/кг) или носитель вводили за 30 мин до теста. На рис. 4а показано среднее число активных нажатий рычага в течение последних 3 дней самоуправления, предшествующих тесту поиска вознаграждения. Нажатие рычага для еды было выше, чем для героина (2-факторный дисперсионный анализ; рычаг: F (1,21) = 49,93, p < 0,0001), но априорных различий между группами лечения не было.
Реакция не различалась между группами лечения во время сеансов FR3, предшествующих тесту поиска награды ( и ). В условиях, когда доступны как героин, так и пищевые сигналы, крысы ищут героин чаще, чем пищу ( b ). Окситоцин (1 мг/кг) и DORA-12 (30 мг/кг) уменьшали поиск героина, но не поиск еды, в присутствии как героина, так и пищевых сигналов. * p < 0,05, *** p < 0,001 по сравнению с группой героин-носитель (Двусторонний RM ANOVA с последующим апостериорным тестом Сидака). Данные представлены как среднее значение ± SEM.
Окситоцин (1 мг/кг) и DORA-12 (30 мг/кг) уменьшали поиск героина, но не поиск еды, в присутствии как героина, так и пищевых сигналов. * p < 0,05, *** p < 0,001 по сравнению с группой героин-носитель (Двусторонний RM ANOVA с последующим апостериорным тестом Сидака). Данные представлены как среднее значение ± SEM.
Изображение в натуральную величину
Во время теста на поиск вознаграждения крысы чаще реагировали на героиновый рычаг для героинового сигнала (рис. 4b; 2-факторный RM-ANOVA: основной эффект рычага, F (1 ,21) = 16,15, p = 0,0006) по сравнению с пищевым рычагом, что согласуется с более высокой мотивацией к поиску героина при наличии обоих сигналов. Лечение агентами окситоцина или орексина приводило к значительному снижению ответа (2-сторонний RM ANOVA: основной эффект препарата, F (2,21) = 5,662, p = 0,0108; рычаг × взаимодействие с наркотиками, F (2,21) = 3,646, p = 0,0437), и апостериорный анализ показал, что это снижение реакции было специфичным для героинового рычага (окситоцин: 0,0000000000000000000000000 , ДОРА-12: p = 0,0006 по сравнению с группой Veh) без существенного влияния на пищевой рычаг. Кроме того, реакция на сигнал героина была выше, чем реакция на сигнал еды только в группе Вех (9).3238 p = 0,0003). Эти результаты показывают, что активация системы окситоцина с помощью экзогенного окситоцина или ингибирование системы орексина с помощью DORA-12 способна нормализовать уровень поиска вознаграждения в присутствии героина по сравнению с пищевыми сигналами.
Кроме того, реакция на сигнал героина была выше, чем реакция на сигнал еды только в группе Вех (9).3238 p = 0,0003). Эти результаты показывают, что активация системы окситоцина с помощью экзогенного окситоцина или ингибирование системы орексина с помощью DORA-12 способна нормализовать уровень поиска вознаграждения в присутствии героина по сравнению с пищевыми сигналами.
Количество окситоциновых и орексиновых клеток по-разному связано с потребностью в еде и героине
Мы подсчитали количество орексиновых нейронов в ЛГ и DMH/PF и количество окситоциновых нейронов в PVN в мозге крыс из нашего предыдущего исследования [6]. ]. Важно отметить, что эти крысы никогда не подвергались воздействию фармакологических агентов, воздействующих на системы орексина или окситоцина, что могло повлиять на уровни экспрессии этих нейропептидов [66, 67]. В соответствии с отсутствием влияния окситоцина и DORA-12 на выбор опиоидов мы не наблюдали корреляции между количеством нейронов окситоцина или орексина и поведением выбора (дополнительная рис. 4a, b).
4a, b).
Затем мы изучили корреляции между этими подсчетами и поведенческими экономическими переменными из кривых спроса каждой отдельной крысы на героин и еду, а также поиск вознаграждения во время теста на сигнал. На рис. 5a–c показано репрезентативное изображение гипоталамического поля орексина. Мы обнаружили, что количество орексиновых нейронов ЛГ положительно коррелирует с ЭВ героина (рис. 5г; Pearson’s r = 0,5992, p = 0,0142) и P max (рис.3239 = 0,6827, p = 0,0036) и отрицательно коррелирует с героином α (рис. 5е; Pearson’s r = -0,528, = -0,528, = 0,39). Интересно, что никакие пищевые переменные не коррелировали с количеством орексиновых клеток (данные не показаны). Более того, количество орексиновых нейронов в DMH / PF не коррелировало с какими-либо поведенческими экономическими переменными для героина или еды (дополнительная рис. 4c – e). Это подчеркивает специфику орексиновой системы ЛГ в мотивации употребления героина по сравнению с естественным вознаграждением (еда). Затем мы исследовали корреляцию между числом клеток окситоцина и поведенческими экономическими переменными. На рис. 6a–c показаны репрезентативные изображения нейронов окситоцина в PVN. Количество клеток окситоцина положительно коррелирует как с героином α (рис. 6D; Пирсона R = 0,5371, р = 0,0312) и пищи α (рис. 6E; ) Пирсона). Никакие другие переменные не коррелировали с количеством клеток окситоцина (данные не показаны). Это предполагает возможное общее участие системы окситоцина в мотивации как наркотиков, так и естественных вознаграждений.
Затем мы исследовали корреляцию между числом клеток окситоцина и поведенческими экономическими переменными. На рис. 6a–c показаны репрезентативные изображения нейронов окситоцина в PVN. Количество клеток окситоцина положительно коррелирует как с героином α (рис. 6D; Пирсона R = 0,5371, р = 0,0312) и пищи α (рис. 6E; ) Пирсона). Никакие другие переменные не коррелировали с количеством клеток окситоцина (данные не показаны). Это предполагает возможное общее участие системы окситоцина в мотивации как наркотиков, так и естественных вознаграждений.
a Репрезентативные изображения окрашивания нейронов (DAPI), b иммунофлуоресценции орексина и c показаны наложения, показывающие анатомические границы между латеральным гипоталамусом (LH) и дорсомедиальным (DMH) и перифорникальным (PF) ) области (третий желудочек 3V, свод FX. Масштабная линейка = 500 мкм). Количество орексиновых нейронов ЛГ положительно коррелировало с героином EV ( d ) и P max ( e ) и отрицательно коррелировало с героином α ( ф ). Этот профиль предполагает, что орексиновая система ЛГ является движущей силой героинового мотивационного состояния. * p < 0,05, ** p < 0,01 достоверная корреляция.
Масштабная линейка = 500 мкм). Количество орексиновых нейронов ЛГ положительно коррелировало с героином EV ( d ) и P max ( e ) и отрицательно коррелировало с героином α ( ф ). Этот профиль предполагает, что орексиновая система ЛГ является движущей силой героинового мотивационного состояния. * p < 0,05, ** p < 0,01 достоверная корреляция.
Изображение в полный размер
Рис. 6: Количество окситоциновых нейронов в паравентрикулярном гипоталамусе коррелирует с эластичностью потребности как в героине, так и в пище. a Репрезентативные изображения гипоталамуса (DAPI), b иммунофлуоресценция окситоцина и c наложение, показывающее анатомические границы паравентрикулярного гипоталамуса (PVN). 3V третий желудочек. Масштабная линейка = 100 мкм. Количество окситоциновых нейронов PVN положительно коррелировало как с героином α ( d ), так и с пищей α ( e ). Этот профиль подразумевает систему окситоцина как ограничитель мотивационных состояний. * p < 0,05 значимая корреляция.
Этот профиль подразумевает систему окситоцина как ограничитель мотивационных состояний. * p < 0,05 значимая корреляция.
Изображение в полный размер
Обсуждение
В целом эти результаты свидетельствуют о том, что два гипоталамических нейропептида, окситоцин и орексин, двунаправленно регулируют способность опиоидных сигналов влиять на выбор при острой (~24 ч) абстиненции. Мы подтвердили предыдущие выводы в аналогичной модели выбора, согласно которой крысы готовы работать больше за героин, чем за естественное вознаграждение (еду) [6]. Действительно, спрос на героин был более неэластичным, чем спрос на продукты питания, что позволяет предположить, что крысы в этом исследовании относились к героину как к предмету первой необходимости, а к еде как к предмету роскоши. Множественные переменные, полученные из индивидуальных кривых спроса, указывали на повышенную мотивацию к употреблению героина по сравнению с едой. Эссенциальная ценность (EV) героина была выше, чем у продуктов питания, при этом EV отражала нормализованное значение 9. 3238 α , что позволяет нам напрямую сравнивать эластичность спроса между этими двумя разными вознаграждениями. P max , или максимальная цена, которую животное готово заплатить (в рычажном прессе) для защиты желаемого потребления ( Q 0 ), также была выше для героина, чем для еды. Более того, героин α коррелировал как с количеством нейронов орексина, так и с окситоцином, что указывает на то, что эти гипоталамические системы лежат в основе мотивации к употреблению героина.
3238 α , что позволяет нам напрямую сравнивать эластичность спроса между этими двумя разными вознаграждениями. P max , или максимальная цена, которую животное готово заплатить (в рычажном прессе) для защиты желаемого потребления ( Q 0 ), также была выше для героина, чем для еды. Более того, героин α коррелировал как с количеством нейронов орексина, так и с окситоцином, что указывает на то, что эти гипоталамические системы лежат в основе мотивации к употреблению героина.
В нескольких доклинических исследованиях изучалась взаимосвязь переменных поведенческой экономики и выбора между наркотиками и альтернативными вознаграждениями, не связанными с наркотиками. Ранние работы предполагали, что грызуны ценят сладкое вознаграждение (например, сахарозу или сахарин) так же или даже больше, чем вознаграждение наркотиками [68, 69].]. В этом исследовании тип пищи в домашней клетке был подобен по составу типу пищевых гранул, доступных в операционных камерах, и крысы не были лишены пищи. Это может частично объяснить более равное предпочтение между едой и героином, наблюдаемое в использованных здесь условиях выбора. С другой стороны, в более поздних работах предполагается, что интервал между выборочными испытаниями и фармакодинамика препарата (в данном случае героина) являются критическими факторами, влияющими на поведение при выборе [70, 71]. При сравнении двух разных вознаграждений, таких как еда и героин, EV является полезным показателем, поскольку он обеспечивает нормализацию первичной переменной α, указывающей на эластичность спроса. В этой области предыдущие исследования продемонстрировали положительную корреляцию между EV кокаина или героина и выбором наркотиков и отрицательную корреляцию между EV еды или сахарина и выбором наркотиков [59]., 62]. В настоящем исследовании выбор героина не коррелировал с какими-либо переменными поведенческой экономики, что указывает на то, что это принципиально разные показатели тяжести OUD. Кроме того, EV героина был выше, чем EV пищи, тогда как предыдущие исследования показали, что EV еды или сахарина выше, чем EV наркотиков (кокаина или героина) [59, 62].
Это может частично объяснить более равное предпочтение между едой и героином, наблюдаемое в использованных здесь условиях выбора. С другой стороны, в более поздних работах предполагается, что интервал между выборочными испытаниями и фармакодинамика препарата (в данном случае героина) являются критическими факторами, влияющими на поведение при выборе [70, 71]. При сравнении двух разных вознаграждений, таких как еда и героин, EV является полезным показателем, поскольку он обеспечивает нормализацию первичной переменной α, указывающей на эластичность спроса. В этой области предыдущие исследования продемонстрировали положительную корреляцию между EV кокаина или героина и выбором наркотиков и отрицательную корреляцию между EV еды или сахарина и выбором наркотиков [59]., 62]. В настоящем исследовании выбор героина не коррелировал с какими-либо переменными поведенческой экономики, что указывает на то, что это принципиально разные показатели тяжести OUD. Кроме того, EV героина был выше, чем EV пищи, тогда как предыдущие исследования показали, что EV еды или сахарина выше, чем EV наркотиков (кокаина или героина) [59, 62].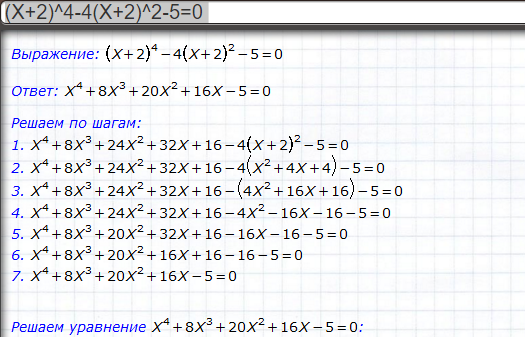 В соответствии с нашей предыдущей работой [6], пища α была выше, чем героин α , что снова указывает на более высокое мотивационное состояние для героина, чем еда, вопреки другим сообщениям [59]., 72, 73]. Тем не менее, это подчеркивает повышенную достоверность этой модели выбора поведенческой экономики для OUD.
В соответствии с нашей предыдущей работой [6], пища α была выше, чем героин α , что снова указывает на более высокое мотивационное состояние для героина, чем еда, вопреки другим сообщениям [59]., 72, 73]. Тем не менее, это подчеркивает повышенную достоверность этой модели выбора поведенческой экономики для OUD.
Гипоталамус, особенно его нейропептидные системы окситоцина и орексина, сильно вовлечен в поведение, связанное с зависимостью [31, 41, 74, 75]. Системное введение антагониста Ox1R SB-334867 снижает потребление опиоидов при самостоятельном приеме героина, опиоидную точку останова при тестах с прогрессивным соотношением и сигнальный поиск опиоидов [76, 77]. Системное введение SB-334867 также снижает поведенческие экономические показатели мотивации для фентанила и ремифентанила [39]., 40, 76]. Несмотря на растущее количество литературы об эффективности терапии на основе орексина, нацеленной на Ox1R [38], меньше известно об эффективности двойного антагонизма к рецептору орексина при приеме и поиске наркотиков. Новые данные в этой области многообещающие; например, острое лечение альморексантом DORA ослабляет обусловленное предпочтение места, вызванное кокаином и метамфетамином [50]. Точно так же неотложное лечение суворексантом DORA снижает потребление кокаина при самостоятельном приеме, гедонистические реакции на кокаин, кокаин-индуцированное повышение уровня дофамина, а также импульсивное поведение, вызванное кокаином [47, 48]. Наши результаты также показывают, что острое лечение с помощью DORA-12 снижает стремление к вознаграждению в присутствии сигналов героина, но не одновременно доступных сигналов пищи, подчеркивая очевидную специфичность орексиновой системы в содействии мотивированному поведению в отношении очень важных вознаграждений, включая злоупотребление наркотиками. 78]. Наши данные также согласуются с выводом о том, что острое лечение антагонистом Ox2R специфически снижает потребление героина при самостоятельном приеме, но не потребление сахарозы [42]. В совокупности эти результаты свидетельствуют о том, что терапия на основе DORA обладает большим потенциалом для лечения расстройств, связанных с употреблением психоактивных веществ (SUD).
Новые данные в этой области многообещающие; например, острое лечение альморексантом DORA ослабляет обусловленное предпочтение места, вызванное кокаином и метамфетамином [50]. Точно так же неотложное лечение суворексантом DORA снижает потребление кокаина при самостоятельном приеме, гедонистические реакции на кокаин, кокаин-индуцированное повышение уровня дофамина, а также импульсивное поведение, вызванное кокаином [47, 48]. Наши результаты также показывают, что острое лечение с помощью DORA-12 снижает стремление к вознаграждению в присутствии сигналов героина, но не одновременно доступных сигналов пищи, подчеркивая очевидную специфичность орексиновой системы в содействии мотивированному поведению в отношении очень важных вознаграждений, включая злоупотребление наркотиками. 78]. Наши данные также согласуются с выводом о том, что острое лечение антагонистом Ox2R специфически снижает потребление героина при самостоятельном приеме, но не потребление сахарозы [42]. В совокупности эти результаты свидетельствуют о том, что терапия на основе DORA обладает большим потенциалом для лечения расстройств, связанных с употреблением психоактивных веществ (SUD). Важно отметить, что в настоящее время для лечения бессонницы клинически используются три DORA (например, суворексант, лемборексант и даридорексант), которые можно легко перепрофилировать в качестве терапевтических средств против ССН.
Важно отметить, что в настоящее время для лечения бессонницы клинически используются три DORA (например, суворексант, лемборексант и даридорексант), которые можно легко перепрофилировать в качестве терапевтических средств против ССН.
Как клинические, так и доклинические исследования подтверждают терапевтический потенциал препаратов на основе окситоцина для лечения ССН, включая ОСН [79]. Недавнее клиническое исследование показало, что однократная интраназальная доза окситоцина снижает тягу и показатели синдрома отмены у потребителей героина во время воздержания [27]. Ранние доклинические исследования показали, что системное введение экзогенного окситоцина снижает как приобретение, так и поддержание самостоятельного приема героина у крыс [80, 81], а также уменьшает симптомы отмены, вызванные налоксоном, у морфинзависимых мышей [82]. Более того, интрацеребровентрикулярное введение окситоцина уменьшает восстановление предпочтения места, обусловленного оксикодоном [83, 84], а системное введение карбетоцина, аналога окситоцина, уменьшает вызванное стрессом [85] и индуцированное праймом [86] восстановление предпочтения места, обусловленного морфином. Поразительно, но на сегодняшний день ни одно доклиническое исследование не исследовало эффективность системного введения окситоцина при поиске героина. Наши результаты показывают, что острое лечение окситоцином снижает потребность в опиоидах в присутствии опиоидных сигналов, конкурирующих с сигналами, связанными с естественным вознаграждением, расширяя наши знания о доменах, посредством которых окситоцин проявляет мультимодальные антиаддиктивные свойства [87].
Поразительно, но на сегодняшний день ни одно доклиническое исследование не исследовало эффективность системного введения окситоцина при поиске героина. Наши результаты показывают, что острое лечение окситоцином снижает потребность в опиоидах в присутствии опиоидных сигналов, конкурирующих с сигналами, связанными с естественным вознаграждением, расширяя наши знания о доменах, посредством которых окситоцин проявляет мультимодальные антиаддиктивные свойства [87].
Интересно, что ни окситоцин, ни DORA не влияли на выбор поведения, когда присутствовали героин и пища. В соответствии с этими негативными поведенческими данными ни количество клеток окситоцина, ни орексина не коррелировало с поведением выбора. Тем не менее, оба соединения были эффективны в снижении потребности в опиоидах в присутствии героиновых сигналов (одновременно доступных пищевых сигналов). Таким образом, активация системы окситоцина или ингибирование системы орексина снижает поиск вознаграждения, вызванный сигналами героина, до уровней, аналогичных сигналам пищи. Несколько ключевых различий между условиями испытаний могут объяснить эти очевидные несопоставимые результаты. Во-первых, во время тестов выбора процент ответов низок, а вознаграждения доступны и потребляются. Этот тип поведения может быть менее поддающимся разрушению, чем поведение в таких условиях, как тест на сигнал, когда доступны конкурирующие сигналы героина и еды, но нет соответствующих вознаграждений, а скорость реакции высока. Кроме того, используемые здесь конкретные условия выбора не охватывают все элементы свободной экономики, поскольку героин был доступен только во время оперативных сеансов [88,89].,90]. Это могло ограничивать поведение выбора и повышать его устойчивость к нарушению фармакологическими агентами. Тем не менее, наша модель выбора дает ценную информацию о способности агентов окситоцина и орексина изменять реакцию на героин и пищу, когда доступны оба вознаграждения. Модели выбора обладают преимуществами по сравнению с процедурами самостоятельного введения отдельных оперантов благодаря присущей им чувствительности к обнаружению общих изменений двигательной активности и мотивации [91, 92].
Несколько ключевых различий между условиями испытаний могут объяснить эти очевидные несопоставимые результаты. Во-первых, во время тестов выбора процент ответов низок, а вознаграждения доступны и потребляются. Этот тип поведения может быть менее поддающимся разрушению, чем поведение в таких условиях, как тест на сигнал, когда доступны конкурирующие сигналы героина и еды, но нет соответствующих вознаграждений, а скорость реакции высока. Кроме того, используемые здесь конкретные условия выбора не охватывают все элементы свободной экономики, поскольку героин был доступен только во время оперативных сеансов [88,89].,90]. Это могло ограничивать поведение выбора и повышать его устойчивость к нарушению фармакологическими агентами. Тем не менее, наша модель выбора дает ценную информацию о способности агентов окситоцина и орексина изменять реакцию на героин и пищу, когда доступны оба вознаграждения. Модели выбора обладают преимуществами по сравнению с процедурами самостоятельного введения отдельных оперантов благодаря присущей им чувствительности к обнаружению общих изменений двигательной активности и мотивации [91, 92].
Несмотря на соображения, отмеченные выше, специфичность эффектов DORA-12 и окситоцина на стимулы к поиску героина предполагает, что эти методы лечения могут быть особенно эффективными для предотвращения рецидивов, вызванных сигналами, связанными с наркотиками. Хотя мы не исследовали здесь нейронные схемы, лежащие в основе этих терапевтических эффектов, тот факт, что DORA-12 и окситоцин влияют на одни и те же поведенческие результаты, но в противоположных направлениях, повышает вероятность того, что их действия опосредованы через схожие области мозга и механизмы. Потенциальным общим местом действия является базолатеральная миндалина; Входы орексина в базолатеральную миндалевидное тело, особенно вовлекающие Ox1R, вовлечены в сигнальное восстановление поиска наркотиков [9].3], и данные свидетельствуют о том, что они также обрабатывают информацию, связанную со стрессом, в рамках этой цепи [94, 95], что согласуется с ролью орексина в стресс-индуцированных формах рецидива [96, 97]. Также было показано, что интраназальная окситоциновая терапия для лечения посттравматического стрессового расстройства нормализует функциональную связь в базолатеральных цепях миндалины [98]. Более того, связывание как с рецепторами орексина, так и с окситоциновыми рецепторами задействует нижестоящие пути фосфолипазы С (PLC) [99, 100], а дисфункция изоформы PLCβ1 связана со стрессом и зависимостью [9].4, 101]. Хотя существует много других областей мозга и внутриклеточных путей, которые могут быть частью схемы, опосредующей наблюдаемые терапевтические эффекты окситоцина и DORA-12 на вызванный героиновым рецидивом [15, 84], требуется дополнительная работа, чтобы идентифицировать не только цепь на уровне механизмы, но также молекулярные и G-белковые сигнальные механизмы, лежащие в основе этих результатов.
Более того, связывание как с рецепторами орексина, так и с окситоциновыми рецепторами задействует нижестоящие пути фосфолипазы С (PLC) [99, 100], а дисфункция изоформы PLCβ1 связана со стрессом и зависимостью [9].4, 101]. Хотя существует много других областей мозга и внутриклеточных путей, которые могут быть частью схемы, опосредующей наблюдаемые терапевтические эффекты окситоцина и DORA-12 на вызванный героиновым рецидивом [15, 84], требуется дополнительная работа, чтобы идентифицировать не только цепь на уровне механизмы, но также молекулярные и G-белковые сигнальные механизмы, лежащие в основе этих результатов.
Хотя ни количество клеток окситоцина, ни орексина не коррелировало с поиском героина во время теста поиска вознаграждения с сигналом, корреляции с α наблюдались. Неоднократно было показано, что переменная α коррелирует с поиском наркотиков для злоупотребления несколькими наркотиками [61] и связана со склонностью к развитию более тяжелого фенотипа SUD у крыс, самостоятельно принимающих кокаин [102].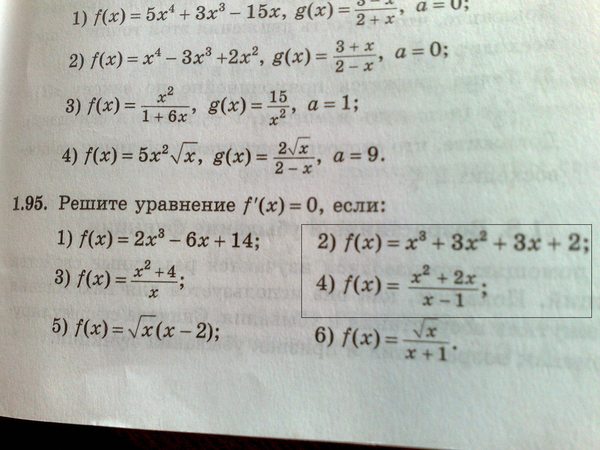 В соответствии с несколькими предыдущими исследованиями, указывающими на функциональную дихотомию орексиновых клеток LH и DMH/PF в процессах вознаграждения и стресса, соответственно [60, 64, 103, 104], мы обнаружили, что количество орексиновых клеток LH (но не DMH/PF) отрицательно коррелирует с героином α. Интересно, что мы не наблюдали связи между числом орексиновых клеток ни в ЛГ, ни в ДМГ/ПФ, ни в пищевых продуктах α, что указывает на явную специфическую взаимосвязь между орексиновой системой ЛГ и мотивацией к употреблению героина. Кроме того, наблюдалась положительная корреляция между количеством клеток орексина ЛГ (но не ДМГ/ПФ) и героином 9.3238 P макс . Примечательно, что максимальное количество усилий, прилагаемых для поддержания потребления наркотиков на уровне P max , привлекло значительное внимание как надежный предиктор тяжести ВНС у людей, особенно при алкоголизме. У людей с недавними эпизодами пьянства кривая спроса на алкоголь становится более неэластичной [105], и даже без переедания поведенческие экономические показатели коррелируют с еженедельным потреблением алкоголя [106], что снова подтверждает кажущуюся достоверность поведенческой экономики для оценки тяжести ВНС в человека [107].
В соответствии с несколькими предыдущими исследованиями, указывающими на функциональную дихотомию орексиновых клеток LH и DMH/PF в процессах вознаграждения и стресса, соответственно [60, 64, 103, 104], мы обнаружили, что количество орексиновых клеток LH (но не DMH/PF) отрицательно коррелирует с героином α. Интересно, что мы не наблюдали связи между числом орексиновых клеток ни в ЛГ, ни в ДМГ/ПФ, ни в пищевых продуктах α, что указывает на явную специфическую взаимосвязь между орексиновой системой ЛГ и мотивацией к употреблению героина. Кроме того, наблюдалась положительная корреляция между количеством клеток орексина ЛГ (но не ДМГ/ПФ) и героином 9.3238 P макс . Примечательно, что максимальное количество усилий, прилагаемых для поддержания потребления наркотиков на уровне P max , привлекло значительное внимание как надежный предиктор тяжести ВНС у людей, особенно при алкоголизме. У людей с недавними эпизодами пьянства кривая спроса на алкоголь становится более неэластичной [105], и даже без переедания поведенческие экономические показатели коррелируют с еженедельным потреблением алкоголя [106], что снова подтверждает кажущуюся достоверность поведенческой экономики для оценки тяжести ВНС в человека [107]. В совокупности эти результаты указывают на то, что орексиновая система является потенциальным биомаркером склонности к развитию ВНС.
В совокупности эти результаты указывают на то, что орексиновая система является потенциальным биомаркером склонности к развитию ВНС.
В отличие от отрицательной корреляции, наблюдаемой между количеством клеток орексина и героином α, количество клеток окситоцина положительно коррелировало как с героином α, так и с пищей α, подчеркивая двунаправленную функциональную роль этих систем в мотивации и предполагая более общее участие окситоциновой системы в мотивации как наркотиков, так и немедикаментозных вознаграждений. Например, однократное введение окситоцина снижает потребление сахарозы при самостоятельном приеме, а также поиск, вызванный сигналами сахарозы [57]. Хотя это противоречит нашим нынешним выводам о том, что окситоцин специфически снижает рецидивы для героина, но не для пищевых сигналов, это согласуется с нашими выводами о том, что количество окситоцина коррелирует как с героином, так и с пищей α.
Наконец, и окситоцин, и орексин играют важную роль в пробуждении и сне, и при некоторых обстоятельствах сообщалось о снотворном эффекте экзогенного окситоцина и DORA.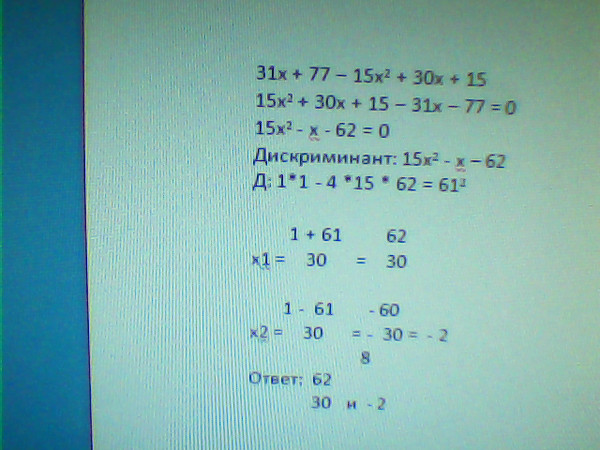 Однако маловероятно, что поведенческие эффекты окситоцина и DORA-12 на поведение, связанное с поиском опиоидов, наблюдаемые здесь, являются результатом нарушения общей активности, поскольку (1) эти соединения не влияли на поведение выбора, задача, которая требовала устойчивого оперантного поведения. ответы на протяжении всего сеанса; и (2) в случае с DORA-12 в нескольких исследованиях не сообщалось о влиянии подобных соединений на профиль двигательной активности животных, прием лекарств с низким усилием или выполнение когнитивных задач, требующих высокого уровня вовлеченности и реакции на задачу. 47,48,49]. Тем не менее, любая разработка фармакологических стратегий, нацеленных на системы окситоцина и/или орексина, должна учитывать потенциальные нежелательные эффекты на общее возбуждение и связанные с ним результаты [44].
Однако маловероятно, что поведенческие эффекты окситоцина и DORA-12 на поведение, связанное с поиском опиоидов, наблюдаемые здесь, являются результатом нарушения общей активности, поскольку (1) эти соединения не влияли на поведение выбора, задача, которая требовала устойчивого оперантного поведения. ответы на протяжении всего сеанса; и (2) в случае с DORA-12 в нескольких исследованиях не сообщалось о влиянии подобных соединений на профиль двигательной активности животных, прием лекарств с низким усилием или выполнение когнитивных задач, требующих высокого уровня вовлеченности и реакции на задачу. 47,48,49]. Тем не менее, любая разработка фармакологических стратегий, нацеленных на системы окситоцина и/или орексина, должна учитывать потенциальные нежелательные эффекты на общее возбуждение и связанные с ним результаты [44].
Таким образом, эти результаты указывают на то, что гипоталамические системы окситоцина и орексина являются двумя потенциальными терапевтическими мишенями, способными двунаправленно регулировать поиск вознаграждения в мире конкурирующих лекарственных и немедикаментозных сигналов. Поскольку рецидив редко возникает в изолированных условиях, когда доступны только сигналы от наркотиков, эти результаты имеют значение для рецидива, который возникает в условиях, когда доступны альтернативы. Будущие исследования должны тщательно изучить потенциал использования систем окситоцина и орексина для достижения ремиссии при НСС путем смещения выбора в пользу естественных вознаграждений и уменьшения тяги, вызванной сигналами, связанными с наркотиками.
Поскольку рецидив редко возникает в изолированных условиях, когда доступны только сигналы от наркотиков, эти результаты имеют значение для рецидива, который возникает в условиях, когда доступны альтернативы. Будущие исследования должны тщательно изучить потенциал использования систем окситоцина и орексина для достижения ремиссии при НСС путем смещения выбора в пользу естественных вознаграждений и уменьшения тяги, вызванной сигналами, связанными с наркотиками.
Ссылки
Fredriksson I, Venniro M, Reiner DJ, Chow JJ, Bossert JM, Shaham Y. Модели рецидива употребления наркотиков и тяги к наркотикам на животных после добровольного воздержания: обзор. Pharmacol Rev. 2021;73:1050–83.
КАС пабмед Статья Google ученый
Ахмед Ш. Попытка понять поведение грызунов при выборе наркотиков. Прог Нейропсихофармакол Биол Психиатрия.
 2018;87:3–10.
2018;87:3–10.КАС пабмед Статья Google ученый
Венниро М., Каприоли Д., Чжан М., Уитакер Л.Р., Чжан С., Уоррен Б.Л. и др. Глутаматергический путь передняя островковая кора -> центральная миндалина имеет решающее значение для рецидива после экстренного лечения. Нейрон 2017; 96: 414–27.e418.
КАС пабмед ПабМед Центральный Статья Google ученый
Venniro M, Zhang M, Caprioli D, Hoots JK, Golden SA, Heins C, et al. Волевое социальное взаимодействие предотвращает наркоманию в крысиных моделях. Нат Нейроски. 2018;21:1520–9.
КАС пабмед ПабМед Центральный Статья Google ученый
Бенишек Л.А., Дугош К.Л., Кирби К.С., Матейковски Дж., Клементс Н.Т., Сеймур Б.Л. и соавт. Управление непредвиденными обстоятельствами на основе призов для лечения лиц, злоупотребляющих психоактивными веществами: метаанализ.
 Наркомания 2014; 109: 1426–36.
Наркомания 2014; 109: 1426–36.ПабМед ПабМед Центральный Статья Google ученый
Heinsbroek JA, Giannotti G, Mandel MR, Josey M, Aston-Jones G, James MH, et al. Общая ограничительная схема для выбора опиоидов и рецидива, идентифицированная в модели зависимости грызунов. Нац коммун. 2021;12:4788.
КАС пабмед ПабМед Центральный Статья Google ученый
Ким С., Стратерн Л. Окситоцин и пластичность материнского мозга. Новый режиссёр Child Adolesc Dev. 2016; 2016: 59–72.
ПабМед ПабМед Центральный Статья Google ученый
Долен Г., Дарвишзаде А., Хуанг К.В., Маленко Р.С. Социальное вознаграждение требует скоординированной активности окситоцина и серотонина прилежащего ядра. Природа 2013; 501:179–84.
ПабМед ПабМед Центральный Статья Google ученый
">Clark-Elford R, Nathan PJ, Auyeung B, Voon V, Sule A, Muller U, et al. Влияние окситоцина на социальное вознаграждение у людей. Int J Neuropsychopharmacol. 2014;17:199–209.
КАС пабмед Статья Google ученый
Li XH, Matsuura T, Xue M, Chen QY, Liu RH, Lu JS и другие. Окситоцин в передней части поясной извилины ослабляет невропатическую боль и эмоциональную тревогу, ингибируя пресинаптическое долговременное потенцирование. Cell Rep. 2021; 36:109411.
КАС пабмед Статья Google ученый
">Sippel LM, Allington CE, Pietrzak RH, Harpaz-Rotem I, Mayes LC, Olff M. Окситоцин и расстройства, связанные со стрессом: нейробиологические механизмы и возможности лечения. Хронический стресс. 2017. https://doi.org/10.1177/2470547016687996.
Ши Д.Д., Чжан Ю.Д., Рен Ю.Ю., Пэн С.Ю., Юань Т.Ф., Ван З. Предсказуемое разлучение с матерью придает взрослым стрессоустойчивость через сигнальный путь окситоцина медиальной префронтальной коры у крыс. Мол Психиатрия. 2021;26:7296–307.
КАС пабмед Статья Google ученый
">Lee MR, Weerts EM. Окситоцин для лечения расстройств, связанных с употреблением наркотиков и алкоголя. Бихав Фармакол. 2016;27:640–8.
КАС пабмед ПабМед Центральный Статья Google ученый
Кокс Б.М., Янг А.Б., См. Р.Е., Райхель К.М. Половые различия в поиске метамфетамина у крыс: влияние окситоцина. Психонейроэндокринология 2013;38:2343–53.
КАС пабмед ПабМед Центральный Статья Google ученый
Чжоу Л., Сун В.Л., Янг А.Б., Ли К., МакГинти Дж.Ф., см. RE. Окситоцин снижает потребность в кокаине и обращает вспять хронические вызванные кокаином изменения в функции глутаматных рецепторов.
 Int J Neuropsychopharmacol. 2014;18:pyu009.
Int J Neuropsychopharmacol. 2014;18:pyu009.Боуэн М.Т., Карсон Д.С., Спиро А., Арнольд Д.С., МакГрегор И.С. Воздействие окситоцина на подростков вызывает стойкое снижение тревожности и потребления алкоголя, а также повышает общительность у крыс. ПЛОС ОДИН. 2011;6:e27237.
КАС пабмед ПабМед Центральный Статья Google ученый
Макфадьен К., Лавлесс Р., ДеЛукка Б., Уордли К., Деоган С., Томас С. и др. Периферическое введение окситоцина снижает потребление этанола у крыс. Фарм Биохим Поведение. 2016;140:27–32.
КАС Статья Google ученый
Cox BM, Bentzley BS, Regen-Tuero H, See RE, Reichel CM, Aston-Jones G. Окситоцин действует в прилежащем ядре, чтобы ослабить поиск и потребность в метамфетамине. Биол психиатрия. 2017; 81: 949–58.
КАС пабмед Статья Google ученый
">Баллас Х.С., Уилфур С.М., Фрекер Н.А., Леонг К.С. Окситоцин ослабляет вызванное стрессом восстановление тяги к алкоголю у самцов крыс: роль центральной миндалины. Биомедицина 2021;9:1919.
Педерсен К.А., Смедли К.Л., Лезерман Дж., Ярског Л.Ф., Рау С.В., Кампов-Полевой А. и др. Интраназальный окситоцин блокирует алкогольную абстиненцию у людей. Алкоголь Clin Exp Res. 2013; 37: 484–9.
КАС пабмед Статья Google ученый
Мелби К., Граве Р.В., Аамо Т.О., Сковлунд Э., Спигсет О. Эффективность самостоятельного интраназального введения окситоцина при употреблении алкоголя и тяге к алкоголю после детоксикации у пациентов с алкогольной зависимостью.
 двойное слепое плацебо-контролируемое исследование. Алкоголь Алкоголь. 2021; 56: 565–72.
двойное слепое плацебо-контролируемое исследование. Алкоголь Алкоголь. 2021; 56: 565–72.КАС пабмед Статья Google ученый
Hansson AC, Koopmann A, Uhrig S, Buhler S, Domi E, Kiessling E, et al. Окситоцин снижает реактивность алкогольных сигналов у зависимых от алкоголя крыс и людей. Нейропсихофармакология 2018;43:1235–46.
КАС пабмед Статья Google ученый
Моейни М., Омиди А., Сехат М., Банафше Х.Р. Влияние окситоцина на абстиненцию, тягу и реакцию на стресс у героинозависимых пациентов: рандомизированное двойное слепое клиническое исследование. Европейский наркоман Res. 2019;25:41–47.
ПабМед Статья Google ученый
Stauffer CS, Musinipally V, Suen A, Lynch KL, Shapiro B, Woolley JD. Двухнедельное пилотное исследование интраназального окситоцина для лиц с кокаиновой зависимостью, получающих поддерживающую терапию метадоном по поводу расстройства, связанного с употреблением опиоидов.
 Теория наркомании. 2016;24:490–8.
Теория наркомании. 2016;24:490–8.ПабМед ПабМед Центральный Статья Google ученый
Quintana DS, Lischke A, Grace S, Scheele D, Ma Y, Becker B. Достижения в области исследования интраназального окситоцина: извлеченные уроки и будущие направления клинических исследований. Мол Психиатрия. 2021;26:80–91.
КАС пабмед Статья Google ученый
Джеймс М.Х., Малер С.В., Мурман Д.Е., Астон-Джонс Г. Десятилетие орексина/гипокретина и зависимости: где мы сейчас? Curr Top Behav Neurosci. 2017; 33: 247–81.
ПабМед ПабМед Центральный Статья Google ученый
Малер С.В., Мурман Д.Э., Смит Р.Дж., Джеймс М.Х., Астон-Джонс Г. Мотивационная активация: объединяющая гипотеза функции орексина/гипокретина. Нат Нейроски. 2014;17:1298–303.

КАС пабмед ПабМед Центральный Статья Google ученый
Мехр Дж. Б., Билотти М. М., Джеймс М. Х. Орексин (гипокретин) и зависимость. Тренды Нейроси. 2021;44:852–5.
КАС пабмед Статья Google ученый
Хэмлин А.С., Ньюби Дж., МакНалли Г.П. Нейронные корреляты и роль дофаминовых рецепторов D1 в восстановлении угасшего влечения к алкоголю. Неврология 2007; 146: 525–36.
КАС пабмед Статья Google ученый
Dayas CV, McGranahan TM, Martin-Fardon R, Weiss F. Стимулы, связанные с наличием этанола, активируют гипоталамические CART и нейроны орексина в модели восстановления рецидива. Биол психиатрия. 2008; 63: 152–7.
КАС пабмед Статья Google ученый
">Harris GC, Wimmer M, Aston-Jones G. Роль нейронов латерального гипоталамуса орексина в поиске вознаграждения. Природа 2005; 437: 556–9..
КАС пабмед Статья Google ученый
Moorman DE, James MH, Kilroy EA, Aston-Jones G. Активация нейронов орексина/гипокретина коррелирует с поиском и предпочтением алкоголя топографически специфическим образом. Евр Джей Нейроски. 2016;43:710–20.
ПабМед ПабМед Центральный Статья Google ученый
Perrey DA, Zhang Y. Разработка терапии зависимости: антагонисты рецепторов орексина-1.
 Мозг Res. 2020;1731:145922.
Мозг Res. 2020;1731:145922.КАС пабмед Статья Google ученый
Fragale JE, Pantazis CB, James MH, Aston-Jones G. Роль передачи сигналов рецептора орексина-1 при спросе на опиоидный фентанил. Нейропсихофармакология 2019;44:1690–7.
КАС пабмед ПабМед Центральный Статья Google ученый
Mohammadkhani A, James MH, Pantazis CB, Aston-Jones G. Стойкие эффекты антагониста рецептора орексина-1 SB-334867 на мотивацию быстродействующего опиоида ремифентанила. Мозг Res. 2020;1731:146461.
КАС пабмед Статья Google ученый
Matzeu A, Martin-Fardon R. Нацеливание на систему орексина при расстройстве, связанном с употреблением опиоидов, отпускаемых по рецепту: Блокада рецептора орексина-1 предотвращает прием и поиск оксикодона у крыс.
 Нейрофармакология 2020;164:107906.
Нейрофармакология 2020;164:107906.КАС пабмед Статья Google ученый
Schmeichel BE, Barbier E, Misra KK, Contet C, Schlosburg JE, Grigoriadis D, et al. Антагонизм к гипокретиновым рецепторам 2 дозозависимо снижает эскалацию самостоятельного приема героина у крыс. Нейропсихофармакология 2015;40:1123–9.
КАС пабмед Статья Google ученый
Браун Р.М., Кху С.И., Лоуренс А.Дж. Антагонизм к центральному рецептору орексина (гипокретина) 2 снижает самостоятельный прием этанола, но не обусловленный сигналом поиск этанола у крыс, предпочитающих этанол. Int J Neuropsychopharmacol. 2013;16:2067–79.
КАС пабмед Статья Google ученый
Джеймс М. Х., Фрагале Дж. Э., Аврора Р. Н., Куперман Н. А., Ланглебен Д. Д., Астон-Джонс Г.
 Перепрофилирование двойного антагониста рецепторов орексина суворексанта для лечения расстройства, связанного с употреблением опиоидов: зачем спать на этом дольше? Нейропсихофармакология 2020;45:717–9.
Перепрофилирование двойного антагониста рецепторов орексина суворексанта для лечения расстройства, связанного с употреблением опиоидов: зачем спать на этом дольше? Нейропсихофармакология 2020;45:717–9.ПабМед ПабМед Центральный Статья Google ученый
Khoo SY, Brown RM. Фармакотерапия на основе орексина/гипокретина для лечения зависимости: DORA или SORA? Препараты ЦНС. 2014;28:713–30.
КАС пабмед Статья Google ученый
Джеймс М.Х., Aston-Jones G. Предисловие к специальному выпуску: «Превращение в реальность методов лечения зависимости на основе орексина: каковы дальнейшие шаги?». Мозг Res. 2020;1731:146665.
КАС пабмед ПабМед Центральный Статья Google ученый
Gentile TA, Simmons SJ, Barker DJ, Shaw JK, Espana RA, Muschamp JWSuvorexant.
 антагонист орексиновых/гипокретиновых рецепторов, ослабляет мотивационные и гедонистические свойства кокаина. Наркоман биол. 2018;23:247–55.
антагонист орексиновых/гипокретиновых рецепторов, ослабляет мотивационные и гедонистические свойства кокаина. Наркоман биол. 2018;23:247–55.КАС пабмед Статья Google ученый
Gentile TA, Simmons SJ, Watson MN, Connelly KL, Brailoiu E, Zhang Y, et al. Влияние суворексанта, антагониста рецепторов двойного орексина и гипокретина, на импульсивное поведение, связанное с кокаином. Нейропсихофармакология 2018;43:1001–9.
КАС пабмед Статья Google ученый
O’Connor SL, Fragale JE, James MH, Aston-Jones G. Суворексант, антагонист рецепторов двойного орексина/гипокретина, снижает поведение, подобное зависимости, от опиоидного фентанила. bioRxiv: 2020.04.25.061887 [Препринт]. 2020 : [цитировано 27 апреля 2020 г.]: [27 стр.]. Доступно по адресу: https://doi.org/10.1101/2020.04.25.061887.
">Сухтинг Р., Юн Дж. Х., Мигель Г. Г. С., Грин К. Э., Уивер М. Ф., Винсент Дж. Н. и др. Предварительное исследование системы орексина на факторы, связанные с рецидивом расстройства, связанного с употреблением кокаина. Мозг Res. 2020;1731:146359.
КАС пабмед Статья Google ученый
Huhn AS, Finan PH, Gamaldo CE, Hammond AS, Umbricht A, Bergeria CL, et al. Суворексант уменьшал нарушения сна, синдром отмены опиоидов и тягу к бупренорфину. Sci Transl Med. 2022;14:eabn8238.
КАС пабмед Статья Google ученый
">Хурш С.Р., Зильберберг А. Экономический спрос и существенная ценность. Psychol Rev. 2008; 115: 186–98.
ПабМед Статья Google ученый
Национальный исследовательский совет. Руководство по уходу и использованию лабораторных животных. 8-е изд. Вашингтон, округ Колумбия: Издательство национальных академий; 2011. 246 стр.
Кинг К.Э., Гриффин В.К., Людерман Л.Н., Кейтс М.М., МакГинти Дж.Ф., Беккер Х.К. Окситоцин снижает самостоятельный прием этанола у мышей. Алкоголь Clin Exp Res. 2017;41:955–64.
КАС пабмед ПабМед Центральный Статья Google ученый
">Boulet NP, Cloutier CJ, Ossenkopp KP, Kavaliers M. Окситоцин, социальные факторы и выражение условного отвращения (упреждающая тошнота) у самцов крыс. Бихав Фармакол. 2016;27:718–25.
КАС пабмед Статья Google ученый
Шварц Л.П., Ким Дж.С., Зильберберг А., Кернс Д.Н. Спрос и предпочтение героина и сахарина у крыс. Наркотики Алкогольная зависимость. 2017; 178:87–93.
КАС пабмед ПабМед Центральный Статья Google ученый
James MH, Stopper CM, Zimmer BA, Koll NE, Bowrey HE, Aston-Jones G.
 Увеличение количества и активности латеральной субпопуляции гипоталамических орексиновых/гипокретиновых нейронов лежит в основе проявления наркозависимости у крыс. Биол психиатрия. 2019;85:925–35.
Увеличение количества и активности латеральной субпопуляции гипоталамических орексиновых/гипокретиновых нейронов лежит в основе проявления наркозависимости у крыс. Биол психиатрия. 2019;85:925–35.КАС пабмед Статья Google ученый
Бенцли Б.С., Фендер К.М., Астон-Джонс Г. Поведенческая экономика самостоятельного приема лекарств: обзор и новый аналитический подход к внутрисессионным процедурам. Психофармакология 2013;226:113–25.
КАС пабмед Статья Google ученый
Кернс Д.Н., Ким Дж.С., Танстолл Б.Дж., Силберберг А. Существенные ценности кокаина и немедикаментозных альтернатив предсказывают выбор между ними. Наркоман биол. 2017;22:1501–14.
КАС пабмед Статья Google ученый
Simmons SJ, Martorana R, Philogene-Khalid H, Tran FH, Gentile TA, Xu X, et al.
 Роль блокады гипокретиновых/орексиновых рецепторов при приеме наркотиков и ультразвуковых вокализациях (USV), связанная с самостоятельным введением 3,4-метилендиоксипировалерона, производного катинона (MDPV), у крыс без особых усилий. Психофармакология 2017; 234:3207–15.
Роль блокады гипокретиновых/орексиновых рецепторов при приеме наркотиков и ультразвуковых вокализациях (USV), связанная с самостоятельным введением 3,4-метилендиоксипировалерона, производного катинона (MDPV), у крыс без особых усилий. Психофармакология 2017; 234:3207–15.КАС пабмед ПабМед Центральный Статья Google ученый
Fragale JE, James MH, Aston-Jones G. Периодический самостоятельный прием фентанила вызывает состояние многогранной зависимости, связанное с постоянными изменениями в орексиновой системе. Наркоман биол. 2021;26:e12946.
КАС пабмед Статья Google ученый
Giannotti G, Gong S, Fayette N, Heinsbroek JA, Orfila JE, Herson PS, et al. Угасание притупляет вклад паравентрикулярного таламуса в героиновый рецидив. Представитель ячейки 2021; 36:109605.
КАС пабмед ПабМед Центральный Статья Google ученый
">Рассел Дж. А., Ленг Г., Дуглас А. Дж. Магноцеллюлярная система окситоцина, источник материнства: адаптация во время беременности. Передний нейроэндокринол. 2003; 24:27–61.
КАС пабмед Статья Google ученый
Ahmed SH, Guillem K, Vandaele Y. Сахарная зависимость: доведение до предела аналогии с наркотиками и сахаром. Curr Opin Clin Nutr Metab Care. 2013;16:434–9.
КАС пабмед Статья Google ученый
Ленуар М., Серр Ф., Кантин Л., Ахмед Ш. Интенсивная сладость превосходит кокаиновое вознаграждение. ПЛОС ОДИН. 2007;2:e698.

ПабМед ПабМед Центральный Статья Google ученый
Канши Л., Жирардо П., Дюран А., Вуйак-Мендоса С., Ахмед Ш. Фармакокинетика превосходит фармакодинамику при выборе кокаина: примирение с дофаминовой гипотезой зависимости. Нейропсихофармакология. 2021; 46: 288–96.
КАС пабмед Статья Google ученый
Вандале Ю., Ахмед Ш. Выбор между кокаином и сахарозой под воздействием: проверка влияния кокаиновой толерантности. Психофармакология 2022;239: 1053–63.
КАС пабмед Статья Google ученый
Christensen CJ, Silberberg A, Hursh SR, Huntsberry ME, Riley AL. Эссенциальная ценность кокаина и пищи для крыс: тесты экспоненциальной модели спроса. Психофармакология 2008;198:221–9.
КАС пабмед Статья Google ученый
">Чжан С., Жорницкий С., Ле Т.М., Ли Ч.Р. Гипоталамические реакции на кокаин и пищевые сигналы у людей с кокаиновой зависимостью. Int J Neuropsychopharmacol. 2019;22:754–64.
КАС пабмед ПабМед Центральный Статья Google ученый
ДиЛеоне Р.Дж., Джорджеску Д., Нестлер Э.Дж. Латеральные нейропептиды гипоталамуса в вознаграждении и наркомании. Жизнь наук. 2003;73:759–68.
КАС пабмед Статья Google ученый
Портер-Странски К.А., Бенцли Б.С., Астон-Джонс Г.
 Индивидуальные различия в модуляции рецептора орексина-I мотивации для опиоида ремифентанила. Наркомания биол. 2017;22:303–17.
Индивидуальные различия в модуляции рецептора орексина-I мотивации для опиоида ремифентанила. Наркомания биол. 2017;22:303–17.КАС Статья Google ученый
Smith RJ, Aston-Jones G. Антагонист рецепторов орексина/гипокретина 1 уменьшает самоуправление героином и поиск героина, вызванный сигналом. Евр Джей Нейроски. 2012;35:798–804.
ПабМед ПабМед Центральный Статья Google ученый
Хопф Ф.В. Недавние взгляды на орексин/гипокретин, стимулирующий поведение, связанное с зависимостью. Нейрофармакология 2020;168:108013.
КАС пабмед Статья Google ученый
Занос П., Георгиу П., Вебер С., Робинсон Ф., Куимцидис С., Нифорушан Р. и др. Новый взгляд на окситоцин и опиоидную зависимость: старый препарат, новые применения. Бр Дж.
 Фармакол. 2018;175:2809–24.
Фармакол. 2018;175:2809–24.КАС пабмед Статья Google ученый
Ковач С.Л., Ван, Ри Дж.М. Поведенчески активные фрагменты окситоцина одновременно ослабляют самостоятельное введение героина и толерантность у крыс. Жизнь наук. 1985; 37: 1895–1900.
КАС пабмед Статья Google ученый
Kovacs GL, Borthaiser Z, Telegdy G. Окситоцин снижает внутривенное введение героина у крыс, толерантных к героину. Жизнь наук. 1985;37:17–26.
КАС пабмед Статья Google ученый
Kovacs GL, Horvath Z, Sarnyai Z, Faludi M, Telegdy G. Окситоцин и С-концевое производное (Z-пролил-D-лейцин) ослабляют толерантность к морфину и зависимость от него и взаимодействуют с дофаминергической нейротрансмиссией у мышей мозг. Нейрофармакология 1985; 24:413–9.

КАС пабмед Статья Google ученый
Fan XY, Shi G, Zhao P. Изменение обусловленного оксикодоном предпочтения места окситоцином: содействие глобальному метилированию ДНК в гиппокампе. Нейрофармакология 2019;160:107778.
КАС пабмед Статья Google ученый
Фан XY, Ши Г, Хэ XJ, Ли XY, Ван YX, Цзянь LY. Окситоцин предотвращает вызванное сигналом восстановление поиска оксикодона: участие в метилировании ДНК в гиппокампе. Наркоман биол. 2021;26:e13025.
КАС пабмед Статья Google ученый
Занос П., Георгиу П., Райт С.Р., Хурани С.М., Китчен И., Вински-Соммерер Р. и др. Аналог окситоцина карбетоцин предотвращает эмоциональное ухудшение и вызванное стрессом восстановление поиска опиоидов у мышей, воздерживающихся от морфина.
 Нейропсихофармакология 2014;39:855–65.
Нейропсихофармакология 2014;39:855–65.КАС пабмед Статья Google ученый
Георгиу П., Занос П., Гарсия-Кармона Дж.А., Хурани С., Китчен И., Киффер Б.Л. и др. Аналог окситоцина карбетоцин предотвращает индуцированное праймингом восстановление поиска морфина: вовлечение дофаминергической, норадренергической и MOPr систем. Евро Нейропсихофармакол. 2015;25:2459–64.
КАС пабмед Статья Google ученый
Lee MR, Rohn MC, Tanda G, Leggio L. Ориентация на систему окситоцина для лечения зависимостей: обоснование и прогресс на сегодняшний день. Препараты ЦНС. 2016;30:109–23.
КАС пабмед ПабМед Центральный Статья Google ученый
Ахмед Ш. Кризис валидации в животных моделях наркомании: от беспорядочного употребления наркотиков к наркомании.
 Neurosci Biobehav Rev. 2010; 35:172–84.
Neurosci Biobehav Rev. 2010; 35:172–84.КАС пабмед Статья Google ученый
Хурш С.Р. Экономические концепции для анализа поведения. J Exp анальное поведение. 1980;34:219–38.
КАС пабмед ПабМед Центральный Статья Google ученый
Ким Дж.С., Гунаван Т., Триполи К.С., Зильберберг А., Кернс Д.Н. Влияние типа экономики на спрос и предпочтение кокаина и сахарина у крыс. Наркотики Алкогольная зависимость. 2018;192:150–7.
КАС пабмед ПабМед Центральный Статья Google ученый
Негус С.С., Бэнкс М.Л. Противостояние проблеме неудачного перевода в разработку лекарств от расстройств, связанных с употреблением психоактивных веществ. Фармакол Биохим Поведение. 2021;210:173264.
КАС пабмед ПабМед Центральный Статья Google ученый
">Юпп Б., Крстью Э., Дези Г., Лоуренс А.Дж. Дискретный поиск алкоголя, обусловленный сигналом, после длительного воздержания: характер нервной активации и участие рецепторов орексина (1). Бр Дж. Фармакол. 2011; 162:880–9.
КАС пабмед ПабМед Центральный Статья Google ученый
Yaeger JDW, Krupp KT, Jacobs BM, Onserio BO, Meyerink BL, Cain JT, et al. Антагонизм к рецептору орексина 1 в базолатеральной миндалине смещает баланс от про- к антистрессовой передаче сигналов и поведению.
 Биол психиатрия. 2022;91: 841–52.
Биол психиатрия. 2022;91: 841–52.КАС пабмед Статья Google ученый
Yaeger JDW, Krupp KT, Summers TR, Summers CH. Контекстуальная генерализация обучения социальному стрессу модулируется орексиновыми рецепторами в базолатеральной миндалевидном теле. Нейрофармакология 2022;215:109168.
КАС пабмед ПабМед Центральный Статья Google ученый
Norwood VMT, Brice-Tutt AC, Eans SO, et al. Предотвращение поведения, связанного с поиском морфина, путем изменения биологической активности винкамина. J Med Chem. 2020;63:5119–38.
ПабМед ПабМед Центральный Статья Google ученый
Шмейхель Б.Е., Герман М.А., Роберто М., Кооб Г.Ф. Нейротрансмиссия гипокретина в центральной миндалине опосредует эскалацию самостоятельного приема кокаина и вызванное стрессом восстановление у крыс.
 Биол психиатрия. 2017; 81: 606–15.
Биол психиатрия. 2017; 81: 606–15.КАС пабмед Статья Google ученый
Koch SB, van Zuiden M, Nawijn L, Frijling JL, Veltman DJ, Olff M. Интраназальный окситоцин нормализует функциональную связность миндалины при посттравматическом стрессовом расстройстве. Нейропсихофармакология 2016;41:2041–51.
КАС пабмед ПабМед Центральный Статья Google ученый
Холмквист Т., Акерман К.Е., Кукконен Дж.П. Передача сигналов орексина в рекомбинантных нейроноподобных клетках. ФЭБС лат. 2002; 526:11–14.
КАС пабмед Статья Google ученый
Zingg HH, Laporte SA. Рецептор окситоцина. Тенденции Эндокринол Метаб. 2003; 14: 222–7.
КАС пабмед Статья Google ученый
">James MH, Bowrey HE, Stopper CM, Aston-Jones G. Эластичность спроса предсказывает эндофенотипы зависимости и терапевтическую эффективность антагониста рецептора орексина/гипокретина-1 у крыс. Евр Джей Нейроски. 2019;50:2602–12.
ПабМед Статья Google ученый
Пантазис С.Б., Джеймс М.Х., Бенцли Б.С., Астон-Джонс Г. Количество орексиновых/гипокретиновых нейронов латерального гипоталамуса способствует индивидуальным различиям в потребности в кокаине. Наркоман биол. 2020;25:e12795.
КАС пабмед Статья Google ученый
">Мерфи Дж. Г., МакКиллоп Дж. Относительная укрепляющая эффективность алкоголя среди пьющих студентов колледжей. Exp Clin Psychopharmacol. 2006; 14: 219–27.
ПабМед Статья Google ученый
Мерфи Дж.Г., МакКиллоп Дж., Скидмор Дж.Р., Педерсон А.А. Надежность и обоснованность кривых спроса на алкогольное подкрепление. Exp Clin Psychopharmacol. 2009 г.;17:396–404.
ПабМед Статья Google ученый
Маккиллоп Дж., Мерфи Дж. Г., Тайди Дж. В., Калер К. В., Рэй Л. А.
 , Бикель В. К. Скрытая структура аспектов подкрепления алкоголем из поведенческой кривой экономического спроса. Психофармакология 2009; 203:33–40.
, Бикель В. К. Скрытая структура аспектов подкрепления алкоголем из поведенческой кривой экономического спроса. Психофармакология 2009; 203:33–40.КАС пабмед Статья Google ученый
Хунг Л.В., Нойнер С., Полепалли Дж.С., Бейер К.Т., Райт М., Уолш Дж.Дж. и др. Блокирование социального вознаграждения окситоцином в вентральной области покрышки. Наука 2017;357:1406–11.
КАС пабмед ПабМед Центральный Статья Google ученый
Ван Дж.С., Лю Дж.Л., Чжан Дж., Тан Дж., Хуан Т., Лу С.С. и др. Наследственное социальное тревожное расстройство и тяга к героину у женщин, вызванные физическими упражнениями, вызывают повышение уровня окситоцина в плазме. Фронтовая психиатрия. 2021;12:624993.
ПабМед ПабМед Центральный Статья Google ученый
Леонг К.С., Кокс С., Кинг С., Беккер Х., Райхель К.М. Окситоцин и модели зависимости у грызунов. Int Rev Neurobiol. 2018;140:201–47.
КАС пабмед ПабМед Центральный Статья Google ученый
King CE, Becker HC. Окситоцин ослабляет вызванное стрессом восстановление поведения, связанного с поиском алкоголя, у самцов и самок мышей. Психофармакология 2019;236:2613–22.
КАС пабмед ПабМед Центральный Статья Google ученый
Лоуренс А.Дж., Коуэн М.С., Ян Х.Дж., Чен Ф., Олдфилд Б. Система орексина регулирует поиск алкоголя у крыс. Бр Дж. Фармакол. 2006; 148: 752–9.
КАС пабмед ПабМед Центральный Статья Google ученый
Steiner MA, Lecourt H, Jenck F. Альморексант, антагонист рецепторов двойного орексина, сам по себе и в сочетании с морфином, кокаином и амфетамином, на предпочтение условного места и локомоторную сенсибилизацию у крыс. Int J Neuropsychopharmacol. 2013;16:417–32.
КАС пабмед Статья Google ученый
Расмуссен К., Уайт Д.А., Акри Дж.Б. Приоритеты NIDA в области разработки лекарств в ответ на опиоидный кризис: десять самых разыскиваемых. Нейропсихофармакология 2019;44:657–9.
ПабМед Статья Google ученый
Чжоу Л., Топленое масло С.М., См. Р.Е., Райхель К.М. Окситоцин по-разному влияет на потребление и поиск сахарозы у самцов и самок крыс. Поведение мозга Res. 2015; 283:184–90.
КАС пабмед ПабМед Центральный Статья Google ученый
Барсон Дж.Р., Лейбовиц С.Ф. Система орексин/гипокретин: роль в чрезмерном потреблении пищи и лекарств. Int Rev Neurobiol. 2017; 136:199–237.
КАС пабмед ПабМед Центральный Статья Google ученый
Галушка С.М., Банна К.М., Виллсе Л.В., Яхьяви-Фируз-Абади Н., См. РЭ. Сравнение экономического спроса и условного восстановления поиска метамфетамина или поиска пищи у крыс. Бихав Фармакол. 2011;22:312–23.
ПабМед ПабМед Центральный Статья Google ученый
Таунсенд Э.А., Швинтек К.Л., Робинсон Х.Л., Лоусон С.Т., Бэнкс М.Л. Процедура «выбора» лекарства или пищи у крыс для исследования фармакологических и экологических механизмов расстройств, связанных с употреблением психоактивных веществ. J Neurosci Методы. 2021;354:109110.
КАС пабмед ПабМед Центральный Статья Google ученый
Кабана-Домингес Дж., Ронсеро С., Пинеда-Сирера Л., Пальма-Альварес РФ, Рос-Кукурулл Э., Грау-Лопес Л. и др. Ассоциация гена PLCB1 с лекарственной зависимостью. Научный доклад 2017;7:10110.
ПабМед ПабМед Центральный Статья Google ученый
Пантазис К.Б., Джеймс М.Х., О'Коннор С., Шин Н., Астон-Джонс Г. Передача сигналов рецептора орексина-1 в вентральной области покрышки опосредует стимулируемый сигналом спрос на кокаин. Нейропсихофармакология 2022;47:741–51.
КАС пабмед Статья Google ученый
Ссылки на скачивание
Благодарности
Авторы выражают благодарность Программе снабжения лекарствами NIDA за поставку героина и Merck за поставку ДОРА-12.
Финансирование
Это исследование финансировалось NIDA R01 DA045836, R21 DA044524, K01 DA038235 (JP), K99 DA048974 (GG), DP5 OD026407 (JAH), R00 DA045765 (MHJ).
Информация об авторе
Примечания автора
Эти авторы внесли равный вклад: Джузеппе Джаннотти, Франческа Моттарлини.
Авторы и филиалы
Кафедра анестезиологии Университета Колорадо, Медицинский кампус Аншутц, Аврора, Колорадо, 80045, США
Джузеппе Джаннотти, Франческа Моттарлини, Джаспер А.
 Хайнсбрук, Митчел Р. Мандель и Джейми Питерс 19892 Фармакологическое отделение
Хайнсбрук, Митчел Р. Мандель и Джейми Питерс 19892 Фармакологическое отделение9202 920 и биомолекулярных наук, Миланский университет, 20133, Милан, Италия
Франческа Моттарлини
Кафедра психиатрии, Медицинская школа Роберта Вуда Джонсона, Университет Ратгерса, Пискатауэй, Нью-Джерси, 08854, США
Morgan H. James
Department of Pharmacology, University of Colorado, Anschutz Medical Campus, Aurora, CO, 80045, USA
Jamie Peters
Authors
- Giuseppe Giannotti
View author publications
You также можете искать этого автора в PubMed Google Scholar
- Francesca Mottarlini
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Jasper A. Heinsbroek
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Mitchel R.
 Mandel
MandelПросмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Morgan H. James
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Jamie Peters
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Взносы
GG и JP разработали исследование. GG, FM, MRM и MHJ провели эксперименты. GG, FM, JAH и JP проанализировали данные. GG, FM и JP написали рукопись при участии всех авторов.
Автор, ответственный за переписку
Переписка с Джейми Питерс.
Декларации этики
Конкурирующие интересы
JP является консультантом Delix Therapeutics, Inc.
Дополнительная информация
Примечание издателя Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.

 и др. Алгебра, 6-8. / Пробный учебник для 6-8 классов средней школы. — М., Просвещение, 1981.
и др. Алгебра, 6-8. / Пробный учебник для 6-8 классов средней школы. — М., Просвещение, 1981. – 2-е издание, испр. и доп. – М.:Педагогика, 1989.
– 2-е издание, испр. и доп. – М.:Педагогика, 1989.

 1 Произведение нескольких слагаемых равно нулю.
1 Произведение нескольких слагаемых равно нулю. 1 Найдите вершину y = x 2 -10x-24
1 Найдите вершину y = x 2 -10x-24
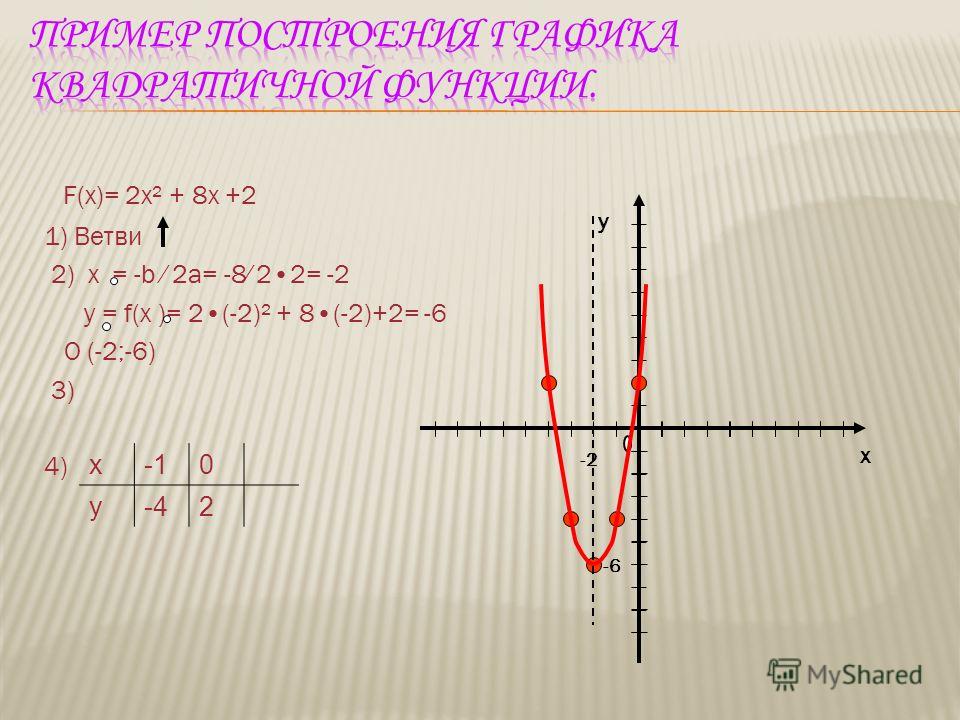 Поскольку
Поскольку  е. второй корень). 14
е. второй корень). 14  2018;87:3–10.
2018;87:3–10. Наркомания 2014; 109: 1426–36.
Наркомания 2014; 109: 1426–36. Int J Neuropsychopharmacol. 2014;18:pyu009.
Int J Neuropsychopharmacol. 2014;18:pyu009. двойное слепое плацебо-контролируемое исследование. Алкоголь Алкоголь. 2021; 56: 565–72.
двойное слепое плацебо-контролируемое исследование. Алкоголь Алкоголь. 2021; 56: 565–72. Теория наркомании. 2016;24:490–8.
Теория наркомании. 2016;24:490–8.
 Мозг Res. 2020;1731:145922.
Мозг Res. 2020;1731:145922. Нейрофармакология 2020;164:107906.
Нейрофармакология 2020;164:107906. Перепрофилирование двойного антагониста рецепторов орексина суворексанта для лечения расстройства, связанного с употреблением опиоидов: зачем спать на этом дольше? Нейропсихофармакология 2020;45:717–9.
Перепрофилирование двойного антагониста рецепторов орексина суворексанта для лечения расстройства, связанного с употреблением опиоидов: зачем спать на этом дольше? Нейропсихофармакология 2020;45:717–9. антагонист орексиновых/гипокретиновых рецепторов, ослабляет мотивационные и гедонистические свойства кокаина. Наркоман биол. 2018;23:247–55.
антагонист орексиновых/гипокретиновых рецепторов, ослабляет мотивационные и гедонистические свойства кокаина. Наркоман биол. 2018;23:247–55. Увеличение количества и активности латеральной субпопуляции гипоталамических орексиновых/гипокретиновых нейронов лежит в основе проявления наркозависимости у крыс. Биол психиатрия. 2019;85:925–35.
Увеличение количества и активности латеральной субпопуляции гипоталамических орексиновых/гипокретиновых нейронов лежит в основе проявления наркозависимости у крыс. Биол психиатрия. 2019;85:925–35. Роль блокады гипокретиновых/орексиновых рецепторов при приеме наркотиков и ультразвуковых вокализациях (USV), связанная с самостоятельным введением 3,4-метилендиоксипировалерона, производного катинона (MDPV), у крыс без особых усилий. Психофармакология 2017; 234:3207–15.
Роль блокады гипокретиновых/орексиновых рецепторов при приеме наркотиков и ультразвуковых вокализациях (USV), связанная с самостоятельным введением 3,4-метилендиоксипировалерона, производного катинона (MDPV), у крыс без особых усилий. Психофармакология 2017; 234:3207–15.
 Индивидуальные различия в модуляции рецептора орексина-I мотивации для опиоида ремифентанила. Наркомания биол. 2017;22:303–17.
Индивидуальные различия в модуляции рецептора орексина-I мотивации для опиоида ремифентанила. Наркомания биол. 2017;22:303–17. Фармакол. 2018;175:2809–24.
Фармакол. 2018;175:2809–24.
 Нейропсихофармакология 2014;39:855–65.
Нейропсихофармакология 2014;39:855–65. Neurosci Biobehav Rev. 2010; 35:172–84.
Neurosci Biobehav Rev. 2010; 35:172–84. Биол психиатрия. 2022;91: 841–52.
Биол психиатрия. 2022;91: 841–52. Биол психиатрия. 2017; 81: 606–15.
Биол психиатрия. 2017; 81: 606–15. , Бикель В. К. Скрытая структура аспектов подкрепления алкоголем из поведенческой кривой экономического спроса. Психофармакология 2009; 203:33–40.
, Бикель В. К. Скрытая структура аспектов подкрепления алкоголем из поведенческой кривой экономического спроса. Психофармакология 2009; 203:33–40. Хайнсбрук, Митчел Р. Мандель и Джейми Питерс 19892 Фармакологическое отделение
Хайнсбрук, Митчел Р. Мандель и Джейми Питерс 19892 Фармакологическое отделение Mandel
Mandel