Кольцевая прокладка 11,91 х 2,62 nbr 5408270 BAXI — оригинальная продукция от официального дилера БАКСИ
O-RING 11,91 X 2,62 NBR
Кольцевая прокладка 11,91 х 2,62 nbr 5408270 совместим со следующими моделями:
ECO Four 1.14 CSE461143540
ECO Four 1.14 F CSE465143540
ECO Four 1.14 F CSE465143541
ECO Four 1.24 CSE461243540
ECO Four 1.24 F CSE465243540
ECO Four 1.24 F CSE465243541
ECO-3 240 Fi CSB456243680
ECO-3 240 Fi CSB456243681
ECO-3 240 i CSB452243680
ECO-3 240 i CSB452243681
ECO-3 280 Fi CSB456283680
ECO-3 280 Fi CSB456283681
ECO-3 COMPACT 1.140 Fi CSB445143681
ECO-3 COMPACT 1.140 Fi CSB445143682
ECO-3 COMPACT 1.140 i CSB441143680
ECO-3 COMPACT 1.140 i CSB441143681
ECO-3 COMPACT 1.240 Fi CSB445243680
ECO-3 COMPACT 1.240 Fi CSB445243681
ECO-3 COMPACT 1.240 Fi CSB445243682
ECO-3 COMPACT 1.240 i CSB441243680
ECO-3 COMPACT 1.240 i CSB441243681
ECO-3 COMPACT 240 Fi CSB446243681
ECO-3 COMPACT 240 Fi CSB446243682
ECO-3 COMPACT 240 Fi CSB446243683
ECO-3 COMPACT 240 Fi CSB446243684
ECO-3 COMPACT 240 i CSB442243681
ECO-3 COMPACT 240 i CSB442243682
ECO-3 COMPACT 240 i CSB442243683
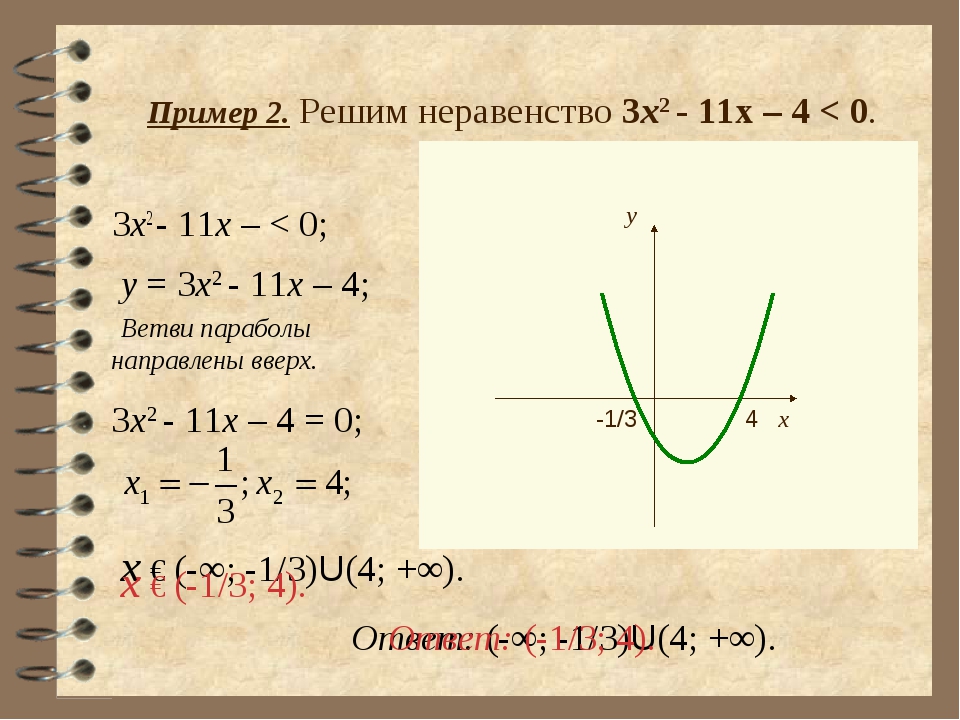 310 Fi CSE455313660
310 Fi CSE455313660LUNA-3 COMFORT 1.240 Fi CSE455243580
LUNA-3 COMFORT 1.240 Fi CSE455243581
LUNA-3 COMFORT 1.240 Fi CSE455243582
LUNA-3 COMFORT 1.240 i CSE451243580
LUNA-3 COMFORT 1.240 i CSE451243581
LUNA-3 COMFORT 1.240 i CSE451243582
LUNA-3 COMFORT 1.310 Fi CSE455313580
LUNA-3 COMFORT 1.310 Fi CSE455313581
LUNA-3 COMFORT 1.310 Fi CSE455313582
LUNA-3 COMFORT 240 Fi CSE456243580
LUNA-3 COMFORT 240 Fi CSE456243581
LUNA-3 COMFORT 240 i CSE452243580
LUNA-3 COMFORT 240 i CSE452243581
LUNA-3 COMFORT 310 Fi CSE456313580
LUNA-3 COMFORT 310 Fi CSE456313581
LUNA-3 COMFORT AIR 250 Fi CSB456253690
LUNA-3 COMFORT AIR 310 Fi CSB456313690
MAIN Four 18 F BSR466183411
MAIN Four 18 F BSR466183412
MAIN Four 18 F BSR466183413
MAIN Four 24 BSB462243650
MAIN Four 24 BSB462243651
MAIN Four 24 BSB462243652
MAIN Four 240 F BSE466243650
MAIN Four 240 F BSE466243651
MAIN Four 240 F BSE466243652
MAIN Four 240 F BSE466243653
MAIN Four 240 F BSE466243654
Старое написание артикула:
JJJ005408270, JJJ 005408270, JJJ 5408270
Номер позиции на чертеже: Подходит к следующим типам котлов: Подходит к сериям котлов BAXI: Используется в моделях котлов БАКСИ: ECO Four 1. 24 F, ECO Four 1.24, ECO Four 1.14, ECO-3 240 Fi, ECO Four 1.14 F, ECO-3 240 i, ECO-3 280 Fi, ECO-3 COMPACT 1.140 Fi, ECO-3 COMPACT 1.140 i, ECO-3 COMPACT 1.240 Fi, ECO-3 COMPACT 1.240 i, ECO-3 COMPACT 240 Fi, ECO-3 COMPACT 240 i, LUNA-3 1.310 Fi, LUNA-3 COMFORT 1.240 Fi, LUNA-3 COMFORT 1.240 i, LUNA-3 COMFORT 1.310 Fi, LUNA-3 COMFORT 240 Fi, LUNA-3 COMFORT 240 i, LUNA-3 COMFORT 310 Fi, LUNA-3 COMFORT AIR 250 Fi, LUNA-3 COMFORT AIR 310 Fi, MAIN Four 18 F, MAIN Four 24, MAIN Four 240 F
Гарантия:
24 F, ECO Four 1.24, ECO Four 1.14, ECO-3 240 Fi, ECO Four 1.14 F, ECO-3 240 i, ECO-3 280 Fi, ECO-3 COMPACT 1.140 Fi, ECO-3 COMPACT 1.140 i, ECO-3 COMPACT 1.240 Fi, ECO-3 COMPACT 1.240 i, ECO-3 COMPACT 240 Fi, ECO-3 COMPACT 240 i, LUNA-3 1.310 Fi, LUNA-3 COMFORT 1.240 Fi, LUNA-3 COMFORT 1.240 i, LUNA-3 COMFORT 1.310 Fi, LUNA-3 COMFORT 240 Fi, LUNA-3 COMFORT 240 i, LUNA-3 COMFORT 310 Fi, LUNA-3 COMFORT AIR 250 Fi, LUNA-3 COMFORT AIR 310 Fi, MAIN Four 18 F, MAIN Four 24, MAIN Four 240 F
Гарантия:Италия
Лезвие для ножа FATMAX STANLEY 2-11-718, с 18-мм лезвием с отламывающимися сегментами х 10шт.
Купить STANLEY 2-11-718 лезвие для ножа FATMAX STANLEY, с 18-мм лезвием с отламывающимися сегментами х 10шт. Цена на СТЭНЛИ 2-11-718 в официальном интернет-магазине пн–пт 9–21, сб–вс 9–19Скорее всего в вашем браузере отключён JavaScript.
Вы должны включить JavaScript в вашем браузере, чтобы использовать все возможности этого сайта.
Лезвие для ножа FATMAX STANLEY 2-11-718, с 18-мм лезвием с отламывающимися сегментами х 10шт.
Индукционная закалка режущей кромки для высокой прочности
Все характеристикиГород доставки:
Хотите дешевле?
Описание
- Лезвие запасное «FatMax» шириной 18 мм с отламывающимися сегментами.
- Индукционная закалка режущей кромки для высокой прочности
- Новая геометрия лезвия: увеличенная кромка
- Лезвие имеет 7 отделяемых сегментов (8 режущих кромок)
Характеристики
Основные характеристики
- Тип инструмента:
- Лезвие для ножа
- Длина, мм:
- 18
- Материал лезвия:
- сталь
- Количество изделий в упаковке, шт.:
- 10
Ножи строительные
- Длина лезвия, мм:
- 110
- Ширина лезвия, мм:
- 4.
 75
75
Гарантия
- Страна производства:
- Великобритания
- Разработано в:
- США
Дополнительная информация
- Обратите внимание:
- Производитель вправе изменять параметры продукции без дополнительного уведомления. Информация о технических характеристиках, комплекте поставки, стране изготовления и внешнем виде товара может отличаться от фактической и основывается на последних доступных к моменту публикации данных.
Вопросы и ответы
Лезвие для ножа FATMAX STANLEY 2-11-718, с 18-мм лезвием с отламывающимися сегментами х 10шт.
По этому товару ещё не задавали вопросов
Есть Вопрос? Спросите:
Пожалуйста, заполните все поля. Ответ на непубличный вопрос мы пришлём вам на электронную почту. Убедитесь, что ввели адрес правильно.
НазадОтзывы покупателей
Назад
Загружается…Мы используем файлы cookies! Оставаясь на нашем сайте, вы соглашаетесь на их использование. OK
OKSG @ 2021-07-17 02:38:21:G0:1.547:R145438
Дисковая пилорама ПТ-06 «КРОНА» (11 кВт х 2)
Пилорама обеспечивает производительность в зависимости от твердости древесины, сортамента пиломатериалов, от опыта оператора станка до 12…20м3 в смену. Дисковая пилорама ПТ-06 «КРОНА» позволяет получить высокую точность изделия за счет того, что пильные диски находятся на шпиндельном узле, который в отличии от вала двигателя не имеет хода в вертикальной плоскости. В отличии от ленточной, дисковая пилорама гарантирует отсутствие волнообразного эффекта. На практике дисковую пилораму часто используют в паре с ленточной. С помощью ленточной пилорамы делают лафет, а затем при помощи дисковой получают обрезную доску с высокой геометрией.
| Наименование параметров | Ед. изм. | ПТ-06 |
Напряжение | В | 380 |
Электродвигатель привода пилы дисковой (2шт. — номинальная мощность — число оборотов |
кВт об/мин |
11 3000 |
Электродвигатель подъема/опускания каретки: — номинальная мощность — число оборотов |
кВт об/мин |
0,55 950 |
| Режущий инструмент — пила дисковая (2шт.), — диаметр пил — толщина |
|
|
Максимальные размеры бревна: — диаметр в комле — высота бруса |
мм мм |
300 150 |
Расстояние от диска пилы до горизонтальной базы основания, — наибольший — наименьший | |
|
Длина бревна, — наибольшая — наименьшая |
мм мм |
6500 1000 |
Масса станка | кг | 800 |
Масса дороги направляющей | кг | 534 |
Шкаф-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Ясень Шимо Темный
Характеристики шкаф-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Ясень Шимо Темный
Описание шкаф-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Ясень Шимо Темный
Преимущества шкафа-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Ясень Шимо Темный
- Полноцветная печать делается на японском оборудовании, что позволяет обеспечить высочайшее качество и четкость рисунка.
 Вариаций изображений в большом ассортименте и можно легко подобрать шкаф-купе в комнату девочки или мальчика
Вариаций изображений в большом ассортименте и можно легко подобрать шкаф-купе в комнату девочки или мальчика - Уникальные запатентованные алюминиевые раздвижные двери Футурум. Оттенок серебра идеально подойдет почти в любой современный интерьер дома. Эргономика дверей рассчитана до мельчайших деталей и, следовательно, удобна для каждодневного пользования. Ну и сам материал(алюминий) как говорится «навсегда».
Шкаф-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Ясень Шимо Темный изготавливается из древесно-стружечной плиты.
Данная модель шкафа доступна в разных размерах:
- ширина шкафа: 120 см, 136.2 см, 168.2 см, 177 см, 201.4 см, 236 см;
- высота: 220 см, 230 см или 240 см;
- глубина шкафа-купе 62 сантиметра.
Небольшая ширина 120 см позволяет поставить шкаф-купе компактно в помещении. Но, большая глубина 62 см даст возможность расположить большое количество одежды и прочей утвари.
Дополнительные опции
- Комплект амортизационных щеток является доп.
 опцией для этого шкафа-купе.
опцией для этого шкафа-купе. - В данный шкаф возможно дополнить встраиваемую тумбу с двумя ящиками (фурнитура тумбы к шкафу-купе входят в состав тумбы). Дополнительную тумбу возможно закрепить в любой отдел с полками, за исключением нижнего и верхнего.
- Шкаф можно дополнить боковой консолью с необходимой стороны, либо с обеих сторон. То есть, вместе со шкафом-купе сделать стеллаж.
Мебель цвета «Ясень шимо темный» кажется элегантно и нежно. Данное цветовое решение соединяет в себе сдержанность и строгость с уютом и теплотой. За счет четко выраженной текстуры дерева и оттенка капучино такой шкаф-купе поможет создать приятную гармоничную обстановку в помещении. Шкаф-купе цвета «Ясень шимо темный» визуально освежает и расширяет пространство. Значит, он подойдёт даже для небольших помещений. Нейтральный изящный цвет шкафа позволяет создать органичные комбинации собстановкой, реализованной в зеленых, голубых, серых, белых, коралловых и иных цветах теплых и холодных тонов. Данный шкаф идеально выглядит в современных минималистичных, классических интерьерах.
Данный шкаф идеально выглядит в современных минималистичных, классических интерьерах.
Наша компания производит доставку мебели в Самаре и в Самарской области. Кроме того, доставка возможна почти по всей РФ и странам Таможенного союза:
- Киргизия
- Казахстан
- Беларусь
- Армения
Инструкции
Информация о доставке шкаф-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Ясень Шимо Темный
| Способ доставки | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Самовывоз | Бесплатно — самостоятельный вывоз с пункта выдачи. Пункт выдачи расположен по адресу г. Самара, ул. Береговая, 30. Режим работы: пн — пт, c 09:00 по 18:00, сб, c 09:00 по 13:00. Всего пунктов: 7 получения готовой мебели (посмотреть) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Доставка до подъезда дома из пункта выдачи | Время доставки согласуется дополнительно. Выгрузка из машины и подъём на нужный этаж осуществляется Вами лично, либо за дополнительную плату после согласования с менеджером. 2-30x+100$ равна $6$. После деления на два заданных бинома степень заданного многочлена уменьшится на $2$, т.е. станет равна $4$. 2-30x+100$ равна $6$. После деления на два заданных бинома степень заданного многочлена уменьшится на $2$, т.е. станет равна $4$.Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целочисленных корней метод довольно-таки неплох. Уравнения 5 класса | МатематикаСегодня мы рассмотрим более сложные уравнения 5 класса, содержащие несколько действий. Чтобы найти неизвестную переменную, в таких уравнениях надо применить не одно, а два правила.1) x:7+11=21 Выражение, стоящее в левой части — сумма двух слагаемых
Таким образом, переменная x является частью первого слагаемого. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое: x:7=21-11 x:7=10 Получили простое уравнение 5 класса, из которого надо найти неизвестное делимое. Чтобы найти неизвестное делимое, нужно частное умножить на делитель: x=10∙7 x=70 Ответ: 70. 2) 65-5z=30 Правая часть уравнения представляет собой разность:
Переменная z является частью неизвестного вычитаемого. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность: 5z=65-30 5z=35 Получили простое уравнение, в котором z — неизвестный множитель. z=35:5 z=7 Ответ: 7. 3) 120:y-23=17 В правой части уравнения — разность. Переменная y является частью неизвестного уменьшаемого.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое: 120:y=17+23 120:y=40 Здесь y — неизвестный делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное: y=120:40 y=3 Ответ: 3. 4) (48+k)∙8=400 Левая часть уравнения представляет собой произведение.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель: 48+k=400:8 48+k=50 В новом уравнении k — неизвестное слагаемое: k=50-48 k=2 Ответ: 2. Здесь мы решали уравнения 5 класса без использования свойств сложения и вычитания. В 6 классе правила раскрытия скобок упрощаются, и решать такие уравнения становится проще. Шкаф-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Белая Шагрень в Петропавловске-Камчатском заказать выгодно за 24097 рХарактеристики шкаф-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Белая Шагрень Описание шкаф-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Белая Шагрень Маленькая ширина 120 см позволяет поставить шкаф-купе компактно в помещении. Дополнительный функционал
Корпусные шкафы с оттенком «Белая шагрень» могут быть использованы в интерьере в любом стиле: от современного до классического, а также, возможно их применение в качестве одного из элементов эклектики. Светлые цвета расширяют и «разгружают» пространство квартиры, потому, белая шагрень — это довольно частый выбор в маленькие помещения. Шкаф-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Белая Шагрень производится из древесно-стружечной плиты (ДСП). Данная модель возможна в разных размерах:
Преимущества шкафа-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Белая Шагрень
Наш магазин доставляет мебель в Петропавловске-Камчатском и на Камчатке. Кроме того, доставка возможна почти по всей Российской федерации и странам Евразийского экономического союза:
ИнструкцииИнформация о доставке шкаф-купе 2-х дверный 2400х1200х620 ХИТ 24-12/2-11 Белая Шагрень
Пошаговое решение:Шаг 1:Калькулятор полиномиальных корней: 1.1 Найдите корни (нули): F (x) = x 2 +11 Rational Roots Test является одним из вышеупомянутых инструментов. Теорема рационального корня утверждает, что если полином обнуляется для рационального числа P / Q, то P является множителем конечной константы и Q является множителем ведущего коэффициента В этом случае ведущий коэффициент равен 1, а конечная константа — 11. Фактор (ы): ведущего коэффициента: 1 Давайте проверим ….
Уравнение в конце шага 1:x 2 + 11 = 0 Шаг 2:Решение уравнения с одной переменной:2.1 Решите: x 2 +11 = 0 Вычтем 11 из обеих частей уравнения: В математике i называется мнимой единицей. Он удовлетворяет i 2 = -1. Оба i и -i являются квадратными корнями из -1 Соответственно, √ -11 = Уравнение не имеет реальных решений. У него есть 2 воображаемых или сложных решения. x = 0,0000 + 3,3166 i Было найдено два решения:
Algebra Calculator Tutorial — MathPapaЭто руководство по использованию калькулятора алгебры , пошагового калькулятора для алгебры. Решение уравненийСначала перейдите на главную страницу калькулятора алгебры.В текстовом поле калькулятора вы можете ввести математическую задачу, которую хотите вычислить. Например, попробуйте ввести уравнение 3x + 2 = 14 в текстовое поле. После того, как вы введете выражение, Калькулятор алгебры распечатает пошаговое объяснение того, как решить 3x + 2 = 14. ПримерыЧтобы увидеть больше примеров задач, которые понимает калькулятор алгебры, посетите Страница примеров. Вы можете попробовать их прямо сейчас.2.Вычисление выражений Калькулятор алгебры может вычислять выражения, содержащие переменную x. Чтобы оценить выражение, содержащее x, введите выражение, которое вы хотите оценить, затем знак @ и значение, которое вы хотите вставить для x. Например, команда 2x @ 3 вычисляет выражение 2x для x = 3, что равно 2 * 3 или 6. Калькулятор алгебры также может вычислять выражения, содержащие переменные x и y.Чтобы оценить выражение, содержащее x и y, введите выражение, которое вы хотите оценить, затем знак @ и упорядоченную пару, содержащую ваше значение x и значение y. Вот пример вычисления выражения xy в точке (3,4): xy @ (3,4). Проверка ответов для решения уравненийТак же, как калькулятор алгебры можно использовать для вычисления выражений, Калькулятор алгебры также можно использовать для проверки ответов на решение уравнений, содержащих x. В качестве примера предположим, что мы решили 2x + 3 = 7 и получили x = 2.Если мы хотим вставить 2 обратно в исходное уравнение, чтобы проверить нашу работу, мы можем сделать это: 2x + 3 = 7 @ 2. Если вместо этого мы попробуем значение, которое не работает, скажем, x = 3 (попробуйте 2x + 3 = 7 @ 3), вместо этого калькулятор алгебры покажет красный знак «не равно». Чтобы проверить ответ на систему уравнений, содержащую x и y, введите два уравнения, разделенные точкой с запятой, за которыми следует знак @ и упорядоченную пару, содержащую ваше значение x и значение y.Пример: x + y = 7; х + 2у = 11 @ (3,4). Режим планшетаЕсли вы используете планшет, например iPad, войдите в режим планшета, чтобы отобразить сенсорную клавиатуру. Статьи по темеВернуться к калькулятору алгебры » квадратичное разложение с использованием разделения среднего членаCovid-19 привел мир к феноменальному переходу. За электронным обучением будущее уже сегодня. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!! Квадратичная факторизация с использованием разбиения среднего члена: В этом методе разбиение среднего члена на два фактора.
В квадратичной факторизации с использованием разбиения среднесрочного члена x-член представляет собой сумму двух факторов и произведение, равное последнему члену.
Квадратичная факторизация с использованием разделения среднесрочного периода
Корни уравнения равны 3x — 2 = 0 ⇒ 3x = 2, поэтому x = 2/3 2x — 3 = 0 ⇒ 2x = 3, поэтому x = 3/2 Корни равны {2/3, 3/2} Примеры квадратичной факторизации с разделением среднесрочной перспективы 1) 12x 2 -15 = 11x Решение: 12x 2 -15 + 11x = 0 [добавить + 11x 12x 2 + 11x -15 = 0 12x 2 + 20x — 9x -15 = 0 4x (3x + 5) — 3 (3x + 5) = 0 (3x + 5) (4x — 3) = 0 3x + 5 = 0 или 4x — 3 = 0 3x = — 5 или 4x = 3 x = -5/3 или x = 3/4 Решение: (-5 / 3,3 / 4) _________________________________________________________________ Решение: ⇒ 3x (x — 1) + (x — 1) = 0 ⇒ (x — 1) (3x + 1) = 0 ⇒ x = 1 и x = -1/3 ________________________________________________________________ 3) Произведение двух последовательных положительных целых чисел равно 240. Решение: x (x + 1) = 240 x 2 + x = 240 x 2 + x — 240 = 0 x 2 + 16x — 15x — 240 = 0 x ( x + 16) — 15 (x -16) = 0 (x + 16) (x -15) = 0 x = -16 и x = 15 Таким образом, положительные целые числа равны 15 и 16. Введение в квадратные уравнения • Квадратичная факторизация с использованием разделения среднего срока Covid-19 повлиял на физические взаимодействия между людьми. Не позволяйте этому влиять на ваше обучение. Решение системных уравнений | Уравнения и неравенства \ (- 10 x = -1 \) и
\ (- 4 х + 10 у = -9 \). Решить относительно \ (x \): \ begin {align *} — 10х = -1 \\ \ поэтому x = \ frac {1} {10} \ end {выровнять *}Подставляем значение \ (x \) во второе уравнение и решаем относительно \ (y \): \ begin {align *} -4x + 10y & = -9 \\ -4 \ left (\ frac {1} {10} \ right) + 10y & = -9 \\ \ frac {-4} {10} + 10y & = -9 \\ 100л & = -90 + 4 \\ y & = \ frac {-86} {100} \\ & = \ frac {-43} {50} \ end {выровнять *} Следовательно, \ (x = \ frac {1} {10} \ text {и} y = — \ frac {43} {50} \). \ (3x — 14y = 0 \) и \ (x — 4y + 1 = 0 \) Запишите \ (x \) через \ (y \): \ begin {align *} 3х — 14лет & = 0 \\ 3х & = 14л \\ x & = \ frac {14} {3} y \ end {выровнять *}Подставьте значение \ (x \) во второе уравнение: \ begin {align *} х — 4у + 1 & = 0 \\ \ frac {14} {3} y — 4y + 1 & = 0 \\ 14лет — 12лет + 3 & = 0 \\ 2у & = -3 \\ y & = — \ frac {3} {2} \ end {выровнять *}Подставить значение \ (y \) обратно в первое уравнение: \ begin {align *} x & = \ frac {14 \ left (- \ frac {3} {2} \ right)} {3} \\ & = -7 \ end {выровнять *} Следовательно, \ (x = -7 \ text {и} y = — \ frac {3} {2} \). \ (x + y = 8 \) и \ (3x + 2y = 21 \) Запишите \ (x \) через \ (y \): \ begin {align *} х + у & = 8 \\ х & = 8 — у \ end {выровнять *}Подставьте значение \ (x \) во второе уравнение: \ begin {align *} 3х + 2у & = 21 \\ 3 (8 — у) + 2у & = 21 \\ 24 — 3л + 2у & = 21 \\ y & = 3 \ end {выровнять *}Подставить значение \ (y \) обратно в первое уравнение: \ [x = 5 \]Следовательно, \ (x = 5 \ text {и} y = 3 \). \ (y = 2x + 1 \) и \ (x + 2y + 3 = 0 \) Запишите \ (y \) через \ (x \): \ [y = 2x + 1 \]Подставьте значение \ (y \) во второе уравнение: \ begin {align *} х + 2у + 3 & = 0 \\ х + 2 (2х + 1) + 3 & = 0 \\ х + 4х + 2 + 3 & = 0 \\ 5x & = -5 \\ х & = -1 \ end {выровнять *}Подставить значение \ (x \) обратно в первое уравнение: \ begin {align *} у & = 2 (-1) + 1 \\ & = -1 \ end {выровнять *} Следовательно, \ (x = -1 \ text {и} y = -1 \). \ (5x-4y = 69 \) и \ (2x + 3y = 23 \) Сделайте \ (x \) предметом первого уравнения: \ begin {align *} 5х-4л & = 69 \\ 5х & = 69 + 4у \\ x & = \ frac {69 + 4y} {5} \ end {выровнять *}Подставьте значение \ (x \) во второе уравнение: \ begin {align *} 2х + 3у & = 23 \\ 2 \ left (\ frac {69 + 4y} {5} \ right) + 3y & = 23 \\ 2 (69 + 4у) +3 (5) у & = 23 (5) \\ 138 + 8л + 15л & = 115 \\ 23лет & = -23 \\ \ поэтому y & = -1 \ end {выровнять *}Подставить значение \ (y \) обратно в первое уравнение: \ begin {align *} x & = \ frac {69 + 4y} {5} \\ & = \ frac {69 + 4 (-1)} {5} \\ & = 13 \ end {выровнять *} Следовательно, \ (x = 13 \ text {и} y = -1 \). \ (x + 3y = 26 \) и \ (5x + 4y = 75 \) Сделайте \ (x \) предметом первого уравнения: \ begin {align *} х + 3у & = 26 \\ x & = 26 — 3 года \ end {выровнять *}Подставьте значение \ (x \) во второе уравнение: \ begin {align *} 5х + 4у & = 75 \\ 5 (26 — 3л) + 4л & = 75 \\ 130 — 15л + 4л & = 75 \\ -11л & = -55 \\ \ поэтому y & = 5 \ end {выровнять *}Подставить значение \ (y \) обратно в первое уравнение: \ begin {align *} х & = 26 — 3у \\ & = 26 — 3 (5) \\ & = 11 \ end {выровнять *} Следовательно, \ (x = 11 \ text {и} y = 5 \). \ (3x — 4y = 19 \) и \ (2x — 8y = 2 \) Если мы умножим первое уравнение на 2, то коэффициент при \ (y \) будет одинаковым в обоих уравнениях: \ begin {align *} 3х — 4л & = 19 \\ 3 (2) х — 4 (2) у & = 19 (2) \\ 6x — 8 лет & = 38 \ end {выровнять *}Теперь мы можем вычесть второе уравнение из первого: \ [\ begin {array} {cccc} & 6x — 8лет & = & 38 \\ — & (2x — 8y & = & 2) \\ \ hline & 4x + 0 & = & 36 \ конец {массив} \]Решить относительно \ (x \): \ begin {align *} \ поэтому x & = \ frac {36} {4} \\ & = 9 \ end {выровнять *}Подставьте значение \ (x \) в первое уравнение и решите относительно \ (y \): \ begin {align *} 3х-4л & = 19 \\ 3 (9) -4y & = 19 \\ \ поэтому y & = \ frac {19-3 (9)} {- 4} \\ & = 2 \ end {выровнять *} Следовательно, \ (x = 9 \ text {и} y = 2 \). \ (\ dfrac {a} {2} + b = 4 \) и \ (\ dfrac {a} {4} — \ dfrac {b} {4} = 1 \) Сделайте \ (a \) предметом первого уравнения: \ begin {align *} \ frac {a} {2} + b & = 4 \\ а + 2b & = 8 \\ а & = 8 — 2b \ end {выровнять *}Подставьте значение \ (a \) во второе уравнение: \ begin {align *} \ frac {a} {4} — \ frac {b} {4} & = 1 \\ а — б & = 4 \\ 8 — 2б — б & = 4 \\ 3b & = 4 \\ b & = \ frac {4} {3} \ end {выровнять *}Подставить значение \ (b \) обратно в первое уравнение: \ begin {align *} a & = 8 — 2 \ left (\ frac {4} {3} \ right) \\ & = \ frac {16} {3} \ end {выровнять *} Следовательно, \ (a = \ frac {16} {3} \ text {и} b = \ frac {4} {3} \). \ (- 10x + y = -1 \) и \ (- 10x — 2y = 5 \) Если мы вычтем второе уравнение из первого, то мы сможем решить для \ (y \): \ [\ begin {array} {cccc} & -10x + y & = & -1 \\ — & (-10x — 2y & = & 5) \\ \ hline & 0 + 3г & = & -6 \ конец {массив} \]Решить относительно \ (y \): \ begin {align *} 3лет & = -6 \\ \ поэтому y & = -2 \ end {выровнять *}Подставьте значение \ (y \) в первое уравнение и решите относительно \ (x \): \ begin {align *} -10x + y & = -1 \\ -10x — 2 & = -1 \\ -10x & = 1 \\ x & = \ frac {1} {- 10} \ end {выровнять *} Следовательно, \ (x = \ frac {-1} {10} \ text {и} y = -2 \). \ (- 10 x — 10 y = -2 \) и \ (2 x + 3 y = 2 \) Сделайте \ (x \) предметом первого уравнения: \ begin {align *} — 10 х — 10 у = -2 \\ 5х + 5у & = 1 \\ 5x & = 1 — 5л \\ \ поэтому x = -y + \ frac {1} {5} \ end {выровнять *}Подставляем значение \ (x \) во второе уравнение и решаем относительно \ (y \): \ begin {align *} 2х + 3у & = 2 \\ 2 \ left (-y + \ frac {1} {5} \ right) + 3y & = 2 \\ -2y + \ frac {2} {5} + 3y & = 2 \\ y & = \ frac {8} {5} \ end {выровнять *}Подставьте значение \ (y \) в первое уравнение: \ begin {align *} 5х + 5у & = 1 \\ 5x + 5 \ влево (\ frac {8} {5} \ right) & = 1 \\ 5х + 8 & = 1 \\ 5x & = -7 \\ x & = \ frac {-7} {5} \ end {выровнять *} Следовательно, \ (x = — \ frac {7} {5} \ text {и} y = \ frac {8} {5} \). \ (\ dfrac {1} {x} + \ dfrac {1} {y} = 3 \) и \ (\ dfrac {1} {x} — \ dfrac {1} {y} = 11 \) Переставьте оба уравнения, умножив на \ (xy \): \ begin {align *} \ frac {1} {x} + \ frac {1} {y} & = 3 \\ у + х & = 3xy \\\\ \ frac {1} {x} — \ frac {1} {y} & = 11 \\ у — х & = 11xy \ end {выровнять *}Сложите два уравнения вместе: \ [\ begin {array} {cccc} & y + x & = & 3xy \\ + & (у — х & = & 11xy) \\ \ hline & 2y + 0 & = & 14xy \ конец {массив} \]Решить относительно \ (x \): \ begin {align *} 2y & = 14xy \\ у & = 7xy \\ 1 & = 7x \\ х & = \ гидроразрыв {1} {7} \ end {выровнять *}Подставить значение \ (x \) обратно в первое уравнение: \ begin {align *} y + \ frac {1} {7} & = 3 \ left (\ frac {1} {7} \ right) y \\ 7у + 1 & = 3у \\ 4г & = -1 \\ y & = — \ frac {1} {4} \ end {выровнять *} Следовательно, \ (x = \ frac {1} {7} \ text {и} y = — \ frac {1} {4} \). Поскольку это верно для всех \ (x \) в действительных числах, \ (x \) может быть любым действительным числом. Посмотрите, что происходит с \ (y \), когда \ (x \) очень маленький или очень большой: Наименьшее значение \ (x \) может быть равно 0. Когда \ (x = 0 \), \ (y = 2- \ frac {3} {2} = \ frac {1} {2} \).2 & = 3 — ab \ end {выровнять *} Обратите внимание, что это то же самое, что и второе уравнение \ (a \) и \ (b \) может быть любым действительным числом, кроме \ (\ text {0} \). % PDF-1. Калькулятор дробей Правила для выражений с дробями:Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже). Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 . Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций: Задачи с дробями:следующие математические задачи » ЖК-калькуляторКак найти ЖК-дисплей? Чтобы найти ЖКИ, сначала переводим все целые числа и смешанные дроби в дроби.
Затем находим НОК знаменателей. Результатом является ЖК-дисплей, и каждая дробь должна быть записана как эквивалентная дробь с тем же ЖК-дисплеем.2y $. В общем, наименьший общий знаменатель может быть числом, переменной или комбинацией чисел и переменных.
Чтобы найти LCM с двумя или более числами, обратитесь к калькулятору LCM . Здесь мы покажем, как найти ЖК-дисплей $ \ frac {4} {5}, \ frac {6} {8}, \ frac {13} {11}, \ frac {2} {10} $ с помощью простые множители. LCM (5, 8, 11, 10) = 5 1 x 2 3 x 11 1 = 440 = LCD (4/5, 6/8, 13/11, 2 / 10) Если мы перепишем исходные входные данные как эквивалентные дроби с помощью ЖК-дисплея, мы получим дроби $$ \ frac {352} {440}, \ frac {330} {440}, \ frac {520} {440}, \ frac {88} {440} $$ Работа с общим знаменателем с шагами показывает полное пошаговое вычисление для нахождения наименьшего общего знаменателя для данного набора чисел: $ \ frac {4} {5}, \ frac {6} {8}, \ frac { 13} {11}, \ frac {2} {10} $ с использованием факторизации на простые множители.Для любой другой набор чисел, просто укажите список чисел и нажмите кнопку «Создать работу». Учащиеся начальной школы могут использовать этот общий знаменатель для расчета работать, проверять результаты сложения, вычитания или сравнения дробей, полученных вручную, или эффективно выполнять домашние задания.  |

 75
75 ),
), Вариаций изображений в большом ассортименте и можно легко подобрать шкаф-купе в комнату девочки или мальчика
Вариаций изображений в большом ассортименте и можно легко подобрать шкаф-купе в комнату девочки или мальчика опцией для этого шкафа-купе.
опцией для этого шкафа-купе.
 Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель:
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель:
 Но, достаточно большая глубина 62 см даст возможность расположить приличное количество ваших вещей.
Но, достаточно большая глубина 62 см даст возможность расположить приличное количество ваших вещей.

 Он может найти только рациональные корни, то есть числа x, которые можно выразить как частное двух целых чисел
Он может найти только рациональные корни, то есть числа x, которые можно выразить как частное двух целых чисел 00
00

 Поскольку ответ правильный, калькулятор алгебры показывает зеленый знак равенства.
Поскольку ответ правильный, калькулятор алгебры показывает зеленый знак равенства. Факторизуйте каждую пару, найдя общие факторы.
Факторизуйте каждую пару, найдя общие факторы.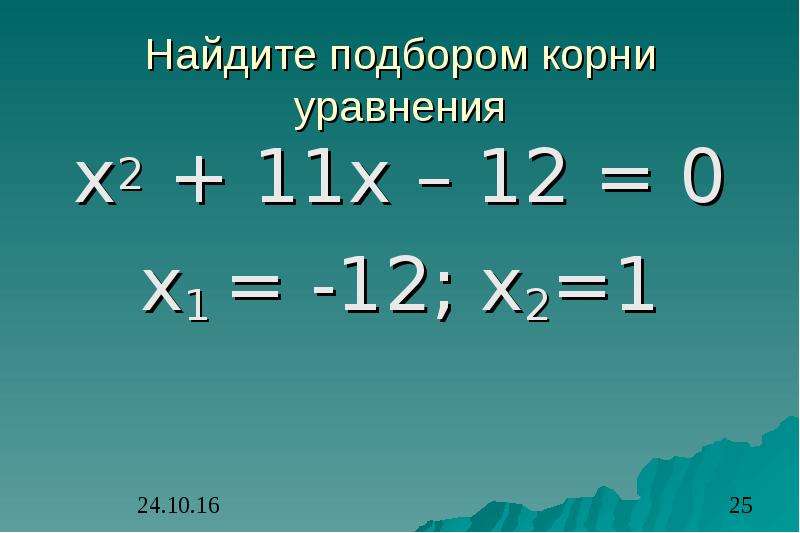 Найдите целые числа.
Найдите целые числа.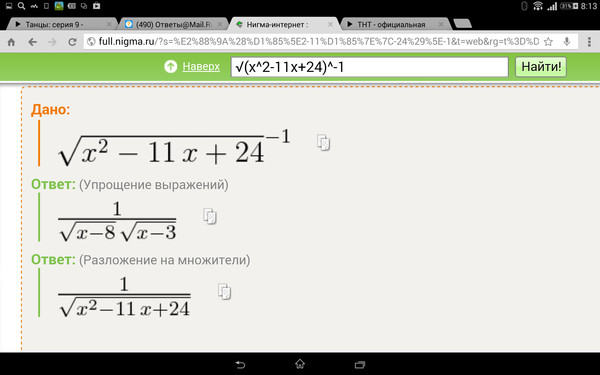



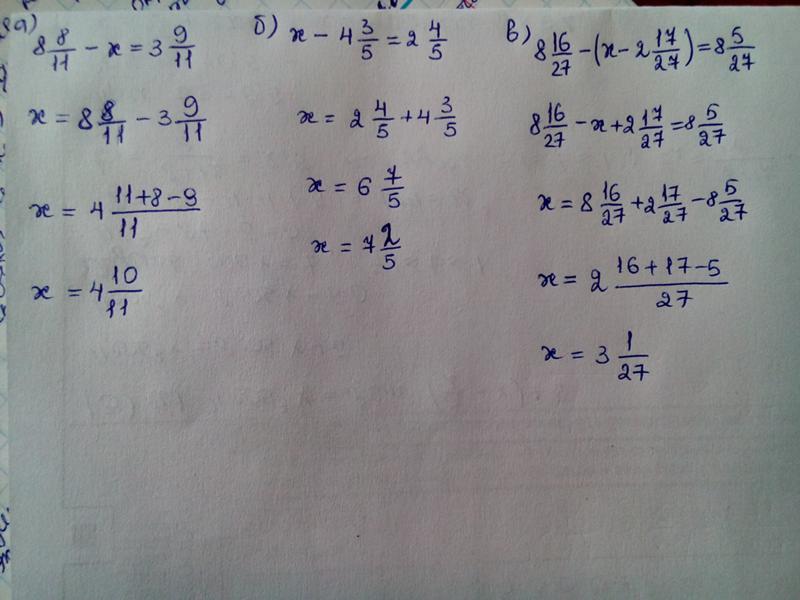
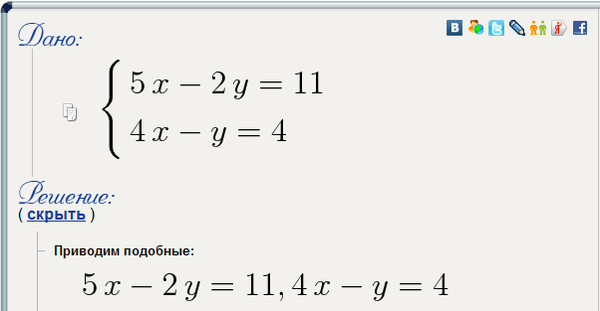




 2 + 1 \\
0 & = 0
\ end {выровнять *}
2 + 1 \\
0 & = 0
\ end {выровнять *} 4
%
1374 0 объект
>
эндобдж
xref
1374 80
0000000016 00000 н.
0000002429 00000 н.
0000002577 00000 н.
0000003363 00000 н.
0000003688 00000 н.
0000003768 00000 н.
0000005982 00000 п.
0000006187 00000 н.
0000007970 00000 п.
0000008701 00000 н.
0000009210 00000 п.
0000009447 00000 н.
0000010502 00000 п.
0000011691 00000 п.
0000012851 00000 п.
0000014015 00000 п.
0000015732 00000 п.
0000015989 00000 п.
0000016073 00000 п.
0000016130 00000 п.
0000016166 00000 п.
0000016196 00000 п.
0000016273 00000 п.
0000016388 00000 п.
0000035570 00000 п.
0000035892 00000 п.
0000035961 00000 п.
0000036079 00000 п.
0000036196 00000 п.
0000036232 00000 п.
0000036309 00000 п.
0000044980 00000 п.
0000045314 00000 п.
0000045383 00000 п.
0000045501 00000 п.
0000045617 00000 п.
0000045730 00000 п.
0000047075 00000 п.
0000047395 00000 п.
0000047758 00000 п.
0000047844 00000 п.
0000050958 00000 п.
0000051374 00000 п.
0000051884 00000 п.
0000053259 00000 п.
0000053618 00000 п.
4
%
1374 0 объект
>
эндобдж
xref
1374 80
0000000016 00000 н.
0000002429 00000 н.
0000002577 00000 н.
0000003363 00000 н.
0000003688 00000 н.
0000003768 00000 н.
0000005982 00000 п.
0000006187 00000 н.
0000007970 00000 п.
0000008701 00000 н.
0000009210 00000 п.
0000009447 00000 н.
0000010502 00000 п.
0000011691 00000 п.
0000012851 00000 п.
0000014015 00000 п.
0000015732 00000 п.
0000015989 00000 п.
0000016073 00000 п.
0000016130 00000 п.
0000016166 00000 п.
0000016196 00000 п.
0000016273 00000 п.
0000016388 00000 п.
0000035570 00000 п.
0000035892 00000 п.
0000035961 00000 п.
0000036079 00000 п.
0000036196 00000 п.
0000036232 00000 п.
0000036309 00000 п.
0000044980 00000 п.
0000045314 00000 п.
0000045383 00000 п.
0000045501 00000 п.
0000045617 00000 п.
0000045730 00000 п.
0000047075 00000 п.
0000047395 00000 п.
0000047758 00000 п.
0000047844 00000 п.
0000050958 00000 п.
0000051374 00000 п.
0000051884 00000 п.
0000053259 00000 п.
0000053618 00000 п. ; p! XW | / d2] ZGx4 ## \ T { -Xa @
; p! XW | / d2] ZGx4 ## \ T { -Xa @ 1/2
1/2 
 1}} \ end {align} $$
При умножении наибольшей степени 2, 11 и 5, образующих эти факторизации, НОК 5, 8, 11, 10 равно НОК $ \ frac {4} {5}, \ frac {6} {8}, \ frac {13} {11}, \ frac {2} {10}.$ Это означает, что
1}} \ end {align} $$
При умножении наибольшей степени 2, 11 и 5, образующих эти факторизации, НОК 5, 8, 11, 10 равно НОК $ \ frac {4} {5}, \ frac {6} {8}, \ frac {13} {11}, \ frac {2} {10}.$ Это означает, что