X в кубе минус y в кубе. Формулы сокращенного умножения
Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.
Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).
Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.
Квадрат суммы
Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².
Квадрат разности
Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².
Разность квадратов
Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).
Куб суммы
Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого.
Сумма кубов
Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).
Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.
Если значения сторон небольшие, то выполнить вычисления просто.
Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.
Куб разности
Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.
Разность кубов
Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).
Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.
Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.
Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой , которую мы рекомендуем распечатать и все время держать перед глазами:
Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений.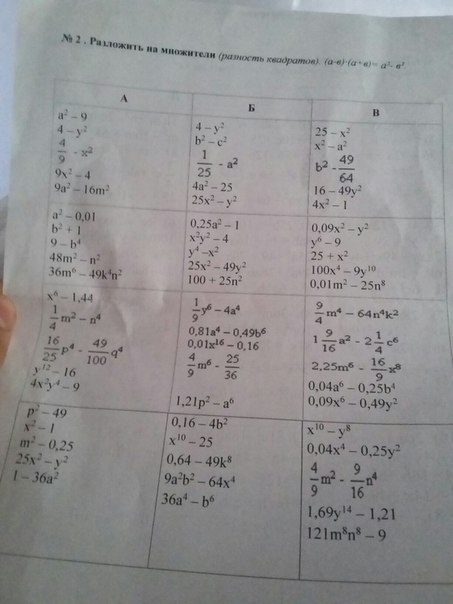 Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a
и b
на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2
) и разности двух выражений a
и b
на неполный квадрат их суммы (a 2 +a·b+b 2
) соответственно.
Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a
и b
на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2
) и разности двух выражений a
и b
на неполный квадрат их суммы (a 2 +a·b+b 2
) соответственно.
Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество . Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.
При решении примеров, особенно в которых имеет место разложение многочлена на множители , ФСУ часто используют в виде с переставленными местами левыми и правыми частями:
Три последних тождества в таблице имеют свои названия. Формула a 2 −b 2 =(a−b)·(a+b)
называется формулой разности квадратов , a 3 +b 3 =(a+b)·(a 2 −a·b+b 2
) — формулой суммы кубов , а a 3 −b 3 =(a−b)·(a 2 +a·b+b 2
) — формулой разности кубов . Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.
Дополнительные формулы
В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.
Сферы применения формул сокращенного умножения (фсу) и примеры
Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.
Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений . Наиболее часто эти формулы используются в процессе упрощения выражений .
Пример.
Упростите выражение 9·y−(1+3·y) 2 .
Решение.
В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y) 2 =9·y−(1 2 +2·1·3·y+(3·y) 2) . Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1 2 +2·1·3·y+(3·y) 2)= 9·y−1−6·y−9·y 2 =3·y−1−9·y 2 .
При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения .
Следует также помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.
Разность квадратов
Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.
a 2 — b 2 = (a — b)(a + b)
Квадрат суммы
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
(a + b) 2 = a 2 + 2ab + b 2
Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел , не используя калькулятор или умножение в столбик. Поясним на примере:
Найти 112 2 .
Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.2
112 = 100 + 1
Запишем сумму чисел в скобки и поставим над скобками квадрат.
Воспользуемся формулой квадрата суммы:
112 2 = (100 + 12) 2 = 100 2 + 2 x 100 x 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544
Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.
(8a + с) 2 = 64a 2 + 16ac + c 2
Предостережение!!!
(a + b) 2 не равно a 2 + b 2
Квадрат разности
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.
(a — b) 2 = a 2 — 2ab + b 2
Также стоит запомнить весьма полезное преобразование:
(a — b)
2
= (b — a)
2
Формула выше доказывается простым раскрытием скобок:
(a — b)
2
= a
2
— 2ab + b
2
= b
2
— 2ab + a
2
= (b — a)
2
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
Запомнить эту «страшную» на вид формулу довольно просто.
Выучите, что в начале идёт a 3 .
Два многочлена посередине имеют коэффициенты 3.
В
спомним, что любое число в нулевой степени есть 1. (a 0 = 1, b 0 = 1). Легко заметить, что в формуле идёт понижение степени a и увеличение степени b. В этом можно убедиться:
(a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3
Предостережение!!!
(a + b) 3 не равно a 3 + b 3
Куб разности
Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+» и «-». Перед первым членом a 3 стоит «+» (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «-», затем опять «+» и т.д.
(a — b) 3 = + a 3 — 3a 2 b + 3ab 2 — b 3 = a 3 — 3a 2 b + 3ab 2 — b 3
Сумма кубов ( Не путать с кубом суммы!)
Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.
a 3 + b 3 = (a + b)(a 2 — ab + b 2)
Сумма кубов — это произведение двух скобок.
Первая скобка — сумма двух чисел.
Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:
A 2 — ab + b 2
Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.
Разность кубов (Не путать с кубом разности!!!)
Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.
a 3 — b 3 = (a — b)(a 2 + ab + b 2)
Будьте внимательны при записи знаков. Следует помнить, что все формулы, приведённые выше, используется также и справа налево.
Трудно запоминаются формулы сокращенного умножения? Делу легко помочь. Нужно просто запомнить, как изображается такая простая вещь, как треугольник Паскаля. Тогда вы вспомните эти формулы всегда и везде, вернее, не вспомните, а восстановите.
Что же такое треугольник Паскаля? Этот треугольник состоит из коэффициентов, которые входят в разложение любой степени двучлена вида в многочлен.
Разложим, например, :
В этой записи легко запоминается, что вначале стоит куб первого, а в конце — куб второго числа. А вот что посередине — запоминается сложно. И даже то, что в каждом следующем слагаемом степень одного множителя все время уменьшается, а второго — увеличивается — несложно заметить и запомнить, труднее дело обстоит с запоминанием коэффициентов и знаков (плюс там или минус?).
Итак, сначала коэффициенты. Не надо их запоминать! На полях тетрадки быстренько рисуем треугольник Паскаля, и вот они — коэффициенты, уже перед нами. Рисовать начинаем с трех единичек, одна сверху, две ниже, правее и левее — ага, уже треугольник получается:
Первая строка, с одной единичкой — нулевая. Потом идет первая, вторая, третья и так далее. Чтобы получить вторую строку, нужно по краям снова приписать единички, а в центре записать число, полученное сложением двух чисел, стоящих над ним:
Записываем третью строку: опять по краям единицы, и опять, чтобы получить следующее число в новой строке, сложим числа, стоящие над ним в предыдущей:
Как вы уже догадались, мы получаем в каждой строке коэффициенты из разложения двучлена в многочлен:
Ну а знаки запомнить еще проще: первый — такой же, как в раскладываемом двучлене (раскладываем сумму — значит, плюс, разность — значит, минус), а дальше знаки чередуются!
Вот такая это полезная штука — треугольник Паскаля. Пользуйтесь!
Пользуйтесь!
Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук. Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей , решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
И так вот они:
Первая х 2 — у 2 = (х — у) (х+у) .Чтобы рассчитать разность квадратов двух выражений надо перемножить разности этих выражений на их суммы.
Вторая (х + у) 2 = х 2 + 2ху + у 2 .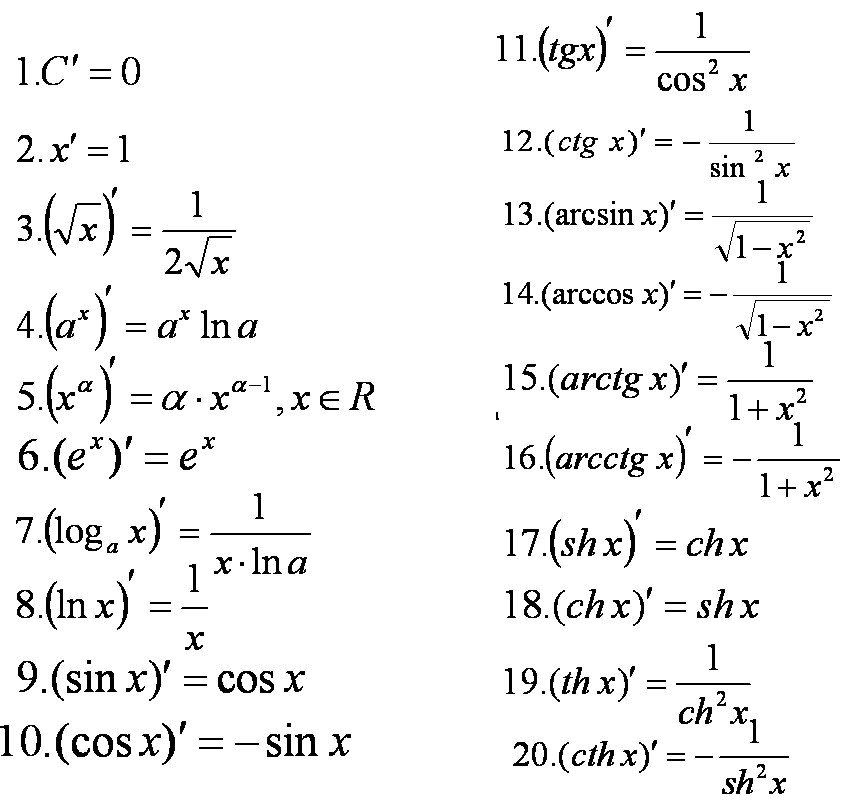 Чтобы найти квадрат суммы двух выражений нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Чтобы найти квадрат суммы двух выражений нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Третья (х — у) 2 = х 2 — 2ху + у 2 . Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Четвертая (х + у) 3 = х 3 + 3х 2 у + 3ху 2 + у 3. Чтобы вычислить куб суммы двух выражений нужно к кубу первого выражения прибавить утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
Пятая (х — у) 3 = х 3 — 3х 2 у + 3ху 2 — у 3 . Чтобы рассчитать куб разности двух выражений необходимо от куба первого выражения отнять утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
Шестая х 3 + у 3 = (х + у) (х 2 — ху + у 2) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.
Седьмая х 3 — у 3 = (х — у) (х 2 + ху + у 2) Чтобы произвести вычисление разности кубов двух выражений надо умножить разность первого и второго выражения на неполный квадрат суммы этих выражений.
Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).
О существовании этих закономерностей з нали еще около 4 тысяч лет тому назад. Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.
Разберем доказательство квадрата суммы (а + b) 2 = a 2 +2ab +b 2 .
Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н. э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.
э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
Обогреватель мощностью P = 6500 Вт соединён с сетью постоянного напряжения двумя алюминиевыми проводами. Длина каждого l = 600 м, площадь поперечного сечения S = 140 мм2. Сила тока в цепи I = 100 А.
Длина каждого l = 600 м, площадь поперечного сечения S = 140 мм2. Сила тока в цепи I = 100 А.
Мальчик, находясь на плоском склоне горы с углом наклона alpha=30 градусов , бросает камень в сторону подъёма горы, сообщив ему начальную скорость v0=20м/с, направленную под углом beta=30
Решено
Даны координаты вершин треугольника АВС. НАЙТИ: 1) длину стороны АВ; 2) уравнение сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол В; 4) уравнение медианы АЕ; 5) уравнение и длину
Решено
Радиус окружности,вписанной в прямоугольную трапецию,равен 7.Большая боковая сторона трапеций равна 23.Найдите периметр трапеций.
Решено
1. Развёртка боковой поверхности цилиндра является квадратом, диагональ которого равна 10 см. Найдите S (площадь т.е.) боковой поверхности цилиндра. 2. Плоскость, параллельная оси цилиндра, отсекает
Пользуйтесь нашим приложением
TSI Math: Использование простой факторизации для нахождения кубических корней Видео
множителей под кубом, так что это выглядит так до
Пятый, который такой же, как и корень куба
из отрицательного в один раз корень куба от шестна это до шестнадцати, потому что это особенная
Номер. будет выглядеть так Отрицательное от одного до шестнадцати Пятьдесят
будет выглядеть так Отрицательное от одного до шестнадцати Пятьдесят
Да Теперь пришло время найти каждого из этих трех
кубических корней Медленные и стабильные победы
220000 Гонка шла00:49
приходить по одному Вот и мы Куб
корень отрицательного числа один отрицательный один правильный Потому что отрицательный Когда
это сделано, мы обратим наше внимание на кубический корень
из шестнадцати.0004
два шестнадцать и так много троек И
вы знаете это, потому что вы можете добавить два плюс один
плюс шесть, что дает вам четные девять, и это делится
на три, так что вы знаете, что три будут
Один из этих факторов правильно, чтобы сделать это, мы
. Возможны малые простые числа Здесь показано
Возможны малые простые числа Здесь показано
Мы получили два шестнадцати равных равенства одного раза OH EH
с транспортными средствами два раза два раза пятьдесят, для которых равен
умножить на два два двадцать семь, что равно
все это прямо здесь, в конце
день Это два в кубе умножить на три в кубе и все Тогда
2 01:31
мы разделяем множители и это позволяет нам взять
кубический корень здесь Таким образом, кубический корень из шестнадцати
три в третьем, что равно кубу
корень из двух в третьем, что тоже
кубический корень из трех в третью
всего три, так что лихорадочный ответ — шесть лет,
мог бы получить туда, зная, что шесть раз шесть
Мне шесть это два Шестнадцать Вот что
мы подразумеваем под этим одним из тех специальных чисел Вы будете
видите, что много тестов Так что можете я
просто хочу заметить, что это в вашем мозгу
А. Куб X, который такой же, как x до
Куб X, который такой же, как x до
Три плюс два, что и x до
Второе питание там Orjust x квадрат, поэтому еще раз разделяйте
Факторы под корнем куба.
дает нам кубический корень из х, умноженный на
, кубический корень из х в квадрате, который равен х, умноженному на
.0002 02:27
кубический корень из x в квадрате прямо здесь Итак, мы нашли
каждый из трех кубических корней, которые мы первоначально установили
пора решать задачу
Соедините их все вместе и упростите правильно
до шестнадцати умножить на кубический корень из х в пятой раз
то же, что и родной Один раз шесть раз действует раз
кубический корень из х в квадрате что то же самое, что и отрицательные шесть
x умножить на кубический корень из x в квадрате ничего себе, что
было некрасиво, но было сделано И ответ v 00:02:57. 46 —> [endTime] и давайте просто двигаться дальше
46 —> [endTime] и давайте просто двигаться дальше
раз3 (раз х раз х раз) — ПРОТОТИП
Такие странные времена требуют нового тактового размера. Есть ли еще время, чтобы посидеть в центре города и послушать поток машин? Чтобы услышать сердцебиение? Таймс-сквер — это время, умноженное на время; и раз в трех измерениях? Времена в кубе. Раз раз раз раз раз раз. Пять раз. Пять глобальных вымираний. Одна планета. Один город. 8,4 млн человек. Скажи это в пять раз быстрее.
Композитор Памела Зи и театральный художник Джефф Собель вместе отправляются в звуковое путешествие по Таймс-сквер — прошлое, настоящее и воображаемое… Что это было за место? Что это за место? И как мы сюда попали? В этой работе звука и пространства слушатель переносится в мир, где город и партитура сходятся, разваливаются и снова сходятся.
Прогуляйтесь по Таймс-сквер и послушайте музыку, созданную специально для вашего опыта. Или послушайте, не выходя из дома, и представьте себе город, вырезанный бесчисленными руками из места, когда-то густо заросшего деревьями… которое может снова уйти в ту сторону. Эта музыка, созданная из впечатлений от пространства, была написана для того, чтобы слушатели могли настроиться на силы под ногами, назад во времени и в будущем. Это звуковой ландшафт, созданный для вашего знакомства с городом.
Эта музыка, созданная из впечатлений от пространства, была написана для того, чтобы слушатели могли настроиться на силы под ногами, назад во времени и в будущем. Это звуковой ландшафт, созданный для вашего знакомства с городом.
Раз 3 (Times x Times x Times) — это четвертая итерация PROTOTYPE Out of Bounds, платформы для новых вокальных композиций, происходящих в неожиданных местах по всему Нью-Йорку. Благодаря работам общественные сайты станут временными пространствами контактов, обмена и обновленной социальной динамики.
Скачать цифровую программу
Соавтор:
Джефф Собель и Памела З.

Составитель:
Pamela Z
Written by
Geoff Sobelle
Instrumentalists
Tom Dambly, Crystal Pascucci, Todd Reynolds
Vocals
Pamela Z
Voices sampled from
Eric Sanderson, Алан Вейсман, Робин Орлин, Лиза МакГинн, Стефани Собель, Крейг Дайкерс, Эрик Грегори, Коллин Дженнингс-Роггенсак, Джек Чен, Эдриенн Браун, Памела Зи и Джефф Собель
Джефф Собель
(Соавтор) — театральный художник, посвятивший себя «возвышенному смеху». Он является со-художественным руководителем Rainpan 43, ренегатской абсурдистской организации, занимающейся созданием оригинальных перформансов, управляемых актерами. Используя иллюзию, пленку и устаревшую механику, R43 создает сюрреалистичные поэтические произведения, которые ищут человечность там, где вы меньше всего этого ожидаете, и находят благодать там, где никто не смотрит. Спектакли R43 включают: котелков в полном обмундировании (Innovative Theatre Award, номинация Drama Desk), Amnesia Curiosa , машины машины машины машины машины машины машины (награда OBIE — дизайн) и Elephant Room (по заказу Center Theater Group). Его независимая работа включает Flesh and Blood & Fish and Fowl (Первая премия Edinburgh Fringe) и The Object Lesson (Первая премия Edinburgh Fringe, Премия Кэрол Тамбор, Total Theater Award, NYTimes Critics Pick). С 2001 года он является членом труппы Филадельфийского театра Pig Iron Theater Company.0006
Спектакли R43 включают: котелков в полном обмундировании (Innovative Theatre Award, номинация Drama Desk), Amnesia Curiosa , машины машины машины машины машины машины машины (награда OBIE — дизайн) и Elephant Room (по заказу Center Theater Group). Его независимая работа включает Flesh and Blood & Fish and Fowl (Первая премия Edinburgh Fringe) и The Object Lesson (Первая премия Edinburgh Fringe, Премия Кэрол Тамбор, Total Theater Award, NYTimes Critics Pick). С 2001 года он является членом труппы Филадельфийского театра Pig Iron Theater Company.0006
Премьера всех его работ на сегодняшний день состоялась на Фестивале живых искусств в Филадельфии, после чего он отправился в турне по стране и за рубежом. Работы Джеффа были представлены в Бруклинской музыкальной академии (BAM), St. Ann’s Warehouse, HERE Arts Center, The Kirk Douglas Theater (CTG), Berkeley Rep, La Jolla Playhouse, Arena Stage, Studio Theater (DC), Museum. современного искусства (Чикаго), Bard College, Barbican Center (Лондон), гастролировал в Германии, Италии, Франции и Южной Корее.
современного искусства (Чикаго), Bard College, Barbican Center (Лондон), гастролировал в Германии, Италии, Франции и Южной Корее.
В качестве учителя Джефф проводил мастер-классы по всему миру, посвященные театральному творчеству, физическому подходу к персонажу, клоунаде и «игрушкам». Он преподает в школе Pig Iron в Филадельфии (APT) и преподает в Бард-колледже. Его проекты были поддержаны Фондом MAP, Фондом независимости, Филадельфийской театральной инициативой, Фондом Винкота, US Arts International, Принстонским ателье и Фондом искусств Новой Англии. Он является членом Pew Fellow 2006 года и стипендиатом 2009 года.Грантополучатель Креативного капитала. Джефф с отличием окончил Стэнфордский университет и обучался физическому театру в Школе Жака Лекока в Париже.
Памела Z
(соавтор) — композитор/исполнитель и медиа-художник, работающий в основном с голосом, живой электронной обработкой, семплированным звуком и видео. Пионер в области живых цифровых лупов, она обрабатывает свой голос в режиме реального времени, создавая плотные, сложные звуковые слои. Ее сольные работы сочетают в себе экспериментальные расширенные вокальные техники, оперное бельканто, найденные объекты, текст, цифровую обработку и беспроводные MIDI-контроллеры, которые позволяют ей управлять звуком с помощью физических жестов. В дополнение к своей сольной работе ей было поручено сочинять музыку для танцев, театра, кино и камерных ансамблей, включая Kronos Quartet, Eighth Blackbird, The Bang on a Can All Stars, Ethel и San Francisco Contemporary Music Players. Ее междисциплинарные перформансы были представлены на таких площадках, как The Kitchen (Нью-Йорк), Yerba Buena Center for the Arts (SF), REDCAT (LA) и MCA (Чикаго), а ее инсталляции были представлены на таких выставочных площадках, как Whitney. (Нью-Йорк), Diözesanmuseum (Кёльн) и Krannert (Иллинойс). Pamela Z много гастролировала по США, Европе и Японии. Она выступала на многочисленных фестивалях, включая Bang on a Can (Нью-Йорк), Interlink (Япония), Other Minds (Сан-Франциско), La Biennale di Venezia (Италия), Dak’Art (Сенегал) и фестиваль Tanztheater Pina Bausch (Вупперталь, Германия).
Ее сольные работы сочетают в себе экспериментальные расширенные вокальные техники, оперное бельканто, найденные объекты, текст, цифровую обработку и беспроводные MIDI-контроллеры, которые позволяют ей управлять звуком с помощью физических жестов. В дополнение к своей сольной работе ей было поручено сочинять музыку для танцев, театра, кино и камерных ансамблей, включая Kronos Quartet, Eighth Blackbird, The Bang on a Can All Stars, Ethel и San Francisco Contemporary Music Players. Ее междисциплинарные перформансы были представлены на таких площадках, как The Kitchen (Нью-Йорк), Yerba Buena Center for the Arts (SF), REDCAT (LA) и MCA (Чикаго), а ее инсталляции были представлены на таких выставочных площадках, как Whitney. (Нью-Йорк), Diözesanmuseum (Кёльн) и Krannert (Иллинойс). Pamela Z много гастролировала по США, Европе и Японии. Она выступала на многочисленных фестивалях, включая Bang on a Can (Нью-Йорк), Interlink (Япония), Other Minds (Сан-Франциско), La Biennale di Venezia (Италия), Dak’Art (Сенегал) и фестиваль Tanztheater Pina Bausch (Вупперталь, Германия).

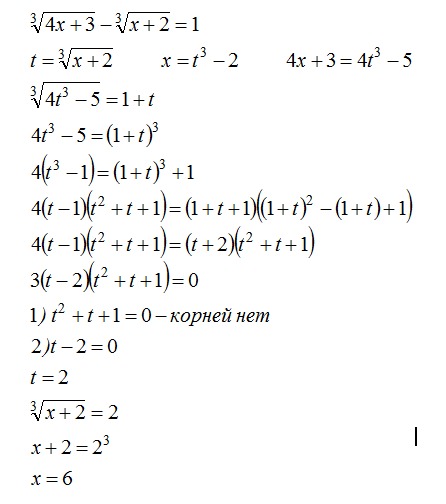
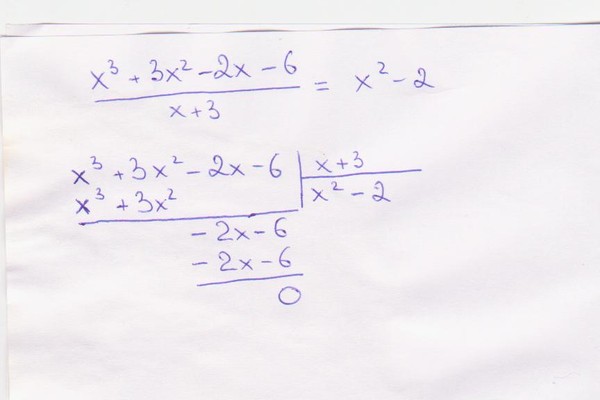 11.18
11.18