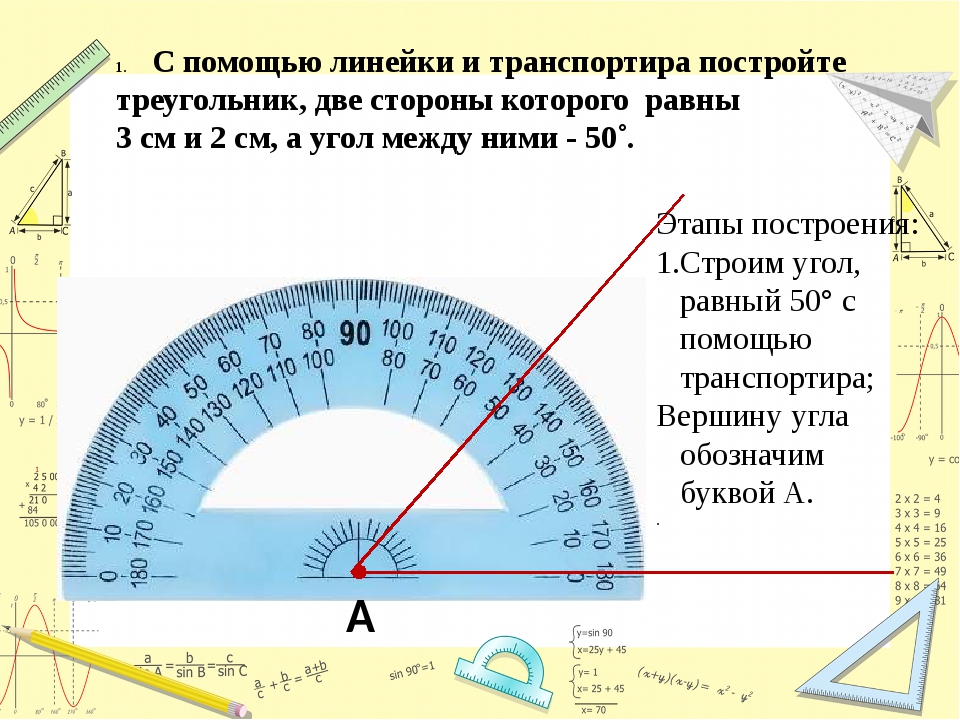
В градусах
Вы не задавались вопросом, почему в градусах измеряют настолько не связанные между собой вещи — углы и температуру? Скажем больше, градусами меряют плотность жидкости и качество молока и (да, мы не забыли) долю спирта. Gradus — латинское слово, означающее шаг, ступень или степень. Иными словами, у градуса, в отличие от метрических единиц измерения, нет конкретной величины, и он не соответствует никакому эталону, привязанному к тем или иным физическим параметрам. При этом размер градуса можно всякий раз устанавливать по-разному, и ничего не изменится. Кому и зачем могла понадобиться такая единица измерения? Давайте разбираться.
Углы
Со школы все мы знаем, что в окружности содержится ровно 360 градусов. Но почему именно 360? Ответить на этот вопрос можно по-разному.
По одной версии, древние астрономы, скорее всего персы и каппадокийцы, заметили, что солнце оказывается в одной и той же точке небосвода лишь один раз в 365 дней.
Они объяснили это тем, что солнце совершает полный оборот вокруг земли за год и возвращается в исходную точку.
Возможно, они округлили число 365, а может, и просто пропустили пять дней, но в итоге заключили: солнце сдвигается на одну трехсот шестидесятую долю окружности в день.
Другая теория объясняет 360-градусный полный угол совсем другими причинами. Шумеры и вавилоняне пользовались (не самой удобной) шестидесятеричной системой счисления. Большие числа они считали шестидесятками (например, число 1020 это 17 шестидесятков).
Вписав в окружность правильный шестиугольник, вавилоняне заметили, что в круг отлично помещаются шесть равносторонних треугольников. Каждому треугольнику они приписывали по шестидесятку. В итоге, шесть треугольников по шестидесятку дали известные 360 градусов.
Шестидесятизначная система объясняет и деление градуса на 60 минут (‘) и 3600 секунд (“). Знак, которым мы сегодня обозначаем градусы (°), впервые был использован в математике в 1569 году, по аналогии с верхним штриховым индексом для минут и секунд.
Независимо от истории, полный угол в 360 градусов — лучший вариант из возможных, ведь 360 — сверхсоставное число (натуральное число, с бoльшим числом делителей, чем все предыдущие). Оно делится на все числа от 1 до 10 за исключением семи, а еще и на: 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 и 180. На такое количество частей вы можете разделить окружность простым вычислением в уме.
Геометрические градусы прошли проверку временем и оказались самой удобной единицей измерения углов. Но есть и другие.
Так, если у вас есть инженерный калькулятор, то, переключаясь между градусами (DEG) и радианами (RAD), вы, возможно, попадали в режим GRAD — это исчисление в градах (или гонах). Один град — это одна сотая часть прямого угла, а значит, полный угол равен 400 град.
Такая единица измерения появилась во времена Французской революции вместе с метрической системой и быстро всех запутала. Кроме проблем с названием, — в некоторых странах grad обозначали привычные градусы, — возникли трудности и с вычислением.
Например, как известно, углы равностороннего треугольника равны друг другу и составляют 60 градусов. Переведем это в грады — 66 целых и шесть в периоде, ужасно неудобно.
В отличие от метрической системы, без которой трудно представить нашу жизнь, вычисления в градах оказались не самыми простыми, сейчас их практически нигде не используют.
Но свой след в истории они оставили — именно благодаря градам стоградусная температурная шкала получила название шкалы Цельсия.
Температура
Как ни странно, температурные шкалы появились гораздо раньше термометров. Создателем первой шкалы можно считать Галена — древнеримского медика, хирурга и философа.
Гален утверждал, что существует некая нейтральная температура — он определил ее как температуру смеси одинакового количества кипящей воды и льда. От нейтральной температуры он отсчитал по четыре шага (ступени) в сторону тепла и холода.
Шведский теолог и физик Иоганн Хаслер на основании работ Галена построил таблицу температуры, опубликованную на страницах труда «De Logistica Medica problematis novem» в 1578 году.
Он отложил те же четыре шага тепла и холода по разные стороны от нейтральной температуры, а также заметил, что шкалу можно заменить на последовательность чисел от единицы до девяти.
В таблице значения температуры называются просто «номерами», но в тексте Хаслер использует слово «градус». Нейтральная температура в его системе будет соответствовать числу пять.
Первое устройство, похожее на современный термометр, создал Галилео Галилей приблизительно в 1597 году. Вслед за этим ученые почти 200 лет искали универсальную, удобную и точную шкалу температур.
Например, в 1701 году Исаак Ньютон в опубликованной анонимно работе (в ней он уже использует слово gradus для обозначения единиц тепла) предлагат 18 реперных точек, часть из которых формирует геометрическую, а другая — арифметическую прогрессии. В градусах Ньютона точка замерзания воды равна 0 градусов, а температура человеческого тела — 12 градусов.
В том же году известный астроном Оле Ремер (первым измеривший скорость света) предложил свой вариант.
Нулем своей шкалы он выбрал температуру соленой воды со льдом, а вот температуру кипения воды — снова это магическое число — он обозначил как 60 градусов. Эту шкалу позаимствовал знакомый Ремера, Габриэль Фаренгейт.
Фаренгейт избавился от неудобных дробей, возникавших при измерении температуры человеческого тела (22,5 градуса) и замерзания пресной воды (7,5 градуса), заменив их на 24 и 8 градусов соответственно. Вода стала кипеть при 64 градусах Фаренгейта.
Некоторое время он производил термометры с такой шкалой, но потом, в 1724 году, умножил ее на 4. По одной версии, Фаренгейт просто хотел сделать шкалу точнее, поэтому увеличил количество рисок на градуснике, по другой — он сделал это, чтобы увеличение температуры на один Фаренгейт приводило к увеличению объема ртути ровно на одну десятитысячную.
Так появилась знаменитая шкала Фаренгейта, которой люди пользуются и сегодня. Некоторое время она была лучшей из возможных, но затем ей смену пришел более совершенный вариант.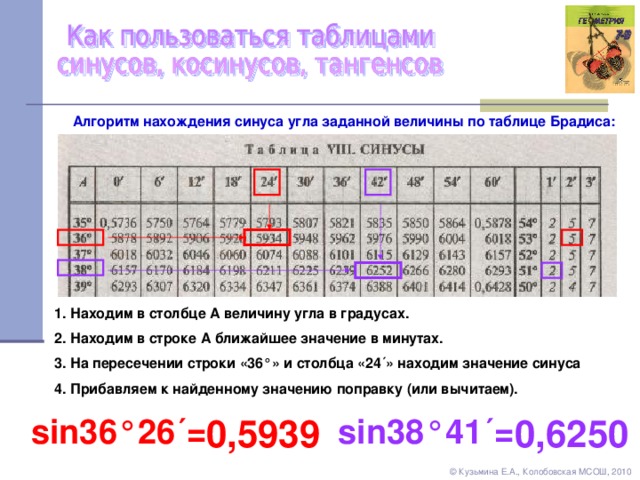
Хотя жители США навряд ли согласились бы с нами.
Жозеф Николя Делиль пошел несколько другим путем. Он выбрал всего одну реперную точку, температуру кипения воды, и обозначил ее за ноль. Градуировать шкалу он решил по расширению ртути в термометре — понижение температуры, приводящее к уменьшению объема ртути на одну стотысячную, Делиль обозначил за один градус.
Температура замерзания воды в таком случае — 2400 градусов, шкала оказалась излишне мелкой, поэтому в 1738 году Иосия Вейтбрехт изменил ее. Он задал температуру замерзания воды в 150 градусов.
Такие термометры стали удобными и получили широкое распространение. Ими примерно сто лет пользовались в России, Ломоносов использовал термометр Делиля (правда, перевернув шкалу) в своих опытах.
Только в этот момент на сцене появляется Андерс Цельсий. В 1741 году он наносит на термометр Делиля свою шкалу — 0 градусов в точке кипения и 100 градусов в точке замерзания воды. Перевернули шкалу (скорее всего, это сделал Карл Линней) через год после смерти Цельсия (он умер в 1744 году от туберкулеза).
Кстати, к 1745 году уже существовал термометр с нулем в точке замерзания и сотней градусов в точке кипения воды. Он называется термометром Лиона, его изобретатель — французский физик Жан-Пьер Кристен.
Заслуга Цельсия в другом — он провел эксперименты, продемонстрировавшие, что температура плавления льда практически не зависит от давления. Более того, он с высокой точностью определил, как температура кипения воды изменяется в зависимости от атмосферного давления.
Цельсий предложил калибровать ноль своей температурной шкалы (в тот момент, точку кипения воды) по атмосферному давлению, определить которое можно по среднему уровню моря.
Эта калибровка наконец сделала термометры по-настоящему универсальными. Вероятно, именно поэтому прогноз погоды, который вы смотрели сегодня утром, был в градусах Цельсия.
Но стоградусную температурную шкалу назвали в честь Цельсия только в 1948 году. До этого она так и называлась — стоградусной температурной (centigrade temperature scale).
Но во французском (где использовали грады) термин centigrade уже был занят в геометрии.
Чтобы избежать путаницы, Международное бюро мер и весов переименовало шкалу в честь Андерса Цельсия. Так градусы температуры стали градусами Цельсия.
Шкала Цельсия оказалась идеальной для применения в быту, но физики остались ею недовольны.
Привязка реперных точек к свойствам воды очень удобна для экспериментов, ведь воду можно найти практически где угодно. А вот для теоретических вычислений, например, связи энергии молекул с температурой, требовалось найти абсолютную шкалу.
Ее создал Уильям Томсон в 1848 году — нулевая точка его шкалы соответствует абсолютному нулю, а цена деления равна градусу Цельсия. Новую шкалу назвали в честь Томсона (ставшего лордом Кельвином), а градус Цельсия в ней превратился в Кельвин. Но почему Кельвин — это не градус?
Дело в том, что шкала Кельвина — это шкала абсолютной температуры. Все шкалы, о которых шла речь выше — произвольные, ведь для их градуировки были выбраны произвольные точки.
Шкалу Кельвина отсчитывают от абсолютного нуля — минимального предела температуры во Вселенной, она тесно связана с энергией молекул через постоянную Больцмана. Чтобы подчернуть, что речь идет об абсолютной температуре, Кельвин не называют градусом.
Цвет
Получается, температура в Кельвинах нужна только физикам? Нет, вы наверняка пользовались Кельвинами в бытовом отделе супермаркета, просто не подозревали об этом.
Выбирая оттенок света лампочки, мы обращаем внимание на цветовую температуру (например, 2800К), она измеряется в Кельвинах.
Такой свет будет испускать абсолютно черное тело, нагретое до указанной температуры. Так цвет измеряют температурой, а не в длинной волны, ведь излучение нагретого тела, как и лампочки, не монохроматично (состоит из множества частот).
Алкоголь
Из бытового отдела переместимся в отдел алкоголя и снова увидим там градусы. А точнее — объемные проценты, называемые градусами.
В России крепость алкогольных напитков в градусах Гесса стали измерять с 1847 года, когда академик Герман Гесс выпустил книгу «Учет спиртов».
В этой книге Гесс приводил спиртовые таблицы и инструкции по использованию спиртомера. А сам спиртомер Гесса показывал «не содержание алкоголя, а число ведер воды, имеющей температуру 12,44 Р[еомюра], которое надобно добавить к 100 ведрам испытываемого спирта, чтобы получить полугар, то есть такую смесь, которая содержит 38% алкоголя». Например, к 100 ведрам водки нужно добавить примерно пять ведер воды для получения полугара.
Официально перестали оценивать крепость в градусах Гесса уже в 1863 году, когда на их место пришли объемные проценты — отношение объема этилового спирта к общему объему напитка. А слово «градус» осталось.
Кстати, английское degree (градус) не имеет никакого отношения к алкоголю, а вот во Франции скажут, что в коньяке 40 градусов Гей-Люссака.
Плотность, кислотность молока
До середины XX века в химии и фармакологии широко использовались градусы Боме, предложенные Антуаном Боме в 1768 году для измерения плотности жидкости.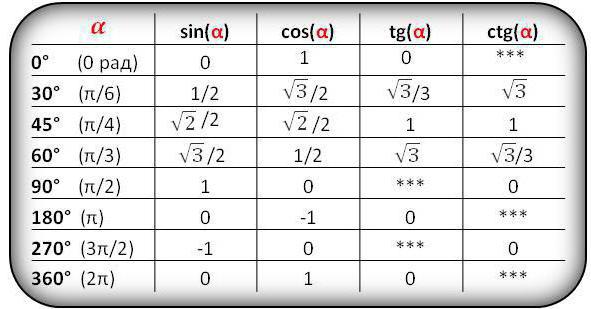
В физике и химии градусы Боме были вытеснены нынешней единицей СИ — килограммом на метр в кубе, но их продолжают использовать в пивоварении, переработке сахарной свеклы и других областях.
Кислотность молока также измеряют в градусах — в градусах Тернера. Это число миллилитров децинормального (0,1 н.) раствора гидроксида натрия, необходимое для нейтрализации 100 миллилитров молока. Молоко высшего сорта должно обладать градусом Тернера в пределах от 16 до 18.
Олег Макаров
Градусная мера угла равна сумме. Определение
Градусная мера угла – это положительное число, показывающее сколько раз градус и его части укладываются в угле.
У слова «угол» есть разные толкования. В геометрии углом называют часть плоскости, ограниченную двумя лучами, которые выходят из одной точки, так называемой вершины. Когда рассматриваются прямые, острые и развёрнутые углы, имеются ввиду именно геометрические углы.
Как и любые геометрические фигуры, углы можно сравнивать.
В области геометрии описать, что один угол большего или меньшего размера по сравнению с другим, сегодня несложно.
За единицу измерения углов взят градус – 1/180 часть развернутого угла.
У каждого угла есть градусная мера, больше нуля. Развёрнутый угол соответствует 180 градусам. Градусная мера угла ровна сумме всех градусных мер углов, на которые можно разбить исходный угол лучами.
От любого луча к заданной плоскости можно отложить угол с градусной мерой не более 180 градусов. Мера плоского угла, являющаяся частью полуплоскости – это градусная мера угла, имеющая аналогичные стороны. Меру плоскости угла, в составе которого находится полуплоскость, обозначают числом 360 – ?, где? является градусной мерой дополнительного плоского угла.
Прямой угол всегда равен 90 градусам, тупой – менее 180 градусам, но более 90, острый – не превышает 90 градусов.
Кроме градусной меры угла существует радианная. В планиметрии длину дуги окружности обозначают как L, радиус – r, а соответствующему центральному углу досталось обозначение – ?.
. Соотношение этих параметров выглядит так: ? = L/r.
Градусная мера угла. Радианная мера угла. Перевод градусов в радианы и обратно.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы освоили отсчёт углов на тригонометрическом круге. Узнали, как отсчитывать положительные и отрицательные углы. Осознали, как нарисовать угол больше 360 градусов. Пришла пора разобраться с измерением углов. Особенно с числом «Пи», которое так и норовит запутать нас в хитрых заданиях, да…
Стандартные задания по тригонометрии с числом «Пи» решаются неплохо. Зрительная память выручает. А вот любое отклонение от шаблона — валит наповал! Чтобы не свалиться — понимать надо. Что мы с успехом сейчас и сделаем. В смысле — всё поймём!
Итак, в чём считаются углы? В школьном курсе тригонометрии используются две меры: градусная мера угла и радианная мера угла . Разберём эти меры. Без этого в тригонометрии — никуда.
Градусная мера угла.
К градусам мы как-то привыкли. Геометрию худо-бедно проходили… Да и в жизни частенько встречаемся с фразой «повернул на 180 градусов», например. Градус, короче, штука простая…
Да? Ответьте мне тогда, что такое градус? Что, не получается с ходу? То-то…
Градусы придумали в Древнем Вавилоне. Давненько это было… Веков 40 назад… И придумали просто. Взяли и разбили окружность на 360 равных частей. 1 градус — это 1/360 часть окружности. И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее… Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона?
Где-то в то же время, в Древнем Египте мучились другим вопросом. Во сколько раз длина окружности больше длины её диаметра? И так измеряли, и этак… Всё получалось немного больше трёх. Но как-то лохмато получалось, неровно.
.. Но они, египтяне не виноваты. После них ещё веков 35 мучились. Пока окончательно не доказали, что как бы мелко не нарезать окружность на равные кусочки, из таких кусочков составить ровно длину диаметра нельзя… В принципе нельзя. Ну, во сколько раз окружность больше диаметра установили, конечно. Примерно. В 3,1415926… раз.
Это и есть число «Пи». Вот уж лохматое, так лохматое. После запятой — бесконечное число цифр без всякого порядка… Такие числа называются иррациональными. Это, кстати, и означает, что из равных кусочков окружности диаметр
Для практического применения принято запоминать всего две цифры после запятой. Запоминаем:
Раз уж мы поняли, что длина окружности больше диаметра в «Пи» раз, имеет смысл запомнить формулу длины окружности:
Где L — длина окружности, а d — её диаметр.
В геометрии пригодится.
Для общего образования добавлю, что число «Пи» сидит не только в геометрии… В самых различных разделах математики, а особенно в теории вероятности, это число возникает постоянно! Само по себе.
Вне наших желаний. Вот так.
Но вернёмся к градусам. Вы сообразили, почему в Древнем Вавилоне круг разбили на 360 равных частей? А не на 100, к примеру? Нет? Ну ладно. Выскажу версию. У древних вавилонян не спросишь… Для строительства, или, скажем, астрономии, круг удобно делить на равные части. А теперь прикиньте, на какие числа делится нацело 100, и на какие — 360? И в каком варианте этих делителей нацело — больше? Людям такое деление очень удобно. Но…
Как выяснилось много позже Древнего Вавилона, не всем нравятся градусы. Высшей математике они не нравятся… Высшая математика — дама серьёзная, по законам природы устроена. И эта дама заявляет: «Вы сегодня на 360 частей круг разбили, завтра на 100 разобьёте, послезавтра на 245… И что мне делать? Нет уж…» Пришлось послушаться. Природу не обманешь…
Пришлось ввести меру угла, не зависящую от человеческих придумок. Знакомьтесь — радиан!
Радианная мера угла.
Что такое радиан? В основе определения радиана — всё равно окружность.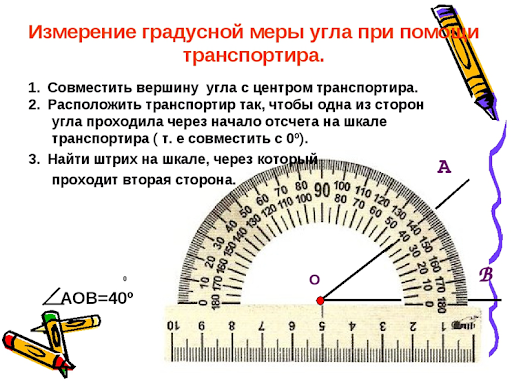
Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой (
Маленький такой угол, почти и нет его… Наводим курсор на картинку (или коснёмся картинки на планшете) и видим примерно один радиан . L = R
Чувствуете разницу?
Один радиан много больше одного градуса. А во сколько раз?
Смотрим следующую картинку. На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.
А теперь я нарежу этот полукруг радианами! Наводим курсор на картинку и видим, что в 180° укладывается 3 с хвостиком радиана.
Кто угадает, чему равен этот хвостик!?
Да! Этот хвостик — 0,1415926…. Здравствуй, число «Пи», мы тебя ещё не забыли!
Действительно, в 180° градусах укладывается 3,1415926… радиан. Как вы сами понимаете, всё время писать 3,1415926… неудобно. Поэтому вместо этого бесконечного числа всегда пишут просто:
А вот в Интернете число
писать неудобно.
Вот теперь совершенно осмысленно можно записать приближённое равенство:
Или точное равенство:
Определим, сколько градусов в одном радиане. Как? Легко! Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула — это тоже уравнение!) на 3,14:
Это соотношение полезно запомнить В одном радиане примерно 60°. В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.
Но главное умение этой темы — перевод градусов в радианы и обратно.
Если угол задан в радианах с числом «Пи», всё очень просто. Мы знаем, что «Пи» радиан = 180°. Вот и подставляем вместо «Пи» радиан — 180°. Получаем угол в градусах. Сокращаем, что сокращается, и ответ готов. Например, нам нужно выяснить, сколько
Или, более экзотическое выражение:
Легко, верно?
Обратный перевод чуть сложнее.
Но не сильно. Если угол дан в градусах, мы должны сообразить, чему равен один градус в радианах, и умножить это число на количество градусов. Чему равен 1° в радианах?
Смотрим на формулу и соображаем, что если 180° = «Пи» радиан, то 1° в 180 раз меньше. Или, другими словами, делим уравнение (формула — это тоже уравнение!) на 180. Представлять «Пи» как 3,14 никакой нужды нет, его всё равно всегда буквой пишут. Получаем, что один градус равен:
Вот и всё. Умножаем число градусов на это значение и получаем угол в радианах. Например:
Или, аналогично:
Как видите, в неспешной беседе с лирическими отступлениями выяснилось, что радианы — это очень просто. Да и перевод без проблем… И «Пи» — вполне терпимая штука… Так откуда путаница!?
Вскрою тайну. Дело в том, что в тригонометрических функциях значок градусов — пишется. Всегда. Например, sin35°. Это синус 35 градусов . А значок радианов (рад ) — не пишется! Он подразумевается.
То ли лень математиков обуяла, то ли ещё что… Но решили не писать. Если внутри синуса — котангенса нет никаких значков, то угол — в радианах ! Например, cos3 — это косинус трёх радианов .
Это и приводит к непоняткам… Человек видит «Пи» и считает, что это 180°. Всегда и везде. Это, кстати, срабатывает. До поры до времени, пока примеры — стандартные. Но «Пи» — это число! Число 3,14, а никакие не градусы! Это «Пи» радиан = 180°!
Ещё раз: «Пи» — это число! 3,14. Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…
«Пи» — это число! Что, достал я вас этой фразой? Вы уже всё давно поняли? Ну ладно. Проверим. Скажите-ка, какое число больше?
Или, что меньше?
Это из серии слегка нестандартных вопросов, которые могут и в ступор вогнать…
Если вы тоже в ступор впали, вспоминаем заклинание: «Пи» — это число! 3,14.
В самом первом синусе четко указано, что угол — в градусах ! Стало быть, заменять «Пи» на 180° — нельзя! «Пи» градусов — это примерно 3,14°. Следовательно, можно записать:
Во втором синусе обозначений никаких нет. Значит, там — радианы ! Вот здесь замена «Пи» на 180° вполне прокатит. Переводим радианы в градусы, как написано выше, получаем:
Осталось сравнить эти два синуса. Что. забыли, как? С помощью тригонометрического круга, конечно! Рисуем круг, рисуем примерные углы в 60° и 1,05°. Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, что sin60° существенно больше, чем sin1,05° .
Совершенно аналогично поступим и с косинусами. На круге нарисуем углы примерно 4 градуса и 4 радиана (не забыли, чему примерно равен 1 радиан?). Круг всё и скажет! Конечно, cos4 меньше cos4°.
Потренируемся в обращении с мерами угла.
Переведите эти углы из градусной меры в радианную:
360°; 30°; 90°; 270°; 45°; 0°; 180°; 60°
У вас должны получиться такие значения в радианах (в другом порядке!)
Я, между прочим, специально выделил ответы в две строчки. Ну-ка, сообразим, что за углы в первой строчке? Хоть в градусах, хоть в радианах?
Да! Это оси системы координат! Если смотреть по тригонометрическому кругу, то подвижная сторона угла при этих значениях точно попадает на оси . Эти значения нужно знать железно. И угол 0 градусов (0 радиан) я отметил не зря. А то некоторые этот угол никак на круге найти не могут… И, соответственно, в тригонометрических функциях нуля путаются… Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге — сплошь и рядом.
Во второй строчке — тоже углы специальные… Это 30°, 45° и 60°. И что в них такого специального? Особо — ничего. Единственное отличие этих углов от всех остальных — именно про эти углы вы должны знать всё .
И где они располагаются, и какие у этих углов тригонометрические функции. Скажем, значение sin100° вы знать не обязаны. А sin45° — уж будьте любезны! Это обязательные знания, без которых в тригонометрии делать нечего… Но об этом подробнее — в следующем уроке.
А пока продолжим тренировку. Переведите эти углы из радианной меры в градусную:
У вас должны получиться такие результаты (в беспорядке):
210°; 150°; 135°; 120°; 330°; 315°; 300°; 240°; 225°.
Получилось? Тогда можно считать, что перевод градусов в радианы и обратно — уже не ваша проблема.) Но перевод углов — это первый шаг к постижению тригонометрии. Там же ещё с синусами-косинусами работать надо. Да и с тангенсами, котангенсами тоже…
Второй мощный шаг — это умение определять положение любого угла на тригонометрическом круге. И в градусах, и в радианах. Про это самое умение я буду вам во всей тригонометрии занудно намекать, да…) Если вы всё знаете (или думаете, что всё знаете) про тригонометрический круг, и отсчёт углов на тригонометрическом круге, можете провериться.
Решите эти несложные задания:
1. В какую четверть попадают углы:
45°, 175°, 355°, 91°, 355° ?
Легко? Продолжаем:
2. В какую четверть попадают углы:
402°, 535°, 3000°, -45°, -325°, -3000°?
Тоже без проблем? Ну, смотрите…)
3. Сможете разместить по четвертям углы:
Смогли? Ну вы даёте..)
4. На какие оси попадёт уголок:
и уголок:
Тоже легко? Хм…)
5. В какую четверть попадают углы:
И это получилось!? Ну, тогда я прям не знаю…)
6. Определить, в какую четверть попадают углы:
1, 2, 3 и 20 радианов.
Ответ дам только на последний вопрос (он слегка хитрый) последнего задания. Угол в 20 радианов попадёт в первую четверть.
Остальные ответы не дам не из жадности.) Просто, если вы не решили чего-то, сомневаетесь в результате, или на задание №4 потратили больше 10 секунд, вы слабо ориентируетесь в круге.
Это будет вашей проблемой во всей тригонометрии. Лучше от неё (проблемы, а не тригонометрии!)) избавиться сразу. Это можно сделать в теме: Практическая работа с тригонометрическим кругом в разделе 555.
Там рассказано, как просто и правильно решать такие задания. Ну и эти задания решены, разумеется. И четвёртое задание решено за 10 секунд. Да так решено, что любой сможет!
Если же вы абсолютно уверены в своих ответах и вас не интересуют простые и безотказные способы работы с радианами — можете не посещать 555. Не настаиваю.)
Хорошее понимание — достаточно веская причина, чтобы двигаться дальше!)
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Как найти градусную меру угла?
Для многих в школе геометрия — это настоящее испытание.
Одной из базовых геометрических фигур является угол. Под этим понятием подразумевают два луча, которые берут начало в одной точке. Для измерения значения (величины) угла используют градусы или радианы. Как найти градусную меру угла, вы узнаете из нашей статьи.
Виды углов
Допустим, у нас есть угол. Если мы его разложим в прямую, тогда его величина будет равняться 180 градусам. Такой угол называют развернутым, а одним градусом считают 1/180 его часть.
Кроме развернутого угла различают еще острые (меньше 90 градусов), тупые (больше 90 градусов) и прямые (равные 90 градусам) углы. Эти термины используют для характеристики величины градусной меры угла.
Измерение угла
Величину угла измеряют с помощью транспортира. Это специальный прибор, на котором полукруг уже разбит на 180 частей. Приложите транспортир к углу так, чтобы одна из сторон угла совпадала с нижней частью транспортира. Второй луч должен пересекать дугу транспортира. Если этого не происходит, уберите транспортир и с помощью линейки удлините луч.
Если угол «открывается» вправо от вершины, считывают его значение по верхней шкале, если влево — по нижней.
В системе СИ принято измерять величину угла в радианах, а не в градусах. В развернутом угле помещается всего 3,14 радиана, поэтому эта величина неудобна и на практике почти не применяется. Именно поэтому необходимо знать, как перевести радианы в градусы. Для этого существует формула:
- Градусы = радианы/π х 180
Например, величина угла равняется 1,6 радиана. Переводим в градусы: 1,6/3,14 * 180 = 92
Свойства углов
Теперь вы знаете, как измерять и пересчитывать градусные меры углов. Но для решения задач необходимо еще знать свойства углов. На сегодняшний день сформулированы следующие аксиомы:
- Любой угол можно выразить в градусной мере, большей нуля. Величина развернутого угла — 360.
- Если угол состоит из нескольких углов, то его градусная мера равняется сумме всех углов.
- В заданную полуплоскость от любого луча можно построить угол заданной величины, меньший 180 градусов, причем только один.
- Величины равных углов одинаковы.
- Чтобы сложить два угла, надо сложить их величины.
Понимание этих правил и умение измерять углы — ключ к успешному изучению геометрии.
Углом называется фигура, которая состоит из точки — вершины угла и двух различных полупрямых, исходящих из этой точки, — сторон угла (рис. 14). Если стороны угла являются дополнительными полупрямыми, то угол называется развернутым.
Угол обозначается либо указанием его вершины, либо указанием его сторон, либо указанием трех точек: вершины и двух точек на сторонах угла. Слово «угол» иногда заменяют
символом Угол на рисунке 14 можно обозначить тремя способами:
Говорят, что луч с проходит между сторонами угла если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.
На рисунке 15 луч с проходит между сторонами угла так как он пересекает отрезок
В случае развернутого угла любой луч, исходящий из его вершины и отличный от его сторон, проходит между сторонами угла.
Углы измеряются в градусах. Если взять развернутый угол и разделить его на 180 равных углов то градусная мера каждого из этих углов называется градусом.
Основные свойства измерения углов выражены в следующей аксиоме:
Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Это значит, что если луч с проходит между сторонами угла то угол равен сумме углов
Градусная мера угла находится при помощи транспортира.
Угол, равный 90°, называется прямым углом. Угол, меньший 90°, называется острым углом. Угол, больший 90° и меньший 180°, называется тупым.
Сформулируем основное свойство откладывания углов.
От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
Рассмотрим полупрямую а. Продлим ее за начальную точку А.
Полученная прямая разбивает плоскость на две полуплоскости. На рисунке 16 показано, как с помощью транспортира отложить от полупрямой а в верхнюю полуплоскость угол с данной градусной мерой 60°.
Т. 1. 2. Если от данной полупрямой отложить в одну полуплоскость два угла, то сторона меньшего угла, отличная от данной полупрямой, проходит между сторонами большего угла.
Пусть — углы, отложенные от данной полупрямой а в одну полуплоскость, и пусть угол меньше угла . В теореме 1. 2 утверждается, что луч проходит между сторонами угла (рис. 17).
Биссектрисой угла называется луч, который исходит из его вершины, проходит между сторонами и делит угол пополам. На рисунке 18 луч — биссектриса угла
В геометрии существует понятие плоского угла. Плоским углом называется часть плоскости, ограниченная двумя различными лучами, исходящими из одной точки. Эти лучи называются сторонами угла. Существуют два плоских угла с данными сторонами. Они называются дополнительными. На рисунке 19 заштрихован один из плоских углов со сторонами а и
Углы измеряют в разных единицах измерениях.
Это могут быть градусы, радианы. Чаще всего углы измеряют в градусах. (Не следует путать этот градус с мерой измерения температуры, где также используется слово «градус).
1 градус — это угол, который равен 1/180 части развернутого угла. Другими словами, если взять развернутый угол и поделить его на 180 равных между собой частей-углов, то каждый такой маленький угол будет равен 1 градусу. Размер всех других углов определяется тем, сколько таких маленьких углов можно внутри измеряемого угла уложить.
Обозначается градус знаком °. Это не ноль и не буква О. Это такой специальный, введенный для обозначения градуса, символ.
Таким образом, развернутый угол равен 180°, прямой угол равен 90°, острые углы имеют размер меньший, чем 90°, а тупые — больший, чем 90°.
В метрической системой для измерения расстояния используется метр. Однако используются и более крупные и мелкие единицы. Например, сантиметр, миллиметр, километр, дециметр. По аналогии с этим в градусной мере углов также выделяют минуты и секунды.
Одна градусная минута равна 1/60 градуса. Обозначается она одним знаком «.
Одна градусная секунда равна 1/60 минуты или 1/3600 градуса. Обозначается секунда двумя знаками «, то есть «».
В школьной геометрии градусные минуты и секунды используются редко, однако надо уметь понимать, например, такую запись: 35°21″45″». Это значит, что угол равен 35 градусов + 21 минута + 45 секунд.
С другой стороны, если угол нельзя измерить точно лишь в целых градусах, то не обязательно вводить минуты и секунды. Достаточно использовать дробные значения градуса. Например, 96,5°.
Понятно, что минуты и секунды можно перевести в градусы, выразив их в долях градуса. Например, 30″ равно (30/60)° или 0,5°. А 0,3° равно (0,3 * 60)» или 18″. Таким образом, использование минут и секунд — это лишь вопрос удобства.
{»}}\]. Примечание: Градусы и радианы используются для измерения углов. Радиан равен величине, на которую должен быть открыт угол, чтобы захватить дугу окружности круга, длина которой равна радиусу круга.
Недавно обновленные страницы
Рассчитайте изменение энтропии, связанное с преобразованием химии класса 11 JEE_Main
Закон, сформулированный доктором Нернстом, является первым законом термодинамики 11 класса химии JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении А класс 11 химии JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 химии JEE_Main
Для реакции rm2Clg в rmCrmlrm2rmg признаки перехода 11 класса JEE_Main
3 жидкая вода класс 11 химия JEE_Main
Рассчитать изменение энтропии, связанное с конверсией 11 класс химия JEE_Main
Закон, сформулированный доктором Нернстом, является первым законом термодинамики 11 класс химии JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении А класс 11 химии JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 химии JEE_Main
Для реакции rm2Clg в rmCrmlrm2rmg знаки перехода 11 класса 9 JEE_Main жидкой воды, класс 11, химия JEE_Main
Тенденции сомнений
Студенты также читают
Степень — определение, символ и преобразование степени в радиан
градусов в Radian
Radian меру
Преобразование рупий в Paise
Степень полиномиального
угол 180 градусов
45 -градусный угол
и степень дифференциальных уравнений
.