Интеграл dx cos 2 x: интеграл dx/cos^2 2x — ответ на Uchi.ru

Интеграл от cos 2x НЕ совпадает с интегралом от cos

Найдем интеграл от cos 2x и интеграл от cos ² x, а также решим некоторые задачи, связанные с этими интегралами.

Чему равен интеграл от Cos 2x dx?

Интеграл от cos 2x  обозначается ∫ cos 2x dx, а его значение равно (sin 2x) / 2 + C, где «C» — постоянная интегрирования. Для доказательства воспользуемся методом подстановки. Для этого предположим, что 2x = u. Тогда 2 dx = du (или) dx = du/2. Подставляя эти значения в интеграл ∫ cos 2x dx,

∫ cos 2x dx = ∫ cos u (du/2)

= (1/2) ∫ cos u du

Мы знаем, что интеграл от cos x равен sin x + C. Итак,

Подставив здесь u = 2x,

∫ cos 2x dx = (1/2 ) sin (2x) + C

Это интеграл формулы cos 2x.

Определенный интеграл от Cos 2x

Определенный интеграл есть не что иное, как интеграл с нижними и верхними границами. По основной теореме математического анализа, чтобы вычислить определенный интеграл, мы сначала подставляем верхнюю границу, а затем нижнюю границу в интеграл, а затем вычитаем их в том же порядке. В этом процессе мы можем игнорировать постоянную интегрирования. Вычислим здесь некоторые определенные интегралы от интеграла cos 2x dx.

Интеграл от Cos 2x От 0 до 2pi

∫ ₀ ^2π cos 2x dx = (1/2) sin (2x) | ₀ ^2π

= (1/2) sin 2(2π) — (1/2) sin 2(0)

= (1/2) sin 4π — sin 0

= (1/2) ) 0 — 0

= 0

Таким образом, интеграл от cos 2x от 0 до 2pi равен 0.

Интеграл от Cos 2x от 0 до pi

∫ ₀ ^{πx 92908 2) грех (2x) | ₀ π}

Чтобы найти интеграл от cos ² x, мы используем формулу двойного угла для cos. Одна из формул cos 2x: cos 2x = 2 cos ² x — 1. Добавляя 1 с обеих сторон, мы получаем 1 + cos 2x = 2 cos ² x. Разделив обе части на 2, мы получим cos ² x = (1 + cos 2x) / 2. Мы используем это, чтобы найти ∫ cos ² x dx. Тогда мы получаем

∫ cos ² x dx = ∫ (1 + cos 2x) / 2 dx

= (1/2) ∫ (1 + cos 2x) dx 92x Используя интегрирование по частям

Мы знаем, что можем записать cos ² x как cos x · cos x. Поскольку это произведение, мы можем использовать интегрирование по частям, чтобы найти ∫ cos x · cos x dx. Тогда мы получаем

∫ cos ² x dx = ∫ cos x · cos x dx = ∫ u dv

Здесь u = cos x и dv = cos x dx.

Тогда du = — sin x dx и v = sin x.

По формуле интегрирования по частям0911

∫ cos ² x dx = (1/2) (2 sin x cos x) + ∫ sin ² x dx

По формуле двойного угла sin, 2 sin x cos x = sin 2x и тригонометрическое тождество, sin ² x = 1 — cos ² x. Итак,

∫ cos ² x dx = (1/2) sin 2x + ∫ (1 — cos ² x) dx

∫ cos ² x dx = (1/2) sin 2×1 + ∫ dx — ∫ cos ² x dx

∫ cos ² x dx + ∫ cos ² x dx = (1/2) sin 2x + x + C₁ 92x От 0 до пи

∫ ₀ ^π cos ² x dx = [x/2 + (sin 2x)/4] | ₀ ^π

= [π/2 + (sin 2π)/4] — [0 + (sin 0)/4]

= π/2 + 0/4

= π/2

Следовательно, интеграл от cos ² x от 0 до π равен π/2.

Важные замечания по интегралу от Cos 2x и интегралу от Cos ² x:

• ∫ cos 2x dx = (sin 2x)/2 + C
• ∫ потому что 2 9092x

  Что такое интеграция Cos 2x dx?

  Интегрирование  cos 2x dx записывается как ∫ cos 2x dx и ∫ cos 2x dx = (sin 2x)/2 + C, где C – постоянная интегрирования.

  Как найти интеграл от Cos 2x?

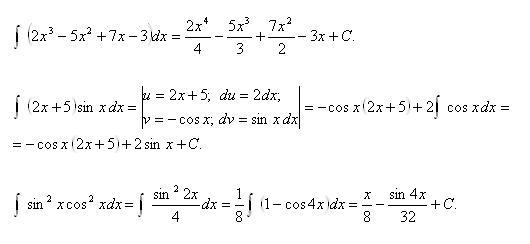  Интеграл от cos 2x находится методом подстановки. При этом мы предполагаем, что 2x = u, тогда 2 dx = du, откуда dx = du/2. Тогда интеграл принимает вид (1/2) ∫ cos u du = (1/2) sin u + C = (1/2) sin 2x + C. Таким образом, интеграл от cos 2x равен (1/2) sin 2x + C, где C — постоянная интегрирования. 93x дх?

  ∫ cos ³ x dx = ∫ cos ² x cos x dx = ∫ (1 — sin ² x) cos x dx. Подставим sin x = u. Тогда cos x dx = du. Тогда приведенный выше интеграл принимает вид ∫ (1 — u ² ) du = u — u ³ /3 + C. Подставив здесь u = sin x, ∫ cos ³ x dx = sin x — sin ³ x/3 + C.

  В чем разница между интегрированием Cos 2x и интегралом Cos x?

  • Интеграл от cos 2x равен ∫ cos 2x dx = (sin 2x)/2 + C. 92x от 0 до 2Pi?

    Мы знаем, что ∫ cos ² dx = x/2 + (sin 2x)/4 + C. Подставляя сюда пределы, мы получаем значение определенного интеграла как [π/2 + (sin 2π)/ 4] — [0 + (sin 0)/4] = π/2.

    Является ли интеграл Cos 2x dx таким же, как квадрат интеграла Cos x dx?

    Нет, значения этих двух интегралов НЕ совпадают.

    No related posts.

    Добавить комментарий Отменить ответ

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    Комментарий *

    Имя *

    Email *

    Сайт