Гипербола
К содержанию
Гипербола — это плоская кривая второго порядка, которая состоит из двух отдельных кривых, которые не пересекаются.
Формула гиперболы y = k/x, при условии, что k не равно 0. То есть вершины гиперболы стремятся к нолю, но никогда не пересекаются с ним.
Гипербола — это множество точек плоскости, модуль разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.
Основные понятия
- Гипербола состоит из двух отдельных кривых, которые называют ветвями.
- Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
- Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
- Середина большой оси называется центром гиперболы.
- Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы. Обычно обозначается a.
- Расстояние от центра гиперболы до одного из фокусов называется
 Обычно обозначается c.
Обычно обозначается c. - Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.
- Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой или сопряженной осью гиперболы.
- Отрезок между фокусом гиперболы и гиперболой, перпендикулярный к её действительной оси, называется фокальным параметром.
- Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром. Обычно обозначается b.
- Каноническое уравнение гиперболы в декартовых координатах:
x2 / a2 — y2 / b2 = 1
- Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:
xox / a2 — yoy / b2 = 1
или
y = yo + (b2xo)(x — xo) / (a2yo)
- Уравнение нормали к гиперболе имеет вид:
y = yo — (a2yo)(x — xo) / (b2xo)
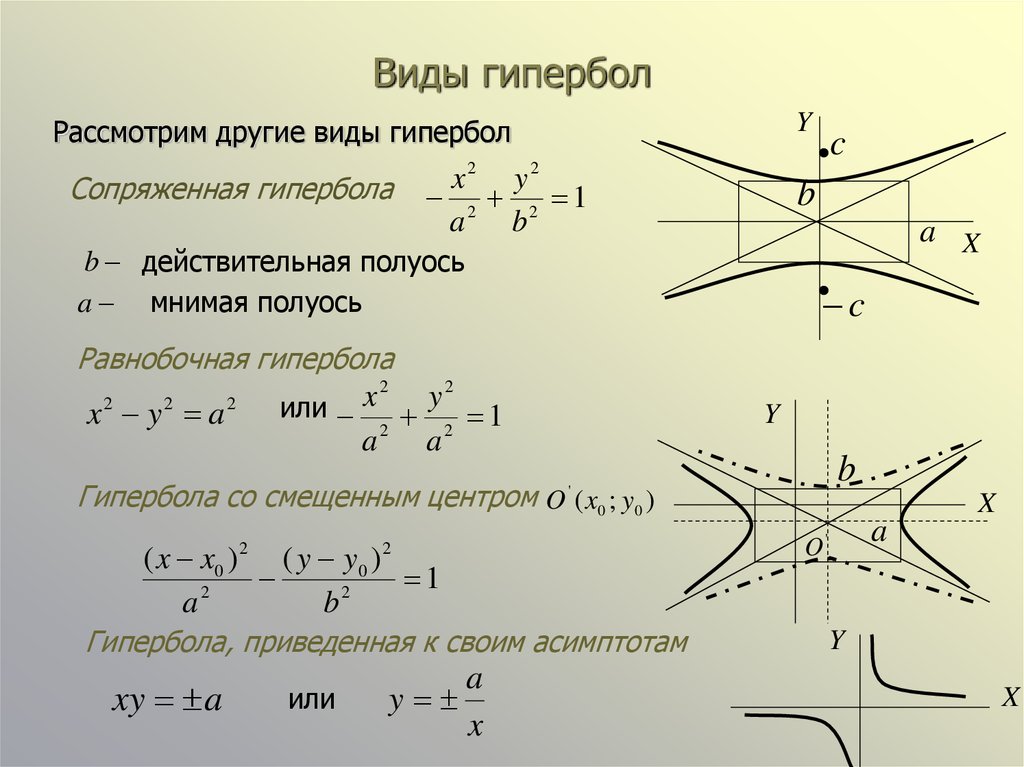
Некоторые типы гипербол
Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением:
Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением:
xy = a2 / 2,
при этом фокусы гиперболы располагаются в точках (a, a) и (−a,−a).
Гиперболы, связанные с треугольником:
- гипербола Киперта — кривая, изогонально сопряженная прямой проходящей через точку Лемуана и центр описанной окружности данного треугольника.
Свойства гиперболы
- Оптическое свойство: свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
Иначе говоря, если F1 и F2 фокусы гиперболы, то касательная в любой точки X гиперболы является биссектрисой угла ∠F1XF2. - Для любой точки, лежащей на гиперболе, отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.

- Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
- Каждая гипербола имеет сопряженную гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними.
Другие заметки по алгебре и геометрии
Полезная информация?
Гипербола и её каноническое уравнение
О чем статья
Что такое гипербола
Гипербола – это множество точек плоскости, разница расстояний которых от двух заданных точек, фокусов, есть постоянная величина и равна .
Аналогично эллипсу фокусы размещаем в точках , (см. рис. 1).
Рис. 1
Видно из рисунка, что могут быть случаи и , тогда согласно определению
Известно, что в треугольнике разница двух сторон меньше третьей стороны, поэтому, например, с у нас получается:
. Значит, для гиперболы .
Дальше запишем значение выражений и через координаты точек
.
Поднесём к квадрату обе части и после дальнейших преобразований найдём:
.
(1)
где . Уравнение гиперболы (1) – это каноническое уравнение гиперболы.
Гипербола симметрична относительно координатных осей, поэтому, как и для эллипса, достаточно построить её график в первой четверти, где:
. Область значения для первой четверти .
При у нас есть одна из вершин гиперболы . Вторая вершина . Если , тогда из (1) – действительных корней нет. Говорят, что и – мнимые вершины гиперболы. Из соотношением получается, что при достаточно больших значениях есть место ближайшего равенства . Поэтому прямая есть линией, расстояние между которой и соответствующей точкой гиперболы направляется к нулю при .
Форма и характеристики гиперболы
Исследуем уравнение (1) форму и расположение гиперболы.
- Переменные и входят в уравнение (1) в парных степенях. Поэтому, если точка принадлежит гиперболе, тогда и точки также принадлежат гиперболе.
 Значит, фигура симметрична относительно осей и , и точки , которая называется центром гиперболы.
Значит, фигура симметрична относительно осей и , и точки , которая называется центром гиперболы. - Найдём точки пересечения с осями координат. Подставив в уравнение (1) получим, что гипербола пересекает ось в точках . Положив получим уравнение , у которого нет решений. Значит, гипербола не пересекает ось . Точки называются вершинами гиперболы. Отрезок = и называется действительной осью гиперболы, а отрезок – мнимой осью гиперболы. Числа и называются соответственно действительной и мнимой полуосями гиперболы. Прямоугольник, созданный осями и называется главным прямоугольником гиперболы.
- С уравнения (1) получается, что , то есть . Это означает, что все точки гиперболы расположены справа от прямой (правая ветвь гиперболы) и левая от прямой (левая ветвь гиперболы).
- Возьмём на гиперболе точку в первой четверти, то есть , а поэтому . Так как , при , тогда функция монотонно возрастает при . Аналогично, так как при , тогда функция выпуклая вверх при .

Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Асимптоты гиперболы
Есть две асимптоты гиперболы. Найдём асимптоту к ветви гиперболы в первой четверти, а потом воспользуемся симметрией. Рассмотрим точку в первой четверти, то есть . В этом случае , , тогда асимптота имеет вид: , где
= x = ,
= x = x =
Значит, прямая – это асимптота функции . Поэтому в силу симметрии асимптотами гиперболы есть прямые .
За установленными характеристиками построим ветвь гиперболы, которая находится в первой четверти и воспользуемся симметрией:
Рис. 2
В случае, когда , то есть гипербола описывается уравнением . В этой гиперболе асимптоты, которые и есть биссектрисами координатных углов .
Примеры задач на построение гиперболы
Пример 1
Задача
Найти оси, вершины, фокусы, ексцентриситет и уравнения асимптот гиперболы. Построить гиперболу и её асимптоты.
Построить гиперболу и её асимптоты.
Решение
Сведём уравнение гиперболы к каноническому виду:
.
Сравнивая данное уравнение с каноническим (1) находим , , . Вершины , фокусы и . Ексцентриситет ; асмптоты ; Строим параболу. (см. рис. 3)
Рис. 3
Пример 2
Задача
Даны фокусы гиперболы и её асимптота . Написать уравнение гиперболы:
Решение
Записав уравнение асимптоты в виде находим отношение полуосей гиперболы . По условию задачи следует, что . Поэтому Задачу свели к решению системы уравнений:
Подставляя во второе уравнение системы, у нас получится:
,
откуда . Теперь находим .
Следовательно, у гиперболы получается такое уравнение:
.
Ответ
Уравнение гиперболы .
Средняя оценка 0 / 5. Количество оценок: 0
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
6517
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Уравнение, формулы, свойства, примеры и часто задаваемые вопросы
Гипербола — это коническое сечение, которое образуется, когда плоская поверхность пересекает двойной конус, но, конечно, не в центре. В результате пересечения двойного конуса и плоской поверхности образуются две неограниченные кривые, являющиеся зеркальным отражением друг друга. Гипербола симметрична относительно сопряженной оси и во многом напоминает эллипс. Давайте узнаем о гиперболе, ее свойствах и многом другом в этой статье.
В результате пересечения двойного конуса и плоской поверхности образуются две неограниченные кривые, являющиеся зеркальным отражением друг друга. Гипербола симметрична относительно сопряженной оси и во многом напоминает эллипс. Давайте узнаем о гиперболе, ее свойствах и многом другом в этой статье.
Что такое гипербола?
Гипербола — это геометрическое место точек, разность расстояний которых от двух фокусов является фиксированной величиной. Эта разница получается путем вычитания расстояния до ближнего фокуса из расстояния до дальнего фокуса. Если P (x, y) — точка на гиперболе и F, F’ — два фокуса, то геометрическое место гиперболы равно PF-PF’ = 2a.
Стандартное уравнение гиперболыСтандартное уравнение гиперболы:
OR,
Гипербола имеет два стандартных уравнения. Эти уравнения гиперболы основаны на ее поперечной оси и сопряженной оси.
- Стандартное уравнение гиперболы: [(x 2 /a 2 ) – (y 2 /b 2 )] = 1, где ось X – это поперечная ось, а ось Y -ось — сопряженная ось.

- Кроме того, другое стандартное уравнение гиперболы [(y 2 /a 2 )- (x 2 /b 2 )] = 1, где ось Y — поперечная ось, а ось X — сопряженная ось.
| . 0) Координаты вершины: (а, 0) и (-а, 0) Координаты очагов: (с, 0) и (-с, 0) Длина поперечной оси = 2a Длина сопряженной оси = 2b Длина широкой прямой кишки = 2b 2 /a Уравнения асимптот: a y = ( x и y = -(b /a) x Эксцентричность (e) = √ [1 + (B 2 /A 2 )] | ||||
|---|---|---|---|---|
| 9 9003 | 9 | 9003 центр: (0, 0) |
- Стандартное уравнение гиперболы с центром (h, k) и осью X в качестве поперечной оси и осью Y в качестве сопряженной оси,
- Кроме того, другое стандартное уравнение гиперболы с центром (h, k) и осью Y в качестве поперечной оси и осью X в качестве сопряженной оси:
Equation of the Hyperbola
Hyperbola
Formulae of parameters of a hyperbola
Координаты центра: (h, k)
Координаты вершины:
(h + a, k) и (h – a, k)
Координаты очагов: (h + c, k) и (h – c, k)
Длина поперечной оси = 2a
Длина сопряженной оси = 2b
Длина широкой прямой кишки = 2b 2 /a
Уравнения асимптот:
y = (b/a) (x – h) + k и
y = -(b/a) (x – h) + k
Координаты центра: (h, k)
Координаты вершины:
(h, k + a) и (h, k – a) Координаты 3:
(h, k + c) и (h, k – c)
Длина поперечной оси = 2a
Длина сопряженной оси = 2b
Длина широкой прямой кишки = 2b 2 /a
Уравнения асимптот:
y = (a/b) (x – h) + k и
y = -(a/b) (x – h) + k
Рассмотрим точку P на гиперболе с координатами (x, y).
 Из определения гиперболы мы знаем, что разница между расстоянием точки Р от двух фокусов F и F’ равна 2а, т. е. PF’-PF = 2а.
Из определения гиперболы мы знаем, что разница между расстоянием точки Р от двух фокусов F и F’ равна 2а, т. е. PF’-PF = 2а.Пусть координаты фокусов равны F(c, o) и F'(-c, 0).
Теперь, используя формулу координатного расстояния, мы можем найти расстояние от точки P (x, y) до фокусов F (c, 0) и F’ (-c, 0).
√[(x + c) 2 + (y – 0) 2 ] – √[(x – c) 2 + (y – 0) 2 ] = 2a
√[ x + c) 2 + y 2 ] = 2a + √[(x – c) 2 + y 2 ]
Теперь, возведя обе стороны в квадрат, мы получим
(x + c 2 + Y 2 = 4a 2 + (x — c) 2 + y 2 + 4A√ [(x — c) 2 + Y 2 ]
4CX — 4а 2 = 4а√[(х – с) 2 + y 2 ]
cx – a 2 = a√[(x – c) 2 + y 2 ]
3Возведение в квадрат 3 с обеих сторон
[(х 2 /а 2 ) – (у 2 /(с 2 – а 2 ))] = 1
Имеем, с 2 b 2 , поэтому, подставив это в приведенное выше уравнение, мы получим
x 2 /a 2 – y 2 /b 2 = 1
Отсюда выводится стандартное уравнение гиперболы.

Аналогично можно вывести стандартные уравнения другой гиперболы, т.е. В аналитической геометрии гипербола — это коническое сечение, которое получается, когда плоскость пересекает двойной прямой круговой конус под углом, так что обе половины конуса соединяются. Гипербола может быть описана с использованием таких понятий, как фокусы, директриса, широкая прямая кишка и эксцентриситет.
Давайте проверим несколько важных терминов, относящихся к различным параметрам гиперболы.
- Фокусы: Гипербола имеет два фокуса с координатами F(c, o) и F'(-c, 0).
- Центр гиперболы: Центр гиперболы — это середина линии, соединяющей два фокуса.
- Большая ось : Длина большой оси гиперболы составляет 2а единиц.
- Малая ось: Длина малой оси гиперболы составляет 2b единиц.
- Вершины: Точки пересечения гиперболы с осью называются вершинами. (а, 0) и (-а, 0) — вершины гиперболы.

- Широкая прямая кишка гиперболы: Широкая прямая кишка гиперболы — это линия, проходящая через любой из фокусов гиперболы и перпендикулярная поперечной оси гиперболы. Концы широкой прямой кишки лежат на гиперболе, а ее длина равна 2b 2 /a.
- Поперечная ось: Поперечная ось гиперболы — это линия, проходящая через два фокуса и центр гиперболы.
- Сопряженная ось: Сопряженная ось гиперболы — это линия, проходящая через центр гиперболы и перпендикулярная поперечной оси.
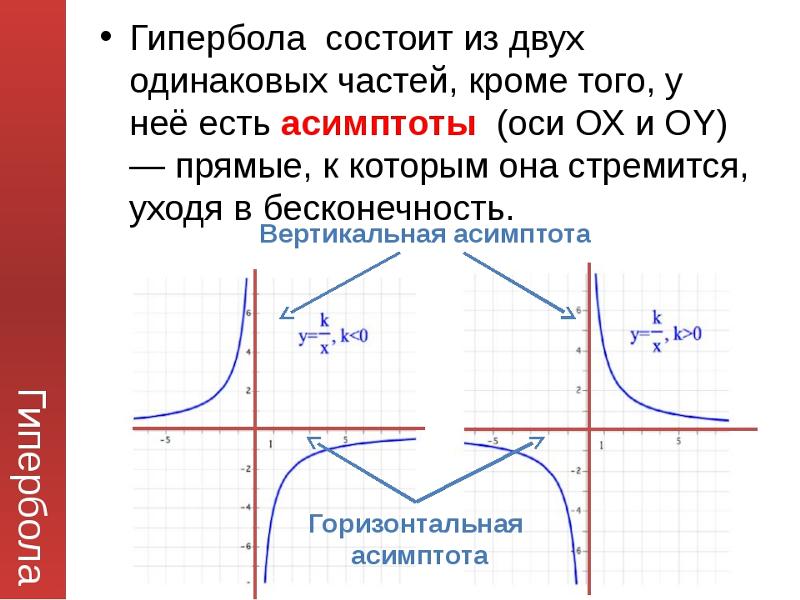
- Асимптоты: Гипербола имеет пару асимптот, где асимптота — это прямая линия, приближающаяся к гиперболе на графике, но никогда не касающаяся ее. Уравнения асимптот пары асимптот гиперболы,
y = (b/a) x
y = -(b/a) x
- Директриса: перпендикуляр к оси гиперболы гипербола.

- Эксцентриситет гиперболы: Эксцентриситет гиперболы – это отношение расстояния точки от фокуса до ее перпендикулярного расстояния от директрисы. Эксцентриситет гиперболы больше 1, т. е. e > 1.
e = √[1 + (b 2 /a 2 )]
Гипербола — это незамкнутая кривая, имеющая две ветви, которые выглядят как зеркальные отражения друг друга. Для любой точки любой из ветвей абсолютная разница между точкой и фокусами постоянна и равна 2а, где а — расстояние ветви от центра. Формула гиперболы помогает нам найти различные параметры и связанные части гиперболы, такие как уравнение гиперболы, большую и малую оси, эксцентриситет, асимптоты, вершину, фокусы и полуширотную прямую кишку
Что такое сопряженная гипербола?
Сопряженные гиперболы — это 2 гиперболы, у которых поперечная и сопряженная оси одной гиперболы являются соответственно сопряженной и поперечной осью другой гиперболы.

Конъюгатная гипербола (x 2 / A 2 ) — (Y 2 / B 2 ) = 1 IS,
(x 2 / A 2 ) — (y / A 2 ) — (y / A 2 ) — (x 2 / A 2 ) — (x 2 / A 2 ) — (x 2 / A 2 ) — (x 2 / A 2 ) — (x 2 / A 2 ) 2 / б 2 ) = 1 и,
а 2 = б 2 (e 2 − 1)
где
e — эксцентриситет параболы.Some Important points on Conjugate Hyperbola
- If the eccentricities of the hyperbola and its conjugate are e 1 , and e 2 then,
(1 / e 1 2 ) + (1 / e 2 2 ) = 1
- Фокусы гиперболы и сопряженной ей концикличны и образуют вершины квадрата.

- Гиперболы равны, если они имеют одинаковую прямую кишку.
Вспомогательные окружности гиперболы
Вспомогательная окружность — это окружность, центр которой C и диаметр которой являются поперечной осью гиперболы. Вспомогательная окружность уравнения гиперболы
x 2 + y 2 = a 2
Параметрическое представление
Параметрическое представление вспомогательных окружностей гиперболы
002 x = a sec θ, y = b tan θПрямоугольная гипербола
Гипербола с поперечной осью, сопряженной осью 2a единиц и сопряженной осью 2b единиц равной длины называется прямоугольной гиперболой. Эксцентричность прямоугольной гиперболы составляет √2
Уравнение прямоугольной гиперболы составляет
x 2 — Y 2 = A 2
Tangengular of Rectangular Hyperbola
Tangengular of Rectangular Gyperbola
966Tangengular Gyperbola
Tangengular gyperbola
.
 0002 Линия, которая касается прямоугольной гиперболы в любой точке кривой прямоугольной гиперболы, называется касательной к прямоугольной гиперболе.
0002 Линия, которая касается прямоугольной гиперболы в любой точке кривой прямоугольной гиперболы, называется касательной к прямоугольной гиперболе.Уравнение Tangent
для гиперболы x 2 /A 2 — Y 2 /B 2 = 1 The Tangent,
Y = MX + C
, если C 2 52 Y = MX + C
, если C 2 55559. = a 2 /m 2 – b 2
Форма наклона касательной
Для гиперболы x 2 /A 2 — Y 2 /B 2 = 1 Форма наклона тангенса IS,
Y = MX ± √ (A 2 M 2 — B 24 2 )
для гиперболы x 2 /A 2 — Y 2 /B 2 = 1 Уравнение тангенса в точке (x 1 , Y 1 ),
99999999999949949999. (xx 1 )/a 2 – (yy 1 )/b 2 = 1
Также, прочитайте
- Parabola
- Circle
- Эллипс
Решенные примеры на гиперболе
Пример 1: Определите Eccentrity of The Hyperbola X 24242424242454444444444444424 4002 4.
 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 9002
9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 90022 9002 9002 9002
/A 2 — Y 2 /B 2 = 1, мы получаем2 9002
. 36 = 1.
Решение:
Уравнение гиперболы x 2 /64 – y 2 /36 = 0
Сравнивая данное уравнение гиперболы со стандартным уравнением гиперболы0024 2
A 2 = 64, B 2 = 36
A = 8, B = 6
We have,
Эксцентриситет гиперболы (e) = √(1 + b 2 /a 2 )
e = √(1 + 6 2 /8 2 ) e + 36/64)
e = √(64 + 36)/64) = √(100/64)
e = 10/8 = 1,25Следовательно, эксцентриситет данной гиперболы равен 1,25.
Пример 2: Если уравнение гиперболы имеет вид [(x-4) 2 /25] – [(y-3) 2 /9] = 1, найдите длины большой оси, малой оси, и широкая прямая кишка.

Решение:
Уравнение гиперболы: стандартное уравнение гиперболы, (x – h) 2 /a 2 – (y – k) 2 /b 2 = 1
Здесь x = 4 — большая ось, а y = 3 — малая ось.
A 2 = 25 A = 5
B 2 = 9 B = 3
Длина основной оси = 2A
Длина минорного оси = 2B
= 2 × (5)
= 10 единиц
= 2 × (3)
= 6 единицДлина широкой прямой кишки = 2b 2 /a
0024 2 /5
= 18/5
= 3,6 единицыПример 3: Найдите вершину, асимптоту, основную ось, незначительную ось и Directrix, если уравнение гиперболы равен [(x-6) 2 / / 7 2 ]-[(y-2) 2 /4 2 ] = 1.
Решение:
Уравнение гиперболы: [(00-6) 2 ] – [(у-2) 2 /4 2 ] = 1
Сравнивая данное уравнение со стандартным уравнением гиперболы, (x – h) 2 /a 2 – (y – k) 2 /b 2 = 1
h = 6, k = 2, a = 7, b = 4
Вершина гиперболы: (h + a, k) и (h – a, k) = (13, 2) и (-1, 2)
Большая ось гиперболы: x = h x = 6
Малая ось гиперболы: y = k y = 2
Уравнения асимптот гиперболы:
y = k − (b / a)x + (b / а)h и y = k+ (b / a)x – (b / a)h
y = 2 – (4/7)x + (4/7)6 и y = 2 + (4/7)x – (4/7)6
y = 2 – 0,57x + 3,43 и y = 2 + 0,57x – 3,43
y = 5,43 – 0,57x и y = -1,43 + 0,57x
Уравнение направляющей гиперболы: x = ± a 2 /√(a 2 2 + b 2 900 )
x = ± 7 2 /√ (7 2 + 4 2 )
= ± 49 /√65x = ± 6,077
Пример 4: Найдите эсцентричность чья широкая прямая кишка составляет половину ее сопряженной оси.

Решение:
Длина широкой прямой кишки составляет половину ее сопряженной оси.
Пусть уравнение гиперболы будет [(x 2 / a 2 ) – (y 2 / b 2 )] = 1
Тогда длина сопряженной оси = 2b
(2b 2 / a)
Из приведенных данных, (2b 2 / a) = (1/2) × 2b
2b = a
Имеем,
Эксцентриситет гиперболы (e) = √[1 + (b 2 /a 2 )]
Теперь подставим a = 2b в формулу эксцентриситета
e = √[1 + (b 2 /(2b) 2 ]
e = √1 + (b 2 /4b 2 )] = √(5/4)
e = √5/2Следовательно, искомый эксцентриситет равен √5/2.
Пример 5. Найдите вершину фокусов и уравнения асимптот, если уравнение гиперболы имеет вид [y 2 /25]-[x 2 /9] = 1,
Решение:
Уравнение гиперболы: [y 2 /25]-[x 2 /9] = 1
Сравнивая данное уравнение со стандартным уравнением гиперболы y 2 /a 2 – x 2 /b 2 = 1, получаем
a 2 = 25, b 2 = 9 a = 5, b = 3
Координаты вершины: (0, 5) и (0, -5)
Координаты фокусов: (0, c) и (0, -c)
Мы знаем, что c = √(a 2 + b 2 )
= √ (5 2 + 3 2 )
= √34
= 5,83Отсюда : y = (a/b) x и y = -(a/b) x
y = (5/3)x и y = -(5/3)x
Таким образом, уравнения асимптот таковы: 5x – 3y = и 5x + 3y = 0
Часто задаваемые вопросы о гиперболе
Вопрос 1: Что такое гипербола?
Ответ:
Геометрическое место точки на плоскости, для которой отношение расстояния от фиксированной точки к расстоянию от фиксированной прямой является константой, превышающей 1, называется гиперболой.

Вопрос 2: Что такое эксцентриситет гиперболы?
Ответ:
Для гиперболы эксцентриситет всегда больше 1.
Вопрос 3: Какова формула эксцентриситета гиперболы?
Ответ:
Формула эксцентриситета гиперболы: e = √(1 + (b 2 /a 2 ))
Вопрос 4: Что такое стандартное уравнение гиперболы?
Answer:
Standard Equation of the hyperbola is
(x 2 /a 2 ) – (y 2 /b 2 ) = 1
Question 5: Каковы фокусы гиперболы?
Ответ:
Гипербола имеет два фокуса. Для гиперболы (x 2 /a 2 ) – (y 2 /b 2 ) = 1 фокусы задаются формулами (ae, 0) и (-ae, 0)
Вопрос 6: Что такое поперечная ось гиперболы?
Ответ:
Для гиперболы (x 2 /a 2 ) – (y 2 /b 2 ) = 1, ось x.
 Его длина равна 2а. Прямая, проходящая через центр и фокусы гиперболы, называется поперечной осью гиперболы.
Его длина равна 2а. Прямая, проходящая через центр и фокусы гиперболы, называется поперечной осью гиперболы.Вопрос 7: Каковы асимптоты гиперболы?
Ответ:
Прямые, параллельные гиперболе, пересекающие гиперболу на бесконечности, называются асимптотами гиперболы.
Параметрическая форма, касательные и нормали
Гипербола представляет собой коническое сечение, построенное путем соединения прямого круглого конуса с плоскостью под углом таким образом, что обе половины конуса соединяются. Это пересечение создает две отдельные неограниченные кривые, которые являются зеркальным отображением друг друга. Конические сечения составляют неотъемлемую часть аналитической геометрии, такой как парабола, эллипс и гипербола. Как и эллипс, гиперболу также можно интерпретировать как набор точек на координатной плоскости. Набор всех точек (x, y) на плоскости, для которых разность длин между (x, y) и фокусами является положительной константой, является определением гиперболы.

Определение гиперболы: гипербола — это набор точек, разность расстояний которых от двух фокусов является фиксированным значением. Эта разница получается из расстояния до дальнего фокуса минус расстояние до ближнего фокуса.
Для точки (x, y) гиперболы и двух фокусов (−c, 0) и (c, 0) геометрическое место гиперболы равно \(|d_2-d_1|=2a \)
, где \(d_2\) — расстояние от (−c,0) до (x,y), а \(d_1\) — расстояние от (c,0) до (x,y).
92}=1. \)Параметрическое уравнение имеет вид \(x=a\secθ,\ y=b\tanθ \), а параметрические координаты точки, покоящейся на нем, представлены \((a\secθ,b\tanθ).\)
Уравнение касательных и нормалей к гиперболеГипербола представляет собой набор всех точек на плоскости, разность длин которых от двух фиксированных точек на плоскости постоянна. «Разница» здесь означает расстояние до «дальней» позиции минус расстояние до «ближней» точки. Две фиксированные точки являются фокусами, а середина отрезка, соединяющего фокусы, является центром гиперболы.
 92}=1 \)
92}=1 \)Координаты центра (0, 0) (0, 0) Координаты вершин и (-a, 0 0 63) и (-a, 0 0 63) ) (0, а) и (0, – а) Координаты очагов (в, 0) и (-в, 0) (0, в) и (0, -в ) Длина поперечной оси 2а 2а Длина сопряженной оси 2b 92}{a} \) Все гиперболы имеют общие черты, состоящие из двух кривых, каждая с вершиной и фокусом. Поперечная ось гиперболы — это ось, проходящая через вершины и фокусы, а сопряженная ось гиперболы перпендикулярна поперечной оси.
Мы можем распознать график гиперболы в стандартных формах, как показано ниже. Если уравнение представленной гиперболы не в стандартном виде, то требуется заполнить квадрат, чтобы получить его в стандартном виде. 92. \)
- Уравнения асимптот: \(y=\pm\left(\frac{a}{b}\right)\left(x-h\right)+k.
 2. \) 9{2}}{36}=1. \)
2. \) 9{2}}{36}=1. \)Мы надеемся, что приведенная выше статья об уравнении гиперболы поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы об уравнении гиперболыВ.1 Что такое гипербола?
Ответ 1 Гипербола представляет собой набор точек, разность расстояний которых от двух фокусов является фиксированной величиной. Эта разница получается из расстояния до дальнего фокуса минус расстояние до ближнего фокуса. 92}=1 \)
Q.3 Каковы вершины гиперболы?
Ответ 3 Вершины гиперболы — это точки, где гипербола встречается с осью.
Q.4 Что является сопряженной осью гиперболы?
Ans.


 Обычно обозначается c.
Обычно обозначается c.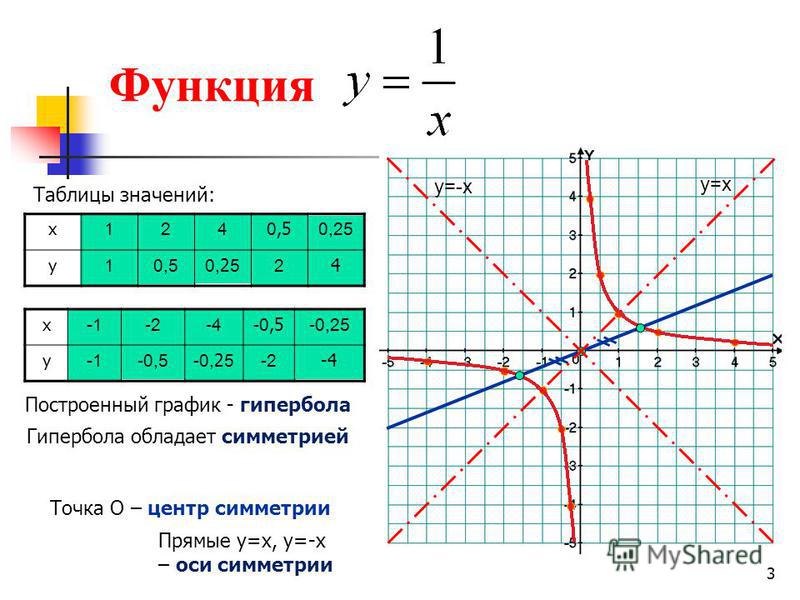
 Значит, фигура симметрична относительно осей и , и точки , которая называется центром гиперболы.
Значит, фигура симметрична относительно осей и , и точки , которая называется центром гиперболы.

 Из определения гиперболы мы знаем, что разница между расстоянием точки Р от двух фокусов F и F’ равна 2а, т. е. PF’-PF = 2а.
Из определения гиперболы мы знаем, что разница между расстоянием точки Р от двух фокусов F и F’ равна 2а, т. е. PF’-PF = 2а.


 0002 Линия, которая касается прямоугольной гиперболы в любой точке кривой прямоугольной гиперболы, называется касательной к прямоугольной гиперболе.
0002 Линия, которая касается прямоугольной гиперболы в любой точке кривой прямоугольной гиперболы, называется касательной к прямоугольной гиперболе. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 9002
9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 4. 9002 9002

 Его длина равна 2а. Прямая, проходящая через центр и фокусы гиперболы, называется поперечной осью гиперболы.
Его длина равна 2а. Прямая, проходящая через центр и фокусы гиперболы, называется поперечной осью гиперболы.
 92}=1 \)
92}=1 \) 2. \) 9{2}}{36}=1. \)
2. \) 9{2}}{36}=1. \)