Высшая математика Т2
Высшая математика Т2
ОглавлениеПРЕДИСЛОВИЕГлава 1. ВВЕДЕНИЕ § 1.1. Предмет математики. Переменные и постоянные величины, множества § 1.2. Операции над множествами § 1.3. Символика математической логики § 1.4. Действительные числа § 1.5. Определение равенства и неравенства § 1.6. Определение арифметических действий 1.6.1. Общие соображения 1.6.2. Стабилизирующиеся последовательности 1.6.3. Определение арифметических действий § 1.7. Основные свойства действительных чисел § 1.8. Аксиоматический подход к понятию действительного числа § 1.9. Неравенства для абсолютных величин § 1.10. Отрезок, интервал, ограниченное множество § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел Глава 2. Предел последовательности § 2.1. Понятие предела последовательности § 2.  2. Арифметические действия с переменными, имеющими предел§ 2.3. Бесконечно малая и бесконечно большая величины § 2.4. Неопределенные выражения § 2.5. Монотонные последовательности § 2.6. Число e § 2.7. Принцип вложенных отрезков § 2.8. Точные верхняя и нижняя грани множества § 2.9. Теорема Больцано-Вейерштрасса § 2.10. Верхний и нижний пределы § 2.11. Условие Коши сходимости последовательности § 2.12. Полнота и непрерывность множества действительных чисел Глава 3. Функция. Предел функции § 3.1. Функция 3.1.1. Функция от одной переменной. 3.1.2. Функции многих переменных. 3.1.3. Полярная система координат § 3.2. Предел функции § 3.3. Непрерывность функции § 3.4. Разрывы первого и второго рода § 3.5. Функции, непрерывные на отрезке § 3.7. Равномерная непрерывность функции § 3.8. Элементарные функции § 3.9. Замечательные пределы § 3.10. Порядок переменной. Эквивалентность Глава 4.  Дифференциальное исчисление функций одной переменной§ 4.1. Производная § 4.2. Геометрический смысл производной § 4.3. Производные элементарных функций § 4.4. Производная сложной функции § 4.5. Производная обратной функции § 4.6. Производные элементарных функций (продолжение) § 4.7. Дифференциал функции 4.7.1. Дифференцируемые функции 4.7.2. Дифференциал функции 4.7.3. Приближенное выражение приращения функции § 4.8. Другое определение касательной § 4.9. Производная высшего порядка § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка § 4.11 Дифференцирование параметрически заданных функций § 4.12. Теоремы о среднем значении § 4.13. Раскрытие неопределенностей § 4.14. Формула Тейлора § 4.15. Ряд Тейлора § 4.16. Формулы и ряды Тейлора элементарных функций § 4.17. Локальный экстремум функции § 4.18. Экстремальные значения функции на отрезке § 4.19. Выпуклость кривой.  Точка перегиба§ 4.20. Асимптота графика функции § 4.21. Непрерывная и гладкая кривая § 4.22. Схема построения графика функции § 4.23. Вектор-функция. Векторы касательной и нормали Глава 5. неопределенные интегралы § 5.1. Неопределенный интеграл. Таблица интегралов § 5.2. Методы интегрирования § 5.3. Комплексные числа § 5.4. Теория многочлена n-й степени § 5.5. Действительный многочлен n-й степени § 5.6. Интегрирование рациональных выражений § 5.7. Интегрирование иррациональных функций Глава 6. Определенный Интеграл § 6.2. Свойства определенных интегралов § 6.3. Интеграл как функция верхнего предела § 6.4. Формула Ньютона – Лейбница § 6.5. Остаток формулы Тейлора в интегральной форме § 6.6. Суммы Дарбу. Условия существования интеграла § 6.7. Интегрируемость непрерывных и монотонных функций § 6.8. Несобственные интегралы § 6.  9. Несобственные интегралы от неотрицательных функций§ 6.10. Интегрирование по частям несобственных интегралов § 6.11. Несобственный интеграл с особенностями в нескольких точках Глава 7. Приложения интегралов. Приближенные методы § 7.1. Площадь в полярных координатах § 7.2. Объем тела вращения § 7.3. Гладкая кривая в пространстве. Длина дуги § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента § 7.5. Площадь поверхности вращения § 7.6. Интерполяционная формула Лагранжа § 7.7. Квадратурные формулы прямоугольников и трапеций § 7.8. Формула Симпсона Глава 8. Дифференциальное исчисление функций многих переменных § 8.1. Предварительные сведения § 8.2. Предел функции § 8.3. Непрерывная функция § 8.4. Частные производные и производная по направлению § 8.5. Дифференцируемые функции § 8.6. Применение дифференциала в приближенных вычислениях § 8.7. Касательная плоскость. Геометрический смысл дифференциала § 8.  8. Производная сложной функции. Производная по направлению. Градиент8.8.1. Производная сложной функции 8.8.2. Производная по направлению 8.8.3. Градиент функции 8.8.4. Однородные функции § 8.9. Дифференциал функции. Дифференциал высшего порядка § 8.10. Формула Тейлора § 8.11. Замкнутое множество § 8.13. Экстремумы § 8.14. Нахождение наибольших и наименьших значений функции § 8.15. Теорема существования неявной функции § 8.16. Касательная плоскость и нормаль § 8.17. Системы функций, заданных неявно § 8.18. Отображения § 8.19. Условный (относительный) экстремум Глава 9. Ряды § 9.1. Понятие ряда § 9.2. Несобственный интеграл и ряд § 9.3. Действия с рядами § 9.4. Ряды с неотрицательными членами § 9.5. Ряд Лейбница § 9.6. Абсолютно сходящиеся ряды § 9.7. Условно сходящиеся ряды с действительными членами § 9.8. Последовательности и ряды функций. 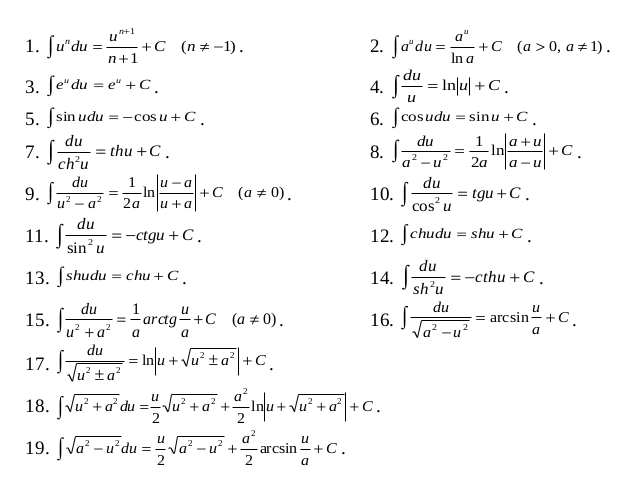 Равномерная сходимость§ 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов § 9.10. Перемножение абсолютно сходящихся рядов § 9.11. Степенные ряды § 9.12. Дифференцирование и интегрирование степенных рядов § 9.13. Функции exp(z), sinz, cosz от комплексного переменного § 9.14. Ряды в приближенных вычислениях § 9.15. Понятие кратного ряда § 9.16. Суммирование рядов и последовательностей |
Неопределенный интеграл, таблица интегралов — Интегралы и дифференциальные уравнения
Лекция 1 Неопределенный интеграл, таблица интегралов.
Функция называется первообразной для функции , если .
Теоремы о первообразных.
Теорема. Если — первообразная для функции , то (- константа) — тоже первообразная для функции .
Доказательство. .
Теорема. Пусть — две первообразных для функции , тогда они различаются на некоторую константу (- константа).
Рассмотрим функцию , она непрерывна и дифференцируема на всей числовой оси, как и функции . Тогда для любых конечных значений по формуле конечных приращений Лагранжа .
Следовательно,
Неопределенным интегралом (интеграл от функции по ) называется совокупность всех первообразных функций для функции .
.
Функция , стоящая под знаком интеграла, называется подинтегральной функцией, а выражение — подинтегральным выражением..
Свойства неопределенного интеграла.
Свойства неопределенного интеграла можно условно разделить на две группы. В первую группу собраны свойства, вытекающие из того, что интегрирование – операция, обратная дифференцированию. Во вторую группу собраны свойства линейности. Эти свойства вытекают из того, что интегрирование, как и дифференцирование – линейная операция и определяют линейную операцию.
Первая группа свойств.
1) .
2)
3)
4) .
Докажем первое свойство.
Так как
Здесь — первообразная для .
Докажем второе свойство.
Обозначим Тогда , а по первому свойству. Поэтому функции являются первообразными для функции . Следовательно, по теоремам о первообразных, они различаются на константу, т.е. или
Третье свойство следует из первого:
Четвертое свойство следует из второго, если вспомнить, что с дифференциалом первого порядка можно обращаться как с алгебраическим выражением (свойство инвариантности формы записи первого дифференциала).
Поэтому надо доказать два первых свойства.
Вторая группа свойств.
1) свойство суперпозиции
2) свойство однородности .
Доказательства того и другого свойств проводятся аналогично. Дифференцируем (по свойствам первой группы) левую и правую часть равенства, приходим к тождеству. Затем из теорем о первообразных заключаем, что левая и правая часть равенства, как первообразные одной и той же функции, различаются на константу. Эта константа может быть формально включена в неопределенный интеграл в левой или правой части равенства.
Для того, чтобы вычислить интеграл от функции, проще всего «угадать» первообразную для этой функции по таблице для производных, переписав эту таблицу в обратном порядке. Запишем интегралы для основных элементарных функций.
1) . Эти формулы лучше запомнить, они очень часто встречаются.
2)
3)
4)
Справедливость этих формул легко проверить, дифференцируя правую часть соотношения и получая подинтегральную функцию.
Основные формулы
Интегралы от рациональных функций (23 шт)
Интегралы от трансцендентных функций (15 шт)
Бесплатная лекция: «Комбинаторная литература, факториальные перестановки» также доступна.
Интегралы от иррациональных функций (27 шт)
Интегралы от тригонометрических функций (31 шт)
Интеграционные таблицы: определения и экспоненциальные
Одним из величайших достижений человечества является письмо. Благодаря этому наши знания сохраняются из поколения в поколение посредством книг, поэтому нам не нужно тратить время и силы на то, чтобы открывать все заново!
Одной из самых важных операций в исчислении является интегрирование, которое может занять много времени.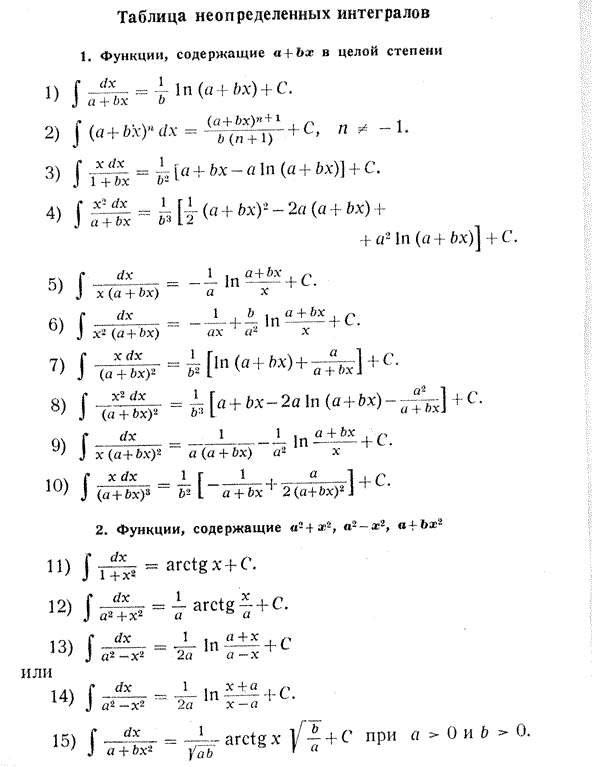
К счастью, точно так же, как информация, полученная человечеством на протяжении веков, содержится в книгах, множество интегралов хранится в Интеграция T Способности.
Метод использования таблиц интеграции
Интеграция может быть трудоемкой операцией. Сначала нужно узнать, какой метод интегрирования больше подходит для данного интеграла. После этого идет сама операция. Кто знает, может быть, вам придется несколько раз делать интеграцию по частям! Это будет трудоемко и сложно.
Вместо прохождения этой пробной версии проще использовать таблицу интеграции .
Но как можно использовать таблицу для интеграции функции? Таблицы интегрирования содержат обобщенных формул для конкретных интегралов . Важно то, что вы определяете переменные и константы, присутствующие в каждой формуле.
Вот быстрый пример. Рассмотрим интеграл
\[ \int \sin{3x} \, \mathrm{d}x.
\]
Чтобы решить этот интеграл, вам нужно выполнить интегрирование путем подстановки, положив
\[u=3x.\]
Вам также необходимо записать дифференциал \( \mathrm{d}x \) через \( u,\), что можно сделать сначала путем дифференцирования
\[ \frac{\mathrm{d}u}{\mathrm{d}x}=3,\]
умножив эту производную на \( \mathrm{d}x,\)
\[ \mathrm {d}u=3\,\mathrm{d}x,\]
и выделение \(\mathrm{d}x,\), поэтому
\[\mathrm{d}x=\frac{1}{ 3}\mathrm{d}u.\]
Теперь вы можете записать исходный интеграл в терминах \(u\), заменив каждый экземпляр \( x \) его эквивалентом в \( u,\) и каждый экземпляр \( \mathrm{d}x \) его эквивалентом в \( \mathrm{d}u,\), то есть
\[ \begin{align} \int \sin{3x} \, \mathrm{ d}x &= \int (\sin{u})\left(\frac{1}{3}\mathrm{d}u\right) \\ &= \frac{1}{3}\int \sin {u} \, \mathrm{d}u, \end{align}\]
, который является интегралом, имеющим общую формулу, которую вы можете проверить в нашей статье «Тригонометрические интегралы», то есть
\[\int \sin{u} \, \mathrm{d}u = -\cos{u} + C.
\]
Зная это, можно записать интеграл
\[ \int \sin{3x}\,\mathrm{d}x = \frac{1}{3} \left( -\cos{u } + C \right),\]
и затем отменить замену. Обычно константа интегрирования добавляется в конце, поэтому
\[ \begin{align} \int \sin{3x}\,\mathrm{d}x &= \frac{1}{3} \left( — \cos{3x} \right) + C \\ &= -\frac{1}{3}\cos{3x}+C. \конец{выравнивание}\]
В приведенном выше примере, просмотрев таблицу интегрирования тригонометрических функций, вы, скорее всего, найдете формулу вида
\[ \int \sin{ax} \, \mathrm{d}x = -\frac{1} {a}\cos{ax}+C.\]
В этом случае вам не нужно делать какую-либо \(u-\)замену, но вы должны указать, что \(a=3.\)
\ [ \begin{align} \int \sin{ax}\,\mathrm{d}x &= \frac{1}{a} \left( -\cos{ax} \right) + C \\ \int \ sin{3x} \, \mathrm{d}x &= -\frac{1}{3}\cos{3x}+C. \конец{выравнивание}\]
Основная идея использования таблиц интеграции состоит в том, чтобы определить, какой интеграл из таблицы имеет тот же вид, что и тот, который вы пытаетесь решить.
Интеграл, приведенный в таблице, уже решен, поэтому его можно использовать как формулу.
Вы можете различать переменные и константы, глядя на дифференциал интеграла. Переменная интегрирования — это та же самая переменная, которая присутствует в дифференциале, и обычно используются \(x\) или \(u\). Остальные буквы, которые вы найдете, скорее всего, являются константами, и обычно выбираются \(a,\) \(b,\) \(k,\) \(n,\) и \(m\).
Поскольку существует множество различных интегралов, таблицы интегрирования обычно разбиваются в зависимости от того, какие функции задействованы. Здесь мы рассмотрим некоторые примеры наиболее распространенных таблиц интеграции.
Таблицы интегрирования экспоненциальных функций
Интегрирование экспоненциальных функций обычно требует многократного интегрирования по частям. Вместо этого вы всегда можете посмотреть таблицы интеграции. Они могут содержать некоторые из следующих формул: 92}{5}-\frac{2x}{25}+\frac{2}{125}\right)+C. \end{align}\]
Довольно просто, правда?
Таблицы интегрирования для тригонометрических функций
Может быть трудно запомнить все первообразные основных тригонометрических функций, не говоря уже о некоторых особых случаях, когда задействованы и их степени.
2{ax}+C\end{align}\] 92}\,\mathrm{d}x\]
становится чрезвычайно актуальным. Поскольку вы не можете использовать основную теорему исчисления для вычисления вышеупомянутого интеграла, вместо этого он вычисляется численно, а его значения организованы в таблицы. Для получения дополнительной информации об этом ознакомьтесь с нашей статьей о нормальном распределении!
Таблицы интегрирования – ключевые выводы
- Таблицы интегрирования содержат обобщенные формулы для конкретных интегралов.
- Основная идея использования таблиц интеграции состоит в том, чтобы идентифицировать интеграл, который имеет ту же форму, что и интеграл из таблицы.
- Существуют таблицы интегрирования экспоненциальных функций, тригонометрических функций и многого другого! Вы должны найти таблицу, которая лучше всего соответствует интегралу, который вам нужно решить.
Интегрировать: по таблице интегралов – А
Загрузка.
Бесплатные разработанные решения
Видео расчетов
Брюс освещает каждое доказательство
Загрузка данных
Загрузка наборов данных в форме электронной таблицы
Вращающиеся графики
Просмотр и вращение трехмерных графиков
Математические графики
Печать собственных рабочих листов
Предыдущий Следующий
ChapterChapter PChapter 1Chapter 2Chapter 3Chapter 4Chapter 5Chapter 6Chapter 7Chapter 8Chapter 9Chapter 10Chapter 11Chapter 12Chapter 13Chapter 14Chapter 15Chapter 16
VideoProof — Substitution for Rational Functions of Sine and CosineIntegrate: using the table of integrals — AIntegrate : с помощью таблицы интегралов — BИспользовать формулы приведения для нахождения неопределенных интегралов
