Практическое занятие 13
Практическое занятие 13
Односторонние пределы. Непрерывность
Задания:
Найти следующие односторонние пределы:
13.1. . 13.2. .
Ответ: Ответ:
13.3. . 13.4. .
Ответ: Ответ:
13.5. . 13.6. .
Ответ: Ответ:
13.7. . 13.8. .
Ответ: Ответ:
13.9. . 13.10. .
Ответ: Ответ:
13.11. . 13.12. а) .
Ответ: Ответ:
б) . Ответ:
Исследовать на непрерывность функции:
13. . 13.14. .13.15. . 13.16. .
13.17. а) ; 13.18. .
б) .
13.19. . 13.20. .
13.21. . 13.22. .
13.23. . 13.24. .
13.25. . 13.26.
Построить график этой функции.
Задана функция . При каком выборе параметров, входящих в ее определение, будет непрерывной?
13.27.
Ответ:
13.28.
Ответ:
13.29.
Ответ:
Найти точки разрыва функции, исследовать их характер, в случае устранимого разрыва доопределить функцию «по непрерывности»:
13.30. .
Ответ: точки разрыва второго рода.
13.31. .
Ответ: точка разрыва первого рода.
13.32. .
Ответ: точка устранимого разрыва,.
13.33. .
Ответ: точка устранимого разрыва,.
13.34. .
Ответ: точка устранимого разрыва,.
13.35. .
Ответ: точки разрыва второго рода.
13.36. .
Ответ: точка разрыва первого рода.
13.37. .
Ответ: точка разрыва первого рода.
Ответ: точка разрыва первого рода.
13.39. .
Ответ: точка
устранимого разрыва,
точка
разрыва второго рода.
1340. .
Ответ: точка устранимого разрыва, точка устранимого разрыва, точка разрыва второго рода.
13.41. .
Ответ: точка устранимого разрыва, .
13.42.
Ответ: точка разрыва первого рода.
13.43. .
Ответ: точка разрыва первого рода.
13.44.
Ответ: точка разрыва первого рода.
13.45.
Ответ: точка разрыва первого рода.
Дополнительные сведения.
1. Непрерывность функции в точке. Классификация точек разрыва. Функция с областью определения называется непрерывной в точке , если выполнены следующие три условия:
а) функция определена в точке
,
т.
е.
;
б) существует ;
в) .
Если а) выполнено, то условия б) и в) эквивалентны следующему:
,
где
– приращение функции в точке , соответствующее приращению аргумента .
Если в точке нарушено хотя бы одно из условий а)-в), то называется точкой разрыва функции . При этом различают следующие случаи:
а) существует, но функция не определена в точке или нарушено условие . В этом случае называется
б) не существует. Если при этом существуют оба односторонних предела и (очевидно, не равные друг другу), то называется точкой разрыва 1-го рода.
в) в остальных случаях называется точкой разрыва 2-го рода.
2. Односторонние
пределы.
Если и
,
то условно пишут
;
аналогично, если и
,
то это записывается так:
.
Числа
и
называются соответственно пределом слева функции в точке и пределом справа функции в точке (если эти числа существуют).
Для существования предела функции при необходимо и достаточно, чтобы имело место равенство
.
Пример 1. Доказать, что функция
непрерывна для любого аргумента .
Решение:
Имеем:
.
Так как
и ,
то при любом имеем
.
Следовательно, функция непрерывна при .
Пример 2. Найти пределы справа и слева функции
при
.
Решение:
Имеем:
и
.
Предела же функции при в этом случае, очевидно, не существует.
Пример 3. Найти левый и правый пределы функции
Решение:
Если , то и . Следовательно, .
Если же , то , и .
Пример 4. Найти левый и правый пределы функции
при .
Решение:
Если , то и .
Если же , то и .
Пример 5. Показать, что при функция имеет разрыв.
Решение:
Находим
,
.
Таким образом, функция при не имеет ни левого, ни правого конечного
предела.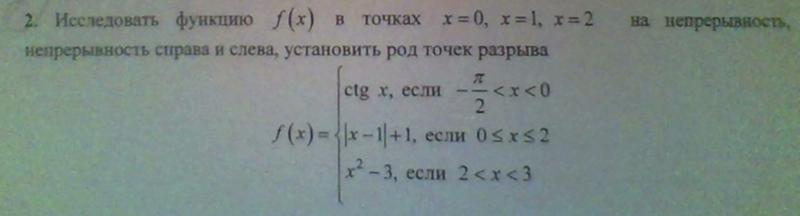
Следовательно, является точкой разрыва II
рода.
Пример 6. Показать, что при функция имеет разрыв.
Решение:
Если , то и . Если же , то и . Итак, при функция имеет как правый так и левый конечный предел, причем эти пределы различны. Следовательно, является точкой разрыва I рода – точкой скачка. Скачок функции в этой точке равен .
Домашнее задание к практическому занятию № 13.
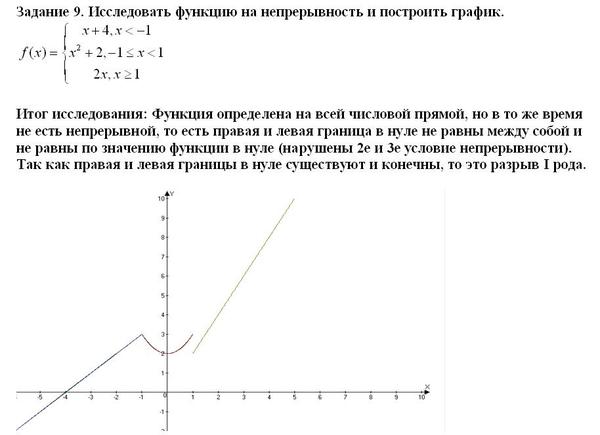
1. Исследовать данные функции на непрерывность и построить их графики.
1) 2)
3) 4)
5) 6)
7) 8)
9) 10)
11) 12)
13) 14) .
15) 16)
17) 18)
19) 20)
21) 22)
23) 24)
25) 26)
27) 28)
29) 30)
2.
1) .
2) .
3) .
4) .
5) .
6) .
7) .
8) .
9) .
10) .
11) .
12) .
13) .
14) .
15) .
16) .
17) .
18) .
19) .
20) .
21) .
22) .
23) .
24) .
25) .
26) .
27) .
28) .
29) .
30) .
Решение типового варианта
1.
Исследовать данную функцию на непрерывность
и построить ее график:
Функция определена и непрерывна на интервалах и , где она задана непрерывными элементарными функциями. Следовательно, разрыв возможен только в точках и . Для точки имеем:
,
т.е. функция в точке имеет разрыв первого рода.
Для точки находим:
, , т.е. в точке функция также имеет разрыв первого рода. График данной функции изображен на рис.1. | Рис.1. |
2. Исследовать функцию на непрерывность в точках .
Для точки имеем:
,
,
т.
е. в точке функция терпит бесконечный разрыв (–точка
разрыва второго рода).
Для точки имеем:
,
.
Следовательно, в точке функция непрерывна.
258
виды разрывов функции
Вы искали виды разрывов функции? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и виды точек разрыва, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «виды разрывов функции».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте.
Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как виды разрывов функции,виды точек разрыва,исследовать на непрерывность функцию и указать характер точек разрыва,исследовать функцию на непрерывность в указанных точках,исследовать функцию на непрерывность и указать характер точек разрыва,как найти точки разрыва,как найти точки разрыва функции,как найти точки разрыва функции и определить их характер,как найти точки разрыва функции и определить характер разрыва,как найти точки разрыва функции онлайн,как найти точку разрыва функции,как определить точки разрыва функции,как устранить разрыв функции,классификация точек разрыва,классификация точек разрыва функции,найти точки разрыва функции,найти точки разрыва функции и определить их характер,найти точки разрыва функции и определить их характер онлайн,найти точки разрыва функции онлайн,найти точки разрыва функции онлайн с подробным решением,найти точку разрыва функции онлайн,нахождение точек разрыва функции,нахождение точек разрыва функции онлайн,непрерывность и точки разрыва функции,непрерывность функции и точки разрыва,непрерывность функции и точки разрыва функции,непрерывность функции точки разрыва,непрерывность функции точки разрыва функции,онлайн найти точку разрыва функции,определение точки разрыва функции,разрыв 1 и 2 рода,разрыв 1 рода,разрыв 2 рода,разрыв второго и первого рода,разрыв второго рода,разрыв первого и второго рода,разрыв первого рода,разрыв первого рода второго рода,разрыв первого рода и второго,разрыв первого рода устранимый,разрыв устранимый,разрыв функции,разрыв функции в точке x0 называется разрывом первого рода если,разрыв функции устранимый,разрывная функция,разрывы 1 и 2 рода,разрывы второго и первого рода,разрывы первого и второго рода,точка разрыва,точка разрыва 1 рода,точка разрыва 2 рода,точка разрыва второго рода,точка разрыва первого и второго рода,точка разрыва первого рода,точка разрыва первого рода второго рода,точка разрыва функции,точка разрыва это,точка устранимого разрыва,точки разрыва,точки разрыва 1 и 2 рода,точки разрыва 1 рода 2 рода,точки разрыва и их классификация,точки разрыва и непрерывность функции,точки разрыва как найти,точки разрыва онлайн,точки разрыва первого и второго рода,точки разрыва функции,точки разрыва функции и их классификация,точки разрыва функции как найти,точки разрыва функции онлайн,точки разрыва функции онлайн калькулятор,устранимый разрыв,устранимый разрыв функции,устраните разрыв функции,устранить разрыв функции,характер точек разрыва.
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и виды разрывов функции. Просто введите задачу в окошко и нажмите
«решить» здесь (например, исследовать на непрерывность функцию и указать характер точек разрыва).
Решить задачу виды разрывов функции вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
исчисление — непрерывность функции без заданной точки
спросил
Изменено 5 лет, 8 месяцев назад
Просмотрено 280 раз
$\begingroup$
Я знаю, как проверить непрерывность функции в данной точке.
2:x\ne 0 \text{ или } y \ne 0\}$. Буду ли я прав, если скажу, что f(x,y) непрерывна, поскольку точки разрывов не лежат в области определения f(x,y)?
- исчисление
$\endgroup$
$\begingroup$
Утверждение, что «$f(x,y)$ непрерывна, поскольку точки разрыва не лежат в области определения $f(x,y)$», не является совершенно строгим (поскольку функция просто не существует вне ее домен, так что нельзя даже сказать, что разрывов в том нет нигде ), но интуицию улавливает правильную.
Вас заботит только то, что происходит в домене функции; так, например, если у вас есть функция, которая где-то непрерывна и прерывна в другом месте, и вы удаляете из области определения все точки разрыва, у вас остается непрерывная функция.
$\endgroup$
$\begingroup$
нет, здесь вообще нет точек разрыва!
быть непрерывной или нет, сначала функция должна быть определена в точке!
(если она не определена, вы не можете сказать, что она непрерывна или прерывиста — см.
определение непрерывности)
в этом примере вы можете сказать, что $f$ непрерывна, поскольку она является частным двух непрерывных функций
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Как определить, является ли функция непрерывной или прерывистой Для чайников
Исследовать Книга Купить на Amazon
Гладкий график функции без дырок, скачков и асимптот называется непрерывным. Ваш учитель математического анализа скажет вам, что три вещи должны быть истинными, чтобы функция была непрерывной при некотором значении c в своем домене:f ( c ) должны быть определены. Функция должна существовать со значением x ( c ), что означает, что в функции не может быть пробела (например, 0 в знаменателе).
Предел функции при приближении x к значению c должен существовать. Левый и правый пределы должны быть одинаковыми; другими словами, функция не может прыгать или иметь асимптоту. Математический способ сказать это так:
должен существовать.
Значение функции при c и предел при приближении x к c должны быть одинаковыми.
непрерывна при x = 4 благодаря следующим фактам:
f (4) существует. Вы можете подставить 4 в эту функцию, чтобы получить ответ: 8.
Если вы посмотрите на функцию алгебраически, то она будет иметь следующие множители:
Ничего не отменяет, но можно еще поставить 4, чтобы получить
что 8.
Обе части уравнения равны 8, поэтому f(x) непрерывна при x = 4.
Функции, которые не являются непрерывными при значении x , имеют либо устранимую неоднородность (отверстие в графике функции), либо неустранимую неустранимую неоднородность (например, скачок или асимптота на графике) :
Если множители функции и нижний член сокращаются, разрыв в значении x , для которого знаменатель был равен нулю, устраним, поэтому на графике есть дыра.
Например, эта функция действует как показано:
После отмены остается x – 7. Следовательно, x + 3 = 0 (или x = –3) является устранимым разрывом — в графике есть дыра, как вы видите на рисунке a.
График устранимого разрыва оставляет ощущение пустоты, тогда как график неустранимого разрыва вызывает нервозность.
Если терм не сокращается, разрыв на этом значении x , соответствующем этому члену, для которого знаменатель равен нулю, является неустранимым, и график имеет вертикальную асимптоту.
Следующие функциональные факторы, как показано:
Поскольку x + 1 отменяется, у вас есть устранимый разрыв в x = –1 (здесь вы увидите дыру на графике, а не асимптоту). Но x – 6 не сокращаются в знаменателе, поэтому у вас есть неустранимый разрыв при x = 6. Этот разрыв создает вертикальную асимптоту на графике при x = 6. На рисунке b показан график г ( х ).
