Признак Даламбера сходимости рядов: теория, примеры
- Теоретические основы
- Решаем примеры
Признак признак Даламбера, как и признак сравнения, радикальный признак Коши и интегральный признак Коши, является достаточным признаком сходимости рядов, так как исследование ряда с помощью этого признака даёт однозначный ответ на вопрос о том, сходится ряд или расходится. Признак Даламбера предполагает найти предел отношения некоторого ряда к предыдущему члену того же ряда. Признак Даламбера, скорее всего, работает, если в выражение ряда входят:
- число в степени,
- факториал,
- цепочки множителей один-три-пять-семь и так далее.
Основной фигурант признака Даламбера — дробь, в числителе которой некоторый член ряда, а
в знаменателе — предыдущий член того же ряда. Вычисляется предел этого отношения… Впрочем, перейдём к научной
форме изложения рассматриваемого признака.
Тогда:
- а) если предел отношения меньше единицы (), то ряд сходится;
- б) если предел отношения больше единицы (), то ряд расходится;
- в) если предел отношения равен единице (), то вопрос о сходимости ряда остаётся нерешённым.
Пример 1. Исследовать сходимость ряда с общим членом
Решение. Найдём отношение
Так как , а , то
и, следовательно,
Установлена сходимость.
Пример 2. Исследовать сходимость ряда
Решение. Общий член данного ряда
а следующий за ним член
Находим их отношение:
Следовательно,
Констатируем расходимость.
Пример 3. Исследовать сходимость ряда с общим членом
Используя признак Даламбера, получаем
Таким образом, получилась неопределённость вида ∞/∞. Раскроем её с помощью правила Лопиталя:
Поскольку l = 1, о сходимости ряда ничего определённого сказать нельзя. Необходимо дополнительное исследование. Сравним данный ряд с гармоническим. Так как при n > 1 получается ln (n + 1) < n, то 1/ln (n + 1) > 1/(n + 1), т.е. члены данного ряда, начиная со второго, больше соответствующих членов расходящегося гармонического ряда, а поэтому данный ряд также расходится.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Ряды
Пример 4. Исследовать сходимость ряда с общим членом
Решение. Так как
Так как
а
то
Поэтому
Признак Даламбера не решает вопроса о сходимости. Продолжим исследование. Поскольку n < n +1, имеем
Следовательно, члены данного ряда меньше соответствующих членов сходящегося ряда, и, значит, данный ряд сходится.
Пример 5. Исследовать сходимость рядаРешение. Запишем n-й член ряда:
Решение. Запишем n+1-й член ряда:
Находим предел их отношения:
Предел отношения больше единицы, поэтому о сходимости не может быть и речи.
Пример 6. Исследовать сходимость ряда
Решение. Запишем n-й член ряда:
Запишем n-й член ряда:
Решение. Запишем n+1-й член ряда:
Находим предел их отношения:
Получили значение меньше единицы и, значит, установили сходимость.
Решение. Запишем n-й член ряда:
Решение. Запишем n+1-й член ряда:
Находим предел их отношения:
Предел отношения членов рядов меньше единицы, поэтому констатируем сходимость.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Ряды
Всё по теме «Ряды»
- Числовые ряды
- Признак сравнения рядов
- Признак Даламбера сходимости рядов
- Радикальный признак Коши сходимости рядов
- Интегральный признак Коши сходимости рядов
- Знакочередующиеся и знакопеременные ряды.
 Признак Лейбница
Признак Лейбница - Функциональные ряды
- Степенные ряды
- Ряды Фурье
Признак Даламбера сходимости ряда
Исследование сходимости рядов является важным с точки зрения их оценки и необходимым в случае вычисления суммы ряда. Признаков сходимости рядов несколько, популярный и достаточно прост в применении для рядов с положительными членами — признак сходимости Даламбера. Ниже будет разобран ряд примеров на установление сходимости ряда по признаку Даламбера, советую для себя взять максимум полезного.
Напомним что предпосылками для применения признака Даламбера служит наличие степенной зависимости (2, 3, a в степени n) или факториалов в формуле общего члена ряда. Будет это знаменатель или числитель дроби совсем не имеет значения, важно что имеем подобную зависимость, ну или факториал и степенную зависимость в одном наборе. С факториалами у многих на первых порах возникают проблемы но с практикой Вы заметете что ничего сложного в факториалах нет. Надо только расписать факториал подробно до тех пор когда в числителе или знаменателе дроби поучим одинаковые множителе. На словах это звучит не всем понятно, но следующие примеры помогут Вам в этом разобраться. Ну и самые сложные примеры предполагают наличие комбинаций факториалов и степенных зависимостей, два или более факториала, тоже и для степенной фунции, всевозможные цепочки множителей и другие каверзные комбинации. Ниже приведены базовые примеры с которых и начинается практика проверки сходимости ряда по Даламберу.
На словах это звучит не всем понятно, но следующие примеры помогут Вам в этом разобраться. Ну и самые сложные примеры предполагают наличие комбинаций факториалов и степенных зависимостей, два или более факториала, тоже и для степенной фунции, всевозможные цепочки множителей и другие каверзные комбинации. Ниже приведены базовые примеры с которых и начинается практика проверки сходимости ряда по Даламберу.
Пример: 2.5 Исследовать сходимость рядов
а)
Вычисления: Поскольку данный ряд имеет положительные члены то исследовать его на сходимость можем с помощью признака Даламбера:
Если А<1 ряд сходящийся, А>1 — ряд расходящийся и при A=0 следует использовать другие признаки сходимости рядов.
Записываем общий член ряда и следующий, идущий после него
И находим границу их доли
Поскольку граница бесконечна то по признаку Даламбера ряд расходящийся. Если искать суму ряда то она будет бесконечная.
б)
Вычисления: Члены ряда положительные поетому исследуем на сходимость по признаку Даламбера — записываем формулы последовательных членов ряда
И находим предел отношения следующего члена к предыдущему при n стремящемуся к бесконечности
Граница равна нулю так как показатель стремится к бесконечности, а в скобках имеем значение меньше единицы.
По теореме Даламбера A = 0 <1 ряд сходится!
Пример: 2.8 Исследовать ряды на сходимость:
а)
Вычисления: Как Вы уже убедились все примеры которые здесь рассматриваются следует проверять по признаку Даламбера.
В результате упрощения придем ко второму замечательному пределу — экспоненте
В общем граница меньше единицы следовательно ряд сходится.
б)
Вычисления: Для проверки на сходимость ряда по признаку Даламбера вычисляем предел
Предел равен 0 (A = 0 <1) следовательно ряд сходится!
Пример: 2.14 Исследовать ряд на сходимость
а)
Вычисления: Находим предел следующего члена ряда к предыдущему
Для удобства чтения формул следующий член ряда выделенный в формулах черным цветом. Хорошо разберитесь как делить факториал на факториал, как показывает статистика множество неверных ответов Вы у Вас выходит в примерах с факториалами.
По признаку Даламбера ряд сходится.
б)
Вычисления: Записываем формулу общего члена ряда и последовавшего за ним
Подставляем их в формулу Даламбера и вычисляем предел
Граница равна нулю 0 <1, а это значит что данный ряд сходящийся.
Пример: 2.16 Исследовать ряд на сходимость:
а)
Вычисления: По признаку Даламбера проверяем границу общего члена ряда на ограниченность
Превратив множители в числителе и знаменателе дроби сведем функцию в скобках ко второму замечательному пределу
Поскольку граница меньше единицы
то согласно теореме Даламбера ряд сходящийся.
б)
Вычисления: Задан числовой степенной ряд с положительными членами. Найдем предел отношения последующего члена ряда к предыдущему
При исчислении границы считаю все моменты Вам понятны, если нет то Вам нужно прочесть статьи с категории «предел функций».
Получили предел меньше единицы,
следовательно ряд сходится за Даламбером .
Пример: 2.26 Исследовать сходимость ряда:
а)
Вычисления: Для применения признака Даламбера выпишем общий член ряда и последующий за ним
Далее подставим их и найдем предел дроби
Предел равен A = 3/2> 1, а это значит что данный ряд расходящийся.
б)
Вычисления: Записываем два последовательных члены положительного ряда
Находим границу для оценки сходимости ряда по теореме Даламбера.
В ходе вычислений получим второй замечательный предел (экспоненту) как в числителе, так и в знаменателе. Результирующая граница больше единицы , следовательно делаем вывод о расхождении ряда.
- Назад
- Вперёд
Сходимость рядов. Признак Даламбера
Сходимость рядов. Признак Даламбера
Сходимость рядов. Признак Даламбера
Пусть задана бесконечная последовательность чисел . Выражение называется числовым рядом. При этом числа называются членами ряда.
Числовой ряд часто записывают в виде .
Теорема (необходимый признак сходимости ряда). Если ряд сходится,
то его -й
член стремится к нулю при неограниченном возрастании .
Следствие. Если -й
член ряда не стремится к нулю при ,
то ряд расходится.
Теорема
— ряд сходится в случае ,
— ряд расходится в случае .
В случаях, когда предел не существует или он равен единице, ответа на вопрос о сходимости или расходимости числового ряда теорема не дает. Необходимо провести дополнительное исследование.
Примеры решения задач
Пример 1. Исследовать сходимость ряда .
Решение.
Применим признак сходимости
Даламбера. Сначала запишем формулы для -го
и -го
членов ряда:
Затем найдем предел отношения -го
члена ряда к -му
при :
И последнее, сделаем вывод о сходимости ряда, сравнив полученное значение предела
с 1.
Ответ: ряд
расходится.
Пример 2. Исследовать сходимость ряда .
Решение.
Применим признак сходимости Даламбера. Запишем формулы для -го и -го членов ряда:
Найдем предел отношения -го
члена ряда к -му
при :
Сравним полученное значение предела с 1. Поскольку ,
то данный ряд сходится.
Ответ: ряд сходится.
Пример 3. Исследовать сходимость ряда .
Решение.
Используем признак сходимости Даламбера, а также определение функции факториал. Поскольку для каждого целого положительного числа функция (читается «n факториал»), по определению, равна произведению всех целых чисел от 1 до , т.е. , то .
С учетом вышесказанного найдем предел отношения -го
члена ряда к -му
при :
Вывод о сходимости ряда: сравнив полученное значение предела с 1 ,
устанавливаем, что данный ряд сходится.
Ответ: ряд сходится.
Пример 4. Исследовать сходимость ряда .
Решение.
Используем признак сходимости Даламбера. Запишем формулы для -го и -го членов ряда:
С учетом того, что ,
найдем предел отношения -го
члена ряда к -му
при :
Вывод о сходимости ряда: сравнив полученное значение предела с 1 ,
устанавливаем, что данный ряд расходится.
Ответ: ряд
расходится.
Пример 5. Исследовать сходимость ряда , пользуясь признаком сходимости Даламбера.
Решение.
Запишем формулы для -го и -го членов ряда:
.
Далее найдем предел отношения -го
члена ряда к -му
при :
Вывод о сходимости ряда: сравнив полученное значение предела с 1 ,
устанавливаем, что данный ряд расходится.
Ответ: ряд
расходится.
Пример 6. Исследовать сходимость ряда ,
пользуясь признаком сходимости Даламбера.
Решение.
Запишем формулы для -го и -го членов ряда:
Далее найдем предел отношения -го
члена ряда к -му
при :
И последнее, сделаем вывод о сходимости ряда, сравнив полученное значение предела
с 1. Поскольку ,
то данный ряд сходится.
Ответ: ряд
сходится.
Пример 7. Исследовать сходимость ряда , пользуясь признаком сходимости Даламбера.
Решение.
Сначала запишем формулы для -го и -го членов ряда:
Затем найдем предел отношения -го
члена ряда к -му
при :
Сравним полученное значение предела с 1. Поскольку ,
то данный ряд сходится.
Ответ: ряд
сходится.
Пример 8. Исследовать сходимость ряда , пользуясь признаком сходимости Даламбера.
Решение.
Предварительно вспомним, что для каждого целого положительного числа функция , по определению, равна произведению всех целых чисел от 1 до , т.е. .
Тогда для
и
получим: ,
.
Теперь запишем формулы для -го
и -го
членов ряда:
Далее найдем предел отношения -го
члена ряда к -му
при :
Вывод о сходимости ряда: сравнив полученное значение предела с 1 ,
устанавливаем, что данный ряд сходится.
Ответ: ряд
сходится.
Задания для самостоятельной работы
Исследовать сходимость
ряда, пользуясь признаком сходимости Даламбера:
1. . Ответ: ,
ряд расходится.
2. . Ответ: ,
ряд сходится.
3. . Ответ: , ряд расходится.
4. . Ответ: , ряд сходится.
5. . Ответ: , ряд расходится.
6. . Ответ: , ряд расходится.
7. . Ответ: , ряд сходится.
8. . Ответ: , ряд сходится.
9. . Ответ: , ряд сходится.
10. . Ответ: , ряд сходится.
11. . Ответ: , ряд сходится.
12. . Ответ: , ряд сходится.
13. . Ответ: , ряд расходится.
14. . Ответ: , ряд сходится.
15. . Ответ: ,
ряд расходится.
16. . Ответ: , ряд сходится.
исследование сходимости числовых положительных рядов
Оглавление:
Задание: Исследование сходимости числовых положительных рядов.
Цель: формирование умения применять достаточные признаки (сравнения, Даламбера, радикальный и интегральный Коши) при исследовании рядов на сходимость.
Задание для самостоятельной внеаудиторной работы:
39.1. Выучите определение положительного (знакоположительного) ряда. Сформулируйте признак сравнения. Выясните, какова техника его применения для исследования сходимости положительных рядов. Запомните ряды, традиционно использующиеся в качестве «эталонных» для исследования сходимости ряда по признаку сравнения.
39.2. С помощью признака сравнения исследуйте на сходимость положительные ряды:
39.3. Сформулируйте признак Даламбера. Постарайтесь освоить алгоритм, позволяющий исследовать сходимость положительного ряда по признаку Даламбера. Изучите пример исследования сходимости ряда по этому признаку.
Изучите пример исследования сходимости ряда по этому признаку.
39.4. С помощью признака Даламбера исследуйте на сходимость положительные ряды:
39.5. Сформулируйте признак Коши (радикальный). Постарайтесь освоить алгоритм, позволяющий исследовать сходимость положительного ряда по признаку Коши. Изучите пример исследования сходимости ряда по этому признаку.
39.6. С помощью признака Коши исследуйте на сходимость положительные ряды:
39.7. Выясните, в чём заключается интегральный признак Коши, и как он применяется для исследования сходимости положительных рядов.
39.8. С помощью интегрального признака Коши исследуйте на сходимость положительные ряды:
39.9. Проанализируйте, в каких случаях исследовать положительный ряд на сходимость целесообразно с помощью признака сравнения, в каких — с помощью признака Даламбера, а в каких — с помощью признаков Коши.
39.10. Исследуйте на сходимость положительные ряды:
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала: Числовой ряд с неотрицательными членами называется положительным (знакоположительным).
Признак сравнения позволяет исследовать положительный ряд на сходимость путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет.
Признак сравнения: Пусть даны два положительных ряда и . Если, начиная с некоторого номера, выполняется неравенство , то
- из сходимости ряда следует сходимость ряда ;
- из расходимости ряда следует расходимость ряда .
Другими словами:
- если общий член исследуемого ряда меньше общего члена сходящегося ряда, то исследуемый ряд сходится;
- если общий член исследуемого ряда больше общего члена расходящегося ряда, то исследуемый ряд расходится.
В качестве «эталонных» обычно используют следующие ряды:
1. — расходящийся гармонический ряд;
2. , если — расходящийся обобщённый гармонический ряд,
, если — сходящийся обобщённый гармонический ряд;
3. , если — расходящийся ряд геометрической прогрессии,
, если — сходящийся ряд геометрической прогрессии.
Рассмотрим примеры использования признака сравнения для исследования сходимости положительных рядов.
Пример 1.Исследуйте ряд на сходимость, применяя признак сравнения.
Решение:
Сравним данный ряд с «эталонным» рядом геометрической прогрессии , который сходится . Имеем: . Таким образом, общий член нашего ряда меньше общего члена сходящегося ряда. Следовательно, по признаку сравнения, ряд сходится.
Ответ: сходится.
Пример 2.Исследуйте ряд на сходимость, применяя признак сравнения.
Решение:
Рассмотрим ряд . Поскольку он получается из расходящегося гармонического ряда умножением на 2, то, по свойству числовых рядов (свойство 2), он расходится. Сравним исследуемый ряд с рядом . Имеем: , т.е. . Таким образом, общий член исследуемого ряда больше общего члена расходящегося ряда. Следовательно, по признаку сравнения, ряд расходится.
Ответ: расходится.
В отличие от признака сравнения, где многое зависит от догадки и запаса «эталонных» рядов, признак Даламбера часто позволяет исследовать сходимость ряда, проделав лишь некоторые операции над ним.
Признак Даламбера: Пусть дан положительный числовой ряд и существует конечный или бесконечный предел . Тогда:
- если , то ряд сходится;
- если , то ряд расходится;
- если , то признак не применяется (вопрос о сходимости ряда остается открытым).
Исследовать ряд на сходимость по признаку Даламбера удобно по следующему алгоритму:
1) найти ;
2) найти ;
3) найти ;
4) найти предел отношения на бесконечности и проанализировать полученное значение:
- если , то ряд сходится;
- если , то ряд расходится;
- если , то признак Даламбера ответа не дает (требуется дополнительное исследование).
Рассмотрим пример использования признака Даламбера для исследования сходимости положительных рядов.
Исследуйте ряд на сходимость, применяя признак Даламбера.
Решение:
Для исследования сходимости ряда по признаку Даламбера воспользуемся алгоритмом:
1) найдём
2) найдём
3) найдём
4) найдём (при раскрытии неопределенности использовали правило Лопиталя). Получили, что . Значит, по признаку Даламбера ряд расходится.
Ответ: расходится.
Заметим, что признак Даламбера целесообразно применять в том случае, когда общий член ряда содержит выражение вида или .
Иногда для исследования сходимости положительного ряда удобно использовать радикальный признак Коши, во многом схожий с признаком Даламбера.
Признак Коши (радикальный): Пусть дан положительный числовой ряд , и существует конечный или бесконечный предел . Тогда:
- если , то ряд сходится;
- если , то ряд расходится;
- если , признак не применяется (вопрос о сходимости ряда остается открытым).

Исследовать ряд на сходимость по признаку Коши удобно по следующему алгоритму:
1) найти ;
2) найти ;
3) найти и проанализировать полученное значение:
- если , то ряд сходится;
- если , то ряд расходится;
- если , то признак Коши ответа не дает (требуется дополнительное исследование).
Исследуйте ряд на сходимость, применяя признак Коши.
Решение:
Для исследования сходимости ряда по признаку Коши воспользуемся алгоритмом:
1) найдём
2) найдём
3) найдём . Получили, что . Значит, по признаку Коши ряд сходится.
Ответ: сходится.
Заметим, что признак Коши целесообразно применять в том случае, когда общий член ряда представляет собой -ую степень выражения.
В некоторых ситуациях, когда ни один из признаков сравнения, Даламбера, Коши не дает ответ о сходимости положительного ряда, исследовать ряд на сходимость позволяет интегральный признак Коши.
Интегральный признак Коши: Если члены положительного ряда могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке функции так, что , то данный ряд и несобственный интеграл одновременно сходятся или расходятся.
Пример 5.Исследуйте ряд на сходимость, применяя интегральный признак Коши.
Решение:
Рассмотрим функцию . Эта функция непрерывна, монотонно убывает на , и , следовательно, можно применить интегральный признак Коши.
Выясним, будет ли несобственный интеграл сходиться или расходиться.
Имеем: .
Отдельно найдём неопределённый интеграл методом замены переменной:
Найдем предел: .
Таким образом, получили . Следовательно, несобственный интеграл расходится. Значит, в силу интегрального признака Коши, ряд также будет расходиться.
Ответ: расходится.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение… Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит… Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Интересное: Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны. Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 5Следующая ⇒ Перед тем как сформулировать сам признак, рассмотрим важный вопрос: !!! Основные предпосылки для применения признака Даламбера следующие: 1) В общий член ряда («начинку» ряда) входит какое-нибудь число в степени, например, , , и так далее. 2) В общий член ряда входит факториал. Что такое факториал? ! При использовании признака Даламбера нам как раз придется расписывать факториал подробно. Как и в предыдущем пункте, факториал может располагаться вверху или внизу дроби. 3) Если в общем члене ряда есть «цепочка множителей», например, . Этот случай встречается редко. ! Вместе со степенями или (и) факториалами в начинке ряда часто встречаются многочлены, это не меняет дела – нужно использовать признак Даламбера. ! Кроме того, в общем члене ряда может встретиться одновременно и степень и факториал; может встретиться два факториала, две степени, важно чтобы там находилось хоть что-то из рассмотренных пунктов – и это как раз предпосылка для использования признака Даламбера. Признак Даламбера: Рассмотрим положительный числовой ряд . !!! Без понимания предела и умения раскрывать неопределенность дальше, к сожалению, не продвинуться. Пример: Исследовать ряд на сходимость Используем признак Даламбера:
Радикальный признак Коши. Признак сходимости Коши для положительных числовых рядов чем-то похож на только что рассмотренный признак Даламбера. Радикальный признак Коши:Рассмотрим положительный числовой ряд . Если существует предел: , то: ! Интересно отметить, что если признак Коши не даёт нам ответа на вопрос о сходимости ряда, то признак Даламбера нам тоже не даст ответа. Но если признак Даламбера не даёт ответа, то признак Коши вполне может «сработать». То есть, признак Коши является в этом смысле более сильным признаком. !!! Когда нужно использовать радикальный признак Коши? Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда ПОЛНОСТЬЮ находится в степени, зависящей от «эн». Либо когда корень «хорошо» извлекается из общего члена ряда. Пример: Исследовать ряд на сходимость Решение: Мы видим, что общий член ряда полностью находится под степенью, зависящей от , а значит, нужно использовать радикальный признак Коши:
Интегральный признак Коши. Для того чтобы применять интегральный признак Коши необходимо более или менее уверенно уметь находить производные, интегралы, а также иметь навык вычисления несобственного интеграла первого рода. Сформулирую своими словами (для простоты понимания). Интегральный признак Коши: Рассмотрим положительный числовой ряд . Данный ряд сходится или расходится вместе с соответствующим несобственным интегралом. !!! Основной предпосылкой использования интегрального признака Коши является тот факт, что в общем члене ряда есть некоторая функция и её производная. Пример: Исследовать ряд на сходимость Решение: Из темы Производная вы наверняка запомнили простейшую табличную вещь: , и у нас как раз такой канонический случай. Как использовать интегральный признак? Сначала берем значок интеграла и переписываем со «счётчика» ряда верхний и нижний пределы: . Затем под интегралом переписываем «начинку» ряда с буковкой «икс»: . Теперь нужно вычислить несобственный интеграл . При этом возможно два случая: 1) Если выяснится, что интеграл сходится, то будет сходиться и наш ряд . 2) Если выяснится, что интеграл расходится, то наш ряд тоже будет расходиться. Используем интегральный признак: Подынтегральная функция непрерывна на Таким образом, исследуемый ряд расходится вместе с соответствующим несобственным интегралом.
Пример: Исследовать сходимость ряда Решение: прежде всего, проверяем необходимый признак сходимости ряда. Числовая последовательность более высокого порядка роста, чем , поэтому , то есть необходимый признак сходимости выполнен, и ряд может, как сходиться, так и расходиться. Таким образом, нужно использовать какой-либо признак. Но какой? Предельный признак сравнения явно не подходит, поскольку в общий член ряда затесался логарифм, признаки Даламбера и Коши тоже не приводят к результату. Если бы у нас был , то худо-бедно можно было бы вывернуться через интегральный признак. «Осмотр места происшествия» наводит на мысль о расходящемся ряде (случай обобщенного гармонического ряда), но опять же возникает вопрос, как учесть логарифм в числителе? Остаётся самый первый признак сравнения, основанный на неравенствах, который часто не принимается во внимание и пылится на дальней полке. Распишем ряд подробнее: Напоминаю, что – неограниченно растущая числовая последовательность: В итоге, ряду ничего не остаётся, как тоже расходиться. !!! Сходимость или расходимость числового ряда зависит от его «бесконечного хвоста» (остатка). В нашем случае мы можем не принимать во внимание тот факт, что неравенство неверно для первых двух номеров – это не оказывает влияния на сделанный вывод. Чистовое оформление примера должно выглядеть примерно так: Сравним данный ряд с расходящимся рядом .
Знакочередующиеся ряды. Признак Лейбница. Примеры решений. Что такое знакочередующийся ряд?Это понятно или почти понятно уже из самого названия. Сразу простейший пример. Рассмотрим ряд и распишем его подробнее:
!!! В практических примерах знакочередование членов ряда может обеспечивать не только множитель , но и его родные братья: , , , …. !!! Подводным камнем являются «обманки»: , , и т.п. – такие множители не обеспечивают смену знака. Совершенно понятно, что при любом натуральном : , , . Как исследовать знакочередующийся ряд на сходимость?Использовать признак Лейбница. Признак Лейбница: Если в знакочередующемся ряде выполняются два условия: 1) члены ряда монотонно убывают по абсолютной величине . 2) предел общего члена по модулю равен нулю , то ряд сходится, и модуль суммы этого ряда не превосходит модуля первого члена. Краткая справка о модуле: Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду . Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Теперь немного про монотонность. Члены ряда строго монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю МЕНЬШЕ, чем предыдущий: . Члены ряда нестрого монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю НЕ БОЛЬШЕ предыдущего: . Рассмотрим ряд с факториалом: Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего: . !!! В условиях теоремы Лейбница должна выполняться монотонность убывания (неважно, строгая или нестрогая). При этом члены ряда могут даже некоторое время возрастать по модулю, но «хвост» ряда обязательно должен быть монотонно убывающим. Пример: Исследовать ряд на сходимость Решение: В общий член ряда входит множитель , а значит, нужно использовать признак Лейбница 1) Проверка ряда на монотонное убывание. 1<2<3<…, т.е. 2) – второе условие тоже не выполнено. Вывод: ряд расходится.
Определение: Если ряд сходится по признаку Лейбница и ряд, составленный из модулей: тоже сходится, то говорят, что ряд сходится абсолютно. Если ряд сходится по признаку Лейбница, а ряд, составленный из модулей: расходится, то говорят, что ряд сходится условно. Достаточный признак сходимости знакочередующегося ряда:Если ряд, составленный из модулей сходится, то сходится и данный ряд. !!! Поэтому знакочередующейся сходящийся ряд необходимо исследовать на абсолютную или условную сходимость. Пример: Исследовать ряд на условную или абсолютную сходимость Решение: Используем признак Лейбница: 1) Каждый следующий член ряда по модулю меньше, чем предыдущий: – первое условие выполнено. 2) – второе условие тоже выполнено. Вывод: ряд сходится. Проверим на условную или абсолютную сходимость.
Составим ряд из модулей – опять просто убираем множитель, который обеспечивает знакочередование: Таким образом, наш ряд не является абсолютно сходящимся.
Пример: Исследовать ряд на условную или абсолютную сходимость Решение: Используем признак Лейбница: 2) Дело в том, что не существует стандартных обыденных приемов для решения подобных пределов. Куда стремится такой предел? К нулю, к бесконечности? Здесь важно, ЧТО на бесконечности растёт быстрее – числитель или знаменатель. Если числитель при растёт быстрее факториала, то . Если, на бесконечности факториал растёт быстрее числителя, то он, наоборот – «утянет» предел на ноль: . А может быть этот предел равен какому-нибудь отличному от нуля числу? Записали несколько первых членов ряда: Создается стойкое впечатление, что , но где гарантия, что при очень больших «эн» факториал не «обгонит» числитель и не утащит предел на ноль? Обратимся к теории математического анализа: !!! Справка – Факториал растёт быстрее, чем любая показательная последовательность, иными словами: или . – Факториал растёт быстрее, чем любая степенная последовательность или многочлен, иными словами: или . Вместо можно подставить какой-нибудь многочлен тысячной степени, это опять же не изменит ситуацию – рано или поздно факториал всё равно «перегонит» и такой страшный многочлен. Факториал более высокого порядка роста, чем любая степенная последовательность. – Факториал растёт быстрее, чем произведение любого количества показательных и степенных последовательностей (наш случай). – Любая показательная последовательность растёт быстрее, чем любая степенная последовательность, например: , . Показательная последовательность более высокого порядка роста, чем любая степенная последовательность. Аналогично факториалу, показательная последовательность «перетягивает» произведение любого количества любых степенных последовательностей или многочленов: . – А есть ли что-нибудь «сильнее» факториала? Есть! Степенно-показательная последовательность («эн» в степени «эн») растёт быстрее факториала. На практике встречается редко, но информация лишней не будет. Конец справки Таким образом, второй пункт исследования можно записать так: Вывод: ряд сходится. !!! Вот здесь как раз тот любопытный случай, когда члены ряда сначала растут по модулю, из-за чего у нас сложилось ошибочное первоначальное мнение о пределе. Но, начиная с некоторого номера «эн», факториал обгоняет числитель, и «хвост» ряда становится монотонно убывающим, что является принципиально важным для выполнения условия теоремы Лейбница. Чему конкретно равно данное «эн», выяснить достаточно трудно. Исследуем ряд на абсолютную или условную сходимость: А тут уже работает признак Даламбера: Используем признак Даламбера: Таким образом, ряд сходится. Исследуемый ряд сходится абсолютно. Разобранный пример можно решить другим способом (используем достаточный признак сходимости знакочередующегося ряда). Достаточный признак сходимости знакочередующегося ряда:Если ряд составленный из абсолютных величин членов данного ряда, сходится, то сходится и данный ряд.
Второй способ: Исследовать ряд на условную или абсолютную сходимость Решение: Исследуем ряд на абсолютную сходимость: Используем признак Даламбера: Таким образом, ряд сходится. Вывод: Исследуемый ряд сходится абсолютно.
Для вычисления суммы ряда с заданной точностьюбудем использовать следующую теорему: Пусть знакочередующийся ряд удовлетворяет условиям признака Лейбница и пусть – его n-ая частичная сумма.
Функциональные ряды. Степенные ряды. Для успешного освоения темы нужно хорошо разбираться в обычных числовых рядах.
⇐ Предыдущая12345Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим. Приведём понятие сходящегося числового ряда и расходящегося. Введём обозначение некоторой конечной суммы первых $n$ членов: $S_n=w_1,+w_2+w_3+…+w_n$. Такая сумма называется $n$-й частичной суммой ряда. Определение 2 Числовой ряд сходящийся, если существует предел вида $S=\lim\limits_{n\to\infty} S_n$. Иначе ряд расходящийся. В теории числовых рядом первым вопросом является вопрос о сходимости данного ряда. Если доказана сходимость, то следующий вопросом встаёт его сумма. Она вычисляется приближённо, с большим количеством членов в составе. Существуют несколько признаков сходимости рядов с положительными членами:
В рамках данной статьи перейдём сразу ко второму признаку. Теорема 1 Пусть существует предел Рисунок 1. Предел. Автор24 — интернет-биржа студенческих работ Если $D$ $1$, то ряд расходится. Замечание 1 Если $D=1$, то теорема не даёт ответа на вопрос о сходимости ряда. Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ Далее Рисунок 5. Пример. Автор24 — интернет-биржа студенческих работ Получилось $D$ > $1 \Rightarrow$ ряд расходится. Пример 2 Рисунок 6. Пример. Автор24 — интернет-биржа студенческих работ Так как в знаменателе $n!$, то дробь быстро убывает. Значит, наиболее эффективно рассмотреть признак Даламбера. Рисунок 7. Пример. Автор24 — интернет-биржа студенческих работ Рисунок 8. Пример. Автор24 — интернет-биржа студенческих работ $D$ Пример 3 Рисунок 9. Пример. Автор24 — интернет-биржа студенческих работ Рисунок 10. Пример. Автор24 — интернет-биржа студенческих работ Ряд сходится. Другие примеры исследования сходимости ряда производятся по аналогии. Сообщество экспертов Автор24 Автор этой статьи
Дата последнего обновления статьи: 15. Выполнение любых типов работ по математике Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами Подбор готовых материалов по теме Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы Коэффициент Даламбера Проверка сходимости рядапо Гаурав Тивари В этой статье мы сформулируем критерий коэффициента Даламбера сходимости ряда. Начнем. Утверждение теста отношения ДаламбераРяд положительных членов $ \sum {u_n}$ сходится, если от и после некоторого фиксированного члена $ \dfrac {u_{n+1}} {u_n} < r < { 1} $ , где r — фиксированное число. Ряд расходится, если $ \dfrac{u_{n+1}} {u_n} > 1$ после некоторого фиксированного члена. 9\infty a_n$ сходится абсолютно. Определения для обычных читателей(Определение 1) Бесконечный ряд $ \sum {u_n}$, т. е. $ \mathbf {u_1+u_2+u_3+….+u_n}$, называется сходящимся , если $ S_n$, сумма его первых $n$ членов, стремится к конечному пределу $S$, когда n стремится к бесконечности. Мы называем $ S$ суммой ряда и пишем $ S=\displaystyle {\lim_{n \to \infty} } S_n$ . Таким образом, бесконечный ряд $ \sum {u_n}$ сходится к сумме S, если для любого заданного положительного числа $ \epsilon $ , каким бы малым оно ни было, существует натуральное число $ n_0$ такое, что $ |S_n-S| < \epsilon$ для всех $ n \ge n_0$ . (Определение 2) (Определение 3) Доказательство и обсуждение теста отношенийПусть ряд равен $ \mathbf {u_1+u_2+u_3+…….}$ . Будем считать, что приведенные выше неравенства верны. Из первой части утверждения: $ \dfrac {u_2}{u_1} < r$ , $ \dfrac {u_3}{u_2} < r $ ……… где r <1. Следовательно, $$ {u_1+u_2+u_3+….}$$ $$= u_1 {(1+\frac{u_2}{u_1}+\frac{u_3}{u_1}+….)}$$ Поскольку $ \dfrac{u_{n+1}}{u_n} > 1$, тогда $ \dfrac{u_2}{u_1} > 1$ , $ \dfrac{u_3}{u_2} > 1$ Поэтому $ u_2 > u_1$ $u_3 >u_2>u_1$ $u_4 >u_3 > u_2 >u_1$ и так далее. Следовательно, $ \sum {u_n}=u_1+u_2+u_3+….+u_n$ > $nu_1$ . Взяв n достаточно большим, мы увидим, что $ nu_1$ можно сделать больше любой фиксированной величины. Следовательно, ряд расходится. Академическое доказательство Из формулировки теоремы необходимо, чтобы $\forall n: a_n \ne 0$; в противном случае ${\dfrac {a_{n + 1}} {a_n}}$ не определен. Абсолютная сходимость Комментарии
Рекомендуемая литература 92}}$ сходится.Следовательно, $ \sum {u_n}$ также сходится. Загрузить эту статью в формате PDFD Тест на соответствие коэффициента Аламберта. доказательство будет состоять из двух частей:
Странно сходящиеся последовательности | Александр Харазишвили Классический математический анализ включает в себя интригующее взаимодействие между конечными и бесконечными наборами и между дискретными и непрерывными структурами. Что делает взаимодействие интригующим, так это возникновение из самых элементарных соображений результатов, которые парадоксальны или, по крайней мере, совершенно нелогичны. Сумма ? Конечно, эта последовательность чисел просто становится все больше и больше; и сверх этого он ни к чему не сходится. Не так. Сумма равна –1/12. Нильс Абель назвал расходящиеся ряды изобретением дьявола. 1 Внося выдающийся вклад в изучение предмета как игрушки дьявола, он знал, о чем говорил. Бесконечные последовательностиМатематический анализ начинается с рассмотрения бесконечных последовательностей действительных чисел и определения их предела. На данный момент я буду рассматривать действительные числа и только действительные числа. Бесконечная последовательность — это произвольная функция, область определения которой совпадает с множеством ℕ = {0, 1, 2, …, n , …} натуральных чисел или с некоторыми из его бесконечных подмножеств, и диапазон которых содержится в действительной строке R. Таким образом, an:n∈N или более явно, если менее компактно а0, а1, а2, …, ан, … . Члены таких последовательностей часто генерируются по фиксированному правилу или путем применения определенного алгоритма к каждому n. Ограничения следующие. Вещественное число a является пределом последовательности an:n∈N, если для любого ε>0 существует натуральное число n0=n0(ε) такое, что an-a<ε всякий раз, когда n>n0. Если это так, последовательность сходится (или стремится) к a, когда n стремится к бесконечности: a=liman:n∈N. Легко показать, что a единственно. 2 После того как было дано определение предела — как оказалось, Огюстеном-Луи Коши, — математики, естественно, пожелали знать, существуют ли такие пределы и при каких условиях. Классический критерий — снова по Коши, как это происходит снова — утверждает, что an:n∈N сходится тогда и только тогда, когда для любого ε>0 существует натуральное число n0=n0(ε), такое что an-am< ε при n>n0 и m>n0. 3 Среди славы математического анализа никто, кроме Коши, никогда не находил эти идеи легкими, и никто, кроме Леонарда Эйлера, никогда не находил их очевидными. Критерий Коши отражает свойство полноты действительных чисел, из которого почти сразу следуют необходимое и достаточное условие существования предела. Многие другие условия сходимости на практике более удобны. Если последовательность действительных чисел монотонна и ограничена, то она обязательно имеет предел. Если две последовательности an:n∈N и bn:n∈N сходятся к a и b соответственно, то для любых действительных r и t последовательность ran+tbn:n∈N сходится к ra+tb. Предположим, что для двух последовательностей an:n∈N и bn:n∈N можно найти два натуральных числа m и n такие, что am+i=bn+i всякий раз, когда i∈N. Тогда an:n∈N сходится тогда и только тогда, когда сходится bn:n∈N, и в этом случае сходится равенство лиман:n∈N=конечность:n∈N Сходимость последовательности действительных чисел зависит только от ее хвоста. Пример 1.Последовательность 1,21/2,31/3,… ,n1/n,… сходится и ее предел равен 1. Пример 2. Последовательность an:n∈N, где an=1+1/nn при n>0, сходится к константе Непера, e = 2,71828… . Пример 3.Последовательность an:n∈N, где an=1+1/2+…+1/n-ln(n) при n>0, сходится к константе Эйлера C = 0,57721… . Если не существует предела последовательности an:n∈N, то эта последовательность расходится. В некотором смысле большинство реальных последовательностей расходятся. Пример 4.Любая неограниченная последовательность расходится; в частности, неограниченная последовательность bn:n∈N, где bn=1+1/2+…+1/n при n>0. Пример 5.Последовательность an:n∈N, где an=1 для всех четных n и an=-1 для всех нечетных натуральных n, расходится. Пример 6.Последовательность an:n∈N, где an=(n!)1/n при n>0, неограничена и, следовательно, расходится. Иногда удобно рассматривать некоторые расходящиеся последовательности так, как будто они сходятся к бесконечности. Последовательность an:n∈N стремится к +∞, если для любого r>0 существует n0=n0(r) такое, что an>r всякий раз, когда n>n0. Данной последовательности an:n∈N можно связать с ней другую последовательность sn:n∈N, где sn=Σak:k≤n обозначает сумму первых n+1 членов последовательности an:n∈N. Заметим, что начальная последовательность an:n∈N полностью определяется sn:n∈N, потому что an=sn-sn-1, точка, действительная для всех n∈N. Пара an:n∈N,sn:n∈N называется бесконечной серией, сокращенно серией. 4 С гораздо меньшим количеством обозначений математики пишут а0+а1+а2+…+ан+… . Ряд a0+a1+a2+…+an+… сходится, если соответствующая последовательность sn:n∈N имеет конечный предел s, сумма ряда; в противном случае он расходится. Критерий сходимости Коши теперь следует: бесконечный ряд имеет сумму тогда и только тогда, когда для любого ε>0 существует n0=n0(ε) такое, что an+1+an+2+…+an+m<ε всякий раз, когда n>n0 и m∈N. Из сходимости a0+a1+a2+…+an+… следует, что пределan:n∈N=0. В области, где мало времени, используются более простые тесты: критерий Даламбера, критерий n -го корня, критерий Лейбница, критерий Раабе, критерий Куммера, критерий Бертрана, критерий Гаусса, интегральный критерий, критерий Абеля, проба Дирихле, проба Ермакова. 5 Существует достаточно много тестов, чтобы проводить бесконечную серию экзаменов для студентов. Пример 7.Ряд 1/12+1/22+1/32+…+1/n2+… сходится, так как все его члены 1/n2, где n>1, меньше 1/(nn-1)=1/ (n-1)-1/n и серия 1+1/2+1/6+1/12+…+1/(nn-1)+… сходится к 2. Здесь так называемый сравнительный тест делает свое дело. Более тонкий расчет показывает, что сумма 1/12+1/22+1/32+…+1/n2+… равна π2/6. 6 Это результат, хорошо скрытый от чьей-либо интуиции. Как и следовало ожидать, серии бывают особых типов. Существуют геометрические ряды, гармонические ряды, гипергеометрические ряды, знакопеременные ряды и многое другое. Во многих случаях серия вида а0х+а1х+а2х+…+анх+… , Можно взять, где anxn∈N — действительные функции вещественной переменной x. а0р+а1р+а2р+…+анр+… . Я упоминал степенные ряды, ряды Тейлора, ряды Лорана, ряды Дирихле, тригонометрические ряды, ряды Фурье и всегда популярный биномиальный ряд? Пример 8.Геометрический ряд 1+q1+q2+…+qn+… , где q<1. Пример 9.Ряд Гранди: 1-1+1-1+…+-1n-1+… и, в более общем случае, для любого строго положительного целого числа k ряд 1-k1+k2-k3+…+-1n-1kn-1+ … . Пример 10.Серия 0!-1!+2!-3!+…+-1nn!+… . Пример 11.Серия Дирихле: fx=a1/1x+a2/2x+a3/3x+…+an/nx+… , , где x∈R, а an:n∈N — последовательность действительных чисел. В частности, почти везде встречается обобщенный гармонический ряд, являющийся частью дзета-функции Римана: ζx=1/1x+1/2x+1/3x+…+1/nx+… , и обобщенный знакопеременный гармонический ряд, являющийся частью эта-функции Дирихле ηx=1/1x-1/2x+1/3x-…+(-1)n-1/nx+… , получается таким образом. Пример 12.Ряд a0+a1+a2+…+an+… называется абсолютно сходящимся, если ряд a0+a1+a2+…+an+… сходится. Каждый абсолютно сходящийся ряд сходится. Обратное, увы, неверно. Переменный гармонический ряд 1-1/2+1/3-1/4+…+(-1)n-1(1/n)+… , сходится, и его сумма равна ln(2), 7 , но этот ряд не является абсолютно сходящимся, как может показать пример 4. Сходящийся ряд a0+a1+a2+…+an+… условно сходится, если связанный с ним ряд a0+a1+a2+…+an+… расходится. Если ряд сходится условно, то для любого действительного r существует такая перестановка его членов, что новый ряд сходится к r. Это классическая теорема Римана, допускающая нетривиальное обобщение на серию векторов в конечномерном евклидовом пространстве. Странно расходящиеся серии Странно расходящиеся ряды, такие как 1+2+3+4+…, являются прямыми, поскольку они расходятся; они странные, поскольку это не так. Много расходящихся рядов; и так много сумм; много сумм и так много методов суммирования: метод суммирования Абеля, метод суммирования Бореля, метод суммирования Чезаро, метод суммирования Эйлера, метод суммирования Гельдера, метод суммирования Куммера, метод суммирования Ламберта, метод суммирования Линделёфа, метод суммирования Пуассона, метод суммирования Вороного и многие другие. Самый простой метод суммирования назван в честь Эрнесто Чезаро. Если задан ряд a0+a1+…+an+…, то иногда — не всегда, не во всяком случае — может случиться, что соответствующая последовательность средних арифметических ее частичных сумм s0,s0+s1/2,(s0+s1+s2)/3,… , сходится к некоторому вещественному числу. Это его сумма Чезаро. Понятие суммы Чезаро совместимо с обычным понятием суммы сходящегося ряда. Действительно, согласно одной из классических теорем Коши, если последовательность вещественных чисел имеет предел, то последовательность средних арифметических этих вещественных чисел также сходится и имеет тот же предел. Простые контрпримеры показывают, что обратное неверно. Следует также отметить, что метод суммирования Чезаро вдохновил тауберовы результаты в общей теории рядов. Эти результаты позволяют математикам установить сходимость заданного ряда a0+a1+…+an+… , если ряд a0+a1+…+an+… суммируется каким-либо методом и удовлетворяет некоторым дополнительным ограничениям. Побродив в сарае с инструментами Дьявола, Абель предложил технику, теперь известную как метод суммирования Абеля, или, иногда, метод суммирования Абеля-Пуассона. Дьявол, как известно, найдет работу для праздных рук. Предположим, что задан ряд a0+a1+…+an+…, и для переменной x, лежащей в открытом интервале (0,1), рассмотрим соответствующий степенной ряд a0+a1x1+a2x2+…+anxn+… . Может случиться, что этот ряд сходится для каждого r из (0,1) и, следовательно, определяет конкретную функцию f(x) на интервале. Может случиться так, что существует предел f(x) при стремлении x к 1. Такова сумма Абеля ряда. Метод Чезаро совместим с обычным понятием суммы сходящегося ряда. Как и метод Абеля. Если ряд a0+a1+…+an+… сходится к s, то в силу классической теоремы Абеля 10 сумма Абеля a0+a1+…+an+… также равна s. Обратное не удается. Чеки Дьявола никогда не бывают пустыми. Пример 13.Для любого строго положительного целого числа k метод Абеля подразумевает, что расходящийся ряд 1-к1+к2-к3+…+-1н-1кн-1+… , в сумме дает 1/(k+1) и, в частности, ряд Гранди 1-1+1-…+-1n-1+… сумов 1/2. 1-к1+к2-к3+…+-1н-1кн-1+… , не суммируется по Чезаро. Есть много других примеров рядов, которые можно суммировать методом Абеля, а не методом Чезаро. Пример 14. Рассмотрим ряд 1-2+3-4+…+-1n-1n+…, который тривиально расходящийся и не суммируется по Чезаро. Метод Абеля работает, но метод Чезаро дает сбои. Действительно, если 0 Метод Абеля очень полезен при работе с произведениями бесконечных рядов. Нижеследующее представляет собой одну формулу, но два ряда: a0+a1+…+an+… , Их произведение c0+c1+…+cn+… определяется равенством cn=a0bn+a1bn-1+a2bn-2+…+anb0 (n∈N) Произведение двух условно сходящихся рядов, вообще говоря, не сходится. Это удивительно изящный результат и, пожалуй, самый простой из доступных интуиции результатов, говорящий о том, что придуманные по определению приемы имеют богатую внутреннюю структуру. Используя тот факт, что сумма произведений является произведением сумм — выше, чуть выше — сразу получается равенство 1-1+1-1+…1-1+1-1+… Эмиль Борель создал или открыл несколько важных методов суммирования. Если а0+а1+…+ан+… , серия рысью мчится в неизвестность, потом функция fx=ex(Σsnxn/n!:n∈N) , имеет смысл — на самом деле, полный смысл — применительно к множеству действительных чисел x, для которых эта функция определена корректно. Может случиться так, что f(x) имеет конечный предел y при стремлении x к +∞. Доказательство простое. Далее используется тот же Борель, но другой метод: борелевское интегральное суммирование. Ряд 0!-1!+2!-3!+…+(-1)nn!+… имеет борелевскую сумму ∫0∞e-t1+tdt. 11 Рассмотрим частичную дзета-функцию Римана ζ(x) и частичную эта-функцию Дирихле η(x) для всех действительных чисел x, строго больших 1. Сходимость 1/1x+1/2x+1/3x+…+1/nx+… , легко подразумевает: ηx=(1-21-x)ζ(x). Еще лучше, можно рассматривать 1/1x-1/2x+1/3x-…+-1n-1/nx+… для комплексных чисел z. Заменяя x на z, получаем 1/1z-1/2z+1/3z-…+-1n-1/nz+…, которое сходится к комплексному значению всякий раз, когда действительная часть z строго больше 1. Это η( х) допускает аналитическое продолжение на всю комплексную плоскость С — доказуемый факт жизни. ηz=(1-21-z)ζ(z), , где ζ(z) — аналитическая функция на открытом множестве C\{1}, продолжающая ζ(x). Вспомнив, что η-1=1/4, можно, наконец, понять, что, вопреки всем ожиданиям, 1+2+3+…+n+…=ζ-1=-1/12. Это выдающийся результат в математике, но это также выдающийся результат в математике, имеющий нетривиальные приложения в современной теоретической физике. Видел ли это вдохновенный Эйлер, слепой с зрелых лет и так много видевший? Предположим, что на некотором подмножестве D множества R задана последовательность функций gn:n∈N, для которой существует точка накопления d множества D. Предположим также, что для каждого n∈N существует предел gnt при t∈ D стремится к d, и что этот предел равен 1, Рассмотрим ряд a0+a1+…+an+… и пусть ряд функций gt=a0g0t+a1g1t+…+angnt+… (t∈D) будет его естественным партнером. Может случиться, что функция g(t) корректно определена в некоторой окрестности точки d и, кроме того, существует предел s=sa0+a1+…+an+… функции g(t) при t∈D склоняется к д. Предположим, что последовательность функций gn:n∈N удовлетворяет этим двум условиям: Если S сходится к s, то сумма S равна s. Многие классические методы суммирования соответствуют соответствующему выбору последовательности функций, удовлетворяющих 1) и 2). Для метода суммирования Чезаро функции gnn∈N можно определить на N следующим образом: gnm=m+1-n/m+1, если n≤m, Для метода суммирования Абеля функции gnn∈N могут быть определены на открытом интервале (0,1) gnt=tn 0 Взять положительный луч (0,+∞) R в качестве D и определить функции gnn∈N по формуле gnt=1-∑tk/k!:k получается некий вариант борелевского метода суммирования. Есть и другие общие схемы. Довольно часто схема суммирования формулируется в терминах действительнозначной матрицы T со счетным числом строк и столбцов. Методы T-суммирования преобразуют одну бесконечную последовательность в другую в ожидании или в надежде, что это преобразование даст последовательность с лучшим поведением в плане сходимости. Знаменитая теорема Сильвермана–Теплица устанавливает необходимые и достаточные условия, при которых класс всех сходящихся последовательностей преобразуется T в себя. 13 Среди множества интересных и важных утверждений о суммируемости матриц я хочу отметить один результат. 14 Для данной матрицы T и ряда a0+a1+…+an+… рассмотрим все те перестановки членов a0+a1+…+an+…, которые дают T-суммируемый ряд, и обозначим символом S(a0+ a1+…+an+… , T) множество всех T-сумм, полученных таким образом. Различные схемы суммирования естественным образом приводят к большому семейству точечных множеств в R и связаны с более или менее тонкими фактами классической дескриптивной теории множеств. Связи такого рода касаются даже проблемы измеримости по Лебегу всех подмножеств R. С более общей точки зрения любой метод суммирования может быть описан как функционал f, определенный на некотором векторном подпространстве L = dom(f) пространства RN всех бесконечных вещественных последовательностей. Элементы L имеют вид sn:n∈N, где sn(n∈N) — частичные конечные суммы ряда. Как правило, методы суммирования удовлетворяют условиям как линейности, так и регулярности. Линейность означает, что f — линейный функционал на L; Регулярность состоит в том, что f расширяет стандартный линейный функциональный предел, определенный на пространстве c всех сходящихся последовательностей в RN. Иногда накладывается третье условие, некий аналог трансляционной инвариантности. Если s является суммой ряда a0+a1+…+an+… и r является суммой a1+…+an+… , то s=a0+r. К ряду 1+1+1+…+1+… нельзя применить метод суммирования, удовлетворяющий условию переноса. Доказательство очевидно: s=1+1+1+1+…+1+…=1+s, откуда следует, что 0=1. Теперь, если последовательность tn:n∈N не принадлежит L и r — произвольное действительное число, функционал f может быть расширен до линейного функционала g, определенного на большем векторном подпространстве K пространства RN, такое что tn:n∈N∈K, gtn:n∈N=r. Это утверждение допускает конструктивное доказательство, не опирающееся на аксиому выбора. Прекрасная интуиция Эйлера теперь подтвердилась: Сразу следует оговорка. Существует нет методов линейного суммирования, удовлетворяющих условию переноса, которое присваивает конечную сумму
на 1+2+3+…+n+… . Предположим, что 1+2+3+…+n+…=с, , где s — действительное число. Тогда: с-1=2+3+…+n+… и -1=s-1-s=2-1+3-2+…+n+1-n+… что невозможно. Если кто-то хочет приписать некоторые обобщенные суммы сразу всем расходящимся рядам, то он должен обратиться к сильным формам аксиомы выбора. Например, стандартное применение леммы Цорна показывает, что существует линейный регулярный метод суммирования, областью определения которого является все RN. Этот результат практически бесполезен в силу его крайне неконструктивного характера. С другой стороны, из фундаментального результата Роберта Соловея следует, что при счетных формах аксиомы выбора логически непротиворечиво предположить, что областью применения любого линейного регулярного метода суммирования является подпространство первой категории в RN. Используя несчетные формы аксиомы выбора, математики смогли построить некоторые замечательные линейные функционалы на различных векторных подпространствах RN. Среди них наиболее известен функциональный предел Банаха, или Lim, определенный на пространстве всех ограниченных вещественных последовательностей, Lim линейен, расширяет стандартный функциональный предел и является инвариантным относительно переноса. 17 Но существование таких функционалов всегда влечет за собой существование предельно патологических подмножеств R, а именно множеств, неизмеримых по Лебегу, или множеств, не обладающих так называемым свойством Бэра. Рассмотрим следующую серию функций FS: cos(t)+cos2t+cos4t+…+cos2nt+… , , где переменная t лежит в пределах R. Предположим, что для каждого t из измеримого по Лебегу подмножества R со строго положительной мерой эта FS суммируется с f(t) по некоторой линейной регулярной схеме суммирования, удовлетворяющей условию переноса. Отсюда следует, что f неизмерима в смысле Лебега. Такова теорема Колмогорова. 19 Глубокий результат Соловея показывает, что нет никакой надежды на эффективное построение нелебеговского измеримого подмножества R или, что эквивалентно, нелебеговской измеримой функции, действующей из R в R. 21 Содержание Настоящая статья кратко знакомит с теорией бесконечных рядов. В отличие от конечного ряда сумма произвольного бесконечного ряда не может быть получена. Когда это получается, бесконечный ряд называется сходящимся рядом. В этом В статье мы кратко обсудим Примечание: s n называется n-й частичной суммой ряда.
Рассмотрим ряд \[\frac{1}{1.2}+{\frac{1}{1.2}+{\frac{1}{2.3} …~~to~~\infty \] Здесь \[{{u}_{n}}=\frac{1}{n\left( n+1 \right)}=\frac{1} {n}-\frac{1}{n+1}\] \[\поэтому ~~{{u}_{1}}=1-\frac{1}{2}\] \[ \поэтому ~~{{u}_{2}}=\frac{1}{2}-\frac{1}{3}\] \[\поэтому ~~{{u}_{3}} =\frac{1}{3}-\frac{1}{4}\] \[…………………..\] \[\поэтому ~~{{u}_{n}}=\frac{1}{n}-\frac{1}{n+1}\] \[\поэтому {{s}_ {n}}={{u}_{1}}+{{u}_{2}}+{{u}_{3}}+…+{{u}_{n}}\] \[\Rightarrow {{s}_{n}}=\left( 1-\frac{1}{2} \right)+\left( \frac{1}{2}-\frac{1}{3 } \right)+\left( \frac{1}{3}-\frac{1}{4} \right)+…+\left( \frac{1}{n}-\frac{1}{n +1} \right)\] \[\Стрелка вправо {{s}_{n}}=1-\frac{1}{n+1}\] \[\поэтому \underset{n\to \ infty {\ mathop{\ lim }} \, {{s} _ {n}} = \ underset {n \ to \ infty } {\ mathop {\ lim }} \, \ left ( 1- \ frac { 1}{n+1} \справа)=1-0=1\] Следовательно, серия сходится и сходится к 1. Divergent Infinite SeriesA Series σu N из реальных чисел, как говорят, является дивергентной, если последовательность (S N 8888888888888888888888888 88888888 8888888 8888888 8888888 8888888 888888 888888 888888444444444444444444444444444 лет. Разное, где S N = U 1 + U 2 +… + U N , для n = 1, 2, .then, мы напишу n = 1, 2, . = 9{2}}\] \[\следовательно {{s}_{n}}=\frac{n\left( n+1 \right)\left( 2n+1 \right)}{6}\] \[\поэтому \underset{n\to \infty}{\mathop{\lim }}\,{{s}_{n}}=\underset{n\to \infty}{\mathop{\lim }}\,\frac{n\left( n+1 \right)\left( 2n+1 \right)}{6}=\infty \] Следовательно, ряд расходится и расходится до +∞. Осциллятор Бесконечный ряд Ряд Σu n действительных чисел называется осциллятором, если последовательность {S N } является колебательным, где S N = U 1 + U 2 +… + N 919, для 8 + N 919, для + N 9, для + N 9, для … . Примечание: Если ряд не сходится и не расходится, то ряд является колебательным.
Рассмотрим ряд 1 – 1 + 1 – 1 + … до {n-1}}\] Итак, n-я частичная сумма, \[{{s}_{n}}={{u}_{1}}+{{u}_{2} }+{{u}_{3}}+…+{{u}_{n}}\] \[\Стрелка вправо {{s}_{n}}=1-1+1-1+… ~~to~~n~~terms\] \[\Rightarrow {{s}_{n}}=0~~или~~1,~~в соответствии~~как~~n~~~~четно ~~или~~нечетное\] Таким образом, последовательность частичных сумм равна {1, 0, 1, 0, …}. Таким образом, последовательность {s n } колеблется конечно. Следовательно, ряд является колебательным. Геометрическая серия InfiniteРяд Σ x n = 1 + x + x 2 + x 3 + … ∞ известен как геометрический ряд с обыкновенным отношением 9 1 0 0 0 3 9 .
A geometric series Σ x n is convergent if -1 < x < 1 , divergent if x ≥ 1 9{2}}}+…~~to~~\infty \] Очевидно, что ряд является геометрическим рядом со знаменателем ½ (< 1). Следовательно, ряд сходится. Некоторые свойства бесконечной серии , если σu N и σu N = S , затем = S , затем = S , затем = S , затем = S , затем = S = S = S . Если Σu n расходится, то Σku n расходится, где k Если σu N и σv N и сходится к S 1 и S 7 2 1 и S 7 2 1 и S 7 2 1 и S 7 2 и S 7 2 и S 7 2 и S 7 2 и . U N + K 2 V N ) — это конверген и преобразование K 1 S 1 + K 2 S 2 + K 2 S 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 . Характер сходимости или расходимости бесконечного ряда остается неизменным при добавлении или удалении конечного числа его членов.
Если ряд вещественных чисел Σu n сходится, то \[\underset{n\to \infty }{\mathop{\lim }}\,~~{{u} _{n}}=0\] Доказательство: \[Позвольте~~\sum{{{u}_{n}}=s}\] \[\поэтому \underset{n\ to \infty }{\mathop{\lim }}\,~~{{s}_{n}}=s\] Где s n — n-я частичная сумма ряда. Очевидно, тогда \[\поэтому \underset{n\to \infty }{\mathop{\lim }}\,~~{{s}_{n-1}}=s\] \[\поэтому \underset{n\to \infty }{\mathop{\lim }}\,~~\left( {{s}_{n}}-{{s}_{n-1} } \right)=s-s=0\] \[Следовательно~~\underset{n\to \infty }{\mathop{\lim }}\,~~{{u}_{n}}=0. \] Примечание: Обратная теорема неверна.
Положительный ряд либо сходится, либо расходится к +∞, не колеблясь. Сравнительный тест
Let Σu n and Σv n be two series of positive numbers and Σv n is convergent. Тогда Σu n сходится, если (1) Существует натуральное число N такое, что u n ≤ kv n , где k — константа, где k ≥ N. Или (2) Если l конечное число (l может быть равно нулю) \[\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{u} _ {n}}} {{{v} _ {n}}} = L \]
|
86
. n — два ряда положительных чисел, а Σv n — расходящийся ряд. Затем Σu n сходится, если
n — два ряда положительных чисел, а Σv n — расходящийся ряд. Затем Σu n сходится, если(1) Существует натуральное число N такое, что u n ≥ kv n для всех n ≥ N, где k — константа.
Или
(2) Если l ненулевое число (l может быть ∞)
\[\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{ u} _ {n}}} {{{v} _ {n}}} = L \]
| Теорем 03 |
| Пример 01 |
Показать, что ряд
\[1+\frac{1}{1.13}+ ~to~~\infty ~~сходится.\]
Решение:
Пусть u n (n = 1, 2, 3, …) обозначает n-й член данный сериал. 9{2}}}}=\frac{1}{1+0}=1,~~a~~конечное~~число.\]
Следовательно, по тесту сравнения Σ u n сходится или расходится, если Σ v n сходится или расходится. Но Σ v n является сходящимся рядом (будучи p-рядом с p = 3/2 > 1). Следовательно, ряд Σ u n сходится.
| Пример 02 | 9{2}}\left( 2n+4 \right)}{\left( 2n-1 \right)\left( 2n+1 \right)\left( 2n+3 \right)}\]
| Theorem |
Let Σ u n be a series of positive numbers such that
\[\ underset{n\to \infty}}{\mathop{\lim}}\,~~\frac{{{u}_{n+1}}}{{{u}_{n}}}~ ~ существует~~конечно~~и~~\underset{n\to \infty }{\mathop{\lim }}\,~~\frac{{{u}_{n+1}}}{{{u }_{n}}}=l. \]
\]
Тогда ряд сходится, если l < 1 , и расходится, если l > 1 .
Примечание: Приведенный выше тест не пройден, если l = 1 .
| Пример 01 |
Следовательно, по критерию отношения Даламбера данный ряд сходится.
Raabe’s Test
| Theorem |
Let Σ u n be a series of positive numbers such that
\[\underset{n\to \infty }{ \mathop{\lim }}\,~~\left\{ n\left( \frac{{{u}_{n}}}{{{u}_{n+1}}}-1 \right) \right\}~~существует~~конечно~~и~~\underset{n\to \infty }{\mathop{\lim }}\,~~\left\{ n\left( \frac{{{u }_{n}}}{{{u}_{n+1}}}-1 \right) \right\}=l. \]
\]
Тогда ряд сходится, если l > 1 , и расходится, если l < 1 .
Примечание: Приведенный выше тест не пройден, если l = 1 .
| Пример 01 +\frac{\left( 1+\alpha \right)\left( 2+\alpha \right)}{\left( 1+\beta \right)\left( 2+\beta \right)}+…~ ~к~~\infty \] Решение: Опустив первый член, обозначим через u n (n = 1, 2, 3, …) n-й член данного ряда. Затем \[{{u}_{n}}=\frac{\left( 1+\alpha \right)\left( 2+\alpha \right)….\left( n-1+\alpha \ right)}{\left( 1+\beta \right)\left( 2+\beta \right)\left( n-1+\beta \right)}\] \[\следовательно {{u}_ {n+1}}=\frac{\left( 1+\alpha \right)\left( 2+\alpha \right)….\left( n-1+\alpha \right)\left( n+\alpha \right)}{\left( 1+\beta \right)\left( 2+\beta \right)\left( n-1+\beta \right)\left( n+\beta \right)}\] \[\поэтому \underset{n\to \infty }{\mathop{\lim }}\,~\frac{{{u}_{n+1}}}{{{u}_{n} }} = \ underset {n \ to \ infty} }{\ mathop {\ lim }} \, ~ \ frac {n + \ alpha} {n + \ beta} = \ underset {n \ to \ infty} {\ mathop {\ lim }} \, ~ \ frac {1+ \ frac {\ alpha {n}} {1+ \ frac {\ beta} {n}} = \ frac {1 + 0} {1 + 0} = 1 \ ] Таким образом, тест отношения Д’Аламбера не проходит. Теперь, \[\underset{n\to \infty}{\mathop{\lim}}\,~~\left\{ n\left(\frac{{{u}_{n}}} {{{u}_{n+1}}}-1 \right) \right\}=\underset{n\to \infty }{\mathop{\lim }}\,~n\left\{ \frac {n+\beta} }{n+\alpha}-1 \right\}=\underset{n\to \infty}{\mathop{\lim}}\,\frac{n\left(\beta -\alpha \right )}{п+\альфа }\] \[=\underset{n\to \infty}{\mathop{\lim}}\,\frac{\beta -\alpha}}{1+\frac{\alpha}{n}}=\frac{ \beta -\alpha }{1+0}=\beta -\alpha \] Отсюда по критерию Раабе данный ряд сходится при β – α > 1 и расходится при β – α < 1 .
; бесконечный ряд — Everything2.comСумма бесконечного геометрического ряда — замечательная вещь… с ее помощью можно доказать, что 0,99999… (девять навсегда) равно , равно 1. Дано 0,99999… = 0,9 + 0,09 + 0,009 + … Сумма бесконечного геометрического ряда определяется как сумма = t/(1-r), где t — первый член, а r — отношение между членами. 1 = 0,9/(1-0,1) Если не верите, спросите у профессора математики. Ряды иногда могут сбивать с толку (или, по крайней мере, быть полезными при доказательстве того, что сумма бесконечного ряда положительных чисел отрицательна или что 0 = 1), поэтому определение значения ряда может оказаться полезным. (Для педантичности выражение «сумма ряда» излишне, поскольку ряд это сумма). Серия A T 1 + T 2 + T 3 + … = сумма i=1 до бесконечности T i считается сходящейся к значению S, если предел S S = lim n->бесконечность sum i=1 to n T i существует. В этом случае говорят, что ряд сходится. Если предел не существует, он расходится. Обратите внимание, что сумма до n может быть ограничена даже для расходящегося ряда: например. 1-1+1-1+1… Исторически сложилось так, что это определение является «обратным», потому что серии были определены первыми. инф --- 1 \ ---- /___ пер(н) п=2 Расходится, хотя lim n->inf 1/ln(n) = 0… n-членный тест на расхождение Если последовательность {a n } не сходится к 0, то ряд Сигма(а n ) расходится. Это означает, что , а не означает, что если последовательность {a n } сходится к 0, то ряд Sigma (a n ) сходится; тест просто неубедительный. Другими словами… инф --- н \ ---- /___ 2 п=1 Расходится, потому что lim n->inf n/2 = бесконечность, которой не существует. Геометрический ряд Геометрический ряд довольно прост, когда дело доходит до определения их сходимости или расхождения. Во-первых, было бы лучше определить геометрические ряды.
9п +. Термин r называется отношением. Если 0 < |r| < 1, то геометрический ряд сходится. Чтобы определить ряд, если он сходится, просто следуйте формуле S = a/(1-r). Интегральный тест Это еще один довольно простой тест, который прекрасно работает для всех легко интегрируемых задач. Если f положительная, непрерывная, убывающая функция для n >= 1, и если f(n) = a n , то оба 9п /___ п=1 Чтобы выяснить расходимость или сходимость этих рядов, достаточно посмотреть на стр. Если 0 < p <= 1, то ряд расходится. Если p > 1, ряд сходится. Сравнительные тесты Если a n <= c n для всех n, и
инф
---
\ с н сходится, то
/___
п=1
инф
---
\ a n сходится
/___
п=1
И если c n <= a n ,
инф
---
\ c n расходится, то
/___
п=1
инф
---
\ а n расходится
/___
п=1
Аналогично, предположим, что a n > 0 и d n > 0. инф --- \ д н и /___ п=1 инф --- \ а н /___ п=1 оба либо сходятся, либо расходятся. Есть несколько других тестов на расхождение и сходимость, но предыдущие тесты являются прочной основой для работы с бесконечными рядами. 9n Такие серии полезны для анализа множества различных интересных ситуаций. Далее я покажу, как найти
значение частичной суммы n th и бесконечного ряда. Мне это нравится, потому что это простое доказательство, но оно показывает действительно
интересный результат. Можно заметить два разных способа получить частичную сумму ( n+1 ) th (имеется в виду сумма
геометрический ряд от 0 до n+1 9(n+1) превращается в ноль (потому что каждый раз, когда вы умножаете два числа на
| р | < 1 вместе вы получите еще меньший). S = а(1-0)/(1-r) = а/(1-r) Определение сходимости ряда 2 Поскольку существует лишь (относительно) небольшое число теорем, применимых к определению сходимости бесконечных рядов, вполне возможно определить «алгоритмический» процесс решения вопроса: Сходится/расходится ли Σu n ? Обратите внимание на использование кавычек вокруг слова алгоритмический выше: здесь подчеркивается тот факт, что я не буду использовать какие-либо формальные мета-нотации и что я не претендую на выполнение фактических требований алгоритма в этом методе . Это просто попытка организовать все общие тесты и инструменты, доступные для работы с рядами, в связный и простой в использовании список утверждений «если, то». В любом случае, допустим, у вас есть бесконечный ряд Σu n и вы хотите/надеетесь/надеетесь определить, сходится он или расходится.
 207206206207206206206206206206206206206206206206206206206206206206206206206202н. f (n) = u n for all n ≥ 1 then Σu n is convergent if and only if ∫ 1 +∞ f (x)dx сходится (подробности см. В статье выше) 207206206207206206206206206206206206206206206206206206206206206206206206206202н. f (n) = u n for all n ≥ 1 then Σu n is convergent if and only if ∫ 1 +∞ f (x)dx сходится (подробности см. В статье выше)8 9
Хотя мне хотелось бы верить, что приведенный выше список близок к исчерпывающему, это, скорее всего, совсем не так. Из-за невежества, глупости, банальной лени или сочетания этих трех факторов я мог бы пропустить полезные тесты или идеи. Если вы знаете о каком-либо полезном дополнении к этой методологии, пожалуйста, дайте мне знать (постарайтесь оставаться в строгом поле бесконечных рядов, поскольку я не пытаюсь здесь переписывать Principia Mathematica). Доказательство формулы суммы бесконечных членов геометрического ряда S=a/(1-r) , довольно просто. Во-первых, напомним формулу суммы конечных членов геометрического ряда S n = (a(1-r n ))/(1-r) Замените n на бесконечность. |

 Признак Лейбница
Признак Лейбница
 — КиберПедия
— КиберПедия ..
..
 Причем, совершенно не важно, где эти функции располагается, в числителе или в знаменателе – важно, что они там присутствуют.
Причем, совершенно не важно, где эти функции располагается, в числителе или в знаменателе – важно, что они там присутствуют. Если существует предел отношения последующего члена к предыдущему: , то:
Если существует предел отношения последующего члена к предыдущему: , то:
 Есть еще экзотические случаи, но ими голову забивать не будем.
Есть еще экзотические случаи, но ими голову забивать не будем.
 Это не формальность, а отличный шанс расправиться с примером «малой кровью».
Это не формальность, а отличный шанс расправиться с примером «малой кровью».
 Например:
Например: Для ряда выполнена строгая монотонность убывания, её можно расписать подробно:
Для ряда выполнена строгая монотонность убывания, её можно расписать подробно: n+1>n – первое условие не выполняется
n+1>n – первое условие не выполняется
 Да хоть миллион в степени «эн», это не меняет дела. То есть, факториал более высокого порядка роста, чем любая показательная последовательность.
Да хоть миллион в степени «эн», это не меняет дела. То есть, факториал более высокого порядка роста, чем любая показательная последовательность.

 Тогда ряд сходится и погрешность при приближенном вычислении его суммы S по абсолютной величине не превосходит модуля первого отброшенного члена:
Тогда ряд сходится и погрешность при приближенном вычислении его суммы S по абсолютной величине не превосходит модуля первого отброшенного члена: \infty w_n$.
\infty w_n$. n$. Возьмём $(n-1)$ вместо $n$.
n$. Возьмём $(n-1)$ вместо $n$. 05.2022
05.2022
 2+…..)$$ 9n \to 0$
2+…..)$$ 9n \to 0$ 

 Те студенты, которые не изучали формальное определение предела, могут обратиться к учебнику по математическому анализу по этому вопросу (любой из учебников, перечисленных на странице «Рекомендуемые ресурсы», охватывает его).
Те студенты, которые не изучали формальное определение предела, могут обратиться к учебнику по математическому анализу по этому вопросу (любой из учебников, перечисленных на странице «Рекомендуемые ресурсы», охватывает его). {\ infty} | a_ {n} | = | a_ {N + 1} | + | a_ {N + 2} | + | a_ {N + 3} |+\ldots }
9{\ infty} а_ {к}}
{\ infty} | a_ {n} | = | a_ {N + 1} | + | a_ {N + 2} | + | a_ {N + 3} |+\ldots }
9{\ infty} а_ {к}} Отсюда ясно следует, что последовательность
{
а
н
}
{\ Displaystyle \ {а_ {п} \}}
не может сходиться к 0. Следовательно, данный ряд расходится по признаку расходимости.
9{\infty} u_{n}\), или просто \(\sum u_{n}\), для бесконечного ряда \(u_{0} + u_{1} + u_{2} + \dots\). 1
Отсюда ясно следует, что последовательность
{
а
н
}
{\ Displaystyle \ {а_ {п} \}}
не может сходиться к 0. Следовательно, данный ряд расходится по признаку расходимости.
9{\infty} u_{n}\), или просто \(\sum u_{n}\), для бесконечного ряда \(u_{0} + u_{1} + u_{2} + \dots\). 1 
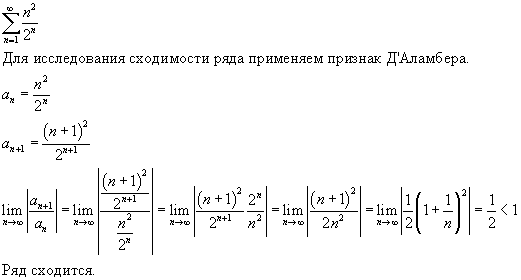 {n}\). Этот тест известен как тест Даламбера . Позже мы увидим, что он теоретически менее общий, чем критерий Коши, в том смысле, что критерий Коши может быть применен всякий раз, когда можно применить тест Даламбера, а иногда и тогда, когда последний не может. Более того, критерий расходимости, соответствующий критерию сходимости Даламбера, гораздо менее общий, чем критерий, данный теоремой 2. Верно, как легко докажет читатель, что если \(v_{n+1}/ v_{n} \geq r \geq 1\) для всех значений \(n\) или всех достаточно больших значений, то \(\sum v_{n}\) расходится. Но это неправда (см. Ex LXVII. 9).{2}} + \dots\right),\end{aligned}\] по теоремам (8) и (6) § 77.]
{n}\). Этот тест известен как тест Даламбера . Позже мы увидим, что он теоретически менее общий, чем критерий Коши, в том смысле, что критерий Коши может быть применен всякий раз, когда можно применить тест Даламбера, а иногда и тогда, когда последний не может. Более того, критерий расходимости, соответствующий критерию сходимости Даламбера, гораздо менее общий, чем критерий, данный теоремой 2. Верно, как легко докажет читатель, что если \(v_{n+1}/ v_{n} \geq r \geq 1\) для всех значений \(n\) или всех достаточно больших значений, то \(\sum v_{n}\) расходится. Но это неправда (см. Ex LXVII. 9).{2}} + \dots\right),\end{aligned}\] по теоремам (8) и (6) § 77.] ] 9{2} + \dots\: для них последнее обозначение явно удобнее. Поэтому мы примем это в качестве нашего стандартного обозначения. Но мы не будем придерживаться его систематически и будем предполагать, что \(u_{1}\) является первым членом всякий раз, когда этот ход более удобен. Например, при работе с рядом \(1 + \frac{1}{2} + \frac{1}{3} + \dots\) удобнее считать, что \(u_{n} = 1/n\) и что ряд начинается с \(u_{1}\), чем предположить, что \(u_{n} = 1/(n + 1)\) и что ряд начинается с \(u_{ 0}\). Это замечание применимо, 9{1/n} \к л\). То, что обратное неверно, можно увидеть, предположив, что \(v_{n} = 1\), когда \(n\) нечетно, и \(v_{n} = 2\), когда \(n\) четно. ↩︎
] 9{2} + \dots\: для них последнее обозначение явно удобнее. Поэтому мы примем это в качестве нашего стандартного обозначения. Но мы не будем придерживаться его систематически и будем предполагать, что \(u_{1}\) является первым членом всякий раз, когда этот ход более удобен. Например, при работе с рядом \(1 + \frac{1}{2} + \frac{1}{3} + \dots\) удобнее считать, что \(u_{n} = 1/n\) и что ряд начинается с \(u_{1}\), чем предположить, что \(u_{n} = 1/(n + 1)\) и что ряд начинается с \(u_{ 0}\). Это замечание применимо, 9{1/n} \к л\). То, что обратное неверно, можно увидеть, предположив, что \(v_{n} = 1\), когда \(n\) нечетно, и \(v_{n} = 2\), когда \(n\) четно. ↩︎ Какова, например, сумма 1 + 2 + 3 + … + п + …?
Какова, например, сумма 1 + 2 + 3 + … + п + …?

 Последовательность bn:n∈N стремится к –∞, если для любого r<0 существует n0=n0(r) такое, что bn
Последовательность bn:n∈N стремится к –∞, если для любого r<0 существует n0=n0(r) такое, что bn
 Для каждого значения r параметра x имеется обычный ряд
Для каждого значения r параметра x имеется обычный ряд Ряд 1/1x+1/2x+1/3x+…+1/nx+… сходится для всех действительных x>1, а ряд 1/1x-1/2x+1/3x-…+(-1)n- 1/nx+… сходится для всех действительных x>0.
Ряд 1/1x+1/2x+1/3x+…+1/nx+… сходится для всех действительных x>1, а ряд 1/1x-1/2x+1/3x-…+(-1)n- 1/nx+… сходится для всех действительных x>0. Это утверждение, казалось бы, на цыпочках приближается к самому краю парадокса. Тем не менее Эйлер систематически имел дело со странно расходящимися рядами; он мог успешно манипулировать ими. После многих хитрых манипуляций Эйлеру пришло в голову утверждать, что любой расходящийся ряд должен иметь определенную сумму. Позиция Эйлера подверглась критике со стороны привередливого Жана Д’Аламбера, столь же привередливого Абеля и других математиков, всем им было безразлично, что Эйлер мог быть прав, а они неправы. Лишь много позже какой-то рациональный фрагмент идеи Эйлера трансформировался в богатую теорию суммируемости расходящихся рядов.
Это утверждение, казалось бы, на цыпочках приближается к самому краю парадокса. Тем не менее Эйлер систематически имел дело со странно расходящимися рядами; он мог успешно манипулировать ими. После многих хитрых манипуляций Эйлеру пришло в голову утверждать, что любой расходящийся ряд должен иметь определенную сумму. Позиция Эйлера подверглась критике со стороны привередливого Жана Д’Аламбера, столь же привередливого Абеля и других математиков, всем им было безразлично, что Эйлер мог быть прав, а они неправы. Лишь много позже какой-то рациональный фрагмент идеи Эйлера трансформировался в богатую теорию суммируемости расходящихся рядов. 8
8  9
9  Ряд Гранди также суммируется по методу Чезаро, и его чезаровская сумма снова равна 1/2. Это не просто счастливое совпадение. Метод Абеля значительно сильнее метода Чезаро. С другой стороны, для натурального числа k, строго большего 1, ряд
Ряд Гранди также суммируется по методу Чезаро, и его чезаровская сумма снова равна 1/2. Это не просто счастливое совпадение. Метод Абеля значительно сильнее метода Чезаро. С другой стороны, для натурального числа k, строго большего 1, ряд Но если оба ряда a0+a1+…+an+… и b0+b1+…+bn+… суммируемы по Абелю, то их произведение c0+c1+…+cn+… также суммируемо по Абелю и равно произведению абелевых сумм ряда a0+ a1+…+an+… и b0+b1+…+bn+… .
Но если оба ряда a0+a1+…+an+… и b0+b1+…+bn+… суммируемы по Абелю, то их произведение c0+c1+…+cn+… также суммируемо по Абелю и равно произведению абелевых сумм ряда a0+ a1+…+an+… и b0+b1+…+bn+… . Если это так, то у называется борелевской суммой ряда. Если ряд a0+a1+…+an+… сходится, то он также суммируем по Борелю и его обычная сумма совпадает с его борелевской суммой.
Если это так, то у называется борелевской суммой ряда. Если ряд a0+a1+…+an+… сходится, то он также суммируем по Борелю и его обычная сумма совпадает с его борелевской суммой. Кроме того, есть
Кроме того, есть Ряд S=a0+a1+…+an+… суммируем, и его обобщенная сумма равна s.
Ряд S=a0+a1+…+an+… суммируем, и его обобщенная сумма равна s. 12 Не все идет гладко. Две разные схемы могут оказаться несовместимыми в том смысле, что для некоторого конкретного ряда они дают две различные обобщенные суммы.
12 Не все идет гладко. Две разные схемы могут оказаться несовместимыми в том смысле, что для некоторого конкретного ряда они дают две различные обобщенные суммы. Оказывается, что, меняя a0+a1+…+an+… и T всеми возможными способами, семейство всех множеств S(a0+a1+…+an+… , T) дает семейство всех аналитических, или суслинских, подмножеств R Это семейство намного шире, чем семейство всех борелевских подмножеств R. 15
Оказывается, что, меняя a0+a1+…+an+… и T всеми возможными способами, семейство всех множеств S(a0+a1+…+an+… , T) дает семейство всех аналитических, или суслинских, подмножеств R Это семейство намного шире, чем семейство всех борелевских подмножеств R. 15 

 16 Поскольку RN является польским топологическим пространством, RN имеет вторую категорию само по себе. Следовательно, область определения любой конструктивно определенной схемы линейной и регулярной суммируемости составляет очень малую часть RN. В рамках того же слабого фрагмента теории множеств можно предположить, что класс всех линейных регулярных методов суммирования, снабженный его естественной частичной упорядоченностью, не имеет максимальных элементов.
16 Поскольку RN является польским топологическим пространством, RN имеет вторую категорию само по себе. Следовательно, область определения любой конструктивно определенной схемы линейной и регулярной суммируемости составляет очень малую часть RN. В рамках того же слабого фрагмента теории множеств можно предположить, что класс всех линейных регулярных методов суммирования, снабженный его естественной частичной упорядоченностью, не имеет максимальных элементов. 18
18  Начнем с определений сходимости, расхождения и колебательного ряда. Кроме того, мы вводим ряд полезных признаков сходимости бесконечных рядов. 9{\infty}{{{u}_{n}}}~~или~~подробнее~~кратко~~\sum{{{u}_{n}}}\]
Начнем с определений сходимости, расхождения и колебательного ряда. Кроме того, мы вводим ряд полезных признаков сходимости бесконечных рядов. 9{\infty}{{{u}_{n}}}~~или~~подробнее~~кратко~~\sum{{{u}_{n}}}\]