Полная таблица неопределенных интегралов: Большая таблица интегралов (первообразных). Таблица интегралов полная для студентов. Интегралы от рациональных функций. Интегралы от трансцендентных функций. Интегралы от иррациональных функций. Интегралы от тригонометрических функций.

Содержание

XYZ — Таблица первообразных. Таблица интегралов. Таблица неопределенных интегралов. Формулы интегралов. Формулы первообразных.

Проект Карла III Ребане и хорошей компании

Раздел недели: Перевод единиц измерения величин. Перевод единиц измерения физических величин. Таблицы перевода единиц величин. Перевод химических и технических единиц измерения величин. Величины измерения. Таблицы соответствия величин.

Техническая информация тут

Поиск на сайте DPVA

Полезные ссылки

О проекте

Обратная связь

Оглавление

Адрес этой страницы (вложенность) в справочнике DPVA.xyz: главная страница / / Техническая информация/ / Математический справочник / / Интегральное и дифференциальное исчисление. Табличные производные и интегралы. Таблица производных. Таблица интегралов. Таблица первообразных. Найти производную. Найти интеграл. Диффуры.

/ / Таблица первообразных. Таблица интегралов. Таблица неопределенных интегралов. Формулы интегралов. Формулы первообразных.

Таблица первообразных («интегралов»). Таблица интегралов. Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница. Версия для печати.

Справочно: Таблица производных.
Справочно: Таблицы неопределенных интегралов. Смолянский М.Л. ГИФМЛ 1963. (.djvu — 1Mb)

(Простейшие интегралы и интегралы с параметром).»>

Таблица первообразных («интегралов»). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром).
Интеграл степенной функции.	Интеграл степенной функции.
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала.
—
Интеграл экспоненциальной функции.	Интеграл экспоненты, где a-постоянное число.
Интеграл сложной экспоненциальной функции.	Интеграл экспоненциальной функции.
—
Интеграл, равняющийся натуральному логарифму.	Интеграл : «Длинный логарифм».
	Интеграл : «Длинный логарифм».
Интеграл : «Высокий логарифм».	Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логарифму.
Интеграл : «Высокий логарифм».
—
Интеграл косинуса.	Интеграл синуса.
Интеграл, равный тангенсу.	Интеграл, равный котангенсу.
—
Интеграл, равный как арксинусу, так и арккосинусу	Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл, равный как арксинусу, так и арккосинусу.	Интеграл, равный как арктангенсу, так и арккотангенсу.

Интеграл равный косекансу.	Интеграл, равный секансу.
Интеграл, равный арксекансу.	Интеграл, равный арккосекансу.
Интеграл, равный арксекансу.	Интеграл, равный арксекансу.
—
Интеграл, равный гиперболическому синусу.	Интеграл, равный гиперболическому косинусу.
Интеграл, равный гиперболическому тангенсу.	Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому синусу, где sinhx — гиперболический синус в ангийской версии.	Интеграл, равный гиперболическому косинусу, где sinhx — гиперболический синус в ангийской версии.
Интеграл, равный гиперболическому тангенсу.	Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому секансу.	Интеграл, равный гиперболическому косекансу.

Кликабельная картинка
для печати

Справочно: Таблица производных.
Справочно: Таблицы неопределенных интегралов. Смолянский М.Л. ГИФМЛ 1963. (.djvu — 1Mb)

Формулы интегрирования по частям. Правила интегрирования.

*Формулы интегрирования по частям. Формула Ньютона-Лейбница.Правила интегрирования.*
Интегрирование произведения (функции) на постоянную:
Интегрирование суммы функций:
Формула интегрирования по частям неопределенные интегралы:
Формула интегрирования по частям определенные интегралы:
Формула Ньютона-Лейбница определенные интегралы:	Где F(a),F(b)-значения первообразных в точках b и a соответственно.

Описание раздела: Таблица первообразных. Таблица интегралов.

Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела:

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.xyz
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления.

Владельцы сайта www.DPVA.xyz не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.

Таблица неопределенных интегралов тригонометрических функций

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Интегралы тригонометрических функций

Ниже в табличном виде представлены формулы неопределенных интегралов тригонометрических функций: прямых, производных и обратных.

Содержание

Прямые и производные функции: sin, cos, tg, ctg
Обратные функции: arcsin, arccos, arctg, arcctg

Прямые и производные функции: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg).


Действие	Формула
Интеграл синуса	∫ sin x dx = -cos x + C
Интеграл косинуса	∫ cos x dx = sin x + C
Интеграл тангенса	∫ tg x dx = -ln \|cos x\| + C
Интеграл котангенса	∫ ctg x dx = ln \|sin x\| + C

microexcel. ru

Обратные функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).


Действие	Формула
Интеграл арксинуса	ru/wp-content/uploads/2020/02/arcsinus-formula-exc-7.png" class="stbSkipLazy aligncenter size-full" width="300" height="612" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arcsinus-formula-exc-7.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arcsinus-formula-exc-7.png" class="stbSkipLazy aligncenter size-full" width="300" height="612" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arcsinus-formula-exc-7.png" />»>
Интеграл арккосинуса	ru/wp-content/uploads/2020/02/arccos-exc-4.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arccos-exc-4.png" class="stbSkipLazy aligncenter size-full" width="320" height="630" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arccos-exc-4.png" />»>
Интеграл арктангенса	ru/wp-content/uploads/2020/02/arktangets-formuly-exc-5.png" class="stbSkipLazy aligncenter size-full" width="320" height="670" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arktangets-formuly-exc-5.png" />»>
Интеграл арккотангенса	ru/wp-content/uploads/2020/02/arkkotangens-formuly-exc-5.png" />»>

microexcel.ru

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Что такое интеграл простым языком

Содержание

Интегралы – что это, как решать, примеры решений и объяснение для чайников
Почему вы не знаете, как решать интегралы
Интеграл – что это?
Объясняем понятие «Интеграл»
Неопределённый интеграл
Определённый интеграл
Таблица интегралов для студентов (основные формулы)
Как вычислять интеграл правильно
Примеры вычисления интегралов
Решение неопределенного интеграла
Решение определенного интеграла
Базовые понятия для понимания темы
Заключение
Интеграл простыми словами
Простыми словами…
Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.
Зачем нужен интеграл
Еще примеры из жизни
Интегралы для чайников: как решать, правила вычисления, объяснение
Изучаем понятие « интеграл »
Неопределенный интеграл
Полная таблица интегралов для студентов
Определенный интеграл
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Свойства определенного интеграла
Примеры решения интегралов
Видео

Интегралы – что это, как решать, примеры решений и объяснение для чайников

За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов

Почему вы не знаете, как решать интегралы

Внимание!

Если вам нужна помощь с академической работой, то рекомендуем обратиться к профессионалам. Более 70 000 экспертов готовы помочь вам прямо сейчас.

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Объясняем понятие «Интеграл»

Если вы не уверены, что справитесь с работой, обратитесь за помощью к профессионалам. Работу могут написать преподаватели, доцены вузов

Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.

Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».

Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.

Интеграл записывается так:

Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования.

Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».

Определённый интеграл

В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.

Точки A и B на оси X – есть ограничение зоны определения интеграла

Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:

Таблица интегралов для студентов (основные формулы)

Скачайте формулы интегралов, они вам еще пригодятся

Как вычислять интеграл правильно

Существует несколько простейших операций для преобразования интегралов. Вот основные из них:

Вынесение константы из-под знака интеграла

Разложение интеграла суммы на сумму интегралов

Если поменять местами a и b, знак изменится

Можно разбить интеграл на промежутки следующим образом

Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.

Примеры вычисления интегралов

Когда нет времени!

Помощь в написании работы от 1 дня. Гарантируем сдачу работу к сроку без плагиата, только авторский текст. Оформление + сопровождеие в подарок!

Решение неопределенного интеграла

Решение определенного интеграла

Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Заключение

Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.

Источник

Интеграл простыми словами

Интегралы начинают изучать еще в школе. Но никто из учителей не говорит, зачем это нужно, как использовать эти знания в жизни. Мало кто вообще способен объяснить простыми словами, что такое интеграл, даже в университете. А мы попробуем.

Простыми словами…

Если коротко — интеграл, это сумма маленьких частей. Да, точно так же как и сложение 2+2, только части бесконечно маленькие, естественно и количество их — бесконечно.

Знак интеграла ∫ — это вытянутая буква s (длинная «эс» существовала до начала 19-ого века писалась так — ſ). Первая буква слова summa.

Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.

Почему обычного «плюсования» не достаточно? Просто в алгебре нет никаких бесконечно малых или больших.

Бесконечно малая величина, это не какое-то конкретное число. Это абстракция, в реальном мире аналогов просто нет. Мы придумали так для удобства. Что-то настолько маленькое, что измерять его бессмысленно, но в расчетах использовать можно.

Слово «интеграл» происходит от латинского integer, что означает «целый». Даже в названии есть намек некое действие, что-то вроде восстановления чего-то целого.

Лучше всего показать «на пальцах», точнее на примере. Предположим, мы хотим узнать площадь фигуры как на картинке (она называется криволинейная трапеция, потому, что одна из сторон создана кривой линией). Зачем нам это нужно? Например, это часть крыла самолета и нужно знать его площадь.

Можно, конечно, разбить фигуру на две, прямоугольник и треугольник.

Но останется «пробел», площадь которого будет неизвестна. Чтобы увеличить точность, можно разделять на большее количество фигур, но все равно будет оставаться какая-то, пусть и небольшая, но «не закрашенная» область. Фигуры будут становиться все меньше и меньше… Очевидно, что процесс измельчения будет бесконечным, по крайней мере в воображении.

Но, в реальности, бесконечный процесс попросту не нужен. На самом деле вычислить такие вещи как площадь круга, длину диагонали квадрата или объем пирамиды невозможно, значение будет бесконечным, естественно, практического смысла бесконечные числа не имеют и мы их «округляем» до нужного предела точности — приблизительно.

Такой метод в Древней Греции назывался «исчерпание». Аналогия с водой тут очень уместна, если представить, что черпаешь из ведра при помощи кружки, то сначала кружки будут полные, но чем ближе ко дну, тем меньший объем будет попадать в кружку. Первой известной личностью «взявшей интеграл» был Архимед, он фактически решил задачу по нахождению площади круга и площади параболы ничего не зная ни про пределы, но даже про число «пи».

Чем больше будет фигур, тем больше будет и точность расчета и тем меньше будут сами фигурки. Если площадь маленьких фигурок будет бесконечно малой, то есть стремится к нулю (но не равняться ему), сумма всех этих площадей будет равна сумме большой фигуры с бесконечно большой точностью.

То же самое происходит при интегрировании:

Фигура на картинке разбивается на столбцы бесконечно маленькой ширины. Ширина у нас Х. Бесконечно малое число обозначается d. То есть dx — это бесконечно малый «икс».

Сложение бесконечного числа частей бесконечно маленького размера это и есть интегрирование.

Чтобы узнать площадь фигуры нужна еще высота, а это y. Высота везде не одинаковая, она постоянно меняется. И мы знаем как именно! Ведь кривая может быть (а может и не быть, но в нашем случае так и есть) функцией y=f(x), то есть значение у меняется по закону (буква f об этом говорит) зависимому от х. Поэтому «эф от икс». Значит высота это f(x). Функция, кстати, тоже бесконечная.

Высота конкретного прямоугольничка, это значение функции в этой конкретной точке (почему точке, потому, что ширина полоски у нас бесконечно маленькая, мы так договорились в самом начале).

Площадь, это высота умноженная на ширину. За высоту можем брать и y и f(x), они равны. За ширину у нас играет dx. Итак, момент истины:

f(x)dx — площадь нашего маленького столбика. В если собрать из все вместе, будет сумма бесконечно маленьких столбиков.

А площадь нужна не бесконечной фигуры, а той что начинается от 1 и закачивается на 5. Если написать эти цифры над и под значком интеграла, получится определенный интеграл.

Собственно и все, интеграл — это сумма бесконечно малых приращений (то есть значений) какой-то функции. Не сложно и не страшно, если не усложнять.

Что мы делаем? Разрезаем фигуру на «ленточки» изменяем площадь этих ленточек и собираем все обратно (суммируем).

Интересно, везде идет речь о сумме, а площадь считается умножением.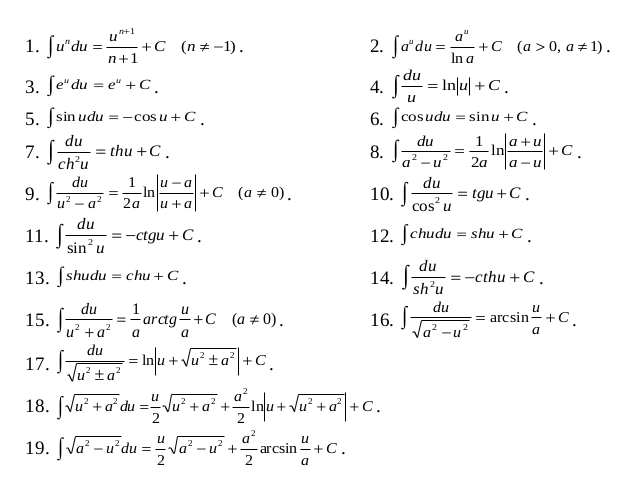 Парадокс? Нет, умножение это ведь то же самое, что и сложение: 2+2+2+2=2*4. То же самое происходит и с площадью. Чтобы выяснить какова площадь прямоугольника со сторонами 5 и 4, перемножаем 5 на 4, или разделяем прямоугольник на 5 полосок шириной в «единицу» и складываем 4+4+4+4+4=5*4=20.

Никакого противоречия здесь нет. Вот только умножение работает в случае одинаковых величин, простых фигур или прямолинейного движения без ускорения. В остальных случаях — интегрирование.

Зачем нужен интеграл

Из примера выше уже понято, что одна из полезных задач интегрирования — это расчет площади криволинейных фигур. В любой сложной ситуации, если сложность эта заключается криволинейности или неравномерности мы используем интеграл.

Но лучший способ объяснить, что такое интеграл простыми словами — показать еще пару примеров. Как когда-то в детстве объяснили сложение на яблоках. Для чего интеграл может понадобиться?

Предположим, нужно построить храм кому-то из древнегреческих богов, такой чтобы место в нем хватило всем, крыша была прямоугольной, а колоны круглыми, ведь так красивее (а еще прочнее).

Давление колонны на фундамент легко посчитать, если она квадратного сечения, делим силу на площадь и вуаля. А если колонна круглого сечения? Какова площадь круга?

Можно конечно, не напрягаться, и заменить круг эквивалентным квадратом (квадратура круга), но каким? На всякий случай побольше, чтобы наверняка ничего не развалилось. Но это не наш метод, особенно, если ни бесконечного числа рабочих, ни бесконечного числа мрамора в действительности нет и взять негде, а казнить за неэффективное использование бюджета никто не запрещает.

Прием с эквивалентом площади на самом деле простой, использовался древними людьми. Очень-очень древние греки ничего не знали об интегрировании, а Архимед еще не родился, тем не менее, чтобы рассчитать площадь круга, в него выкладывались камешки. Когда круг заполнялся, камешки собирались и раскладывались в виде квадрата. Чем меньше камешки тем… Ничего не напоминает?

Еще примеры из жизни

Конечно, в физике интеграл «берут» постоянно. Вместо Х, может быть время, и тогда мы будем иметь дело с функцией времени, такой, например, как скорость. Ускорение — это скорость изменения скорости. Скорость, это скорость изменения координат. Пробежавшись от ускорения к скорости мы уже дважды использовали интеграл.

В обратную сторону: первая производная пути, это скорость, вторая производная — ускорение. Если ускорение равно нулю, значит скорость не менялась.

Интегрирование и дифференцирование, такие же «парочка» как и умножение и деление, суммирование и вычитание, только не с цифрами, а с функциями. Это взаимно-обратные операции. В случае производной, мы не «складываем», а «отнимаем».

Если проинтегрировав функцию изменения скорости (ускорение) получим константу (число, например, 60, а не формулу y=2x), значит, скорость не изменялась со временем, ускорения не было. Если, взяв приводную (дифференциал) функции скорости по времени, получим ноль — скорость не менялась, ускорение равно нулю.

То есть, имея в своем распоряжении какую-то функцию (зависимость чего-то от чего-то), мы можем ее дифференцировать или интегрировать. Точно также как если бы умножали и или, вычитали и складывали обычные числа.

Например, у нас есть функция изменения координат от времени. В реальном мире мы вышли на пробежку. Бежал наш виртуальный спортсмен 30 минут, первые 10 минут очень быстро, вторые 10 минут уже с одышкой, ну а последние 10 прошел пешком.

Очевидно, что координаты бегуна в начале и в конце разные (он же не стоял на месте). Если координаты менялись — скорость не равнялась нулю.

Скорость не была одинаковой, а менялась в зависимости от времени (больше времени, больше усталость, меньше скорость).

Итак, у нас есть функция изменения координат. Первая производная даст нам новую функцию — изменения координат, вторая производная — функцию ускорения. И первая и вторая функции зависят от одной и той же переменной — времени.

Еще один пример, вычисление массы. Масса, это произведение плотности на объем. Если плотность и объем одинаковы (это стакан воды) никаких проблем нет. А если плотность меняется (тот же стакан, только с коктейлем в несколько слоев)? В таком случае нужно знать закон (зависимость с которой изменяться плотность жидкости в стакане).

Если вам такие примеры не близки, то представьте себе, что взяли кредит под сложный процент. Тогда ваш долг будет расти не линейно. И вы будете интегрировать…

Если нужно узнать какую работу нужно затратить на перемещение предмета не по прямой, а если, нужно рассчитать лучшую цену, зная зависимость спроса от предложения, а если нужно посчитать за какое время рабочие выкопают яму, если это не роботы, а живые люди, которые устают со временем, а если…

Если посмотреть вокруг, не найдется в реальном мире ни идеальных фигур, ни ровных графиков, ни равномерного движения без ускорения, ни линейных зависимостей в поведении человека «разумного».

Все эти простые штуки из науки, просто частные случаи. А значит, в реальном мире интеграл более полезен, чем кажется. Конечно, кривые сложнее прямых и именно поэтому всю свою историю люди упрощали себе жизнь: делили поле прямыми, на квадраты и прямоугольники при помощи натянутой веревки. Считали среднюю скорость, а не мгновенную в каждой точке маршрута, полагали, что тело прошенное под углом к горизонту летит по параболе, а не баллистической кривой… Но, просто — не значит точно.

Говоря простым языком, интегрирование — это такой же инструмент, как и суммирование, в нем нет никаких особых тайн и сложностей. Кроме одной — представить себе бесконечность сложнее, чем натуральные числа, у которых есть наглядные представления в природе. Но справляемся же мы как-то с представлениями таких абстракций как «ноль» или «отрицательное число». С матанализом просто нужно чуть больше воображения.

Ну а если уж совсем просто, для гуманитариев, то производная винограда — это вино. Интеграл вина — это виноград.

Источник

Интегралы для чайников: как решать, правила вычисления, объяснение

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие « интеграл »

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

Свойства определенного интеграла

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Видео

ИНТЕГРАЛ С НУЛЯ | определенный интеграл | ТАБЛИЦА ИНТЕГРАЛОВ | сумма Римана

Математика без ху{a47c00a1996a64a2145764bc9f608acb943865b2eadd21c2af8fa308981ee3ea}!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.

Зачем нужен ИНТЕГРАЛ. Объяснение математического смысла.

Определенные и неопределенные интегралы для чайников. Свойства интегралов.

✓ Формула Ньютона-Лейбница.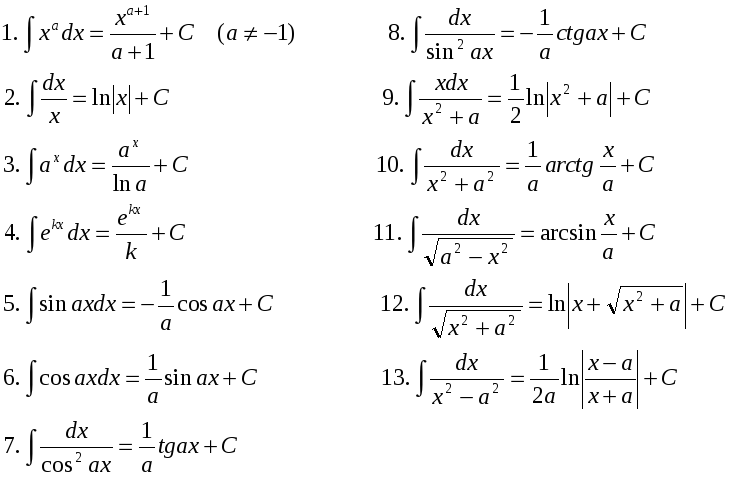 Что такое первообразная и интеграл | Осторожно, спойлер! | Борис Трушин

Смысл интеграла и производной. В помощь студенту

05. Что такое интеграл?

ЧТО ТАКОЕ ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ. Артур Шарифов

Интеграл: Азы интегрирования. Высшая математика

Определенный интеграл. 11 класс.

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Справочник по математике

Элементы математического анализа

Интегралы

Первообразная

Неопределенный интеграл

Правила интегрирования. Замена переменной в неопределенном интеграле

Таблица интегралов

Примеры решения задач

Первообразная

Определение 1. Функцию F (x) , определенную на интервале (a, b), называют первообразной функции f (x) , определенной на интервале (a, b), если для каждого выполнено равенство

F’ (x) = f (x) .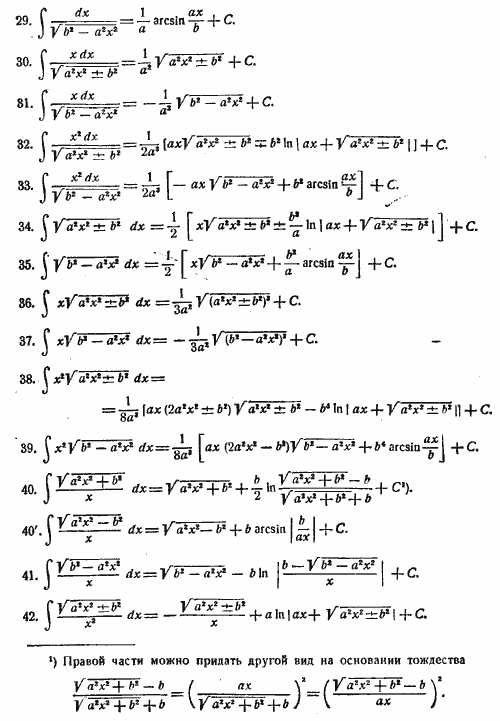

Например, из справедливости равенства

(sin 2x)’ = 2 cos 2x

вытекает, что функция F (x) = sin 2x является первообразной функции f (x) = 2 cos 2x .

Замечание. Функция F (x) = sin 2x не является единственной первообразной функции f (x) = 2 cos 2x , поскольку функция F (x) = sin 2x + 10 , или функция F (x) = sin 2x – 3 , или функции вида F (x) = sin 2x + c , где c – любое число, также являются первообразными функции f (x) = 2 cos 2x .

Справедлива следующая теорема, доказательство которой выходит за рамки школьного курса математики.

Теорема 1. Если функция F (x) является первообразной функции f (x) на интервале (a, b) , то любая другая первообразная функции f (x) на интервале (a, b) имеет вид

F (x) + с ,

где c – некоторое число.

Неопределенный интеграл

Определение 2. Множество всех первообразных функции f (x) называют неопределенным интегралом от функции f (x) и обозначают

(1)

Обозначение (1) читается так: «Неопределенный интеграл от функции f (x) по dx» .

Если F (x) является первообразной f (x) , то в силу теоремы 1 смысл формулы (1) заключается в следующем:

(2)

Однако для упрощения формулу (2) принято записывать в виде

(3)

подразумевая, но не указывая специально, что c – любое число.

В формуле (3) функцию f (x) называют подынтегральной функцией, выражение f (x) dx нызывают подынтегральным выражением, а число c называют постоянной интегрирования.

Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.

Правила интегрирования. Замена переменной в неопределенном интеграле

Вычисление интегралов (интегрирование) основано на применении следующих правил, которые непосредственно вытекают из правил вычисления производных.

Правило 1 (интеграл от произведения числа на функцию). Справедливо равенство

где k – любое число.

Другими словами, интеграл от произведения числа на функцию равен произведению этого числа на интеграл от функции.

Правило 2 (интеграл от суммы функций). Интеграл от суммы функций вычисляется по формуле

то есть интеграл от суммы функций равен сумме интегралов от этих функций.

Правило 3 (интеграл от разности функций). Интеграл от разности функций вычисляется по формуле

то есть интеграл от разности функций равен разности интегралов от этих функций.

Правило 4 (интегрирование при помощи замены переменной). Из справедливости формулы

вытекает, что

(4)

если все входящие в формулу (4) функции f (φ (x)), φ’ (x), F (φ (x)) определены.

Доказательство правила 4. Воспользовавшись формулой для производной сложной функции, вычислим производную от правой части формулы (4):

Мы получили подынтегральную функцию из левой части формулы (4), что и требовалось.

Замечание. Рассмотрим частный случай формулы (4), когда функция φ (x) является линейной функцией, то есть

φ (x) = kx + b ,

что k и b – произвольные числа, .

В этом случае

φ’ (x) = k ,

и формула (4) принимает вид

(5)

Формула (5) часто используется при решении задач.

Таблица интегралов

Следующая таблица неопределенных интегралов составлена на основе таблицы производных часто встречающихся функций, а также на основе таблицы производных сложных функций

Основная формула

Обобщения

, где k – любое число

где n – любое число, не равное – 1

где n, k, b – любые числа, ,

где n – любое число,

, x > 0

где k, b – любые числа, ,
kx + b > 0

где φ (x) > 0

где k, b – любые числа,

где a – любое положительное число, не равное 1

где a – любое положительное число, не равное 1, k, b – любые числа,

где a – любое положительное число, не равное 1

где k, b – любые числа,

где k, b – любые числа, ,

| x | < 1

где k, b – любые числа, ,
| kx + b | < 1

| φ (x) | < 1

где a, b – любые числа,

где k, b – любые числа,

где a, b – любые числа,

Основная формула:

Обобщения:

, где k – любое число

Основная формула:

где n – любое число, не равное – 1 .

Обобщения:

где n, k, b – любые числа, ,

_____

где n – любое число,

Основная формула:

, x > 0

Обобщения:

где k, b – любые числа, , kx + b > 0

_____

где φ (x) > 0

Основная формула:

Обобщения:

где k, b – любые числа,

_____

Основная формула:

где a – любое положительное число, не равное 1 .

Обобщения:

где a – любое положительное число, не равное 1, k, b – любые числа,

_____

где a – любое положительное число, не равное 1

Основная формула:

Обобщения:

где k, b – любые числа,

_____

Основная формула:

Обобщения:

где k, b – любые числа,

_____

Основная формула:

где

Обобщения:

где k, b – любые числа, ,

_____

где

Основная формула:

где

Обобщения:

где k, b – любые числа, ,

_____

Основная формула:

| x | < 1

Обобщения:

где k, b – любые числа, , | kx +b | < 1

_____

где | φ (x) | < 1

_____

где a, b – любые числа,

Основная формула:

Обобщения:

где k, b – любые числа,

_____

где a, b – любые числа,

Примеры решения задач

Пример 1. Вычислить интеграл

Решение. Воспользовавшись свойствами степеней, а затем правилами интегрирования и формулами из таблицы неопределенных интегралов формулами из таблицы неопределенных интегралов, получаем

Ответ.

Пример 2. Значение первообразной F (x) функции f (x) = – 4 sin x в точке x = 0 равно 9. Найти .

Решение. Поскольку Поскольку

то

F (x) = 4 cos x + c,

(6)

Подставляя в формулу (6) значение x = 0 , находим значение постоянной интегрирования c:

F (0) = 4 cos 0 + c = 9,

4 + c = 9, c = 5.

Следовательно,

F (x) = 4 cos x + 5

Поэтому

Ответ. 7

Пример 3. Найти первообразную F (x) функции

если F (2π) = 2e + 3.

Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов

для функции φ (x) = cos x , получаем

Следовательно,

(7)

Подставляя в формулу (7) значение x = 2π, находим значение постоянной интегрирования c:

Итак,

c = 3e +3 .

Ответ.

Пример 4. Вычислить интеграл

для функции φ (x) = e^x, получаем

Ответ.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

\prime\left( x \right) = f\left( x \right).\]

В этом определении ∫ называется символом интеграла, f ( x ) называется подынтегральной функцией, x называется переменной интегрирования, d x называется дифференциалом переменной x , а C называется константой интегрирования.

Неопределенный интеграл некоторых общих функций

Интегрирование – процесс, обратный дифференцированию, поэтому таблица основных интегралов следует из таблицы производных.

Здесь предполагается, что $a,$ $p\left( {p \ne 1} \right),$ $C$ — вещественные константы, $b$ — основание экспоненты функция $\left( {b \ne 1, b \gt 0} \right).$

Свойства неопределенного интеграла

Если $а$ некоторая константа, то
\[\int {af\left( x \right)dx} = a\int {f\left( x \right)dx},\]
т. е. постоянный коэффициент можно вынести за знак интеграла.
Для функций $f\left( x \right)$ и $g\left( x \right),$
\[\int {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} \pm \int {г\влево( х \вправо)dx} ,\]
т. е. неопределенный интеграл суммы (разности) равен сумме (разности) интегралов.

Вычисление интегралов с использованием линейных свойств неопределенных интегралов и таблицы основных интегралов называется прямым интегрированием.

Решенные проблемы

Щелкните или коснитесь проблемы, чтобы увидеть решение. 94}}}}}{4} + С.\]

Пример 5.

Найдите неопределенный интеграл \[\int {\frac{{x + 1}}{{\sqrt x }} dx}.\]

Раствор.

Интегралы запишем в виде суммы двух интегралов и вычислим их по отдельности:

\[\ int {\ frac {{x + 1}}{{\ sqrt x}} dx} = \ int {\ left ({\ frac {x} {{\ sqrt x}} + \ frac {1} {{\ sqrt x }}} \ right) dx} = \ int {\ left ( {\ sqrt x + \ frac {1} {{\ sqrt x }}} \ right) dx} = \ int {\ sqrt x dx} + \ int {\ frac {{dx}} {\ sqrt x }}} = \ frac {{{x ^ {\ frac {3} {2}}}}} {{\ frac {3} { 2}}} + 2\sqrt x + C = \frac{{2\sqrt {{x^3}} }}{3} + 2\sqrt x + C. \] 93}х + С.\]

Дополнительные проблемы см. на стр. 2.

Исчисление I — Неопределенные интегралы

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 5-1: Неопределенные интегралы

В предыдущих двух главах нам давали функцию $f\left( x \right)$, и мы спрашивали, какова производная этой функции. 4} + 3х — 92} — 9x + c,\,\,\hspace{0,25in}c{\mbox{ является константой}}\]

даст $f\left( x \right)$ после дифференцирования.

В этом последнем примере было два момента. Первый пункт состоял в том, чтобы заставить вас думать о том, как решать эти задачи. Сначала важно помнить, что на самом деле мы просто спрашиваем, что мы дифференцировали, чтобы получить данную функцию.

Другой момент заключается в том, чтобы признать, что на самом деле существует бесконечное количество функций, которые мы могли бы использовать, и все они будут отличаться на константу.

Теперь, когда мы поработали с примером, давайте избавимся от некоторых определений и терминологии.

Определения

Для данной функции $f\left( x \right)$ антипроизводной функции $f\left( x \right)$ является любая функция $F\left( x \right)$ такой, что

\[F’\влево(х\вправо) = f\влево(х\вправо)\]

Если $F\left( x \right)$ является любой антипроизводной $f\left( x \right)$, то наиболее общая антипроизводная $f\left( x \right)$ )\) называется неопределенный интеграл и обозначенный,

\[\int{{f\left( x \right)\,dx}} = F\left( x \right) + c,\hspace{0. 25in}\,\,\,\,c{\mbox{ произвольная константа}}\]

В этом определении $\int{{}}$ называется интегральным символом , $f\left( x \right)$ называется подынтегральным выражением , $x$ называется переменная интегрирования и «$c$» называются константой интегрирования .

Обратите внимание, что часто мы будем говорить просто интеграл вместо неопределенного интеграла (или определенного интеграла в этом отношении, когда мы доберемся до них). Из контекста задачи будет понятно, что речь идет о неопределенном интеграле (или определенном интеграле).

Процесс нахождения неопределенного интеграла называется интегрированием или интегрированием $f\left( x \right)$ . Если нам нужно уточнить переменную интегрирования, мы скажем, что мы 92} — 9х + с\]

Несколько предупреждений. Одна из наиболее распространенных ошибок, которую студенты допускают при работе с интегралами (как неопределенными, так и определенными), заключается в том, что они пропускают dx в конце интеграла. Это необходимо! Думайте о знаке интеграла и dx как о наборе скобок. Вы уже знаете и, вероятно, вполне довольны идеей, что каждый раз, когда вы открываете скобку, вы должны ее закрывать. В интегралах думайте о знаке интеграла как о «открытой скобке», а 95} + c + 3x — 9\end{выравнивание*}\]

Вы интегрируете только то, что находится между знаком интеграла и dx . Каждый из приведенных выше интегралов заканчивается в другом месте, поэтому мы получаем разные ответы, потому что каждый раз интегрируем разное количество членов. Во втором интеграле «-9» находится вне интеграла и поэтому не интегрируется. Точно так же в третьем интеграле «$3x — 9$» находится вне интеграла и поэтому оставлено в покое.

Знание того, какие термины интегрировать, — не единственная причина для записи $dx$. В разделе «Правило подстановки» мы фактически будем работать с $dx$ в задаче, и если у нас нет привычки записывать его, то можно легко забыть об этом, и тогда мы получим неверный ответ на тот этап.

Мораль этого состоит в том, чтобы убедиться и поставить $dx$! На данном этапе это может показаться глупым, но это просто необходимо, хотя бы по той причине, что нужно знать, где останавливается интеграл.

Кстати, обозначение $dx$ должно показаться вам немного знакомым. Мы видели такие вещи пару разделов назад. Мы назвали $dx$ дифференциалом в этом разделе, и да, это именно то, чем оно является. $dx$, которым заканчивается интеграл, есть не что иное, как дифференциал. 92} — 9w + c\end{выравнивание*}\]

Изменение переменной интегрирования в интеграле просто меняет переменную в ответе. Однако важно отметить, что когда мы меняем переменную интегрирования в интеграле, мы также изменяем дифференциал ($dx$, $dt$ или $dw$) в соответствии с новой переменной. Это важнее, чем мы можем себе представить на данный момент.

Дифференциал в конце интеграла используется также для того, чтобы сообщить нам, по какой переменной мы интегрируем. На данном этапе это может показаться неважным, поскольку большинство интегралов, с которыми мы собираемся здесь работать, будут включать только одну переменную. Однако, если вы находитесь на пути к получению степени, который приведет вас к исчислению с несколькими переменными, это будет очень важно на этом этапе, поскольку в задаче будет более одной переменной. Вам нужно выработать привычку записывать правильный дифференциал в конце интеграла, чтобы, когда он станет важным в этих классах, вы уже привыкли записывать его. 92} + с\]

Второй интеграл тоже достаточно прост, но нужно быть осторожным. dx сообщает нам, что мы интегрируем $x$. Это означает, что мы интегрируем только те $x$, которые входят в подынтегральную функцию, а все остальные переменные в подынтегральной функции считаются константами. Тогда второй интеграл равен

. \[\int{{2t\,dx}} = 2tx + c\]

Может показаться глупым всегда ставить dx , но это важная часть записи, которая может привести к тому, что мы получим неверный ответ, если не введем его.

Теперь есть некоторые важные свойства интегралов, на которые мы должны обратить внимание.

Свойства неопределенного интеграла

$\displaystyle \int{{k\,f\left( x \right)\,dx}} = k\int{{f\left( x \right)\, dx}}$, где $k$ — любое число. Таким образом, мы можем выносить мультипликативные константы из неопределенных интегралов.
Доказательство этого свойства см. в разделе «Доказательство различных интегральных формул» в главе «Дополнительно».
$\displaystyle \int{{ — f\left( x \right)\,dx}} = — \int{{f\left( x \right)\,dx}}$. Это действительно первое свойство с $k = -1$, поэтому доказательство этого свойства не приводится.
$\displaystyle \int{{f\left( x \right) \pm g\left( x \right)\,dx}} = \int{{f\left( x \right)\,dx}} \pm \int{{g\left( x \right)\,dx}}$. Другими словами, интеграл суммы или разности функций есть сумма или разность отдельных интегралов. Это правило можно распространить на столько функций, сколько нам нужно.
Доказательство этого свойства см. в разделе «Доказательство различных интегральных формул» главы «Дополнительно».

Обратите внимание, что когда мы работали над первым примером выше, мы использовали в обсуждении первое и третье свойство. Мы интегрировали каждый член по отдельности, вернули все константы, а затем соединили все вместе с соответствующим знаком.

В приведенных выше свойствах не указаны интегралы от произведений и частных. Причина этого проста. Как и в случае с производными, каждое из следующих действий НЕ будет работать.

\[\int{{f\left( x \right)g\left( x \right)\,dx}} \ne \int{{f\left( x \right)dx}}\int{{g\ влево ( х \ вправо) \, dx}} \ hspace {0,75 дюйма} \ int {{\ гидроразрыва {{f \ влево ( х \ вправо)}} {{g \ влево ( х \ вправо)}} \, dx }} \ne \frac{{\int{{f\left( x \right)\,dx}}}}{{\int{{g\left( x \right)\,dx}}}}\]

С производными у нас было правило произведения и правило частного для решения этих случаев. Однако для интегралов таких правил нет. Столкнувшись с произведением и частным в интеграле, у нас будет множество способов справиться с ним в зависимости от того, что представляет собой подынтегральная функция. 92} — 9х + с\]

В этом разделе мы продолжали вычислять один и тот же неопределенный интеграл во всех наших примерах. Цель этого раздела заключалась не в том, чтобы вычислять неопределенные интегралы, а в том, чтобы познакомить нас с обозначениями и некоторыми основными идеями и свойствами неопределенных интегралов. Следующие несколько разделов посвящены фактическому вычислению неопределенных интегралов.

Таблица интегралов, рядов и произведений

ScienceDirect

РегистрацияВход

Книга • Седьмое издание • 2007

Отредактировано:

Алан Джеффри и Даниэль Цвиллингер

Книга • Седьмое издание • 2007

Под редакцией:

Алан Джеффри и Даниэль Цвиллингер

Просмотрите эту книгу

Arrow DownПо содержанию

Описание книги

Таблица интегралов, рядов и произведений — это основной справочник по интегралам на английском языке. Математики, ученые и инженеры полагаются на него при идентификации . .. прочитайте полное описание

Search in this book

Browse content

Actions for selected chapters

Select all / Deselect all

Select all Front Matter
Full text access
Front Matter
Copyright
Предисловие к седьмому изданию
Благодарности
Порядок представления формул
Использование таблиц
Указатель специальных функций
Обозначение
ПРИМЕЧАНИЕ О библиографических ссылках
Выбор 0 — Введение
Книга Capterno Access
0 — Введение
Страницы 1-23
93
Страницы 1-23
93.
1 — Элементарные функции
Страницы 25-62
Выбор 2 — Неопределенные интегралы элементарных функций
Глава книги Нет доступа
2 — Неопределенные интегралы элементарных функций
Страницы 63-245
SELECT 3–4 — Определенные интегралы элементарных функций
Книга Capterno Access
3–4 — Определенные интегралы элементарных функций
7 -67-617 3–4 — Определенные интегралы элементарных функций
7-67-617 247-617 3–4 — Определенные интегралы элементационных функций
7-67-67-617 247-617 247-617.
Select 5 — Неопределенные интегралы специальных функций
Глава книги Нет доступа
5 — Неопределенные интегралы специальных функций
Страницы 619-630
Select 6–7 — Определенные интегралы специальных функций
Глава книги Нет доступа
6–7 — Определенные интегралы специальных функций
Страницы 631–857
Select Chapter 901 Доступ к специальным функциям 8–99
8–9 — Специальные функции
Страницы 859-1048
Выбрать 10 — Векторная теория поля
Глава книги Нет доступа
10 — Векторная теория поля
-1 Страницы0019
Select 11 — Algebraic Inequalities
Book chapterNo access
11 — Algebraic Inequalities
Pages 1059-1061
Select 12 — Integral Inequalities
Book chapterNo access
12 — Integral Inequalities
Pages 1063
13.
Матрицы и связанные результаты-1074
SELECT 14 — Degrinants
Книга Capterno Access
14 — Детерминанты
Страницы 1075-1080
SELECT 15 — Нормы
Книга Chapterno Access
9074
. Select 15 — Нормы
4004
9073
.
Select 16 — Обыкновенные дифференциальные уравнения
Глава книги Нет доступа
16 — Обыкновенные дифференциальные уравнения
Страницы 1093-1106
Select0019
Книга Capterno Access
17 — Фурье, Лаплас и Меллин Трансформации
Страницы 1107-1133
SELECT 18 — Z -Transform
Книга Capterno Access
18 — The Z -Transform
333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333н. -1140
Выбор библиографических ссылок, используемых при подготовке текста
Глава книги Нет доступа
Библиографические ссылки, используемые при подготовке текста
Страницы 1141-1144
Select Classified Дополнительные ссылки
Книга Capterno Access
Классифицированные дополнительные ссылки
Страницы 1145-1150
Индекс функций и константы
КОНДЕРСКОЙ КОНФЕРСА
9047.
Выберите Указатель понятий
Глава книги Нет доступа
Указатель понятий
Страницы 1161-1171

Основные характеристики

— компакт-диск с возможностью полного поиска, на котором информация всегда под рукой
, включая текст
— самый последний список интегралов, рядов и продуктов
информация у вас под рукой
вместе с текстом
— Самый последний список интегралов, серий и продуктов

— Обеспечивает точность и эффективность в работе

В настоящее время у вас нет доступа к этой книге, однако вы можно приобрести отдельные главы прямо из оглавления или купить полную версию.

КорзинаКупить книгу

Авторы

И.С. Gradshteyn

I.M. Ryzhik

Редакторы

Alan Jeffrey

Университет Ньюкасла на Tyne, Англия

Daniel Zwillinger

Rensesselaer Polytechn, USA Daniel Zwillinger

Rensesselaer PolyeChnININES, USA

из Renselaer. Основные методы интегрирования

Определение 1

Первообразной $F(x)$ функции $y=f(x)$ на отрезке $$ называется функция, дифференцируемая в каждой точке этого отрезка, и выполняется равенство для его производной:

Определение 2

Множество всех первообразных заданной функции $y=f(x)$, определенных на некотором отрезке, называется неопределенным интегралом данной функции $y=f(x)$. Неопределенный интеграл обозначается символом $\int f(x)dx $.

Из таблицы производных и определения 2 получаем таблицу основных интегралов.

Пример 1

Проверить справедливость формулы 7 по таблице интегралов:

\[\int tgxdx =-\ln |\cos x|+C,\, \, C=const.\]

Продифференцируем правую часть: $-\ln |\cos x|+C$.

\[\left(-\ln |\cos x|+C\right)»=-\frac(1)(\cos x) \cdot (-\sin x)=\frac(\sin x)( \cos x)=tgx\]

Пример 2

Проверить справедливость формулы 8 по таблице интегралов:

\[\int ctgxdx =\ln |\sin x|+C,\, \, C= const. \]

Дифференцируем правую часть: $\ln |\sin x|+C$.

\[\left(\ln |\sin x|\right)»=\frac(1)(\sin x) \cdot \cos x=ctgx\]

Производная оказалась равна подынтегральной функции. Следовательно, формула верна. 9(2) ) ) \]

Производная оказалась равна подынтегральной функции. Следовательно, формула верна.

Пример 7

Найдите интеграл:

\[\int \left(\cos (3x+2)+5x\right) dx.\]

Воспользуемся теоремой интеграла суммы: \left(\cos (3x+2)+5x\right) dx=\int \cos (3x+2)dx +\int 5xdx .\]

Воспользуемся теоремой о вынесении постоянного множителя из-под знака интеграла :

\[\int \cos (3x+2)dx +\int 5xdx =\int \cos (3x+2)dx +5\int xdx .\] 9(2) )(2) +C,\, \, C=C_(1 ) +C_(2) \]

Главные интегралы, которые должен знать каждый студент

Перечисленные интегралы являются основой, основой фонды. Эти формулы, конечно, следует запомнить. При вычислении более сложных интегралов вам придется использовать их постоянно.

Обратите особое внимание на формулы (5), (7), (9), (12), (13), (17) и (19). Не забудьте при интегрировании добавить к ответу произвольную константу C!

Интеграл от константы

∫ A d x = A x + C (1)

Интегрирование степенной функции

Фактически можно было бы ограничиться формулами (5) и (7), но остальные интегралы из этой группы настолько обычны, что стоит уделить им немного внимания.

∫ x d x = x 2 2 + C (2)
∫ x 2 d x = x 3 3 + C (3)
∫ 1 x d x = 2 x + C (4)
∫ 1 x d x = log | х | +C(5)
∫ 1 x 2 d x = − 1 x + C (6)
∫ x n d x = x n + 1 n + 1 + C (n ≠ − 1) (7)

Интегралы показательной функции и гиперболические функции

Конечно, формулу (8) (пожалуй, наиболее удобную для запоминания) можно рассматривать как частный случай формулы (9). Формулы (10) и (11) для интегралов гиперболического синуса и гиперболического косинуса легко выводятся из формулы (8), но лучше просто запомнить эти соотношения. (9)
11)

Основные интегралы тригонометрических функций

Ошибка, которую часто допускают студенты: они путают знаки в формулах (12) и (13). Помня о том, что производная синуса равна косинусу, многие почему-то считают, что интеграл от функции sinx равен cosx. Это неправда! Интеграл от синуса равен «минус косинус», а интеграл от cosx равен «просто синусу»:

∫ sin x d x = − cos x + C (12)
∫ cos x d x = sin x + C (13)
∫ 1 cos 2 x d x = t g x + C (14)
∫ 1 sin 2 x d x = − c t g x + C (15)

Интегралы, сводящиеся к обратным тригонометрическим функциям

Формула (16), приводящая к арктангенсу, естественно, является частным случаем формулы (17) при a=1. Точно так же (18) является частным случаем (19).

∫ 1 1 + x 2 d x = a r c t g x + C = − a r c c t g x + C (16)
∫ 1 x 2 + a 2 = 1 a a r c t g x a + C (a ≠ 0) (17)
∫ 1 1 − x 2 d x = arcsin x + C = − arccos x + C (18)
∫ 1 a 2 − x 2 d x = arcsin x a + C = − arccos x a + C (a > 0) (19)

Более сложные интегралы

Эти формулы тоже желательно запомнить. Они также используются довольно часто, и их вывод довольно утомителен.

Общие правила интегрирования

1) Интеграл от суммы двух функций равен сумме соответствующих интегралов: ∫ (f (x) + g (x)) d x = ∫ f (x) d x + ∫ g (x) d x (25)

2) Интеграл от разности двух функций равен разности соответствующих интегралов: ∫ (f (x) − g (x)) d x = ∫ f (x) d x − ∫ g (x) d x (26)

3) Постоянную можно вынести из-под знака интеграла: ∫ C f (x) d x = C ∫ f (x) d x (27)

Легко видеть, что это свойство (26) представляет собой просто комбинацию свойств (25) и (27).

4) Интеграл комплексной функции, если внутренняя функция линейна: ∫ f (A x + B) d x = 1 A F (A x + B) + C (A ≠ 0) (28)

Здесь F(x) является первообразной функции f(x). Обратите внимание, что эта формула работает только тогда, когда внутренняя функция равна Ax + B.

Важно: не существует универсальной формулы для интеграла от произведения двух функций, а также для интеграла от дроби:

∫ f (x ) г (х) d х = ? ∫ ж (х) г (х) d х = ? (тридцать)

Это, конечно, не означает, что дробь или произведение нельзя интегрировать. Просто каждый раз, когда вы видите интеграл типа (30), вам приходится изобретать способ «бороться» с ним. В некоторых случаях вам поможет интегрирование по частям, где-то придется сделать замену переменной, а иногда могут помочь даже «школьные» формулы алгебры или тригонометрии.

Простой пример вычисления неопределенного интеграла

Пример 1. Найти интеграл: ∫ (3 x 2 + 2 sin x − 7 e x + 12) d x

Используем формулы (25) и (26) (интеграл суммы или разности функций равна сумме или разности соответствующих интегралов, получаем: ∫ 3 x 2 d x + ∫ 2 sin x d x − ∫ 7 e x d x + ∫ 12 d x

Напомним, что константу можно вынести знака интеграла (формула (27)), выражение преобразуется к виду

3 ∫ x 2 d x + 2 ∫ sin x d x − 7 ∫ e x d x + 12 ∫ 1 d x

Теперь воспользуемся таблицей основных интегралов. Нам потребуется применить формулы (3), (12), (8) и (1). Проинтегрируем степенную функцию, синус, показатель степени и константу 1. Не забываем в конце добавить произвольную константу C:

3 x 3 3 — 2 cos x — 7 e x + 12 x + C

После элементарных преобразований получаем получить окончательный ответ:

X 3 − 2 cos x − 7 e x + 12 x + C

Проверь себя дифференцированием: возьми производную от полученной функции и убедись, что она равна исходному подынтегральному выражению.

Сводная таблица интегралов

∫ A d x = A x + C

∫ х d х = х 2 2 + С

∫ х 2 d х = х 3 3 + С

∫ 1 х d х = 2 х + С

∫ 1 х d х = журнал | х | +С

∫ 1 х 2 d х = — 1 х + С

∫ х n d х = х n + 1 n + 1 + C (n ≠ — 1)

∫ е х d х = е х + С

∫ a x d x = a x ln a + C (a > 0, a ≠ 1)

∫ с ч х d х = с ч х + С

∫ sin x d x = — cos x + C

∫ cos x d x = sin x + C

∫ 1 cos 2 x d x = t g x + C

∫ 1 sin 2 x d x = − c t g x + C

∫ 1 1 + x 2 d x = a r c t g x + C = − a r c c t g x + C

∫ 1 x 2 + a 2 = 1 a a r c t g x a + C (a ≠ 0)

∫ 1 1 − x 2 d x = arcsin x + C = − arccos x + C

∫ 1 a 2 − x 2 d x = arcsin x a + C = − arccos x a + C (a > 0)

∫ 1 х 2 + а 2 d х знак равно пер | х + х2 + а2 | +С

∫ 1 Икс 2 — а 2 d Икс знак равно пер | Икс + Икс 2 — а 2 | +С

∫ a 2 − x 2 d x = x 2 a 2 − x 2 + a 2 2 arcsin x a + C (a > 0)

∫ Икс 2 + а 2 d Икс знак равно Икс 2 Икс 2 + а 2 + а 2 2 пер | х + х2 + а2 | + С (а > 0)

∫ Икс 2 — а 2 d Икс знак равно Икс 2 Икс 2 — а 2 — а 2 2 пер | Икс + Икс 2 — а 2 | + С (а > 0)

Скачать таблицу интегралов (часть II) по этой ссылке

Если вы учитесь в вузе, если у вас возникли трудности с высшей математикой(математический анализ, линейная алгебра, теория вероятностей, статистика), если вам нужно услуги квалифицированного преподавателя, перейдите на страницу репетитора по высшей математике. Давайте решать ваши проблемы вместе!

Вас также может заинтересовать

Интегрирование — одна из основных операций математического анализа. Таблицы известных первообразных могут быть полезны, но теперь, после появления систем компьютерной алгебры, они теряют свое значение. Ниже приведен список наиболее распространенных первообразных производных.

Таблица основных интегралов

Другая компактная версия

Таблица интегралов от тригонометрических функций

От рациональных функций

От иррациональных функций

Интегралы трансцендентных функций

«С» — произвольная постоянная интегрирования, которая определяется, если известно значение интеграла в какой-то точке. Каждая функция имеет бесконечное число первообразных.

У большинства школьников и студентов возникают проблемы с вычислением интегралов. Эта страница содержит таблиц интегралов от тригонометрических, рациональных, иррациональных и трансцендентных функций, которые помогут в решении. Таблица производных также поможет вам.

Видео — как находить интегралы

Если вы не совсем разбираетесь в этой теме, посмотрите видео, где все подробно объясняется.

Решение интегралов — простая задача, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но мало или совсем ничего о них не знает. Интеграл… Зачем он нужен? Как его рассчитать? Что такое определенные и неопределенные интегралы?

Если единственное известное вам применение интеграла — доставать что-то полезное из труднодоступных мест с помощью крючка в виде значка интеграла, то добро пожаловать! Узнайте, как решать простые и другие интегралы и почему без этого не обойтись в математике.

Изучаем понятие « интеграл »

Интеграция была известна еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали на эту тему множество книг. Особо отличившиеся Ньютон и Лейбниц но суть вещей не изменилась.

Как понять интегралы с нуля? Ни за что! Чтобы разобраться в этой теме, вам все равно потребуются базовые знания основ. математический анализ. Информация о , которая также необходима для понимания интегралов, уже есть в нашем блоге.

Неопределенный интеграл

Пусть есть функция f(x) .

Неопределенный интеграл функции f(x) такая функция называется F(x) , производная которой равна функции f(x) .

Другими словами, интеграл — это обратная производная или первообразная. Кстати, о том, как читайте в нашей статье.

Примитив существует для каждой непрерывной функции. Также к первообразной часто добавляют знак константы, так как производные функций, отличающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не вычислять примитивы элементарных функций, их удобно свести в таблицу и использовать уже готовые значения.

Полная таблица интегралов для студентов

Определенный интеграл

Говоря об интеграле, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, прошедшего через неровный путь движения и другое. Следует помнить, что интеграл представляет собой сумму бесконечно большого числа бесконечно малых членов.

В качестве примера представьте график некоторой функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом, рисунок будет разделен на тонкие столбцы. Сумма площадей столбов и будет площадью трапеции. Но помните, что такой расчет даст приблизительный результат. Однако чем меньше и уже сегменты, тем точнее будет расчет. Если уменьшить их до такой степени, чтобы длина стремилась к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это определенный интеграл, который записывается следующим образом:

Точки a и b называются пределами интегрирования.

« Интеграл »

Кстати! Для наших читателей действует скидка 10% на

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые будут полезны при решении примеров.

Производная интеграла равна подынтегральной функции:

Постоянную можно вынести из-под знака интеграла:

Интеграл от суммы равен сумме интегралов. Также верно для разницы:

Свойства определенного интеграла

Линейность:

Знак интеграла меняется, если пределы интегрирования меняются местами:

В любые точек a , b и с :

Мы уже выяснили, что пределом суммы является определенный интеграл. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже мы рассмотрим неопределенный интеграл и примеры с решениями. Предлагаем вам самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавать вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаивайтесь, если интеграл не дан сразу. Обратитесь в профессиональную студенческую службу, и любой тройной или криволинейный интеграл на замкнутой поверхности будет вам под силу.

Первообразная функция и неопределенный интеграл

Факт 1. Интегрирование есть противоположность дифференцированию, а именно восстановление функции по известной производной этой функции. Восстановленная таким образом функция F ( x ) вызывается примитивом для функции f ( x ).

Определение 1. Функция F ( x F ( x ) На некотором интервале x , если для всех значений x Из этого интервала равенство F «( x ) = f ( x ), т.е. заданная функция f ( x ) является производной первообразной функции F ( х ). .

Например, функция F ( x ) = sin x является первообразной функции f ( x ) = cos x на всей числовой прямой, так как для любого значения x (sin x )» = (cos x ) .

Определение 2. Неопределенный интеграл функции f ( x ) есть совокупность всех ее первообразных . При этом используется обозначение

∫

f ( x ) дх

где знак ∫ называется знаком интеграла, функция f ( x ) является интегралом, и f ( x ) dx является интегралом.

Таким образом, если F ( x ) является некоторой первообразной для f ( x ), то

∫

f ( x ) dx = F ( x ) + C

где С — произвольная постоянная (константа).

Чтобы понять смысл множества первообразных функции как неопределенного интеграла, уместна следующая аналогия. Пусть будет дверь (традиционная деревянная дверь). Его функция – «быть дверью». Из чего сделана дверь? Из дерева. Это означает, что множество первообразных подынтегральной функции «быть дверью», т. е. ее неопределенного интеграла, есть функция «быть деревом + С», где С — константа, которую в данном контексте можно обозначить, для например, порода дерева. Точно так же, как дверь сделана из дерева с помощью некоторых инструментов, производная функции «сделана» из первообразной функции с помощью 9Формула 1067, которую мы узнали, изучая производную .

Тогда таблица функций обычных предметов и соответствующих им примитивов («быть дверью» — «быть деревом», «быть ложкой» — «быть металлом» и т. д.) аналогична таблице таблица основных неопределенных интегралов, которая будет приведена ниже. В таблице неопределенных интегралов перечислены общие функции с указанием первообразных, из которых эти функции «сделаны». В рамках заданий на нахождение неопределенного интеграла даются такие подынтегральные выражения, которые можно интегрировать непосредственно без особых усилий, то есть по таблице неопределенных интегралов. В более сложных задачах подынтегральная функция должна быть сначала преобразована, чтобы можно было использовать табличные интегралы.

Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную константу (константу) C , а чтобы не писать список первообразных с различными константами от 1 до бесконечности, нужно написать вниз по набору первообразных с произвольной константой C , например: 5 x ³+C. Итак, в выражение первообразной входит произвольная константа (константа), так как первообразная может быть функцией, например, 5 х ³+4 или 5 х ³+3 и при дифференцировании 4 или 3 или любая другая константа обращается в нуль.

Ставим задачу интегрирования: по заданной функции f ( x ) найти такую функцию F ( x ), производная которой равна f ( x ).

Пример 1 Найти множество первообразных функции

Решение. Для этой функции первообразной является функция

Функция F ( х ) называется первообразной для функции f ( х ), если производная F ( х ) равна х (900), или то же самое, дифференциал F ( x ) равен f ( x ) dx , т.е. Однако это не единственная первообразная для . Они также являются функциями

где С — произвольная константа. В этом можно убедиться дифференцированием.

Таким образом, если у функции имеется одна первообразная, то для нее существует бесконечное множество первообразных, отличающихся постоянным слагаемым. Все первообразные для функции записываются в приведенном выше виде. Это следует из следующей теоремы.

Теорема (формальная формулировка факта 2). Если F ( x ) является первообразной для функции f ( x ) на некотором интервале X , то любая другая первообразная для f ( x ) на том же интервале может быть представлена как F ( x ) +

5 C, где

С — произвольная константа.

В следующем примере мы уже обратимся к таблице интегралов, которая будет приведена в пункте 3, после свойств неопределенного интеграла. Делаем это до ознакомления со всей таблицей, чтобы была понятна суть вышеизложенного. А после таблицы и свойств мы будем использовать их целиком при интеграции.

Пример 2 Найти наборы первообразных:

Решение. Находим наборы первообразных функций, из которых эти функции «сделаны». При упоминании формул из таблицы интегралов пока просто примите, что такие формулы есть, а таблицу неопределённых интегралов полностью мы изучим чуть дальше.

1) Применяя формулу (7) из таблицы интегралов для n = 3, получаем

2) Используя формулу (10) из таблицы интегралов для n = 1/3 имеем

3) Так как

то по формуле (7) при n = -1/4 находим

Под знаком интеграла саму функцию не пишут f , а его произведение на дифференциал dx . Это делается в первую очередь для того, чтобы указать, по какой переменной ищется первообразная. Например,

, ;

здесь в обоих случаях подынтегральная функция равна , но ее неопределенные интегралы в рассмотренных случаях оказываются разными. В первом случае эта функция рассматривается как функция переменной х , а во втором — как функция z .

Процесс нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Геометрический смысл неопределенного интеграла

Пусть требуется найти кривую y=F(x) и мы уже знаем, что тангенс наклона касательной в каждой ее точке задан функцией f (x) абсцисс этой точки.

Согласно производной в геометрическом смысле, тангенс наклона касательной в данной точке кривой y=F(x) равно значению производной F»(x) . Итак, нам нужно найти такую функцию F(x) , для которой F»(x)=f( х) . Требуемая функция в задаче F(x) получена из f(x) . Условию задачи удовлетворяет не одна кривая, а семейство кривых. y=F(x) — одна из этих кривых, а из нее можно получить любую другую кривую параллельным переносом вдоль оси Oy .

Назовем график первообразной функции f(x) интегральная кривая. Если a F»(x)=f(x) , то график функции y=F(x) является интегральной кривой.

Факт 3. Неопределенный интеграл геометрически представляется семейством все интегральные кривые как на картинке ниже. Расстояние каждой кривой от начала координат определяется произвольной константой (константой) интегрирования C .

Свойства неопределенного интеграла

Факт 4. Теорема 1. Производная неопределенного интеграла равна подынтегральной функции, а ее дифференциал равен подынтегральной функции.

Факт 5. Теорема 2. Неопределенный интеграл от дифференциала функции f ( x ) равен функции f ( x ) с точностью до постоянного члена , т. е.

(3)

Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно обратными операциями.

Факт 6. Теорема 3. Постоянный множитель под интегралом можно вынести из-под знака неопределенного интеграла , то есть

4.0: Антипроизводные и неопределенное интегрирование (повторное рассмотрение)

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 13743

Мы потратили много времени на рассмотрение производных функции и их приложений. В следующих главах мы начнем думать «в другом направлении». То есть, учитывая функцию $f(x)$, мы будем рассматривать функции $F(x)$ такие, что $F'(x) = f(x)$. 2 + 123 456 789\) также имеет производную от $2x$. Дифференциальное уравнение $y’ = 2x$ имеет много решений. Это приводит нас к некоторым определениям.

Определение $\PageIndex{1}$: первообразные и неопределенные интегралы

Пусть задана функция $f(x)$. Первопроизводная функции $f(x)$ — это функция $F(x)$ такая, что $F'(x) = f(x)$.

Множество всех первообразных $f(x)$ есть неопределенный интеграл от $f$ , обозначаемый

\[\int f(x) \ dx.\]

Обратите внимание на наше определение: мы ссылаемся на как на первообразную производную от $f$, в отличие от на первопроизводную $f$, поскольку всегда бесконечное число. Мы часто используем заглавные буквы для обозначения первообразных.

Зная одну первообразную $f$, мы можем найти бесконечно больше, просто добавляя константу. Это не только дает нам еще 90 231 90 232 первообразных, но и 90 231 всех 90 232 из них.

Теорема $\PageIndex{1}$: формы первообразных

Пусть $F(x)$ и $G(x)$ первообразные $f(x)$. Тогда существует константа $С$ такая, что

\[G(x) = F(x) + C.\]

Для данной функции $f$ и одной из ее первообразных $F$ мы знаем, что все первообразные функции $f$ имеют вид $F(x) + C$ для некоторой константы $ С$. Используя определение $\PageIndex{1}$, мы можем сказать, что

\[\int f(x) \ dx = F(x) + C.\]

Давайте проанализируем это неопределенное целочисленное обозначение.

Рисунок $\PageIndex{1}$: Знакомство с записью неопределенного интеграла.

На рисунке $\PageIndex{1}$ показаны типичные обозначения неопределенного интеграла. Символ интегрирования $\int$ на самом деле представляет собой «удлиненную букву S», означающую «возьмите сумму». Позже мы увидим, как связаны суммы и первообразные .

Функция, для которой мы хотим найти первообразную, называется подынтегральной функцией . Он содержит дифференциал переменной, по которой мы интегрируем. Символ $\int$ и дифференциал $dx$ не являются «форзацами» с зажатой между ними функцией; скорее, символ $\int$ означает «найти все первообразные следующего за ним», а функции $f(x)$ и $dx$ перемножаются; $dx$ не «просто сидит там».

Давайте попрактикуемся в использовании этих обозначений.

Пример $\PageIndex{1}$: вычисление неопределенных интегралов

Вычисление $\displaystyle \int \sin x\ dx.$

Решение

Нас просят найти все функции $F( х)$ такой, что $F'(x) = \sin x$. Некоторое размышление приведет нас к одному решению: $F(x) = -\cos x$, потому что $\frac{d}{dx}(-\cos x) = \sin x$.

Таким образом, неопределенный интеграл от $\sin x$ равен $-\cos x$ плюс постоянная интегрирования. Итак:

\[\int \sin x \ dx = -\cos x + C.\]

Часто задаваемый вопрос: «Что случилось с $dx$?» Непросветленный ответ: «Не беспокойтесь об этом. Это само пройдет». Полное понимание включает следующее.

Этот процесс антидифференциации на самом деле решает дифференциальный вопрос. Интеграл

\[\int \sinx\dx\]

представляет нам дифференциал $dy = \sin x\ dx$. Он спрашивает: «Что такое $y$?» Мы нашли множество решений, все вида $y = -\cos x+C$.

Пусть $dy = \sin x\ dx$, переписать

\[\int \sin x \ dx \quad \text{as}\quad \int dy.\]

Это вопрос: «Какие функции имеют дифференциал вида $dy$?» Ответ: «Функции вида $y+C$, где $C$ — константа». Что такое $у$? У нас есть много вариантов, все они отличаются на константу; самый простой выбор — $y = -\cos x$.

Понимание всего этого важнее позже, когда мы попытаемся найти первообразные более сложных функций. В этом разделе мы просто изучим правила неопределенного интегрирования, и на данный момент можно добиться успеха, ответив на вопрос «Что случилось с $dx$?» с «Это ушло». 92+4х+5\).

Этот последний шаг «проверки нашего ответа» важен как с практической, так и с теоретической точки зрения. В общем, брать производные легче, чем находить первообразные, поэтому проверять нашу работу легко и важно по мере обучения.

Мы также видим, что производная от нашего ответа возвращает функцию под интегралом. Таким образом, мы можем сказать, что:

\[\frac{d}{dx}\left(\int f(x)\ dx\right) = f(x).\]

Дифференциация «отменяет» работу антидифференцировки.

Теорема 27 дала список производных общих функций, которые мы узнали к тому моменту. Мы повторяем здесь часть этого списка, чтобы подчеркнуть взаимосвязь между производными и первообразными. Этот список также будет полезен в качестве глоссария общих первообразных производных по мере нашего изучения.

Теорема $\PageIndex{2}$: производные и первообразные

92\большой)\)). Пример:

\[\int 5\cos x\ dx = 5\cdot\int \cos x\ dx = 5\cdot (\sin x+C) = 5\sin x + C. 2+5x+C \end{выравнивание}\] 90+C\)»; скорее см. Правило №14.

Мы представляем антидифференцировку как «операцию, обратную» дифференцировке. Вот полезная цитата для запоминания: «Обратные операции делают противоположные вещи в обратном порядке».
При построении производной с помощью Степенного правила мы сначала умножаем на степень, затем секунду вычитаем из степени 1. Чтобы найти первообразную, выполните противоположные действия в обратном порядке: первые прибавить к степени единицу, затем секунд разделить на степень.

Обратите внимание, что Правило №14 включает абсолютное значение $x$. Упражнения помогут читателю понять, почему это так; на данный момент знайте, что абсолютное значение важно и его нельзя игнорировать.

Задачи с начальными значениями

В разделе 2.3 мы видели, что производная функции положения дает функцию скорости, а производная функции скорости описывает ускорение. Теперь мы можем пойти «другим путем»: первообразная функции ускорения дает функцию скорости и т. д. Хотя существует только одна производная данной функции, существует бесконечное количество первообразных. Поэтому мы не можем спрашивать: «Что такое 92\). В момент времени $t=3$ падающий объект имел скорость $-10$ футов/с. Найдите уравнение скорости тела.

Решение

Мы хотим знать функцию скорости $v(t)$. Мы знаем две вещи:

Ускорение, т. е. $v'(t)=-32$, и
скорость в конкретный момент времени, т. е. $v(3) = -10$.

Используя первую часть информации, мы знаем, что $v(t)$ является первообразной $v'(t)=-32$. Итак, начнем с нахождения неопределенного интеграла от $-32$:

\[\int (-32)\ dt = -32t+C=v(t).\]

Теперь воспользуемся тем, что $v(3)=-10$, чтобы найти \(C\ ):

\[\begin{align} v(t) &= -32t+C \\ v(3) &= -10 \\ -32(3)+C &= -10\\ C &= 86 \end{align}\]

Таким образом, $v(t)= -32t+86$. Мы можем использовать это уравнение, чтобы понять движение объекта: когда $t=0$, объект имел скорость $v(0) = 86$ фут/с. Поскольку скорость положительна, объект двигался вверх.

Когда объект начал двигаться вниз? Сразу после $v(t) = 0$:

\[-32t+86 = 0 \quad \Rightarrow\quad t = \frac{43}{16} \приблизительно 2,69\text{s}.\]

Признать, что мы можем довольно немного определить о путь объекта, зная только его ускорение и скорость в один момент времени.

Пример $\PageIndex{4}$: Решение задач с начальными значениями

Найти $f(t)$, учитывая, что $f»(t) = \cos t$, $f’ (0) = 3$ и $f(0) = 5$.

Решение

Начнем с нахождения $f'(t)$, которая является первообразной $f»(t)$:

\[\int f»(t)\ dt = \int \cos t\ dt = \sin t + C = f'(t).\]

Итак, $f'(t) = \sin t+C$ для правильного значения $C$. Нам дано, что $f'(0) = 3$, поэтому:

\[f'(0) = 3 \quad \Rightarrow \quad \sin 0+C = 3 \quad \Rightarrow \quad C= 3. \]

Используя начальное значение, мы нашли $f'(t) = \sin t+ 3.$

Теперь найдем $f(t)$ путем повторного интегрирования.

\[f(t)=\int f'(t) \ dt = \int (\sin t+3)\ dt = -\cos t + 3t + C.\]

Нам дано, что $ f(0) = 5$, поэтому

\[\begin{align} -\cos 0 + 3(0) + C &= 5 \\ -1 + C &= 5\\ C &= 6 \end{align}\]

Таким образом $ f(t) = -\cos t + 3t + 6$.

В этом разделе представлены первообразные и неопределенный интеграл. Мы обнаружили, что они необходимы при поиске функции с учетом информации о ее производной (производных). Например, мы нашли функцию положения по заданной функции скорости.

В следующем разделе мы увидим, как положение и скорость неожиданно связаны площадями определенных областей на графике функции скорости. Затем, в разделе 5.4, мы увидим, как тесно связаны друг с другом площади и первообразные.

Авторы и ссылки

Грегори Хартман (Вирджинский военный институт). Свой вклад внесли Трой Симерс и Димплекумар Чалишаяр из VMI, а также Брайан Хейнольд из Университета Маунт-Сент-Мэри. Авторские права на этот контент защищены некоммерческой лицензией Creative Commons Attribution (BY-NC). http://www.apexcalculus.com/
Интегрировано Джастином Маршаллом.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Лицензия
СС BY-NC-SA
Показать страницу TOC
да
Теги
1. расчетный график:да
2. юпитер: питон

Неопределенный интеграл — определение, вычисление, формулы

Неопределенный интеграл — это интегрирование функции без каких-либо ограничений. Интегрирование является обратным процессом дифференцирования и называется первообразной функции. Неопределенный интеграл — важная часть исчисления, и приложение предельных точек к интегралу превращает его в определенный интеграл. Интегрирование определено для функции f(x) и помогает найти площадь, ограниченную кривой, относительно одной из осей координат.

Неопределенные интегралы далее решаются с помощью различных методов интегрирования по частям, интегрирования с подстановкой, интегрирования неполных дробей и интегрирования обратных тригонометрических функций. Давайте узнаем больше о неопределенных интегралах, важных формулах, примерах и разнице между неопределенными интегралами и определенными интегралами.

Общие правила дифференцирования

Общие неопределенные правила интеграции

1.	Что такое неопределенный интеграл?
2.	Важные формулы неопределенных интегралов
3.	Разница между неопределенным интегралом и определенным интегралом
4.	Примеры на неопределенный интеграл
5.	Практические вопросы
6.	Часто задаваемые вопросы о неопределенном интеграле

Что такое неопределенный интеграл?

Неопределенные интегралы — это интегралы, которые могут быть вычислены обратным процессом дифференцирования и называются первообразными функций. Для функции f(x), если производная представлена f'(x), интегрирование равнодействующей f'(x) возвращает исходную функцию f(x). Этот процесс интегрирования можно определить как определенные интегралы. Давайте поймем это из приведенного ниже выражения.

Если d/dx f(x) = f'(x), то ∫ f'(x) dx = f(x) + C

Здесь C — константа интегрирования, и вот пример того, почему нам нужно добавлять ее после значения каждого неопределенного интеграла.

Пример: Пусть f(x) = x ² и по степенному правилу f ‘(x) = 2x. Тогда интеграл от f ‘(x) равен x ² + C, поскольку дифференцирование не только x ², но и таких функций, как x ² + 2, x ² — 1 и т. д., дает 2x. Неопределенный интеграл технически определяется, как показано ниже.

В приведенном выше определении:

f(x) называется подынтегральной функцией
dx означает, что переменная интегрирования равна x
F(x) — значение неопределенного интеграла

, т. е. неопределенный интеграл функции f(x) равен F(x) + C, где производная от F(x) — исходная функция f(x).

Вычисление неопределенного интеграла

Процесс вычисления неопределенного интеграла зависит от заданной функции. Вот шаги для вычисления неопределенных интегралов различных типов функций:

Простые неопределенные интегралы можно решить с помощью формул прямого интегрирования, которые упомянуты в разделе ниже.
Рациональные функции могут быть решены методом частных дробей. т. е. мы разделяем подынтегральное выражение на частичные дроби, а затем интегрируем каждую дробь отдельно.
Некоторые неопределенные интегралы можно решить методом подстановки.
Если подынтегральное выражение является произведением, то его можно решить с помощью интегрирования по частям.
Чтобы вычислить определенный интеграл, сначала вычислите первообразную, используя один из вышеуказанных методов, а затем примените пределы, используя формулу ∫ _a ^b f(x)dx = F(b) — F(a).

Пример: Вычислить неопределенный интеграл ∫ 3x ² sin x ³ dx.

Решение:

Данный интеграл можно вычислить методом подстановки. Предположим, что x ³ = t, тогда 3x ² дх = дт. Тогда данный интеграл принимает вид ∫ sin t dt. Используя одно из правил интегрирования, его значение равно — cos t + C. Подставляя t = x ³ обратно, значение данного неопределенного интеграла равно — cos x ³ + C.

Важные формулы неопределенных интегралов

Ниже перечислены некоторые важные формулы неопределенных интегралов. Чтобы узнать больше об этих формулах и правилах, нажмите здесь.

∫ x ⁿ dx = x ^{n + 1} / (n + 1) + C
∫ 1 дх = х + С
∫ е ^х dx = е ^х + С
∫1/x dx = ln |x| + С
∫ a ^x dx = a ^x / ln a + C
∫ cos x dx = sin x + C
∫ sin x dx = -cos x + C
∫ сек ² х dx = тангенс х + С

Свойства неопределенного интеграла

Нам может понадобиться применить следующие свойства при вычислении неопределенного интеграла.

Свойство суммы : ∫ [f(x) + g(x)]dx = ∫ f(x)dx + ∫ g(x)dx
Отличие: ∫ [f(x) — g(x)]dx = ∫ f(x)dx — ∫ g(x)dx
Свойство постоянного кратного: ∫ k f(x)dx = k∫ f(x)dx
∫ f(x) dx = ∫ g(x) dx, если ∫ [f(x) — g(x)]dx = 0
∫ [k ₁ f ₁ (x) + k ₂ f ₂ (x) + . ..+k _n f _n (x)]dx = k 929212 1 ∫ 113 f ₁ (x)dx + k ₂ ∫ f ₂ (x)dx + … + k _n ∫ f _n (x)dx

Разница между неопределенным интегралом и определенным интегралом

Неопределенный интеграл используется для нахождения интеграла функции, а результирующее выражение представляет площадь, ограниченную функцией относительно одной из осей. Определенный интеграл имеет определенное значение. Определенный интеграл представляется как ∫ ^b _a f(x)dx, где a — нижний предел, а b — верхний предел, для функции f(x), определенной относительно оси x. Определенные интегралы являются первообразной функции f(x) для получения функции F(x), а верхний и нижний пределы применяются для нахождения значения F(b) — F(a). Это следует из основной теоремы исчисления.

Кроме того, многочисленные формулы и теоремы, используемые для неопределенного интеграла, можно использовать и для определенных интегралов. Основное различие между неопределенными интегралами и определенными интегралами состоит в том, что неопределенные интегралы не имеют пределов, а у определенных интегралов есть верхний предел и нижний предел.

☛ Связанные темы:

Формулы дифференцирования и интегрирования
Дифференциальное уравнение

Часто задаваемые вопросы о неопределенном интеграле

В чем разница между неопределенными интегралами и определенными интегралами?

Определенный интеграл и неопределенный интеграл отличаются применением предельных точек. В неопределённых интегралах нижний предел и верхний предел применяются к точкам, а в неопределённых интегралах вычисляются для всего диапазона без каких-либо ограничений.

Каковы свойства неопределенных интегралов?

Свойства неопределенных интегралов аналогичны свойствам дифференцирования. Неопределенные интегралы обратны дифференцированию. Дифференцирование f(x) дает f'(x), которое при применении неопределенного интеграла возвращает функцию f(x).

Какие методы используются для вычисления неопределенных интегралов?

Мы используем следующие методы для вычисления/вычисления неопределенных интегралов:

Использование формул интегрирования
Использование метода u-замены
Использование УФ-метода
Путем разбиения на неполные дроби
Путем применения тригонометрических формул

Каковы важные правила неопределенных интегралов?

Вот некоторые из важных правил неопределенных интегралов.

∫ x ⁿ dx = x ^{n + 1} / (n + 1) + C
∫ 1 дх = х + С
∫ е ^х dx = е ^х + С
∫ 1/x dx = ln |x| + С

Каковы приложения неопределенных интегралов?

Тема неопределенного интеграла имеет множество применений в исчислении. Понятие неопределенного интеграла можно использовать для нахождения площади, ограниченной данным уравнением кривой. Далее при наложении ограничений неопределенный интеграл преобразуется в определенный интеграл, что помогает в вычислении площади, ограниченной этой кривой.

XYZ — Таблица первообразных. Таблица интегралов. Таблица неопределенных интегралов. Формулы интегралов. Формулы первообразных.

Таблица неопределенных интегралов тригонометрических функций

Прямые и производные функции: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg).

Обратные функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Что такое интеграл простым языком

Интегралы – что это, как решать, примеры решений и объяснение для чайников

Почему вы не знаете, как решать интегралы

Интеграл – что это?

Объясняем понятие «Интеграл»

Неопределённый интеграл

Определённый интеграл

Таблица интегралов для студентов (основные формулы)

Как вычислять интеграл правильно

Примеры вычисления интегралов

Решение неопределенного интеграла

Решение определенного интеграла

Базовые понятия для понимания темы

Заключение

Интеграл простыми словами

Простыми словами…

Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.

Зачем нужен интеграл

Еще примеры из жизни

Интегралы для чайников: как решать, правила вычисления, объяснение

Изучаем понятие « интеграл »

Неопределенный интеграл

Полная таблица интегралов для студентов

Определенный интеграл

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Свойства определенного интеграла

Примеры решения интегралов

Видео

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Первообразная

Неопределенный интеграл

Правила интегрирования. Замена переменной в неопределенном интеграле

Таблица интегралов

Примеры решения задач

Неопределенный интеграл некоторых общих функций

Свойства неопределенного интеграла

Решенные проблемы

Пример 5.

Исчисление I — Неопределенные интегралы

Раздел 5-1: Неопределенные интегралы

Определения

Свойства неопределенного интеграла

Таблица интегралов, рядов и произведений

Просмотрите эту книгу

Описание книги

Browse content

Table of contents

Actions for selected chapters

Front Matter

Copyright

Предисловие к седьмому изданию

Благодарности

Порядок представления формул

Использование таблиц

Указатель специальных функций

Обозначение

ПРИМЕЧАНИЕ О библиографических ссылках

0 — Введение

1 — Элементарные функции

2 — Неопределенные интегралы элементарных функций

3–4 — Определенные интегралы элементарных функций

5 — Неопределенные интегралы специальных функций

6–7 — Определенные интегралы специальных функций

8–9 — Специальные функции

10 — Векторная теория поля

11 — Algebraic Inequalities

12 — Integral Inequalities

13.

14 — Детерминанты

16 — Обыкновенные дифференциальные уравнения

17 — Фурье, Лаплас и Меллин Трансформации

18 — The Z -Transform

Библиографические ссылки, используемые при подготовке текста

Классифицированные дополнительные ссылки