Векторное Произведение Векторов. Свойства, определение
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.

- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
, где
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
или
- Сочетательное свойство
или
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
По определению
и
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
Как решаем:
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Ответ:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Ответ:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
Как решаем:
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Ответ:
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Как решаем:
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Ответ:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
формула, как найти по координатам, примеры решения
Содержание:
- Что такое произведение векторов
-
Основные типы перемножения векторов
- Скалярное
- Векторное
- Смешанное умножение векторов
- Произведение векторов, примеры и решения
Содержание
- Что такое произведение векторов
-
Основные типы перемножения векторов
- Скалярное
- Векторное
- Смешанное умножение векторов
- Произведение векторов, примеры и решения
Что такое произведение векторов
Определение
Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.
Это одна из основных операций над векторами в векторной алгебре. Вектор, в отличие от обычного отрезка, имеет не только длину, но и направление в пространстве.
Основные типы перемножения векторов
В математике есть два основных вида умножения векторов: скалярное и векторное. Результатом первого является число, результатом второго — вектор. Оба произведения применяются к двум векторам. Также выделяют смешанное произведение векторов, которое является комбинацией двух вышеописанных. Оно применяется, когда необходимо узнать результат умножения трех векторов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Скалярное
Определение
Скалярным произведением двух векторов называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними. Длина вектора является его модулем.
Длина вектора является его модулем.
Записывается скалярное произведение двумя способами: \( (\overline a,\;\overline b) \) или \( \overline a\cdot\overline b.\)
Алгебраические свойства скалярного произведения
- Перестановочность. Произведение не меняется от перемены мест множителей: \(\overline a\cdot\overline b=\overline b\cdot\overline a.\)
- Сочетательность относительно числа. Умножение одного из векторов на число равносильно умножению обоих векторов на это число: \((\lambda\overline a)\cdot\overline b=\lambda(\overline a\cdot\overline b)(\lambda\overline a)\cdot(\mu\overline b)=(\lambda\mu)(\overline a\cdot\overline b).\)
- Распределительный закон. Скалярное произведение суммы двух векторов на третий равносильно сумме скалярных произведений этих векторов на третий вектор: \((\overline a+\overline b)\cdot\overline c=\overline a\cdot\overline c+\overline b\cdot\overline c.\)
Примечание
Таким образом, при выполнении алгебраических действий, связанных со скалярным произведением, с векторами можно обращаться как с числами.
Геометрический смысл
Скалярное произведение двух векторов равно произведению модуля одного из них на проекцию второго вектора на первый.
\(\overline a\cdot\overline b=\left|\overline a\right|\cdot пр_\overline a\overline b=\overline{\left|b\right|}\cdot пр_\overline b\overline a\)
\(пр_\overline b\overline a=\frac{\overline a\cdot\overline b}{\left|\overline b\right|}\)
Физический смысл
Скалярное произведение применяется для расчета работы, выполняемой при перемещении материальной точки вдоль вектора \(\overline s\) под действием силы \(\overline F\), приложенной под некоторым углом \(\varphi.\)
Рисунок 1. Физический смысл скалярного произведения
Силу \(\overline F\) необходимо разложить на ортогональные компоненты \(\overline{F_1}\) и \(\overline{F_2}. \) Тогда \(\overline{F_1}\) будет являться проекцией силы \(\overline F\) на вектор \(\overline s:\)
\) Тогда \(\overline{F_1}\) будет являться проекцией силы \(\overline F\) на вектор \(\overline s:\)
\(\left|\overline{F_1}\right|=\left|\overline F\right|\cdot\cos\left(\varphi\right).\)
В свою очередь, работа A вычисляется по формуле:
\(A=\left|\overline{F_1}\right|\cdot\left|\overline S\right|.\)
Соединив данные формулы получим:
\(A=\left|\overline F\right|\cdot\left|\overline S\right|\cdot\cos\left(\varphi\right),\)
что является скалярным произведением векторов \(\overline F\) и \(\overline s:\)
\(A=\overline F\cdot\overline S.\)
Векторное
Определение
Векторным произведением векторов \overline a и \overline b называют перпендикулярный им вектор \overline c из правой тройки, модуль которого равняется произведению модулей векторов \overline a и \overline b на синус угла между ними.
Упорядоченная тройка некомпланарных векторов называется правой, если с конца третьего вектора кратчайший поворот от первого ко второму совершается против часовой стрелки. В противном случае такая тройка называется левой.
В противном случае такая тройка называется левой.
Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Векторное произведение может выражаться в записи двумя способами: \(\overline a\times\overline b\) и \(\lbrack\overline a,\overline b\rbrack.\)
Алгебраические свойства
- Антиперестановочность. В отличие от скалярного произведения, в векторном при перемене мест множителей знак меняется на противоположный: \(\overline a\times\overline b=-(\overline b\times\overline a)\)
- Сочетательность относительно числа. Как и в случае со скалярным умножением, произведение числа на один из векторов равняется произведению его на другой или на оба вектора: \((\lambda\overline a)\times\overline b=\overline a\times(\lambda\overline b)=\lambda(\overline a\times\overline b).\)
- Распределительный закон. Векторное произведение суммы двух векторов на третий равносильно сумме векторных произведений этих векторов на третий вектор: \((\overline a+\overline b)\times\overline c=\overline a\times\overline c+\overline b\times\overline c.
 \)
\)
Из этого следует, что при выполнении алгебраических действий, связанных с векторным произведением, скобки можно раскрывать так же, как при работе с числами, с поправкой на правило антиперестановочности.
Геометрические свойства
- Если вектора \(\overline a\) и \(\overline b\) параллельны, то их векторное произведение равняется нулю.
- Векторное произведение векторов с известными координатами выражается в матричном виде: \(\overline a\times\overline b=\begin{vmatrix}i&j&k\\a_x&a_y&a_z\\b_x&b_y&b_z\end{vmatrix}=\left(\begin{vmatrix}a_y&a_z\\b_y&b_z\end{vmatrix};\;-\begin{vmatrix}a_x&a_z\\b_x&b_z\end{vmatrix};\;\begin{vmatrix}a_x&a_y\\b_x&b_y\end{vmatrix}\right).\)
Геометрический смысл
Модуль векторного произведения двух векторов равняется площади параллелограмма, сторонами которого являются эти вектора.
Рисунок 2. Геометрический смысл векторного произведения
Из определения векторного умножения следует, что модуль полученного вектора равняется произведению модулей исходных векторов на синус угла между ними:
\(\left|\overline c\right|=\left|\overline a\right|\cdot\left|\overline b\right|\cdot\sin\left(\varphi\right)\)
Площадь параллелограмма вычисляется так:
\(S=\left|\overline a\right|\cdot h, где h=\left|\overline b\right|\cdot\sin\left(\varphi\right). \)
\)
Таким образом, получаем:
\(S=\left|\overline a\right|\cdot\left|\overline b\right|\cdot\sin\left(\varphi\right)=\left|\overline a\times\overline b\right|\)
Отсюда следует формула для площади треугольника:
\(S_\bigtriangleup=\frac12\left|\overline a\times\overline b\right|\)
Физический смысл
В физике векторное произведение применяется для расчета момента силы, приложенной к одной точке относительно другой:
\(\overline M=\overline{AB}\times\overline F\)
Смешанное умножение векторов
Фактически, смешанное произведение векторов представляется как скалярное умножение одного вектора на векторное произведение двух других. Результатом смешанного произведения является число.
Свойства смешанного умножения
- \((\overline a\times\overline b)\cdot\overline c=\overline a\cdot(\overline b\times\overline c)=\overline a\cdot\overline b\cdot\overline c.\)
- Если \(\overline a\cdot\overline b\cdot\overline c\) больше нуля, тройка векторов — правая.

- Если\( \overline a\cdot\overline b\cdot\overline c\) меньше нуля, тройка векторов — левая.
- Если вектора \(\overline a, \overline b\) и \(\overline c\) компланарны, то их смешанное произведение равняется нулю.
Геометрический смысл
Если вектора \overline a, \overline b и \overline c не компланарны, то их смешанное произведение равно объему параллелепипеда, построенного на этих векторах. Число будет положительным, если тройка векторов правая, и отрицательным, если тройка левая.
\(V_{пар.}=\overline a\cdot\overline b\cdot\overline c\)
Следствием этого является формула нахождения объема пирамиды:
\(V_{пир.}=\frac16\left(\overline a\cdot\overline b\cdot\overline c\right)\)
Произведение векторов, примеры и решения
Задача №1
Даны вектора \(\overline a=(-1,\;0,\;3) и \overline b=(2,\;-3,\;1).\)
Найти их скалярное произведение.
Решение
Возьмем формулу скалярного произведения для векторов с известными координатами:
\(\overline a\cdot\overline b=a_x\cdot b_x+a_y\cdot b_y+a_z\cdot b_z\) и подставим имеющиеся значения:
\(\overline a\cdot\overline b=(-1)\cdot2+0\cdot(-3)+3\cdot1=1\)
Задача №2
Найти площадь треугольника с известными координатами угловых точек
Координаты точек: \(A(-1,\;2,\;3), B(0,\;-2,\;1), C(1,\;2,\;1)\)
Решение
Для решения этой простейшей задачи из геометрии воспользуемся следствием геометрического смысла векторного произведения:
\(S_\bigtriangleup=\frac12\left|\overline a\times\overline b\right|\)
В данном случае треугольник построен на векторах\( \overline{AB}\) и \(\overline{AC}\). Чтобы рассчитать их координаты, необходимо вычесть из координат конечной точки координаты начальной:
Чтобы рассчитать их координаты, необходимо вычесть из координат конечной точки координаты начальной:
\(\overline{AB}=(0-(-1),\;(-2)-2,\;1-3)=(1,\;-4,\;-2)\)
\(\overline{AC}=(1-(-1),\;2-2,\;1-3)=(2,\;0,\;-2)\)
Векторное произведение векторов с известными координатами выполняется в матричном виде:
\(\overline a\times\overline b=\begin{vmatrix}i&j&k\\a_x&a_y&a_z\\b_x&b_y&b_z\end{vmatrix}=\left(\begin{vmatrix}a_y&a_z\\b_y&b_z\end{vmatrix};\;-\begin{vmatrix}a_x&a_z\\b_x&b_z\end{vmatrix};\;\begin{vmatrix}a_x&a_y\\b_x&b_y\end{vmatrix}\right)\)
Подставляем значения векторов\( \overline{AB}\) и \(\overline{AC}\) в матрицу и производим вычисления:
\(\overline{AB}\times\overline{AC}=\begin{vmatrix}i&j&k\\1&-4&-2\\2&0&-2\end{vmatrix}=\left(i\begin{vmatrix}-4&-2\\0&-2\end{vmatrix};\;-j\begin{vmatrix}1&-2\\2&-2\end{vmatrix};\;k\begin{vmatrix}1&-4\\2&0\end{vmatrix}\right)=8i-2j+8k\)
Подставляем полученное значение в формулу вычисления площади треугольника, учитывая, что в ней фигурирует модуль произведения:
\(S_\bigtriangleup=\frac12\left|\overline{AB}\times\overline{AC}\right|=\frac12\sqrt{8^2+{(-2)}^2+8^2}=\sqrt{132}=11. 49\)
49\)
Насколько полезной была для вас статья?
Рейтинг: 4.00 (Голосов: 5)
Поиск по содержимому
Скалярное умножение
Скалярное умножениеВ. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников
Суперобложка / Обложка / Содержание
|
От автора Введение Векторы .Геометрическое определение вектора .Алгебраические операции над направленными отрезками ..Сложение направленных отрезков ..Умножение направленных отрезков на число .Проекции вектора ..Параллельное проектирование вектора в пространстве ..Параллельное проектирование вектора в пространстве . …Проекция вектора на плоскость ..Ортогональная проекция вектора в пространстве …Ортогональная проекция вектора на плоскость …Ортогональная проекция вектора на прямую и направленную ось .Метод координат ..Коллинеарные векторы ..Компланарные векторы ..Векторы в трехмерном геометрическом пространстве ..Линейная зависимость векторов и размерность пространства .Декартова система координат ..Различные формы записи векторов ..Линейные операции над векторами в координатной форме ..Скалярное умножение векторов …Свойства скалярного умножения …Скалярное умножение в декартовых координатах ..Некоторые примеры использования скалярного умножения . ..Площадь параллелограмма, построенного на векторах ..Свойства определителя второго порядка ..Задачи на применение определителей ..Объем параллелепипеда, построенного на векторах ..Определитель третьего порядка и его свойства ..Векторное произведение векторов ..Векторное умножение векторов базиса декартовой системы координат На подступах к тензорам .Преобразования координат .Скалярное умножение векторов в произвольных косоугольных координатах .Метрический тензор .Взаимный координатный базис .Ковариантные и контравариантные координаты вектора .Площадь и объем в косоугольных координатах ..Индексная форма записи для выражений с определителями ..Символы Веблена . ..Тензор Леви-Чивиты ..Операция векторного умножения в произвольных косоугольных координатах .Линейные преобразования или операторы .Линейный оператор и его матрица ..Примеры линейных операторов .Доказательство теоремы об определителе Тензоры .Определение тензора .Общие определения алгебраических операций с тензорами .Примеры на применение тензоров в физике ..Тензор инерции ..Тензор напряжений .Задачи ..Задачи на тождественные преобразования Методические комментарии Литература |
|
Пусть нам даны два вектора и , которые заданы своими координатами в произвольной косоугольной системе координат , и :
;
.
Как вычислить скалярное произведение этих векторов? Чему равно
Если бы речь шла о декартовой системе координат, то все было бы просто: . Однако для произвольной системы координат это равенство не выполняется. Тем не менее мы можем им воспользоваться. Для этого нам всего лишь необходимо перейти от произвольной системы координат к декартовой.
и
.
Теперь мы можем записать:
.
Введем обозначение:
.
Матрицу будем называть таблицей или матрицей координат метрического тензора.
Очевидно, что , или
.
Перепишем теперь формулу для скалярного умножения с учетом введенных обозначений:
, и в индексной форме:
.
Данная формула для скалярного произведения является общей. Она справедлива для произвольной косоугольной системы координат. В декартовой же системе матрица координат метрического тензора совпадает с единичной матрицей.
В самом деле, для декартовой системы
, и , следовательно, и
.
Метрический
тензор представляет собой набор коэффициентов
,
привязанный к определенной системе координат. Если мы переходим к
другой системе, то в общем случае будем иметь и другие коэффициенты
метрического тензора, которые принято называть координатами.
Координаты метрического тензора зависят от выбранной координатной
системы и непосредственно выражаются через ее базисные векторы. Тем
не менее метрический тензор, также как и вектор, отражает вполне
определенную геометрическую реальность, поскольку его координаты в
различных координатных системах связаны известным законом
преобразования.
Найдем закон преобразования координат метрического тензора.
, следовательно,
и есть искомый закон преобразования координат метрического тензора в индексной и в матричной формах. Мы обвели этот закон рамочкой, поскольку в тензорной алгебре он играет принципиальную роль, а нам он встретился впервые. В дальнейшем мы сможем убедиться, что этот закон проявляется при изучении самых разнообразных объектов. Для начала следует обратить внимание на принципиальное сходство его с законом преобразования координат вектора:
|
Закон преобразования координат вектора |
Закон преобразования координат метрического тензора |
|
|
|
Свойства метрического тензора.
1. Матрица координат метрического тензора симметрична.
Это свойство непосредственно следует из определения. В самом деле:
, но и, следовательно, .
2. Матрица метрического тензора определяет линейные размеры базисных векторов и углы между ними.
и .
.
В этих формулах не используется правило суммирования по повторяющимся индексам.
Метрический тензор аккумулирует в себе информацию о метрических
свойствах пространства. Он необходим для вычисления длин векторов,
углов между ними, расстояний между точками, площадей фигур и объемов
тел. Иногда даже говорят, что метрический тензор определяет метрику
пространства, хотя, если мы имеем дело с классической евклидовой
геометрией, метрика всегда предполагается заданной. Необходимо только
определиться с масштабами длин и углов. Но если мы имеем дело с
некоторым абстрактным векторным пространством, понимая под векторами
нечто отличное от направленных отрезков, мы можем столкнуться со
случаями, когда расстояние между точками пространства определяется по
другим правилам. Возможны также случаи, когда расстояние вообще
нельзя никак определить. Векторные пространства, в которых правила
для определения расстояниями между его точками не определены или не
имеют смысла, называются аффинными, а свойства таких пространств
изучает аффинная геометрия. Так вот, аффинную геометрию можно
наделить метрическими свойствами и можно это сделать различными
способами. Выбор способа и конкретного правила зависит от того, какую
реальность мы хотим таким образом смоделировать. Одним из таких
способов и является задание координат метрического тензора. В этом
случае метрический тензор будет определять метрику пространства.
Возможны также случаи, когда расстояние вообще
нельзя никак определить. Векторные пространства, в которых правила
для определения расстояниями между его точками не определены или не
имеют смысла, называются аффинными, а свойства таких пространств
изучает аффинная геометрия. Так вот, аффинную геометрию можно
наделить метрическими свойствами и можно это сделать различными
способами. Выбор способа и конкретного правила зависит от того, какую
реальность мы хотим таким образом смоделировать. Одним из таких
способов и является задание координат метрического тензора. В этом
случае метрический тензор будет определять метрику пространства.
3. Матрица метрического тензора в ортонормированном базисе совпадает с единичной.
-
;
;
;
;
;
.

4. Закон преобразования координат метрического тензора
.
5. Определитель матрицы метрического тензора на плоскости равен квадрату площади базисного параллелограмма.
Докажем это.
Обозначим площадь базисного параллелограмма , тогда .
Но . А . Следовательно,
.
Учитывая, что , получаем: .
6. Определитель матрицы метрического тензора в трехмерном пространстве равен квадрату объема базисного параллелепипеда.
Построим параллелепипед на векторах
,
и
(рис. 43). Из конца вектора
опустим перпендикуляр h на
основание: параллелограмм, построенный на векторах
и
. Объем параллелепипеда
равен
,
где
– площадь основания.
Объем параллелепипеда
равен
,
где
– площадь основания.
.
Для того чтобы вычислить объем, нам осталось найти высоту параллелепипеда h. Из точки пересечения высоты h и плоскости основания опустим перпендикуляры x и y на боковые ребра параллелепипеда. Перпендикуляры отсекут на ребрах при этом отрезки a и b. Длины отрезков мы можем найти как
, .
Из уравнения мы смогли бы найти h, если бы знали x.
Для того чтобы найти x, обратимся к рис. 44, на котором изображен вид сверху на плоскость основания параллелепипеда.
Точка O является основанием высоты
h, которая на рисунке не показана. x
и y – перпендикуляры, опущенные на
стороны параллелограмма, следовательно, треугольники
и
прямоугольные. Вертикальные углы
и
равны углу
.
Вертикальные углы
и
равны углу
.
Катет BC прямоугольного треугольника с одной стороны равен
, с другой стороны, тот же катет равен .
Приравнивая эти выражения и умножая на , получаем первое уравнение:
.
Рассматривая второй прямоугольный треугольник , мы приходим ко второму уравнению: .
Заменяя a и b соответствующими выражениями, мы приходим к системе уравнений:
,
решая которую, находим x; y нам не нужен.
.
Подставляя x в уравнение , получаем:
.
Решая уравнение относительно , получаем:
.
Подставим полученное выражение в формулу для объема и произведем необходимые преобразования
.
Вот и все, осталось только узнать в полученном результате выражение для определителя. Развернем определитель метрического тензора, учитывая симметрию его элементов.
.
Теперь мы можем констатировать, что определитель матрицы метрического тензора равен квадрату объема параллелепипеда, построенного на векторах базиса:
.
Определитель метрического тензора часто возникает в уравнениях, поэтому для него используется специальное обозначение: .
Приведенное нами доказательство является чисто геометрическим. Оно не
зависит от случайностей произвольного выбора координатных систем, оно
использует только испытанные и вызывающие доверие приемы элементарной
геометрии и в этом его достоинство. Однако, как и многие другие
прямые геометрические доказательства, оно трудоемко и требует
терпения и аккуратности.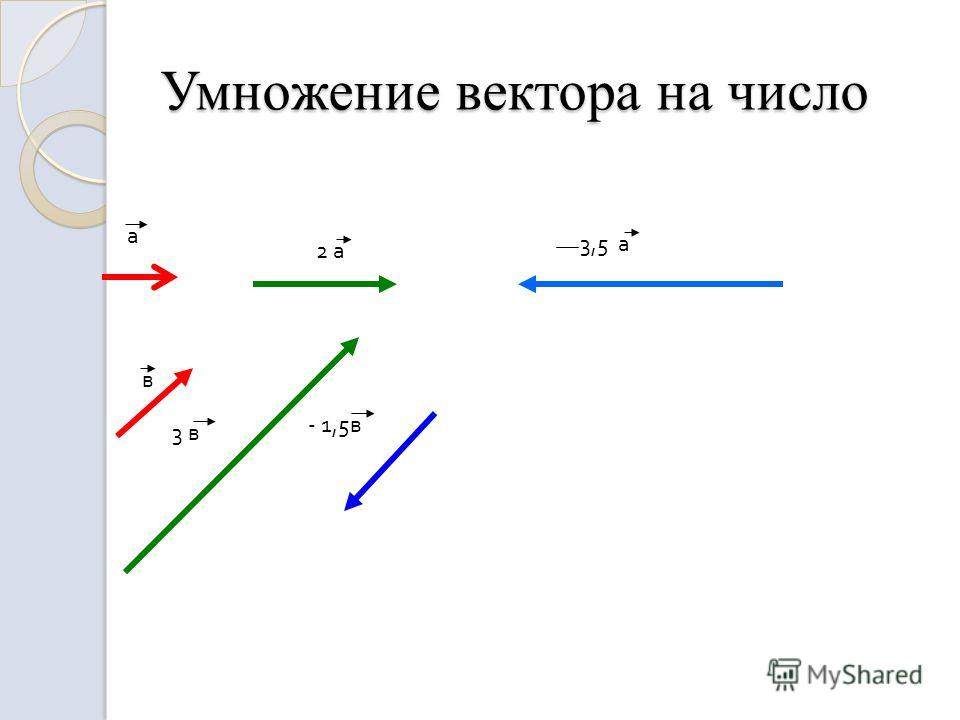 Развивая алгебраические идеи теории
векторов, мы готовы дать другое, менее мучительное доказательство
шестого свойства метрического тензора.
Развивая алгебраические идеи теории
векторов, мы готовы дать другое, менее мучительное доказательство
шестого свойства метрического тензора.
Воспользуемся законом преобразования координат метрического тензора. Пусть нам известны координаты метрического тензора в некоторой системе координат:
.
Перейдем к некоторой ортонормированной системе и найдем координаты метрического тензора в ней, воспользовавшись для этого законом преобразования координат.
, где звездочкой обозначен, как всегда, индекс, соответствующий названиям базисных векторов декартовой системы координат, а – матрица метрического тензора в декартовой системе. Но в декартовой системе координат матрица метрического тензора совпадет с единичной матрицей, следовательно: . Умножив полученное уравнение справа и слева на матрицы и , получим:
.
Теперь вспомнив, что ,
выразим
.
Чтобы яснее было видно, что получилось, выпишем матрицы подробно:
.
Матрица составлена из координат векторов базиса в ортонормированной системе координат. Следовательно, ее определитель равен ориентированному объему параллелепипеда, построенного на векторах , и . А так как определитель произведения матриц равен произведению определителей, и определитель матрицы не изменяется от ее транспонирования, то:
, где s означает, как всегда, знак ориентированного объема.
Продемонстрируем еще одну идею доказательства.
Воспользуемся на этот раз определением
.
Воспользуемся некоторой ортонормированной системой координат. Выражая скалярные произведения через координаты векторов , и в ортонормированной системе, получим:
.
Ну а дальше, все как в предыдущем доказательстве.
7. Матрица метрического тензора симметричная и положительно определенная.
О том, что матрица симметричная мы уже говорили в первом нашем свойстве. Но между первым свойством и седьмым мы говорили об очень многих разных вещах, так что не грех будет и повториться. Что касается положительной определенности (напомним, что положительно определенной матрицей называется матрица, определитель которой больше нуля), то из шестого свойства сразу следует .
На этом, пожалуй, можно и закончить разговор о метрическом тензоре.
К оглавлению
Скалярное произведение векторов, его основные свойства, выражение через координаты перемножаемых векторов.
Скалярным произведением векторов и
называется число, обозначаемое и равное произведению длин этих векторов на косинус угла между ними:
(
– угол между векторами и
).
Свойства скалярного произведения:
1. ;
2. ;
3. ;
4.
Выражение скалярного произведения через координаты сомножителей
,
т.е. скалярное произведение векторов равно сумме произведений одноименных координат.
Векторное произведение векторов, его основные свойства, выражение через координаты перемножаемых векторов.
Векторным произведением векторов и называется вектор , обозначаемый , который удовлетворяет следующим трём условиям:
1.
2. , ;
3. тройка – правая (т.е. при наблюдении из конца вектора кратчайший поворот от к виден совершающимся против часовой стрелки
Свойства векторного произведения
1. ;
;
2.;
3.;
4..
Выражение векторного произведения через координаты сомножителей
Свойства смешанного произведения.
1. ;
2. ;
3. – компланарны;
Смешанное произведение векторов, его основные свойства, выражение через координаты перемножаемых векторов
Смешанным произведением трех векторов
, , называется число
Выражение смешанного произведения через координаты сомножителей
Приложения скалярного, векторного и смешанного произведений векторов в геометрии и механике.
Приложения скалярного произведения к задачам геометрии и механики
Угол между векторами
2. Проекция вектора на направление другого
вектора
Проекция вектора на направление другого
вектора
Так как = то
,
3. Работа силы (механический смысл скалярного произведения).
Работа А силы при прямолинейном перемещении тела на вектор под действием силы равна скалярному произведению вектора силы на вектор перемещения:
.
Приложения векторного произведения к задачам геометрии и механики
Площадь параллелограмма (геометрический смысл векторного произведения).
Площадь параллелограмма, построенного на векторах и находится по формуле .
Площадь треугольника .
2. Момент
силы (механический
смысл векторного произведения). Пусть
точка А твердого тела закреплена, а в точке В приложена сила
. Тогда возникает вращающий момент
,
равный векторному произведению плеча
силы на вектор силы
,
т.е.
Тогда возникает вращающий момент
,
равный векторному произведению плеча
силы на вектор силы
,
т.е.
Приложения смешанного произведения к задачам геометрии
Объём параллелепипеда, построенного на векторах ,,, равен
.
Объём пирамиды .
Условие компланарности векторов в координатной форме:
– компланарны
Декартовы и полярные координаты на плоскости. Уравнения линий в декартовых, полярных координатах и в параметрическом виде. Примеры.
Упорядоченная система двух или трёх пересекающихся перпендикулярных друг другу осей с общим началом отсчёта (началом координат) и общей единицей длины называется прямоугольной декартовой системой координат.
Две
перпендикулярные оси на плоскости с
общим началом и одинаковой масштабной
единицей образуют декартову прямоугольную
систему координат на плоскости. Одна
из этих осей называется осью Ox, или осью
абсцисс, другую — осью Oy, или осью ординат.
Одна
из этих осей называется осью Ox, или осью
абсцисс, другую — осью Oy, или осью ординат.
Полярная система координат
Суть задания какой-либо систем координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствующую пару действительных чисел, орпеделённое положение этой точки на плоскости.
В случае полярной системы координат роль этих чисел играют расстояния точки от полюса и угол между полярной осью и радиус-вектора этой точки. Этот угол называется полярным углом, а точка О называется полюсом, а луч l— полярной осью.
Можно установить связь между полярной и декартовой системой координат, если поместить начало декартовой системы в полюс, а полярную ось направить вдоль положительного направления оси Ox.
Тогда координаты произвольной точки в двух различных системах координат связывают соотношением
x = r cos φ y = r sin φ
r=
Прямая на плоскости и ее основные уравнения: общее, векторно-параметрическое, каноническое, по двум точкам, с угловым коэффициентом, «в отрезках».
 Условия
параллельности и перпендикулярности
прямых, вычисление угла между двумя
прямыми, расстояния от точки до прямой.
Условия
параллельности и перпендикулярности
прямых, вычисление угла между двумя
прямыми, расстояния от точки до прямой.
Уравнение называется общим уравнением прямой на плоскости.
Векторно-параметрическое уравнение прямой
Каноническое уравнение прямой
Уравнение прямой по двум точкам
Уравнение прямой вида , где x и y — переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент).
Уравнение прямой в отрезках на плоскости в прямоугольной системе координатOxy имеет вид , где a и b — некоторые отличные от нуля действительные числа.
Условие параллельности прямых заключается в равенстве их угловых коэффициентов.
tgφ1=tgφ2 или k1=k2
Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1
k1k2=-1
Угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:
угол между двумя прямыми на плоскости
Угол между двумя прямыми, заданными уравнениями: l1: и l2: можно найти по формуле
расстояние от точки до прямой на плоскости
Расстояние от точки до прямой вычисляется по формуле
.
Формула для вычисления расстояния от точки до прямой в пространстве
Если s = {m; n; p} — направляющий вектор прямой l, M1(x1, y1, z1) — точка лежащей на прямой, тогда расстояние от точки M0(x0, y0, z0) до прямой l можно найти, используя формулу
d = | |M0M1×s| |
|s| | |
Плоскость и ее основные уравнения: по точке и нормальному вектору, общее, по трём точкам, «в отрезках». Взаимное расположение двух плоскостей: условия их параллельности, перпендикулярности, совпадения, вычисление угла между ними. Вычисление расстояния от точки до плоскости.

общее уравнение плоскости
Частные случаи расположения плоскости, определяемой общим уравнением
по точке и нормальному вектору
A(x − x0) + B(y − y0) + C(z − z0) = 0
уравнение плоскости, проходящей через три точки
Получим уравнение плоскости в отрезках:
где – это величины направленных отрезков, отсекаемых плоскостью на осях координат.
Угол между двумя плоскостями равен углу между их векторами нормали :
.
взаимное расположение плоскостей (условие перпендиулярности плоскостей),
(условие параллельности плоскостей).
расстояние от точки до п лоскости
Расстояние от точки до плоскости определяется по формуле
Скалярное произведение в координатах
На
прошлых занятиях к уже известным действиям над векторами, а именно сложению,
вычитанию и умножению вектора на число, мы добавили скалярное умножение
векторов.
Мы говорили, что результатом первых трёх действий является некоторый вектор, а вот результатом скалярного умножения векторов — число.
Причём скалярное произведение равно 0, если хотя бы один из векторов нулевой. В случае, когда оба вектора ненулевые, скалярное произведение может принимать положительное значение, если угол между векторами острый, отрицательное значение, если угол между векторами тупой. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Вы знаете, что каждый вектор имеет свои координаты. В связи с этим ранее нами были получены правила, позволяющие выражать координаты вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Так каждая координата вектора суммы равна сумме соответствующих координат данных векторов.
,
Каждая
координата вектора разности двух векторов равна разности соответствующих
координат данных векторов.
,
И каждая координата произведения вектора на число равна произведению соответствующих координат данного вектора на это число.
Понятно, что и скалярное произведение векторов можно выразить некоторым образом через координаты данных векторов.
Теорема. В прямоугольной системе координат скалярное произведение векторов и выражается формулой:
Доказательство.
,
,
,
, , то
,
Что и требовалось доказать.
Скалярное произведение векторов равно сумме произведений их соответствующих координат.
Выполним задание, где применим эту формулу.
Задача.
Найти скалярное произведение векторов ,
,
,
если ,
,
.
Решение.
Получается, что, зная координаты векторов, мы можем выяснить, перпендикулярны они или нет.
И в связи с изученной сегодня формулой, можно записать следствие из теоремы.
Следствие 1. Ненулевые векторы и перпендикулярны тогда и только тогда, когда .
Какие из данных векторов являются перпендикулярными для вектора ?
Для этого сумма произведений соответствующих координат векторов должна быть равна нулю.
Составим такие выражения для вектора с каждым из векторов , и .
Проверим пары векторов.
Мы получили, что только два вектора, и , являются перпендикулярными вектору .
А теперь рассмотрим ещё одно следствие из теоремы.
Следствие
2.
Косинус угла между
ненулевыми векторами и
выражается
формулой: .
Действительно, из формулы скалярного произведения
.
Найти косинусы углов между векторами , , . Если , , , , , .
Запишем формулу косинуса угла между векторами
Так мы рассмотрели примеры вычисления косинуса угла между векторами по их координатам.
А теперь выполним такое задание.
Задача. Определить, при каких значениях переменной .
,
,
,
,
Решение.
По следствию, записанному сегодня, можно записать, что для того, чтобы векторы были перпендикулярны, сумма произведений их координат должна равняться нулю.
В каждом из этих пунктов мы определили значение переменной x, при котором векторы будут перпендикулярны.
Задача.
Доказать, что треугольник с вершинами ,
и
тупоугольный
и найти косинус тупого угла.
Решение.
Нужно доказать, что треугольник с вершинами А, B и C тупоугольный и найти косинус тупого угла.
В нашем треугольнике ABC три угла. Чтобы доказать, что он тупоугольный достаточно найти косинус каждого угла и проанализировать его величину.
Если косинус одного из углов окажется меньшим нуля, то тем самым мы докажем, что данный угол тупой, а треугольник — тупоугольный.
Мы умеем находить косинус угла между векторами по их координатам.
Чтобы воспользоваться изученной формулой косинуса угла между векторами, нужно знать их координаты.
Найдём их как разности соответствующих координат конца и начала вектора.
острый
острый
тупой
Тем самым мы доказали, что треугольник ABC — тупоугольный, и нашли косинус тупого угла.
Что
и требовалось доказать.
Ответ: .
Подведём итоги урока.
Сегодня мы с вами получили формулу скалярного произведения векторов в координатах.
А также сформулировали следствия из данной теоремы.
Первое из них гласит, что ненулевые векторы перпендикулярны тогда и только тогда, когда сумма произведений их соответствующих координат равна нулю.
Второе следствие позволяет находить косинус угла между векторами через их координаты.
Векторы и действия над векторами
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения направлено к поверхности Земли, а величина его равна 9,8 м/с2. Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Вот другой пример.
Автомобиль движется из A в B. Конечный результат — его перемещение из точки A в точку B, то есть перемещение на вектор .
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или
Длиной вектора называется длина этого отрезка. Обозначается: или
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1. Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y, абсцисса и ордината.
Вектор также задается двумя координатами:
Здесь в скобках записаны координаты вектора — по x и по y.
Находятся они просто: координата конца вектора минус координата его начала.
Если координаты вектора заданы, его длина находится по формуле
Сложение векторов
Для сложения векторов есть два способа.
1. Правило параллелограмма. Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и .
Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
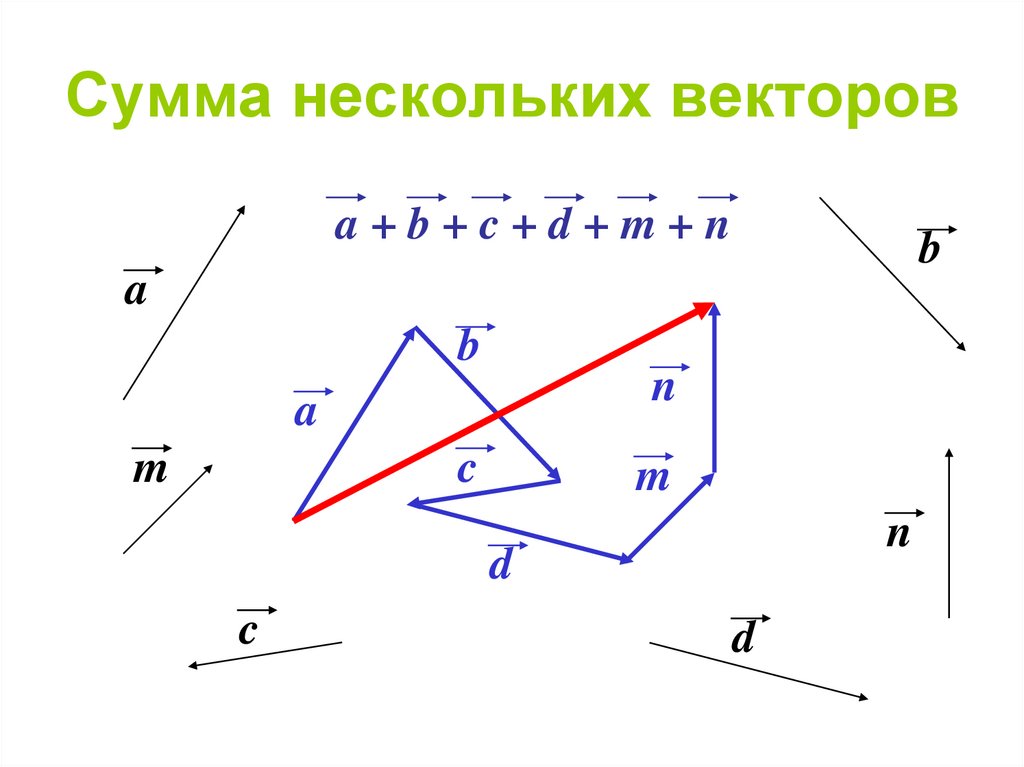
2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и .
Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и .
По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
Представьте, что вы идете из пункта А в пункт В, из В в С, из С в D, затем в Е и в F. Конечный результат этих действий — перемещение из А в F.
При сложении векторов и получаем:
Вычитание векторов
Вектор направлен противоположно вектору . Длины векторов и равны.
Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора .
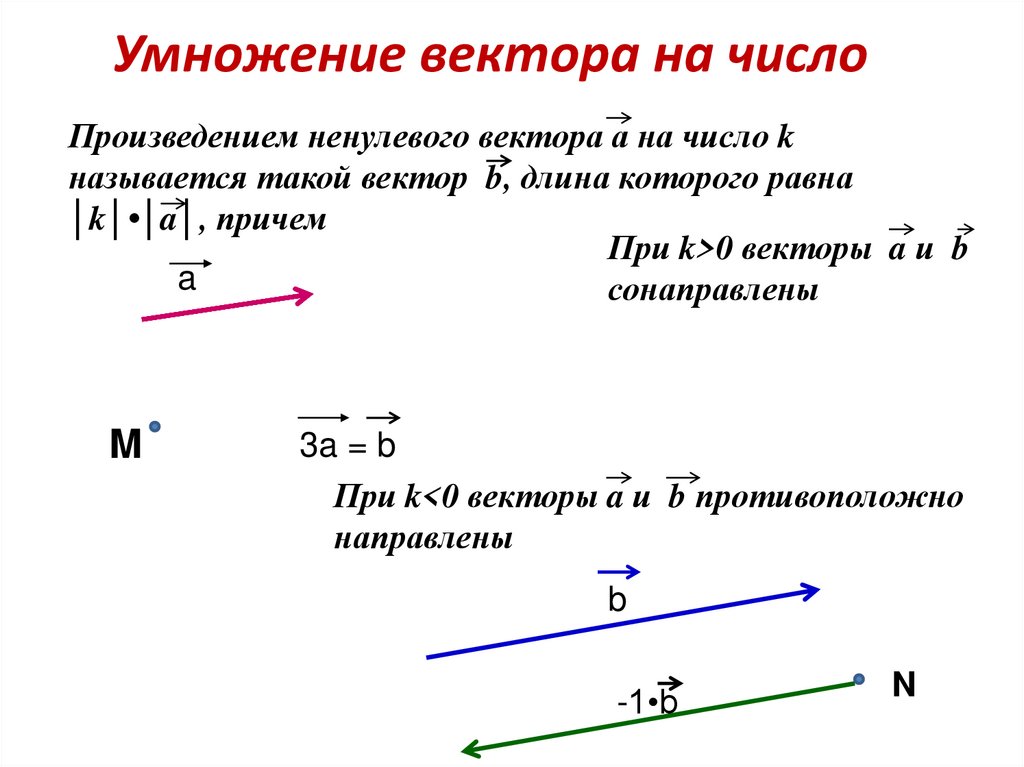
Умножение вектора на число
При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля.
Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов и :
Из формулы для скалярного произведения можно найти угол между векторами:
Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
ПОДРОБНЕЕ
Умножение векторов — Гиперучебник по физике
[закрыть]
умножение скаляра на вектор
Умножение вектора на скаляр изменяет величину вектора, но оставляет его направление неизменным. Скаляр изменяет размер вектора. Скаляр «масштабирует» вектор. Например, полярный форм-вектор…
Скаляр «масштабирует» вектор. Например, полярный форм-вектор…
r = r r̂ + θ θ̂
умножить на скаляр a равно…
a r = ar r̂ + θ θ̂
Умножение вектора на скаляр является дистрибутивным.
a ( A + B ) = a A + a B
Следовательно, прямоугольный форм-вектор…
r = x х + у х
умножить на скаляр а это…
a r = ax î + ау ĵ
скалярное произведение
Геометрически скалярное произведение двух векторов равно единице, умноженной на проекцию второго на первый.
Символ, используемый для обозначения этой операции, представляет собой небольшую точку средней высоты (·), откуда и произошло название «точечный продукт». Поскольку этот продукт имеет только величину, он также известен как 9.0087 скалярное произведение .
Поскольку этот продукт имеет только величину, он также известен как 9.0087 скалярное произведение .
A · B = AB cos θ
Скалярный продукт является распределительным…
А · ( В + С ) = А · В + А · С033
и коммутативный…
А · Б = Б · А
Поскольку проекция вектора на самого себя оставляет его величину неизменной, скалярное произведение любого вектора на самого себя равно квадрату величины этого вектора.
А · А = AA cos 0° = А 2
Применение этого следствия к единичным векторам означает, что скалярное произведение любого единичного вектора с самим собой равно единице. Кроме того, поскольку вектор не имеет перпендикулярной к себе проекции, скалярное произведение любого единичного вектора на любой другой равно нулю.
х · х = х · х = k̂ · k̂ ° = 9 (1)(0)0003
х · х = х · k̂ = k̂ · х 3 0 = 9(1)(0)
Используя эти знания, мы можем вывести формулу скалярного произведения любых двух векторов в прямоугольной форме. Полученный продукт выглядит так, как будто это будет ужасный беспорядок, но он состоит в основном из членов, равных нулю.
| А · В = | ( А x î + A y ĵ + A z k̂ ) · ( B x î + B y ĵ + B z k̂ ) | |||||||||||
| А · Б = | А x î | · | В x î | + | А x î | · | Б у х | + | А x î | · | B z k̂ | |
| + | А у х | · | В x î | + | А у х | · | Б у х | + | А у х | · | B z k̂ | |
| + | А z к̂ | · | В x О | + | А z к̂ | · | Б у х | + | А z к̂ | · | B z k̂ | |
| А · В = | A x B x + A y B y + A z B z | |||||||||||
Таким образом, скалярное произведение двух векторов равно сумме произведений их параллельных компонентов. Отсюда мы можем вывести теорему Пифагора для трех измерений.
Отсюда мы можем вывести теорему Пифагора для трех измерений.
A · A = AA cos 0° = A x A x + A y A y + A z А z
A 2 = A x 2 + A y 2 + A z 2
перекрестное произведение
Геометрически перекрестное произведение двух векторов представляет собой площадь параллелограмма между ними.
Символ, используемый для обозначения этой операции, представляет собой большой диагональный крест (×), откуда и произошло название «перекрестное произведение». Поскольку это произведение имеет величину и направление, оно также известно как число 9.0087 векторный продукт .
A × B = AB sin θ n̂
Вектор n̂ (n hat) представляет собой единичный вектор, перпендикулярный плоскости, образованной двумя векторами. Направление n̂ определяется правилом правой руки, которое мы вскоре обсудим.
Направление n̂ определяется правилом правой руки, которое мы вскоре обсудим.
Перекрестное произведение является распределительным…
A × ( B + C ) = ( A × B ) + ( А × С )
, но не коммутативный…
А × В = — В × А
Изменение порядка перекрестного умножения на противоположное меняет направление произведения.
Поскольку два одинаковых вектора образуют вырожденный параллелограмм без площади, то векторное произведение любого вектора на самого себя равно нулю…
А × А = 0
Применение этого следствия к единичным векторам означает, что векторное произведение любого единичного вектора с самим собой равно нулю.
х × х = х х х = k̂ × k̂ °= 90(1)(1)
Следует отметить, что векторное произведение любого единичного вектора на любой другой будет иметь модуль, равный единице. (В конце концов, синус 90° — это единица.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение равно не коммутативный, важен порядок операций.
(В конце концов, синус 90° — это единица.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение равно не коммутативный, важен порядок операций.
- Держите правую руку горизонтально, большой палец должен быть перпендикулярен остальным. Ни в коем случае не сгибайте большой палец.
- Укажите пальцем в направлении первого вектора.
- Расположите ладонь так, чтобы при сгибании пальцев они указывали в направлении второго вектора.
- Теперь ваш большой палец указывает в направлении векторного произведения.
A правая система координат , которая является обычной системой координат, используемой в физике и математике, является той, в которой любое циклическое произведение трех координатных осей положительно, а любое антициклическое произведение отрицательно. Представьте себе часы с тремя буквами x-y-z вместо обычных двенадцати цифр. Любое произведение этих трех букв, которое работает круглосуточно в том же направлении, что и последовательность x-y-z, равно , циклическому и положительному. Любой продукт, который работает в противоположном направлении, является антициклическим и отрицательным.
Любое произведение этих трех букв, которое работает круглосуточно в том же направлении, что и последовательность x-y-z, равно , циклическому и положительному. Любой продукт, который работает в противоположном направлении, является антициклическим и отрицательным.
| Перекрестное произведение циклической пары единичных векторов равно положительному . | Перекрестное произведение антициклической пары единичных векторов равно отрицательному . |
Используя эти знания, мы можем вывести формулу векторного произведения любых двух векторов в прямоугольной форме. Полученный продукт выглядит так, как будто он будет ужасным беспорядком, и это так!
А × В = ( A x î + A y ĵ + A z k̂ ) × ( B x î + B y ĵ + B z k̂ )
Произведение двух трехчленов состоит из девяти членов.
| А × В | = | А x î | × | В x î | + | А x î | × | Б у х | + | А x î | × | B z k̂ |
| + | А у х | × | В x î | + | А у х | × | Б у х | + | А у х | × | B z k̂ | |
| + | A z k̂ | × | В x î | + | А z к̂ | × | Б у х | + | А z к̂ | × | B z k̂ |
Три из них равны нулю. Устраните их.
Устраните их.
| А × Б | = | A x B y k̂ | − | А х В z х |
| − | A y B x k̂ | + | A y B z î | |
| + | А z B x х | − | A z B y î |
Сгруппируйте термины по единичному вектору и фактору.
A × B = ( A y B z − A z B y ) î Есть более простой способ написать это. Расширение определителя 3×3 по его первой строке — это первый шаг. Это дает нам три определителя 2×2. Эти определители 2×2 можно быстро найти. A × B = ( A y B z − A z B y ) î Умножение векторов бывает двух типов. Вектор имеет как величину, так и направление, и, исходя из этого, двумя способами умножения векторов являются скалярное произведение двух векторов и перекрестное произведение двух векторов. Скалярное произведение двух векторов также называется скалярным произведением, поскольку результирующее значение является скалярной величиной. Перекрестное произведение называется векторным произведением, так как в результате получается вектор, перпендикулярный этим двум векторам. Давайте узнаем о двух умножениях векторов, рабочем правиле, свойствах, использовании, примерах этого умножения векторов. Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов является определителем матрицы, первая строка которой представляет собой единичные векторы, вторая строка — первый вектор, а третья строка — второй вектор. Символически…
Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов является определителем матрицы, первая строка которой представляет собой единичные векторы, вторая строка — первый вектор, а третья строка — второй вектор. Символически… А × В = или — к̂ А x А у А z В x Б у Б г А × В = А у А z î — А x А z х + А x А у к̂ Б у Б г В x Б г В x Б у  Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать члены и множители.
Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать члены и множители. Умножение векторов — определение, формула, примеры
1. Как сделать умножение векторов? 2. Рабочее правило умножения векторов 3. Свойства умножения векторов 4. Применение умножения векторов 5. Примеры умножения векторов 6. Практические вопросы по умножению векторов 7. Часто задаваемые вопросы об умножении векторов Как сделать умножение векторов?
Вектор имеет как величину, так и направление. Мы можем умножать два или более векторов на скалярное произведение и перекрестное произведение. Давайте разберемся подробнее о каждом умножении векторов.
Скалярное произведение
Скалярное произведение векторов также называется скалярным произведением векторов. Результат скалярного произведения векторов является скалярным значением. Скалярное произведение векторов равно произведению величин двух векторов и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом или отрицательным действительным числом.
Результат скалярного произведения векторов является скалярным значением. Скалярное произведение векторов равно произведению величин двух векторов и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом или отрицательным действительным числом.
Пусть a и b — два ненулевых вектора, а θ — угол между векторами. Тогда скалярное произведение или скалярное произведение обозначается буквой a.b, которая определяется как:
\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ .
Здесь \(|\overrightarrow a|\) — величина \(\overrightarrow a\), \(|\overrightarrow b|\) — величина \(\overrightarrow b\), а θ — величина угол между ними.
Перекрестное произведение
Перекрестное произведение также называется векторным произведением. Перекрестное произведение — это форма умножения векторов, выполняемая между двумя векторами разной природы или вида. Когда два вектора перемножаются друг с другом, и умножение также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.
Когда два вектора перемножаются друг с другом, и умножение также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.
Понять это можно на примере: если у нас есть два вектора, лежащих в плоскости X-Y, то их векторное произведение даст результирующий вектор в направлении оси Z, которая перпендикулярна плоскости XY. Символ × используется между исходными векторами. Умножение векторов или перекрестное произведение двух векторов показано следующим образом.
\(\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}\)
Здесь \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — два вектора, и \(\overrightarrow{c}\) — результирующий вектор. Пусть θ — угол, образованный между \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а \(\hat n\) — единичный вектор, перпендикулярный плоскости, содержащей обе \(\overrightarrow{a }\) и \(\overrightarrow{b}\). Перекрестное произведение двух векторов определяется следующей формулой:
Перекрестное произведение двух векторов определяется следующей формулой:
\(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)
Рабочее правило умножения векторов
Рабочее правило умножения векторов, которое включает скалярное произведение и векторное произведение, можно понять из приведенных ниже предложений.
Скалярное произведение
Для скалярного умножения векторов два вектора выражаются через единичные векторы i, j, k вдоль осей x, y, z, затем скалярное произведение получается следующим образом:
Если \(\overrightarrow a = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow b = a_2 \hat i + b_2 \hat j + c_2\hat k\), то
\(\overrightarrow a. \overrightarrow b\) = \((a_1 \hat i + b_1 \hat j + c_1 \hat k)(a_2 \hat i + b_2 \hat j + c_2 \hat k)\)
= \((a_1a_2) (\hat i. \hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1c_2) (\hat i. \hat k) + \\(b_1a_2) ( \hat j. \hat i) + (b_1b_2)(\hat j. \hat j) + (b_1c_2 (\hat j. \hat k) + \\(c_1a_2)(\hat k. \hat i) + ( c_1b_2)(\шляпа k.\шляпа j) + (c_1c_2)(\шляпа k.\шляпа k)\)
\hat j) + (b_1c_2 (\hat j. \hat k) + \\(c_1a_2)(\hat k. \hat i) + ( c_1b_2)(\шляпа k.\шляпа j) + (c_1c_2)(\шляпа k.\шляпа k)\)
\(\overrightarrow a. \overrightarrow b\) = \(a_1a_2 + b_1b_2+ c_1c_2\)
Перекрестное произведение
Предположим, что \(\overrightarrow{a}\) и \(\overrightarrow{b}\ ) — два вектора, такие, что \(\overrightarrow{a}\)= \(a_1\hat i+b_1 \hat j+c_1 \hat k\) и \(\overrightarrow{b}\) = \(a_2 \ шляпа i+b_2 \ шляпа j+c_2 \ шляпа k\), то с помощью определителей мы могли бы найти векторное произведение векторов, используя следующую матричную запись.
Перемножение векторов также представляется с помощью формулы перекрестного произведения как:
\(\overrightarrow{a} \times \overrightarrow{b} = \hat i (b_1c_2-b_2c_1) — \hat j (a_1c_2-a_2c_1) + \hat k (a_1b_2-a_2b_1)\)
Примечание: \ ( \hat i, \hat j, \text{ и } \hat k \) — единичные векторы в направлении оси x, оси y и оси z соответственно.
Свойства умножения векторов
Скалярное произведение единичного вектора изучается путем взятия единичных векторов \(\hat i\) вдоль оси x, \(\hat j\) вдоль оси y и \(\hat k\) по оси Z соответственно. Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0.
Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0.
- \(\hat i.\hat i\) = \(\hat j.\hat j\) = \(\hat k.\hat k\)= 1
- \(\шляпа i.\шляпа j\) = \(\шляпа j.\шляпа k\) = \(\шляпа k.\шляпа i\)= 0
Перекрестное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и перекрестное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их векторное произведение равно 0. А угол между двумя перпендикулярными векторами равен 90º, и их векторное произведение дает вектор, который перпендикулярен двум заданным векторам.
- \(\overrightarrow{i}\times \overrightarrow{i} =\overrightarrow{j}\times \overrightarrow{j} = \overrightarrow{k}\times \overrightarrow{k} = 0\)
Перекрестное произведение двух векторов следует циклическому порядку, как показано на изображении ниже. Перекрестное произведение двух векторов в циклической последовательности дает третий вектор в последовательности.
Перекрестное произведение двух векторов в циклической последовательности дает третий вектор в последовательности.
- \(\overrightarrow{i}\times \overrightarrow{j} = \overrightarrow{k}; \overrightarrow{j}\times \overrightarrow{k}= \overrightarrow{i}; \overrightarrow{k} \times \overrightarrow{i} = \overrightarrow{j}\)
- \(\overrightarrow{j}\times \overrightarrow{i} = \overrightarrow{-k}; \overrightarrow{k}\times \overrightarrow{j}= \overrightarrow{-i}; \overrightarrow{i}\times \overrightarrow{k} = \overrightarrow{-j}\)
Свойства умножения векторов помогают получить подробное представление об умножении векторов, а также выполнять многочисленные вычисления с использованием векторов. Здесь перечислены несколько важных свойств умножения векторов.
- Перекрестное произведение двух векторов определяется формулой \( \overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta)\).
- Скалярное произведение двух векторов определяется формулой \( \overrightarrow{a} .
 \overrightarrow{b} = |a| |b| \cos(\theta)\).
\overrightarrow{b} = |a| |b| \cos(\theta)\). - Скалярное произведение двух векторов подчиняется свойству коммутативности. \(\vec a. \vec b = \vec b. \vec a \)
- Перекрестное произведение двух векторов не соответствует свойству коммутативности. \( \vec a \times \vec b\neq \vec b \times \vec a \)
- Антикоммутативное свойство: \(\overrightarrow{a} \times \overrightarrow{b} = — \overrightarrow{b} \times \overrightarrow{a}\)
- Распределительное свойство: \(\overrightarrow{a} \times (\overrightarrow{b} + \overrightarrow{c}) = (\overrightarrow{a}\times \overrightarrow{b} )+ (\overrightarrow{a}\times \overrightarrow{с})\)
- Перекрестное произведение нулевого вектора: \(\overrightarrow{a}\times \overrightarrow{0} = \overrightarrow{0}\)
- Перемножение вектора с самим собой: \(\overrightarrow{a}\times \overrightarrow{a} = \overrightarrow{0}\)
- Умножить на скалярную величину: \(c(\overrightarrow{a}\times \overrightarrow{b}) = c\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{a}\times c\overrightarrow{ б}\)
- Скалярное произведение двух векторов является скаляром и лежит в плоскости двух векторов.

- Перекрестное произведение двух векторов — это вектор, который перпендикулярен плоскости, содержащей эти два вектора.
Применение умножения векторов
Ниже приведены некоторые из важных применений умножения векторов. Давайте разберемся с каждым из этих применений в следующих параграфах.
- Проекция вектора
- Угол между двумя векторами
- Продукт тройного креста
- Площадь параллелограмма
- Объем параллелепипеда
Проекция вектора
Скалярное произведение полезно для нахождения компонента одного вектора в направлении другого. Проекция вектора одного вектора на другой вектор — это длина тени данного вектора на другой вектор. Он получается путем умножения величины данных векторов на косеканс угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.
Здесь \(\overrightarrow a\) и \(\overrightarrow b\) — два вектора, а θ — угол между двумя векторами. 2}}\)
2}}\)
Тройное перекрестное произведение
Перекрестное произведение вектора на произведение двух других векторов представляет собой тройное перекрестное произведение векторов. Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:
\((\overrightarrow{a}\times \overrightarrow{b}) \times \overrightarrow{c} = (\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b} -(\overrightarrow{b}\cdot \overrightarrow{c}) \overrightarrow{a}\)
Площадь параллелограмма
Две смежные стороны параллелограмма могут быть представлены векторами \(\overrightarrow a\) и \(\overrightarrow b\). Площадь параллелограмма равна произведению основания и высоты параллелограмма. Рассмотрим основание параллелограмма как \(|\overrightarrow a|\), а высоту параллелограмма как \(|\overrightarrow b|\)sin θ.
Здесь Основание = \(|\overrightarrow a|\), Высота = \(|\overrightarrow b|\)sin θ, а Площадь параллелограмма = Основание x Высота
Площадь параллелограмма = \(|\overrightarrow a|.|\overrightarrow b|\)sin θ = \(\overrightarrow a \times \overrightarrow b \)
Объем параллелепипеда
Параллелепипед равен шести двусторонняя фигура, каждая из сторон которой является параллелограммом. Здесь параллелограммы противоположных сторон одинаковы. Объем V параллелепипеда можно получить со стороны ребер a, b, c. Объем параллелепипеда можно получить из произведения площади основания на высоту параллелепипеда. Площадь основания параллелепипеда равна |b x c| а высота параллелепипеда равна |a|. Формула расчета объема параллелепипеда выглядит следующим образом.
V = a.(b x c)
Связанные темы
Следующие темы помогают лучше понять умножение векторов.
- Коллинеарные векторы
- Векторы
- Типы векторов
- Сложение векторов
- Перекрестное произведение двух векторов
Часто задаваемые вопросы по умножению векторов
Что такое скалярное умножение векторов?
Скалярное умножение векторов также называется скалярным произведением двух векторов и имеет два определения. Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного умножения векторов является скалярным значением.
Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного умножения векторов является скалярным значением.
Как вычислить скалярное произведение векторов?
Скалярное умножение векторов можно вычислить в три простых шага. Сначала найдите величину двух векторов a и b, т.е. |a| и |б|. Во-вторых, найдите косеканс угла θ между двумя векторами. Наконец, возьмите произведение величины двух векторов и косеканса угла между двумя векторами, чтобы получить скалярное произведение двух векторов. (a.b = |a|.|b|.Cosθ). Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.
Почему скалярное произведение называется скалярным умножением векторов?
Скалярное произведение называется скалярным умножением векторов, поскольку все отдельные составляющие ответа являются скалярными величинами. В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные величины. Следовательно, скалярное произведение также называют скалярным умножением векторов.
В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные величины. Следовательно, скалярное произведение также называют скалярным умножением векторов.
Почему мы используем косинус в скалярном умножении векторов?
Чтобы найти скалярное произведение векторов, нам нужно, чтобы два вектора a, b были направлены в одном направлении. Поскольку векторы a и b расположены под углом друг к другу, значение acosθ является компонентом вектора a в направлении вектора b. Следовательно, мы находим cosθ в скалярном произведении или скалярном умножении двух векторов.
Что такое векторное умножение векторов?
Перемножение двух векторов при умножении дает третий вектор, перпендикулярный двум исходным векторам. Величина результирующего вектора определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. a × b = c, где c — перекрестное произведение или векторное произведение двух векторов a и b.
Что такое скалярное умножение и векторное умножение векторов?
Векторы можно умножать двумя разными способами: точечным произведением и перекрестным произведением. Результаты обоих этих умножений векторов различны. Скалярное умножение векторов или скалярное произведение дает в результате скалярную величину, тогда как векторное умножение векторов или перекрестное произведение дает векторную величину. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).
Результаты обоих этих умножений векторов различны. Скалярное умножение векторов или скалярное произведение дает в результате скалярную величину, тогда как векторное умножение векторов или перекрестное произведение дает векторную величину. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).
В чем разница между скалярным умножением и векторным умножением векторов?
При умножении векторов скалярное умножение векторов или скалярное произведение исходных векторов дает скалярную величину, тогда как векторное умножение двух векторов или перекрестное произведение двух векторов дает векторную величину. Скалярное произведение — это произведение величины векторов на косинус угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
а × б = | а | |б| грех θ.
Что такое правило большого пальца правой руки для перекрестного произведения векторов?
Правило правой руки для векторного произведения двух векторов помогает определить направление результирующего вектора. Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора.
Объяснение урока: Скалярное умножение и единичные векторы
В этом объяснении мы узнаем, как умножить вектор на скаляр и как найти единичный вектор в Направление любой заданный вектор путем деления вектора на скаляр.
Вектор — это величина, которая имеет как величину, так и направление. Совокупность этих признаков делает
вектор универсальный инструмент, который имеет множество применений. Некоторые примеры
включать описание положения точки в
пространстве относительно другой точки и выражает скорость движущегося тела.
Векторы часто выражаются путем соотнесения их с набором координат и, следовательно, имеют более чем один компонент. А Трехмерный вектор ⃑𝑉 часто выражается в декартовых координатах. 𝑥, 𝑦 и 𝑧, ⃑𝑉=(𝑥,𝑦,𝑧), или используя единичные векторы, ⃑𝑉=𝑥⃑𝑖+𝑦⃑𝑗+𝑧⃑𝑘.
В отличие от этого, скаляр — это величина, величина которой но без направления. Скаляр часто может быть представлен по одному номеру, без дополнительной информации.
Перемножить два скаляра просто, но в этом объяснении мы собираемся изучить скалярное умножение числа вектор. Как следует из названия, это включает в себя умножение вектора на скаляр.
Рассмотрим частицу, движущуюся со скоростью ⃑𝑉. Если частица продолжает двигаться в том же направлении, но ее скорость удваивается по величине, как мы можем описать это? Простой ответ: 2⃑𝑉. Поскольку мы умножили скаляр на вектор, это пример скалярного умножения.
Давайте посмотрим, как это относится к компонентам вектора.
Определение: скалярное умножение
Умножение скаляра на вектор известно как скалярное умножение.
Рассмотрим вектор ⃑𝑉 и скаляр 𝑘: ⃑𝑉=(𝑥,𝑦,𝑧).
При скалярном умножении скаляр может быть распределен по компонентам вектора: 𝑘⃑𝑉=𝑘(𝑥,𝑦,𝑧)=(𝑘𝑥,𝑘𝑦,𝑘𝑧).
Результат скалярного умножения также является вектором, где величина исходного вектора умножается на значение, представленное скаляром.
Мы рассмотрим простой пример, прежде чем перейти к более интуитивным интерпретациям скалярного умножения.
Пример 1. Умножение двумерного вектора на скаляр
Учитывая, что ⃑𝐴=(−1,−8), найти 3⃑𝐴.
Ответ
На этот вопрос нам дали двумерный вектор и попросили выполнить умножение на скалярную величину числа 3.
Чтобы сделать это, мы можем просто умножить оба 𝑥
и 𝑦 компонента вектора по заданному
скаляр:
3⃑𝐴=3(−1,−8)=(3(−1),3(−8))=(−3,−24).
С некоторым упрощением мы находим, что наш результат — вектор с 𝑥 компонент −3 и 𝑦 составляющая −24.
Обратите внимание, что вектор 3⃑𝐴 имеет то же направление, что и ⃑𝐴, но его величина теперь больше, поскольку была масштабирована на коэффициент 3.
Приведенный выше вопрос дает нам численный пример скалярного умножения на положительное число. Так как векторы часто изображаются в виде стрелок, давайте взглянем на некоторые наглядные примеры.
Как мы видели, умножение вектора на положительную скалярную величину не изменить направление результирующего вектора, но масштабирует его величину.
Рассмотрим визуальное представление вектора ⃑𝑉, при различных формах скалярного умножения.
Обратите внимание на часть (A) схемы. Умножающий вектор
⃑𝑉
на 1 даст нам тот же результат, что и исходный
вектор, а его величина останется неизменной; однако, умножая на 3
увеличит магнитуду в 3,9 раза. 0003
0003
Раздел (B) диаграммы показывает, что важно понимать, что умножение вектора на отрицательное число меняет направление . Рассмотрим простейший случай, когда вектор ⃑𝑉 умножается на −1. Величина вектор останется неизменным, но его направление изменится на противоположное так как все компоненты меняют знак: ⃑𝑉=(𝑥,𝑦)−⃑𝑉=(−𝑥,−𝑦).
Умножение на отрицательное число, отличное от −1 изменит направление, а также масштабирует величину вектора.
Наконец, для части (C) диаграммы мы отмечаем, что скалярное умножение не ограничивается целыми числами или числами которые больше 1. Если величина скаляра меньше 1, скалярное умножение приведет к вектору с меньшей величиной (или меньшей длиной), чем оригинал.
Пример 2. Умножение двумерного вектора на скаляр Графически
⃑𝐴 представлен следующим графиком.
Какой из следующих графиков представляет −2⃑𝐴?
Ответ
Давайте сначала рассмотрим менее формальное решение этой задачи.
Вопрос дает нам вектор ⃑𝐴 и просит нас выполнить скаляр умножение на коэффициент −2. С мы имеем дело с отрицательным скаляром, мы знаем, что эта операция изменит направление нашего исходного вектора.
Вектор ⃑𝐴 имеет начальную точку в начале и его конечной точке в верхнем правом квадранте. Если бы результирующий вектор был чтобы также начать с исходной точки (как видно во всех вариантах), мы знаем, что его конечная точка должен лежать внизу слева квадрант, так как направление обратное.
Единственным графиком, соответствующим этому описанию, является вариант (а), и так что, кажется, это правильный ответ.
Мы также можем рассмотреть величину нашего скаляра. С |−2|=2, вектор, полученный из нашего скаляра умножение будет иметь удвоенную длину оригинала. При визуальном осмотре вариант (а) кажется наиболее подходящим. кейс!
Для дальнейшей проверки нашего решения мы можем использовать более формальный подход. по первому определяющему вектору ⃑𝐴. От нашего
график, мы видим, что начальная точка ⃑𝐴
это начало координат, которое имеет координаты (0,0),
и конечная точка лежит в (1,1). Отсюда следует, что
⃑𝐴=(1,1)−(0,0)=(1,1).
по первому определяющему вектору ⃑𝐴. От нашего
график, мы видим, что начальная точка ⃑𝐴
это начало координат, которое имеет координаты (0,0),
и конечная точка лежит в (1,1). Отсюда следует, что
⃑𝐴=(1,1)−(0,0)=(1,1).
Теперь, когда мы определили вектор ⃑𝐴, мы можем выполнить скалярное умножение следующим образом: −2⃑𝐴=−2(1,1)=(−2(1),−2(1))=(−2,−2).
Как уже упоминалось, все имеющиеся у нас варианты множественного выбора включают вектор, который начинается в начале координат. Если вектор (−2,−2), начинается в начале координат, его конечная точка будет в координатах (−2,−2).
Граф, который соответствует этому описанию, является вариантом (а), и, следовательно, мы подтверждаем, что это правильный ответ.
Еще одна важная концепция, связанная со скалярным умножением.
является единичным вектором. Мы знакомы
с единичными векторами ⃑𝑖,
⃑𝑗, и
⃑𝑘. Это векторы величины 1 в
𝑥-, 𝑦- и
𝑧-направления соответственно.
Это векторы величины 1 в
𝑥-, 𝑦- и
𝑧-направления соответственно.
На самом деле любой вектор длины 1 можно считать единичным вектором! Таким образом, мы можем определить единичный вектор в любой заданном направлении или для любого набора координат. Давайте формально обобщить это понятие.
Определение: единичные векторы
Единичный вектор — это вектор, длина которого равна 1. ⃑𝑉 путем деления вектора на его величину: ⃑𝑣=⃑𝑉‖‖⃑𝑉‖‖.
Напомним, что величина вектора ⃑𝑉=(𝑥,𝑦,𝑧) определяется как ‖‖⃑𝑉‖‖=√𝑥+𝑦+𝑧.
Учитывая приведенное выше определение единичного вектора, мы должны отметить, что эквивалент математическое утверждение ⃑𝑣=⃑𝑉‖‖⃑𝑉‖‖.
Обратите внимание, что величина ‖‖⃑𝑉‖‖ не имеет чувства направления и, следовательно, является скаляром. Это означает, что 1‖‖⃑𝑉‖‖ также является скаляром.
Оглядываясь назад на нашу формулу, мы можем признать, что она включает в себя
умножение скаляра
1‖‖⃑𝑉‖‖
и вектор
⃑𝑉. Процесс поиска единицы
вектор в заданном направлении, следовательно, можно рассматривать как
«частный случай» скалярного умножения!
Процесс поиска единицы
вектор в заданном направлении, следовательно, можно рассматривать как
«частный случай» скалярного умножения!
Вместо умножения вектора на заданный скаляр мы находим скаляр, который даст желаемый результат величина. В случае ⃑𝑉=(𝑥,𝑦,𝑧), наш расчет может выглядеть так: ⃑𝑣=1‖‖⃑𝑉‖‖⃑𝑉=1√𝑥+𝑦+𝑧(𝑥,𝑦,𝑧).
Поскольку скалярное умножение на положительное число не меняет направление вектора, результатом будет новый вектор, который указывает в том же направлении, что и ⃑𝑉 но имеет величину 1. Это определение ⃑𝑉.
В качестве краткого примечания, хотя стандартно используется акцент (или «шляпа»), например 𝑉 для обозначения единичного вектора, вы обычно будет видеть ̂𝑖, ̂𝑗, и ̂𝑘 без этого обозначения. Поскольку эти три единичных вектора широко используются, их часто представлен как просто ⃑𝑖, ⃑𝑗, и ⃑𝑘.
Давайте рассмотрим пример нахождения единичного вектора.
Пример 3. Нахождение единичного вектора по исходному вектору
Нахождение единичного вектора в том же направлении, что и вектор ⃑𝑖−⃑𝑗−⃑𝑘.
Ответ
Этот вопрос дал нам вектор ⃑𝑖−⃑𝑗−⃑𝑘 и попросил нас найти единичный вектор в том же направлении. Это будет — вектор величины 1. Обратите внимание, что нам дано наш вектор через единичные векторы ⃑𝑖, ⃑𝑗, и ⃑𝑘 но это не влияет на метод, который мы будем использовать.
Наш первый шаг — найти величину ⃑𝑖−⃑𝑗−⃑𝑘. Обратите внимание, что хотя отдельные компоненты этого вектора в 𝑥-, 𝑦- и 𝑧-направления все равны 1, это не означает, что сам вектор имеет величину 1: ‖‖⃑𝑖−⃑𝑗−⃑𝑘‖‖=1+(−1)+(−1)=√1+1+1=√3.
Теперь вспомним, что для нахождения единичного вектора некоторого вектора ⃑𝑉, делим на величину: ⃑𝑣=⃑𝑉‖‖⃑𝑉‖‖=1‖‖⃑𝑉‖‖⃑𝑉.
Чтобы найти единичный вектор для данного вопроса,
поэтому мы можем выполнить следующий расчет:
1√3⃑𝑖−⃑𝑗−⃑𝑘=√33⃑𝑖−⃑𝑗−⃑𝑘.
На предыдущих шагах мы выполнили обычную технику рационализации знаменатель, чтобы получить ответ. Эта форма ответа совершенно верна, поскольку она выражает единичный вектор как кратное исходному вектору.
Эквивалентное выражение может быть получено путем умножения отдельных компоненты вектора скаляром: =√33⃑𝑖−√33⃑𝑗−√33⃑𝑘.
В нашем последнем примере мы объединим наши навыки скалярного умножения с другими векторными операциями в для решения задачи об единичных векторах.
Пример 4. Сочетание скалярного умножения, векторных операций и вычислений с единичным вектором
Дано ⃑𝐴=(2,0,−2) а также ⃑𝐵=(1,−1,1), определить единичный вектор в направлении 2⃑𝐵−⃑𝐴.
Ответ
Этот вопрос требует от нас найти единичный вектор в направлении 2⃑𝐵−⃑𝐴, и для этого нам понадобится величина вектора 2⃑𝐵−⃑𝐴.
Чтобы найти эту величину, давайте сначала найдем компоненты числа 2⃑𝐵−⃑𝐴. Для этого потребуется комбинация скаляра
умножение и вычитание векторов:
2⃑𝐵−⃑𝐴=2(1,−1,1)−(2,0,−2).
Для этого потребуется комбинация скаляра
умножение и вычитание векторов:
2⃑𝐵−⃑𝐴=2(1,−1,1)−(2,0,−2).
Мы можем составить уравнение, используя векторы ⃑𝐴 и ⃑𝐵 указано в вопросе. Обратите внимание, что первый член в правой части является скалярным умножением. Скаляр 2 может быть распределяется между компонентами ⃑𝐵. Следующий это, мы сможем выполнить векторное вычитание: 2⃑𝐵−⃑𝐴=(2,−2,2)−(2,0,−2)=(0,−2,4).
Теперь, когда у нас есть компоненты 2⃑𝐵−⃑𝐴, мы можем найти его величину: ‖‖2⃑𝐵−⃑𝐴‖‖=0+(−2)+4=√0+4+16=√20=2√5.
Обратите внимание, что для нашего последнего шага мы упростили нашу величину, взяв коэффициент 2 вне радикала.
Теперь, когда мы нашли компоненты 2⃑𝐵−⃑𝐴 и его величины, мы можем найти единичный вектор в направлении из 2⃑𝐵−⃑𝐴 применяя следующее правило: ⃑𝑣=⃑𝑉‖‖⃑𝑉‖‖=1‖‖⃑𝑉‖‖⃑𝑉.
Чтобы найти наш единичный вектор, мы разделим 2⃑𝐵−⃑𝐴
по своей величине. Другой способ выразить это — умножить
величина, обратная исходному вектору:
1‖‖2⃑𝐵−⃑𝐴‖‖2⃑𝐵−⃑𝐴=12√5(0,−2,4)=√510(0,−2,4)=0,−2√510,4√510= 0,−√55,2√55.
Другой способ выразить это — умножить
величина, обратная исходному вектору:
1‖‖2⃑𝐵−⃑𝐴‖‖2⃑𝐵−⃑𝐴=12√5(0,−2,4)=√510(0,−2,4)=0,−2√510,4√510= 0,−√55,2√55.
После нескольких шагов упрощения мы пришли к нашему ответу.
В заключение, можно выполнить быструю проверку, подтвердив, что наш ответ является вектором величины 1: 0+−√55+2√55=525+2025=2525=1.
Конечно, в данном случае этот шаг необязателен, но иногда может быть полезно при работе с более длинными расчеты.
Давайте обобщим некоторые ключевые моменты, касающиеся скалярного умножения и единичных векторов.
Key Points
- Умножение скаляра на вектор известно как скалярное умножение.
- При выполнении скалярного умножения скаляр может быть распределены по компонентам вектора: 𝑘⃑𝑉=𝑘(𝑥,𝑦,𝑧)=(𝑘𝑥,𝑘𝑦,𝑘𝑧).
- Результат скалярного умножения также является вектором, где умножается величина исходного вектора
значением, представленным скаляром.

- Если скаляр является положительным числом, результирующий вектор имеет то же направление, что и исходный. Когда скаляр отрицателен, результирующий вектор находится в направлении, противоположном исходному.
- Единичный вектор — это вектор, длина которого равна 1.
- Мы можем найти единичный вектор, обозначаемый ⃑𝑣, в сторону ⃑𝑉 путем деления исходного вектора на его величину: ⃑𝑣=⃑𝑉‖‖⃑𝑉‖‖=1‖‖⃑𝑉‖‖⃑𝑉.
Умножение векторов — Nexus Wiki
До сих пор мы сосредоточились на том, как складывать и вычитать векторы. Это просто, поскольку векторы — это математические структуры, которые ведут себя как пространственные смещения. Добавление означает просто выполнение одного за другим, точно так же, как прохождение последовательных смещений. Вычитание означает изменение направления (умножение на -1) и сложение. Но можем ли мы умножать векторы?
Оказывается, мы можем, и что различные способы умножения векторов служат для выделения физически существенных элементов пар векторов, которые объединяются для получения важного физического результата. Два примера включают:
Два примера включают:
- Концепция работы — когда сила перемещает объект, что приводит к изменению его энергии движения (кинетической энергии). В этом случае имеет значение та часть силы, которая направлена вдоль (или против) смещения. (Требуется скалярное произведение)
- Понятие крутящего момента — когда сила перемещает объект, заставляя его вращаться вокруг центра на некотором расстоянии. В данном случае имеет значение та часть силы, которая перпендикулярна смещению к центру вращения. (Требуется перекрестное произведение)
Мы предпочитаем вводить математику там, где это необходимо, поэтому мы будем обсуждать концептуальные идеи, лежащие в основе точечного и перекрестного произведений, когда мы будем обсуждать работу (и теорему о работе-энергии) и вращательное движение. Здесь мы представляем математические определения точечных и перекрестных произведений, которые служат справочными материалами, когда эти темы представляются в контексте физики.
Математика умножения матриц
Предположим, у нас есть два трехмерных вектора, которые мы запишем в виде троек $(a_x, a_y, a_z)$ и $(b_x, b_y, b_z)$, опустив пока $\hat{i }, \hat{j}$ и $\hat{k}$, определяющие направления $x$, $y$ и $z$ соответственно. Можем ли мы перемножить эти векторы?
Можем ли мы перемножить эти векторы?
Каждый вектор состоит из трех чисел, поэтому в принципе мы можем умножать их девятью разными способами. Мы могли бы создать девять продуктов $a_xb_x, a_xb_y, a_xb_z, a_yb_x,..,a_zb_z$. Это в значительной степени математический ответ, но нас интересует не просто «что мы можем сделать», а «что имеет физический смысл». Оказывается, комбинации этих девяти продуктов имеют важное физическое значение.
Скалярный продукт
Комбинация произведений трех пар
$$\overrightarrow{a} \cdot \overrightarrow{b} = a_xb_x + a_yb_y + a_zb_z $$
оказывается хорошим (если это удивительно) свойство, что на самом деле это скаляр : то есть изменение нашего выбора осей изменяет каждое из чисел, которые входят в это вычисление, но комбинация остается прежней! (Это верно даже в том случае, если мы находимся в 2D и имеем только первые два члена.) Эта комбинация называется 9.1319 скалярное произведение двух векторов. Он возникает, когда мы хотим взять компонент одного вектора в направлении другого.
Он возникает, когда мы хотим взять компонент одного вектора в направлении другого.
Физически скалярное произведение полезно, когда мы хотим использовать часть второго закона Ньютона, которая говорит нам о том, как объект меняет свою скорость. Мы знаем, что силы, действующие в направлении движения или против него, изменяют скорость — силы, перпендикулярные движению, изменяют только направление. Итак, мы хотим взять скалярное произведение векторной формы второго закона Ньютона со скоростью (или смещением). Это дает теорему о работе и энергии, ключ к нашему развитию концепции энергии.
Скалярное произведение также появляется, когда мы хотим рассчитать поток через поверхность, которая не перпендикулярна к ней. Только поток, перпендикулярный поверхности (в том же направлении, что и нормаль к поверхности), пропускает жидкость. Поток, параллельный поверхности (перпендикулярный нормали к поверхности), просто течет жидкость параллельно поверхности.
Перекрестное произведение
Другие комбинации наших 9 произведений из наших двух векторов могут быть объединены для создания вектора, известного как перекрестное произведение . Компонент x вектора состоит из компонентов y и z двух векторов и так далее, например:
Компонент x вектора состоит из компонентов y и z двух векторов и так далее, например:
$$(\overrightarrow{a} \times \overrightarrow{b})_x = a_yb_z — a_zb_y $ $
$$(\overrightarrow{a} \times \overrightarrow{b})_y = a_zb_x — a_zb_x $$
$$(\overrightarrow{a} \times \overrightarrow{b})_z = a_xb_y — a_yb_x $ $
Эти три комбинации ведут себя как компоненты вектора, когда мы меняем системы координат. (Хотя они ведут себя иначе, когда вы смотрите на них в зеркало.)
Перекрестное произведение используется в физике, когда нам нужна составляющая вектора, перпендикулярная другому вектору, например, когда мы рассматриваем силы, воздействующие на протяженные объекты. Составляющая силы, направленная вдоль линии от точки вращения, пытается растянуть или сжать объект, но не стремится повернуть его вокруг точки вращения. Только компонент, перпендикулярный линии от точки опоры, стремится повернуть объект. Это мотивация для введения понятия крутящего момента. Взаимное произведение также появляется при построении магнитных сил.
А что насчет остальных?
Мы нашли полезными 4 комбинации произведений компонент вектора, но начали с 9 объектов. Разве не должно быть еще 5 комбинаций? На самом деле есть. Они образуют не скаляр и не вектор, а нечто иное — симметричную бесследовую матрицу. Эти математические структуры полезны при преобразовании векторов, но выходят за рамки этого класса. Их изучение — это шаг в математику, известную как тензорный анализ 9.0564 . Это полезно для понимания того, как квантовые электронные орбитали сочетаются в химии и передовой механике. Такого рода рассуждения также играют важную роль в специальной и общей теориях относительности Эйнштейна.
Для получения более подробной информации о точечных и перекрестных произведениях читайте последующие страницы.
Joe Redish 06.11.11
Вектор координат
Марко Табога, доктор философии
В векторном пространстве любой вектор можно представить в виде линейной комбинации
основа. Коэффициенты линейной комбинации называются координатами
вектора относительно базиса.
Коэффициенты линейной комбинации называются координатами
вектора относительно базиса.
Table of contents
Motivation
Definition
Examples
Example 1
Example 2
Addition of coordinate vectors
Multiplication of координатные векторы скалярами
Числовые массивы являются координатными векторами относительно канонического базиса
Решенные упражнения
Упражнение 1
Упражнение 2
Мотивация
Ранее мы предоставили два определения векторного пространства:
неформальное определение: вектор — это конечный массив чисел, и множество таких массивы называются векторным пространством тогда и только тогда, когда они замкнуты относительно принимать линейные комбинации;
формальное определение: векторное пространство — это множество, снабженное двумя операциями, называется векторным сложением и скалярным умножением, которые удовлетворяют ряду аксиомы.

Более простое неформальное определение вполне совместимо с более формальным. определение, как множество числовых массивов удовлетворяет всем свойствам векторное пространство при условии, что векторное сложение и скалярное умножение определяется обычным образом и что множество замкнуто относительно линейных комбинации.
Теперь мы вводим новое понятие, понятие вектора координат, которое делает два определения почти эквивалентны: если мы имеем дело с рефератом векторное пространство , но его размерность конечна и мы можем идентифицировать базис для пространства, то мы можем записать каждый вектор в виде линейной комбинации основы; как следствие, мы можем представить вектор как массив , называемый вектором координат, который содержит коэффициенты линейная комбинация.
Как только мы получили это простое представление, мы можем применить обычные правила
матричной алгебры к координатным векторам, даже если мы имеем дело с
абстрактное векторное пространство.
Это не только очень удобно, но и стирает различия между двумя подходы к определению векторов и векторных пространств (по крайней мере, для конечномерный случай).
Определение
Теперь мы готовы дать определение вектора координат.
Определение Позволять — конечномерное линейное пространство. Позволять быть основой для . Для любого , взять уникальный набор скаляры такой чтоЗатем, в векторис называется координатным вектором по отношению к основе .
Заметим, что единственность скаляров гарантируется уникальность представления в терминах базиса.
Примеры
Приведем несколько примеров.
Пример 1
Позволять быть векторным пространством и основу для него.
Предположим, что вектор можно записать в виде линейной комбинации базиса как следует:
Тогда координатный вектор в отношении
Пример 2
Рассмотрите пространство
второго порядка
полиномыгде
коэффициенты
и аргумент
являются скалярами.
Как мы уже говорили в лекции о линейные пространства, является векторным пространством при условии, что сложение полиномов и их умножение на скаляры производится обычным образом.
Рассмотрим полиномы
Эти три полинома образуют базис за потому что они линейны независимыми (никакая их комбинация не равна нулю ни при каком ) и их можно линейно комбинировать так, чтобы получить любой формы выше:
Координатный вектор относительно базиса, который мы только что нашли is
Сложение векторов координат
Добавление двух векторов можно выполнить, выполнив обычный операция сложения векторов на соответствующие им координатные векторы.
Предложение Позволять быть линейным пространством и основа для . Позволять . Тогда координатный вектор относительно базиса равна сумме координатных векторов а также по тому же основанию, что есть,
Доказательство
Предположим, что представления в терминах основа так что координатные векторы по коммутативные и дистрибутивные свойства векторного сложения и скалярного умножение в абстрактных векторных пространствах, мы имеем чтоТаким образом, координатный вектор is
Умножение векторов координат на скаляры
Умножение вектора на скаляр можно выполнить, выполнив
обычная эксплуатация
умножение
скаляром на его координатном векторе.
Предложение Позволять быть линейным пространством и основа для . Позволять и разреши быть скаляром. Тогда координатный вектор по базе равен произведению и координатный вектор , что есть,
Доказательство
Предположим, что представление в терминах основа иссо что вектор координат это по ассоциативные и дистрибутивные свойства скалярного умножения в абстрактные векторные пространства, мы имеем чтоТаким образом, координатный вектор
Числовые массивы являются координатными векторами относительно каноническая основа
Когда элементы линейного пространства представляют собой одномерные массивы чисел (векторы в простейшем смысле терм), то они совпадают со своими координатными векторами относительно стандартная основа.
Пример
Позволять
быть пространством всех
векторы-столбцы. Позволять
— его каноническая основа, где
вектор, элементы которого все
,
кроме
-й,
что равно
:
Брать
Любые
Затем,
совпадает с его вектором координат относительно базиса
,
что
это потому что
Позволять
— его каноническая основа, где
вектор, элементы которого все
,
кроме
-й,
что равно
:
Брать
Любые
Затем,
совпадает с его вектором координат относительно базиса
,
что
это потому что
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Позволять — векторное пространство всех полиномов третьего порядка.
Выполнить сложение двух многочленыandby используя их координатные векторы относительно базис
Убедитесь, что результат тот же, что и при суммировании двух полиномы напрямую.
Раствор
Представления в терминах основы Таким образом, два координатных вектора их сумма иссо что это тот же результат, который мы получаем, выполняя добавление напрямую:
Упражнение 2
Позволять
быть пространством всех
векторы.
Рассмотрим основу где
Найдите координатный вектор с отношении к данному основанию.
Решение
У нас есть чтоПоэтому, координатный вектор
Как указывать
Пожалуйста, указывайте как:
Taboga, Marco (2021). «Координатный вектор», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/координата-вектор.
Скалярное умножение | Математика и физика для начинающих программистов игр
Я уверен, что уже много лет вы умножаете скаляры на другие скаляры. Помните, скалярная величина — это просто обычное число. Давайте обратим наше внимание на скаляр, умноженный на вектор. Если вы думаете о векторе, выраженном в полярных координатах, все, что у вас есть, это величина и направление. Когда вы умножаете скаляр на этот вектор, все, что вы на самом деле делаете, — это меняете величину, увеличивая или уменьшая ее. Если скалярное значение является целым числом, величина становится больше. Точно так же, если скаляр меньше 1, величина становится меньше.
Точно так же, если скаляр меньше 1, величина становится меньше.
Скалярное умножение в полярных координатахдля любого скаляра c и вектора . |
Пример 4.10: Скаляр * вектор в полярных координатах
Рассчитайте 5a, если вектор a = 3ft @ 22.
Раствор
5a = 5 (3ft @ 22) = 15ft @ 22
,
5a = 5 (3ft @ 22) = 15ft @ 22
6
, но и » @ 22
6, 40006, но и » @ 22
, но и » @ 22
, но и » @ 22
,
,
5a = 5 (3ft @ 22) = 15ft @ 22
, потому что вы. Пытаясь визуализировать влияние скалярного умножения на вектор, взгляните на рис. 4.17.
Рисунок 4.17. 2 * вектор A.
Помните, что векторы часто представляются стрелками, длина которых соответствует величине, а то, как указывает вектор, указывает направление. Как видите, вектор 2А в два раза длиннее вектора А, но по-прежнему указывает в том же направлении.
Если вы уже настроены для программирования вектора и он находится в декартовых координатах, вы все равно можете выполнять скалярное умножение без обратного преобразования в полярные координаты. Просто умножьте каждый компонент на скалярное значение, и это будет иметь тот же эффект.
Скалярное умножение в декартовых координатахдля любого скаляра c и вектора . |
Пример 4.11: Скаляр * Вектор в декартовых координатах
Вычислить A, если вектор .
Решение
Довольно часто в программировании вы будете слышать термин нормализация . На самом деле это просто красивое слово для масштабирования величины вектора до 1. Довольно часто вектор используется, чтобы просто установить направление. На самом деле, и являются прекрасными примерами этого. На самом деле это просто вектор длиной в одну единицу в положительном направлении x. Точно так же это вектор с величиной 1 в положительном направлении y. В следующих разделах вы увидите приложения, в которых для определения направления используется вектор длины 1.
Точно так же это вектор с величиной 1 в положительном направлении y. В следующих разделах вы увидите приложения, в которых для определения направления используется вектор длины 1.
Нормировать вектор в полярных координатах очень просто. Просто измените величину на 1 и оставьте направление прежним. Однако в контексте программирования вектор, скорее всего, будет в декартовых координатах, прежде чем вам потребуется его нормализовать. В этом случае вы должны сначала вычислить величину вектора, а затем разделить каждую составляющую на величину. По сути, вы выполняете скалярное умножение на 1 по величине.
Нормализация двумерного векторадля любого вектора A = [a 1 a 2 ]. |
Этот процесс еще чаще происходит в 3D.
Нормализация трехмерного вектора для любого вектора A = [a 1 a 2 a 3 ]. |
ПРИМЕЧАНИЕ
Символом нормализованного вектора является заглавная буква. Например, когда A имеет величину 1, ее можно записать как .
Пример 4.12: Нормализация вектора
Нормализация вектора A = [5 0 12].
Решение
Первое, что вам нужно найти, это величина A. (Вам может понадобиться обратиться к разделу «Полярные координаты в сравнении с декартовыми координатами» ранее в этой главе.)
Теперь что вы знаете величину, все, что осталось сделать, это разделить каждую составляющую на нее:
ПРИМЕЧАНИЕ
Чтобы проверить себя, вы всегда можете рассчитать . Он всегда должен быть равен 1, если вы правильно нормализовали.
Как видите, скалярное умножение приводит к увеличению или уменьшению величины вектора. Направление всегда остается одним и тем же; меняется только величина. Кроме того, процесс нормализации — отличный пример скаляра, умноженного на вектор.


 \)
\)
 ..Проекция точки на плоскость
..Проекция точки на плоскость
 Измерение площадей и объемов
Измерение площадей и объемов
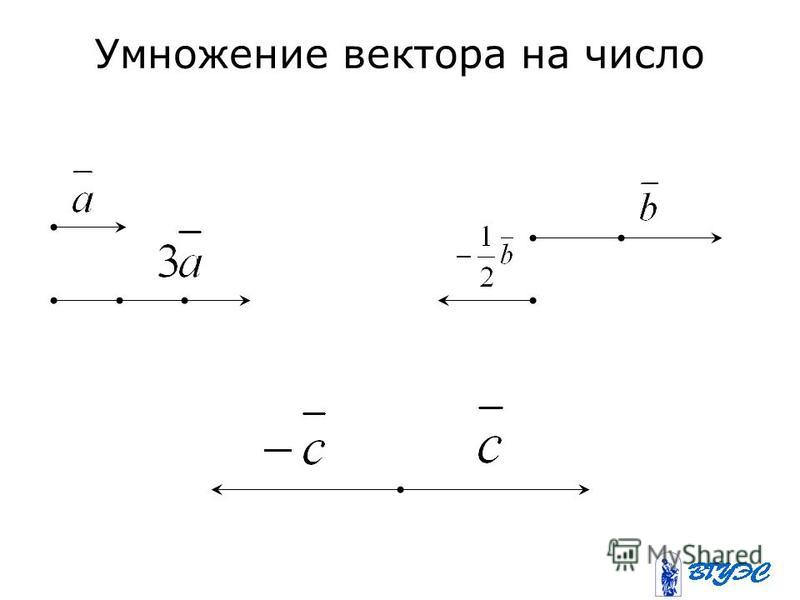 .Свойства символов Веблена
.Свойства символов Веблена

 Условия
параллельности и перпендикулярности
прямых, вычисление угла между двумя
прямыми, расстояния от точки до прямой.
Условия
параллельности и перпендикулярности
прямых, вычисление угла между двумя
прямыми, расстояния от точки до прямой. 