|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности… Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Интересное: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным. Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 4 из 5Следующая ⇒ При решении инженерных задач достаточно часто приходится сталкиваться с решением систем линейных алгебраических уравнений (СЛАУ). СЛАУ называется совместной, если имеет хотя бы одно решение, и несовместной, если не имеет ни одного решения. Таким образом, решить СЛАУ – значит определить, является ли она совместной или нет. Существуют точные и приближенные (итерационные) методы решения СЛАУ. К точным относятся методы, которые дают точное решение задачи после конечного числа арифметических и логических операций. К указанным методам относятся, например, матричный метод, метод Крамера, метод Гаусса и т. д. К приближенным – метод Якоби, метод Гаусса – Зейделя и др. Для определения совместности системы можно использовать теорему Кронекера-Капелли, согласно которой для того, чтобы СЛАУ была совместной, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу ее расширенной матрицы. Напомним, что расширенная матрица получается после дополнения матрицы коэффициентов столбцом свободных членов. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решение. На рис. 5.1 представлен пример исследования на совместность следующей системы уравнений:
Рис. 5.1. Пример исследования на совместность заданной СЛАУ. В результате исследования получили, что ранг расширенной матрицы равен рангу матрицы коэффициентов СЛАУ, следовательно, данная система совместна. При этом ранг совместной системы равен числу неизвестных, поэтому система имеет единственное решение. Рассмотрим точные методы решения СЛАУ в системе MATLAB. Одним из таких методов является матричный метод решения СЛАУ, который предусматривает выполнение следующих шагов: 1. Убедиться в том, что система не является вырожденной (определитель ее не равен нулю), т. е. существует обратная матрица. 2. Найти обратную матрицу . 3. Найти вектор – столбец X, вычислив произведение . На рис. 5.2 приводится пример решения представленной выше системы уравнений с помощью матричного метода.
Рис. 5.2. Пример решения СЛАУ с помощью матричного метода.
Рассмотренный матричный метод решения требует определения обратной матрицы, для вычисления которой требуется значительное время, поэтому на практике данный метод не применяется.
В основе решения СЛАУ с помощью формул Крамера лежит теорема Крамера: система n уравнений с n неизвестными, определитель которой отличен от нуля всегда имеет решение, и притом единственное.
Пусть дана система n линейных уравнений с n неизвестными:
Обозначим определитель системы: . Заменим поочередно столбцы коэффициентов при на столбец свободных членов и получим n определителей: .
Формулы Крамера для решения системы уравнений имеют вид: .
Решение СЛАУ из предыдущего примера с помощью формул Крамера представлено на рис. 5.3.
Рис. 5.3. Пример решения СЛАУ с помощью формул Крамера.
Вычисление определителей, используемое в методе Крамера, занимает очень много времени, поэтому этот метод также редко используется на практике.
Существо метода Гаусса состоит в последовательном исключении неизвестных. Этот метод в MATLAB реализован в функции rref(), которая на его основании осуществляет приведение расширенной матрицы к треугольной форме. Пример ее применения для решения СЛАУ представлен на рис. 5.4.
Рис. 5.4. Пример решения СЛАУ с помощью метод Гаусса с частичным выбором главного элемента.
Как было сказано выше, помимо точных методов решения СЛАУ существует ряд итерационных методов. Одним их них является метод наименьших квадратов , реализованный в системе MATLAB функцией lsqr().
На рис. 5.5 приведен пример решения СЛАУ с использованием функции lsqr(A, B). В данном примере процесс итераций сходится на четвертом шаге с относительным остатком (отношением вторых норм векторов невязки и свободных членов) 1.7∙10
Рис. 5.5. Пример решения СЛАУ методом наименьших квадратов.
Помимо рассмотренных методов решения СЛАУ в MATLAB реализован еще ряд методов решения с помощью функций, расположенных в ядре системы.
Рис. 5.6. Пример решения СЛАУ. ⇐ Предыдущая12345Следующая ⇒ Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого. |
I.5. Исследование неоднородных систем линейных алгебраических уравнений
(схема 18)
Пусть задана неоднородная система линейных алгебраических уравнений размерности m×n. Матрицаназывается
расширенной матрицей системы, если наряду с коэффициентами при
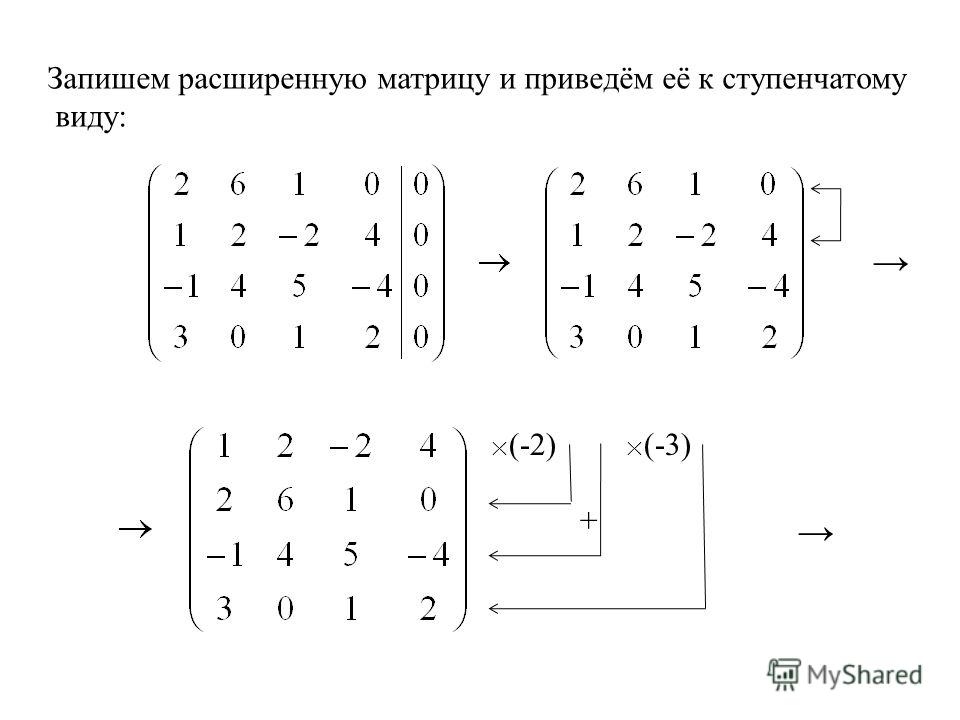
неизвестных, она содержит столбец свободных членов. Следовательно, размерность Исследование любой системы линейных алгебраических уравнений начинается с преобразования ее расширенной матрицы методом Гаусса, который основан на следующих элементарных преобразованиях: – перестановка строк матрицы; – умножение строк матрицы на действительное отличное от руля число; – поэлементное сложение строк матрицы; – вычеркивание нулевой строки; – транспонирование матрицы (в этом случае
преобразования производятся по
столбцам). Элементарные преобразования приводят первоначальную систему к системе, ей эквивалентной. Системы называются эквивалентными, если они имеют одно и то же множество решений. Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Элементарные преобразования ранга матрицы не меняют. На вопрос о наличии решений у неоднородной системы линейных уравнений отвечает следующая теорема. Теорема 1.3 (теорема Кронекера-Капелли). Неоднородная система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу ее главной матрицы, то есть Обозначим количество строк, оставшихся в матрице после метода Гаусса, через r (соответственно, в системе остается r уравнений). Эти строки матрицы называются базисными. Если r=n, то
система имеет единственное решение (является совместной определенной), ее
матрица элементарными преобразованиями приводится к треугольному виду. Если r<n (количество переменных в системе больше количества уравнений), матрица элементарными преобразованиями приводится к ступенчатому виду. Такая система имеет множество решений и является совместной неопределенной. В данном случае для нахождения решений системы необходимо выполнить ряд операций. 1. Оставить в левых частях уравнений системы r неизвестных (базисные переменные), остальные n—r неизвестных перенести в правые части (свободные переменные). После разделения переменных на базисные и свободные система принимает вид: . (1.10) 2. Из коэффициентов при базисных переменных составить
минор (базисный минор), который должен быть отличен от нуля. 3. Если базисный минор системы (1.10) равен нулю, то одну из базисных переменных следует заменить на свободную; полученный базисный минор снова проверить на отличие от нуля. 4. Применяя формулы (1.6) метода Крамера, считая правые части уравнений их свободными членами, найти выражение базисных переменных через свободные в общем виде. Полученный при этом упорядоченный набор переменных системы является ее общим решением. 5. Придавая свободным переменным в (1.10) произвольные значения, вычислить соответствующие значения базисных переменных. Получаемый при этом упорядоченный набор значений всех переменных называется частным решением системы, соответствующим данным значениям свободных переменных. Система имеет бесконечное множество частных решений. 6. Получить базисное решение системы – частное решение, получаемое при нулевых значениях свободных переменных. Заметим, что количество базисных наборов
переменных системы (1. Пусть строки матрицы обозначены соответственно l1;l2;…;ln. Строка l называется линейной комбинацией строк l1;l2;…;ln матрицы, если она равна сумме произведений этих строк на произвольные действительные числа, то есть ,. Однородная система уравнений всегда совместна, так как
имеет хотя бы одно – нулевое (тривиальное) решение. Для того чтобы однородная
система n линейных уравнений с n переменными имела ненулевые решения, необходимо и
достаточно, чтобы ее главный определитель ∆ был равен нулю. Теорема 1.4. Общее решение неоднородной системы уравнений представляет собой сумму общего решения соответствующей однородной системы и некоторого частного решения неоднородной системы уравнений Пример 1.7. Исследовать заданную систему уравнений и найти одно частное решение: . Решение. Выпишем расширенную матрицу системы и применим к ней элементарные преобразования: Так как r(A)=2 и , то по теореме 1. Вспомогательные определители . По формулам (1.6) имеем . Данное выражение базисных переменных через свободные представляет собой общее решение системы: . При конкретных значениях свободных переменных из общего решения получаем частное решение системы. Например, частное решение соответствует значениям свободных переменных x3=x4=17. При x3=0 x4=0 получаем базисное решение системы Вопросы для самопроверки |
Системы линейных алгебраических уравнений Ø Виды систем линейных
Системы линейных алгебраических уравнений Ø Виды систем линейных алгебраических уравнений (СЛАУ) Ø Решение СЛАУ в матричном виде Ø Решение СЛАУ методом Крамера Ø Решение СЛАУ методом Гаусса Ø Решение СЛАУ в общем случае
Системы линейных алгебраических уравнений Пусть задана система, состоящая из m уравнений с n неизвестными вида: (1) где а — заданные числа, — неизвестные
Системы линейных алгебраических уравнений Систему (1) можно записать в виде или Решением системы (1) называется такая совокупность чисел при подстановки которых каждое уравнение системы обращается в верное тождество
Системы линейных алгебраических уравнений Система (1) называется совместной, если у нее существует решение. Если решения нет, то система называется несовместной. Система, имеющая единственное решение называется определенной. Если система имеет более одного решения, то она называется неопределенной Система (1) называется однородной, если все свободные члены в ней равны нулю. В противном случае она называется неоднородной.
Если решения нет, то система называется несовместной. Система, имеющая единственное решение называется определенной. Если система имеет более одного решения, то она называется неопределенной Система (1) называется однородной, если все свободные члены в ней равны нулю. В противном случае она называется неоднородной.
Решение СЛАУ в матричном виде Коэффициенты при неизвестных в уравнениях системы (1) образуют матрицу размера которую обозначим и назовем матрицей системы (1).
Решение СЛАУ в матричном виде Вектор — столбец неизвестных системы (1): Вектор — столбец свободных членов системы (1):
Решение СЛАУ в матричном виде Рассмотрим произведение матриц: Таким образом систему (1) можно записать в матричном виде:
Решение СЛАУ в матричном виде Рассмотрим случай, когда m=n, то есть количество уравнений в системе (1) равно количеству неизвестных. Матрица системы А – квадратная матрица порядка n.
Решение СЛАУ в матричном виде Будем считать, что матрица А – невырожденная матрица, то есть Пусть система записывается в матричном виде (2) У матрицы А существует, причем единственная матрица. Умножим слева обе части уравнения (2) на матрицу. (3)
Умножим слева обе части уравнения (2) на матрицу. (3)
Решение СЛАУ в матричном виде Если задано матричное уравнение вида: (4) , то для его решения умножим обе части уравнения (4) справа на матрицу. (5)
Решение СЛАУ методом Крамера Рассмотрим невырожденную линейную систему алгебраических уравнений в матричном виде где А – квадратная матрица порядка n и Решение системы:
Решение СЛАУ методом Крамера Таким образом, имеем:
Решение СЛАУ методом Крамера Составим определитель , который получается из определителя путем замены первого столбца столбцом из свободных членов
Решение СЛАУ методом Крамера Составим определитель , который получается из определителя путем замены n -ого столбца столбцом из свободных членов
Решение СЛАУ методом Крамера Таким образом, была доказана следующая теорема Пусть — определитель матрицы системы А и — определитель матрицы, полученной из матрицы А заменой j-ого столбца столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам Крамера
Тогда, если , то система имеет единственное решение, определяемое по формулам Крамера
Решение СЛАУ методом Гаусса Метод последовательного исключения неизвестных Этот метод заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних по номеру элементов находятся все остальные элементы
Решение СЛАУ в общем случае Пусть дана произвольная система m линейных уравнений с n неизвестными (1)
Решение СЛАУ в общем случае Рассмотрим для системы (1) матрицу системы А и расширенную матрицу , дополненную столбцом свободных членов
Решение СЛАУ в общем случае Исследуем систему (1) на совместность Для того, чтобы система (1) была совместна необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы
Решение СЛАУ в общем случае Из теоремы Кронекера-Капелли следует: 1. Если , то система (1) несовместна, то есть не имеет решения. 2. Если (n – число неизвестных системы), то система имеет единственное решение, которое можно найти, например, по формулам Крамера. 3. 3. Если , то система (1) имеет бесконечно много решений.
Если , то система (1) несовместна, то есть не имеет решения. 2. Если (n – число неизвестных системы), то система имеет единственное решение, которое можно найти, например, по формулам Крамера. 3. 3. Если , то система (1) имеет бесконечно много решений.
Пример Исследовать систему на совместность система несовместна
Решение систем линейных неоднородных уравнений Алгоритм построения общего решения неоднородной системы 1. Вычислить и и установить совместность системы (1). Пусть. 2. 2. Выделим в матрице А базисный минор: 3. (считаем, что он расположен в левом верхнем углу матрицы А)
Решение систем линейных неоднородных уравнений 3. Рассмотрим уравнения системы (1), соответствующие базисному минору. Их будет r. 4. Неизвестные , коэффициенты которых соответствуют базисному минору, назовем базисными. Неизвестные назовем свободными.
Решение систем линейных неоднородных уравнений 5. Запишем уравнения системы (1), соответствующие базисному минору, в виде: слагаемые с базисными переменными оставим в левой части, а слагаемые со свободными переменными перенесем вправо:
Решение систем линейных неоднородных уравнений 6. Обозначим свободные переменные Выразим базисные переменные формулам Крамера через параметры по :
Обозначим свободные переменные Выразим базисные переменные формулам Крамера через параметры по :
Решение систем линейных неоднородных уравнений В результате получим решение системы (1), которое называю общим решением системы. Если придать свободным переменным конкретные числовые значения, то получим частное решение системы (1).
Пример Найти общее и указать некоторое частное решение системы система совместна
Пример Базисный минор: Система из двух уравнений, соответствующих базисному минору: — базисные переменные — свободные переменные
Пример Базисные переменные модели выразим через свободные: Обозначим свободные переменные: Имеем:
Пример Выразим базисные переменные по формулам Крамера через параметры. Общее решение системы
Пример Частное решение системы
90 000 COVID сорвало обучение 1,6 миллиарда учащихся. Вот как школы могут помочь им наверстать упущенное
Вот как школы могут помочь им наверстать упущенноеК октябрю прошлого года Мэг Брайдон увидела ужасные потери, которые пандемия нанесла детям в ее школе. Брайдон был учителем в средней школе Эшвуда в пригороде Мельбурна, Австралия — городе, который провел больше времени в изоляции от COVID-19, чем любой другой город в мире. Школа то и дело закрывалась около семи месяцев.
До пандемии около 10% детей, присоединившихся к Ashwood в возрасте 12 лет, были ниже ожидаемого национального стандарта. Но в последней когорте Брайдон мог видеть, что шокирующие 30% из них отстали. И ущерб оказался еще глубже. Так много детей имели поведенческие или психологические проблемы после самоизоляции, что некоторые из них становились агрессивными, и школа наняла штатного психолога, чтобы помочь. «Количество обращений к ней было астрономическим, — говорит Брайдон.
Подобные сценарии разыгрывались в классах по всему миру. К февралю этого года школы во всем мире были закрыты из-за COVID-19 в среднем на 4,5 месяца, что затронуло примерно 1,6 миллиарда учащихся и привело к тому, что Организация Объединенных Наций назвала крупнейшим нарушением образования в истории. По данным культурной организации ООН ЮНЕСКО, даже спустя 2 года после начала пандемии 48 стран еще не полностью открыли свои школы.
По данным культурной организации ООН ЮНЕСКО, даже спустя 2 года после начала пандемии 48 стран еще не полностью открыли свои школы.
Последствия этих закрытий печальны, но предсказуемы. В богатых странах больше всего отстали обездоленные и уязвимые дети. Больше всего пострадали жители более бедных стран, и миллионы людей вообще никогда не вернутся в школу. По оценкам ЮНЕСКО, нынешнее поколение студентов может потерять 17 триллионов долларов США заработка в течение жизни при текущих значениях из-за отсутствия знаний и навыков. «На самом деле мы говорим о потере поколений», — говорит Маргарет Сакс-Исраэль, руководитель отдела инклюзивного качественного образования в ЮНЕСКО в Бангкоке.
Теперь правительствам и школам необходимо знать, как лучше помочь детям наверстать упущенное, и исследования могут показать путь. За последние 20–30 лет исследователи в области образования, экономики и международного развития накопили значительный объем фактических данных, включая банки рандомизированных контролируемых испытаний, демонстрирующих стратегии, которые эффективны для повышения посещаемости школы и повышения успеваемости. Они показывают, например, что репетиторство — один из самых экономически эффективных способов помочь детям наверстать упущенное. И некоторые страны опираются на эти данные в своих исследованиях COVID-19.ответов, сосредоточив внимание на репетиторстве и других программах, эффективность которых была доказана образовательными исследованиями.
Они показывают, например, что репетиторство — один из самых экономически эффективных способов помочь детям наверстать упущенное. И некоторые страны опираются на эти данные в своих исследованиях COVID-19.ответов, сосредоточив внимание на репетиторстве и других программах, эффективность которых была доказана образовательными исследованиями.
Поколение COVID: как пандемия влияет на детский мозг?
Но эксперты указывают на ряд опасений. Истинные масштабы потерь в обучении во время пандемии еще не ясны; образовательные исследования редко дают простые ответы о том, что делать; и страны могут не использовать эту возможность для осуществления столь необходимых системных изменений. «Каждый раз, когда в мире происходит бедствие, мы возвращаемся к старому нормальному голоданию», — говорит Джон Хэтти, исследователь в области образования из Мельбурнского университета. «Самая большая пародия на COVID — это если мы ничему не научимся».
Более того, масштаб предстоящей задачи огромен. Исследователи и эксперты в области образования обеспокоены тем, что инвестируемые суммы смехотворно недостаточны, учитывая количество студентов, нуждающихся в помощи. «Это настоящее испытание для мирового сообщества», — говорит Кеннет Рассел, специалист по образованию в Детской благотворительной организации ООН ЮНИСЕФ в Нью-Йорке. «И я не думаю, что величина ответа соответствует величине потребности».
Исследователи и эксперты в области образования обеспокоены тем, что инвестируемые суммы смехотворно недостаточны, учитывая количество студентов, нуждающихся в помощи. «Это настоящее испытание для мирового сообщества», — говорит Кеннет Рассел, специалист по образованию в Детской благотворительной организации ООН ЮНИСЕФ в Нью-Йорке. «И я не думаю, что величина ответа соответствует величине потребности».
Несмотря на это, пандемия может в конечном итоге привести к некоторым трансформационным изменениям в образовании, которые улучшат практику и охватят больше учащихся, говорят исследователи. «Я действительно думаю, что это развеяло многие наши предположения об образовании», — говорит Ли Эллиот Мейджор, изучающая социальную мобильность в Эксетерском университете, Великобритания.
Жесткая реклама Концепция использования научных исследований в образовании долго и упорно продавалась. «Основная проблема заключается в том, что многие практики не верят, что это когда-либо станет наукой», — говорит Андреас Шлейхер, возглавляющий управление образования и навыков Организации экономического сотрудничества и развития (ОЭСР) в Париже. От учителей не ожидают, что они просматривают академические журналы, а образовательная политика часто определяется идеологией бюрократов, а не исследованиями, показывающими, что на самом деле работает. «Многие из них используют доказательства, чтобы подтвердить то, что они хотят сделать», — говорит Шлейхер.
От учителей не ожидают, что они просматривают академические журналы, а образовательная политика часто определяется идеологией бюрократов, а не исследованиями, показывающими, что на самом деле работает. «Многие из них используют доказательства, чтобы подтвердить то, что они хотят сделать», — говорит Шлейхер.
Некоторые исследователи и преподаватели десятилетиями пытались изменить эту точку зрения. Они хотят, чтобы образование было больше похоже на медицину, где эффективность лекарства обычно должна быть доказана в ходе рандомизированных контролируемых испытаний, прежде чем оно будет использовано. Сторонники образования, основанного на фактических данных, утверждают, что методы преподавания и обучения также должны быть подтверждены исследованиями, а не использоваться из-за традиций, мнений или последних причуд. Но они признают, что проверить, улучшает ли тот или иной метод результаты обучения, зачастую сложнее, чем проверить, улучшает ли лекарство здоровье.
Студент из Токио получает индивидуальное обучение через прозрачный барьер в августе 2020 года. Фото: Тору Ханай/Bloomberg/Getty
Фото: Тору Ханай/Bloomberg/Getty
В конце 2010 года образование на основе фактических данных получило один из самых больших импульсов, когда правительство Великобритании инвестировало 125 миллионов фунтов стерлингов (156 миллионов долларов США) в повышение стандартов в школах. Это привело к созданию Education Endowment Foundation (EEF), некоммерческой организации в Лондоне, которая с тех пор стала лидером в исследованиях в области образования. Она профинансировала не менее 160 рандомизированных контролируемых испытаний в сфере образования, вероятно, больше, чем любая другая организация в мире. Около половины английских школ приняли участие в этих испытаниях. Инвестиции в EEF «имели волновой эффект во всем мире», — говорит Аннет Боаз, изучающая фактические данные и политику в Лондонской школе гигиены и тропической медицины.
Расцвели и другие базы данных образовательных исследований. Хэтти возглавила ранний новаторский проект по обобщению данных со всего мира о том, что влияет на обучение 1 . Кроме того, Институт педагогических наук Министерства образования США в Вашингтоне, округ Колумбия, поддерживает Информационный центр What Works, источник информации об образовательных программах, эффективность которых доказана тщательными исследованиями. Хэтти утверждает, что с такими базами данных области не нужно больше доказательств — проблема заключается в том, чтобы получить информацию, используемую правительствами и школами. «Мы безнадежны в этом», — говорит он.
Кроме того, Институт педагогических наук Министерства образования США в Вашингтоне, округ Колумбия, поддерживает Информационный центр What Works, источник информации об образовательных программах, эффективность которых доказана тщательными исследованиями. Хэтти утверждает, что с такими базами данных области не нужно больше доказательств — проблема заключается в том, чтобы получить информацию, используемую правительствами и школами. «Мы безнадежны в этом», — говорит он.
Теоретически пандемия может помочь преодолеть этот разрыв. Страны во всем мире хотят знать, как лучше всего инвестировать в восстановление образования, и миллиарды долларов уже вливаются в школы. «Этот момент времени действительно уникален, потому что изменил разговор о доказательствах в образовании», — говорит Нэнси Мэдден, психолог и исследователь из Педагогической школы Университета Джона Хопкинса в Балтиморе, штат Мэриленд. «Людям нужно что-то, что работает, а не просто заниматься бизнесом, как обычно».
Разрушение догмы Жемчужиной ВЭФ является его Инструментарий для преподавания и обучения, который основан на систематических обзорах и мета-анализах исследований, таких как рандомизированные контролируемые испытания, которые протестировали 30 образовательных подходов. Инструментарий переводит результаты в простую для понимания метрику: количество месяцев дополнительного прогресса, достигнутого в среднем за год детьми, получающими вмешательство, по сравнению с аналогичными детьми, не получающими вмешательства. Он также отображает силу лежащих в основе доказательств и стоимость вмешательства (см. «Какие образовательные методы получают высшие оценки?» и go.nature.com/3nbhdzm).
Инструментарий переводит результаты в простую для понимания метрику: количество месяцев дополнительного прогресса, достигнутого в среднем за год детьми, получающими вмешательство, по сравнению с аналогичными детьми, не получающими вмешательства. Он также отображает силу лежащих в основе доказательств и стоимость вмешательства (см. «Какие образовательные методы получают высшие оценки?» и go.nature.com/3nbhdzm).
Источник: EEF
Инструментарий опровергает многие распространенные убеждения, показывая, что умеренное сокращение размера класса (например, с 30 до 20 учеников), ношение школьной формы и группировка детей в соответствии с уровнем успеваемости имеют незначительный эффект, если вообще имеют какое-либо влияние, на основе имеющихся данных. . К наиболее эффективным стратегиям относятся те, которые помогают детям понять то, что они читают; предоставление им значимой обратной связи; и подходы, улучшающие метапознание — способность учащихся думать, планировать и оценивать собственное обучение. Каждый из них дает детям в среднем шесть или семь месяцев прогресса.
Каждый из них дает детям в среднем шесть или семь месяцев прогресса.
Более 70% руководителей средних школ в Англии теперь используют набор инструментов при принятии решений о том, как расходовать финансирование. EEF сотрудничает с группами, чтобы адаптировать его для использования в Австралии и некоторых частях Латинской Америки, Ближнего Востока и Африки.
Задолго до пандемии было ясно, что одним из самых рентабельных подходов является репетиторство, как в небольших группах, так и индивидуально. Инструментарий говорит, что это может купить четыре-пять месяцев дополнительного прогресса при относительно низких затратах. И, в отличие от некоторых других эффективных методов, программы репетиторства можно быстро наращивать и внедрять. Итак, в 2020 году EEF быстро рассмотрел данные о возможных последствиях закрытия школ в Соединенном Королевстве по всей стране9.0035 2 и подчеркнул, что репетиторство, вероятно, будет особенно эффективным способом помочь детям наверстать упущенное. В то время «репетиторство казалось вполне правдоподобным ответом», — говорит Бекки Фрэнсис, исследователь в области образования и исполнительный директор EEF. По ее словам, в то время эта рекомендация «приземлилась в пустоту и была с готовностью подхвачена политиками».
В то время «репетиторство казалось вполне правдоподобным ответом», — говорит Бекки Фрэнсис, исследователь в области образования и исполнительный директор EEF. По ее словам, в то время эта рекомендация «приземлилась в пустоту и была с готовностью подхвачена политиками».
Как COVID меняет изучение человеческого поведения
В июне 2020 года правительство Великобритании объявило о создании Национальной программы репетиторства стоимостью 350 миллионов фунтов стерлингов в рамках своего более широкого догоняющего финансирования для детей в размере 1 миллиарда фунтов стерлингов. (ВЭФ был одним из нескольких партнеров, которые управляли программой в течение первого года; голландская компания Randstad приняла ее на второй год). выиграют от этого больше всего. «Я думаю, что она не нацелена должным образом на самых обездоленных учеников. Это не покорило учителей», — говорит Эллиот Мейджор. «И отчасти это потому, что есть некоторый скептицизм в отношении качества репетиторов».
В марте этого года правительство расторгло контракт с Randstad и объявило, что в 2022–2023 учебном году финансирование репетиторства будет направлено непосредственно школам. Национальный фонд исследований в области образования в Слау, Великобритания, проводит независимую оценку влияния программы репетиторства на успеваемость учащихся.
И EEF, и Randstad говорят, что гордятся тем, чего они добились благодаря программе репетиторства. В заявлениях для Nature EEF сообщил, что к июлю 2021 года 60% средних школ получили доступ к репетиторству, а Randstad заявил, что утроил количество учащихся, участвующих в программе репетиторства.
Примеры из практики Еще одна программа, основанная на фактических данных, была широко и менее противоречиво внедрена в Англии. В рандомизированных контролируемых исследованиях было показано, что раннее вмешательство Наффилда (NELI) улучшает языковые навыки у детей в возрасте 4–5 лет посредством серии учебных занятий в небольших группах (см. go.nature.com/39xtgsk). В настоящее время NELI используется в двух третях английских начальных школ, чтобы компенсировать пропущенное во время пандемии обучение, и его результаты оцениваются независимо. «Хотя у него был огромный радиус действия, он почти полностью остался незамеченным», — говорит Фрэнсис.
go.nature.com/39xtgsk). В настоящее время NELI используется в двух третях английских начальных школ, чтобы компенсировать пропущенное во время пандемии обучение, и его результаты оцениваются независимо. «Хотя у него был огромный радиус действия, он почти полностью остался незамеченным», — говорит Фрэнсис.
Некоторые исследователи указывают на то, что Нидерланды применили образцовый подход к восстановлению образования, основанный на фактических данных. Там правительство выделило школам 4,2 миллиарда евро (4,4 миллиарда долларов США) на финансирование для поддержки учащихся и потребовало, чтобы они тратили их, выбирая из «карточки меню» научно обоснованные подходы, в значительной степени основанные на наборе инструментов EEF. «Мы хотим максимально убедиться, что школы будут основывать свои решения на имеющихся знаниях об эффективных подходах», — говорит Фемке Бинк, старший советник Департамента среднего образования Министерства образования, культуры и науки в Гааге.
Двое детей посещают школу удаленно с помощью смартфона в Дехрадуне, Индия, в конце января. По словам их матери, к тому моменту пандемии COVID-19 они лично ходили в школу всего один месяц с марта 2020 года. Фото: Atul Loke/The New York Times/Redux/eevine
По словам их матери, к тому моменту пандемии COVID-19 они лично ходили в школу всего один месяц с марта 2020 года. Фото: Atul Loke/The New York Times/Redux/eevine
А в Панаме, где школы были полностью закрыты более года, Министерство образования в апреле запустило ресурсы и тренинги для учителей, показывающие, как внедрять практики, основанные на фактических данных, включая обратную связь с учащимися. «Учителя устали и напряжены, поэтому мы пытаемся сказать им: «Мы хотим направить ваши усилия на то, что действительно работает», — говорит Хавьер Гонсалес, директор SUMMA в Сантьяго, Чили. SUMMA стремится улучшить системы образования в Латинской Америке и Карибском бассейне с помощью исследований и помогла разработать обучение.
Соединенные Штаты также уделяют особое внимание доказательствам в своих планах восстановления. В 2021 году гигантский законопроект о стимулировании экономики направил школам 122 миллиарда долларов. Закон требует, чтобы не менее 20% средств, получаемых округами, использовались на научно обоснованные меры для удовлетворения академических, социальных и эмоциональных потребностей учащихся. На практике, однако, трудно понять, как используются эти деньги, говорит Майк Петрилли, президент Института Томаса Б. Фордхэма, образовательного фонда в Вашингтоне, округ Колумбия. «Основываясь на прошлом опыте, мы должны ожидать, что большая часть денег будет потрачена не лучшим образом».
На практике, однако, трудно понять, как используются эти деньги, говорит Майк Петрилли, президент Института Томаса Б. Фордхэма, образовательного фонда в Вашингтоне, округ Колумбия. «Основываясь на прошлом опыте, мы должны ожидать, что большая часть денег будет потрачена не лучшим образом».
Еще одна сложность заключается в том, что обучение проводится в разных стилях: индивидуально или в небольших группах; онлайн или лично; доставляется учителями-людьми или цифровыми учителями. Нет никакой гарантии, что конкретная программа будет эффективной или что она будет успешной в конкретной школе или для определенного ребенка. «Это не просто нанять людей, которые называют себя репетиторами, и поместить их в комнату с детьми — таким образом вы можете потратить много денег», — говорит Мэдден.
В Мельбурне Брайдон увидел проблемы с внедрением программы обучения. Ее школа смогла разместить дополнительного учителя в некоторых классах, чтобы помочь отстающим детям, используя деньги, полученные в рамках программы наверстывания от правительства. Но школа изо всех сил пытается найти учителей для заполнения вакансий, говорит она, потому что измученные коллеги увольняются с работы. «Нам нужно более десяти замещающих учителей каждый день только для того, чтобы школа продолжала работать», — говорит она.
Но школа изо всех сил пытается найти учителей для заполнения вакансий, говорит она, потому что измученные коллеги увольняются с работы. «Нам нужно более десяти замещающих учителей каждый день только для того, чтобы школа продолжала работать», — говорит она.
В других частях мира дела обстоят еще хуже. По оценкам ЮНЕСКО, к апрелю 2020 года более 1,2 миллиарда детей в густонаселенном Азиатско-Тихоокеанском регионе пострадали от закрытия школ. И если в Японии и Сингапуре школы закрылись всего на месяц или около того, то в Бангладеш и на Филиппинах произошли одни из самых серьезных сбоев в мире: школы были полностью закрыты более 13 месяцев.
Еще до COVID-19По словам Сакс-Исраэль, в регионе был кризис обучения, потому что так много детей не достигли ожидаемого уровня успеваемости в школе. По оценкам, 10 миллионов детей в Азиатско-Тихоокеанском регионе не вернутся в школу, и ожидается, что число ранних или принудительных браков и детского труда резко возрастет.
COVID и школы: доказательства безопасного открытия
Масштабы этой проблемы не могут быть решены одним дополнительным обучением. Поскольку многие школы все еще закрыты, очевидным главным приоритетом, по словам специалистов в области образования, является открытие классов, чтобы дети могли вернуться, даже если COVID-19случаи снова начинают расти. Sachs-Israel говорит, что школы должны быть гостеприимными и безопасными, а также должны преодолевать любые опасения, которые могут возникнуть у родителей, учителей и детей по поводу рисков заражения.
Согласно отчету 3 за 2020 год, подготовленному международной группой Global Education Evidence Advisory Panel, одним из экономически эффективных подходов для школ является нацеливание обучения на уровень обучения ребенка, а не на его возраст. А исследователи в области образования говорят, что школы должны оценивать каждого возвращающегося ученика.
Это стратегия основанной на фактических данных программы под названием «Преподавание на правильном уровне», проводимой учебной организацией Pratham в Нью-Дели. Исполнительный директор организации Рукмини Банерджи говорит, что она работает с правительствами нескольких штатов в Индии и других странах и заметила, что дети добиваются успехов в обучении грамоте и счету всего за несколько недель. «Мы чувствуем, что это то, что действительно нужно во всем мире», — говорит она.
Исполнительный директор организации Рукмини Банерджи говорит, что она работает с правительствами нескольких штатов в Индии и других странах и заметила, что дети добиваются успехов в обучении грамоте и счету всего за несколько недель. «Мы чувствуем, что это то, что действительно нужно во всем мире», — говорит она.
Несмотря на всю поддержку использования фактических данных в образовании, существуют давние опасения по поводу того, насколько надежны некоторые из этих доказательств.
В 2019 году пара исследователей изучила 141 крупное рандомизированное контролируемое испытание, проведенное по заказу EEF и расположенного в США Национального центра оценки образования и региональной помощи. Они пришли к выводу, что 40% испытаний были неинформативными, поскольку их эффекты были небольшими или неточными 4 .
«Итак, вначале вы не знали, работает ли вмешательство или нет. Но, в конце концов, мы все еще не уверены, работает ли это», — говорит автор исследования Хьюго Лорти-Форгес, изучающий математическое образование в Университете Лафборо, Великобритания. По его словам, это могло быть связано с тем, что ранние многообещающие исследования подхода оказались ошибочными, метод было трудно масштабировать или исследование было плохо спланировано.
По его словам, это могло быть связано с тем, что ранние многообещающие исследования подхода оказались ошибочными, метод было трудно масштабировать или исследование было плохо спланировано.
Это не стало большим сюрпризом для исследователей, которые проводят такие исследования. Подобно тому, как большинство новых лекарств оказываются неэффективными в крупных клинических испытаниях, самые блестящие идеи по улучшению обучения оказываются малоэффективными, когда их подвергают испытанию. И в то время как в медицине врачи начинают с больного и пытаются сделать его заметно лучше, в образовании многие страны начинают с довольно здоровой системы образования, поэтому любой новый метод, скорее всего, принесет лишь незначительные выгоды. «Возможно, немного наивно предполагать, что учителя со временем не обнаружили некоторые из подходов, которые с большей вероятностью будут успешными», — говорит Стив Хиггинс из Даремского университета, Великобритания, руководивший работой над инструментарием EEF.
Поскольку данные все еще поступают, есть некоторые предположения, что закрытие школ могло оказать меньшее влияние на достижения некоторых детей, чем предполагают многие мрачные заголовки, или что ученики могут быстро прийти в себя.
Когда Хэтти изучил последствия закрытия школ в штате Виктория, Австралия, где школы (в том числе школа Брайдона) были закрыты в течение длительного времени, он пришел к выводу, что удивительно, что траектории обучения снизились лишь незначительно (см. go.nature.com/3mtxucq ). Одна из возможных причин заключается в том, что некоторые учащиеся, работая в одиночку, были более эффективны, чем в школе. Шлейхер добавляет, что технологии также стали более приемлемыми, учителя сплотились, чтобы поддержать детей в социальном и эмоциональном плане, а родители стали более активно участвовать в образовании своих детей. Глядя на общее воздействие пандемии на образование, он говорит, что «в балансе есть плюсы и минусы».
Подготовка учителей
В более долгосрочной перспективе ключевым способом более регулярного использования исследований в образовании будет включение их в подготовку учителей и непрерывное профессиональное развитие. Одна модель пришла из Японии, где учителя десятилетиями проводили «изучение уроков». Это форма исследования, в которой они разрабатывают цель — например, улучшить понимание дробей — затем пишут подробный план урока, наблюдают за уроком в действии и обсуждают то, что они узнали. Школы опираются на внешние исследования и часто консультируются в процессе с учеными. Такой тип непрерывного профессионального развития необычен, говорит специалист по математическому образованию Тошиакира Фуджи из Токийского университета Гакугей. Учителя развивают глубокое понимание учебных материалов, «но что более важно, они учатся учиться как учителя».
Одна модель пришла из Японии, где учителя десятилетиями проводили «изучение уроков». Это форма исследования, в которой они разрабатывают цель — например, улучшить понимание дробей — затем пишут подробный план урока, наблюдают за уроком в действии и обсуждают то, что они узнали. Школы опираются на внешние исследования и часто консультируются в процессе с учеными. Такой тип непрерывного профессионального развития необычен, говорит специалист по математическому образованию Тошиакира Фуджи из Токийского университета Гакугей. Учителя развивают глубокое понимание учебных материалов, «но что более важно, они учатся учиться как учителя».
Другие страны также начинают использовать фактические данные в подготовке учителей. EEF и SUMMA сотрудничают с Университетом Вест-Индии в Кейв-Хилл, Барбадос, над обучением учителей методам, основанным на фактических данных, таким как эффективная обратная связь со студентами. А начиная с этого года все 650 студентов, обучающихся в магистратуре Гарвардской высшей школы образования в Кембридже, штат Массачусетс, должны будут пройти курс по доказательствам, говорит старший преподаватель Кэрри Конауэй. «Идея в том, что у нас есть поколение лидеров, которые понимают ценность этого как части процесса принятия решений», — говорит она.
«Идея в том, что у нас есть поколение лидеров, которые понимают ценность этого как части процесса принятия решений», — говорит она.
Брайдон говорит, что во время обучения ее почти ничему не учили использовать данные исследований — «вы знакомитесь с парой крупных теоретиков, и тогда это действительно так». Но теперь она является частью Q Project, усилия в Австралии по улучшению использования доказательств в школах. Однако она считает, что самым большим препятствием является нехватка времени. «Мы так загружены, и когда вам нужно выбирать между тем, чтобы отметить свои эссе для 12-летнего класса, или чтением каких-либо научных данных, я знаю, что я выберу каждый день недели».
Прямо сейчас Брайдон и ее коллеги все еще борются за то, чтобы помочь детям наверстать упущенное, на фоне кипящих опасений, что следующий вариант коронавируса может снова закрыть школы. Когда люди спрашивали Брайдон о ее работе, она говорила им, что преподавание — самая лучшая работа в мире. Но теперь впервые у нее другая реакция. «Есть некоторые части, которые мне очень нравятся, — говорит она, — но есть и те, которые очень усложняют работу».
«Есть некоторые части, которые мне очень нравятся, — говорит она, — но есть и те, которые очень усложняют работу».
Прикладные исследования
Загрязняющие вещества и вредоносное цветение водорослей представляют серьезную опасность как для здоровья человека, так и для здоровья экосистемы в Дельте. Загрязняющие вещества в системе происходят из различных источников, включая сточные воды, исторические побочные продукты добычи полезных ископаемых, сельскохозяйственные и городские стоки. Вредоносное цветение водорослей, сокращенно «ВЦВ», происходит, когда колонии определенных видов водных водорослей размножаются и выделяют токсины, вредные для животных, включая человека. Загрязняющие вещества и ВЦВ могут оказывать прямое видимое воздействие на организмы (например, опухоли, поражения, смерть) или косвенное воздействие (например, изменения в поведении, угнетение размножения, снижение роста). И то, и другое оказывает важное влияние на экосистему Дельты и людей, которые воссоздают и живут в ней.
Прикладные исследования загрязняющих веществ и ВЦВ в Отделе экологических услуг направлены на понимание причин и последствий воздействия этих компонентов на организмы и экосистемы в Дельте. Конкретные области исследований включают:
• Какие условия вызывают и влияют на цветение цианобактерий, Microsystis в Дельте
• Местные источники и перемещение ртути в системе
• 0003
Меркурий
Секция мониторинга и оценки ртути была создана в 2012 году после того, как Региональный совет по контролю качества воды Центральной долины принял Программу контроля ртути в дельте. Этот раздел обеспечивает соблюдение DWR правил, касающихся ртути и метилртути в Калифорнии. Это включает в себя разработку и проведение исследований качества воды, сбор и анализ данных, а также использование в качестве информационного ресурса для сотрудников ДВХ, работающих над проектами с ртутным компонентом.
Заключительный отчет Mercury Open Water был представлен DWR в соответствии с Программой контроля Delta Mercury, обнародованной Центральным Региональный совет по контролю качества воды долины. Отчет состоит из резюме и семи отдельных глав. В отчете обобщаются результаты сочетания моделирования и научных исследований в Дельте и обходе Йоло для оценки источников ртути и метилртути в открытых водах и возможных методов управления (только обход Йоло) для снижения нагрузки по метилртути. Заключительный отчет Mercury Open Water о соответствии программе Delta Mercury Control Program
Технические приложения, содержащие подробную информацию о моделировании и научных исследованиях, предоставляются по запросу. Направляйте запросы на техническое приложение по адресу [email protected] или [email protected].
Для получения информации об исследованиях по моделированию или по вопросам загрузки и запуска модели Delta Mercury (DSM2-Hg) отправляйте запросы на моделирование по адресу Prabhjot. [email protected].
[email protected].
микроцистис
Microcystis — это разновидность цианобактерий (фотосинтезирующих бактерий), которые могут вырабатывать токсины, вызывающие серьезные проблемы со здоровьем у животных и людей. Люди, купающиеся в густых цветках Microcystis, испытывают раздражение, такое как кожная сыпь, ожоги и пр. Проглатывание может вызвать рвоту, тошноту, головные боли, диарею, пневмонию, лихорадку и повреждение печени. Случаев смерти людей не зарегистрировано, но собаки, дикие животные и домашний скот погибли в результате воздействия этого токсина. Специальные исследования Microcystis сосредоточены на причинах и последствиях этого цветения в эстуарии.
Отчеты и публикации
1. Ли, П. и Мэннинг, Дж. 2020. Импорт и экспорт ртути из четырех приливных водно-болотных угодий в дельте Сакраменто-Сан-Хоакин, объездная дорога Йоло и Суйсун Марш для соблюдения программы контроля ртути в дельте. Департамент водных ресурсов Калифорнии. Апрель 2020 г.
Ли, П. и Мэннинг, Дж. 2020. Импорт и экспорт ртути из четырех приливных водно-болотных угодий в дельте Сакраменто-Сан-Хоакин, объездная дорога Йоло и Суйсун Марш для соблюдения программы контроля ртути в дельте. Департамент водных ресурсов Калифорнии. Апрель 2020 г.
2. Lehman P, T Kurobe, S Lesmeister, M Mizel, D Baxa, A Tung, S Teh (2017) Воздействие сильной засухи 2014 года на цветение Microcystis в устье Сан-Франциско. Вредоносные водоросли 63: 94-108.
3. Lehman PW, C Kendall, MA Guerin, MB Young, SR Silva, GL Boyer, SJ Teh (2015) Характеристика цветения Microcystis и его снабжения азотом в эстуарии Сан-Франциско с использованием стабильных изотопов. Estuaries and Coasts Estuaries and Coasts (2015) 38:165-178
4. Lehman PW, K Marr, GL Boyer, S Acuna, SJ Teh (2013) Долгосрочные тенденции и причинные факторы, связанные с обилием и токсичностью Microcystis в Сан Эстуарий Франсиско и последствия изменения климата. Гидробиология 718:141-158
5. Acuna S, DF Deng, P Lehman, S Teh (2012) Сублетальные диетические эффекты Microcystis на расщепленном хвосте Сакраменто, Pogonichthys macrolepidotus. Aquatic Toxicology 110-111 (2012) 1-8
Aquatic Toxicology 110-111 (2012) 1-8
6. Baxa DV, T Kurobe, K Ger, PW Lehman, SJ Teh (2010) Оценка численности токсичных видов Microcystis в эстуарии Сан-Франциско с использованием количественной ПЦР в реальном времени . Вредные водоросли 9:342-349
7. Дэн Д.Ф., К. Чжэн, Ф.С. Тех, П. В. Леман, С. Дж. Тех (2010) Порог токсичности диетического микроцистина (-LR) для Quart Medaka. Токсикон 55:787-794
8. Henery RE, TR Sommer, CR Goldman (2010) Рост и накопление метилртути в молоди чавычи в реке Сакраменто и ее пойме, объездная дорога Йоло. Transactions of the American Fisheries Society, 139: 550-563
9. Lehman PW, SJ Teh, GL Boyer, ML Nobriga, E Bass, C Hogle (2009) Первоначальное воздействие Microcystis aeruginosablooms на водную пищевую сеть в Сан-Франциско. Устье. Hydrobiologia DOI 101007/s10750-009-9999-y
10. Moisander PH, PW Lehman, M Ochiai, S Corum (2009).) Разнообразие Microcystis aeruginosa в реке Кламат и дельте залива Сан-Франциско, Калифорния. Aquatic Microbial Ecology 57:19-31
Aquatic Microbial Ecology 57:19-31
11. Lehman PW, G Boyer, M Satchwell, S Waller (2008) Влияние условий окружающей среды на сезонные колебания плотности клеток Microcystis и концентрации микроцистинов в эстуарии Сан-Франциско. Гидробиология 600:187-204.
Все организмы нуждаются в достаточном количестве пищи, чтобы выжить и размножаться. Таким образом, понимание пищевой сети Дельты имеет решающее значение для поддержки основы экосистемы. В Отделе экологических услуг прикладные исследования пищевой сети направлены на то, чтобы понять, как функционирует сложная, взаимосвязанная и изменяющаяся пищевая сеть Дельты, как на нее влияет окружающая среда и как научно обоснованное управление может смягчить воздействие человека.
Конкретные исследования включают:
• Как продуктивность и видовой состав фитопланктона (микроскопические водные растения), зоопланктона (почти микроскопические водные животные), моллюсков и других беспозвоночных изменяются в разных местах обитания и при различных условиях воды (например, течение, химический состав
• Влияние управленческих действий на продуктивность пищевой сети
• Воздействие, которое один вид или группа видов оказывает на другую популяцию в результате выпаса или нападения на них хищников.
• Как доступность пищи и хищничество влияют на уязвимые и внесенные в списки виды, включая дельта-корюшку и чавычу.
Действие продовольственной сети Северной Дельты
Этот проект представляет собой межведомственное сотрудничество под руководством DWR в рамках стратегии обеспечения устойчивости Delta Smelt Агентства по ресурсам. Утрата планктона в дельте является основным фактором, ответственным за сокращение численности многих рыб, в том числе находящейся под угрозой исчезновения дельтовой корюшки, состояние которой влияет на надежность водоснабжения в штате. Это исследование направлено на то, чтобы понять, может ли поток воды через богатые планктоном районы обхода Йоло и комплекса Cache Slough переносить «семя» продуктивности в нижнюю часть дельты, что увеличивает производство пищи для Delta Smelt.
Производство пищевой сети Duck Club
Утрата запасов пищи для зоопланктона связана с сокращением численности многих видов рыб в дельте, в том числе аборигенной длинноперой корюшки и находящейся под угрозой исчезновения дельта-корюшки. Это исследование является результатом сотрудничества между DWR и Университетом штата Сан-Франциско для изучения производства и экспорта зоопланктона из управляемых и естественных водно-болотных угодий в болоте Суисун в окружающие приливные и открытые воды.
Это исследование является результатом сотрудничества между DWR и Университетом штата Сан-Франциско для изучения производства и экспорта зоопланктона из управляемых и естественных водно-болотных угодий в болоте Суисун в окружающие приливные и открытые воды.
Публикации в пищевой сети
Corline NJ, Sommer T, Jeffres CA, Katz J (2017) Экология зоопланктона и трофические ресурсы для выращивания местной рыбы в сельскохозяйственной пойме в обходе Йоло, Калифорния, США. Экология и управление водно-болотными угодьями doi:101007/s11273-017-9534-2
Браун, Л.Р., В. Киммерер, Дж.Л. Конрад, С. Лесмайстер и А. Мюллер-Зольгер, 2016 г. Пищевые сети дельты, залива Суйсан и болота Суйсан: обновленная информация о текущем понимании и возможностях для управления Устье Сан-Франциско и наука о водоразделах 14( 3)
Lehman PW, S Mayr, L Leiji and A Tang (2015) Дневной поток органических и неорганических материалов из прудов на пресноводных приливных заболоченных территориях острова Свободы.
 СпрингерПлюс 4:273
СпрингерПлюс 4:273Лобощефски Э., Г. Бениньо, Т. Соммер, К. Роуз, Т. Джинн, А. Массуди и др. (2012) Исторический спрос на добычу полосатого окуня в устье Сан-Франциско на индивидуальном и популяционном уровне с использованием биоэнергетической модели. Наука об устье и водоразделе Сан-Франциско 10 (1)
Lehman PW, S Mayr, L Mecum, C Enright (2010) Пресноводная приливная заболоченная местность острова Свободы, Калифорния, была как источником, так и поглотителем неорганических и органических материалов в устье Сан-Франциско. Водная экология 44:359-372
Lehman PW (2007) Влияние состава сообщества фитопланктона на первичную продуктивность вдоль приливно-отливного континуума от реки до пресной воды в реке Сан-Хоакин, Калифорния. Эстуарии и побережья 30: 82-93.
Lehman PW, T Sommer, L Rivard (2007) Влияние пойменной среды обитания на количество и качество углерода речного фитопланктона, образующегося во время паводков в эстуарии Сан-Франциско.
 Водная экология 42: 363-378
Водная экология 42: 363-378Nobriga M, F Feyrer (2007) Динамика мелководных рыбоядных и жертв в дельте Сакраменто-Сан-Хоакин. Устье Сан-Франциско и наука о водоразделах. 5(2)
Lehman PW (2004) влияние климата на механистические пути, которые влияют на снижение производства пищевых сетей в северной части устья залива Сан-Франциско. Устья 27: 311-324.
Schemel LE, TR Sommer, AB Muller-Solger, WC Harrell (2004) Гидрологическая изменчивость, химический состав воды и биомасса фитопланктона в большой пойме реки Сакраменто, Калифорния, США. Гидробиология 513:129-139
Качественная среда обитания является важнейшим компонентом экосистемы дельты и ключом к выживанию и долгосрочному сохранению видов, обитающих в устье. Понимание того, как организмы взаимодействуют с окружающей средой и зависят от нее в плане выращивания, питания, укрытия и воспроизводства, поэтому необходимо для создания устойчивых ландшафтов. Прикладные исследования в Отделе экологических услуг сосредоточены на понимании того, как организмы используют среду обитания и как изменения в этих средах обитания влияют на популяции. Это исследование помогает DWR выполнять свои обязательства по восстановлению среды обитания, информируя разработчиков проекта о передовых научных данных. Выводы также помогают департаменту разрабатывать инновационные управленческие решения, которые могут предотвратить или смягчить негативное воздействие деятельности человека.
Прикладные исследования в Отделе экологических услуг сосредоточены на понимании того, как организмы используют среду обитания и как изменения в этих средах обитания влияют на популяции. Это исследование помогает DWR выполнять свои обязательства по восстановлению среды обитания, информируя разработчиков проекта о передовых научных данных. Выводы также помогают департаменту разрабатывать инновационные управленческие решения, которые могут предотвратить или смягчить негативное воздействие деятельности человека.
Исследовательские проекты включают:
Как перечисленные и уязвимые виды, такие как дельтакорюшка, чавыча и зеленый осетр, используют различные среды обитания (например, открытую воду, реку, пойму, приливные водно-болотные угодья).
Воздействие засух и наводнений, которые, как ожидается, будут происходить чаще с изменением климата, на основные места обитания и организмы, которые их используют.
Как улучшить управление приливными водно-болотными угодьями и пойменными сельскохозяйственными угодьями, чтобы сбалансировать использование обоих видов (например, водоплавающих птиц, рыб, планктона) и людей.

Публикации в пищевой сети
Поймы и другие участки за пределами русла имеют решающее значение в качестве мест нагула для молоди лососевых из-за их богатой кормовой базы по сравнению с местами в русле. Обход Йоло — это обширная пойма в Центральной долине Калифорнии, которая поддерживает сельское хозяйство, а также среду обитания для рыб и птиц благодаря мозаике сезонных водно-болотных угодий, прибрежных районов и горных мест обитания. Управляемое сельскохозяйственное исследование поймы исследует взаимосвязь между кормовой базой молоди лосося, использованием среды обитания, ростом и выживанием на сельскохозяйственных угодьях поймы, когда они затапливаются зимой.
Программа управляемых исследований водно-болотных угодий Suisun Marsh
Марш Суисун — крупнейшее непрерывное солоноватое болото, оставшееся на западном побережье Северной Америки. Исследование среды обитания на болоте направлено на то, чтобы лучше понять, как сохранить и увеличить ценность среды обитания Суйсан-Марш для водоплавающих и других водоплавающих птиц. Эта работа направлена на лучшее понимание факторов, влияющих на продуктивность водоплавающих птиц, использование зимней среды обитания и производство корма для водоплавающих птиц, особенно в том, что касается методов управления водно-болотными угодьями.
Исследование среды обитания на болоте направлено на то, чтобы лучше понять, как сохранить и увеличить ценность среды обитания Суйсан-Марш для водоплавающих и других водоплавающих птиц. Эта работа направлена на лучшее понимание факторов, влияющих на продуктивность водоплавающих птиц, использование зимней среды обитания и производство корма для водоплавающих птиц, особенно в том, что касается методов управления водно-болотными угодьями.
Публикации среды обитания
1. Таката Л., Т. Р. Соммер, Дж. Л. Конрад и Б. М. Шрайер (2017) Выращивание и миграция молоди чавычи (Oncorhynchus tshawytscha) в пойме крупной реки. Экологическая биология рыб. 100(9), 1105-1120. 10.1007/s10641-017-0631-0
2. Конрад Дж. Л., Э. Холмс, С. Джеффрес, Л. Таката, Н. Икемияги (2016) Применение технологии пассивных интегрированных транспондеров для использования среды обитания молоди лосося в экспериментальной сельскохозяйственной пойме. Североамериканский журнал управления рыболовством. 36:30-39
Североамериканский журнал управления рыболовством. 36:30-39
3. Джеффрис К.М., Коннон Р.Е., Бьельде Б.Е., Комороске Л.М., Бриттон М.Т., Соммер Т., Тодгам А.Е., Фангу Н. (2016)Влияние высоких температур на эстуарные рыбы, которым угрожает опасность, в периоды сильной засухи. Журнал экспериментальной биологии 2019 г.: 1705-1716
4. Цао, округ Колумбия, Р. Е. Мейсер-младший, М. Брэдбери (2015) Распространение и ассоциации местообитаний калифорнийского черного рельса (Laterallus jamaicensis cortuniculus) в дельте Сакраменто-Сан-Хоакин. Устье Сан-Франциско и наука о водных ресурсах 13(4)
5. Б. Гербольд, Д. М. Бальц, Л. Браун, Р. Гроссингер, В. Киммерер, П. Леман, П. Б. Мойл, М. Нобрига, К. А. Сименстад (2014) Роль восстановления приливных болот в Управление рыбным хозяйством в устье Сан-Франциско. Наука об устье и водоразделе Сан-Франциско 12 (1)
6. Seesholtz AM, MJ Manuel, JP Van Eenennaam (2014) Первое задокументированное нерест и связанные с ним условия обитания зеленого осетра в реке Перо, Калифорния. Экологическая биология рыб 98 (3): 905–912.
Экологическая биология рыб 98 (3): 905–912.
7. Соммер Т., Ф. Мехиа (2013) Место, которое можно назвать домом: синтез среды обитания дельты корюшки в устье Верхнего Сан-Франциско. San Francisco Estuary and Watershed Science 11(2), 27 p
8. Фейер Ф., М. Нобрига, Т. Соммер (2007) Многодесятилетние тенденции для трех исчезающих видов рыб: модели и механизмы среды обитания в эстуарии Сан-Франциско, Калифорния, США. Канадский журнал рыболовства и водных наук 64:723-734
9. Соммер, Т., К. Армор, Р. Бакстер, Р. Брейер, Л. Браун, М. Хотковски, С. Калберсон, Ф. Фейрер, М. Гинграс, Б. Хербольд, В. Киммерер, А. Мюллер-Зольгер, М. Нобрига, К. Соуза (2007 г. ) Гибель пелагических рыб в верхнем эстуарии Сан-Франциско. Fisheries 32:270-277
10. Sommer T, B Harrell, M Nobriga, R Brown, P Moyle, W Kimmerer, L Schemel (2001) Калифорнийский обход Йоло: свидетельство того, что борьба с наводнениями может быть совместима с рыболовством, водно-болотными угодьями, дикой природой , и сельское хозяйство. Рыболовство 26:6-16
Рыболовство 26:6-16
Неместные или «инвазивные» виды — это организмы, переносимые людьми в регион, где они не встречаются в природе. Оказавшись на новом месте, инвазивные виды могут изменить новую среду, изменяя пищевые сети, структурную среду обитания и экологическое сообщество. Более того, залив-Дельта, пожалуй, самый заселенный эстуарий в мире. В Дельте инвазивные виды часто негативно воздействуют на местные организмы и могут создавать серьезные проблемы для использования человеком и водными операциями.
Прикладные исследования инвазивных видов в Отделе экологических служб направлены на понимание истории жизни неместных организмов в Дельте, их влияния на важные местные организмы и экосистемы и того, как это воздействие можно смягчить или избежать с помощью управления и восстановления. .
Инвазивная водная растительность
Затопленные, плавающие и всплывающие виды инвазивной водной растительности расширились в дельте и в настоящее время занимают большую часть мелководных и прибрежных районов системы. Существует много неблагоприятных последствий водных сорняков, включая сокращение среды обитания в открытой воде, негативное воздействие на воду и продвижение других чужеродных видов, включая неместных рыбных хищников. В этом исследовании будет изучено, как химическая обработка инвазивной водной растительности, чтобы определить, влияют ли изменения в среде обитания на качество воды, пищевую сеть и могут ли эти эффекты быть полезными для Delta Smelt.
Существует много неблагоприятных последствий водных сорняков, включая сокращение среды обитания в открытой воде, негативное воздействие на воду и продвижение других чужеродных видов, включая неместных рыбных хищников. В этом исследовании будет изучено, как химическая обработка инвазивной водной растительности, чтобы определить, влияют ли изменения в среде обитания на качество воды, пищевую сеть и могут ли эти эффекты быть полезными для Delta Smelt.
Публикации об инвазивных видах
- Махарджа Б., Фарруджиа М.Дж., Шрайер Б., Соммер Т. (2017) Доказательства сдвига в прибрежном рыбном сообществе дельты Сакраменто-Сан-Хоакин. PLoS ONE 12(1): e0170683 doi:101371/journalpone0170683
- Махарджа Б., Дж. Л. Конрад, Л. Люшер, Б. Шрайер (2016) Тенденции численности, распространение и ассоциации местообитаний инвазивной Миссисипи Сильверсайд (Menidia audens) в дельте Сакраменто-Сан-Хоакин, Калифорния, США.
 Наука об устье и водоразделе Сан-Франциско 14(1): Статья 2
Наука об устье и водоразделе Сан-Франциско 14(1): Статья 2 - Шрайер, Б.М., М.Р. Бэрвальд, Дж.Л. Конрад, Г. Шумер и Б. Мэй (2016 г.) Изучение хищничества корюшки дельты на ранней стадии жизни в эстуарии Сан-Франциско с использованием анализа диеты ДНК. Сделки Американского рыболовного общества 145: 723-733
- Браун Т., К.А. Хиб (2013) Статус сибирской креветки Exopalaemon Modetus в эстуарии Сан-Франциско. Устье Сан-Франциско и наука о водоразделах. 12(1)
- Феррари, MCO, Л. Ранокер, К.Л. Вайнерсмит, М.Дж. Янг, А. Сих, Дж.Л. Конрад (2013) Влияние мутности и инвазивных водорослей на хищничество интродуцированного большеротого окуня. Экологическая биология рыб Опубликовано в Интернете в марте 2013 г.
- Фейрер Ф., Т. Соммер, С. Слейтер (2009) Старая школа против новой школы: статус Threadfin Shad через пять десятилетий после его появления в дельте Сакраменто-Сан-Хоакин. Устье Сан-Франциско и наука о водоразделах 7 (1).
- Фейрер Ф.
 (2004) Экологическая сегрегация местных и чужеродных сообществ личинок рыб в южной части дельты Сакраменто-Сан-Хоакин. Страницы 67–79 в книге Ф. Фейрера, Л. Р. Брауна, Р. Л. Брауна и Дж. Дж. Орси, редакторов «История ранней жизни рыб в устье и водоразделе Сан-Франциско». Американское рыболовное общество, Симпозиум 39, Бетесда, Мэриленд
(2004) Экологическая сегрегация местных и чужеродных сообществ личинок рыб в южной части дельты Сакраменто-Сан-Хоакин. Страницы 67–79 в книге Ф. Фейрера, Л. Р. Брауна, Р. Л. Брауна и Дж. Дж. Орси, редакторов «История ранней жизни рыб в устье и водоразделе Сан-Франциско». Американское рыболовное общество, Симпозиум 39, Бетесда, Мэриленд - Фейрер Ф., Б. Хербольд, С. А. Матерн, П. Б. Мойл (2003) Диетические сдвиги в стрессовом сообществе рыб: последствия вторжения двустворчатых моллюсков в устье Сан-Франциско. Экологическая биология рыб 67:277-288
- Тофт Дж. Д., К. А. Сименстад, Дж. А. Корделл, Л. Ф. Гримальдо (2003) Влияние интродуцированного водного гиацинта на структуру среды обитания, сообщества беспозвоночных и рацион рыб. Устья 26: 746-758
Разработка технологий и инструментов
Новые научные технологии и аналитические инструменты позволяют исследователям улучшить качество и количество данных об окружающей среде, собираемых в Дельте. Это может позволить собирать полевые данные о труднодоступных или уязвимых для традиционных методов отлова видах, таких как дельтакорюшка. Следовательно, новые инструменты и технологии могут дать новое понимание, которое было невозможно с помощью традиционных методов. В некоторых случаях новые технологии позволяют собирать больше информации, используя аналогичные объемы ресурсов и рабочей силы.
Это может позволить собирать полевые данные о труднодоступных или уязвимых для традиционных методов отлова видах, таких как дельтакорюшка. Следовательно, новые инструменты и технологии могут дать новое понимание, которое было невозможно с помощью традиционных методов. В некоторых случаях новые технологии позволяют собирать больше информации, используя аналогичные объемы ресурсов и рабочей силы.
Прикладные исследования новых технологий и инструментов в Отделе экологических служб направлены на поиск новых способов максимизации ресурсов и позволяют DWR выполнять свои экологические обязательства, одновременно удовлетворяя потребности людей в Дельте. Темы исследований включают:
• Генетика: тестирование и совершенствование генетических методов для: 1) обнаружения очень редких видов в дикой природе; 2) Идентификация присутствующих рас чавычи; 3) Определите, какие виды поедаются хищниками.
• Наблюдение: оценка и совершенствование новых технологий камер и гидролокаторов для быстрого количественного определения и идентификации рыбы и планктона, часто без необходимости захвата или обработки.
• Моделирование: разработка и тестирование компьютерных моделей для прогнозирования того, как организмы могут распределяться в различных условиях окружающей среды и течения в дельте.
Дрон, следящий за Элкхорн-Слау – Монтерей Геральд
Дрон летает над Элкхорн-Слау, перемещаясь взад и вперед по вытянутому зигзагообразному узору. Когда он скользит по воздуху, он делает снимки поверхности, чтобы отслеживать жизнь растений и высоту земли.
Обследование земли с помощью дрона — это метод, используемый для отслеживания деликатного восстановления Хестер Марш, продолжающегося проекта с 2017 года.
Исторически сложилось так, что болота были обвалованы и осушены для создания пастбищ, в результате чего губчатая земля сокращалась. Теперь ученые собирают грязь и восстанавливают местные растения, чтобы вернуть солончаку его былую славу. Они также поднимают его, чтобы противодействовать будущему повышению уровня моря, вызванному изменением климата.
Джон Хаскинс указывает траекторию полета дрона на пульте дистанционного управления устройства. (Маккензи Прилламан, корреспондент Herald)
(Маккензи Прилламан, корреспондент Herald)Но это непростая задача с такой привередливой экосистемой.
Для того, чтобы болото процветало и было здоровым, требуется частый и точный контроль, который может занять несколько часов труда, проведенного в грязи. Однако сбор данных с помощью дронов делает процесс более быстрым и точным, чем когда-либо.
«Само болото похоже на Златовласку», — сказал Джон Хаскинс, специалист по мониторингу качества воды Национального эстуарного исследовательского заповедника Элкхорн-Слау и один из руководителей проекта по использованию дронов. «Он хочет быть в идеальной зоне приливной рамки, чтобы иметь возможность расти».
Если болото слишком высокое, оно не получает достаточно воды для роста растений. Но если она слишком низкая, затопление убивает растения. Золотая середина, как объяснил Хаскинс, существует в пределах 3-футовой области внутри 8-футовой приливной рамки, полного диапазона, которого могут достичь океанские приливы на западном побережье США.
Традиционно ученые исследуют, как поживает растительность, вручную. С помощью метровых стержней и рулеток они подсчитывают количество растений каждого типа на небольшой площади и рассчитывают приблизительный растительный покров по всему региону. 900:03 Дрон приземляется после полета над территорией фазы II реставрации Хестер Марш. (Маккензи Прилламан, корреспондент Herald)
Однако совершенно белый беспилотник длиной в фут с двумя прикрепленными к нему камерами может обследовать всю площадь в 35 акров реставрации Хестер Марш, этап II, примерно за 45 минут. Кроме того, моментальный снимок всего региона означает точный подсчет растений, а не оценки.
«Мы обнаружили, что для проекта восстановления, подобного этому, где сейчас не так много растительности, это действительно быстрый и простой способ отслеживать изменения во времени», — сказал Чарли Эндрис, научный сотрудник и специалист по ГИС из Moss Landing Marine Laboratories и один из руководителей проекта по созданию дронов.
Во время полета одна из камер дрона делает около 1000 изображений, которые затем объединяются для создания трехмерной карты высот всего региона. Другой делает снимки с двумя длинами волн света, невидимыми для человеческого глаза, которые помогают идентифицировать определенные сорта растений на болоте.
Не выходя из своего офиса, Хаскинс вставляет в приложение аэрофотоснимок Хестер Марш. Затем он рисует траекторию полета дрона, по которому он перемещается взад и вперед по земле, гарантируя, что изображения будут накладываться друг на друга, чтобы их можно было позже собрать воедино.
Выехав на болото, Хаскинс разгружает дрон, на управление которым у него есть специальная лицензия пилота, и отправляет ему инструкции через приложение. Он и Эндрис впервые подумали о наблюдении за болотом с помощью дрона в 2015 году, когда они вышли к болоту с кем-то, управляющим дроном с неподвижным крылом, по сути, миниатюрным самолетом.
Дрон Хаскинса взлетает и автоматически следует по намеченному ранее маршруту. Устройство скользит на высоте 50 метров над землей, делая снимки каждые пару секунд, обнаруживая и избегая других объектов в воздухе, таких как птицы. Он возвращается на посадочную площадку примерно каждые 15 минут для подзарядки батарей.
Устройство скользит на высоте 50 метров над землей, делая снимки каждые пару секунд, обнаруживая и избегая других объектов в воздухе, таких как птицы. Он возвращается на посадочную площадку примерно каждые 15 минут для подзарядки батарей.
Когда полет завершен и дрон возвращается в офис, Хаскинс и Эндрис обрабатывают «гигабайты и гигабайты» данных, собранных дроном. По словам Эндриса, требуется несколько дней, чтобы преобразовать все изображения в продукт, который можно интерпретировать. Иногда ему и Хаскинсу помогают студенты местного университета, но дуэт ищет способ загрузить данные в Интернет и превратить их в научный проект.
Конечным результатом является трехмерная модель рельефа с точностью до сантиметра, разделенная на различные зоны, такие как болота с растительностью, болота без растительности и луга. Используя этот инструмент, ученые из Элкхорн-Слау могут определить, насколько нагроможденные отложения уплотняются с течением времени, оценить сорта и местонахождение растений, отследить формирование и развитие ручьев и многое другое.
Исследователи также могут использовать эту модель для изучения результатов различных экспериментов по управлению земельными ресурсами. Эндрис объяснил, что данные беспилотников помогли им определить, что плотное заполнение краев водных каналов грязью помогает предотвратить эрозию. После тестирования этого метода на уже завершенном восстановлении участка площадью 65 акров на этапе I они применили тот же метод на продолжающемся этапе этапа II.
Опираясь на свою успешную методологию мониторинга с помощью дронов, Хаскинс и Эндрис теперь пытаются запустить общенациональную программу дронов на 30 прибрежных участках, входящих в Национальную систему эстуарных исследовательских заповедников, в сеть которой входит Элкхорн-Слау.
«(Дрон) только что взорвал количество возможностей, которые вы можете использовать», — сказал Хаскинс.

 ..
..
 Как известно, обычная СЛАУ может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений размера m x n, X — искомый вектор неизвестных с n компонентами и В — вектор свободных членов, также содержащий n компонент. Решением системы называется совокупность чисел , при подстановке которых все уравнения системы обращаются в тождества.
Как известно, обычная СЛАУ может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений размера m x n, X — искомый вектор неизвестных с n компонентами и В — вектор свободных членов, также содержащий n компонент. Решением системы называется совокупность чисел , при подстановке которых все уравнения системы обращаются в тождества.

 Значение каждого из неизвестных в этом случае равно дроби, знаменателем которой является определитель системы, а числитель равен определителю системы, в которой вместо столбца коэффициентов при неизвестном располагается столбец свободных членов.
Значение каждого из неизвестных в этом случае равно дроби, знаменателем которой является определитель системы, а числитель равен определителю системы, в которой вместо столбца коэффициентов при неизвестном располагается столбец свободных членов.
 При вызове функции lsqr(A, B) итерации производятся либо до сходимости к решению, либо до появления ошибки, либо до достижения максимального числа итераций (по умолчанию равного min(20, m, n), где m – число уравнений, n – число неизвестных). Сходимость достигается, когда отношение вторых норм векторов norm(B-Ax)/norm(B) меньше или равно погрешности метода tol (по умолчанию 1е-6). Функция lsqr(A, B, tol) — возвращает решение с заданной погрешностью tol.
При вызове функции lsqr(A, B) итерации производятся либо до сходимости к решению, либо до появления ошибки, либо до достижения максимального числа итераций (по умолчанию равного min(20, m, n), где m – число уравнений, n – число неизвестных). Сходимость достигается, когда отношение вторых норм векторов norm(B-Ax)/norm(B) меньше или равно погрешности метода tol (по умолчанию 1е-6). Функция lsqr(A, B, tol) — возвращает решение с заданной погрешностью tol. Описание этих функций можно посмотреть с помощью команды help имя_функции. Функция mldivide() или оператор «\» самостоятельно выбирают лучший метод решения заданной системы уравнений (см. рис. 5.6).
Описание этих функций можно посмотреть с помощью команды help имя_функции. Функция mldivide() или оператор «\» самостоятельно выбирают лучший метод решения заданной системы уравнений (см. рис. 5.6). ..
..
 Такую
систему можно решить также методом Крамера и с помощью обратной матрицы.
Такую
систему можно решить также методом Крамера и с помощью обратной матрицы.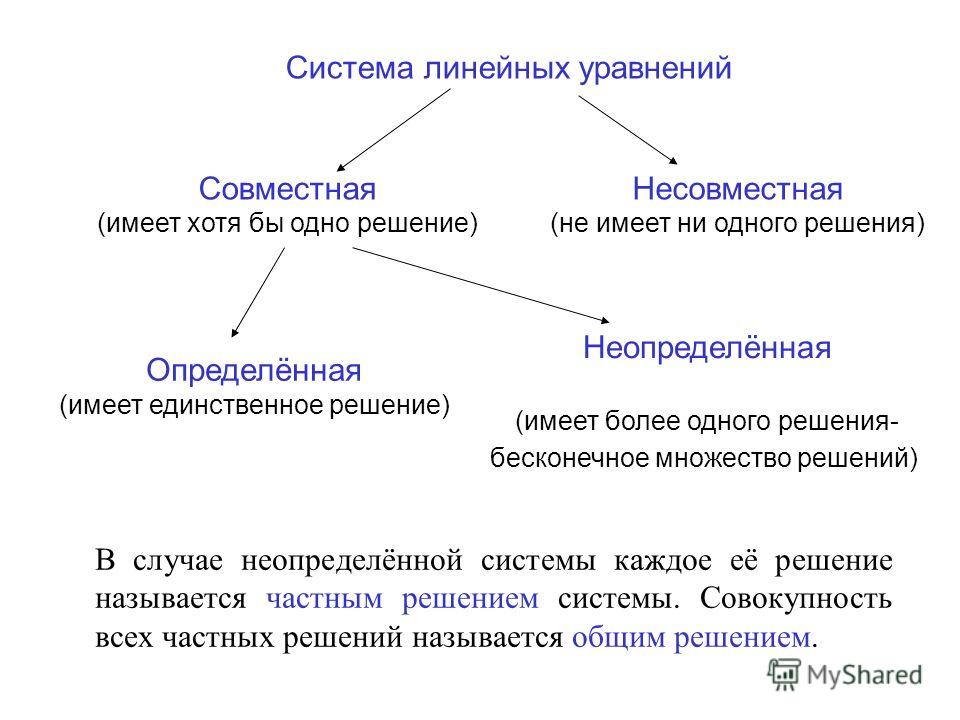
 10) равно числу
сочетаний из n элементов по r элементов Cnr. Так как каждому базисному набору переменных соответствует
свое базисное решение, следовательно, количество базисных решений у системы
также равно Cnr.
10) равно числу
сочетаний из n элементов по r элементов Cnr. Так как каждому базисному набору переменных соответствует
свое базисное решение, следовательно, количество базисных решений у системы
также равно Cnr. Это означает, что ранг r ее главной матрицы меньше числа n неизвестных (r<n). В этом случае исследование однородной системы
уравнений на общее и частные решения проводится аналогично исследованию
неоднородной системы. Решения однородной системы уравнений обладают важным
свойством: если известны два различных решения однородной системы линейных алгебраических
уравнений, то их линейная комбинация также является решением этой системы.
Нетрудно убедиться в справедливости следующей теоремы.
Это означает, что ранг r ее главной матрицы меньше числа n неизвестных (r<n). В этом случае исследование однородной системы
уравнений на общее и частные решения проводится аналогично исследованию
неоднородной системы. Решения однородной системы уравнений обладают важным
свойством: если известны два различных решения однородной системы линейных алгебраических
уравнений, то их линейная комбинация также является решением этой системы.
Нетрудно убедиться в справедливости следующей теоремы. 3
(Кронекера-Капелли) заданная система линейных алгебраических уравнений
совместна. Количество переменных n=2, т.е. r<n, значит,
система является неопределённой.
Количество базисных наборов переменных системы равно . Следовательно, базисными могут быть 6 комплектов
переменных: {x1;x2}, {x1;x3}, {x1;x4}, {x2;x3}, {x2;x4}, {x3;x4}. Рассмотрим один из них {x1;x2}. Тогда
систему, полученную в результате метода Гаусса, можно переписать в виде . Главный определитель . С помощью метода Крамера ищем общее решение системы.
3
(Кронекера-Капелли) заданная система линейных алгебраических уравнений
совместна. Количество переменных n=2, т.е. r<n, значит,
система является неопределённой.
Количество базисных наборов переменных системы равно . Следовательно, базисными могут быть 6 комплектов
переменных: {x1;x2}, {x1;x3}, {x1;x4}, {x2;x3}, {x2;x4}, {x3;x4}. Рассмотрим один из них {x1;x2}. Тогда
систему, полученную в результате метода Гаусса, можно переписать в виде . Главный определитель . С помощью метода Крамера ищем общее решение системы.
 СпрингерПлюс 4:273
СпрингерПлюс 4:273 Водная экология 42: 363-378
Водная экология 42: 363-378
 Наука об устье и водоразделе Сан-Франциско 14(1): Статья 2
Наука об устье и водоразделе Сан-Франциско 14(1): Статья 2 (2004) Экологическая сегрегация местных и чужеродных сообществ личинок рыб в южной части дельты Сакраменто-Сан-Хоакин. Страницы 67–79 в книге Ф. Фейрера, Л. Р. Брауна, Р. Л. Брауна и Дж. Дж. Орси, редакторов «История ранней жизни рыб в устье и водоразделе Сан-Франциско». Американское рыболовное общество, Симпозиум 39, Бетесда, Мэриленд
(2004) Экологическая сегрегация местных и чужеродных сообществ личинок рыб в южной части дельты Сакраменто-Сан-Хоакин. Страницы 67–79 в книге Ф. Фейрера, Л. Р. Брауна, Р. Л. Брауна и Дж. Дж. Орси, редакторов «История ранней жизни рыб в устье и водоразделе Сан-Франциско». Американское рыболовное общество, Симпозиум 39, Бетесда, Мэриленд