Тригонометрические неравенства с примерами решения
Оглавление:
Рассмотрим примеры тригонометрических неравенств. При решении таких неравенств используются свойства тригонометрических функций и их графики.
Примеры с решениями
Пример №303.Решить неравенство
Решение:
Первый способ. Построим график функции и проведем прямую (рис. 25.1).
Решить неравенство (1) — значит найти все значения , при которых соответствующие точки графика функции лежат ниже прямой и на этой прямой.
Так как функция является периодической с периодом , то достаточно найти решения неравенства (1) на отрезке длиной . В качестве такого отрезка возьмем отрезок
Прямая при пересекает график функции в точках и (рис. 25.1), абсциссы которых служат
корнями уравнения на отрезке Одним из корней этого уравнения является другим — значение
Следовательно, значения из отрезка и значения, являются решениями неравенства (1) на отрезке а множество всех решений неравенства (1) — это объединение всех отрезков каждый из которых получается из отрезка сдвигом по оси на где т. е. совокупность отрезков вида
е. совокупность отрезков вида
Ответ.
Второй способ. Решим неравенство (1) с помощью единичной окружности. Построим угол, косинус которого равен . Для этого отметим на оси точку с абсциссой, равной , и проведем через эту точку прямую , параллельную оси (рис. 25.2).
Прямая пересекает единичную окружность в точках и .
Точке соответствует угол в радиан, а точке — угол в радиан.
Из рис. 25.2 видно, что абсциссу, меньшую или равную , имеют все точки единичной окружности, расположенные слева от прямой и на самой прямой. Итак, множество всех решений неравенства (1) представляет собой совокупность отрезков вида (2).
Пример №304.Решить неравенство
Решение:
Построим график функции на отрезке и проведем прямую рис. 25.3).
Эта прямая пересекает график функции , в точках и , абсциссы и которых равны и соответственно.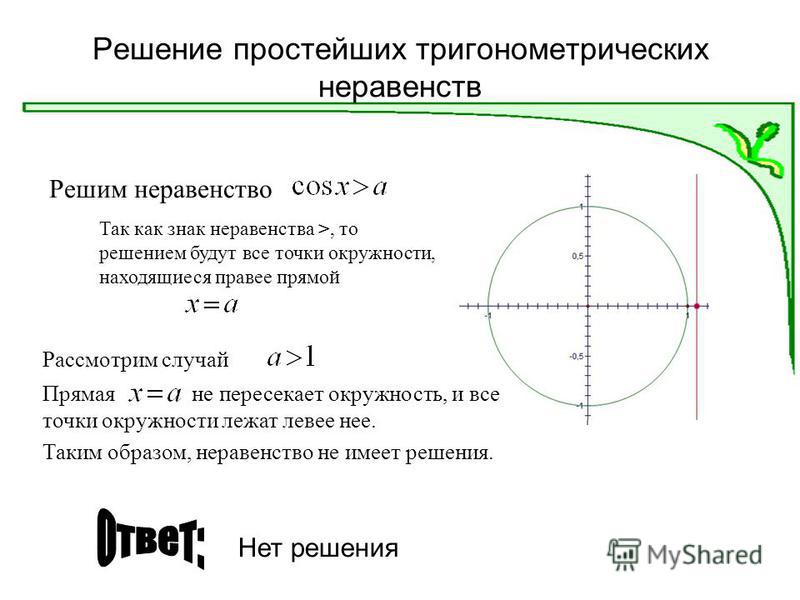 Из рис. 25.3 видно, что решения неравенства (3) на отрезке образуют интервал а множество всех решений неравенства (3) — это совокупность интервалов, каждый
Из рис. 25.3 видно, что решения неравенства (3) на отрезке образуют интервал а множество всех решений неравенства (3) — это совокупность интервалов, каждый
из которых можно получить сдвигом интервала по оси на , где
Ответ.
Пример №305.Решить неравенство
Решение:
Первый способ. Построим графики функций и (рис. 25.4). Функция является периодической с периодом . Поэтому достаточно найти решения неравенства (4) на отрезке длиной . В качестве такого отрезка выберем отрезок . На этом отрезке прямая пересекает график функции в точках и , абсциссыи которых равны и соответственно. Из рис. 25.4 видно, что решениями неравенства (4) на отрезке являются все числа интервала
Поэтому множество всех решений неравенства (4) — это объединение интервалов вида
Ответ.
Второй способ. Построим единичную окружность и проведем через точку оси с ординатой прямую , параллельную оси (см.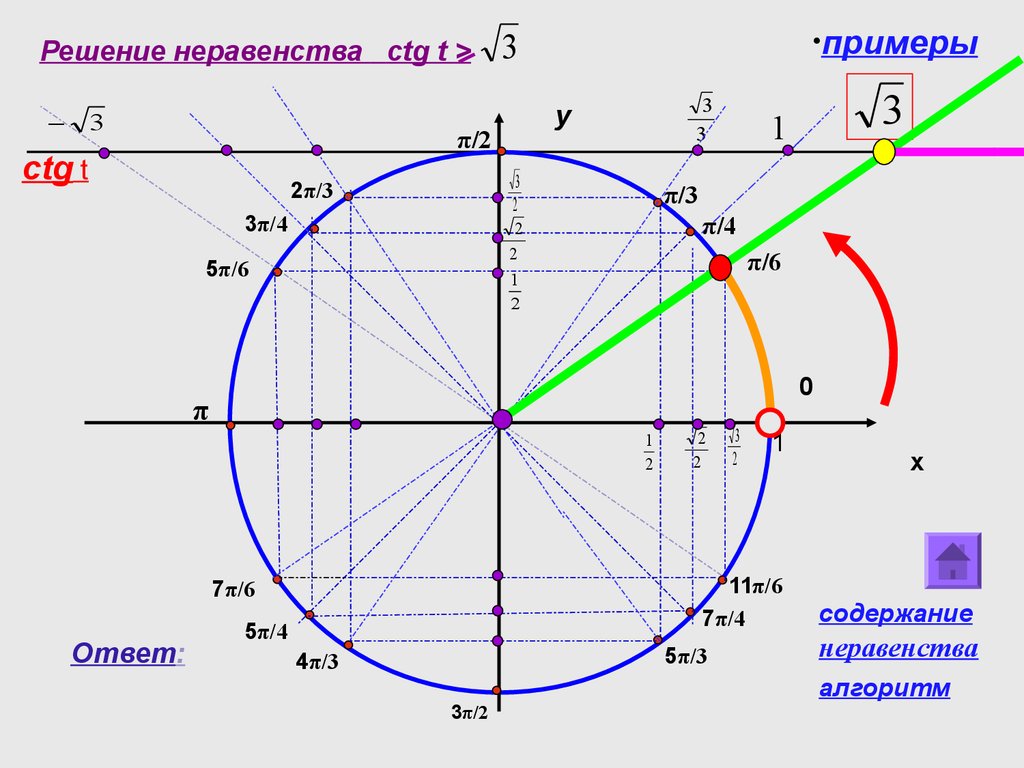 рис. 25.5).
рис. 25.5).
Прямая пересекает единичную окружность в точках и
Точке соответствует угол в радиан, а точке — угол в радиан. Из рис. 25.5 видно, что все точки единичной окружности, расположенные ниже прямой , имеют ординату, меньшую
Итак, множество всех решений неравенства (4) представляет собой совокупность интервалов вида (5).
Пример №306.Решить неравенство
Решение:
Неравенство (6) равносильно неравенству
Построим график функции и проведем прямую (рис. 25.6). Функция является периодической с периодом , а на отрезке уравнение имеет корни и Из рис. 25.6 видно, что решениями неравенства (7) на отрезке являются все числа из интервала Множество решений неравенства (7) — это объединение интервалов, каждый из которых можно получить сдвигом интервала по оси на , где
Ответ.
Пример №307.Решить неравенство
Решение:
Функция является периодической с периодом .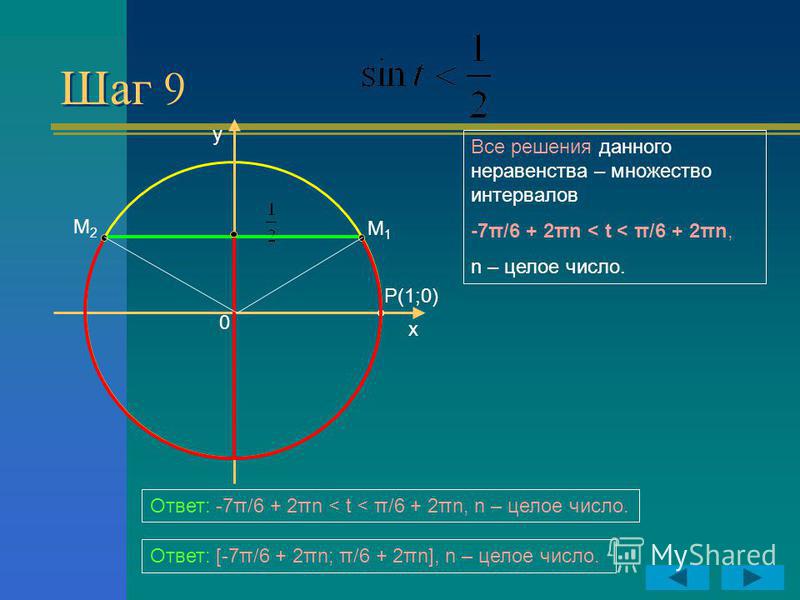 Построим график функции : на интервале и проведем прямую (см. рис. 25.7). Функция возрастает на интервале , а прямая пересекает график этой функции в точке с абсциссой .
Построим график функции : на интервале и проведем прямую (см. рис. 25.7). Функция возрастает на интервале , а прямая пересекает график этой функции в точке с абсциссой .
Поэтому решениями неравенства (8) на интервале являются все числа из интервала а множество всех решении неравенства (8) представляет собой совокупность интервалов вида
Ответ.
Пример №308.Решить неравенство
Решение:
Полагая , получаем квадратное неравенство , равносильное неравенству
Поэтому неравенство (9) равносильно каждому из неравенств
На отрезке уравнение имеет корни и (см. рис. 25.1), а решениями неравенства (10) на этом отрезке являются все числа из интервала.
Множество решений неравенства (10) и равносильного ему неравенства (9) представляет собой объединение интервалов вида
Ответ.
Пример №309.Решить неравенство
Решение:
Первый способ. Используя тождество заменим неравенство (11) равносильным ему:
Используя тождество заменим неравенство (11) равносильным ему:
Как и при решении однородных тригонометрических уравнений, сведем неравенство (12) к квадратному относительно Рассмотрим два возможных случая:
1) Пусть, тогда и неравенство (12) примет вид Следовательно, все значения , удовлетворяющие уравнению , т. е. числа
являются решениями неравенства (12).
2) Пусть тогда и неравенство (12) равносильно каждому из неравенств
а неравенство (14) равносильно совокупности неравенств
На интервале решения неравенства (15) — это все числа из интервала , а решения неравенства (16) все числа из интервала Следовательно, на интервале решениями неравенства (12), равносильного (11), являются все числа из интервалов и , а также число , т. е. все числа , принадлежащие интервалу
Так как функция периодическая с периодом , то множество всех решений неравенства (12) представляет собой совокупность интервалов вида
Ответ.
Второй способ. Неравенство (11) равносильно каждому из следующих неравенств:
где Отсюда находим
Заметим, что
где Поэтому двойное неравенство (18) но записать в виде (17).
Пример №310.Решить неравенство
Решение:
Найдем решения неравенства на отрезке длиной . Все значения из интервала — решения неравенства, так как при а левая часть неравенства определена и неотрицательна при всех .
Пусть , тогда исходное неравенство равносильно каждому из неравенств
Так как то откуда
Итак, на отрезке , решениями исходного неравенства являются все числа из интервала
Ответ.
Пример №311.Доказать, что если — углы треугольника, то
Решение:
Обозначим левую часть неравенства (19) через и выразим произведение синусов через разность косинусов.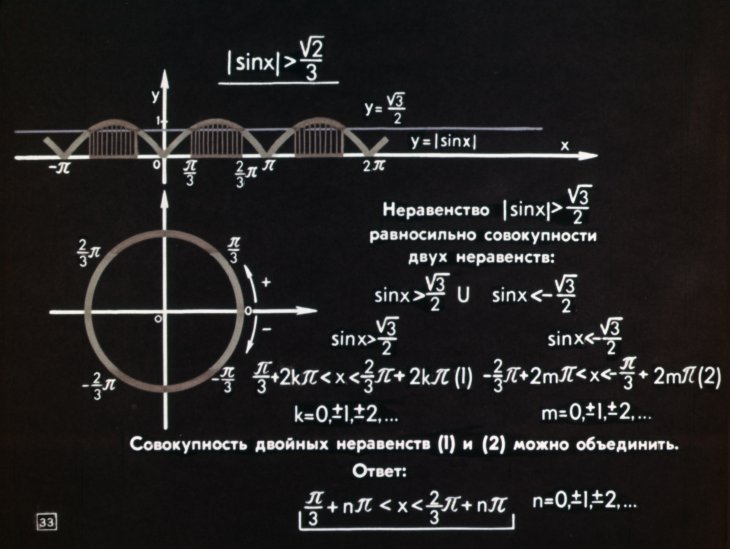 Тогда получим
Тогда получим
так как Полагая и применяя метод выделения полного квадрата, имеем
откуда следует, что
Неравенство (19) доказано.
Пример №312.Доказать, что если то верно неравенство
Решение:
Так как при то, разделив числитель и знаменатель левой части неравенства (20) на получим равносильное ему неравенство 1
Обозначим левую часть неравенства (21) через и воспользуемся формулой Тогда задача сведется к доказатель- ству неравенства
Полагая получаем где Заметим, что
при
и поэтому
т. е. что и требовалось доказать.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Решение задач по математике
Возможно вам будут полезны эти страницы:
Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет.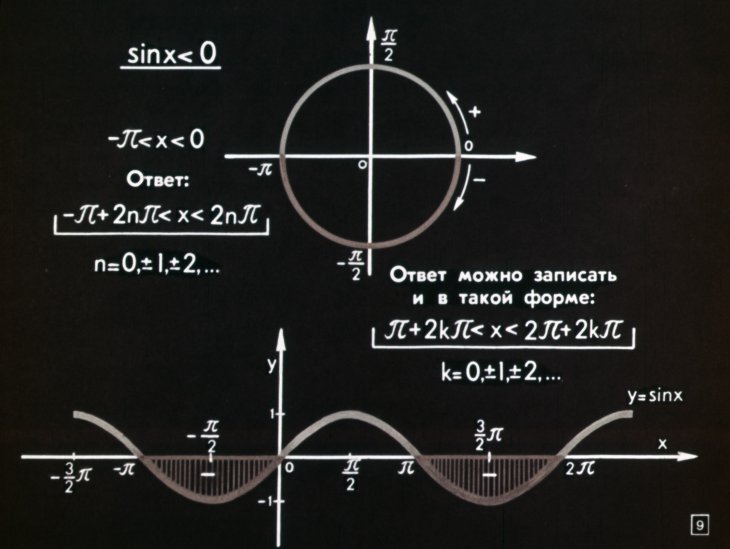 На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
Вам нужно написать сообщение в Telegram .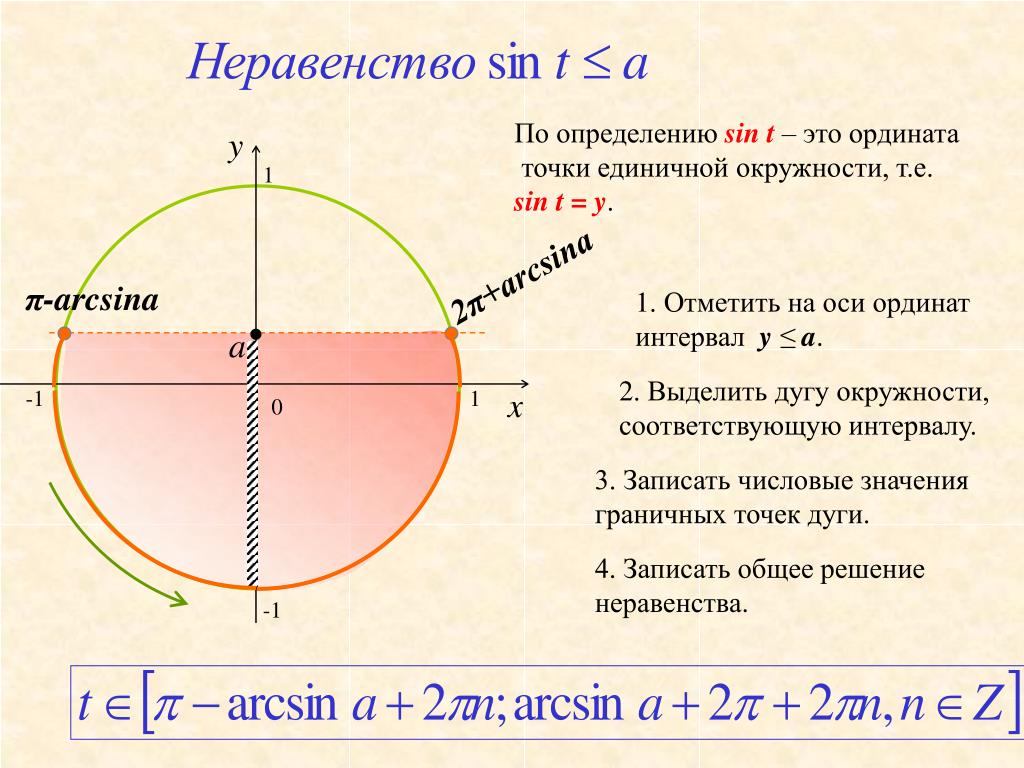 После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа?Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.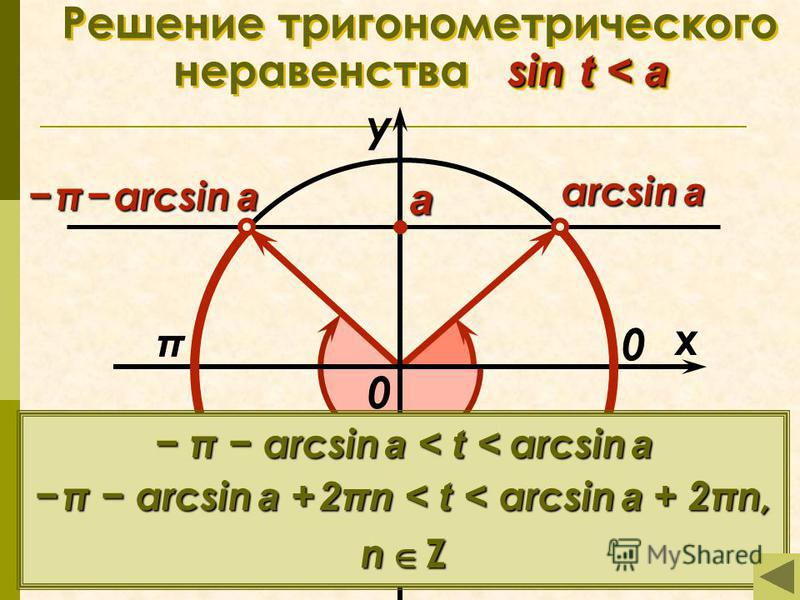
В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню.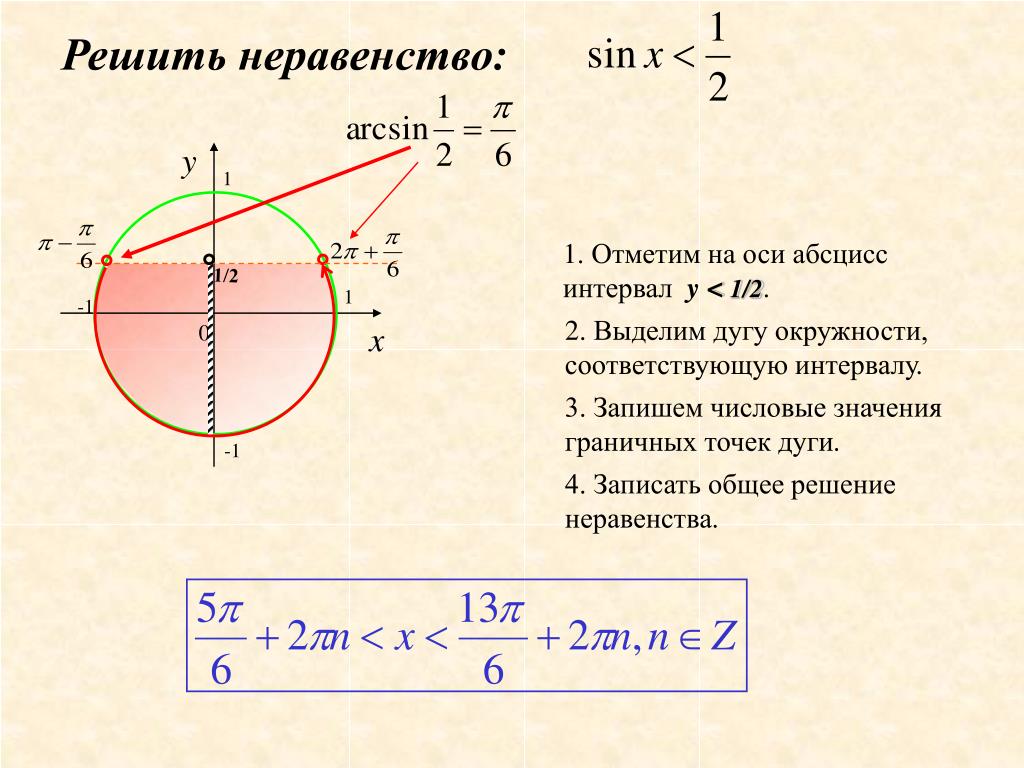
youtube.com/embed/vOuj6t2Zyeg» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/ElMEic2MJ-U» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.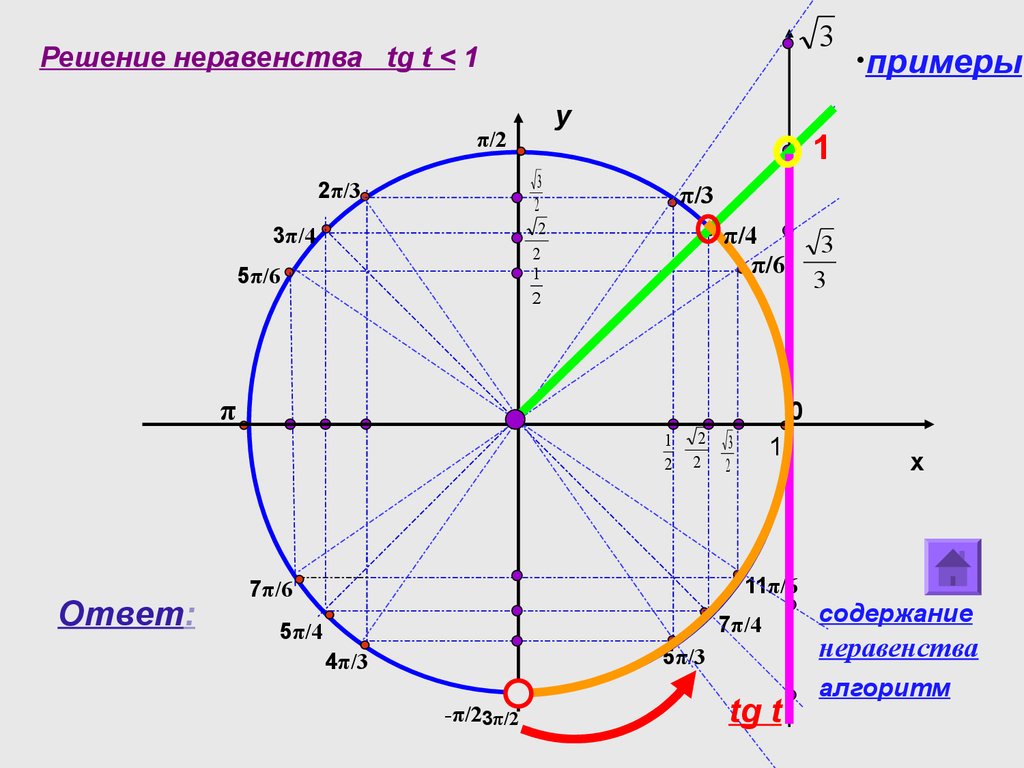
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Сколько может стоить заказ?Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.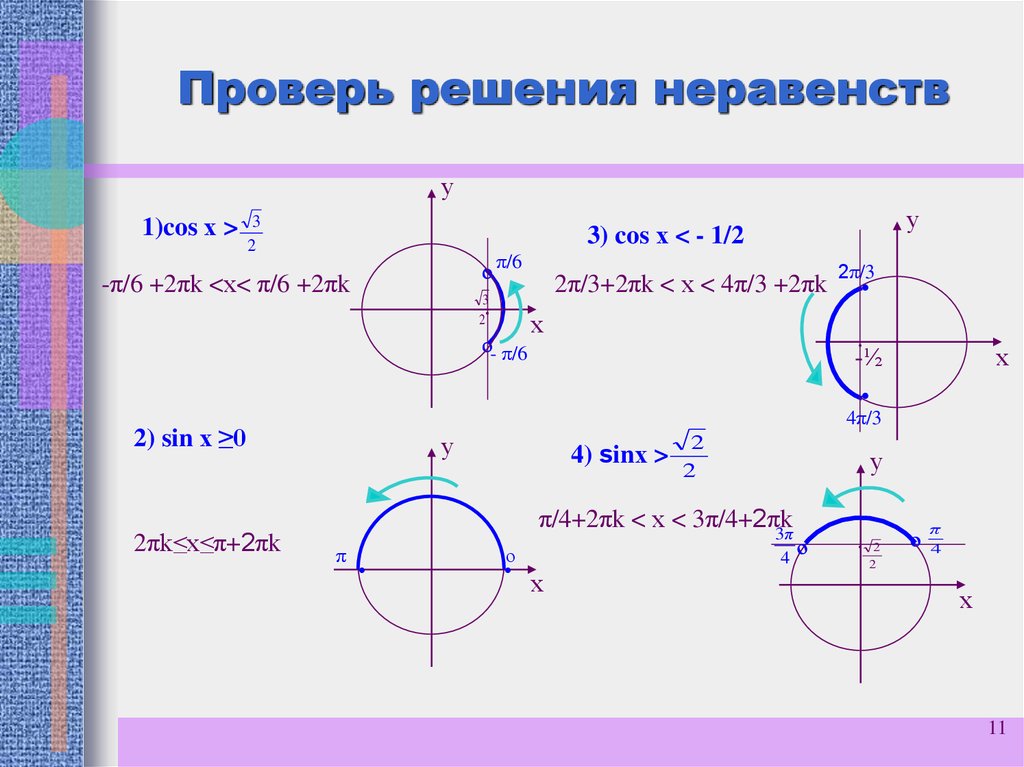
Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Какие гарантии и вы исправляете ошибки?В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
youtube.com/embed/FTtp-vAv3lI» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/7LD4euDcivY» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/ZfNUaigadEY» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
Основные тригонометрические неравенства
Неизвестная переменная (угол): x
Набор целых чисел: ℤ
Целое число: n
Набор действительных чисел: ℝ
Реальное число: A
Тригонометрические функции: SIN x , COS X , TAN X , COT X
Обратные тригонометрические функции: Arcsin A , Arccos A , Arctan A A , Arccos A , Arctan A 44444444444444444 A 444444444444444 A 444444444444444 A 444444444444444 A 444444444444444.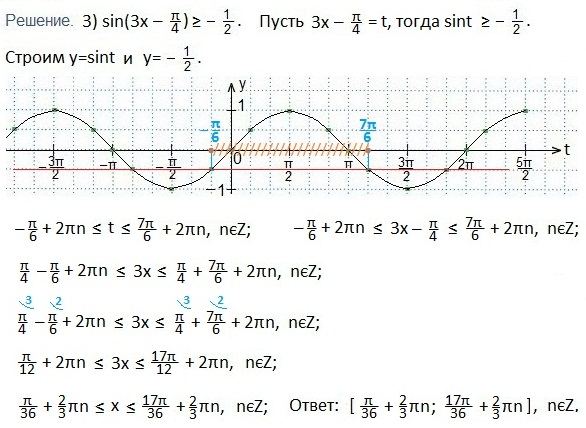 , арккот и
, арккот и
Неравенство, включающее тригонометрические функции неизвестного угла, называется тригонометрическим неравенством.
Следующие \(16\) неравенства относятся к основным тригонометрическим неравенствам:
\[\sin x \gt a,\; \sin x \ge a,\; \sin x \lt a,\; \sin x \le a,\]
\[\cos x \gt a,\; \cos x \ge a,\; \cos x \lt a,\; \cos х \ле а,\]
\[\tan x \gt a,\; \тан х \ге а,\; \загар х \lt а,\; \загар х \ле а,\]
\[\cot x \gt a,\; \cot x \ge a,\; \кот х \lt а,\; \cot x \le a.\]
Здесь \(x\) неизвестная переменная, \(a\) может быть любым вещественным числом.
Неравенства вида \(\sin x \gt a,\) \(\sin x \ge a,\) \(\sin x \lt a,\) \(\sin x \le a\)
Неравенство \(\sin x \gt a\)
Если \(\left| a \right| \ge 1\), то неравенство \(\sin x \gt a\) не имеет решений: \(x \in \varnothing.\)
Если \(a \lt -1\), то решением неравенства \(\sin x \gt a\) является любое действительное число: \(x \in \mathbb{R}.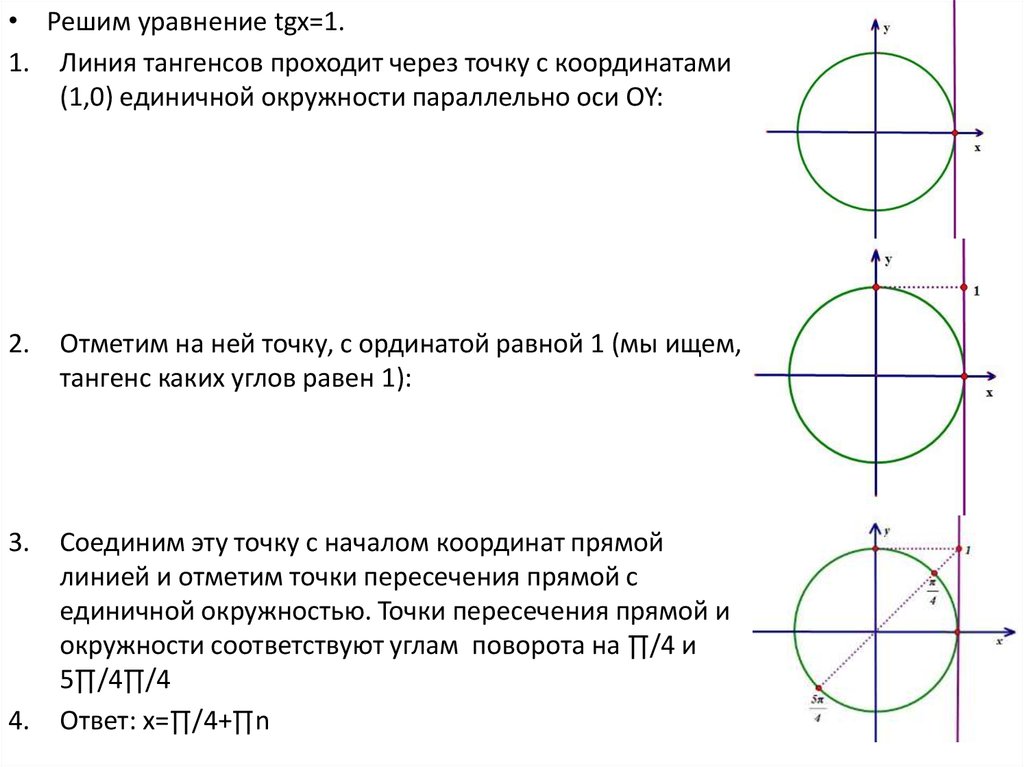 \)
\)
При \(-1 \le a \lt 1\) решение неравенства \(\sin x \gt a\) выражается в виде
\[\arcsin a + 2\pi n \lt x \lt \pi — \arcsin a + 2\pi n, \;n \in \mathbb{Z}.\]
Рис. 1.Неравенство \(\sin x \ge a\)
Если \(a \gt 1\), то неравенство \(\sin x \ge a\) не имеет решений: \(x \in \varnothing.\)
Если \(a \le -1\), то решением неравенства \(\sin x \ge a\) является любое действительное число: \(x \in \mathbb{R}.\)
Случай \(а = 1:\)
\[x = \pi/2 +2\pi n,\; n \in \mathbb{Z}.\]
При \(-1 \lt a \lt 1\) решение нестрогого неравенства \(\sin x \ge a\) включает граничные углы и имеет вид
\[\arcsin a + 2\pi n \le x \le \pi — \arcsin a + 2\pi n,\;n \in \mathbb{Z}.\]
Неравенство \(\sin x \lt a\)
Если \(a \gt 1\), то решением неравенства \(\sin x \lt a\) является любое действительное число: \(x \in \mathbb{R}.\)
Если \(a \le -1\), то неравенство \(\sin x \lt a\) не имеет решений: \(x \in \varnothing.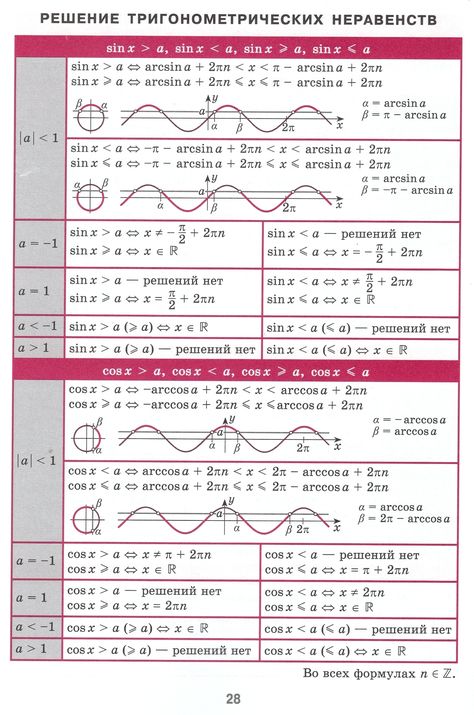 \)
\)
При \(-1 \lt a \le 1\) решение неравенства \(\sin x \lt a\) лежит в интервале
\[-\pi — \arcsin a + 2\pi n \lt x \lt \arcsin a + 2\pi n,\;n \in \mathbb{Z}.\]
Рис. 2.Неравенство \(\sin x \le a\)
Если \(a \ge 1\), то решением неравенства \(\sin x \le a\) является любое действительное число: \(x \in \mathbb{R}.\)
Если \(a \lt -1\), то неравенство \(\sin x \le a\) не имеет решений: \(x \in \varnothing.\)
Случай \(а = -1:\)
\[x = -\pi/2 + 2\pi n,\;n \in \mathbb{Z}.\]
При \(-1 \lt a \lt 1\) решение нестрогого неравенства \(\sin x \le a\) находится в интервале
\[-\pi — \arcsin a + 2\pi n \le x \le \arcsin a + 2\pi n,\;n \in \mathbb{Z}.\]
Неравенства вида \(\cos x \gt a,\) \(\cos x \ge a,\) \(\cos x \lt a,\) \(\cos x \le a\)
Неравенство \(\cos x \gt a\)
Если \(a \ge 1\), то неравенство \(\cos x \gt a\) не имеет решений: \(x \in \varnothing.\)
Если \(a \lt -1\), то решением неравенства \(\cos x \gt a\) является любое действительное число: \(x \in \mathbb{R}.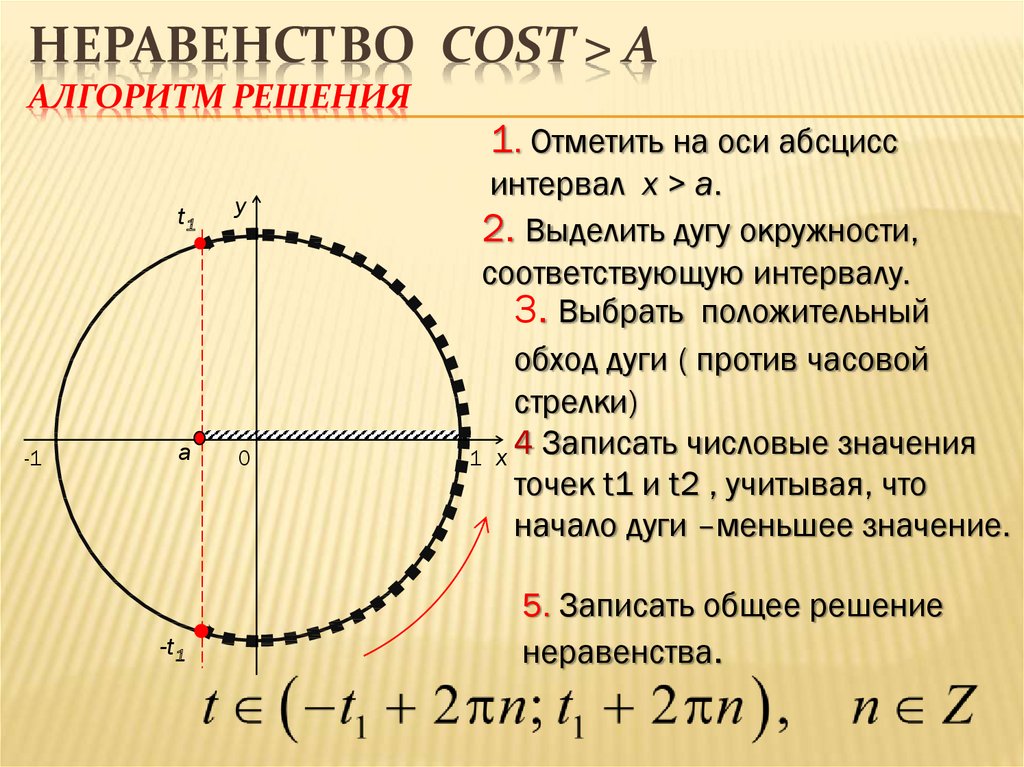 \)
\)
При \(-1 \le a \lt 1\) решение неравенства \(\cos x \gt a\) имеет вид
\[-\arccos a + 2\pi n \lt x \lt \arccos a + 2\pi n,\;n \in \mathbb{Z}.\]
Рис. 3.Неравенство \(\cos x \ge a\)
Если \(a \gt 1\), то неравенство \(\cos x \ge a\) не имеет решений: \(x \in \varnothing.\)
Если \(a \le -1\), то решением неравенства \(\cos x \ge a\) является любое действительное число: \(x \in \mathbb{R}.\)
Случай \(а = 1:\)
\[x = 2\pi n,\;n \in \mathbb{Z}.\]
При \(-1 \lt a \lt 1\) решение нестрогого неравенства \(\cos x \ge a\) выражается формулой
\[-\arccos a + 2\pi n \le x \le \arccos a + 2\pi n,\;n \in \mathbb{Z}.\]
Неравенство \(\cos x \lt a\)
Если \(a \gt 1\), то неравенство \(\cos x \lt a\) верно для любого действительного значения \(x\): \(x \in \mathbb{R}.\)
Если \(a \le -1\), то неравенство \(\cos x \lt a\) не имеет решений: \(x \in \varnothing.\)
При \(-1 \lt a \le 1\) решение неравенства \(\cos x \lt a\) записывается в виде
\[\arccos a + 2\pi n \lt x \lt 2\pi — \arccos a + 2\pi n,\;n \in \mathbb{Z}. \]
\]
Неравенство \(\cos x \le a\)
Если \(a \ge 1\), то решением неравенства \(\cos x \le a\) является любое действительное число: \(x \in \mathbb{R}.\)
Если \(a \lt -1\), то неравенство \(\cos x \le a\) не имеет решений: \(x \in \varnothing.\)
Случай \(а = -1:\)
\[x = \pi + 2\pi n,\;n \in \mathbb{Z}.\]
Для \(-1 \lt a \lt 1\) решение нестрогого неравенства \(\cos x \le a\) записывается как
\[\arccos a + 2\pi n \le x \le 2\pi — \arccos a + 2\pi n,\;n \in \mathbb{Z}.\]
Неравенства вида \(\tan x \gt a,\) \(\tan x \ge a,\) \(\tan x \lt a,\) \(\tan x \le a\)
Неравенство \(\tan x \gt a\)
Для любого действительного значения \(a\) решение строгого неравенства \(\tan x \gt a\) имеет вид
\[\arctan a + \pi n \lt x \lt \pi/2 + \pi n,\;n \in \mathbb{Z}.\]
Рис. 5.Неравенство \(\tan x \ge a\)
Для любого действительного значения \(a\) решение неравенства \(\tan x \ge a\) выражается в виде
\[\arctan a + \pi n \le x \lt \pi/2 + \pi n,\;n \in \mathbb{Z}.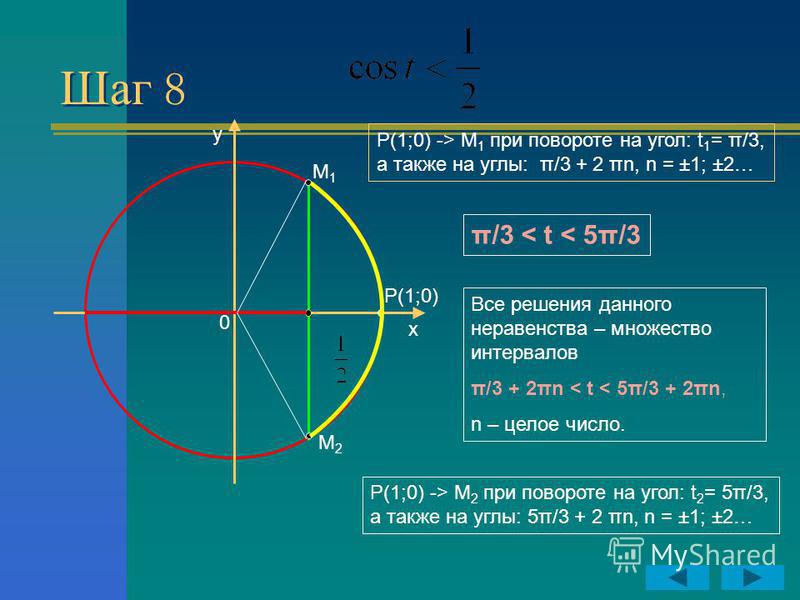 \]
\]
Неравенство \(\tan x \lt a\)
При любом значении \(a\) решение неравенства \(\tan x \lt a\) записывается в виде
\[-\pi/2 + \pi n \lt x \lt \arctan a + \pi n,\;n \in \mathbb{Z}.\]
Рис. 6.Неравенство \(\tan x \le a\)
Для любого значения \(a\) неравенство \(\tan x \le a\) имеет следующее решение:
\[-\pi/2 + \pi n \lt x \le \arctan a + \pi n,\;n \in \mathbb{Z}.\]
Неравенства вида \(\cot x \gt a,\) \(\cot x \ge a,\) \(\cot x \lt a,\) \(\cot x \le a\)
Неравенство \(\cot x \gt a\)
При любом значении \(а\) решение неравенства \(\cot x \gt a\) имеет вид
\[\pi n \lt x \lt \text {arccot } a + \pi n,\;n \in \mathbb{Z}.\]
Рис. 7.Неравенство \(\cot x \ge a\)
Нестрогое неравенство \(\cot x \ge a\) имеет аналогичное решение:
\[\pi n \lt x \le \text {arccot } a + \pi n,\;n \in \mathbb{Z}.\]
Неравенство \(\cot x \lt a\)
При любом значении \(a\) решение неравенства \(\cot x \lt a\) лежит на открытом интервале
\[\text {arccot} a + \pi n \lt x \lt \pi + \pi n,\;n \in \mathbb{Z}.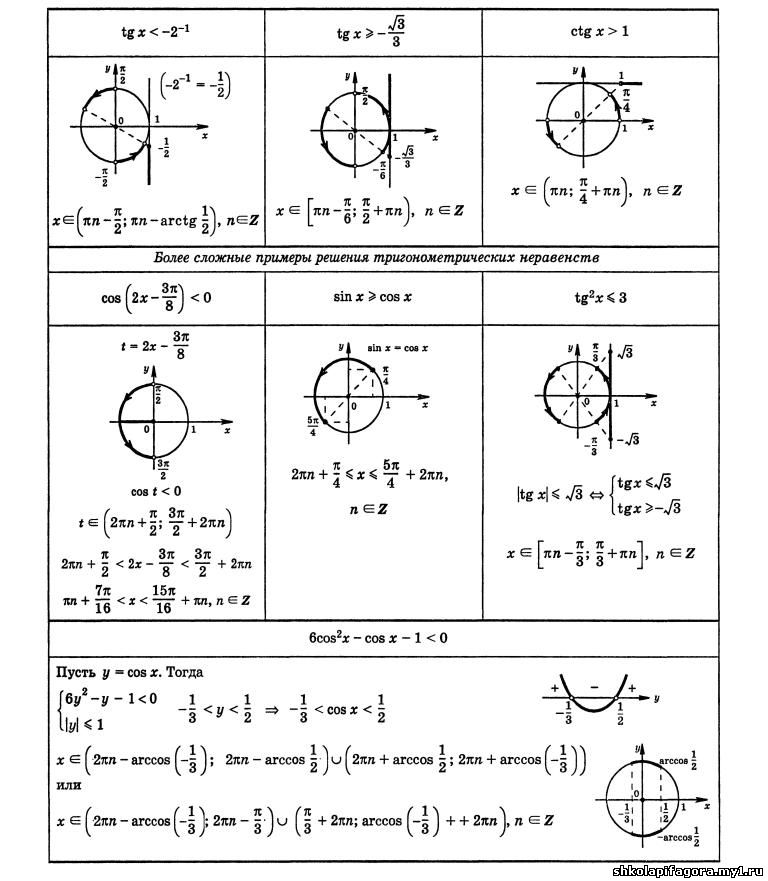 \]
\]
Неравенство \(\cot x \le a\)
При любом значении \(a\) решение нестрогого неравенства \(\cot x \le a\) находится в полуинтервале
\[\text {arccot} a + \pi n \le x \lt \pi + \pi n,\;n \in \mathbb{Z}.\]
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Решить неравенство
\[\sin x \ge -\frac{1}{2}.\]
Пример 2
Решить неравенство
\[\cos x \lt -\frac{\sqrt{2}}{2}.\]
Пример 3
Решите неравенство
\[\tan x \gt -\sqrt{3}. \]
Пример 4
Решить неравенство
\[\cot x \ge \frac{1}{\sqrt{3}}.\]
Пример 1.
Решить неравенство
\[\sin x \ge -\frac{1}{2}.\]
Раствор.
Отметить на оси \(y-\) точку \(y = -\frac{1}{2}.\) Найти углы, соответствующие данному значению синуса:
\[\sin x = -\frac{1}{2}, \стрелка вправо\]
\[x_1 = \arcsin{\left({-\frac{1}{2}}\right)} = — \ arcsin{\left({\frac{1}{2}}\right)} = — \фракция{\пи}{6};\]
\[x_2 = \pi — {x_1} = \pi — \left({-\frac{\pi}{6}}\right) = \pi + \frac{\pi}{6} = \frac{ 7\pi}{6}. \]
\]
Решение неравенства \(\sin x \ge -\frac{1}{2}\) на единичной окружности представляется в виде сектора \(\left[-\frac{\pi}{6} , \frac{7\pi}{6}\right].\) Не забудьте добавить в ответ периодические члены:
\[-\frac{\pi}{6} + 2\pi n \le x \le \frac{7\pi}{6} + 2\pi n,\;n \in \mathbb{Z}. \]
Пример 2.
Решить неравенство
\[\cos x \lt -\frac{\sqrt{2}}{2}.\]
Раствор.
Решая уравнение \(\cos x = -\frac{\sqrt{2}}{2}\) находим:
\[x = \pm\arccos\left({-\frac{\sqrt{2}}{2}}\right) + 2\pi n = \pm\left({\pi — \arccos{\frac {\ sqrt {2}} {2}}} \ справа) + 2 \ pi n = \ pm \ слева ({\ pi — \ frac {\ pi} {4}} \ справа) + 2 \ pi n = \ pm\frac{3\pi}{4} + 2\pi n,\;n \in \mathbb{Z}.\]
Обратите внимание, что угол \(-\frac{3\pi}{4}\) можно записать в виде \(\frac{5\pi}{4}.\) Следовательно, решение неравенства лежит в интервале \(\left[{\frac{3\pi}{4}, \frac{5\pi}{4}}\right].\)
Рисунок 10.Ответ дается
\[\frac{3\pi}{4} + 2\pi n \lt x \lt \frac{5\pi}{4} + 2\pi n,\;n \in \mathbb{Z}.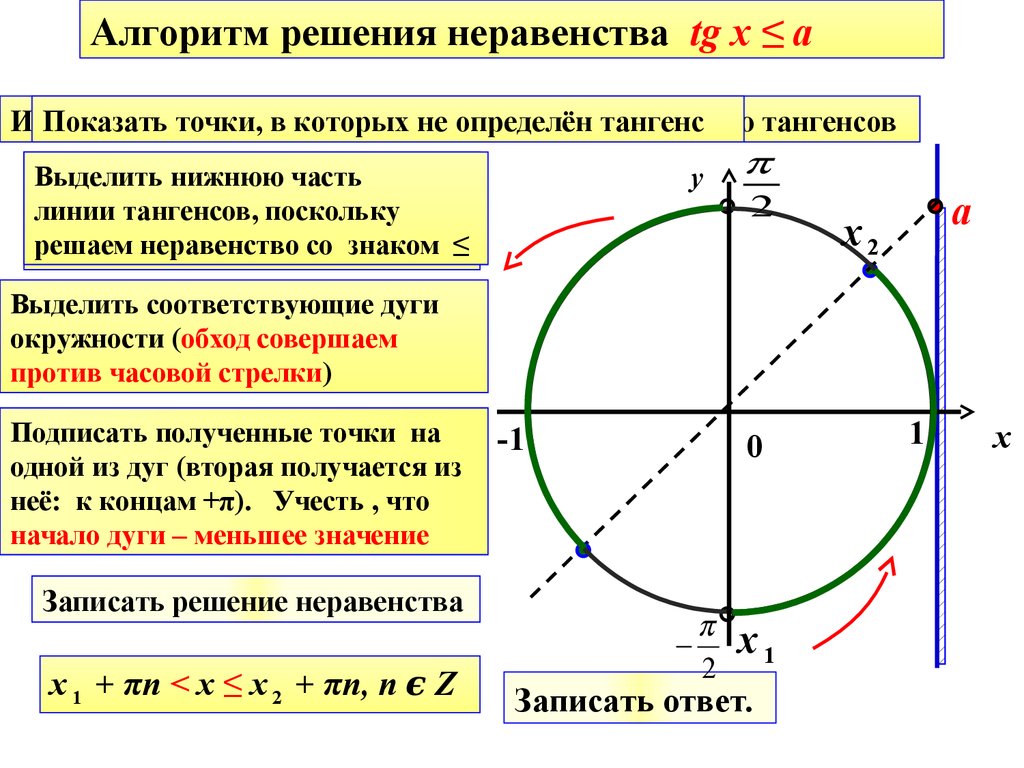 \]
\]
Пример 3.
Решить неравенство
\[\tan x \gt -\sqrt{3}.\]
Раствор.
Решение неравенства \(\tan x \gt a\) записывается в виде
\[\arctan a + \pi n \lt x \lt \pi/2 + \pi n,\;n \in \mathbb{Z}.\]
В нашем случае:
\[\arctan a = \arctan\left({-\sqrt{3}}\right) = — \arctan\sqrt{3} = -\frac{\pi}{3}.\]
Следовательно, имеем:
\[-\frac{\pi}{3} + \pi n \lt x \lt \pi/2 + \pi n,\;n \in \mathbb{Z}.\]
Рис. 11.Пример 4.
Решить неравенство
\[\cot x \ge \frac{1}{\sqrt{3}}.\]
Раствор.
Мы знаем, что решение нестрогого неравенства \(\cot x \ge a\) дается выражением
\[\pi n \lt x \le \text {arccot } a + \pi n,\;n \in \mathbb{Z}.\]
С
\[\text{arccot}\frac{1}{\sqrt{3}} = \frac{\pi}{3},\]
мы можем написать
\[\pi n \lt x \le \frac{\pi}{3} + \pi n,\;n \in \mathbb{Z}.\]
Рис. 12.Тригонометрические неравенства
11,5
Теперь мы завершим изучение неравенств рассмотрением неравенств, включающих тригонометрические члены.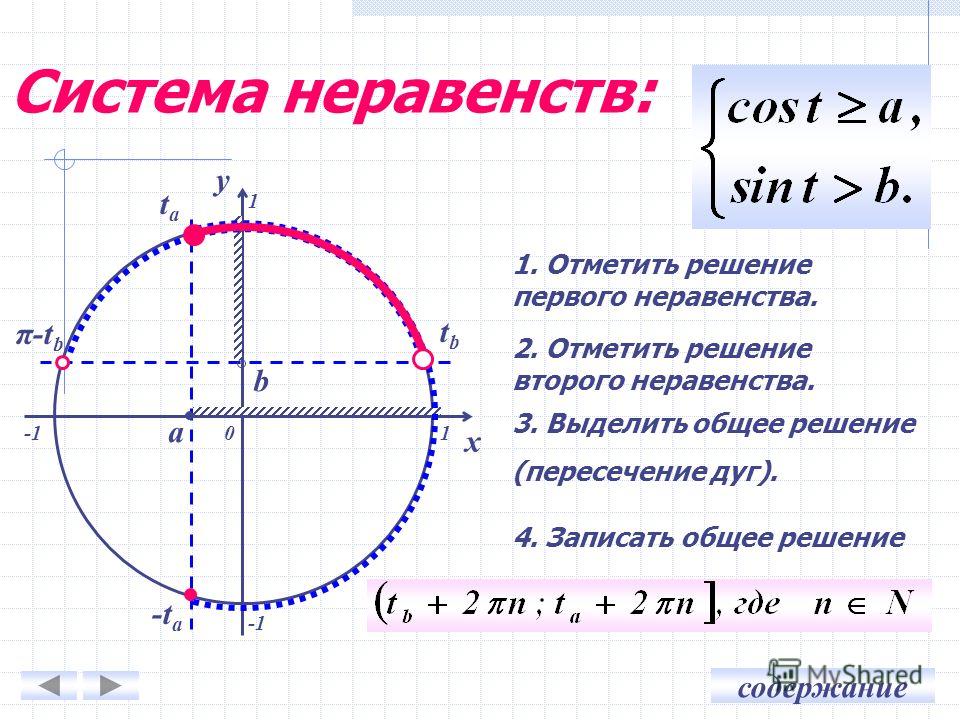
21.2
Надо сказать, что они сложнее, чем экспоненциальные или логарифмические неравенства вообще. На самом деле, я бы сказал, что они в значительной степени находятся на переднем крае того, что могут делать люди, прошедшие курс предварительного исчисления. Одна из причин, по которой они сложнее, заключается в том, что монотонность, которую мы имели для экспоненциальных функций, гораздо менее полезна, чем была. И его заменяет периодичность. А также, конечно, как обычно в тригонометрии, вам нужно хорошо разбираться во всех тех тождествах и свойствах, которые, как мы знаем, имеют место для тригонометрических функций. В качестве общего принципа можно сначала рассмотреть неравенство на подходящем интервале, охватывающем период задействованных функций, а затем найти другие решения неравенства, ссылаясь на периодичность.
72.3
Эти, возможно, расплывчатые замечания станут яснее, если мы рассмотрим определенное количество примеров. Начнем с простого неравенства типа косинус х больше или равно альфа, или, возможно, меньше или равно альфа. Первое замечание состоит в том, что если абсолютное значение альфы больше 1, то множество решений будет очевидным. Это будет либо реальная линия, либо пустой набор. Почему? Ну, потому что, например, косинус х больше минус 2 всегда верен для любого х. Или косинус х больше 3, например, невозможен. Таким образом, действительно интересен случай, когда абсолютное значение альфы меньше или равно 1,9.0013
Первое замечание состоит в том, что если абсолютное значение альфы больше 1, то множество решений будет очевидным. Это будет либо реальная линия, либо пустой набор. Почему? Ну, потому что, например, косинус х больше минус 2 всегда верен для любого х. Или косинус х больше 3, например, невозможен. Таким образом, действительно интересен случай, когда абсолютное значение альфы меньше или равно 1,9.0013
115,5
В этом случае существует конкретный угол a, косинус которого равен альфа. Это угол, который мы назвали арккосинусом альфа, и он лежит, как вы помните, в интервале 0 pi. Таким образом, два рассматриваемых нами неравенства будут косинусом x больше или равным cos a или меньшим или равным. Начнем с первого. Как решить это неравенство? Один из способов сделать это — посмотреть на график функции косинуса, что мы действительно должны знать очень хорошо. Вот угол а. Он находится между 0 и пи и генерирует определенное значение косинуса.
153.8
И мы ищем те точки, для которых косинус x будет хотя бы равен этому же значению.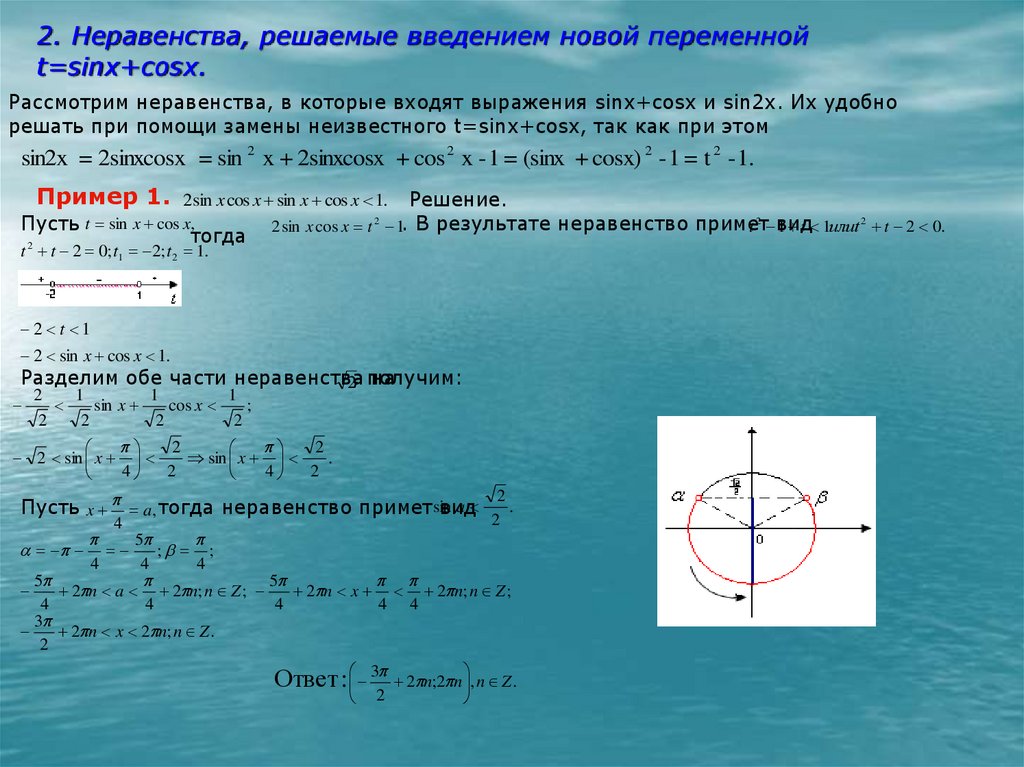 Ну, если вы посмотрите вокруг точки а, вы увидите, что эти точки будут слева от а, пока вы не достигнете определенного другого угла. Что это за другой угол? Ну, вы можете видеть по симметрии, что это угол минус а, тот, у которого тот же косинус, что и а.
Ну, если вы посмотрите вокруг точки а, вы увидите, что эти точки будут слева от а, пока вы не достигнете определенного другого угла. Что это за другой угол? Ну, вы можете видеть по симметрии, что это угол минус а, тот, у которого тот же косинус, что и а.
177,6
Кроме того, вы можете видеть, что в интервале минус пи до пи, который является интервалом длины 2 пи, который является периодом задействованной функции, единственные решения, для которых cos x будет больше или равен cos a — это те, которые находятся в интервале от минус a до a. И это говорит вам, где должен лежать x, чтобы быть решением нашего неравенства относительно интервала минус пи до пи. Конечно, учитывая, что косинус периодичен с периодом 2 пи, будет много других значений x, удовлетворяющих тому же неравенству.
212,2
Они будут в каком-то другом интервале, и мы можем получить их все, просто добавив к тем, которые мы уже идентифицировали, любое целое число, кратное 2 pi, где целое число k либо положительное, либо отрицательное. Условное обозначение здесь: когда я беру интервал минус -а, а и добавляю число вроде 2k pi, это означает, что я взял интервал, состоящий из всех чисел в исходном интервале, к которому я добавил это. Другими словами, это интервал от минус плюс плюс 2 к пи до плюс 2 к пи. Нотативное соглашение. Теперь давайте рассмотрим другой случай, когда косинус x меньше или равен cos a.
Условное обозначение здесь: когда я беру интервал минус -а, а и добавляю число вроде 2k pi, это означает, что я взял интервал, состоящий из всех чисел в исходном интервале, к которому я добавил это. Другими словами, это интервал от минус плюс плюс 2 к пи до плюс 2 к пи. Нотативное соглашение. Теперь давайте рассмотрим другой случай, когда косинус x меньше или равен cos a.
253,8
Это можно решить довольно похожим образом, взглянув на график функции косинуса. Вот угол а. Он генерирует определенный косинус. Теперь мы ищем x, чье значение косинуса меньше косинуса a. И мы видим, что справа, под определенным углом, который, как мы видим по симметрии, равен 2 пи минус а, эти косинусы будут меньше или равны тому, что они были в точке а. И далее мы видим, что относительно интервала 0, 2 пи, это единственные иксы, те, что в этом интервале, от а до 2 пи минус а, для которых косинус будет меньше, чем он был при а.
296
Это немедленно дает нам первую оценку нашего набора решений, интервал от a до 2 pi минус a. Но, конечно, будет много других решений на других интервалах длины 2 pi. И мы фиксируем их, добавляя к этому интервалу 2k pi, где k — любое положительное или отрицательное целое число. Итак, мы нашли решения в обоих случаях нашего простого неравенства. Давайте используем пример того, как мы можем применить это к неравенствам, таким как cos x меньше минус 1/2. Что мы должны сделать в первую очередь? Итак, нам нужно найти угол, косинус которого равен минус 1/2. Достаточно легко сделать. Это 2 пи больше 3,
Но, конечно, будет много других решений на других интервалах длины 2 pi. И мы фиксируем их, добавляя к этому интервалу 2k pi, где k — любое положительное или отрицательное целое число. Итак, мы нашли решения в обоих случаях нашего простого неравенства. Давайте используем пример того, как мы можем применить это к неравенствам, таким как cos x меньше минус 1/2. Что мы должны сделать в первую очередь? Итак, нам нужно найти угол, косинус которого равен минус 1/2. Достаточно легко сделать. Это 2 пи больше 3,
339,8
Итак, мы находим cos x меньше косинуса 2 pi больше 3. Мы могли бы сделать это графически, как я только что проиллюстрировал. Но есть еще одна техника, которую я хотел бы показать вам. Он использует круговое определение синуса и косинуса, вещь единичного круга. Если вы посмотрите на угол 2 пи на 3 и посмотрите на соответствующую ему точку на единичной окружности, косинус минус 1/2 будет координатой x этой точки. Какие точки на единичной окружности будут иметь координату x меньше минус 1/2? Ну, вы можете определить их довольно легко. Они будут слева от этого вертикального сегмента.
Они будут слева от этого вертикального сегмента.
381,3
И синяя точка, которая дает вам нижнюю точку, соответствует углу минус 2 пи на 3. Помните, что косинус четный, и косинус минус 2 пи на 3 будет таким же, как косинус 2 число пи больше 3. Теперь какие точки вы пытаетесь захватить? Те точки, которые лежат слева от этого вертикального сегмента. Как вы выражаете этот вертикальный сегмент? Какие в нем углы? Ну, это будут углы между этим. Теперь я выразил свой угол минус 2 пи на 3 в эквивалентной форме как 4 пи на 3. Это будут углы до этой точки, но начиная с 2 пи на 3,9.0013
420,3
Другими словами, это будут все углы между 2 пи на 3 и 4 пи на 3. И это наш набор решений. За исключением того, что периодичность даст нам другие решения. Так что, конечно, мне нужно добавить к этому любое целое число, кратное 2 пи, положительное или отрицательное. Мы могли бы решить это, взглянув на график косинуса, а также альтернативный метод. Кому-то проще. Некоторые люди предпочитают единичный круг. Как бы это работало графически? Итак, мы смотрим на наш угол 2 пи на 3. Он генерирует определенное значение косинуса. Мы ищем x, которые дают вам что-то меньшее. Они явно смещены вправо. Они доходят до 4 пи на 3,9.0013
Как бы это работало графически? Итак, мы смотрим на наш угол 2 пи на 3. Он генерирует определенное значение косинуса. Мы ищем x, которые дают вам что-то меньшее. Они явно смещены вправо. Они доходят до 4 пи на 3,9.0013
466,1
И когда мы смотрим на интервал 0, 2 пи, мы видим, что это единственные x, которые будут генерировать косинус меньше минус 1/2. И это дает нам тот же ответ. Теперь точно такие же рассуждения, какие мы применяли к косинусу, применимы и к синусу. И мы можем решать такие неравенства, как синус х меньше или равно синусу а, почти таким же образом. Теперь а будет между минус пи более 2 и пи более 2, потому что именно здесь функция арксинуса принимает свои значения. Простой пример. Найдите x, для которых синус x меньше или равен корню 3 из 2. Начнем с поиска угла, синус которого равен корню 3 из 2.
511,6
Это, конечно, пи больше 3. Это одно из наших известных значений, которое мы знаем наизусть. И как мы поступим? Ну, графически мы смотрим на число пи больше 3, и оно генерирует определенный синус.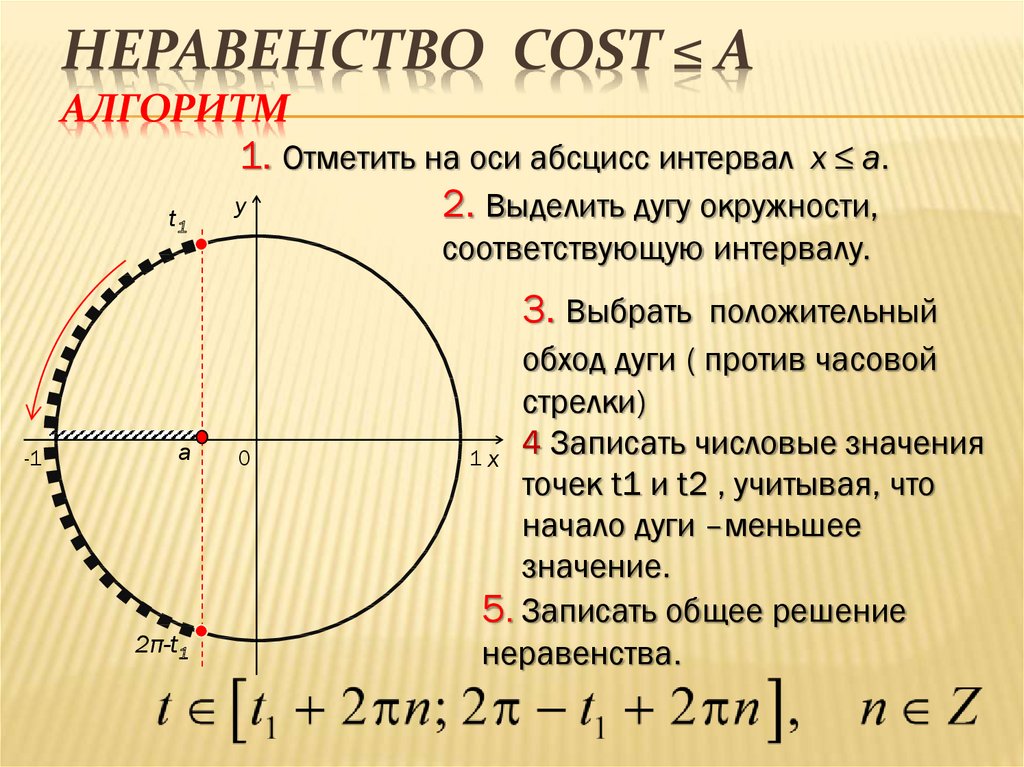 И мы ищем x, для которых синус не больше. Настолько ясно, что мы сдвинулись влево до определенного угла, у которого такой же синус, как и у пи на 3. Что это за угол? Это дополнительный угол. В данном случае минус 4 пи больше 3. Теперь на интервале от минус пи до пи не совсем понятно, есть ли у нас единственные решения.
И мы ищем x, для которых синус не больше. Настолько ясно, что мы сдвинулись влево до определенного угла, у которого такой же синус, как и у пи на 3. Что это за угол? Это дополнительный угол. В данном случае минус 4 пи больше 3. Теперь на интервале от минус пи до пи не совсем понятно, есть ли у нас единственные решения.
550,7
Поэтому лучше сдвинуть интервал влево, чтобы мы, очевидно, захватили все возможные решения неравенства на интервале длины 2 pi. Этот интервал, конечно, представляет собой интервал минус 3 пи на 2 до пи на 2. Теперь мы можем быть совершенно уверены, что в этом интервале единственными решениями являются те, которые находятся в обозначенном интервале. Итак, мы берем этот интервал, но, конечно же, мы продолжаем добавлять 2k pi, чтобы захватить по периодичности все остальные решения.
586,4
Мы могли бы решить эту задачу с помощью метода единичного круга. Укажем, как это будет работать. Это изображение, которое вы будете использовать для решения этого неравенства.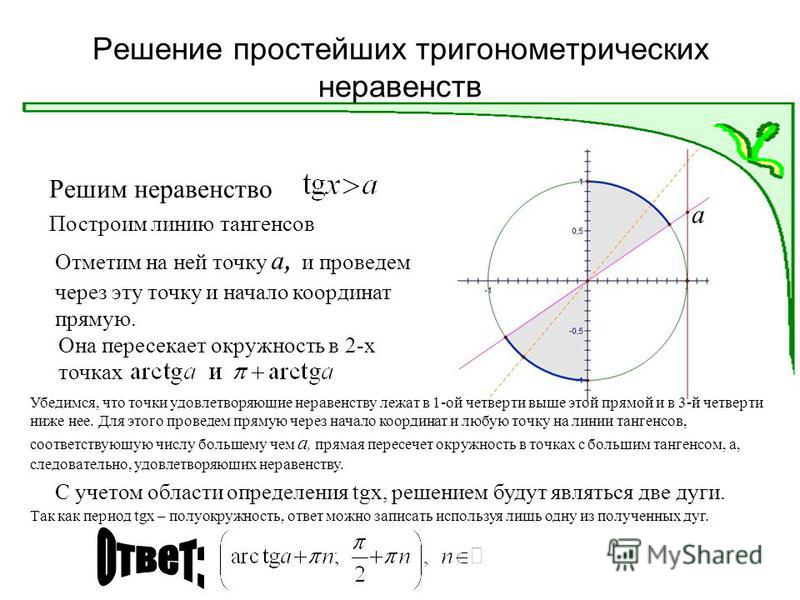 Чему соответствует эта картинка? Ну, во-первых, мы определили угол пи над 3 и поставили точку на единичной окружности, которой он соответствует. Затем мы нашли угол, для которого синус был одинаковым, а именно дополнительный угол 2 пи к 3. А теперь мы смотрим на точки, которые мы хотим определить как решения нашего неравенства на единичной окружности. Это означает, что координата y, синус x, не должна быть больше, чем для этих двух точек.
Чему соответствует эта картинка? Ну, во-первых, мы определили угол пи над 3 и поставили точку на единичной окружности, которой он соответствует. Затем мы нашли угол, для которого синус был одинаковым, а именно дополнительный угол 2 пи к 3. А теперь мы смотрим на точки, которые мы хотим определить как решения нашего неравенства на единичной окружности. Это означает, что координата y, синус x, не должна быть больше, чем для этих двух точек.
629.1
Это означает, что мы не в секторе выше. Мы скорее в составе этого сектора. Как мы выражаем дополнение этого сектора? Что ж, мы видим, что он состоит из всех углов между минус 4 пи на 3 и пи на 3, что дает нам этот интервал как наш начальный набор решений. А затем применяем периодичность. Мы добавляем к этому 2 k pi, чтобы найти множество всех решений. И, конечно же, мы получаем тот же ответ, что и графическим методом. Теперь вы заметили, что даже при решении этих простых неравенств вам действительно приходилось учитывать задействованный метод.
669,2
И вам пришлось немало поразмыслить на всем протяжении, будь то графически или с единичными кругами. Я бы сказал, что если вы можете правильно решить такие виды неравенства, вы принадлежите к элите неравенства.
Методы решения тригонометрических неравенств и их систем. Простейшие и сложные тригонометрические неравенства
Неравенства — это отношения вида а › b, где а и b — выражения, содержащие хотя бы одну переменную. Неравенства могут быть строгими — ‹, › и нестрогими — ≥, ≤.
Тригонометрические неравенства представляют собой выражения вида: F(x) > a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, в которых F(x) представлен одним или несколькими тригонометрические функции.
Пример простейшего тригонометрического неравенства: sin x ‹ 1/2. Такие задачи принято решать графически; для этого разработаны два метода.
Способ 1. Решение неравенств путем построения графика функции
Чтобы найти интервал, удовлетворяющий условиям неравенства sin x ‹ 1/2, необходимо сделать следующее:
- По оси координат построить синусоиду y = sin x.

- Начертите график на той же оси числового аргумента неравенства, т. е. прямой линии, проходящей через точку ½ ординаты y.
- Отметьте точки пересечения двух графиков.
- Закрасьте отрезок, являющийся решением примера.
Если в выражении есть сильные знаки, точки пересечения не являются решениями. Так как наименьшая синусоида положительного периода равна 2π, то ответ запишем так:
Если знаки выражения нестрогие, то интервал решений должен быть заключен в квадратные скобки- . Ответ на задачу также можно записать в виде другого неравенства:
Способ 2 — Решение тригонометрических неравенств с помощью единичной окружности
Подобные задачи легко решаются с помощью тригонометрической окружности. Алгоритм поиска очень прост:
- Сначала нарисуйте единичный круг.
- Затем нужно отметить значение дуговой функции аргумента правой части неравенства на дуге окружности.
- Необходимо провести прямую линию, проходящую через значение функции дуги параллельно оси x (OX).

- После этого остается только выбрать дугу окружности, являющуюся множеством решений тригонометрического неравенства.
- Запишите ответ в нужной форме.
Разберем шаги решения на примере неравенства sin x › 1/2. На окружности отмечены точки α и β – значения
Точки дуги, расположенные выше α и β, являются интервалом решения данного неравенства.
Если нужно решить пример на cos, то дуга ответов будет располагаться симметрично оси ОХ, а не OY. Разницу между интервалами решения для sin и cos можно рассмотреть на диаграммах ниже по тексту.
Графические решения для тангенса и котангенса неравенств будут отличаться как от синуса, так и от косинуса. Это связано со свойствами функций.
Арктангенс и арктангенс касаются тригонометрической окружности, а минимальный положительный период для обеих функций равен π. Для того, чтобы быстро и правильно использовать второй способ, нужно помнить, на какой оси лежат значения sin, cos, tg и ctg.
Тангенс Тангенс проходит параллельно оси OY. Если на единичную окружность нанести значение arctg a, то вторая искомая точка будет располагаться в диагональной четверти. углы
Они являются точками останова для функции, так как график стремится к ним, но никогда не достигает их.
В случае котангенса тангенс проходит параллельно оси OX, и функция прерывается в точках π и 2π.
Если аргумент функции неравенства представлен не просто переменной, а целым выражением, содержащим неизвестную, то речь уже идет о комплексном неравенстве. Ход и порядок ее решения несколько отличаются от описанных выше способов. Предположим, нам нужно найти решение следующего неравенства:
Графическое решение предусматривает построение обыкновенной синусоиды y = sin x для произвольно выбранных значений x. Рассчитаем таблицу с координатами опорных точек графика:
В результате должна получиться красивая кривая.
Для простоты поиска решения заменяем аргумент сложной функции
Алгоритм решения простейших тригонометрических неравенств и распознавания способов решения тригонометрических неравенств.
Преподаватели высшей квалификационной категории:
Ширко Ф.М. Поселок Прогресс, МОБУ-СОШ №6
Санкина Л.С. Армавир, ДОУ СОШ «Новый путь»
Не существует универсальных приемов преподавания дисциплин естественно-математического цикла. Каждый учитель находит свои способы преподавания, приемлемые только для него.
Наш многолетний опыт преподавания показывает, что учащиеся могут легче усваивают материал, требующий концентрации внимания и хранения большого количества информации в памяти, если их учат использовать алгоритмы в своей работе Начальный этап изучения трудной темы Такой темой, на наш взгляд, является тема решения тригонометрических неравенств.
Итак, прежде чем мы начнем вместе со студентами выявлять приемы и способы решения тригонометрических неравенств, отработаем и закрепим алгоритм решения простейших тригонометрических неравенств.
Алгоритм решения простейших тригонометрических неравенств
Отмечаем точки на соответствующей оси ( для грех x — ось Y, для cos x — Ось OX )
Восстанавливаем перпендикуляр к оси, который будет пересекать окружность в двух точках.
Сначала на окружности подписываем точку, принадлежащую интервалу диапазона значений дуговой функции по определению.
Начиная с отмеченной точки, заштриховываем дугу окружности, соответствующую заштрихованной части оси.
Особое внимание обращаем в сторону обхода. Если обход по часовой стрелке (т.е. есть переход через 0), то вторая точка на окружности будет отрицательной, если против часовой стрелки — положительной.
Ответ запишем в виде интервала с учетом периодичности функции.
Рассмотрим работу алгоритма на примерах.
1) грех ≥ 1/2;
Решение:
Начертить единичный круг.;
Отмечаем точку ½ на оси Y.
Восстановление перпендикуляра к оси,
, который пересекает окружность в двух точках.
По определению арксинуса сначала отмечаем
точка π/6.
Заштриховываем ту часть оси, которая соответствует
при заданном неравенстве выше точки ½.
Заштриховываем дугу окружности, соответствующую заштрихованной части оси.
Обход производится против часовой стрелки, мы получили точку 5π/6.
Ответ запишем в виде интервала с учетом периодичности функции;
Ответ: x ;[π/6 + 2π n , 5π/6 + 2π n ], n Z.
Простейшее неравенство, если решить по тому же алгоритму нет табличного значения в записи ответа.
Учащиеся, на первых уроках, решая неравенства у доски, проговаривают вслух каждый шаг алгоритма.
2) 5 потому что х – 1 ≥ 0;
R Решение: at
5 cos x – 1 ≥ 0;
x ≥ 1/5;
Нарисуйте единичный круг.
Отмечаем на оси ОХ точку с координатой 1/5.
Восстанавливаем перпендикуляр к оси, который
пересекает окружность в двух точках.
Сначала на окружности подписываем точку, которая принадлежит интервалу диапазона значений арккосинуса по определению (0; π).
Заштриховываем ту часть оси, которая соответствует этому неравенству.
Начиная с точки со знаком arccos 1/5, заштрихуйте дугу окружности, соответствующую заштрихованной части оси.
Обход производится по часовой стрелке (т.е. идет переход через 0), значит вторая точка на окружности будет отрицательной — arccos 1/5.
Ответ запишем в виде интервала с учетом периодичности функции от меньшего значения к большему.
Ответ: x [- Arccos 1/5 + 2π N , Arccos 1/5 + 2π N ], N Z.
Улучшая способность к мощности. неравенствам облегчают вопросы: «Как будем решать группу неравенств?»; «Чем одно неравенство отличается от другого?»; «Чем одно неравенство похоже на другое?»; Как изменится ответ, если будет задано строгое неравенство? Как бы изменился ответ, если бы вместо знака «» стоял знак «»
Задача анализа списка неравенств с точки зрения способов их решения позволяет отработать их распознавание.
