Как определить точку разрыва функции через предел. Точки разрыва функции и их виды
Если функция f (x ) не является непрерывной в точке x = a , то говорят, что f (x ) имеетразрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a , а две имеют разрыв.
Непрерывна при x = a . | Имеет разрыв при x = a . | |
Непрерывна при x = a . | Имеет разрыв при x = a . | |
Рисунок 1. | ||
Классификация точек разрыва функции
Все точки разрыва функции разделяются наточки разрыва первого и второго рода .
Говорят, что функция f (x ) имеетточку разрыва первого рода при x = a , если в это точке
При этом возможно следующие два случая:
Функция f (x )
имеетточку разрыва второго рода при x = a , если по крайней мере один из односторонних пределов не существует или равен бесконечности.
Пример3 .13 Рассмотрим функцию(функция Хевисайда ) на отрезке,. Тогданепрерывна на отрезке(несмотря на то, что в точкеона имеет разрыв первого рода).
Рис.3 .15 .График функции Хевисайда
Аналогичное определение можно дать и для полуинтервалов видаи, включая случаии. Однако можно обобщить данное определение на случай произвольного подмножестваследующим образом. Введём сначала понятиеиндуцированной
набазы: пусть — база, все окончаниякоторой имеют непустые пересечения с. Обозначимчерези рассмотрим множество всех. Нетрудно тогда проверить, что множествобудет базой. Тем самым дляопределены базы,и, где,и — базы непроколотых двусторонних (соответственно левых, правых) окрестностей точки(их определение см.
Свойства функций, непрерывных на отрезке.
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [ a , b ] выполняется условие — M £ f (x ) £ M .
Доказательство этого свойства основано на том, что функция, непрерывная в точке х 0 , ограничена в некоторой ее окрестности, а если разбивать отрезок [ a , b ] на бесконечное количество отрезков, которые “стягиваются” к точке х 0 , то образуется некоторая окрестность точки х 0 .
Свойство 2: Функция, непрерывная на отрезке [ a , b ], принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения х 1 и х 2 , что f (x 1 ) = m , f (x 2 ) = M , причем
m £ f (x ) £ M
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например —
f
(x
) =
sinx
).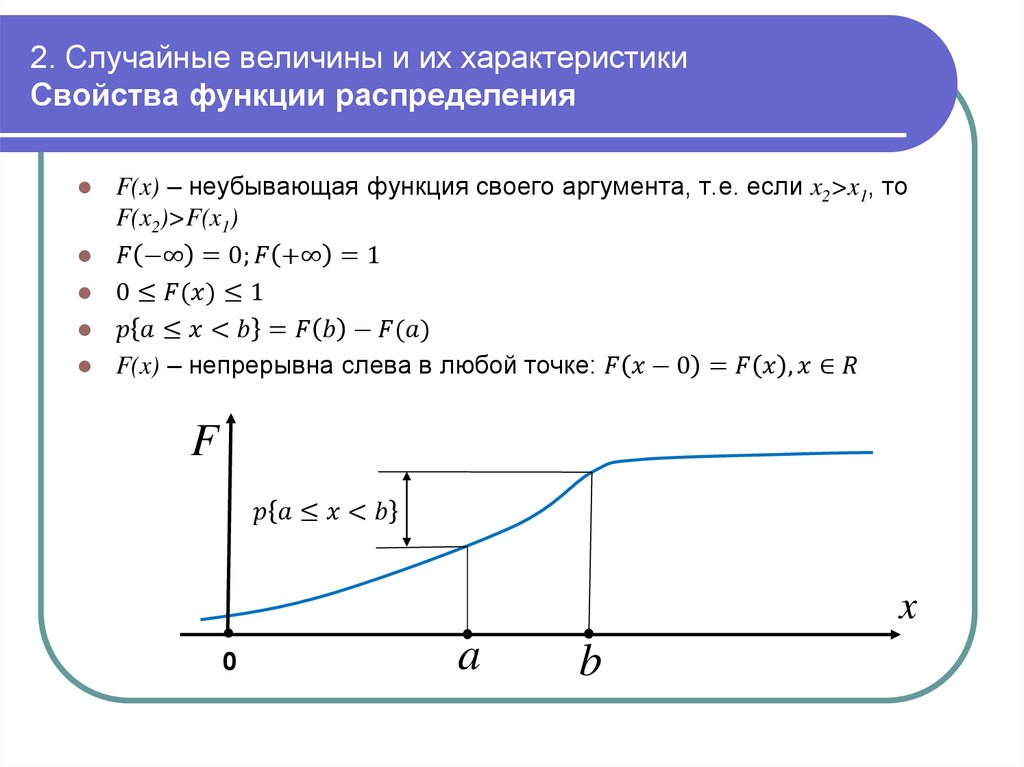
Разность между наибольшим и наименьшим значением функции на отрезке называетсяколебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано — Коши). Функция, непрерывная на отрезке [ a , b ], принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция f (x ) непрерывна в точке х = х 0 , то существует некоторая окрестность точки х 0 , в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) — Коши). Если функция f (x )- непрерывная на отрезке [ a , b ] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f (x ) = 0.
Т . е . если sign(f(a)) ¹ sign(f(b)), то $ х 0 : f(x 0) = 0.
Определение. Функция f (x ) называетсяравномерно непрерывной на отрезке [ a , b ], если для любого e >0 существует D >0 такое, что для любых точек х 1 Î [ a , b ] и x 2 Î [ a , b ] таких, что
ï х 2 — х 1 ï
верно неравенство ï f (x 2 ) — f (x 1 ) ï
Отличие равномерной непрерывности от “обычной” в том, что для любого
e
существует свое
D
, не зависящее от х, а при “обычной” непрерывности
D
зависит от
e
и х.
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Пример .
Непрерывность функции в точке. Функция y = f (x ) называется непре-
рывной в точке x 0 , если:
1) эта функция определена в некоторой окрестности точки x 0 ;
2) существует предел lim f (x ) ;
→ x 0
3) этот предел равен значению функции в точке x 0 , т.е. limf (x )= f (x 0 ) . | ||
x→ x0 | ||
Последнее условие равносильно условию lim | y = 0 , гдеx = x − x 0 – при- | |
x→ 0 | ||
ращение аргумента, y = f (x 0 + | x )− f (x 0 ) – приращение функции, соответст- | |
вующее приращению аргумента | x
, т. | f (x ) непрерывна в точкеx 0 |
тогда и только тогда, когда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Односторонняя непрерывность. Функцияy = f (x ) называется непрерыв-
ной слева в точкеx 0 , если она определена на некотором полуинтервале(a ;x 0 ]
и lim f (x )= f (x 0 ) .
x→ x0 − 0
Функция y = f (x ) называется непрерывнойсправа в точкеx 0 , если она оп-
ределена на некотором полуинтервале [ x 0 ;a ) и limf (x )= f (x 0 ) .
x→ x0 + 0
Функция y = f (x ) | непрерывна в точке x 0 | тогда и только тогда, когда она | ||||||
непрерывна | ||||||||
lim f (x )= limf (x )= limf (x )= f (x 0 ) . | ||||||||
x→ x0 + 0 | x→ x0 − 0 | x→ x0 | ||||||
Непрерывность функции на множестве. Функция
y
=
f
(x
) называется
Функция
y
=
f
(x
) называется
непрерывной на множестве X , если она является непрерывной в каждой точкеx этого множества. При этом если функция определена в конце некоторого промежутка числовой оси, то под непрерывностью в этой точке понимается непрерывность справа или слева. В частности, функцияy = f (x ) называетсяне-
прерывной на отрезке [ a; b] , если она
1) непрерывна в каждой точке интервала (a ;b ) ;
2) непрерывна справа в точке a ;
3) непрерывна слева в точке b .
Точки разрыва функции. Точкаx 0 , принадлежащая области определения функцииy = f (x ) , или являющаяся граничной точкой этой области, называется
точкой разрыва данной функции , еслиf (x ) не является непрерывной в этой точке.
Точки разрыва подразделяются на точки разрыва первого и второго рода:
1) Если существуют конечные пределы lim f (x )= f (x 0 − 0) и
x→ x0 − 0
f (x )= f (x 0 + 0) , причем не все три числаf (x 0 − 0) ,f (x 0 + 0) , | f (x 0 ) равны | ||
x→ x0 + 0 | |||
между собой, то x 0 | называется
точкой разрыва I рода. | ||
В частности, если левый и правый пределы функции в точке x 0 | равны меж- | ||
собой, но | не равны значению функции в этой точке: | ||
f (x0 − 0) = f(x0 + 0) = A≠ f(x0 ) , то x 0 называется точкой устранимого разрыва.
В этом случае, положив f (x 0 )= A , можно видоизменить функцию в точкеx 0
так, чтобы она стала непрерывной (доопределить функцию по непрерывности ). Разностьf (x 0 + 0)− f (x 0 − 0) называетсяскачком функции в точке x 0 .
Скачок функции в точке устранимого разрыва равен нулю.
2) Точки разрыва, не являющиеся точками разрыва первого рода, называются точками разрыва II рода . В точках разрыва II рода не существует или бесконечен хотя бы один из односторонних пределовf (x 0 − 0) иf (x 0 + 0) .
Свойства функций, непрерывных в точке.
f (x) | и g (x ) непрерывны в точкеx 0 , то функции | ||
f (x )± g (x ) , | f (x )g (x ) и | f (x) | (где g
(x
)≠
0) также непрерывны в точкеx
. |
g(x) | |||
2) Если функция u (x ) непрерывна в точкеx 0 , а функцияf (u ) непрерывна
в точке u 0 = u (x 0 ) , то сложная функцияf (u (x )) непрерывна в точкеx 0 .
3) Все основные элементарные функции (c , x a ,a x , loga x , sinx , cosx , tgx , ctgx , secx , cosecx , arcsinx , arccosx , arctgx , arcctgx ) непрерывны в каж-
дой точке своих областей определения.
Из свойств 1)–3) следует, что все элементарные функции (функции, полученные из основных элементарных функций с помощью конечного числа арифметических операций и операции композиции) также непрерывны в каждой точке своих областей определения.
Свойства функций, непрерывных на отрезке.
1) (теорема о промежуточных значениях) Пусть функция f(x) определе-
на и непрерывна на отрезке [ a ;b ] . Тогда для любого числаC , заключенного
между числами f (a ) иf (b ) , (f (a )
2) (теорема Больцано – Коши
рывна на отрезке [
a
;b
]
и принимает на его концах значения различных знаков.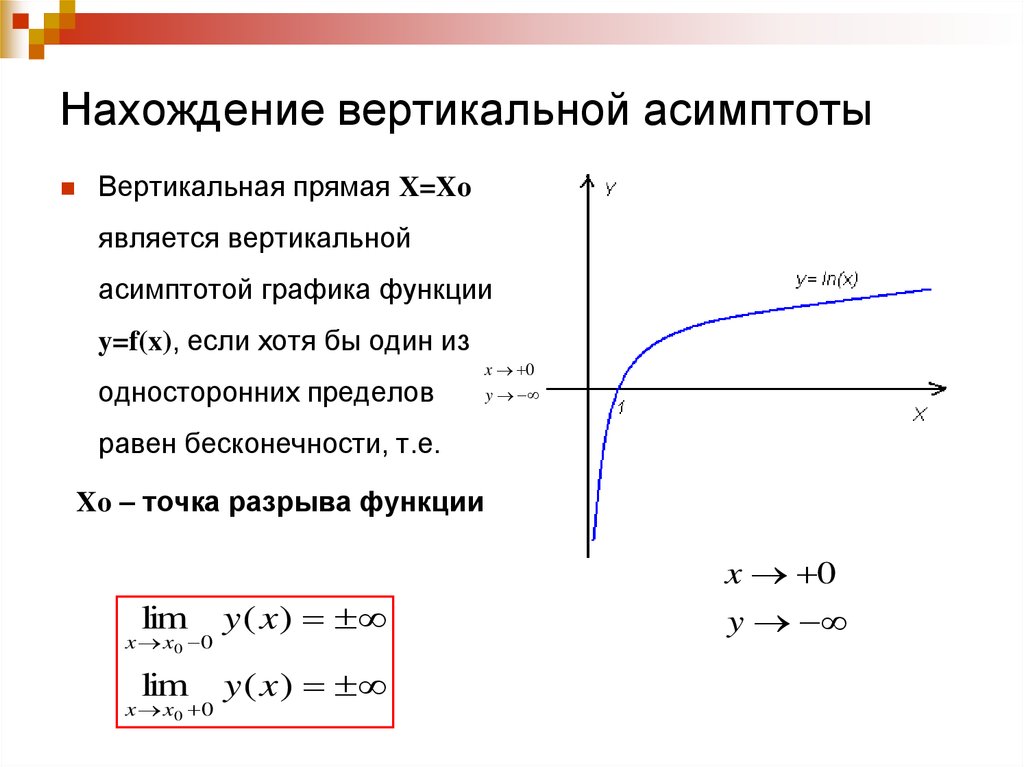
Тогда найдется хотя бы одна точка x 0 [ a ;b ] , такая, чтоf (x 0 )= 0 .
3) (1-я теорема Вейерштрасса ) Пусть функцияf (x ) определена и непре-
рывна на отрезке [ a ;b ] . Тогда эта функция ограничена на этом отрезке.
4) (2-я теорема Вейерштрасса ) Пусть функцияf (x ) определена и непре-
рывна на отрезке | [ a ;b ] . Тогда эта функция достигает на отрезке[ a ;b ] | |||||
наибольшего | наименьшего | значений, т.е. | существуют | |||
x1 , x2 [ a; b] , | для любой | точки x [ a ;b ] | справедливы | неравенства | ||
f (x 1 )≤ f (x )≤ f (x 2 ) .
Пример 5.17.
Пользуясь определением непрерывности, доказать, что функцияy
=
3x
2
+
2x
−
5 непрерывна в произвольной точкеx
0
числовой оси.
Решение: 1 способ: Пусть x 0 – произвольная точка числовой оси. Вы-
числим сначала предел функции f (x ) приx → x 0 , применяя теоремы о пределе суммы и произведения функций:
lim f (x )= lim(3x 2 + 2x − 5)= 3(limx )2 + 2 limx − 5= 3x 2 | − 5. | ||||||
x→ x0 | x→ x0 | x→ x0 | x→ x0 | ||||
Затем вычисляем значение функции в точке x :f (x )= 3x 2 | − 5 . | ||||||
Сравнивая полученные результаты, видим, | lim f (x )= f (x 0 ) , что согласно | ||||||
x→ x0 | |||||||
определению и означает непрерывность рассматриваемой функции в точке x
0
.
2 способ: Пусть | x – приращение аргумента в точкеx 0 . Найдем соот- | |||
ветствующее | приращение | y = f(x0 + x) − f(x0 ) = | ||
3(x + x )2 + 2(x + x )− 5− (3x 2 + 2x − 5) | ||||
6 x x+ (x) 2 | 2x = (6x + 2)x + (x )2 . | |||
Вычислим теперь предел приращения функции, когда приращение аргу- | ||||
стремится | ||||
y = lim (6x + 2) | x + (x )2 = (6x + 2) lim | x
+
(limx
)2
=
0 . | |||
x→ 0 | x→ 0 | x→ 0 | x→ 0 | ||
Таким образом, lim y = 0 , что и означает по определению непрерывность
x→ 0
функции для любого x 0 R .
Пример 5.18. Найти точки разрыва функцииf (x ) и определить их род. В
случае устранимого разрыва доопределить функцию по непрерывности:
1) f (x ) = 1− x 2 приx
5x приx ≥ 3
2) f (x )= x 2 + 4 x + 3 ;
x + 1
f (x) = | |||||
x4 (x− 2) | |||||
f (x )= arctg | |||||
(x − 5) | |||||
Решение: 1) Областью определения данной функции является вся число-
вая ось (−∞
;+∞
)
.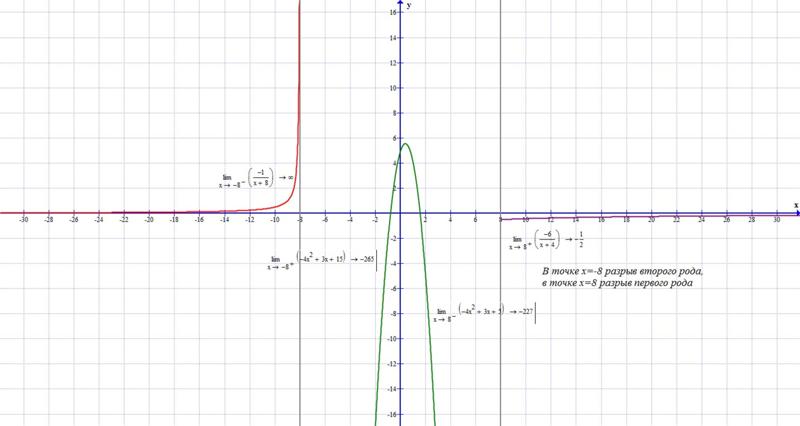 На интервалах(−∞
;3)
,(3;+∞
)
функция непрерывна. Разрыв возможен лишь в точкеx
=
3 , в которой изменяется аналитическое задание функции.
На интервалах(−∞
;3)
,(3;+∞
)
функция непрерывна. Разрыв возможен лишь в точкеx
=
3 , в которой изменяется аналитическое задание функции.
Найдем односторонние пределы функции в указанной точке:
f (3− 0)= lim (1− x 2 )= 1− 9= 8;
x →3 −0
f (3+ 0)= lim 5x = 15.
x →3 +0
Мы видим, что левый и правый пределы конечны, поэтому x = 3 | |||||
разрыва I | f (x ) . Скачок функции в | ||||
f (3+ 0)− f (3− 0)= 15− 8= 7 . | |||||
f (3)= 5 3= 15= f (3+ 0) , поэтому в точке | x = 3 | ||||
f (x ) непрерывна справа.
2) Функция непрерывна на всей числовой оси, кроме точки x = − 1, в которой она не определена. Преобразуем выражение дляf (x ) , разложив числитель
дроби на множители: | f (x) = | 4 x +3 | (x + 1)(x + 3) | X
+
3 приx
≠ −
1. | |||||
x + 1 | x + 1 | ||||||||
Найдем односторонние пределы функции в точке x = − 1: | |||||||||
f (x )= lim | f (x )= lim(x + 3)= 2 . | ||||||||
x →−1 −0 | x →−1 +0 | x →−1 | |||||||
Мы выяснили, что левый и правый пределы функции в исследуемой точке существуют, конечны и равны между собой, поэтому x = − 1 – точка устранимо-
прямую y = x + 3 с «выколотой» точкойM (− 1;2) . Чтобы функция стала непре-
рывной, следует положить f (− 1)= f (− 1− 0)= f (− 1+ 0)= 2 .
Таким образом, доопределив f
(x
) по непрерывности в точкеx
= −
1, мы получили функциюf
*
(x
)=
x
+
3 с областью определения(−∞
;+∞
)
.
3) Данная функция определена и непрерывна для всех x , кроме точек
x = 0 ,x = 2 , в которых знаменатель дроби обращается в ноль.
Рассмотрим точку x = 0:
Поскольку в достаточно малой окрестности нуля функция принимает толь-
ко отрицательные значения, то f (− 0)= lim | = −∞ = f (+0) | Т.е. точка | |||
(x − 2) | |||||
x →−0 | |||||
x = 0 является точкой разрыва II рода функции | f (x ) . | ||||
Рассмотрим теперь точку x = 2:
Функция принимает отрицательные значения вблизи слева от рассматри-
ваемой точки и положительные – справа, поэтому | f (2− 0)= | = −∞, | ||||||
x4 (x− 2) | ||||||||
x →2 −0 | ||||||||
f (2+ 0)= lim | = +∞
. | |||||||
(x − 2) | ||||||||
x →2 +0 | ||||||||
ция не имеет ни левого, ни правого конечного пределов, т.е. терпит в этой точке разрыв II рода.
x = 5 . | ||||||||||||||||||
f (5− 0)= lim arctg | π ,f (5+ 0)= lim arctg | x = 5 | ||||||||||||||||
(x − 5) | (x − 5) | |||||||||||||||||
x →5 −0 | x →5 +0 | |||||||||||||||||
ка разрыва | ||||||||||||||||||
f (5+ 0)− f (5− 0)= | π − (− | π
)=
π
(см. | ||||||||||||||||
Задачи для самостоятельного решения
5. 174.
Пользуясь лишь определением, доказать непрерывность функцииf
(x
) в
174.
Пользуясь лишь определением, доказать непрерывность функцииf
(x
) в
каждой точке x 0 R :
а) f(x) = c= const; | б) f (x )= x ; | ||
в) f (x )= x 3 ; | г) f (x )= 5x 2 − 4x + 1; | ||
д) f (x )= sinx . | |||
5.175. Доказать, что функция | f (x) = x 2 | 1 приx ≥ 0, | является непрерывной на |
1 при x | |||
всей числовой оси. Построить график этой функции. | |||
5.176. Доказать, что функция | f (x) = x 2 | 1 приx ≥ 0, | не является непрерывной |
0 при x | |||
в точке x
=
0 , но непрерывна справа в этой точке. Построить график функцииf
(x
) .
Построить график функцииf
(x
) .
рывной в точке x = | Но непрерывна слева в этой точке. Построить график | |||||||||||||
функции f (x ) . | ||||||||||||||
5.178. Построить графики функций | ||||||||||||||
а) y = | x + 1 | б) y= x+ | x + 1 | |||||||||||
x + 1 | x + 1 | |||||||||||||
Какие из условий непрерывности в точках разрыва этих функций выполнены, и какие не выполнены?
5. 179.
Указать точку разрыва функции
179.
Указать точку разрыва функции
sin x | При x ≠ 0 | ||
при x = 0 | |||
Какие из условий непрерывности в этой точке выполнены, и какие не выполнены?
4.1. Основные теоретические сведения
Определение. Функция у = f (x ) называется непрерывной в точке х 0 , если эта функция определена в какой-нибудь окрестности точки х 0 и если
то есть бесконечно малому приращению аргумента в окрестности точки х 0 соответствует бесконечно малое приращение функции.
Определение. Функция у= f (x ) непрерывна в точке х 0 , если она определена в некоторой окрестности этой точки и если предел функции при стремлении независимой переменной х к х 0 существует и равен значению функции при х=х 0 , то есть
Определение. Пусть х → х 0 ,
оставаясь все
время слева от х 0 . Если при
этом условии f (x ) стремится
к пределу, то он называется левым пределом
функции f (x ) в точке х 0 ,
то есть
Пусть х → х 0 ,
оставаясь все
время слева от х 0 . Если при
этом условии f (x ) стремится
к пределу, то он называется левым пределом
функции f (x ) в точке х 0 ,
то есть
Аналогично определяется и правый предел
Определение. Функция непрерывна в точке х 0 если:
функция определена в точке х 0 ;
существуют левый и правый пределы функции f (x ) при х → х 0 ;
все три числа (х 0 ), f (x 0 –0), f (x 0 +0) совпадают, то есть
Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой его точке.
Теорема .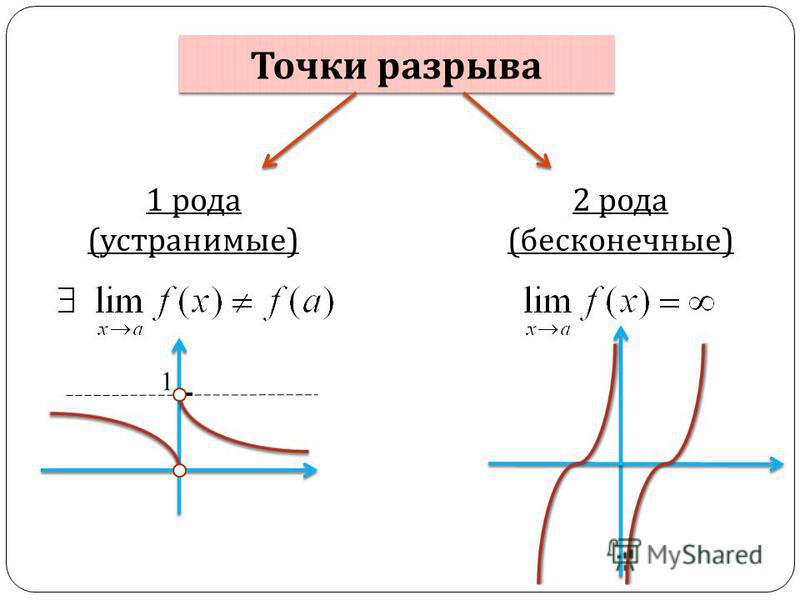 Если две
функции f (x )
и g (x )
определены в одном и том же
Если две
функции f (x )
и g (x )
определены в одном и том же
интервале и обе непрерывны в точке х 0 , то в той же точке будут непрерывны и функции
Теорема. Сложная функция, состоящая из конечного числа непрерывных функций, является непрерывной.
Все основные элементарные функции непрерывны в своей области определения.
Определение. Если в какой-либо точке х 0 функция не является непрерывной, то точка х 0 называется точкой разрыва функции, а сама функция – разрывной в этой точке.
Определение. Если в точке х 0 существует конечный lim f (x ) = А
(левосторонний и
правосторонний пределы существуют,
конечны и равны между собой), но
он не совпадает со значением функции в
точке, или же функция в точке не определена,
то точка х 0 называется
точкой устранимого разрыва. Принятое изображение точки устранимого
разрыва представлено на
рис. 1.
Принятое изображение точки устранимого
разрыва представлено на
рис. 1.
Определение. Точкой разрыва первого рода или точкой конечного разрыва называется такая точка х 0 , в которой функция имеет левый и правый конечные пределы, но они не равны между собой.
На рис. 2 приведено графическое представление разрыва функции первого рода в точке х 0
Определение. Если хотя бы один из пределов f (x 0 – 0) или f (x 0 + 0) не существует или бесконечен, то точка х 0 называется точкой разрыва, второго рода.
Графические представления разрывов функций второго рода в точке х 0 приведены на рис. 3 (а, б, в).
Приведенные выше определения непрерывности функции f (x ) в точке х 0
представлены на
рис.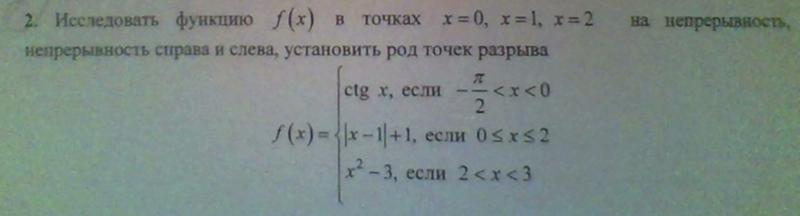 4, где отмечено, что основной посылкой
при определении непрерывности функции
(необходимым условием) в точке х 0 является то, что f (x )
определена в точке и ее окрестности.
4, где отмечено, что основной посылкой
при определении непрерывности функции
(необходимым условием) в точке х 0 является то, что f (x )
определена в точке и ее окрестности.
Пример Исследовать на непрерывность, определить характер точек разрыва,
изобразить в окрестности точек разрыва функцию
Это рациональная функция Она определена и непрерывна при всех значениях х, кроме х = 1, так как при х = 1 знаменатель обращается, в нуль. В точке х = 1 функция терпит разрыв. Вычислим предел этой функции при
х → 1, имеем
Конечный предел функции при х → 1 существует, а функция в точке
х = 1 не определена; значит точка х = 1 является точкой устранимого разрыва.
Если доопределить функцию, то есть положить f (1) = 5, то функция
будет непрерывной.
х = 1
изображено на
рис. 4.
Замечание. Данная функция
Данная функция
неопределенная при х = 1, совпадает с непрерывной функцией
во всех точках кроме х =1
Исследовать на непрерывность функцию и определить характер ее точек разрыва
Область определения функции – вся числовая ось. На интервалах(–, 0), (0,+) функция непрерывна. Разрыв возможен только в точке х = 0, в которой изменяется аналитическое задание функции.
Найдем односторонние пределы функции:
Левый и правый пределы хотя и конечны, но не равны между собой. Поэтому в точке х = 0 функция имеет разрыв первого рода. Скачок функции в точке разрыва равен
Поведение функции в окрестности точки х = 0 изображено на рис. 5.
Рис. 5
Пример Исследовать функцию f (x ) на непрерывность, определить характер ее точек разрыва, изобразить ее поведение в окрестности точек разрыва.
Функция определена и непрерывна на всей числовой оси, кроме точек х , = –2 и х 2 = 2, причем
не
существует.
Вычисляем односторонние пределы в точке х , = –2.
Итак, в точке х = – 2 функция терпит разрыв второго рода. Исследуем характер разрыва функции в точке х 2 = 2. Имеем
В точке х 2 = 2 функция также терпит разрыв второго рода.
Поведение функции в окрестности точек х х = – 2 и х 2 = 2 изображено на рис. 6.
Исследовать функцию f (x ) = e x + i на непрерывность, определить характер точек разрыва, изобразить поведение функции в окрестности точек разрыва.
Функция
неопределена прих = –3, поэтому
функция
непрерывна при всех
кромех =
–3. Определим
характер разрыва функции. Имеем
то есть один из пределов равен бесконечности, а значит функция терпит разрыв
второго
рода.
Поведение функции f (x ) = e x +3 в окрестности точки разрыва х = –3 изображено на рис. 7
4.2. Упражнения для самостоятельной работы студентов
1. Исследовать функции на непрерывность, определить характер их точек разрыва, изобразить графически поведение функций в окрестности
2. Исследовать функции на непрерывность, определить характер их точек разрыва, изобразить графически поведение функций в окрестности точек разрыва
Определение точки разрыва функции
Конечная точка x 0
называется точкой разрыва функции f(x)
,
если функция определена на некоторой проколотой окрестности точки x 0
,
но не является непрерывной в этой точке.
То есть, в точке разрыва, функция либо не определена, либо определена, но хотя бы один односторонний предел в этой точке или не существует, или не равен значению f(x 0
)
функции в точке x 0
.
См. «Определение непрерывности функции в точке ».
Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода , если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.
Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.
Определение точки устранимого разрыва
Точка называется точкой устранимого разрыва , если существует предел
,
но функция в точке или не определена, или не равна предельному значению: .
Таким образом, точка устранимого разрыва — это точка разрыва первого рода, в которой скачек функции равен нулю.
Определение точки разрыва 2-го рода
Точка разрыва называется точкой разрыва второго рода , если она не является точкой разрыва 1-го рода.
То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.
Исследование функций на непрерывность
При исследовании функций на непрерывность мы используем следующие факты.
- Элементарные функции и обратные к ним непрерывны на своей области определения. К ним относятся следующие функции:
, а также постоянная и обратные к ним функции. См. «Справочник по элементарным функциям ». - Сумма, разность и произведение непрерывных, на некотором множестве функций, является непрерывной, функцией на этом множестве.
Частное двух непрерывных, на некотором множестве функций, является непрерывной, функцией на этом множестве, за исключением точек, в которых знаменатель дроби обращается в нуль. См. «Арифметические свойства непрерывных функций » - Сложная функция непрерывна в точке , если функция непрерывна в точке , а функция непрерывна в точке . См. «Предел и непрерывность сложной функции »
Примеры
Пример 1
Задана функция и два значения аргумента и .
Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа, установить вид разрыва; 3) сделать схематический чертеж.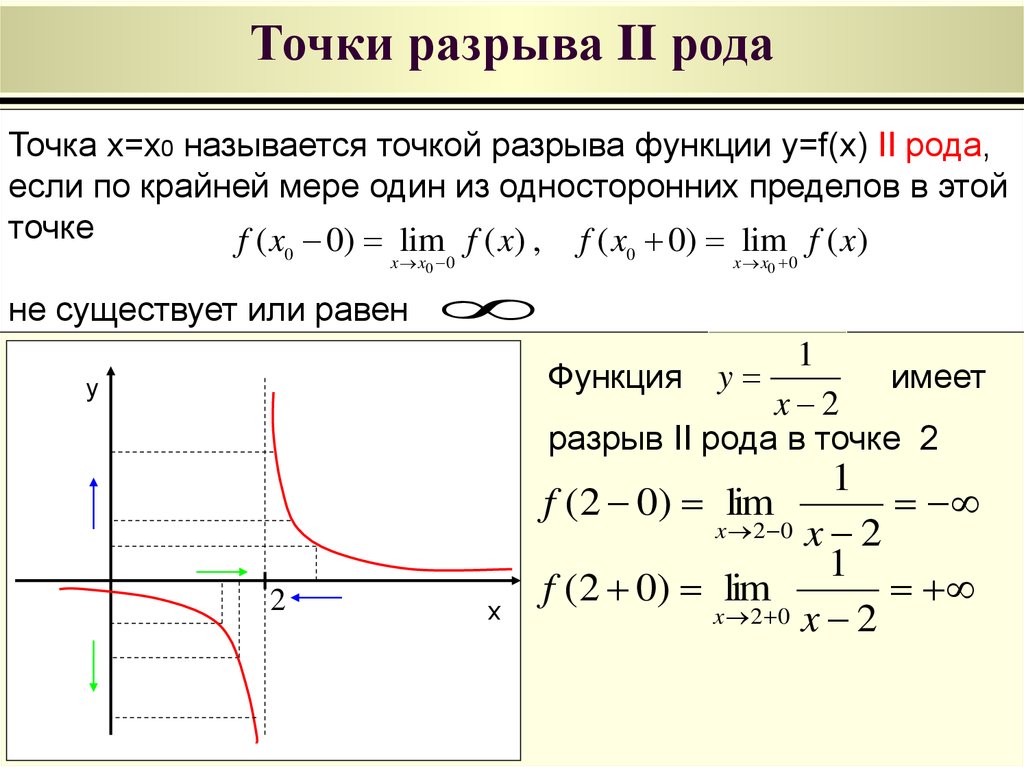
.
Заданная функция является сложной. Ее можно рассматривать как композицию двух функций:
,
.
Тогда
.
Рассмотрим функцию .
Она составлена из функции и постоянных с помощью арифметических операций сложения и деления. Функция является элементарной — степенной функцией с показателем степени 1
. Она определена и непрерывна для всех значений переменной .
Поэтому функция определена и непрерывна для всех ,
кроме точек, в которых знаменатель дроби обращается в нуль. Приравниваем знаменатель к нулю и решаем уравнение:
.
Получаем единственный корень .
Итак, функция определена и непрерывна для всех ,
кроме точки .
Рассмотрим функцию .
Это показательная функция с положительным основанием степени. Она определена и непрерывна для всех значений переменной .
Поэтому заданная функция определена и непрерывна для всех значений переменной ,
кроме точки .
Таким образом, в точке , заданная функция является непрерывной.
График функции y = 4 1/(x+2)
.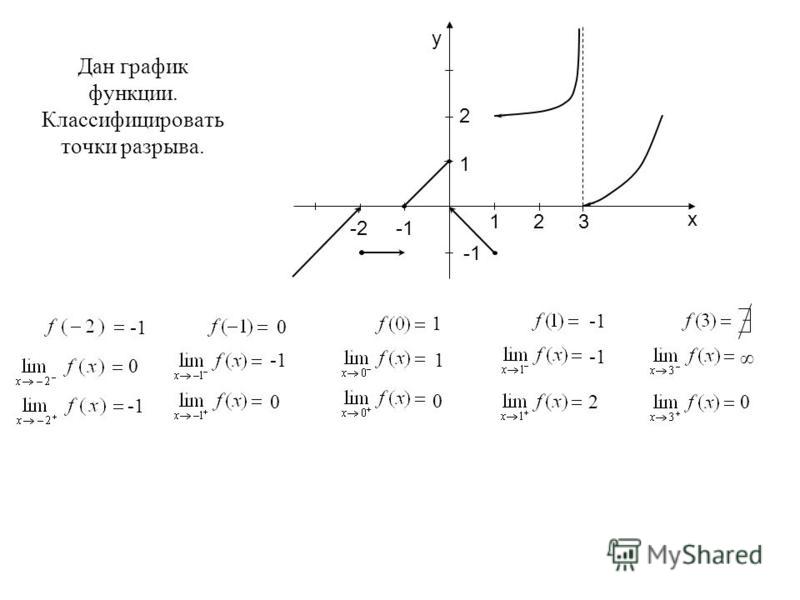
Рассмотрим точку . В этой точке функция не определена. Поэтому она не является непрерывной. Установим род разрыва. Для этого находим односторонние пределы.
Используя связь между бесконечно большими и бесконечно малыми функциями , для предела слева имеем:
при ,
,
,
.
Здесь мы использовали следующие общепринятые обозначения:
.
Также мы использовали свойство показательной функции с основанием :
.
Аналогично, для предела справа имеем:
при ,
,
,
.
Поскольку один из односторонних пределов равен бесконечности, то в точке разрыв второго рода.
В точке функция непрерывна.
В точке разрыв второго рода,
.
Пример 2
Задана функция .
Найти точки разрыва функции, если они существуют. Указать род разрыва и скачек функции, если есть. Сделать чертеж.
.
График заданной функции.
Функция является степенной функцией с целым показателем степени, равным 1
.
Такую функцию также называют линейной. Она определена и непрерывна для всех значений переменной .
Она определена и непрерывна для всех значений переменной .
В входят еще две функции: и .
Они составлены из функции и постоянных с помощью арифметических операций сложения и умножения:
,
.
Поэтому они также непрерывны для всех .
Поскольку функции, входящие в состав непрерывны для всех , то может иметь точки разрыва только в точках склейки ее составляющих. Это точки и . Исследуем на непрерывность в этих точках. Для этого найдем односторонние пределы.
Рассмотрим точку .
Чтобы найти левый предел функции в этой точке, мы должны использовать значения этой функции в любой левой проколотой окрестности точки .
Возьмем окрестность .
На ней .
Тогда предел слева:
.
Здесь мы использовали тот факт, что функция является непрерывной в точке (как и в любой другой точке). Поэтому ее левый (как и правый) предел равен значению функции в этой точке.
Найдем правый предел в точке .
Для этого мы должны использовать значения функции в любой правой проколотой окрестности этой точки.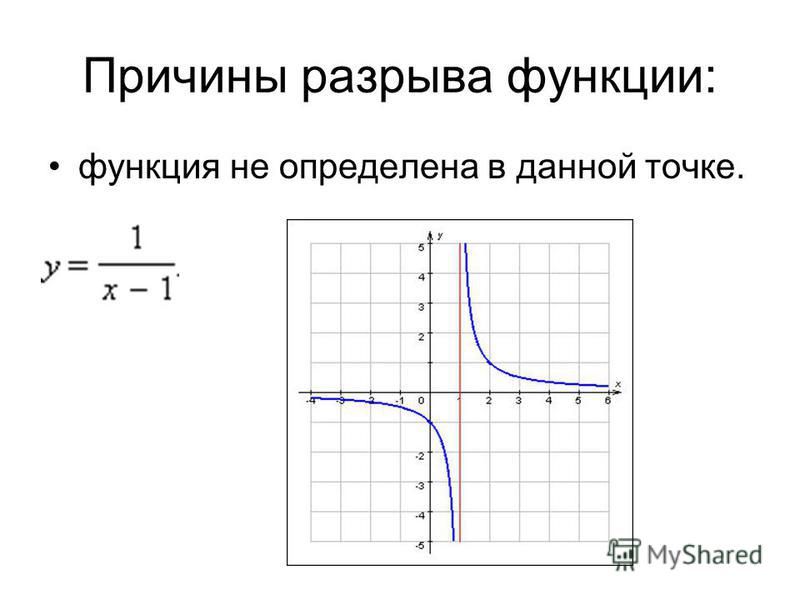 Возьмем окрестность .
На ней .
Тогда предел справа:
Возьмем окрестность .
На ней .
Тогда предел справа:
.
Здесь мы также воспользовались непрерывностью функции .
Поскольку, в точке ,
предел слева не равен пределу справа, то в ней функция не является непрерывной — это точка разрыва. Поскольку односторонние пределы конечны, то это точка разрыва первого рода. Скачек функции:
.
Теперь рассмотрим точку .
Тем же способом вычисляем односторонние пределы:
;
.
Поскольку функция определена в точке и левый предел равен правому, то функция непрерывна в этой точке.
Функция имеет разрыв первого рода в точке . Скачек функции в ней: . В остальных точках функция непрерывна.
Пример 3
Определить точки разрыва функции и исследовать характер этих точек, если
.
Воспользуемся тем, что линейная функция определена и непрерывна для всех .
Заданная функция составлена из линейной функции и постоянных с помощью арифметических операций сложения, вычитания, умножения и деления:
.
Поэтому она определена и непрерывна для всех ,
за исключением точек, в которых знаменатель дроби обращается в нуль.
Найдем эти точки. Приравниваем знаменатель к нулю и решаем квадратное уравнение :
;
;
;
.
Тогда
.
Используем формулу:
.
С ее помощью, разложим числитель на множители:
.
Тогда заданная функция примет вид:
(П1) .
Она определена и непрерывна для всех ,
кроме точек и .
Поэтому точки и являются точками разрыва функции.
Разделим числитель и знаменатель дроби в (П1) на :
(П2) .
Такую операцию мы можем проделать, если .
Таким образом,
при .
То есть функции и отличаются только в одной точке: определена при ,
а в этой точке не определена.
Чтобы определить род точек разрыва, нам нужно найти односторонние пределы функции в точках и .
Для их вычисления мы воспользуемся тем, что если значения функции изменить, или сделать неопределенными в конечном числе точек, то это не окажет ни какого влияние на величину или существование предела в произвольной точке (см. «Влияние значений функции в конечном числе точек на величину предела »). То есть пределы функции в любых точках равны пределам функции .
То есть пределы функции в любых точках равны пределам функции .
Рассмотрим точку .
Знаменатель дроби в функции ,
при в нуль не обращается. Поэтому она определена и непрерывна при .
Отсюда следует, что существует предел при и он равен значению функции в этой точке:
.
Поэтому точка является точкой устранимого разрыва первого рода.
Рассмотрим точку .
Используя связь бесконечно малых и бесконечно больших функций , имеем:
;
.
Поскольку пределы бесконечные, то в этой точке разрыв второго рода.
Функция имеет точку устранимого разрыва первого рода при , и точку разрыва второго рода при .
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Практикум 7. Непрерывность функции
Цель работы – изучение понятия непрерывности функции в точке, классификация точек разрыва, использование функции fzero для нахождения нулей функции и корней уравнения, символическое решение уравнений и систем
Продолжительность
работы —
3 часа.
Оборудование, приборы, инструментарий – работа выполняется в компьютерном классе с использованием пакета MatLab.
Порядок выполнения
Упражнения выполняются параллельно с изучением теоретического материала.
После выполнения каждого упражнения результаты заносятся в отчёт.
При выполнении упражнений в случае появления сообщения об ошибке рекомендуется сначала самостоятельно выяснить, чем оно вызвано, и исправить команду; если многократные попытки устранить ошибку не привели к успеху, то проконсультироваться с преподавателем.
Дома доделать упражнения из раздела «Краткие теоретические сведения и практические упражнения», которые Вы не успели выполнить во время аудиторного занятия.
После выполнения упражнений выполнить дополнительные упражнения для самостоятельной работы и ответить на контрольные вопросы и (см.
 ниже).
ниже).Подготовить отчёт, в который включить упражнения из раздела «Краткие теоретические сведения и практические упражнения» и упражнения для самостоятельной работы. Отчёт представить в виде документа Microsoft Word, имя файла (пример): mp_10_Ivanov_P_01_s_1 (факультет_группа_Фамилия студента_Инициал_номер лабораторной, семестр). Отчет должен содержать по каждому выполненному упражнению: № упражнения, текст упражнения; команды, скопированные из командного окна, с комментариями к ним и результаты их выполнения, включая построенные графики; тексты М-сценариев и М-функций; выводы.
Краткие теоретические сведения и практические упражнения
1. Непрерывность функции в точке и точки разрыва функции.
Определение. Функция называется непрерывной в точке , если.
Если функция не
является непрерывной в точке области определения функции или функция
не определена в этой точке, но определена
в некоторой её окрестности, то точка называется точкой
разрыва функции.
Точки разрыва классифицируются следующим образом:
1) если оба предела и конечны и , то такая точка является точкой устранимого разрыва, причем может быть и определена, и не определена в точке ;
2) если оба предела и конечны и , то функция имеет в точке разрыв первого рода;
3) если хотя бы один из односторонних пределов не существует или бесконечен, то функция имеет в точке разрыв второго рода.
2. Нули непрерывной функции. Численное решение уравнений
Из курса математического анализа нам известно следующее свойство непрерывной функции:
если , то существует точка такая, что . Это утверждение означает, что график функции непрерывной на отрезке , хотя бы в одной точке пересекает отрезок ось , если точки и лежат по разные стороны от оси .
Найти приближенно точку можно с помощью функции fzero.
Базовый формат вызова этой функции включает два аргумента и имеет один из двух видов:
fzero (fun, [a b])
fzero (fun, x1)
Аргумент
fun
может быть задан так же как первый
аргумент функции fplot
(т. е. как указатель на функцию или строка
функции).
е. как указатель на функцию или строка
функции).
Второй аргумент в форме [a b] представляет собой интервал, на концах которого функция fun меняет знак, что гарантирует нахождение, по крайней мере, одного корня на этом интервале. Второй аргумент в форме x1 представляет собой скалярное значение, в окрестности которого предполагается нахождение корня. В этом случае функция fzero сама пытается найти отрезок с центром в заданной точке x1, на концах которого функция меняет знак.
Пример 1.
Нули функции на отрезке можно найти с помощью команды
>>fzero(@(x) cos(x) — sin(x), [0, pi/2])
ans =
0.7854
Если мы хотим получить не только значение корня, но и узнать значение функции в найденной точке, то к функции fzero можно обратиться с двумя выходными параметрами
>> [x,f]=fzero(@(x) cos(x) — sin(x), [0, pi/2])
x =
0.7854
f =
-1.1102e-016
Судя по значению
функции точность нахождения нуля функции
достаточно высока.
Поскольку fzero не проверяет функцию fun на непрерывность, то применение fzero в некоторых случаях может привести к парадоксальным (на первый взгляд) результатам. Например, попытка найти нули функции вблизи точки 1,5 приводит к следующему.
Пример 2.
>> [x,f]=fzero(@tan, 1.5)
x =
1.5708
f =
1.9789e+015
Полученное значение аргумента соответствует приближенному значению и на самом деле является не нулем функции , а ее точкой разрыва, при переходе через которую функция меняет знак. Выведенное значение функции в найденной точке показывает нам, что найден не корень.
Условие обнаружение интервала, на концах которого функция принимает значения разных знаков, является принципиальным для алгоритма, использованного в функции fzero. Например, для такой тривиальной функции, как , функция fzero найти нуля не может.
Логично задать
вопрос: как мы можем получить начальное
приближение или отрезок, на концах
которого функция принимает значения с
разными знаками? Часто это проще всего
сделать, построив график функции.
Пример 3.
Хотим решить уравнение Преобразуем его к виду и воспользуемся тем, что корни уравнения можно интерпретировать как нули функции . Теперь задаём анонимную функцию и строим график:
>>f = @(x) sin(x) — 1 + 0.25*x;
>>fplot(f, [0 10]) % почему мы знаем, что все корни лежат в этом промежутке?
>>grid on
Из рисунка видно, что корни уравнения лежат на отрезках , и . (Можно было использовать другой подход: построить графики функций и в одном окне и увидеть, в каких точках они пересекаются.)
>>x1 = fzero(f, [0 1])
x1 = 0.8905
>>x2 = fzero(f, [2 3])
x2 = 2.8500
>>x3 = fzero(f, [5 6])
x3 = 5.8128
Упражнение 1. Для следующих функций найти точки разрыва, исследовать их характер, сделать геометрическую иллюстрацию:
а) , б) .
Упражнение 2.
Найдите все корни уравнений:
а) б)
Непрерывность функции.
 Точки разрыва и их классификация. Построение графиков. — Студопедия
Точки разрыва и их классификация. Построение графиков. — СтудопедияПоделись
Номер: 7.1.А
Задача: Используя понятие точки разрыва функции и определения типов точек разрыва, выяснить является ли точка точкой разрыва данной функции (в случае утвердительного ответа определить тип разрыва).
Ответы: 1). не является точкой разрыва 2). точка устранимого разрыва
3). точка разрыва I рода 4). точка разрыва II рода 5). нет ответа
Номер: 7.2.А
Задача: Используя понятие точки разрыва функции и определения типов точек разрыва, выяснить является ли точка точкой разрыва данной функции (в случае утвердительного ответа определить тип разрыва).
Ответы: 1). не является точкой разрыва 2). точка устранимого разрыва
3). точка разрыва I рода 4). точка разрыва II рода 5). нет ответа
Номер: 7.10.А
Задача: Используя понятие точки разрыва функции и определения типов точек разрыва, выяснить является ли точка точкой разрыва данной функции (в случае утвердительного ответа определить тип разрыва).
Ответы: 1). не является точкой разрыва 2). точка устранимого разрыва
3). точка разрыва I рода 4). точка разрыва II рода 5). нет ответа
Номер: 7.19.А
Задача: Используя понятие точки разрыва функции и определения типов точек разрыва, выяснить является ли точка точкой разрыва данной функции (в случае утвердительного ответа определить тип разрыва).
Ответы: 1). не является точкой разрыва 2). точка устранимого разрыва
3). точка разрыва I рода 4). точка разрыва II рода 5). нет ответа
Номер: 7.21.А
Задача: Используя понятие точки разрыва функции и определения типов точек разрыва, выяснить является ли точка точкой разрыва данной функции (в случае утвердительного ответа определить тип разрыва).
Ответы: 1). не является точкой разрыва 2). точка устранимого разрыва
3). точка разрыва I рода 4). точка разрыва II рода 5). нет ответа
Номер: 7. 25.А
25.А
Задача: Используя понятие точки разрыва функции и определения типов точек разрыва, выяснить является ли точка точкой разрыва данной функции (в случае утвердительного ответа определить тип разрыва).
Ответы: 1). не является точкой разрыва 2). точка устранимого разрыва
3). точка разрыва I рода 4). точка разрыва II рода 5). нет ответа
Номер: 7.29.А
Задача: Используя понятие точки разрыва функции и определения типов точек разрыва, выяснить является ли точка точкой разрыва данной функции (в случае утвердительного ответа определить тип разрыва).
Ответы: 1). не является точкой разрыва 2). точка устранимого разрыва
3). точка разрыва I рода 4). точка разрыва II рода 5). нет ответа
Номер: 7.33.В
Задача: Используя определения непрерывности функции в точке, найти такие значения , при которых функция будет непрерывна в указанной точке :
Ответы: 1). 2). 3). таких значений нет 4). 5).
таких значений нет 4). 5).
Номер: 7.37.В
Задача: Используя определения непрерывности функции в точке, найти такие значения , при которых функция будет непрерывна в указанной точке :
Ответы: 1). 2). 3). 4). 5). нет таких значений
Номер: 7.41.В
Задача: Используя определения непрерывности функции в точке, найти такие значения , при которых функция будет непрерывна в указанной точке :
Ответы: 1). 2). 3). 4). нет таких значений 5).
Номер: 7.42.В
Задача: Используя определения непрерывности функции в точке, найти такие значения , при которых функция будет непрерывна в указанной точке :
Ответы: 1). 2). 3). 4). нет таких значений 5).
Номер: 7.50.В
Задача: Используя определения непрерывности функции в точке, найти такие значения , при которых функция будет непрерывна в указанной точке :
Ответы: 1). 2). 3). 4). 5). таких значений нет
4). 5). таких значений нет
Номер: 7.51.В
Задача: Используя определения непрерывности функции в точке, найти такие значения , при которых функция будет непрерывна в указанной точке :
Ответы: 1). 2). 3). 4). 5). таких значений нет
Номер: 7.55.В
Задача: Используя определения непрерывности функции в точке, найти такие значения , при которых функция будет непрерывна в указанной точке :
Ответы: 1). 2). 3). 4). 5). таких значений нет
Номер: 7.56.В
Задача: Используя определения непрерывности функции в точке, найти такие значения , при которых функция будет непрерывна в указанной точке :
Ответы: 1). 2). 3). 4). 5). таких значений нет
Номер: 7.63.В
Задача: Найти точки разрыва, исследовать их характер
Ответы: 1). функция непрерывна 2). точка разрыва II рода
3). точка разрыва I рода 4). точка устранимого разрыва
5). нет правильного ответа
нет правильного ответа
Номер: 7.66.В
Задача: Найти точки разрыва, исследовать их характер
Ответы: 1). функция непрерывна 2). точка разрыва II рода
3). точка разрыва I рода 4). точка разрыва I рода
5). точка разрыва II рода
Номер: 7.67.В
Задача: Найти точки разрыва, исследовать их характер
Ответы: 1). функция непрерывна 2). точка разрыва II рода
3). точка разрыва I рода 4). точка разрыва устранимого
5). точка разрыва II рода
Номер: 7.68.В
Задача: Найти точки разрыва, исследовать их характер
Ответы: 1). точка разрыва II рода, точка устранимого разрыва
2). точка разрыва II рода; точка разрыва I рода
3). точка разрыва I рода; точка устранимого разрыва
4). точка разрыва II рода; точка
5). точка разрыва II рода, функция непрерывна
Начало работы с анализом точек останова в Python | Анжелика Ло Дука
Анализ данных
Готовое руководство по сравнению библиотек Ruptures и Jenkspy для анализа точек останова в Python
Изображение автора При работе с временными рядами очень важно определить точки останова. На самом деле наличие точек останова в данных может привести к ошибкам и нестабильности модели при выполнении прогнозов.
На самом деле наличие точек останова в данных может привести к ошибкам и нестабильности модели при выполнении прогнозов.
Точка останова — это структурное изменение данных, такое как аномалия или ожидаемое событие.
Существует множество методов определения точек останова. В целом эти методы можно разделить на две категории:
- обнаружение — обнаружение одной или нескольких точек останова
- проверка — по заданной точке проверить, является ли она точкой останова или нет. К этой категории техник относится знаменитый тест Чоу.
В этом коротком руководстве я сосредоточусь на первой категории точек останова и сравню две библиотеки Python для анализа точек останова: рвет и jenkspy .
Код доступен в виде блокнота Jupyter и может быть загружен из моего репозитория Github.
Сначала я загружаю набор данных как кадр данных pandas . В качестве набора данных я использую тенденцию аудитории Giallozafferano с 2015 по 2020 год. Giallozafferano — очень известный итальянский блог о еде. Данные были извлечены из Audiweb, итальянского веб-сайта, который анализирует использование Интернета в Италии, а затем обработаны с помощью программного обеспечения под названием LEX, созданного одним из моих студентов. LEX — очень полезная программа, которая преобразует несколько файлов Microsoft Excel, разделенных по датам, в один файл CSV. Если вы хотите узнать больше об этом программном обеспечении, напишите мне сообщение 🙂
В качестве набора данных я использую тенденцию аудитории Giallozafferano с 2015 по 2020 год. Giallozafferano — очень известный итальянский блог о еде. Данные были извлечены из Audiweb, итальянского веб-сайта, который анализирует использование Интернета в Италии, а затем обработаны с помощью программного обеспечения под названием LEX, созданного одним из моих студентов. LEX — очень полезная программа, которая преобразует несколько файлов Microsoft Excel, разделенных по датам, в один файл CSV. Если вы хотите узнать больше об этом программном обеспечении, напишите мне сообщение 🙂
импорт панд как pddf = pd.read_csv('GialloZafferano.csv')
df.head() Изображение автораТеперь я конвертирую кадр данных во временной ряд. Это можно сделать в три шага:
- преобразовать
поле данныхв поле даты и времени - установить столбец даты как индекс временного ряда
- назначить столбец значений новой переменной с именем
ts.
df['date'] = pd.to_datetime(df['date'])
df.set_index(df['date'], inplace = True)
ts = df['audience']
Я рисую временной ряд. Я использую библиотеку matplotlib .
Глядя на график, я отмечаю, что основных разрывов примерно три. Таким образом, я решаю искать 3 разрыва.
Изображение автораn_breaks = 3
Я готовлю данные для ввода в качестве входных данных протестированных библиотек. Я конвертирую временные ряды в массив.
import numpy as npy = np.array(ts.tolist())
Первой библиотекой обнаружения точек останова является Ruptures, которую можно установить с помощью команды pip установить разрыв .
Ruptures предоставляет шесть различных моделей для обнаружения точек останова: Dynp , KernelCPD , Pelt , Binseg , BottomUp , Window . Каждая модель должна быть построена, обучена (с помощью функции fit() ) и затем использована для прогнозирования. Функция
Функция predict() получает в качестве входных данных количество точек останова (минус 1), которые необходимо идентифицировать. В этом примере я использую модель Dynp , которая соответствует динамическому программированию.
импортировать разрывы как rptmodel = rpt.Dynp(model="l1")
model.fit(y)
breaks = model.predict(n_bkps=n_breaks-1)
Поскольку разрывов возвращает индекс, при котором структурный происходит изменение, я получаю дату из исходного временного ряда ts .
breaks_rpt = []
для i в перерывах:
breaks_rpt.append(ts.index[i-1])
breaks_rpt = pd.to_datetime(breaks_rpt)
breaks_rpt
что дает следующий вывод:
DatetimeIndex(['2016-03-01', '2018-04-01', '2020-11-01'], dtype='datetime64[ns]', freq=None)
Теперь я рисую результаты.
plt.plot(ts, label='data')Изображение автора
plt.title('Аудитория')
print_legend = True
для i in breaks_rpt:
if print_legend:
plt.axvline(i, color='red', linestyle='штрих', label='разрывы')
print_legend = False
else:
plt.axvline(i, color='красный',linestyle='штрих')
plt.grid()
plt.legend()
plt.show()
Вторая библиотека обнаружения точек останова — Jenkspy, которую можно установить с помощью следующей команды: pip install jinkspy . Эта библиотека вычисляет естественные разрывы массива в соответствии с алгоритмом Фишера-Дженкса.
Я импортирую библиотеку ( import jekspy ), а затем вызываю функцию jenks_breaks() , которая получает в качестве входных данных массив значений и количество обнаруживаемых разрывов. На выходе функция возвращает значения, соответствующие идентифицированным разрывам. Напоминаем, что вместо этого Ruptures возвращает индексы разрывов.
import jenkspybreaks = jenkspy.jenks_breaks(y, nb_class=n_breaks-1)
Я вычисляю индексы перерывов, проходя по массиву breaks .
breaks_jkp = []
для v в разрывах:
idx = ts.index[ts == v]
breaks_jkp.append(idx)
breaks_jkp
, что дает следующий результат:
[DatetimeIndex(['20177 07-01'], dtype='datetime64[ns]', name='date', freq=None),
DatetimeIndex(['2018-04-01'], dtype='datetime64[ns]', name= 'дата', частота = нет),
DatetimeIndex(['2020-04-01'], dtype='datetime64[ns]', name='date', freq=None)]
И я рисую результаты.
plt.plot(ts, label='data')Изображение автора
plt.title('Аудитория')
print_legend = True
для i in breaks_jkp:
if print_legend:
plt.axvline(i, color='red', linestyle='штрих', label='разрывы')
print_legend = False
else:
plt.axvline(i, color='красный',linestyle='штрих')
plt.grid()
plt.legend()
plt.show()
Наконец, я сравниваю результаты, полученные двумя библиотеками. Делаю визуальное сравнение.
Я вычисляю идеальный случай, когда оба алгоритма дают одинаковый результат.
x_ideal = ts.index
y_ideal = x_ideal
Я сравниваю два алгоритма с помощью точечной диаграммы. Идеальный случай показан красным цветом. Замечу, что есть только общий излом (тот, что пересекает идеальный случай). Первая точка останова совершенно другая, а третья очень похожа.
plt.figure(figsize=(5, 5), dpi=80)Изображение автора
plt.scatter(breaks_rpt,breaks_jkp)
plt.xlabel('Разрывы')
plt.ylabel('Jenkspy')
plt.title('Jenskpy VS Ruptures')
plt.xlim(ts.index[0], ts.index[len(ts)-1])
plt.ylim(ts .index[0], ts.index[len(ts)-1])
plt.plot(x_ideal,y_ideal, color='r', linestyle='dashed')
plt.grid()
plt.show( )
В этом уроке я показал, как обнаруживать точки останова в Python с помощью двух библиотек: ruptures и jenkospy . Две библиотеки производят разные выходные данные. Сравнивая выходные данные с визуальными точками останова, в этом конкретном примере алгоритм Jenkspy, кажется, превосходит динамическое программирование.
Если вы хотите быть в курсе моих исследований и другой деятельности, вы можете подписаться на меня в Twitter, Youtube и Github.
Как обнаружить выбросы с помощью Python pyod
Краткое руководство по использованию библиотеки pyod.
в направлении datascience.com
4 различных подхода к анализу временных рядов
в направлении datascience.com
Полный рабочий процесс анализа данных в Python и scikit-learn
в направлении datascience.com
Отладка Golang с помощью Delve [шаг за шагом]
В этой статье мы рассмотрим, как отлаживать программы Go (Golang) с помощью Delve. Delve — это сторонний отладчик для языка программирования Go, доступный на github https://github.com/go-delve/delve. Это достойная альтернатива отладчику GDB golang (https://golang.org/doc/gdb), поскольку он более многофункционален, как указано на официальном веб-сайте Go GDB
.Обратите внимание, что Delve является лучшей альтернативой GDB при отладке программ Go, созданных с помощью стандартной цепочки инструментов.
Он понимает среду выполнения Go, структуры данных и выражения лучше, чем GDB. Delve в настоящее время поддерживает Linux, OSX и Windows на
amd64. Актуальный список поддерживаемых платформ см. в документации Delve.
Цель
К концу этой статьи вы сможете легко отлаживать и проверять программы Go с помощью инструмента командной строки отладчика delve. Мы увидим, как просматривать, добавлять и изменять точки останова в программе Go, перемещаться по программе построчно или через точки останова, проверять значения переменных, функций и выражений и, наконец, подробно анализировать все наши программы.
Загрузите и установите Go Delve
Go delve можно загрузить и установить, просто используя команду go get
Linux, Windows, OS X
$ зайдите на github.com/go-delve/delve/cmd/dlv
- Если вы используете модули Go, вы можете выполнить эту команду вне каталога вашего проекта, чтобы избежать добавления delve в качестве зависимости в файл go.
 mod
mod
Следующее должно быть уже настроено, если у вас есть работающая установка Go:
- Убедитесь, что переменная env GOBIN правильно установлена, которая будет указывать каталог, в котором будет храниться команда
dlv(delve). Вы можете проверить, набравgo env GOBIN - Убедитесь, что PATH содержит GOBIN, что позволит вам запускать исполняемые файлы Go без указания абсолютного пути
OSX
В mac OS вам также может понадобиться включить инструменты разработчика, введя следующую команду
xcode-выбрать --установить
Проверьте свою установку
После завершения установки вы можете убедиться, что delve успешно установлена, проверив версию
.$ dlv версия Отладчик погружения Версия: 1.5.1 Сборка: $Id: bca418ea7ae2a4dcda985e623625da727d4525b5 $
Это означает, что вы успешно установили delve. Теперь приступим к отладке.
Начать отладку (Delve Server)
Когда мы начинаем отладку, мы обычно имеем в виду, что начинаем «сеанс отладки». Чтобы начать сеанс отладки, вы можете использовать одну из команд, доступных в справке командной строки dlv 9.0007
Чтобы начать сеанс отладки, вы можете использовать одну из команд, доступных в справке командной строки dlv 9.0007
$ dlv помощь ... Применение: dlv [команда] Доступные команды: attach Присоединитесь к запущенному процессу и начните отладку. connect Подключиться к безголовому серверу отладки. core Изучите дамп ядра. dap [ЭКСПЕРИМЕНТАЛЬНАЯ ВЕРСИЯ] Запускает TCP-сервер, обменивающийся данными через протокол адаптера отладки (DAP). debug Скомпилировать и начать отладку основного пакета в текущем каталоге или в указанном пакете. exec Выполнить предварительно скомпилированный двоичный файл и начать сеанс отладки. help Справка по любой команде запустить устаревшую команду. Вместо этого используйте «отладку». test Скомпилируйте тестовый двоичный файл и начните отладку программы. trace Скомпилируйте и начните трассировку программы. версия Печатает версию.
Нам интересны команды dlv debug и dlv exec , которые обе используются для запуска сеанса отладки, с той лишь разницей, что одна (dlv debug) также компилирует двоичный файл из исходного кода, а другая (dlv exec) ожидает скомпилированный двоичный файл.
Команда test также полезна, если мы хотим отладить тест Go.
Пример отладочного кода Golang
Приведенный ниже фрагмент кода представляет пример кода, который мы собираемся использовать для нашего сеанса отладки, это реализация Фибоначчи.
пакет основной
импортировать "фмт"
var m = make(map[int]int, 0)
основная функция () {
для _, n := диапазон [] int {5, 1, 9, 98, 6} {
х := фиб(п)
fmt.Println(n, "выдумка", x)
}
}
func fib(n int) int {
если п < 2 {
вернуть н
}
вар е целое число
если v, то := m[n]; Ok {
ф = v
} еще {
f = выдумка (n-2) + выдумка (n-1)
м [п] = е
}
возврат f
}
Вы можете проверить и запустить этот фрагмент кода на игровой площадке Go
Нам нужно передать основной пакет, который будет скомпилирован и выполнен для отладки.
dlv отладка main.go Введите «помощь» для списка команд. (длв)
Это запустит сеанс отладки. Это также известно как сервер delve, так как это запущенный процесс, ожидающий инструкций.
Это также известно как сервер delve, так как это запущенный процесс, ожидающий инструкций.
Клиент Delve
После того, как наш сеанс отладки начался, мы скомпилировали и присоединили к двоичному файлу Go, мы можем начать отладку нашей программы. Теперь нам представлен новый repl, который является просто интерпретатором delve, который вы также можете назвать «клиентом delve», который будет отправлять инструкции по отладке на наш ранее созданный сервер delve.
Мы можем увидеть все доступные команды, набрав следующее.
Введите 'help' для списка команд. (длв) помощь Доступны следующие команды: Запуск программы: call ------------------------ Возобновляет процесс, вводя вызов функции (ЭКСПЕРИМЕНТАЛЬНО!!!) continue (псевдоним: c) --------- Выполнять до точки останова или завершения программы. next (псевдоним: n) ------------- Переход к следующей строке исходного кода. перестроить --------------------- Перестроить целевой исполняемый файл и перезапустить его.Это не работает, если исполняемый файл не был собран delve. перезапустить (псевдоним: r) ---------- Перезапустить процесс. шаг (псевдоним: s) ------------- Пошаговое выполнение программы. пошаговая инструкция (псевдоним: si) Один шаг одиночной инструкции процессора. stepout (псевдоним: so) --------- Выйти из текущей функции. Управление точками останова: break (псевдоним: b) ------- Устанавливает точку останова. точки останова (псевдоним: bp) Вывести информацию об активных точках останова. clear ------------------ Удаляет точку останова. clearall --------------- Удаляет несколько точек останова. условие (псевдоним: cond) Установить условие точки останова. on --------------------- Выполняет команду при достижении точки останова. trace (псевдоним: t) ------- Установить точку трассировки. Просмотр переменных программы и памяти: args ------------------ Вывести аргументы функции. display -------------- Выводить значение выражения каждый раз, когда программа останавливается. exammem (псевдоним: x) Проверить память: locals --------------- Вывести локальные переменные.
print (псевдоним: p) ----- Вычислите выражение. regs ------------------ Вывести содержимое регистров процессора. set ------------------ Изменяет значение переменной. vars ------------------ Вывести переменные пакета. whatis --------------- Выводит тип выражения. Листинг и переключение между потоками и горутинами: goroutine (псевдоним: gr) — показывает или изменяет текущую goroutine goroutines (псевдоним: grs) Список программных goroutines. thread (псевдоним: tr) ----- Переключиться на указанный поток. threads ---------------- Распечатать информацию для каждого трассируемого потока. Просмотр стека вызовов и выбор кадров: deferred --------- Выполняет команду в контексте отложенного вызова. вниз ------------- Переместить текущий кадр вниз. кадр ------------ Установить текущий кадр или выполнить команду на другом кадре. stack (псевдоним: bt) Печать трассировки стека. вверх --------------- Переместить текущий кадр вверх. Другие команды: config --------------------- Изменяет параметры конфигурации.
дизассемблировать (псевдоним: дизассемблировать) Дизассемблер. редактировать (псевдоним: ed) ----------- Открыть там, где вы находитесь, в $DELVE_EDITOR или $EDITOR exit (псевдоним: quit | q) ----- Выйти из отладчика. funcs ---------------------- Вывести список функций. help (псевдоним: h) ------------ Выводит справочное сообщение. библиотеки ------------------ Список загруженных динамических библиотек list (псевдоним: ls | l) ------- Показать исходный код. source --------------------- Выполняет файл, содержащий список команд delve источники -------------------- Распечатайте список исходных файлов. типы ---------------------- Распечатать список типов Введите help, а затем команду для получения полной документации.
Есть несколько доступных команд, но мы можем легко разделить их по разным областям, чтобы лучше понять, как работать с клиентом delve.
Общие команды Спуска
Первая команда, на которую я хотел бы обратить ваше внимание, это команда list , которая позволяет нам просмотреть исходный код данного местоположения. Мы можем указать местоположение, передав имя пакета и функцию или путь к файлу и строку. Например
Мы можем указать местоположение, передав имя пакета и функцию или путь к файлу и строку. Например
Список
показывает исходный код по имени пакета и функции
(dlv) список main.main
Отображение /workspace/tutorials/delve/main.go:7 (ПК: 0x10d145b)
2:
3: импортировать "FMT"
4:
5: var m = make(map[int]int, 0)
6:
7: основная функция () {
8: для _, n := диапазон []int{5, 1, 9, 98, 6} {
9: х := фиб(п)
10: fmt.Println(n, "fib", x)
11: }
12: }
(длв)
Список
показывает исходный код по имени файла и номеру строки
(dlv) список ./main.go:14
Отображение /workspace/tutorials/delve/main.go:14 (ПК: 0x10d1713)
9: х := фиб(п)
10: fmt.Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
15: если n < 2 {
16: вернуть п
17: }
18:
19: вар целое число
(длв)
Также есть команда поиска функций по шаблону
Функции
(dlv) функции fib main.fib
Выход
если вы застряли в сеансе отладки, вы можете выйти
(длв) выход
Добавление точек останова с помощью Delve
Как только вы научитесь отображать на экране часть вашего исходного кода с помощью команды delve list , вы можете начать добавлять точки останова в свою программу в тех областях, где вы хотите затем остановиться и проверить переменные и другие значения выражений. .
.
Для этого базового примера предположим, что мы хотим добавить точку останова в строке 10 в файле main.go, которую мы уже видели в предыдущем примере list . Это будет сделано с помощью ключевого слова break , за которым следует место, где вы хотите добавить точку останова.
break
Это добавит точку останова в указанное место, а также список, где эта точка останова будет использоваться в строке 10
(dlv) перерыв ./main.go:10
Точка останова 1 установлена на 0x10d155d для main.main() ./main.go:10
(dlv) список ./main.go:10
Отображение /workspace/tutorials/delve/main.go:10 (ПК: 0x10d155d)
5: var m = make(map[int]int, 0)
6:
7: основная функция () {
8: для _, n := диапазон [] int {5, 1, 9, 98, 6} {
9: х := фиб(п)
10: fmt.Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
15: если n < 2 {
(длв)
точек останова
Список всех текущих точек останова для этого сеанса отладки
(dlv) точки останова Точка останова runtime-fatal-throw по адресу 0x10388c0 для runtime.fatalthrow() /usr/local/go/src/runtime/panic.go:1162 (0) Точка останова невосстановленная-паника по адресу 0x1038940 для runtime.fatalpanic() /usr/local/go/src/runtime/panic.go:1189 (0) печать runtime.curg._panic.arg Точка останова 1 по адресу 0x10d155d для main.main() ./main.go:10 (0)
В этом примере мы видим 3 точки останова. Первые 2 автоматически добавляются delve и используются для защиты от паники и фатальных ошибок, чтобы мы могли точно определить статус нашей программы и проверить переменные, трассировку стека и статус.
Третья точка останова с надписью Breakpoint 1 — это та, которую мы добавили в строке 10.
Попробуйте добавить новые точки останова и посмотрите, как они потом отображаются в списке здесь!
прозрачный
Чтобы удалить определенную точку останова из сеанса отладки
(dlv) очистить 1 Точка останова 1 очищена по адресу 0x10d155d для main.main() ./main.go:10
Это полезно, если вы хотите удалить определенную точку останова, которую вы добавили по ошибке или просто потому, что вам нужно удалить и начать отладку какой-либо другой области той же программы.
clearall
Для очистки всех добавленных вручную точек останова
(dlv) перерыв ./main.go:8 Точка останова 1 установлена на 0x10d1472 для main.main() ./main.go:8 (dlv) перерыв ./main.go:9Точка останова 2 установлена на 0x10d154a для main.main() ./main.go:9 (dlv) перерыв ./main.go:10 Точка останова 3 установлена на 0x10d155d для main.main() ./main.go:10 (dlv) точки останова Точка останова runtime-fatal-throw по адресу 0x10388c0 для runtime.fatalthrow() /usr/local/go/src/runtime/panic.go:1162 (0) Точка останова невосстановленная-паника по адресу 0x1038940 для runtime.fatalpanic() /usr/local/go/src/runtime/panic.go:1189 (0) печать runtime.curg._panic.arg Точка останова 1 по адресу 0x10d1472 для main.main() ./main.go:8 (0) Точка останова 2 по адресу 0x10d154a для main.main() ./main.go:9(0) Точка останова 3 по адресу 0x10d155d для main.main() ./main.go:10 (0) (dlv) очистить все Точка останова 1 очищена по адресу 0x10d1472 для main.main() ./main.go:8 Точка останова 2 очищена по адресу 0x10d154a для main.main() ./main.go:9 Точка останова 3 очищена по адресу 0x10d155d для main.main() ./main.go:10
В приведенном выше примере мы создали 3 точки останова , строки 8, 9 и 10 . Мы отображаем все точки останова, а затем удаляем все точки останова сразу. Это может быть очень удобно, когда вы хотите очистить все точки останова сразу и перейти к отладке другой области той же программы.
Запуск и навигация по программе с помощью Delve
После того, как мы установили все точки останова и можем проверить любую часть нашего исходного кода с помощью списка, мы теперь можем увидеть, как мы можем на самом деле «отлаживать» и запускать нашу программу в режиме отладки, используя набор очень мощных команд.
продолжить
Запускает программу до следующей точки останова или до завершения программы
(dlv) перерыв ./main.go:10 Точка останова 1 установлена на 0x10d155d для main.main() ./main.go:10 (длв) продолжить > main.main() ./main.go:10 (попадает в goroutine(1):1, всего:1) (ПК: 0x10d155d) 5: var m = make(map[int]int, 0) 6: 7: основная функция () { 8: для _, n := диапазон [] int {5, 1, 9, 98, 6} { 9: х := фиб(п) => 10: fmt.Println(n, "fib", x) 11: } 12: } 13: 14: func fib(n int) int { 15: если n < 2 {
После установки точки останова на строку 10 в файле main.go мы можем просто запустить continue , и наш отладчик будет запускать программу до следующей точки останова, которая в нашем случае является просто точкой останова 1 в строке 10. На этом мы можем делать довольно много вещей, например, проверять и изменять содержимое переменных. Но сначала давайте посмотрим, какие другие команды мы можем использовать для навигации по нашей программе Go.
следующий
Переход к следующей исходной строке
(dlv) следующий 5 фиб 5 > main.main() ./main.go:8 (ПК: 0x10d1693) 3: импортировать "FMT" 4: 5: var m = make(map[int]int, 0) 6: 7: основная функция () { => 8: для _, n := диапазон []int{5, 1, 9, 98, 6} { 9: х := фиб(п) 10: fmt.Println(n, "fib", x) 11: } 12: } 13:
Вот так просто! Команда next просто позволяет нам выполнять одну инструкцию за раз, как указано в исходном коде, независимо от того, есть точки останова или нет. Это весьма полезно, если вы хотите проанализировать программу шаг за шагом
step
Шаг, или, как мне нравится его называть, «вход», используется, чтобы указать отладчику перейти внутрь вызова функции, это похоже на следующий, но используется для перехода на уровень глубже при вызове функций.
(dlv) следующий
> main.main() ./main.go:9 (ПК: 0x10d154a)
4:
5: var m = make(map[int]int, 0)
6:
7: основная функция () {
8: для _, n := диапазон []int{5, 1, 9, 98, 6} {
=> 9: х := фиб(п)
10: fmt. Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
(длв) шаг
> main.fib() ./main.go:14 (ПК: 0x10d1713)
9: х := фиб(п)
10: fmt.Println(n, "fib", x)
11: }
12: }
13:
=> 14: func fib(n int) int {
15: если n < 2 {
16: вернуть п
17: }
18:
19: вар целое число
Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
(длв) шаг
> main.fib() ./main.go:14 (ПК: 0x10d1713)
9: х := фиб(п)
10: fmt.Println(n, "fib", x)
11: }
12: }
13:
=> 14: func fib(n int) int {
15: если n < 2 {
16: вернуть п
17: }
18:
19: вар целое число
С помощью шага мы можем перейти внутрь определения функции вместо того, чтобы просто вычислять ее значение и двигаться дальше. Это весьма полезно, если следовать логике множественных вызовов функций, которые возвращают результаты, природу и происхождение которых мы хотим исследовать. При использовании шаг в строках, не являющихся вызовами функций, она будет вести себя точно так же, как инструкция next delve. Проходит строчка за строчкой.
stepout
Причина, по которой я предпочитаю называть step stepin, заключается в том, что его аналог stepout является полной противоположностью step. Это возвращает нас к вызывающему объекту функции, в которой мы находимся.
Это возвращает нас к вызывающему объекту функции, в которой мы находимся.
(dlv) ступенчатый выход
> main.main() ./main.go:9 (ПК: 0x10d1553)
Возвращаемые значения:
~r1: 1
4:
5: var m = make(map[int]int, 0)
6:
7: основная функция () {
8: для _, n := диапазон [] int {5, 1, 9, 98, 6} {
=> 9: х := фиб(п)
10: fmt.Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
перезагрузка
Перезагрузка позволит нам перезапустить программу в случае ее завершения, а мы все еще хотим отладить. Это особенно полезно, если мы не хотим потерять все наши точки останова и не хотим выходить и создавать новый сервер отладки delve с нуля
(длв) очистить все Точка останова 4 очищена по адресу 0x10d155d для main.main() ./main.go:10 (длв) продолжить 1 выдумка 1 9выдумка 34 98 фиб 6174643828739884737 6 фиб 8 Процесс 39014 завершился со статусом 0 (длв) перезагрузка Процесс перезапущен с PID 39050
В нашем примере мы просто очищаем все точки останова, продолжаем, чтобы программа выполнялась до конца, и снова перезапускаем процесс. Теперь мы можем сделать новый шаг и снова начать отладку без необходимости перезапускать отладку с нуля.
Теперь мы можем сделать новый шаг и снова начать отладку без необходимости перезапускать отладку с нуля.
Как просмотреть программные переменные с помощью Delve
До сих пор мы видели, как добавлять точки останова и управлять ими, как легко перемещаться по программе с помощью delve. Теперь нам просто нужно иметь возможность просматривать и редактировать программные переменные и память, что является фундаментальной частью процесса отладки. Есть множество очень полезных команд delve, которые мы можем использовать для этой цели.
print
Print самый простой и позволяет нам видеть содержимое переменных и вычислять выражения
(dlv) перерыв ./main.go:10
Точка останова 1 установлена на 0x10d155d для main.main() ./main.go:10
(длв) продолжить
> main.main() ./main.go:10 (попадает в goroutine(1):1, всего:1) (ПК: 0x10d155d)
5: var m = make(map[int]int, 0)
6:
7: основная функция () {
8: для _, n := диапазон []int{5, 1, 9, 98, 6} {
9: х := фиб(п)
=> 10: fmt. Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
15: если n < 2 {
(длв) печать х
5
Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
15: если n < 2 {
(длв) печать х
5
В приведенном выше примере мы только что установили точку останова на наш main.go в строке 10 и напечатали значение переменной x, которая является значением Фибоначчи для последовательности в позиции 5, как указано в приведенном выше коде.
Теперь вы можете попытаться перейти внутрь функции fib и попробовать вывести различные значения, такие как
nили переменная картыm!
locals
Команда locals может оказаться весьма полезной для исследования содержимого всех локальных переменных
(длв) список
> main.main() ./main.go:10 (попадает в goroutine(1):1, всего:1) (ПК: 0x10d155d)
5: var m = make(map[int]int, 0)
6:
7: основная функция () {
8: для _, n := диапазон []int{5, 1, 9, 98, 6} {
9: х := фиб(п)
=> 10: fmt.Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
15: если n < 2 {
(dlv) местные жители
п = 5
х = 5
Выводы
Этого набора команд должно быть более чем достаточно для уверенной отладки приложений Go. Отладчик Go delve также доступен для использования во всех основных редакторах Go и IDE. Вы можете проверить список доступных интеграций здесь https://github.com/go-delve/delve/blob/master/Documentation/EditorIntegration.md.
Отладчик Go delve также доступен для использования во всех основных редакторах Go и IDE. Вы можете проверить список доступных интеграций здесь https://github.com/go-delve/delve/blob/master/Documentation/EditorIntegration.md.
Если вы освоите отладчик командной строки Go Delve, вам будет еще проще работать с другими интегрированными версиями редактора, которые следуют той же концепции и структуре.
Я планирую выпустить вторую часть руководства по отладке Go Delve, посвященную исключительно отладке горутин. Спасибо за чтение, и я надеюсь, что вам понравился этот контент!
Перейти к отладке с помощью Delve YouTube Tutorial
Р для экологов: Собираем кусочную регрессию
[Эта статья была впервые опубликована на Экология изменения климата » R и любезно предоставлена R-блогерами]. (Вы можете сообщить о проблеме с содержанием на этой странице здесь)
Хотите поделиться своим контентом с R-блогерами? нажмите здесь, если у вас есть блог, или здесь, если у вас его нет.

Кусочная регрессия возникает, когда у вас есть «точки останова», когда в данных явно присутствуют две разные линейные зависимости с внезапным резким изменением направления. Это иногда возникает в экологии, когда речь идет, например, о видовом богатстве растений подлеска и возрасте леса. Сначала происходит быстрое падение по мере развития сукцессии (быстрые колонизирующие растения умирают, когда свет становится более ограниченным), затем внезапный перелом и более умеренный рост видового богатства, поскольку более теневыносливые растения и саженцы старых деревьев начинают колонизировать зрелый лес. .
Если вы погуглите «R кусочная регрессия», вы можете получить множество методов и советов о том, как запустить кусочную регрессию. По сути, вы можете сделать это вручную или использовать готовый пакет для запуска регрессии. Если вы похожи на меня, вам может быть интересно: эти методы одинаковы? Если нет, то что лучше? Как я на самом деле их использую? Что ж, надеюсь, я отвечу на некоторые из этих вопросов.
По сути, я рассмотрю два метода: итеративный подход методом грубой силы (как в «Книге R» Кроули) и «сегментированный» пакет. Использование этих подходов позволяет вам статистически оценить точку останова, что лучше, чем просто на глазок и подгонка двух моделей к тому, что вы думаю, что является точкой останова. Позвольте статистике работать за вас объективно.
Во-первых, давайте сгенерируем некоторые сегментированные данные:
x <- c(1:10, 13:22) у <- числовой (20) ## Создать первый сегмент у[1:10] <- 20:11 + rнорма(10, 0, 1,5) ## Создать второй сегмент y[11:20] <- seq(11, 15, len=10) + rnorm(10, 0, 1.5) ## Нарисуйте это пар(мар=с(4,4,1,1)+0,2) график (x, y, ylim = c (5, 20), pch = 16)
У вас должен получиться V-образный участок, правая сторона которого имеет более пологий уклон.
Вот так
МЕТОД 1: ИТЕРАТИВНЫЙ ПОИСК
Сначала мы смоделируем данные, используя процедуру итеративного поиска, описанную Кроули. Мы собираемся использовать модель, которая выглядит следующим образом:
Мы собираемся использовать модель, которая выглядит следующим образом:
Обратите внимание, что символ умножения используется в смысле определения модели R, а не в математическом смысле, что означает основные эффекты и взаимодействия для обеих переменных
В этом случае c - это точка останова. I ( x ) и I ( x > c ) по сути являются фиктивными переменными. I ( x ) равно 1, если x меньше точки останова, и 0, если выше. I ( x > c ) — это фиктивная переменная, которая равна 1, если x выше точки останова, и 0, если она ниже. Должно быть очевидно, что моделируются два набора параметров в зависимости от значения x.
Самый сложный бит — это выбор точки останова. Мы можем просмотреть данные и сказать, что точка останова находится где-то между 9и 17. Выбирайте более широкий диапазон, чем вы думаете, просто на всякий случай. Создайте переменную с именем breaks для хранения этих точек останова:
breaks <- x[that(x >= 9 & x <= 17)]
Теперь мы будем итеративно искать в этих контрольных точках модель с наименьшим остаточным MSE, используя ее в качестве критерия для наилучшей модели. Создайте пустой контейнер для значений MSE из каждой модели и используйте цикл for() для запуска линейной регрессии для каждой возможной точки останова. Сформулируйте линейную модель точно так же, как приведенная выше формула.
Создайте пустой контейнер для значений MSE из каждой модели и используйте цикл for() для запуска линейной регрессии для каждой возможной точки останова. Сформулируйте линейную модель точно так же, как приведенная выше формула.
mse <- числовой (длина (разрывы))
для (я в 1: длина (разрывы)) {
кусочно1 <- lm(y ~ x*(x =breaks[i]))
mse[i] <- итог(кусочно1)[6]
}
mse <- as.numeric(mse)
Если построить MSE по точкам останова, мы можем визуально оценить точку останова как самую низкую точку на кривой:
Легко может быть 13 или 15, поэтому я просто выбираю точку останова с наименьшей ошибкой:
разрывов [который (mse == мин (mse))]
Это говорит мне, что точка останова в моей симуляции была 15. Я запускаю свою окончательную модель с моей новой оценочной точкой останова:
кусочно2 <- lm(y ~ x*(x < 15) + x*(x > 15)) резюме(кусочно2)
Итог выглядит так:
Это довольно неприятный результат.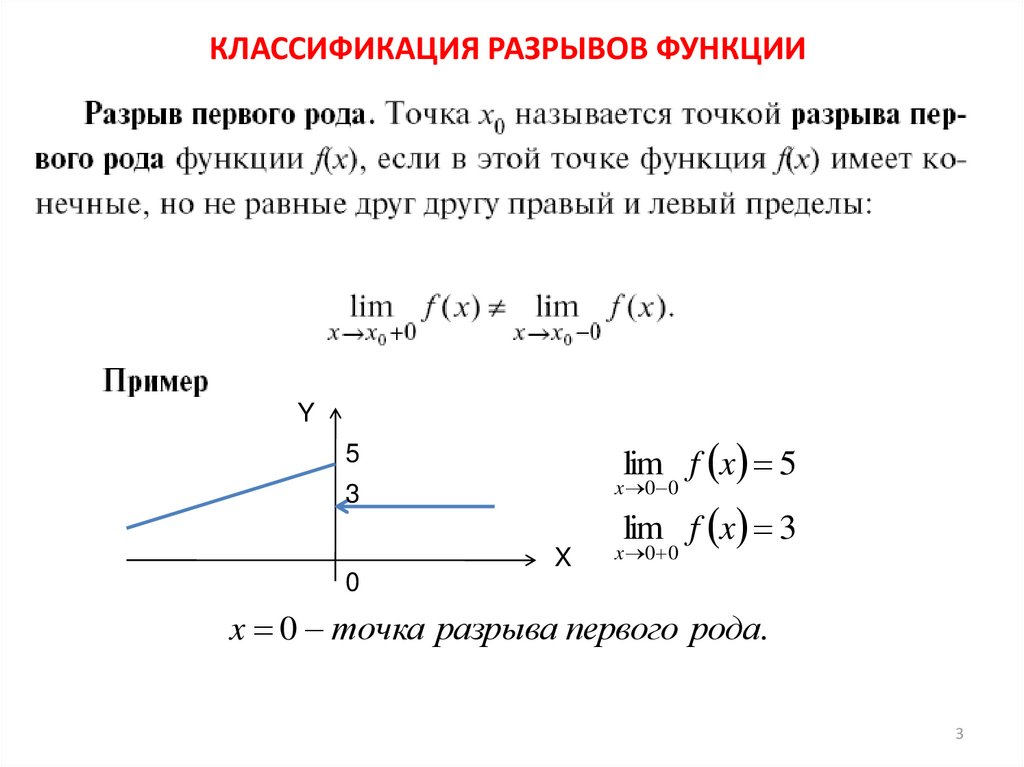 Прочитайте это так: (Перехват) более или менее бесполезен сам по себе. Перехват линии при x
Прочитайте это так: (Перехват) более или менее бесполезен сам по себе. Перехват линии при x
Когда x больше 15, точка пересечения составляет 3,3133 – 0,9116 = 2,4017, а наклон представляет собой просто переменную x, 0,5843. Таким образом, когда x больше 15, линия имеет уравнение 2,4017 + 0,5843x. Обратите внимание, что в этой таблице исключены коэффициенты с оценками NA. Они возникают из сингулярностей и могут быть проигнорированы.
сюжет(x,y, ylim=c(5, 20), pch=16) кривая ((3,3133 + 16,6352) + (0,5843-1,3025)*x, добавить=T, от=1, до=15) кривая ((3,3133 - 0,9116) + 0,5843*x, добавить=T, от=15, до=max(x)) аблин (v=15, lty=3)
Обратите внимание, что сегменты не были ограничены соприкасающимися или непрерывными. Это заложено в алгоритме, который мы использовали.
СПОСОБ 2: ИСПОЛЬЗОВАНИЕ «СЕГМЕНТИРОВАННОГО» ПАКЕТА
Чтобы использовать «сегментированный» пакет, вам, конечно же, необходимо установить и загрузить его. Процедура «сегментирования» использует максимальное правдоподобие, чтобы соответствовать несколько иной параметризации модели:
Процедура «сегментирования» использует максимальное правдоподобие, чтобы соответствовать несколько иной параметризации модели:
Более или менее. Это не совсем так, но достаточно близко
I ( x > c ) является фиктивной переменной, как указано выше, поэтому, когда x
Член γ — это просто мера расстояния между концом первого сегмента и началом следующего. Модель сходится, когда γ минимизируется, таким образом, этот метод ограничивает сегменты (почти) непрерывными . Это 90 378 основных 90 379 отличий от итеративного подхода в методе 1 выше.
Чтобы использовать этот метод, вы сначала подбираете общую линейную модель. Затем вы используете функцию segmented(), чтобы подогнать кусочную регрессию. Функция segmented() принимает в качестве аргументов общую линейную модель, seg.Z, которая представляет собой одностороннюю формулу, описывающую предиктор с сегментом (у нас есть только один предиктор, x, который имеет сегмент), и psi, который является начальное значение точки останова (как и в nls(), вам необходимо указать наилучшую оценку). Более сложные модели немного сложнее с точки зрения аргументов, но это хороший начальный пример.
Более сложные модели немного сложнее с точки зрения аргументов, но это хороший начальный пример.
В нашем случае x — это предиктор с сегментом (это единственный предиктор), и, основываясь на моей самой первой диаграмме рассеяния (первый график на странице), я предполагаю, что точка останова равна 14.
лин. мод <- lm(y~x) segmented.mod <- segmented(lin.mod, seg.Z = ~x, psi=14)
Используя команду summary(segmented.mod), вы получите предполагаемую точку останова +/- некоторую ошибку (12.07 для меня), точку пересечения и наклон для первого сегмента, а также U1.x, который является наклоном второго сегмент.
ОБНОВЛЕНИЕ:
U1.x не наклон второго сегмента. Это разница наклонов между первым и вторым сегментом. Итак, если ваши коэффициенты x = -0,9699 и U1.x = 1,4163, то наклон второго сегмента равен -0,9699 + 1,4163 = 0,4464. Использование команды наклона (segmented.mod) даст вам наклоны каждого сегмента, которые должны соответствовать приведенному выше расчету.
Построить это просто:
plot(x,y, pch=16, ylim=c(5,20)) график (segmented.mod, добавить = T)
Итак, два метода кусочной регрессии. Каждый из них относительно прост в реализации, но они делают очень разные вещи. Если вы твердо настроены на кусочную регрессию, убедитесь, что вы выбрали тот, который наиболее подходит для вашего вопроса: должны ли сегменты быть непрерывными или они могут быть прерывистыми? Убедитесь, что у вас есть обоснование для любого из них.
Также обратите внимание, что эти модели являются , а не вложенными, , поэтому вы не можете использовать тесты отношения правдоподобия для выбора модели. Вы можете попробовать использовать AIC для выбора модели, но вместо этого я советую вам логически подумать о непрерывности сегментов.
К оставьте комментарий для автора, перейдите по ссылке и оставьте комментарий в их блоге: Изменение климата Экология » R .

 е. функция
е. функция


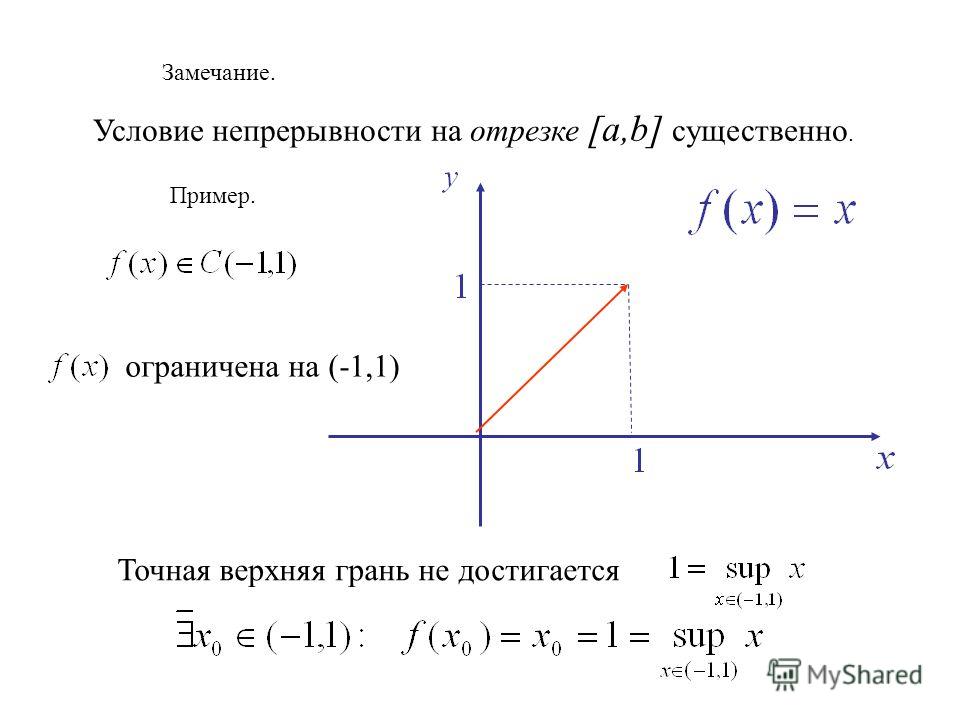
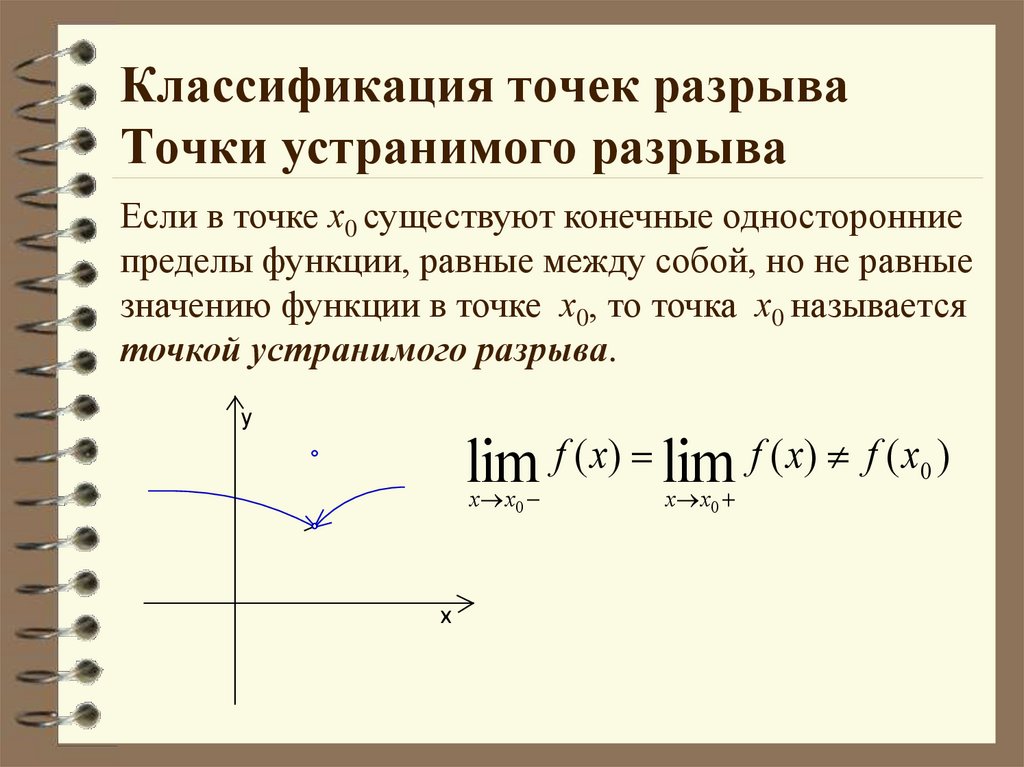 Как и в предыдущем случае, в точкеx
=
2
Как и в предыдущем случае, в точкеx
=
2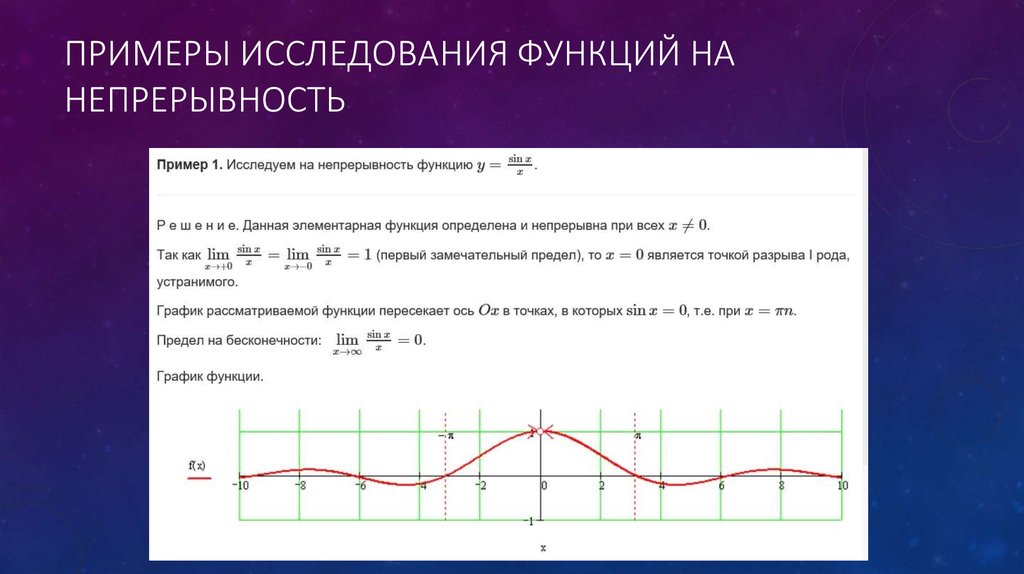 рис. 5.2).
рис. 5.2). ниже).
ниже).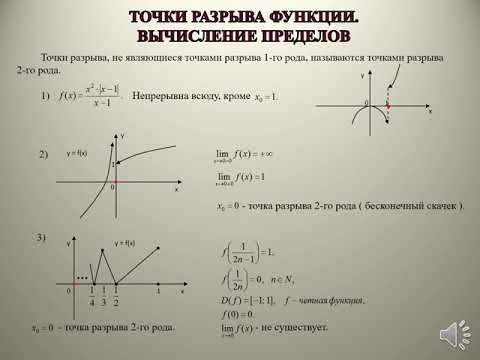
 axvline(i, color='red', linestyle='штрих', label='разрывы')
axvline(i, color='red', linestyle='штрих', label='разрывы') 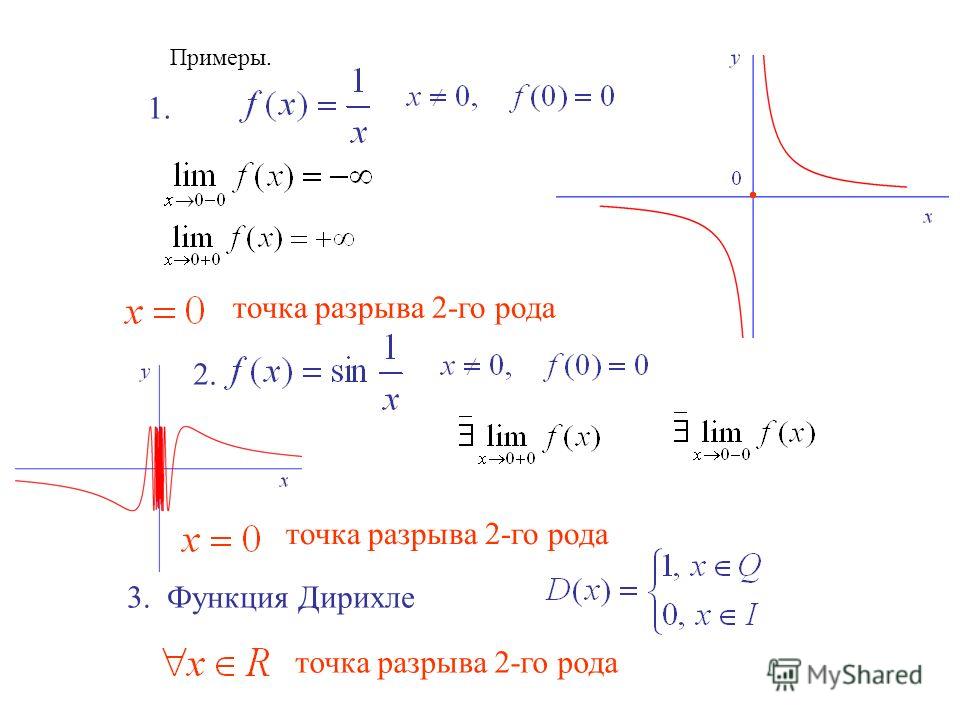 Он понимает среду выполнения Go, структуры данных и выражения лучше, чем GDB. Delve в настоящее время поддерживает Linux, OSX и Windows на
Он понимает среду выполнения Go, структуры данных и выражения лучше, чем GDB. Delve в настоящее время поддерживает Linux, OSX и Windows на  mod
mod Это не работает, если исполняемый файл не был собран delve.
перезапустить (псевдоним: r) ---------- Перезапустить процесс.
шаг (псевдоним: s) ------------- Пошаговое выполнение программы.
пошаговая инструкция (псевдоним: si) Один шаг одиночной инструкции процессора.
stepout (псевдоним: so) --------- Выйти из текущей функции.
Управление точками останова:
break (псевдоним: b) ------- Устанавливает точку останова.
точки останова (псевдоним: bp) Вывести информацию об активных точках останова.
clear ------------------ Удаляет точку останова.
clearall --------------- Удаляет несколько точек останова.
условие (псевдоним: cond) Установить условие точки останова.
on --------------------- Выполняет команду при достижении точки останова.
trace (псевдоним: t) ------- Установить точку трассировки.
Просмотр переменных программы и памяти:
args ------------------ Вывести аргументы функции.
display -------------- Выводить значение выражения каждый раз, когда программа останавливается.
exammem (псевдоним: x) Проверить память:
locals --------------- Вывести локальные переменные.
Это не работает, если исполняемый файл не был собран delve.
перезапустить (псевдоним: r) ---------- Перезапустить процесс.
шаг (псевдоним: s) ------------- Пошаговое выполнение программы.
пошаговая инструкция (псевдоним: si) Один шаг одиночной инструкции процессора.
stepout (псевдоним: so) --------- Выйти из текущей функции.
Управление точками останова:
break (псевдоним: b) ------- Устанавливает точку останова.
точки останова (псевдоним: bp) Вывести информацию об активных точках останова.
clear ------------------ Удаляет точку останова.
clearall --------------- Удаляет несколько точек останова.
условие (псевдоним: cond) Установить условие точки останова.
on --------------------- Выполняет команду при достижении точки останова.
trace (псевдоним: t) ------- Установить точку трассировки.
Просмотр переменных программы и памяти:
args ------------------ Вывести аргументы функции.
display -------------- Выводить значение выражения каждый раз, когда программа останавливается.
exammem (псевдоним: x) Проверить память:
locals --------------- Вывести локальные переменные.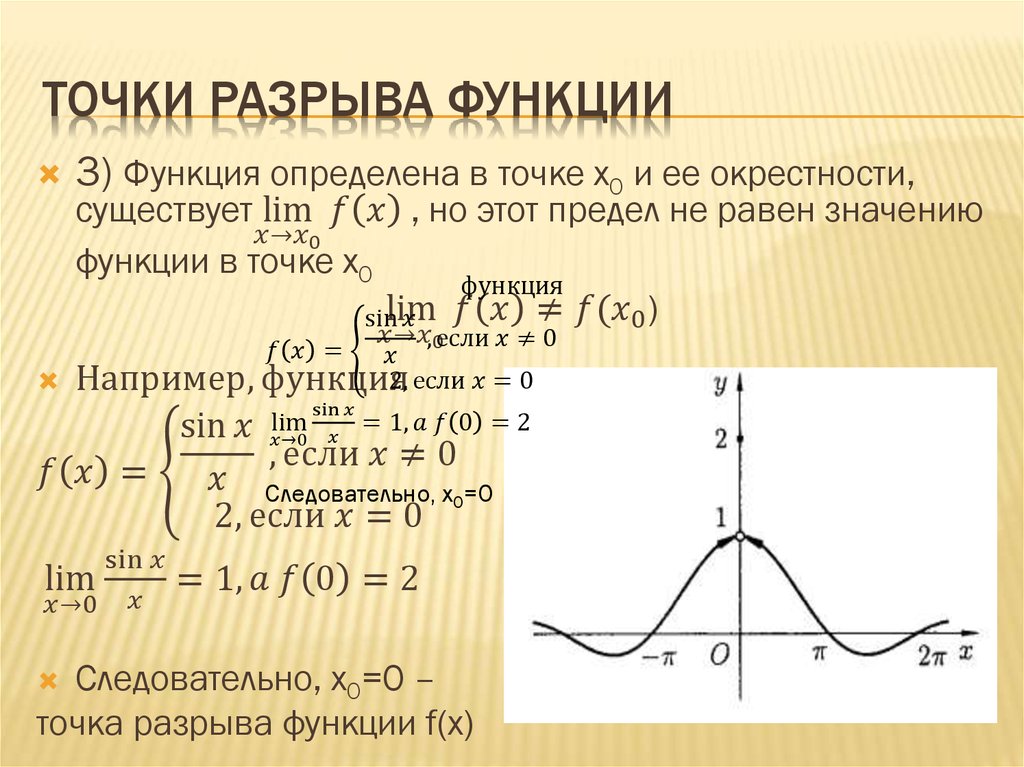 print (псевдоним: p) ----- Вычислите выражение.
regs ------------------ Вывести содержимое регистров процессора.
set ------------------ Изменяет значение переменной.
vars ------------------ Вывести переменные пакета.
whatis --------------- Выводит тип выражения.
Листинг и переключение между потоками и горутинами:
goroutine (псевдоним: gr) — показывает или изменяет текущую goroutine
goroutines (псевдоним: grs) Список программных goroutines.
thread (псевдоним: tr) ----- Переключиться на указанный поток.
threads ---------------- Распечатать информацию для каждого трассируемого потока.
Просмотр стека вызовов и выбор кадров:
deferred --------- Выполняет команду в контексте отложенного вызова.
вниз ------------- Переместить текущий кадр вниз.
кадр ------------ Установить текущий кадр или выполнить команду на другом кадре.
stack (псевдоним: bt) Печать трассировки стека.
вверх --------------- Переместить текущий кадр вверх.
Другие команды:
config --------------------- Изменяет параметры конфигурации.
print (псевдоним: p) ----- Вычислите выражение.
regs ------------------ Вывести содержимое регистров процессора.
set ------------------ Изменяет значение переменной.
vars ------------------ Вывести переменные пакета.
whatis --------------- Выводит тип выражения.
Листинг и переключение между потоками и горутинами:
goroutine (псевдоним: gr) — показывает или изменяет текущую goroutine
goroutines (псевдоним: grs) Список программных goroutines.
thread (псевдоним: tr) ----- Переключиться на указанный поток.
threads ---------------- Распечатать информацию для каждого трассируемого потока.
Просмотр стека вызовов и выбор кадров:
deferred --------- Выполняет команду в контексте отложенного вызова.
вниз ------------- Переместить текущий кадр вниз.
кадр ------------ Установить текущий кадр или выполнить команду на другом кадре.
stack (псевдоним: bt) Печать трассировки стека.
вверх --------------- Переместить текущий кадр вверх.
Другие команды:
config --------------------- Изменяет параметры конфигурации. дизассемблировать (псевдоним: дизассемблировать) Дизассемблер.
редактировать (псевдоним: ed) ----------- Открыть там, где вы находитесь, в $DELVE_EDITOR или $EDITOR
exit (псевдоним: quit | q) ----- Выйти из отладчика.
funcs ---------------------- Вывести список функций.
help (псевдоним: h) ------------ Выводит справочное сообщение.
библиотеки ------------------ Список загруженных динамических библиотек
list (псевдоним: ls | l) ------- Показать исходный код.
source --------------------- Выполняет файл, содержащий список команд delve
источники -------------------- Распечатайте список исходных файлов.
типы ---------------------- Распечатать список типов
Введите help, а затем команду для получения полной документации.
дизассемблировать (псевдоним: дизассемблировать) Дизассемблер.
редактировать (псевдоним: ed) ----------- Открыть там, где вы находитесь, в $DELVE_EDITOR или $EDITOR
exit (псевдоним: quit | q) ----- Выйти из отладчика.
funcs ---------------------- Вывести список функций.
help (псевдоним: h) ------------ Выводит справочное сообщение.
библиотеки ------------------ Список загруженных динамических библиотек
list (псевдоним: ls | l) ------- Показать исходный код.
source --------------------- Выполняет файл, содержащий список команд delve
источники -------------------- Распечатайте список исходных файлов.
типы ---------------------- Распечатать список типов
Введите help, а затем команду для получения полной документации.
 fatalthrow() /usr/local/go/src/runtime/panic.go:1162 (0)
Точка останова невосстановленная-паника по адресу 0x1038940 для runtime.fatalpanic() /usr/local/go/src/runtime/panic.go:1189 (0)
печать runtime.curg._panic.arg
Точка останова 1 по адресу 0x10d155d для main.main() ./main.go:10 (0)
fatalthrow() /usr/local/go/src/runtime/panic.go:1162 (0)
Точка останова невосстановленная-паника по адресу 0x1038940 для runtime.fatalpanic() /usr/local/go/src/runtime/panic.go:1189 (0)
печать runtime.curg._panic.arg
Точка останова 1 по адресу 0x10d155d для main.main() ./main.go:10 (0)
 /main.go:8
Точка останова 2 очищена по адресу 0x10d154a для main.main() ./main.go:9
Точка останова 3 очищена по адресу 0x10d155d для main.main() ./main.go:10
/main.go:8
Точка останова 2 очищена по адресу 0x10d154a для main.main() ./main.go:9
Точка останова 3 очищена по адресу 0x10d155d для main.main() ./main.go:10
 go:10
Точка останова 1 установлена на 0x10d155d для main.main() ./main.go:10
(длв) продолжить
> main.main() ./main.go:10 (попадает в goroutine(1):1, всего:1) (ПК: 0x10d155d)
5: var m = make(map[int]int, 0)
6:
7: основная функция () {
8: для _, n := диапазон [] int {5, 1, 9, 98, 6} {
9: х := фиб(п)
=> 10: fmt.Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
15: если n < 2 {
go:10
Точка останова 1 установлена на 0x10d155d для main.main() ./main.go:10
(длв) продолжить
> main.main() ./main.go:10 (попадает в goroutine(1):1, всего:1) (ПК: 0x10d155d)
5: var m = make(map[int]int, 0)
6:
7: основная функция () {
8: для _, n := диапазон [] int {5, 1, 9, 98, 6} {
9: х := фиб(п)
=> 10: fmt.Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
15: если n < 2 {
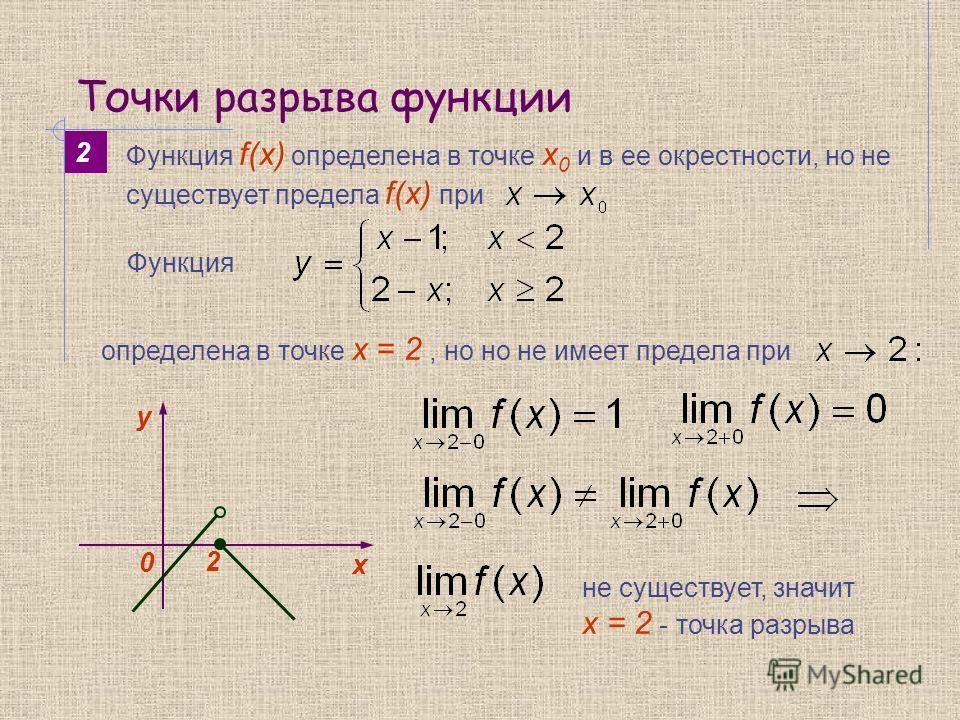 main() ./main.go:8 (ПК: 0x10d1693)
3: импортировать "FMT"
4:
5: var m = make(map[int]int, 0)
6:
7: основная функция () {
=> 8: для _, n := диапазон []int{5, 1, 9, 98, 6} {
9: х := фиб(п)
10: fmt.Println(n, "fib", x)
11: }
12: }
13:
main() ./main.go:8 (ПК: 0x10d1693)
3: импортировать "FMT"
4:
5: var m = make(map[int]int, 0)
6:
7: основная функция () {
=> 8: для _, n := диапазон []int{5, 1, 9, 98, 6} {
9: х := фиб(п)
10: fmt.Println(n, "fib", x)
11: }
12: }
13:
 Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
(длв) шаг
> main.fib() ./main.go:14 (ПК: 0x10d1713)
9: х := фиб(п)
10: fmt.Println(n, "fib", x)
11: }
12: }
13:
=> 14: func fib(n int) int {
15: если n < 2 {
16: вернуть п
17: }
18:
19: вар целое число
Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
(длв) шаг
> main.fib() ./main.go:14 (ПК: 0x10d1713)
9: х := фиб(п)
10: fmt.Println(n, "fib", x)
11: }
12: }
13:
=> 14: func fib(n int) int {
15: если n < 2 {
16: вернуть п
17: }
18:
19: вар целое число
 Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
15: если n < 2 {
(длв) печать х
5
Println(n, "fib", x)
11: }
12: }
13:
14: func fib(n int) int {
15: если n < 2 {
(длв) печать х
5