Правила область определения функции: § Область определения функции

3.7. Правила нахождения области определения и множества значений функции

Область определения функции , то . ,то . , то . , то . , то . , то . , то	(20)
Множество значений функции ; . .	(21)

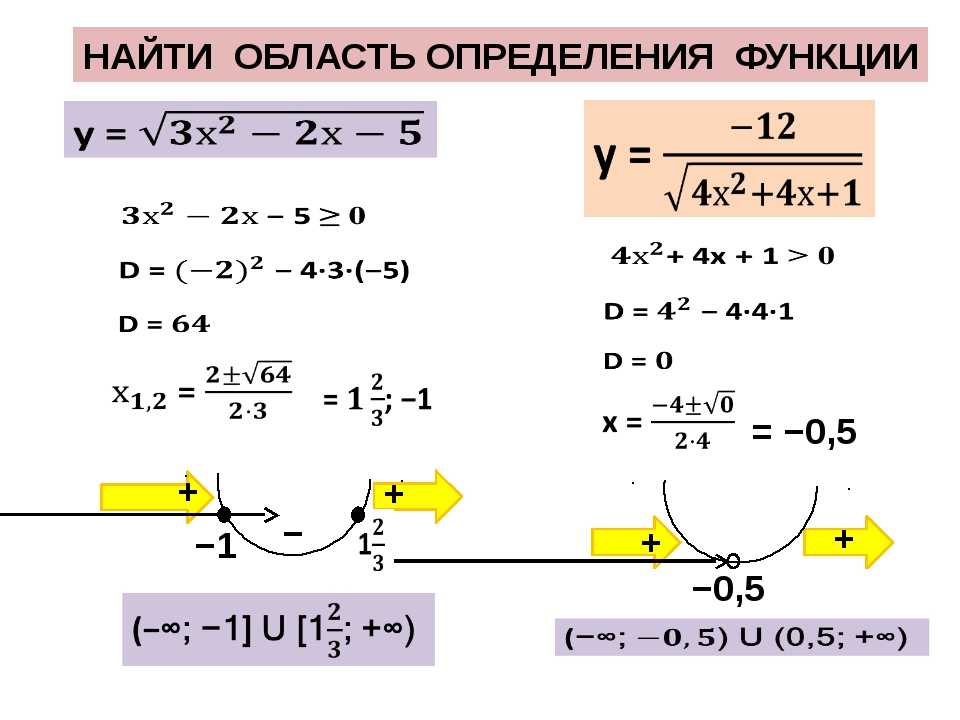
Пример. Найти область определения функции ,

►а)

б)

Рисунок 11

◄

4.1. Углы измеряются в градусах и радианах, соотношение между ними

180⁰= радиан

Поэтому 1⁰= радиан и 1 радиан= градусов.

4.2. Угол, отложенный по часовой стрелке, считается отрицательным, а угол, отложенный против часовой стрелки, считается положительным.

Будем откладывать углы от положительного направления оси Ox.

4.3. Круг, с центром в начале координат и радиусом 1, называется единичным или тригонометрическим кругом.

4.4. Каждому углу соответствует точка , ее координаты называются соответственно косинусом и синусом угла :

Рисунок 12

4. 5. В прямоугольном треугольнике:

Синус угла есть отношение противолежащего катета к гипотенузе.

Косинус угла есть отношение прилежащего катета угла к гипотенузе.

Тангенс угла есть отношение противолежащего катета к прилежащему катету.

Котангенс угла есть отношение прилежащего катета к противолежащему катету.

4.6. Область определения тригонометрических функций

D ( )= D ( )=

D (tg ): D (ctg ):

D (tg .ctg ):

4.7. Множество значений тригонометрических функций

, т.е.

, т.е.

4.8. Периодичность тригонометрических функций

и есть периодические функции с наименьшим периодом и

и есть периодические функции с наименьшим периодом и

4. 9. Знаки тригонометрических функций

Рисунок 13

4.10. Четность тригонометрических функций

— функция четная

— функция нечетная

— функция нечетная

— функция нечетная

4.11.Формулы приведения. Они позволяют отбросить числа , пользуясь двумя правилами:

1. находим четверть, в которой расположен угол, и определяем знак приводимой функции в этой четверти и ставим его перед приведенной функцией;

2. меняем функцию на кофункцию, если аргументом являются углы или , т.е. если отбрасываем угол или ;

3. не меняем название функции, если аргументом являются углы или , т.е. если отбрасываем угол или .

4. 12. Тригонометрические функции одного и того же угла.

4.13. Формулы сложения

4.14. Формулы двойных углов

1). sin2α = 2 sin α cos α	1а). sin α cos α = sin2α	1б). sin2 α cos2 α = sin22α
2). cos2α = cos2α – sin2α	3). tg2α =	3). сtg2α =

4. 15. Выражения тригонометрических функций через косинус двойного угла (формулы понижения степени)

1).	1а)		1б)
2)	2а)		2б)
3)		4)

4.16. Выражение тригонометрических функций через тангенс половинного угла (универсальная подстановка)

1)

2)

3)

4. 17. Преобразование суммы тригонометрических функций в произведение

1) sin α +sin β =	2) sin α -sin β =
3)cos α + cos β =	4) cos α – cos β =
5)	6)

4.18. Преобразование произведения тригонометрических функций в сумму

4.19.Обратные тригонометрические функции

20. Формулы решения простейших тригонометрических уравнений

a	где |a|<1,	где |a|<1,	,	,
a=0	,	,	,	,
a=1	,	,	,	,
a=-1	,	,	,	,

4. 21. Таблица значений тригонометрических функций некоторых углов

α	00	300	450	600	900	1800	2700	3600
	0
sinα	0				1	0	-1	0
cosα	1				0	-1	0	1
tgα	0		1			0	—	0
ctgα			1		0	—	0

Функции.

Область определения функции. | Методическая разработка по алгебре (9 класс) на тему:

Конспект урока алгебры по теме

«Функция. Область определения функции». 9 класс.

Цели:

Обучающая цель: систематизировать знания учащихся по теме; ввести понятия области определения, формировать умение их находить.

Развивающая цель: способствовать развитию наблюдательности, умения анализировать; побуждать учеников к самоконтролю, самоанализу своей учебной деятельности, развитие грамотной математической речи обучающихся.

Воспитательная: воспитывать такие качества личности, как познавательная активность, самостоятельность при работе на уроке.

Ход урока

1. Организационный момент. Сообщение  темы  и  целей  урока.
2. Актуализация  знаний.  

В курсе алгебры 7 и 8 классов вы уже многое узнали о функциях. Вспомним: какие функции мы изучали – название функций, каков вид графиков этих функций, формулы, задающие данные функции. (Презентация, слайды 2,3).

3. Изучение нового материала.

— Что же такое функция?  (Опр. Функцией называют такую зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение переменной у).

— Как называют переменные x и y? ( x называют независимой переменной или аргументом. Переменную y называют зависимой переменной, говорят также, что переменная y является функцией от переменной x).

— Как читают запись y = f(x)? (Читают:«y равно f от x») Символом f(x) обозначают значение функции, соответствующее значению аргумента, равному x.

— Пусть, например, функция задана формулой у = 2×2 – 6.Тогда можно записать, что

f (x)= 2×2 – 6. Найдём значения функции f для значений x, равных 2,5 и -3:

f (2,5) = 2 · 2,52 – 6 = 6,5; f(-3) = 2 · (-3)2 – 6 = 12.(Презентация, слайд 4 ).

4. Закрепление.

Решить из учебника №1(в) и №2(f(-1)) с последующей самопроверкой (два ученика решают эти номера с обратной стороны доски).

5. Решить устно. Найдите g(5), если g(x) =  . Сделайте вывод. (Вывод: выражение не имеет смысла, так как делить на 0 нельзя).

— В каких случаях выражение может не иметь смысла? (Выражение может не иметь смысла, если оно представлено в виде дроби с переменной в знаменателе или в виде корня четной степени из выражения с переменной).

6. Изучение нового материала.

— Что такое область определения функции ? (Все значения независимой переменной образуют область определения функции). Область определения может быть бесконечным и конечным множеством чисел.

— Попробуем вывести правила для нахождения области определения функции, в зависимости от её вида.

После обсуждения с классом данной проблемы, приходим к следующим выводам (правила и примеры записываем в тетрадь).

Правило 1. Если функция представлена в виде многочлена, то областью её определения является множество действительных чисел. (Презентация, слайд 5).

Пример. Областью определения функции  f(x) = 5×2 + 6x – 4 является множество всех действительных чисел, т.к. 5×2 + 6x – 4 – многочлен.

Правило 2.Если функция представлена в виде дроби, то областью её определения является множество действительных чисел, при которых знаменатель отличен от нуля. ( Презентация, слайд 6).

Пример. Найдите область определения функции, заданной формулой: у = .

Решение. Так как в области действительных чисел делить на нуль нельзя, то область определения функции найдем из условия: знаменатель не равен нулю.

x 2  — 6x + 8 ≠ 0, отсюда x ≠ 2. x ≠ 4.

Ответ: областью определения функции у =  является множество действительных чисел, кроме х = 2 и х = 4.

Правило 3. Если функция представлена в виде корня четной степени из выражения с переменной, то областью её определения является множество действительных чисел, при которых подкоренное выражение неотрицательно. (Презентация, слайд 7).

Пример. Найдите область определения функции, заданной формулой: у = .

Решение. Так как в области действительных чисел под знаком квадратного корня может находиться только неотрицательное число, то область определения функции найдем из условия: подкоренное выражение больше либо равно нуля.

-6х + 8 ≥ 0, отсюда x ≤  .

Ответ: (-.

Пример. Найдите область определения функции, заданной формулой: у =  .

Решение. Учитывая, что в области действительных чисел под знаком квадратного корня может находиться только неотрицательное число и делить на нуль нельзя, то область определения функции найдем из условия: подкоренное выражение больше нуля.

-6х + 8  0, отсюда х   .

Ответ: (-.

Пример. Найдите область определения функции, заданной формулой: у = .

Решение. Областью определения функции  у =  является множество всех действительных чисел, т.к.  – многочлен.

7. Закрепление. Решить из учебника № 11 (под диктовку).
8. Обучающая самостоятельная работа из сборника Л.А.Александрова. Вариант 1, стр.26,  №1 (а, б, в). Вариант 2, стр.27, №1 (а, б, в). (По окончании работы взаимопроверка по образцу). (Презентация, слайды 8, 9)
9. Итоги урока.

— Что называют областью определения функции?

— Назовите области определения всех элементарных функций.

— Какие выражения должны входить в формулу записи функции, чтобы областью её определения не являлось множество всех чисел?

X.  Домашнее  задание. п.1, № 3, № 9, № 29.

Функция. Зависимые и независимые переменные. Область определения и область значений функции.

теория по математике 🎲 функции

Определение понятия функции. Переменные.

Определение

Зависимость переменной у от переменной х, при которой любому значению переменной х соответствует единственное значение переменной у, называют функцией.

• х – это независимая переменная, ее называют аргумент.
• у – это зависимая переменная.

Ключевое слово, которое нужно запомнить в определении функции – это зависимость.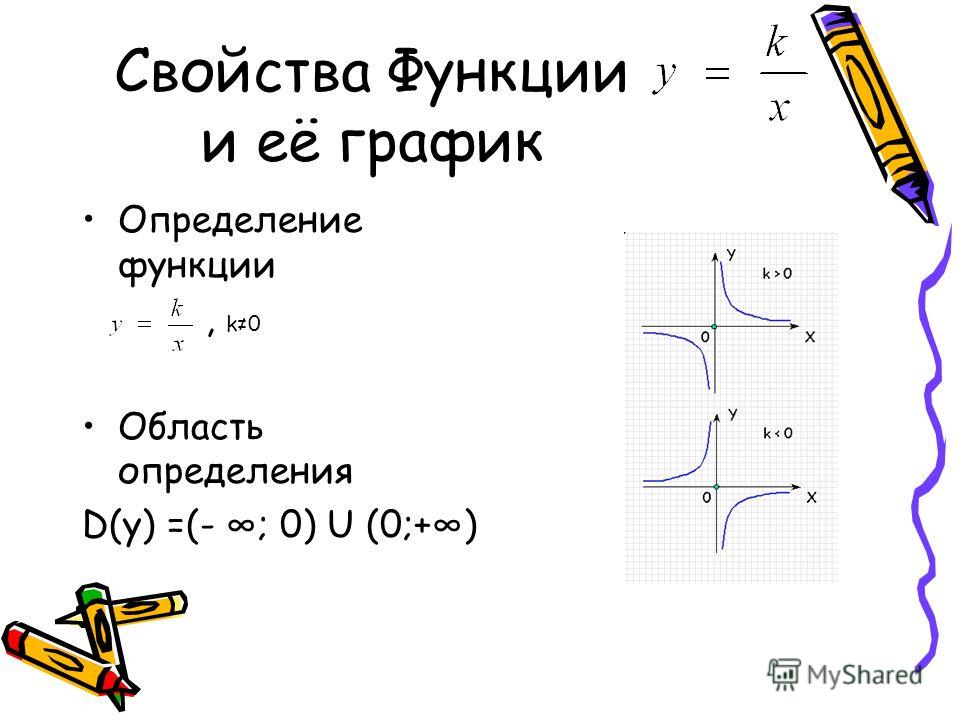

Например, человек идет на деловую встречу, но чувствует, что он опаздывает. Он ускоряет свой шаг, потому что от его скорости зависит время. Чем быстрее он двигается, тем меньше времени уйдет у него на дорогу. То есть время зависит от скорости.

Или, например, спортсмен метает ядро на дальнее расстояние. Чем сильнее будет бросок, тем дальше полетит ядро. Скорость полета зависит от силы толчка. Здесь опять прослеживается зависимость.

Функцию коротко записывают так: y = f(x). Вместо буквы f может быть использована и другая буква. Чтение данной записи следующее: “у равно f от х”.

Например, функция задана формулой у = – 3х² – 7. Равносильная ей запись такая: f(x)= – 3х² – 7.

Пример 1. Найти значение функции f(x)= – 3х² – 7 для значений аргумента, равных –5 и 4. Подставим в формулу вместо х значения, сначала (-5), а затем 4 f (–5) = – 3^. (–5)² – 7 = –75–7 = –82 f (4) = – 3^.(4)² – 7 = – 48 – 7 = –55 Пример 2. Найти значение х, при котором функция, заданная формулой f (х) = 3х+2, принимает значение равное 5. Так как дано, что значение равно 5, то значит f (х) = 5, составим и решим уравнение: 5=3х + 2 выполним перенос слагаемого 2 в левую часть, изменяя при этом знак: 5 – 2 = 3х приведем подобные слагаемые в левой части уравнения: 3 = 3х найдем неизвестный множитель делением: х = 1Ответ: х=1.

Области определения и значения функции

Определение

Все возможные значения независимой переменной (х) называют областью определения функции.

Все значения, которые принимает зависимая переменная (у) называют областью значений функции.

Если какая-либо функция у=f(x) задана формулой, а при этом ее область определения не указана, то считается, что она состоит из любых значений переменной, при которых выражение имеет смысл.

Области определения и значений школьных функций

1. Для линейной функции областью определения будет являться любое число.

Если у такой функции k≠0, то областью ее значений также будет являться любое число.

При k=0 область значений этой функции состоит из единственного числа b.

Например, функция задана формулой у = 7. Тогда ее область значения — это число 7, а область определения – любое число.

2. Гипербола задается формулой вида y = k/x.

Область определения такой функции – любое число, кроме нуля.

Область значений такой функции – аналогичная.

3. Функция, заданная формулой y= |x|, имеет область определения – любое число.

4. У функций у = х²  и у = х³ область определения  – любое число.

Для того чтобы понимать, как находится область определения функции и рассмотреть примеры заданий на нахождение области определения функции, вспомним правила, при которых существуют ограничения и выражение не имеет смысл: нельзя делить на нуль; нельзя извлекать квадратный корень из отрицательного числа.

Пример 3. Рассмотрим, как находится область определения функций, которые заданы следующими формулами:

• у = 5х + 2

Данное выражение будет иметь смысл при любом значении х, так как все действия здесь выполнимы. Например, подставив нуль, получим, что 5×0 + 2 = 2. Также при любых отрицательных или положительных значениях х выражение будет иметь смысл.

• у = – 8х² – 4

Данное выражение содержит степень. Все действия здесь так же выполнимы при любом значении х.

• у = 87/(х + 11)

В знаменателе этого выражения содержится переменная х, поэтому надо проверить, при каком значении он может быть равным нулю и исключить это значение из области определения, так как на знаменатель делят, а на нуль делить нельзя.

Итак, имеем знаменатель х + 11. Приравниваем его к нулю, получаем х + 11 = 0. Решаем простое уравнение на нахождение неизвестного слагаемого и получаем х= – 11. Это число исключаем из области определения функции.

• у = √х

Выражение содержит квадратный корень из переменной х.  Знаем, что он может извлекаться только из положительного или равного нулю числа. Поэтому область определения будет х≥0.

Ответ: (1) и (2) – множество всех чисел; (3) – любое число, кроме (-11) или х ≠ – 11; (4) х ≥0.

Нахождение области определения функции

1. Если выражение целое и не содержит квадратного корня, то оно имеет смысл при любом значении независимой переменной. Следовательно, областью определения будет являться множество всех чисел.
2. Если выражение дробное, то необходимо исключить те значения, которые обращают знаменатель в нуль. Для этого знаменатель дроби приравнять к нулю и решить полученное уравнение. Областью определения будут являться все числа, кроме тех, которые получились при решении уравнения.

Даниил Романович | Просмотров: 11.2k | Оценить:

Краткое изложение правил области действия | Microsoft Узнайте

Обратная связь Редактировать

Твиттер LinkedIn Фейсбук Эл. адрес

• Статья
• 03.08.2021
• 2 минуты на чтение

Использование имени должно быть однозначным в пределах его области действия (до момента определения перегрузки). Если имя обозначает функцию, функция должна быть однозначной по количеству и типу параметров. Если имя остается однозначным, применяются правила доступа к членам.

Инициализаторы конструктора

Инициализаторы конструктора оцениваются в области самого внешнего блока конструктора, для которого они указаны. Следовательно, они могут использовать имена параметров конструктора.

Глобальные имена

Имя объекта, функции или перечислителя является глобальным, если оно введено вне какой-либо функции или класса или предваряется глобальным унарным оператором области действия ( :: ) и если оно не используется в сочетании с любым из этих бинарных операторов:

• Разрешение области ( :: )

• Выбор элементов для объектов и ссылок (. )

• Выбор элемента для указателей ( -> )

Квалифицированные имена

Имена, используемые с бинарным оператором разрешения области видимости ( :: ), называются «полными именами». Имя, указанное после бинарного оператора разрешения области видимости, должно быть членом класса, указанного слева от оператора, или членом его базового класса(ов).

Имена, указанные после оператора выбора члена ( . или -> ), должны быть членами типа класса объекта, указанного слева от оператора, или членами его базового класса (ов). Имена, указанные справа от оператора выбора члена ( -> ), также могут быть объектами другого типа класса при условии, что левая часть -> является объектом класса и что класс определяет перегруженный член. -оператор выбора ( -> ), который оценивается как указатель на какой-либо другой тип класса. (Более подробно это положение обсуждается в разделе «Доступ к членам класса».)

Компилятор ищет имена в следующем порядке, останавливаясь, когда имя найдено:

1. Область действия текущего блока, если имя используется внутри функции; в противном случае — глобальная область.

2. Вовне через каждую охватывающую область блока, включая самую внешнюю область действия (которая включает в себя параметры функции).

3. Если имя используется внутри функции-члена, поиск имени выполняется в области видимости класса.

4. Базовые классы класса ищутся по имени.

5. Просматривается объемлющая вложенная область класса (если есть) и его базы. Поиск продолжается до тех пор, пока не будет найдена самая внешняя область охвата класса.

6. Поиск в глобальной области.

Однако вы можете изменить этот порядок поиска следующим образом:

1. Имена, которым предшествует :: , заставляют поиск начинаться в глобальном масштабе.

2. Names preceded by the class , struct , and union keywords force the compiler to search only for class , struct , or union имена.

3. Имена слева от оператора разрешения прицела ( :: ) может быть только class , struct , namespace , или union имен.

Если имя относится к нестатическому элементу, но используется в статической функции-члене, создается сообщение об ошибке. Точно так же, если имя относится к любому нестатическому члену включающего класса, генерируется сообщение об ошибке, поскольку вложенные классы не имеют вмещающего класса this указатели.

Имена параметров функций

Имена параметров функций в определениях функций считаются находящимися в области действия самого внешнего блока функции. Следовательно, они являются локальными именами и выходят за пределы области видимости при выходе из функции.

Имена параметров функций в объявлениях функций (прототипах) находятся в локальной области действия объявления и выходят за ее пределы в конце объявления.

Параметры по умолчанию входят в область действия параметра, для которого они используются по умолчанию, как описано в предыдущих двух абзацах. Однако они не могут получить доступ к локальным переменным или нестатическим членам класса. Параметры по умолчанию оцениваются в момент вызова функции, но они оцениваются в исходной области действия объявления функции. Поэтому параметры по умолчанию для функций-членов всегда оцениваются в области класса.

См. также

Наследство

Обратная связь

Отправить и просмотреть отзыв для

Этот продукт Эта страница

Просмотреть все отзывы о странице

python — Краткое описание правил области видимости?

Подробного ответа о времени Python3 не было, поэтому я написал ответ здесь. Большая часть описанного здесь подробно описана в разделе 4.2. 2 Разрешение имен документации Python 3.

Как указано в других ответах, существует 4 основных области действия: LEGB, для локальной, внешней, глобальной и встроенной. В дополнение к ним существует специальная область, тело класса , которое не включает объемлющую область для методов, определенных в классе; любые присваивания в теле класса делают переменную оттуда связанной в теле класса.

В частности, нет оператора блока , помимо def и class , создайте переменную область. В Python 2 понимание списка не создает область действия переменной, однако в Python 3 переменная цикла в включении списка создается в новой области.

Для демонстрации особенностей тела класса

 x = 0
класс X (объект):
    у = х
    x = x + 1 # x теперь переменная
    г = х
    Метод защиты (сам):
        печать(я.x) # -> 1
        print(x) # -> 0, глобальный x
        print(y) # -> NameError: глобальное имя 'y' не определено
инст = Х()
print(inst. x, inst.y, inst.z, x) # -> (1, 0, 1, 0)
 

Таким образом, в отличие от тела функции, вы можете переназначить переменную с тем же именем в теле класса, чтобы получить переменную класса с тем же именем; дальнейшие поиски по этому имени разрешаются вместо этого в переменную класса.

---

Одним из самых больших сюрпризов для многих новичков в Python является то, что цикл for не создает область переменных. В Python 2 генераторы списков также не создают область видимости (в отличие от генераторов и генераторов словарей!) Вместо этого они пропускают значение в функции или в глобальную область видимости:

 >>> [ i для i в диапазоне (5) ]
>>> я
4
 

Включения можно использовать как хитрый (или ужасный, если хотите) способ сделать модифицируемые переменные в лямбда-выражениях в Python 2 — лямбда-выражение действительно создает переменную область видимости, как оператор def , но внутри лямбда нет заявления разрешены. Присваивание, являющееся оператором в Python, означает, что никакие присвоения переменных в лямбда-выражении не допускаются, но понимание списка является выражением. ..

Это поведение было исправлено в Python 3 — никакие выражения понимания или генераторы не пропускают переменные.

---

Global действительно означает область действия модуля; основной модуль Python — это __main__ ; все импортированные модули доступны через переменную sys.modules ; чтобы получить доступ к __main__ можно использовать sys.modules['__main__'] или import __main__ ; вполне приемлемо получать доступ и назначать атрибуты там; они будут отображаться как переменные в глобальной области видимости основного модуля.

---

Если имя когда-либо присваивается в текущей области (кроме области класса), оно будет считаться принадлежащим этой области, в противном случае оно будет считаться принадлежащим любой охватывающей области, которая присваивается переменной (оно может еще не назначена или вообще не назначена) или, наконец, глобальная область. Если переменная считается локальной, но еще не установлена ​​или удалена, чтение значения переменной приведет к ошибке UnboundLocalError , которая является подклассом NameError 9. 0028 .

 х = 5
деффубар():
    print(x) # вызывает UnboundLocalError!
    x += 1 # потому что здесь присваивание делает x локальной переменной внутри функции
# вызов функции
Фубар()
 

Область может объявить, что она явно хочет изменить глобальную переменную (область модуля) с ключевым словом global:

 x = 5
деффубар():
    глобальный х
    печать (х)
    х += 1
foobar() # -> 5
напечатать(х) # -> 6
 

Это также возможно, даже если оно было затенено в охватывающей области:

 х = 5
у = 13
защита make_close():
    х = 42
    у = 911
    Функция определения():
        global x # видит глобальное значение
        напечатать (х, у)
        х += 1
    функция возврата
функция = make_close()
функция() # -> 5 911
напечатать(х, у) # -> 6 13
 

В python 2 нет простого способа изменить значение в охватывающей области; обычно это моделируется наличием изменяемого значения, такого как список длиной 1:

 def make_closure():
    значение = [0]
    защита get_next_value():
        значение[0] += 1
        возвращаемое значение[0]
    вернуть get_next_value
get_next = сделать_закрытие()
print(get_next()) # -> 1
print(get_next()) # -> 2
 

Однако в python 3 на помощь приходит нелокальный :

 def make_closure():
    значение = 0
    защита get_next_value():
        нелокальное значение
        значение += 1
        возвращаемое значение
    вернуть get_next_value
get_next = make_closure() # поведение идентично предыдущему примеру. 
 

В нелокальной документации говорится, что

Имена, перечисленные в нелокальном операторе, в отличие от перечисленных в глобальном операторе, должны ссылаться на уже существующие привязки во внешней области (область, в которой должна быть создана новая привязка, не может быть определена однозначно).

т. е. нелокальный всегда относится к самой внутренней внешней неглобальной области, где имя было привязано (т. е. присвоено, в том числе используется в качестве целевой переменной для , в предложении с или в качестве параметра функции) .

---

Любая переменная, не считающаяся локальной для текущей области или любой окружающей области, является глобальной переменной. Глобальное имя ищется в глобальном словаре модуля; если он не найден, глобальный объект ищется из встроенного модуля; изменено название модуля с python 2 на python 3; в питоне 2 было __builtin__ , а в python 3 теперь он называется встроенный . Если вы назначите атрибут встроенного модуля, после этого он будет виден любому модулю как доступная для чтения глобальная переменная, если этот модуль не затеняет их своей собственной глобальной переменной с тем же именем.

---

Также может быть полезно чтение встроенного модуля; предположим, что вам нужна функция печати в стиле python 3 в некоторых частях файла, но в других частях файла по-прежнему используется оператор print . В Python 2.6-2.7 вы можете получить Python 3 функция печати с:

 import __builtin__
print3 = __builtin__.__dict__['print']
 

из __future__ import print_function на самом деле не импортирует функцию print нигде в Python 2 - вместо этого он просто отключает правила синтаксического анализа для оператора print в текущем модуле, обрабатывая print как любой другой идентификатор переменной, и, таким образом, позволяет print искать функцию во встроенных функциях.

Правила области действия

Вы объединяете правила участников и администраторов с правилами области действия. Правила области действия ограничивают объекты, на которых может использоваться роль.

cim1265

Вы объединяете правила участника и администратора с правилами области действия.

Правила области действия

ограничивают объекты, на которых можно использовать эту роль.

Область применения относится к основному объекту задачи. Например, пользователь является основным объектом задачи «Создать пользователя». Однако область не применяется к группам для этого пользователя, поскольку группа является вторичным объектом.

Для большинства типов объектов можно указать типы правил области в следующей таблице.

9

Rule Condition	Example	Rule Syntax
All	Role members can управлять всеми объектами	Все
Объект должен соответствовать одному или нескольким значениям атрибута.	Пользователи, где название начинается с старший	где <фильтр>

При выборе параметра фильтра

Identity Manager

отображает два типа фильтров:

Дополнительные параметры, описанные в следующих таблицах, доступны для объектов пользователя, группы и организации.

Следующие правила области пользователя являются примерами. Вы можете создать другие правила для управления различными отношениями между администратором и пользователями, которыми может управлять администратор.

Rule Condition	Example	Rule Syntax
The user must match one attribute value.	Пользователи, у которых участник групповых продаж или сотовый телефон не равен нулю	где
Пользователь должен соответствовать нескольким значениям атрибутов.	Пользователи, где title=manager и locality=USA	где
Пользователь должен принадлежать к названным организациям.	Пользователи в организации Австралия или Новая Зеландия Примечание: Правило области действия организации применяется к дочерним организациям организации, которые соответствуют правилу. Например, если правило организации «в организации1», правило области применяется к организации1.1 и организации1.2, но не применяется к организации1.	в
Пользователь должен принадлежать к организациям, которые соответствуют условию, указанному в атрибутах организации.	Пользователи в организациях, где бизнес-тип = золотой или платиновый	в организациях, где
Пользователь должен принадлежать к определенным организациям и соответствовать определенным атрибутам пользователя.	Пользователи, у которых title=manager и locality=east и которые занимаются продажами или маркетингом организации	, где и кто находится в
Атрибут в профиле пользователя должен совпадать с атрибутом в профиле администратора.	Пользователи, где менеджер = идентификатор пользователя администратора	где <атрибут пользователя> <компаратор> <атрибут пользователя> администратора Примечание: .
Пользователь находится в той же организации, что и администратор.	Пользователи организации, членом которой является Джефф (администратор).	Пользователи отдела продаж или маркетинга	организация, которая является значением в администратора

Следующие правила области действия группы являются только примерами. Вы можете создать другие правила для управления различными отношениями между администратором и группами, которыми администратор может управлять.

Rule Condition	Example	Rule Syntax
The group must match one attribute value.	Имя группы, где Имя группы = 401K	, где <групповой фильтр>
Группы должны принадлежать названным организациям.	Группы в учете организации и ниже	в
Группа должна соответствовать одному значению атрибута и принадлежать именованной организации.	Группы, где BusinessType = финансы и кто занимается продажами организации и ниже	где и кто находится в
Группа должна быть указана в атрибуте администратора.	Группы, где Описание = Engineering	где admin’s Примечание: Используйте многозначный атрибут Not Equal To с компаратором.

Следующие правила области действия организации являются только примерами. Вы можете создать другие правила для управления различными отношениями между администратором и организациями, которыми администратор может управлять.

Rule Condition	Example	Rule Syntax
The organization must match one attribute value. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт