Объем куба и прямоугольного параллелепипеда: Объём прямоугольного параллелепипеда — урок. Математика, 5 класс.

Объемы. Объем прямоугольного параллелепипеда

Урок 22. Математика 5 класс

В этом уроке мы сформируем представление об объеме, единицах измерения объемов. Познакомим с понятиями объем фигуры, единичный куб. Познакомим с формулами для вычисления объемов прямоугольного параллелепипеда, куба. Установим соотношения между различными единицами объема

Конспект урока «Объемы. Объем прямоугольного параллелепипеда»

На этом уроке мы узнаем, что такое объём. Научимся находить объём прямоугольного параллелепипеда.

Для начала давайте вернёмся к предыдущим урокам. Мы с вами изучали фигуры, которые расположены в плоскости – это точка, прямая, отрезок, прямоугольник и т.д.. Такие фигуры называют плоскими.

Также мы с вами уже успели познакомиться с прямоугольным параллелепипедом.

Скажите, чем он отличается, например, от прямоугольника? Правильно! Прямоугольный параллелепипед имеет 3 измерения.

Такие фигуры как прямоугольный параллелепипед, пирамида, шар и т.д. называют объёмными.

Значит, мы с вами можем найти объём тела. А теперь давайте разберёмся, как же мы будем его вычислять.

Чтобы измерить объём, надо выбрать единицу измерения объёмов.

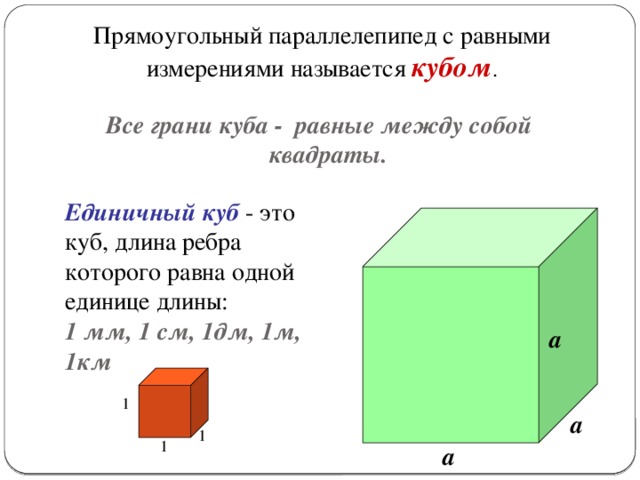
Определение

Куб, ребро которого равно единице измерения длины, называется единичным.

Объём единичного куба принимается за единицу измерения объёмов.

Например

Точно также определяются и

Легко заметить, что название единицы объёма получается из названия единицы длины присоединением прилагательного «кубический».

Измерить объём тела означает найти число, которое показывает, сколько единичных кубов содержится в этом теле.

Проще всего измерить объём прямоугольного параллелепипеда.

Найдём правило вычисления объёма прямоугольного параллелепипеда

.

Пусть у нас есть прямоугольный параллелепипед с измерениями: длина 5 см, ширина 2 см и высота 3 см.

Посчитаем, сколько единичных кубов вмещается в нём. Нижняя грань параллелепипеда имеет длину 5 см и ширину 2 см. Поэтому на ней можно расположить 5 ∙ 2 единичных кубов. Чтобы заполнить весь прямоугольный параллелепипед, нужно вложить 3 таких слоя, т.к. высота параллелепипеда 3 см.

Значит, всего таких кубов, которые вместятся в этом параллелепипеде, будет равно

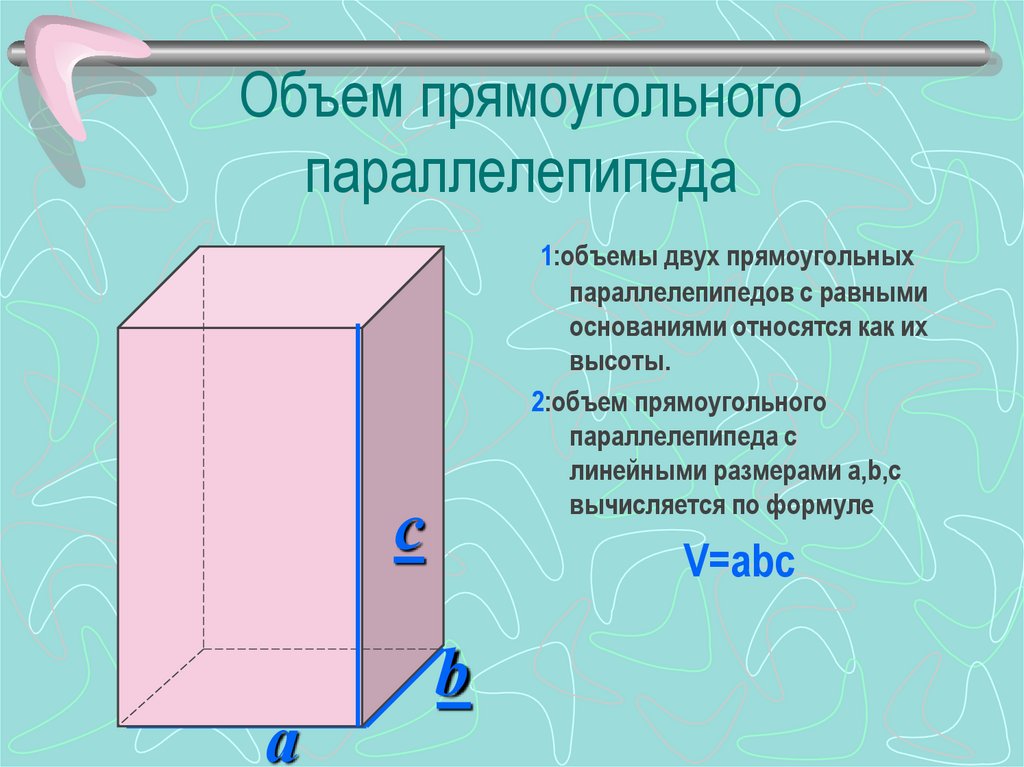
Запомните, объём прямоугольного параллелепипеда равен произведению трёх его измерений, т.е. длины, ширины и высоты.

Если обозначить объем буквой V, а его измерения: длину – а, ширину – b, высоту – с, то это утверждение можно записать формулой:

При вычислениях нужно обязательно обращать внимание, чтобы все измерения прямоугольного параллелепипеда были выражены в одинаковых единицах.

Если S – площадь основания прямоугольного параллелепипеда, следовательно,

Тогда объём прямоугольного параллелепипеда можно переписать так:

где с – высота параллелепипеда.

Запомните ещё одно утверждение: объём прямоугольного параллелепипеда равен произведению площади основания и высоты.

Найдём правило вычисления объёма куба с ребром а.

Значит, объём куба можно вычислить так

Именно поэтому  читается «а куб», или «а в кубе».

Равенство V =  даёт возможность выражать одни единицы объёма через другие. Например

Единица объёма 1  имеет ещё и другое название

Итоги

Итак, объём прямоугольного параллелепипеда равен произведению трёх его измерений, т.е. длины, ширины и высоты, V = a ∙ b ∙ c. И ещё объём прямоугольного параллелепипеда равен произведению площади основания и высоты, т.е. V = S ∙ c.

Предыдущий урок 21 Прямоугольный параллелепипед

Следующий урок 23 Окружность и круг

Получите полный комплект видеоуроков, тестов и презентаций Математика 5 класс

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Мерзляк 5 класс — § 23. Объём прямоугольного параллелепипеда

• Ответы к учебнику для 5 класса. А. Г. Мерзляк
• Переход на главную страницу сайта

Вопросы к параграфу

1. Какими свойствами обладает объём фигуры?

1. Равные фигуры имеют равные объёмы.
2. Объём фигуры равен сумме объёмов фигур, из которых она состоит.

2. Какой куб называют единичным?

Единичным называют куб, ребро которого равно единичному отрезку.

3. Приведите примеры единиц измерения объёма.

• 1 мм³ — один кубический миллиметр
• 1 см³ — один кубический сантиметр
• 1 дц³ — один кубический дециметр
• 1 м³ — один кубический метр
• 1 л — один литр (при измерении жидкостей, 1 л = 1 дм³)

4. Что означает измерить объём фигуры?

Измерить объем фигуры — значит подсчитать, сколько единичных кубов в ней помещается.

5. Чему равен объём прямоугольного параллелепипеда с измерениями а, b, с?

V = abc

6. По какой формуле вычисляют объём куба?

V= a³

7. Как вычислить объём прямоугольного параллелепипеда, зная его площадь основания и высоту?

V = Sh

Решаем устно

1. Заполните пропуски в цепочке вычислений: 

2. Сколько необходимо использовать кубиков с ребром 1 см, чтобы сложить кубик с ребром 2 см?

Чтобы сложить кубик с ребром 2 см, надо использовать 8 кубиков с ребром 1 см.

3. Сколько сантиметров проволоки необходимо для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 3 см, 5 см и 6 см?

3 • 4 + 5 • 4 + 6 • 4 = 12 + 20 + 24 = 56 (см) — проволоки.

Ответ: 56 см.

4. Расставьте вместо звёздочек знаки «+» и «—» так, чтобы запись 20 * 30 * 10 * 80 * 70 = 50 стала верным равенством.

20 + 30 — 10 + 80 — 70 = (20 + 30) + (80 — 10 — 70) = 50 + 0 = 50

Упражнения

617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?

• 1 дм = 10 см
• 1 дм² = 10 см • 10 см = 100 см²
• 1 дм³ = 10 см • 10 см • 10 см = 1 000 см³

2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?

• 1 м = 100 см
• 1 м² = 100 см • 100 см = 10 000 см²
• 1 м³ = 100 см • 100 см • 100 см = 1 000 000 см³

618. Фигуры, изображённые на рисунке 179, сложены из кубиков, рёбра которых равны 1 см. Найдите объём каждой фигуры.

Для того, чтобы найти объём фигуры, надо посчитать количество единичных кубов, из которых она состоит.

1 фигура (на рисунке слева):

V = 5 • 2 + 3 + 3 + 2 = 10 + 8 = 18 см³

2 фигура (на рисунке справа):

V = 6 • 3 + 2 +2 + 3 • 2 + 5 + 2 = 18 + 4 + 6 + 7 = 18 + 17 = 35 см³

Ответ: 18 см³ и 35 см³.

619. Вычислите объём прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.

Дано:

a = 12 м
b = 15 м
c = 6 м
V = ? м³

Решение:

V = abc = 12 • 15 • 6 = 12 • 90 = 1 080 м³

Ответ: 1 080 м³.

620. Чему равен объём куба, ребро которого равно 6 см?

Дано:

a = 12 см
V = ? см³

Решение:

V= a³ = 6³ = 36 • 6 = 216 см³

Ответ: 216 см³.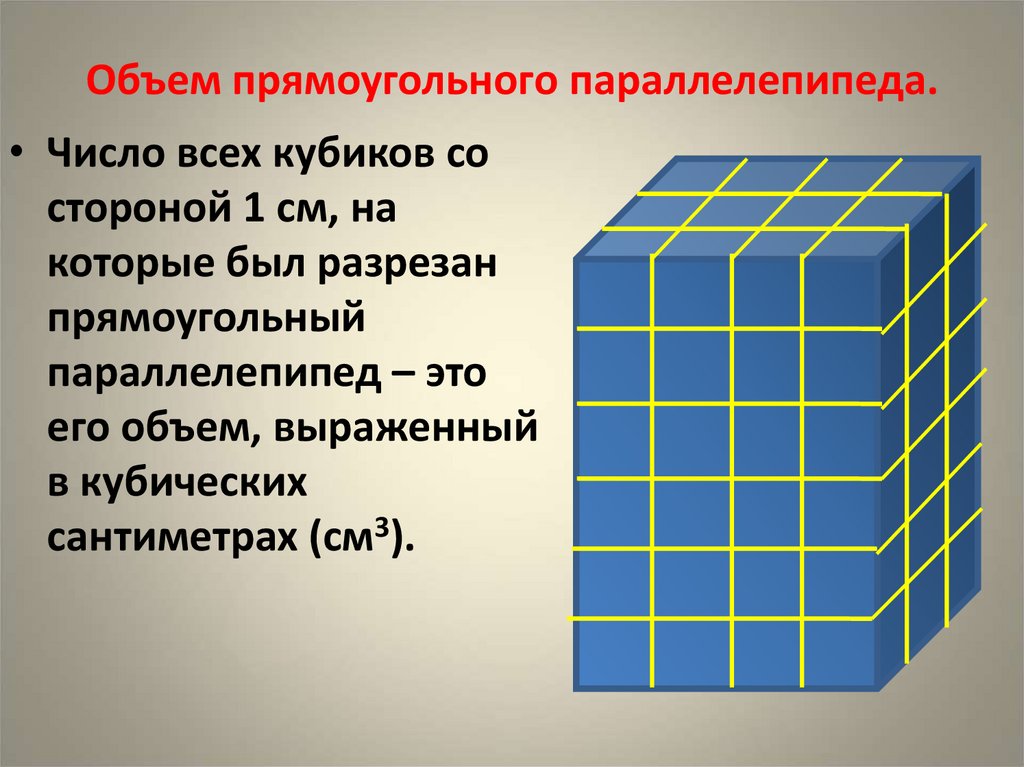

621. Чему равен объём прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?

Дано:

a = 10 дм
b = 8 дм
c = 4 дм
V = ? дм³

Решение:

V = abc = 10 • 8 • 4 = 10 • 32 = 320 дм³

Ответ: 320 дм³.

622. Выразите:

1) в кубических миллиметрах:

7 см³ = 7 000 мм³

38 см³ = 38 000 мм³

12 см³ 243 мм³ = 12 000 мм³ + 243 мм³ = 12 243 мм³

42 см³ 68 мм³ = 42 000 мм³ + 68 мм³ = 42 068 мм³

54 см³ 4 мм³; = 54 000 мм³ + 4 мм³ = 54 004 мм³

1 дм³ 20 мм³ = 1 000 000 мм³ + 20 мм³ = 1 000 020 мм³

 18 дм³ 172 см³ = 18 000 000 мм³ + 172 000 мм³ = 18 172 000 мм³

35 дм³ 67 см³ 96 мм³ = 35 000 000 мм³ + 67 000 мм³ + 96 мм³ = 35 067 096 мм³

2) в кубических дециметрах:

4 м³ = 4 000 дм³

264 м³ = 264 000 дм³

10 м³ 857 дм³ = 10 000 дм³ + 857 дм³ = 10 857 дм³

28 м³ 2 дм³ = 28 000 дм³ + 2 дм³ = 28 002 дм³

44 000 см³ = 44 дм³

5 430 000 см³ = 5 430 дм³

623. Выразите в кубических сантиметрах:

8 дм³ = 8 000 см³

62 дм³ = 62 000 см³

378 000 мм³ = 378 см³

520 000 мм³ = 520 см³

78 дм³ 325 см³ = 78 000 см³ + 325 см³ = 78 325 см³

56 дм³ 14 см³ = 56 000 см³ + 14 см³ = 56 014 см³

8 м³ 4 дм³ 6 см³ = 8 000 000 см³ + 4 000 см³ + 6 см³ = 8 004 006 см³

624. Ширина прямоугольного параллелепипеда равна 15 дм, длина — на 3 дм больше ширины, а высота — в 3 раза меньше длины. Найдите объём данного параллелепипеда.

Дано:

a = ? см, на 3 дм больше, чем ребро b
b = 15 дм
c = ? см, в 3 раза меньше, чем ребро a
V = ? см³

Решение:

1) 15 + 3 = 18 (дм) — длина прямоугольного параллелепипеда.

2) 18 : 3 = 6 (дм) — высота прямоугольного параллелепипеда.

V = abc

3) 18 • 15 • 6 = 18 •  90 = 1 620 (дм³) — объем V прямоугольного параллелепипеда.

Ответ: V= 1 620 дм³.

625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины.

Вычислите объём данного параллелепипеда.

Дано:

a = ? см, на 4 см больше, чем ребро с
b = ? см, в 5 раз меньше, чем ребро c
c = 20 см
V = ? см³

Решение:

1) 20 + 4 = 24 (см) — длина прямоугольного параллелепипеда.

2) 20 : 5 = 4 (см) — ширина прямоугольного параллелепипеда.

V = abc

3) 24 • 5 • 20 = 24 • 80 = 1 920 (дм³) — объем V прямоугольного параллелепипеда.

Ответ: V= 1 920 дм³.

626. Объём прямоугольного параллелепипеда равен 560 см³, длина — 14 см, ширина — 8 см. Найдите высоту данного параллелепипеда.

Дано:

a = 14 см
b = 8 см
V = 560 см³
h = ? см

Решение:

V = Sh, значит h = V : S

1) 14 • 8 = 122 (см²) — площадь основания S прямоугольного параллелепипеда.

2) 560 : 120 = 5 (см) — высота h прямоугольного параллелепипеда.

Ответ: 5 см.

627. Длина прямоугольного параллелепипеда равна 18 см, высота — 15 см, а объём — 3 240 см³. Найдите ширину данного параллелепипеда.

Дано:

a = 18 см
h = 15 см
V = 3 240 см³
b = ? см

Решение:

V = Sh, значит S = V : h

1) 3 240 : 15 = 216 (см²) — площадь основания S прямоугольного параллелепипеда.

S = a • b, значит b = S : a

2) 216 : 18 = 12 (см) — ширина b прямоугольного параллелепипеда.

Ответ: 12 см.

628. Объём комнаты, имеющей форму прямоугольного параллелепипеда, равен 144 м³, а высота — 4 м. Найдите площадь пола комнаты.

Дано:

h = 4 м
V = 144 м³
S = ? м²

Решение:

V = Sh, значит S = V : h

1) 144 : 4 = 36 (м²) — площадь пола комнаты.

Ответ: 36 м².

629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объём равен 960 м³, а площадь пола равна 192 м².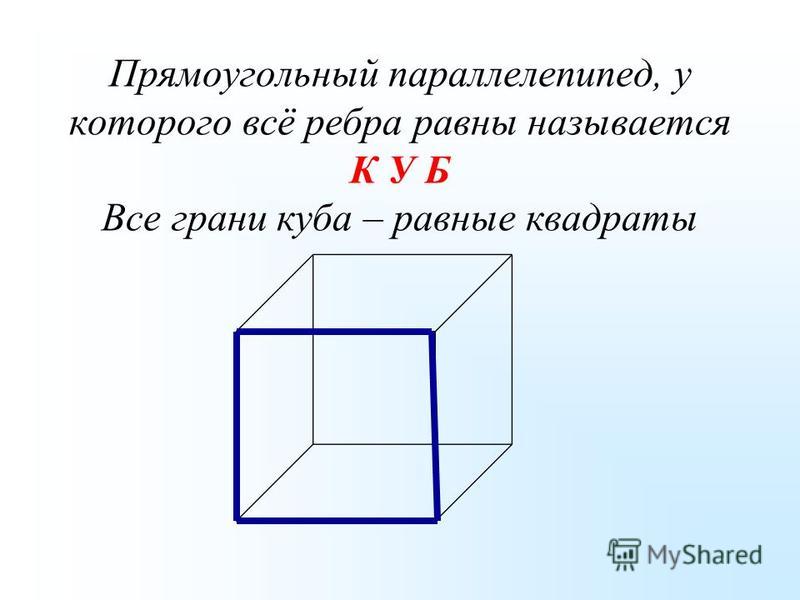 Найдите высоту спортивного зала.

Дано:

S = 192 м²
V = 960 м³
h= ? м

Решение:

V = Sh, значит h = V : S

1) 960 : 192 = 5 (м) — высота спортивного зала.

Ответ: 5 м.

630. Найдите объём фигуры, изображённой на рисунке 180 (размеры даны в сантиметрах).

Выполним дополнительное построение: проведём линии, соединяющие выступающие части исходной фигуры. Теперь можно сказать, что V = V_А— V_В, где:

• V — объем искомой фигуры.
• V_А — объем большого прямоугольного параллелепипеда, измерения которого равны 30 см, 20 см и 25 см.
• V_В — объем малого прямоугольного параллелепипеда (красный), который вырезали из большого параллелепипеда для получения искомой фигуры.  Его измерения: 15 см, 5 см и 20 см.

V = abc

V_А = 30 • 20 • 25 = 600 • 25 = 15 000 (cм³)

V_А = 15 • 5 • 20 = 15 •  100 = 1 500 (cм³)

V = V_А— V_В = 15 000 — 1 500 = 13 500 (cм³)

Ответ: V= 13 500 cм³

631. Найдите объём фигуры, изображённой на рисунке 181 (размеры даны в сантиметрах).

Фигуру, изображенную на рисунке 181, можно разделить на три прямоугольных параллелепипеда:

1. жёлтый
2. зелёный 
3. красный

Рассмотрим прямоугольный параллелепипед № 3 (красный):

• длина равна 15 см
• ширина равна 8 + 8 = 16 см
• высота равна 14 см

V = abc

V₃ = 15 • 16 • 14 = 240 • 14 = 3 360 (cм³)

Рассмотрим прямоугольный параллелепипед № 2 (зелёный):

• длина равна 8 см
• ширина равна 8 см
• высота равна 14 + 8 = 22 см

V = abc

V₂ = 8 • 8 • 22 = 64 • 22 = 1 408 (cм³)

Рассмотрим прямоугольный параллелепипед № 1 (жёлтый):

• длина равна 12 см
• ширина равна 8 + 8 = 16 см
• высота равна 14 см

V = abc

V₁ = 12 • 16 • 14 = 192 • 14 = 2 688 (cм³)

Объем фигуры равен сумме объемов фигур, из которых она состоит.

V = V₁ + V₂ + V₃= 2 688 + 1 408 + 3 360 = 7 456 (cм³)

Ответ: V = 7 456 cм³.

632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если масса 1 см³ цинка составляет 7 г.

Дано:

a = 4 cм²
Масса 1 cм³ = 7 г
Масса куба = ? г

Решение:

V = a³

V = 4 • 4 • 4 = 16 • 4 = 64 (см³)

Масса 1 см³ куба равна 7 г, значит масса 64 см³ равна: 

64 • 7 = 448 (г)

Ответ: 448 г.

633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работу скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм³ земли?

150 м = 15 000 см

1) 15 000 • 80 • 60 = 1 200 000 • 60 = 72 000 000 (см³) — объем выкопанной машиной траншеи.

72 000 000 см³ = 72 м³

2) 72 : 8 = 9 (м³) — выкапывает машина за 1 час.

72 м³ = 72 000 дм³

3) 72 000 : 240 = 300 (человек) — коротышек могут заменить 1 машину.

Ответ: 9 м³, 300 коротышек.

634. Куб и прямоугольный параллелепипед имеют равные объёмы. Найдите площадь поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высоты параллелепипеда.

1) 12 • 2 = 6 (см) — сторона b прямоугольного параллелепипеда.

2) 12 • 4 = 3 (см) — сторона с прямоугольного параллелепипеда.

3) V = a • b • c = 12 • 6 • 3 = 72 • 3 = 216 (см³) — объём прямоугольного параллелепипеда.

V (прямоугольного параллелепипеда) = V (куба) = a³ = 216 (см³)

Значит сторона куба равна такому числу, которое при возведении в третью степень равно 216. Методом подбора можем определить что это число 6, то есть сторона квадрата а = 6 см.

У куба 6 одинаковых граней, площадь каждой из которых равна а².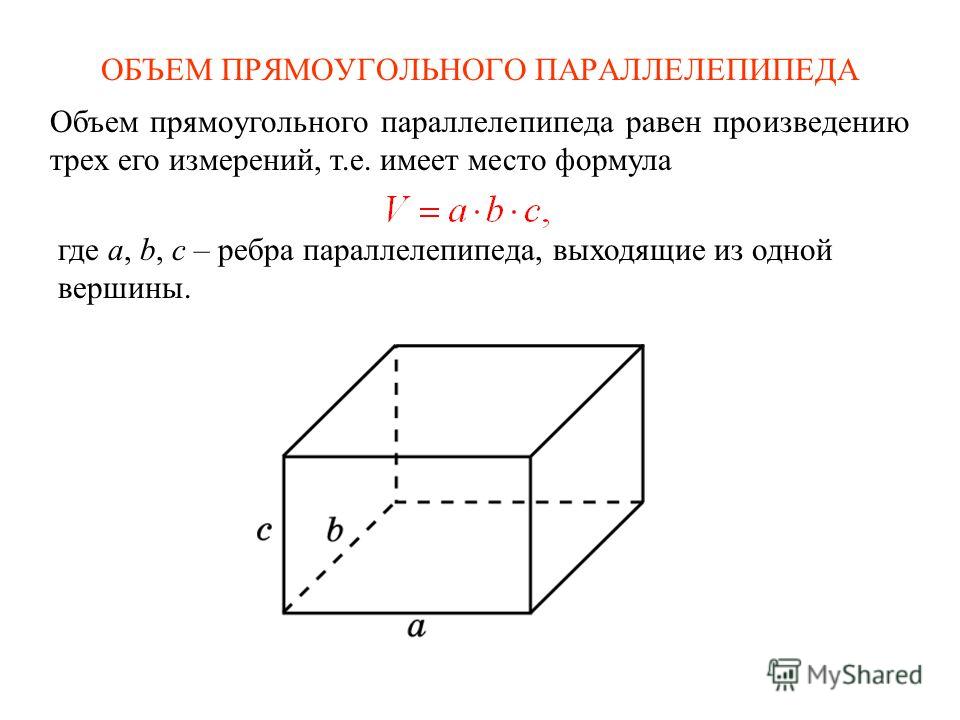

4) а² = 6 • 6 = 36 (см²) — площадь поверхности одной грани куба.

5) 36 • 6 = 216 (см²) — площадь поверхности куба.

Ответ: Площадь поверхности куба равна 216 см².

635. Ребро одного куба в 4 раза больше ребра второго. Во сколько раз: 1) площадь поверхности первого куба больше площади поверхности второго; 2) объём первого куба больше объёма второго?

Пусть длина ребра второго куба равна х единиц, тогда длина ребра первого куба будет равна 4х единиц.

S = 6a²

S₂ = 6a² = 6x² (ед²) — площадь поверхности второго куба.

S₁ = 6a² = 6(4x)² = 6 • (4 • 4 • x • x) = 6 • 16 x² = 96 x² (ед²) — площадь поверхности первого куба.

S₂ : S₁ =96 x² : 6x² = 96 : 6 = 16 (раз) — площадь поверхности первого куба больше площади поверхности второго куба.

V = a³

V₂ = a³ = х³ (ед³)  — объём второго куба.

V₁ = a³ = (4х)³ = 4 • 4 • 4 • x • x • x = 16 • 4 • х³ = 64 х³ (ед³)  — объём второго куба.

V₁ : V₂= 64 х³ : х³ = 64 (раза) — объём первого куба больше объёма второго куба.

Ответ: Площадь поверхности больше в 16 раз, объём больше в 64 раза.

636. Как изменится объём прямоугольного параллелепипеда, если:

1) длину увеличить в 4 раза, ширину — в 2 раза, высоту — в 5 раз

V = abc

V₁ = (4 • a) • (2 • b) • (5 • c) = (4 • 2 • 5) abc = 40 abc

V₁ : V = 40 abc : abc = 40 (раз)

Ответ: объём увеличится в 40 раз.

2) ширину уменьшить в 4 раза, высоту — в 2 раза, а длину увеличить в 16 раз

V = abc

V₁ = (16 • a) • (b : 4) • (c : 2) = (16 : 4 : 2) abc = (4 : 2) abc = 2 abc

V₁ : V = 2 abc : abc = 2 (раза)

Ответ: объём увеличится в 2 раза.

637. Как изменится объём прямоугольного параллелепипеда, если:

1) каждое измерение увеличить в 2 раза

V = abc

V₁ = (2 • a) • (2 • b) • (2• c) = (2 • 2 • 2) abc = 8 abc

V₁ : V = 8 abc : abc = 8 (раз)

Ответ: объём увеличится в 8 раз.

2) длину уменьшить в 3 раза, высоту — в 5 раз, а ширину увеличить в 15 раз

V = abc

V₁ = (a : 3) • (b • 15) • (c : 5) = (15 : 3 : 5) abc = (5 : 5) abc = abc

V₁ : V = abc : abc = 1 (раз)

Ответ: объём не изменится.

638. В бассейн, площадь дна которого равна 1 га, налили 1 000 000 л воды. Можно ли в этом бассейне провести соревнования по плаванию?

S = 1 га = 10 000 м² = 1 000 000 дм²

V = 1 000 000 л = 1 000 000 дм³ 

V = S • h,  значит h = V : S

h = V : S = 1 000 000 дм³ : 1 000 000 дм² = 1 дм = 10 см — высота налитой в басейн воды.

Это значит, что плавать в этом бассейне невозможно.

Ответ: Нет, соревнования по плаванию провести нельзя.

639. В кубе с ребром 3 см проделали три сквозных квадратных отверстия со стороной 1 см (рис. 182). Найдите объём оставшейся части.

1) V (куба) = a³ = 3³ = 9 • 3 = 27 (см³) — объём куба с ребром 3 см.

2) V (одного отверстия) = abc = 1 • 1 • 3 = 3 (см³) — объем одного сквозного отверстия со стороной 1 см.

Так как все три отверстия пересекаются в центре куба, то объём вырезанной части: 

3) V (вырезанной части) = 3 см³ • 3 ( размер трёх сквозных отверстий) — 1 см³ (размер пересечения второго отверстия в первым и третьим) —  1 см³ размер пересечения третьего отверстия с первым и вторым) = 9 — 1 — 1 = 7 (см³) — объём вырезанной части.

4) V (оставшейся части) = V (куба) — V (вырезанной части) = 27 — 7 = 20 (см³) — объём оставшейся части.

Ответ: 20 см³.

640. Размеры куска мыла, имеющего форму прямоугольного параллелепипеда, равны 12 см, 6 см и 4 см. Каждый день используют одинаковую массу мыла. Через 14 дней все размеры куска мыла уменьшились в 2 раза. На сколько дней хватит оставшегося куска мыла?

1) 12 • 6 • 4 = 72 • 4 = 288 (см³) — объём нового куска мыла.

2) (12 : 2) • (6 : 2) • (4 : 2) = 6 • 3 • 2 = 18 • 2 = 36 (см³) — объём мыла через 14 дней использования.

3) 288 — 36 = 252 (см³) — мыла было использовано за 14 дней.

4) 252 : 14 = 18 (см³) — мыла используется за 1 день.

5) 36 : 18 = 2 (дня) — хватит оставшегося мыла.

Ответ: на 2 дня.

Упражнения для повторения

641. В школьном коридоре, длина которого равна 30 м, ширина — 35 дм, надо заменить линолеум. Какое наименьшее количество рулонов линолеума для этого нужно, если длина рулона линолеума равна 12 м, а ширина — 160 см?

35 дм = 350 см

1) 350 = 2 • 160 + 30 (см)

Значит, для того, чтобы покрыть линолеумом в один ряд пол по ширине коридора необходимо использовать 2 рулона материала и ещё полосу шириной в 30 см.

2) 30 = 12 • 2 + 6 (м)

Значит, для того, чтобы покрыть линолеумом в один ряд пол по длине коридора необходимо использовать 2 целых рулона и ещё одну половину рулона (6 = 12 : 2).

Сделаем раскладку:

• 1 ряд по длине — 2 рулона + полоса 12 м х 30 см 
• 2 ряд по длине — 2 рулона + полоса 12 м х 30 см
• 3 ряд по длине — (половина рулона + половина рулона) + полоса  6 м х 30 см.

Половина рулона + половина рулона = 1 целый рулон.

Полосы 12 м х 30 см, 12 м х 30 см и 6 м х 30 см можно выкроить из 1 целого рулона.

Значит нам потребуется:

3) 2 + 2 + 1 + 1 = 6 (шт) — рулонов линолеума потребуется для замены линолеума в школьном коридоре.

Ответ: 6 рулонов.

642. Из двух населённых пунктов, расстояние между которыми равно 54 км, одновременно выехали навстречу друг другу два велосипедиста и встретились через 2 ч после начала движения. Скорость движения первого велосипедиста составляла 12 км/ч. С какой скоростью двигался второй велосипедист?

1) 12 •  2 = 24 (км) — проехал первый велосипедист до места встречи.

2) 54 — 24 = 30 (км) — проехал второй велосипедист до места встречи.

3) 30 : 2 = 15 (км/ч) — скорость второго велосипедиста.

Ответ: 15 км/ч.

643. Найдите значение выражения:

1) 7a + 7b, если a + b = 14

7a + 7b = 7 (a + b) = 7 •  14 = 98

2) m • 17 + n • 17, если m + n = 1 000

m • 17 + n • 17 = 17 (m + n) = 17 • 1 000 = 17 000

3) k • 9 + 9l, если k + l = 12

k • 9 + 9l = 9 (k + l) = 9 • 12 = 108

4) 4c — 4d, если с — d = 125

4c — 4d = 4 (c — d) = 4 • 125 = 500

5) x • 23 — 23y, если x — у = 4

x • 23 — 23y = 23 (x — y) = 23 • 4 = 92

6) 56p — r • 56, если р — r = 11

56p — r • 56 = 56 (p — r) = 56 • 11 = 616

Задача от мудрой совы

644. В записи первого трёхзначного числа используются только цифры 2 и 3, а в записи второго — только цифры 3 и 4. Может ли произведение этих чисел записываться только цифрами 2 и 4?

Если в записи первого трёхзначного числа используются только цифры 2 и 3, то таким трёхзначным числом могут быть числа: 

• 222, 223, 232, 322, 233, 323, 332, 333.

Если в записи второго трёхзначного числа используются только цифры 3 и 4, то таким трёхзначным числом могут быть числа:

• 333, 334, 343, 433, 344, 434, 443, 444.

Расположим их в виде таблицы: 

• в первом столбце напишем все возможные варианты первого числа;
• в верхней строке — все возможные варианты второго числа;
• на пересечении — произведение соответствующего варианта первого и второго числа (можно их посчитать при помощи калькулятора).

	333	334	343	433	344	434	443	444
222	73926	74148	76146	96126	76368	96348	98346	98568
223	74259	74482	76489	96559	76712	96782	98789	99012
232	77256	77488	79576	100456	79808	100688	102776	103008
322	107226	107548	110446	139426	110768	139748	142646	142968
233	77589	77822	79919	100889	80152	101122	103219	103452
323	107559	107882	110789	139859	111112	140182	143089	143412
332	110556	110888	113876	143756	114208	144088	147076	147408
333	110889	111222	114219	144189	114552	144522	147519	147852

Мы видим, что ни одно произведение не удовлетворяет условию. Значит записать такое произведения только цифрами 2 и 4 невозможно.

Ответ: Нет, нельзя.

• Ответы к учебнику для 5 класса. А. Г. Мерзляк
• Переход на главную страницу сайта

Урок математики на тему «Понятие объема. Объем прямоугольного параллелепипеда. Объем куба». 11-й класс

Цели урока: сформировать понятия объема, объема прямоугольного параллелепипеда и объема куба.

Задачи:

• закрепить понятие объема, объема прямоугольного параллелепипеда и объема куба; рассмотреть следствие об объеме прямой призмы, основанием которой является прямоугольный треугольник (следствие 2) и доказать его.
• формировать навыки нахождения объема прямоугольного параллелепипеда и объема куба;
• способствовать воспитанию ответственности, организованности, самостоятельности

Тип урока: урок совершенствования ЗУН

Оборудования: компьютер, демонстрационный материал

Ход урока

I. Организационный момент.

Сообщение темы урока, сформулировать цели урока, психологический настрой на урок.

II. Актуализация знаний учащихся

Устный опрос по вопросам (1 ученик готовит доказательство теоремы об объеме прямоугольного параллелепипеда у доски, пока другие отвечают на вопросы учителя):

1. Что за величина объем?

— Объем – это положительная величина, одна из основных величин, связанных с геометрическими телами. Задача вычисления объема простейших тел, идущая от практических потребностей, была одним из стимулов развития геометрии. Математика Древнего Востока располагала рядом правил для вычисления объема тел, с которыми чаще всего приходилось встречаться на практике (призматические брусья, пирамиды полные и усеченные, цилиндры.

Чтобы найти объем, сначала выбирают единицу измерения. В Древнем Риме, например, одной из единиц объема служила амфора (около 25,5 л). Нефть во всем мире принято сейчас измерять в англо-американских единицах – бареллях, т.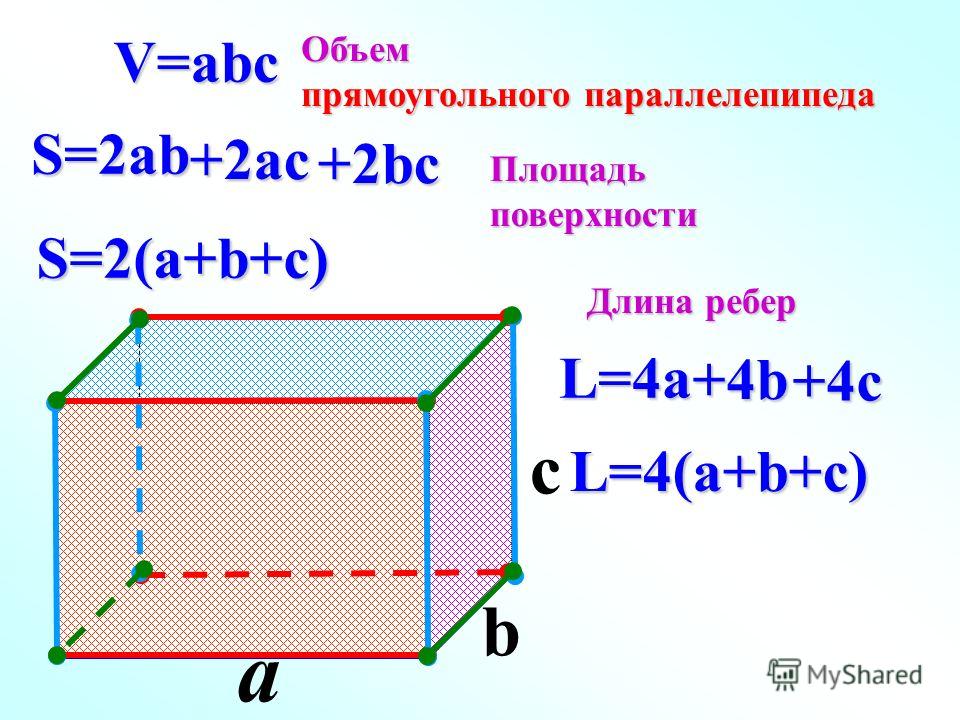 е в бочках е костью 159 л. В России распространенная в быту мера объема – ведро.

2. Какую единицу принимают за единицу объема?

— В геометрии за единицу объема принимают объем куба с ребром единичной длины. Объем куба полностью определяется длиной ребра.

• 1 см³ – это куб с ребром 1 см,
• 1 м³ – это куб с ребром 1 м и т.д.

3. Назовите свойства объема

— Равные тела имеют равные объемы

— Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.

— Если одно тело содержит другое, то объем первого тела не меньше объема второго.

Следствие: объем куба с ребром 1/n равен 1/n³

Для закрепления ответов учащихся прслушать фрагмент видиоурока №21 (на 2 мин) по геометрии от инфоурок (Приложение 1)

Доказательство теоремы (слушаем ученика)

Теорема: Объем прямоугольного параллелепипеда равен произведению трех его измерений.

V = авс

Следствие 1. Объем прямоугольного параллелепипеда равен произведению основания на высоту. V = Sh

4. Проверка выполнения домашнего задания.

• П.74-75, №647(б), №648(в), №649(б), стр.161
• №647(б) Решение: V = V₁ + V₂ – 1/3 V₁ = 2/3 V₁+ V₂
• №648(в) Решение: V = 18**13 = 1170
• №649(б) Ответ: 6 см³

Рисунок 1

Работа по готовым чертежам:

Презентация №22, слайд №6 от инфоурок (Приложение 2)

Задача 1. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение:

Объем прямоугольного параллелепипеда находим по формуле:

V=abc

Данная фигура состоит из двух прямоугольных параллелепипедов.

Пусть — это объем полного параллелепипеда с измерениями 4, 3, 3. Тогда это объем малого “вырезанного” параллелепипеда с измерениями 3, 1, 1.

Чтобы найти объем многогранника, необходимо найти разность объемов V₁ и V₂

Находим объем V₁ как произведение его измерений обозначим их а₁, b₁, c₁, получаем объем его равен

Для малого “вырезанного” параллелепипеда объем V₂ равен произведению его измерений, их обозначим как а₂, b₂, c₂, тогда получим

Объем многогранника V равен разности объемов V₁ и V₂, получим

V= V₁ — V₂

V=36-3=33

Ответ: V многогранника равен 33 кубическим единицам.

Рисунок  3

2. Рис. 3 Ответ: 250

III. Изучение нового материала

Рассмотреть следствие 2 и доказать его.

Следствие 2. Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.

V = S_осн. h

Дана прямоугольная призма , угол А в основании является прямым.

Рисунок 2

Достроим прямоугольную призму до прямоугольного параллелепипеда (смотрите чертеж). Прямоугольный параллелепипед состоит из двух прямоугольных призм, которые равны, так как имеют равные основания и высоты. Соответственно, площадь прямоугольника равна двум площадям прямоугольных треугольников АВС Следовательно, объем прямоугольной призмы равен половине объема прямоугольного параллелепипеда (при умножении ) или произведению основания прямоугольного треугольника на высоту.

IV. Применение знаний

1. Решить задачу №653

Решение по рис. 4:

Рисунок 4

Рассмотрим треугольник D₁C₁B:

Рассмотрим треугольник D₁BВ_1. Он прямоугольный. Тогда

Диагональ и измерения прямоугольного параллелепипеда связаны соотношением: . Значит, , . Тогда . Ответ:

Самостоятельная работа. Найти объем по готовым чертежам:

Рисунок 5

Рисунок 6

Ответы: 40; 24

Проверить решения – взаимопроверка, обмениваются тетрадями и проверяют.

V. Рефлексия.

Подведение итогов урока. Назвать свойства объема, написать формулы известных объемов.

Оценить работы учащихся.

VI. Домашняя работа.

П 74-75, №651, стр.161. Вспомнить формулу нахождения массы тела через плотность и объем. Индивидуальные задания по сборнику для подготовки к ЕГЭ по математике.

Литература.

(Приложение 3)

Объем куба, прямоугольного параллелепипеда и цилиндра

Куб, прямоугольный параллелепипед и цилиндр являются частью трехмерных фигур. Как правило, в трехмерной фигуре вы найдете меру длины, ширины и высоты. Напротив, в случае 2D-фигуры у вас есть только длина и высота. Некоторыми примерами двумерных фигур являются треугольник, квадрат и круг. Теперь давайте посмотрим, что такое объем? Студентам обычно трудно иметь дело с 3D-фигурами. Одна из причин — их склонность запоминать формулы, не понимая, что это такое. Итак, хорошо бы начать с понимания того, что означает объем любой формы?

 

Причина разницы между объемом куба и цилиндра

Объем любой трехмерной фигуры — это мера площади, заключенной в площадь фигуры. В буквальном смысле объем обозначает общую емкость или пространство, занимаемое объектом, который имеет все три элемента: длину, высоту и ширину. Различные формулы для каждой трехмерной формы выводятся в зависимости от структуры пласта. Например, структурное различие между кубом и цилиндром вызывает необходимость в разных формулах объема для каждой из рассматриваемых форм.

   

Куб

Куб — первая трехмерная фигура, которую довольно утомительно составлять на карте. Это фигура, заключенная в шесть одинаковых квадратов. Одна из интересных особенностей куба заключается в том, что одна вершина образуется в точке встречи трех ребер.

Свойства куба

• Куб является своего рода квадратной призмой.

• Имеет 6 граней, 8 вершин и 12 ребер.

• Поскольку грани куба имеют форму квадрата, длина, ширина и высота куба одинаковы.

• Угол между любыми двумя поверхностями равен 90 градусов.

• В кубе противоположные грани и ребра параллельны друг другу.

• Каждая грань куба соприкасается с четырьмя другими гранями.

• Каждая вершина куба соприкасается с тремя ребрами и тремя гранями.

 

Прямоугольный

Напомню, что любой объект в форме коробки является прямоугольным. Прямоугольный параллелепипед, по сути, представляет собой трехмерную форму, которая характеризуется шестью прямоугольными гранями. Каждая вершина образована под прямым углом.

 

Свойства кубоида

• Поверхности прямоугольного параллелепипеда.

• Имеет 8 вершин, 12 ребер, 6 граней.

• Две поверхности прямоугольного параллелепипеда образуют угол 90 градусов в вершинах.

• Количество диагоналей, проведенных на каждой грани прямоугольного параллелепипеда, равно 2.

• В параллелепипеде противоположные ребра параллельны друг другу.

• Количество диагоналей пространства и диагоналей граней в прямоугольном параллелепипеде равно 4 и 12 соответственно.

• Значения длины, ширины и высоты прямоугольного параллелепипеда различны.

  

Цилиндр 

Основное различие между кубом и цилиндром, структурой-wsie, заключается в наличии третьего измерения, т. е. высоты. Банка диетической колы, которую вы, возможно, держите в руке, читая эту статью, является подходящим примером цилиндра.

 

Цилиндр представляет собой трехмерную фигуру с двумя параллельными сторонами и круглыми или овальными отверстиями вверху и внизу. Теперь проемы могут быть полыми или сплошными.

 

Свойства цилиндра

• Цилиндр — это трехмерный объект, который имеет одну изогнутую поверхность и две плоские поверхности.

• Две плоские поверхности имеют круглую форму и идентичны.

• Размер цилиндра зависит от радиуса основания и высоты криволинейной поверхности.

• В цилиндре нет вершины.

• В цилиндре везде одинаковое поперечное сечение, как у призмы.

  

Как рассчитать объем куба, прямоугольного параллелепипеда и цилиндра

Вычисление объема куба, прямоугольного параллелепипеда и цилиндра довольно просто, если вы знаете обходные пути для получения измерений имеющейся фигуры.

 

Разница между кубом и цилиндром или прямоугольным параллелепипедом и цилиндром весьма существенна. Кроме того, цилиндры не принадлежат к семейству трехмерных многогранников. 3).

 

Этапы вычисления объема прямоугольного параллелепипеда

Процедура нахождения объема прямоугольного параллелепипеда описана ниже:

• Шаг 1 — Измерьте длину, ширину и высоту цилиндра.

• Шаг 2 — Преобразуйте все единицы измерения в одну единицу, если единицы измерения различны.

• Шаг 3 — Подставьте значения размеров в данную формулу (Д x Ш x В), чтобы найти объем. 92ч.

• Шаг 3 — Выполните расчеты и запишите ответ в кубических метрах.

Решенные примеры

Теперь мы рассмотрим некоторые из решенных примеров объема куба и цилиндра

1. Найдите объем куба со стороной 9 м?

Пусть объем куба равен V. Используя формулы V=a3, имеем

V= (9м)3 = 729

2. Найдите объем прямоугольного параллелепипеда длиной 12м, высотой 8м и шириной 6м ?

Используя формулы для объема прямоугольного параллелепипеда, т.е. V=LBH, имеем

V= (12X8X6)м3 = 576м3

3. Найдите объем цилиндра с радиусом 14м и высотой 10м?

Используя формулы для расчета объема цилиндра, т.е. V=𝚷 R2H.

У нас V= 22/7 x (14 м)2 X (10 м)= 6 160 м3.

Объем цилиндра с применением теоремы Пифагора для нахождения фактической высоты.

4. Найдите объем цилиндра с наклонной высотой 10 см и радиусом 3 см?

(Примечание: **наклонная высота представляет собой гипотенузу, образованную соединением верхнего конца овального отверстия с противоположным нижним концом. Для большей ясности см. рисунок ниже.)

Как вы можете видеть, наклонная высота обозначается д. Теперь формула для расчета объема цилиндра включает высоту. Но в вопросе у нас нет значения высоты, поэтому приходится вычислять высоту по теореме Пифагора.

h3 (гипотенуза) = L2 (длина) + B2 (ширина квадрата)  

Аналогично, здесь мы имеем d2=h3 + D2 (диаметр) 

(10 см)2= h3 + (6)2 

Решая приведенное выше уравнение, мы получаем h= 8 см 

Теперь V= 𝚷 R2H 

V= 22/7 x (3)2 x (8)

Решая приведенное выше уравнение, мы получаем V= 226 (приблизительно).

Факты о кубе, параллелепипеде и цилиндре

• Квадрат часто называют двумерной заменой куба.

• Прямоугольный параллелепипед очень похож на куб, главное отличие заключается в том, что параллелепипед не имеет трех ребер одинаковой длины.

• В отличие от большинства трехмерных фигур, многогранный цилиндр не является одной из них. Причина, по которой цилиндр не является многогранником, заключается в наличии площади поверхности.

Объем прямоугольного параллелепипеда – формула, определение, примеры

Объем прямоугольного параллелепипеда – это величина, которая используется для измерения пространства прямоугольного параллелепипеда. Прямоугольник — это трехмерная фигура, которую очень часто можно увидеть вокруг нас. Термин объем используется для измерения емкости любой формы на основе ее размеров, таких как длина, ширина и высота. Для расчета объема прямоугольного параллелепипеда будет использоваться формула, специфичная для формы прямоугольного параллелепипеда. В этом разделе мы изучим формулу для расчета объема прямоугольного параллелепипеда и решим несколько примеров, чтобы лучше понять концепцию.

1.	Каков объем прямоугольного параллелепипеда?
2.	Объем кубовидной формулы
3.	Как рассчитать объем прямоугольного параллелепипеда?
4.	Часто задаваемые вопросы по Volume of Cuboid

Каков объем прямоугольного параллелепипеда?

Объем прямоугольного параллелепипеда является мерой пространства, занимаемого прямоугольным параллелепипедом. Кубоид представляет собой трехмерную фигуру, которая имеет длину, ширину и высоту. Если у нас есть прямоугольный лист, и мы продолжаем складывать такие листы, мы в конечном итоге получим форму, которая имеет некоторую длину, ширину и высоту. Эта стопка листов выглядит как фигура с 6 гранями, 12 ребрами и 8 вершинами, что дает нам форму прямоугольного параллелепипеда. Единицей объема прямоугольного параллелепипеда является (единица измерения) 9.0339 3 . Метрическими единицами объема являются кубические метры или кубические сантиметры, а единицами объема в системе обычного права США (USCS) являются кубические дюймы или кубические футы. Объем прямоугольного параллелепипеда зависит от длины, ширины и высоты прямоугольного параллелепипеда, поэтому изменение любой из этих величин изменяет объем формы.

Объем кубовидной формулы

Формула объема прямоугольного параллелепипеда может быть получена из понятия, объясняемого на прямоугольных листах. Пусть площадь прямоугольного листа бумаги равна «A», высота, до которой они сложены, равна «h», а объем прямоугольного параллелепипеда равен «V». Затем объем прямоугольного параллелепипеда определяется путем умножения площади основания и высоты.
Объем прямоугольного параллелепипеда = площадь основания × высота
Площадь основания прямоугольного параллелепипеда = l × b
Следовательно, объем прямоугольного параллелепипеда V = l × b × h = lbh

Как рассчитать объем прямоугольного параллелепипеда?

Объем прямоугольного параллелепипеда – это пространство, занимаемое внутри прямоугольного параллелепипеда. Если все три измерения прямоугольного параллелепипеда равны, он становится кубом. Объем прямоугольного параллелепипеда можно рассчитать по формуле объема прямоугольного параллелепипеда. Шаги для вычисления объема прямоугольного параллелепипеда:

• Шаг 1: Проверьте, находятся ли заданные размеры прямоугольных параллелепипедов в одних и тех же единицах измерения. Если нет, преобразуйте размеры в те же единицы.
• Шаг 2: После того, как размеры будут в одинаковых единицах измерения, умножьте длину, ширину и высоту прямоугольного параллелепипеда.
• Шаг 3: Запишите единицу измерения в конце после получения значения.

Давайте рассмотрим пример, чтобы узнать, как вычислить объем прямоугольного параллелепипеда, используя его формулу.

Пример: Найдите объем прямоугольного параллелепипеда, имеющего длину 7 дюймов, ширину 5 дюймов и высоту 2 дюйма.
Решение: Как мы знаем, объем прямоугольного параллелепипеда V = lbh
Здесь длина l = 7 дюймов, ширина b = 5 дюймов и высота h = 2 дюйма
Таким образом, объем прямоугольного параллелепипеда V = lbh = (7 × 5 × 2) в ³
⇒ V = 70 в ³
\(\следовательно\) Объем прямоугольного параллелепипеда равен 70 в ³ .

 

Объем параллелепипеда Примеры

1. Пример 1: Если размеры кубовидного аквариума для рыб составляют 30 дюймов, 20 дюймов и 15 дюймов. Можно ли определить объем аквариума с рыбками?
   Решение: Как известно, аквариум с рыбками имеет прямоугольную форму. Отсюда размеры рыбного аквариума:
   Длина аквариума = 30
   Ширина аквариума = 20
   Высота аквариума = 15

   Объем аквариума:
   Объем = Длина × Ширина × Высота
   ⇒ Объем = 30 × 20 × 15 дюймов ³ = 9000 дюймов ³
   ∴ Объем кубовидного аквариума для рыб составляет 9000 кубических дюймов.

2. Пример 2: Какой будет длина прямоугольного параллелепипеда, если его объем равен 3000 в ³ , ширина 15 дюймов, а высота 10 дюймов?
   Решение: Как мы знаем, объем прямоугольного параллелепипеда определяется как Объем = Длина × Ширина × Высота. Данные размеры для прямоугольного параллелепипеда:
   Объем = 3000 дюймов ³
   Ширина = 15 в
   Высота = 10 в
   Пусть длина прямоугольного параллелепипеда равна х дюймов.

   Следовательно, объем прямоугольного параллелепипеда будет:
   Объем = Длина × Ширина × Высота
   ⇒ Объем = x × 15 × 10 = 3000 в ³
   ⇒ х = (3000/(15 × 10)) = 20 в
   ∴ Длина прямоугольного параллелепипеда составляет 20 дюймов.

3. Пример 3: Найдите объем прямоугольного параллелепипеда, если его длина 10 дюймов, ширина 20 дюймов, а высота 30 дюймов.

   Решение: объем прямоугольного параллелепипеда определяется как Объем = Длина × Ширина × Высота. Данные размеры для прямоугольного параллелепипеда:
   Длина = 10 в
   Ширина = 20 в
   Высота = 30 в
   ⇒ Объем = 10 × 20 × 30 дюймов ³ = 6000 дюймов ³
   ∴ Объем прямоугольного параллелепипеда составляет 6000 кубических дюймов.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.

Записаться на бесплатный пробный урок

Практические вопросы по объему прямоугольного параллелепипеда

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по Volume of Cuboid

Что вы подразумеваете под объемом прямоугольного параллелепипеда?

Объем прямоугольного параллелепипеда — это пространство, заключенное внутри прямоугольного параллелепипеда. Например, чтобы налить воду в аквариум, мы должны знать его объем.

Как найти объем прямоугольного параллелепипеда?

Объем прямоугольного параллелепипеда вычисляется путем умножения его длины, ширины и высоты. Например, объем прямоугольного параллелепипеда длиной, шириной и высотой 2 дюйма, 3 дюйма и 4 дюйма определяется как Объем = длина × ширина × высота = 2 × 3 × 4 = 24 дюйма ³

Что такое формула объема прямоугольного параллелепипеда?

Формула объема прямоугольного параллелепипеда = длина × ширина × высота. Формула объема прямоугольного параллелепипеда выводится путем укладки прямоугольных листов друг на друга, что дает нам три параметра в формуле: длину, ширину и высоту.

Если единицы измерения прямоугольного параллелепипеда различны, то как найти его объем?

Если единицы данных измерений прямоугольного параллелепипеда различны, то сначала нам нужно заменить единицы измерений любых двух измерений на единицы третьего измерения. После этого перемножьте все три известных нам измерения, чтобы вычислить объем прямоугольного параллелепипеда.

Имеет ли значение порядок высоты, ширины и длины при расчете объема прямоугольного параллелепипеда?

Нет, порядок высоты, ширины и длины не имеет значения при нахождении объема прямоугольного параллелепипеда, потому что для его определения нам нужно перемножить все три величины. Поскольку умножение ассоциативно, следовательно, независимо от того, в каком порядке умножаются измерения, объем прямоугольного параллелепипеда остается одним и тем же.

Как изменится объем прямоугольного параллелепипеда, если длину стороны уменьшить вдвое?

Объем прямоугольного параллелепипеда уменьшится вдвое, когда длина стороны уменьшится вдвое, так как l = l/2. Так как объем прямоугольного параллелепипеда = длина × ширина × высота = (l/2) × b × h = (lbh)/2 = объем/2. Таким образом, объем прямоугольного параллелепипеда уменьшится вдвое, как только его длина уменьшится вдвое.

Загрузить БЕСПЛАТНЫЕ учебные материалы

Загрузить рабочие листы по измерению и измерению тел

Вычисление объема и вместимости кубов и прямоугольных параллелепипедов ｜ Хацуди

В математике мы часто думаем о фигурах с точки зрения трехмерных объектов, а не двухмерных объектов. На самом деле все вокруг нас трехмерно.

Итак, давайте удостоверимся, что мы можем вычислить размер трехмерных объектов. В начальной школе геометрии мы изучаем формулы для вычисления размеров трехмерных фигур. Также размер трехмерной фигуры называется объемом. Используя формулу, вы сможете рассчитать объем.

Итак, давайте сначала вычислим объем куба и прямоугольного параллелепипеда. Тогда мы сможем понять вместимость сосуда. В этом разделе мы объясним, как рассчитать объем и вместимость кубов и прямоугольных параллелепипедов.

Содержание

• 1 Что такое кубы и прямоугольные параллелепипеды?
  • 1.1 Как рассчитать объем куба и параллелепипеда
• 2 Расчет вместимости сосуда: объем воды, заполненный трехмерным объектом
  • 2.1 Случаи, когда объем и вместимость различаются
• 3 Почему мы можем рассчитать объем и емкость?
  • 3.1 Расчет длин сторон по объему
• 4 Узнайте, как рассчитать объем и вместимость

Что такое кубы и прямоугольные параллелепипеды?

Во-первых, давайте разберемся, что такое куб и прямоугольный параллелепипед. Куб — это объект, окруженный шестью квадратами. Кроме того, прямоугольный параллелепипед — это объект, окруженный шестью прямоугольниками.

Ниже приведены куб и прямоугольный параллелепипед.

Вы должны быть в состоянии рассчитать размер таких фигур.

Как рассчитать объем куба и прямоугольного параллелепипеда

Поймите, что объем — это размер трехмерного объекта. Вы будете вычислять размер объекта, который имеет высоту, а также длину и ширину.

При расчете объема куба или параллелепипеда используйте следующую формулу.

• Объем трехмерного объекта = длина × ширина × высота

Например, каков объем следующего куба и параллелепипеда?

В случае куба все стороны имеют одинаковую длину. Итак, давайте умножим одно и то же число три раза. Так как длина стороны 3 см, объем куба следующий.

• $3×3×3=27$

Таким образом, ответ равен 27 см ³ . В площади длина стороны умножается в два раза, поэтому единица измерения равна см ² . С другой стороны, при вычислении объема длина стороны умножается на три раза, поэтому единицей измерения является см ³ .

Далее вычислим объем прямоугольного параллелепипеда, у которого длины сторон прямоугольника различны. Итак, давайте умножим длину, ширину и высоту соответственно. Результат следующий.

• $4×3×2=24$

Таким образом, мы видим, что объем прямоугольного параллелепипеда равен 24 см ³ .

Расчет вместимости сосуда: объем воды, заполненный трехмерным объектом

После понимания объема давайте узнаем о вместимости сосуда. Когда жидкость (например, воду) наливают в сосуд, емкость показывает, сколько жидкости можно налить в этот сосуд. Объем и вместимость сосуда — это одни и те же понятия, и формула используется одна и та же.

При вычислении объема мы умножали длину, ширину и высоту соответственно. При расчете вместимости сосуда умножьте длину, ширину и высоту сосуда соответственно.

В этом случае вместимость судна следующая.

• 15×8×10=1200$

Таким образом, мы можем рассчитать, что этот сосуд может быть наполнен до 1200 см ³ воды. 1 л равен 1000 см ³ , поэтому мы также можем видеть, что этот сосуд может вместить 1,2 л воды.

Случаи, когда объем и вместимость различаются

Как упоминалось ранее, формула для расчета объема и вместимости судна одинакова. Однако в реальности объем и емкость могут отличаться. Это связано с толщиной контейнера.

Например, каковы объем и вместимость следующего контейнера?

Объем равен размеру всего контейнера. Итак, давайте умножим на внешнюю длину контейнера. Так как длина 8 см, ширина 6 см и высота 5 см, объем следующий.

• $8×6×5=240$

С другой стороны, как рассчитать вместимость судна? В емкости важно знать, сколько воды можно залить. Только внутренняя часть контейнера может удерживать воду. Итак, давайте умножим внутреннюю длину контейнера. Так как длина 6 см, ширина 4 см и высота 4 см, объем следующий.

• $6×4×4=96$

Таким образом, мы можем рассчитать объем и вместимость сосуда. Поймите, что если емкость имеет толщину, то объем и вместимость будут другими.

Почему мы можем рассчитать объем и емкость?

Почему можно вычислить объем и вместимость сосуда путем умножения длины, ширины и высоты? Давайте выясним, почему.

Прежде всего, каков объем куба со стороной 1 см?

Поскольку все стороны имеют длину 1 см, объем этого куба равен 1 см ³ . Тогда каков объем этого куба, если он устроен следующим образом?

Всего кубиков 12. Следовательно, мы знаем, что это 12 см ³ . Однако подсчет количества кубиков по одному затруднителен. Итак, посчитаем объем.

В отличие от куба, все стороны которого имеют длину 1 см, кубоид на рисунке выше имеет высоту 1 см, но его вертикальная и горизонтальная длины различны. Итак, давайте умножим длину на ширину так же, как вычисляем площадь.

• $3×4×1=12$

Высота 1 см. Однако умножение на единицу не меняет ответ. Следовательно, в этом прямоугольном параллелепипеде вычисление площади такое же, как вычисление объема.

Далее рассмотрим прямоугольный параллелепипед высотой 3 см вместо 1 см. Результат следующий.

В этом прямоугольном параллелепипеде есть три параллелепипеда размером $3×4×1$, поставленные друг на друга. Поскольку блоки имеют высоту 3 см, мы вычисляем высоту в 3 см вместо 1 см следующим образом.

• $3×4×3=36$

Когда вы думаете об этом таким образом, вы можете понять, почему умножение на длину, ширину и высоту позволит вам вычислить объем.

Расчет длин сторон по объему

Если объем известен, в некоторых случаях можно рассчитать длины сторон. Например, если объем следующего прямоугольного параллелепипеда равен 16 см3, какова длина $a$?

Мы уже знаем объем. Кроме того, мы знаем длину и высоту. Итак, если мы установим ширину как $□$, мы можем составить следующее уравнение.

• $16=4×2×□$

Теперь давайте посчитаем стоимость $□$. Измените его на следующее уравнение.

• $□=16÷4÷2$

Вычислив это выражение, мы видим, что ширина равна 2 см.