Исследуйте функцию на экстремум онлайн: Экстремумы функции онлайн

Исследовать на экстремум функцию. — примеры, решения

Пример 1:

Исследовать функцию на экстремум и вычислить значение функции в точках экстремума:

Решение от преподавателя:

Решение.

Найдем частные производные. 


2. Решим систему уравнений. 
-4*x-4*y+4 = 0 
-4*x-6*y+10 = 0 
Получим: 
а) Из первого уравнения выражаем x и подставляем во второе уравнение: 

2*y-6 = 0 
Откуда y = 3 
Данные значения y подставляем в выражение для x. Получаем: x = -2 
Количество критических точек равно 1. 
M₁(-2;3) 
3. Найдем частные производные второго порядка. 



4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀). 
Вычисляем значения для точки M₁(-2;3) 



AC — B² = 8 > 0 и A 1(-2;3) имеется максимум z(-2;3) = 16 
Вывод: В точке M₁(-2;3) имеется максимум z(-2;3) = 16; 

Пример 2:

Исследуйте на экстремум функцию.

y = х² – 10х + 5

Решение от преподавателя:

Пример 3:

Найти экстремумы функций двух переменных

z = 2x³ + 6xy² – 30x – 24y.

Решение от преподавателя:

Пример 4:

Исследовать на экстремум:

Решение от преподавателя:

Необходимое условие экстремума функции одной переменной. 

Уравнение f’₀(x*) = 0 — это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает. 

Достаточное условие экстремума функции одной переменной. 
Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f»₀(x*) > 0 
то точка x* является точкой локального (глобального) минимума функции.  
Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f»₀(x*) то точка x* — локальный (глобальный) максимум. 
Решение. 
Находим первую производную функции: 
y’ = 6x²+6x 
или 
y’ = 6x(x+1) 
Приравниваем ее к нулю: 
6x²+6x = 0 
x₁ = 0 
x₂ = -1 
Вычисляем значения функции 
f(0) = -11 
f(-1) = -10 
Ответ: 
f_min = -11, f_max = -10 
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную: 
y» = 12x+6 
Вычисляем: 
y»(0) = 6>0 — значит точка x = 0 точка минимума функции. 
y»(-1) = -6

Пример 5:

Найти стационарные точки и исследовать на экстремум функцию

z = x² + y² – 2x – 2y+ 8

Решение от преподавателя:

Исследовать на экстремум функцию z = x² + y² – 2x – 2y+ 8

 

1. Найдем частные производные. 


2. Решим систему уравнений. 
2x-2 = 0 
2y-2 = 0 
Получим: x = 1, y = 1 
критическая  точка   M₁(1;1) 
3. Найдем частные производные второго порядка. 



4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀). 
Вычисляем значения для точки M₁(1;1) 



AC — B² = 4 > 0 и A > 0 , то в точке M₁(1;1) имеется минимум z(1;1) = 6 
Вывод: В точке M₁(1;1) имеется минимум z(1;1) = 6;

Пример 6:

Исследовать на экстремум функцию:

Решение от преподавателя:

Пример 7:

Исследовать функцию z(x,y) на экстремум

Решение от преподавателя:

Пример 8:

Исследовать на экстремум функцию:

Решение от преподавателя:

Вычислим производную этой функции и найдем стационарные точки, в которых она обращается в нуль:

Решая это уравнение, находим корни x₁ = 1 и x₂ = 2. Они являются подозрительными на экстремум в данной задаче. При этом знаки производной нашей функции распределены следующим образом:

Согласно теореме о достаточном условии экстремума первого порядка, полученные точки являются точками локального экстремума, а именно: x₁ = 1 — точка локального максимума, причем f(x₁) = 11, а x₂ = 2 — точка локального минимума, причем f(x₂) = 10.

Глобальных экстремумов в этой задаче нет. Это видно из того, что

Итак, локальный максимум достигается в точке x = 1 и равен 11, локальный минимум достигается в точке x = 2, и равен 10.

 

Пример 9:

Исследуйте на экстремум функцию z = z(x;y).

Решение от преподавателя:

Пример 10:

Исследовать на экстремум:

y = (2*x-8)*(9*x+1) 

Решение от преподавателя:

Необходимое условие экстремума функции одной переменной.  

Уравнение f’₀(x*) = 0 — это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает. 
Достаточное условие экстремума функции одной переменной. 

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f»₀(x*) > 0 
то точка x* является точкой локального (глобального) минимума функции. 
Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f»₀(x*) то точка x* — локальный (глобальный) максимум. 
Решение. 
Находим первую производную функции: 
y’ = 36x-70 
Приравниваем ее к нулю: 
36x-70 = 0 

Вычисляем значения функции 

Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную: 
y» = 36 
Вычисляем: 

значит эта точка — минимума функции.

Пример 11:

Найти экстремумы функции z(x,y) при данном условии:

Решение от преподавателя:

Пример 12:

Исследовать на экстремум функцию:

Решение от преподавателя:

Найдем производную f′ (x) = e^x − e^−x . Чтобы найти критические точки функции f(x), приравняем эту производную к нулю:

Очевидно, что точка x = 0 является решением последнего уравнения. Функция f′(x) строго возрастает (поскольку ). Поэтому она отрицательна при x 0.

Следовательно, точка x = 0 является точкой строгого локального минимума функции f(x), и f(0) = 2 — соответствующее минимальное значение.

В данной ситуации можно также применить теорему о достаточном условии экстремума второго порядка. Поскольку f′′(0) = 2 > 0, функция f(x) имеет строгий локальный минимум в точке x = 0.

Кроме того, этот минимум глобальный, потому что

Ответ: точка x = 0 является точкой глобального минимума для исследуемой функции и f_min = f(0) = 2.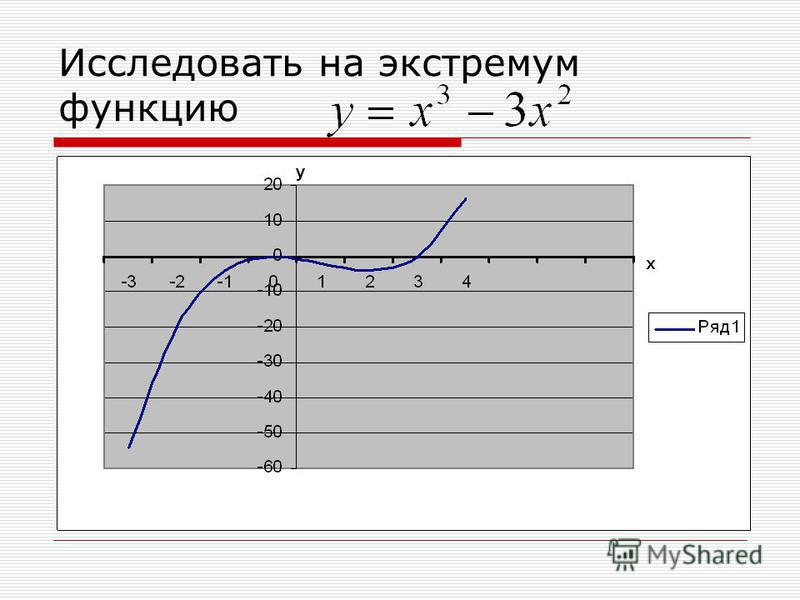

Пример 13:

Найти наибольшее и наименьшее значения функции z(x,y) в области D:

Решение от преподавателя:

Пример 14:

Исследовать на экстремум функцию:

y = x³+6*x²-4, [-4;1]. 

Решение от преподавателя:

Необходимое условие экстремума функции одной переменной. 

Уравнение f’₀(x*) = 0 — это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает. 
Достаточное условие экстремума функции одной переменной. 

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f»₀(x*) > 0 
то точка x* является точкой локального (глобального) минимума функции. 
Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f»₀(x*) то точка x* — локальный (глобальный) максимум.  
Решение. 
Находим первую производную функции: 
y’ = 3x²+12x 
или 
y’ = 3x(x+4) 
Приравниваем ее к нулю: 
3x(x+4) = 0 
x₁ = 0 
x₂ = -4 
Вычисляем значения функции на концах отрезка 
f(0) = -4 
f(-4) = 28 
f(-4) = 28.0000000000000 
f(1) = 3.00000000000000 

Ответ: f_min = -4, f_max = 28.

Пример 15:

Исследовать на экстремум функцию

Решение от преподавателя:

Как обычно, начнем с нахождения производной исследуемой функции и точек, подозрительных на экстремум:

Легко видеть, что точка x = 0 является критической.

Найдем вторую производную:

Очевидно, f′′(0) = 0. Воспользуемся теоремой о достаточном условии экстремума n-го порядка и будем дифференцировать функцию до того момента, пока не появится отличная от нуля производная:

Значит, x = 0 — точка локального минимума функции f(x).

Из предыдущего примера следует, что при . В то же время . Поэтому f′′(x) > 0 при . Отсюда следует, что производная f′(x) обращается в нуль в единственной точке x = 0.

Так как ,  минимум в точке x = 0 является глобальным.

Ответ: есть один глобальный минимум f(0) = 4.

Пример 16:

С помощью второй производной исследуйте на экстремум функцию . Найдите наибольшее М и наименьшее m значения этой функции на отрезке [-1, 2].

Решение от преподавателя:

Определяем критические точки

Определяем вторую производную функции

Определяем знаки второй производной в критических точках

Т. к. вторая производная положительная, то в точке х=0 минимум

Т. к. вторая производная отрицательная, то в точке х=1 максимум

Наибольшее М и наименьшее m значения этой функции на отрезке [-1, 2]

Т. к. обе критические точки принадлежат указанному отрезку, то определяем значения функции в полученных точках и на концах отрезка

 

 

 

Т. о., М=у(-1)=6 m=у(2)=-3

Пример 17:

Исследовать на экстремум функцию:

Решение от преподавателя:

Подозрительные на экстремум точки найдем с помощью леммы Ферма. Так как

то единственная подозрительная на экстремум точка (в которой все частные производные обращаются в нуль) — это точка a = (3, −2, −1).

Определим, есть ли в этой точке экстремум. Для этого найдем все частные производные второго порядка

и составим из них матрицу полной второй производной f′′(a):

Главные миноры этой матрицы чередуют знаки:

По теореме (достаточное условие экстремума второго порядка) в точке a локальный максимум. Ответ: локальный максимум достигается в точке a = (3, −2, −1) и равен 14.

Ответ: локальный максимум достигается в точке a = (3, −2, −1) и равен 14.

 

Пример 18:

Найти экстремумы функции:

Решение от преподавателя:

Подозрительные на экстремум точки найдем с помощью леммы Ферма. Так как

то единственной стационарной точкой будет точка a = (0, 0).

Посмотрим, есть ли в ней экстремум. Для этого вычислим частные производные второго порядка

и составим из них матрицу второй производной в точке a:

Очевидно, ее определитель равен нулю. Значит, достаточные условия экстремума из теоремы (достаточное условие экстремума второго порядка) в данном случае не применимы.

Придется использовать определение экстремума. Рассмотрим разность . Она больше нуля при всех y > 0 и меньше нуля при y

Ответ: у функции f нет экстремумов.

Пример 19:

Найти экстремумы функции

Решение от преподавателя:

Очевидно,

и единственная стационарная точка — это a = (0, 0).

Далее вычисляем частные производные второго порядка

и выписываем матрицу второй производной в точке a:

Ее определитель равен нулю. Достаточные условия экстремума опять не работают. С другой стороны, . Поэтому в точке (0, 0) глобальный минимум.

Ответ: есть один глобальный минимум f(0, 0) = 0.

Пример 20:

Исследовать на экстремумы функцию.

Решение от преподавателя:

Работа вам нужна срочно. Не волнуйтесь, уложимся!

Заполните, пожалуйста, данные для автора:

• 22423 авторов готовы помочь тебе.
• 2402 онлайн

Применение производной для исследования функции на монотонность и экстремумы

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Дом. : РАЗОБРАТЬ ВСЕ ПРИМЕРЫ В ПРЕЗЕНТАЦИИ,Решу ЕГЭ.№ 7, (3, ТАМ 30 ЗАД.) будет с.р. ( геом. и прим. производной)

Применение
производной для
исследования
функции на
монотонность и
экстремумы

3. Применение производной к исследованию функции

1. Промежутки монотонности
2. Точки экстремума и значение
функции в этих точках
3. Наибольшее и наименьшее
значение функции
4. Построение графика функции
f ( x0 ) tg k
У
y f (x)
k – угловой коэффициент
прямой (касательной)
y k x b
α
0
x0
Х
Геометрический смысл производной: если к графику функции y = f(x)
в точке с абсциссой x0 можно провести касательную, непараллельную оси у,
то f ( x0 ) выражает угловой коэффициент касательной, т.е.
f ( x0 ) k
Поскольку
, то верно равенство
f ( x0 ) tg
Если α < 90°, то k > 0. Если α > 90°, то k < 0.
у
x2 x3
у f (x)
x1
0
х
Если α = 0°, то k = 0.
Касательная параллельна оси ОХ.

7. Монотонность функции

•Если производная функции y=f(x)
положительна на некотором интервале, то
функция в этом интервале монотонно
возрастает
•Если производная функции y=f(x)
отрицательна на некотором интервале, то
функция в этом интервале монотонно
убывает.
На рисунке изображен график функции у = f(x), определенной на
интервале (-9; 8). Определите количество целых точек, в которых
производная функции положительна.
Решение: 1. f/(x) > 0, значит, функция возрастает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
y
5
4
3
2
1
-9 -8 -7 -6 -5 — 4 -3 -2 -1
-1
-2
-3
-4
y = f (x)
x
1 2 3 4 5 6 7 8
Ответ: 8
На рисунке изображен график функции у = f(x), определенной на
интервале (-5; 5). Определите количество целых точек, в которых
производная функции отрицательна.
Решение: 1. f/(x) < 0, значит, функция убывает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
y
5
4
3
2
1
-9 -8 -7 -6 -5 — 4 -3 -2 -1
-1
-2
-3
-4
y = f (x)
x
1 2 3 4 5 6 7 8
Ответ: 5
Точки экстремума
Если функция y=f(x) имеет экстремум в точке x=x0,
то в этой точке производная функции
или равна нулю,
или не существует
Стационарные точки
Касательная
в таких точках
графика параллельна оси ОХ
Критические точки
Касательная в
таких точках графика
не существует
Непрерывная функция у = f(x) задана на отрезке [a;b]
На рисунке изображен ее график. В ответе укажите количество
точек графика этой функции, в которых касательная
параллельна оси Ох.
y
y = f(x)
a
b
x
Ответ: 5

12. Достаточное условие существования экстремума функции:

Если при переходе через стационарную точку х0 функции
f(x) ее производная меняет знак с «+» на «-», то х0 – точка
максимума функции f(x).
Если при переходе через стационарную точку х0 функции
f(x) ее производная меняет знак с «-» на «+», то х0 – точка
минимума функции f(x).
Если при переходе через стационарную точку х0 функции
f(x) ее производная не меняет знака, то в точке х0
экстремума нет.
12
Возрастает: (-9;-3) и (3;6)
Убывает:
(-3;3)
Максимум:
Минимум;
— 3; 6
3
На рисунке изображен график производной функции у
=f (x), заданной на промежутке (- 8; 8).
Найти точки, в которых f /(x)=0 (это нули функции).
y
+
-7 -6 -5 -4 -3 -2 -1
–
f/(x)
f(x)
-5
4
3
2
1
-1
-2
-3
-4
-5
0
y = f /(x)
+
+
1 2 3 4 5 6 7
–
3
7
x
x
Исследуйте функцию у =f (x) на экстремум и укажите
количество ее точек минимума.
y
4
y = f /(x)
-7 -6 -5 -4 -3 -2 -1
3
2
1
-1
-2
-3
-4
-5
f/(x)-8 +
-5
f(x)
1 2 3 4 5 6 7
+
–
0
+ 8
–
3
x 4 точки экстремума
7
x
Ответ:2
Найдите количество точек экстремума функции у =f (x)
на отрезке [– 3; 7]
y
-7 -6 -5 -4 -3 -2 -1
f/(x) -8 +
-5
f(x)
4
3
2
1
y = f /(x)
-1
-2
-3
-4
-5
1 2 3 4 5 6 7
–
+
0
+ 8
–
3
x
7
x
Ответ: 3
На рисунке изображен график производной функции
y=f(x), определенной на интервале ( — 11; 3). 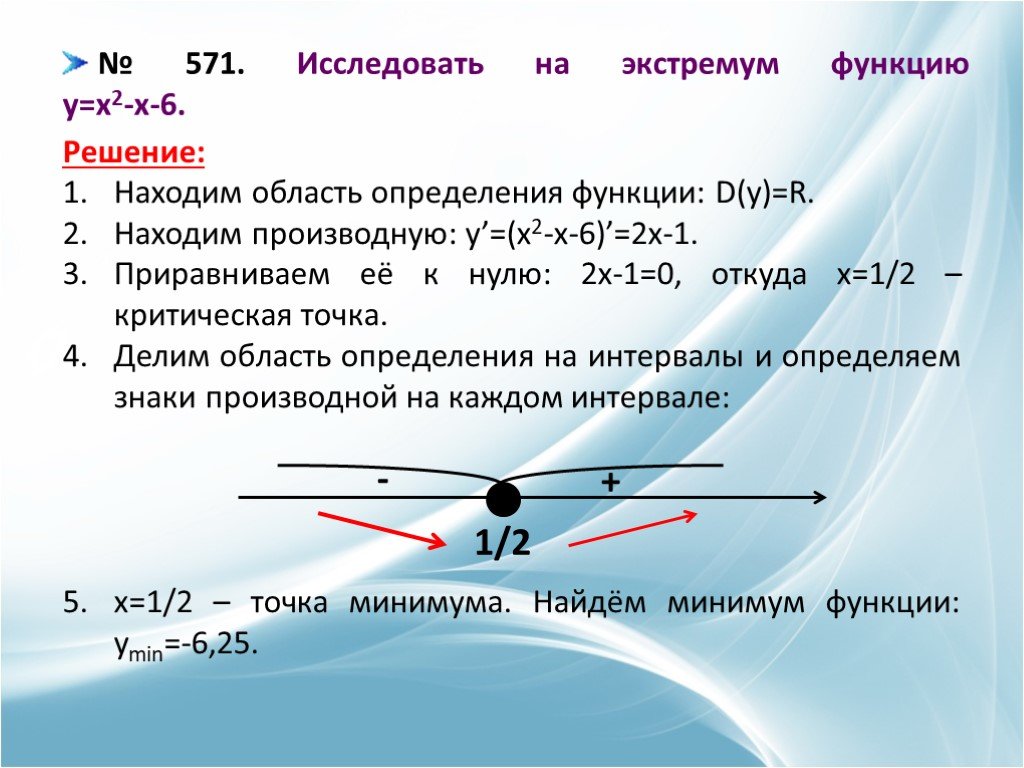Найти
промежутки возрастания функции. В ответе указать
длину наибольшего из них
17
На рисунке изображен график функции
f(x),
определенной на интервале (-3;10) . Найдите сумму
точек экстремума функции f(x) .
-1 0 1 2 3
6 7 8 9
-1 + 0 + 1+2 + 3 + 6 + 7+ 8 + 9= 35
Ответ: 35

19. Исследование функции на монотонность

Найти D(f) и исследовать на непрерывность
функцию f (х).
Найти производную f ´.
Найти стационарные и критические точки
функции f (х).
Отметить промежутки знакопостоянства f ´.
и промежутки монотонности функции f (х).
Найти промежутки монотонности функции
y=2x³-3x²-36x+5
1.
2.
3.
Область определения: R. Функция непрерывна.
Вычисляем производную : y’=6x²-6x-36.
Находим стационарные точки: y’=0.
x²-x-6=0
Д=1-4*(-6)*1=1+24=25
—
+
-2
+
3
5.Функция возрастает при xϵ (-∞; -2)υ(3; +∞),
функция убывает при xϵ (-2; 3).
20
Найти промежутки монотонности функции
y=x³-3x²
1.
2.
3.
4.
Область определения: R. Функция непрерывна.
Вычисляем производную : y’=3x²-6x.
Находим критические точки: y’=0.
x²-2x= 0
x(x-2)= 0
x1=0 и x2=2
Делим область определения на интервалы:
+
—
2
0
5. Функция возрастает при xϵ(-∞;0]υ[2;+∞),
функция убывает при xϵ[0;2].
+
21

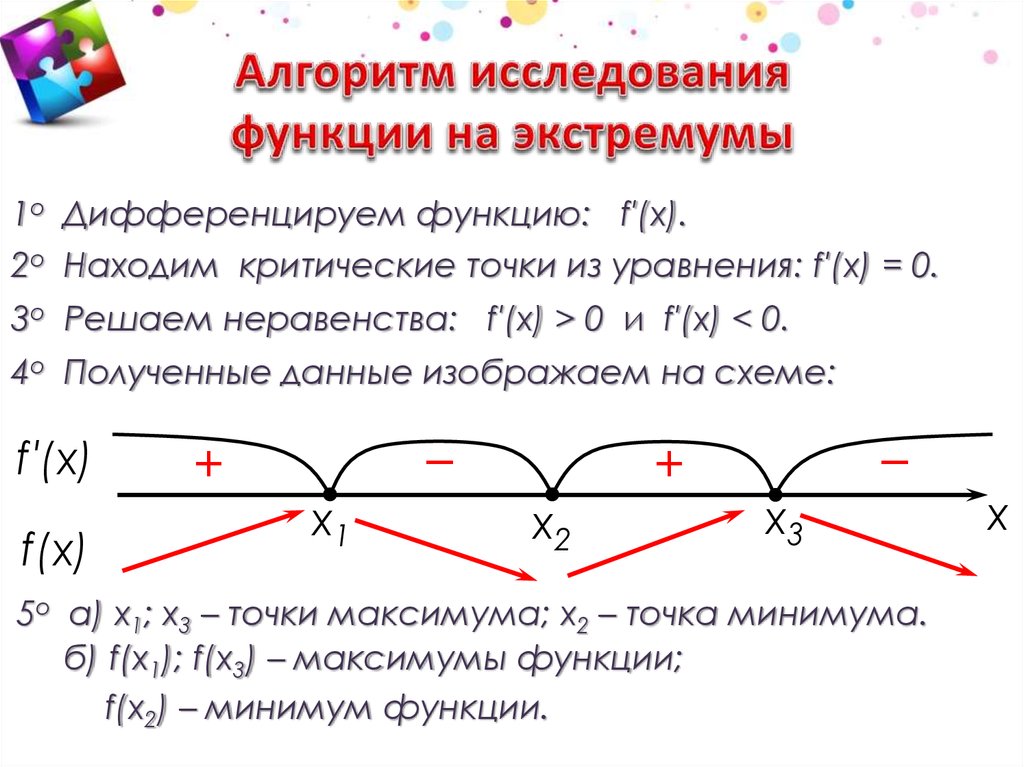
22. Алгоритм исследования функции f(х) на экстремум с помощью производной :

Найти D(f) и исследовать на непрерывность
функцию f (х).
Найти производную f ´
Найти стационарные и критические точки
функции f(х) и на координатной прямой
отметить промежутки знакопостоянства f ´.
Посмотрев на рисунок знаков f ´, определить
точки минимума и максимума функции и
вычислить значения f(х) в этих точках.
Исследовать на экстремум функцию
y=x2+2.
Решение:
1. Находим область определения функции: D(y)=R.
2. Находим производную: y’=(x2+2)’=2x.
3. Приравниваем её к нулю: 2x= 0, откуда x = 0 –
критическая точка.
4. Делим на интервалы и определяем знаки производной
на каждом интервале:
—
+
0
5. х =0 – точка минимума.
Найдём минимум функции ymin=2.
23
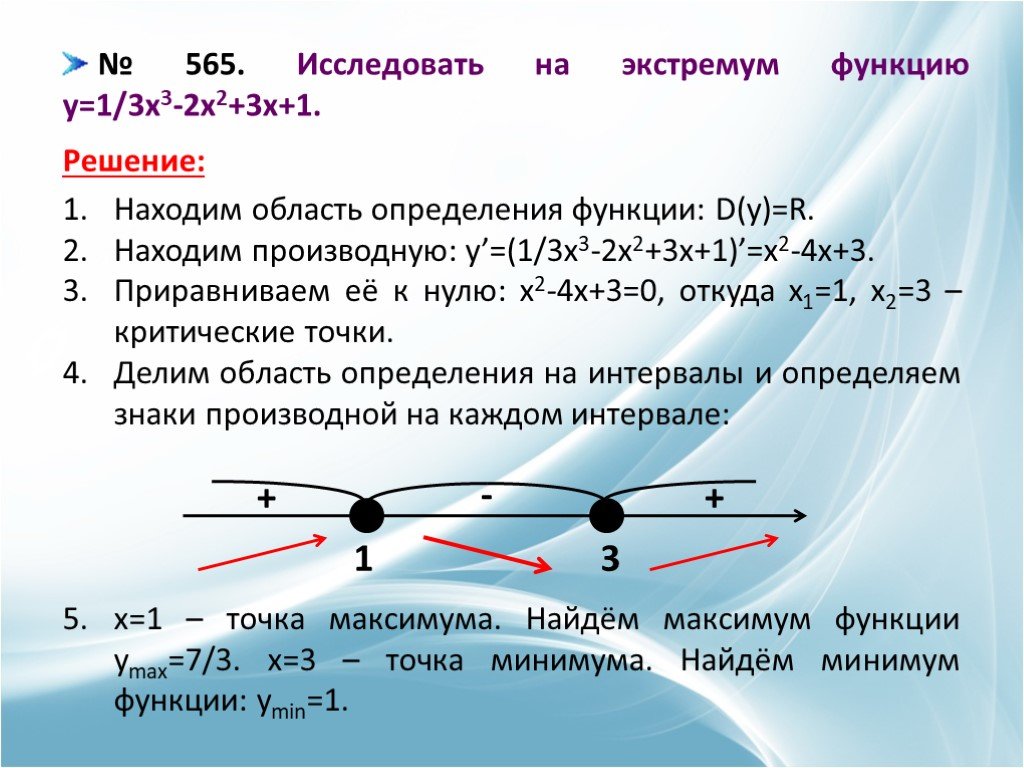
Исследовать
y=1/3×3-2×2+3x+1.
на
экстремум
функцию
Решение:
1. Находим область определения функции: D(y)=R.
2. Находим производную: y’=(1/3×3-2×2+3x+1)’=x2-4x+3.
3. Приравниваем её к нулю: x2-4x+3=0, откуда x1=1, x2=3 –
критические точки.
4. Делим на интервалы и определяем знаки производной
на каждом интервале:
+
—
+
1
3
5. x=1 – точка максимума. Найдём максимум функции
ymax=7/3.
x=3 – точка минимума. Найдём минимум функции: ymin=1.
24

25. Общая схема исследования функции

Найти область определения функции f(х).
Выяснить, обладает ли функция особенностями,
облегчающими исследование, то есть является ли
функция f(х):
а) четной или нечетной;
б) периодической.
Вычислить координаты точек пересечения графика с
осями координат.
Найти промежутки знакопостоянства производной
функции f(х) .
Выяснить, на каких промежутках функция f (х)
возрастает, а на каких убывает.
Найти точки экстремума (максимум или минимум) и
вычислить значения f (х) в этих точках.
Исследовать поведение функции f (х) в окрестности
характерных точек не входящих в область определения.
Построить график функции.

26. Исследовать функцию f(x)=x4-2×2-3

Область определения: D (f)=R
Четность – нечетность функции:
f (-x)=x4-2×2-3,
значит f (-x) = f (x) для любого х, принадлежащего D (f) –
функция является чётной.
Координаты точек пересечения графика с осями
координат
с ось Оу: f(x)=0: (x2-3)(x2+1)=0; x=± 3 ;
с осью Ох: f(0)=-3
Промежутки знакопостоянства производной f’.
f’(x)=4х3-4x=4х(x-1)(x+1) =0
х = -1; 0; 1.
Промежутки монотонности функция f(х).
Точки экстремума и значения f в этих точках.
Составить таблицу.
x
f’(x)
f(x)
(- ∞; -1) -1 (-1;0)
−
0
+
0
(0;1)
1
0
—
0
-4
-3
-4
mi
n
max
min
(1;+
∞)
+
Построить график функции.

29. Правило нахождения наибольшего и наименьшего значений функции f(x) на отрезке [a;b]

Чтобы найти наибольшее и наименьшее значения
непрерывной функции f(x) на промежутке [a;b],
нужно
вычислить её значения f(a) и f(b) на концах
данного промежутка;
вычислить её значения в точках экстремума,
принадлежащих этому промежутку;
Выбрать из них наибольшее и наименьшее.
Записывают : max f(x) и min f(x)
[a;b]
[a;b]

30. Найти наибольшее и наименьшее значение функции

English     Русский Правила

относительных экстремумов — определение, производные тесты, графики, примеры Точки относительных экстремумов можно получить с помощью критерия второй производной, проверяя знак второй производной в критических точках, или с помощью критерия первой производной, проверяя изменение знака первой производной функции в ближайшей окрестности критической точка. Тест первой производной и Тест второй производной — два наиболее часто используемых метода для определения относительных экстремумов.

В этой статье мы узнаем, как находить относительные экстремумы функции, используя тесты производных и графики. Мы также будем решать различные примеры, чтобы понять шаги по нахождению относительных экстремумов и для ясности концепции.

1.	Что такое относительные экстремумы?
2.	Определение относительного экстремума
3.	Поиск относительных экстремумов
4.	Тест первой производной относительных экстремумов
5.	Тест второй производной относительного экстремума
6.	Относительный экстремум на графике
7.	Часто задаваемые вопросы об относительных экстремумах

Что такое относительные экстремумы?

Относительные экстремумы — это входные значения функции f(x), где f(x) имеет минимальное или максимальное значение.

Они могут быть двух типов — относительные максимумы и относительные минимумы. Графически относительные экстремумы — это пики и впадины графика функции, причем пики — это точки относительных максимумов, а долины — точки относительных минимумов. Сочетание относительных максимумов и минимумов называется относительными экстремумами.

Определение относительного экстремума

Относительные экстремумы функции — это точки на графике функции, в которых получаются минимальные или максимальные значения функции на некотором интервале области определения функции. Пройдемся по определениям относительных максимумов и относительных по отдельности:

• Относительные максимумы — Говорят, что точка x = b является точкой относительных максимумов для f(x), если она находится в 𝛿-окрестности b, т.е. (b−𝛿, b+𝛿), где 𝛿 можно сделать сколь угодно малым, f(x) < f(b) для всех x ∈ (b−𝛿, b+𝛿)∖{b}. Другими словами, если мы рассмотрим небольшую область (интервал) вокруг x = b, f(b) должно быть максимальным в этом интервале.
• Относительные минимумы — Точка x = a называется точкой относительных минимумов для f(x), если она находится в окрестности точки a, т. е. в (a−𝛿,a+𝛿), где 𝛿 можно сделать сколь угодно малым , f(x) > f(a) для всех x ∈ (a−𝛿,a+𝛿)∖{a}. Проще говоря, если мы рассмотрим небольшой интервал вокруг x = a, f(a) должно быть минимумом в этом интервале.

Обратите внимание, что функция f(x) может иметь более одного относительного экстремума. С другой стороны, может быть только один абсолютный экстремум (один абсолютный максимум и один абсолютный минимум) функции во всей области.

Поиск относительных экстремумов

Мы можем оценить относительные экстремумы функции, используя тесты производных. Есть два теста, а именно:

• Первый производный тест
• Тест второй производной

Мы подробно изучим два теста с помощью примеров, чтобы понять их применение. В тесте первой производной мы проверяем знак первой производной при движении через критические точки, а в тесте второй производной мы проверяем знак второй производной в критических точках. Давайте подробно рассмотрим эти два теста в следующих разделах.

Тест первой производной относительного экстремума

Теперь, чтобы найти относительные экстремумы с помощью критерия первой производной, мы проверим изменение знака первой производной функции при движении через критические точки. Наклон графика функции определяется первой производной. Рассмотрим непрерывную дифференцируемую функцию f(x) с критической точкой при x = c, такую, что f'(c) = 0. Тогда имеем следующие условия для точек относительных экстремумов:0005

• Относительный максимум: если знак f'(x) меняется с положительного на отрицательный при движении слева направо через точку x = c, т. е. если f'(x) > 0 для значений x слева 𝛿-окрестности c и f'(x) < 0 для значений x в правой 𝛿-окрестности c, где 𝛿 может быть сколь угодно малым, то x = c является точкой относительных максимумов.
• Относительные минимумы: если знак f'(x) меняется с отрицательного на положительный при движении слева направо через точку x = c, т. е. если f'(x) < 0 для значений x слева 𝛿- окрестность c и f'(x) > 0 для значений x в правой 𝛿-окрестности c, где 𝛿 может быть сколь угодно малым, то x = c является точкой относительных минимумов.
• Тест не пройден: если знак первой производной f(x) не меняется при движении через точку c, то x = c называется точкой перегиба.

Давайте рассмотрим пример, чтобы понять, как найти точки относительных экстремумов с помощью теста первой производной пошагово. Для этого рассмотрим функцию f(x) = 2x

3 — 3x ² + 6. Теперь выполните указанные шаги, чтобы найти ее точки относительных экстремумов:

Шаг 1: Определите производную от f(x)

f'(x) = 6x ² — 6x

Шаг 2: Приравняйте производную к 0, т. е. f'(x) = 0, чтобы найти критические точки.

f'(x) = 0

⇒ 6x ² — 6x = 0

⇒ 6x(x — 1) = 0

⇒ x = 0, или x = 1

и, следовательно, x = 1 — критические точки.

Теперь для определения точек относительных экстремумов рассмотрим точки слева и справа от этих критических точек.

Шаг 3: Найдите точки слева и справа от критических точек и проверьте значение производной в этих точках.

Рассмотрим x = -1 слева и x = 1/2 справа от критической точки x = 0 и проверьте значение f'(x) в этих точках.

f'(-1) = 6(-1) ² — 6(-1) = 6 + 6 = 12 > 0

f'(1/2) = 6(1/2) ² — 6(1/2) = 6/4 — 6/2 = 3/2 — 3 = -3/2 < 0

Поскольку значение f'(x) меняется с положительного на отрицательное, поэтому x = 0 точка относительных максимумов.

Аналогично рассмотрим x = 1/2 слева и x = 2 справа от критической точки x = 1 и проверьте значение f'(x) в этих точках.

f'(1/2) = 6(1/2) ² — 6(1/2) = 6/4 — 6/2 = 3/2 — 3 = -3/2 < 0

f ‘(2) = 6(2) ² — 6(2) = 24 — 12 = 12 > 0

Поскольку значение f'(x) меняется с отрицательного на положительное, поэтому x = 1 является точкой относительные минимумы.

Чтобы определить относительное максимальное и минимальное значения, мы можем найти значения f(0) и f(1) соответственно.

Тест второй производной относительного экстремума

Далее, чтобы найти точки относительных экстремумов с помощью критерия второй производной, мы проверяем знак второй производной функции в критических точках. Как правило, если первая проверка производной не проходит, мы используем вторую проверку производной, чтобы найти точки относительных экстремумов. Рассмотрим функцию f(x), которая дважды дифференцируема, и критическую точку x = c в области определения функции f(x), такую, что f'(c) = 0, тогда выполняются следующие условия:0005

• Если f»(c) < 0, то x = c является точкой относительных максимумов.
• Если f»(c) > 0, то x = c является точкой относительных минимумов.
• Тест не пройден, если f»(c) = 0. В этом случае x = c называется точкой перегиба.

Рассмотрим пример, чтобы понять, как пошагово находить точки относительных экстремумов с помощью теста второй производной. Для этого рассмотрим функцию f(x) = 2x ³ + 3x ² — 12x + 5.

Теперь выполните указанные шаги, чтобы найти ее точки относительных экстремумов:

Шаг 1: Определите производную f(x)

f'(x) = 6x ² + 6x — 12

Шаг 2: Приравняйте производную к 0, т. е. f'(x) = от 0 до найти критические точки.

f'(x) = 0

⇒ 6x ² + 6x — 12 = 0

⇒ 6(x ² + x — 2) = 0

⇒ -2 x 90 =

+ 1 2 90 0

⇒ х ² + 2х — х — 2 = 0

⇒ х(х + 2) — 1(х + 2) = 0

⇒ (х — 1) (х + 2) = 0

⇒ х = 1 или х = -2

Следовательно, x = -2 и x = 1 являются критическими точками.

Шаг 3: Определите вторую производную f(x).

f»(x) = 12 x + 6

Шаг 4: Подставьте критические точки в f»(x) и проверьте знак второй производной.

f»(-2) = 12(-2) + 6 = -24 + 6 = -18 < 0 ⇒ x = -2 — точка относительных максимумов.

f»(1) = 12(1) + 6 = 12 + 6 = 18 >

0 ⇒ x = 1 — точка относительных минимумов.

Относительный экстремум на графике

Мы научились определять точки относительных экстремумов алгебраически, используя тесты производных. Далее мы научимся определять относительные экстремумы функции с помощью графика. Пики и впадины на графике указывают на относительные экстремумы функции. Как мы видим на графике ниже, в точках x = a и x = c есть долины, и функция имеет минимальные значения в этих точках, следовательно, x = a и x = c являются точками относительных минимумов. Точно так же мы видим пики при x = b и x = d на графике. В этих точках функция имеет максимальные значения, поэтому x = b и x = d являются точками относительных максимумов.

Важные примечания относительно относительных экстремумов

• Функция может иметь несколько относительных экстремумов, но может быть только одна точка абсолютного максимума и абсолютного минимума.
• Значение x в области определения f(x), которое не является ни локальным максимумом, ни локальным минимумом, называется точкой перегиба.

Темы, связанные с относительными экстремумами

• Относительные максимумы
• Первый производный тест
• Тест второй производной
• Применение деривативов

Часто задаваемые вопросы об относительных экстремумах

Что такое относительный экстремум в исчислении?

Относительные экстремумы — это входные значения функции f(x), где f(x) имеет минимальное или максимальное значение. Они могут быть двух типов — относительные максимумы и относительные минимумы.

Что такое относительные экстремумы на графике?

Пики и впадины на графике обозначают относительные экстремумы функции, пики — это точки относительных максимумов, а впадины — точки относительных минимумов.

Когда нет относительных экстремумов?

Относительные экстремумы не встречаются на концах области определения функции.

Как найти относительные экстремумы?

Мы можем найти относительные экстремумы, используя график. Их также можно определить алгебраически, используя критерии первой и второй производной.

Как найти относительные экстремумы с помощью теста второй производной?

Рассмотрим функцию f(x), дважды дифференцируемую, и критическую точку x = c в области определения f(x), такую, что f'(c) = 0, тогда выполняются следующие условия:

• Если f»(c) < 0, то x = c является точкой относительных максимумов.
• Если f»(c) > 0, то x = c является точкой относительных минимумов.
• Тест не пройден, если f»(c) = 0. В этом случае x = c называется точкой перегиба.

Что такое тест первой производной для относительных экстремумов?

Для теста первой производной для нахождения относительных экстремумов рассмотрим непрерывную дифференцируемую функцию f(x) с критической точкой при x = c, такой что f'(c) = 0. Тогда у нас есть следующие условия для точек относительных экстремумы:

• Относительный максимум: если знак f'(x) меняется с положительного на отрицательный при движении слева направо через точку x = c, т. е. если f'(x) > 0 для значений x слева 𝛿-окрестности c и f'(x) < 0 для значений x в правой 𝛿-окрестности c, где 𝛿 может быть сколь угодно малым, то x = c является точкой относительных максимумов.
• Относительные минимумы: если знак f'(x) меняется с отрицательного на положительный при движении слева направо через точку x = c, т. е. если f'(x) < 0 для значений x слева 𝛿- окрестность c и f'(x) > 0 для значений x в правой 𝛿-окрестности c, где 𝛿 может быть сколь угодно малым, то x = c является точкой относительных минимумов.
• Тест не пройден: если знак первой производной f(x) не меняется при движении через точку c, то x = c называется точкой перегиба.

В чем разница между абсолютным и относительным экстремумами?

Функция может иметь один абсолютный экстремум (один абсолютный максимум и один абсолютный минимум). С другой стороны, функция может иметь как можно больше относительных экстремумов. Кроме того, абсолютные экстремумы являются только одним из относительных экстремумов.

Является ли точка перегиба относительным экстремумом?

Точка перегиба может быть или не быть относительным экстремумом. Например, рассмотрим (x) = x ² для x ≤ 0. Здесь x = 0 является точкой перегиба с использованием теста первой производной, но x = 0 также является точкой относительного минимума.

Типы объяснений в данных объяснения

Каждый раз, когда вы выбираете новую отметку в визуализации или панели инструментов и запускаете «Объяснение данных», Tableau запускает новый статистический анализ с учетом этой отметки и базовых данных в рабочей книге. Возможные объяснения отображаются в расширяемых разделах панели «Объяснение данных». Для получения информации о том, как объяснения данных анализируются и оцениваются, см. раздел «Как работает объяснение данных».

Изучение базовых значений

В этом разделе приведены пояснения для каждого показателя, который можно объяснить (называемый целевыми показателями ). Каждое перечисленное здесь объяснение описывает взаимосвязь со значениями целевого показателя, которые проверяются на анализируемой метке. Используйте свое реальное практическое понимание данных, чтобы определить, являются ли взаимосвязи, обнаруженные с помощью объяснения данных, значимыми и заслуживающими изучения.

В этом примере целевым показателем является расстояние поездки.

Базовые характеристики

Эти пояснения описывают, как базовые записи меток в представлении могут влиять на агрегированное значение объясняемого показателя. Атрибуты метки могут включать экстремальные значения, нулевые значения, количество записей или среднее значение метки.

Примечание . Определения общих терминов, используемых в пояснениях, см. в разделе Термины и понятия в пояснениях(ссылка откроется в новом окне).

Экстремальные значения

Этот тип пояснения указывает, имеют ли одна или несколько записей значения, которые значительно выше или ниже, чем у большинства записей. Если объяснение подтверждается моделью, это указывает на то, что экстремальное значение влияет на целевой показатель анализируемой отметки.

Когда метка имеет экстремальные значения, это не означает автоматически, что она имеет выбросы или что вы должны исключить эти записи из представления. Этот выбор зависит от вашего анализа. Объяснение просто указывает на экстремальное значение отметки. Например, это может выявить ошибочное значение в записи, где банан стоит 10 долларов вместо 10 центов. Или это может показать, что у конкретного продавца был отличный квартал.

Примечание : это объяснение должно быть включено автором, чтобы оно отображалось в режиме просмотра опубликованной книги. Дополнительные сведения см. в разделе Управление доступом к объяснению данных.

Это пояснение показывает: Количество базовых записей в анализируемой метке. Экстремальное значение или значения, влияющие на значение целевой меры. Распределение значений в марке. Сведения о записи, соответствующие каждому значению распределения. Варианты исследования: Наведите указатель мыши на кружок на диаграмме, чтобы увидеть соответствующее значение. Щелкните стрелку влево или вправо под списком сведений, чтобы просмотреть сведения о записи. Если доступно, щелкните Просмотр полных данных , а затем щелкните вкладку Полные данные , чтобы просмотреть все записи в таблице. Щелкните значок «Открыть», чтобы просмотреть увеличенную версию визуализации. Следующие шаги анализа: Если количество записей невелико, проверьте эти значения по сравнению с максимальным значением. Если экстремальное значение значительно выше или ниже других значений записи, исключите его и посмотрите, как оно изменяет значение анализируемой отметки. При рассмотрении данных с экстремальным значением и без него используйте это как возможность применить свои практические знания о данных.		В этом примере единственное экстремальное значение, равное 463 часам аренды, способствует более высокой, чем ожидалось, сумме общего времени аренды, равной 613 часам. Вероятной причиной такого высокого значения может быть то, что кто-то забыл пристыковать велосипед, когда возвращал его. В этом случае автор может захотеть исключить это значение для будущего анализа.
Визуализируйте разницу В этом разделе показаны: Как изменяется значение анализируемой отметки при исключении экстремального значения.               Варианты исследования: Щелкните значок «Открыть», чтобы просмотреть увеличенную версию визуализации. Исследуйте разницу с экстремальным значением (или значениями) и без него. Авторы могут открыть представление как новый лист и применить фильтр, чтобы исключить экстремальное значение. Следующие шаги анализа: Если экстремальное значение значительно выше или ниже других значений записи, исключите его и посмотрите, как оно изменяет значение анализируемой отметки. При рассмотрении данных с экстремальным значением и без него используйте это как возможность применить свои практические знания о данных.		В этом примере, когда исключено крайнее значение 483, анализируемая метка больше не является высокой по сравнению с другими метками в представлении. Другие знаки теперь выделяются. Автор может захотеть изучить другие марки, чтобы понять, почему в этих других местах часы проката велосипедов больше.

Null Values ​​

Тип пояснения Null Values ​​указывает на ситуации, когда количество отсутствующих данных в метке превышает ожидаемое. Он указывает долю значений целевой меры, которые являются нулевыми, и то, как нулевые значения могут влиять на совокупное значение этой меры.

Это пояснение показывает: Процент нулевых значений в целевой мере для анализируемой метки (синий кружок). Варианты исследования: Наведите указатель мыши на каждый кружок на точечной диаграмме, чтобы увидеть его детали. Прокрутите, чтобы увидеть больше диаграммы. Щелкните значок «Открыть», чтобы просмотреть увеличенную версию визуализации. Следующие шаги анализа: При необходимости исключить нулевые значения в метке для дальнейшего анализа.

В этом примере процент нулевых значений в целевой мере показан синим кругом.

Количество записей

Этот тип объяснения описывает, когда количество базовых записей соотносится с суммой. Анализ выявил взаимосвязь между количеством записей, агрегируемых в отметке, и фактическим значением отметки.

Хотя это может показаться очевидным, этот тип объяснения помогает выяснить, влияет ли на значение метки величина значений в ее записях или просто количество записей в анализируемой метке.

Это пояснение показывает: Количество записей в целевом показателе для анализируемой отметки (синяя полоса). Количество записей в целевой мере для других меток в исходной визуализации (голубая полоса). Варианты исследования: Наведите указатель мыши на каждую полосу, чтобы просмотреть сведения о ней. Прокрутите, чтобы увидеть больше диаграммы. Щелкните значок «Открыть», чтобы просмотреть увеличенную версию визуализации. Следующие шаги для анализа: Сравните, являются ли отдельные значения записей низкими или высокими, или количество записей в анализируемой отметке низким или высоким. Авторы, если вас удивляет большое количество записей, вам может потребоваться нормализовать данные.

В этом примере количество записей для параметра «Расстояние поездки» указано для каждого значения параметра «Месяц поездки», который является измерением в исходной визуализации. Август имеет самое высокое значение общей дальности поездки. Вы можете выяснить, имеет ли август наибольшее значение расстояния поездки, потому что в августе было больше поездок, или он имеет самое большое расстояние поездки, потому что некоторые поездки были более продолжительными.

Среднее значение оценки

Этот тип пояснения описывает, когда среднее значение показателя соотносится с суммой. Сравните, является ли среднее значение низким или высоким, или количество записей низким или высоким.

Это пояснение показывает: Среднее значение целевой меры для каждого значения измерения, используемого в исходной визуализации. Варианты исследования: Наведите указатель мыши на каждую полосу, чтобы просмотреть сведения о ней. Прокрутите, чтобы увидеть больше диаграммы. Щелкните значок «Открыть», чтобы просмотреть увеличенную версию визуализации. Следующие шаги анализа: Сравните, является ли среднее значение низким или высоким, или количество записей низким или высоким. Например, высока ли прибыль, потому что вы продали много товаров или потому что вы продали дорогие товары? Попробуйте выяснить, почему анализируемая оценка имеет значительно большее или меньшее среднее значение.

В этом примере среднее расстояние поездки в августе незначительно выше или ниже, чем в большинстве месяцев. Это говорит о том, что расстояние поездки в августе выше, потому что в августе было больше поездок, а не из-за того, что люди совершали более длительные поездки.

 

Внесение одного значения

Используйте это пояснение, чтобы понять состав значений записи, составляющих анализируемую метку.

Этот тип пояснения указывает, когда отдельное значение в невизуализируемом измерении может вносить вклад в совокупное значение анализируемой отметки. Невизуализированное измерение — это измерение, существующее в источнике данных, но не используемое в данный момент в представлении.

Это пояснение указывает, когда каждая базовая запись измерения имеет одинаковое значение или когда значение измерения выделяется, потому что многие или несколько записей имеют одно и то же значение для анализируемой метки.

Примечание .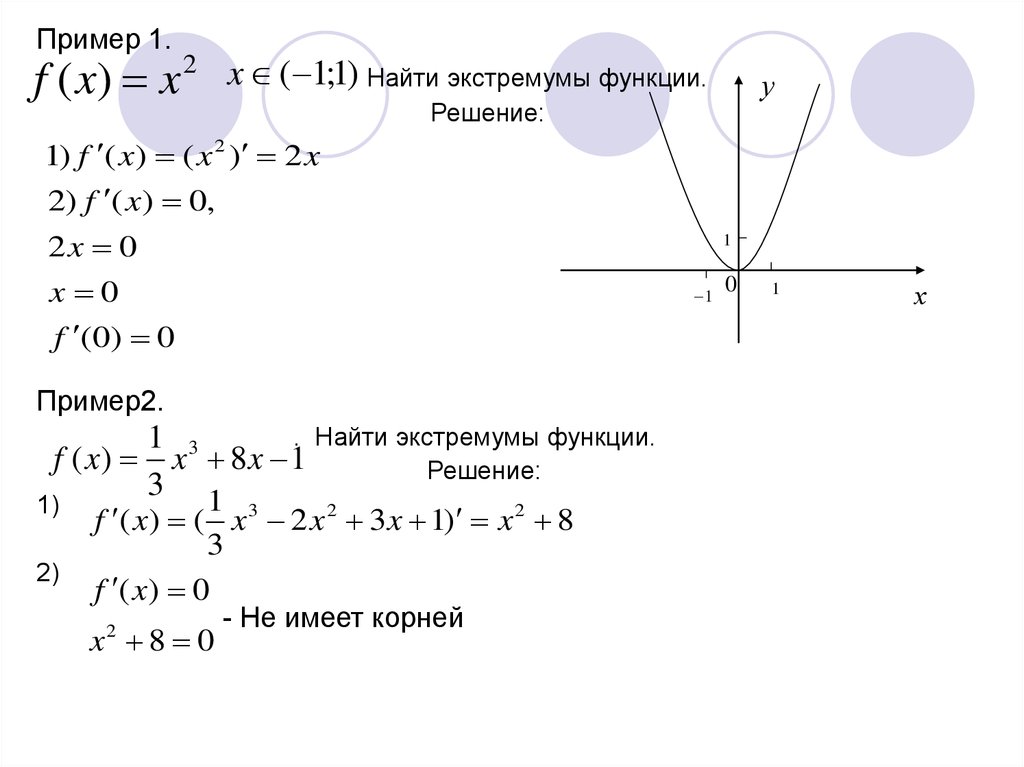  Определения общих терминов, используемых в пояснениях, см. в разделе Термины и понятия в пояснениях(ссылка откроется в новом окне).

Это пояснение показывает: Процент количества записей для одного значения измерения для анализируемой метки (синяя полоса) по сравнению со всеми метками (серая полоса) в исходной визуализации. Процент от количества записей для всех других значений измерения для анализируемой метки (синяя полоса) по сравнению со всеми метками (серая полоса) в исходной визуализации. Среднее значение целевого показателя для одного значения параметра в анализируемой метке (синяя полоса) по сравнению со всеми метками (серая полоса). Среднее значение целевой меры для всех других значений измерения для анализируемой метки (синяя полоса) по сравнению со всеми метками (серая полоса) в исходной визуализации. Варианты исследования: Наведите указатель мыши на каждую полосу, чтобы просмотреть сведения о ней. Щелкните значок «Открыть», чтобы просмотреть увеличенную версию визуализации. Следующие шаги анализа: Используйте это объяснение, чтобы понять состав значений записи, составляющих анализируемую метку. Авторы могут захотеть создать новую визуализацию для изучения любого невизуализированного измерения, всплывающего в этом объяснении.

В этом примере статистический анализ показал, что многие поездки осуществляются из района станции Бэк-Бэй. Обратите внимание, что Station Neighborhood — это невизуализированное измерение, которое имеет некоторую связь с Trip Distance в базовых данных для исходной визуализации.

 

Сопутствующие измерения

Используйте это объяснение, чтобы понять состав значений записи, составляющих анализируемую метку.

Этот тип объяснения показывает, что распределение невизуализированного параметра может влиять на совокупное значение анализируемой отметки. Этот тип объяснения используется для целевых сумм мер, подсчетов и средних значений. Невизуализированное измерение — это измерение, существующее в источнике данных, но не используемое в данный момент в представлении.

Примечание . Определения общих терминов, используемых в пояснениях, см. в разделе Термины и понятия в пояснениях(ссылка откроется в новом окне).

Это пояснение показывает: Процент количества записей для всех значений измерения для анализируемой метки (синяя полоса) по сравнению со всеми значениями измерения для всех меток (серая полоса) в исходной визуализации. Среднее целевого показателя для всех значений измерения для анализируемой метки (синяя полоса) всех значений измерения для всех меток (серая полоса). Варианты исследования: Наведите указатель мыши на каждую полосу, чтобы просмотреть сведения о ней. Прокрутите, чтобы увидеть больше диаграммы. Щелкните значок «Открыть», чтобы просмотреть увеличенную версию визуализации. Следующие шаги анализа: Используйте это объяснение, чтобы понять состав значений записи, составляющих анализируемую метку. Авторы могут захотеть создать новую визуализацию для изучения любых невизуализированных измерений, всплывающих в этом объяснении.

В этом примере статистический анализ показал, что больше поездок было совершено из Южного вокзала и Массачусетского технологического института, а меньше — из Чарльза Серкла и Кендалла, по сравнению с поездками, взятыми для оценки в целом. Обратите внимание, что название станции является невизуализированным измерением, которое имеет некоторое отношение к расстоянию поездки в базовых данных для исходной визуализации.

 

Сопутствующие показатели

Этот тип объяснения показывает, что среднее значение невизуализированного показателя может вносить вклад в совокупное значение анализируемой оценки. Невизуализированная мера — это мера, существующая в источнике данных, но не используемая в данный момент в представлении.

Это объяснение может выявить линейную или квадратичную зависимость между невизуализируемым показателем и целевым показателем.

Примечание . Определения общих терминов, используемых в пояснениях, см. в разделе Термины и понятия в пояснениях(ссылка откроется в новом окне).

Это пояснение показывает: Связь между суммой целевого показателя и средним значением невизуализированного показателя для анализируемой метки (синий кружок) и всех меток (серые кружки) в представлении. Если сумма целевого показателя высокая или низкая, поскольку среднее значение невизуализированного показателя высокое или низкое. Варианты исследования: Наведите указатель мыши на каждый кружок, чтобы увидеть его детали. Щелкните значок «Открыть», чтобы просмотреть увеличенную версию визуализации. Следующие шаги анализа: Авторы могут захотеть создать новую визуализацию для изучения любых невизуализированных мер, встречающихся в этом объяснении.

В этом примере одной из возможных причин большого расстояния поездки является то, что среднее общее время аренды также велико.

Другие вещи для изучения

В этом разделе приведены возможные причины того, почему анализируемый знак является уникальным или необычным. Эти объяснения:

• Не объясняйте, почему значение этого знака такое, какое оно есть.
• Никоим образом не связаны со значением мер в исходной визуализации.
• Не учитывать никаких целевых показателей.

Другие интересующие параметры

Используйте это объяснение, чтобы понять состав значений записи, составляющих анализируемую метку.

Распределение невизуализируемого измерения в анализируемой метке необычно по сравнению с распределением значений для всех других меток в представлении. Невизуализированное измерение — это измерение, существующее в источнике данных, но не используемое в данный момент в представлении.

Примечание . Определения общих терминов, используемых в пояснениях, см. в разделе Термины и понятия в пояснениях(ссылка откроется в новом окне).

Это пояснение показывает: Процент количества записей для всех значений измерения для анализируемой метки (синяя полоса) по сравнению со всеми значениями измерения для всех меток (серая полоса) в исходной визуализации. Варианты исследования: Наведите указатель мыши на каждую полосу, чтобы просмотреть сведения о ней. Прокрутите, чтобы увидеть больше диаграммы. Щелкните значок «Открыть», чтобы просмотреть увеличенную версию визуализации. Следующие шаги анализа: Используйте это объяснение, чтобы понять состав значений записи, составляющих анализируемую метку. Авторы могут захотеть создать новую визуализацию для изучения любых невизуализированных измерений, всплывающих в этом объяснении.

В этом примере высокий процент записей связан с пасмурной погодой. Поскольку данные относятся к аренде велосипедов в Бостоне, а анализируемая отметка — расстояние поездки за август, мы можем предположить, что погода обычно теплая и влажная. Люди могли чаще брать велосипеды напрокат в пасмурные дни, чтобы избежать жары. Также возможно, что в августе было больше пасмурных дней. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт