Разность двух углов 25 градусов: РЕШИТЕ СРОЧНО ПРОШУРазность двух углов 25градусов. Доказать, что эти углы не могут быть вертикальными….

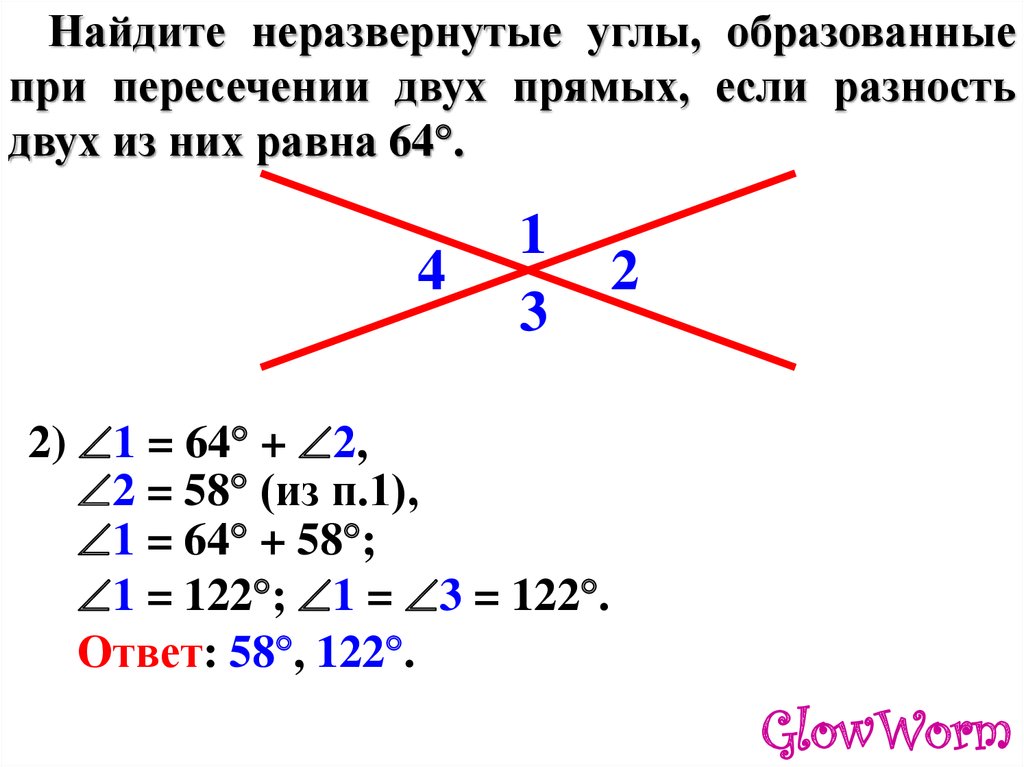
2) разность двух углов 10 градусов. докажите, что эти углы не могут быть вертикальными. — Школьные Знания.net

• Все предметы

• Математика

• Литература

• Алгебра

• Русский язык

• Геометрия

• Английский язык

• Физика

• Биология

• Другие предметы

• История

• Обществознание

• Окружающий мир

• География

• Українська мова

• Информатика

• Українська література

• Қазақ тiлi

• Экономика

• Музыка

• Беларуская мова

• Французский язык

• Немецкий язык

• Психология

• Оʻzbek tili

• Кыргыз тили

• Астрономия

• Физкультура и спорт

Ответ дан

sharofat0

Ответ:

Теорема о вертикальных углах.

Объяснение:

По этой теореме вертикальные углы равны, следовательно их разность равна 0.Так как по условию разность заданных углов 10° , то они не могут быть вертикальными.

Ответ дан

nikitagorkovoi1

Ответ:Вертикальные углы имеют одну общую вершину и стороны одного угла являются лучами, противоположными сторонам другого. Вертикальные углы равны ==их разность равна нулю. Значит, если разность двух углов 25 градусов, они не могут быть вертикальными

Объяснение:

Итоговый тест по геометрии за 7 класс

Итоговый тест по геометрии 7

Цель работы: выявление уровня сформированности предметных результатов по геометрии за 7 класс.

Содержание работы определяется на основе требований Федерального государственного образовательного стандарта основного общего образования. Контрольно-измерительные материалы позволяют осуществить диагностику достижения предметных и метапредметных результатов обучения.

Работа рассчитана на учащихся 7 класса средних общеобразовательных учреждений.

Работа состоит из 13 заданий.

В заданиях 1, 2, 7, 8, 9, 10, 13 необходимо записать краткое решение и ответ. В заданиях 3-6, 11, 12 нужно записать ответ и краткое объяснение.

На выполнение экзаменационной работы отводится 60 минут.

№ 1. Найдите угол 2, если угол 1 равен 67 о. Запишите решение и ответ.

№ 2. Найдите углы 2 и 3, если угол 1 равен 129 о. Запишите решение и ответ.

№ 3. Прямая а пересекает стороны угла А в точках P и Q. Могут ли обе прямые AP и AQ быть перпендикулярными к прямой а? Объясните почему.

№ 4. По рисунку укажите равные треугольники. Объясните почему.

№ 5. Известно, что в треугольнике MNK и треугольнике PHS : MN = PH, угол N равен углу H, угол M равен углу S. Равны ли эти треугольники? Объясните ответ.

№ 6. Известно, что AB = EF, BC = FK, AC = EK. Будут ли равны треугольники ABC и FKE? Ответ объясните.

№ 7.Треугольник PQF – равнобедренный с основанием PQ. Найдите углы P и F, если угол Q равен 32 о.

№ 8. Дан равнобедренный треугольник ABC. Известно, что AB =5 см, BD =3см. Найдите периметр треугольника ABC.

№ 9. Прямые a и b параллельны. Найдите углы 2,3,4, если угол 1 равен 47 о.

№ 10. В треугольнике ABC проведена биссектриса AL, угол ALB равен 102°, угол ACB равен 52°. Найдите угол ABC. Ответ дайте в градусах.

№ 11. Может ли существовать треугольник со сторонами 3, 5, 9? Ответ объясните.

№ 12. В треугольнике ABC : угол A равен 40 о, угол B =50 о. Верно ли, что сторона AC – наименьшая? Объясните свой ответ.

№ 13. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены три точки: A, B и C. Найдите расстояние от точки B до прямой AC.

№ 1. Найдите угол 1, если угол 2 равен 167 о. Запишите решение и ответ.

№ 2. Найдите углы 2 и 3, если угол 1 равен 153 о. Запишите решение и ответ.

№ 3. Прямая а пересекает стороны угла С в точках E и F. Могут ли обе прямые CF и CE быть перпендикулярными к прямой а? Объясните почему.

№ 4. По рисунку укажите равные треугольники. Объясните почему.

№ 5. Известно, что в треугольнике MNK и треугольнике PHS : MN = PH, MK = PH, угол N равен углу H. Равны ли эти треугольники? Объясните ответ.

№ 6. Известно, что AB = FK, BC = FE, AC = KE. Будут ли равны треугольники ABC и FKE? Ответ объясните.

№ 7.Треугольник PQF – равнобедренный с основанием PQ. Найдите углы P и Q, если угол F равен 32 о.

№ 8. Дан равнобедренный треугольник ABC. Известно, что A С=6 см, BD =5см. Найдите периметр треугольника ABC.

№ 9. Прямые a и b параллельны. Найдите углы 1,2,3, если угол 4 равен 58 о.

№ 10. В треугольнике ABC проведена биссектриса AL, угол ALC равен 84°, угол ABC равен 54°. Найдите угол ACB. Ответ дайте в градусах.

№ 11. Может ли существовать треугольник со сторонами 12, 5, 9? Ответ объясните.

№ 12. В треугольнике ABC : угол A равен 30 о, угол B равен 56 о. Верно ли, что сторона A В – наибольшая? Объясните свой ответ.

№ 13. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены три точки: A, B и C. Найдите расстояние от точки C до прямой AB.

Ответ объясните.

Xn—j1ahfl. xn--p1ai

18.12.2018 21:27:29

2018-12-18 21:27:29

Источники:

Https://xn--j1ahfl. xn--p1ai/library/itogovij_test_po_geometrii_za_7_klass_195346.html

Итоговый контрольный тест по геометрии за курс 7 класса » /> » /> .keyword { color: red; }

Итоговый тест по геометрии 7

На выполнение теста дается 45 минут. Работа состоит из двух частей, включающих в себя 14 заданий.

Часть 1 содержит 12заданий с кратким ответом базового уровня по материалу курса геометрии. Ответом является целое число или конечная десятичная дробь.

Часть 2 содержит 2 более сложных задания по материалу курса геометрии. При их выполнении надо записать полное обоснованное решение и ответ.

При выполнении работы разрешается использовать линейку, циркуль.

Использование калькулятора не допускается.

Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо только указать его номер.

За каждое правильно выполненное задание части1 выставляется 1 балл. Задания части 2 расположены по нарастанию сложности и оцениваются в 2 и 3 балла соответственно.

Максимальное количество баллов: 17.

Критерии оценивания: «5» — 13 -17 баллов

«4» — 10 -12 баллов

«2» — менее 6 баллов

· Для заданий с выбором ответа из четырех предложенных вариантов выберите один верный

· Для заданий с кратким ответом полученный ответ запишите в указанных единицах измерений.

1. Через точку, не лежащую на прямой, можно провести …

1) две прямые, параллельные данной прямой

2) только одну прямую, параллельную данной

3) ни одной прямой, параллельной данной

4) множество параллельных прямых

2. На луче с началом в точке А отмечены точки В и С. АВ = 19,2 см, АС=12,4 см.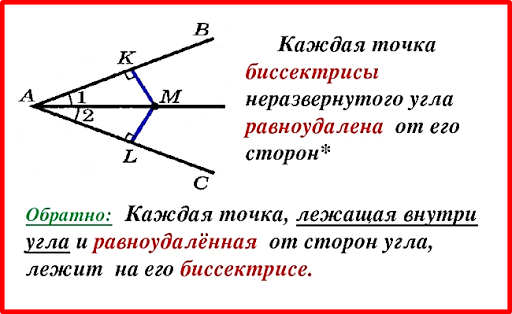 Чему равен отрезок ВС?

1. 6,8 см 2. 5,8 см 3. 31,6 см 4. Недостаточно условий

3. Точка М делит отрезок АВ на две части, одна из которой на 12 см больше другой. Найдите длину большей части, если длина отрезка АВ равна 60 см.

1. 24 см 2. 36 см 3. 42 см 4. другой ответ

4. Один из смежных углов в 5 раз больше другого. Найдите больший угол.

1. 144 0 2. 36 0 3. 30 0 4. 150 0

5. Периметр равнобедренного треугольника равен 36 см, а его основание 10 см. Найдите длину боковой стороны треугольника.

1. 26 см 2. 13 см 3. 20 см 4. Недостаточно условий

6. По данным рисунка ответьте на следующий вопрос: в какой из указанных пар углы являются соответственными?

1. 1 и 4 2. 1 и 5 3. 4 и 6 4. 4 и 5

7. С какими из предложенных измерений сторон может существовать треугольник?

1. 10 см, 6 см, 8 см 2. 70 см, 30 см, 30 см

3.60 см, 30 см, 20 см 4. 30 см, 30 см, 80 см

8. Выберите верное утверждение.

1. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны

2.Каждая сторона треугольника меньше суммы двух других сторон

3.Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны

4.Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны

9. В треугольнике АВС угол С равен 90 0 , угол А равен 60 0 , АС= 8 см. Найдите АВ.

10. Прямые M и N параллельны. Найдите ∠ 3 , если ∠ 1 =48 0 , ∠ 2 = 57 0 . Ответ дайте в градусах.

11. В треугольнике ABC проведена биссектриса AL , угол LАC равен 24 0 , угол ABC равен 54 0 . Найдите угол ACB . Ответ дайте в градусах.

12. В треугольнике ABC BM – медиана и BH – высота. Известно, что AC = 84 и BC = BM . Найдите AH .

Ответ_____________

При выполнении заданий 13 и 14 укажите полное решение.

13. Два острых угла прямоугольного треугольника относятся как 4 : 5. Найдите больший острый угол. Ответ дайте в градусах.

14. В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 143 0 . Найдите величину угла АВС. Ответ дайте в градусах.

· Для заданий с выбором ответа из четырех предложенных вариантов выберите один верный

· Для заданий с кратким ответом полученный ответ запишите в указанных единицах измерений

1. Через две любые точки А и В можно провести:

1. только две прямые 2.только одну прямую

3. ни одной прямой 4. множество прямых

2. На луче с началом в точке М отмечены точки В и С. МВ = 18,2 см, МС=9,4 см. Чему равен отрезок ВС?

1. 8,8 см 2. 9,8 см 3. 27,6 см 4. Недостаточно условий

3. Точка М делит отрезок АВ на две части, одна из которой на 8 см меньше другой. Найдите длину меньшей части, если длина отрезка АВ равна 54 см.

1. 19 см 2. 31 см 3. 23 см 4. другой ответ

4. Один из смежных углов в 9 раз больше другого. Найдите больший угол.

1. 162 0 2. 20 0 3. 18 0 4. 160 0

5. Периметр равнобедренного треугольника равен 46 см, а его боковая сторона 17 см. Найдите длину основания треугольника.

1. 29 см 2. 12 см 3. 14,5 см 4. Недостаточно условий

6. По данным рисунка ответьте на следующий вопрос: в какой из указанных пар углы являются односторонними?

1. 1 и 4 2. 1 и 5 3. 4 и 6 4. 4 и 5

7. С какими из предложенных измерений сторон может существовать треугольник?

1. 10 см, 6 см, 8 см 2. 7 см, 3 см, 3 см

1. 54 см, 30 см, 20 см 4. 40 см, 40 см, 90 см

8. Выберите верное утверждение.

1.Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны

2.Каждая сторона треугольника больше суммы двух других сторон

3.Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны

4. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны

9. В треугольнике АВС угол С равен 90 0 , угол А равен 60 0 , АВ= 18 см. Найдите АС.

10. Прямые M и N параллельны. Найдите ∠ 3 , если ∠ 1 =56 0 , ∠ 2 = 49 0 . Ответ дайте в градусах.

11. В треугольнике ABC проведена биссектриса AL , угол В АL равен 26 0 , угол ACB равен 61 0 . Найдите угол ABC . Ответ дайте в градусах.

12. В треугольнике ABC BM – медиана и BH – высота. Известно, что AC = 76 и BC = BM . Найдите AH .

Ответ: ________________

При выполнении заданий 13 и 14 укажите полное решение.

13. Разность двух острых углов прямоугольного треугольника равна 20 0 . Найдите больший острый угол. Ответ дайте в градусах.

14. В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине А равен 138 0 . Найдите величину угла АВС.

Ответ дайте в градусах.

Ответ: ________________

Ответ_____________

Разность двух острых углов прямоугольного треугольника равна 20 0.

Infourok. ru

21.10.2020 23:56:18

2020-10-21 23:56:18

Источники:

Https://infourok. ru/itogovyj-kontrolnyj-test-po-geometrii-za-kurs-7-klassa-4277425.html

Итоговый тест по геометрии за курс 7 класса » /> » /> .keyword { color: red; }

Итоговый тест по геометрии 7

Г) если две стороны и угол между ними одного треугольника равны двум сторонам и углу другого треугольника, то такие треугольники равны.

7. Если прямые параллельны, то внутренние односторонние…

А) углы равны; б) углы в сумме дают 180 ° ;

В) стороны равны; г) углы в сумме дают 90 ° .

8. Треугольник называется прямоугольным, если у него…

А) один угол острый; б) два угла прямые;

В) два угла острые; г) один угол прямой.

9. Сторона равнобедренного треугольника, отличная от двух других сторон называется…

А) боковой стороной; б) гипотенузой;

В) основанием; г) катетом.

10. Сумма углов треугольника равна…

А) 90 ° ; б) 180 ° ; в) 360 ° ; г) нет правильного ответа.

11. D MPK = D PMN (см. рисунок) по …, если Ð KMP = Ð NPM.

А) гипотенузе и катету; б) катету и острому углу;

В) двум катетам; г) гипотенузе и острому углу.

12. Найдите третий угол треугольника, если два его угла 36 ° и 57 ° .

А) 36 ° ; б) 57 ° ; в) 93 ° ; г) 87 ° ; д) нет правильного ответа.

13. Найдите углы при основании равнобедренного треугольника, если угол при вершине равен 38 ° .

А) 71 ° и 71 ° ; б) 38 ° и 76 ° ; в) 38 ° и 104 ° ; г) нет правильного ответа.

14. Прямые параллельны, если равны…

А) вертикальные углы; б) внутренние накрест лежащие углы;

В) соответственные углы; г) внутренние односторонние углы.

15. Начертите две пересекающиеся прямые AB и CD в точке О. Ð BOC и … вертикальные углы.

А) Ð COA ; б) Ð AOD ; в) Ð DOB ; г) нет правильного ответа.

16. Точка С принадлежит отрезку АВ. Чему равна длина отрезка АВ, если АС=3,4 см, ВС=1,5 см. а ) 1,9 б) 7,2 в) 6,1 г) 4,9

17. Найдите острый угол прямоугольного треугольника, если другой острый угол равен 69 ° .

А) 21 ° ; б) 69 ° ; в) 90 ° ; г) 180 ° ; д) нет правильного ответа.

18. Известны стороны равнобедренного треугольника: 4 см и 1 см. Чему равен его периметр? А) 5 б) 6 в) 9 г) 14

19. Сколько прямых можно провести через одну точку? А) 1 б) 2 в) 3 г) бесконечно много

20. Каждая сторона треугольника:

А) Равна сумме двух других его сторон;

Б) больше суммы двух других его сторон;

В) меньше или равна сумме двух других его сторон;

Г) меньше суммы двух других его сторон.

21. Угол — это геометрическая фигура, которая состоит:

А) из точки и пересекающихся лучей;

Б) из точки и двух лучей, исходящих из этой точки;

В) из точки и двух прямых, проходящих через эту точку;

Г) из двух пересекающихся прямых.

22. Отрезок – это:

А) часть прямой;

Б) часть прямой, ограниченная двумя точками;

В) часть прямой, на которой отмечены две точки;

Г) прямая, имеющая начало и конец.

23. Биссектриса угла – это луч, который:

А) делит угол пополам;

Б) исходит из вершины угла и проходит между его сторонами;

В) исходит из вершины угла и проходит во внутренней области угла;

Г) исходит из вершины угла и делит его на два равных угла.

24. Треугольник – это геометрическая фигура, состоящая:

А) из трех точек, не лежащих на одной прямой, и трех отрезков, их соединяющих;

Б) из трех точек и трех отрезков, их соединяющих;

В) из трех отрезков;

Г) из трех точек и трех отрезков.

25. Две прямые на плоскости называются параллельными, если они:

А) перпендикулярны одной прямой;

Б) находятся на одинаковом расстоянии друг от друга;

В) не пересекаются на данном чертеже;

Г) не пересекаются.

26. Один из признаков параллельности прямых двух прямых гласит:

А) если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;

Б) если при пересечении двух прямых секущей сумма соответственных углов равна 180 градусов, то прямые параллельны;

В) если при пересечении двух прямых секущей односторонние углы равны, то прямые параллельны;

Г) если при пересечении двух прямых секущей вертикальные углы равны, то прямые параллельны;

27. Внешний угол треугольника:

А) это угол, градусная мера которого равна сумме градусных мер двух углов треугольника;

Б) это угол, который расположен вне данного треугольника;

В) это угол, смежный с каким-нибудь углом этого треугольника;

Г) это угол, который равен сумме двух других углов.

28. В треугольнике:

А) Против большего угла лежит меньшая сторона;

Б) против большей стороны лежит больший угол;

В) против меньшего угла лежит большая сторона;

Г) против большей стороны лежит тупой угол.

29. Для доказательства равенства треугольников АВС и NКМ достаточно доказать, что…

А) С = К;

Б) С = М;

В) В = М.

30. Для доказательства равенства треугольников АВС и КМР достаточно доказать, что…

Тест по геометрии за курс 7 класса

Фамилия, имя _____________________________________ класс _______

Вариант № 2

Продолжите предложения:

Два угла называются смежными, если…

А) у них одна сторона общая, а две другие являются продолжениями одна другой;

Б) их сумма равна 180 ° ;

В) они равны;

Г) стороны одного угла являются продолжениями сторон другого.

А) часть прямой;

Б) часть прямой, ограниченная двумя точками;

В) часть прямой, на которой отмечены две точки;

Г) прямая, имеющая начало и конец.

Середина отрезка – это:

А) точка, которая принадлежит данному отрезку;

Б) точка, которая делит данный отрезок на части;

В) точка отрезка, делящая его пополам;

Г) точка, равноудаленная от концов отрезка.

4. Если сумма двух углов равна 180 ° , то:

А) эти углы смежные; б) эти углы вертикальные;

В) эти углы перпендикулярные; г) нельзя определить.

5. Периметр треугольника – это:

А) длина всех его сторон; б) сумма длин всех его сторон;

В) сумма длин всех отрезков; г) произведение всех его сторон.

6. Второй признак равенства треугольника гласит:

А) если сторона и два прилежащих к ней угла одного треугольника равны стороне и двум углам другого треугольника, то такие треугольники равны;

Б) если сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны;

В) если сторона и прилежащий к ней угол одного треугольника соответственно равны стороне и прилежащему к ней углу другого треугольника, то такие треугольники равны;

Г) если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

7. Диаметр окружности – это:

А) отрезок, равный двум радиусам;

Б) отрезок, соединяющий две точки окружности;

В) хорда, проходящая через центр окружности;

Г) отрезок, проходящий через центр окружности.

8. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:

А) смежные и вертикальные; б) острые, прямые и тупые;

В) параллельные и перпендикулярные;

Г) накрест лежащие, соответственные и односторонние.

9. Расстоянием от точки до прямой называется:

А) длина отрезка, проведенного из данной точки к данной прямой;

Б) длина перпендикуляра, проведенного из данной точки к прямой;

В) расстояние от данной точки до какой-нибудь точки данной прямой;

Г) длина отрезка, соединяющего данную точку с какой-нибудь точкой данной прямой.

10. . Вертикальные углы изображены на рисунке…

11. Для сторон данного треугольника справедливо равенство…

1) M = K ; 2) K = 2 N ; 3) N = M .

12. Найдите третий угол треугольника, если два его угла 35 ° и 97 ° .

А) 35 ° ; б) 97 ° ; в) 48 ° ; г) 132 ° ; д) нет правильного ответа.

13. Найдите угол при вершине равнобедренного треугольника, если угол при основании равен 52 ° .

А) 76 ° ; б) 104; в) 100 ° ; г) нет правильного ответа.

14. Аксиома – это:

А) положение геометрии, требующее обоснований;

Б) положение геометрии, не требующее доказательства;

В) положение геометрии, имеющее следствие;

Г) положение геометрии, обратное к которому верно.

15. Начертите две пересекающиеся прямые AB и CD в точке О. Ð D О B и … вертикальные углы.

А) Ð COA ; б) Ð AOD ; в) Ð DOB ; г) нет правильного ответа.

16. Точка С принадлежит отрезку АВ. Чему равна длина отрезка АВ, если АС=4,4 см, ВС=10,5 см. а ) 6,1 б) 7,2 в) 14,9 г) 4,9

17. Найдите острый угол прямоугольного треугольника, если другой острый угол равен 52 ° .

А) 38 ° ; б) 52 ° ; в) 90 ° ; г) 180 ° ; д) нет правильного ответа.

18. Известны стороны равнобедренного треугольника: 6 см и 3 см. Чему равен его периметр? А)15 б) 8 в) 15 г) 12

20. В треугольнике:

А) Против большего угла лежит прямой угол;

Б) против большей стороны лежит тупой или прямой угол;

В) против меньшего угла лежит большая сторона;

Г) против меньшего угла лежит острый угол.

21. Прямоугольные треугольники равны, если:

А) Гипотенуза и угол одного треугольника равны гипотенузе и углу другого треугольника;

Б) два угла одного треугольника равны двум углам другого треугольника;

В) гипотенуза и катет одного треугольника равны гипотенузе и катету другого треугольника;

Г) катет и угол одного треугольника равны катету и углу другого треугольника.

25. Угол называют тупым, если его градусная мера:

А) меньше 90 градусов; б) больше 90 градусов, но меньше 180;

В) меньше развернутого угла; г) больше прямого угла.

26. Если две параллельные прямые пересечены третьей, то:

А) сумма накрест лежащих углов равна 180 ° ;

Б) односторонние углы равны;

В) сумма односторонних углов равна 180 ° ;

Г) сумма соответственных углов равна 180 ° .

27. Выберите верное утверждение:

А) через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, параллельные данной;

Б) если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;

В) если две прямые параллельны третьей, то они пересекаются;

Г) если прямая пересекает одну из двух прямых, то она пересекает и другую.

28. Один из признаков параллельности прямых двух прямых гласит:

А) если при пересечении двух прямых секущей сумма смежных углов равна 180 ° , то прямые параллельны;

Б) если при пересечении двух прямых секущей сумма накрест лежащих углов равна 180 ° , то прямые параллельны;

В) если при пересечении двух прямых секущей односторонние углы равны, то прямые параллельны;

Г) если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

29. Для доказательства равенства треугольников АPK и DCE достаточно доказать, что…

а) АР = CD ; б) AP = DE ; в) AP = CE .

30. Из равенства треугольников АРК и MFN следует, что…

а) АК = MF ; б) AK = MN ; в) A = M .

1) M = K ; 2) K = 2 N ; 3) N = M .

а) АР = CD ; б) AP = DE ; в) AP = CE .

При пересечении двух прямых секущей образуются углы, имеющие специальные названия.

Infourok. ru

07.08.2019 1:45:16

2019-08-07 01:45:16

Источники:

Https://infourok. ru/itogovyj-test-po-geometrii-za-kurs-7-klassa-6159443.html

Как решить треугольник, если вы знаете две меры угла

Если вы знаете две величины угла и длину стороны треугольника, вы можете использовать Закон синусов, чтобы найти недостающие части треугольника. В этом случае вам нужно знать либо два угла и сторону между ними (угол-сторона-угол, или ASA), либо два угла и последовательную сторону (угол-угол-сторона, или AAS).

Если у вас есть два угла, вы можете сразу же найти третий и работать с ним. В обоих этих случаях можно найти ровно одно решение для рассматриваемого треугольника.

Решение треугольника с помощью ASA

Треугольник ASA означает, что в задаче даны два угла и сторона между ними. Например, в задаче может быть указано, что

, как показано на рисунке. Вам также могут дать

На этой фигурке промаркированы все заданные и неизвестные части.

Маркированный треугольник ASA.

Чтобы найти недостающую информацию с помощью закона синусов, выполните следующие действия:

1. Определите меру третьего угла.

   Как правило,

   Итак, подставив в эту задачу то, что вы знаете об углах, вы можете найти недостающий угол:

2. Составьте формулу закона синусов, введя то, что вы знаете.

   Учитывая, что формула закона синусов выглядит так:

   формула здесь выглядит так:

3. Приравняйте дробь с неизвестным числителем и дробь с известным числителем и перемножьте их.

   Если использовать, скажем, первую и третью дроби, уравнение будет выглядеть так:

   Умножение креста, у вас есть

4. Найдите десятичную аппроксимацию отсутствующей стороны с помощью калькулятора.

   Поскольку sin 101 градус — это просто число, вы можете разделить на него обе части уравнения, чтобы выделить переменную:

5. Повторите шаги 3 и 4, чтобы найти другую отсутствующую сторону.

   Приравняв вторую и третью дроби друг к другу, вы получите следующее уравнение:

   Это уравнение становится

   при перекрестном умножении. Изолируйте переменную и решите для нее:

6. В качестве окончательного ответа укажите все части треугольника.

   Некоторые ответы могут быть приблизительными, поэтому убедитесь, что вы используете правильные знаки:

Решение треугольника с помощью AAS

Во многих задачах на триггеры вам даны два угла и сторона, которая не находится между ними. Этот тип проблемы называется проблемой AAS. Например, вам могут дать

, как показано на этом рисунке.

Маркированный треугольник AAS.

Обратите внимание, что если вы начнете со стороны b и будете двигаться против часовой стрелки вокруг треугольника, вы придете к

.

Эта проверка — хороший способ проверить, является ли треугольник примером AAS.

После того, как вы найдете третий угол, задача AAS станет частным случаем ASA. Вот шаги для решения:

1. Определите меру третьего угла.

   Можно сказать, что

2. Составьте формулу закона синусов, введя то, что вы знаете.

3. Установите одну дробь с неизвестным числителем и дробь с известным числителем равными друг другу, а затем перемножьте.

   Скажите, что вы решили использовать a и b:

   Умножение креста, у вас есть

4. Найдите недостающую сторону.

   Делишь на грех 68 градусов, значит

5. Повторите шаги 3 и 4, чтобы найти другую отсутствующую сторону.

   Установив b и c равные друг другу, у вас есть это уравнение:

   Перекрестное умножение:

   Разделите на sin 68 градусов, чтобы изолировать переменную и решить:

6. В качестве окончательного ответа укажите все части треугольника.

   Ваш окончательный ответ выглядит следующим образом:

Об этом артикуле

Этот артикул можно найти в категории:

• Предварительное исчисление ,

Один из углов треугольника равен 130, а два других угла равны Какова мера каждого…

Перейти к

• Свойства треугольника. Упражнение 15.1.
• Свойства треугольника. Упражнение 15. 2.
• Свойства треугольника. Упражнение 15.3.
• Свойства треугольника. Упражнение 15.4.
• Свойства треугольника. Упражнение 15.5.

• Целые числа
• Фракции
• Десятичные
• Рациональное число
• Операции над рациональными числами
• Экспоненты
• Алгебраические выражения
• Линейные уравнения с одной переменной
• Соотношение и пропорция
• Унитарный метод
• Процент
• Доходы и расходы
• Простой интерес
• Линии и углы
• Свойства треугольника
• Конгруэнтность
• Конструкции
• Симметрия
• Визуализация твердых фигур
• Измерение 1
• Измерение 2 Площадь круга
• Данные организации по обработке и сбору данных
• Обработка данных — основные ценности
• Обработка данных — построение гистограмм
• Обработка данных-вероятность

Главная > РД Шарма Решения Класс 7 Математика > Глава 15. Свойства треугольника > Свойства треугольника. Упражнение 15.2. > Вопрос 2

Вопрос 2 Свойства треугольника Упражнение 15.2

Один из углов треугольника равен 130, а два других угла равны. Какова мера каждого из этих равных углов?

Ответ:

Учитывая, что один из углов треугольника равен 130

Также учитывая, что оставшиеся два угла равны

Итак, пусть второй и третий углы равны х

Мы знаем, что сумма всех углов треугольника = 180

130 + х + х = 180

130 + 2x = 180

2x = 180 – 130

2x = 50 x = 50/2 x = 25

Therefore the two other angles are 25 degree each

Video transcript

hello everybody welcome чтобы узнать лидера, я раджна чаудхари, и мы собираемся решить этот вопрос, мы можем видеть, что написано, что один из углов треугольника равен 130 градусам, и два угла равны, какова мера каждого из этих равных углов, поэтому мы известно, что первый угол равен 130 градусов, а остальные два угла равны, поэтому пусть второй и третий углы равны x, поэтому второй и третий углы оба должны быть равны, поэтому x теперь мы знаем, что сумма всех углов треугольника равна 180 градусов согласно к свойству суммы углов, поэтому 130 плюс x плюс x должно быть равно 180, поэтому 130 плюс 2x равно 180 2x равно 180 минус 130 сдвиг, поэтому 130 имеет знак минус, когда мы сдвинули его вправо, теперь 2x равно 50 градусов теперь x равно 50 разделить на 2, что равно 2 5, так что у нас есть значение x, которое было вторым и третьим углом, поэтому второй и третий углы равны 25 градусам каждый, так что это ответ на вопрос, я надеюсь, вы понимаете метод, увидимся в моем следующем видео и не не забудьте лайкнуть комментарий и подписаться на канал обучения лидеров, спасибо

Связанные вопросы

Два угла треугольника имеют размеры 150 градусов и 30 градусов. Найдите градус третьего угла…

Три угла треугольника равны друг другу. Какова мера каждого из углов?

Если углы треугольника относятся как 1:2:3, определите три угла

Углы треугольника равны (х — 40) ⁰ , (х — 20) ⁰ и (1/2 — 10) ⁰ . Найдите значение х.

Углы треугольника расположены в порядке возрастания величины. Если разница между двумя…

Два угла треугольника равны, а третий угол больше каждого из этих углов на 30 градусов…

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Свойства упражнения треугольник 15.