Комплексные числа и функции
Комплексные числа имеют геометрическую интерпретацию как точки на плоскости или двумерные векторы.
Комплексная плоскость
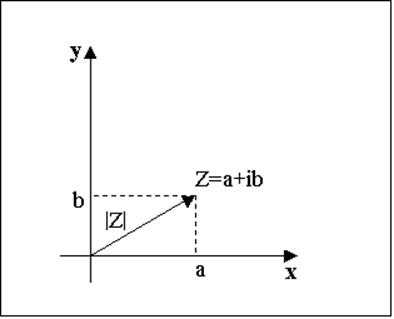
Рассмотрим плоскость и прямоугольную систему координат на ней. Ось абсцисс обозначим $\operatorname{Re} z$ и будем называть действительной осью, а ось ординат обозначим $\operatorname{Im} z$, будем называть мнимой осью. Каждому комплексному числу $z=x+iy$ сопоставим точку на этой плоскости с координатами $(x,y)$, и, другими словами, радиус-вектор с координатами $(x,y)$.
Заметим, что соответствие между комплексными числами и точками на комплесной плоскости является взаимнооднозначным соответствием (а в случае с вещественными числами, соответствие строится с точкам на вещественной прямой).
Модуль комплексного числа $z=x+iy$ равен длине вектора, соответствующего данному числу на комплексной плоскости, $$|z|= \sqrt{x^2+y^2}.$$ Несложно проверить, что расстояние между двумя точками комплексной плоскости $z_1$ и $z_2$ равно $|z_1-z_2|$. То есть, модуль разности двух комплексных чисел есть расстояние между точками на комплексной плоскости, которым соответствуют этим числам.
Определение.
Аргументом комплексного числа $z=x+iy$ называется угол $\varphi$ между вектором $(x,y)$
и положительным направлением действительной оси $\operatorname{Re} z$ измеряемый против хода часовой стрелки.
Аргумент числа $z$ обозначается $\operatorname{Arg} z$.
Строго говоря, аргумент комплексного числа определен не однозначно, в общем виде аргумент можно записать как
$$
\operatorname{Arg} z = \arg z + 2\pi k ,\text{ где } k\in\mathbb Z,
$$
где $\arg z$ — главное значение аргумента
Единственное комплексное число, для которого значение аргумента не определяют, это $z=0$.
Впрочем, это также единственное число, у которого модуль равен нулю, поэтому неопределённость аргумента в данном случае не является проблемой.
Также можно отметить: для действительных чисел $\arg z=0$, если число положительное, и $\arg z = \pi$, если число отрицательное.
Геометрически сложение чисел $z_1$ и $z_2$ производится по правилу сложения векторов (по правилу параллелограмма).
СуммаРазность $z_1-z_2$ представляется вектором, конец которого находится в точке $z_1$, а начало — в точке $z_2$.
РазностьГеометрический смысл умножения на мнимую единицу $i$ состоит в повороте на угол $\pi/2$. Действительно, пусть $z=x+iy$, тогда $i\cdot z = -y + ix$. Преобразование $(x,y)\mapsto(-y,x)$ — это поворот вектора $(x,y)$ на $\pi/2$ против часовой стрелки.
Умножение комплексного числа $z=x+iy$ на комплексную экспоненту $e^{i\theta}$ соответстует повороту на угол $\theta$ против часовой стрелки.
Комплексным сопряжением числа $z$ на комплексной плоскости является вектор, симметричный вектору $z$, относительно оси абсцисс.
В качестве несложного упражнения, изобразите как на комплексной плоскости будет выглядеть вектор $-z$.
Пример 1. Зафиксируем $z_0\in\mathbb C$ и $r\in\mathbb R$, $r>0$. Изобразить на комплексной плоскости множество точек, соответствующих комплексным числам $z$, которые удовлетворяют условиям: $$ 1) \ |z-z_0|=r, \quad 2) \ |z-z_0|\leqslant r. $$
Решение.
1) Пусть $z=x+iy$ и $z_0=x_0+iy_0$. Распишем модуль комплексного числа $|z-z_0|$ по определению: \begin{multline*} |z-z_0| = |x+iy — (x_0+iy_0)| =\\ |x-x_0 + i(y-y_0)|= \sqrt{(x-x_0)^2 + (y-y_0)^2}. \end{multline*} Тогда равенство $|z-z_0|=r$ равносильно \begin{equation*} \sqrt{(x-x_0)^2 + (y-y_0)^2} = r \quad \text{ или } \quad (x-x_0)^2 + (y-y_0)^2 = r^2. \end{equation*} В свою очередь, уравнение $(x-x_0)^2 + (y-y_0)^2 = r^2$ задаёт окружность с центром в точке $(x_0,y_0)$ и радиусом $r$.
Окружность2) Рассуждая аналогичным образом, приходим к выводу, что неравенство $|z-z_0|\leqslant r$ равносильно неравенству $(x-x_0)^2 + (y-y_0)^2 \leqslant r^2$, которое задаёт круг.
КругПример 2. Исходя из геометрических рассуждений, доказать неравенство \begin{equation*} \left|\frac{z}{|z|}-1\right| \leqslant \arg z. \end{equation*}
Решение.
Число $\frac{z}{|z|}$ находится на единичной окружности. Построим на комплексной плоскости вектор, соответствующий разности $\frac{z}{|z|} — 1$.
Длина дуги больше длины отрезкаДлина дуги единичной окружности, соединяющей точки $1$ и $\frac{z}{|z|}$, равна $\arg z$ и не может быть меньше длины отрезка соединяющего эти точки.
Тригонометрическая форма записи
Пусть $z=x+iy$ и $\varphi = \operatorname{Arg} z$, тогда \begin{equation}\label{eq:cossin} \cos\varphi = \frac{x}{\sqrt{x^2+y^2}}, \quad \sin\varphi = \frac{y}{\sqrt{x^2+y^2}}. \end{equation} Обозначим $\rho = \sqrt{x^2+y^2}$. Из \eqref{eq:cossin} выводим \begin{equation}\label{eq:ReIm} \operatorname{Re} z = x = \rho\cos\varphi \quad\text{ и }\quad \operatorname{Im} z = y = \rho\sin\varphi. \end{equation} В итоге из \eqref{eq:ReIm} имеем \begin{equation}\label{eq:trig_forma} z = \rho(\cos\varphi+i\sin\varphi). \end{equation}
Запись \eqref{eq:trig_forma} называется тригонометрической формой комплексного числа, где $\rho=|z|$, а $\varphi = \operatorname{Arg} z$.
Например, найдём число $z=1+i$ в тригонометрической форме.
Данное число $z$ на комплексной плоскости является вектором с координатами $(1,1)$.
Вектор направлен по диагонали единичного квадрата, и поэтому угол $\varphi=\pi/4$.
Длина вектора (модуль $z$) $\rho = \sqrt{1+1} = \sqrt{2}$.
Таким образом,
$$z=\sqrt{2}(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4}).$$
Задачи
1. $z=1-i$. Найти $|z|$ и $\arg z$.
Ответ.$|z|=\sqrt{2}$, $\arg z = \frac{7\pi}{4}$.
2. Пусть $|z|=2$ и $\arg z = \frac{\pi}{6}$. Представить $z$ в виде $x+iy$.
Ответ.3. Найти геометрическое место точек $z$ на комплексной плоскости, которые удовлетворяют соотношению $|z-i| + |z+i| = 16$.
Ответ.Эллипс с фокусами в точках $-i$ и $i$, каноническое уравнение $\frac{x^2}{63}+\frac{y^2}{64} =1$.
4. Представить $z=\sqrt{3}+i$ в тригонометрической форме.
Ответ.$z = 2(\cos\frac{\pi}{6} + i\sin\frac{\pi}{6})$.
5. Представить $z=-2+i2\sqrt{3}$ в тригонометрической форме.
Ответ.$z=4(\cos2\pi/3+i\sin2\pi/3)$.
6. Вычислить $(1+\sqrt{3}i)^9$.
Ответ.7. Вычислить $(1+\cos\theta+i\sin\theta)^n$, где $n\in\mathbb N$.
Ответ.$\left(2\cos\frac{\theta}{2}\right)^n\cdot\left(\cos\frac{n\theta}{2} + i\sin\frac{n\theta}{2}\right)$.
www.phys.nsu.ru
Изображение комплексных чисел и областей на плоскости
Для изображения комплексного числа на плоскости необходимо построить точку с координатами (x; y), где x и y соответственно равны действительной и мнимой частям
заданного комплексного числа. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось Ox называется действительной осью ,а ось Oy
— мнимой осью.
Пример 1. Изобразить на комплексной плоскости числа z1 = 1 — 3i, z2 = 4 + i, z3 = 5, найти их модули и аргументы.
Согласно теоретической сноске выше, имеем, что числу z1 = 1 — 3i соответствует точка с координатами (1; -3), z2 = 4 + i — точка (4; 1), а комплексному числу z3 = 5 соответствует точка с координатами (5; 0).
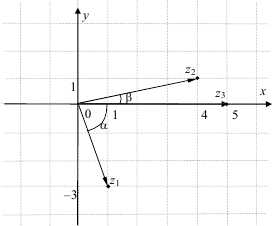
Комплексные числа можно отобразить просто точками, а можно сделать по-другому, как в данном примере, изобразить радиус-вектором точки с началом в точке О.
Длина этого вектора называется модулем числа z и обозначается |z|. По определению, модуль комплексного числа:
где x и y соответственно действительная и мнимая части комплексного числа.
Найдем модули и аргументы для каждого заданного числа (см. рисунок)
Ответ:
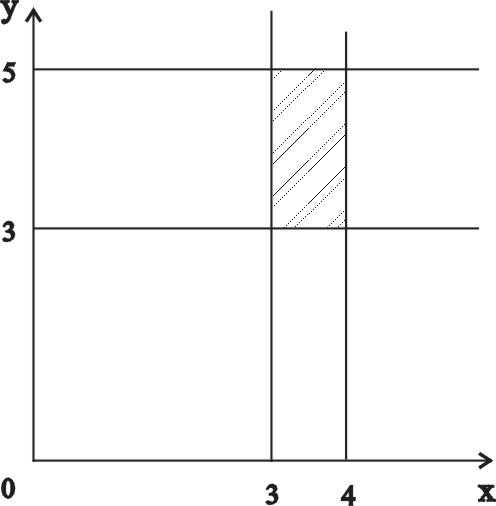
Пример 2. Найти и построить на комплексной плоскости области, которым принадлежат точки z = x + iy, удовлетворяющие условию 2 ≤ Re(z + 1) ≤ 4.
Преобразуем заданное неравенство: 2 ≤ Re(x + 1 + iy) ≤ 4.
Поскольку выражение Re (x + 1 + iy) определяет действительную часть числа, записанного в скобках, то можно перейти к следующему неравенству: 2 ≤ x + 1 ≤ 4. Или: 1 ≤ x ≤ 3.
Таким образом, условие 2 ≤ Re(z + 1) ≤ 4 определяет на комплексной плоскости область, множество точек (x; y) которой, удовлетворяют системе:
matematyka.ru
Области в комплексной плоскости | Математика
Рассмотрим задачи на нахождение областей в комплексной плоскости, заданных неравенствами. Чтобы решить данные неравенства с комплексными числами, вначале необходимо перейти к декартовым координатам, т.е. перейти к действительному представлению.
Чтобы представить комплексное число в действительной форме, нужно заменить комплексную переменную z действительными переменными
x = Re(z), y = Im(z).
Пример 1. Найти на комплексной плоскости множество точек, удовлетворяющих неравенству
|z + i| < 2.
Решение неравенства с комплексными числами начинается с представления числа в действительной форме. Неравенство примет вид:
или
Для того, чтобы избавиться от ограждающего знака модуля, используют стандартную замену:
или
Как мы знаем из начальных уроков, |z| это модуль комплексного числа, х — действительная часть комплексного числа, y — это мнимая часть комплексного числа, которая находится в связке с мнимой единицей. Итоговый ответ, область решения — это часть плоскости, расположенная внутри круга
Пример 2. Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству
Заменяем переменную z представлением в действительной форме z = x + iy, приводим подобные члены, берем действительную часть от получившегося комплексного числа и
приводим к стандартному виду получившееся комплексное число:
Областью решения неравенства
является плоскость, расположенная выше прямой у = 1. Рисунок не прикрепляю, все просто — чертим прямую у = 1 и штрихуем область выше этой прямой.
Чтобы изобразить область, заданную несколькими неравенствами, нужно изобразить области, задаваемые отдельными неравенствами, а затем найти их общую часть.
Пример 3. Построить область, заданную неравенствами
Вначале, заменяем z=x+iy, затем группируем подобные члены, чтобы сформировать действительное представление комплексного числа.
Первое неравенство задает внешнюю часть окружности радиуса 1 с центром в точке (-1; 0) с границей (белый круг). Второе неравенство задает внутреннюю часть окружности радиуса 1 с центром в точке
Сделаем рисунок в качестве графического доказательства. Область окружности, закрашенная зеленым цветом, является графическим ответом к решению заданного неравенства с комплексными числами:
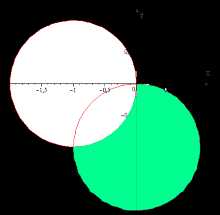
matematyka.ru
Множества на комплексной плоскости.
Для того, чтобы
правильно строить типичные кривые на
комплексной плоскости, прежде всего
надо помнить, что 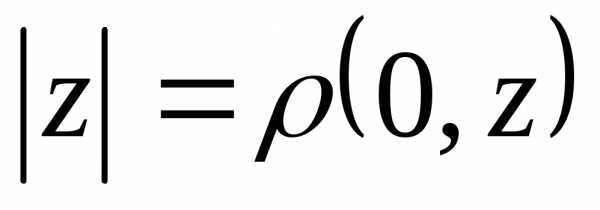 .
Следовательно,
.
Следовательно,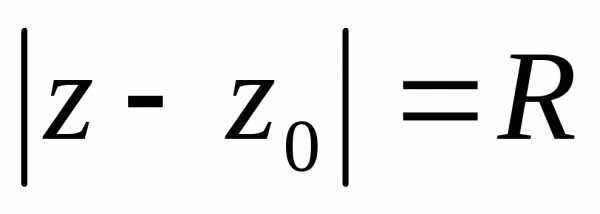 — это окружность радиуса
— это окружность радиуса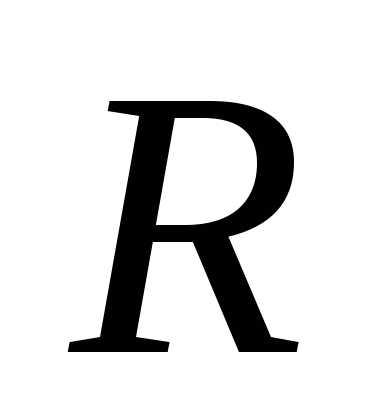
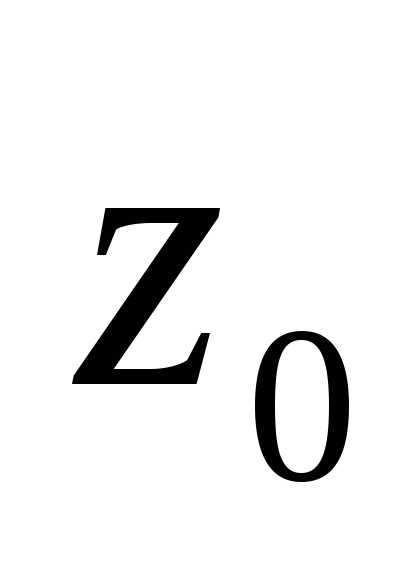 на комплексной плоскости (расстояние
от точки
на комплексной плоскости (расстояние
от точки до точки
до точки 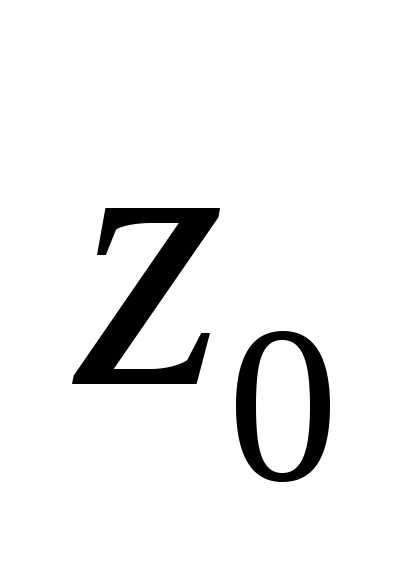 равно
равно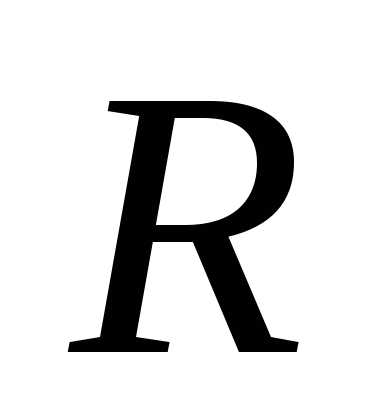 ).- это круговое кольцо с центром в точке
).- это круговое кольцо с центром в точке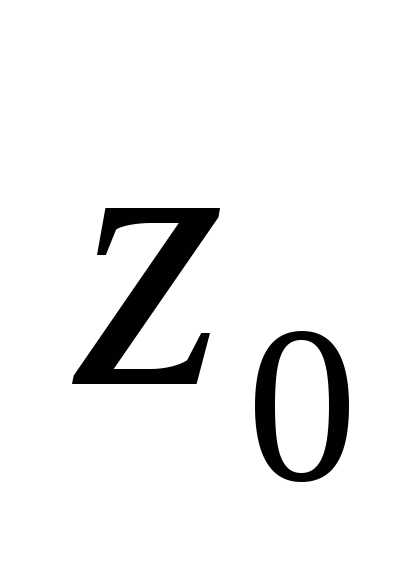 ,
включая внутреннюю окружность радиусом
,
включая внутреннюю окружность радиусом ,
исключая внешнюю окружность радиусом
,
исключая внешнюю окружность радиусом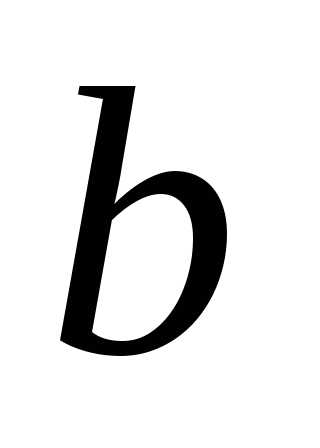 .
.— это прямая линия на комплексной плоскости,- угол наклона прямой к действительной оси. Некоторые часто встречающиеся кривые и области изображены ниже
|
|
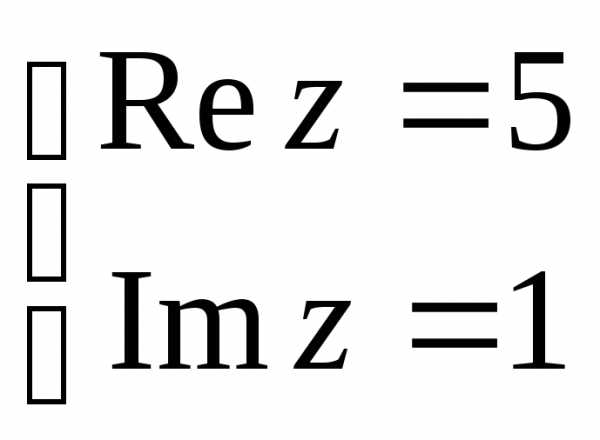
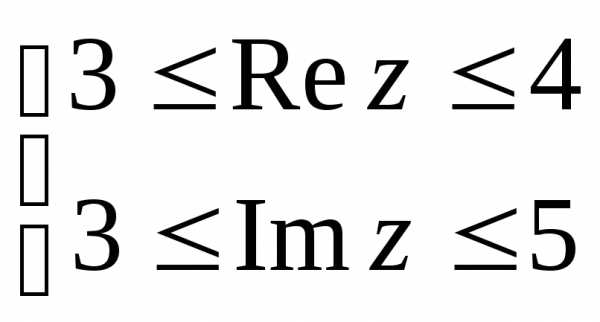
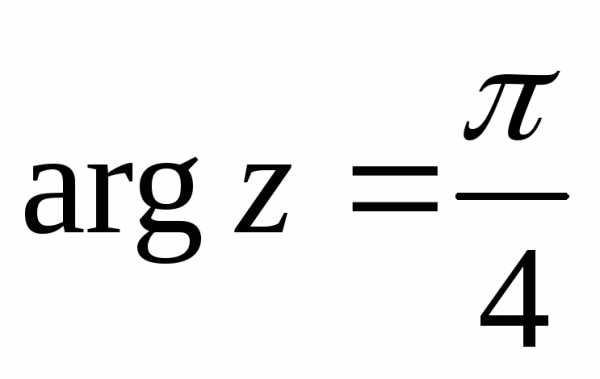
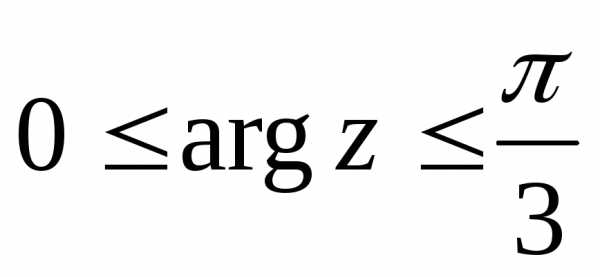
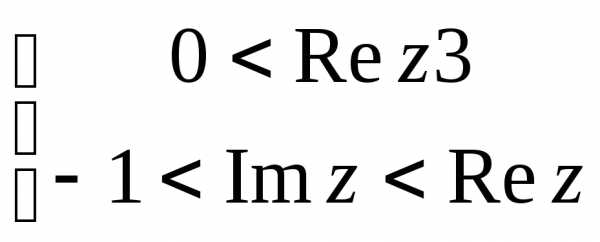
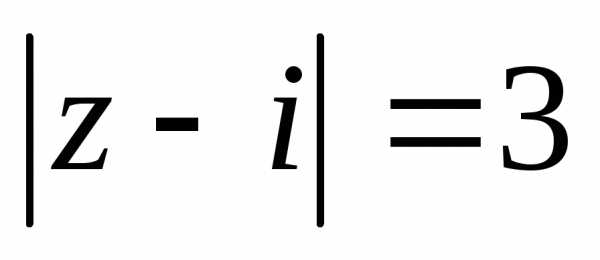
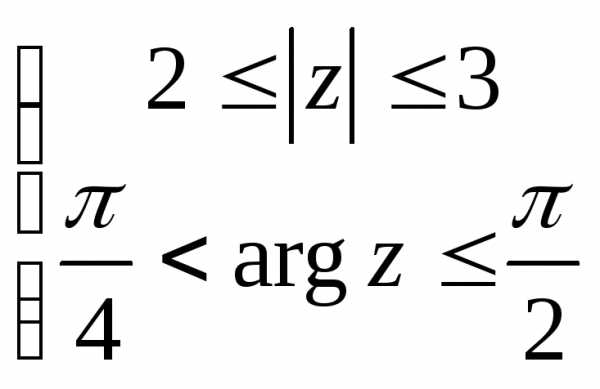
|
|
При построении двух последних
областей надо вспомнить определение
эллипса (геометрическое место точек
плоскости, сумма расстояний которых от
двух фиксированных точек плоскости 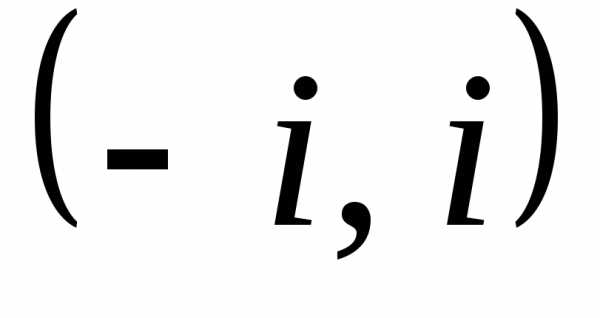 постоянна
и равна
постоянна
и равна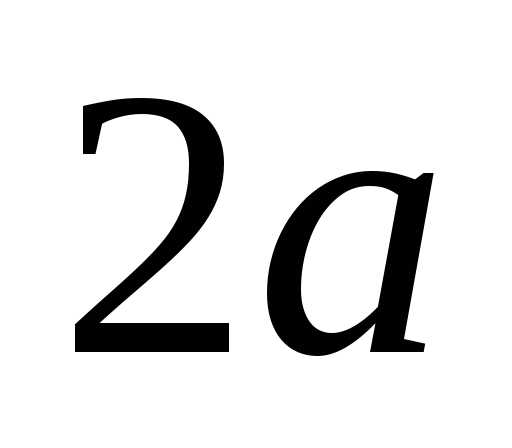 (
(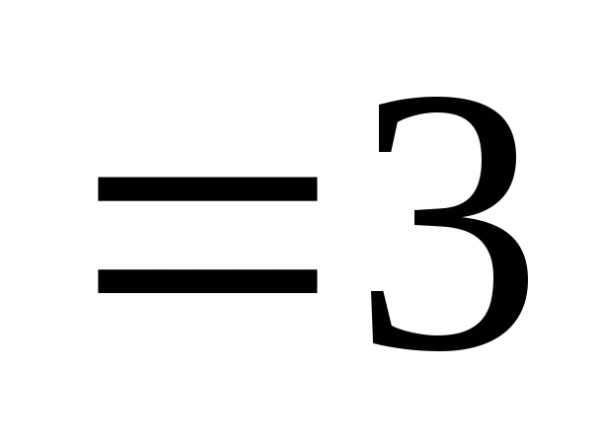 ))
и определение параболы (геометрическое
место точек плоскости, расстояние
которых от фиксированной точки плоскости
))
и определение параболы (геометрическое
место точек плоскости, расстояние
которых от фиксированной точки плоскости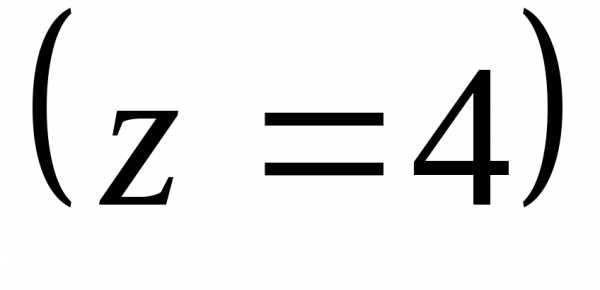 равно расстоянию до фиксированной
прямой
равно расстоянию до фиксированной
прямой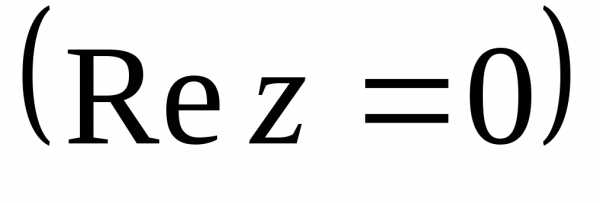 ).
).
Открытые и замкнутые множества, односвязное множество.
называется множество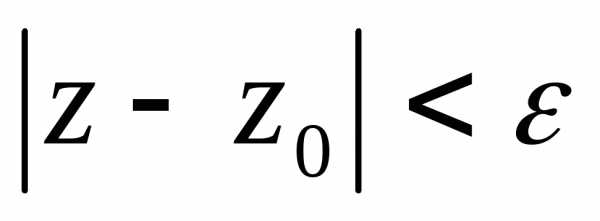
Точка  называетсявнутренней точкой множества,если существует ее окрестность, целиком
принадлежащая этому множеству. Например,
все точки круга
называетсявнутренней точкой множества,если существует ее окрестность, целиком
принадлежащая этому множеству. Например,
все точки круга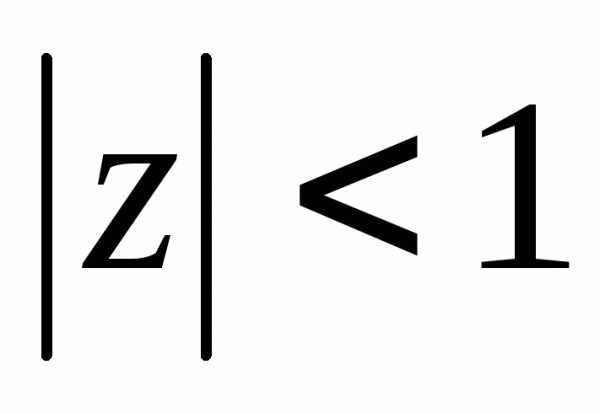 — внутренние.
— внутренние.
Точка 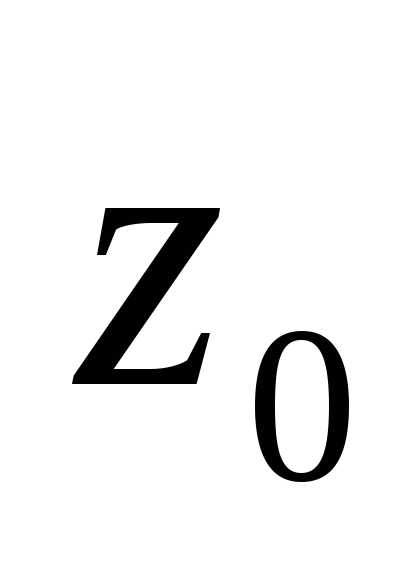 называетсяграничной точкой множества,
если в любой ее окрестности найдутся
как точки, принадлежащие множеству, так
и точки, не принадлежащие множеству.Границей множества называется
совокупность его граничных точек.
Например, окружность
называетсяграничной точкой множества,
если в любой ее окрестности найдутся
как точки, принадлежащие множеству, так
и точки, не принадлежащие множеству.Границей множества называется
совокупность его граничных точек.
Например, окружность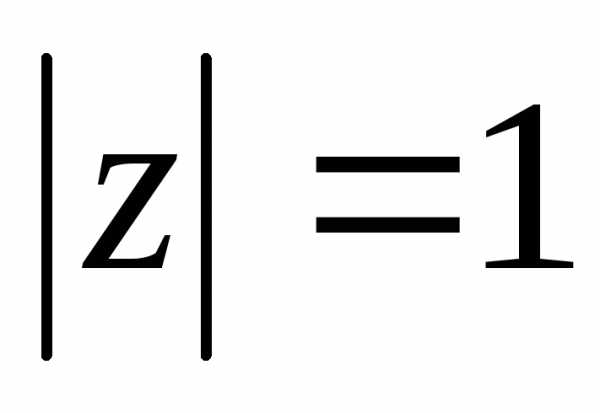 — граница круга
— граница круга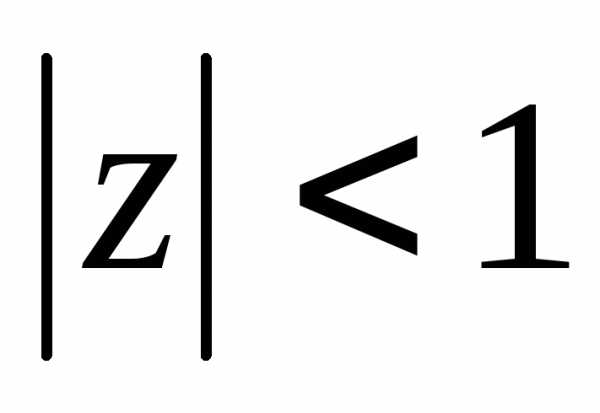 .
.
Множество
называется открытым, если оно состоит
только из внутренних точек. Например,
круг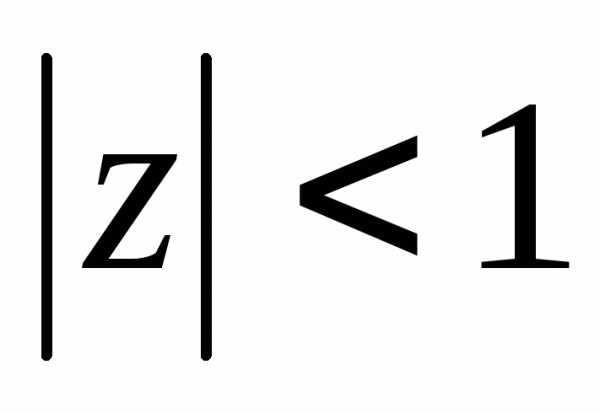
Замыканием множества называется объединение множества и его границы.Замкнутымназывается множество, совпадающее со своим замыканием.
Множество называется ограниченным,если его можно накрыть кругом конечного радиуса.
Открытой областью (или просто областью) называется открытое множество, любые две точки которого можно соединить ломаной, целиком принадлежащей множеству.
Замкнутой областью называется объединение открытой области и ее границы.
Рассмотрим последовательность комплексных чисел . Последовательность называетсянеограниченно возрастающей, если. То есть все элементы неограниченно возрастающей последовательности нельзя накрыть кругом конечного радиуса.
По определению полагают, что все неограниченно возрастающие последовательности сходятся к (единственной) бесконечно удаленной точке (или
Пояснить единственность бесконечно удаленной точки можно, рассматривая сферу Римана
| Сфера находится на комплексной
плоскости. Проведем прямую из верхней
точки сферы (ее северного полюса) в
какую-либо точку |
Кривой на
комплексной плоскости называется
однопараметрическое семейство точек
плоскости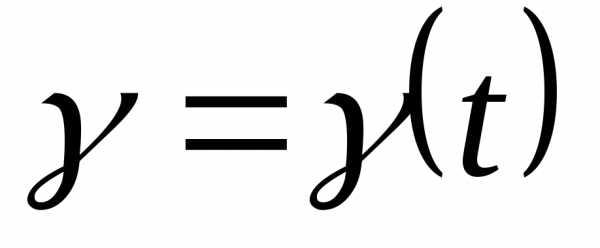 .Точкой самопересечения или кратной
точкой кривойназывается точка,
отвечающая двум или более значениям
параметра.
.Точкой самопересечения или кратной
точкой кривойназывается точка,
отвечающая двум или более значениям
параметра.
Кривая, не содержащая кратных точек, называется простой или жордановой кривой. Кривая называется замкнутой, если ее начало совпадает с ее концом.
Теорема Жордана. Любая замкнутая жорданова кривая делит расширенную комплексную плоскость на две области, общей границей которых она является. Одна из этих областей ограничена и называется внутренностью кривой. Вторая не ограничена и называется внешностью кривой.
Множество  называетсяодносвязным,если
для любой замкнутой кривой
называетсяодносвязным,если
для любой замкнутой кривой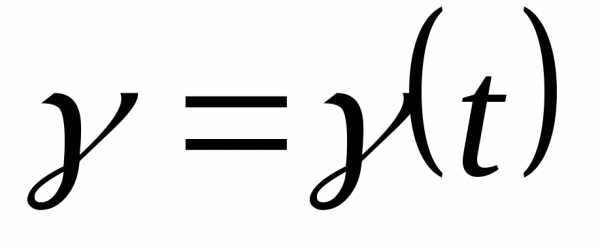
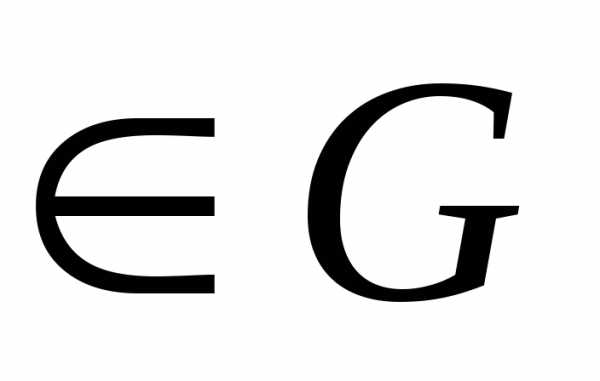 либо внутренность кривой принадлежит
либо внутренность кривой принадлежит ,
либо внешность кривой принадлежит
,
либо внешность кривой принадлежит .
Например, множества,
да и все изображенные на рисунках
области, за исключением кругового кольца-
односвязные, они «не содержат дыр».
.
Например, множества,
да и все изображенные на рисунках
области, за исключением кругового кольца-
односвязные, они «не содержат дыр».
studfiles.net
4. Множества точек на комплексной плоскости. задание геометрических м
При решении геометрических задач используется геометрический смысл модуля комплексного числа, его аргумента, геометрический смысл введенных алгебраических операций и пр. Приведем конкретные примеры.
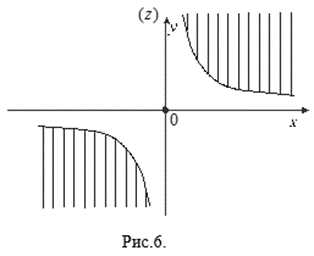
Пример 1. Какое множество точек на плоскости (z) определяется условием
Решение. Имеем и, стало быть, . По условию или . Последнее неравенство определяет множество точек в первом и третьем квадрантах, соответственно над и под гиперболой (см. рис.6).
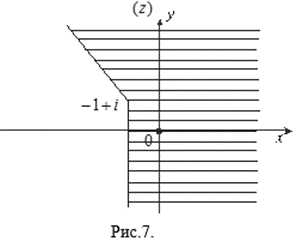
Пример 2. Какое множество точек на плоскости (Z) определяется условием ?
Решение. Комплексное число изображается вектором, началом которого является точка –1+I и концом – точка z. Угол между этим вектором и осью Ox есть , и он меняется в пределах от до . Следовательно, данное неравенство определяет угол между прямыми, выходящими из точки –1+ I и образующими с осью Ox углы в и
(рис.7).
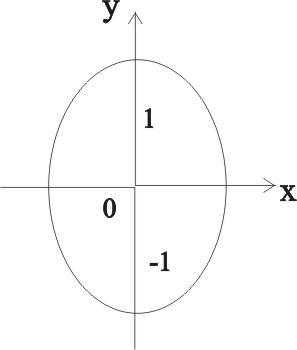
Пример 3. Какая кривая задается уравнением , где C и A – действительные положительные числа, причем A >C.
Решение. Модуль Есть расстояние между точками Z и – C; — расстояние между точками Z и C. По условию сумма расстояний от точки Z до двух данных точек —C и C есть величина постоянная. Значит, точка Z лежит на эллипсе. Уравнение этого эллипса имеет вид , где
(рис.8).
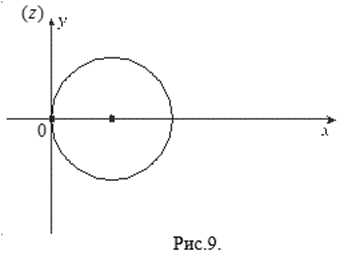
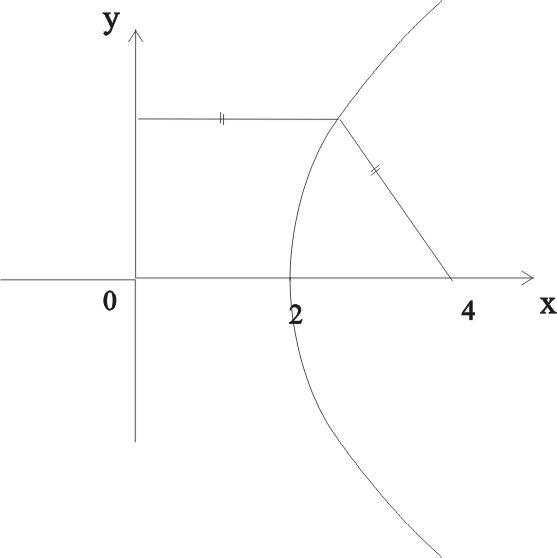
Пример 4. Какая кривая определяется уравнением ?
Решение. Имеем (см.(1.9)) . По условию или — это окружность (рис.9).
Пример 5. Написать в комплексной форме уравнение прямой .
Решение. Подставляя X и Y по формуле (1.9) в уравнение прямой, получим , или . Обозначив , получим уравнение: — уравнение прямой в комплексной форме.
Задачи для самостоятельного решения
1. Доказать следующие соотношения:
А) ; б) ; в) ; г) .
2. Найти:
А) ; б) ; в) ; г) ; д) .
3. Найти действительные решения уравнений:
А) ;
Б) , где A, B – заданные действительные числа, ;
В) .
4. Представить комплексное число в алгебраической форме.
5. Вычислить (X— действительное число).
6. Выделить X и Y через U и V (X,…,V – действительные числа), если .
7. Найти все числа, удовлетворяющие условию .
8. Решить системы уравнений:
А) б)
В) г)
9. Найти модуль и главное значение аргумента комплексного числа. Записать число в тригонометрической и показательной формах:
А) –2; б) 2I; в) ; г) –Z — I; д) 4-3I; е)
ж) ; з) ;
И) .
10. Вычислить:
А) ; б) ; в) ; г) ;
Д) .
11. Найти все значения корней:
А) ; б) ; в) ; г) ; д) ; е) ;
Ж) ; з) ; и); к) ; л) ; м) .
12. Решить квадратные уравнения:
А) ; б) ;
В) .
13. Решить уравнения:
А); б) ; в) ;
Г) ; д) .
14. Найти множества точек на плоскости (Z), определяемые заданными условиями:
А) ; б) ; в) ; г) ;
Д) ; е) ; ж) ;
з) .
15. Какие линии определяются следующими уравнениями:
А) ; б) ; в) ;
Г) ; д) ; е) ; ж) .
16. Написать в комплексной форме уравнение следующих линий:
А) координатных осей Ox и Oy; б) прямой Y = X; в) прямой , — действительные числа; г) гиперболы ; д) окружности .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Комплексные числа и комплексная плоскость
1. КОМПЛЕКСНЫЕ ЧИСЛА, КОМПЛЕКСНАЯ ПЛОСКОСТЬ
Поле комплексных чисел. . Напомним, что комплексными называют числа вида , где и – действительные числа, – мнимая единица. Число называется действительной частью комплексного числа, число – мнимой частью. Вводятся обозначения .
Для комплексных чисел определяют арифметические действия:
Если и , то
В частности, если , то . Если — действительное число, то . Иными словами с выражениями поступают как с многочленами с переменной , при этом считаем, что . В частности, два числа и считаются равными, если и .
Если (т. е. ), то существует обратное к число. Действительно, попробуем найти в виде . Тогда должно выполниться равенство
Вычисляя произведение, получим , откуда и .
В алгебре показывается, что множество комплексных числе с введенными операциями образует поле. Это, в частности, означает, что общие правила действий с комплексными числами такие же как и с вещественными. Это поле обозначается буквой С.
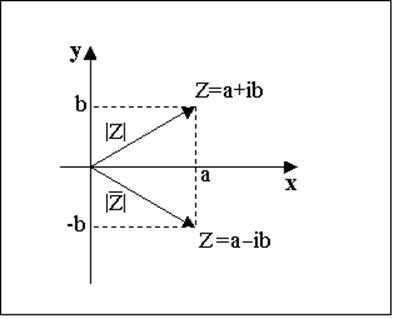
Кроме арифметических операций в С вводится операция сопряжения:
.
Легко проверяется, что и , .
Множество действительных чисел рассматривается как множество всех тех комплексных чисел, для которых мнимая часть равна нулю. Для таких комплексных числе действия совпадают с обычными арифметическими.
Заметим, что
(1.1)
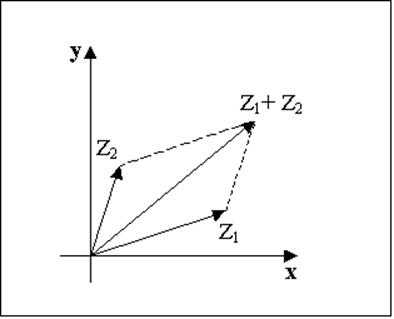
Комплексная плоскость. Комплексные числа естественно изображаются точками на плоскости. Если на плоскости выбрать прямоугольную систему координат и на оси абсцисс откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть, то этим устанавливается взаимно однозначное соответствие между комплексными числами и точками плоскости. Тем самым комплексному числу ставится в соответствие точка с абсциссой и ординатой . Точку плоскости можно еще описывать ее радиусом–вектором. Тогда становится ясным, что сложению комплексных чисел отвечает сложение радиусов-векторов, их изображающих.
Легко видеть также, что точки и симметричны относительно оси абсцисс. Ось абсцисс теперь естественно называть действительной осью, поскольку на оси абсцисс лежат вещественные числа.
Плоскость, точки которой отождествлены с комплексными числами, называется комплексной плоскостью. Обозначается она также, как поле комплексных чисел через С.
Тригонометрическая форма комплексного числа. Комплексное число иногда удобно записывать в следующей форме
,
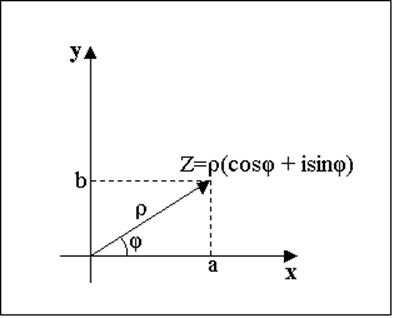
где вещественное число строго большее нуля, а некоторое вещественное число. Такая форма записи называется тригонометрической.
Величина в силу периодичности функции и определяется с точностью до целого кратного . Она называется аргументом комплексного числа. Иногда, чтобы подчеркнуть многозначность, ее обозначают через , иногда пишут , помня, что она определяется с точностью до слагаемого вида , где — целое.
Из равенства
и (1.2)
следует, что . Это число называется модулем комплексного числа и обозначается . Геометрически модуль комплексного числа представляет собой расстояние от начала координат до точки с координатами и , то есть длину радиуса-вектора, изображающего на плоскости число
Равенство (1.1) теперь означает, что . Формулу для числа, обратного к можно записать в виде .
Модуль обладает свойствами:
1. (неравенство треугольника)
2.
3. .
Свойства 1 и 3 геометрически очевидны, как только мы изобразим комплексные числа точками плоскости. Обоснование свойства 2 дается ниже.
Рассмотрим вопрос о том, у всякого ли комплексного числа есть тригонометрическая форма и сколькими способами можно записать число в этой форме?
Если на плоскости ввести систему полярных координат , то, как известно из курса аналитической геометрии, декартовы координаты и выражаются через полярные координаты по формулам
,
следовательно, любое комплексное число имеет вид
Значит и . Иными словами аргумент комплексного числа -это угол, образованный радиусом-вектором, идущим из начала координат в точку а модуль – это длина этого радиуса-вектора. То есть для отыскания тригонометрической формы достаточно найти полярные координаты соответствующей точки на комплексной плоскости. Так как для начала координат (нуля) вторая полярная координата (угол) не определяется, то тригонометрическая форма нулевого комплексного числа не рассматривается.
Если каким–то образом получены две тригонометрические формы одного числа, то есть
то очевидно . Поэтому, сокращая равные между собой и , получим
,
или
Из тригонометрии известно, что отсюда следует
для некоторого целого.
Таким образом разные тригонометрические формы могут отличаться только своими аргументами, причем разные аргументы отличаются на слагаемое кратное .
Для чего нужна тригонометрическая форма?
Пусть и Тогда
Таким образом при перемножении комплексных числе их модули перемножаются, а аргументы складываются:
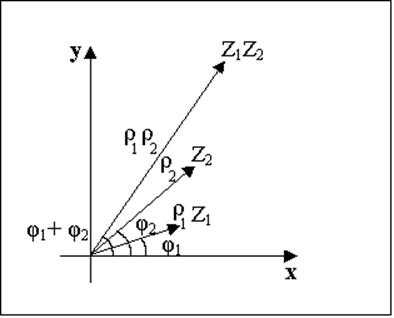
(последнее равенство понимается с точностью до слагаемого , где целое).
В частности, при возведении числа в целую положительную степень, аргумент умножается на показатель степени:
Частным случаем этого равенства при является замечательная формула Муавра
(1.3)
Извлечение корней из комплексных чисел. Корнем -ой степени из комплексного числа называется решение уравнения
. (1.4)
Основное преимущество от введения комплексных чисел состоит в том, что во множестве комплексных числе это уравнение всегда имеет решение, чего как известно, не было, когда мы находились во множестве вещественных чисел. Например, извлечь корень из отрицательного числа во множестве вещественных чисел невозможно. Покажем как можно решить уравнение (1.4).
Если , то решение, очевидно, равно нулю.
Если , рассмотрим число в тригонометрической форме Тогда
и поэтому
и
для некоторого целого
Следовательно, . Поэтому решение уравнения (1.4) равно
где — любое целое число. На первый взгляд получается бесконечное множество корней, соответствующих бесконечному множеству целых чисел . На самом же деле, как известно, при разных числа вида
повторяются при разных , и получается ровно различных комплексных корней вида
при
В частности при получается ровно два корня.
Множества на комплексной плоскости. Если и – точки на комплексной плоскости, то расстояние между ними равно длине вектора, соединяющего и , то есть расстояние между ними равно .
Окрестностью точки радиуса называется множество всех для которых . Геометрически такая окрестность является открытым кругом с центром в и радиусом . В дальнейшем окрестность точки радиуса будем обозначать через .
Множество называется открытым, если каждая его точка входит в него вместе с некоторой окрестностью. Дополнение к открытому множеству называется замкнутым.
Открытое множество называется связным, если две любые его точки можно соединить ломаной, целиком лежацей в этом множестве.
Открытое связное множество называется областью. Это понятие является основным для всего курса.
Области часто описываются с помощью неравенств.
ПРИМЕРЫ
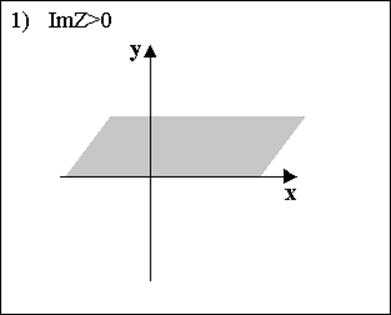
1. Im z > 0 — верхняя полуплоскость без вещественной оси.
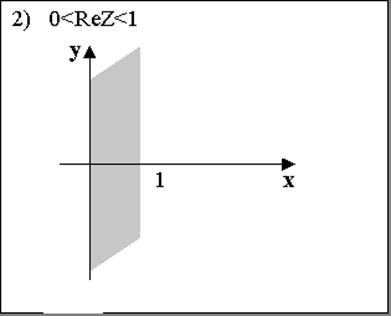
2. 0 < Re z < 1 — вертикальная бесконечная полоса, лежащая между прямыми x = 0 и x = 1, не включая эти прямые.
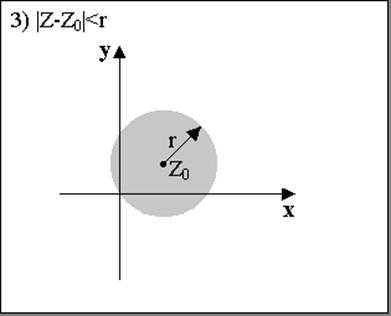
3. |z — z0| < r — внутренность круга радиусом r с центром в z0.
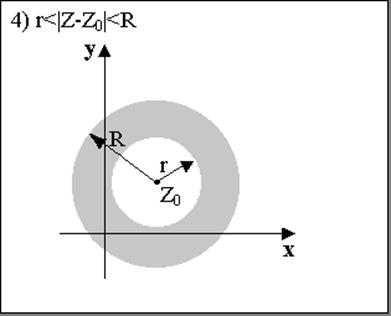
4. — внутренность кольца между окружностями и .
5. — внутренность прямого угла, биссектриса которого совпадает с положительной полуосью .
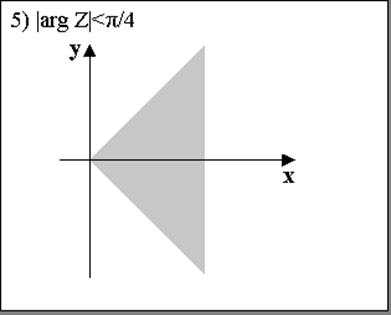
Множество называется ограниченным, если существует такое число , что при всех . Геометрически это означает, что множество лежит внутри некоторого круга с центром в начале координат. Из всех перечисленных выше примеров только круг из примера 3 является ограниченным множеством.
matematiku5.ru
Комплексная плоскость | Математика, которая мне нравится
Рассмотрим координатную плоскость и поставим в соответствие каждому комплексному числу точку с координатами . Тогда устанавливается взаимно однозначное соответствие между полем и множеством точек координатной плоскости. Координатную плоскость в этом случае будем называть комплексной плоскостью. Ось абсцисс будем называть вещественной осью, а ось ординат — мнимой осью.
С каждой точкой комплексной плоскости можно связать вектор, идущий из нуля в эту точку (радиус-вектор). Координаты этого вектора — вещественная и мнимая части его конца.
Радиус-вектор числа равен сумме радиус-векторов чисел и .
Аналогично с вычитанием.

Полярная система координат
Выберем в плоскости точку (полюс) и луч с началом в точке (полярную полуось). Тогда положение любой точки плоскости , отличной от точки , однозначно характеризуется двумя числами: длиной отрезка (полярный радиус точки ) и величиной угла, образованного лучом с полярной полуосью (полярный угол точки ). При этом полярный угол отсчитывается в некотором фиксированном направлении, одном и том же для всех точек.
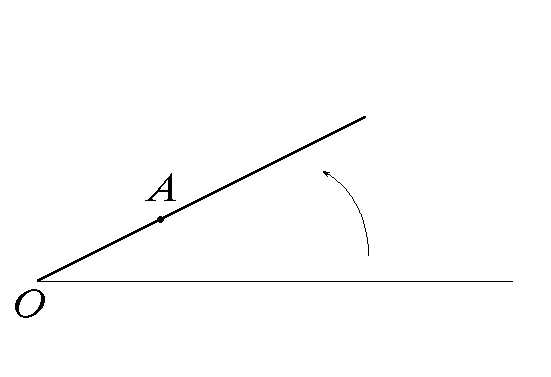
Полярный угол определен с точностью до . Полярный радиус точки считается равным нулю, а полярного угла у нее нет.
Модуль и аргумент комплексного числа
Модулем комплексного числа называется расстояние от до нуля на комплексной плоскости.
Обозначение. . (Модуль — длина радиус-вектора.) Если , это определение не противоречит определению модуля вещественного числа.
Пусть и — комплексные числа. — длина радиус-вектора числа — длина вектора — расстояние между и на комплексной плоскости.
Пусть . Тогда Следовательно, .
Теорема. .
Доказательство.
Теорема.
Доказательство аналогично.
Теорема.
Доказательство. Следует из определения модуля и геометрического смысла сложения и вычитания комплексных чисел.
Определение. Пусть — комплексное число, не равное нулю, пусть , тогда
Следовательно, точка лежит на единичной окружности с центром в нуле.
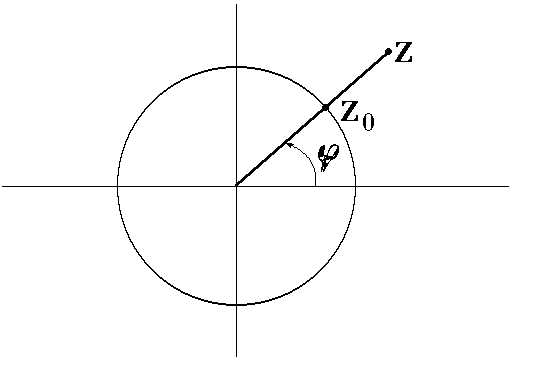
Существует вещественное число такое, что
Таких чисел бесконечно много, и любые два из них различаются на , где — произвольное целое число. Любое такое число называется аргументом числа .
Обозначение. .
Итак, любое комплексное число можно представить в виде
где .
Такое представление комплексного числа называется его тригонометрической формой.
Формула Муавра
Абрахам де Муавр (1667–1754) был выходцем из Франции, прожил долгую жизнь в Англии и умер в Лондоне. Однажды, незадолго до смерти, Муавр заявил, что ему необходимо ежедневно увеличивать время сна на 10–15 минут. Достигнув, таким образом, в сумме продолжительность сна более 23 часов, он на следующие сутки проспал все 24 часа и умер во сне.
С именем Муавра связаны правила возведения в -ю степень и извлечения корня -й степени для комплексных чисел. Муавр много занимался исследованием рядов и доказал частный случай предельной теоремы в теории вероятностей.
Лемма. Пусть , где . Тогда .
Доказательство.
Пусть . Тогда . Но
Следовательно, числам и соответствует одна и та же точка числовой окружности. Значит, . Значит, — одно из значений .
Теорема. Пусть . Тогда .
Доказательство. Представим и в тригонометрической форме:
Тогда
Так как , то можно применить лемму. — одно из значений .
Следствие.
— формула Муавра.
Следствие. В условиях теоремы .
Доказательство.
Пусть . По теореме
Следствие. Формула Муавра верна для любого целого показателя (целая отрицательная и нулевая степень для комплексных чисел вводится так же, как и для вещественных).
Доказательство. Пусть .
Следствие.
Доказательство.
Задачи.
1. Изобразите на комплексной плоскости числа
1)
2) ;
3) .
2. Найдите модуль и аргумент чисел
1) ;
2) ;
3) ;
4) .
3. Изобразите на комплексной плоскости множество точек z, задаваемых условиями
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
7) и .
4. Найдите множество значений функций с областью определения :
1) , ;
2) , .
5. Используйте тригонометрическую форму и формулу Муавра для вычисления значений:
1) ;
2) ;
3) ;
4) .
hijos.ru

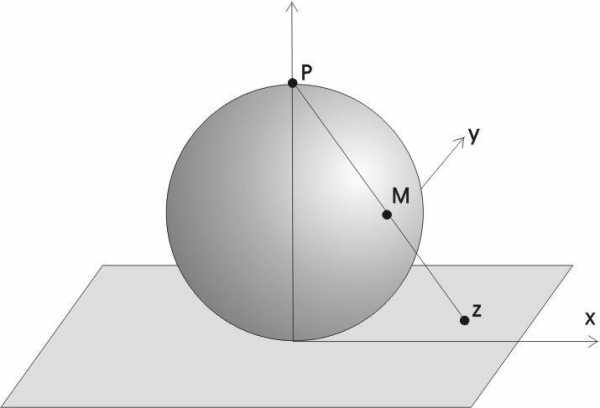
 комплексной плоскости. Прямая «проткнет»
сферу в некоторой точкеM.
Организуем из точекzплоскости неограниченно возрастающую
последовательность. Образы этих точек
стремятся к точкеP, а
сама точкаPявляется
отображением бесконечно удаленной
точки плоскости.
комплексной плоскости. Прямая «проткнет»
сферу в некоторой точкеM.
Организуем из точекzплоскости неограниченно возрастающую
последовательность. Образы этих точек
стремятся к точкеP, а
сама точкаPявляется
отображением бесконечно удаленной
точки плоскости.