|
Каталог Поиск книг Электронные приложения Авторизация Подписка на рассылку Стихи о нас Богатство Трудности эти уже превратились в смыслы. Тивикова С.К., зав. каф. начального образования НИРО Обратная связь Отправить сообщение с сайта Партнёры |
Цикл 2«Разработка алгоритмов средствами языка программирования Паскаль»
Цикл 1«Алгоритмы решения задач и их реализация средствами языка программирования Паскаль» Цикл 1 проводился с 5 марта по 20 апреля 2013 года Лекция 1. Линейные алгоритмы и их реализация средствами языка Паскаль
Домашнее задание. Решить задачи:
Запись видеолекции Лекция 2. Целочисленная арифметика и средства языка Паскаль.
Домашнее задание. Решить задачи:
Запись видеолекции Лекция 3. Алгоритм с проверкой условия и его реализация средствами языка Паскаль. .
Домашнее задание.
Запись видеолекции Лекция 4. Сложные ветвления.
Домашнее задание.
Запись видеолекции Лекция 5. Алгоритм с циклом и его реализация средствами языка Паскаль.
Домашняя работа: Решение задач:
Запись видеолекции Лекция 6. Понятие массива.
Домашняя работа. Решение задач лекции. Лекция 7 Решение сложных задач.
Запись видеолекции |
Задачи для решения в pascal — Информатика, информационные технологии
Варианты задач по теме «Операторы ветвления»
1.Даны действительные числа a, b, c. Проверить, выполняются ли неравенства a
2.Даны два действительных числа. Заменить первое число нулем, если оно равно второму, и оставить числа без изменения в противном случае.
3.Даны три вещественных числа. Выбрать те из них, которые принадлежат интервалу [1,3].
4.Даны три действительных числа. Возвести в квадрат те из них, значения которых неотрицательны.
5.Даны положительные действительные числа x, y, z. Выяснить существует ли треугольник с длинами сторон x, y, z.
6.Даны целые числа a, b. Если числа не равны, то заменить каждое из них одним и тем же числом, равным большему из исходных, а если равны, то заменить числа нулями.
7.Даны три вещественных числа x, y, z. Вычислить значения выражений x + y + z и xyz и вывести максимальное из них.
8.Даны две точки: А(x1,y1) и B(x2,y2). Составить алгоритм, определяющий, которая точка находится ближе к началу координат.
9.Заданы координаты вершин треугольника и точки. Определить, лежит ли точка внутри треугольника.
10.Заданы два целых числа. Определить являются ли они оба четными или оба нечетными или какое из них четное, а какое нечетное.
11.Проверить имеет ли квадратное уравнение вида ax2+bx+c=0 действительные корни. Если да, то найти их.
Если да, то найти их.
12.Составить программу упорядочивания трех чисел x, y, z по возрастанию.
13.Составить программу, проверяющую верно ли утверждение, что сумма цифр введенного двузначного целого числа делится без остатка на 5.
14.Дано некоторое целое двузначное число. Проверить, равна ли сумма его цифр числу 7.
15.Определить, находится ли точка с координатами x, y во второй координатной четверти.
16.Даны две переменные целого типа А и В. Если их значение не равны, то присвоить каждой переменной сумму этих значений, а если равны, то присвоить переменным нулевые значения.
17.Известны площади круга и квадрата. Определить, поместится ли круг в квадрате?
18 Определите номер квадранта, в котором находится точка с заданными координатами x,y.
Варианты задач по теме «Цикл с параметром»
| №варианта | Ряд | Количествознаков после десятичнойточки |
Варианты задач по теме «Итерационные циклы»
| №варианта | Вид функции y=f(x) | xнач | xкон | s |
| 0,2 | 0,5 | 0,1 | ||
| 0,3 | 3,7 | 0,4 | ||
| 0,2 | 0,2 | |||
| 0,5 | ||||
| 0,3 | 0,9 | 0,1 | ||
| 0,1 | 0,9 | 0,1 | ||
| 0,2 | 0,2 | |||
| -2 | 0,5 | |||
| 0,2 | ||||
| -2 | 0,5 | |||
| 0,5 | ||||
| -2 | 0,5 | |||
| 0,2 | ||||
| 2,5 | 0,1 | |||
| -5 | -3 | 0,5 | ||
| 0,5 | ||||
| -1 | 0,2 | |||
| -1 | 0,2 |
Приложение Г
Вопросы для самостоятельного изучения
1. Информатика как наука. Информация, виды информации
Информатика как наука. Информация, виды информации
2.Понятие информации, единицы измерения информации
3.Аппаратное устройство ПК (основные части, их назначение)
4.Системный блок ПК, основные узлы (системная плата, технические характеристики)
5.Внутренняя и внешняя память ПК
6.Устройства ввода и вывода информации (основные характеристики)
7.Периферийные устройства ПК (основные характеристики)
8.Программное обеспечение ПК, классификация
9.Инструментальное программное обеспечение. Понятие математической модели задачи
10.Прикладное программное обеспечение, их состав. Пакеты прикладных программ, назначение и примеры
11.Системное программное обеспечение, их состав
12.Операционная система: назначение и состав
13.Операционная система Windows: возможности и назначение системы
14.MS Windows : объекты рабочего стола (папки, ярлыки, панель задач), их назначение
15.MS Windows : понятие окон, элементы окон, действия с окнами
16. MS Windows : понятие документа и приложения. Назначение офисных приложений
MS Windows : понятие документа и приложения. Назначение офисных приложений
17.Возможности операционной системы MS Windows по работе с файловой структурой. Понятие файла и файловой структуры (имя файла, файловая система, путь к файлу)
18.Назначение стандартных приложений MS Windows
19.MS Windows : работа с документами (создание, хранение, открытие и печать)
20.OLE – технологии: принципы внедрения и связывания объектов
21.Понятие «Буфера обмена» его назначение и использование в приложениях MS Windows. Назначение и возможности текстовых редакторов и процессоров
22.Основные режимы отображения документов в текстовых процессорах (обычный, Web-документ, разметка, обычный)
23.Основные приемы работы с текстами в процессоре MS Word
24.Основные приемы форматирования в текстовом процессоре MS Word
25.Приемы и средства автоматизации разработки документов в текстовом процессоре MS Word (стили, шаблоны)
26.MS Word: работа с таблицами (создание, редактирование, форматирование)
27. MS Word: возможности по работе с графическими объектами (рисунки, изображения, надписи)
MS Word: возможности по работе с графическими объектами (рисунки, изображения, надписи)
28.MS Word: возможности по вводу и редактированию формул (редактор формул)
29.MS Word: преобразование текста в список, оформление текста в несколько столбцов
30.Назначение и возможности электронных таблиц. MS Excel
31.MS Excel: вычислительные возможности, абсолютная и относительная ссылки
32.MS Excel: автоматизация ввода (автозаполнение числами, формулами), оформление таблиц
33.MS Excel: приемы связывания рабочих листов
34.Основные понятия баз данных (БД): структура БД, этапы разработки
35.Этапы создания многотабличных баз данных в СУБД MS Access
36.Назначение объектов в СУБД MS Access (таблицы, запросы, формы, отчеты)
37.Общее понятие о компьютерной графике. Примеры графических редакторов
38.Понятие компьютерных вирусов. Защита данных, основные методы
39.Понятие локальных и глобальных компьютерных сетей, топология сетей
40. Сеть Internet: основные понятия (протоколы TCP/IP), программное обеспечение
Сеть Internet: основные понятия (протоколы TCP/IP), программное обеспечение
41.Сеть Internet: основные службы
42.Сеть Internet: основные понятия World Wide Web (Web-каналы, Web- страница, гиперссылки, средства просмотра)
43.Сеть Internet: работа с электронной почтой
44.Основные этапы решения задач на ЭВМ
45.Понятие алгоритмизации задачи. Алгоритм, основные типы алгоритмов их свойства. Формы представления алгоритмов
46.Языки программирования, уровни языков программирования, примеры
47.Pascal: алфавит и структура программы
48.Pascal: структура данных (типы данных)
49.Pascal: линейные алгоритмы и их операторы
50.Pascal: разветвляющиеся алгоритмы и их операторы
51.Pascal: циклические алгоритмы и их операторы
52.Pascal: работа с массивами данных
53.Работа в среде программирования Pascal: создание, сохранение, отладка и запуск программ
Статьи к прочтению:
- Задачи для самостоятельного решения
- Задачи и функции администрирования в информационных системах
Паскаль с нуля [ч1].
 Первая программа.
Первая программа.Похожие статьи:
Блок-схема алгоритма решения задачи
СОДЕРЖАНИЕ Введение………………………………………………………………………3 Постановка задачи……………………………………………………………5 Блок – схема…………………………………………………………………..6 Описание блок-схемы…
Технология решения задач на компьютере.
Предмет информатики. Информатика: определение, история, составные части, сферы применения, информационное общество. Информация: определение,…
Pascal-SC — 1st Edition
Select country/regionUnited States of AmericaUnited KingdomAfghanistanÅland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Sint Eustatius and SabaBosnia and HerzegovinaBotswanaBrazilBritish Indian Ocean TerritoryBritish Virgin IslandsBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCanary IslandsCape VerdeCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongoCook IslandsCosta RicaCroatiaCubaCuraçaoCyprusCzech RepublicDemocratic Republic of the КонгоДанияДжибутиДоминикаДоминиканская РеспубликаЭквадорЕгипетСальвадорЭкваториальная ГвинеяЭритреяЭстонияЭфиопияФолклендские (Мальвинские) островаФарерские островаФедеративные Штаты МикронезииФиджиФинляндияФранцияФранцузская ГвианаФранцузская ПолинезияГабонГамбияГрузияГерманияГанаГибралтарГрецияГренландияГренадаГуадело upeGuamGuatemalaGuernseyGuineaGuinea-BissauGuyanaHaitiHondurasHong KongHungaryIcelandIndiaIndonesiaIranIraqIrelandIsle of ManIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKuwaitKyrgyzstanLaoLatviaLesothoLiberiaLibyaLiechtensteinLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNepalNetherlandsNew CaledoniaNew ZealandNicaraguaNigerNiueNorfolk IslandNorth KoreaNorthern Mariana IslandsNorwayOmanPakistanPalauPanamaPapua New GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarRéunionRomaniaRwandaSaint BarthélemySaint HelenaSaint Kitts and NevisSaint LuciaSaint Martin (French part)Saint Pierre and MiquelonSaint Vincent and the GrenadinesSamoaSan MarinoSao Tome and PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSint Maarten (Dutch part)SlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia и South Sandwich IslandsSouth KoreaSouth SudanSpainSri LankaSudanSurinameSvalbard and Jan MayenSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzaniaThailandTimor LesteTogoTokelauTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUruguayUS Virgin IslandsUzbekistanVanuatuVatican CityVenezuelaVietnamWallis and FutunaWestern SaharaYemenZambiaZimbabwe
Варианты покупки Ebook 25% скидка $ 72,95 $ 54,71
Налог с продаж будет рассчитываться по выбору
Бесплатная глобальная доставка
NO Минимальный заказ
Описание
. В комплекте. 17: Pascal-SC: Компьютерный язык для научных вычислений фокусируется на применении Pascal-SC, языка программирования, разработанного как расширение стандартного Pascal, в научных вычислениях. В публикации сначала подробно рассказывается о введении в Pascal-SC, обзоре стандартного Pascal и реальной арифметике с плавающей запятой. Обсуждения сосредоточены на оптимальном скалярном произведении, стандартных функциях, реальных выражениях, структуре программы, простых расширениях, реальной арифметике с плавающей запятой, векторной и матричной арифметике и динамических массивах. Затем в тексте рассматриваются функции и операторы с произвольными типами результатов и решение проблем с Pascal-SC. В книге рассматриваются строки и обработка текста, динамические массивы и модули. Темы включают объявление и использование модулей, совместимость статических и динамических массивов, динамические типы результатов функций и операторов, строки в процедурах, функции и операторы, а также объявление строковых переменных.
В комплекте. 17: Pascal-SC: Компьютерный язык для научных вычислений фокусируется на применении Pascal-SC, языка программирования, разработанного как расширение стандартного Pascal, в научных вычислениях. В публикации сначала подробно рассказывается о введении в Pascal-SC, обзоре стандартного Pascal и реальной арифметике с плавающей запятой. Обсуждения сосредоточены на оптимальном скалярном произведении, стандартных функциях, реальных выражениях, структуре программы, простых расширениях, реальной арифметике с плавающей запятой, векторной и матричной арифметике и динамических массивах. Затем в тексте рассматриваются функции и операторы с произвольными типами результатов и решение проблем с Pascal-SC. В книге рассматриваются строки и обработка текста, динамические массивы и модули. Темы включают объявление и использование модулей, совместимость статических и динамических массивов, динамические типы результатов функций и операторов, строки в процедурах, функции и операторы, а также объявление строковых переменных. Публикация является надежным справочником для экспертов в области компьютерных наук и исследователей, заинтересованных в применении Pascal-SC в научных вычислениях.
Публикация является надежным справочником для экспертов в области компьютерных наук и исследователей, заинтересованных в применении Pascal-SC в научных вычислениях.
Содержание
-
Глава I. Введение в Pascal-SC
1.1 Почему Pascal-SC?
1.2 Распространение ошибки круглосуточности
1.3 Реальная арифметика с плавающей точкой
1.4 Комплексная арифметика с плавающей точкой
1.5 Интервальная арифметика
1,6 Вектор и матричная арифметика
1,7 Динамические массивы
1.8 Перегрузка операторов и функционирование
1,9 Модиальные массивы
1.8 Перегрузка операторов и функционирование названий
1,9 Модиальные массивы
1.8. Концепция струн
Глава II. Обзор стандартного Паскаля
2.1 Структура программы
2.2 Объявления и определения
2.3 Операторы
2.4 Выражения
2.5 Простые расширения
2.5.1 Идентификаторы
2.5.2 Подмассивы
2.5.3 Оператор Case
2.5.4 Глава 9 Переписка III. Вещественная арифметика с плавающей запятой — сердце научного языка программирования
Вещественная арифметика с плавающей запятой — сердце научного языка программирования
3.1 Арифметика с плавающей запятой
3.2 Вещественные выражения
3.3 Ввод и вывод
3.4 Стандартные функции
3.5 Оптимальное скалярное произведение
3.6 Тип данных Dotprecision
Глава IV. Функции и операторы с произвольными типами результатов
4.1 Структурированные типы данных в Standard Pascal
4.2 Функции с произвольными типами результатов
4.3 Операторы
4.4 Идентификаторы операторов и определение приоритета
4.5 Перегрузка функций, процедур и операторов
4.6 Примеры Глава
Задачи с Pascal-SC
5.1 Комплексная арифметика
5.2 Интервальная арифметика
5.3 Векторная и матричная арифметика
5.3.1 Вещественная векторная и матричная арифметика
5.3.2 Комплексный вектор и матричная арифметика
5.3.3 Интервальный вектор и матричная арифметика
5.4 Дифференцирование
5.4.1 Действительное дифференцирование
5. 4.2 Интервальное дифференцирование
4.2 Интервальное дифференцирование
5.4.3 Тейлоровские разложения
Глава VI. Строки и обработка текста
6.1 Объявление строковых переменных
6.2 Манипуляции со строками
6.3 Строки в процедурах, функциях и операторах
6.4 Примеры
Глава VII. Динамические массивы
7.1 Декларация и квалификация
7.2 Динамические массивы как аргументы подпрограмм
7.3 Динамические типы результатов функций и операторов
7.4 Совместимость статических и динамических массивов
7.5 Примеры
Глава VIII. Модули
8.1 Вводные примеры
8.2 Объявление и использование модулей
8.3 Определение и реализация модулей
8.4 Примеры
Приложение A: Диаграммы синтаксиса
A.1 Синтаксис Pascal-SC
A.2 Синтаксис выражений для отдельных типов данных
A .2.1 Целочисленные выражения
A.2.2 Вещественные выражения (с плавающей запятой)
A.2.3 Булевы выражения
A.2.4 Выражения для символьных и перечисляемых типов
A. 2.5 Выражения множеств
2.5 Выражения множеств
A.2.6 Строковые выражения
A.2.7 Выражения для массивов, записей и Указатели
A.2.8 Комплексные выражения
A.2.9 Вещественные интервальные выражения
A.2.10 Комплексные интервальные выражения
A.2.11 Вещественные векторные и матричные выражения
A.2.12 Комплексные векторные и матричные выражения
A.2.13 Вещественные интервальные векторные и матричные выражения
A.2.14 Комплексные интервальные векторные и матричные выражения
A.2.15 Обзор векторных и матричных выражений
Приложение B: Дополнительные расширения и ограничения существующих реализаций
B.1 Идентификаторы
B.2 Концепция файла
B.3 Операторы
B .3.1 Расширенный оператор Case
B.3.2 Ограничения на операторы goto
B.4 Стандартные процедуры
B.5 Расширение целочисленной арифметики
B.6 О скалярном произведении
B.6.1 Округления и функциональные режимы
B.6.2 Скалярные произведения для Сложные и интервальные векторы
B. 7 Директива о компиляторах
7 Директива о компиляторах
Приложение C: Указатель синтаксических диаграмм, словесных символов, стандартных идентификаторов и примеров
C.1 Синтаксические диаграммы
C.2 Словесные символы
C.3 Стандартные идентификаторы
C.4 Примеры
Библиография
Тема Индекс
Информация о продукте
- Кол-во страниц: 304
- Язык: английский
- Авторское право: © Academic Press 1987
- Опубликовано: 28 января 1987 г.781483268859
About the Authors
Gerd Bohlender
Christian Ullrich
Jürgen Wolff von Gudenberg
About the Editors
Werner Rheinboldt
Daniel Siewiorek
Affiliations and Expertise
Carnegie -Mellon University
Рейтинги и обзоры
Написать отзыв
На данный момент нет отзывов для «Pascal-SC»
Биномиальная теорема, биномиальные расширения с использованием треугольника Паскаля, подмножества
Биномиальные расширения с использованием треугольника Паскаля
Рассмотрим следующие расширенные степени (a + b) n , где a + b — любой двучлен, а n — целое число. Ищите закономерности.
Ищите закономерности.
Каждое расширение является многочленом. Следует отметить некоторые закономерности.
1. На один член больше, чем степень показателя степени, n. То есть в разложении (a + b) 9 есть члены0182 n .
2. В каждом члене сумма показателей равна n, степени, в которую возводится двучлен.
3. Показатели степени начинаются с n, степени бинома, и уменьшаются до 0. Последний член не имеет множителя a. Первый член не имеет множителя b, поэтому степени b начинаются с 0 и увеличиваются до n.
4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения примерно «на полпути», а затем уменьшаются на те же значения обратно до 1.
Давайте рассмотрим коэффициенты подробнее. Предположим, что мы хотим найти разложение (a + b) 6 . Только что отмеченные закономерности показывают, что в расширении 7 терминов:
a 6 + c 1 a 5 b + c 2 a 4 b 2 + c 2 a 3 3 b 3 + c 4 a 2 b 4 + c 5 ab 5 + b 6 .
Как определить значение каждого коэффициента c i ? Мы можем сделать это двумя способами. Первый метод включает запись коэффициентов в треугольный массив следующим образом. Это известно как Треугольник Паскаля :
В треугольнике много паттернов. Найдите столько, сколько сможете.
Возможно, вы нашли способ записать следующий ряд чисел, учитывая числа в ряду над ним. Снаружи всегда есть 1. Каждое оставшееся число является суммой двух чисел над ним. Попробуем найти расширение для (a + b) 6 , добавив еще одну строку, используя обнаруженные закономерности:
Мы видим, что в последней строке
первая и последняя цифры 1 ;
2-е число равно 1+5, или 6 ;
3-е число равно 5+10, или 15 ;
4-е число равно 10+10, или 20 ;
5-е число равно 10+5, или 15 ; а
6-е число равно 5+1, или 6 .
Таким образом, расширение для (A + B) 6 составляет
(A + B) 6 = 1 A 6 + 6 A 5 B + 15 A 4 B B 15 A 4 B B 15 A 4 B B + 15 A 5 B + 15 A 2 + 20 а 3 б 3 + 15 а 2 б 4 + 6 аб 5 + 2 6 1 б 3 6
Чтобы найти разложение для (a + b) 8 , заполним еще две строки треугольника Паскаля:
Таким образом, разложение
(a + b) 8 = a 8 + 8a 7 б + 28а 6 б 2 + 56а 5 б 3 + 70а 4 б 4 + 56а 3 б 5 + 28а 2 б 6 + 8аб 7 + б 8 .
Мы можем обобщить наши результаты следующим образом.
Биномиальная теорема с использованием треугольника Паскаля Для любого бинома a + b и любого натурального числа n,
(a + b) n = c 0 a n b 0 + c 1 a n-1 9182 b + c 2 a n-2 b 2 + …. + c n-1 a 1 B N-1 + C N A 0 B N ,
, где числа C 0 , C 1 , C 2 , C N N N N N N N. -1 , c n взяты из (n + 1)-й строки треугольника Паскаля.
Пример 1 Расширить: (u — v) 5 .
Решение Имеем (a + b) n , где a = u, b = -v и n = 5. Используем 6-ю строку треугольника Паскаля:
1 5 10 10 0028 Тогда имеем
(и — v) 5 = [и + (-v)] 5 = 1 (и) 5 + 5 (и) 4 (-82) 900 1 + 10 (и) 3 (-в) 2 + 10 (и) 2 (-в) 3 + 90905 5 90)() 3 9 0)() + 1 (-V) 5 = U 5 — 5U 4 V + 10U 3 V 2 — 10U 2 V 3 + 5uv 2 V 3 + 5uv 2 V 3 + 5uv 2 . 0183 .
0183 .
Обратите внимание, что знаки терминов чередуются между + и -. Когда степень -v нечетная, знак -.
Пример 2 Расширить: (2t + 3/t) 4 .
Решение Имеем (a + b) n , где a = 2t, b = 3/t и n = 4. Воспользуемся 5-й строкой треугольника Паскаля:
1 4 6 0
Биномиальное разложение с использованием факториальной записи
Предположим, что мы хотим найти разложение (a + b) 11 . Недостатком использования треугольника Паскаля является то, что мы должны вычислить все предыдущие строки треугольника, чтобы получить строку, необходимую для расширения. Следующий метод позволяет избежать этого. Это также позволяет нам найти конкретный член — скажем, 8-й член — без вычисления всех остальных членов разложения. Этот метод полезен в таких курсах, как конечная математика, исчисление и статистика, и он использует обозначение биномиального коэффициента .
Мы можем переформулировать биномиальную теорему следующим образом.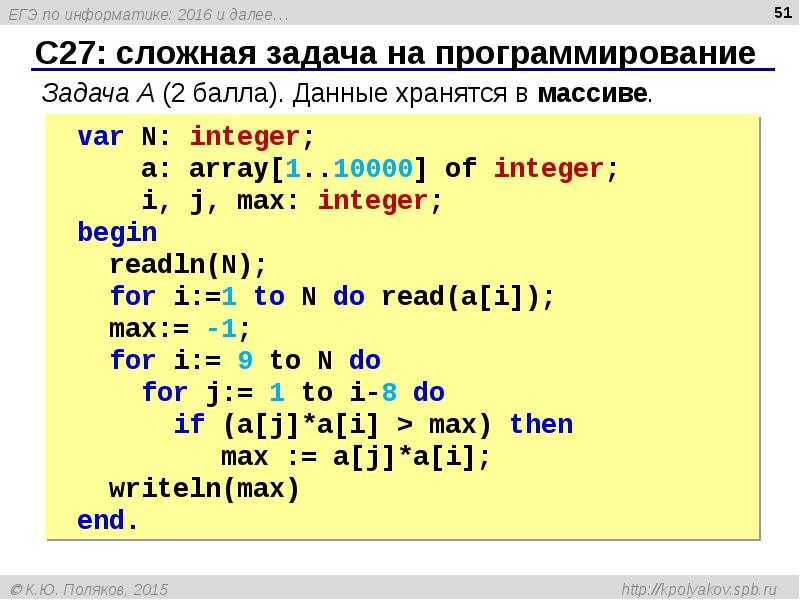
Для любого двучлена (a + b) и любого натурального числа n,
.
Биномиальную теорему можно доказать с помощью математической индукции. (Видеть Упражнение 63.) Эта форма показывает, почему называется биномиальным коэффициентом .
Пример 3 Расширить: (x 2 — 2y) 5 .
Решение Имеем (a + b) n , где a = x 2 , b = -2y и n = 5. Тогда, используя биномиальную теорему, имеем
Finally (x 2 — 2y) 5 = x 10 — 10x 8 y + 40x 6 y 2 — 80x 4 y 3 + 80x 2 y 4 — 32г 5 .
Пример 4 Расширить: (2/x + 3√x) 4 .
Решение Имеем (a + b) n , где a = 2/x, b = 3√x и n = 4. Тогда, используя биномиальную теорему, имеем
Наконец, (2/x + 3 √x) 4 = 16/x 4 + 96/х 5/2 + 216/х + 216х 1/2 + 81х 2 .
Поиск конкретного термина
Предположим, что мы хотим определить только конкретный член разложения. Разработанный нами метод позволит найти такое слагаемое без вычисления всех строк треугольника Паскаля или всех предшествующих коэффициентов.
Обратите внимание, что в биномиальной теореме дает нам 1-й член, дает нам 2-й член, дает нам 3-й член и так далее. Это можно обобщить следующим образом.
Нахождение (k + 1)-го члена(k + 1)-й член (a + b) n равен .
Пример 5 Найдите 5-й член в разложении (2x — 5y) 6 .
Решение Прежде всего заметим, что 5 = 4 + 1. Таким образом, k = 4, a = 2x, b = -5y и n = 6. Тогда 5-й член разложения равен
Пример 6 Найдите восьмой член в разложении (3x — 2) 10 .
Решение Сначала заметим, что 8 = 7 + 1. Таким образом, k = 7, a = 3x, b = -2 и n = 10. Тогда 8-й член разложения равен
Общее количество подмножеств
Предположим, что набор содержит n объектов. Количество подмножеств, содержащих k элементов. Общее количество подмножеств набора — это количество подмножеств с 0 элементами, плюс количество подмножеств с 1 элементом, плюс количество подмножеств с 2 элементами и так далее. Общее количество подмножеств множества из n элементов равно
Количество подмножеств, содержащих k элементов. Общее количество подмножеств набора — это количество подмножеств с 0 элементами, плюс количество подмножеств с 1 элементом, плюс количество подмножеств с 2 элементами и так далее. Общее количество подмножеств множества из n элементов равно
.
Теперь рассмотрим разложение (1 + 1) п :
.
Таким образом, общее количество подмножеств равно (1 + 1) n или 2 n . Мы доказали следующее.
Общее количество подмножеств множества из n элементов равно 2 n .
Пример 7 Сколько подмножеств имеет множество {A, B, C, D, E}?
Решение Набор состоит из 5 элементов, поэтому количество подмножеств равно 2 5 или 32.
Пример 8 Национальная сеть ресторанов Wendy’s предлагает следующие начинки для своих гамбургеров:
{ кетчуп, горчица, майонез, помидоры, листья салата, лук, рассол, приправы, сыр }.

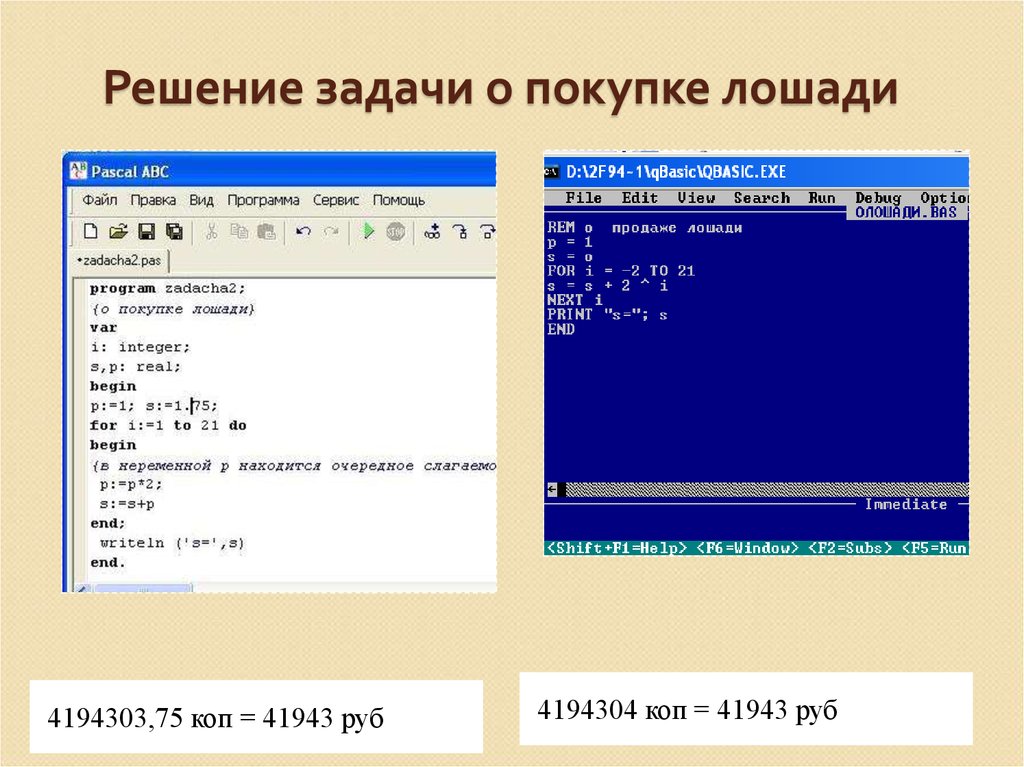
 Базовые алгоритмические конструкции. Линейные команды. Ветвление. Циклы. Задача «Дружественные числа».
Базовые алгоритмические конструкции. Линейные команды. Ветвление. Циклы. Задача «Дружественные числа».
 org;
org; Решение Задачи «Среднее арифметическое трех чисел» средствами оператора присваивания и записи арифметического выражения. Стандартные функции. Решение Задачи «Среднее арифметическое трех чисел» средствами использования стандартной функции. Датчик случайных чисел. Решение Задачи «Сумма трех чисел» средствами датчика случайных чисел (Задача «Бросание кости 3 раза»).
Решение Задачи «Среднее арифметическое трех чисел» средствами оператора присваивания и записи арифметического выражения. Стандартные функции. Решение Задачи «Среднее арифметическое трех чисел» средствами использования стандартной функции. Датчик случайных чисел. Решение Задачи «Сумма трех чисел» средствами датчика случайных чисел (Задача «Бросание кости 3 раза»).


 Определить, в какой из пяти кружков сможет записаться ученик, если запись в кружки осуществляется по конкурсу на основе сдачи экзамена по трем предметам (набор предметов одинаковый для всех пяти кружков). По итогам сдачи учеником трех экзаменов (баллы по пятибальной системе задаются из ввода) определяется его средний балл (округление до десятых долей). Приемная комиссия вывешивает проходные баллы для каждого кружка с учетом десятых долей ( проходные баллы генерируются датчиком случайных чисел). Следует распечатать на экране информацию, в какой кружок (по номеру) принят ученик.
Определить, в какой из пяти кружков сможет записаться ученик, если запись в кружки осуществляется по конкурсу на основе сдачи экзамена по трем предметам (набор предметов одинаковый для всех пяти кружков). По итогам сдачи учеником трех экзаменов (баллы по пятибальной системе задаются из ввода) определяется его средний балл (округление до десятых долей). Приемная комиссия вывешивает проходные баллы для каждого кружка с учетом десятых долей ( проходные баллы генерируются датчиком случайных чисел). Следует распечатать на экране информацию, в какой кружок (по номеру) принят ученик.  Далее программа должна выводить информацию: стойте, идите, внимание.
Далее программа должна выводить информацию: стойте, идите, внимание.  «Сумма арифметического ряда».
«Сумма арифметического ряда». 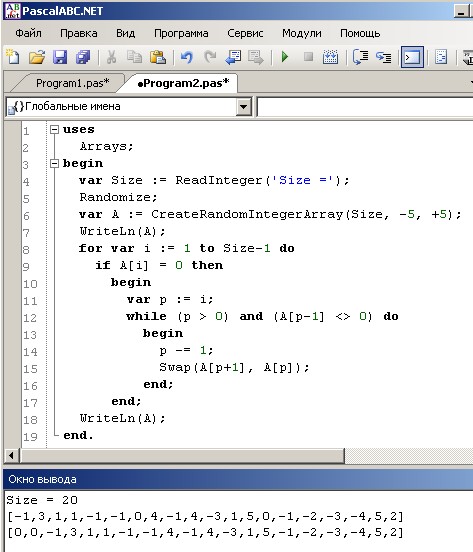 )
)  Вещественная арифметика с плавающей запятой — сердце научного языка программирования
Вещественная арифметика с плавающей запятой — сердце научного языка программирования 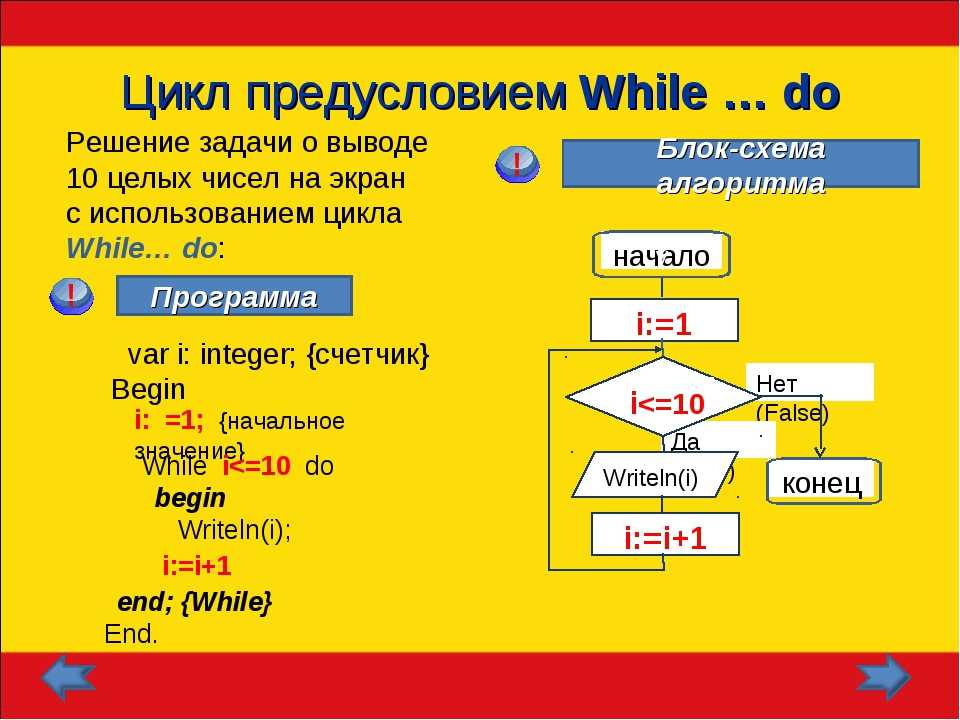 4.2 Интервальное дифференцирование
4.2 Интервальное дифференцирование  2.5 Выражения множеств
2.5 Выражения множеств 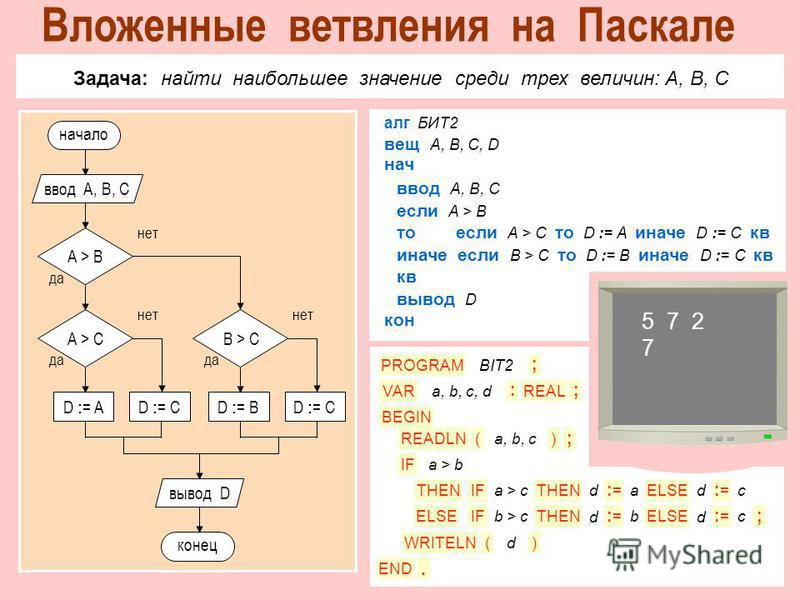 7 Директива о компиляторах
7 Директива о компиляторах