Приклади:
Приклад №1.
Обчислити детермінант
Розв’язання.
1-й спосіб. Скористаємося формулою для обчислення детермінанта третього порядку:
2-й спосіб. Відмітимо, що в другому стовпці всі елементи, крім одного, дорівнюють нулю. Тоді розкладемо детермінант за елементами другого стовпця:
Зауваження. Перший і третій доданки в розкладі можна було не вписувати.
Приклад №2.
Обчислити детермінант
Розв’язання.
Якщо детермінант розкласти за елементами якого-небудь рядка або стовпця, то його обчислення зводиться до обчислення чотирьох детермінантів третього порядку. Очевидно, що це не кращий шлях. Застосуємо спосіб одержання в якому-небудь рядкові або стовпцеві нулів: якщо із другого рядка відняти перший, із третього – подвоєний перший, із четвертого – потроєний перший, то одержимо детермінант
,
рівний даному. Розкладемо його за елементами першого стовпця:
Тепер треба обчислити лише один детермінант третього порядку.
Якщо продовжити процес «одержання нулів» (наприклад, із другого рядка відняти перший), то
Приклад №3.
Не обчислюючи детермінанта, знайти член детермінанта, який утримує x2:
Розв’язання.
За означенням детермінанта це буде алгебраїчна сума наступних трьох елементів: 4x2—x2-12x2=-9x2
Приклад №4.
Розв’язати рівняння.
Розв’язання. За третьою властивістю детермінанта коренями даного рівняння будуть числа: x1=2, x2=3,…, xn=n
Обернена матриця
Матриця А-1називається оберненою по відношенню до матриці А, якщо АА-1=А-1А=Е, де Е – одинична матриця.
Для того, щоб для матриці А існувала обернена, необхідно і достатньо, щоб детермінант матриці А був відмінний від нуля.
Квадратна матриця, детермінант якої відмінний від нуля, називається невиродженою (або неособливою), в противному випадку – виродженою (або особливою). Вироджені матриці обернених матриць не мають. Будь-яка невироджена матриця А має єдину обернену матрицю А-1:
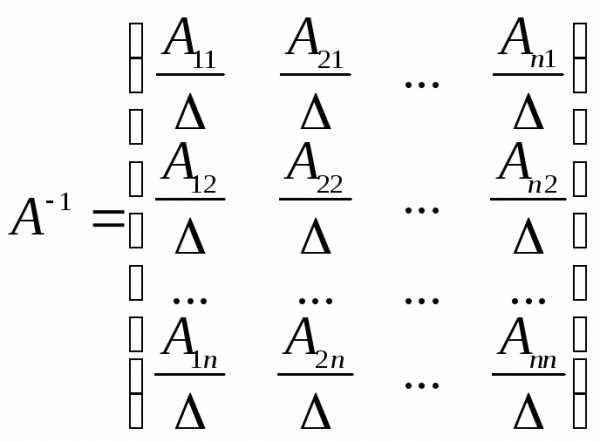
де А, Аij— алгебраїчні доповнення елемента аij матриці А, утворену за правилом: кожен елемент матриці А заміняється його алгебраїчним доповненням, потім одержана матриця транспонується і кожен її елемент ділиться на детермінант матриці А.
Для невироджених матриць вірне співвідношення:
Приклад №1.
Обчислити матрицю А-1, обернену до матриці А
Розв’язання.
Відомо, що обернена матриця існує тоді і тільки тоді, коли задана матриця неособлива. Оскільки
то А – неособлива матриця і А-1 існує. Відомо також, що
де Аij – алгебраїчне доповнення елемента аij. Знаходимо послідовно
Зауваження Найпростішою перевіркою правильності знаходження оберненої матриці є множення заданої і знайденої матриць: якщо добуток їх дорівнює одиничній матриці, то обернену матрицю знайдено правильно.
Зробимо перевірку:
Матричні рівняння
Приклад.
Розв’язати матричне рівняння
Розв’язання.
Позначимо матрицю через А, а матрицю черезВ.
Матричне рівняння набуває вигляду: AX
=B X=A-1B.Обчислимо детермінант матриці А:
Отже, матриця А має обернену матрицю А-1. Знаходимо А-1, для чого обчислимо алгебраїчне доповнення елементів А:
Матриця А-1 має вигляд:
Зробимо перевірку:
Матриця А-1 обчислена вірно.
Знайдемо матрицю X:
Перевірка:
Матриця X знайдена вірно.
studfiles.net
Система лінійних рівнянь. Матричний метод
Маричний метод обчислення СЛАР не такий поширений як метод Крамера, однак він присутній в авчальній програмі з лінійної алгебри і його вивчають як один із способів розв’язання системи рівнянь.
Нехай маємо систему N лінійних алгебраїчних рівнянь (СЛАР) з N невідомими x1, x2,…, xN.,коефіцієнтами при яких є елементи матриці A(aij), а вільними членами є числа b1, b2,…, bN.
Позначимо через X – матрицю-стовпець невідомих, через B– матрицю-стовпець вільних членів. Тоді попередню систему рівнянь можна записати у вигляді матричного рівняння:
A*X=B
Якщо квадратна матриця A має відмінний від нуля визначник , то для неї існує обернена A-1. Помноживши зліва в цьому рівнянні на A-1, одержимо
Враховуючи, що добуток оберненої матриці на саму матрицю дає одиничну , а також формулу , одержимо матричний розв’язок системи
X=A-1*B
Знаходження матричного розв’язку називається матричним способом розв’язування системи лінійних алгебраїчних рівнянь (СЛАР).
Приклад 1. Розв’язати систему лінійних рівнянь матричним методом.
Розв’язок. Маємо систему з трьох рівнянь. Позначимо матрицю і вектори літерами
Матричний розв’язок системи алгебраїчних рівнянь шукаємо за формулою X=A-1*B. Для знаходження оберненої матриці A-1 обчислимо визначник
Оскільки він відмінний від нуля , то задана система рівнянь сумісна і має єдиний розв’язок.
Знайдемо транспоновану матрицю A
Обчислимо алгебраїчні доповнення до елементів заданої матриці:
Обернену матрицю отримаємо за формулою
Знайдемо розв’язок СЛАР
Розв’язок системи рівнянь x1=3; x2=-5; x3=-7.
Розрахунки для системи із трьох рівнянь достатньо прості і зводяться на практиці до обчислень оберненої матриці, що теж не складно. У випадку системи чотирьох рівнянь обчислень буде куда більше і для визначення оберненої матриці доведеться шукати 16 визначників матриць розміром 3×3. Для системи рівнянь 5 порядку при визначенні оберненої матриці необхідно знаходити 25 визначників 4 порядку, або методом розкладу куда більше визначників 3 порядку. Перемножити обернену матрицю на праву частину рівняння після всіх операцій досить просто, і з цим справляються усі. Труднощі лише у обчисленні обернених матриць!
yukhym.com
Метод оберненої матриці. Матричні рівняння
ЛЕКЦІЯ 4: ЕЛЕМЕНТИ МАТРИЧНОГО АНАЛІЗУ
Розглянемо квадратну не вироджену СЛР у матричному вигляді
. (3.1)
Оскільки , то існує, причому єдина, обернена до матриці А матриця . Помножимо обидві частини рівності (4) зліва на матрицю . Маємо . Тобто розв’язок СЛР (3.1) обчислюється за формулою
(3.2)
Єдиність отриманого розв’язку випливає з єдиності оберненої матриці.
Приклад 1. Розв’язати методом оберненої матриці наступну СЛР:
Матриця даної системи має вигляд , стовпчик вільних членів . Матрицю, обернену до матриці А, було знайдено у прикладі 8 розділу 2: . Отже, єдиний розв’язок даної СЛР має вигляд:
Узагальнюючи наведений метод, розглянемо найпростіші матричні рівняння, тобто рівняння, що містять матрицю невідомих Х. Виділимо три типи таких рівнянь.
1. . За умови, що , маємо
.
Зауважимо, що СЛР (4) є частинним випадком цього матричного рівняння, коли m=1.
2. . За умови, що , маємо
.
3. . За умови, що та , маємо
.
Приклад 2. Розв’язати матричне рівняння , де , , .
Обернені до матриць А і В можна знайти за правилом, сформульованим у прикладі 7 розділу ІІ.
, .
Отже, шукана матриця
studlib.info
Метод оберненої матриці. Матричні рівняння
ЛЕКЦІЯ 4: ЕЛЕМЕНТИ МАТРИЧНОГО АНАЛІЗУ
Розглянемо квадратну не вироджену СЛР у матричному вигляді
. (3.1)
Оскільки , то існує, причому єдина, обернена до матриці А матриця . Помножимо обидві частини рівності (4) зліва на матрицю . Маємо . Тобто розв’язок СЛР (3.1) обчислюється за формулою
(3.2)
Єдиність отриманого розв’язку випливає з єдиності оберненої матриці.
Приклад 1.Розв’язати методом оберненої матриці наступну СЛР:
Матриця даної системи має вигляд , стовпчик вільних членів . Матрицю, обернену до матриці А, було знайдено у прикладі 8 розділу 2: . Отже, єдиний розв’язок даної СЛР має вигляд:
Узагальнюючи наведений метод, розглянемо найпростіші матричні рівняння, тобто рівняння, що містять матрицю невідомих Х. Виділимо три типи таких рівнянь.
1. . За умови, що , маємо
.
Зауважимо, що СЛР (4) є частинним випадком цього матричного рівняння, коли m=1.
2. . За умови, що , маємо
.
3. . За умови, що та , маємо
.
Приклад 2. Розв’язати матричне рівняння , де , , .
Обернені до матриць А і В можна знайти за правилом, сформульованим у прикладі 7 розділу ІІ.
, .
Отже, шукана матриця
5rik.ru
1. Матричний спосіб розв’язання
Через
те, що 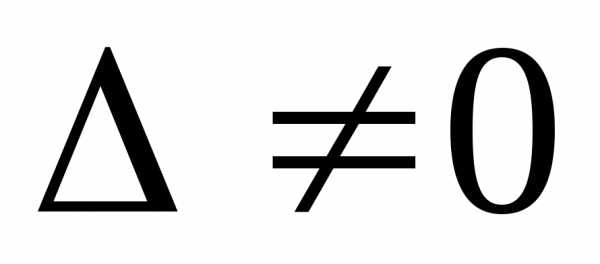 ,
то для матриціА існує
обернена матриця
,
то для матриціА існує
обернена матриця 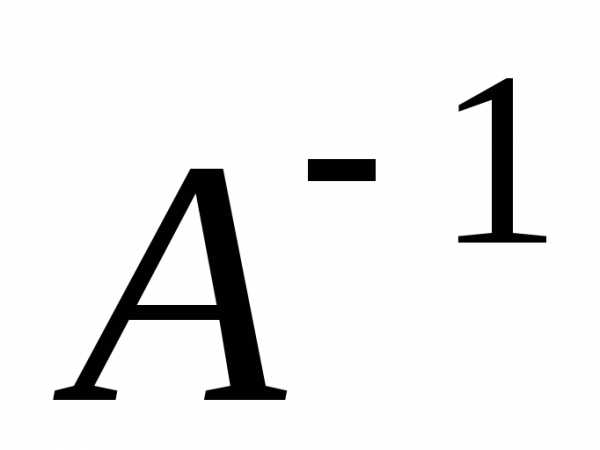 й
й
. (1.7)
Помноживши обидві частини рівняння ліворуч на матрицю, одержимо Оскільки й, то .
Відшукання розв’язку системи (1.6) за формулою (1.7) називають матричним способом розв’язання даної системи.
2. Формули Крамера (Крамер Г. ( 1704-1752) – швейцарський математик)
Формули
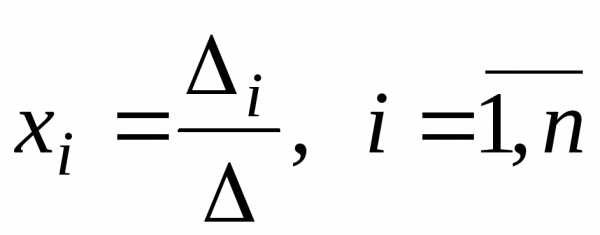 (1.8)
(1.8)
називаються формулами
Крамера, де 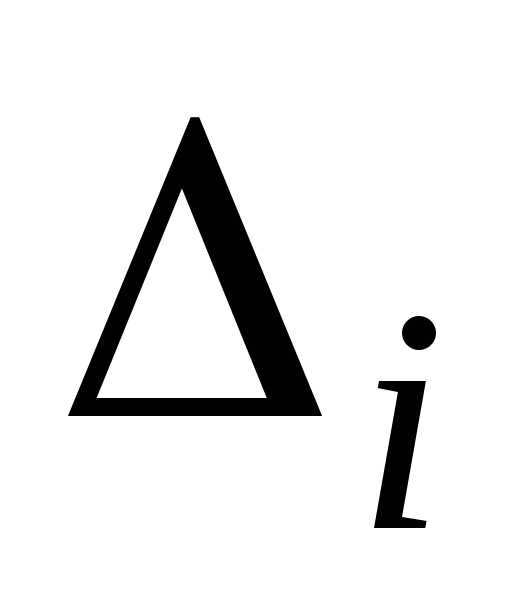 – визначник, отриманий з визначника
– визначник, отриманий з визначника  заміною i-го
стовпця стовпцем вільних членів.
заміною i-го
стовпця стовпцем вільних членів.
Доведення.
Для доведення матричну рівність (1.7) запишемо у вигляді

тобто
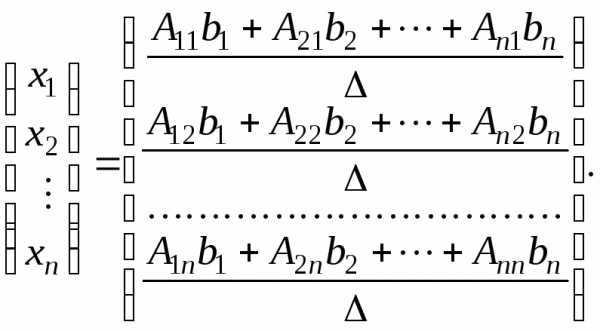
Звідси маємо, що
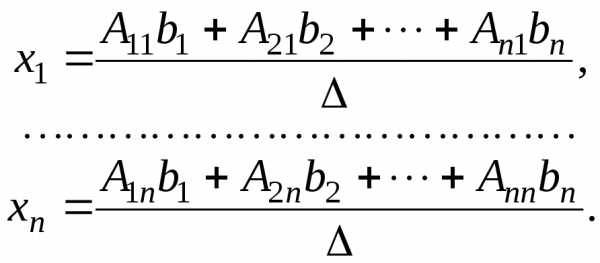
Але є розкладанням визначника
 за
елементами першого стовпця. Визначник
за
елементами першого стовпця. Визначник 
 заміною першого стовпця коефіцієнтів
стовпцем з вільних членів.
заміною першого стовпця коефіцієнтів
стовпцем з вільних членів. Отже, 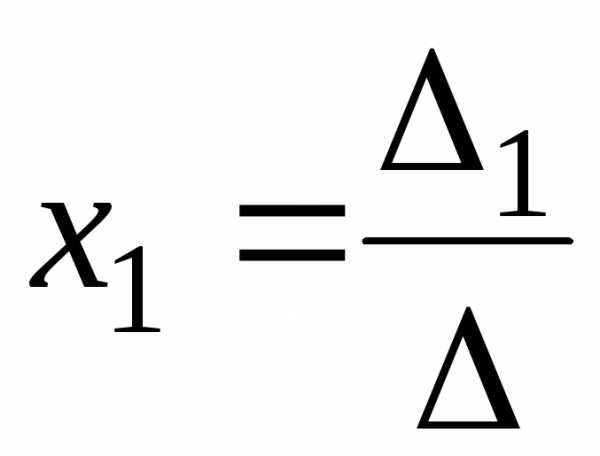 .
.
Аналогічно
можна показати, що 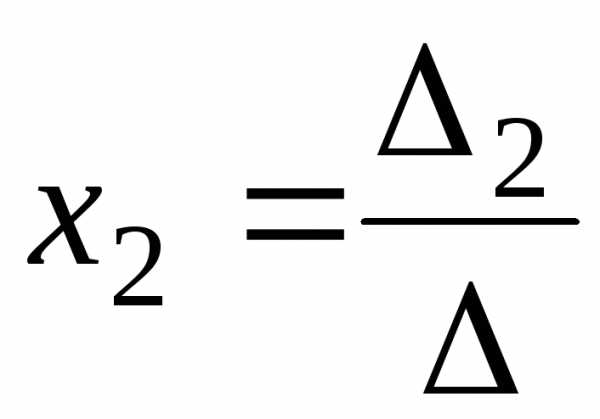 ,
де
,
де отримано з
отримано з шляхом заміни другого стовпця коефіцієнтів
стовпцем з вільних членів і т.д.:
шляхом заміни другого стовпця коефіцієнтів
стовпцем з вільних членів і т.д.:
.
Теорему доведено.
Приклад.
Розв’язати
систему 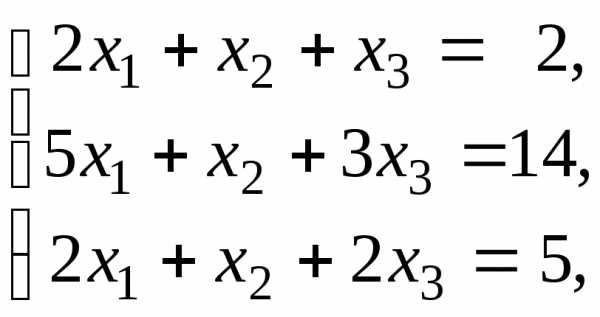 двома методами: 1) матричним способом;
2) за формулами Крамера.
двома методами: 1) матричним способом;
2) за формулами Крамера.
Розв’язання.
1. У матричному вигляді система має вигляд , де
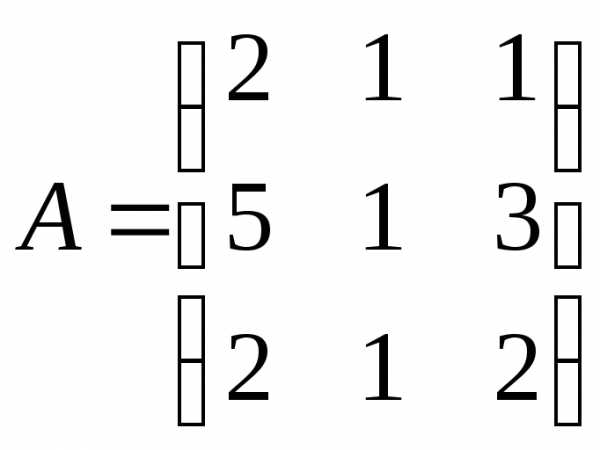
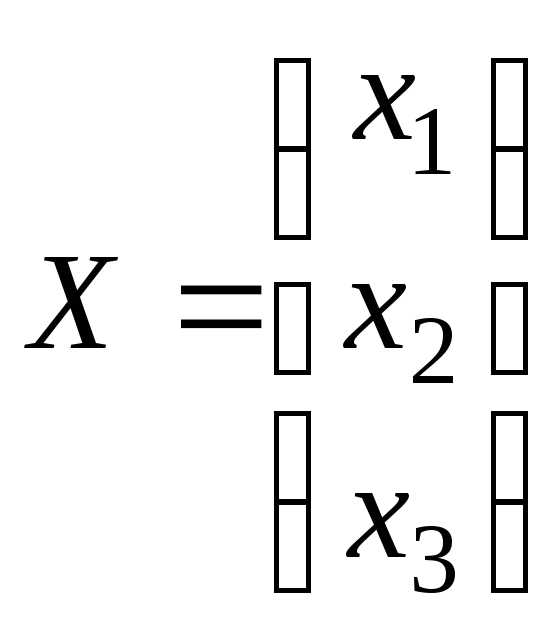 ,
, .
.З матричного рівняння . Розв’язання матричним методом можливо, якщо матрицяА є невиродженою, тобто при :
,
тобто
обернена матриця 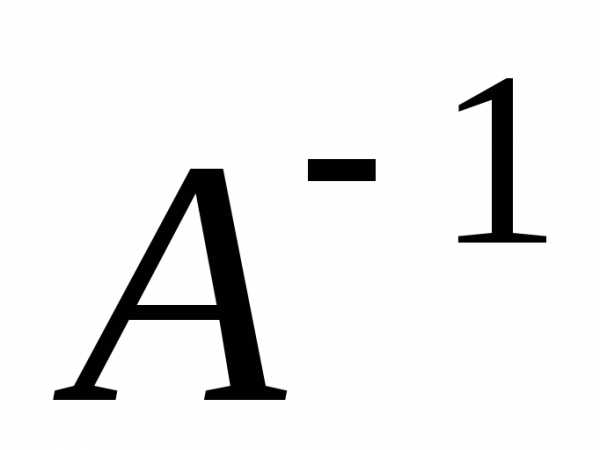 існує.
існує.
Знайдемо
обернену матрицю 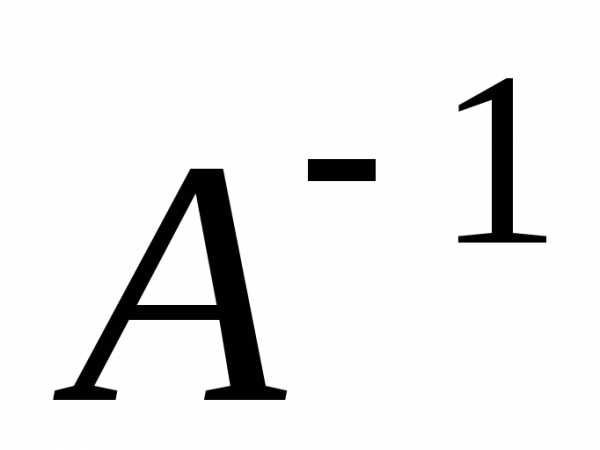 :
:
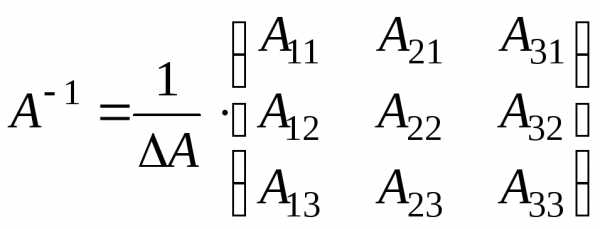 .
.
Обчислимо алгебраїчні доповнення:
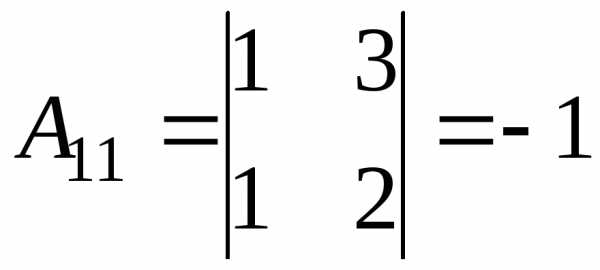 ;
; 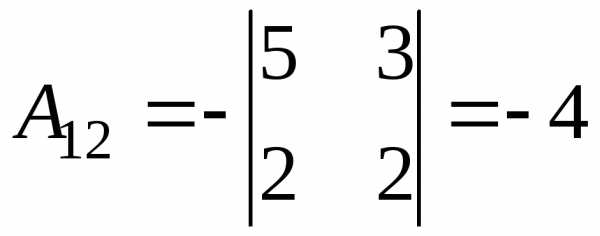 ;
;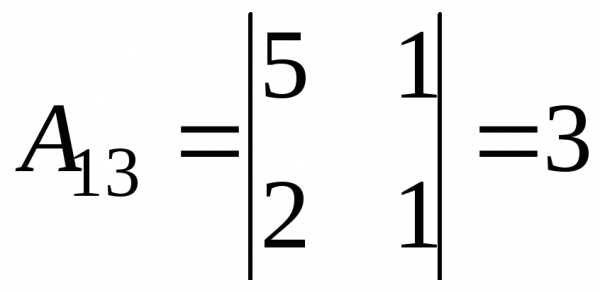 ;
;
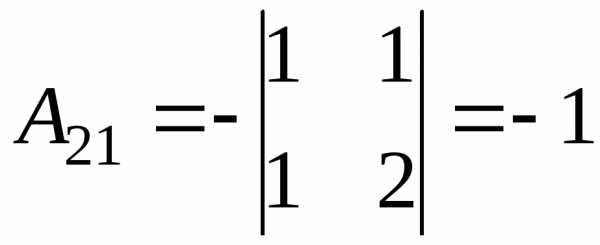 ;
; 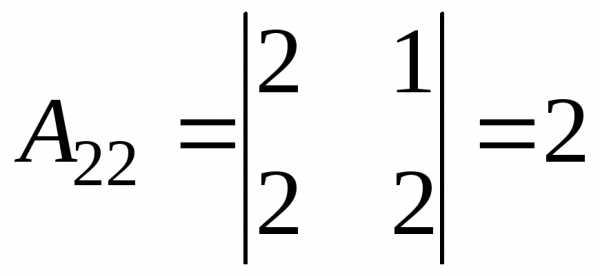
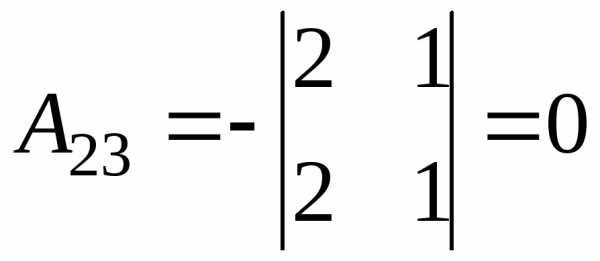 ;
; 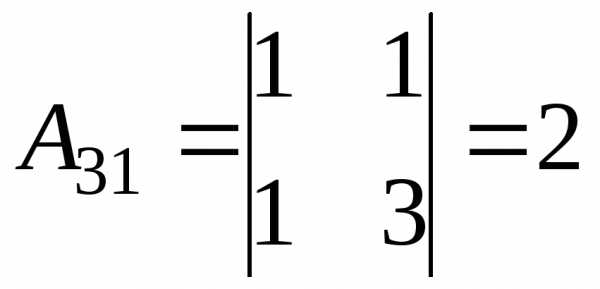 ;
; 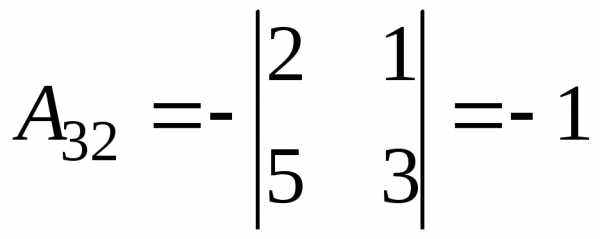 ;
;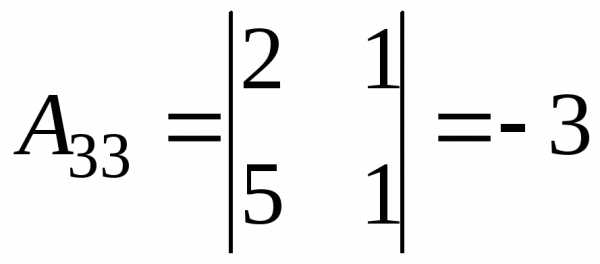 ;
;
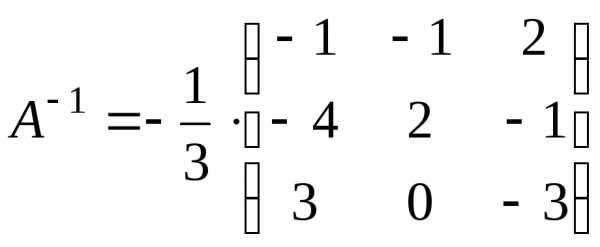 .
.
Тоді .
Таким
чином 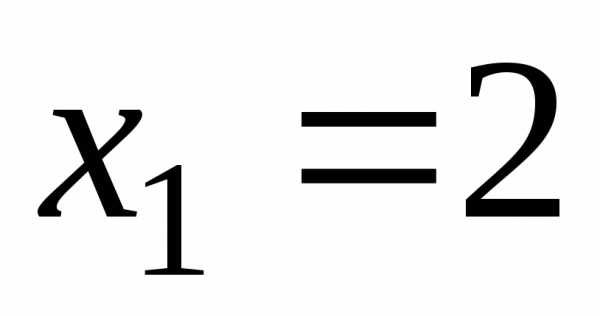 ,
,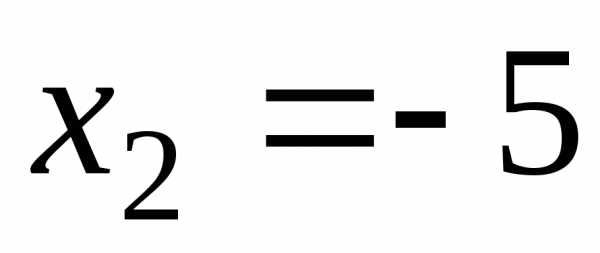 ,
,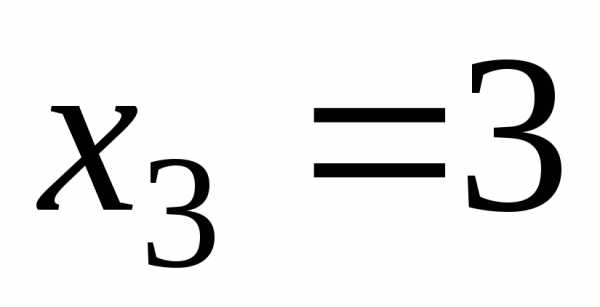 .
.
2. За формулами Крамера
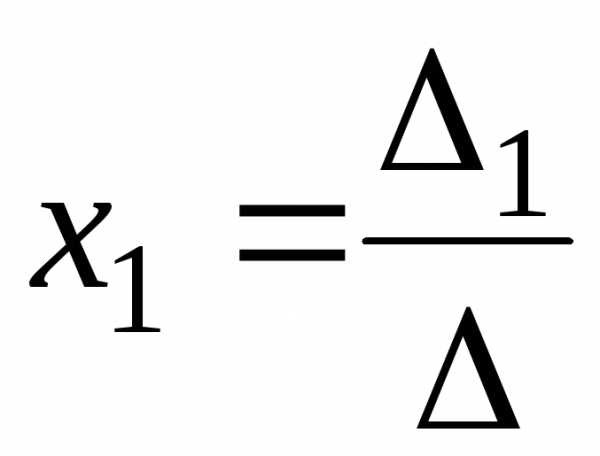 ,
, 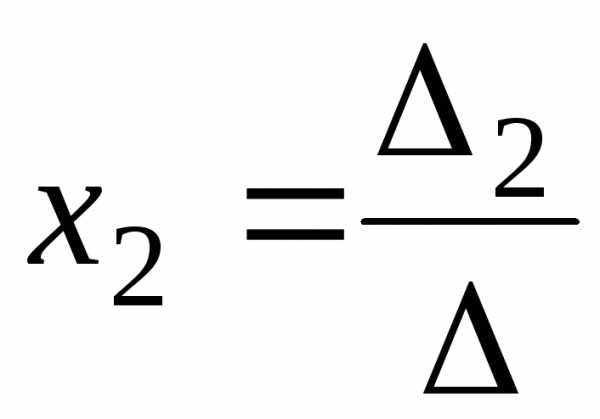 ,
,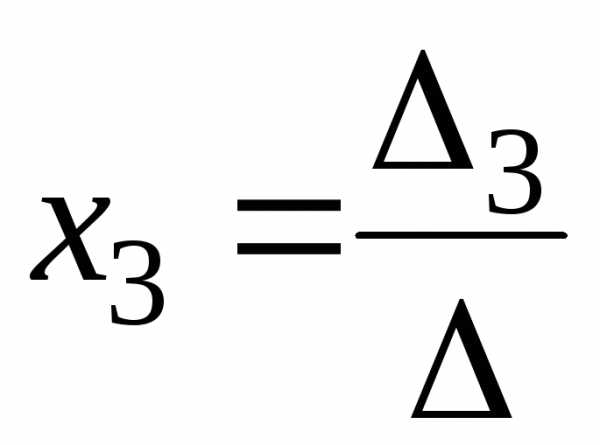 .
.
Визначник
системи  знайшли в попередньому пункті:
знайшли в попередньому пункті: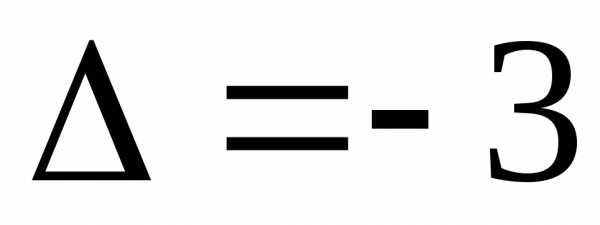 .
Обчислимо
.
Обчислимо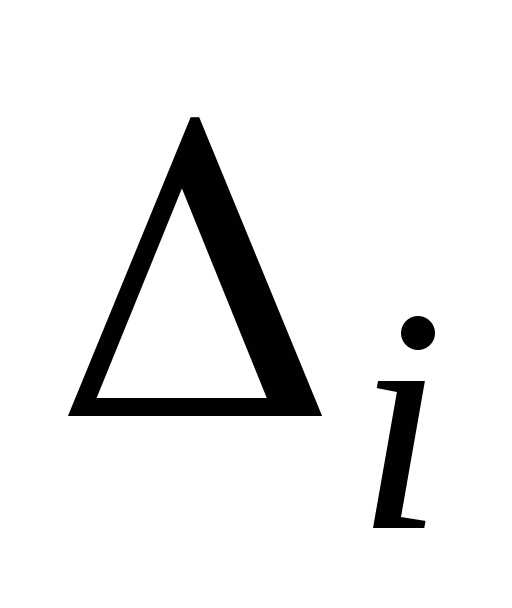
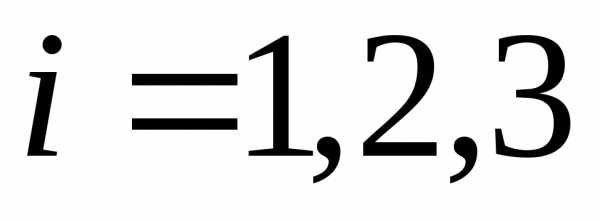 :
:;
;
.
Тоді 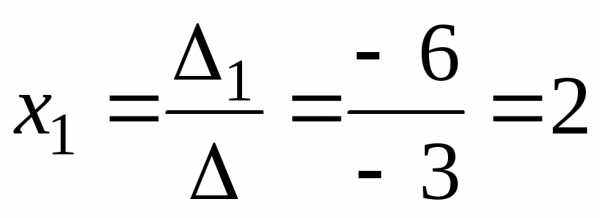 ,,
,,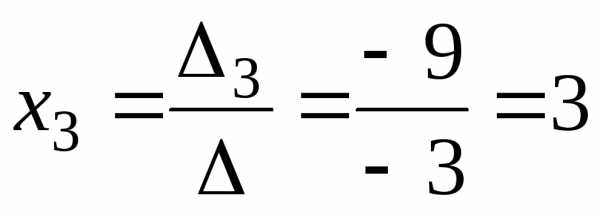 .
.
Правила практичного знаходження всіх розв’язків сумісної системи лінійних рівнянь випливають із наслідків теореми.
Алгоритм розв’язання довільної системи лінійних рівнянь
1. Знайти ранги основної й розширеної матриць системи. Якщо , то система несумісна.
2. Якщо ,
то система
сумісна. Виділяють базисний мінор
порядку 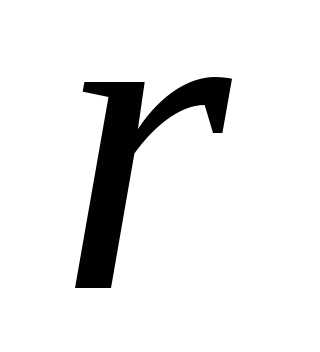 (нагадування: мінор, порядок якого
визначає ранг матриці, називається
базисним). Невідомі, коефіцієнти за яких
становлять базисний мінор, називаютьбазисними,
а інші (п –
(нагадування: мінор, порядок якого
визначає ранг матриці, називається
базисним). Невідомі, коефіцієнти за яких
становлять базисний мінор, називаютьбазисними,
а інші (п – 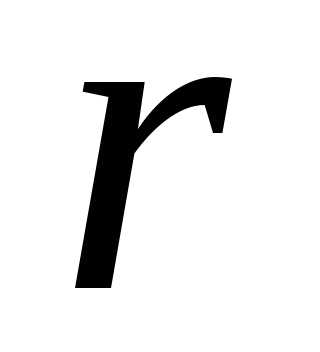 ) невідомих
називають вільними.
) невідомих
називають вільними.
3. Дану
систему замінюють рівносильною їй
системою, що складається з тих 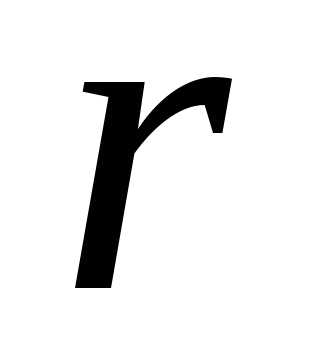 рівнянь, у які ввійшли елементи базисного
мінору (інші рівняння відкинути). Базисні
невідомі залишають ліворуч, а вільні
переносять у праві частини рівнянь.
рівнянь, у які ввійшли елементи базисного
мінору (інші рівняння відкинути). Базисні
невідомі залишають ліворуч, а вільні
переносять у праві частини рівнянь.
4. Якщо число базисних невідомих дорівнює числу невідомих системи, то система має єдиний розв’язок, і його знаходять або матричним способом, або за формулами Крамера.
5. Якщо число базисних невідомих не дорівнює числу невідомих системи, то система має незліченну множину розв’язків. Із системи, отриманої на кроці 3, знаходять вираження базисних невідомих через вільні. Надаючи вільним невідомим довільні значення, одержимо загальний розв’язок системи. Розв’язок, що виходить із загального при конкретних значеннях вільних невідомих, називається частинним розв’язком.
Приклад.
Дослідити на сумісність та розв’язати системи:
1) 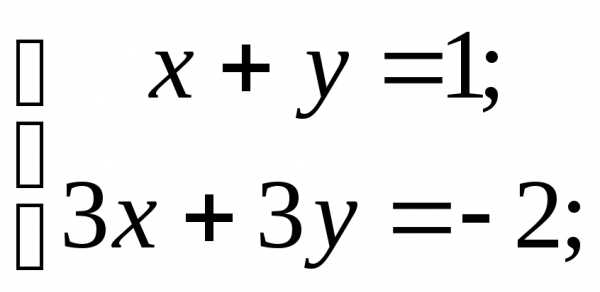 2)
2)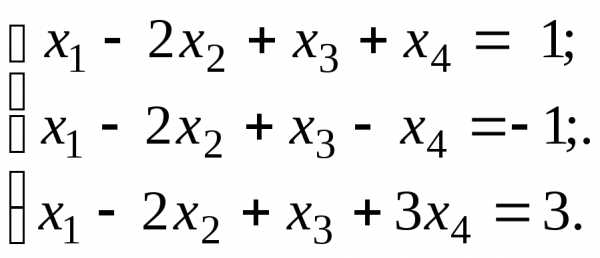
Розв’язання.
1)
через
те, що 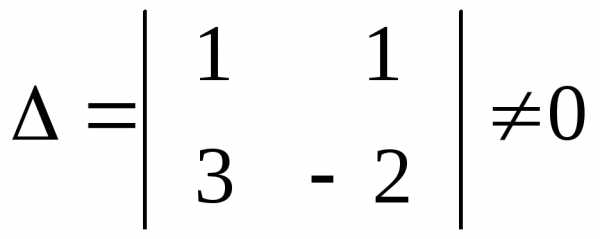 .
.
Таким чином, , отже, система несумісна.
2)
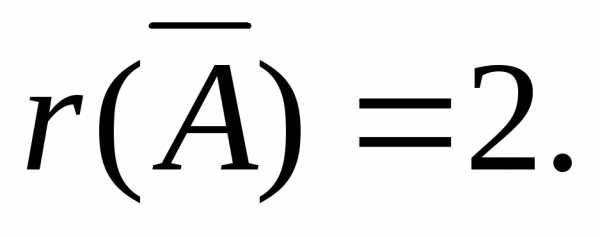
Через те, що , то система сумісна і базисних невідомих буде 2. Беремо два перших рівняння:
Виразимо
базисні невідомі 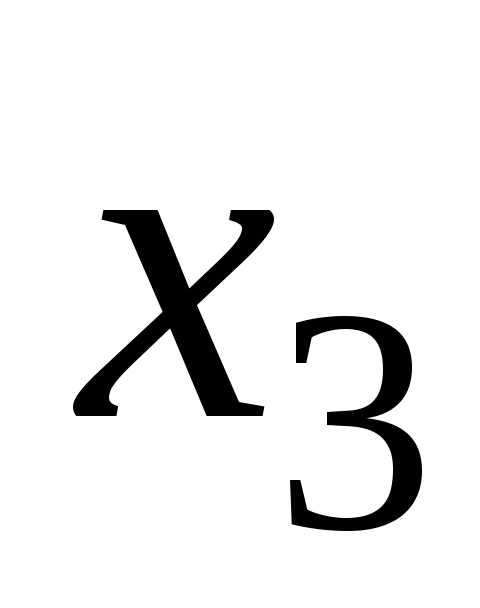 та
та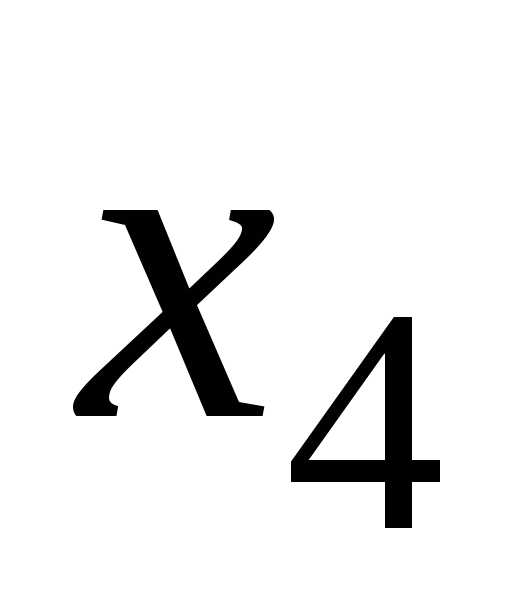 через
вільні
через
вільні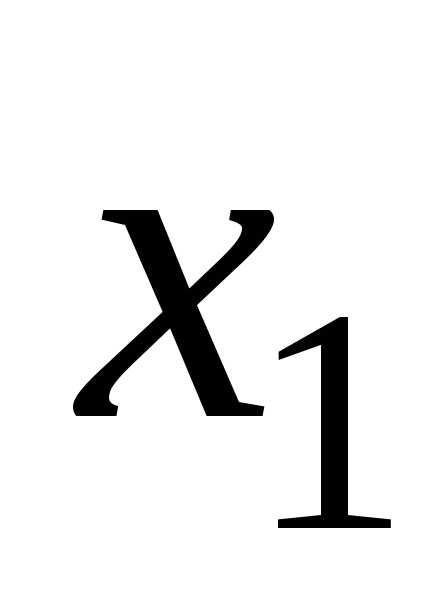 та
та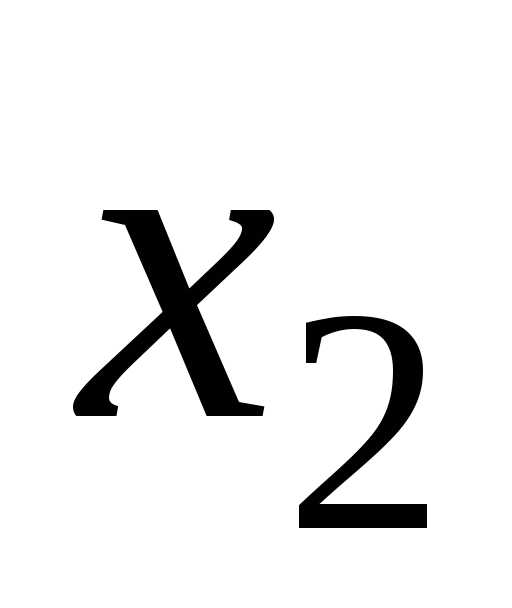 :
:
Використовуючи формули Крамера, маємо
, .
Отже,
,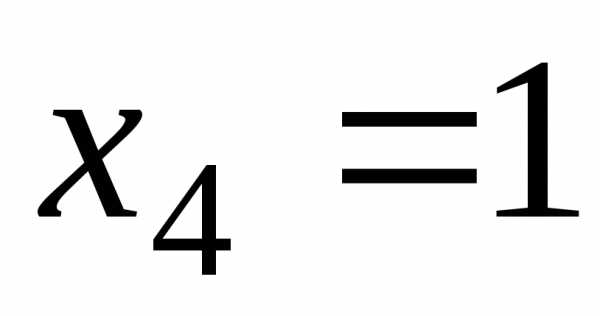 – загальнийрозв’язок.
Нехай,
наприклад, отримаємо
один
з
часткових
розв’язків:
– загальнийрозв’язок.
Нехай,
наприклад, отримаємо
один
з
часткових
розв’язків:
Контрольні запитання та завдання
1. Дайте визначення сумісної і несумісної, означеної і неозначеної системи алгебраїчних лінійних рівнянь.
2. Запишіть систему рівнянь у матричній формі.
3. Сформулюйте теорему Кронекера-Капеллі.
4. В чому полягає матричний спосіб розв’язання системи алгебраїчних рівнянь?
5. Дайте виведення формул Крамера.
6. Наведіть алгоритм розв’язання системи алгебраїчних рівнянь.
7. Які невідомі називають «вільними»?
8. Скільки базисних невідомих має система?
9. Скільки вільних невідомих має система?
studfiles.net
Матричний спосіб розв’язання слар
Систему 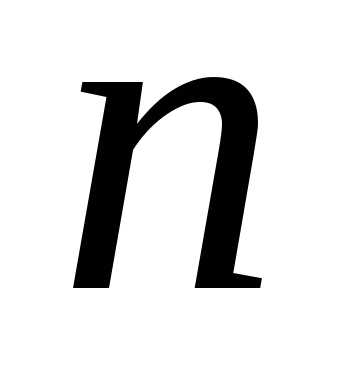 лінійних алгебраїчних рівнянь ізn невідомими (*) можна записати в матричному
виді:
,
деA – матриця системи, X – матриця-стовпець невідомих
,
аB – матриця-стовпець вільних членів. Якщо A – невироджена матриця, то після множення
ліворуч на
лінійних алгебраїчних рівнянь ізn невідомими (*) можна записати в матричному
виді:
,
деA – матриця системи, X – матриця-стовпець невідомих
,
аB – матриця-стовпець вільних членів. Якщо A – невироджена матриця, то після множення
ліворуч на 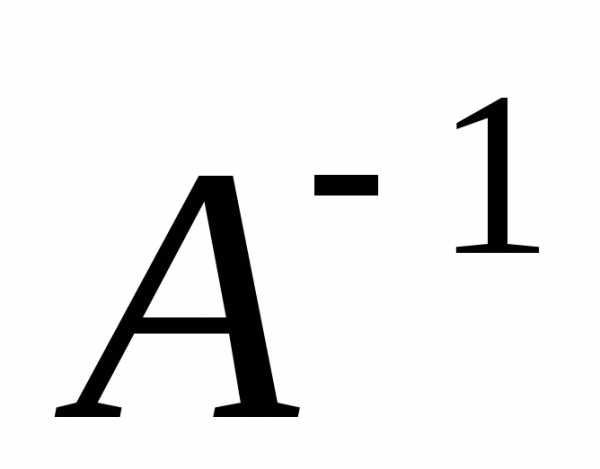 обидві частини матричного рівняння,
одержимо.
Taк як,
то очевидно
обидві частини матричного рівняння,
одержимо.
Taк як,
то очевидно
.
Приклади розв’язування задач
Розв’яжіть систему лінійних алгебраїчних рівнянь: а) за теоремою Крамера; б) матричним способом:
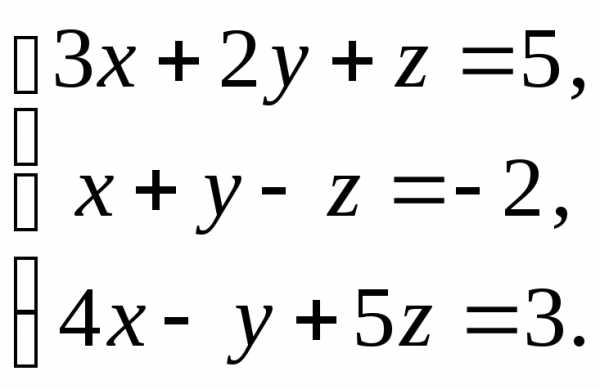
Розв’язання:
а)
Обчислимо визначник системи  й визначники
й визначники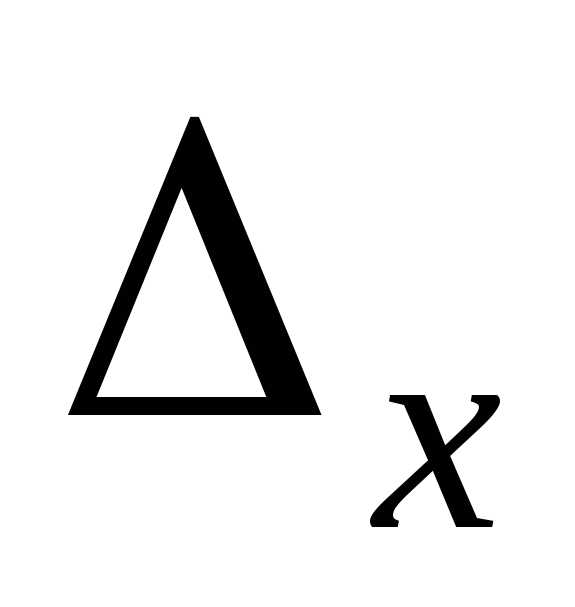 ,
,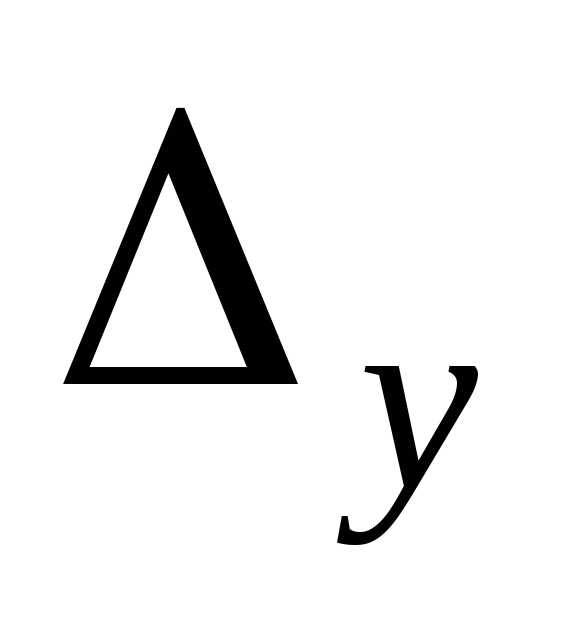 ,
, ,
що отримані з визначника
,
що отримані з визначника заміною першого, другого, третього
стовпців стовпцем вільних членів:
заміною першого, другого, третього
стовпців стовпцем вільних членів:
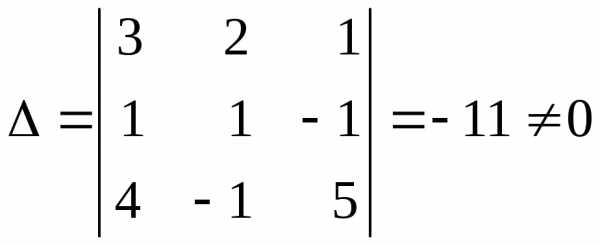 ,
,  ,
,
 ,
,  .
.
За формулами Крамера одержуємо єдиний розв’язок системи:
, 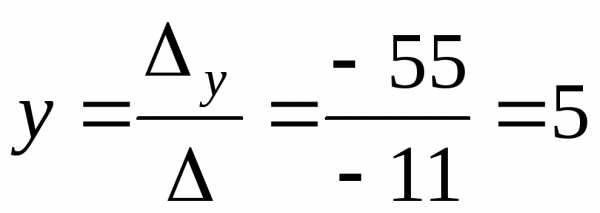 ,
,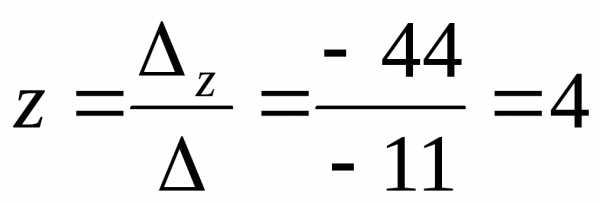 .
.
Відповідь: 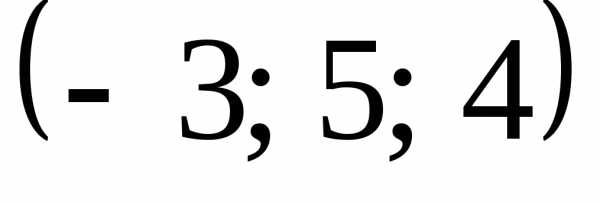 .
.
б) Перепишемо вихідну систему у вигляді
,
де 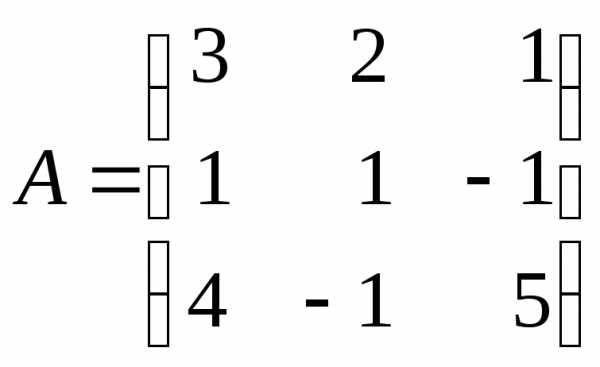 ,
,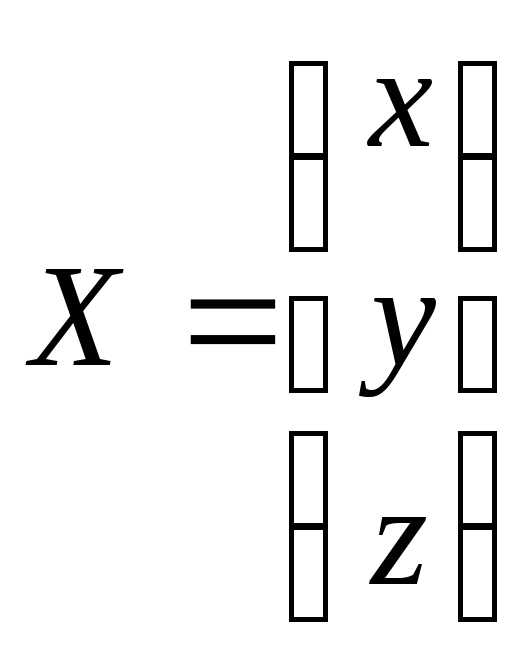 ,
,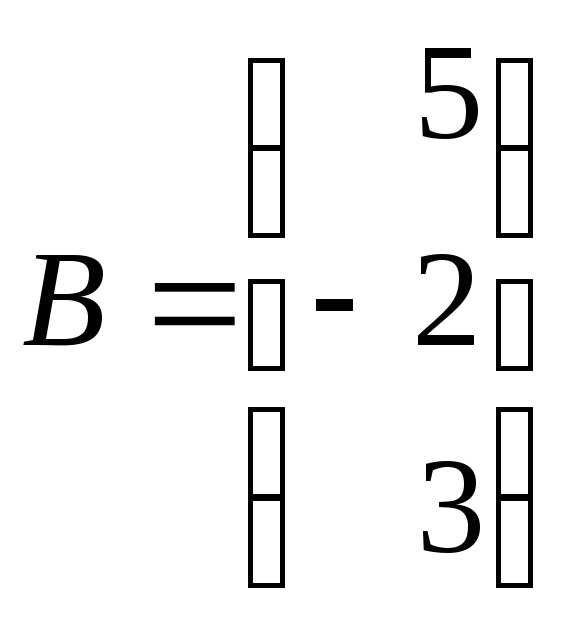 .
.
Оскільки 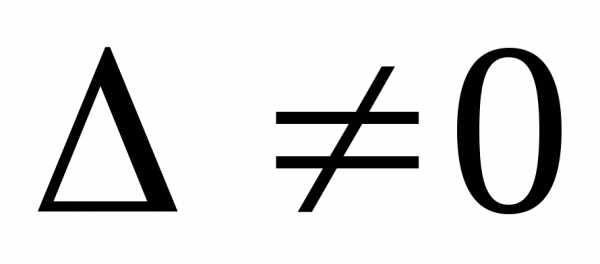 ,
то матриця
,
то матриця має обернену. Знайдемо її методом
алгебраїчних доповнень:
має обернену. Знайдемо її методом
алгебраїчних доповнень:
, ,,
, ,,
, ,,
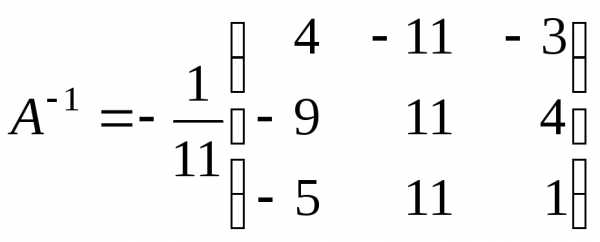 .
.
Знайдемо розв’язок:
.
Відповідь: 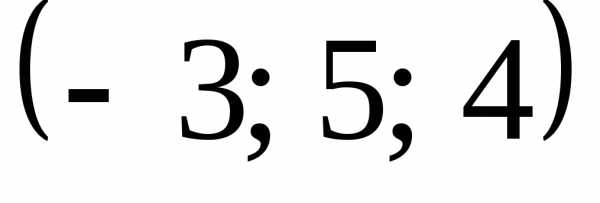 .
.
Розв’яжіть СЛАР: а) за правилом Крамера; б) шляхом зведення її до матричного рівняння. Порівняйте отримані результати.
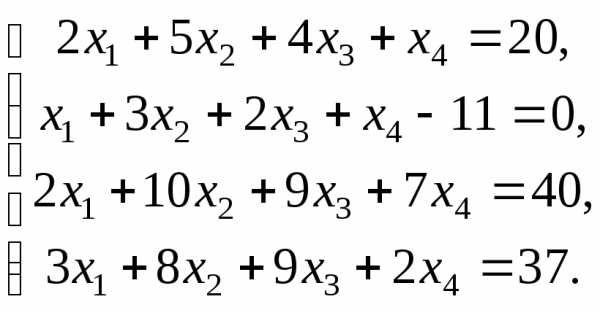
Розв’язання:
а) Знайдемо визначник матриці системи:
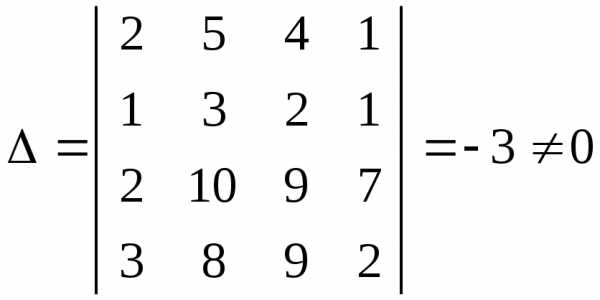 .
.
За
теоремою Крамера дана СЛАР має єдиний
розв’язок. Знайдемо значення визначників 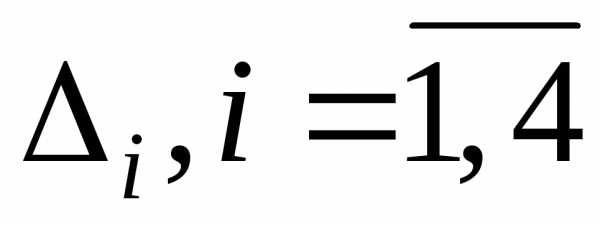 матриць, отриманих з вихідної заміною
матриць, отриманих з вихідної заміною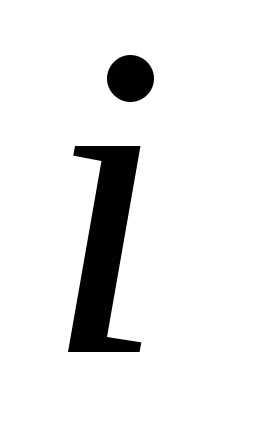 -ого
стовпця стовпцем вільних членів.
Отримаємо:
-ого
стовпця стовпцем вільних членів.
Отримаємо:
 ,
,  ,
,
 ,
,  .
.
Значення змінних знайдемо зі співвідношень:
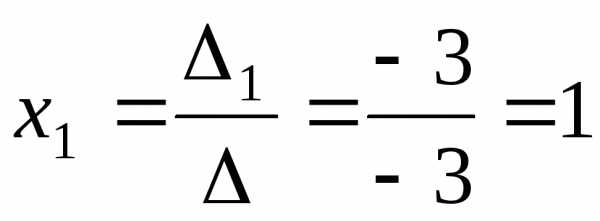 ,
, 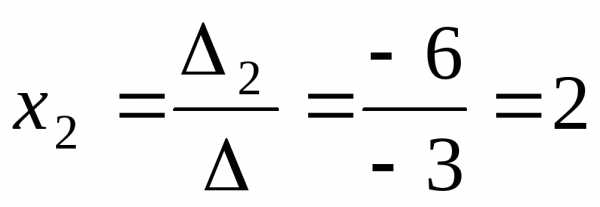 ,
,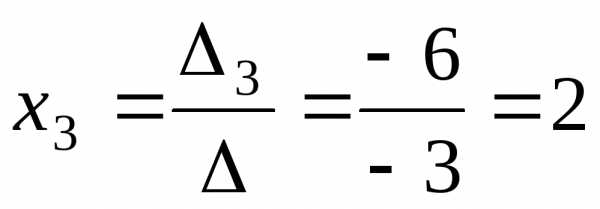 ,
,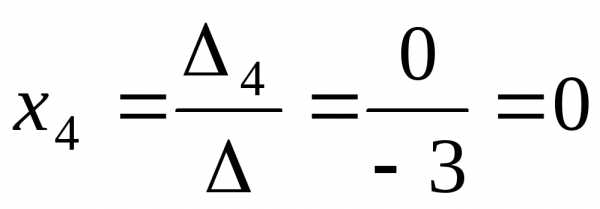 .
.
б) Запишемо вихідну систему у матричному вигляді:
.
На стор. 26-28 знайдено обернену матрицю:
.
Тоді:
.
Отже, . Як бачимо, розв’язки СЛАР, що знайдені різними методами, співпадають між собою.
Підстановкою
отриманих значень у вихідну систему
легко переконатись, що набір 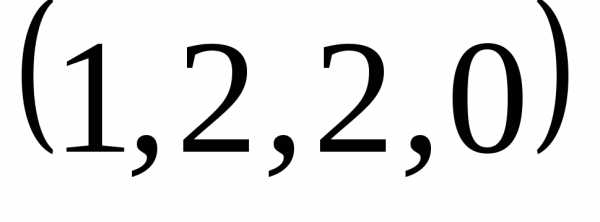 дійсно є її розв’язком.
дійсно є її розв’язком.
Задачі для самостійного розв’язування
Розв’яжіть наступні СЛАР за теоремою Крамера:
а)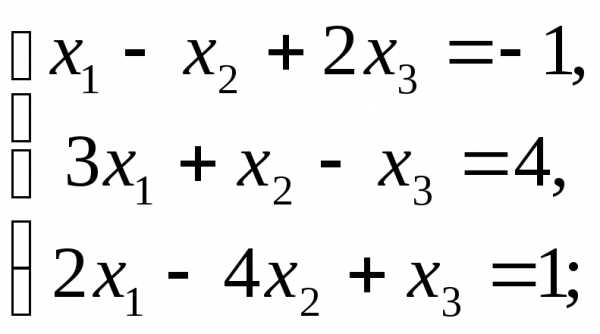 б)
б)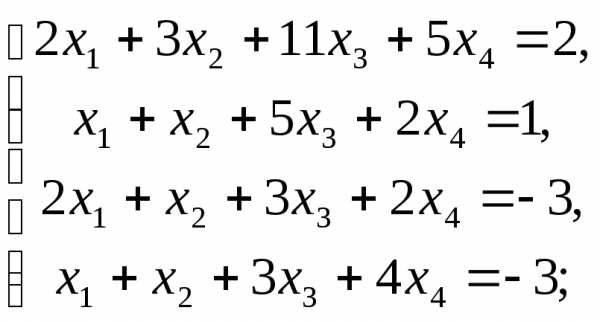 в)
в)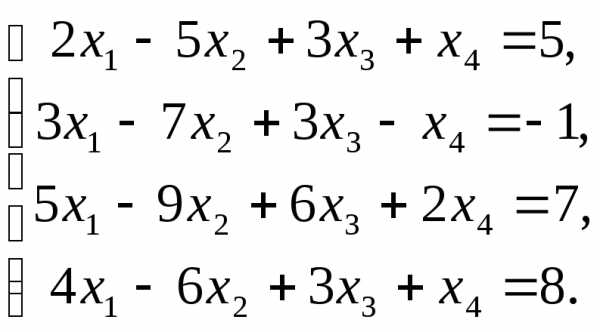
Якщо система визначена, то знайдіть її розв’язок: а) за теоремою Крамера; б) матричним методом:
1) 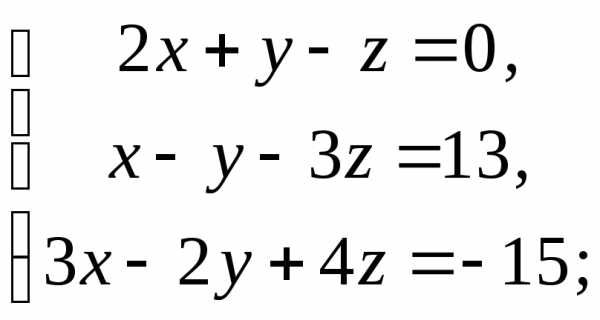 2)
2)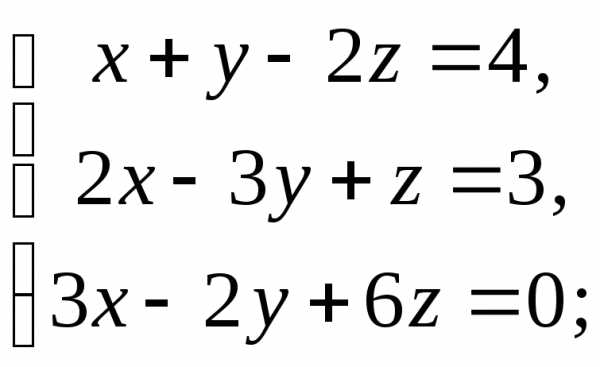 3)
3)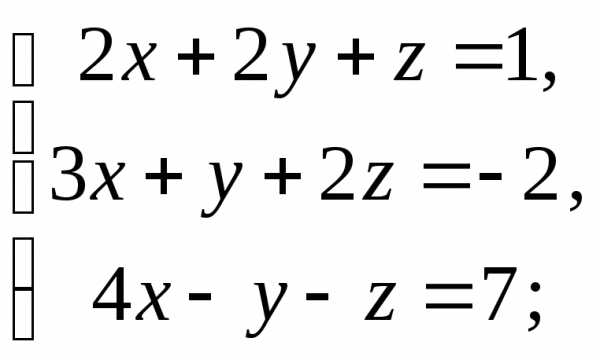
4) 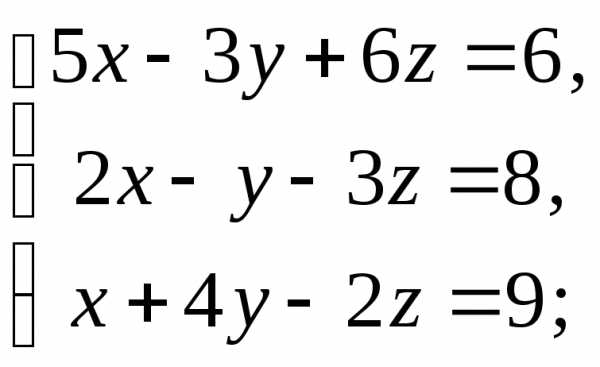 5)
5)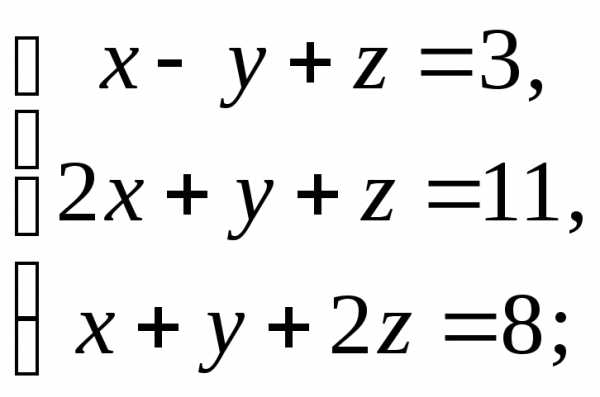 6)
6)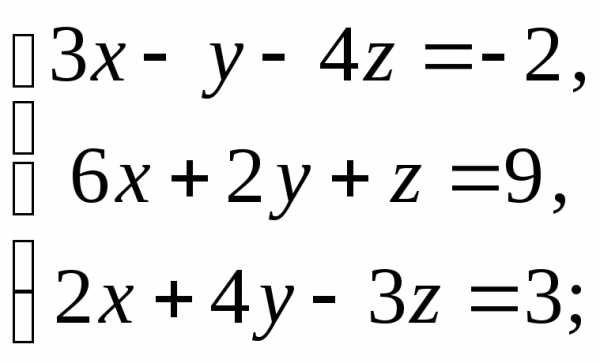
7) 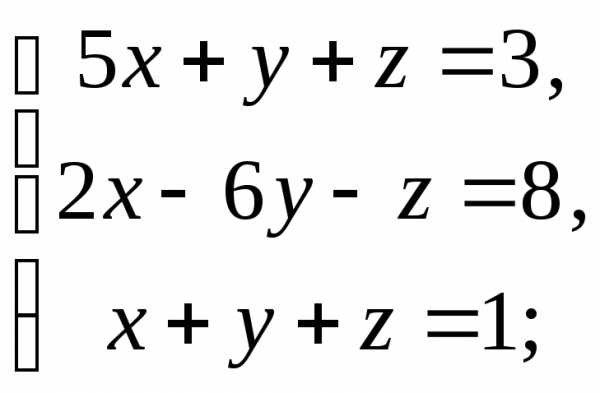 8)
8)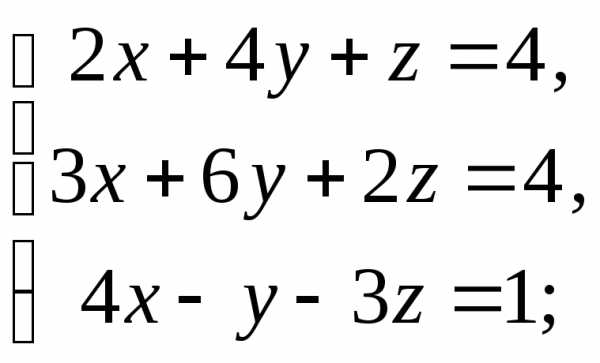 9)
9)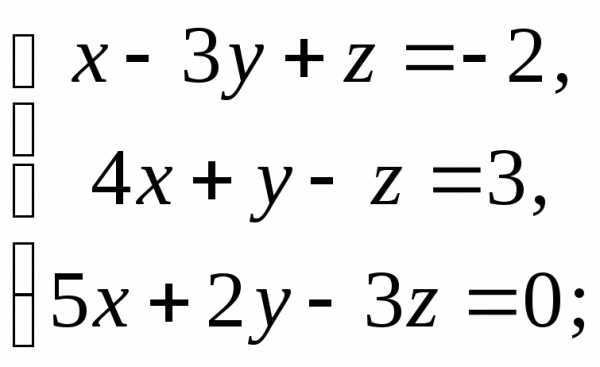
10) 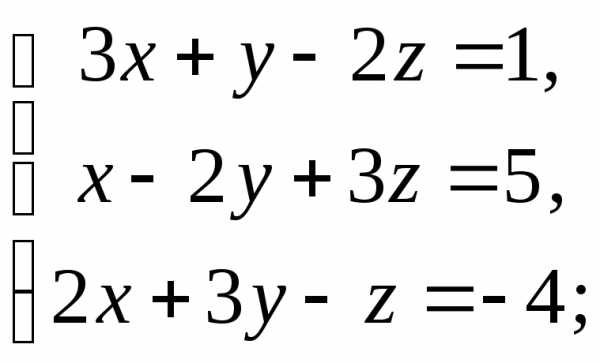 11)
11)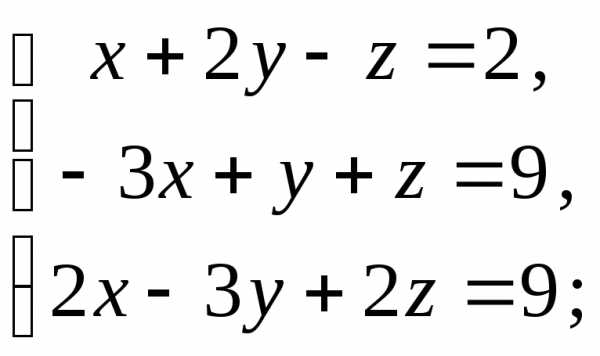 12)
12)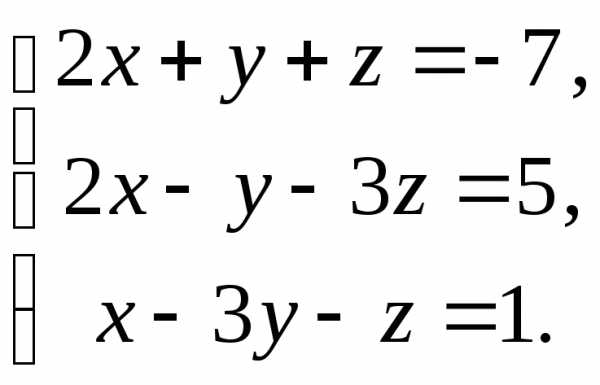
Практичне заняття № 5 Тема: Ранг матриці. Теорема Кронекера-Капеллі. Метод Гауса розв’язання слар
Елементарними перетвореннями рядів матриці називають: 1) переміна місцями двох рядків матриці; 2) додавання до елементів одного рядка відповідних їм елементів іншого, помножених на ненульове число.
Теорема. Якщо від матриці  до матриці
до матриці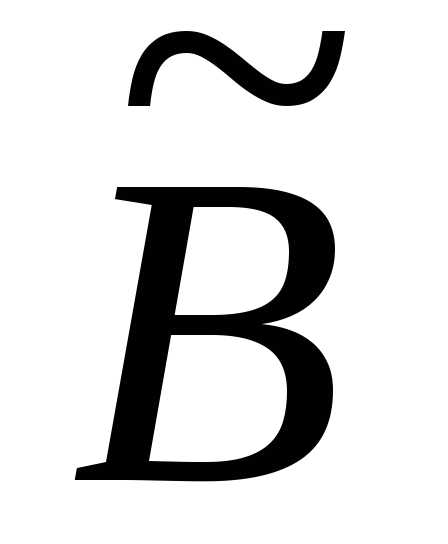 можна перейти скінченим числом
елементарних перетворень рядків, то
всякий розв’язок системи лінійних
алгебраїчних рівнянь, що відповідає
матриці
можна перейти скінченим числом
елементарних перетворень рядків, то
всякий розв’язок системи лінійних
алгебраїчних рівнянь, що відповідає
матриці ,
служить розв’язком системи з матрицею
,
служить розв’язком системи з матрицею і навпаки, тобто розглянуті системи
рівнянь еквівалентні.
і навпаки, тобто розглянуті системи
рівнянь еквівалентні.
Матриця називається ступінчастою, якщо в ній під кожним першим ненульовим елементом рядка стоять тільки нулі.
Рангом
матриці  називається число
називається число ненульових рядків в матриці ступінчастого
виду.
ненульових рядків в матриці ступінчастого
виду.
Теорема (теорема Кронекера-Капеллі) Система лінійних алгебраїчних рівнянь сумісна тоді й тільки тоді, коли ранг матриці системи дорівнює рангу розширеної матриці цієї системи, тобто .
Зауваження. 1) Якщо ранг матриці сумісної СЛАР дорівнює числу невідомих, то система має єдиний розв’язок, тобто є визначеною. 2) Якщо ранг матриці сумісної СЛАР менше числа невідомих, то система має нескінченну множину розв’язків, тобто є невизначеною.
Алгоритм розв’язку системи рівнянь (*) методом Гауса:
Запишемо розширену матрицю
 вихідної системи рівнянь.
вихідної системи рівнянь.Приведемо матрицю
 до ступінчастого виду за допомогою
елементарних перетворень рядків. Якщо
в отриманій ступінчастій матриці
до ступінчастого виду за допомогою
елементарних перетворень рядків. Якщо
в отриманій ступінчастій матриці є рядок, у якому перший ненульовий
елемент перебуває на останньому місці,
то вихідна система розв’язків не має
(несумісна).
є рядок, у якому перший ненульовий
елемент перебуває на останньому місці,
то вихідна система розв’язків не має
(несумісна).Якщо система рівнянь сумісна, то в системі рівнянь із матрицею
 необхідно відкинути рівняння, які
відповідають нульовим рядкам матриці
необхідно відкинути рівняння, які
відповідають нульовим рядкам матриці .
У рівняннях, що залишилися, виділяємо
головні невідомі (визначник, складений
з коефіцієнтів при них, не дорівнює
нулю), а члени з вільними невідомими
переносимо в праві частини.
.
У рівняннях, що залишилися, виділяємо
головні невідомі (визначник, складений
з коефіцієнтів при них, не дорівнює
нулю), а члени з вільними невідомими
переносимо в праві частини.Послідовно виражаємо головні невідомі через вільні, рухаючись від останнього рівняння до першого, отримаємо загальний розв’язок системи.
Надаючи вільним невідомим різні числові значення й обчислюючи відповідні значення головних невідомих, одержимо різні розв’язки вихідної системи лінійних алгебраїчних рівнянь, тобто отримаємо частинні розв’язки системи.
Приклад. Розв’яжіть системи лінійних алгебраїчних рівнянь:
1) 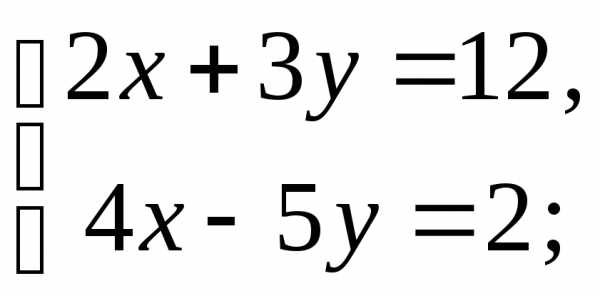 2)
2)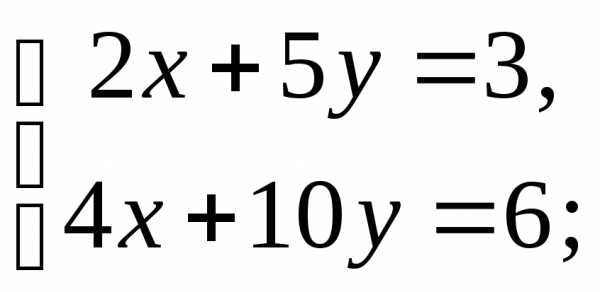 3)
3)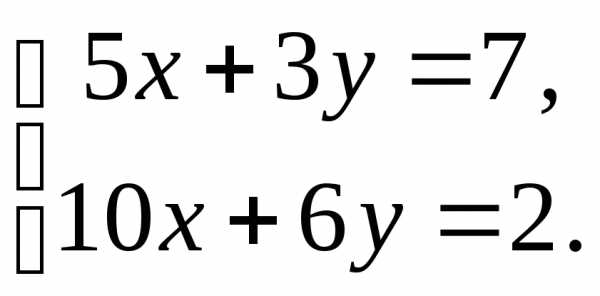
Відповідь: 1) 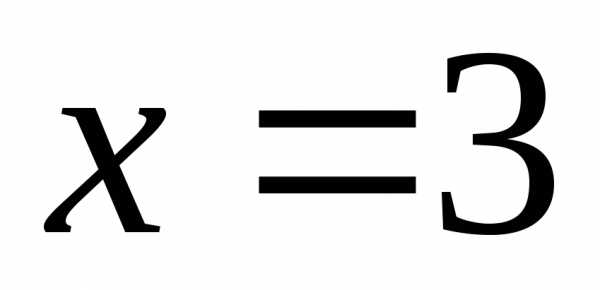 ,
,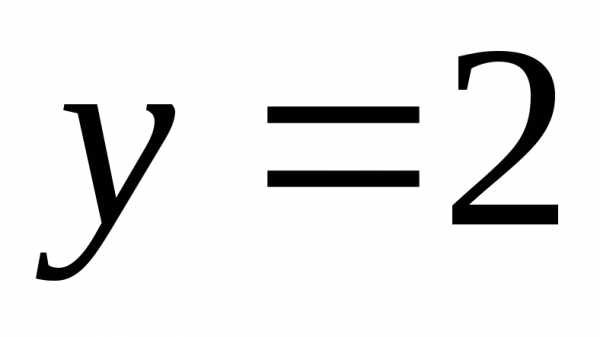 ;
2);
3)
;
2);
3) .
.
studfiles.net
Матриці та матричні рівняння – Механіко-математичний факультет
Тип: На вибір студента
Кафедра: алгебри і логіки
Навчальний план
| Семестр | Кредити | Звітність |
| 7 | 4 | Іспит |
Лекції
Практичні
Опис курсу
Метою спеціальної дисципліни “Матриці та матричні рівняння” є вивчення питань про існування, єдиність та знаходження розв’язків різних типів лінійних матричних рівнянь та їх застосування в різних задачах лінійної алгебри, теорії кілець, теорії диференціальних рівнянь.
Завдання дисципліни: поглибити підготовку, одержану в процесі вивчення нормативної дисципліни “Лінійна алгебра”, а саме акцентувати увагу на структурі алгебри матриць над різними полями, матрицях спеціального вигляду, вивчити поняття прямого (кронекерівського) добутку матриць і його властивості з метою застосування його до дослідження питання про існування, єдиність і розв’язування лінійних матричних рівнянь.
У результаті вивчення навчальної дисципліни “Матриці та матричні рівняння” студент повинен
знати: основні поняття теорії матриць над різними полями і їх застосування до питання про наявність розв’язків лінійних матричних рівнянь та методи розв’язування цих рівнянь;
вміти: досліджувати питання про існування та єдиність розв’язків лінійних матричних рівнянь на основі поняття спектру матриці, її жорданової форми, подібності матриць, розв’язувати різні типи лінійних матричних рівнянь залежно від структури їхніх матричних коефіцієнтів, а також від полів, над якими розглядаються ці матриці.
Рекомендована література
Базова
- Гантмахер Ф.Р. Теорія матриц. М.: Наука, 1967. –549 с.
- Завало С.Т. Курс алгебри. К.: Вища школа,1985. – 503 с.
- Зеліско В.Р., Зеліско Г.В. Основи лінійної алгебри і аналітичної геометрії. – Львів: Львівський національний університет імені Івана Франка, 2011. – 326 с.
- Ланкастер П. Теорія матриц. М.: Наука, 1978. – 280 с.
- Хорн Р. Джонсон Ч. Матричный анализ, М.: Мир, 1989. – 655 с.
Допоміжна
- Шестопал В.Е. Решение матричного уравнения AX−XB=C // Матем. заметки, 1976, Т. 19, вып 3, с. 449-451.
- Gustafson W. H. Rot’s theorem over commutative ring // Linear Algebra and Appl., – 1979, – v. 23, -P. 245-251.
- Roth W. E. The equation AX-YB=C and AX-XB=C in matrices // Proc. Amer. Math. Soc., 1952, № 3, – P. 392-396.
new.mmf.lnu.edu.ua

 вихідної системи рівнянь.
вихідної системи рівнянь. до ступінчастого виду за допомогою
елементарних перетворень рядків. Якщо
в отриманій ступінчастій матриці
до ступінчастого виду за допомогою
елементарних перетворень рядків. Якщо
в отриманій ступінчастій матриці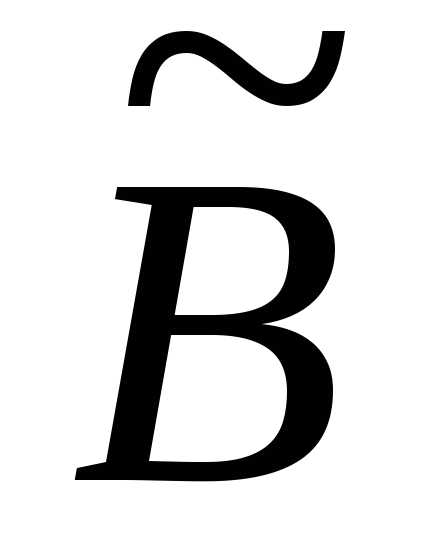 є рядок, у якому перший ненульовий
елемент перебуває на останньому місці,
то вихідна система розв’язків не має
(несумісна).
є рядок, у якому перший ненульовий
елемент перебуває на останньому місці,
то вихідна система розв’язків не має
(несумісна).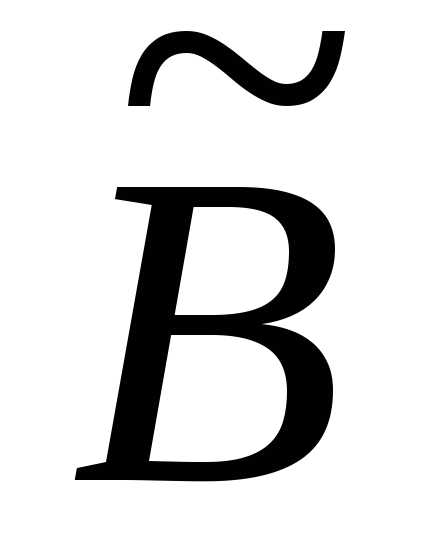 необхідно відкинути рівняння, які
відповідають нульовим рядкам матриці
необхідно відкинути рівняння, які
відповідають нульовим рядкам матриці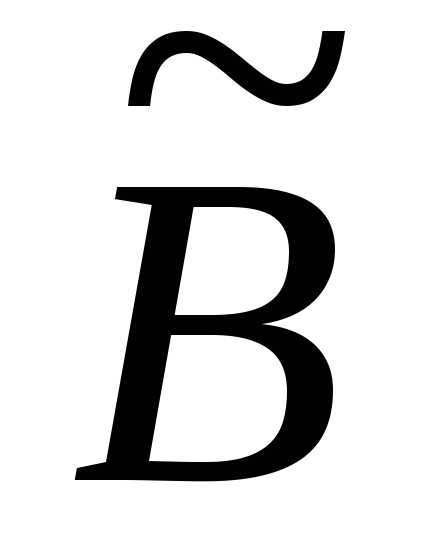 .
У рівняннях, що залишилися, виділяємо
головні невідомі (визначник, складений
з коефіцієнтів при них, не дорівнює
нулю), а члени з вільними невідомими
переносимо в праві частини.
.
У рівняннях, що залишилися, виділяємо
головні невідомі (визначник, складений
з коефіцієнтів при них, не дорівнює
нулю), а члени з вільними невідомими
переносимо в праві частини.