Пример конечного множества чисел – Придумайте примеры конечных и бесконечных множеств. Задайте их, указав характеристическое свойство и перечислив элементы,

Конечные и бесконечные множества.

Прежде всего, множества можно разделить на конечные и бесконечные.

Конечным множеством называется множество, состоящее из конечного числа элементов. Примерами конечных множеств могут быть множество корней алгебраического уравнения n-й степени, множество букв русского алфавита, множество персонажей романа Михаила Булгакова «Мастер и Маргарита», множество атомов Солнечной системы. Причем неважно, известно число элементов множества или нет, главное, чтобы оно существовало.

В математике приходится сталкиваться и с другими – неконечными, или, как принято говорить, с бесконечными множествами. Множество называется бесконечным, если оно состоит из бесконечного числа элементов. Таковы, например, множество всех натуральных чисел, множество точек окружности, множество прямых, проходящих через точку плоскости, и т.д.

К конечным множествам относится и множество, не содержащее элементов вообще. Такое множество называют пустым и обозначают Æ. Необходимость его введения вызвана тем, что, определяя множество с помощью некоторого условия, мы не всегда можем сказать заранее, содержит ли оно элементы или нет. Например, в 101-й группе может не быть отличников и тогда А={а | а – отличник 101-й группы}=Æ.

Пустым множеством является и множество корней системы уравнений:

Х^2 + 1 = 0

Без введения пустого множества мы не могли бы, скажем, говорить о множестве корней произвольного уравнения, не убедившись предварительно, что данное уравнение имеет хотя бы один корень. Существование этого понятия сокращает и упрощает формулировки многих теорем, облегчает введение новых понятий.

 

3. Равенство множеств. Подмножества. Способы задания множеств.

Множество однозначно определяется своими элементами. Поэтому множества А и В следует считать равными лишь в том случае, когда они состоят из одних и тех же элементов, т.е. тогда и только тогда, когда . Например, если А={а, b, с, d} и В={b, d, c, a}, то А=В. В частности, порядок расположения элементов в записи множеств при их сравнении во внимание не принимается. Рассмотрим еще пример. Пусть в плоскости заданы две точки: А и В. Обозначим середину отрезка АВ через O. Рассмотрим два множества: и Очевидно, что X=Y, так как оба множества представляют собой множество точек срединного перпендикуляра к отрезку АВ. Особо следует отметить, что каждый объект может быть элементом множества только один раз. Пусть, например, X ={х|х -гласный звук слова «математика»} . Выписывая все гласные звуки, получим: {а, е, а, и, а}. Звук «а» перечислен трижды. Вместе с тем ясно, что все звуки «а» тождественны, так что X ={а, е, и}. Имеем: {а, е , а ,и, а}={а, е, и }.

Определение. Пусть A и B — какие-то два множества. Если любой элемент x множества A является элементом множества B, то говорят, что множество A является подмножеством множества B и обозначают этот факт следующим образом или .

Это же определение можно переписать на языке кванторов «если элемент x принадлежит множеству A, то x принадлежит множеству B». Из введенного определения очевидно следует утверждение, если и , то A = B, т.е. множества A и B состоят из одних и тех же элементов.

Пустое множество по определению считается подмножеством любого множества множества A имеем, что .

Определение. Подмножество A множества B, отличное от самого множества B и называется собственным подмножеством.

На языке кванторов это записывается следующим образом: .

Это, так называемое, «строгое» включение множества A в множество B.

Способы задания множеств.

1) Перечислением — и перечислении множества его элементы принято заключать в фигурные скобки:

{2,4,6,…} — множество четных чисел,

{3,6,9,…}— множество чисел кратных трем.

Под многоточием в данных случаях подразумеваются все последующие числа: в первом случае — четные, а во втором — кратные трем.

2) Описание свойств — для задания (описания) некоторого множества

X, состоящего из элементов, обладающих свойством

α, используют

запись X={x |α(x)}. Читается как: «

X — множество элементов

x таких, что

α(x)».

Например, Y={y | y∈N и y<7} — множество натуральных чисел, меньших 7.

Числовые множества.

Множество натуральных чисел N включают числа вида 1, 2, 3 и т.д., которые используются для счёта предметов.

Множество целых чисел Z состоят из натуральных чисел 1, 2, 3,…, числа 0 и чисел, противоположных к натуральным: -1, -2, -3,… .

Множество рациональных чисел Q включают в себя выше перечисленные множества и числа вида m/n, где m и n целые числа. Рациональные числа могут быть записаны в виде конечных или бесконечных периодических десятичных дробей.

К множеству иррациональных чисел I относятся числа, которые представляются в зиде конечных десятичных дробей или в виде бесконечной периодической дроби. Например: число п .

При объединении множества рациональных чисел Q и множества иррациональных чисел Iобразуется множество действительных чисел R.

Действительные числа можно изображать в виде точек на числовой прямой. Чтобы задать числовую прямую необходимо отметить на прямой точку, которой будет соответствовать число 0- начало отсчёта, а затем выбрать единичный отрезок и указать положительнео направление.

Каждой точке на координатной прямой соответствует число, которое определяется как длина отрезка от начала отсчета до рассматриваемой точки, при этом за единицу измерения принимается единичный отрезок. Это число -координата точки. Если точка взята справа от начала отсчета, то ее координата положительная, а если слева — отрицательная. Например точки О и А имеют координаты 0 и 2, соответственно, что можно записать так: 0(0), А(2).

Модуль или абсолютная величина числа х обозначается х . Модуль числа всегда положителен. Определение модуля можно записать с помощью системы:

В геометрическом смысле модуль х представляет собой расстояние отточки А(х) до начала координат.

 



infopedia.su

Эквивалентность множеств. Счетные и несчетные множества

Определение. Мощностью конечного множества называется число элементов в этом множестве.

Обозначение. Мощность множества будем обозначать .

Любые два конечные множества можно сравнивать по их мощности.

Пример 1. Пусть , . Тогда , так как .

Однако для бесконечных множеств такой способ сравнения не подходит (возьмем, например, множество прямоугольников и множество рациональных чисел).

Рассмотрим способ сравнения множеств, применимый как для конечных, так и для бесконечных множеств. Для этого нам понадобится следующее определение.

Определение. Говорят, что между множествами и установлено взаимно однозначное соответствие, если:

1) каждому элементу множества соответствует только один элемент множества ;

2) каждый элемент множества при этом соответствует некоторому элементу множества ;

3) разным элементам множества соответствуют разные элементы множества .

Тогда можно определить и эквивалентные множества:

Определение. Множества и называются эквивалентными или равномощными, если между ними можно установить взаимно однозначное соответствие.

Таким образом, мы имеем теперь возможность сравнивать по количеству элементов как конечные, так и бесконечные множества.

Приведем несколько примеров.

Пример 2. Покажем, что множество натуральных чисел эквивалентно множеству четных положительных чисел. Для этого установим между этими множествами взаимно однозначное соответствие следующим образом:

   

иначе: каждому элементу поставим в соответствие элемент множества четных положительных чисел.

Так как множество четных положительных чисел является подмножеством множества натуральных чисел, то этот пример показывает, что бесконечное множество может быть эквивалентно своему подмножеству. В случае конечных множеств такая ситуация невозможна: между конечными множествами и можно установить взаимно однозначное соответствие тогда и только тогда, когда .

Пример 3. Покажем, что множество целых чисел эквивалентно множеству натуральных чисел . Для этого установим между этими множествами взаимно однозначное соответствие следующим образом:

   

иначе: каждому элементу поставим в соответствие элемент , если , и элемент , если множества натуральных чисел.

Определение. Множество называется счетным, если оно эквивалентно множеству натуральных чисел.

Иначе говоря, множество счетно, если все элементы этого множества можно занумеровать. Таким образом, множества четных положительных чисел и множество целых чисел счетны.

Пример 4. Покажем, что множество положительных рациональных чисел счетно. В самом деле, запишем каждое положительное рациональное число в виде несократимой дроби, запишем его в бесконечную таблицу, а затем перенумеруем числа в таблице способом, указанным на рис. 4:

Рис. 4

   

Пример 5. Множества

   

счетны, а следовательно, эквивалентны. В самом деле, установим взаимно однозначное соответствие следующим образом:

   

Пример 6. Любой отрезок эквивалентен отрезку . Искомое взаимно однозначное соответствие можно установить как аналитически, например, формулой:

   

так и геометрически (см. рис. 5):

Рис. 5

Пример 7. Установим взаимно однозначное соответствие между точками интервала и точками полуинтервала . Заметим, что множество и множество равны (множества и определены в примере 4; обозначим . Тогда , . Пусть . Если , то поставим ему в соответствие по закону, описанному в примере 4; если же , то поставим ему в соответствие себя: . Таким образом, устанавливается взаимно однозначное соответствие между и . Следовательно, множества и эквивалентны.

В заключение заметим, что не все бесконечные множества являются счетными. Так, например, можно доказать, что множество точек любого отрезка не является счетным.

Задачи.

1. Докажите, что множество рациональных чисел счетно.

2. Докажите, что множества и равномощны.

3. Установите взаимно однозначное соответствие между элементами множеств и .

hijos.ru

Конечные и бесконечные множества — Приведите по 2-3 примера конечных, бесконечных и пустых множеств — 22 ответа



Бесконечное множество

В разделе Домашние задания на вопрос Приведите по 2-3 примера конечных, бесконечных и пустых множеств заданный автором

Ёергио лучший ответ это Конечные множества:
1. Зрители в зале,
2. Множество корней 5-й степени из числа (на множестве комплексных чисел) .
3. Множество самолетов отлетающих за неделю из аэропорта.
Бесконечные множества:
1. Множество звезд вселенной.
2. Множество натуральных чисел.
Пустые множества:
1. Множество действительных решений уравнения х^2+4=0
2. Множество студентов 8 курса.

Ответ от 22 ответа[гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Приведите по 2-3 примера конечных, бесконечных и пустых множеств

Ответ от сложносочиненный[активный]
конечное множество — множество чисел (1,2,3,4,5), бесконечное множество — множество действительных чисел (-бесконечность; 0) пустое множество — пересечение интервалов (-бесконечность; 1) и (3; + бесконечность) бесконечность пишется спец. знаком перевернутая цифра 8

Ответ от Европейский[новичек]
К пустому множеству относится весь открытый ряд чисел, его подмножества, не калиброванные базовыми векторами ПСО (Привилегированной системы отсчета).

Ответ от 2 ответа[гуру]

Привет! Вот еще темы с нужными ответами:

Бесконечное множество на Википедии
Посмотрите статью на википедии про Бесконечное множество

Конечное множество на Википедии
Посмотрите статью на википедии про Конечное множество

Пустое множество на Википедии
Посмотрите статью на википедии про Пустое множество

 

Ответить на вопрос:

22oa.ru

1.3.5. Мощности бесконечных множеств. Счетные множества

Определение. Говорят, что множества А и В имеют одинаковую мощность (или, что они равномощны), если между А и В можно установить биекцию. Множества, равномощные множеству натуральных чисел, называются Счетными.

Установить биекцию с множеством натуральных чисел N фактически означает: сопоставить каждому элементу рассматриваемого множества номер, т. е. пронумеровать все элементы, или другими словами – пересчитать.

Конечное или счетное множество называется Не более чем счетным.

Примеры и свойства счетных множеств.

· Множество четных чисел 2N – счетное. Действительно, биекцию задает, например, отображение .

Задача гостинице “Бесконечность”.

В гостинице имеется счетное количество номеров, но все они заняты. Приехали еще 100 посетителей. Можно ли их разместить? А если приехали еще столько же, сколько уже имеется?

· Множество целых чисел Z счетно. Соответствующей биекцией, очевидно, является следующее отображение

· Объединение не более чем счетного множества счетных множеств – счетно.

Доказательство. Можно считать, что все множества и элементы в них уже пронумерованы. Пусть , , , … . Расположим все элементы объединения следующим образом и пронумеруем в порядке, указанном стрелкой:

Понятно, что при указанном способе рассмотрения элементов всякий элемент рано или поздно получит свой номер. Если имеют непустые пересечения и в процессе нумерации встречаются элементы уже ранее пронумерованные, то их будем пропускать и переходить к следующим элементам.

· Прямое произведение конечного числа счетных множеств – счетно.

Доказательство. Пусть . Элементы декартового произведения расположим так же, как и в предыдущем примере (в виде бесконечной вправо и вниз прямоугольной таблицы) и пронумеруем аналогично. Таким образом, произведение двух счетных множеств — счетно. Дальше по индукции для любого числа множителей.

· Множество Q — рациональных чисел счетно.

Доказательство. Представим множество всех рациональных чисел в виде , где Q+ И Q — — подмножества положительных и отрицательных рациональных чисел, соответственно. Достаточно показать, что Q+ Счетно. А это действительно так, поскольку

Есть объединение счетного количества счетных множеств.

· Множество алгебраических чисел A (корней всевозможных многочленов с целыми коэффициентами) – счетно (докажите).

< Предыдущая		Следующая >

matica.org.ua

1.5. Конечные и бесконечные множества. Мощность множества

Множества бывают конечные и бесконечные, счетные и несчетные. В конечном множестве число элементов конечно. Бесконечное множество содержит бесконечное число элементов.

Для сравнения множеств между собой вводят понятие мощности множества. Для конечных множеств понятие мощности соответствует числу элементов множества. Бесконечные множества можно сравнивать по мощности путем установления взаимнооднозначного соответствия между элементами одного и другого множества.

Два множества M и N, называются эквивалентными по мощности (обозначение MN), если между их элементами можно установить биекцию.

Множество называется счетным, если оно эквивалентно множеству натуральных чисел.

Рассмотрим несколько примеров счетных множеств.

1. Множество всех целых чисел. Установим биекцию между множеством всех целых чисел и множеством всех натуральных чисел. Для этого расположим элементы этих множеств друг под другом попарно следующим образом

0	-1	1	-2	2	-3	3	-4	4	.	.	.
1	2	3	4	5	6	7	8	9	.	.	.

Этим самым биекция установлена, значит эквивалентность этих множеств доказана.

2. Множество всех рациональных чисел. Каждое рациональное число записывается однозначно в виде несократимой дроби: =p/q, q>0. Назовем сумму +q высотой рационального числа α. Число дробей с данной высотой конечно. Например, высоту 1 имеет только число 0/1. Высоту 2 — числа 1/1 и -1/1. высоту 3 — числа 2/1, 1/2, -2/1 и -1/2 и т.д. Будем нумеровать все рациональные числа по возрастанию высоты. При этом всякое рациональное число получит некоторый номер, т.е. будет установлена биекция между всеми натуральными и всеми рациональными числами.

Среди всех бесконечных множеств существуют такие, которые не являются счетными — это несчетные множества. Между счетным множеством и несчетным множеством биекцию провести нельзя, в последнем всегда элементов “больше”. Покажем, что множество действительных чисел, заключенных между нулем и единицей, несчетно.

Пусть множество P=[0,1] счетно, т.е. все точки этого отрезка можно последовательно пронумеровать: x₁,x₂,…, x_n,… Разделим отрезок [0,1] на три равных отрезка. Тогда по крайней мере один из отрезков не содержит точки x₁. Точка x₁ может принадлежать либо одному отрезку либо двум, если она лежит на их границе. Отрезок A₁, который не содержит точки x₁, снова разделим на три равных отрезка. По крайней мере один из них A₂ не содержит точки x₂. Отрезок A₂ который не содержит x₂, снова разделим на три равных отрезка и т.д. В результате получим последовательность вложенных один в другой отрезков A₁,A₂,…, A_n. Пусть x_k— точка, которая принадлежит всем этим отрезкам. Тогда, с одной стороны, x_k[0,1] и в силу счетности точек отрезка входит в последовательность x₁,x₂,…, x_n,… С другой стороны, точка x_k не может совпасть ни с одной из точек этой последовательности, поскольку отрезки A₁, A_2… так построены, что ни одна из точек счетного множества x₁,x₂,…, x_n,… им не принадлежит. Из этого следует, что принятое допущение о том, что множество P=[0,1]счетное неверно, т.е. множество несчетно.

Несчетные множества тоже можно сравнивать между собой путем построения биекции. Если биекцию удается построить, то этим самым доказывается эквивалентность множеств.

Рассмотрим примеры. Множества точек на любых двух отрезках эквивалентны между собой. На рис.4 показано, как можно установить биекцию между двумя различными отрезками ab и cd.

Рис.4. Построение биекции между элементами множеств ab и cd

Множество точек в интервале 0,1 эквивалентно множеству всех точек на прямой. Биекцию можно установить, например, с помощью функции

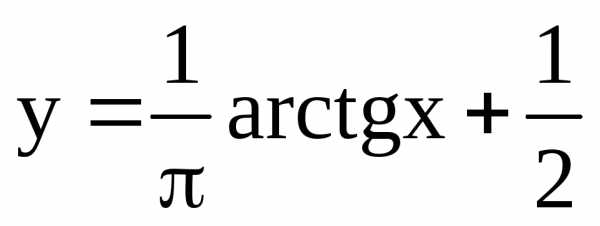, —<x<, 0<y<1

Из приведенных примеров следует, что множество точек любого отрезка эквивалентно множеству точек бесконечной прямой; любые отрезки эквивалентны между собой.

Нетрудно установить из приведенных примеров, что всякое бесконечное множество (счетное и несчетное) эквивалентно своему истинному подмножеству (бесконечному).

Например, натуральных чисел оказывается “столько же” сколько и всех целых, сколько всех четных, нечетных, рациональных и т.д. На любом отрезке можно выделить часть его, а затем построить биекцию между отрезком и его частью, т.е. часть оказывается эквивалентной целому. Это свойство характерно для любого бесконечного множества. Мощность бесконечного множества точек на прямой называется мощностью континуума.

Пусть M — некоторое множество и пусть 2^m — множество — степень M. Тогда 2^m имеет мощность большую, чем мощность исходного множества M. Если рассмотреть множество-степень счетного множества, то оказывается, что его мощность равна мощности континуума. Для любого множества мощности континуума можно рассмотреть его множество-степень и мощность этого нового множества будет больше мощности континуума. Затем можно рассмотреть опять множество-степень этого нового множества и опять его мощность будет больше. Таким образом, не существует верхней границы мощности множеств, подобно тому как не существует “самого большого” числа.

МАТРИЧНЫЙ ФОРМАЛИЗМ В ТЕОРИИ СИСТЕМ.

ЛИНЕИНЫЕ ОПЕРАТОРЫ

Рассмотрим линейное n — мерное пространство U_n. Пусть задано правило, которое ставит в соответствии произвольному вектору X пространства U_n определенный вектор Y того же пространства. В этом случае вектор X называется прообразом, а вектор Y — образом вектора X. Это правило называется преобразованием пространства U_n или оператором, заданном в пространстве U_n.

Преобразования (операторы) будем условно обозначать буквами А,В,С,… Например можно написать, что:

(1) АХ=Y

Равенство (1) читается так: преобразование (оператор) А, примененное к вектору Х, ставит ему в соответствие вектор Y.

Преобразование (оператор) называется линейным преобразованием (линейным оператором), если выполнено условие:

(2) A(Х+Y)=АХ+АY

(3) А(ℷХ)=ℷ(АХ), где ℷ- произвольное число

таким образом, линейное преобразование переводит сумму векторов в сумму их образов, а произведение вектора на число в произведение образа того вектора на это же число.

ИНВАРИАНТНОЕ ПОДПРСТРАНСТВО.

Пусть Х n — мерное линейное пространство и у=Ах -линейное преобразование на пространстве Х. Пусть X₁∈X является некоторым подпространством Х, обладающим однако, тем свойством, что если х∈Х₁, то и у=Ах∈Х₁. Подпространство Х1, обладающее подобными свойством, называют инвариантным относительно линейного преобразования у=Ах.

Особенно интересны одномерные инвариантные пространства, представляющие собой прямые в пространстве Х, проходящем через начало координат.

Если х — произвольная точка пространства Х α — вещественная переменная, меняющаяся от -∞ до +∞, то dx будет представлять собой одномерное подпространство Х, проходящее через х(при α =0), как показано на рисунке 2.

x₂

3

dx

2 x₁

Такое одномерное подпространство будем обозначать R₁. Предположим, что среди бесконечного множества одномерных пространств R₁ найдутся такие, которые инвариантны относительно у=Ах, т.е. для любого x∈R₁, имеет место у=Ах∈R₁.

Обозначим через ℷ отношение у к х, которое при этом будет просто вещественным числом, т.е. можно записать у=ℷх, таким образом если R₁ -инвариантное пространство, то для х∈R₁ имеет место равенство:

(4) Ах=ℷх

Вектор х≠0, удовлетворяющий соотношению (4) называют собственным вектором матрицы А, а число ℷ — собственным значением матрицы А.

Для определения характеристических чисел матрицы перепишем соотношение (4) в ином виде, введя тождественное преобразование х=Iх. При этом получим:

(5) (А-ℷI)х=0

Соотношение (5) представляет собой систему линейных однородных уравнений, которая может быть записана в явном виде как:

(a₁₁-ℷ)x₁+a₁₂x₂+…+a_1nx_n=0;

(6) a₂₁x₁+(a₂₂-ℷ)x₂+…+a_2nx_n=0;

…………………….

a_n1 x₁+a_n2x₂+…+(a _nn-ℷ)x_n=0;

Матрица вида (А-ℷI) (6) называется характеристической матрицей А. Определитель характеристической матрицы называется характеристическим многочленом матрицы А. Корни характеристического многочлена матрицы называются характеристическими числами этой матрицы. Из свойств решения уравнения (6) нетривиальное решение (отличное от нуля) возникает только тогда, когда имеется бесчисленное множество решений:

(7) det(A-ℷI)+a₀ℷⁿ+a₁ℷ^n-1+….+a_n-1ℷ=0

Подставив любое собственное значение в исходную систему уравнений (6), получим уравнение:

(8) (А-ℷ_iI)х=0

которое имеет непрерывное решение, так как det(A-ℷ_iI)=0

Это решение дает вектор хⁱ, определяемый с точностью до скалярного множителя. Этот вектор называется собственным вектором матицы А.

Свойства:

1. Если собственные числа матрицы А различны (корни характеристического уравнения не равны), то порождаемые или собственные векторы образуют систему линейно независимых векторов.

2. Если матрица А симметрическая, то собственные числа такой матрицы всегда вещественны, а собственный вектор в матрице образует систему ортогональных векторов.

Линейные пространства, элементами которых являются, упорядоченные последовательности n-вешественных чисел называются векторами.

ДЕЙСТВИЯ НАД ВЕКТОРАМИ.

Упорядоченные последовательности из n — чисел х⁽¹⁾,…,х⁽ⁿ⁾, могут быть записаны в виде вектор — столбца или вектор — строки;

x⁽¹⁾ _{n n}

(9) х= ….. = x⁾ⁱ⁾ ; (x⁽¹⁾,…,x⁽ⁿ⁾)=(x⁽ⁱ⁾)

x^{(n) 1 1}

Эти числа, составляющие вектор, называются компонентами вектора.

Если один из этих векторов обозначить буквой х, то другой будем обозначать х и называть транспонированным вектором.

_n

(10) х=(х⁽ⁱ⁾) =(х⁽¹⁾,…,х⁽ⁿ⁾)

¹

Число n компонент вектора называется его размерностью.

СВОИСТВА ВЕКТОРОВ.

а) х=у, если равны их компоненты:

x⁽ⁱ⁾=y⁽ⁱ⁾

x⁽¹⁾ y⁽¹⁾ x⁽¹⁾+y⁽¹⁾

б) х+у= …… + …… = ……….. -сумма векторов.

x⁽ⁿ⁾ y⁽ⁿ⁾ x⁽ⁿ⁾+y⁽ⁿ⁾

в) Разность векторов х-у представляет собой вектор z, такой, что у+z=х.

г) умножение вектора на скаляр

x⁽¹⁾ αx⁽¹⁾

αx=хα=α ……. = ………

x⁽ⁿ⁾ αx⁽ⁿ⁾

СКАЛЯРНОЕ ПРИЗВЕДЕНИЕ ВЕКТОРОВ.

x₁ y₁

Пусть х= х₂ и у= у₂ два вектора в трех мерном

x₃ y₃

пространстве. Скалярным произведением этих векторов называют скалярную величину:

(11) х^Tу=у^Tх=х₁у₁+х₂у₂+х₃у₃

Нормой или длинной вектора х в евклидовом пространстве называют число:

(12) х = х =(х^Tх)^½ , где х -норма вектора х.

Линейное пространство в котором определено скалярное произведение называется евклидовым пространством.

БАЗИС ЛИНЕЙНОГО ПРОСТРАНСТВА.

Пусть имеем систему векторов

(13) х₁, х₂, х₃,…, х_n

Базисом (базой) системы векторов (13) называется такая линейно-независимая ее подсистема, через которую линейно выражаются все указанные векторы.

УГОЛ МЕЖДУ ВЕКТОРАМИ. ОРТОГОНАЛЬНЫЕ ВЕКТОРЫ.

Пусть х=(х₁, х₂) и у=(у₁, у₂) — два вектора на плоскости. Выберем систему координат так, чтобы ось абсцисс совпадала с направлением вектора х, так что x₁= x , х₁ =0 (рис.3)

2

y₂ y

α x

y₁ 1

обозначим через угол α между векторами х и у при этом

х^Tу=х₁у₁+х₂у₂= х * у cosα

Угол между векторами определяется:

α=arccos(x^Ty/ x y )

при │х│=1 скалярное произведение х^Tу определяет проекцию вектора у называется ортогональным, если угол между ними равен 90^○, т.е.

если х^Tу=0.

МАТРИЦЫ И ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ.

ПОНЯТИЕ МАТРИЦ.

Матрицей А размером m*n называют таблицу, содержащую m-строк и n-столбцов, элементами которой являются вещественные или комплексные числа

a₁₁ ………. a_1n

A= …………………. =[a_ij]

a_m1 ………. a_mn

Если m=n, то матрицу называют квадратной.

Матрицы А=[а_ij] и В=[в_ij] равны (А=В) в том и только в том случае, если имеют один и тот же размер а_ij=в_ij для всех ij.

Преобразованием линейного n-мерного пространства Х называют оператор А, отображающий это пространство в m — мерное линейное пространство Y:

(1) А:Х→Y

Таким образом, преобразование А ставит в соответствие каждому вектору х пространства Х вектор

(2) Y=А-х, пространства Y.

Преобразование А называют линейным, если выполняется условие:

(3) А(х₁+х₂)=Ах₁+Ах₂, А(ℷх_i)=ℷАх

Условие (3) будет выполнятся, если между компонентами хⁱи у^j векторов х и у имеется линейная зависимость вида:

n ___

(4) у⁽ⁱ⁾= ∑ a_ijx^(j), i=1,m ,где а_ij — произвольное число

j=1 ____ ___

Совокупность чисел а_ij, i=1,m; ;j=1,n образуют матрицу:

a₁₁……a_1n

A= ……………. = [a_ij]

a_m1……a_mn

которую называют матрицей линейного преобразования.

у=Ах можно записать в виде умножения матрицы на вектор:

y⁽¹⁾ a₁₁……a_1n x⁽¹⁾

(5) …. = …………… * …..

y⁽ⁿ⁾ a_m1……a_mn x⁽ⁿ⁾

ОПЕРАЦИИ НАД МАТРИЦАМИ. УМНОЖЕНИЕ МАТРИЦЫ НА ЧИСЛО.

Пусть А матрица линейного преобразования Ах, α- число.

(6) αА=[α а_ij ]

При умножении матрицы А на число α все ее члены умножаются на это число.

СУММА МАТРИЦ.

Пусть у=Ах и v=Вх — два линейных преобразования с матрицами А=[a_ij] и В=[в_ij] размером m*n.

Рассмотрим новое линейное преобразование, ставшее в соответствие каждому вектору х∈Х вектор у+v∈Y

(7) у+v=Ах+Вх=(А+В)х

Преобразование (А+В)х называют суммой линейных преобразований Ах и Вх, или:

(8) А+В=[a_ij]+[в_ij]

При сложении двух матриц одинакового размера получается новая матрица того же размера, элементы которой равны сумме элементов складываемых матриц.

ПРОИЗВЕДЕНИЕ МАТРИЦ.

Пусть X,Y,Z-линеиные пространства размерностью m, r, n и пусть у=Вх, z=Ау — линейные преобразования пространства Х в пространство Y, и пространства Y в пространство Z, где В=[в_kj] и A=[a_ik] матрицы размером m*k и k*n соответственно. Произведением преобразований Ау и Вх называют новое линейное преобразование Сz.

(9) Z=Cx=A(Bx)=ABx

Матрицу С=АВ размером n*n называют произведением матриц А и В.

n ___ ___

(10) С_ij= ∑ а_ikв_kj , i=1,n , j=1,m

k=1

Согласно (10) элемент С_ij матрицы С представляет собой скалярное произведение i-й строки матрицы А на j-й столбец матрицы В, так что произведение матриц АВ символически может быть представлено в виде:

a₁₁…a_1k в₁₁…в_1m

(11) АВ= ………… * ………….

a_n1…a_nk в_k1….в_km

ТРАНСПОНИРОВАНАЯ МАТРИЦА.

Пусть А=[a_ij] — матрица размером m*n. Матрица А^T=[а’_ij] размером m*n, строки которой являются столбцами матрицы А, столбцы строками матрицы А.

Элемент а’_ij матрицы А^T определяют по элементам а_ij матрицы А из соотношения:

(12) а’_ij=а_ji

ОСОБЕННОСТИ КВАДРАТНЫХ МАТРИЦ.

В квадратной матрице число строк равно числу столбцов.

Определителем квадратной матрицы называют, определитель составленный из элементов a_ij этой матрицы и обозначают det A.

Определитель det A обладает следующими свойствами:

1) при умножении на ℷ любого столбца матрицы А определитель det A умножается на ℷ;

2) перемена местами двух соседних столбцов меняет знак det A на противоположный;

3) если любые два столбца матрицы равны между собой, то det A=0;

4) добавление к любому столбцу матрицы любого другого столбца, умноженного на произвольный скалярный множитель, оставляет det A неизменным;

5) если столбцы матрицы линейно зависимы, то det A=0;

ТЕОРЕМА ГАМИЛЬТОНА-КЕЛЛИ.

Каждая квадратная матрица является корнем своего характеристического уравнения.

(13) det (A-ℷI)=a₀ℷⁿ+a₁ℷ^n-1+…+a_n-1ℷ a_n=0

(14) a₀Aⁿ+a₀A^n-1+a_n-1A+a_nI=0_[n*n]

ОБРАТНАЯ МАТРИЦА.

Матрицей, обратной по отношению к квадратной матрице А размером n*n, назовем такую матрицу А^-1 того же размера, для которой справедливо соотношение:

(15) А*А^-1=А^-1*А=Е

Пусть у=Ах — линейное преобразование с квадратной матрицей А=[x_ij]. Обратным преобразованием называют преобразование х=А^-1у. Матрицу А^-1 этого преобразования называют обратной по отношению к матрице А.

(16) А^-1=(1/detA) [A_ij]^T , где А_ij — алгебраическое

дополнение элемента а в определителе матрицы.

Система уравнений Ах=у называется определенной и имеет единственное решение, если detA≠0. Матрица А, для которой выполнено это условие, называют невырожденной.

ДИАГоНАЛИЗАЦИЯ МАТРИЦ.

Вид квадратной матрицы А линейного преобразования у=Ах, может быть изменен без изменения характеристического уравнения этой матрицы путем использования преобразования подобия.

Пусть А — квадратная матрица; С — произвольная невырожденная матрица. Преобразованием подобия называют преобразование:

(17) В=С^-1*А*С

Преобразование подобия позволяет приводить некоторые виды квадратных матриц к диагональной форме, являющейся наиболее удобным видом матрицы.

ℷ₁ 0 0

(18) diag[ℷ₁ ℷ₂ ……ℷ_n ]= 0 ℷ₂ 0

0 0 ℷ_n

Нормой матрицы А размер m*n называется сумма модулей ее элементов:

m n

(19) │А│= ∑ ∑ │a _ij │

i=1 j=1

При решении задач удобно ввести матрицы, элементы которых являются функциями независимой переменной t.

Эти матрицы имеют вид:

a₁₁(t) a₁₂(t) …… a_1n(t)

(20) А(t)= a₂₁(t) a₂₂(t) …… a_2n(t)

……………………….

a_m1(t) a_m2(t) ….. a_mn(t)

и называются функциональными матрицами.

Производной матрицы А(t) по независимому переменному называется матрица А(t) вида:

da₁₁(t)/dt da₁₂(t)/dt …… da_1n(t)/dt

(21) А(t)= dA(t)/dt = ……………………………………………………. =

da_m1(t)/dt ad_m2(t)/dt …… da_mn(t)/dt

=[da_ij(t)/dt]

studfiles.net

Числовые множества — определение основных

Числовые множества — введение

Словосочетание «числовые множества» довольно часто встречается в учебниках математики. Там очень часто можно встретить фразы такого плана:

«Бла-бла-бла, где принадлежит множеству натуральных чисел».

Частенько вместо окончания фразы можно увидеть вот такую запись . Она означает то же что и текст немного выше — число принадлежит множеству натуральных чисел. Многие довольно часто не придают внимания в каком множестве определена та или иная переменная. В результате применяться совершенно неверные методы при решении задачи или доказательстве теоремы. Это происходит из-за того, что свойства чисел принадлежащих  различным множествам могут иметь различия.

Числовых множеств не так уж и много. Ниже можно увидеть определения различных числовых множеств.

Множество натуральных чисел

Множество натуральных чисел включает в себя все целые числа больше нуля — положительные целые числа.

Например: 1, 3, 20, 3057. Множество не включает в себя цифру 0. 

Множество целых чисел

В это числовое множество входят все целые числа больше и меньше нуля, а так же ноль.

Например: -15, 0, 139.

Множество рациональных чисел

Рациональные числа, вообще говоря, представляют собой множество дробей, которые не сокращаются (если дробь сокращается, то это уже будет целое число, и для этого случая не стоит вводить еще одно числовое множество).

Пример чисел входящих в рациональное множество: 3/5, 9/7, 1/2.

Множество вещественных чисел

,

где – конечная последовательность цифр целой части числа, принадлежащего множеству вещественных чисел. Эта последовательность является конечной, то есть количество цифр в целофй части вещественного числа конечное количество.

– бесконечная последовательность чисел, стоящих в дробной части вещественного числа. Выходит, что в дробной части присутствует бесконечное количество чисел. 

Такие числа невозможно представить в виде дроби. В противном случае, подобное число можно было бы отнести к множеству рациональных чисел.

Примеры вещественных чисел:

Давайте рассмотрим значение корня из двух внимательнее. В целочисленной части представлена только одна цифра — 1, поэтому мы можем записать:

В дробной части (после точки) последовательно идут числа 4, 1, 4, 2 и так далее. Поэтому для первых четырех цифр можно записать:

.

Смею надеяться, что теперь запись определения множества вещественных чисел стала понятней.  

Заключение

Следует помнить, что одна и та же функция может проявлять совершенно разные свойства в зависимости от того к какому множеству будет принадлежать переменная. Так что помните основы – они вам пригодятся.

Post Views: 5 805

Похожее

optoelectrosys.ru

§6. Счётные множества

Понятие равномощности множеств и его свойства позволяют выделить классы равномощных множеств. Интересно знать, как много существует неравномощных множеств и иметь в некотором смысле «эталонные множества», чтобы, сравнивая с ними другие, было легче устанавливать равномощность множеств или её отсутствие.

1. Конечных, но не равномощных множеств, бесконечно много. Их классов столько же, сколько натуральных чисел.

2. Бесконечных, но не равномощных множеств, также бесконечно много.

Возникает вопрос: есть ли среди бесконечных множеств множество наименьшей мощности? Да. Это счётные множества.

Определение 1.ПустьN— множество натуральных чисел. МножествоSназываетсясчётным множеством,если оно равномощноN, то естьSN.

Мощность счётного множества имеет специальное обозначение: (первая буква алфавита иврит, читается «алеф-нуль»). Мы будем обозначать мощность счётного множества буквойа:

m(S)=a.

Примеры счётных множеств

1. 2N;

2. Q;

3. Z;

4. Множество квадратов натуральных чисел.

Основные свойства счётных множеств

Теорема 1. Для того чтобы множествоSбыло счётным необходимо и достаточно, чтобы его элементы можно было занумеровать в последовательность, члены которой попарно различны:

.

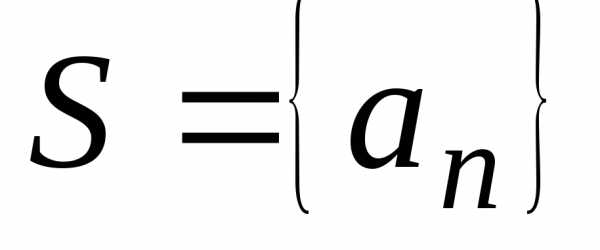Доказательство:

1. Необходимость.

Пусть S— счётное множество, тогда существует биекцияf: NS. В этой биекции образ элементаnобозначима_n, тем самым будут занумерованы все элементы множестваS, то есть. Так как все элементы множестваSразличны, то и все члены последовательностипопарно различны.

2. Достаточность.

Пусть ,а_nпопарно различны. Сопоставим элементуа_nего номерn.Полученное соответствие изSвNявляется биекцией. Следовательно, по определениюS— счётное множество.

Теорема 2.Во всяком бесконечном множествеА имеется счётное подмножество.

Доказательство:

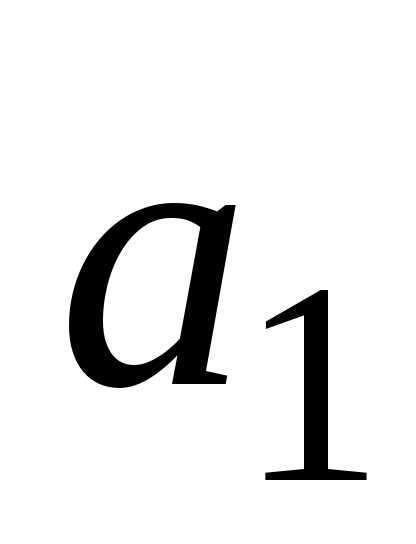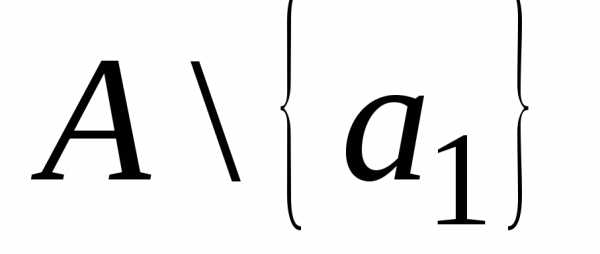Возьмём во множестве Апроизвольный элемент. Множество бесконечное (доказывается от противного). Из множества 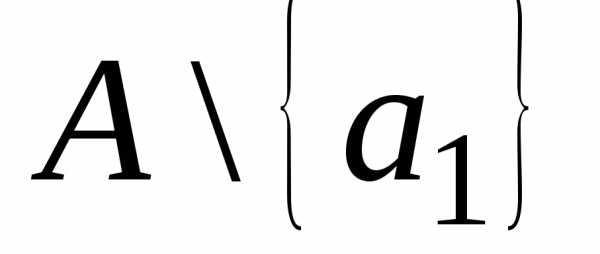выберем элеме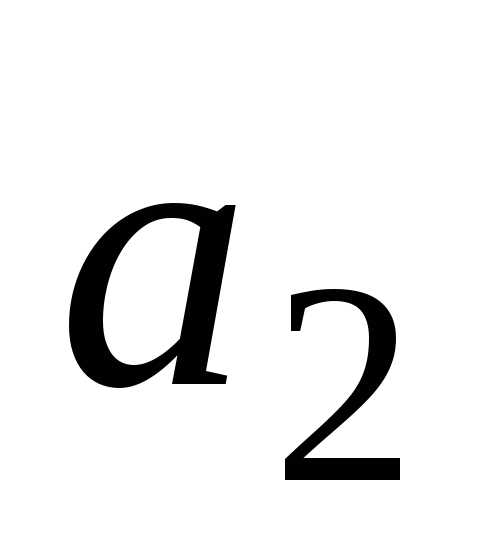нт. Множество — бесконечное. Из множества выбираем элементи так далее. Так какА– бесконечное множество, то этот процесс продолжим до бесконечности. В результате получим последовательность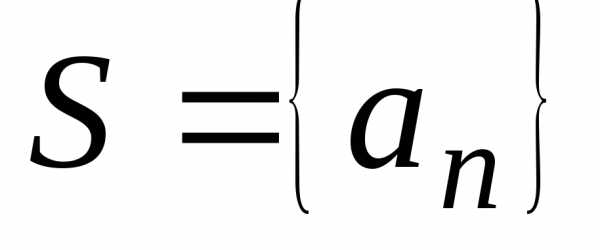. Так как во множествеАвсе элементы попарно различны, по теореме 1S— счётное множество.

Следствие. Счётная мощность является наименьшей из мощностей бесконечных множеств.

Доказательство:

Пусть А — произвольное бесконечное множество. По теореме 2 оно содержит счётное подмножествоS, то естьm(S)=а. Так какS, тоm(S)m(А)илиаm(А).

Теорема3.Всякое бесконечное подмножествоВсчётного множестваS счётно:

ВS; m(S)=а  m(В)=а.

Доказательство:

Так как ВS,тоm(В)m(S)=а. Но по следствиюm(В)а.Таким образом,m(В)аиm(В)а. По теореме Кантора-Бернштейнаm(В)=а.

Теорема 4.Бесконечное множествоВсчётно, если существует сюрьекцияfкакого-нибудь счётного множестваSнаВ.

Доказательство:

Не умоляя общности доказательства можно считать, что S=N. По условиюf: N — сюрьекция (В– это образNпри отображенииf, то естьf(N)=В). Возьмём любой элемент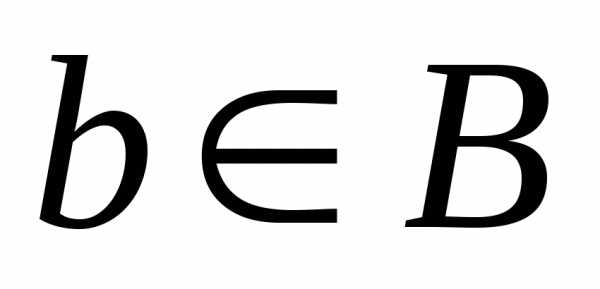,b– образ какого-либо натурального числа. При отображенииfего прообразом является некоторое множество натуральных чиселf ^-1(b), состоящее из тех элементов, образ которых равенb, то естьf ^-1(в)={nN: f(n)=b}. В этом множестве существует наименьшее натуральное число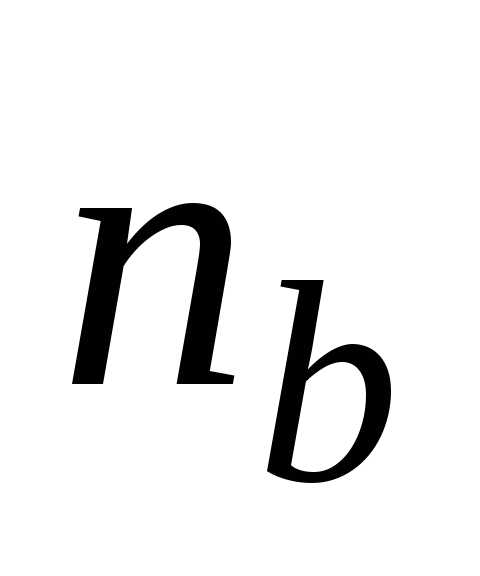. Рассмотрим множество- бесконечное множество (От противного: пустьАконечно. Тогда для бесконечного числа элементов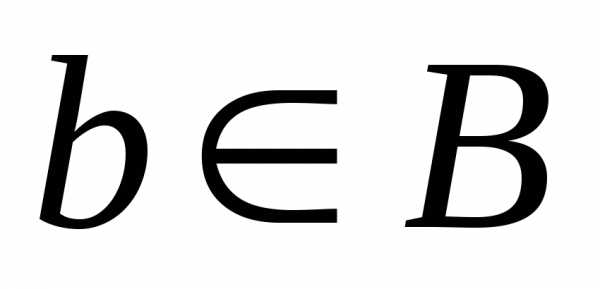существует один элемент 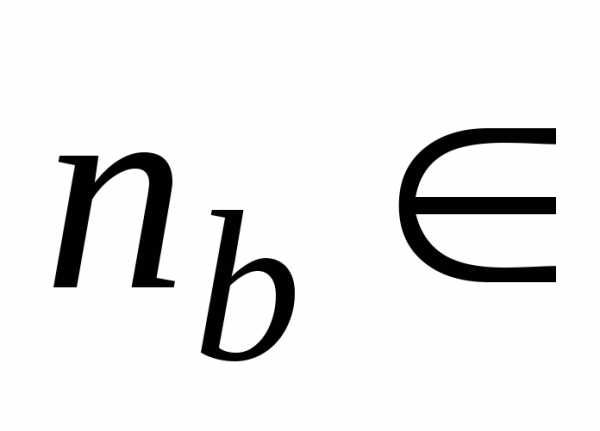N, то есть одному элементуnNсоответствует бесконечно много элементов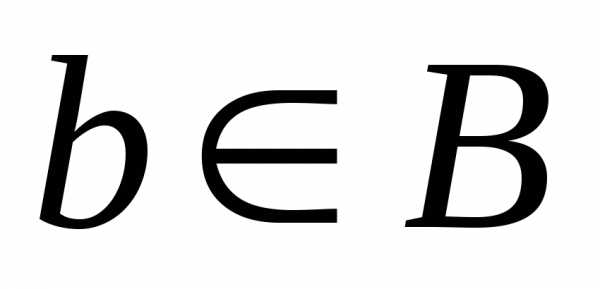. Это означает, что соответствиеNне является отображением. Получили противоречие с условием. Следовательно, предположение не верно.). Так какАNиА– бесконечное множество, то по теореме 3 множествоАсчётно. Рассмотрим соответствие,при котором. Это соответствие является биекцией. Следовательно,АВиВсчётно.

Определение 2. Кортежемназывается конечное множество элементов.

Теорема 5.МножествоКвсевозможных кортежей, составленных из натуральных чисел, счётно.

Доказательство:

Пусть Р— множество всех простых чисел, расположенных в порядке возрастания:

Р=(р_к), р₁=2, р₂=3, р₃=5,… .

Возьмём любой кортеж из натуральных чисел (n₁,n₂,…,n_k)и поставим в соответствие ему число

N.

Например,

.

На основании теоремы о единственности разложения чисел на простые множители различным кортежам соответствуют различные натуральные числа, то есть если

, то.

Рассмотрим соответствие f:KА, гдеА– некоторое бесконечное подмножество множестваN, то естьА— счётно (по теореме 3). Указанное соответствие является биекцией. Так какАсчётно и, тоK также счётно.

Определение 3.Декартовым произведением А₁А₂…А_mназывается множество, состоящее из кортежей, где.

Теорема 6.Декартово произведение конечного числа счётных множеств счётно.

Доказательство:

Пусть А₁,А₂,…,А_m — счётные множества. Докажем, чтоА₁А₂…А_m=А — счётное множество. Счётные множестваА_k,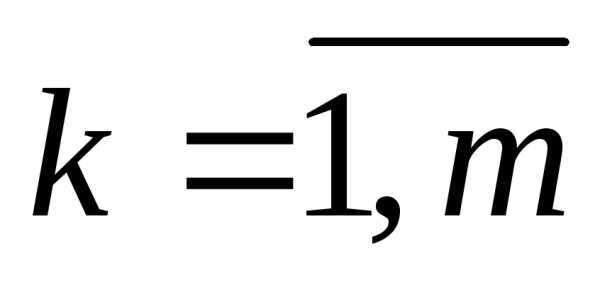, представим в виде последовательностей

;

;

…………………………………

;

.

Возьмём , поставим ему в соответствие кортеж из натуральных чисел. Обозначим. Указанное соответствие является биекциейf:А₁. Но₁– бесконечное подмножество счётного множестваиз теоремы 5. По теореме 3₁ счётно. Так какf— биекция, тоА счётно.

Теорема 7. Объединение конечной или счётной совокупности счётных множеств счётно.

Доказательство:

Пусть А₁,А₂,…,А_m,… — счётные множества. Докажем, что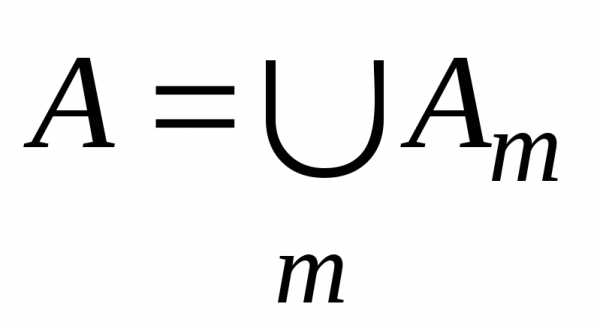 — счётное множество.

1. Пусть 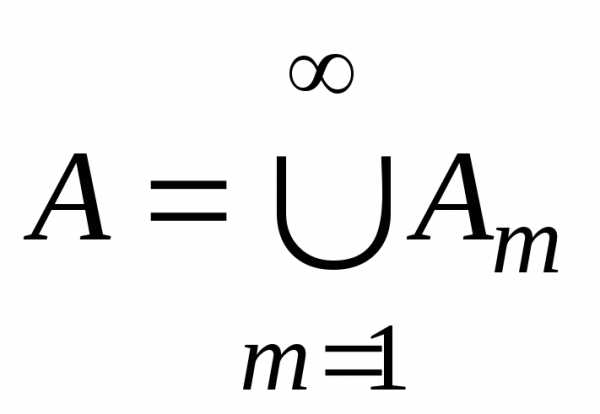— объединение счётного числа счётных множеств. Счётные множестваА_mпредставим в виде последовательностей

;

;

…………………………………

;

……………………………………

,

где — это элемент множествас номером. Рассмотрим множествоN²=N´N. Оно счётно по теореме 6. Возьмём любой элемент(p,q)ÎN². Сопоставим ему элемент. Так как любой элемент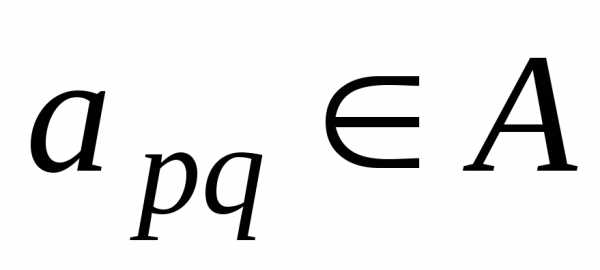принадлежит хотя бы одному из множествА_pи имеет в нём определённый номерq, то указанное соответствие является сюрьекциейf:N²®A. Так как множествоN²счётно, то по теореме 4 множествоАсчётно.

2. Пусть 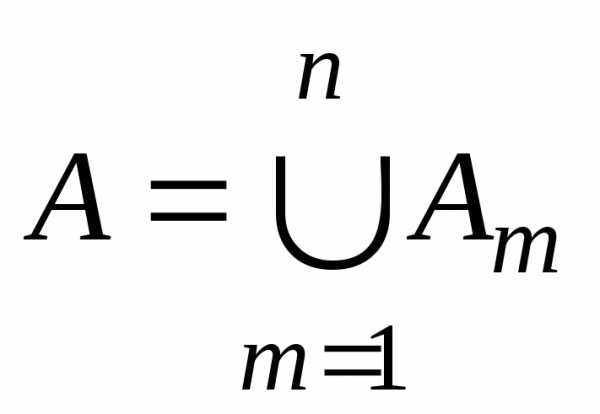— объединение конечного числа счётных множеств. Положим

,

тогда 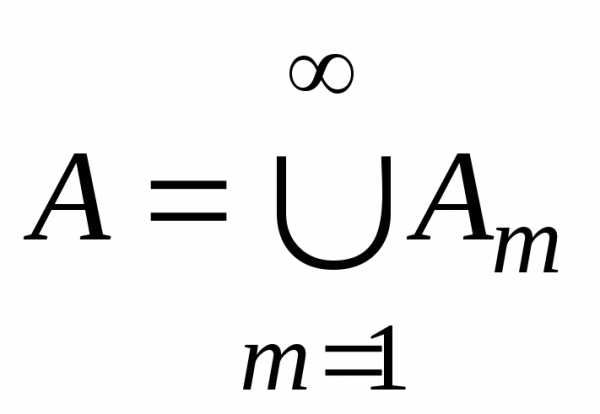. По первой части теоремы множествоАсчётно.

Теорема 8.МножествоQрациональных чисел счётно.

Доказательство:

Представим множество Qв виде

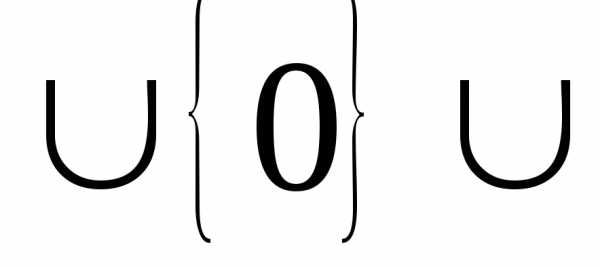Q =Q₊Q_—,

Q₊={m/n, m,nN, (m,n)=1},

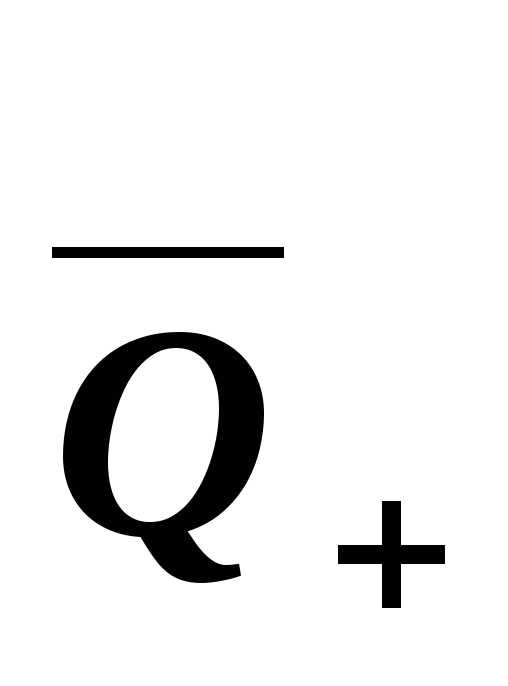={m/n, m,n},

Q₊,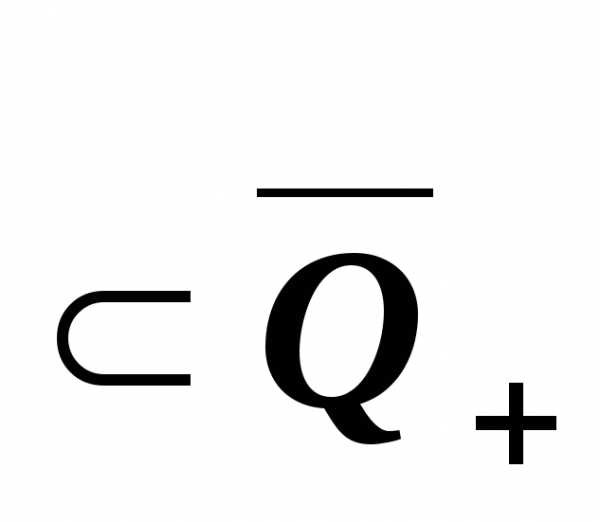

,

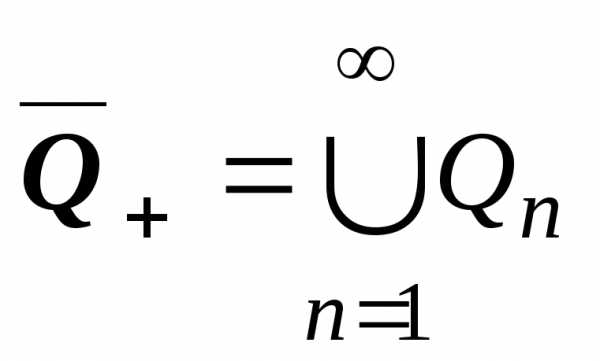где Q_n— множество дробей видас фиксируемым знаменателем. Очевидно, чтоQ_n, то естьQ_nсчётное множество. Тогда по теореме 7 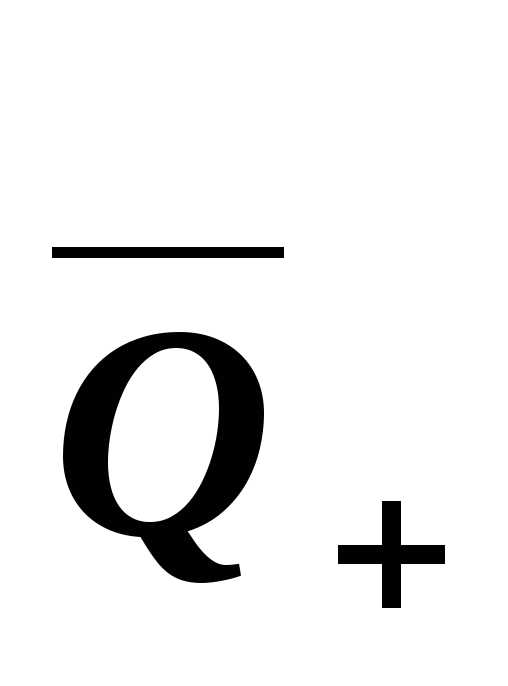также счётно. НоQ₊является бесконечным подмножеством счётного множества 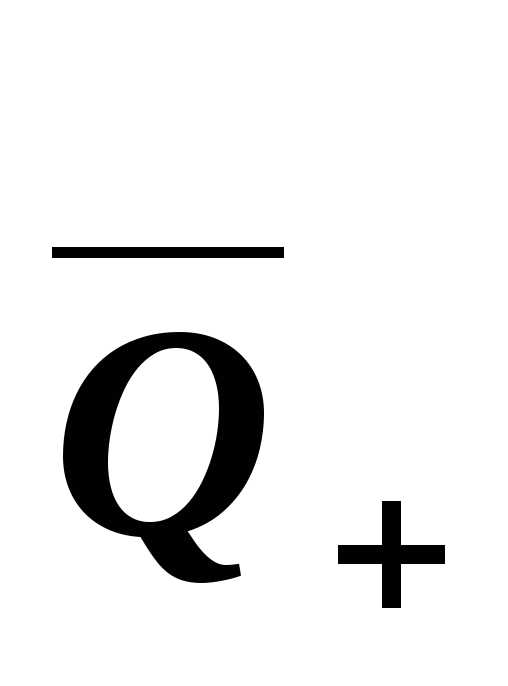. Тогда по теореме 3 множествоQ₊счётно. В силу того, чтоQ₊~ Q_—, заключаем, что множествоQ_—счётно. По теореме 7 множествоQ₊Q_—счётно, тогда по теореме 1 множествоQсчётно.

Теорема 9.Объединение счётной совокупности конечных множеств конечно или счётно.

Доказательство:

Пусть — конечные множества,.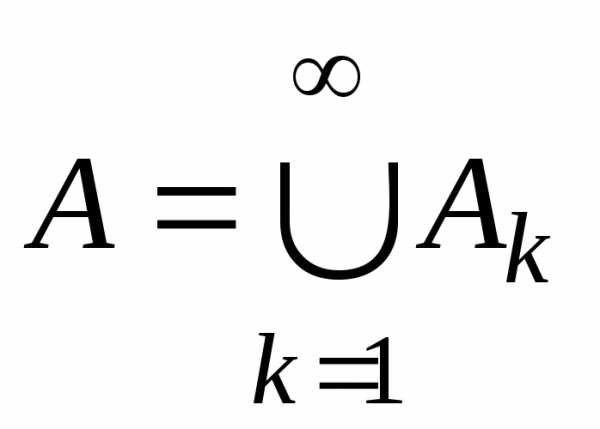

1. Множество А может быть конечным (например, если все множестваА_kравны:N).

2. Рассмотрим случай, когда множество А— бесконечно. Пусть множествоА_k имеетn_kэлементов. Присоединим к этому множеству все натуральные числа, большие чемn_k, получим счётное множествоВ_k. Проделаем это для всехk. Рассмотрим множеств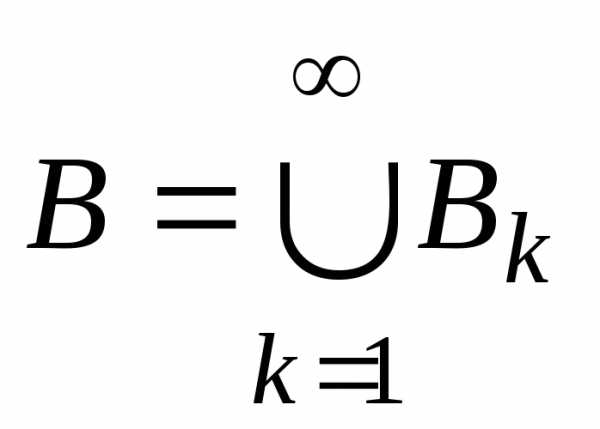о. По теореме 7 множествоВсчётно. НоАи является его бесконечным подмножеством. По теореме 3 множествоАсчётно.

Теорема 10.Мощность бесконечного множества не изменяется, если к нему присоединить конечное или счётное множествоS.

Доказательство:

Случай конечного множества Sне интересен, так как является следствием теоремы 1. Рассмотрим случай счётного множестваS. Не нарушая общности доказательства будем считать, что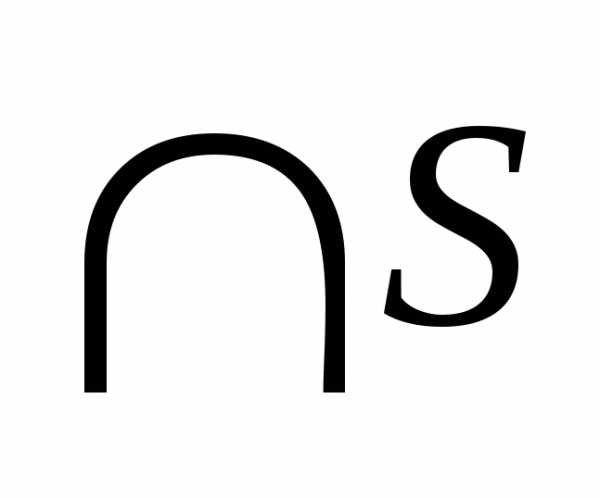=. По теореме 2 множествоВможно представить в виде, гдеS₁— счётное множество множестваS. Тогда

.

Так как множества иS₁— счётные множества, то существует биекцияf:S₁.Рассмотрим отображение, определяемое следующим образом:

Это отображение является биекцией . Следовательно,, то есть.

Определение 4.Если бесконечное множество не является счётным, то оно называетсянесчётным.

Теорема 11. Мощность несчётного множестваМне изменяется, если из него удалить конечное или счётное подмножествоS.

Доказательство:

Пусть М– несчётное множество, тогдаМ\S– бесконечное множество (доказательство от противного). Тогда по теореме 10 .

Определение 5.Числоназываетсяалгебраическим,если оно является корнем некоторого многочлена с целыми коэффициентами.

Теорема 12. МножествоАвсех алгебраических чисел счётно.

Доказательство:

Пусть М– множество всех многочленов с целыми коэффициентами,М_n– множество многочленов с целыми коэффициентами и с фиксированной степеньюn. Возьмём любой многочлен,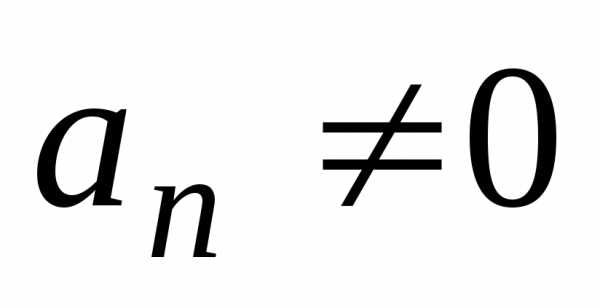, из множестваМ_n. Этому многочлену сопоставим кортеж из его коэффициентов(а_n ,…,а₀). Множество таких кортежей обозначимТ. Очевидно, чтоТ=(Z\{0})Z ⁿ. Построенное соответствие является биекциейf:М_nT. Так как множествоZсчётно, то по теореме 3 множествоZ\{0}также счётно. Следовательно, по теореме 6 множествоТсчётно. Так какf– биекция, тоМ_n~T, то естьМ_n счётно. 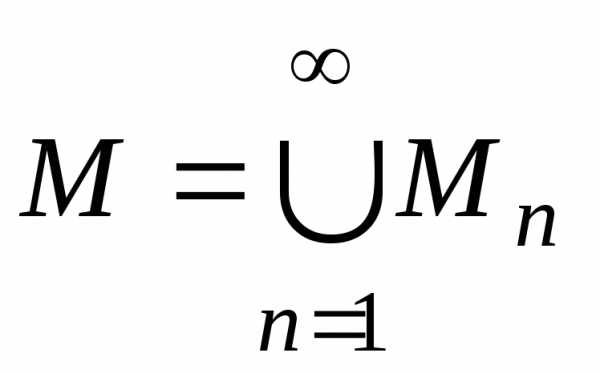Так каки все множестваМ_n счётны, то по теореме 7 множествоМсчётно. Итак, множество всех многочленов с целыми коэффициентами счётно и любой многочлен имеет конечное число корней. Следовательно, множествоАпредставляет собой объединение счётного числа конечных множеств. Так какА– бесконечное множество, то по теореме 9 оно счётно.

studfiles.net