Арксинус, арккосинус и арктангенс числа
Функции с приставкой arc — это функции, обратные тригонометрическим. Например, для функции $sinα$ обратной функцией является её арксинус, записывается как $arcsinα$, а для функции косинуса обратной будет функция арккосинус, записывается как $arccosα$. Проще говоря, обратные тригонометрическим функции с приставкой $arc$ являются множеством значений углов $α$, от которых берётся какая-либо обычная тригонометрическая функция, также иногда функции с приставкой $arc$ используют как меру длины дуги, ограничивающей угол $α$.
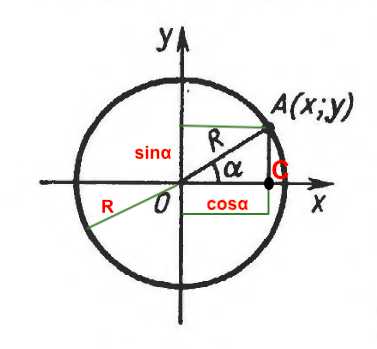
Рисунок 1. Единичная окружность. Автор24 — интернет-биржа студенческих работ
Рассмотрим теперь непосредственно определения для функций арксинус, арккосинус, арктангенс и арккотангенс по отдельности.
Арксинус числа
Определение 1
Арксинус числа $x$ — это множество значений углов, для которых $sinα = x$. Также определение арксинуса можно записать так: $arcsin(x) = α$.
Рассмотрим рисунок 1, на котором изображена окружность с радиусом, равным единице. Как мы помним, $sinα$ — это отношение противолежащей стороны к гипотенузе, численно он равен длине стороны $AC$. Так как арксинус его обратная функция и есть не что иное как угол, от которого берётся синус, свойства арксинуса очень похожи на свойства синуса:
- Область определения функции арксинуса $D(y)= \ [-1;1\ ]$, для синуса $D(y)=\ [-\frac{π}{2};\frac{π}{2}\ ]$;
- Область значения для арксинуса $E = \ [-\frac{π}{2};\frac{π}{2}\ ]$, для синуса $E = \ [-1;1\ ]$
- Функции синуса и арксинуса обе возрастающие;
- Функции арксинуса и синуса обе нечётные, то есть: $arcsin(-x)= -arcsinx$;
- Функция $y=arcsin(x)$ равна нулю при $x=0$.
График арксинуса выглядит следующим образом:
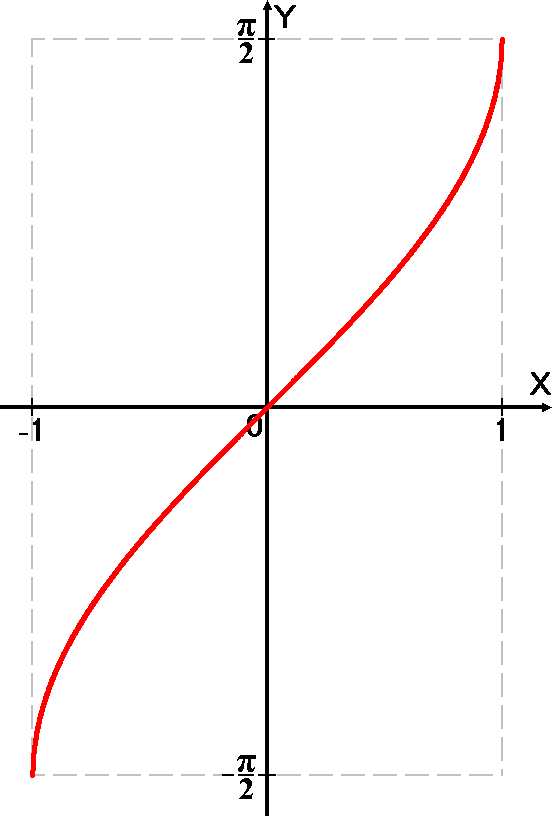
Рисунок 2. График арксинуса. Автор24 — интернет-биржа студенческих работ
Арккосинус числа
Определение 2
Арккосинус числа $x$ — это множество значений углов, для которых $cosα = x$, то есть это значение угла.
Свойства арккосинуса в сравнении с косинусом:
- Область определения функции арккосинуса $D(y)= \ [-1;1\ ]$, для косинуса $D(y)=\ [0; π\ ]$;
- Область значения для арккосинуса $E = \ [0; π\ ]$, для косинуса $E = \ [-1;1\ ]$;
- График функции арккосинуса симметричен относительно точки $(0; \frac{ π}{2})$, следовательно, он не является ни чётным, ни нечётным, в отличии от функции косинуса, которая является чётной;
- График функции арккосинуса $y= arccos(x)$ является убывающим, это происходит на всей его области определения, так же, как и c графиком косинуса.
- Функция $y=arccos(x)$ равна нулю при $x=1$.

Рисунок 3. График арккосинуса. Автор24 — интернет-биржа студенческих работ
Арктангенс числа
Определение 3
Арктангенс числа $x$ — это множество значений углов, для которых $tgα = x$.
Свойства арктангенса:
- $D(y)= \ [-\infty;1\ ]$;
- $E = \ [-\frac{π}{2};\frac{π}{2}\ ]$;
- Данная функция нечётная;
- Функция $y= arctgx$ возрастающая на всей области определения;
- Функция $y= arctgx$ равна нулю при $x=0$.

Рисунок 4. График арктангенса. Автор24 — интернет-биржа студенческих работ
Арккотангенс
Определение 4
Арккотангенс числа $x$ — это множество значений углов, для которых $ctgα = x$.
Свойства функции арккотангенса:
- $D(y)= \ [-\infty;1\ ]$;
- $E = \ [0; π\ ]$;
- Данная функция не является ни чётной, ни нечётной;
- Функция $y= arcсtgx$ убывает на всей области определения;

Рисунок 5. График арккотангенса. Автор24 — интернет-биржа студенческих работ
Пример 1
Найдите значение следующих выражений: $arcsin(\frac{1}{2}), arccos(-\frac{\sqrt{2}}{2}), arcctg(\frac{\sqrt{3}}{3}), arccos(-\frac{1}{2})$.
Решение:
$arcsin(\frac{1}{2}) = \frac{π}{6}$
$arccos(\frac{\sqrt{2}}{2}) = \frac{π}{4}$
$arcctg(\frac{\sqrt{3}}{3}) = \frac{π}{4}$
Здесь мы имеем арккосинус отрицательного числа $arccos(-\frac{-1}{2})$, для того чтобы его вычислить, необходимо прибегнуть к следующей формуле: $arccos(-α) = π – arccos(α)$
$arccos(-\frac{-1}{2}) = π – arccos(\frac{-1}{2}) = π – \frac{π}{3} = \frac{2π}{3}$
spravochnick.ru
Определения и свойства обратных тригонометрических функций
by Колпаков А.Н. on 15 сентября 2010
Обратные тригонометрические функции:

Определение:
Арксинусом числа а называется угол из отрезка , синус которого равен числу а.
Свойство арксинуса от отрицательного угла :
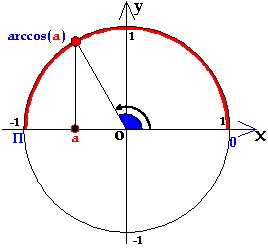
Определение:
Аркосинусом числа а называется угол из отрезка , косинус которого равен числу а.
Свойство арккосинуса от отрицательного угла :

Определение:
Арктангенсом числа а называется угол из интервала , тангенс которого равен числу а.
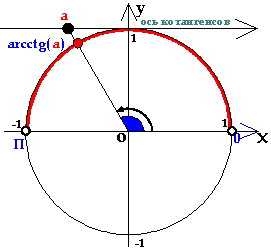
Определение:
Арккотангенсом числа а называется угол из интервала , котангенс которого равен числу а.
Свойство арккотангенса от отрицательного угла :
Дополнительные свойства обратных тригонометричесикх функций:
, если ;
, если ;
, если ;
, если ;
, если ;
, если ;
, если ;
, если
, если
, если
Справочные материалы по обратным тригонометрическим функциям предназначены для учащихся 10-11 классов, школьных преподавателей и репетиторов по математике. Рекомендуется использовать материалы на уроках по тригонометрии и подготовке к ЕГЭ по математике.
Колпаков Александр Николаевич, репетитор по математике.
Метки: Справочник репетитора, Тригонометрия, Ученикам
ankolpakov.ru
Арккосинус | Алгебра
Что такое арккосинус? Для чего вводится понятие арккосинуса?
Функция y=cosx не является монотонной на всей своей области определения. Поэтому для нахождения обратной функции выбираем промежуток [0;π], на котором косинус убывает, то есть выполняется условие обратимости функции:
1) В формулу y=cos x вместо x подставим y, вместо y — x:
x=cos y.
2) Из этого равенства нужно выразить y через x. Для этого вводится определение арккосинуса (арккосинус икс обозначают как arccos x).
Определение.
Арккосинусом числа a называется такое число b из промежутка [0;π], косинус которого равен a:
Отсюда решение уравнения x=cos y на промежутке [0;π] — y=arccos x.
Таблица значений косинусов на промежутке [0;π] —
Таблица значений арккосинусов —
Графики взаимно обратных функций y=arccos x и y=cos x (на рассматриваемом промежутке) симметричны относительно прямой y=x:
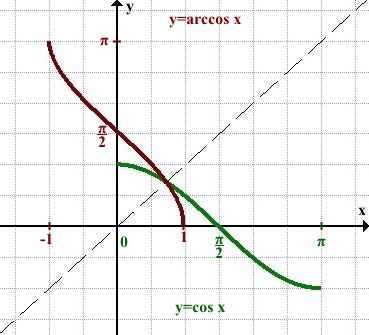
В алгебре (в тригонометрии) введение понятия арккосинуса позволяет найти решение простейшего тригонометрического уравнения вида cosx=a.
www.algebraclass.ru
Тригонометрия: арккосинус
Абитуриентам и старшеклассникам – для повторения и закрепления
Уравнение cos x = a, где -1 ≤ a ≤ 1, на отрезке [0; π] имеет решение и при том только одно. Действительно, функция y = cos x непрерывна и на концах отрезка [0; π] принимает значения -1 (в точке π) и 1 (в точке 0) – это обеспечивает существование корня, а единственность следует из монотонности функции (убывает) на указанном отрезке (рис.1).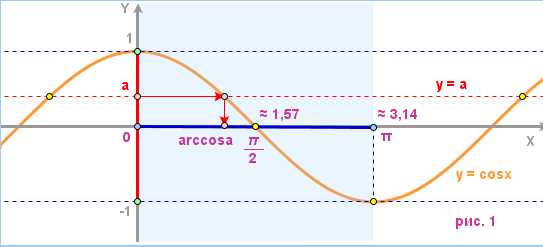
Записывают этот корень (это число) в виде arccos a. Можно сказать и так: arccos a – это единственный корень системы
Итак, под записью arccos a мы понимаем число, которое удовлетворяет двум условиям:
1) 0 ≤ arccos a ≤ π и 2) cos(arccos a) = a.
Отметим, что запись «arccos a» будет числом, если -1 ≤ a ≤ 1. В противном случае эта запись теряет смысл. На практике удобно работать с числовой окружностью (рис.2).
Из точки a оси абсцисс проведем перпендикуляр к этой оси и точку его пересечения с верхней полуокружностью обозначим буквой М. На точке М имеем бесконечно много чисел. Среди них находится и число arccos a – число из отрезка [0 ; π]. Число arccos a , при девяти значениях числа a, можно (и нужно) записать в более простой форме (см.рис.3).
Задача 1.
Почему данные записи не имеют смысла (не являются числами) ?
Решение.
arccos a имеет смысл лишь при -1 ≤ a ≤ 1. Данные записи не являются числами, так как
Задача 2.
При каких значениях переменной x, выражение arccos(|x| — 3) имеет смысл (будет числом) . Решение.
arccosa имеет смысл лишь при -1 ≤ a ≤ 1. Следовательно:
Задача 3.
Найти значение числового выражения (вычислить).
Решение.
Воспользуемся таблицей значений арккосинуса (их нужно помнить!).
Задача 4.
Вычислить cos(arccos 0,7) + cos(arccos(-0,3)) .
Решение.
Воспользуемся равенством cos(arccosa) = a. cos(arccos 0,7) + cos(arccos(-0,3)) = 0,7 – 0,3 = 0,4
Задача 5.
Вычислить
Решение.
Задача 6.
Вычислить sin(arccos 0,8).
Решение.
Заметим, что 0 ≤ arccos 0,8 ≤ π , следовательно, sin(arccos0,8) ≥ 0. Воспользуемся основным тригонометрическим тождеством и заметим, что
Абитуриентам на заметку
Задача 7.
Вычислить cos(arccos0,6 +arccos0,8) .
Решение.
Воспользуемся тождеством cos (x + y) = cosx•cosy – sinx•siny и указанной выше формулой.
Уравнение cosx = a Так как областью значений функции y = cosx является отрезок [-1 ; 1], то уравнение имеет решение тогда и только тогда, когда -1≤ a ≤ 1. Пусть a некоторое внутреннее число из отрезка [-1 ; 1]. На числовой окружности имеем две точки, ордината которых равна числу a: точки M и K на рисунке 2. Решить уравнение cosx = a – это значит найти все числа на этих точках. Одно из чисел на точке М мы знаем – это число arccosa, следовательно, с его помощью можем получить все числа этой точки: x = arccosa + 2πn, где n = 0; ±1; ±2; … . Теперь найдем все числа точки K. Так как точки M и K симметричны относительно оси абсцисс (MK – вертикальная хорда окружности), то число (-arccosa) находится на точке K и, значит, все числа точки K можно задать формулой: x = = -arccosa + 2πn, где n = 0; ±1; ±2; … . Объединив эти две формулы, запишем ответ в виде: x = ± arccosa + 2πn , n = 0; ±1; ±2; … . Для частных случаев числа a (девять значений) ответы записываются в упрощенном виде http://www.tutoronline.ru/blog/prosteishie-trigonometricheskie-uravnenia
Задача 8.
Решить уравнение cosx = π .
Решение.
Уравнение решений не имеет, т.к. π > 1.
Задача 9.
Решить уравнение cosx = 0,3 .
Решение. x = ± arccos0,3 + 2πn , n = 0; ±1; ±2; … .
Три свойства arccosa , которые должен знать абитуриент.
1. Сумма арккосинусов двух противоположных чисел равна π:
arccos(-a) + arccosa =π , или в виде arccos(-a) = π – arccosa . Действительно, числа arccos(-a) и arccosa равноудалены от точки π/2 (строгое доказательство мы опустим, но из рисунков 4 или 5 в этом легко убедиться). И так, π/2 – среднее арифметическое этих чисел, следовательно
Задача 10.
Вычислить.
.
Решение.
Так как ( a – b ) и (b – a) противоположные числа, то arccos(a –b) = π – arccos(b –a ).
2. Если b < a , то arccos b > arccos a и обратно, если arccos b > arccos a , то b < a. Понятно, что числа a и b принадлежат отрезку [-1 ; 1]. Убедиться в этом не сложно, если внимательно изучим рисунки 4 или 5.
Задача 11.
Расположить числа в порядке возрастания.
Решение.
Задача 12.
Принадлежит ли число arccos(-0,6) интервалу (2,08 ; 2,37) ?
Решение.
Ответить на данный в задаче вопрос нам поможет рисунок 3.
Ответ: да, принадлежит.
Задача 13 .
Решить неравенство: arccos(x – 2) > arccos( 2x –3).
3. Равенство arccos a = arccos b равносильно системе из двух условий: 1) a = b ; 2) -1 ≤ a ≤ 1 Разумеется, что в двойном неравенстве вместо числа a можно взять число b.
Задача 14.
Решить уравнение
arccos(x – 2) = arccos(3|x| – 7).
Решение.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
2) Понятие арксинуса и арккосинуса числа. Примеры. И 3 вопрос Арксинус, арккосинус, арктангенс и арккотангенс – основные сведения.
1)Понятие степени. Свойства степеней. Примеры.
Степенью называется выражение вида: , где:
Степень с натуральным показателем {1, 2, 3,…}
Определем понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
По определению: .
Возвести число в квадрат — значит умножить его само на себя:
Возвести число в куб — значит умножить его само на себя три раза: .
Возвести число в натуральную степень — значит умножить число само на себяраз:
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
, n > 0
Возведение в нулевую степень:
, a ≠ 0
Если показателем степени является целое отрицательное число:
, a ≠ 0
Прим: выражение не определено, в случаеn ≤ 0. Если n > 0, то
Пример 1.
Степень с рациональным показателем
Если:
Тогда:
Пример 2.
Свойства степеней
Произведение степеней | |
Деление степеней | |
Возведение степени в степень |
Пример 3.
Корень
Арифметический квадратный корень
Уравнение имеет два решения:x=2 и x=-2. Это числа, квадрат которых равен 4.
Рассмотрим уравнение . Нарисуем график функциии увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.
Но в данному случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.
Арифметический квадратный корень — это неотрицательное число, квадрат которого равен,a ≥ 0. При a < 0 — выражение не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу.
Корень из квадрата
Например, . А решения уравнениясоответственнои
Кубический корень
Кубический корень из числа — это число, куб которого равен. Кубический корень определен для всех. Его можно извлечь из любого числа:.
Корень n-ой степени
Корень -й степени из числа— это число,-я степень которого равна.
Если — чётно.
Тогда, если a < 0 корень n-ой степени из a не определен.
Или если a ≥ 0, то неотрицательный корень уравнения называется арифметическим корнемn-ой степени из aи обозначается
Если — нечётно.
Пример 4.
Задача, обратная нахождению значений синуса, косинуса, тангенса и котангенса данного угла, подразумевает нахождение угла по известным значениям тригонометрических функций. Она приводит к понятиям арксинуса, арккосинуса, арктангенса и арккотангенса числа.
В этой статье мы дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа, введем принятые обозначения, а также приведем примеры арксинуса, арккосинуса, арктангенса и арккотангенса. В заключение обговорим некоторые тонкости, касающиеся этой темы, и покажем, как арксинус, арккосинус, арктангенс и арккотангенс связаны с единичной окружностью.
Навигация по странице.
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа.
Обозначения arcsin, arccos, arctg и arcctg.
Примеры.
Арксинус, арккосинус, арктангенс и арккотангенс числа или угла?
Арксинус, арккосинус, арктангенс и арккотангенс на единичной окружности.
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа
Дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа.
Определение.
Арксинус числа a из интервала от −1 до 1 включительно – это такой угол, лежащий в пределах от −π/2 до π/2 (от −90 до 90 градусов) включительно, синус которого равен a.
Определение.
Арккосинусом числа a, −1≤a≤1, называется такой угол из отрезка [0, π] (от нуля до180 градусов включительно), косинус которого равен a.
Определение.
Арктангенсом числа a, a – любое действительное число, называется угол из интервала(−π/2, π/2) (от −90 до 90 градусов не включительно), тангенс которого равен a.
Определение.
Арккотангенс числа a, a – любое действительное число, — это такой угол из интервала(0, π) (от нуля до 90 градусов не включительно), котангенс которого равен a.
Из приведенных определений видно, что арксинус и арккосинус числа определены для чисел, лежащих в интервале [−1, 1], для остальных чисел арксинус и арккосинус не определяются. Например, не определены arcsin 2, арксинус пяти, арксинус минус корня из трех, арккосинус семи целых двух третьих и арккосинус минус пи, так как числа 2, 5, не лежат в интервале от−1 до 1.
В свою очередь определения арктангенса и арккотангенса даются для любых действительных чисел a. То есть, имеют смысл и арктангенс нуля, и арктангенс −500,2, и арккотангенс миллиарда, и арккотангенс −π/3, как и арктангенс, и арккотангенс любого другого действительного числа.
Также стоит отметить, что при условиях, указанных для числа a в определениях, арксинус, арккосинус, арктангенс и арккотангенс существуют, причем они определены однозначно, то есть, для данного числа a имеют единственное значение.
К началу страницы
Обозначения arcsin, arccos, arctg и arcctg
Для записи арксинуса, арккосинуса, арктангенса и арккотангенса приняты следующиеобозначения: arcsin, arccos, arctg и arcctg. То есть, арксинус числа a можно записать какarcsin a, арккосинус, арктангенс и арккотангенс числа a запишутся соответственно как arccos a,arctg a и arcctg a.
Также можно встретить обозначения arctan и arccot, они являются другой формой обозначения арктангенса и арккотангенса, принятой в англоязычной литературе. Мы же арктангенс и арккотангенс будем обозначать как arctg и arcctg.
В свете введенных обозначений, определения арксинуса, арккосинуса, арктангенса и арккотангенса числа запишутся как:
arcsin a, где −1≤a≤1, есть угол α, если sinα=a и −π/2≤α≤π/2;
arccos a, где −1≤a≤1, есть угол α, если cosα=a и 0≤α≤π;
arctg a, где a – любое действительное число, есть угол α, если tgα=a и −π/2≤α≤π/2;
arcctg a, где a – любое действительное число, есть угол α, если ctgα=a и 0≤α≤π.
К началу страницы
Примеры
Самое время привести примеры арксинуса, арккосинуса, арктангенса и арккотангенса числа.
Начнем с примеров арксинуса. Угол π/3 является арксинусом числа , это действительно так, так как числопринадлежит интервалу от−1 до 1, угол π/3 лежит в пределах от −π/2до π/2 и . Приведем еще несколько примеров арксинуса числа:arcsin(−1)=−π/2,arcsin(0,5)=π/6, .
А вот π/10 не является арксинусом 1/2, так как sin(π/10)≠1/2. Еще пример: не смотря на то, что синус 270 градусов равен −1, угол 270 градусов не является арксинусом минус единицы, так как 270 градусов не является углом в пределах от −90 до 90 градусов. Более того, угол 270градусов вообще не может быть арксинусом какого-либо числа, так как арксинус числа должен лежать в пределах от −90 до 90 градусов.
Для полноты картины осталось привести примеры арккосинуса, арктангенса и арккотангенса числа. Например, угол 0 радиан является арккосинусом единицы (так как выполняются все условия из определения арккосинуса: число 1 лежит в отрезке от −1 до 1, угол нуль радиан лежит в пределах от нуля до пи включительно и cos0=1), угол π/2 есть арккосинус нуля. По определению арктангенса числа arctg(−1)=−π/4 и арктангенс корня из трех равен 60 градусам (π/3 рад). А из определения арккотангенса можно заключить, чтоarcctg0=π/2, так как π/2 лежит в открытом интервале от 0 до пи и ctg(π/2)=0.
К началу страницы
Арксинус, арккосинус, арктангенс и арккотангенс числа или угла?
В первом пункте данной статьи мы дали определения арксинуса, арккосинуса, арктангенса и арккотангенса числа. Таким образом, мы говорим именно об арксинусе, арккосинусе, арктангенсе и арккотангенсе числа, а не угла.
Для себя нужно четко разграничить, что существует синус, косинус, тангенс и котангенс УГЛА, их значениями являются числа, и обратно: существует арксинус, арккосинус, арктангенс и арккотангенс ЧИСЛА, их значениями являются углы.
К началу страницы
Арксинус, арккосинус, арктангенс и арккотангенс на единичной окружности
Чтобы получить наглядное представление об арксинусе, арккосинусе, арктангенсе и арккотангенсе числа a, взглянем на них с позиций геометрии. Это несложно сделать, если знать про линии синусов, косинусов, тангенсов и котангенсов.
arcsin a, arccos a, arctg a и arcctg a можно связать с дугами единичной окружности, стягивающими углы, соответствующие значениям арксинуса, арккосинуса, арктангенса и арккотангенса числа a.
Для примера получим дугу, соответствующую арксинусу числа a. Для этого на линии синусов отметим точку, отвечающую числу a, после чего из нее проведем луч, параллельно и в положительном направлении оси абсцисс. Этот луч будет пересекать единичную окружность в некоторой точке. Дуга единичной окружности от этой точки до начальной точки с координатами(1, 0) и будет отвечать арксинусу числа a.
По схожим принципам можно получить дуги, отвечающие арккосинусу, арктангенсу и арккотангенсу числа a. На рисунке ниже синими линиями показаны дуги, отвечающие арккосинусу, арктангенсу и арккотангенсу числа a.
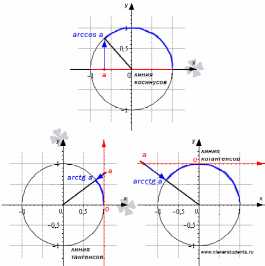
4) Показатели функции, ее свойства и график.
В практике часто используются функции y=2x,y=10x,y=(12)x,y=(0,1)x и т. д., т. е. функция вида y=ax, где a — заданное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Функция, заданная формулой y=ax(где a>0,a≠1), называется показательной функцией с основанием a.
Сформулируем основные свойства показательной функции:
1. Область определения — множество R действительных чисел.
2. Область значений — множество R+ всех положительных действительных чисел.
3. При a>1 функция возрастает на всей числовой прямой; при 0<a<1 функция убывает на множестве R.
ax1<ax2, если x1<x2,(a>1),
ax1>ax2, если x1<x2,(0<a<1)
4. При любых действительных значениях x и y справедливы равенства
axay=ax+yaxay=ax−y(ab)x=axbx(ab)x=axbx(ax)y=axy
Графики показательных функций изображены на рисунках:
1) для случая a>1
2) для случая 0<a<1
Логарифм и его свойства. Примеры
Логарифмом числа по основанию() называется такое число, что, то есть записииравносильны. Логарифм имеет смысл, если.
Если немного перефразировать — Логарифм числа по основаниюопределяется как показатель степени, в которую надо возвести число, чтобы получить число(Логарифм существует только у положительных чисел).
Логарифм в переводе с греческого буквально означает «число, изменяющее отношение».
Специальные обозначения:
Натуральный логарифм — логарифм по основанию, где-число Эйлера.
Десятичный логарифм — логарифм по основанию 10.
Свойства логарифмов:
1° —основное логарифмическое тождество.
2°
3°
Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.
4° —логарифм произведения.
Логарифм произведения равен сумме логарифмов сомножителей.
5° —логарифм частного.
Логарифм частного (дроби) равен разности логарифмов сомножителей.
6° —логарифм степени.
Логарифм степени равен произведению показателя степени на логарифм ее основания.
7°
8°
9° — переход к новому основанию.
Вычислить , если
Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:
Ответ.
studfiles.net
Арксинус и арккосинус числа
Просмотр содержимого документа
«Арксинус и арккосинус числа»

Урок алгебры в 10 классе

Работам устно
- Определите знак произведения
Sin157 °·sin275°·cos157°
Cos73°·cos140°·cos(-384°)
- Существует ли угол, для которого
- Упростите выражение:
Sin² α +cos² α =
1-cos² α =
Sin ² α – 1=
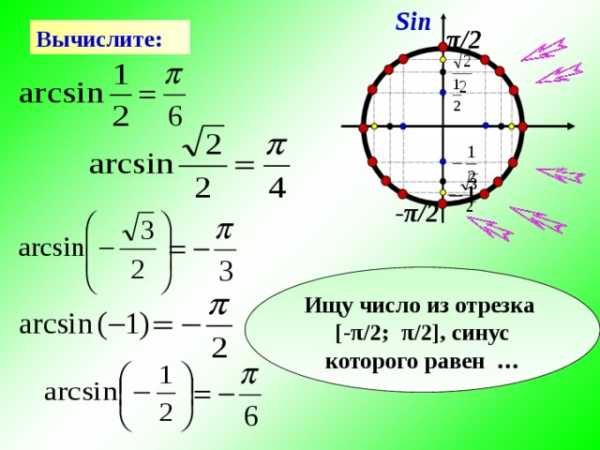
Вычислите

Определение арксинуса, арккосинуса числа а
Цель урока: ввести понятие арксинуса и арккосинуса числа; рассмотреть их свойства и научиться применять при упрощении выражений
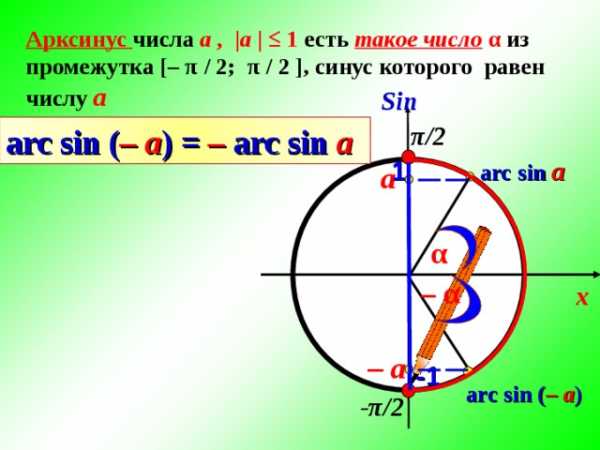
Арксинус числа а , |а | ≤ 1 есть такое число α из промежутка [– π / 2; π / 2 ], синус которого равен числу а
Sin
π /2
arc sin ( – a ) = – arc sin a
1
arc sin a
а
α
– α
x
– a
-1
arc sin ( – a )
— π /2
Sin
π /2
Вычислите :
— π /2
Ищу число из отрезка
[ — π /2; π /2] , синус которого равен …
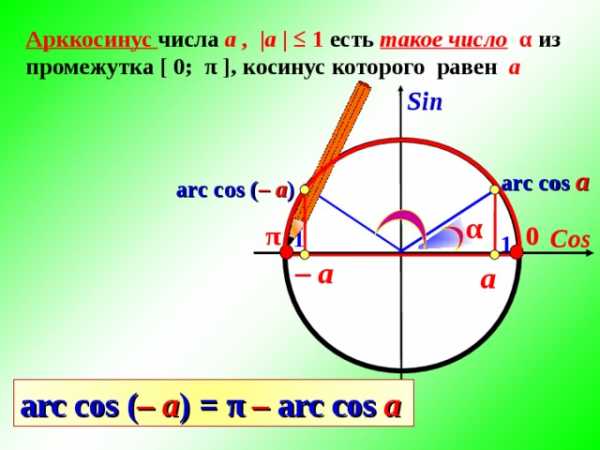
Арккосинус числа а , |а | ≤ 1 есть такое число α из промежутка [ 0; π ], косинус которого равен а
Sin
arc cos a
arc со s ( – a )
α
0
π
Cos
-1
1
– a
а
arc cos ( – a ) = π – arc cos a

Вычислите :
Cos
π
0
Ищу число из отрезка [0; π ] , косинус которого равен…..

Имеет ли смысл выражение?
а rcsin (-1/2) arccos arcsin
да нет нет
а rcsin 1,5 arccos arccos
нет да да

Историческая справка.
- Современные обозначения arcsin и arccos появляются в 1772 в работах великого математика Шерфера и известного французского ученого Ж.Л. Лагранжа, хотя несколько ранее их уже рассматривал Д. Бернули, который употреблял иную символику. Но общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка « arc » происходит от латинского « arcus » (лук, дуга), что вполне согласуется со смыслом понятия: arcsin x , например, — это угол (а можно сказать и дуга), синус которого равен x .

π
1
=
arcsin
6
2
3
π
3
arcsin
=
2
π
1
—
)
(
arcsin
—
6
=
2
π
arcsin
1 =
2
π
2
arcsin
—
=
(
)
4
2
10

π
1
3
arccos
=
2
π
3
arccos
=
2
6
2 π
1
1
arccos
)
arccos
π ̶
=
−
=
(
2
2
3
2
3 π
)
(
arccos
=
2
4
π
0
=
arccos
2

Работаем вместе
- № 7.78
- № 7.86
- № 7.100(а,б,в)
- № 101 ( а,б,в)
- № 102
- № 103

Домашнее задание
№ 7.79
№ 7.87
№ 7.100(г,д,е)
№ 101 ( г,д,е)
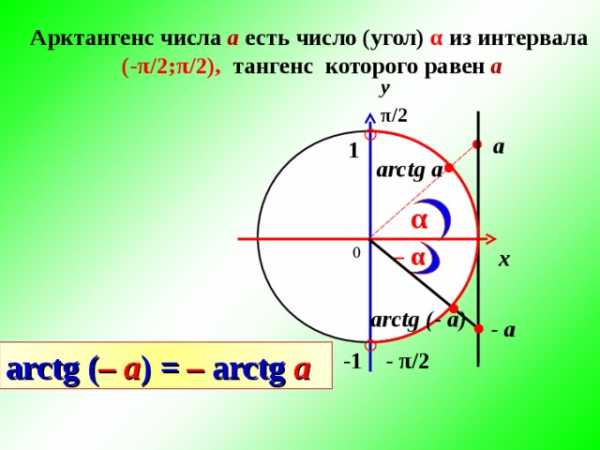
Арктангенс числа а есть число (угол) α из интервала
(- π /2; π /2), тангенс которого равен а
у
π /2
○
а
1
arctg a
α
– α
х
0
arctg (- a )
— а
○
— π /2
arctg ( – a ) = – arctg a
-1
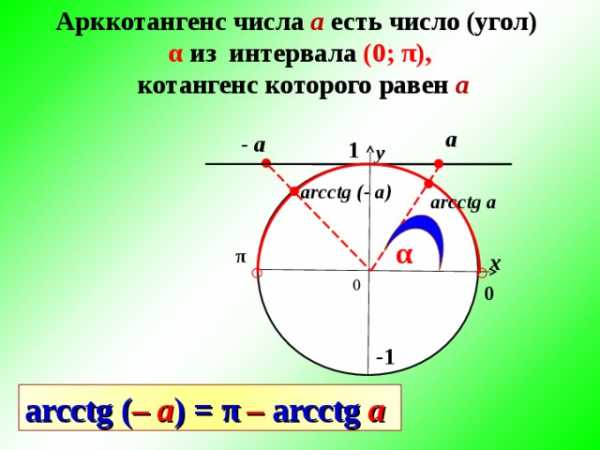
Арккотангенс числа а есть число (угол)
α из интервала (0; π ),
котангенс которого равен а
а
— а
1
у
arcctg (- a)
arcctg a
α
π
х
○
○
0
0
-1
arcctg ( – a ) = π – arcctg a

1
П
ar с tg
=
6
3
П
ar с ctg
1
=
4
П
3
ar с tg
=
3
3
3
П
П
П
+
arccos
arcsin
=
+
=
6
3
2
2
2
1
П
1
П
arccos
П
+
=
+
=
arcsin
2
2
6
2
3
16
multiurok.ru
Обратные тригонометрические комплексного числа
В данном материале мы рассмотрим способы вычисления и рассчитаем значения обратных тригонометрических функций в поле комплексных чисел. Результат выдается как в радианах, так и в градусах.
Арксинус комплексного числа
Если представить
То арксинус числа, выраженный через логарифм
Арккосинус комплексного числа
Если представить
То арккосинус числа, выраженный через логарифм
Введите в поле число, комплексное или вещественное и программа выдаст результат
http://abak.pozitiv-r.ru
http://abak.pozitiv-r.ru
Арктангенс комплексного числа
Если представить
То артангенс числа, выраженный через логарифм
Через арксинус
Через арккосинус
Или вот так
АРКкоТАНГЕНС КОМПЛЕКСНОГО ЧИСЛА
Арккотангенс комплексного числа легко решается через связь с арктангенсом
- Онлайн калькулятор. Расчет произвольных выражений. >>
abakbot.ru
