Геометрия высота треугольника – Высота треугольника | Формулы и расчеты онлайн

Высоты треугольника / Треугольники / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Треугольники
5. Высоты треугольника

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Треугольник

Равенство треугольников

Первый признак равенства треугольников

Перпендикуляр к прямой

Медианы треугольника

Биссектрисы треугольника

Равнобедренный треугольник

Свойства равнобедренного треугольника

Второй признак равенства треугольников

Третий признак равенства треугольников

Окружность

Построения циркулем и линейкой

Треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 154, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 263, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 320*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 348, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 360, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 489, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 543, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 667, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 932, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© 2019 — budu5.com, Буду отличником!

budu5.com

Медианы, биссектрисы и высоты треугольника. Видеоурок. Геометрия 7 Класс

Определение: Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

         

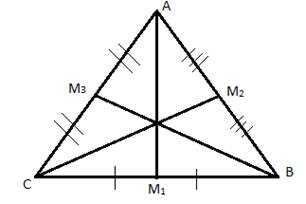
Рис. 1. Медианы треугольника

А, В, С – вершины треугольника.

 – середины сторон треугольника. 

  – медианы треугольника.

У каждого треугольника есть три медианы. В дальнейшем мы докажем, что все медианы треугольника пересекаются в одной точке. И эта точка обладает замечательными свойствами и называется «центром тяжести» треугольника.

Определение: Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. Стоит заметить, что биссектриса угла – это луч, делящий угол на два равных, а биссектриса треугольника – это отрезок, часть луча, ограниченная стороной треугольника.

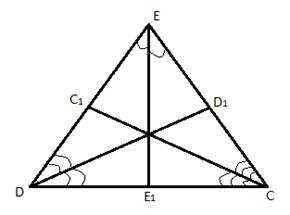
Рис. 2. Биссектрисы треугольника

C, D, E – вершины треугольника.

   – биссектрисы треугольника.

Три биссектрисы любого треугольника пересекаются в одной точке, которая также имеет важное свойство.

Определение: Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется

высотой треугольника.

 

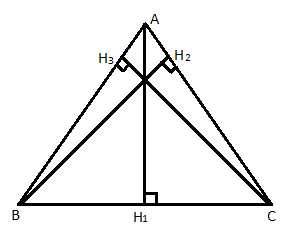
Рис. 3. Высоты остроугольного треугольника

А, В, С – вершины треугольника. 

  – высоты треугольника.

Поскольку у треугольника три вершины, а значит, и три высоты. Далее мы выясним, что все три высоты пересекаются в одной точке. Но в тупоугольном треугольнике высоты расположены следующим образом:

 

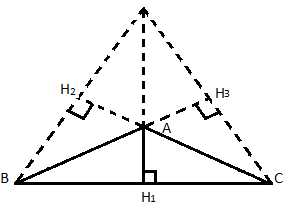
Рис. 4. Высоты тупоугольного треугольника

Перпендикуляр, опущенный с вершины С на прямую ВА, это перпендикуляр , который является высотой треугольника.  – это перпендикуляр, опущенный с вершины В на прямую СА, которая содержит сторону АС.  – это вторая высота треугольника. – третья высота треугольника. Высоты или их продолжения пересекаются в одной точке. Это будет доказано далее.

Пример 1: Медиана AD треугольника АВС продолжена за сторону ВС на отрезок DE, равный AD, и точка Е соединена с точкой С.

1.  Докажите, что ∆АВD = ∆ECD.

2.  Найдите ∠АСЕ, если ∠ACD = , ∠ABD = .

Дано: BD = CD, AD = ED.

Доказать: ∆ABD = ∆ECD.

Доказательство: Выполним пояснительный рисунок:

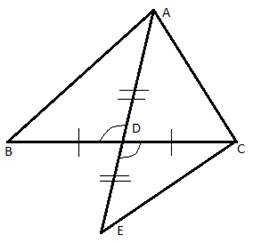
Рис. 5. Чертеж к примеру 1

 

треугольник ABD = треугольнику ECD по первому признаку равенства треугольников, что и требовалось доказать.

Дано: BD = CD, AD = ED, ∠ACD = , ∠ABD = .

Найти: ∠АСЕ.

Решение: Выполним пояснительный рисунок:

Рис. 6. Чертеж к примеру 1

Воспользуемся результатами предыдущей задачи, что треугольник ABD = треугольнику ECD. Треугольники равны, значит, и равны их соответствующие элементы. ∠ECD =∠ABD = .∠ACE = ∠ECD + ∠ACD = +=.

Ответ: ∠ACE = .

Пример 2: треугольник АВС =  треугольнику .

Доказать: медианы ВМ и  равны.

Доказательство: Выполним пояснительный рисунок:

Рис.7. Чертеж к примеру 2

1 способ:

. 

Отсюда следует, что треугольник АВМ = треугольнику . А из равенства треугольников следует, что ВМ = , что и требовалось доказать.

2 способ: совмещение треугольников АВС и . При этом точка В перейдет в точку , а точка М в точку . Значит, отрезки ВМ и  совместятся. ВМ = .

Ответ: Доказано.

На сегодняшнем уроке мы познакомились с медианами, биссектрисами и высотами треугольника. С этими важными элементами мы будем встречаться неоднократно. На следующем уроке мы рассмотрим равнобедренный треугольник и его свойства.

 

Список рекомендованной литературы

1. Александров  А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.

2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.

3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.

 

Рекомендованные ссылки на интернет-ресурсы

1. Обобщающий урок по геометрии в 7-м классе (Источник).

2. Прямая линия, отрезок (Источник).

 

Рекомендованное домашнее задание

1. №28(а). Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А.  – М.: Просвещение, 2010.

2. На стороне АС треугольника АВС отмечена такая точка К, что периметры треугольников АВК и ВСК отличаются на 5 см. Найдите периметр треугольника АВС, если АВ + АК = 30 см.

3. Какие элементы (части) треугольника совпадут при перегибании его по биссектрисе?

4. *Докажите, что если в треугольнике медиана равна половине стороны, к которой она проведена, то угол, из вершины которого проведена медиана, равен сумме двух других углов. 

interneturok.ru

Высота треугольника — Википедия

Материал из Википедии — свободной энциклопедии

Высота в треугольниках различного типа

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.

Свойства точки пересечения трех высот треугольника (ортоцентра)[ | ]

Высоты треугольника

• Все три высоты треугольника пересекаются в одной точке, называемой ортоцентром. Это утверждение легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E{\displaystyle A,\ B,\ C,\ E}, не обязательно даже лежащих в одной плоскости:

EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}

(Для доказательства тождества следует воспользоваться формулами

AB→=EB→−EA→,BC→=EC→−EB→,CA→=EA→−EC→{\displaystyle {\overrightarrow {AB}}={\overrightarrow {EB}}-{\overrightarrow {EA}},\,{\overrightarrow {BC}}={\overrightarrow {EC}}-{\overrightarrow {EB}},\,{\overrightarrow {CA}}={\overrightarrow {EA}}-{\overrightarrow {EC}}}

В качестве точки E следует взять пересечение двух высот треугольника.)

encyclopaedia.bid

Высота треугольника Википедия

Высота в треугольниках различного типа

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.

Свойства точки пересечения трех высот треугольника (ортоцентра)[ | ]

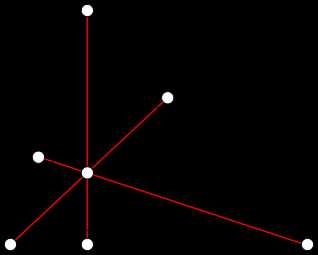Высоты треугольника

• Все три высоты треугольника пересекаются в одной точке, называемой ортоцентром. Это утверждение легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E{\displaystyle A,\ B,\ C,\ E}, не обязательно даже лежащих в одной плоскости:

EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}

(Для доказательства тождества следует воспользоваться формулами

AB→=EB→−EA→,BC→=EC→−EB→,CA→=EA→−EC→{\displaystyle {\overrightarrow {AB}}={

ru-wiki.ru

Высота треугольника — Википедия

Высота в треугольниках различного типа

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или прямую, совпадающую с противоположной стороной. В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника.

Свойства точки пересечения трех высот треугольника (ортоцентра)[править]

Высоты треугольника

• Высоты треугольника пересекаются в одной точке, называемой ортоцентром. Это утверждение легко доказать, используя векторное тождество, справедливое для любых точек , не обязательно даже лежащих в одной плоскости:

(Для доказательства тождества следует воспользоваться формулами

В качестве точки E следует взять пересечение двух высот треугольника.)

• Ортоцентр изогонально сопряжен центру описанной окружности.
• Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
• Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
• Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
• Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
• Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
• Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
• Если О — центр описанной окружности ΔABC, то ,
• Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
• Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
• Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
• Следствия теоремы Гамильтона:
  • Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
  • Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.
• В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.

Свойства высот равнобедренного треугольника[править]

Свойства оснований высот треугольника[править]

• Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.
• Описанная около ортотреугольника окружность — окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
• Другая формулировка последнего свойства:
  • Теорема Эйлера для окружности девяти точек. Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек).
• Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
• Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.

Другие свойства высот треугольника[править]

Свойства минимальной из высот треугольника[править]

Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:

• Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
• Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
• При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
• Минимальная высота в треугольнике всегда проходит внутри этого треугольника.

Основные соотношения[править]

где  — основание.

•  — высота в равностороннем треугольнике.

Теорема о высоте прямоугольного треугольника[править]

Если высота в прямоугольном треугольнике ABC длиной , проведённая из вершины прямого угла, делит гипотенузу длиной на отрезки и , соответствующие катетам и , то верны следующие равенства:

Высота

Похожа на кота,

Она красива и стройна.

Но провести её легко

Ты лишь начертишь эту подругу под прямым углом,

Она тот час же соединит вершину фигуры своим челом,

Дотянется до стороны хвостом.

(Правил К.Волков Дв.Хаб.)

www.wiki-wiki.ru

Высота (геометрия) — Википедия

Высота в элементарной геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.

Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.

Высота треугольника[править]

Высота треугольника — отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.

Все высоты треугольника пересекаются в одной точке, называемой ортоцентром этого треугольника. — Эту теорему легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E, не обязательно даже лежащих в одной плоскости:

(Для доказательства следует взять в качестве точки E пересечение двух высот треугольника.)

Площадь треугольника равна половине произведения высоты треугольника на соответствующее основание. Кроме формулы, удобной для расчёта площади, из этого также следует, что длины высот треугольника обратно пропорциональны длинам соответствующих сторон.

Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:

1. Минимальная [ортогональность|ортогональная]] проекция треугольника на прямую, лежащую в плоскости треугольника, имеет длину, равную наименьшей из его высот.

2. Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.

3. При непрерывном движении двух точек по периметру треугольника друг навстречу другу, если они встречаются хотя бы дважды, тогда максимальное расстояние между точками во время их движения не может быть меньше длины наименьшей из высот треугольника.

К:ВП: Статьи без изображений (тип: )К:ВП: Статьи без изображений (указано в Викиданных)

www.wikiznanie.ru

Высота (геометрия) — Википедия

Высота в элементарной геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.

Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.

Высота треугольника[править]

Высота треугольника — отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.

Все высоты треугольника пересекаются в одной точке, называемой ортоцентром этого треугольника. — Эту теорему легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E, не обязательно даже лежащих в одной плоскости:

(Для доказательства следует взять в качестве точки E пересечение двух высот треугольника.)

Площадь треугольника равна половине произведения высоты треугольника на соответствующее основание. Кроме формулы, удобной для расчёта площади, из этого также следует, что длины высот треугольника обратно пропорциональны длинам соответствующих сторон.

Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:

1. Минимальная [ортогональность|ортогональная]] проекция треугольника на прямую, лежащую в плоскости треугольника, имеет длину, равную наименьшей из его высот.

2. Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.

3. При непрерывном движении двух точек по периметру треугольника друг навстречу другу, если они встречаются хотя бы дважды, тогда максимальное расстояние между точками во время их движения не может быть меньше длины наименьшей из высот треугольника.

К:ВП: Статьи без изображений (тип: )К:ВП: Статьи без изображений (указано в Викиданных)

www.wiki-wiki.ru