Логарифмирование и потенцирование выражений | План-конспект занятия по алгебре (10, 11 класс):
Практическая работа № 9 на тему «Логарифмирование и потенцирование выражений»
Порядок выполнения работы
1. Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
2. Решите самостоятельную работу. Оформите решение письменно в тетради.
Теоретический материал
Определение. Логарифмом числа b по основанию a называется показатель степени, в которую нужно взвести основание a, чтобы получить число b.
Логарифм определен только при b>0, a>0 и a1.
Обозначается logab
Пример: log28 = 3, так как 23 = 8
log525 = 2, так как 52 = 25
Свойства логарифмов:
1. alogab = b — основное свойство
2. loga(xy) = logax + logay
3. loga() = logax — logay
4. logaxn = nlogax
5. loga1 = 0
6.
logaa = 1
7. logab = — формула перехода
8. logab =
9. logab = log an bn = nlog an b
Определение. Логарифм по основанию 10 называется десятичным и обозначается символом lg.
lg x = log10 x
Определение. Логарифм по основанию e называется натуральным и обозначается символом ln.
ln x = log e x, где e = 2,7
Примеры применения свойств логарифмов
а) Основное свойство логарифмов:
Вычислить:
1) log644 = =
2) = log416 = 2 (свойство №7)
3) = log5125 = 3 (свойство №9)
Определение: Операция нахождения логарифма выражения называется логарифмированием.
Пример: Прологарифмировать выражение по основанию 3.
Решение:
= =
= log35 + log3a3 + log3b4 + log3c — log33 — log3x3 — log3y =
= log35 + 3log3a + 4log3b + log3c — 1 — 3log3x — log3y
Определение: Операция нахождения выражения по его логарифму называется потенцированием.
Пример: Выполнить потенцирование выражения
Решение:
=
Вариант 1
№ 1. Вычислите значение x:
1) ; 2) ; 3) ;
4) ; 5)
№ 2. Найдите значение выражения:
а)
б)
в)
№ 3. Сравните числа:
а) и ;
б) и ;
в) и ;
г) и ;
д) и 1
№ 4. Выполните потенцирование (a>0, b>0, a>b):
1)
2)
3)
№ 5. Прологарифмируйте выражение:
1) ; 2) ; 3)
№6. Упростите выражение:
1) ; 2) ; 3) ; 4)
Вариант 2
№ 1. Вычислите значение x:
1) ; 2) ; 3) ;
4) ; 5)
№ 2. Найдите значение выражения:
а)
б)
в)
№ 3. Сравните числа:
а) и ;
б) и ;
в) и ;
г) и ;
д) и 1
№ 4.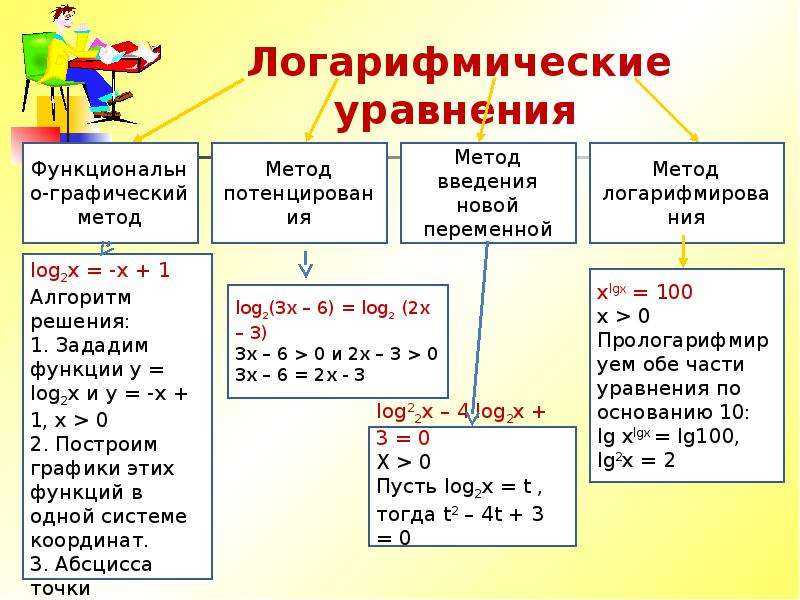
Выполните потенцирование (a>0, b>0, a>b):
1)
2)
3)
№ 5. Прологарифмируйте выражение:
1) ; 2) ; 3)
№6. Дано число а. Выразите через а значение выражения А.
1) ,
2) ,
3) ,
Некоторые методы решения логарифмических уравнений
Рассмотрим некоторые типы логарифмических уравнений, которые не так часто рассматриваются на уроках математики в школе, но широко используются при составлении конкурсных заданий, в том числе и для ЕГЭ.
1. Уравнения, решаемые методом логарифмирования
При решении уравнений, содержащих переменную и в основании и в показателе степени, используют метод логарифмирования. Если, при этом, в показателе степени содержится логарифм, то обе части уравнения надо логарифмировать по основанию этого логарифма.
Пример 1.
Решить уравнение: хlog2х+2 = 8.
Решение.
Прологарифмируем левую и правую части уравнения по основанию 2. Получим
log2 (хlog2х+2) = log2 8,
(log2
Пусть log2 х = t.
Тогда (t + 2)t = 3.
t2 + 2t – 3 = 0.
D = 16. t1 = 1; t2 = -3.
Значит log2 х = 1 и х1 = 2 или log2 х = -3 и х2 =1/8
Ответ: 1/8; 2.
2. Однородные логарифмические уравнения.
Пример 2.
Решить уравнение log23 (х2 – 3х + 4) – 3log3 (х + 5) log3 (х2 – 3х + 4) – 2log23 (х + 5) = 0
Решение.
Область определения уравнения
{х2 – 3х + 4 > 0,
{х + 5 > 0. → х > -5.
log3 (х + 5) = 0 при х = -4. Проверкой определяем, что данное значение х не является корнем первоначального уравнения. Следовательно можно разделить обе части уравнения на log 2 3 (х + 5).
Получим log23 (х2 – 3х + 4) / log23 (х + 5) – 3 log3 (х2 – 3х + 4) / log3 (х + 5) + 2 = 0.
Пусть log3 (х2 – 3х + 4) / log3 (х + 5) = t. Тогда t 2– 3 t + 2 = 0. Корни данного уравнения 1; 2. Возвратившись к первоначальной переменной , получим совокупность двух уравнений
[log3 (х2 – 3х + 4) / log3 (х + 5) = 1
[log3 (х2 – 3х + 4) / log3 (х + 5) = 2. Отсюда
[log3 (х2 – 3х + 4) = log3 (х + 5),
[log3 (х2 – 3х + 4) = 2log3 (х + 5).
Выполнив потенцирование, получим
[х2 – 3х + 4 = х + 5,
[х2 – 3х + 4 = (х + 5)2 ;
[х
[-13х = 21.
[х = 2 – √5,
[х = 2 + √5, [х = -21/13. Все корни входят в область определения.
Ответ: ,-21/13; 2 – √5; 2 + √5.
3. Уравнения, содержащие переменную и в основании логарифма и в выражении, стоящем под знаком логарифма
Пример 3.
Найдите среднее арифметическое корней уравнения log3х+7 (9 + 12х + 4х2) + log2х+3 (6х2 + 23х + 21) = 4.
Решение.
9 + 12х + 4х2 = (2х + 3)2; 6х2 + 23х + 21 = (2х + 3)(3х + 7).
Область определения уравнения
{2х + 3 > 0,
{2х + 3 ≠ 1,
{3х + 7 > 0,
{3х + 7 ≠ 1.
Следовательно х > -1,5 и х ≠ -1
Тогда log3х+7 (2х + 3)2
+ log2х+3 (2х + 3)(3х + 7) = 4;2log3х+7 (2х + 3) + log2х+3 (2х + 3)+ log2х+3 (3х + 7) = 4;
2log3х+7 (2х + 3) + 1 + log2х+3 (3х + 7) = 4;
2log3х+7 (2х + 3) + 1/log3х+7 (2х + 3) = 3;
Введём новую переменную log3х+7 (2х + 3) = t.
Получим 2t + 1/t = 3. 2t2 – 3t + 1 = 0. Корни уравнения 1/2; 1.
Возвращаемся к исходной переменной.
Получаем log3х+7 (2х + 3) = 1/2 или log 3х+7 (2х + 3) = 1
2х + 3 = (3х + 7)1/2;
(2х + 3)2 = 3х + 7;
4х2 + 9х + 2 = 0.
Корни уравнения -2; -0,25.
log3х+7 (2х+3) = 1.
2х + 3 = 3х + 7.
Х = -4.
В область определения уравнения входит только число -0,25.
Среднее арифметическое -0,25,
Ответ: -0,25.
4. Уравнения, требующие использования свойств логарифмических функций (т.е. решаемые функциональным методом).
Пример 4. Какой наибольший корень в уравнении log3 (8 + 2х – х2) = 2х-1 + 21-х
Решение.
Рассмотрим функцию у = 8 + 2х – х2. Её график – парабола, ветви которой направлены вниз.
Координаты вершины (1; 9). Область значений функции (-∞; 9]. Но с учётом существования логарифма нужно рассматривать лишь значения (0; 9]. Значит выражение в левой части принимает наибольшее значение 2 при х = 1. Рассмотрим теперь функцию у = 2х-1 + 21-х . Если принять t = 2x-1,, то она примет вид у = t + 1/t, где t > 0. При таких условиях она имеет единственную критическую точку t = 1. Это точка минимума. У vin = 2. И достигается он при х = 1.
Теперь очевидно, что графики рассматриваемых функций могут пересекаться лишь один раз в точке (1; 2). Получается, что х = 1 единственный корень решаемого уравнения.
Ответ: х = 1.
Пример 5. Решить уравнение log22 х + (х – 1) log2 х = 6 – 2х
Решение.
Решим данное уравнение относительно log2 х. Пусть log2 х = t. Тогда t2 + (х – 1) t – 6 + 2х = 0.
D = (х – 1)2 – 4(2х – 6) = (х – 5)2. t1 = -2; t2 = 3 – х.
Получим уравнение log2 х = -2 или log2 х = 3 – х.
Корень первого уравнения х
Корень уравнения log2 х = 3 – х найдём подбором. Это число 2. Этот корень единственный, так как функция у = log2 х возрастающая на всей области определения, а функция у = 3 – х – убывающая.
Проверкой легко убедится в том, что оба числа являются корнями уравнения
Ответ:1/4; 2.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Как писать в логарифмической форме — mathsathome.com
Как писать в логарифмической форме: видеоурок
youtube.com/embed/Ua_LDHzX5NM?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Что такое логарифмическая форма?
Логарифмическая форма записывается как log a (c)=b. Это перестановка экспоненциальной формы, a b =c. Любое показательное уравнение можно записать в виде логарифма. Логарифмическая форма используется для вычисления показателя степени уравнения.
читается как «логарифмическая база a из c равно b ».
Логарифмическая форма — это просто преобразование уравнения, записанного в экспоненциальной форме. Используются одни и те же числа, но они записываются в другом порядке. Слово log написано, чтобы показать, что используется функция логарифмирования.
Экспоненциальное уравнение содержит показатель степени (небольшое число, записанное сверху справа от другого числа).
Уравнения, записанные в логарифмической форме, содержат три числа:
- Основанием журнала является число, записанное в нижнем индексе рядом со словом «журнал».
- Число после знака равенства является показателем степени.
- Число в журнале перед знаком равенства — это значение основания, возведенное в степень степени.
Например, в экспоненциальном уравнении 3 2 = 9 2 является показателем степени.
Это можно записать в логарифмической форме как .
Ответом на уравнение, записанное в логарифмической форме, является показатель степени.
2 — это показатель степени в экспоненциальной форме, но это ответ, записанный в логарифмической форме.
Почему мы используем логарифмическую форму?
Логарифмическая форма предназначена для вычисления показателей степени и решения экспоненциальных уравнений. Логарифмы можно использовать для понимания размера больших чисел, перестановки уравнений и решения задач роста и распада.
Как логарифмы используются в реальной жизни?
Вот несколько примеров использования логарифмов в реальной жизни:
- Громкость звука. Децибелы измеряются в логарифмической шкале.
- Кислотность измеряется pH в логарифмической шкале.
- Шкала Рихтера, используемая для измерения землетрясений, имеет логарифмическую шкалу.
- Интенсивность света. Яркость звезд измеряется в логарифмической шкале.
- Фокусное отношение в фотографии имеет логарифмическую шкалу
- Сила сигнала Wi-Fi измеряется в логарифмической шкале
- Эффективность компьютерного алгоритма измеряется в логарифмической шкале
- Радиоактивный распад и период полураспада рассчитываются с помощью логарифмов
- Расчет процентных ставок
- Расчет роста населения
Как преобразовать в логарифмическую форму
Можно записать любое экспоненциальное уравнение вида a b 9001 в логарифмической форме, используя log a (c)=b.
Например, экспоненциальное уравнение 2 3 =8 записывается как log 2 (8)=3 в логарифмической форме.
В примере , , и . Поэтому, используя формулу log a (c)=b, это можно записать в экспоненциальной форме как .
Вот экспоненциальное уравнение 3 4 =81. Его можно записать в логарифмической форме как .
Число после знака равенства в логарифмической форме — это степень, в которую возводится основание бревна, чтобы получить число внутри бревна. Здесь 3 возводят в степень 4, чтобы получить 81.
Если основание логарифма равно 10, нет необходимости записывать число 10. Всякий раз, когда в логарифме не записано основание, считается, что оно имеет основание 10.
Например, можно записать в логарифмической форме как .
Вместо записи основания 10 можно удалить и записать как
Как преобразовать логарифмическую форму в экспоненциальную форму
Любое уравнение, записанное в логарифмической форме, можно записать в экспоненциальной форме путем преобразования log в (c )=b в a b =c.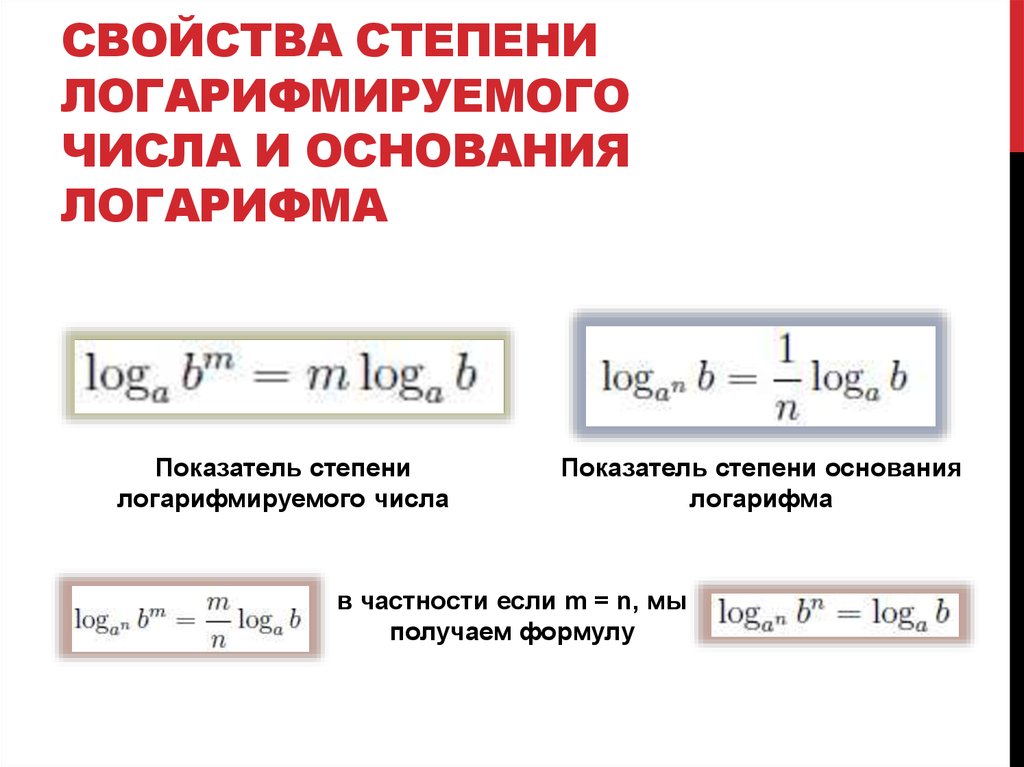
Например, log 5 (25)=2 можно записать как 5 2 =25.
Если уравнение, записанное в логарифмической форме, не имеет записанного основания, то основание принимается равным 10.
Обычно мы не пишем основание числа 10.
Например, означает .
Начиная с 10 2 =100, .
Полученный ответ на логарифм — это степень, в которую возводят 10, чтобы получить 100.
Преобразование натуральных логарифмов в экспоненциальную форму
Число Эйлера, e≈ 2,718 . Натуральный логарифм представляет собой логарифм по основанию e и записывается как ln, а не как log. Например, ln(x) означает log e (x).
Вот несколько примеров работы с натуральным логарифмом.
Если , то .
Поскольку e 1 =e, то .
Если , то .
Правила использования логарифмической формы
Следующие правила применяются при записи чисел в логарифмической форме:
- Если основание логарифма не записано, оно равно 10.
- Натуральный логарифм ln является основанием логарифма e .
- Независимо от основания, логарифм 1 равен 0. Правило log и (1)=0.
- Логарифм основания числа равен 1. Правило log a (a)=1.
- журнал a (0) не определен.
- Логарифмы отрицательных чисел не определены.
- Основание логарифма никогда не бывает отрицательным, ни нулем, ни единицей.
Примеры записи уравнений в логарифмической форме
Вот несколько примеров преобразования показательных уравнений в логарифмическую форму.
| Экспоненциальная форма | Логарифмическая форма | |
| A B = C | Log A (C) = B | |
| 2 5 = 32 | Log 2 (32) = 5 | |
| 10 3 = 1000 | log 1111 3 = 1000 | 11111111 (1000) = 1000). |
| 5 1 =5 | логарифм 5 (5)=1 | |
| 3 0 =1 | log 3 (1)=0 | |
| 9 1 / 2 =3 | log 9 (3)= 1 / 2 | |
| 5 -2 = 1 / 25 | log 5 ( 1 / 25 )=-2 |
2Logarithmic Form with Square Roots
Извлечение квадратного корня из числа равносильно возведению его в половинную степень. Поэтому √9=3 можно записать как 9 1 / 2 =3. Записав это в логарифмической форме, log 9 (3) = 1 / 2 .
Логарифмическая форма с дробями
Правило преобразования экспоненциальных уравнений, a b =c, в логарифмические уравнения, log a (c)=b, также работает для дробей. Например ( 1 / 2 ) 3 = 1 / 8 можно записать как журнал ( 1 / 2 ) ( 1 / 8 )=3.
Логарифмическая форма комплексных чисел
Любое комплексное число z=a+bi может быть записано в виде z=re i θ , где r = √5 5
3b 2901 2 ) и θ =tan -1 (b/a)+2πk. Экспоненциальная форма комплексного числа, z=re i θ можно записать в логарифмической форме как ln(z)=ln(r e i θ ). Это можно записать как ln(z)=ln(r)+ln(e i θ ), что можно упростить до ln(z)=ln(r)+i θ .
Логарифмические функции
Логарифмические функции обратны экспоненциальным функциям, и любая экспоненциальная функция может быть выражена в логарифмической форме. Точно так же все логарифмические функции можно переписать в экспоненциальной форме. Логарифмы действительно полезны, поскольку позволяют нам работать с очень большими числами, манипулируя числами гораздо более удобного размера.
Если бы x = 2 y нужно было решить для y , чтобы его можно было записать в функциональной форме, необходимо было бы ввести новое слово или символ. Если x = 2
y = (степень по основанию 2) равняется x
Это уравнение переписывается как y = log 2 x .
Это читается как « y равно логарифму x по основанию 2» или « y равно логарифму x по основанию 2».
Логарифмическая функция представляет собой функцию вида
, которая читается как « y равно логарифму x , основание b » или « y равно логарифму 0, основание 90 х ».
В обеих формах x > 0 и b > 0, b ≠ 1. На y ограничений нет.
Пример 1
Перепишите каждое показательное уравнение в его эквивалентной логарифмической форме. Решения следуют.
- 5 2 = 25
Пример 2
Перепишите каждое логарифмическое уравнение в эквивалентной ему экспоненциальной форме. Решения следуют.
- журнал 6 36 = 2
- бревно а м = р
Пример 3
Если возможно, решите следующие уравнения.
- журнал 7 49 = у
- логарифм у 8 = 3
- log 4 г = –2
- log 3 (–9) = у
- Это невозможно, так как 3 y всегда будет положительным результатом. Напомним, что логарифмы имеют только положительный домен; следовательно, -9 не находится в области логарифма.
Наиболее часто при работе с логарифмами используются основания 10 и основания e . (Буква e представляет собой иррациональное число, которое имеет множество применений в математике и естественных науках. Значение e примерно равно 2,718281828 …) Логарифмическая база 10, log 10 , известна как десятичный логарифм и записывается как log, при этом основание не записывается, но понимается как 10. Логарифмическая база e , log e , известен как натуральный логарифм и записывается как пер.